Introduction

Landslides are slope failures caused by various external triggers, such as heavy rainfall (Iverson 2000), earthquakes (Malamud et al. 2004), and anthropogenic activities (Lacroix et al. 2019), resulting in fatalities and monetary losses across numerous mountainous regions worldwide (Strozzi et al. 2018). Therefore, long-term landslide monitoring is necessary to track the development of mass activities and potentially predict when the landslide occurs (Utili et al. 2015; Del Soldato et al. 2018b; Strozzi et al. 2018; Lacroix et al. 2019). The movement of landslides generally behaves in a small spatial scale but may follow fractured surfaces due to the internal subdivision of landslide mass (Frattini et al. 2018), leading to multiple sliding directions on a single landslide body. Such spatiotemporal features make it difficult for conventional pointwise landslide monitoring sensors to provide continuous measurements with a sufficient spatial coverage and resolution. Furthermore, the proper location of such sensors is difficult to choose for newly detected landslides when considering multiple failure surfaces (Barla and Antolini 2016), and the installation and maintenance of the sensors are labour-intensive and expensive.

To overcome this, numerous researchers have sought to utilise the spaceborne Interferometric Synthetic Aperture Radar (InSAR) measurement which can map an entire landslide body continuously at a high spatial resolution (Hilley et al. 2004; Calabro et al. 2010; Tomás et al. 2014; Raspini et al. 2019; Dai et al. 2020; Solari et al. 2020) and enables the investigation of the spatiotemporal features of multi-surface failures (Dai et al. 2016; Hu et al. 2018; Intrieri et al. 2020). Since the InSAR can only measure surface landslide movements without the subsurface information (e.g. landslide depth), researchers have proposed strong assumptions such as a spatially uniform landslide rheology and a priori vertical variation of velocity to retrieve the depth of landslides (Booth et al. 2013; Delbridge et al. 2016). However, these assumptions likely do not apply to compound landslides with spatially variable or unknown rheology (Booth et al. 2013). Another strategy to unravel the subsurface structure of landslides is to combine surface deformation with various ground sensors or field surveys, where available. For example, Crosta et al. (2014a) jointly used borehole, Global Positioning System (GPS), optical targets, and InSAR data to comprehensively analyse the movements, depth, and volume of the La Saxe rockslide (Courmayeur, Italy). Carlà et al. (2019) combined InSAR and GPS displacements with a borehole survey to retrieve both deformation fields and stratigraphic information of the Bosmatto landslide (Gressoney St. Jean, Italy). Crippa et al. (2020) reconstructed the morphostructures and basal shear zones of the Mt. Mater landslide (Valle Spluga, Italy) by integrating InSAR measurements with field evidence (e.g. persistent scarps).

Knowledge on the depth of landslides may also be retrieved from geophysical techniques (Pazzi et al. 2019), and among these, seismic noise measurements can be implemented with a high spatial density. For example, Pazzi et al. (2017) used horizontal to vertical spectral ratio (H/V) technique (Nakamura 1989) to identify the depths of slip surfaces on the basis of substantial changes in the seismic impedance between landslide mass and unweather material. Therefore, combining InSAR and a dense network of seismic stations can effectively reveal detailed landslide sliding geometry and in principle can enable an accurate estimation of the landslide volume.

In this study, in order to characterise the landslide motion on a small spatial extent (2 km by 2 km) with high-resolution and long-term observations, we used a combination of 5-year Sentinel-1 images, with a temporal baseline of 6 to 24 days from 2014 to 2019, and a dense seismic noise network, with 120 observation stations carried out between August and September 2017 (dry season). A geometric inversion method combining InSAR descending and ascending measurements to determine the best-fit sliding geometry of the landslide body was proposed. The landslide geometry was further investigated by 120 seismic noise measurements in terms of slip interface depth, and, to the best of our knowledge, such dense seismic noise measurements were employed for the first time together with InSAR to investigate a landslide. The temporal evolution of the landslide has also been traced, and a comparative analysis of InSAR deformation and accumulated precipitation time series has been performed to reveal the impact of rainfall on the landslide.

Study area

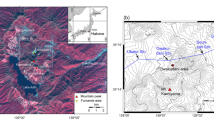
Bolivia is a country highly vulnerable to landslides with roughly one third of its territory located in the Andes and subjected to complex hydrogeological conditions. With the rapid growing population and the expanding settlement areas on unstable slopes since the early twentieth century, Bolivia now suffers from destructive landslides almost every year (Roberts et al. 2014), leading to severe human and economic losses. In Bolivia, landslides are most frequent in the late rainy season (January to March) and usually occur after several weeks of continuous wet periods, indicating a clear hydrometeorological controlling mechanism (Roberts 2016). This mechanism mainly originates from orographically enhanced precipitation which drives the increase of hillslope erosion in steep terrain consisting of high-relief V-shaped valleys. One of such examples is Villa de la Independencia (Fig. 1), the capital of Ayopaya Province, in the Cochabamba Department. Although there has been no written record of landslide occurrences in the town, inhabitants report that the first movement dates back 30 years. In addition, the observed cracks and damage on edifices and structures (Figs. 1d to j) indicate that the landslide motion in the town deserves attention. Moreover, the town lacks an up-to-date systematic monitoring of the slope stability, resulting in a lack of understanding of the landslide dynamic and the safety condition of the population.

Fig. 1
figure 1

a The location of the study area and the coverage of satellite radar imagery. The red star denotes the location of Villa de la Independencia, Bolivia. The purple rectangles outline the spatial coverage of Sentinel-1 frames of paths 156 (descending track) and 76 (ascending track). The solid blue line represents the River Palca close to the town. The solid grey lines indicate the silhouette of Cordillera Oriental Mountains. b Geological map of the study area (by Julio Torres Navarro, August 2017, as internal and unpublished output of the project “Proyecto Integral de Estudios de Movimientos en Masa PIEMM”) with 100-m contour lines (in grey). The landslide boundaries are in red, the H/V measurements are black dots, the soil samples are yellow dots, the rock samples are blue dots, and the boreholes are purple triangles. c The stratigraphy of the three boreholes shown from North to South. d to j Seven photos we took at the locations indicated by yellow rounded rectangles in b, showing the damage on edifices and structures. All the photos were taken during the 2017 field survey (between the last days of August and the first days of September)

Full size image

From a geological point of view, the town is settled on an ancient alluvial terrace formed by the dissection of the River Palca and surrounded by large river deposits, where the presence of erosion landforms in furrows and gullies reflects strong erosive activity (Fig. 1). The deposits of terraces (Qd, as pebbles, gravel, sand, silt, and clay) and colluvial-fluvial sediments (Qcf, mainly gravel, sand, silt, and clay) rest on the Anzaldo Formation (Oan, as siltstones, shales, and greenish-grey-to-light brown sandstones). In the east side of the landslide area outcrops are the Capinota formation (Ocp, dark grey shales with horizons of light brown sandstones at the top), while in the west side outcrops are the Amutara formation (Oam, as quartzitic sandstones and grey sandstones and grey sandstones with shales and siltstones) (Raventós et al. 2017). The rock and soil properties are summarised in Table 1, while the location of the samples is shown in Fig. 1b. The soil exhibits a texture that varies from “fine grain” to “very fine grain”. Figure 1 c shows the stratigraphy as inferred from three boreholes performed in the landslide body whose locations are indicated in Fig. 1b. The average annual rainfall in the municipality recorded by Servicio Nacional de Meteorología e Hidrología (SENAMHI) of Bolivia is 789.3 mm, where the precipitation reaches an average of 189.4 mm in the dry season (April to October) and of 599.9 mm in the wet season (November to March).

Table 1 Rock and soil sample properties. The location of the samples is shown in Fig. 1b. Note that missing values imply measurements were impossible to read at the time of observation
Full size table

On a broad scale, the landslide mass includes three sectors (Fig. 1b): (i) mass I: the main one affecting the town centre and the upper portion with a length of about 2700 m and an average width of about 950 m; (ii) mass II: a second one affecting the eastern portion of the municipality with a length of approximately 1700 m and a width, in the lower portion, of approximately 1100 m (such as the eastern bus station and the cemetery shown in Figs. 1h and i); (iii) mass III: the smallest one affecting the western basin close to the main landslide with a length of approximately 2000 m and a width, in the lower portion, of approximately 250 m. This work focuses on the investigation of the surface deformations in the town centre and its closest surroundings (i.e. town centre, upper block, and east block as shown in Fig. 1b) where the InSAR can maintain sufficient coherent pixels and the risk for the population is the highest. In addition, since the seismic noise measurement has a larger coverage than the InSAR measurement, the volume of the entire landslide body can also be estimated.

Data and methodology

InSAR

The SAR images processed are Sentinel-1 Terrain Observation by Progressive Scans (TOPS) (Torres et al. 2012) data in Interferometric Wide (IW) swath mode with a spatial resolution of about 5 m in range and 20 m in azimuth. One hundred sixty-two Sentinel-1 images in the descending track from 16 October 2014 to 31 December 2019 and 135 images in the ascending track from 3 November 2014 to 25 December 2019 with a minimum temporal baseline of 6 days were collected. In the process of grouping interferogram pairs, each image was connected with at least three acquisitions. After excluding image pairs with a long temporal baseline (beyond 3 months), 510 and 503 interferograms respectively for the descending and ascending datasets were obtained (Fig. 2).

Fig. 2
figure 2

Acquisition dates and interferometric pairs of satellite radar imagery in the descending (a) and ascending (b) tracks. Sentinel-1 acquisitions are denoted by blue stars. Y-axis shows the length of perpendicular baselines

Full size image

To keep the original spatial resolution of Sentinel-1 and reduce atmospheric disturbance, a single-look Small BAsline Subset (SBAS) InSAR method integrated with tropospheric delay correction to Sentinel-1 images was applied. As shown in the workflow (Fig. 3), the GAMMA software (Wegmüller et al. 2016) was used to generate interferograms which started with the co-registration of Single Look Complex (SLC) images to a common primary image (2 June 2017 for ascending and 9 April 2017 for descending, chosen as they are in the middle of the time series). After the co-registration, a network of interferograms in single look can be generated and geocoded based on the resampled SLC images and a 30-m Digital Elevation Model (DEM) from the Shuttle Radar Topography Mission (SRTM) (Farr et al. 2007). The tropospheric delay correction from Generic Atmospheric Correction Online Service (GACOS) for InSAR was then applied to these interferograms (Yu et al. 2017; Yu et al. 2018a; Yu et al. 2018b). It should be noted that the tropospheric effect was generally ignored by previous researchers in the study of local-scale landslides (e.g., Lin et al. 2019; Zhang et al. 2020). However, in steep terrains, the stratified tropospheric delay usually presents seasonal oscillations (Samsonov et al. 2014) which may be misinterpreted as rainfall-induced periodic movements (Dong et al. 2019). After manual inspection of the interferograms corrected by GACOS, it emerged that long-wave and terrain-related tropospheric delays were reduced after the tropospheric correction, so these corrected interferograms were used for time series analysis.

Fig. 3
figure 3

Workflow of time series InSAR processing with tropospheric delay correction

Full size image

The interferograms with tropospheric correction were imported into the StaMPS software (Hooper et al. 2012) to perform the single-look SBAS analysis. Pixels with an amplitude dispersion index (Ferretti et al. 2001) lower than 0.6 were selected as the “first-round” coherent pixels. The “second-round” coherent pixels were identified based on the characteristics of their phase noise. After correction of spatially uncorrelated noise (mainly DEM error), the wrapped phase was unwrapped with a 3D unwrapping method (Hooper and Zebker 2007) and the spatially correlated noise, including the residual tropospheric delay, DEM error, and orbital error were removed from the unwrapped phase. The velocity and displacement time series in the line of sight (LOS) were then estimated from the filtered unwrapped phase using singular value decomposition (SVD) (Berardino et al. 2002). The spatial reference value in time series InSAR processing was initially set as the mean phase value in the study area. Then, a stable reference area R1 (marked by a black triangle in Fig. 4) close to the town was selected with which the final displacement time series were re-generated.

Fig. 4
figure 4

Sentinel-1 LOS deformation velocity maps from the descending (a) and ascending (b) tracks, with positive values indicating the surface is moving toward the satellite. The black rectangle covers the location of Independencia (including the town centre, upper block, and east block as shown in Fig. 1b) and the purple line represents the Highway 25 that crosses the town. The red oval delimits the approximate extent of a priori unknown deforming area. The black triangle (R1) denotes the location of the reference area. The standard deviation maps of descending and ascending LOS velocity, respectively (c) and (d)

Full size image

To discuss the relationship between InSAR time series and other external factors (e.g. precipitation and residual atmospheric delays), the wavelet tools including continuous wavelet transform (CWT), cross-wavelet transform (XWT), and wavelet coherence (WTC) (Grinsted et al. 2004) were used. CWT can identify localised intermittent periodicities of a single time series, while XWT and WTC help identify the common power and relative phase between two time series in time-frequency space (Tomás et al. 2016).

Determination of the sliding geometry

A geometric inversion method was designed to determine the best-fit sliding direction (clockwise from the North) and inclination (from horizontal to vertical) of the landslide motion according to the combination of descending- and ascending-track InSAR observations. The method is based on the assumption that the basal failure plane moves approximately but not strictly along the slope surface (Hu et al. 2016) and may have slight deviations from the existing slope geometry.

For a given single landslide sub-block, we assume that it is driven by only one sliding plane with an inclination of β1 and a sliding direction of β2. For each pixel inside this landslide sub-block, a displacement (Dsliding) along the sliding direction and inclination can be projected to the descending (Ddes) and ascending (Dasc) LOS directions following Eqs. (1) and (2).

$$ {D}_{\mathrm{des}}={\left[\begin{array}{c}-\sin {\theta}_{\mathrm{des}\_\mathrm{inc}}\cos {\alpha}_{\mathrm{des}\_\mathrm{head}}\kern0.75em \\ {}\sin {\theta}_{\mathrm{des}\_\mathrm{inc}}\sin {\alpha}_{\mathrm{des}\_\mathrm{head}}\kern0.5em \\ {}\cos {\theta}_{\mathrm{des}\_\mathrm{inc}}\end{array}\ \right]}^T\cdotp \kern0.5em \left[\begin{array}{c}\cos {\beta}_1\sin {\beta}_2\\ {}\cos {\beta}_1\cos {\beta}_2\\ {}-\sin {\beta}_1\end{array}\right]\cdotp {D}_{\mathrm{sliding}} $$
(1)
$$ {D}_{asc}={\left[\begin{array}{c}-\sin {\theta}_{\mathrm{asc}\_\mathrm{inc}}\cos {\alpha}_{asc\_ head}\kern0.75em \\ {}\sin {\theta}_{\mathrm{asc}\_\mathrm{inc}}\sin {\alpha}_{asc\_ head}\kern0.5em \\ {}\cos {\theta}_{asc\_ inc}\end{array}\right]}^T\cdotp \kern0.5em \left[\begin{array}{c}\cos {\beta}_1\sin {\beta}_2\\ {}\cos {\beta}_1\cos {\beta}_2\\ {}-\sin {\beta}_1\end{array}\right]\cdotp {D}_{\mathrm{sliding}} $$
(2)

where θdes _ inc and θasc _ inc are the incidence angles of the descending and ascending satellites, respectively; αdes _ head and αasc _ head are the heading angles of the descending and ascending satellites, respectively.

According to Eqs. (1) and (2), the ratio (r) between the descending and ascending LOS displacements can be expressed as Eq. (3), from which Dsliding is eliminated. Therefore, the descending-to-ascending ratio is only constrained by the satellite radar and sliding geometries. As a scalar, the ratio represents the relative size of the projection of landslide motion on the descending and ascending LOS and, thereby, reflects the relative sensitivity of the descending and InSAR geometries to landslide motion.

$$ {r}_{\mathrm{predicted}}=\frac{{\left[\begin{array}{c}-\sin {\theta}_{\mathrm{des}\_\mathrm{inc}}\cos {\alpha}_{\mathrm{des}\_\mathrm{head}}\kern0.75em \\ {}\sin {\theta}_{\mathrm{des}\_\mathrm{inc}}\sin {\alpha}_{\mathrm{des}\_\mathrm{head}}\kern0.5em \\ {}\cos {\theta}_{\mathrm{des}\_\mathrm{inc}}\end{array}\right]}^T\cdotp \kern0.5em \left[\begin{array}{c}\cos {\beta}_1\sin {\beta}_2\\ {}\cos {\beta}_1\cos {\beta}_2\\ {}-\sin {\beta}_1\end{array}\right]}{{\left[\begin{array}{c}-\sin {\theta}_{\mathrm{asc}\_\mathrm{inc}}\cos {\alpha}_{\mathrm{asc}\_\mathrm{head}}\kern0.75em \\ {}\sin {\theta}_{\mathrm{asc}\_\mathrm{inc}}\sin {\alpha}_{\mathrm{asc}\_\mathrm{head}}\kern0.5em \\ {}\cos {\theta}_{\mathrm{asc}\_\mathrm{inc}}\end{array}\right]}^T\cdotp \kern0.5em \left[\begin{array}{c}\cos {\beta}_1\sin {\beta}_2\\ {}\cos {\beta}_1\cos {\beta}_2\\ {}-\sin {\beta}_1\end{array}\right]} $$
(3)

With the descending and ascending InSAR observations available, the ratio (robserved) between the observed descending (Ddes) and ascending (Dasc) LOS displacements can be calculated according to Eq. (4) for each pixel inside the sub-block.

$$ {r}_{\mathrm{observed}}={D}_{\mathrm{des}}/{D}_{\mathrm{asc}} $$
(4)

Combining Eqs. (3) and (4), β1 and β2 can be solved in a least-squares sense (Grant and Boyd 2008, 2013). Since the assumption is that one landslide sub-block has only one sliding surface, pixels inside each sub-block share the same values of β1 and β2. After β1 and β2 are estimated, they can be substituted into Eq. (3) to obtain the model predictions of r and then the relative root mean square (RMS) of the geometric inversion can be calculated by Eq. (5) to measure the misfit of the determined sliding geometry.

$$ \mathrm{relative}\ \mathrm{RMS}=\sqrt{\frac{1}{n}\sum \limits_{i=1}^n{\left|\frac{r_{\mathrm{predicted}}-{r}_{\mathrm{observed}}}{r_{\mathrm{observed}}}\right|}^2} $$
(5)

where n is the number of pixels inside the landslide sub-block.

Seismic noise measurements (H/V)

The H/V technique analyses the spectral ratio between horizontal and vertical components of motion recorded by a single seismic station and allows for the estimation of the fundamental frequency of soft soils (Nakamura 1989). According to a simplified equation, the frequency of the upper layer is directly proportional to the average shear wave velocity and inversely proportional to four times the layer thickness (Castellaro 2016). In practice, H/V curves show a number of peaks (n) equal to (n + 1) alternating layers of different lithologies or horizontal stratifications in homogeneous layers. As a rule of thumb, a trace recorded on a homogenous soil without a cover layer (the so-called seismic bedrock) has a flat H/V curve, and no seismic wave amplification is expected. According to the SESAME Project guideline (SESAME 2004), a peak has to be taken into account if its amplitude is at least 2. The H/V peak amplitude is proportional to the layers’ seismic impedance contrast and can also indicate the presence of seismic velocity reversals when its value is lower than 1 for a wide range of frequencies (Castellaro and Mulargia 2009). Therefore, knowing the shear velocity (Vs) of the upper layer and its resonant frequency (i.e. an initial constraint is necessary), it is possible to reconstruct the depth (z) of the interface (Pazzi et al. 2017; Del Soldato et al. 2018a).

At the Villa de la Independencia landslide, the H/V seismic noise measurements were designed to cover the entire landslide area (Fig. 1b) and to obtain alignments across the two main directions to generate vertical cross sections of H/V (Pazzi et al. 2017). In total, 120 measurements were collected by means of four triaxial seismometers of the series Tromino® (a 3-directional, compact, all-in-one, and 24-bit digital tromometer developed by MoHo s.r.l.). Each acquisition ran for 20 min at 256 Hz and was processed using the commercial software Grilla® (provided by MoHo s.r.l.), which applied the guideline for processing ambient vibration data according to the H/V technique and SESAME (2004) project standards. To reconstruct the local seismic stratigraphy model (Vs-z profiles), the H/V curves were constrained in terms of velocity. These velocity values were obtained not only by a direct method (Pazzi et al. 2017) but also from a multichannel analysis of surface waves (MASW) and a seismic refraction survey carried out along the road that passes through the town (Highway 25, Fig. 1b). After the H/V data processing, the depth of slip surfaces and the landslide volume were estimated. Furthermore, InSAR and H/V measurements were integrated to reveal the diverse sliding characteristics between landslide sub-blocks during multi-surface fracturing sliding.

Result

The resultant InSAR velocity maps shown in Figs. 4a and b reveal considerable deformation (∼ 10 mm/year) in Independencia (enclosed by a black rectangle) which exerts a direct threat to the lives and properties of its residents. Figs. 4c and d show 0.4-mm and 0.5-mm average standard deviations of the estimated InSAR mean velocity respectively for the descending and ascending satellites, revealing the millimetre-level precision of time series InSAR. The sign of the LOS deformation rate in Independencia is opposite between the descending and ascending tracks, implying the movement has a considerable east-west component. A previously unknown deforming area (red circle in Fig. 4) located 2.5 km southeast of Independencia is also identified, with a LOS velocity of ~ 30 mm/year. Its instability could threaten the public transit safety due to the nearby Highway 25 (solid purple line in Fig. 4). In this section, the InSAR deformation maps and seismic H/V measurements covering the landslide as shown in Fig. 1b will be used to investigate the geometry of the landslide and the spatial pattern of its movements in great detail.

Identification of the fractured sliding surfaces from InSAR

Three sub-blocks were identified in Independencia as shown in Figs. 1b and 5, namely “town centre”, “upper block”, and “east block”, according to their overall slope aspects and the field investigation in 2017 which found a ridgeline and road inside the town (shown in Figs. 5a and b) roughly separating the three sub-blocks from each other. The InSAR measurements were then used to analyse the sliding geometry of each sub-block. As shown in Figs. 5a and b, the town centre block has more InSAR coherent pixels than the upper and east blocks due to the presence of optimal scatterers (e.g. buildings). To check whether the landslide generally moves along the slope, as is the assumption of the geometric inversion method in “Determination of the sliding geometry”, firstly a simulated along-slope displacement (100 mm) of each pixel was projected onto the descending and ascending Sentinel-1 LOS directions and was plotted in Figs. 5c and d. It can be seen that the observed InSAR cumulative displacement and the simulated displacement are largely consistent, with correlations of 0.71 and 0.70 for the descending and ascending tracks, respectively (Figs. 5e and f). The residual discrepancies could be due to the fact that each pixel may not necessarily move with the same magnitude as simulated. But in general, the consistency between observation and simulation verifies the assumption of the geometric inversion method. Note that the purpose of this step is to compare the relative spatial distribution of the simulated and observed displacements and the correlation is calculated from normalised displacements. Therefore, the value of the simulated along-slope displacement is insignificant to the results.

Fig. 5
figure 5

Observed and simulated LOS cumulative displacements around Independencia. a and b The observed LOS cumulative displacements from October 2014 to December 2019 by descending and ascending Sentinel-1, respectively. c and d The simulated descending and ascending LOS displacements, respectively, which are projected from the 100-mm displacement along the slope. The white line represents a road inside the town that roughly separates the town centre and the upper block. The thick magenta line represents a ridgeline separating the upper block and the east block, and the red lines are part of the landslide boundaries shown in Fig. 1b. e and f Scatter plots between observed and simulated LOS displacements for the descending and ascending, respectively. Note that the displacements are normalised between 0 and 1

Full size image

The InSAR measurements within each sub-block were used to execute the geometric inversion method described in “Determination of the sliding geometry”, and to determine a uniform geometry for each of the three sub-blocks. Results are shown in Fig. 6. The basal sliding plane of the upper block has an inclination of about 8° with a sliding direction of about 228°, while that of the flatter town centre has an inclination of about 3° with a sliding direction of about 167°. The inclination of the east block is steeper (~ 14°) than the above two sub-blocks and its sliding direction is about 131°. According to Eq. (5), the relative RMS of the geometric inversion misfit for the town centre, east block, and upper block are calculated to be 0.35, 0.26, and 0.33, respectively. Despite these misfits which could be caused by InSAR outliers, the inversion results can show that most InSAR pixels in each sub-block share the uniform sliding surface. Therefore, the three sub-blocks move downward along three different planar surfaces, suggesting the type of the landslide in Independencia should be classified as a compound type according to the classification of landslides by Hungr et al. (2014).

Fig. 6
figure 6

Determined sliding geometries of the three landslide sub-blocks. a Sliding directions (white arrows) of the three sub-blocks (clockwise from the North). The magenta line represents part of a ridgeline that distinguishes the upper block and the east block, while red lines are part of the landslide boundaries shown in Fig. 1b. The white line represents the road inside the town. The optical base map is from Google Earth, on which the descending InSAR displacements shown in Fig. 5a are also superimposed. b Sectional view of the determined sliding directions. The black vector s indicates the sliding displacement Dsliding, the purple vector d represents the descending LOS displacement Ddes, and the red vector a represents the ascending LOS displacement Dasc. The angle between the sliding direction and LOS is calculated by arccos(Ddes/Dsliding) and arccos(Dasc/Dsliding) according to Eqs. (1) and (2).

Full size image

Sliding interface depth obtained from H/V measurements

Regardless the seismic shear wave velocity, high-frequency peaks of the H/V curves are associated to the shallower interfaces, while low-frequency peaks to the deeper interfaces (Castellaro 2016; Pazzi et al. 2017). Fig. 7 shows the H/V curves of the measurements in the three sub-blocks identified in Fig. 5. Three main frequency ranges associated with natural discontinuities can be recognised. On the basis of the geological map of the area (Fig. 1b) and the results of the three boreholes shown in Fig. 1c, the highest H/V peak (with a frequency range of 40.0–80.0 Hz) can be related to the shallowest discontinuity between the organic/weathered surface layer (Vs range of 90–200 m/s, Vs mean value 100 m/s) and the unconsolidated soil deposits (i.e. silty clay with or without shale fragments, sandstone boulders, and sand with clay) (Vs range of 150–370 m/s, Vs mean value 250 m/s) at a mean depth (z0) of approximately 0.2–0.4 m. The second interface is identified at depths (z1) ranging from 1.5 to 15.0 m (at a frequency of 8.0–40.0 Hz), corresponding to the transition from the unconsolidated soil deposits to the shale and sandstone fragments in clay and silty matrix/highly weathered shale and sandstones (Vs range of 300–900 m/s, Vs mean value 450 m/s). The third peak is characterised by the frequency range of 2.0–8.0 Hz, identifying the seismic interface between the highly weathered shale and sandstones and the slightly weathered shale and sandstones/unweathered shales (the seismic bedrock) (Vs higher than 1000 m/s), at a depth (z2) of approximately 15.0–75.0 m.

Fig. 7
figure 7

A representative selection of H/V curves for the seismic noise measurements carried out in the three landslide sub-blocks (town centre, upper block, and east block)

Full size image

From Fig. 7, it can also be seen that the H/V curves of the three landslide sub-blocks behave in different amplitudes, especially in the frequency range of z1 and z2, indicating that the slip surfaces driving the three sub-blocks vary in seismic impedance contrast. Specifically, the H/V curves of the upper and east blocks are more similar than the town centre, with both of the two areas having a sliding direction of about (±)130° relative to the North revealed by InSAR (Fig. 6a). Compared to them, the H/V curves of the town centre are characterised by the presence of peaks in the frequency range of 2–4 Hz with a higher amplitude. This suggests that in the town centre, the interface between the gravel/consolidated material and the meteorised rock is characterised by a higher seismic impedance contrast, and the landslide motion may occur along both the shallower and deeper interfaces.

Considering the nature of the z0 interface, the landform of the area, and the absence of asphalt in all the streets of the surveyed area (that allowed carrying out H/V measures without amplitude limitations), the identified z0 surface can generate only shallow sliding involving limited volumes. Therefore, this interface is not significant from a geological point of view. Considering that the maximum depth of the houses’ foundations in the whole landslide area is ~ 2 m, it is possible to assess that the z1-related slip surface with depths around 5.0 m (see Fig. 8) is mainly responsible for the buildings’ cracks. Fig. 8 also shows that the deepest interface z2 exhibits a larger range. To observe its spatial distribution, the widely varying z2 values are mapped as dots of different dimensions in Fig. 9a. It can be seen that in the central landslide body they are randomly distributed, whereas in the east side of the landslide, the deeper values are mainly localised near the toe. This is further confirmed by six slip surface profiles (Figs. 9b to g, three in the central landslide and three in the right one) extracted along the slope. Such depth distribution suggests that the eastern part seems to be affected by a rotational movement, while the central one, also considering the slope inclination and that it is in the toe area, is more likely to be controlled by a combination of rotational and translational movements. Figs. 9b to d also show that slip surfaces at the toe of the landslide (> 2100 m from the head) are thin and approximately parallel with the ground surface (as indicated by dot-rectangles), which cross-validates the planar motion in the residential areas of the town observed by InSAR (see Fig. 5). In conclusion, considering the above slip characteristics and the mixture of Qd and Oan in the landslide area (Fig. 1b), the landslide type can be determined as a compound slide with sliding at different interfaces (soil/soil, soil/rock) and depths.

Fig. 8
figure 8

Reconstructed z depth values for seismic noise acquisitions located in the area of town centre (asterisks in yellow), upper block (in purple), and east block (in green). Blue points are all the other measurements carried out in the landslide area that faces to West (L1) and red points are those in the landslide area that faces to east (L2)

Full size image
Fig. 9
figure 9

a Deeper interface depths (z2 values) shown as dots of different dimensions. b–g Ground surface profiles (blue lines) highlighted in panel a and z2 slip interfaces (red dot-lines) derived from the H/V measurements along the profiles

Full size image

Landslide volume estimation

The simplest and commonly used method to calculate the volume is by multiplying the surface area with the average landslide depth (Jaboyedoff et al. 2020). Calculating first the z2 depth average, the volume of the Villa de la Independencia landslide was estimated as 1.35 · 108 m3. All the methods presented in the literature review (Jaboyedoff et al. 2020) were applied to cross sections, so they highlighted the need to assume a slip surface mechanism. However, owing to the wide coverage of H/V measurements in the study area, information about the slip surface depth is available over the whole landslide area, and not just along some cross sections. Therefore, considering the deeper interface (z2), the volume mobilised between the DEM and the interpolated surfaces of z2 depths was estimated by the tool Compute2.5 Volume in CloudCompare2.10.2 software (http://www.danielgm.net/cc/release/). The interpolation was made by means of the Rstudio software adopting the Kriging procedure (Bivand et al. 2013). The best fitting semivariogram (Fig. 10a) was assessed considering a spherical model for designing the sliding surface depths for the entire area of interest (Fig. 10b). The volume estimated by the software is 9.18 · 107 m3. This implies that the simplified method that assumes a single sliding plane of average depth would largely overestimates the volume by 46.7%.

Fig. 10
figure 10

a Experimental (points) and theoretical (line) semivariogram of the z2 values. b Interpolated z2 sliding surface depths of the landslide. The black dashed lines are the landslide boundaries shown in Fig. 1b. Note that the distortion of the interpolation boundary is due to the planar visualisation of a 3D geometry

Full size image

Temporal evolution of the landslide

Coherent pixels within the three sub-blocks shown in Fig. 6a were spatially averaged to generate displacement time series for each of the sub-blocks. Thirty-day cumulated precipitation was also produced according to the Global Precipitation Measurement (GPM) daily records (Hou et al. 2014; Huffman et al. 2019) to investigate the relationship between deformation and precipitation. Figs. 11a and b show how the deformation time series actively response to precipitation, with notable displacement acceleration observed both in the late rainy seasons (January to March) of 2018 and 2019, as indicated by blue dot-rectangles. The deformation magnitudes along the descending and ascending LOS in the upper block are similar, which is evidenced by their nearly identical decomposition angle on the sliding plane shown in Fig. 6b. The starting point of the accelerations in the descending and ascending LOS is also close. However, in the town centre block, the descending and ascending LOS displacements exhibit different sensitivity to the landslide motion. The observed deformation in the ascending track (black dots in Fig. 11a) shows stronger fluctuation but weaker response to the increase of precipitation than the descending track. This is because the sliding direction in the town centre is nearly perpendicular to the ascending LOS vector, as shown in the middle graph in Fig. 6b, resulting in its insensitivity to the displacement on the sliding plane. The insensitivity can be further evidenced by the Sentinel-1 unwrapped interferograms spanning the rainy season from January 2018 to April 2018, where the ascending LOS displacement (Fig. 11e) is smaller in the town centre compared to the descending one (Fig. 11d). The area of east block is less affected by the increase of precipitation, with a relatively stable LOS deformation time series in both descending and ascending modes during the past 5 years. However, there were still oscillations in early 2018 and 2019 marked with blue dot-rectangles in Fig. 11c which occurred well within the time interval of the late rainy season.

Fig. 11
figure 11

InSAR-derived time series from descending and ascending Sentinel-1 images for a the town centre, b the upper block, and c the east block, compared with the precipitation data (green line). The red and black dot-lines represent displacement time series in the descending and ascending LOS, respectively. The green shading in a, b, and c corresponds to the late rainy season in 2018 and 2019. The blue dot-rectangles circle the position of the acceleration phase. The parts enclosed by grey dot-rectangles in a reveal the insensitivity of descending-track Sentinel-1 observation in the town centre. d Sentinel-1 unwrapped interferograms of two descending-track images acquired on 22 January 2018 and 16 April 2018. e Sentinel-1 unwrapped interferograms of two ascending-track images acquired on 16 January 2018 and 22 April 2018. The black circles denote the location of town centre with high coherence (> 0.6). Note that a positive value in d and e means the surface is moving toward the satellite radar

Full size image

The acceleration of the LOS displacement during early 2018 and 2019 presents a precursor signal of the landslide risk. To observe the acceleration of the landslide motion more intuitively, Sentinel-1 LOS displacements were projected onto the sliding surface using a reverse form of Eq. (1) and plotted in Fig. 12. It can be seen that the deformation in the town centre has the largest acceleration compared to the upper and east blocks. Interestingly, the H/V curves shown in Fig. 7 also reveal their difference by presenting a significantly higher seismic impedance contrast of the deeper z2 interface in the town centre. Therefore, combining InSAR and H/V results, it is possible to assess that the town centre could be additionally affected by a deeper sliding interface compared to the other two sub-blocks.

Fig. 12
figure 12

Time series InSAR-derived movements along the sliding surface and 30-day accumulated precipitation total from GPM. The green shading corresponds to the late rainy season in 2018 and 2019. The blue dot-rectangles circle the two acceleration phases of landslide motion with the same time span

Full size image

Despite the fact that there was no increase in rainfall during the 2019 rainy season compared to previous years, the deformation in the study area had been accelerating during this period. The deformation time series projected onto the sliding surface (Fig. 12) reveal that the acceleration signal in 2019 shared similar starting time and duration (the late rainy season) as in 2018. Within the period from 2018 to 2019, the displacement presented a seasonally dominated process, especially in the town centre. This leads to the speculation that further accelerations could recur in the future in the case of substantial precipitation during the late rainy season.

Discussion

The Sentinel-1 data in this study enables us to identify a linear deforming of the landslide before 2018 and then two sudden accelerations during the rainy seasons of 2018 and 2019. It should be noted that the acceleration registered by the landslide in the town centre is larger than the acceleration manifested by the other two sub-blocks. On the other hand, the slope aspect in the town centre is nearly parallel to the flight direction of the ascending satellite so that the ascending LOS observations are insensitive to the along-slope displacement. This may result in an underestimation of displacements as only a small portion of the along-slope displacement is observable by the ascending satellite (~ 5% compared to ~ 23% of the descending satellite). However, considering the millimetre-level precision of time series InSAR shown in Figs. 4c and d, the InSAR-observed acceleration of the landslide movement should be real and worthy of further close monitoring in the future.

Seasonal oscillations in InSAR time series

The displacement time series before 2018 show a stable linear trend. Our analysis identified that there are also substantial seasonal oscillations in the time series. Two possible causes, precipitation and residual stratified tropospheric delays, may contribute to the oscillations as both of them have a similar seasonal variation. To analyse their relationships and identify the most likely factor, the methods of CWT, XWT, and WTC were applied to the detrended time series before the 2018 acceleration. Fig. 13 a shows (i) the detrended Sentinel-1 descending-track LOS displacement time series, which is more sensitive to the landslide movement than the ascending track as discussed in “Result”; (ii) the differential zenith tropospheric delays (dZTD, obtained from GACOS as described in “InSAR”); and (iii) the precipitation. From the CWT results of InSAR time series (Fig. 13b), an annual (365 days) cycle with strong power along the entire recording interval can be observed. In addition, substantial power signals with a period of half a year and 2 to 3 months can be identified around 2016 and 2017.

Fig. 13
figure 13

a InSAR displacement time series, differential zenith tropospheric delays (dZTD), and 30-day accumulated precipitation in the area of town centre. b Continuous wavelet power (CWT) of InSAR time series. The thick contour designates the 5% significance level against noise. The lighter shadow denotes the cone of influence by potential edge effects. c and d Wavelet coherence (WTC) and cross-wavelet transform (XWT) between InSAR time series and dZTD, respectively. e and f WTC and XWT between InSAR time series and precipitation, respectively. The black arrows represent the relative phase shift, with in-phase pointing right (0°) and the first series leading the second 90° pointing down

Full size image

Figs. 13c and d show the WTC and XWT relationship between InSAR time series and dZTD. From the figures, it emerges that the relationship is out of the 5% significance level. On the other hand, InSAR time series are generally in-phase with precipitation, presenting substantial common power in annual and half-year cycles within the 5% significance level as shown by the thick contour in Figs. 13e and f. Therefore, it can be inferred that the seasonal oscillations in InSAR time series are more related to seasonal precipitation than residual tropospheric delays. The in-phase relationship between the annual cycle of InSAR time series and precipitation also shows a phase shift of about 40° as indicated by black arrows in Fig. 13f. This means the onset of deformation in the area of town centre is normally more than a month ahead of the arrival of precipitation peak, since the sliding oscillation tends to initiate shortly after the start of rainy season (Hu et al. 2016) that is before reaching rainwater peak. Here the InSAR time series used for the analysis of seasonal oscillations is before 2018. From Fig. 12, it can be seen that the landslide motion in this phase showed only a moderate response to precipitation (< 30 mm). But after the precipitation peaks in 2018 and 2019, the two observed accelerations represent strong responses (> 70 mm) to the increased precipitation which were substantially different from the seasonal oscillations before 2018.

Instability of the landslide

The ground deformations observed had an important effect on the residential buildings and infrastructures of the town. The examples of the identified damage within the three sub-blocks (Figs. 1d to j) indicate that (i) almost all the buildings exhibit sparse cracks, fine and rarely open; (ii) the church (Fig. 1f) and the opposite garage (Fig. 1g) exhibit big and spread fractures showing up to 5-cm open cracks; (iii) the bus station (Fig. 1h) is completely distorted and partially collapsed with several open fractures; (iv) widespread cracking caused by shear stresses induced by the landslide movement is found in several house walls and at the food market (Fig. 1e).

With InSAR, we further found that the landslide in Villa de la Independencia experienced accelerated deformation since 2018. Because of the increase of precipitation in the rainy season in 2018, more rainwater infiltrated and tended to saturate the landslide body at the base of the slope. This in turn leads to larger porewater pressures and reduces the frictional strength along the failure plane (Hu et al. 2016). Furthermore, the loading by the weight of water on the failure plane can increase the gravitational driving force (Saar and Manga 2003; Schmidt and Bürgmann 2003; Crosta et al. 2014b). These two effects lead to acceleration of the landslide motion. It can be concluded that the landslide is seasonally active and controlled by precipitation, now with a higher risk of failure than before. It is recommended that an early warning system should be installed in this area with, as a minimum, a weather station and a ground total station for constant monitoring of precipitation and surface displacements, respectively. Also, any future construction of residential buildings and infrastructure should be outside the areas identified as most subject to surface displacements.

Conclusions

The work here presented applied both InSAR and seismic noise measurement techniques to the analysis of landslide motion. Combining descending and ascending InSAR displacement maps revealed that the landslide in Independencia is featured by dominant along-slope movements. Three sub-blocks, namely the town centre, upper block, and east block, were identified as shown in Fig. 1b, whose sliding directions were determined by a geometric inversion method. Results show that the sliding directions of the three sub-blocks are about 167°, 228°, and 131° clockwise from the North, respectively, and the inclinations of their sliding planes are about 3°, 8°, and 14°, respectively. Furthermore, the seismic noise measurement analysis revealed that the cracks affecting buildings could be mainly caused by the shallow slip interface (located at a mean depth of 5 m), since the foundation depth of the buildings is at most 2 m. However, the town centre block seems to be additionally affected by the deeper failure surfaces (15 to 75 m), which may be responsible for its different direction and acceleration magnitude of sliding (inferred by InSAR) compared to the other blocks. The combination of InSAR and seismic noise measurements reveals the landslide to be a compound sliding type. The overall landslide volume based on the z2 depth values inferred from the seismic noise measurement is about 9.18 · 107 m3.

In terms of the temporal evolution of the landslide motion, seasonal precipitations contribute most to the seasonal oscillations in deformation time series. More importantly, the deformation time series from Sentinel-1 shows periodic accelerations in early 2018 and 2019. The two accelerations, which are greater in the town centre block than in the other two blocks, were identified at around January to March of each year and last for about 1 month. This is probably due to the sudden increase of precipitation in the late rainy season of 2018 compared to previous years as observed by GPM. This leads to speculate that the landslide could be subject to periodic accelerations in the future following periods of heavy rainfalls.

This study showcases the great potential of combing InSAR with seismic noise measurements in characterising landslide motion. InSAR observations are directly related to the deformation on the ground surface while seismic noise measurements can determine the depth of the failure surface. The combined use of the two techniques allows for full characterisation of the landslide kinematics that dictates the surface movements and the 3D landslide geometry.