Advertisement

Landslides

, Volume 14, Issue 4, pp 1389–1401 | Cite as

Does parameterization influence the performance of slope stability model results? A case study in Rio de Janeiro, Brazil

  • Carolina de Lima Neves Seefelder
  • Sérgio Koide
  • Martin Mergili
Open Access
Original Paper
First Online:
Received:
Accepted:

Abstract

We produce factor of safety (FOS) and slope failure susceptibility index (SFSI) maps for a 4.4-km2 study area in Rio de Janeiro, Brazil, in order to explore the sensitivity of the geotechnical and geohydraulic parameterization on the model outcomes. Thereby, we consider parameter spaces instead of combinations of discrete values. SFSI is defined as the fraction of tested parameter combinations within a given space yielding FOS <1. We repeat our physically based calculations for various parameter spaces, employing the infinite slope stability model and the sliding surface model of the software r.slope.stability for testing the geotechnical parameters and the Transient Rainfall Infiltration and Grid-Based Regional Slope-Stability Model (TRIGRS) for testing the geohydraulic parameters. Whilst the results vary considerably in terms of their conservativeness, the ability to reproduce the spatial patterns of the observed landslide release areas is relatively insensitive to the variation of the parameterization as long as there is sufficient pattern in the results. We conclude that landslide susceptibility maps yielded by catchment-scale physically based models should not be interpreted in absolute terms and suggest that efforts to develop better strategies for dealing with the uncertainties in the spatial variation of the key parameters should be given priority in future slope stability modelling efforts.

Keywords

Parameter sensitivity Parameter space Slope failure susceptibility index Slope stability model TRIGRS Uncertainty 

Introduction

Landslides starting from unstable slopes affect the safety of life as well as of private and public assets. Computer models are employed to identify potentially unstable areas in order to facilitate decision-making at various levels. Whilst statistical models explore the relationships between the spatial patterns of landslide occurrence and a set of predictor layers, physically based models attempt to reproduce or to predict the physical mechanisms involved (Guzzetti et al. 1999; Van Westen 2000; Guzzetti 2006; VanWesten et al., 2006). Physically based models are frequently employed to estimate landslide susceptibility at the scale of small catchments (VanWesten et al., 2006). As long as shallow landslides are considered, these approaches mostly rely on the infinite slope stability model. It is commonly used in raster-based geographic information system (GIS) environments to derive a factor of safety for each pixel. However, the infinite slope stability model is unconditionally suitable only for those areas where shallow translational landslides with a length-to-depth ratio L/D >16–25 are expected (Griffiths et al. 2011; Milledge et al. 2012). As shallow landslides are most commonly triggered by extreme hydrometeorological events, such modelling tools are often coupled with more or less complex hydraulic models (e.g., Montgomery and Dietrich 1994; Van Westen and Terlien 1996; Burton and Bathurst 1998; Pack et al. 1998; Wilkinson et al. 2002; Xie et al. 2004a; Baum et al. 2008; Godt et al. 2008; Muntohar and Liao 2010; Mergili et al. 2012).

For areas with deep-seated landslides, models assuming spherical, ellipsoidal or complex sliding surfaces reproduce the stability situation in a more appropriate way. Whilst they are standard in geotechnical engineering, their implementation with GIS is non-trivial so that catchment-scale applications are less commonly applied (e.g. Xie et al. 2003, 2004b, 2006; Jia et al. 2012; Mergili et al. 2014a, b).

Even simple slope stability or hydraulic models rely on parameters which are highly uncertain in their horizontal and vertical distribution. One possible concept to account for parameter uncertainty is the probability of failure (Tobutt 1982) which has started to complement the conventional factor of safety with increasing computational power, considering parameter spaces using random or regular sampling of uncertain parameters (Mergili et al. 2014a). Various authors have introduced and used different types of probability density functions (pdfs) of geotechnical (El-Ramly et al. 2005; Petrovic 2008; Mergili et al. 2014a) and geohydraulic parameters (Mesquita et al. 2002, 2007; Mesquita and Moraes 2004) which can be employed for parameter sampling. Whilst such functions are a smart way to deal with uncertain information, they are not necessarily transferable between different locations and therefore commonly suffer from small sample sizes and, consequently, weakly supported means and standard deviations.

As the challenge of uncertain parameters is encountered in many fields of geosciences, various approaches have been developed in the previous decades to test the sensitivity of the model results or the model performance to the input parameters or to optimize (calibrate) the input parameters in order to bring the model results in line with reference observations. Testing one parameter at a time is thereby considered inappropriate as both the optimum value and the sensitivity may strongly interrelate with the values of other parameters (Saltelli and Annoni 2010). Multi-parameter strategies are therefore required (e.g., Duan et al. 1992; Eberhart and Kennedy 1995; Hay et al. 2006; Vrugt et al. 2008; Fischer 2013). Optimized parameters or parameter sets, however, are not necessarily meaningful from a physical point of view. Particularly when calibrating many parameters at once, a good model performance in terms of reproducing the observation can be achieved despite a poor process understanding. The sensitivity of local-scale slope stability model results to selected input parameters was tested, e.g. by Griffiths and Fenton (2004) or by Wang et al. (2010). Guimarães et al. (2003) and Formetta et al. (2015) have applied parameter optimization strategies at catchment scale.

Almost all documented parameter sensitivity and optimization strategies target at discrete parameter values. We think that, particularly at broader scales, sensitivity analysis and optimization of parameter values is inappropriate as it disregards the inherent fine-scale spatial variability of the parameters. Instead, we suggest performing sensitivity analysis and optimization of parameter ranges.

The present article demonstrates such a strategy, employing a modification of the probability of failure concept. We investigate how the considered ranges of geotechnical and geohydraulic input parameters influence the results and performance of GIS-based catchment-scale slope stability models. For this purpose, we apply the infinite slope stability model, the sliding surface model of the tool r.slope.stability and the software Transient Rainfall Infiltration and Grid-Based Regional Slope-Stability Model (TRIGRS) to the Quitite and Papagaio catchments, Rio de Janeiro, Brazil. The findings are thought to be useful to identify suitable parameterization strategies for future slope stability modelling efforts.

Next, we introduce the study area (“Study area and data” section) and describe the components of the proposed work flow (“Methods” section). We then demonstrate (“Results” section) and discuss (“Discussion” section) the results obtained before drawing our conclusions (“Conclusions” section).

Study area and data

The study area includes the two landslide-prone Quitite and Papagaio watersheds located in the western part of the city of Rio de Janeiro, Brazil (Fig. 1). Together, they cover an area of 4.4 km2, extending between 12 and 995 m a.s.l. The climate in the area is tropical humid (Guimarães et al. 2009). Due to influence by ocean moisture, the area receives a higher amount of rainfall than the central part of Rio de Janeiro (Hurtado Espinoza 2010). Granitic bedrock dominates both watersheds. The homogeneous, colluvial yellow soil is characterized by sandy-clay features (Hurtado Espinoza 2010; Galindo 2013; Galindo and Campos 2014) and a depth of 1–3 m (Guimarães et al. 2003). Native forest is still the dominant type of vegetation whilst the anthropogenic influence on the land cover is of limited importance (Guimarães et al. 2003; Hurtado Espinoza 2010).
Fig. 1.

The study area, consisting in the two catchments Quitite and Papagaio in Rio de Janeiro, Brazil

Guimarães et al. (2003) optimized values of effective cohesion c’ (kN m−2), normalized to depth d, effective angle of internal friction φ’ and specific weight of the saturated soil γ s (kN m−3) using published parameters for geomorphologically comparable adjacent areas and back-calculations with the software SHALSTAB. These authors arrived at best fit values of c’/d = 2 kN m−3, φ’ = 45° and γ s = 15 kN m−3, but they also indicated that, in general, low values of c’/d, high values of φ’ and values from 15 to 17.5 kN m−3 for γ s would be appropriate for the area. They proposed a general frame of parameter values realistic for the area (in the sense of a parameter space) summarized in Table 1 and, with some modifications, applied to tests A and B (see “Methods” and “Results” sections). Hurtado Espinoza (2010) measured a dry specific weight around 15 kN m−3 for some undisturbed samples taken at 1 m depth. The same authors stated that the slopes in the lower areas would be weaker whilst those in the higher areas would be stronger.
Table 1

Range of parameter values applicable to the Quitite and Papagaio watersheds (Guimarães et al. 2003)

Parameter

Minimum value

Maximum value

c’/d

0 kPa m−1

8 kPa m−1

φ’

25°

45°

γ s

15,000

25,000

Values of soil saturated conductivity K s were measured by Fernandes et al. (2001) using Guelph’s permeameter. The results showed a high variability with values ranging from 10−6 to 10−4 m s−1 as well as some important discontinuities in the profiles, possibly influencing groundwater flow.

We consider a landslide event related to intense rainfall on 13 and 14 February 1996. Within 48 h, 394.3 mm of rainfall was registered at the Alto da Boa Vista station, and 245.9 mm at the Jacarepaguá station, both located in close vicinity to the Quitite and Papagaio catchments and operated by the National Meteorological Institute (INMET; Conti 2012). A landslide inventory developed by Guimarães (2000) is used in the present work. According to this inventory, the rainfall event has triggered 93 landslides, occupying 0.14 km2 (3.1% of the entire area). Table 2 summarizes the main characteristics of the landslide inventory. Most landslides occurred in the native forest areas dominating the study area. Shallow landslides, debris flows and debris avalanches were most common. The sliding surfaces of most landslides coincided with the soil-rock interface (Guimarães et al. 2003; Miqueletto and Vargas, 2009; Hurtado Espinoza 2010). The landslide inventory displays the entire extent of the directly affected areas without distinguishing between release, transit and deposition areas.
Table 2

Main characteristics of the inventoried landslides triggered by the rainfall event of 13 and 14 February 1996 in the Quitite and Papagaio watersheds

Landslide characteristics

Values

Number of landslides

93

Total landslide area (fraction of total area)

0.14 km2 (3.1%)

Average (minimum–maximum) landslide area projected to ground plot

1520 m2 (32–11,904)

Average (minimum–maximum) landslide length in down-slope direction, projected to ground plot

65.9 m (8.0–220.0)

Average (minimum–maximum) landslide width in cross-slope direction

20.0 m (4.0–96.0)

Average (minimum–maximum) landslide inclination in down-slope direction

31.9 (8.5–45.8)°

Besides the geotechnical and geohydraulic information and the landslide inventory, we use a 2-m resolution digital elevation model (DEM).

Methods

Work flow and software

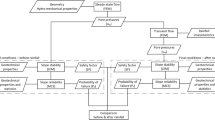
Figure 2 illustrates the general work flow of the study. We compute the slope failure susceptibility index (SFSI) (dimensionless number in the range 0–1) based on sets of factor of safety (FOS) values derived through the controlled variation of selected key parameters within a defined parameter sub-space. This procedure is repeated for various sub-spaces. The resulting SFSI values are evaluated against the inventory of observed landslides, and the findings are compared and interpreted.
Fig. 2.

Work flow of the study

In a first step, we vary the geotechnical parameters (tests A and B) and in a second step, we vary the geohydraulic parameters (test C). Test D uses a simple statistical model for the sake of comparison. Test A builds on the infinite slope stability model, test B on the sliding surface model of the tool r.slope.stability (Mergili et al. 2014a, b), designed as a raster module of the open source GRASS GIS software (Neteler and Mitasova 2008; GRASS Development Team 2016). Test C makes use of TRIGRS (Transient Rainfall Infiltration and Grid-Based Regional Slope-Stability Model; Baum et al. 2008), which is a grid-based tool simulating the permanent and transient rainfall influences on slope stability. Python scripting is used to derive SFSI, and the R Project for Statistical Computing (R Core Team, 2016) is employed for the evaluation of the results. Test D relies entirely on Python and R scripting.

Geotechnical model

Slope stability modelling commonly builds on the limit equilibrium theory (Duncan and Wright 2005): a factor of safety (FOS) is computed as the ratio between resisting forces R and driving forces T:
$$ \mathrm{FOS}=\frac{R}{T} $$
(1)

When FOS = 1, the slope is in static equilibrium. Values of FOS <1 indicate potential failure (in reality, such slopes do not exist), values of FOS >1 indicate stable slopes. The use of this method requires the prior definition of a slip surface, and the soil is considered as rigid material.

For GIS-supported catchment-scale analyses of slope stability, the infinite slope stability model is most commonly employed (Montgomery and Dietrich 1994; Pack et al. 1998; Xie et al. 2004a; Baum et al. 2008). It assumes (i) a uniform slope of infinite length, and (ii) a plane, slope-parallel failure surface. As inter-slice forces do not have to be considered, it is conveniently applied on a pixel-to-pixel basis. Based on Eq. (1), FOS can be expressed in various ways. For fully saturated soil, the equation may be formulated as follows (modified after Baum et al. 2008):
$$ \mathrm{FOS}=\frac{ \tan \phi}{ \tan \alpha}+\frac{c- u \tan \phi}{\gamma_s d \sin \alpha \cos \alpha} $$
(2)

where α is the slope angle, u (N m−2) is the pore water pressure, γ s (N m−3) is the specific weight of the saturated soil and d (m) is the depth of the sliding surface.

In the present work, we use the infinite slope stability model implemented with r.slope.stability and with TRIGRS. Alternatively, we also apply the sliding surface model of r.slope.stability. Thereby, the slope stability is tested for a large number of randomly selected ellipsoid-shaped potential sliding surfaces, truncated at the depth of the soil. R and T are summarized over all pixels intersecting a given sliding surface, and FOS is computed for each surface in a way analogous to Eqs. 1 and 2, applying a modification of the Hovland (1977) model. Finally, the minimum value of FOS resulting from the overlay of all sliding surfaces is applied to each pixel. For a more detailed description of the sliding surface model of r.slope.stability, we refer to Mergili et al. (2014a, b).

Geohydraulic model

In TRIGRS, FOS is computed for one or more user-defined depths. The Richard’s equation is used to calculate the soil transient infiltration for saturated and unsaturated soil conditions (Iverson 2000):
$$ \frac{\partial \psi}{\partial t}\frac{d\theta}{d\psi}=\frac{\partial }{\partial x}\left[{K}_L\left(\psi \right)\left(\frac{\partial \psi}{\partial x}- \sin \alpha \right)\right]+\frac{\partial }{\partial y}\left[{K}_L\left(\psi \right)\left(\frac{\partial \psi}{\partial y}\right)\right]+\frac{\partial }{\partial z}\left[{K}_z\left(\psi \right)\left(\frac{\partial \psi}{\partial z}- \cos \alpha \right)\right] $$
(3)

where ψ (m) is pressure head, θ is soil volumetric water content, t (s) is time, K L (m s−1) is lateral soil conductivity and K z (m s−1) is soil conductivity in z direction.

To solve the Richards equation, TRIGRS uses an approach developed by Iverson (2000), considering homogeneous soil, isotropic flow, relatively shallow depth, one-dimensional vertical downslope flow and soil moisture close to saturated conditions (Baum et al. 2008; Park et al. 2013), following the heat conduction approach described by Carslaw and Jaeger (1959). We refer to Baum et al. (2008) for a detailed description of the procedure.

For computing the groundwater level, TRIGRS compares the infiltrated water volume V I and the maximum drainage capacity of the soil V D. If V D ≥ V I, the water table remains constant. Otherwise, the water table rises, depending on K s and the transmissivity T. For unsaturated conditions, the maximum value of ψ is the new water level multiplied with β (value set according to the adopted flow condition). The amount of water exceeding the maximum infiltration rate is considered surficial runoff. However, surficial runoff is not taken over from one time step to the next (Baum et al. 2008).

Slope failure susceptibility index

The slope failure susceptibility index (SFSI) in the range 0–1 refers to the fraction of geotechnical and/or geohydraulic parameter combinations resulting in FOS <1, out of an arbitrary number of tested parameter combinations. This means that SFSI for a given pixel increases with each parameter combination where FOS <1 and, finally, low values of FOS correspond to high values of SFSI. The principal concept of the SFSI is identical to the concept of the slope failure probability yielded by r.slope.stability (Mergili et al. 2014a). However, we refer to it as a susceptibility index in the context of the present study as we simply use a uniform probability density function throughout all the computations. Such a distribution does not necessarily capture the real-world parameter distribution (which is unknown) and its use does therefore not justify applying the concept of probability in a strict sense.

Statistical model

In test D, a statistical model is applied for the purpose of comparison, employing the slope angle as the only predictor layer (Table 3). We keep the statistical model as basic as possible in order to evaluate the performance of a simplistic statistical approach in comparison to the physically based models (“Geotechnical model” to “Slope failure susceptibility index” sections). This allows us to conclude on the need of using more complex physically based models for catchment-scale landslide susceptibility analysis. Thereby, we overlay a classified slope map with the map of the observed landslide release areas (ORA; “Model evaluation” section) and, for each slope class, compute the fraction f C of observed landslide release pixels related to all pixels. SFSI—referred to as release probability by Mergili and Chu (2015) who employed a comparable approach—is then computed by applying f C to all pixels of the corresponding slope class. Thereby, it is important to use two different areas for the derivation of f C and for the computation and evaluation of SFSI (“Test layout” section).
Table 3

Summary of all tests performed

Test

Description

A1

The infinite slope stability model is applied with a constant soil depth d = 3 m; the entire OIA is considered for evaluation. This means that all observed landslide pixels are considered OP whilst all observed non-landslide pixels are considered ON.

A2

Infinite slope stability model, constant soil depth d = 3 m; only the ORA is considered for evaluation: the pixels in the upper third of each observed landslide are considered OP, all other observed landslide pixels are considered no data; all observed non-landslide pixels are considered ON. This procedure helps to exclude pixels possibly representing transit or deposition areas from the evaluation procedure.

A3

Infinite slope stability model, variable soil depth and OIA considered for evaluation. According to Guimarães et al. (2003), d is varied between 1 and 3 m. We assume a linear increase of d within a certain range of the topographic wetness index (Moore et al. 1991).

A4

Infinite slope stability model, variable soil depth and ORA considered for evaluation

B

The sliding surface model implemented in r.slope.stability is applied along with the optimized parameters derived from the tests A1–A4. The ellipsoid density per pixel (Mergili et al. 2014a, b) is set to 2500. The ellipsoid dimensions are constrained by the dimensions of the release areas of the observed landslides. All ellipsoids are truncated at the depth of the soil.

C1

TRIGRS, rectangular hydrograph and an assumed rainfall duration of 6 h. The rainfall is considered constant throughout the entire period, resulting in an intensity of 24 mm/h.

C2

TRIGRS, rectangular hydrograph and rainfall duration of 10 h (intensity 14.4 mm/h)

C3

TRIGRS, triangular hydrograph with central peak and rainfall duration of 6 h, resulting in a peak intensity of 48 mm/h

C4

TRIGRS, triangular hydrograph with central peak and duration of 10 h and peak intensity of 28.8 mm/h

D

Simple statistical model employing the slope angle as the only predictor layer. Overlay of a classified slope map with the ORA map and, for each class, computation of the fraction of observed landslide release pixels related to all pixels.

For more details such as the parameters spaces applied please refer to the text

Model evaluation

The landslide inventory for the Quitite and Papagaio watersheds displays the entire observed landslide impact areas (OIAs), i.e. the release, transit and deposition areas without any differentiation. We approximate the ORA as the upper third part of each OIA polygon. Depending on the test (“Test layout” section and Table 3), either the OIA map or the ORA map is overlaid with the corresponding SFSI map. When using the ORA map, the lower two-thirds portion of the OIA is not considered for evaluation. The true positive (TP), true negative (TN), false positive (FP) and false negative (FN) pixel counts are derived for selected levels of SFSI. An ROC curve is produced by plotting the true positive rates TP/(TP + FN) against the false positive rates FP/(FP + TN) derived with each combination of parameters. The area under the ROC curve AUROC indicates the predictive capacity of the model: AUROC = 1.0 (the maximum) means a perfect prediction, AUROC = 0.5 (corresponding to a straight diagonal line) indicates a random prediction, i.e. model failure. AUROC refers to the entire area used for model evaluation.

In addition, we introduce a conservativeness measure:
$$ \mathrm{FoC}=\frac{\mu_{\mathrm{SFSI}}}{r_{\mathrm{OP}}} $$
(4)

where μSFSI is the average of SFSI over the entire study area, and r OP is the observed positive rate, i.e. the fraction of observed landslide pixels out of all pixels in the study area. If FoC >1, the model overestimates the landslide susceptibility, compared to the observation whilst values FoC <1 indicate an underestimation of the landslide susceptibility.

Test layout

Tables 3 and 4 summarize the main characteristics of each test and the parameter values and ranges considered.
Table 4

Geotechnical and geohydraulic parameter values and ranges applied for the tests A–C (Table 3), following Guimarães et al. (2003); Saxton and Rawls (2006); Hurtado Espinoza (2010); Conti (2012); Park et al. (2013)

Symbol

Description

A1–A4

B

C1–C4

φ’

Effective angle of internal friction

21–45°

21–45°

45°

c’

Effective cohesion

0–24 kN m−2

0–24 kN m−2

4.5 kN m−2

γ d

Dry specific weight

13.5 kN m−3

13.5 kN m−3

N/A

γ s

Saturated specific weight

N/A

N/A

16.0 kN m−3

θ s

Saturated water content

40 Vol.%

40 Vol.%

40 Vol.%

θ r

Residual water content

N/A

N/A

5 Vol.%

K s

Saturated hydraulic conductivity

N/A

N/A

10−7–10−4 m s−1

D

Diffusivity

N/A

N/A

200 K s

I 0

Initial infiltration rate

N/A

N/A

1.3 10−6 m s−1

d

Sliding surface depth

3 m

3 ma

3 m

d w

Depth of water table

0 m

0 m

N/A

d i

Initial depth of water table

N/A

N/A

0–3 m

aIn test B, the ellipsoid-shaped random slip surfaces are truncated at a depth of 3 m

In a first step (tests A1–A4 and B), the sensitivity of SFSI and the associated model performance to the geotechnical parameters c′ and φ′ and the shape of the sliding surface is explored, assuming fully water-saturated soils, and the depth of the sliding surface corresponding with the soil depth. The infinite slope stability model and the sliding surface model implemented in r.slope.stability are employed for this purpose. We introduce a two-dimensional parameter space constrained by lower boundaries of c′ = 0 kN m−3 and φ′ = 21°, and upper boundaries of c′ = 24 kN m−3 and φ′ = 45° (Fig. 3a; Table 4). This parameter space accounts for the full ranges of c′ and φ′ considered representative for the area (“Study area and data” section). We note that the resulting values of FOS vary according to φ′ and c′/d, so that the value of FOS obtained with d = 3 m and with a given value of c′ is identical (infinite slope stability model) or similar (sliding surface model) to the value of FOS with other values of c′ and d, but the same c′/d ratio. The dry specific weight of the soil γ d = 13.5 kN m−2 and the volumetric saturated water content θ s = 40 vol.% are set to constant values. We neglect the weight of the trees and the effects of their root systems on the cohesion: sliding surfaces are assumed to develop beneath the rooting depth.
Fig. 3.

Parameter spaces considered for the sensitivity analysis of the a geotechnical and b geohydraulic parameters

The ranges of both c′ and φ′ are (i) considered in their entire extent; (ii) subdivided into two sub-ranges of equal extent and (iii) subdivided into three sub-ranges of equal extent (Fig. 4a, b). Considering all possible combinations of sub-ranges of the two parameters results in 36 partly overlapping parameter sub-spaces with 25 corner points. SFSI is computed for each parameter sub-space, with ten sampled parameters in each dimension (Fig. 4c). This procedure may be extended to three or more dimensions or repeated at a finer level by employing the sub-space with the best model performance as the entire space for the next level. For reasons to be explained in the “Results” section, only one level is applied in the present work. This work flow is repeated for two assumptions of soil depth and two versions of the landslide inventory used for evaluation, resulting in a total of four sub-tests (Table 3).
Fig. 4.

Layout of the parameter sensitivity analysis procedure: a example of an arbitrary parameter space; b sub-setting of the parameter space into sub-spaces of various dimensions; c uniformly distributed parameter sampling within an arbitrary subspace. Each dot represents one parameter combination

Test C explores the sensitivity of SFSI and the associated model performance to K s and the initial depth of the water table d i (m). We introduce a two-dimensional parameter space constrained by lower boundaries of K s  = 10−7 m s−1 and d i = 0 m and upper boundaries of K s  = 10−4 m s−1 and d i = 3 m (Fig. 3b; Table 4). The ranges of values used are based on works of Saxton and Rawls (2006) and Guimarães et al. (2003). We set γ s = 16 kN m−2, θ s  = 40 vol.%, θ r  = 5 vol.%, c′ = 4.5 kN m−2, φ′ = 45° and d = 3 m to constant values. The choice of these values is supported by data from Guimarães et al. (2003) and Hurtado Espinoza (2010). We further assume constant values of diffusivity (D = 200K s ; Park et al., 2013) and initial infiltration rate (I 0 = 1.3 10−6 m s−1; Conti 2012).

In a way analogous to the geotechnical parameters, the ranges of both K s and d i are (i) considered in their entire extent, (ii) subdivided into two sub-ranges of equal extent and (iii) subdivided into three sub-ranges of equal extent, resulting in 36 partly overlapping parameter sub-spaces with 25 corner points. SFSI is computed for each parameter sub-space, with five sampled parameters in each dimension. The landslide inventory used for evaluation is ORA.

This procedure is repeated for four combinations of rainfall duration and type of pluviograph (Table 3). We assume rainfall durations of 6 and 10 h and a total rainfall amount derived from the measurements at the Jacarepaguá and Boa Vista stations on 13 and 14 February 1996 (Conti 2012). The Thiessen method is applied for estimating the precipitation in the catchment, and 20% of interception are deduced (Coelho Netto 2005). The total rainfall considered for the analysis is 144 mm in all the scenarios C1–C4.

In test D, we apply the statistical model introduced in the “Statistical model” section for the purpose of comparison (Table 3). f C is derived for one of the two catchments. SFSI is then computed for the other catchment and evaluated against the corresponding ORA. The entire procedure is repeated in the reverse way, so that a clear separation between the model development and model evaluation areas is ensured.

Results

Tests A and B: geotechnical parameterization

Figure 5 illustrates the results of test A in terms of model performance (AUROC) and conservativeness (FoC). Assuming a constant soil depth, the model performs significantly better when considering only the ORA (test A2; AUROC ≤ 0.741; Fig. 5b) instead of the entire OIA (test A1; AUROC ≤ 0.691; Fig. 5a). This result clearly indicates that the OIA is unsuitable as reference for evaluation, and an appropriate inventory sub-setting is essential. Focusing on Fig. 5b, we note that the model performance in terms of AUROC is insensitive to the variation of the geotechnical parameterization within much of the tested ranges. In particular, the sub-spaces along a diagonal line from medium-high values of c′ and low values of φ′ to low values of c′ and high values of φ′ display almost identical AUROC values to the entire parameter space and to those sub-spaces including broad ranges of c′ or broad ranges of φ′ with medium-low values of c′. Only those sub-ranges limited to high values of c′ or low values of c′ and φ′ yield significantly lower AUROC values. These sub-ranges result in poorly patterned relatively non-conservative and extremely conservative predictions, i.e. they display very low and very high FoC values, respectively. In general, the model results are very conservative, indicated by FoC > > 1. At a lower level of AUROC—and a lower level of FoC caused by a higher number of OP pixels—similar patterns are observed in Fig. 5a.
Fig. 5

Results of tests A1–A4 in terms of model performance (AUROC) and factor of conservativeness (FoC, in italic letters). See Fig. 3 for the configuration of the parameter space

Varying d as a function of the topographic wetness index exerts contrasting effects on the patterns of AUROC, depending on whether the OIA or the ORA is used as reference. With the ORA as reference (Test A4; Fig. 5d), the sub-spaces with low values of c′ perform comparable to test A2 (Fig. 5b). This is not surprising as the influence of d on FOS increases with c′ (with c′ = 0, d has no influence). However, AUROC and also FoC decrease significantly with increasing c′, resulting in a very poor performance associated to those sub-spaces with high c′, and a reduced performance associated to those sub-spaces with broad ranges of c′, compared to Fig. 5b. This trend clearly indicates that most ORA pixels spatially coincide with areas of relatively low topographic wetness index and therefore low values of d (Table 3) resulting in high values of FOS and low values of SFSI in cohesive soils.

The reverse effect occurs when using the entire OIA as reference (test A3; Fig. 5c): many pixels in the lower portions of the landslide polygons coincide with high values of the topographic wetness index. Consequently, d and the resulting values of SFSI are comparatively high for many of the OP pixels, resulting in an improved model performance, compared to the tests A1 – A3 (AUROC ≤ 0.742; Fig. 5b). However, since most of the lower parts of the landslide polygons do most likely not represent release areas, the increased performance represents an artefact of inappropriate assumptions rather than an indicator for model success.

Considering the findings outlined, we identify test A2 as most representative. Even though the full parameter space yields an insignificantly lower value of AUROC than do some of the sub-spaces, there is no basis to support the choice of a particular sub-space in this specific case. The parameter values used and optimized by Guimarães et al. (2003) are mostly located within the parameter sub-spaces with the higher values of AUROC, indicating a certain plausibility of the results (Fig. 5b). Figure 6a shows the spatial patterns of SFSI derived in the tests A1 and A2 with the full parameter space of c′ and φ′. We note that the results of those tests are similar in terms of SFSI, as only the reference information for validation is varied. The same is true for the SFSI maps derived through the tests A3 and A4 (Fig. 6b).
Fig. 6

SFSI maps resulting from the tests a A1 and A2; b A3 and A4 and c B, in each case relating to the full parameter space of c‘ and φ‘. MEA model evaluation area

The spatial patterns of SFIS derived with the sliding surface model of r.slope.stability (test B) are illustrated in Fig. 6c. Applying the full parameter space of c′ and φ′ along with constant soil depth and the ORA as reference, the associated value of AUROC is almost identical to the value yielded with the infinite slope stability model (0.735 vs. 0.734 in test A2). Thereby, the results yielded with the sliding surface model are more conservative: FoC = 59.5, compared to a value of 48.3 yielded with the infinite slope stability model (Fig. 5b).

Test C: geohydraulic parameterization

Figure 7 illustrates the performance (AUROC) and conservativeness (FoC) of the model results for the various parameter sub-spaces of K s and d i. Firstly, we note that the results are largely insensitive to the four assumptions of rainfall duration and hydrograph shape (C1–C4): the patterns yielded are identical for all four scenarios, even though the numbers vary slightly. Within each scenario, the model performance responds highly sensitive to variations of K s and d i: it peaks at AUROC = 0.719–0.724 for the upper sub-range of the hydraulic conductivity (K s  = 10−5–10−4 m s−1) and the lower sub-range of the initial depth of the water table (d i = 0–1 m). However, the model performance drops only slightly when the full range of both parameters K s and d i is applied (AUROC = 0.711–0.712). Figure 8 presents the SFSI maps produced in test C1 with the full space of K s and d i. The SFSI maps resulting from tests C2, C3 and C4 are almost similar to the map resulting from test C1 and are therefore not shown.
Fig. 7

Results of tests C1–C4 in terms of model performance (AUROC) and factor of conservativeness (FoC, in italic letters). See Fig. 3 for the configuration of the parameter space

Fig. 8

SFSI map resulting from test C1with the full parameter range of K s and d i. MEA model evaluation area

Constraining the model input to the lower ranges of hydraulic conductivity or to deeper initial water tables leads to a significant drop in the model performance. Considering K s  ≤ 10–5.5 leads to model failure (AUROC = 0.494), independently of the range applied for d i and the rainfall scenario. In this case, FoC = 3.9 (blue font colour in Fig. 7). As expected, FoC is highest for the configurations with high K s and shallow d i and lowest for the configurations with low K s and deep d i. Its maximum coincides with the best model performance (FoC = 48.0–48.9).

These outcomes reflect the fact that, with K s  ≤ 10–5.5, too little water propagates through the soil to substantially influence slope stability. The effect is similar with higher values of K s if the initial water table is too deep. A shallower initial water table and higher values of K s facilitate increased values of u over broad parts of the study area and, consequently, lead to less stable slopes (Eq. 2) and higher values of FoC. Only combinations of high K s and deep di lead to a sufficient signal to reproduce the observed landslide release patterns with a fair performance. As for tests A and B, all results are very conservative also for test C (FoC > > 1).

Test D: statistical model

The statistical model yields an average AUROC value of 0.737 (values of 0.736 and 0.738 for the two catchments) whilst, as prescribed by the approach chosen, FoC ≈ 1. The model performance corresponds remarkably well to the performance of the physically based models (tests A2 and B in particular), underlining the fact that the slope angle strongly dominates also the pattern of SFSI derived with the physically based models (Fig. 9).
Fig. 9

SFSI map resulting from test D. MEA model evaluation area

Discussion

We have demonstrated that the performance of the physically based-derived slope failure susceptibility index SFSI in our study area reacts conditionally sensitive to variations in the considered spaces of selected geotechnical and geohydraulic input parameters and state variables. Those parameter configurations yielding insufficient pattern in terms of simulated landslide vs. non-landslide areas lead to a significantly poorer performance. With regard to the geotechnical information, comparable AUROC values are displayed throughout much of the parameter space considered relevant for the study area (Guimarães et al. 2003), except for those sub-spaces with low c′ and low φ′ (μSFSI close to 1) and those areas with high c′ and high φ′ (μSFSI close to 0). This constellation underlines a well-known negative relationship between c′ and φ′. Model performance in terms of AUROC responds very sensitive to variations in K s and d i within the tested ranges but insensitive to the variations in the rainfall scenarios applied. Whilst the findings for the geotechnical parameters are claimed to be broadly valid, those for K s and d i may strongly depend on the assumed rainfall duration and intensity in relation to the water capacity of the soil. In this sense, the pattern displayed in Fig. 7 might change for different rainfall events.

Our findings suggest that any further parameter optimization efforts in terms of AUROC may be obsolete: the pattern of SFSI derived with the entire parameter space performs approximately as well in reproducing the observed landslide areas as the patterns of SFSI derived with various sub-spaces do. Applying broad ranges of the key parameters for physically based catchment-scale landslide susceptibility modelling is on the “safe” side as it yields results comparable in quality to those derived with the best-fit narrower ranges. Acknowledging the fact that geotechnical and geohydraulic parameters are spatially highly variable, uncertain and often poorly known, applying a narrow parameter space—or even a singular combination of parameters—bears a considerable risk to be off target. The direct effects of the vegetation (not accounted for in the present study) increase the level of uncertainty particularly in forested areas.

The conservativeness of the result in terms of FoC strongly depends on the parameter sub-spaces used as input. μSFSI is generally much higher than r OP, indicating that the model results tend to be very conservative. The ideal result should correspond to FoC = 1. Theoretically, this could be achieved by increasing the upper thresholds of the geotechnical parameters, i.e. to make the parameter spaces considered broader. However, substantially higher parameter thresholds are not realistic for the soil materials involved. We believe that the key for bringing μSFSI in line with r OP consists in appropriately capturing the fine-scale spatial variation of the geotechnical parameters: sliding surfaces most likely coincide spatially with geotechnically susceptible areas, layers or interfaces, spaced in a more or less irregular way. We consider it almost impossible to parameterize such patterns in a deterministic way. In this context, we note that in Figs. 6 and 8, some landslides coincide spatially with areas of low SFSI. Such mispredictions are most probably related to localized patches of low soil strength, increased water input or increased hydraulic conductivity or the effects of the vegetation. Whilst the variation in the local slope angle explains much of the pattern of SFSI, the residual part is most likely explained by fine-scale spatial variations of the soil and, possibly, the vegetation.

Consequently, physically based landslide susceptibility maps can be produced with a minimum amount of geotechnical data but in this case only provide relative results. There is no benefit in dedicating major resources to the detailed investigation of the geotechnical and geohydraulic parameters for catchment-scale landslide susceptibility maps without accounting in detail for the spatial variation of those parameters. Various studies emphasize the major challenges in capturing the spatial variability of the key parameters such as c′ and φ′ (Mergili et al. 2015), K s (Mesquita et al. 2002, 2007; Mesquita and Moraes 2004) or soil depth (McBratney et al. 2003; Frohn and Müller 2015). More precisely, at this time, there are no means to appropriately regionalize the key input parameters of slope stability models. We have demonstrated that ad-hoc assumptions of parameter variations (soil depth) may result in a decreased model performance or, in combination with inappropriate reference data (an inventory including transit and deposition areas), may pretend an improved model performance. Notwithstanding any possible future progress in this field, we highlight two strategies to deal with the challenges identified:
  1. 1.

    Accepting the limitations described and interpreting the outcomes of physically based landslide susceptibility models in a relative way. The SFSI as suggested in the present work is one possibility to do so; other ways were introduced earlier with SHALSTAB (Montgomery and Dietrich 1994) or SINMAP (Pack et al. 1998). In principle, all slope stability software tools can be used to derive relative indices from multiple results.

     
  2. 2.

    Using probabilistic approaches to deal with the spatial parameter variation, i.e. resulting in the identification of the possible size of weak regions (Fan et al. 2016). Fibre bundle models may then be used to simulate the associated patterns of slope failures (Cohen et al. 2009). However, this method also relies on various assumptions of spatial parameter variability.

    One may argue that also statistical models—employing a black box in terms of relating predictor layers to a landslide inventory—would do the job of producing relative landslide susceptibility maps. In fact, those approaches may be considered a more honest strategy, compared to physically based calculations with uncertain or even unknown geotechnical and geohydraulic parameters. We have shown that even a simplistic statistical model—employing the local slope as the only predictor layer—performs comparable to the more complex physically based models used. This finding reflects the dominant effect of the slope also in the physically based models, as long as the majority of the other key parameters is assumed constant in space. It reminds of the statement of Box (1976) that it would be simple and evocative models pushing science forward rather than over-elaborated, over-parameterized ones. However, it is clear that statistical models would hardly do the work for dynamic analyses such as—with the data usually available—predicting the slope stability response to a particular rainfall event.

     

Conclusions

We have tested the sensitivity of catchment-scale slope stability model results to variations in the geotechnical and geohydraulic parameters. In contrast to many previous studies, we have focused on parameter spaces instead of combinations of parameter values. The results produced with broad parameter sub-spaces show comparable levels of performance in terms of AUROC to those produced with narrow sub-spaces, even though the results vary considerably in terms of FoC. In general, the SFSI maps are classified as very conservative (FoC > > 1). It seems obsolete to optimize the parameters tested by means of statistical procedures.

Considering the uncertainty inherent in all geotechnical and geohydraulic data, and the impossibility to capture the spatial distribution of the parameters by means of laboratory tests in sufficient detail, we conclude that landslide susceptibility maps yielded by catchment-scale physically based models should not be interpreted in absolute terms. We suggest that efforts to develop better strategies for dealing with the uncertainties in the spatial variation of the key parameters should be given priority in future slope stability modelling efforts. Even though we consider it likely that many of our results are valid for most types of landslides or geological settings, more tests including a broad spectrum of situations would be necessary to confirm all statements.

Notes

Acknowledgements

Open access funding provided by University of Natural Resources and Life Sciences Vienna (BOKU). We are grateful to Prof. Renato Guimarães for kindly providing the DEM and the landslide inventory. Further, we thank National Department of Transportation Infrastructure (DNIT, Brazil) for enabling this work and Capes (Coordination of Higher Education Training, Brazil) for their generous support.

References

  1. Baum RL, Savage WZ, Godt JW (2008) TRIGRS—a Fortran program for transient rainfall infiltration and grid-based regional slope-stability analysis, Version 2.0. USGS Open File Report 2008–1159. https://pubs.usgs.gov/of/2008/1159/downloads/pdf/OF08-1159.pdf. Accessed 07 December 2015
  2. Box GE (1976) Science and statistics. J Am Stat Assoc 71:791–799. doi: 10.2307/2286841 CrossRefGoogle Scholar
  3. Burton A, Bathurst JC (1998) Physically based modelling of shallow landslide sediment yield at a catchment scale. Environ Geol 35(2):89–99. doi: 10.1007/s002540050296 CrossRefGoogle Scholar
  4. Carslaw HS, Jaeger JC (1959) Conduction of heat in solids. Oxford University Press, New YorkGoogle Scholar
  5. Coelho Netto AL (2005) Interface florestal-urbana e os desastres naturais relacionados à água no maciço da Tijuca: desafios ao planejamento urbano numa perspectiva sócio- ambiental. Revista do Departamento de Geografia 16:46–60. doi: 10.7154/RDG.2005.0016.0005 Google Scholar
  6. Cohen D, Lehmann P, Or D (2009) Fiber bundle model for multiscale modeling of hydromechanical triggering of shallow landslides. Water Resour Res 45:W10436. doi: 10.1029/2009WR007889 CrossRefGoogle Scholar
  7. Conti A (2012) Desenvolvimento de um modelo matemático transiente para previsão de escorregamentos planares em encostas. Dissertation, PUC-RioGoogle Scholar
  8. Duan Q, Sorooshian S, Gupta V (1992) Effective and efficient global optimization for conceptual rainfall-runoff models. Water Resour Res 28:1015–1031. doi: 10.1029/ 91WR02985 CrossRefGoogle Scholar
  9. Duncan JM, Wright SG (2005) Soil strength and slope stability. Wiley, USAGoogle Scholar
  10. Eberhart RC, Kennedy J (1995) A new optimizer using particle swarm theory. In Proceedings of the Sixth International Symposium on Micro Machine and Human Science 1:39–43. doi:  10.1109/MHS.1995.494215
  11. El-Ramly H, Morgenstern NR, Cruden DM (2005) Probabilistic assessment of stability of a cut slope in residual soil. Géotechnique 55:77–84. doi: 10.1680/geot.2005.55.1.77 CrossRefGoogle Scholar
  12. Fan L, Lehmann P, Or D (2016) Effects of soil spatial variability at the hillslope and catchment scales on characteristics of rainfall-induced landslides. Water Resources Research 52(3):1781-1799Google Scholar
  13. Fernandes NF, Guimarães RF, Gomes RAT, Vieira BC, Montgomery DR, Greenberg H (2001) Condicionantes Geomorfológicos dos Deslizamentos nas Encostas: Avaliação de Metodologias e Aplicação de Modelo de Previsão de Áreas Susceptíveis. Revista Brasileira de Geomorfologia 2(1):51–71. doi: 10.20502/rbg.v2i1.8 CrossRefGoogle Scholar
  14. Fischer JT (2013) A novel approach to evaluate and compare computational snow avalanche simulation. Nat Hazards Earth Syst Sci 13(6):1655–1667. doi: 10.5194/nhess-13-1655-2013 CrossRefGoogle Scholar
  15. Formetta G, Capparelli G, Versace P (2015) Evaluating performances of simplified physically based models for landslide susceptibility. Hydrol Earth Syst Sci Discuss 12:13217–13256. doi: 10.5194/hessd-12-13217-2015 CrossRefGoogle Scholar
  16. Frohn D, Müller J (2015) Spatial distribution of clay minerals and soil depth in the Collazzone area, Umbria, central Italy. Master thesis, University of Natural Resources and Life Sciences (BOKU), ViennaGoogle Scholar
  17. Galindo MSV (2013) Desenvolvimento de uma Metodologia para Determinação da Viscosidade de Solos. Dissertation, PUC-Rio. doi:  10.17771/PUCRio.acad.22977
  18. Galindo MSV, De Campos TMP (2014) Desenvolvimento de uma Metodologia para Determinação da Viscosidade de Solos. XVII Congresso de Mecânica dos Solos e Engenharia Geotécnica, Goiânia - GO - BrasilGoogle Scholar
  19. Godt JW, Baum RL, Savage WZ, Salciarini D, Schulz WH, Harp EL (2008) Transient deterministic shallow landslide modeling: requirements for susceptibility and hazard assessments in a GIS framework. Eng Geol 102:214–226. doi: 10.1016/j.enggeo.2008.03.019 CrossRefGoogle Scholar
  20. GRASS Development Team (2016) Geographic resources analysis support system (GRASS) software. Open Source Geospatial Foundation Project. http://grass.osgeo.org. Accessed 11/05/2016
  21. Griffiths DW, Fenton GA (2004) Probabilistic slope stability analysis by finite elements. J Geotech Geoenviron 130(5):507–518. doi: 10.1061/(ASCE)1090-0241(2004)130:5(507) CrossRefGoogle Scholar
  22. Griffiths DV, Huang J, Dewolfe GF (2011) Numerical and analytical observations on long and infinite slopes. Int J Numer Anal Methods Geomech 35(5):569–585. doi: 10.1002/nag.909 CrossRefGoogle Scholar
  23. Guimarães RF (2000) A modelagem matemática na avaliação de áreas de risco a deslizamentos: o exemplo das bacias dos rios Quitite e Papagaio (RJ). PhD Thesis, Federal University of Rio de JaneiroGoogle Scholar
  24. Guimarães RF, Montgomery DR, Greeberg HM, Fernandes NF, Gomes RAT, Carvalho Júnior OA (2003) Parametrization of soil properties for a model of topographic controls on shallow landsliding: application to Rio de Janeiro. Eng Geol 69:99–108. doi: 10.1016/S0013-7952(02)00263-6 CrossRefGoogle Scholar
  25. Guimarães RF, Gomes RAT, Carvalho Júnior OA, Martins ES, Oliveira SN, Fernandes NF (2009) Análise temporal das áreas susceptíveis a escorregamentos rasos no Parque Nacional da Serra dos Órgãos (RJ) a partir de dados pluviométricos. Revista Brasileira de Geociências 39(1):190–198. http://rbg.sbgeo.org.br/index.php/rbg/article/view/1451. Accessed: 30/11/2015
  26. Guzzetti F (2006) Landslide hazard and risk assessment. PhD Thesis, University of BonnGoogle Scholar
  27. Guzzetti F, Carrara A, Cardinali M, Reichenbach P (1999) Landslide hazard evaluation: a review of current techniques and their application in a multi-scale study, Central Italy. Geomorphology 31:181–216. doi: 10.1016/S0169-555X(99)00078-1 CrossRefGoogle Scholar
  28. Hay LE, Leavesley GH, Clark MP, Markstrom SL, Viger RJ, Umemoto M (2006) Step wise, multiple objective calibration of a hydrologic model for a snowmelt dominated basin. J Am Water Resour Assoc:877–890. doi: 10.1111/j.1752-1688.2006.tb04501.x
  29. Hovland HJ (1977) Three-dimensional slope stability analysis method. J Geotech Eng Div 103(9):971–986Google Scholar
  30. Hurtado Espinoza LO (2010) Avaliação do Potencial de Liquefação de Solos Coluvionares do Rio de Janeiro. Dissertation, PUC-Rio. doi:  10.17771/PUCRio.acad.17520
  31. Iverson RM (2000) Landslide triggering by rain infiltration. Water Resour Res 36(7):897–1910. doi: 10.1029/2000WR900090 CrossRefGoogle Scholar
  32. Jia N, Mitani Y, Xie M, Djamaluddin I (2012) Shallow landslide hazard assessment using a three-dimensional deterministic model in a mountainous area. Comput Geotech 45:1–10. doi: 10.1016/j.compgeo.2012.04.007 CrossRefGoogle Scholar
  33. McBratney AB, Mendonça Santos ML, Minasny B (2003) On digital soil mapping. Geoderma 117:3–52. doi: 10.1016/S0016-7061(03)00223-4 CrossRefGoogle Scholar
  34. Mergili M, Chu H-J (2015) Integrated statistical modelling of spatial landslide probability. Nat Hazards Earth Syst Sci Discuss 3:5677–5715. doi: 10.5194/nhessd-3-5677-2015 CrossRefGoogle Scholar
  35. Mergili M, Fellin W, Moreiras SM, Stötter J (2012) Simulation of debris flow in the Central Andes based on open source GIS: possibilities, limitations, and parameter sensitivity. Nat Hazards 61:1051–1081. doi: 10.1007/s11069-011-9965-7 CrossRefGoogle Scholar
  36. Mergili M, Marchesini I, Alvioli M, Metz M, Schneider-Muntau B, Rossi M, Guzzetti F (2014a) A strategy for GIS-based 3-D slope stability modelling over large areas. Geosci Model Dev 7:2969–2982. doi: 10.5194/gmd-7-2969-2014
  37. Mergili M, Marchesini I, Rossi M, Guzzetti F, Fellin W (2014b) Spatially distributed three-dimensional slope stability modelling in a raster GIS. Geomorphology 206:178–195. doi: 10.1016/j.geomorph.2013.10.008 CrossRefGoogle Scholar
  38. Mergili M, Marchesini I, Rossi M, Alvioli M, Schneider-Muntau B, Cardinali M, Ardizzone F, Fiorucci F, Valigi D, Santangelo M, Bucci F, Guzzetti F (2015) Considering parameter uncertainty in a GIS-based sliding surface model for large areas. In Schweckendiek T, van Tol AF, Pereboom D, van Staveren MT, Cools PMCBM (eds) Geotechnical Safety and Risk V (Proceedings of the 5th International Symposium for Geotechnical Safety and Risk (ISGSR2015), Rotterdam, 13–16 October 2015): 952–957. IOS Press. doi:  10.3233/978-1-61499-580-7-952
  39. Mesquita MGBF, Moraes SOA (2004) Dependência entre a condutividade hidráulica saturada e atributos físicos do solo. Ciência Rural 34(3):963–969. doi: 10.1590/S0103-84782004000300052 CrossRefGoogle Scholar
  40. Mesquita MGBF, Moraes SO, Corrente JE (2002) More adequate probability distributions to represent the saturated soil hydraulic conductivity. Sci Agric 59(4):789–793. doi: 10.1590/S0103-90162002000400025 CrossRefGoogle Scholar
  41. Mesquita MGBF, Moraes SO, Peruchi F, Tereza MC (2007) Alternativa para caracterização da condutividade Hidráulica saturada do solo utilizando probabilidade de ocorrência. Ciência Agrotécnica 31(6):1605–1609. doi: 10.1590/S1413-70542007000600001 CrossRefGoogle Scholar
  42. Milledge DG, Griffiths DV, Lane SN, Warburton J (2012) Limits on the validity of infinite length assumptions for modelling shallow landslides. Earth Surface Process and Landforms 37:1158–1166. doi: 10.1002/esp.3235 CrossRefGoogle Scholar
  43. Miqueletto M, Vargas Jr. EA (2009) Avaliação tridimensional da estabilidade de encostas em escala de bacia de drenagem através do método de talude infinito incorporando o efeito do fluxo saturado-não saturado. Anais da 5ª Conferencia de Estabilidade de Encosta, São Paulo, SP, BrasilGoogle Scholar
  44. Montgomery DR, Dietrich WE (1994) A physically based model for the topographic control on shallow landsliding. Water Resour Res 30:1153–1171. doi: 10.1029/93WR02979 CrossRefGoogle Scholar
  45. Moore ID, Grayson RB, Ladson AR (1991) Digital terrain modeling—a review of hydrological, geomorphological, and biological applications. Hydrol Process 5:3–30. doi: 10.1002/hyp.3360050103 CrossRefGoogle Scholar
  46. Muntohar AS, Liao H-J (2010) Rainfall infiltration: infinite slope model for landslides triggering by rainstorm. Nat Hazards 54:967–984. doi: 10.1007/s11069-010-9518-5 CrossRefGoogle Scholar
  47. Neteler M, Mitasova H (2008) Open source GIS: a GRASS GIS approach. Springer, New York. doi: 10.1007/978-0-387-68574-8 CrossRefGoogle Scholar
  48. Pack RT, Tarboton DG, Goodwin CN (1998) The SINMAP approach to terrain stability mapping. 8th Congress of the International Association of Engineering Geology, Vancouver, BC. doi: 10.1.1.41.5799Google Scholar
  49. Park DW, Nikhil NV, Lee SR (2013) Landslide and debris flow susceptibility zonation using TRIGRS for the 2011 Seoul landslide event. Natural Hazards Earth System Sciences 13:2833–2849. doi: 10.5194/nhess-13-2833-2013
  50. Petrovic I (2008) Probabilistic stability analysis of sanitary landfill Jakusevec. Proceedings of the 1st Middle European Conference on Landfill Technology, Budapest, HungaryGoogle Scholar
  51. R Core Team (2016) R: a language and environment for statistical computing, R foundation for statistical computing. https://cran.r-project.org/doc/manuals/r-release/fullrefman.pdf. Accessed: 11/05/2016
  52. Saltelli A, Annoni P (2010) How to avoid a perfunctory sensitivity analysis. Environmental Modelling and Soft ware 25:1508–1517. doi: 10.1016/j.envsoft.2010.04.012 CrossRefGoogle Scholar
  53. Saxton KE, Rawls WJ (2006) Soil water characteristic estimates by texture and organic matter for hydrologic solutions. Soil Science Society of American Journal 70:1569–1578. doi: 10.2136/sssaj2005.0117 CrossRefGoogle Scholar
  54. Tobutt DC (1982) Monte Carlo simulation methods for slope stability. Comput Geosci 8(2):199–208. doi: 10.1016/0098-3004(82)90021-8 CrossRefGoogle Scholar
  55. Van Westen CJ (2000) The modelling of landslide hazards using GIS. Surveys Geophysics 21:241–255. doi: 10.1023/A:1006794127521 CrossRefGoogle Scholar
  56. Van Westen CJ, Terlien MTJ (1996) An approach towards deterministic landslide hazard analysis in GIS: a case study from Manizales (Colombia). Earth Surfaces Processes Landforms 21:853–868. doi: 10.1002/(SICI)1096-9837(199609)21:9<853::AID-ESP676>3.0.CO;2-C CrossRefGoogle Scholar
  57. VanWesten CJ, Van Asch TWJ, Soeters R (2006) Landslide hazard and risk zonation—why is it still so difficult? Bull Eng Geol Environ 65:167–184. doi: 10.1007/s10064-005-0023-0 CrossRefGoogle Scholar
  58. Vrugt JA, ter Braak CJF, Clark MP, Hyman JM, Robinson BA (2008) Treatment of input uncertainty in hydrologic modeling: doing hydrology backward with Markov chain Monte Carlo simulation. Water Resour Res 44:W00B09. doi: 10.1029/2007WR006720, 2 CrossRefGoogle Scholar
  59. Wang Y, Cao Z, Au SK (2010) Pratical reliability analysis of slope stability by advanced Monte Carlo simulations in spreadsheet. Can Geotech J 48(1):162–172. doi: 10.1139/T10-044 CrossRefGoogle Scholar
  60. Wilkinson PL, Anderson MG, Lloyd DM (2002) An integrated hydrological model for slope stability. Earth Surface Processes Landform 27:1267–1283. doi: 10.1002/esp.409 CrossRefGoogle Scholar
  61. Xie M, Esaki T, Zhou G, Mitani Y (2003) Three-dimensional stability evaluation of landslides and a sliding process simulation using a new geographic information systems component. Environ Geol 43:503–512. doi: 10.1007/s00254-002-0655-3 Google Scholar
  62. Xie M, Esaki T, Cai M (2004a) A time–space based approach for mapping rainfall induced shallow landslide hazard. Environ Geol 46:840–850. doi: 10.1007/s00254-004-1069-1 CrossRefGoogle Scholar
  63. Xie M, Esaki T, Cai M (2004b) A GIS-based method for locating the critical 3D slip surface in a slope. Comput Geotech 31:267–277. doi: 10.1016/j.compgeo.2004.03.003 CrossRefGoogle Scholar
  64. Xie M, Esaki T, Qiu C, Wang C (2006) Geographical information system-based computational implementation and application of spatial three-dimensional slope stability analysis. Comput Geotech 33:260–274. doi: 10.1016/j.compgeo.2006.07.003 CrossRefGoogle Scholar

Copyright information

© The Author(s) 2016

Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.

Authors and Affiliations

  1. 1.National Department of Transportation Infrastructure (DNIT)Brasília – DFBrazil
  2. 2.Department of Civil EngineeringUniversity of BrasíliaBrasília – DFBrazil
  3. 3.Geomorphological Systems and Risk Research, Department of Geography and Regional ResearchUniversity of ViennaViennaAustria
  4. 4.Institute of Applied GeologyUniversity of Natural Resources and Life Sciences (BOKU)ViennaAustria

Personalised recommendations