Abstract
This paper concerns a regional scale warning system for landslides that relies on a decisional algorithm based on the comparison between rainfall recordings and statistically defined thresholds. The latter were based on the total amount of rainfall, which was cumulated considering different time intervals: 1-, 2- and 3-day cumulates took into account the critical rainfall influencing shallow movements, whilst a variable time interval cumulate (up to 240 days) was used to consider the triggering of deep-seated landslides in low permeability terrains. A prototypal version of the model was initially set up to define statistical thresholds. Then, thresholds were calibrated using a database of past georegistered and dated landslides. A validation procedure showed that the calibration highly improves the results and therefore the model was integrated in the regional warning system of Emilia Romagna (Italy) for civil protection purposes. The proposed methodology could be easily implemented in other similar regions and countries where a sufficiently organised meteorological network is present.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
In Italy, landsliding is a recurrent phenomenon responsible for casualties, destruction of assets and infrastructures and major economical loss (Guzzetti 2000). Since rainfall represents the most common triggering factor, many Italian civil protection agencies are setting up warning systems based on the interaction between rainfall and landslides. These agencies are responsible for large territories (e.g. regions or large subdivisions such as provinces), therefore they cannot rely on physically based approaches because of the difficulty of defining the exact spatial and temporal variation of the many involved factors (rainfall variation in space and in time, effect of vegetation, mechanic and hydraulic properties of both bedrock and soil layer). As a consequence, physically based approaches can effectively be applied only over small sites (Segoni et al. 2009), while at regional scale the most diffused methodology is the use of black box models based on empirical or statistical rainfall thresholds. The term ‘black box’ refers to a methodology in which the complex physical processes involved in landslide initiation are ignored (because too difficult to correctly calibrate over large areas) and a more simple and functional empirical correlation is found between the primarily cause (rainfall) and the effect (landslide). Amongst all the factors influencing the triggering of landslides, rainfall is—for instance—one of the most important and the easiest to correctly quantify, e.g. using rain gauges or radar measurements. The majority of the black box approaches are based on an empirical or statistical study of the rainfall characteristics that in the past led to landslides initiation (Caine 1980; Wieczorek 1996; Aleotti 2004; Guzzetti et al. 2008; Brunetti et al. 2010). Such study is aimed at deriving a mathematical equation which represents the threshold beyond which landslides have occurred in the past, and it is assumed they will happen in the future.
The most diffused thresholds are based on the intensity and duration of critical precipitation (Caine 1980; Aleotti 2004; Guzzetti et al. 2008), but also cumulative rain is widely used (Innes 1983; Terlien 1998; Hong et al. 2005; Cardinali et al. 2006). The choice of the right parameters for defining thresholds depends primarily on the landslide typology. There is a general agreement in recognizing that debris flows and shallow landslides are preferentially triggered by short and intense rainfalls (Campbell 1974; Crosta 1998), while deep-seated landslides are more commonly connected with prolonged and less intense rainfall events (Bonnard and Noverraz 2001). Therefore, when trying to predict shallow movements, the study of critical rainfall, defined as in Aleotti (2004), is essential. On the contrary, when studying deep-seated slope movements, the antecedent rain plays a decisive role, but sometimes it can be difficult to assess to which extent a landslide can be influenced by past rainfall events. In other words: How far back in time rainfall has to be considered? In various empirical modeling, very different time intervals have been taken into account, ranging from a few days (Kim et al. 1991; Heyerdahl et al. 2003) to a few months (De Vita 2000; Galliani et al. 2001; Cardinali et al. 2006).
In those areas affected by both shallow and deep-seated landslides, it is essential to define a methodology which could be flexible enough to encompass both of them. This paper presents the results of a co-funded research by the Civil Protection Agency of the Emilia Romagna Region, during which a model was developed for the management of the risk related to rainfall induced landslides (both shallow and deep seated). The developed system is named SIGMA (Sistema Integrato Gestione Monitoraggio Allerta, “Integrated service for the managing and monitoring of the alert”) and it is based on a set of rainfall thresholds, whose overcoming defines different alert levels in accordance with the Regional Civil Protection guidelines. The model was implemented in the regional warning system and it could be easily exported in other areas equipped with an automated network of rain gauges.
Study area
Geographical and geological settings
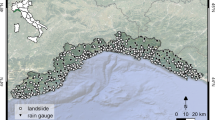
The Emilia Romagna Region (Northern Italy) is bordered by the Apennines mountains on the south and on the west, by the Adriatic Sea on the east and by the Po River on the north. The northern and eastern portions of its territory are a wide flat area constituted by the alluvial plain of the Po, the largest Italian river. Those portions of the region were not considered in the present work, which focuses only on landslide prone areas. The latter are located in the southern and western portions of the region, occupied by the fold and trust belt of the Apennines, whose maximum altitude reaches 2,165 m (Fig. 1).
The very complex geological setting of the study area is connected to the building of the Apennine Range, whose evolution began in the Cretaceous when two separated continental blocks (the European plate and the Adria microplate) collided and started the closing of the ocean called Tethys (Vai and Martini 2001). The present setting was assumed during the Pleistocene, after a rotation and migration toward the northeast due to the opening of the Balearic Basin and the Tyrrhenian Sea. During the Apennine evolution, an alternation between compressive and distensive geodynamic forces took place (and sometimes coexisted) causing a thrust and fold belt with a very complex tectonic and geological setting. In the study area, the Apennines belt is constituted chiefly by turbidite deposits, which in turn consist of alternating massive rocks (mainly sandstones and calcarenites) and pelitic layers of variable thickness (Vai and Martini 2001). Argillaceous geological formations are abundant as well, and during the Holocene, they were extensively affected by large landslides with an intermittent behavior.
Nowadays, the studied area is subject to a wide variety of landslide typologies, but the most frequent phenomena are rotational–translational slides (affecting mainly flysch), slow earth flows (occurring in clayey lithologies) and complex movements (typically rotational failures at the head progressively changing into translational movements throughout the body and toe) (Bertolini and Pellegrini 2001; Bianchi and Catani 2002). Rapid shallow landslides are less recurrent but their frequency is markedly increasing in the last few years (Martina et al. 2010). This could be connected to the recent climatic trends in the Mediterranean area, which are characterized by shortest and more intense rainfalls (Floris et al. 2010). In general, the main triggering factor of all the Emilia Romagna landslides is rainfall. Two different kinds of precipitations can be associated with the initiation of different landslide typologies: debris flows and shallow landslides are usually triggered by short but exceptionally intense rainfalls, while deep-seated landslides and earthflows have a more complex response to rainfalls and are mainly influenced by moderate but exceptionally prolonged (even up to 6 months) periods of rainfalls (Ibsen and Casagli 2004; Benedetti et al. 2005).
The study area is characterized by a typical Mediterranean climate: warm and dry summers (approximately from May to October) and mild/cool and wet winters (approximately from November to April), with a well-defined rainfall regime (Fig. 2).
National and regional civil protection framework
In Italy, the civil protection system is organized as a national service, in force of the 225/1992 Law. This implies that the task is entrusted to the whole state organization, from the governmental bureaus to municipalities; in other words, several agencies and public bodies are involved in the civil protection organization, according to the principle of subsidiarity.
This planning was strengthened in the recent years, according to the general process of devolution from the central government to the regions. At the civil protection organizing level, this led to the establishment of a network of regional functional centers, coordinated by a national one. These centers are in charge of all the civil protection tasks: monitoring, prevention and emergency plans.
In particular, the functional centers collect and elaborate the parameters concerning different hazards to generate real-time risk scenarios. The raw data and their analysis are provided by a network of scientific and technical institutions (called centers of competence) that support the risk management and decisional processes (Bertolaso et al. 2009).
The Regional Functional Centers process environmental data in real time, and the results feed the scenario models of the different types of risks. The main task of the centers of competence is to create and improve these models, in order to define a set of alert levels for the different phenomena and triggering factors (Del Carmen and Siccardi 2010). The reaching of specific thresholds, depending on the event (for instance rainfall and ground displacement for the landslide risk), leads to the issuing of warnings, defined in a system of alert levels. Each level implies different emergency plans, from the involvement of mayors, local and technical agencies to evacuation orders in the most critical cases. The variability and distribution of natural hazards in Italy (meteorological events, earthquakes, volcanic eruptions, landslides, wild fires and others) involved the creation of specific alert systems in different regions and for different risk scenarios.
In this framework, the Emilia Romagna region was a forerunner. From the 1980s an operative approach to the civil protection was established, with the planning of some alert systems (Egidi 1995); for this reason, the Emilia Romagna’s organization is nowadays in the lead. The operative system for flood and landslide risks is currently based on the division of the regional land in eight districts, called alert zones; these areas have been defined following different criteria, both geographical and administrative. The mean extension of the alert zones is about 3,000 km2, so the result is a mid-scale approach that represents a compromise between operational and scientific constraints.
The alert zones that include up to 20 municipalities can be further subdivided in plain and mountain areas, obtaining a more detailed splitting up—the monitoring and forecast data are referred to these subsequent areas. Weather, hydrological, hydrogeological and hydraulic models fed by these data are continuously implemented in each alert zone (or sub-zone), and a bulletin is released twice a day. To this end, the reference is a four-level alert scale (absent, ordinary, moderate, high), and when a threshold is exceeded in one or more zones, a more detailed reporting activity is due.
This paper illustrates some parts of the model for the landslide risk and early warning, built in the framework of the described operational system.
Materials and methods
Data sources
First of all, the study area was partitioned into 19 territorial units (TU), chiefly defined on the basis of different physiographic and environmental features (meteorological, lithological and geographical data) following the approach of previous works (Bertolini and Pellegrini 2001; Ibsen and Casagli 2004; Benedetti et al. 2005) (Fig. 3). However, TU boundaries always match with administrative borders (limits of municipalities); in many cases, these correspond also with physiographic limits (mountain divides), but that is not a general rule. This choice could be considered as a critical one from a scientific point of view but, considering the civil protection organizing structure, it grants a more efficient activation of the response, there is an evident overlapping between these TUs and the above mentioned alert zones.
For each TU, an automated rain gauge was chosen to be used for the calibration of the model and, in the operative scenario, for the monitoring of the TU as well. In order to select the most proper rain gauges, the following criteria were considered: (1) presence of a long historical series of rainfall recordings (60 years for the most part of the rain gauges and at least 30 years for the remaining ones), to ease a statistically correct calibration of the model; (2) hourly automatic recording; (3) central position among the TU; (4) elevation close to the mean elevation of the landslide prone areas of the TU.
These criteria limit the choice of the rain gauges even if in some TUs there are up to six or seven instruments with all these features; in the majority of TUs the number is very low (one or two). We decided for a unique rain gauge for each TU to standardize the accuracy of the model. This choice certainly represents a limit of the model, but it helps to simplify its management and to better understand its outputs.
Historical rain gauge data were used to calibrate the threshold. All the used pluviometers are connected to a regional network, which automatically collects rainfall measurements at hourly time steps. These data are used by the warning system for monitoring purpose. The coupling with rainfall forecasts coming from Local Area Models Italy (Schraff and Hess 2003) allows the estimation of the future evolution of the risk scenario.
For the calibration and validation of the model, landslide data were collected from the records of the regional Civil Protection Department, and they were organized in a geographical database in shapefile format. Landslides were geo-registered, and the triggering dates were entered in a specific field. When available, additional information was added as well (type of landslide, impact in the environment, reference number of the corresponding official report). The 2004–2007 dataset was used for calibration (888 landslides), while the 2008–2010 period was used for the validation (764 landslides) (Fig. 3).
Methodology
Rainfall probability curves and sigma curves
On the hypothesis that anomalous or extreme values of rainfall are responsible for landslide triggering, in the proposed model the statistical distribution of the rainfall series is analysed, and multiples of the standard deviation (σ) are used as thresholds to discriminate between ordinary and extraordinary rainfall events. The name of the model, SIGMA, reflects the central role of the standard deviations in the proposed methodology.
Starting from the original series of daily precipitation (typically 1951–2009), the time series of cumulated data from 1 to 365 days was built for each TU reference rain gauge. To obtain the n-days time series of a rain gauge, the daily recordings are cumulated at n-day intervals, with an n-day-wide moving window shifting at 1-day time steps along the whole rainfall record of the instrument. The procedure was repeated for each time interval n (1 ≤ n ≤ 365) for each reference rain gauge. All cumulated rainfall series were characterized by an asymmetric distribution; the statistical cumulative distributions tend toward lognormal for short periods and toward normal for long periods, but in neither of the cases these theoretic distributions are fully matched (Benedetti et al. 2005). Therefore, to obtain probability values of not exceeding a given rainfall threshold, the data of the original distributions are adapted to a target function chosen as a model (Goovaerts 1997), in our case the standard Gaussian distribution. This transformation, represented in the graphic of Fig. 4, relates the values of the original series of the cumulative rainfall (z) and distribution target (y = α∙σ), where α is a constant and σ is the standard deviation. Each series of cumulative rainfall is sorted in ascending order
and a standard statistical index (plotting position) is used as cumulative sample frequency:
where 1 ≤ k ≤ n. The transformed value y on the original data z is obtained as the quantile of the distribution target
Once the described transformation has taken effect, we can select a probability of not overcoming and applying the procedure in reverse order; to be more precise, from a particular value of σ or its multiples, we calculated the corresponding cumulative frequency sample and from this value the precipitation (in millimetres) of the original series. Proceeding in the same way for the number of cumulative rainfalls between 1 and 365 days, we built the precipitation curves (σ curves) associated with various probabilities of not being overcome (Fig. 5).
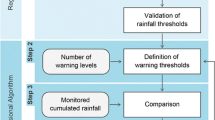
The decisional algorithm of the SIGMA model
The aforementioned σ curves are implemented in a decisional algorithm that constitutes the core of the SIGMA model. The latter operates separately for each TU, and in real-time applications, the model works at daily time steps providing a level of criticality that depends on weather forecasts and rainfall recordings. For each TU, these rainfall amounts are cumulated at increasing time intervals ranging from 1 to 245 days. Such cumulates are compared with the σ curves, which are actually used as thresholds. The decisional algorithm of the SIGMA model was developed to take into account both shallow and deep-seated landslides.
For shallow landslides, the statistical relationship that governs the decisional algorithm can be expressed as:
where C 1–3 is the vector of cumulated rainfall of the daily precipitations P at time of analysis t and S n(Δ) are the thresholds relative to the standard deviation Δ and to cumulative number of days n. In a few words, the algorithm takes into account the cumulative rainfall up to 2 days before the day of analysis (included).
For deep-seated landslides, the algorithm considers the cumulative rainfalls from 4 days up to a period of time that ranges from 63 to 245 days (Eq. 5). The maximum duration of the cumulates depends on the period of the year which is under analysis: during the dry season (from May 1st to October the 31st) the length of the cumulates remains constant (4–63 days), while starting from November 1st it is incremented by one each day, up to a maximum cumulate of 245 days on April the 30th. The use of this variable time window to determine the maximum cumulative rainfall enables to consider the influence of antecedent autumnal rainfall on early spring.
In Eq. 5, the vector C 4–63 + m is incremented by 1 each day (m = 1, 2…, 182) from November 1st to April the 30th. In Eqs. 4 and 5, a given threshold is considered exceeded if at least one element of the vector overcomes it.
The algorithm provides a level of criticality on the basis of which σ curves are exceeded (if any), using the four alert levels adopted in the civil protection procedures: “absent”, “ordinary”, “moderate” and “high” (Fig. 6). The standard sigma curves considered by the algorithm (1.5, 2, 2.5, 3σ) delineate exceptional rainfalls with respect to the characteristics of each TU. The decisional algorithm is organized to provide increasing criticality levels with increasing rainfall amounts.
Model calibration
The correspondence between σ thresholds and expected effects to the ground (landslides) was better constrained performing a calibration with respect to dated landslides of the period 2004–2007. We used an appropriate optimization algorithm that, for the whole calibration period and for each territorial unit, compares the daily model outputs with the corresponding number of occurred landslides. At the first criticality level (ordinary criticality) the algorithm identifies the σ curves that minimize the occurrence of the threshold overcoming in days for which landslides were not reported. An example of the functioning of the optimization algorithm is reported (Fig. 7). At higher criticality levels, the functioning is similar; with a trial and error procedure, thresholds are progressively raised getting rid of unwanted overcoming of threshold. The process stops when the algorithm finds an event characterized by an observed criticality level corresponding to the threshold currently under the calibration procedure.
Visual description of the functioning of the calibration algorithm. Since no landslide was reported in correspondence with this rainfall event, the reference σ value was increased until the cumulative rainfall curve did not overcome the threshold. The procedure is repeated for every event generating a false alarm with the constraint of not reducing the number of the correctly detected landslides
The procedure was repeated separately for each TU; as a result for each of them, the decisional algorithm was provided with specific σ thresholds. It is important to highlight that the calibration procedure does not change the sigma curves, but it chooses a customized set of sigma curves for each TU. On the other hand, the optimized σ curves have been chosen after the calibration, so the original 1.5σ, 2σ, 2.5σ, 3σ curves become different for each TU (Table 1).
Model implementation in the Regional warning system
The described model is nowadays a key element in the Civil Protection Warning System of the Emilia Romagna Region. According to the national legislative and operative framework summarized in the section “National and regional civil protection framework”, this system is based on recorded data and forecasts of rainfall; starting from it, the Civil Protection Service assesses in real time if critical conditions related to certain areas and hydrogeological events are possible.
Twice a day (and with high frequency before and during the passage of rainstorms), the regional service issues a bulletin; overlapping the weather data and the distribution of anthropic elements, an alert level (in a four-stage scale) is associated to each alert zone. In the case of absence of rainfall and when there is no possibility of a significant snowmelt, the landslide alert level is equal to zero (absent criticality).
This operative system is converting from a qualitative to a quantitative approach year by year, at the beginning only for flooding risk (through the implementation of hydrographic models), but in recent years also for landsliding. Now, the SIGMA model is part of the Civil Protection Alert System; for each reference rain gauge, a software combines rainfall recordings from the regional automated network with rainfall forecasts and compares the resulting cumulative rainfalls with the thresholds. In the territorial units where the latter are exceeded, the software provides the corresponding alert level, according to the decisional algorithm (Fig. 6), then the Regional Civil Protection Headquarters weigh up these SIGMA outputs. Normally, at the ordinary criticality level no particular countermeasure is undertaken except for a more frequent monitoring activity, while moderate and high criticalities can be converted in real alerts addressed to municipalities and to other environmental agencies.
Results and validation
The model was validated using landslides and rainfall recordings from the period 2008–2010. In the validation test, the SIGMA model was run with the rainfall recorded by the reference rain gauges in the period 2008–2010, and for each TU, the daily alert level provided by the decisional algorithm was compared with dated and geo-registered landslides from the same period, which were organized in a constantly updated geo database.
Correct predictions (true positives and true negatives) and errors (missed alarms or false negatives and false alarms or false positives) were consequently defined (Table 2) and summarized (Table 3 and Fig. 8) in terms of number of landslides and number of days (in a single TU each day has an alert level but more than a single landslide can happen).
Results showing false alarms (FA), correct predictions (CP) and missed alarms (MA) for the total of territorial units (TU), for the best case (TU 14) and for the worst case (TU 12). See also Table 3
In the validation period 764 landslides occurred, and 84% of them were correctly predicted (i.e. the SIGMA model pointed out a criticality). Taking into account the daily alert level instead of the number of landslides, several statistical attributes were computed to quantitatively define the effectiveness of the SIGMA model; this analysis is reported in the second column of Table 4. In addition, to get a term of comparison to validate these statistical attributes, or, in other words, to validate the robustness of the statistical model, we adopted an algorithmic procedure to generate a random temporal sequence of the Emilia Romagna landslides database, i.e. we considered the real triggering events of landslides, but these were redistributed randomly in the 3 years (2008–2010) of validation. We used a Monte Carlo simulation to obtain a significant value of the parameters a, b, c and d as the average of 1,000 simulations (third column of Table 4).
Discussion
The examination of the results of the model validation revealed a satisfactory correspondence between days with landslides and alert levels provided by the decision-making algorithm. In addition, the comparison between the validation results and the Monte Carlo simulation (Table 4) reveals that the criticality levels provided by the SIGMA model are far from a random distribution.
In general, the model held for both shallow and deep-seated landslides; this result was obtained using two different time intervals for the rainfall cumulates. The “short period” cumulates (1, 2 and 3 days) allowed to correctly identify shallow movements such as soil slips and debris flows, which are usually triggered by short and intense precipitations (Campbell 1974; Crosta 1998). On the other hand, the “long period” cumulates (from 4 to 242 days) accounted for the fundamental role that antecedent rainfall plays in the triggering of deep-seated movements (Bonnard and Noverraz 2001). The double time interval also accounts for the different lithological and hydrogeological conditions that can be found in Emilia Romagna; in permeable terrains, pore water pressure reacts rapidly to rainfall, while in the case of low-permeability terrains the antecedent rainfall is more important. In addition, hydrological response for deep-seated landslides and for terrains with low hydraulic conductivity is governed by more complicated mechanisms which are quite difficult to model with a statistical black box approach. It was so verified that the long-period cumulates generated much more false alarms than the short period cumulates.
The definition of adequate time periods for the rainfall cumulates was not straightforward; several alternative solutions were attempted in the calibration phase, and the adopted version is the one that minimizes errors and is more balanced between missed alarms and false alarms. Reducing the “short period” to 1 or 2 days led to miss several landslide events, while using a longer time interval (up to 4 or 5 days) a state of alert could unnecessarily last for days after the landslide occurrence, providing a high number of false alarms. Concerning the “long period”, the subsequent permanent time intervals were tested: 30, 45, 60, 90, 180 and 365 days. Among these, best results were obtained with the 60-day interval. Missed alarms increased progressively using shorter durations, while longer durations increased the number of false alarms in the dry periods of the year. Therefore, results were further slightly improved introducing the variable time interval discussed in the “Methodology” section.
The percentage of correctly predicted landslides is slightly higher in the validation period (84%) than in the calibration (75%). This outcome highlights the predictive power of the model, and it could have been determined by two concurring factors: (1) in the whole Mediterranean area a general meteorological trend has been recently observed which consists in an increase in frequency and magnitude of high intensity rainfall events (Floris et al. 2010); (2) increased efficiency of the public administration offices in identifying and recording the landslides. In former years (those taken into account for the calibration) the landslide database was incomplete (Benedetti et al. 2005), and we had to discard from the analysis several landslides because any date of occurrence was reported.
The methodology, described in the first part of “Methodology” section (definition of the σ curves and decisional algorithm with nominal σ values), constitutes a prototypal version of the SIGMA model, which was used by the Emilia Romagna Civil Protection in early years when information about landslides were not sufficient to calibrate the model. A similar approach, where landslide occurrence at regional scale is modelled through statistical analyses of rainfall data, is something new in landslide studies. Comparisons could be made more appropriately with some approaches used for solving hydraulic and hydrological problems such as the estimation of river discharges or floods by means of probability curves or by the definition of the return times associated to a certain event (Rossi et al. 1984; Arnel and Gabriele 1988).
After a test period, the calibration procedure described in the last part of the “Methodology” section (model calibration) was specifically designed to lower the number of false alarms leaving the number of correctly predicted landslides unchanged. In the Emilia Romagna case, ordinary level false alarms were reduced by 33.5%, moderate level ones by 31.8% and high-level ones by 88.2%. Despite the coarser results, the “base” uncalibrated version of the SIGMA model has the advantage of requiring only historical rainfall recordings as input data, thus it is easily and rapidly implementable to other contexts. If its use is joined to a recording of the occurred landslides, with time a change to the calibrated version of the SIGMA model can happen smoothly, just adjusting the σ levels in the decisional algorithm (Fig. 5).
Conclusions
In order to forecast the occurrence of landslides at a regional scale, a black box model named SIGMA was defined and was applied to the territory of the Emilia Romagna region, Italy. The model is based on a set of statistical rainfall thresholds defined on the basis of a single parameter (cumulate rainfall). The SIGMA model was implemented in an operative warning system for internal use of the Emilia Romagna regional Civil Protection Department. For each reference rain gauge, a software combines rainfall recordings from the regional automated network with rainfall forecasts and compares the resulting cumulative rainfalls with the thresholds. In the territorial units where the latter are exceeded, the software provides the corresponding alert level according to the decisional algorithm (Fig. 5). The model could theoretically be used to automatically generate warnings and alerts, but longer calibration and validation periods would be required. The direct correspondence between thresholds and warning levels cannot be considered in an absolute sense, but only referring to the spatial distribution of rainfalls and landslides really occurred. Anyhow, at present, the SIGMA model represents a useful tool for civil protection personnel in suggesting an expected warning level to be confirmed or modified by expert evaluations.
The major advantages of the proposed methodology consists of the following:
-
extreme simplicity and rapidity of the forecasting procedure, which can therefore be easily implemented into operational early warning systems;
-
the output of the model can be directly associated to the levels of criticality (absent, normal, moderate, high) to give a quick indication of the warning level even without an expert interpretation;
-
limited number of input data, consisting only in daily precipitation values, easily accessible in countries with sufficiently organized meteorological networks;
-
a calibration of the rainfall thresholds with respect to the severity of landslide events allows to strengthen the correspondence between thresholds and warning levels;
-
all landslide types are taken into account, in particular shallow and deep-seated movements are detected by two different cumulative time intervals.
On the other hand, the accuracy of the results is limited by a few factors, many of which are common to all statistical forecasting models. The number of false alarms is certainly influenced by both the incompleteness and imprecision that characterize all the historical archives of landslides, influencing both the calibration and the validation procedure. Furthermore, the choice of using a single rain gauge for each TU is the most straightforward for an operational civil protection system, but from a scientific point of view, it represents a relevant simplification. Lastly, the model does not differentiate liquid and solid precipitations therefore it does not take into consideration snow accumulation and the subsequent melting process. This last issue will be soon addressed by a simplified model for the snow accumulation/melting, which is currently under study and will be integrated within the SIGMA warning system after a test phase (Martelloni et al. 2010).
References
Aleotti P (2004) A warning system for rainfall-induced shallow failures. Eng Geol 73:247–265
Arnel NW, Gabriele S (1988) The performance of the two-component estreme value distribution in regional flood frequency analysis. Water Resour Res 24(6):879–887
Benedetti A, Casagli N, Bosi V, Dapporto S, Ciolli S, Palmieri M, Zinoni F (2005) Modello statistico per la previsione operativa dei fenomeni franosi nella regione Emilia-Romagna. Boll Soc Geol Italy 124:333–344
Bertolaso G, De Bernardinis B, Bosi V, Cardaci C, Ciolli S, Colozza R, Cristiani C, Mangione D, Ricciardi A, Rosi M, Scalzo A, Soddu P (2009) Civil protection preparedness and response to the 2007 eruptive crisis of Stromboli volcano. Italy J Volcanol Geotherm Res 182(3–4):269–277
Bertolini G, Pellegrini M (2001) The landslides of the Emilia Apennines (Northern Italy) with reference to those which resumed activity in the 1994–1999 period and required civil protection interventions. Quaderni di Geologia Applicata 8(1):27–74
Bianchi F, Catani F (2002) Landscape dynamics risk management in Northern Apennines (Italy). In: Brebbia CA, Zannetti P (eds) Development and application of computer techniques to environmental studies, vol 1. WIT, Southampton, UK, pp 319–328
Bonnard CH, Noverraz F (2001) Influence of climate change on large landslides: assessment of long term movements and trends. In: Proceedings of the International Conference on Landslides causes impact and countermeasures. Gluckauf, Essen, Davos, pp 121–138
Brunetti MT, Peruccacci S, Rossi M, Luciani S, Valigi D, Guzzetti F (2010) Rainfall thresholds for the possible occurrence of landslides in Italy. Nat Hazard Earth Syst Sci 10:447–458
Caine N (1980) The rainfall intensity—duration control of shallow landslides and debris flows. Geogr Ann A 62:23–27
Campbell RH (1974) Debris flows originating from soil slips during rainstorms in Southern California. Quart J Eng Geol 7:339–349
Cardinali M, Galli M, Guzzetti F, Ardizzone F, Reichenbach P, Bartoccini P (2006) Rainfall induced landslides in December 2004 in Southwestern Umbria, Central Italy. Nat Hazard Earth Syst Sci 6:237–260
Crosta GB (1998) Regionalization of rainfall thresholds: an aid to landslide hazard evaluation. Environ Geol 35(2–3):131–145
De Vita P (2000) Fenomeni di instabilità delle coperture piroclastiche dei Monti Lattari, di Sarno e di Salerno (Campania) ed analisi degli eventi pluviometrici determinanti. Quaderni di Geologia Applicata 7:213–235
Del Carmen LM, Siccardi F (2010) A reflection about the social and technological aspects in flood risk management—the case of the Italian Civil Protection. Nat Hazard Earth Syst Sci 10:109–119
Egidi D (1995) The Emilia Romagna approach to civil protection. In: Horlick-Jones T, Amendola A, Casale R (eds) Natural risk and civil protection, E & FN Spon. Chapman & Hall, London, pp 435–446
Floris M, D’Alpaos A, Squarzoni C, Genevois R, Marani M (2010) Recent changes in rainfall characteristics and their influence on thresholds for debris flow triggering in the Dolomitic area of Cortina d’Ampezzo, north-eastern Italian Alps. Nat Hazard Earth Syst Sci 10:571–580
Galliani G, Pomi L, Zinoni F, Casagli N (2001) Analisi meteoclimatologica e soglie di innesco delle frane nella regione Emilia-Romagna negli anni 1994–1996. Quaderni di Geologia Applicata 8:75–91
Goovaerts P (1997) Geostatistics for natural resources evaluation. Oxford University Press, Oxford
Guzzetti F (2000) Landslides fatalities and the evaluation of landslide risk in Italy. Eng Geol 58:89–107
Guzzetti F, Peruccacci S, Rossi M, Stark CP (2008) The rainfall intensity–duration control of shallow landslides and debris flows: an update. Landslides 5(1):3–17. doi:10.1007/s10346-007-0112-1
Heyerdahl H, Harbitz CB, Domaas U, Sandersen F, Tronstad K, Nowacki F, Engen A, Kjekstad O, Devoli G, Buezo SG, Diaz MR, Hernandez W (2003) Rainfall induced lahars in volcanic debris in Nicaragua and El Salvador: practical mitigation. In: Proceedings of International Conference on Fast Slope Movements—Prediction and Prevention for Risk Mitigation, IC-FSM2003. Patron Publication, Naples, pp 275–282
Hong Y, Hiura H, Shino K, Sassa K, Suemine A, Fukuoka H, Wang G (2005) The influence of intense rainfall on the activity of large-scale crystalline schist landslides in Shikoku Island, Japan. Landslides 2(2):97–105
Ibsen M-L, Casagli N (2004) Rainfall patterns and related landslide incidence in the Porretta-Vergato region, Italy. Landslides 1:143–150
Innes JL (1983) Debris flows. Prog Phys Geogr 7:469–501
Kim SK, Hong WP, Kim YM (1991) Prediction of rainfall triggered landslides in Korea. In: Bell DH (ed) Landslides, vol. 2, vol 2. A.A. Balkema, Rotterdam, pp 989–994
Martelloni G, Segoni S, Fanti R, Catani F (2010) Integration of statistical rainfall threshold and snow melt modeling for landslide prediction: applications in the Northern Apennines (Italy). In: International Conference Mountain Risks: bringing science to society, Florence, Italy, pp 73–79
Martina MLV, Berti M, Simoni A, Todini E, Pignone S (2010) Un approccio bayesiano per individuare le soglie di innesco delle frane. In: Picarelli L, Tommasi P, Urcioli G, Versace P (eds) Rainfall-induced landslides: mechanisms, monitoring techniques and nowcasting models for early warning systems, volume 2. CIRAM, Naples
Rossi F, Fiorentino M, Versace P (1984) Two component extreme value distribution for flood frequency analysis. Water Resour Res 20(2):847–856
Schraff C, Hess R (2003) A description of the nonhydrostatic regional Model LM. Available from COSMO web site www.cosmo.model.org. Accessed on Sept 19, 2011
Segoni S, Leoni L, Benedetti AI, Catani F, Righini G, Falorni G, Gabellani S, Rudari R, Silvestro F, Rebora N (2009) Towards a definition of a real-time forecasting network for rainfall induced shallow landslides. Nat Hazard Earth Syst Sci 9:2119–2133
Terlien MTJ (1998) The determination of statistical and deterministic hydrological landslide-triggering thresholds. Environ Geol 35:125–130
Vai GB, Martini IP (2001) Anatomy of an Orogen: the Apennines and adjacent Mediterranean basins. Kluwer Academic Publishers, London, p 636
Wieczorek GF (1996) Landslide triggering mechanism. In: Turner AK, Schuster RL (eds) Landslides investigation and mitigation, special report. Transportation Research Board. National Academy Press, Washington, 247(4):76–89
Acknowledgements
This work has been carried out in the framework of the 2008–2013 project “Scientific and technical support for the Regional Activities of Civil Protection: landslide risk management”, funded by Emilia-Romagna Civil Protection Agency.
Open Access
This article is distributed under the terms of the Creative Commons Attribution Noncommercial License which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This is an open access article distributed under the terms of the Creative Commons Attribution Noncommercial License (https://creativecommons.org/licenses/by-nc/2.0), which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
About this article
Cite this article
Martelloni, G., Segoni, S., Fanti, R. et al. Rainfall thresholds for the forecasting of landslide occurrence at regional scale. Landslides 9, 485–495 (2012). https://doi.org/10.1007/s10346-011-0308-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10346-011-0308-2