Introduction

Wind power is among the fastest-growing renewable energy sectors in Europe, playing a focal role in the transition to a fossil free society. The European Union’s Renewable Energy Directive 2018/2001/EU (RED II 2018) emphasizes the importance of wind energy in achieving these goals. In Finland, the wind energy sector started notably to grow around 2012–2013 and by the of 2023, the number of operational wind turbines reached 1601 generating 14.47 terawatt-hours (TWh) contributing to 18.5% of the country’s total electricity production (FWPA 2024). Technological advancements have facilitated the installation of turbines within forested areas (Sogachev et al. 2020), raising the concerns of audio-visual impact on the landscape (Selkimäki et al. 2024). In Finland, approximately 77% of the land is covered with forest (Kulju et al. 2023) and in recent years there has been a noticeable increase in the construction of wind farms in forested landscapes (FWPA 2024). When initiating new projects, wind farm developers must consider several factors, such as wind resource potential, municipal zoning, proximity to settlements, accessibility to roads and electricity grids, and the soil quality of the site, in addition to land use restrictions (FWPA 2024). It is noteworthy that the construction of a wind turbine requires about one hectare (installation area, cable connection and maintenance roads) which requires clearing, besides there are no restrictions for forest management in the wind farm area (FinSilva 2024).

Simulation and optimization methods are widely employed at the landscape level to address challenges related with land use allocation (Aerts et al. 2005; Zhang et al. 2016), including applications of renewable energy and wind farm siting (Karakostas and Economou 2014; Kamkar and Motieyan 2023). Spatial forest management models and simulation approaches have been developed to address the spatial facets of forestry-related challenges (Heinonen 2007; De Pellegrin Llorente et al. 2017). Spatial interrelationships between stands which are units of forest management and their trade-offs are important considerations in optimizing forest operations during the planning phase (De Pellegrin Llorente et al. 2017). Simulation tools offer the means to study forest development and to produce varying forest management alternatives for individual homogeneous forest stands. Optimization tools can be used to select optimal managements for the stands from the simulated alternatives according to decision makers objectives. For decades in Finland, forest management alternatives have mainly been based on even-aged management, characterised largely by clear cutting and thinnings from below. However, there has been a growing interest in uneven-aged management, characterised thinnings from above without clear cuttings. This approach has gained attention in both research and practical forestry in recent years, with the benefits for several ecosystem services being widely recognized (Puettmann et al. 2015; Pukkala 2016; Savilaakso et al. 2021). Moreover, this forest management alternative could create new economic opportunities for forest owners through Landscape Value Trade (LVT), a concept where monetary compensation is provided to maintain forests as landscape shields to reduce harmful audio and visual effects. (Tyrväinen et al. 2021; Mäntymaa et al. 2021; Selkimäki et al. 2024).

Environmental noises especially from man-made sources as vehicle, industries, aircrafts and railroads can be disturbing for both human and wildlife (WHO 2018; Teff-Seker et al. 2022). In humans, the consequences of such noise range from mere annoyance to sleep disturbances, learning problems and other health issues (; Knopper et al. 2014). In contrast, for wildlife, noise can adversely affect biodiversity by causing species displacement, interrupting communication, and reducing the reproductive success, potentially leading to decreased population densities (EEA 2020; Tolvanen et al. 2023). Green spaces surrounding these noise sources play an important role in noise attenuation and perception (Dzhambov and Dimitrova 2015). Therefore, some regions have incorporated these green spaces into urban planning regulations (Pal et al. 2000; Teff-Seker et al. 2022). In addition, finish government has set maximum guide values for outdoor wind turbine noise, 40dB being the threshold value (Finlex 2015). The propagation of sound in outdoor environments is defined by ground attenuation, atmospheric absorption, turbulence, and refraction depending on wind and temperature gradients (ISO 9613-2 1996). Sound attenuation refers to the energy loss from sound waves. This loss typically occurs through spherical spreading as sound waves propagates uniformly in all directions away from the source. Furthermore, various obstacles or the ground itself can lead to absorption, reflection and diffusion of these waves (Crocker 1998). The capacity of green space to reduce noise level is influenced by several factors, including type of vegetation, prevailing meteorological condition, and the nature of the sound source (EEA 2020). Studies on sound propagation in tree buffers or forest strips, especially in the context of traffic noise, have suggested specific planting schemes and species selection to minimize noise levels (e.g., Defrance et al. 2019; Gaudon et al. 2022). However, there remains no consensus regarding the degree of the noise reduction achievable through vegetation (Albert 2004).

The sound attenuation effect of a forest depends on the ground impedance produced by vegetation of the field layer, tree roots, decaying leaves and needles, and scattering from tree stems, branches, leaves and needles (Attenborough and Taherzadeh 2016). Additionally, meteorological condition under the canopy also plays a role (Albert 2004). Despite this, very few research efforts have investigated noise mitigation through forest management and primarily focused on noise disturbance for sensitive bird species (Iglesias-Merchan et al. 2019) or the effects of forest stand on blast noise (Swearingen and White 2005). This limited research could be due to a lack of environmental noise prediction tools which could be integrated into forest management planning (Iglesias - Merchan et al. 2019). Nevertheless, several studies show that forest structure and tree characteristics affect sound propagation (e.g., Kellomäki et al. 1976; Swearingen and White 2007; Tarrero et al. 2008; Zhao et al. 2021). Variables associated with noise attenuation that have been studied include the spatial variation of tree spacing, species composition, canopy structure, volume, stem density, tree diameter and height. The study conducted by Kellomäki et al. (1976) showed that forest can attenuate 40–60% more compared to clear cut areas. Moreover, spruce and mixed forest stands reduced more noise compared to pine stands. Additionally, the study suggested that different successional stages of the forest have varying effects on noise attenuation, with younger dense and middle aged stands being more effective at reducing noise levels. In contrast, they stated that mature pure pine stands could slightly increase sound levels. Some other researchers have also stated that, in some cases, a forest could actually slightly increase noise levels, especially if tree stems have hard bark, the tree canopy is higher and there is little understorey vegetation, potentially due to backscattering effect of the sound waves from tree trunks (Albert 2004). However, the general understanding is that forest acts effectively as noise barrier (Swearingen and White 2005; Tarrero at al. 2008; Attenborough and Taherzadeh 2016).

One approach to mitigating noise levels from wind turbines in forested landscapes is to understand and consider the relationship between noise levels and forest structure, such as stem density. This relationship could be incorporated systematically into forest planning calculations. The goal of forest planning is to optimise benefits for forest owners and other stakeholders. Forest planning and management should consider multiple and varied uses and objectives (Fürstenau et al. 2007; Pukkala 2016) as well as sustainable use of resources. Forests should be used economically, ecologically and socially in a way, that secures the existence of resources for future generations. Key objectives often include ensuring that forests are not harvested at rates exceeding their grow over the long term, and that forest biodiversity is maintained secured or improved (Davis et al. 2001; Tόth and McDill 2009).

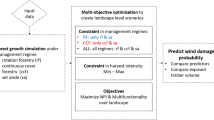
The aim of this study was to develop methods in forest management planning that prevent or attenuate noise from wind turbines. This was implemented by integrating a forest structure-based model into forest planning calculations to assess the forests influence on wind turbines noise and mitigate its adverse effects. The study also assessed whether even-aged forestry (rotation forestry) and uneven-aged forestry, could influence the noise effect. We hypothesised that uneven-aged forest management, which avoid clear cuttings, would create a more noise-friendly landscape. Further, we postulated that a diverse range of forest management alternatives would lead to more effective joint production of timber and noise attenuation. This was studied by constructing trade-off curves of the two. In addition, we compared two different methods for calculating the noise effect of forest as objective variable to evaluate their potential impact on higher noise levels (over government guide value of 40 dB).

Material

Study area

The selected study area locates in Honkajoki (22.296220°E; 61.963800°N), in the Satakunta region of Southern Finland. The Honkajoki wind farm, in operation since 2013, consists of 9 wind turbines with a total production capacity of 21.6 MW (FWPA 2022). The area encompasses various land uses, including agricultural fields, peat production areas, commercial forest land and industrial sites with biogas production, garden, and green house production areas. The nearest population centre lies approximately 2 km to the north. Another wind farm locates 3.5 km to the South and a third one wind farm is under planning about 2 km to the West (FWPA 2022).

The wind farm data of existing and planned farms was retrieved from FWPA (2021). The location of individual wind turbines was collected from National Land Survey database of Topographic database 1:10000 (NLS 2021). The height of each turbine was collected from the online map of FWPA (2021). Forest stand data was collected from Metsäkeskus (2021) which includes the private forest owners forest stand information. Stands around 4 km from nine wind turbines of Honkajoki wind farm were selected as study case totaling 4068 stands. These stands were used as initial state of the forest in the planning area.

Methods

Sound propagation includes several physical factors that influence noise attenuation levels. Sound propagation in the free air was calculated following the principles of the ISO 9613-2 (1996) standard with forest attenuation effect being a modification based on the scattering component of the Nord2000 model (Nord2000, 2000). We adopted standard conditions for temperature (15° C) and air moisture (70%), as recommended by the Finnish Environmental Agency for noise level calculations (Ympäristöhallinnon ohjeita 4/2014, 2014). Noise attenuation, excluding the scattering effect caused by forest, was calculated according to ISO 9613-2 standard for each nominal midband frequency (Hz). To spatially calculate noise levels, we generated 3 raster layers with a pixel size 2 × 2 m for each of the frequency bands (6 midband frequencies) and each of the wind turbines (9 turbines). Noise calculations were performed within 3 km radius of each wind turbines, as the Nord2000 model maintains acceptable accuracy up to this range (Kragh 2000).

Each of these raster layers contained values for the initial sound level, distance attenuation, and ground reflection (Supplementary material Table 1), and geometrical divergence for spherical spreading. The starting noise level was set at 104.5 dB (A), as specified for the wind turbine model in the environmental assessment report (YVA 2014). Data processing involved generating Euclidian distance layers from existing wind turbines with a 2 × 2-meter resolution and then calculating values per frequency using these values. A constant ground reflection value was added for each frequency using the raster calculator. Each component contributing to noise attenuation was initially calculated and then reduced from the starting level of each frequency. The results were then summed up to obtain a cumulative dB level using the specified equation (Eq. 1 Supplementary material). Thereafter, geometrical divergence was calculated for each turbine and reduced from the previous result. The cumulative sound pressure level for the wind farm area was derived by summing up the sound pressure levels from all nine wind turbines using the equation. All spatial noise calculations were performed using ArcGIS 10.5.1 (ESRI) software.

Noise attenuation in forest

The attenuation of noise in forests was calculated using a structural model based on the scattering part of the Nord2000. This model, as modified and developed by Selkimäki et al. (2024) is specifically tailored to assess the scattering effects of forests. This model starts with a baseline noise level of 104.5 dB(A) and the calculation is as follows:

$$\eqalign{\ln ({\rm{ noise }}) = 4.8202389 & - & 0.0256747*\ln ({\rm{ ba }}) \cr - 0.0277844*\ln ({\rm{ distance }}) + \varepsilon \cr}$$
(1)

where noise is the noise attenuation effect (dB), ba is the basal area (m2/ha) and distance (m) is the horizontal path of the sound through the forest.

Forest simulation

Treatment schedules were simulated for 30 years divided into three 10-year periods. Monsu software (Pukkala 2011) was used to simulate forest development and Pukkala et al. (2021) models were used to simulate forest growth and dynamics (diameter increment, survival and ingrowth). Models are adaptable and are able to simulate the stand development in different stand structures, silvicultural systems and transitions from one to another. Pukkala et al. (2009a) models were used to calculate tree height and timber assortment volumes with the Laasasenaho (1982) taper functions. A treatment was simulated in the middle of the 10-year period if predefined thresholds were met. Typically, a treatment schedule includes forest regeneration, treatment of saplings and thinning or regeneration harvest. Harvest treatments adhered to either on even-aged forestry (usually involving thinnings from below and clear cuttings) or a combination of even- and uneven-aged forestry (mainly thinnings from above), depending on the management scenario.

Optimization method of forest management

To select optimal treatment schedules for stands based on the given management objectives, the reduced costs (RC) method (Pukkala et al. 2009b) was used for optimization. The RC executes optimization at the local (stand) level. To incorporate global forest, or landscape level objectives, this method adapts the dual prices from the dual problem related to the theory of linear programming. Due to stand level optimization, the RC is referred to as a decentralized optimization method or decomposition method. In this study, an additive utility function was used as the objective function at the local level.

$${P}_{ij}={\sum }_{l=1}^{L}{w}_{l}{p}_{l}\left({q}_{ijl}\right)$$
(2)

where Pij is the value of schedule i of stand j, L is the number of local (stand level) objectives, wl is the weight of objective l, pl is a sub-utility function for objective l, and qijl is the quantity of objective variable l in schedule i of stand j. The complete stand-level objective function, including dual prices, maximizing reduced costs of individual treatment schedules is:

$$R{C}_{ij}={P}_{ij}-{\sum }_{k=1}^{K}{a}_{ijk}{v}_{k}$$
(3)

where vk are the heuristically up-dated “dual prices”, aijk = quantity of constraining variable k and K is the number of constraints. The main phases of the optimization method were:

  1. 1.

    Produce an initial random solution (select a random schedule for stands).

  2. 2.

    Set initial dual prices (0 in this study).

  3. 3.

    Select the best schedule for every stand using Eq. 3.

  4. 4.

    Calculate the values of forest-level goals (constraining variables, even-flow of timber).

  5. 5.

    Up-date dual prices.

  6. 6.

    Repeat Steps 3–5 until the forest level constraints are satisfied.

A more detailed description of the RC-method can be found in Pukkala et al. (2009a). Trade-off curves between NPV and TN were drawn by modifying the weights (wl) between the objectives in different scenarios. THEOpt forest planning optimization software was used to perform optimization calculations (previously used for example in Heinonen et al. 2018; Heinonen 2019).

Forest management objectives

Net present value (NPV) and turbine noise (TN) were used as management objectives in the planning scenarios. NPV was maximized and TN was minimized. NPV was a sum of discounted values of incomes (harvested timber) and costs (silvicultural actions) during the 30-year planning period. In addition, the discounted value of standing timber at the end of the planning period was added to NPV. Discount rate was 3%, which corresponds to typical rate used in forest management planning calculations in Finland. Value of standing timber was calculated based on the models by Pukkala (2005).

To evaluate the impact of the forest on the turbine noise, we first determined the effect of forests (EF) by deducting the forest structure-based noise (ln(noise)) from the starting noise (IN, 104.5 dB) produced by the turbines. The TN value was then calculated by deducting this EF from the noise due to physical factors (EP) as shown in the following equation:

$${\rm{TN}} = {\rm{EP}} - ({\rm{IN}} - \ln ({\rm{ }}noise{\rm{ }})) = {\rm{EP}} - {\rm{EF}}$$
(4)

EP was calculated with the models presented in Selkimäki et al. (2023) and (ln(noise)) was calculated using Eq. 1. Linear and sigmoid sub-utility functions were used to calculate the scaled value for TN (Fig. 1). Sub-utility function converts objective values comparable between 0 and 1. The sigmoid-shaped sub-utility function for turbine noise was as follows,

$${u}_{s}= 1-\frac{1}{1+{e}^{-(x-{a}_{s}){b}_{s}}}$$
(5)

where us = sub-utility of turbine noise for a schedule, x = turbine noise, as, bs = parameters of sigmoid function (as = 40 and bs = 0.2). The idea behind the sigmoid-shaped function was to convert sub-utility values lower for treatment schedules, that results turbine noise higher than 40 dB. By setting the shape parameter values as mentioned above, sub-utility gets the value of 0.5 at 40 dB and noise over 40 dB is penalized more than with linear function due to parameter bs, which creates more steep slope after 40 dB. For NPV sub-utility function was linear, minimum NPV-value of all stands gave sub-utility 0 and maximum value gave sub-utility 1.

Fig. 1
figure 1

Sub-utility functions for turbine noise. Linear function on the left and sigmoid-shaped sub-utility function on the right

Full size image

Forest management scenarios

Four different management scenarios were developed to study how the use of TN as a planning objective influenced the harvesting methods and NPV (Table 1). In all scenarios, the trade-off between TN and NPV was examined by adjusting the objective weights between 0 and 1, thereby constructing trade-off curves. Two of the scenarios employed solely even-aged forestry, while the other two incorporated both even-aged forestry and uneven-aged forestry management alternatives. The other scenario for the both forest management method was executed with even-flow of timber to achieve more realistic use of forests, with the amount of annual harvested timber being approximately 2,7 m3/ha (80,000–85,000 m3 for 10-year period). In addition, all four scenarios were executed with either a linear- or sigmoid-shaped sub-utility function for TN. The scenario that employed only even-aged forestry, ensured an even-flow of timber and considered net present value as the sole objective (with a weight of 1) can be considered as the business-as-usual alternative.

Table 1 Different management scenarios executed to study the use of turbine noise as a management objective in forest planning calculations. Even = even-aged forest management, EvenUnEven = uneven-aged forest management, EF = even-flow of timber
Full size table

Results

The values of the effect of forest on turbine noise reported are averages of all the stands in the planning area. The average effect of forest ranged between 4.76 dB and 8.77 dB (Fig. 2). The highest average effect was achieved when TN was used as a sole objective (TN weight 1.0). The effect on noise resulted from maximizing NPV and applying even-aged forestry without even-flow of timber. The results indicates that it was possible to reduce noise level substantially by increasing the weight of TN without considerably decreasing the NPV. For example, a 13% decrease in the TN resulted in only a 5% decrease in NPV when applying even- and uneven forest management (blue solid line in Fig. 2). Production possibilities relating to the effect of forest and NPV diminish considerably when even-flow of timber was applied. The maximum effect was 8.35 dB (even- and uneven-aged management and linear sub-utility function) and the minimum value was 7.13 dB (even-aged management). In general, combining even-aged and uneven-aged forest management yielded lower noise level and a higher NPV than even-aged forestry alone.

Fig. 2
figure 2

Trade-off curves of average noise of stands in the study area and net present value. Even = even-aged forest management, EvenUnEven = even- and uneven-aged forest management, EF = even-flow of timber, S = sigmoid-shaped sub-utility function for turbine noise objective

Full size image

In general, the use of linear sub-utility function resulted a lower average turbine noise across the studied landscape. However, as expected, applying sigmoid-shaped sub-utility function reduced the total area of stands where noise exceeded a distracting 40 dB. When both objectives had the same weight and even-flow of timber was applied together with even- and uneven-aged forestry, the area with noise levels above 40 dB reduced by 12% compared to linear function. With only even-aged forestry, this reduction was 24% (Fig. 3). There was no noticeable difference in areas with distracting noise levels between forest management methods when the sigmoid function was employed.

Fig. 3
figure 3

Turbine noise in the wind turbine neighbourhood at the third 10-year period. Noise over 40 dB = colours from orange to red. Even-aged forest management and even-flow of timber, linear-shaped sub-utility function on the left and sigmoid-shaped on the right. Same weight for TN and NPV objectives

Full size image

Total harvest areas for even-aged forestry alone were, on average, about 30% lower across different weight combinations (Fig. 4). In addition, thinning areas constituted roughly half of the areas with even- and uneven-aged management. However, areas designated for regeneration cuttings areas were twice as large for even-aged forestry. The difference in the regeneration cutting area was more pronounced when the even-flow of timber was applied. When even-flow of timber was not applied and TN was the sole objective (weight 1.0), no cuttings were occurred. Otherwise, a higher weight for TN led to larger areas allocated for thinnings. The sole exception was the scenario in which both management methods incorporated a sigmoid-shaped sub-utility function. If the weight of NPV-objective was greater than zero, the total harvest area remained consistent across all scenarios. Even-flow of timber was achieved in all scenarios and weight combinations (Fig. 5). Only exception was the first 10-year period with both management methods, linear sub-utility function and the weight being the same for both objectives. In general, total harvest volume during the whole 30-year was lower as the weight for minimizing turbine noise was high.

Fig. 4
figure 4

Total harvest areas during 30-year planning horizon for regeneration cuttings and thinnings with different turbine noise weights. Even = even-aged forest management, EvenUnEven = even- and uneven-aged forest management, EF = even-flow of timber

Full size image
Fig. 5
figure 5

Total harvest volumes during 30-year planning horizon for scenarios with even-low of timber with different turbine noise weights. Even = even-aged forest management, EvenUnEven = even- and uneven-aged forest management

Full size image

The most realistic scenarios, which include even-flow of timber were visually examined during the third 10-year period for even-aged forest management (Fig. 6) and even- and uneven-aged forest management (Fig. 7). A most essential observation was that even- and uneven-aged forest management resulted a clearly more harvest area, especially thinnings (indicated by the blue color in the figures). Harvest areas were more or less uniformly distributed throughout the study area when the linear sub-utility function was applied for even-aged forest management. In contrast, the sigmoid-shaped sub-utility function seemed to move the cuttings away from the nearby locations of the central wind turbines, where the TN is the highest. As a result, these areas remained forested, to prevent distractive noise of turbines. This effect was clearly evident when the TN was the only objective in optimization.

Fig. 6
figure 6

Harvesting areas at the third 10-year period using even-aged forest management and linear- or sigmoid-shaped sub-utility function for turbine noise objective. Red color = regeneration cutting and blue color = thinning. Even-flow of timber. The number in the parenthesis indicates the weight of the objective in the stand level objective function. Wind turbines are located in the center of the maps. Note, that the white areas have no data and the outermost cray area does not belong to the study area

Full size image
Fig. 7
figure 7

Harvesting areas at the third 10-year period using even- and uneven-aged forest management and linear- or sigmoid-shaped sub-utility function for turbine noise objective. Red color = regeneration cutting and blue color = thinning. Even-flow of timber. The number in the parenthesis indicates the weight of the objective in the stand level objective function. Wind turbines are located in the center of the maps. Note, that the white areas have no data and the outermost cray area does not belong to the study area

Full size image

Discussion

Wind power has many benefits compared to most other ways of energy production and wind energy production in European landscapes has increased rapidly in recent years. This development brings multiple impacts on our environment, making the critical need for precise land-use planning. Numerical optimization methods are used for determining the optimal allocation of limited forest resources and to derive alternative management scenarios (Heinonen 2007). These methods efficiently and reliably tackle challenges presented in numerical models. This study represents one of the pioneering efforts, if not the very first, to incorporate methods that mitigate the noise effects of wind turbines into forest planning and forest management. The method showed great potential and can be seamlessly integrated into practical forestry. Our study findings indicate that forests can provide up to 10 dB of additional noise attenuation. This can be achieved mainly by utilizing uneven-aged forest management and thinnings avoiding clear-cuttings. This confirms the poor noise attenuation ability of treeless areas found in previous studies (Kellomäki et al. 1976). In addition, to avoid higher noise from the turbines (over 40 dB) harvesting should be avoided nearby turbines. Basic forest inventory data with spatial distance information are sufficient to implement the forest-related noise model in planning calculations.

Utility of alternative forest harvesting scenarios were demonstrated when noise model was utilized in planning calculations. The use of noise model as a management objective can lower the noise levels in the study area compared to the so-called business-as-usual management (even-aged forest management). Adapting uneven-aged forest management beside even-aged management kept landscape more forested, which more effectively mitigated noise levels. In addition, the most distracting noise levels nearby wind turbines were reduced by using sigmoid-shaped sub-utility function when optimizing turbine noise - objective.

When sigmoid-shaped sub-utility function was used, the mean noise level across the entire forest area was higher, yet the peak noise levels near the turbines were lower. This can be explained by the larger area of clear cuttings, especially when combining with both even- and uneven-aged forest management. This is because harvest targets needed to be met in smaller areas, leading to harvests being executed farther away from the turbines. In addition, sigmoid sub-utility function did not penalize noise levels generated at these greater distances from the turbines.

The decentralized optimization method used in this study calculates the objective function on a per-stand basis. This approach reduces the search space and makes calculations more efficient, while also enabling for the incorporation of more fine-grained data, such as microsegments or raster cells. Thus, a more detailed description of landscape and forests can be included in the calculation to help mitigate the noise effects of wind turbines. Also, the decentralized method means that planning calculations can be executed in larger areas. For example, land use allocation problems could be address at the scale of a larger, multiple turbine wind power plants. Thus, the method has great potential for future studies related to noise reduction in forest management.

The noise model used in this study is rather simple, relying on the basal area of living trees and their distance from the wind turbines. One of the future steps to develop the noise model for forest effect further could be to calibrate it with tree species. According to Kellomäki et al. (1976) spruce and mixed species forests are more capable to reduce turbine noise compared to pine forests. In fact, mature pine forests might slightly increase noise levels. Real forest stands were used for the optimisation in this study, but the results are still case specific. In order to evaluate only the differences between the different effects, a grid of small microstands, all of a similar shape, could have been a good option (Baskent and Jordan 2002; Heinonen and Pukkala 2007; Heinonen et al. 2009).

In this study, forest management was selected for the stands without considering their spatial location relative to residential areas. The only spatial variable considered was the distance between the stand and the wind turbines. Naturally, noise attenuation would be more effective if noise-friendly management practices would concentrate on stands between the wind turbines and residential areas. This approach would require the development of more specific spatial objectives and optimization methods to create noise barriers between the turbines and residential areas. In the same context, visibility barriers could be generated utilizing turbine visibility models that consider forest characteristics and distance data (Selkimäki et al. 2024). Additionally, integrating a digital elevation data with finer spatial resolution into the planning methodology could facilitate identification of vulnerable locations and mapping the stands which could serve as landscape shields. Identifying the location of these forest shields, their management could be strategically planned to minimize the disturbing audio-visual impact on the surrounding landscape.

In reality, forests closest to wind turbines most probably do not act as a noise barrier. This is because much of the noise is generated at the turbine rotor height, which means it likely pass over forests beneath. In this study, we demonstrated a simple and easy to adapt method to mitigate turbine noise. Thus, this particular aspect was not addressed until more comprehensive information on the subject available. The key point in further developing this methodology is to improve the reliability and precision of spatial models. In forest planning, it may be beneficial to use cell-type of neighbourhoods that consider not only immediate neighbours but also neighbours inside a specific radius (e.g., Heinonen 2007; Heinonen et al. 2018). Forest stand characteristics can be optimised to minimise undesired effects and to address stand features within a specific timespan.

The formulation of preferences over time directly impacts the optimisation results at the landscape level, as demonstrated in this study. Forest management planning commonly involves multiple objectives and constraints, making the effects of introducing new variables not always immediately apparent. Beyond economic values, the forestry planning process frequently incorporate biodiversity and landscape level objectives (e.g., Korosuo et al. 2014). When using empirical forest stand structure data, the optimisation algorithm becomes closely linked to the current spatial structure of the forest landscape (Korosuo et al. 2013). There is ongoing need to improve methodologies and spatial models to ensure stable and realistic outcomes over the time. When the overall objective of the planning is to build a good landscape structure in the future, it is necessary also to analyse results with spatial effects in the more distant periods.