Introduction

Tree rings provide a detailed history of past tree growth at (sub-)annual resolution. This can help to give insights into understanding the negative effects of global change such as rising temperatures, changes in precipitation regimes, increases in the frequency of extreme events or environmental pollution (Schweingruber 2012; Wright et al. 2014). Tree coring has thus been used for decades for various purposes, traditionally with a strong focus on palaeoclimatology. However, the sampling designs behind most tree-ring data target dominant, undisturbed trees growing under marginal growing conditions, thereby maximizing the climate signal. For instance, many such cases can be found in the publicly available data of the International Tree Ring Data Bank (ITRDB). Thus, using existing data to infer climate sensitivities or growth trends of forests across large scales has been shown to yield biased estimates (Cherubini et al. 1998; Nehrbass-Ahles et al. 2014; Babst et al. 2018; Klesse et al. 2018).

When obtained from probabilistic sample surveys, tree-ring data can, however, more accurately estimate forest carbon capture and storage (Canham et al. 2018; Klesse et al. 2018; Evans et al. 2022). As they provide detailed and accurate information on tree and stand age, tree-ring data can overcome different challenges associated with repeated stem diameter measurements at multi-annual intervals (5–10 years), which are among the most important base measures of long-term forest inventories or other long-term monitoring programs (Parr et al. 2002; Tomppo et al. 2010; Nehrbass-Ahles et al. 2014; Gschwantner et al. 2016). These 5- or 10-year remeasurements alone are unable to accurately capture annual growth responses to extreme events that are becoming more frequent in the context of global environmental change. Incorporating tree coring into probabilistic designs developed to be representative of the forest ecosystem under study would provide a more realistic picture. In combination with other tree-based measurements, this would open new opportunities for improved modelling approaches and statistical analyses (Nehrbass-Ahles et al. 2014; Duchesne et al. 2017).

Recognising this potential, some large-scale inventorying and monitoring initiatives across the world have implemented tree coring in their sampling protocols, although mainly in North America where this practice is viewed as minimally invasive and destructive (Bosela et al. 2016; Vallet and Perot 2016; Marin et al. 2019; Kim et al. 2020; Girardin et al. 2021; Evans et al. 2022). Tree coring is now also permitted on the Level II permanent plots UNECE ICP Forests. However, coring is still considered controversial in many European countries. There is indeed limited scientific knowledge around the potential harm coring might cause to trees (see for instance Fig. 1), with potential adverse effects for tree growth, health and mortality (Hepting et al. 1949; Tsen et al. 2016). The main concern for most European long-term inventorying or monitoring programs using permanent plots is that tree coring might bias the repeated measurements of trees, which they rely on to assess the state and long-term changes of forests (Tomppo et al. 2010; Commarmot et al. 2013; Gschwantner et al. 2016). In the absence of sound scientific evidence that coring does not affect measurements, these programs commonly forbid tree coring on permanent plots (Gschwantner et al. 2016). Instead, trees can be cored in the vicinity of the permanent plots, in temporary plots or in abandoned permanent plots (Trotsiuk et al. 2012; Gschwantner et al. 2016). There are additional conservation concerns around the ethics of tree coring for rare species as well as in forest reserves and protected areas. In such forests, the use of invasive techniques is strongly regulated to ensure the natural development of forests and minimise human interventions. When tree coring is not fully prohibited, it requires official permissions and specific restrictions such as a reduced number of cored trees, a limitation to dead trees and/or to specific species (e.g. Trotsiuk et al. 2012; Tsen et al. 2016; Paluch and Jastrzębski 2022; Nagel and Cerioni 2023). Finally, forest practitioners and forest owners can be concerned about the effects of coring on wood quality. Unless financially compensated, they sometimes refuse tree coring to guarantee the economic value of their forests.

Fig. 1
figure 1

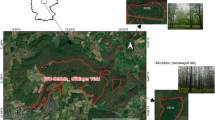
Wound reactions at the coring location and along the stem after approximately 10 years. At the Vordemwald monitoring site in Switzerland, A. alba (a) and P. abies (b) showed minor markings from coring (~ 2–3 cm in width, ~ 4–5 cm in height). In the Uholka-Shyrokyi Luh reserve in Ukraine, F. sylvatica had a stronger wound reaction as well as a bulge along the stem which was generally more pronounced on smaller trees (d) than on larger ones (c). Photos: a and b: J. Portier, c and d J. Stillhard

Full size image

Overall, there are concerns that tree coring could cause surface infections due to wounds, internal decay, reduced growth, and even lead to increased mortality rates of cored trees (Tsen et al. 2016). There is a large body of qualitative literature about the risks of coring for different species in different regions of the world. However, only a few are quantitatively robust studies (Van Mantgem and Stephenson 2004; Wunder et al. 2011, 2013; Helcoski et al. 2019) which generally show no effect of coring on tree mortality. In one of the largest studies on the topic, Van Mantgem and Stephenson (2004) assessed 825 cored and 256 uncored Abies concolor trees and 104 cored and 66 uncored Abies magnifica trees in permanent plots in California. They found no effects of coring on tree mortality 12 years later and they suggest that coring should not be labelled as destructive sampling. In Switzerland, 551 Picea abies trees with a diameter at breast height (DBH) ≥ 8 cm were cored within a 5.9 ha plot in 1965 (Wunder et al. 2011). Following a reassessment of the plot in 2006 (40 years later), no significant influence of coring on tree mortality was found (Wunder et al. 2011).

There is also concern that coring may affect tree growth thereby influencing subsequent inventory remeasurements. However, there is very limited research on the topic and more studies with larger sample sizes and robust statistical analyses are needed (Tsen et al. 2016). In this respect, we only found results of one case study assessing 35 trees in Singapore showing no change in tree diameter growth between cored and uncored trees over a one-year period (Neo et al. 2017). Although limited only to ten cored P. abies trees, another assessment in the Czech Republic showed tree growth returned to normal after three years, but vertical cracking was observed (Fabiánová and Šilhán 2021).

Overall, the longer-term effects of coring are still not well understood and studies that compare multiple species and sites using large sample sizes are rare. An attempt to synthesise different studies was made by Tsen et al. (2016). Their key findings include that vertical discolouration in tree heartwood tissues, internal trunk decay and cambial necrosis in cored trees were common in broadleaved taxa. This can have implications for wood quality and value. Further, their review highlighted that no increase in mortality was observed in conifer species but sometimes to a limited extent in broadleaved species, and that fast-growing, vigorous trees are less affected by coring as their wounds closed more quickly. Accordingly, trees growing at high latitudes and altitudes appeared more sensitive and took longer to heal. However, the authors emphasise that limited evidence prevents generalisation across different contexts and forest tree species, and more quantitative studies with large sample sizes are needed. Accordingly, the aim of this study was to assess the effects of tree coring on both the growth and mortality of three widespread European forest tree species using long-term monitoring plot data in Switzerland (P. abies (L.) H. Karst., Abies alba Mill.) and Ukraine (Fagus sylvatica L.).

Materials and methods

Study areas and sampling designs

Switzerland

Vordemwald, located on the central plateau of Switzerland, is a 2-ha monitoring site belonging to the Long-term Forest Ecosystem Research Programme (LWF; ICP Level II). It is an uneven-aged, mixed-species, forest stand with a basal area of 65.8 m2/ha (Nehrbass-Ahles et al. 2014). The forest has been managed for the past 200 years and is mainly composed of A. alba, P. abies and F. sylvatica. The site is located at 480 m a.s.l. and had a mean annual temperature of 8.4 °C, and mean annual precipitation of ~ 1100 mm over the period 1978–2011 (MeteoSwiss 2013; Nehrbass-Ahles et al. 2014).

The monitoring plot was installed in 1995 and the DBH and tree status (living or dead) have been measured and assessed approximately every five years since. The last inventory before trees were cored was conducted in 2009. After the 2011 growing season, all 298 trees within a defined 0.5 ha fixed sub-plot were cored. Two cores perpendicular to each other were taken at 90 cm above the ground (not at 130 cm to prevent coring wounds from affecting future DBH measurements) from all living and dead trees with a DBH larger than 6 cm; see Nehrbass-Ahles et al. (2014) for further details. The DBH and tree status of cored and uncored trees on the plot were reassessed in the fall of 2020. Although a number of different tree species were cored at Vordemwald in this study we only focus on P. abies and A. alba representing the species with enough records to conduct robust analyses (see Table 1 for the number of trees used in the analyses). We split the dataset into two, one for each species. We will hereafter refer to these two datasets as CH [P. abies] and CH [A. alba].

Table 1 Dates of inventory 1 and 2, year of coring of each dataset and the number of trees (cored/uncored, dead/alive) at the time of inventory 2
Full size table

Ukraine

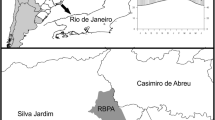
The Uholka-Shyrokyi Luh primeval beech forest covers 102.8 km2 and is situated in southwestern Ukraine within the Carpathian Biosphere Reserve (CBR). It is part of the UNESCO world heritage “Ancient and primeval beech forests of the Carpathians and other regions of Europe”. Elevation ranges from 400 to 1300 m a.s.l., the mean annual temperature across the whole area is ~ 7.7 °C and annual precipitation is ~ 1100 mm (average over 1990–2010; Hobi et al. 2015). Two distinct datasets were used within this reserve based on two different long-term monitoring initiatives. In both, we retained solely data on F. sylvatica, the dominant species in the area.

A 10-ha long-term monitoring plot with a basal area of 38.5 m2/ha was set up in 2000 on the southwestern side of the Uholka part of the reserve, with remeasurements occurring every five years (Stillhard et al. 2019). In 2010, four circular satellite plots of 0.1 ha were set up roughly 200 m apart in the surroundings of the 10-ha plot (Trotsiuk et al. 2012). That year, the DBH and tree status (alive/dead) of all trees with DBH ≥ 6 cm were measured in the four satellite plots and remeasured in the 10-ha plot. In addition, all measured trees in the four satellite plots were cored during the growing season at either 100 cm (143 trees) or 80 cm (21 trees), while no coring occurred in the larger 10-ha plot. In 2021, DBH was remeasured, and tree status was re-assessed in both the 10-ha plot and the four satellites. The 10-ha plot was used as an uncored control site for the cored trees in the four satellites. Therefore, a harmonisation step to ensure comparability of the DBH measurements was needed. Trees’ DBH in the four satellite plots was recorded in centimetres as one floored (rounded to the closest smaller integer) measure per tree. In the 10-ha plot, two crosswise calliper measures were taken per tree, to the millimetre. To match the satellites’ measures, we averaged the two DBH measures of trees in the 10-ha plot and floored the resulting mean. We will hereafter refer to this dataset as UKR [F. sylvatica]-10 ha.

In addition, the sample plot inventory (SPI) is distributed over the entire reserve. The sampling design is based on a systematic 445 m × 1235 m grid of non-stratified clusters. Each cluster is made of a pair of 500 m2 sample plots located 100 m apart from each other (Hobi et al. 2015; Stillhard et al. 2022). During the initial 2010 inventory, 314 sample plots were assessed, and included the measurement of the DBH and status (dead or alive) of all trees with a DBH ≥ 6 cm. The mean basal area of the SPI was 36.6 m2/ha. On 249 of these plots, one (or in rare cases two) living trees with DBH ≥ 16 cm were randomly selected and cored over the months of July and August (Hobi et al. 2015). Cores were taken between 80 and 100 cm above ground and parallel to the slope (for further details see Commarmot et al. 2013 and Hobi et al. 2015). In 2019, 237 plots lying in the core zone of the reserve were revisited. In these plots, DBH was remeasured and tree status (alive/dead/missing) of all trees with DBH ≥ 6 cm was reassessed, including trees that were cored in the first inventory (Stillhard et al. 2022). In total, 192 cored trees were remeasured, distributed in 183 of the 237 revisited plots. We will hereafter refer to this dataset as UKR [F. sylvatica]–SPI.

Pre-processing of the datasets

We define “inventory 1” as the year 2009 for CH [P. abies] and CH [A. alba] and as the year 2010 for UKR [F. sylvatica]–10 ha and UKR [F. sylvatica]–SPI). Similarly, “inventory 2” will hereafter refer to 2020 for CH [P. abies] and CH [A. alba]; 2021 for UKR [F. sylvatica]–10 ha; and 2019 for UKR [F. sylvatica]–SPI (Table 1). In all four datasets, we retained only measured trees that were alive at inventory 1. In UKR [F. sylvatica]–SPI, only plots where at least one tree was cored were used in the analyses (n = 183 plots). All analyses were performed with R version 4.0.3 (R Core Team 2021).

Confounding factors

Tree-level growth and mortality both strongly depend on tree size (DBH): the basal area increment (BAI) (that represents tree growth) tends to increase with DBH (Rohner et al. 2018), and mortality is commonly lowest in medium DBH ranges (Hülsmann et al. 2017). In addition, competition at the tree level can strongly affect growth and mortality through its effects on the availability of nutrients, water and light (Biging and Dobbertin 1995; Cescatti and Piutti 1998). Consequently, to allow the meaningful comparison of growth and mortality between cored and uncored trees, the differences in the distributions of tree size and competition between the two populations should be accounted for. We, therefore, calculated a competition index (CompInd) for each target tree i, following the equation from Hegyi (1974):

$${\mathrm{CompInd}}_{i}= {\sum }_{j=1}^{n}\frac{{\mathrm{DBH}}_{j}/{\mathrm{DBH}}_{i}}{{\mathrm{Distance}}_{ij}}$$

We included neighbouring trees j up to a distance of 8 m (\({\mathrm{Distance}}_{ij}\)). A higher CompInd value indicates higher competitive pressure. For target trees growing closer than 8 m to the plot boundary, we extrapolated CompInd based on the information gained within the plot by the ratio of 201 m2 (the full 8 m competition area) divided by the competition area within the plot boundary, e.g. for a target tree with only half of its 8 m competition circle within the plot, CompInd was multiplied by two.

We then plotted the DBH and CompInd distributions of cored and uncored trees within each dataset to assess how much they differed (Fig. 2).

Fig. 2
figure 2

DBH (a) and CompInd (b) distributions of cored (blue bars) and uncored trees (yellow bars) in each dataset (both living and dead). The distributions of uncored trees are overlayed on the distributions of cored trees, leading to the greenish bars where cored and uncored overlap. Each colour (blue and yellow) in each panel sums up to 100%

Full size image

Contrary to the Vordemwald site in Switzerland and to UKR [F. sylvatica]–10 ha, the UKR [F. sylvatica]–SPI dataset covers a much larger area and thus a substantial gradient of environmental conditions, which are likely to affect both growth and mortality. For this reason, we also extracted the elevation of each plot in the UKR [F. sylvatica]–SPI from a DEM derived from digitized contour lines based on a Ukrainian map (scale 1:50,000) to encompass the topographic variability of the area.

Propensity score matching to improve the comparability of cored and uncored trees

As the DBH and CompInd distributions of cored and uncored trees in most cases strongly differed (Fig. 2), direct comparisons of growth and mortality were not possible. A common way to control for differences in confounding factor distributions between a treatment and a control group (here, cored and uncored trees, respectively) is to use propensity score analyses (Rosenbaum and Rubin 1984; Zhao et al. 2021). The propensity score corresponds to the probability of each observation (each tree) receiving a given treatment (being cored) depending on observed confounding factors (DBH and CompInd). This can be achieved for instance based on logistic regression. The goal of the propensity score is to create comparable datasets (cored and uncored). In propensity score matching, observations in the control group that have the most similar propensity scores as those in the treatment group are selected until the same number of observations are reached in both groups (Rosenbaum and Rubin 1984; Zhao et al. 2021). This new matched dataset, where both groups share the same characteristics in terms of confounding factors, can then be used in further analyses.

We based the propensity score matching between cored and uncored trees on the following model, which was fitted independently for each dataset within a bootstrap procedure (see sub-section ‘Assessing the impact of coring on growth and mortality’ below):

$${\widehat{p}}_{{\mathrm{cored}}_{i}} = \frac{1}{\left(1+ {e}^{-\left({\widehat{\upbeta }}_{0} + {\widehat{\upbeta }}_{1} \cdot {DBH}_{i}+{ \widehat{\upbeta }}_{2} \cdot {\mathrm{CompInd}}_{i}\right)}\right)}$$

where \(\widehat{{p}_{{\mathrm{cored}}_{i}}}\) is the estimated probability of a tree i to be cored, \({\widehat{\upbeta }}_{0}\) is the estimated intercept of the model and \({\widehat{\upbeta }}_{\mathrm{1,2}}\) are the coefficient estimates corresponding to each variable. The previously described model also included elevation as an additional confounding factor for the UKR [F. sylvatica]–SPI dataset.

Propensity score matching was performed based on the previously described model with the function matchit of the MatchIt R package, using the nearest neighbour matching method (Ho et al. 2007). This function calculates the propensity score of each observation based on the provided model formulation. We could then extract a matched dataset containing all observations corresponding to the treatment group as well as the control observations best matching the treatment group based on the propensity score.

Calculation of growth and mortality

Growth at the tree level was represented by annual BAI. We first calculated the basal area (BA) of each tree at each inventory as:

$$\mathrm{BA}= \pi \bullet {\left(\frac{\mathrm{DBH}}{2}\right)}^{2}$$

BAI was then calculated for each tree as the difference in BA between inventory 1 and inventory 2, divided by the number of years between inventory 1 and inventory 2 (\(\Delta t\)) to yield an average annual increment:

$$\mathrm{BAI}=\frac{{BA}_{\mathrm{inv}2}-{BA}_{\mathrm{inv}1}}{\Delta t}$$

Mortality was determined through annual mortality rates (MR), calculated within a bootstrap procedure (see sub-section ‘Assessing the impact of coring on growth and mortality’ below), independently for each dataset and for cored and uncored trees. MRs were calculated according to Sheil and May (1996):

$$\mathrm{MR}=1- {\left(\frac{{N}_{\mathrm{living}}}{{N}_{\mathrm{total}}}\right)}^{\frac{1}{\Delta t}}$$

where Nliving is the number of living trees and Ntotal is the total number of trees (living and dead, Table 1).

Assessing the impact of coring on growth and mortality

To assess the impact of coring on growth and mortality, we used a bootstrap procedure where at each iteration and independently for each dataset, cored and uncored trees data were resampled with replacement. We then applied the matching propensity score process to the resampled data. The comparable matched data were then used to calculate (i) the difference of median BAI between cored and uncored trees, and (ii) their mortality rate. The corresponding 95% bootstrap confidence intervals (bCI) were then calculated from the 1000 bootstrap iterations. No statistical evidence for an effect of coring on tree growth was found when the 95% bCI of the difference in median BAI crossed zero, the same was true for mortality when the 95% bCI of cored trees overlapped that of uncored trees. To evaluate whether the impact of coring could depend on tree size or competition level, we calculated the difference of median BAI between cored and uncored trees for all trees as well as separately for four quantile-defined DBH and CompInd classes. However, the number of dead trees was too small (see Table 1) to allow sound comparisons of mortality rates of cored and uncored trees for different classes.

Results

After accounting for confounding factors with the propensity score analysis, we did not find statistical evidence of an effect of coring on the BAI of trees for any of the three tree species, and with one exception across all DBH and CompInd classes (Fig. 3). In UKR [F. sylvatica]–10 ha, uncored trees with the lowest level of competition had a higher BAI than cored trees. Although the 95% bCI crossed zero, the same pattern was observed in the largest uncored trees of this site (Fig. 3). Large trees have generally little competition, resulting in most trees belonging to the lowest competition class being the same as those from the largest DBH class. The BAI pattern observed in UKR [F. sylvatica]–10 ha thus concerns large trees with low competition.

Fig. 3
figure 3

Difference in median BAI between cored and uncored trees as well as 95% bootstrap confidence intervals based on the propensity score analysis with 1000 iterations. Differences are shown for each dataset for four DBH classes (left four panels), for four CompInd classes (right four panels) as well as for the entire datasets (“Total”). Negative values indicate higher BAI values for uncored trees, positive values indicate higher BAI values for cored trees. Higher values of CompInd indicate higher competition

Full size image

Across all sites and species and after accounting for confounding factors with the propensity score analysis, we did not find any evidence of an effect of coring on tree mortality, as the 95% bCI of mortality rates of cored trees overlapped those of uncored trees (Fig. 4). In both Ukrainian sites, cored trees tended to have lower mortality rates than uncored trees – although the 95% bCI did overlap.

Fig. 4
figure 4

Annual mortality rates of cored and uncored trees for each dataset, along with their 95% bootstrap confidence intervals based on the propensity score analysis with 1000 iterations

Full size image

Discussion

Our study, drawing on data from Switzerland and Ukraine, did not indicate any effects after approximately ten years since coring on tree growth and mortality for three common European tree species F. sylvatica, A. alba and P. abies. With regard to mortality, our results are in line with other quantitative studies from across the world (Van Mantgem and Stephenson 2004; Wunder et al. 2011, 2013; Helcoski et al. 2019). Compared with previously published studies on the effect of coring on tree growth (e.g. Neo et al. 2017; Fabiánová and Šilhán 2021), our study provides quantitative evidence relying on larger species-specific sample sizes and broader scales, thus contributing to an improved understanding of how coring affects trees.

While our results show that there is generally no statistical evidence of tree growth being affected by coring, in the UKR [F. sylvatica]–10 ha site the large uncored trees from the 10-ha plot show a tendency towards higher growth rates than the cored trees in the satellite plots. UKR [F. sylvatica]–10 ha is the only site where cored and uncored trees are located in sampling units that, although in the vicinity of each other, do not spatially overlap. This leads to slight environmental differences between the cored satellite plots and the 10-ha plot. For instance, the 10-ha plot was selected subjectively in a forest patch that displayed characteristics of primeval beech stands. Holeksa et al. (2009) showed that such forest reserves that were subjectively selected tended to have higher growing stocks than those observed from larger-scale inventories. In addition, Peck et al. (2015) found that in 2010, the 10-ha plot had more large trees and a higher basal area compared with the SPI, implying that the 10-ha plot might not be representative of the overall conditions found in the reserve. In contrast, the four satellite plots were randomly selected in the vicinity of the 10-ha plot. These points could have resulted in a selection bias, potentially affecting our results. If more favourable growing conditions prevailed in the 10-ha plot than in the four cored satellite plots, this could explain why uncored trees tended to have a higher BAI than cored trees in this site. Moreover, differences could result from the recent disturbance history of the 10-ha plot, where a large fraction of the plot was affected by windthrow shortly before the 2010 inventory. Although we controlled for differences in competition status between cored and uncored trees using the propensity score, our competition index might not reflect a steady state and underestimates lateral crown extension next to newly formed gaps in the 10-ha plot. It is well-known that gap formation leads to growth spurts in trees newly released from competition (Lorimer and Frelich 1989; Altman et al. 2014).

From a physiological point of view, it is difficult to explain why larger trees should be more negatively impacted by coring. If at all, we would expect this effect to be stronger and significant in the smallest, suppressed trees. There, the wound is larger relative to the size of the tree, i.e. relative to the available resources that can be invested into defence mechanisms and efforts to close the wound. Similarly, the proportion of damaged vessels is higher in smaller trees, thereby reducing water transport and thus potentially photosynthetic capacity more strongly. However, the general redundancy of the hydraulic system (Mackay and Weatherley 1973; Dietrich et al. 2018) likely makes this a rather theoretical argument for all but the very small trees.

Because within each site, cored and uncored trees differed in terms of DBH distributions and competition levels, we could not directly perform comparisons of growth and mortality with the full dataset. For this reason, we used propensity score matching, a widely used approach in medical studies, to account for these confounding factors (Rosenbaum and Rubin 1984; Zhao et al. 2021) and ensure sound comparisons of cored and uncored trees. This technique, however, strongly relies on the correct specification of the model used to estimate the propensity score. It can only control for the confounding variables included in the model, which can lead to biased estimates if some important confounding factors are left out. While this could be the case here, we are confident that controlling for DBH and competition levels—both known to be the primary factors controlling growth rates within a site (Rohner et al. 2018) —sufficiently enhances the comparability of cored and uncored trees.

Although our results did not reveal significant effects of coring on growth or mortality, previous research has shown that it can cause discolouration of wood, internal trunk decay and cambial necrosis, especially in broadleaf species (Tsen et al. 2016). To reduce these impacts best practices should be developed (Tsen et al. 2016). For example, we deem one core per tree enough to get sufficient annually resolved growth information, and coring should not be repeated annually or too often on the same tree. Equally, coring could be conducted at lower stem positions than the traditional breast height to limit impacts on wood quality, but also to avoid biasing future DBH remeasurements in monitoring and inventorying initiatives because of wound reactions. However, a compromise should be found as stem tapering towards the roots can bias the tree ring measurements. It is also obvious that the thinner the borer (i.e. using a 5 mm as opposed to a 10 mm borer) the shorter it takes to close the borehole and the less time there is for pests and pathogens to enter, which potentially lead to wood decay and deterioration of tree health (Shigo and Marx 1977). Further, having a sharp increment borer reduces damage to trees as well as ensures a higher quality of cores (Maeglin 1979).

In their literature review, Tsen et al. (2016) suggest that no interventions after coring are recommended as they either provide no benefits or might even cause further harm. For example, disinfecting increment borers (e.g. with ethanol) does not avoid fungal infestations and could desiccate and kill cambial tissue and thus actually hamper the healing reaction of trees. Similarly, plugging the borehole had no positive effect and may even introduce pathogens (Dujesiefken et al. 1999). Furthermore, Tsen et al. (2016) discuss that trees, especially broadleaved species, should be cored during the peak of the growing season when they are less likely to form serious surface cankers and are more likely to compartmentalise internal decay effectively. They also suggest avoiding coring of species when the spore load of co-occurring pathogens is high. In addition, we recommend avoiding coring during periods of peak drought stress during the growing season to minimize additional stressors on tree health.

Given the limited and avoidable impacts on tree health, growth and wood quality, as well as the great potential of tree rings for improving scientific knowledge, we stress that systematic collection of tree rings should be promoted to overcome past biases of selective sampling approaches (e.g. Babst et al. 2018) and enhance representative estimates of annual growth processes. When incorporated into long-term monitoring and inventorying programs, a careful determination of the coring height and the awareness of possible DBH-dependent reactions could minimise potential risks. Systematic tree core collections according to a sound coring sampling design within plots in long-term monitoring and inventorying programs could improve our understanding of forest changes and dynamics, especially in light of increasing climate variability and extremes (Evans et al. 2022).

Data availability statement

The code used in the analyses as well as the processed data from the Vordemwald site and the Ukrainian 10 ha plot and satellites in the Uholka reserve are available at https://gitlabext.wsl.ch/portier/tree-coring-study.