Skip to main content
SpringerLink
Log in

Nonlinear Dynamics of an Axially Moving Plate Submerged in Fluid with Parametric and Forced Excitation

  • Published:
Acta Mechanica Solida Sinica Aims and scope Submit manuscript

Abstract

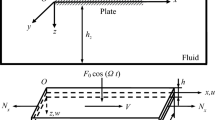
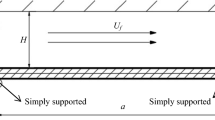
In this study, analytical and numerical methods are applied to investigate the dynamic response of an axially moving plate subjected to parametric and forced excitation. Based on the classical thin plate theory, the governing equation of the plate coupled with fluid is established and further discretized through the Galerkin method. These equations are solved using the method of multiple scales to obtain amplitude-frequency curves and phase-frequency curves. The stability of steady-state response is examined using Lyapunov’s stability theory. In addition, numerical analysis is employed to validate the results of analytical solutions based on the Runge–Kutta method. The multi-value and stability of periodic solutions are verified through stable periodic orbits. Detailed parametric studies show that proper selection of system parameters enables the system to stay in primary resonance or simultaneous resonance, and the state of the system can switch among different periodic motions, contributing to the optimization of fluid–structure interaction system.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

References

  1. Wang L, Ni Q. Vibration and stability of an axially moving beam immersed in fluid. Int J Solids Struct. 2008;45:1445–57.

    Article  Google Scholar 

  2. Ghayesh MH, Kafiabad HA, Reid T. Sub- and super-critical nonlinear dynamics of a harmonically excited axially moving beam. Int J Solids Struct. 2012;49:227–43.

    Article  Google Scholar 

  3. Yang XD, Wu H, Qian YJ, Zhang W, Lim CW. Nonlinear vibration analysis of axially moving strings based on gyroscopic modes decoupling. J Sound Vib. 2017;393:308–20.

    Article  Google Scholar 

  4. Vetyukov Y. Non-material finite element modelling of large vibrations of axially moving strings and beams. J Sound Vib. 2018;414:299–317.

    Article  Google Scholar 

  5. Marynowski K. Free vibration analysis of the axially moving Levy-type viscoelastic plate. Eur J Mech A Solids. 2010;29:879–86.

    Article  Google Scholar 

  6. Ghayesh MH, Amabili M. Non-linear global dynamics of an axially moving plate. Int J Non-Linear Mech. 2013;57:16–30.

    Article  Google Scholar 

  7. Zhou YF, Wang ZM. Dynamic instability of axially moving viscoelastic plate. Eur J Mech A Solids. 2019;73:1–10.

    Article  MathSciNet  Google Scholar 

  8. Banerjee JR, Gunawardana WD. Dynamic stiffness matrix development and free vibration analysis of a moving beam. J Sound Vib. 2007;303:135–43.

    Article  Google Scholar 

  9. Chen LQ, Yang XD. Stability in parametric resonance of axially moving viscoelastic beams with time-dependent speed. J Sound Vib. 2005;284:879–91.

    Article  Google Scholar 

  10. Ding H, Chen LQ. Natural frequencies of nonlinear vibration of axially moving beams. Nonlinear Dyn. 2011;63:125–34.

    Article  MathSciNet  Google Scholar 

  11. Mao XY, Ding H, Lim CW, Chen LQ. Super-harmonic resonance and multi-frequency responses of a super-critical translating beam. J Sound Vib. 2016;385:267–83.

    Article  Google Scholar 

  12. Mao XY, Ding H, Chen LQ. Forced vibration of axially moving beam with internal resonance in the supercritical regime. Int J Mech Sci. 2017;131–132:81–94.

    Article  Google Scholar 

  13. Ghayesh MH, Balar S. Non-linear parametric vibration and stability analysis for two dynamic models of axially moving Timoshenko beams. Appl Math Model. 2010;34:2850–9.

    Article  MathSciNet  Google Scholar 

  14. Sahoo B, Panda LN, Pohit G. Two-frequency parametric excitation and internal resonance of a moving viscoelastic beam. Nonlinear Dyn. 2015;82:1721–42.

    Article  MathSciNet  Google Scholar 

  15. Sahoo B, Panda LN, Pohit G. Combination, principal parametric and internal resonances of an accelerating beam under two frequency parametric excitation. Int J Non-Linear Mech. 2016;78:35–44.

    Article  Google Scholar 

  16. Mao XY, Ding H, Chen LQ. Dynamics of a super-critically axially moving beam with parametric and forced resonance. Nonlinear Dyn. 2017;89:1475–87.

    Article  Google Scholar 

  17. Hatami S, Azhari M, Saadatpour MM. Free vibration of moving laminated composite plates. Compos Struct. 2007;80:609–20.

    Article  Google Scholar 

  18. Yang XD, Zhang W, Chen LQ, Yao MH. Dynamical analysis of axially moving plate by finite difference method. Nonlinear Dyn. 2012;67:997–1006.

    Article  MathSciNet  Google Scholar 

  19. Tang YQ, Chen LQ. Primary resonance in forced vibrations of in-plane translating viscoelastic plates with 3:1 internal resonance. Nonlinear Dyn. 2012;69:159–72.

    Article  MathSciNet  Google Scholar 

  20. Marynowski K, Grabski J. Dynamic analysis of an axially moving plate subjected to thermal loading. Mech Res Commun. 2013;51:67–71.

    Article  Google Scholar 

  21. Hu YD, Zhang JZ. Principal parametric resonance of axially accelerating rectangular thin plate in magnetic field. Appl Math Mech. 2013;34:1405–2013.

    Article  MathSciNet  Google Scholar 

  22. Tang YQ, Chen LQ. Nonlinear free transverse vibrations of in-plane moving plates: without and with internal resonances. J Sound Vib. 2011;330:110–26.

    Article  Google Scholar 

  23. Yao G, Xie ZB, Zhu LS, Zhang YM. Nonlinear vibrations of an axially moving plate in aero-thermal environment. Nonlinear Dyn. 2021;105:2921–33.

    Article  Google Scholar 

  24. Ergin A, Uğurlu B. Linear vibration analysis of cantilever plates partially submerged in fluid. J Fluids Struct. 2003;17:927–39.

    Article  Google Scholar 

  25. Tubaldi E, Alijani F, Amabili M. Non-linear vibrations and stability of a periodically supported rectangular plate in axial flow. Int J Non-Linear Mech. 2014;66:54–65.

    Article  Google Scholar 

  26. Soni S, Jain NK, Joshi PV. Vibration analysis of partially cracked plate submerged in fluid. J Sound Vib. 2018;412:28–57.

    Article  Google Scholar 

  27. Thinh TI, Tu TM, Long NV. Free vibration of a horizontal functionally graded rectangular plate submerged in fluid medium. Ocean Eng. 2020;216:107593.

    Article  Google Scholar 

  28. Li P, Chen H. Vibration analysis of steel strip in continuous hot-dip galvanizing process. J Appl Math Phys. 2013;1:31–6.

    Article  Google Scholar 

  29. Li HY, Lang TY, Liu YJ, Li J. Nonlinear vibrations and stability of an axially moving plate immersed in fluid. Acta Mech Solida Sin. 2019;32:737–53.

    Article  Google Scholar 

  30. Li J, Guo XH, Luo J, Li HY, et al. Analytical study on inherent properties of a unidirectional vibrating steel strip partially immersed in fluid. Shock Vib. 2013;20:793–807.

    Article  Google Scholar 

  31. Li HY, Li J, Liu YJ. Internal resonance of an axially moving unidirectional plate partially immersed in fluid under foundation displacement excitation. J Sound Vib. 2015;358:124–41.

    Article  Google Scholar 

  32. Amabili M. Nonlinear vibrations and stability of shells and plates. New York: Cambridge University Press; 2008.

    Book  Google Scholar 

  33. Wang YQ, Huang XB, Li J. Hydroelastic dynamic analysis of axially moving plates in continuous hot-dip galvanizing process. Int J Mech Sci. 2016;110:201–16.

    Article  Google Scholar 

  34. Permoon MR, Haddadpour H, Javadi M. Nonlinear vibration of fractional viscoelastic plate: primary, subharmonic, and superharmonic response. Int J Non-Linear Mech. 2018;99:154–64.

    Article  Google Scholar 

Download references

Acknowledgements

This work was supported by the National Natural Science Foundation of China (Grant No.11502050 and No.12272091).

Author information

Authors and Affiliations

  1. Key Laboratory of Structural Dynamics of Liaoning Province, College of Sciences, Northeastern University, Shenyang, 110819, China

    Hongying Li, Yijiao Xu, Wenqi Zhang & Jian Li

Authors
  1. Hongying Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Yijiao Xu
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Wenqi Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Jian Li
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Hongying Li.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Li, H., Xu, Y., Zhang, W. et al. Nonlinear Dynamics of an Axially Moving Plate Submerged in Fluid with Parametric and Forced Excitation. Acta Mech. Solida Sin. (2024). https://doi.org/10.1007/s10338-024-00473-9

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s10338-024-00473-9

Keywords

Search

Navigation