1 Introduction

The art of origami folds a flat sheet into a three-dimensional (3D) structure without cutting and adhesion. In recent years, it has received great attention in the fields of deployable space structures [1], functional metamaterials [2, 3] and flexible robotics [4, 5], because of the unusual properties associated with origami-inspired structures such as negative Poisson's ratio [6, 7], multi-stability [8, 9], variable stiffness and configuration [10]. The origin of the unusual properties comes from the rational arrangement of creases and panels. So far, origami optimization has mainly focused on regulating the size, shape and assembly method of typical crease design to meet or improve a certain performance [11,12,13]. However, the conventional origami design methods by regulating and adjusting the known crease patterns cannot satisfy the rapidly growing engineering applications of origami. Therefore, it is necessary to explore new crease design methods.

The wrinkle patterns induced by instability have been related to origami structures as the spontaneous fold behavior results in rich deformation adaptivity, potential functionality and a great assembly property [14, 15]. The well-known Miura-ori structure and Kresling tube are typical representatives of origami designs inspired by wrinkle patterns. The Miura-ori pattern was discovered in a biaxial compression experiment of a thin, stiff, elastic film supported by a thick, soft substrate [16], and the Kresling pattern was originally discovered when twisting thin-walled cylinders [17]. They both have been used successfully in a variety of applications [6,7,8, 18].

Mechanical instability due to local excessive compression is a common natural phenomenon in our daily life, which causes a flat thin sheet to spontaneously transform into a certain 3D wrinkled configuration [19]. This deformation process results in self-organized wrinkle patterns that naturally possess the lowest level of energy [20]. These wrinkle patterns not only are related to material parameters and geometric parameters, but also largely depend on boundary conditions (e.g., loading, deformation constraints, etc.). Different boundary conditions yield drastically different wrinkle patterns and hence lead to different origami designs. To translate wrinkle patterns into corresponding origami designs, we first simulate the wrinkling behavior of thin sheets, and then identify folding creases by certain selection criteria.

Typically, there are two approaches to simulating the wrinkling behaviors of thin film. The first one is to establish a continuum model with finite elements [21, 22]. It can provide detailed physical field information, but needs a lot of elements to describe local strong curvatures which are common in wrinkle patterns. Therefore, more computing resources and time are needed. In addition, local instability may affect convergence of the analysis on the global behavior [23]. The second approach is to simplify the thin film into a discrete bar-and-hinge (or spring-mass) model [23,24,25]. It has an excellent capability in predicting the global deformation as well as local folding behaviors. Comparing with the continuum finite element model, origami mechanical analysis conducted with the bar-and-hinge model needs fewer elements and nodes. And the number of design variables can also be reduced greatly for the origami topology optimization. Therefore, the bar-and-hinge model is the ideal analysis method for our research goal because of the high computational efficiency in structural analysis and solving optimization model.

The design problem of crease layout can be formulated as an origami topology optimization problem [26]. Among the geometric parameter optimization methods [27,28,29,30], the origami topology optimization has the potential to completely obtain the new crease pattern without requiring prescribed initial crease patterns. At present, origami topology optimization was limited to key nodal displacement optimization for actuator designs [26, 30,31,32]. These designs were carried out by the following optimization formulation proposed by Fuchi and Buskohl [26].

$$ \left\{ \begin{gathered} {\text{Max}}\begin{array}{*{20}c} {} \\ \end{array} \, g_{1} ({\varvec{\alpha}}) = {\varvec{c}}^{{\text{T}}} \user2{u } \hfill \\ {\text{s}}{\text{.t}}{.}\begin{array}{*{20}c} { \, g_{2} ({\varvec{\alpha}}) = v_{0} - \frac{1}{{N_{f} }}\sum\limits_{k = 1}^{{N_{f} }} {\alpha_{j} } \le {0 }} \\ \end{array} \hfill \\ \, \quad \quad 0 \le \alpha_{j} \le 1{ (}j = 1, \cdots ,N_{f} {) } \hfill \\ \end{gathered} \right. $$
(1)

where \(g_{1}\) is the objective function, and \({\varvec{u}}\) denotes the nodal displacement vector. Constant vector c is used to prescribe the selection of nodes and direction of the target deflection by assigning “1” or “−1” to locations associated with the target degrees of freedom. The symbol \(g_{2}\) denotes the crease constraint, and \(\alpha_{j}\) indicates the status of creases, which is between 0 and 1. When \(\alpha_{j} = 1\), the hinge element is located on a panel and has a high fold stiffness; when \(\alpha_{j} = 0\), the hinge element is located at a crease and has a low fold stiffness.\(N_{f}\) is the total number of hinge elements. This formulation was applied to the displacement optimization problem of actuators under the load of forces. The creases are selected based on the contribution to the key nodal displacements, although various algorithms have been used to solve the formulation. This topology optimization framework is quite similar to the compliant mechanism design formulation [33], and the types of origami patterns it can design are very limited. With a small twist, we can turn this formulation into a new one that is capable of discovering a wide range of origami patterns based on the idea of instability-induced wrinkle patterns.

The remainder of this paper explains our new formulation in details, supported by numerical examples. The bar-and-hinge model added with a displacement perturbation strategy is employed to simulate the large deformation behavior of a thin sheet under compression. For origami inspired by the wrinkle pattern, the creases should be placed at the central position of the wrinkles where there exists stress concentration. Therefore, a topology optimization framework with minimum strain energy and crease constraint is established to automatically assign creases on a thin sheet. Then, numerical examples are given to illustrate the effectiveness and feasibility of the design method.

2 Mechanical Analysis

2.1 Bar-and-Hinge Model

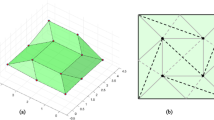
The bar-and-hinge model [24], as shown in Fig. 1a, is adopted for simulation due to high computing efficiency and convenient crease definition. In the bar-and-hinge model, in-plane stretching and compressing are described by the bar elements. Out-of-plane bending and folding deformations are depicted by the hinge elements. Based on this setup, a fully nonlinear, displacement-based quasi-static structural analysis method of origami structures was developed by Liu and Paulino [23], which has been proven effective in analyzing the buckling and post-buckling behavior of origami structures.

Fig. 1
figure 1

Schematic of mechanical analysis model: a bar-and-hinge model; b stiffness switching for a hinge

Full size image

For non-rigid origami structures, the rotational deformation near the crease is far greater than that at the panel. The folding of a crease and the bending of a panel can be described by the folding and bending hinge elements shown in Fig. 1a. In general, the torsional stiffness of a folding hinge \(k_{\rm R}^{{\text{F}}}\) is far less than that of a bending hinge \(k_{\rm R}^{{\text{B}}}\). The same constitutive equation but with different torsional stiffness provides a chance for hinge switching, as illustrated in Fig. 1b.

2.2 Displacement Perturbation

For a thin sheet, instability occurs when the in-plane compressive stress exceeds a critical value. In this paper, the buckling trigger criterion of the bar-and-hinge model is proposed according to the compression state of the bars. As shown in Fig. 2a, the critical buckling load \(F_{{{\text{cr}}}}\) of a bar under compression with one end fixed and the other free is given as follows:

$$ F_{\text{cr}} = \frac{{\pi^{2} EI_{y} }}{(2l)^{2} }$$
(2)

where \(E\) is the elastic modulus, \(I_{y}\) is the moment of inertia along the x-axis, and \(l\) is the length of a bar.

Fig. 2
figure 2

Displacement perturbation to trigger local out-of-plane buckling: a diagram of a bar under compression; b deformation analysis of a compressed sheet before adding displacement disturbance; c deformation analysis of a compressed sheet after adding displacement disturbance

Full size image

When the internal force of a compressed bar exceeds the critical buckling load \(F_{{{\text{cr}}}}\), the out-of-plane deformation of a thin sheet will occur. Here, a displacement perturbation \(\Delta u_{z}\) along the z-direction is added at the free end as follows

$$ \Delta u_{z} = \lambda \sqrt {l^{2} - (l^{2} - \Delta l)^{2} } $$
(3)

where \(\Delta l = \frac{{F_{{{\text{cr}}}} }}{AE}l{ = }\frac{{\pi^{2} I_{{{y}}} }}{{(2l)^{2} A}}l\) is the axial compressive deformation, and \(\lambda\) is the disturbance control parameter, which determines the magnitude of the displacement disturbance. When \(\lambda = 0\), it indicates that the bar remains undeformed in the z-axis. When \(\lambda = 1\), it means that the compressive deformation of the bar is released completely and the displacement disturbance in the z-axis equals to \(\sqrt {l^{2} - (l^{2} - \Delta l)^{2} }\). Therefore, the disturbance control parameter \(\lambda\) is in the range of (0, 1) because the compressive deformation usually does not disappear completely. The exact value of \(\lambda\) is hard to obtain directly because the deformation of a bar after instability is very complex in a structural system. But numerous numerical examples show that final wrinkle pattern after post-buckling analysis always remains the same regardless of the value of \(\lambda\). The deformation diagrams of a thin sheet under displacement compression before and after adding displacement perturbation are illustrated in Fig. 2b and c. It is obvious that the post-buckling deformation is induced by applying displacement disturbance.

3 Origami Topology Optimization

3.1 Crease Assignment

In order to endow a hinge with the ability to evolve into a bending hinge or a folding hinge, an independent and continuous design variable \(\alpha\) is introduced to indicate the state of a hinge inspired by the independent continuous mapping (ICM) method [34]. As shown in Fig. 3, \(\alpha { = }1\) indicates that it has grown into a folding hinge with crease properties. \(\alpha { = }0\) denotes that it is a bending hinge and is located at a panel. \(0 < \alpha < 1\) represents that it is in an intermediate state. The growth process of \(\alpha\) is that one panel is gradually cracked into two panels. The degradation process of \(\alpha\) is regarded as the process of two panels merging into one panel.

Fig. 3
figure 3

Physical properties at the upper and lower limits of the crease indicator

Full size image

Establishment of the relationship between the crease indicator and corresponding physical properties is the premise to realizing origami topology optimization. Referring to the mass and stiffness mapping models in the ICM method [34], the crease length filter function \(f_{{\text{L}}} (\alpha )\) and stiffness filter function \(f_{{\text{k}}} (\alpha )\) are introduced to establish the mapping relationships between crease indicator \(\alpha\) and corresponding physical properties. The equivalent length and stiffness of a crease are calculated as follows:

$$ \begin{aligned} & L(\alpha ) = f_{\text{L}} (\alpha )L^{0} ,\;\;\;\;f_{\text{L}} (\alpha ) = \alpha ,\;\;\;\;L(0) = 0,L(1) = L^{0} , \hfill \\ & k_{\text{R}} (\alpha ) = f_{\text{k}} (\alpha )k_{\text{R}}^{\text{B}} ,\;\;\;\;f_{\text{k}} (\alpha ) = 1 - \beta \alpha^{3} ,\;\;\;\;k_{\text{R}} (0) = k_{\text{R}}^{\text{B}} ,\;\;\;\;\\ & k_{\text{R}} (1) = k_{\text{R}}^{\text{F}} = (1 - \beta )\;k_{\text{R}}^{\text{B}} \hfill \\ \end{aligned} $$
(4)

where \(L(\alpha )\) is the crease equivalent length, \(L^{0}\) is the length of a hinge, and \(k(\alpha )\) is the equivalent torsional stiffness. The constant coefficient of the stiffness filter function \(\beta\) depends on the relationship between the torsional stiffness of the bending and folding hinges. When \(\alpha = 0\), the crease equivalent length is 0, and the equivalent stiffness is \(k_{{\text{R}}}^{{\text{B}}}\). When \(\alpha = 1\), the crease equivalent length is \(L^{0}\), and the equivalent stiffness is \(k_{{\text{R}}}^{{\text{F}}}\). By introducing the relationship between the crease indicator and the corresponding equivalent stiffness, the wrinkle analysis of a thin sheet with an arbitrary set of design variables can be conducted by the mechanical analysis method presented in Part 2.

3.2 Topology Optimization Formulation

It is obvious that high levels of strain and stress at the center lines of the wrinkles contribute significantly to the structural strain energy. Therefore, the position of creases can be quickly selected by taking the minimum total strain energy as the objective function. A topology optimization formulation for origami induced by instability is established as follows

$$ \left\{ \begin{gathered} {\text{Min }}g_{1} ({\varvec{\alpha}}) = U^{\rm T} ({\varvec{u}}, \, {\varvec{\alpha}}) = \sum\limits_{i = 1}^{{N_{1} }} {U_{Bi} ({\varvec{u}}_{i} )} + \sum\limits_{j = 1}^{{N_{2} }} {U_{Sj} (\theta_{j} ,\alpha_{j} )} \hfill \\ s.t.\quad \, g_{2} ({\varvec{\alpha}}) = \sum\limits_{j = 1}^{{N_{2} }} {L_{j}^{0} \alpha_{j} /\sum\limits_{j = 1}^{{N_{2} }} {L_{j}^{0} } \le \overline{C} } \hfill \\ \quad \quad 0 \le \alpha_{j} \le 1 \, (j = 1,\cdots ,N_{2} ) \hfill \\ \end{gathered} \right. $$
(5)

where \(g_{1}\) denotes the structural strain energy \(U^{{\text{T}}}\), which is the sum of the strain energy of all elements. \(U_{Bi}\) is the strain energy of bar element \(i\), and \(U_{Sj}\) is the strain energy of hinge element \(j\). \(\theta\) is the dihedral angle, which is determined by the nodal displacement vector of the corresponding hinge element. \(g_{2}\) equals the crease dosage. \(N_{1}\) and \(N_{2}\) are the total numbers of bar and hinge elements, respectively. \(\overline{C}\) is the upper limit of crease length ratio.

In order to solve Eq. (5), obtaining the explicit objective equation is a crucial step. \(U^{{\text{T}}} ({\varvec{u}}{, }{\varvec{\alpha}})\) is a smooth function of vectors \({\varvec{u}}\) and \({\varvec{\alpha}}\). For each \({\varvec{\alpha}}\), \(U^{{\text{T}}} ({\varvec{u}}{, }{\varvec{\alpha}})\) has a unique minimum point \({\varvec{u}} = {\varvec{u}}({\varvec{\alpha}})\) among all \({\varvec{u}}\) that meet the minimum structural potential energy [35]. According to the theorem for min-functions [36], the partial derivative of total strain energy with respect to \(\alpha_{j}\) is given as follows:

$$\begin{aligned} \left. {\frac{{\partial U^{{\text{T}}} }}{{\partial \alpha_{j} }}} \right|_{{\user2{u = u}{(}{\varvec{\alpha}}{)}}} &= \frac{{\partial U_{Sj} ({\varvec{\alpha}}_{j} )}}{{\partial {\varvec{\alpha}}_{j} }}{ = }\frac{{\partial f_{{\text{k}}} (\alpha_{j} )}}{{\partial {\varvec{\alpha}}_{j} }}U_{Sj} (k_{{\text{R}}}^{{0}} ) \\ &= - 3\beta \alpha_{j}^{2} U_{Sj} (k_{{\text{R}}}^{{0}} ){ = }\frac{{ - 3\beta \alpha_{j}^{2} }}{{1 - \beta \alpha_{j}^{3} }}U_{Sj} (\theta_{j} {, }{\varvec{\alpha}}_{j} )\end{aligned} $$
(6)

The first-order linear Taylor expansion of structural strain energy can be expressed as follows:

$$\begin{aligned} g_{1} ({\varvec{\alpha}})& = U^{{\text{T}}} \approx \, \sum\limits_{i = 1}^{{N_{1} }} {U_{Bi} ({\varvec{u}}_{i}^{(\upsilon )} )}\\& { + }\sum\limits_{j = 1}^{{N_{2} }} {\frac{{ - 3\beta (\alpha_{j}^{(\upsilon )} )^{2} }}{{1 - \beta (\alpha_{j}^{(\upsilon )} )^{3} }}U_{Sj} (\theta_{j}^{(\upsilon )} {, }{\varvec{\alpha}}_{j}^{(\upsilon )} )(\alpha - \alpha^{(\upsilon )} )} \end{aligned}$$
(7)

where the superscript \(\upsilon\) is the iterative number of the optimization algorithm. Because the constant term has no influence on the optimal result, the objective function can be rewritten as follows:

$$ g_{1} ({\varvec{\alpha}}) = \sum\limits_{j = 1}^{{N_{2} }} {a_{j} } \alpha_{j} \to {\text{Min}} $$
(8)

where \(a_{j} { = }\frac{{ - 3\beta (\alpha_{j}^{(\upsilon )} )^{2} }}{{1 - \beta (\alpha_{j}^{(\upsilon )} )^{3} }}U_{Sj} (\theta_{j}^{(\upsilon )} {, }{\varvec{\alpha}}_{j}^{(\upsilon )} )\). Then, the optimization formulation can be simplified as follows:

$$ \left\{ \begin{gathered} {\text{Min}}\begin{array}{*{20}c} {} \\ \end{array} g_{1} ({\varvec{\alpha}}) = \sum\limits_{i = 1}^{{N_{2} }} {a_{j} } \alpha_{j} \hfill \\ {\text{s}}{\text{.t}}{.}\begin{array}{*{20}c} { \, g_{2} ({\varvec{\alpha}}){ = }\sum\limits_{{j{ = }1}}^{{N_{2} }} {\alpha_{j} \le \overline{C} \times N_{2} } } \\ \end{array} \hfill \\ \, \quad \quad 0 \le \alpha_{j} \le 1{ ( }j = 1,\cdots ,N_{2} {)} \hfill \\ \end{gathered} \right. $$
(9)

Based on the explicit formulation of Eq. (9), the optimality criteria (OC)-based algorithm [37] is adopted to solve and update the crease indicator. The convergence condition of the origami topology optimization framework is given as follows:

$$ \left| {\frac{{g_{1} ({\varvec{\alpha}}^{(\upsilon + 1)} ) - g_{1} ({\varvec{\alpha}}^{(\upsilon )} )}}{{g_{1} ({\varvec{\alpha}}^{(\upsilon + 1)} )}}} \right| \le \xi $$
(10)

where \(\xi\) is the convergence precision.

4 Benchmark Problem

In this section, the topology optimization method is used to design the crease pattern of a thin sheet with simple in-plane load boundary conditions. All the examples have the same material parameters, which are shown in Table 1, where Ab is the cross-sectional area of a bar, and E is the elastic modulus. For all examples, the convergence precision \(\xi\) is 0.001.

Table 1 Material parameters
Full size table

4.1 A Straight Fold

The first example is a benchmark problem whose solution is obviously a simple straight fold. The geometry and boundary conditions of the structure are depicted in Fig. 4a. Point A is fixed, and a displacement load of 1.5 is applied at point B along the y-direction. Here, we discuss the influence of the background grid on the optimal crease pattern. A sheet without any creases is considered the initial design. Then, two different background grids are applied on the sheet, which are illustrated in Fig. 4b and c.

Fig. 4
figure 4

Mechanical model: a geometry and boundary conditions; b initial model A; c initial model B

Full size image

Figure 5 illustrates the iterative curves of total energy and crease length ratio. The sheet is easy to lose stability under axial compression, and shows the deformation mode of folding in half. A straight crease is the optimal design for both initial models A and B from the perspective of strain energy. From the iterative curves, we can find that the total strain energy falls first, then converges stably. The crease length ratio increases first and then reaches stable convergence. Stable iterative convergence curves of total energy and actual crease length demonstrate the effectiveness of the optimization design method. The energy iteration curve also shows that a reasonable arrangement of creases makes a huge contribution to energy reduction during folding.

Fig. 5
figure 5

Iterative curves of total energy and crease length ratio with different background grids of a sheet: a starting with initial model A; b starting with initial model B

Full size image

4.2 Tent/Waterbomb

In this example, we explore the instability-induced origami designs of a thin square sheet under biaxial compression. The geometry and boundary conditions are shown in Fig. 6a. The x- and y-directions of the middle point E are fixed, and it can only move along the z-direction. The midpoints of the four sides are fixed along the z-direction. A displacement of 1 toward the middle point E is applied at points A-D. The four initial bar-and-hinge models are shown in Fig. 6 b–e. Figure 7 gives the iterative history of the total energy and crease length ratio.

Fig. 6
figure 6

Mechanical model: a boundary conditions; b initial model A; c initial model B; d initial model C; e initial model D

Full size image
Fig. 7
figure 7

Iterative curves of total energy and crease length ratio with different initial crease patterns: a starting with initial model A; b starting with initial model B; c starting with initial model C; d starting with initial model D

Full size image

From Fig. 7, although the cases starting with model B and C suffer from shock, the iterative processes of strain energy and crease length ratio are of stable convergence. By observing the phenomenon of rocket configuration appearing in cases B and C, it is thought that local penetration causes the anomalous mechanical analysis results. This phenomenon is probably caused by the bifurcation behavior [38]. Unreasonable initial path information also leads to wrong mechanical analysis results. Under such load conditions, the buckling-induced origami designs tend to become a tent or a waterbomb with 8 creases. The final total energies of the tent and the waterbomb are 0.243 and 0.284, and the final crease consumptions are 0.540 and 0.420, respectively. Both designs are reasonable from the aspect of strain energy and crease consumption. Besides, it can be found that the final origami designs depend on the initial crease distribution of the thin sheet, but are generally different from the initial designs.

5 Summary and Outlook

In this paper, we propose a computational origami design method based on topology optimization on a bar-and-hinge model by minimizing the total strain energy of buckled patterns. The straight fold and tent/waterbomb designs demonstrate and prove the effectiveness and feasibility of the design method. From the numerical examples, we find that:

  1. (1)

    The creases perpendicular to in-plane compression are the most easily triggered creases.

  2. (2)

    The optimized design not only is related to the loading condition, but also relies on the initial design.

For a thin sheet with the known wrinkle pattern, it is easy to give the upper limit of crease length ratio. But it is hard to define the crease constraint directly when the potential wrinkle pattern remains unknown. Preliminary wrinkle analysis or repetitive optimization trials are required to find a suitable constraint. Therefore, it is urgent to establish an automatic crease assignment method without presetting crease constraint. Furthermore, numerical instability caused by bifurcation also needs to be overcome in order to ensure stable convergence of the iterative framework.