Abstract
Purpose
To present a modeling workflow for the evaluation of a lead electromagnetic model (LEM) consisting of a transfer function (TF) and a calibration factor. The LEM represents an analytical relationship between the RF response of a lead and the incident electromagnetic field. The study also highlights the importance of including key geometric details of the lead and the electrode when modeling multi-electrode leads.
Methods
The electrical and thermal responses of multi-electrode leads with helical and straight wires were investigated using 3D electromagnetic (EM) and thermal co-simulations. The net dissipated power (P) around each lead electrode and the net temperature increase at the electrodes (ΔT) were obtained for a set of incident EM fields with different spatial distributions. A reciprocity approach was used to determine a TF for each electrode based on the results of the computational model. The evaluation of the calibration factors and the TF validation were performed using the linear regression of P versus the LEM predictions.
Results
P and ΔT were investigated for four multi-electrode leads and four single-electrode leads containing either helical or straight wires. All electrodes of the multi-electrode lead were found to be points of high power deposition and temperature rise. The LEMs for the individual electrodes varied substantially. A significant dependence of the calibration factors on the surrounding tissue medium was also found. Finally, the model showed that the TF, the calibration factor, P and ΔT for multi-electrode leads differ significantly from those for single-electrode leads.
Conclusion
These results highlight the need to evaluate a LEM for each electrode of a multi-electrode lead as well as for each possible surrounding medium. It is also shown that the results derived from simulations based on simplified single-electrode leads can significantly mislead multi-electrode lead analyses.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Radiofrequency (RF)-induced heating of tissues near an electrode of an active implantable medical device (AIMD) is a potential problem for patients undergoing magnetic resonance imaging because tissue damage may occur for sustained exposure above critical temperatures (MRI) [1,2,3,4,5]. Two quantities are typically used to characterize the RF responses of an AIMD: (i) the net dissipated power (P) surrounding the AIMD lead electrode and (ii) the net temperature increase at the electrode (ΔT):
where σ is the electrical conductivity of the surrounding medium, Etotal(v) is the electrical field with the lead in place, Ebackgnd(v) is the electrical field without the lead in place, HSIV is the hot spot integration volume, ΔTtotal is the temperature increase at the electrode with the lead in place, and ΔTbackgnd is the temperature increase at the electrode without the lead in place.
In vivo measurement of P and ΔT during an MRI scan of live human subjects is not currently feasible. ΔT has been evaluated in a limited number of cadaver [6] and animal [7, 8] studies, however. Computational modeling has been identified as a useful approach for understanding the nature of lead interactions with incident electromagnetic (EM) fields in vivo [9]. Recent publications have analyzed leads containing only one electrode [10,11,12], in spite of the fact that multi-electrode leads are more common in AIMDs. Multi-electrode leads have also been analyzed [13,14,15,16,17,18], however substantial simplifications of the lead wire structure were made, e.g., substitution of a multi-wire design with a single wire. These geometric simplifications are a concern because they can have a significant impact on safety assessments.
In spite of continually expanding computational capacity, a prohibitive amount of time is required to conduct electromagnetic (EM) simulations that comprise the full parameter matrix formed by (i) a set of high-resolution human body models that represent the AIMD patient population, (ii) the detailed AIMD model at all possible locations, (iii) a set of MRI RF transmit coils that represent clinically relevant cases, and (iv) a set of relevant patient landmark positions inside the MRI RF transmit coils. Domain decomposition is a common technique to split the solution of a complex problem into a set of substantially simpler sub-tasks. For AIMD RF safety assessments, one possible decomposition consists of separating the human RF exposure due to the MRI RF transmit coil from the assessment of the RF responses of the lead. The former could be accomplished by generating a set of clinically relevant incident tangential RF electric fields (Etan(l)) along the lead pathways, and the latter by evaluating P and ΔT to this set of Etan(l).
Experimental or numerical domain evaluation of lead RF responses to the full set of Etan(l) derived from human RF exposure analysis is still an extremely complex task because (i) the evaluation should represent the matrix of multi-tissue environments that may be encountered by the lead tip in vivo and (ii) the generation of Etan(l) with complex spatial distributions of amplitude and phase requires the construction of a multi-channel RF transmit source with difficult to implement near field directivity of antennas and low mutual coupling between antennas.
The analytical lead electromagnetic model (LEM) was proposed to evaluate the RF responses to a set of clinically relevant Etan(l) in humans [19]:
where A and AT are the calibration factors, S(l) is the transfer function (TF), and L is the lead length. Note that the TF is the same for all RF responses of a given lead electrode because the TF is a relative measure of different lead segment contributions in the EM field radiated by a given electrode [20]. Thus, for a given AIMD electrode, the LEM of an RF response consists of the same TF and a calibration factor specific to this RF response. While concepts for developing a LEM have been published, there have been no publications outlining procedures for assessing a LEM of clinically relevant AIMDs. Indeed, the details are considered trade secrets and are highly guarded by AIMD manufacturers.
Several approaches to determine the TF have been published: piecewise excitation [19], reciprocity [21], transmission line modeling [22, 23], and MRI-based [24]. Evaluation of the calibration factor was rarely described, for example [20, 25]. However, it is impossible to evaluate an RF response of a lead for clinically relevant Etan(l) without knowledge of the calibration factor. Both experimental and numerical TF determination procedures have deficiencies. For example (i) it is impossible to define a piecewise excitation with infinitely short length and (ii) some assumptions of the transmission line model are not valid for all lead types. Thus, the measured or simulated TF should be validated using an approach that is independent from the TF generation procedure (a typical requirement of model validation).
The TF can be obtained for multi-tissue lead environments. However, different lead pathways result in different multi-tissue lead environments and thus varied TFs. To avoid multi-tissue testing requirements, the ISO/TS 10974:2018 Tier3 procedure [26] suggests testing in a homogeneous medium with the electrical properties close to those of the medium (tissue) that is in predominant contact with the AIMD. ISO/TS 10974:2018 also specifies that the AIMD should also be evaluated in several media with appropriate electrical properties if more than 10% of the cumulative physical length of the AIMD pathway spans different tissues.
Following from the above and the facts that (i) the measurement results are rather noisy due to substantial uncertainty of measurement probes and other uncertainties of the measurement setups, and (ii) the high cost of a typical measurement setup (greater than $500,000 US), the main goals of this study were to develop a numerical workflow for modeling the LEM and the RF responses of various multi-electrode lead designs using EM and thermal co-simulation of the entire lead and electrodes. The LEM and RF responses for a range of incident EM fields were evaluated in several tissue media. The calculated RF responses, i.e., P and ΔT, were used to validate the TF and to estimate the correspondent calibration factors. The impact of simplifying a multi-electrode lead to a single electrode was also analyzed.
Methods
Computational model overview
The computational modeling workflow consists of four major steps: (i) obtaining the TF for a given lead, (ii) validating the TF and evaluating the calibration factors of the LEM, (iii) evaluating the power deposition and temperature responses to a set of incident EM fields, and (iv) estimating the power deposition and temperature response to the power injection into a multi-electrode lead. 3D EM simulations at 128 MHz were performed using the frequency-domain solver of ANSYS HFSS (ANSYS, Inc., Canonsburg, PA, USA). Volume and surface losses from the 3D EM simulations were input as thermal sources for the thermal simulations performed using the ANSYS Non-Linear Thermal (NLT) platform (ANSYS, Inc., Canonsburg, PA, USA).
The computational meshes of the 3D EM and thermal numerical domains were independently generated in each solver to ensure the best suitable mesh for each simulation modality. A mesh adaption procedure in HFSS increased the number of mesh elements until the variation of P or ‖S‖max (representing the maximum of the transfer function magnitude ‖S‖ over all spatial points) between two consecutive meshes was less than 3%. Applying this procedure resulted in a mesh size in the region of maximum power deposition that was less than 5 μm. The initial temperature for both the implant and the surrounding medium was 22 °C. The initial time step of the thermal simulation was 125 µs, which is more than 10 times shorter than the shortest thermal constant in the simulation domain. The flux convergence of the thermal solver was set to 0.0001. The convergence of the thermal simulation was obtained by manual refinement of the mesh until the difference between maximum temperature rise (ΔTmax) was less than 3% for two sequential meshes. This resulted in a mesh size in the region of maximum thermal gradient that was less than 8 μm.
Lead description
The exact dimensions and other geometric details of commercially available multi-electrode leads have not been published. We therefore construct the leads used in these studies from literature information [27] as well as publicly available pictures and datasheets. The wire design was estimated based on literature data: (i) the wire diameter is typically less than 0.2 mm and (ii) the distance between adjacent helical wires typically ranges from one to three wire diameters. For mechanical reliability reasons, commercial leads are fabricated using a multi-filament wire. Computational models of multi-filament wires require significant computational resources because each filament must be meshed independently to capture its micrometer-range geometric structure. In our study, the multi-filament wires were substituted with single-filament wires of equivalent cross-section and geometry, namely helical or straight. Mo et al. [28] reported similar temperature rise measurements for leads with seven-filament and bare wires, which indirectly confirms this simplification.
Four 8-electrode lead designs were investigated. The leads were 300 mm in length and 1.35 mm in diameter. Each of the eight titanium alloy electrodes was 3 mm in length with outer and inner diameters of 1.35 mm and 1.15 mm, respectively. The distance between the electrodes was 4 mm (Fig. 1a). The solder connection between the wires and electrodes was modeled as a welded joint that was 0.75 mm in length and 0.2 mm in width at the distal end (Fig. 1c). And while not present in commercial leads, an artificial connector of 1 mm in length was employed at the proximal end of the lead to define realistic impedance between wires (Fig. 1d). This connector consisted of 8 wire pins that were in electrical contact with corresponding lead wires, ground pin, and 8 lumped 3.6 pF capacitors installed between the ground pin and wire pins. These capacitors modeled the input impedance of the implanted pulse generator. An internal air tube with diameter of 0.45 mm was located inside all four leads (Fig. 1c). For leads constructed with straight titanium alloy wire, the thickness of each wire was 0.165 mm (Fig. 1c). For leads constructed with helical titanium alloy wire, each helical structure was made of 0.1 × 0.1 mm rectangular wire with a pitch of 2.0 mm and an external diameter 1 mm (Fig. 1b). The distance between adjacent helical wires was ~ 0.15 mm. The relative electric permittivity of the insulator material (εr) was varied from 2.7 to 5.5 to investigate the effect of this design parameter on lead performance.
a Close-up view of the 8-electrode portion of the lead and hot spot integration volumes (HSIV). b Close-up view of the 8 helical wires. c Cross-section of the straight-wire lead at the solder location of the wire and electrode. d Cross-section of the straight-wire lead in the connector pins region (i.e., proximal end). e Close-up view of the electrode portion of the single-electrode lead
The leads were surrounded by one of three tissue media in each simulation: (i) εr = 78 and σ = 1.2 S/m (approximating blood); (ii) εr = 78 and σ = 0.47 S/m (approximating generic biological tissue, as defined in ASTM 2182-11a and ISO/TS 10974:2018 to represent the global weighted average of human tissues), and (iii) εr = 44 and σ = 0.354 S/m (approximating nerve tissue) [29]. Values of the electrical and thermal properties for all materials are summarized in Table 1.
Single-electrode leads were also investigated and compared to the results for the multi-electrode leads. Many dimensions of the single-electrode lead matched those of the multi-electrode lead, including the length and diameter of the lead as well as the length and inner/outer electrode diameters (Fig. 1e). The helical wire design was constructed from eight 0.1 × 0.1 mm rectangular wires with a pitch of 0.33 mm, resulting in a similar distance between adjacent wire turns in the single and multi-electrode leads. Eight different lead designs were evaluated, four with helical wires and four with straight wires. The four helical wire designs were formed from all four combinations of external wire diameter (0.9 mm and 1.1 mm) and insulator relative permittivity (2.7 and 5.5). Similarly, the four straight wire designs were formed from all four combinations of wire diameter (0.73 and 1.0 mm) and insulator permittivity (2.7 and 5.5). The single-electrode leads were capped at the proximal end. The single-electrode leads were only analyzed for the medium with electrical properties approximating blood, i.e., εr = 78 and σ = 1.2 S/m because the maximum P for multi-electrode leads was observed in this medium.
Transfer function development and calibration factor evaluation
Applying the reciprocity approach and using a current source and 161 numerical current sensors of infinitely short length, the TF was obtained at 161 equidistant points (Fig. 2a). The TF was obtained for each electrode, lead, and surrounding medium using this approach. Each TF was normalized such that \(\mathop \smallint \nolimits_{0}^{L} \left| {S\left( l \right)} \right| \cdot {\text{d}}l\) = 1 and the phase at the first location was shifted such that the phase of S(0) = 0.
Ideally, calibration factor evaluation and validation of the TF at n equidistant points requires a set of n orthogonal non-homogeneous Etan(l) and corresponding RF response measurements, i.e., P or ΔT. In reality, calibration factor evaluation and TF validation is accomplished using a linear regression analysis based on the results obtained for a set of artificial heterogeneous Etan(l). This set of heterogeneous Etan(l) is typically generated in a phantom filled with tissue simulating medium by (i) modifying the lead path within the phantom located inside a RF birdcage coil [26] or (ii) modifying the excitation of a dual-channel RF birdcage coil containing the phantom [30]. These approaches require a curved lead trajectory, which can lead to EM field scattering for certain AIMD lead designs and distances between AIMD lead segments. The scattered EM field from one AIMD lead segment to another should be avoided for reliable LEM validation because the scattered EM field modifies the incident EM field. Because (i) to generate computer-aided design (CAD) models of a helical wire for curved lead trajectories is challenging and (ii) a straight lead trajectory results in the smallest EM field cross-scattering, our previously developed numerical approach to obtain a series of heterogeneous Etan(l) for straight lead trajectories [25] was applied as follows.
Each lead was positioned parallel to the z-axis in the middle of a rectangular box (600 mm × 400 mm × 2400 mm) containing one of the three tissue media (Fig. 2b). The box was surrounded by a perfectly matched layer. Four numerical antennas were located along one (yz) side of the box, generating an EM field at 128 MHz. Each antenna generated an EM field so that the z-component of the electric field was dominant at the lead location. 40 non-uniform Etan(l) were generated using a set of 40 different antenna source amplitudes and phases (Fig. 2c). None of the Etan(l) was a scaled replica of other Etan(l) in the set. Etan(l) along the lead trajectory, \(E_{{{\text{backgnd}}}} \left( v \right)\), and ΔTbackgnd were calculated for the three media without the lead in place.
Two HSIVs were defined: one small and one large (Fig. 1a). Because the evaluation of P was significantly faster than for ΔT, TF validation was performed using the linear regression of P calculated for the small HSIV versus the LEM predictions for the 40 non-uniform Etan(l) as follows:
Note that the smaller HSIV was selected for TF validation to minimize the influence of the scattered EM field. The larger HSIV was used for evaluation of the correlation between P and ΔT. For the thermal analyses, ΔT was analyzed after 10 and 200 s of continuous excitation. ΔT for each electrode was equal to the maximum temperature observed at the electrode external surface. The influence of the medium thermal conductivity on temperature distribution around the electrodes and hot spot determination based on ΔT was evaluated by comparing results at 10 and 200 s.
Another output of the linear regression is the linear coefficient of determination (R2), which is the quotient of the variances of the fitted values and the observed values of the dependent variable. If R2 = 1, all of the data points fall perfectly on the regression line. If R2 = 0, the dependent variable accounts for none of the variation in the observed data. In our case, two reasons that may result in R2 < < 1 are either that the obtained TF is not correct or the LEM is not the right approach for evaluation of the given RF response with a low uncertainty. In our study, the acceptance criterion for TF validation was R2 > 0.95.
The influence of the lead design and the surrounding medium was analyzed using the numerically validated LEMs. It is impossible to specify clinically relevant AIMD trajectories inside the human body and to obtain a set of clinically relevant Etan(l) without indicating a particular type of AIMD. However, the artificial set of 40 Etan(l) distinct from the original 40 Etan(l) supports an initial comparison of P and ΔT for leads with different designs and surrounding media.
The comparison of results for multi-electrode and single-electrode leads was performed based on ΔT at t = 200 s. The same set of Etan(l) was used in the investigation of all leads. Maximum values of ΔT observed in the 3D EM and thermal co-simulation results were compared.
Power injection into leads
There is no standard that defines a safe thermal exposure for each human tissue. Animal studies are one approach to confirm a no-harm condition for a given level of RF-induced heating. However, it is challenging to conduct animal studies in RF exposure environments, e.g., a birdcage of an MRI scanner or an RF exposure system. The major difficulty with performing safety evaluations in animals is to generate clinically relevant distributions of amplitude and phases of Etan. This is because of: (i) substantial differences in the incident EM field generated in humans versus study animals; (ii) difficulty implementing lead trajectories in animals that result in the largest ΔT in humans. Experiments in an MRI environment also require the use of expensive non-magnetic tools and MRI- and RF-compatible temperature probes.
A power injection approach was proposed to address the aforementioned challenges in animal studies [26]. This approach should ensure that the power injection from a power source at the proximal end of the lead results in temperature rises encountered during RF exposure and at relevant distributions of amplitude and phases of Etan. Large inductance-related losses occur in helical wires if the power injection is performed using RF frequencies typical for commercial 3 T MRI scanners (123–128 MHz). Power injection at 0.5 MHz eliminates the lead inductance-related losses and can generate the RF-induced heating in close proximity to an electrode similar to the radiated case at MRI frequencies.
We modeled power injections by connecting a 50 Ω RF power source across the wire pins and the ground pin. The 8 lumped capacitors were removed from the lead model. Continuous injection with Pin = 0.1 W was applied at 128 MHz and at 0.5 MHz. The electrical properties of the medium approximating blood and nerve tissue were adjusted to those for 0.5 MHz using the IT’IS material property database [29]. Variation of electrical properties for the generic tissue medium is not included in the database and was not applied.
Results
Transfer function and calibration factor results
As shown in Fig. 3, the electric field at the location of the leads, and therefore Etan(l), was affected by modification of antenna positions as well as the amplitudes and phases of the RF sources. The influence of the lead on antenna RF field generation was negligible because the leads were located approximately one wavelength from the antennas in the lossy medium. Also, the box was sufficiently large enough in the z-direction to minimize the influence of the perfectly matched layer on field propagation from the antennas to the lead location.
Vector plot of the electric field in the xz plane. a Excitation of one antenna. b Excitation of all antennas simultaneously with the same source amplitudes and phases. c Excitation of all antennas simultaneously with the same source amplitudes, but the phase of the first pair of antennas offset 180° from the second pair of antennas
As shown in Figs. 4 and 5, S(l) varies substantially with changes in wire geometry and surrounding medium for all electrodes. Electrode location also significantly affected S(l) for both straight and helical leads. For the same electrode, a change of surrounding medium primarily resulted in a phase variation of S(l) along the lead length. Changing the lead insulator εr significantly influenced the amplitude and phase shapes of S(l) for all media. Also, increasing εr resulted in higher S(l) phase at all locations along both leads. Similar behavior of S(l) phases was observed for the single-electrode lead (Fig. 6).
Amplitudes and phases of S(l) for single-electrode leads with the straight and helical wires in the blood medium. The leads with straight wire diameters of 0.73 and 1.0 mm are labeled as “straight 0.73” and “straight 1”, respectively. The leads with helical structures consisted of 0.1 × 0.1 mm rectangular wire external diameters of 0.9 mm and 1.1 mm are labeled as “helical 0.9” and “helical 1.1”, respectively
The TF was successfully validated for all electrodes, as demonstrated by R2 values close to 1 (Table 2). The lowest values for R2 were observed for the first electrode of the lead with straight wire and insulator εr = 5.5. The applied set of Etan(l) ensured more than 20 dB dynamic range of P for all electrodes (Fig. 7a). As expected, R2 was close to zero if one electrode was used for TF calculation, but validation was performed for a different electrode (Fig. 7b, c). Thus, the LEM based on the TF developed for one electrode cannot be used to estimate P and ΔT for another electrode.
The calibration factors are also presented in Table 2. The sensitivity of the calibration factor of all electrodes to the dielectric properties of the surrounding medium was significantly higher than the sensitivity of the TF for these electrodes. Dependencies of the calibration factor on the media and the electrode number were substantially different for the lead with straight and helical wires. If the surrounding media was changed from blood to nerve tissue, A decreased by as much as 25% and 75% for the first and eighth electrode, respectively. Variation of AT was smaller than the variation of A for these same cases, for example for the eighth electrode the maximum decrease was 55% (versus 75% for A). If the surrounding media was changed from the global average to nerve tissue, A decreased but AT increased or remained practically unaffected. This result can be attributed to differences in the thermal properties of the global average and nerve tissues. Thus, the evaluation of both the TF and the calibration factors, i.e., A and AT, should be performed for the entire lead parameter matrix.
We observed a significant dependence of A and AT on the surrounding media, with A showing a variation of up to 3.9 and AT of up to 2.2 for the range of electrical properties used, i.e., permittivity εr ranging from 44 to 78 and conductivity σ ranging from 0.354 to 1.2 S/m. Such a large variation in the net dissipated electrode power P and the net temperature rise ΔT makes it difficult to define the electrical properties of the surrounding media conservatively. Further investigations are necessary to propose conservative surrounding media properties.
Regarding the RF exposure, the temperature distributions in close proximity to the electrodes were visibly asymmetric along the electrode length, especially for exposure times less than 100 s (Fig. 8). For an exposure time of 200 s, and only for a surrounding medium of nerve tissue, the regions of highest temperature were cylindrical in nature. The temperature distributions took on the shape of a droplet for all other cases. A rapid decrease of the SAR in close proximity to the electrodes was also observed (Fig. 8g).
Temperature profiles in close proximity to electrodes of the lead with straight wire for RF exposure at 128 MHz after 10 s (left column) and 200 s (right column). Results are presented for leads surrounded by a blood, b generic tissue, and c nerve tissue. d, e Temperature profiles of 8 electrodes for RF exposure of the lead with helical wire in blood at 128 MHz for two different excitations. f Close-up view of the model with the electrodes. g SAR in close proximity to electrodes of the lead with straight wire in blood for an RF exposure of 128 MHz
The results for the influence of lead design and surrounding medium on P are presented in Fig. 9. Use of the artificial set of 40 Etan(l) showed that it is impossible to choose a lead design that always results in either the highest or the lowest combinations of P and ΔT. Therefore, it is impossible to compare P and ΔT for clinically relevant Etan(l) based only on known variations of |S(l)|, A, and AT versus surrounding media. Comparing only these quantities for different surrounding media can result in the incorrect selection of the conservative tissue simulating medium, i.e., a medium that results in the largest heating for a given AIMD lead.
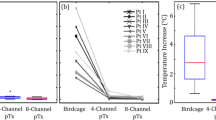
Comparison of the maximum ΔT of the 8-electrode and single-electrode leads for the 40 Etan(l) is presented in Fig. 10. As seen in the figure, the ΔT for single-electrode leads containing helical wire was significantly lower than the ΔT for all multi-electrode leads. Additionally, the ΔT for the single-electrode leads containing straight wire was significantly higher than for all multi-electrode leads. Thus, single-electrode leads cannot be used for “generic” evaluation of multi-electrode leads.
Hot spots around the leads, i.e., the points of high power deposition and temperature rise, were not determined as a separate step in our workflow. Instead, it was more straightforward and even faster to evaluate the LEM for all electrodes without first spending a substantial amount of time to determine the hot spots of each lead. Hot spot evaluation was performed concurrent with the sensitivity analysis. All electrodes were selected as hot spots in all investigated media.
Results for power injection into leads
For power injection into the leads with straight wire at 128 MHz and 0.5 MHz, the temperature distribution in close proximity to the electrodes was cylindrical in shape for all exposure time steps (Fig. 11). Temperature profiles for the power injection at 0.5 MHz were similar for the leads with straight and helical wires to within 3% variation. The power injection into the leads with helical wire at 128 MHz was not modeled because inductance losses were very high.
Six quantities of interest were selected for making quantitative comparisons of the temperature distributions in close proximity to the electrodes: maximum transient temperature rise of the electrode (“electrode max”) and in a small HSIV (“small HSIV max”), minimum temperature rise in a small HSIV (“small HSIV min”), and transient temperature at three locations: 0.5 mm distance from the electrode in the y-direction and opposite electrode left end (“left edge 0.5 mm”), center (“center 0.5 mm”), and right end (“right edge 0.5 mm”) (Fig. 12).
The small HSIV included locations with a maximum distance to the electrode less than 0.35 mm. However, for evaluation of the temperature rise over the small HSIV, the minimum values were approximately 43% and 69% (Table 3) of the maximum values for t = 10 s and t = 200 s, respectively. Higher medium electrical conductivities resulted in increased differences of the temperature rise for the locations “left edge 0.5 mm” and “right edge 0.5 mm”. Also, the difference was larger for the leads with helical wire versus the lead with straight wire.
For the power injection cases at 128 MHz and 0.5 MHz, the values of the temperature rise at the locations “left edge 0.5 mm” and “right edge 0.5 mm” were similar for t = 10 s and t = 200 s (Table 3). Changes in the injection power frequency or the surrounding medium had a negligible impact on the temperature rise quantities when normalized to the maximum electrode temperature rise at 200 s.
Discussion
RF energy absorbed by a human subject undergoing MRI has the potential to increase the local tissue temperature, especially in the presence of an AIMD. To evaluate the risk of the thermal injury, P or ΔT or both are typically used together with the LEM and a set of Etan(l) that is clinically relevant for an AIMD. This study presented a computational modeling workflow for P, ΔT, and LEM of various multi-electrode lead designs using 3D EM and thermal co-simulation. LEM assessment included (i) TF calculation and validation and (ii) evaluation of a calibration factor. Our workflow is targeted at the rapid numerical evaluation of lead design to optimize performance in terms of RF-induced heating. The workflow also extends our understanding of multi-electrode leads with straight and helical wires. For example, it was found that (i) thermal hot spots can occur at all electrodes of a multi-electrode lead in close proximity to the electrode surface and (ii) results for generic single-electrode leads can significantly mislead the analysis of multi-electrode leads, facts that were previously neglected.
The thermal time constants for the electrodes analyzed herein ranged from 55 to 65 s. This is substantially smaller than the maximum thermal simulation time of 200 s. We also tested that the shape of the temperature distribution around the electrodes did not change for times greater than 200 s. Based on these results, it is sufficient to use a thermal exposure time that is approximately three times longer than the thermal time constant to compare different lead designs. Our workflow can accommodate shorter or longer exposure times if ΔT for a particular MRI sequence has to be evaluated.
The work summarized in this paper does not include measurement data. Indirect measurement is required to acquire P because reliable 3D volume dosimetric, i.e., specific absorption rate (SAR), measurement in close proximity to an AIMD electrode is currently not feasible. This is primarily because (i) the electrode diameter is smaller than the field probe tip diameter for most AIMD leads and (ii) the spatial electric field decay is very steep and non-linear. Experimental evaluation of P and ΔT includes uncertainties related to the experimental setup (e.g., probe locations relative to the electrode, reproducibility of the incident RF exposure, etc.), as well as sensor-related uncertainties. Some types of optical temperature sensors, primarily luminescence-based sensors, can be used for ΔT evaluation in an RF exposure environment. The smallest tip diameter of a commercially available fiber optic temperature sensor with an unprotected sensitive element is 0.3 mm, for example the Lsens-B (Rugged Monitoring, Quebec City, QC, Canada). Such probes must be handled with care, which complicates the process of precisely positioning the probe tip in close proximity to the electrode. Another more common option are fiber optic temperature sensors with (i) a sensitive element located at the tip of the probe and with external diameter of more than 0.7 mm, for example the Lsens-P (Rugged Monitoring, Quebec City, QC, Canada) and (ii) a sensitive element coated with a plastic and having an external diameter of more than 0.5 mm, for example the Luxtron Model STB (Lumasense, Santa Clara, CA). These sensors report a spatial average value for the temperature rise with a typical relative temperature accuracy of ± 0.2 °C. Considering the limitations, current thermal measurement technologies make the collection of experimental data at the required resolution of 0.2 mm difficult to obtain and inaccurate. Therefore, verification and validation best practices were identified and followed to ensure the reliability of the simulation outputs for this application.
Regarding software quality assurance, these studies relied on commercial off-the-shelf EM (ANSYS HFSS) and thermal solvers (ANSYS NLT). Both solvers are developed, tested, and released under an ISO-certified quality management system [31]. Without access to the source code, users must in general rely on this certification process to ensure a robust quality assurance process is in place. This helps to ensure the integrity of the source code and executables from release to release. Calculation verification intends to minimize the impact of numerical solver error, discretization error, and use error on the simulation outputs [32]. Numerical solver error refers to the sensitivity of the simulation outputs to the various solver parameters associated with a given simulation, while an evaluation of discretization error ensures that the solution has been sufficiently discretized both in space and time. The spatial convergence of the EM results is ensured by the mesh adaption procedure in HFSS, while the convergence of the thermal results was ensured through manual spatial and temporal mesh convergence. Finally, use error refers to mistakes in the inputs to a computational model. All model inputs were checked visually for accuracy before performing each simulation.
Of course, using a verified modeling workflow does not guarantee that the results accurately describe the behavior of a given AIMD. This is because modeling results depend on a large set of input parameters, i.e., lead geometry, AIMD input impedance, and electrical and thermal properties of the AIMD materials. A number of assumptions and simplifications are also made when constructing the numerical model. The verified modeling workflow is useful for uncovering sensitivities of the RF responses of an AIMD to different design and environmental factors, however. And using a reverse engineering approach, an AIMD model can be adjusted to represent the behavior of a given AIMD.
In our previous study of a helical lead with a single electrode [33], a non-linear dependence of P and the LEM on a small volume of fat tissue surrounding the lead tip was observed. Thus, using LEMs estimated for a homogeneous medium can yield large systematic errors in estimating P, and consequently, the in vivo AIMD lead electrode RF-induced heating. Because it is not required by ISO/TS 10974 Tier 3 Clause #8, it was beyond the scope of this study to provide an evaluation of a multi-electrode lead LEM for a multi-tissue media. The developed numerical workflow can accommodate a multi-tissue environment, however. Future studies should investigate the LEM for other lead and electrode geometries and account for the presence of multiple tissue types surrounding the lead.
Our case study is only a first step in the complex assessment of RF-induced heating for multi-electrode leads. Future research should include, but not be limited to, the following topics: (i) comprehensive uncertainty analysis of LEM-related quantities, (ii) inclusion of temperature probes in the numerical domain, and (iii) reverse engineering of realistic multi-electrode leads.
Conclusion
We successfully developed a numerical workflow for modeling the LEM and the RF responses of realistic multi-electrode leads containing either helical or straight wires. Our workflow is targeted to the R&D of lead design to obtain better performance in terms of RF-induced heating, and better understanding the nature of lead interactions with incident EM fields. The workflow is not expected to be used on its own for clinical trial approval or commercial device clearance. The LEM, P and ΔT were obtained through detailed modeling of the entire lead and electrodes. Our study showed that (i) all electrodes of a multi-electrode lead can be thermal hot spots, (ii) the LEMs of individual electrodes can vary substantially, (iii) the LEM should be evaluated for each electrode, and (iv) the usage of results for generic single-electrode leads can significantly mislead the analysis of multi-electrode leads.
The outcome of this study cannot be readily generalized to the conclusion that the TF for any multi-electrode lead, independent of lead and electrode geometry, can be validated with R2 > 0.95. Credible numerical or experimental LEM estimation should be carried out for each lead and electrode geometry to ascertain the LEM uncertainty. In other words, findings obtained from this numerical workflow may need to be confirmed by measurements before getting clinical trial approval or commercial device clearance.
References
Panych L, Madore B (2018) The physics of MRI safety. J Magn Reson Imaging 47:28–43
Bhusal B et al (2018) Measurements and simulation of RF heating of implanted stereo-electroencephalography electrodes during MR scans. Magn Reson Med 80:1676–1685
Cabot E et al (2013) Evaluation of the RF heating of a generic deep brain stimulator exposed in 1.5 T magnetic resonance scanners. Bioelectromagnetics 34:104–113
Erhardt JB et al (2018) Should patients with brain implants undergo MRI? J Neural Eng 15:041002
Wilkoff BL et al (2013) Safe magnetic resonance imaging scanning of patients with cardiac rhythm devices: a role for computer modeling. Heart Rhythm 10:1815–1821
Eryaman Y et al (2019) A simple geometric analysis method for measuring and mitigating RF induced currents on Deep Brain Stimulation leads by multichannel transmission/reception. NeuroImage 184:658–668
Shrivastava D et al (2012) Heating induced near deep brain stimulation lead electrodes during magnetic resonance imaging with a 3 T transceive volume head coil. Phys Med Biol 57:5651–5665
Coffey RJ, Kalin R, Olsen JM (2014) Magnetic resonance imaging conditionally safe neurostimulation leads: investigation of the maximum safe lead tip temperature. Neurosurgery 74:215–224
Morrison TM, Pathmanathan P, Adwan M, Margerrison E (2018) Advancing regulatory science with computational modeling for medical devices at the FDA’s Office of Science and Engineering Laboratories. Front Med 5:241. https://doi.org/10.3389/fmed.2018.00241
Yu Z, Xin X, Collins CM (2017) Potential for high-permittivity materials to reduce local SAR at a pacemaker lead tip during MRI of the head with a body transmit coil at 3 T. Magn Reson Med 78:383–386
Das R, Yoo H (2017) RF heating study of a new medical implant lead for 1.5 T, 3 T, and 7 T MRI systems. IEEE Trans Electromagn Compat 59:360–366
Bhusal B, Bhattacharyya P, Baig T, Jones S, Martens M (2018) Measurements and simulation of RF heating of implanted stereoelectroencephalography electrodes during MR scans. Magn Reson Med 80(4):1676–1685
Golestanirad L et al (2017) Local SAR near deep brain stimulation (DBS) electrodes at 64 and 127 MHz: a simulation study of the effect of extracranial loops. Magn Reson Med 78:1558–1565
Golestanirad L et al (2017) Construction and modeling of a reconfigurable MRI coil for lowering SAR in patients with deep brain stimulation implants. Neuroimage 147:577–588
Golestanirad L et al (2019) RF-induced heating in tissue near bilateral DBS implants during MRI at 1.5 T and 3T: the role of surgical lead management. NeuroImage 184:566–576
Guerin B et al (2018) Realistic modeling of deep brain stimulation implants for electromagnetic MRI safety studies. Phys Med Biol 63:095015
Zeng Q et al (2018) Evaluation of MRI RF electromagnetic field induced heating near leads of cochlear implants. Phys Med Biol 63:135020
Guerin B et al (2019) The ‘virtual DBS population’: five realistic computational models of deep brain stimulation patients for electromagnetic MR safety studies. Phys Med Biol 64:035021
Park S-M, Kamondetdacha K, Nyenhuis JA (2007) Calculation of MRI-induced heating of an implanted medical lead wire with an electric field transfer function. J Magn Reson Imaging 26:1278–1285
Kozlov M, Kainz W (2019) Comparison of different assessment quantities to evaluate lead electromagnetic model for radio frequency energy-induced heating. IEEE J Electromagn RF Microw Med Biol. https://doi.org/10.1109/JERM.2019.2938166
Feng S, Qiang R, Kainz W, Chen J (2015) A technique to evaluate MRI-Induced electric fields at the ends of practical implanted lead. IEEE Trans Microw Theory Tech 63:305–313
Liu J, Zheng J, Wang Q, Kainz W, Chen J (2018) A transmission line model for the evaluation of MRI RF-induced fields on active implantable medical devices. IEEE Trans Microw Theory Tech 66:4271–4281
Missoffe A, Kabil J, Vuissoz P-A, Felblinger J (2018) transmission line model of an implanted insulated cable for magnetic resonance imaging radiofrequency hazard evaluation. IEEE J Electromagn RF Microw Med Biol 2:201–207
Tokaya JP et al (2018) MRI-based, wireless determination of the transfer function of a linear implant: introduction of the transfer matrix. Magn Reson Med 80(6):2771–2784
Kozlov M, Kainz W (2018) Lead electromagnetic model to evaluate rf-induced heating of a coax lead: a numerical case study at 128 MHz. IEEE J Electromagn RF Microw Med Biol 2:286–293
ISO TS 10974:2018 (2018) Assessment of the safety of magnetic resonance imaging for patients with an active implantable medical device. International Organization for Standardization
Elwassif MM, Datta A, Rahman A, Bikson M (2012) Temperature control at DBS electrodes using a heat sink: experimentally validated FEM model of DBS lead architecture. J Neural Eng 9:1–9
Mo X, Jiang C, Ding J, Zhang F, Li L (2016) Study of deep brain stimulation lead resonant length in 3.0 T MRI RF magnetic field. Electron Lett 52(13):1098–1100
Hasgall PA et al (2018) IT’IS Database for thermal and electromagnetic parameters of biological tissues. Version 4.0. https://doi.org/10.13099/VIP21000-04-0.itis.swiss/database
Yao A, Zastrow E, Kuster N (2017) Test field diversification method for the safety assessment of RF-induced heating of AIMDs during 1.5-T MRI. In: Proceedings of 25th annual ISMRM conference, Honolulu, p 2629
ANSYS, Inc. https://www.ansys.com/-/media/ansys/corporate/files/pdf/about/ansys-iso-cert.pdf?la=en.
ASME V&V40. (2018) Assessing credibility of computational modeling through verification and validation: application to medical devices. The American Society of Mechanical Engineers
Kozlov M, Kainz W (2017) Sensitivity of the transfer function of a helix lead on the dielectric properties of the surrounding media: a case study. In: Proceedings of 2017 IEEE international conference on microwaves, antennas, communications and electronic systems (COMCAS), Tel Aviv, pp 1–6. https://doi.org/10.1109/COMCAS.2017.8244818
Acknowledgement
Open access funding provided by Max Planck Society.
Author information
Authors and Affiliations
Contributions
MK: study conception and design, modeling, analysis and interpretation of data, drafting of manuscript. MH: drafting of manuscript, critical revision. WK: critical revision.
Corresponding author
Ethics declarations
Conflict of interest
The authors have no conflict of interest to declare.
Ethical standards
The editorial does not contain any studies with human participants or animals performed by any of the authors.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Disclaimer
The mention of commercial products, their sources, or their use in connection with material reported herein is not to be construed as either an actual or suggested endorsement of such products by the Department of Health and Human Services.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Kozlov, M., Horner, M. & Kainz, W. Modeling radiofrequency responses of realistic multi-electrode leads containing helical and straight wires. Magn Reson Mater Phy 33, 421–437 (2020). https://doi.org/10.1007/s10334-019-00793-9
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10334-019-00793-9