Keywords

1 Introduction

Generally, patients with active implanted medical devices (AIMD) are denied access to MRI due to the potential for hazardous interactions. It has been estimated that 17% of pacemaker patients will need an MRI within 12 months of device implantation [1]. MR imaging is a highly desirable imaging modality due to its non-ionizing radiation and image quality for soft tissue imaging [2]. Therefore, in recent years device manufacturers, academics, and regulatory agencies have developed standardized test methods for improving the access to this important diagnostic tool for AIMD patients [3, 4].

Several potentially hazardous interactions of implanted medical devices with the MR system have been identified [5, 6]. Computational human models (CHMs) are used in the evaluation of three hazards: RF-induced heating, RF-induced unintended stimulation, and RF-induced malfunction.

2 Utilizing Computational Human Models for the Assessment RF-induced Heating

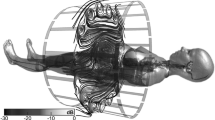
Computational human models have been used for a range of electromagnetic applications [7]. This chapter discusses the specific application of CHMs to MRI RF-induced heating near AIMDs. While some studies have used measurement methods in homogenous phantoms [8], this work focuses on the methods outlined in [3, 4], which are based on the established transfer function method [9, 10]. The benefits of using CHMs in this work have been outlined in [11, 12], which provide a framework for evaluating millions of scenarios and can be contrasted with the testing of pacemaker resilience to Electronic Article Surveillance (EAS) systems [13], which involves physically testing the device in a more limited number of prescribed tests. The general process is illustrated in Fig. 1.

Fig. 1
A flow chart describes the process of calculating, analyzing and determining the deposited power of electronic medical devices planted in human models to assess the risk.

Using CHMs to assess risk to the patient due to RF-induced tissue heating

Full size image

The standardized test methods of [3] outline a 4-tier system for estimating in vivo RF-induced heating utilizing CHMs. Lower-numbered tiers are more conservative than higher-numbered tiers, that is Tier 1 is the most conservative and Tier 4 is considered the most accurate. Tier 1 is impractical and will be removed in the upcoming standard [14].

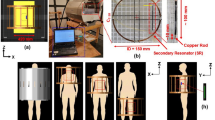
Tiers 2 and 3 both involve simulating a set of CHMs and a set of MR birdcage coils to build a library of expected field distributions within the human body. Examples of CHMs include the Virtual Family [15] and the Visible Human Project [16]. By varying parameters such as landmark position (alignment of the center of the MR coil with the CHM), body position, coil geometry, and using a variety of CHMs (different heights, weights, BMI, ages, etc.), millions of scenarios can be investigated. In a Tier 2 analysis, the risk to the patient is assessed using the maximum fields over the expected implant volume, after taking a 10 g average. In a laboratory setting, the device is then exposed to the appropriate field level and the temperature rise is measured. For elongated devices such as leaded AIMDs, as the maximum field values are taken over a large volume and then applied uniformly over the entire device, this would result in impractically high test conditions and severely over-predict RF-induced heating. A Tier 3 analysis uses the same library of 3-D field distributions, but extracts the incident fields over one or more lead pathways and then combines this with the separately-derived lead model. Then, a probability distribution function of the estimated in vivo RF-induced heating can be carried forward to a safety assessment using an animal model or alternate method of clinical assessment.

The lead models used in Tier 3 analyses are often piecewise excitation models, where the lead response (e.g., RF-induced deposited power or temperature rise near the lead tip) is quantified for the excitation of a section of the lead (e.g., 1 cm). The so-called reciprocity method [10] involves a single excitation and a swept measurement of the response. Whether numerically- or experimentally-derived [17,18,19,20,21], transfer function models are developed within a homogenous medium, commonly referred to as a tissue-simulating medium (TSM). This work focuses on the application of the homogenous TSM used in the lead model to the inhomogeneous CHM used in the generation of the incident fields, and the ultimate impact to the in vivo estimation of RF-induced heating.

3 Tissue-Simulating Media (TSM)

Equivalent medium theorem [22] suggests that there exists an optimal homogenous TSM for agreement between the lead model (transfer function) and predicted in vivo RF-induced heating (in inhomogeneous CHMs). Indeed, recommended procedures for identifying such a medium are becoming standard practice [13] for AIMD manufacturers. The following subsections will discuss what is known about the impact of TSM on the AIMD model.

3.1 Effect of TSM on Computation of RF-induced Heating

The analytical problem of a medical device lead exposed to RF fields from an MR scanner is a particular instance of a wire scatterer in an incident field. Classically, these problems are investigated via the Method of Moments (MoM) [23], though MoM is known to be disadvantageous for analysing problems with multiple material boundaries as are present in the human body. Further, the problem of bare and insulated wire (as antennas or scatterers) in an extended conductive medium has been extensively studied in the literature [24,25,26,27,28], especially for submarine communication and geophysical exploration.

This analytical framework has been extended to the particular problem of implanted medical device leads [29], whereby the particular impact of the TSM to the predicted in vivo RF-induced heating can be quantified. Using a safety index which is proportional to the elevated SAR near the lead tip, general trends are seen for the impact of the TSM on resonant characteristics of the lead geometry. The resonant effect has also been extensively defined in the literature [30,31,32]. One particularly important consequence to the assessment of RF-induced heating near the lead tip is the necessity of elevated Electric field at the lead tip due to the discontinuity in the current distribution, which can be shown using a basic MoM formulation [33]. While the preceding analytical techniques focus on quantifying RF-induced heating in terms of electromagnetic quantities, additional considerations of the TSM for measuring temperature rise are also required [34, 35].

While these studies provide an understanding of the effect of changing the surrounding medium, or TSM, on the lead response, more contemporary research has focused on the impact of the choice of TSM on the overall accuracy of the in vivo prediction of RF-induced heating. This important work is discussed in the next two subsections, which are divided into studies of simplified structures such as a simple wire and more complex geometries representing actual geometries of practical AIMD leads.

3.2 Numerical Studies of Simplified Structures

A basic model for an AIMD lead is an insulated wire with a bare section at the distal end. This simplified structure is useful for its ease in construction and for simplifying analyses, and thus is used for standardization of test methods [3]. Indeed, such structures are often used for numerical simulations of transfer functions, examples include [18, 19].

A transmission-line model of a simplified structure was shown in [36] to give good agreement with measurement for a variety of parameters of the wire (insulation thickness, conductor diameter, insulator dielectric constant, lead length, etc.) and for different TSMs, for RF-induced voltage at the proximal end. While this work did not focus on RF-induced heating, it is still important for any discussion of the impact of TSM properties to highlight the influence of the tip impedance, Ztip, on the ultimate result, a relationship which has been explored in further depth [37]. Still, neither of these works investigated which TSM would then give the most accurate result when compared to a full evaluation with an inhomogeneous CHM. This question for simplified structures is answered in [38], which concludes that the appropriate choice in homogeneous TSM is the TSM with the conductivity which matches that at the lead tip. This conclusion is dependent on the thickness of the insulation surrounding the conductor, as [39] shows that for a given TSM the SAR will plateau for increased insulation thickness. For thin insulation leads, the TSM at the lead tip is no longer dominant and the choice in TSM should align with the average along the lead body [40]. While the focus of this work has been RF-induced heating, most of these principles are extensible to other RF-induced hazards, such as RF-induced unintended stimulation [41].

3.3 Numerical Studies of Realistic Device Geometries

Medical device leads are of course more complex than the simplified structures of the previous subsection. For example, pacemaker leads are helically-wound, with multiple conductors present which may be coaxial or coradial [42]. The current version of the ISO technical specification [3] for MRI safety of AIMDs includes a set of suggested TSMs for manufacturers to consider. For electrically short, non-leaded devices the analysis may be more straightforward. An example of this analysis is shown in [43], which follows the test methods defined in [4]. In this type of analysis, typically two TSMs are used, and the worst-case of these two scenarios is carried forward. In some situations, this may be overly conservative.

Importantly, the set of geometries in [44] included up to four helically wound conductors and includes a parametric study of the helix design, to explore the relationship of the tip impedance to the predicted RF-induced heating. The importance of the lead pathway to the optimal choice of TSM is discussed, and a novel method for constructing an inhomogeneous computational phantom for transfer function generation is proposed.

For a percutaneous SCS lead, the choice of the high conductivity medium (HCM) from [3] was shown to be more accurate, while the low conductivity medium (LCM) would lead to an over-prediction of RF-induced heating by 72–74% [45]. This contrasts with another study of a simplified pacemaker lead [46] which shows that LCM is more accurate while the HCM overpredicted RF-induced heating by 80%. However, exact insulation thicknesses for the lead models used in these two studies were not given. Both studies illustrate the importance of TSM selection on the predicted risk to the patient due to RF-induced heating. While safety assessments should always be conservative, care must be taken to avoid situations where the prediction is so high as to prevent patient access to this important diagnostic tool.

4 Discussion

In this chapter, we have investigated the impact of the CHM on the estimation of MRI RF-induced heating near the tips of AIMD leads through the lens of TSM selection during transfer function development. While general guidance for TSM selection is still being investigated, early evidence exists to recommend that device manufacturers use a TSM similar to that found at the distal end for leads with thick insulation, while for thin insulation, a homogenous TSM should approximate the average properties of tissues in contact with the lead body. The data is supported by experimental, theoretical, and computational analysis of simplified structures as well as practical lead geometries.

4.1 Future Work

The techniques shown in this work are currently being extended to provide general guidelines for the selection of TSM and its applicability to the CHM. AIMD manufacturers desire to have a more defined transition from “thick insulation” to “thin insulation”, a definition which may vary due to the particular lead construction (straight versus helical wires, number of conductors, diameter of the conductors versus outer diameter of the lead, etc.). In addition, these types of sensitivity analyses are enabled mostly by numerical simulation, as to parameterize physical quantities could make prototyping and testing time-consuming and expensive.

The further refinement of numerically derived transfer functions can also enable more solutions for mitigating MRI RF-induced heating. Current practice is still to build prototypes and experimentally confirm the reduction in expected RF-induced heatingRF-induced heating [47, 48]. The investigation of solutions can only be improved by a more thorough understanding of the influence of the computational model on the ultimate results of the safety assessment.