Terraced paddy field rainfall-runoff mechanism and simulation using a revised tank model

Abstract

Terraced paddy fields play important roles in water and soil conservation because their water storage effect reduces and delays flood peaks. This study applies the terraced paddy field rainfall-runoff mechanism to the tank model. Though the traditional four-section tank model can easily simulate rainfall-runoff in a terraced paddy field, it has many parameters that are difficult to calibrate. To address the shortcomings of the traditional four-section tank model, this study develops a revised tank model to simulate rainfall-runoff. This study selects a terraced paddy field located in Hsuing-Pu village in Hsiuing-Chu County as the experimental field. The field under investigation was equipped with automatic monitoring stations, water-stage, and rain gauges. These stations collected data on rainfall and water flow to simulate the rainfall-runoff model in that region. To simulate the runoff behavior of the experimental terraced paddy field, two rainfall events were selected from the gathered data and five normal evaluation indexes based on static and hydrological theory were applied to calculate the results of simulation simultaneously. The revised tank model performed better than expected, and precisely predicted the variations and trends in flow charge. Comparison with representation indexes proved that the revised tank model is an appropriate and valuable tool for rainfall-runoff simulation.

Introduction

Following the fast growth of the economy and society, industrial land has gradually replaced more and more agricultural lands. This has created a serious land-use problem in Taiwan, where more than 75% of the land is covered by mountains, valleys, and hills with steep and varied terrain. To solve the problem of food shortage, farmers cultivate many terraced paddy fields along valleys and hills for rice production.

Compared with dry fields, terraced paddy fields have greater abilities in water and soil conservation (e.g., flood control, water source protection, soil retention, and soil corruption prevention). The storage ability of terraced paddy fields reduces and delays the arrival of flood peaks.

Terraced paddy fields are a cultural legacy of the world and serve many public functions, such as soil-erosion prevention, flood protection, and groundwater conservation. However, Taiwan’s overproduction of rice after becoming a member of WTO has created huge pressure on rice production and particularly for rice production in terraced paddy fields. Disadvantages in hydrology and the limits of terrain make it difficult to cultivate and maintain the function of terraced paddy fields. Aging farmers and a lack of young labors have become another downfall factor of terraced paddy fields. As a result, farmers have switched many terraced paddy fields to other crops or simply abandoned them.

There are some related studies on the terraced paddy fields. Shimur (1982) calculated the total capacity of water storage in paddy fields from a macro perspective. According to his calculations, the total capacity of water storage could be up to 9 billion cubic meters. After eliminating the water needed for rice plantation, the capacity of actual flood control was 8.1 billion cubic meters. According to Shimura’s (1982) estimation, the capacity of flood control of paddy fields was 3.3 times the total capacity of flood controlling dams in Japan in 1980. The flood capacity of the 182 dams in Japan was 2.4 billion cubic meters in 1980.

To evaluate the diminishing influence of the flood control function in abandoned terraced paddy fields, Hayase (1992) conducted run-off simulations using the basin of terraced paddy fields in Satomi Village, Ibaraki County, Japan, as an example. That study shows that the ridge between abandoned fields collapsed from 30 to 5 cm high when the flood peak discharge of a 100-year flood increased 38%. The flood peak discharge of the 50-year flood had become 25-year flood. The flood frequency would likely increase if the terraced paddy field were abandoned.

According to the former research, terraced paddy fields fill a disaster prevention function, and the terraced paddy field rainfall-runoff mechanism needs to be discussed in detail. To discover the rainfall-runoff mechanism and best way of simulation, this study selects a revised tank model (Wen-Pei Peng 2004) that is suitable for simulating the rainfall-runoff of terraced paddy fields. Comparing the simulated data with observed data clearly shows that the revised mechanism of terraced paddy field is appropriate.

Model theoretical analysis

The theoretical analysis of tank model

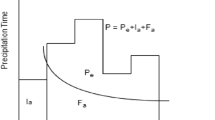
This study uses a tank model proposed by Sugawara, Director, Office of Disaster Prevention, Japan Science and Technology Research Center, in 1972. This model is a hydrological model based on physical concepts. The goal of this method is to replace the runoff mechanism with several storage tanks and consider the complicated hydrological factors existing in a basin. The relevant factors include infiltration, seepage, storage, evaporation, surface runoff, interflow and baseflow. These factors were used to simulate the fixed rate relation of rainfall-runoff in the basin. Figure 1 illustrates the model.

Fig. 1

Sketch of the tank model

During rainfall, part of the rain is stored in surface soil (the top tank), while the other part infiltrates the first aquifer (the second tank). In heavy rain, water in the surface layer eventually reaches the threshold (the water level in the top tank storage overruns the effluent outlet in the lower right corner). In this case, water flows across the surface layer and becomes surface runoff. If rain continues to fall and its magnitude of this runoff, the water content in this layer increases. Therefore, surface runoff can increase rapidly with rain. In this condition, the water level in the top tank storage overruns the effluent outlet in the lower right corner. When water from the top tank continues to infiltrate the second tank, it eventually reaches the threshold (i.e., the water level in the second tank storage overruns the effluent outlet in the lower right corner). Runoff that occurs in this layer is similar to a spring coming out the side of a mountain. The groundwater stored in this layer equals the baseflow that supplies rivers during the dry season. The total runoff in the basin equals the total amount of water flowing out of the lower right corner of each tank.

When using the tank model to illustrate the corresponding outflow components, the top tank outflow represents surface runoff, the second tank outflow represents interflow, and outflow in the third and fourth tanks represents the baseflow. The amount of water infiltrated from the lowest bottom orifice becomes the seepage loss of the base layer. If the storage water level does not reach the height of effluent outlet, there is infiltration, but no outflow. This height represents the first flush loss or rainfall absorbed by dry soil. The tanks often serve as the first or the second tank. Thus, a short duration rainfall with a high intensity can easily cause surface runoff. A long duration rainfall with a low intensity would increase the infiltration and the moisture of the soil, but will not cause surface runoff.

Because the tank model adopts the unit hydrographic method, runoff function method, and storage function method, it is easy to use and produces useful simulation results. For this reason, many researchers have adopted the tank model. The runoff calculation method and characteristics of this model are as follows:

• 1. The model automatically includes the first flush loss and the amount of loss variation during the rain. It can be decided by the effluent height of the top tank and the infiltration hole.

• 2. The model shows that runoff increases with rain intensity. The top tank may have several effluents.

• 3. When the rain intensity increases, the storage height of the top tank also increases, as does the river outflow. When the rain intensity decreases, most of the rainwater infiltrates the tank below, and slowly flows into the river. This study uses a tank model with a single straight column configuration.

• 4. The amount of effluent from each tank has its own steadily descending curve pattern. The sum of runoff components with different descending properties represents the amount of effluent. This study uses several tank combinations of straight column configuration.

• 5. As the rainwater moves from one tank to the tank below, the time will be delayed automatically, so the runoff component of the tank below is delayed naturally. This study uses a tank model with a single straight column configuration.

• 6. The model includes the common features of the unit hydrographic method, runoff function method, and storage function method.

• 7. Only add, subtract, and multiply calculations are required for runoff calculations.

• 8. The greatest shortcoming of the tank model is that its parameters (the height of each tank effluent, the initial value of storage height in each tank, etc.) must be determined by trial and error.

• 9. The tank model cannot express the characteristic spread. When the flow distance of the river tunnel is long, it is necessary to set up the tank model of the river tunnel to ensure accurate calculations.

The theoretical analysis of the revised tank model

Simple tank model A

A paddy field is an area surrounded by a mound. A gap is often opened on the ridge this mound. The bottom of gap is a specific height above the surface of the field to maintain the water level on the field and release excess water. Paddy fields only store enough water to grow rice.

Figure 2 shows the figure of simple tank model A used in this study. This model is a simplified tank model suitable for paddy fields and consists of two tanks in one straight column. The upper tank indicates the surface of the paddy field and the upper effluent indicates the ridge overflow. The lower effluent indicates infiltration from ridges and flow from gaps, and the hole in the bottom of the lower tank indicates vertical infiltration. The effluent of the lower tank indicates groundwater of the paddy field. The infiltrated water eventually becomes groundwater; the only difference is whether it flows into the river directly or to drainage.

Fig. 2

Sketch of simple tank model A

Simple tank model A uses the following calculations:

• (1) The amount of runoff and infiltration from the upper tank is shown as PQ1, PQ2, and PF1

  • I. When PS1 > PZ1

    $$ {\text{PQ1 = Pa1}} \times \left( {{\text{PS1}} - {\text{PZ1}}} \right) $$

    (1)
    $$ {\text{PQ2 = Pa2}} \times \left( {{\text{PS1}} - {\text{PZ2}}} \right) $$

    (2)
    $$ {\text{PF1 = Pb1}} \times {\text{PS1}} $$

    (3)

  • II. When PZ1 > PS1 > PZ2

    $$ {\text{PQ1 = 0}} $$

    (4)
    $$ {\text{PQ2 = Pa2}} \times \left( {{\text{PS1}} - {\text{PZ2}}} \right) $$

    (5)
    $$ {\text{PF1 = Pb1}} \times {\text{PS1}} $$

    (6)

  • III. When PZ2 > PS1

    $$ {\text{PQ1 = PQ2 = 0}} $$

    (7)
    $$ {\text{PF1 = Pb1}} \times {\text{PS1}} $$

    (8)

• (2) The amount of runoff from the lower tank is shown as PQ3

  $$ {\text{PQ3 = Pa3}} \times \left( {{\text{PS2}} - {\text{PZ3}}} \right) $$

  (9)

• (3)
  $$ {\text{Total}}\,{\text{runoff }}\,{\text{PQ}} = {\text{PQ}}1 + {\text{PQ}}2 + {\text{PQ}}3 $$

  (10)

• (4) Total runoff transformed to the flow rate is PQ = (10) × A.

Note that,

PQ1–PQ2:

Runoff of the upper tank (mm)

PQ3:

Runoff of the lower tank (mm)

PQ:

Total runoff value (mm)

PS1–PS2:

The initial tank storage water depth (mm)

PZ1–PZ3:

The tank effluent water depth (mm)

Pa1–Pa3:

The orifice coefficients of side holes (No units)

Pb1:

The orifice coefficient of the infiltration hole (No units)

Simple tank model A still requires irrigation water in the upper tank in addition to rainwater. The amount of irrigation water required is calculated by the paddy field tank model. This study assumes that irrigation and rainfall contribute equally to the paddy field, and irrigation and rainfall are both injected into the upper tank as influent. If the water depth of the upper tank does not reach the threshold for rice cultivation, the paddy field model calculates the difference between the threshold and actual water depth. This total represents the amount of water to the paddy field.

The revision of simple tank model A

Because the parameters of “simple tank model A” have some physical meanings, it is possible to shrink their upper and lower limits during the calibration based on a real scenario. For example the orifice coefficient Pa1 of the upper tank in Fig. 2 is often set to one because a water level higher than the ridge creates flow out. The ridge height parameter represents the ridge height of the area, but not every ridge in every paddy field has the same height. While ridge overflow may occur in some fields, it does not mean ridge overflow happening every field. We can only indicate Pa1 approaching 1, but not definitely 1. The lower effluent of the upper tank can be viewed as the seepage from the ridge. Assume that PZ1 is the ordinary ridge height, which is 100–200 mm. PZ2 is the ridge gap height, which is 0–150 mm. The lower tank represents groundwater outflow. Therefore, the tank water depth represented by PS2 represents the corresponding depth of groundwater. The height of groundwater effluent, PZ3, has no important meaning, and simply serves as fixed soil moisture. It is also possible to transfer the moisture conserved in soil to the water level height of the tank, but depending on the soil component, it does not affect effluent. This study uses the global auto-search Multi-start Powell method to calibrate each effluent parameter. The PZ3 parameter does not affect the convergence of target function, though it does affect effluent. Thus, PZ3 jumps randomly during calibration. To avoid trouble in determining PZ3 during the calibration, PZ3 in Fig. 2 is set to 0.

Evaluation index of tank model

To discuss the feasibility of using the revised tank model in terraced paddy field rainfall-runoff simulation, this study uses different error indexes in hydrological simulation testing. Flow rate evaluation was based on the relation between measured and simulated flow rate. This study uses five common indicators in statistics and hydrology to assess the performance of each simulation model (Table 1).

Table 1 Formula of the tank model evaluation index

The closer the root mean squared error (RMSE) gets to zero, the better model performance will be. The closer the percent error of peak discharge (EQ_p) and percent error of total volume (EV) get to zero, the more accurate the estimated hydrological data will be. The smaller the error of time to peak (ET_p) is, the better the estimated time to peak will be. The closer the coefficient of efficiency (CE) gets to one, the closer the simulated and observed data will be.

Case study

Site description

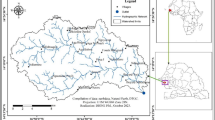
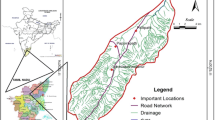
A terraced paddy field in Hsuing-Pu village, Hsiuing-Chu County, was selected as the test zone. This field is near the border of land owned by Hsiuing-Chu Irrigation Association. The total area is 7,434 m². The slope is 25°, as Fig. 3 shows. Hydrological measurement stations were installed in the upstream influent and downstream effluent. S1 was located downstream, which is the effluent of this paddy field. A rain gauge was set up near the station. S2 as located upstream, which is the influent of this paddy field. Figure 4 shows the locations of S1, S2, and the rain gauge. The instruments in S1 and S2 include aqueducts, flumes, and recording stage gages, and the weir has a rectangular triangle. Information was recorded every 5 min. Date, rainfall, water level, and other data were included in the information sheet to measure the rainfall, influent, and effluent in the test zone. The following sections of this study analyze this data.

Fig. 3

The location of test zone

Fig. 4

Location of hydrological measurement stations

Analytical method

Two hydrological measurement stations and one rain gauge were installed in the test zone. Flow rate and rainfall data were continuously collected over the long term to establish the hydrological database needed for parameter calibration and model analysis and verification.

Therefore most suitable for rice terraces of selected rainfall-runoff simulation of the hydrological model, which is the revision of tank model A (hereinafter referred to as the revised tank model), used in 2005 and 2008 to collect the flow, rainfall measured data, the actual rainfall-runoff simulation, analysis of the hydrological model simulation results and the differences in assessment of the accuracy of their model.

Figure 5 illustrates the detailed calculation process adopted in this study.

Fig. 5

Revised tank model calculation process

Parameter calibration

The revised tank model in this study requires the calibration of eight parameters. This study uses the Multi-start Powell method [5] for parameter calibration.

Table 2 shows the upper and lower limits of the revised tank model. The reasonability of calibrated parameter was considered when the initial parameter values were given, and the following limitation conditions were added:

Table 2 Upper and lower limits of the revised tank model parameters

$$ {\text{Pa}}1 + {\text{Pa}}2 + {\text{Pb}}1 \leqq 1 $$

(11)

$$ {\text{Pa}}3 \leqq 1 $$

(12)

The conditions of Formulas (11) and (12) are that the sum of outflow and infiltration orifice factors must not exceed 1. Formula (13) shows the least square error evaluation function (x²-base).

$$ {\text{object}}\_{\text{function}} = \frac{1}{N}\sum\limits_{i = 1}^{N} {{\frac{{(Q_{\text{sim}} (i) - Q_{\text{obs}} (i))^{2} }}{{Q_{\text{obs}} (i)}}}} $$

(13)

Q_sim(i):

simulated flow rate i

Q_obs(i):

observed flow rate I

N :

number of data

The penalty functions of the tank model are as follows:

• (1) If the sum of each tank coefficient exceeds or equals 1,

  $$ f_{\text{P1}} = c \times ({\text{Pa1 + Pa2 + Pb}}1) $$

  (14)
  $$ f_{\text{P2}} = c \times {\text{Pa3}} $$

  (15)

• (2) If the value of each standardized parameter is not located between 1 and 0,

  $$ f_{\text{P3}} = c \times (\left| {N_{i} } \right| + 1) $$

  (16)

  If >1,

  $$ f_{{{\text{P}}4}} = c \times (N_{i} ) $$

  (17)
  $$ N_{i} = \left( {X_{i} - X_{i}^{\text{lower}} } \right)/\left( {X_{i}^{\text{upper}} - X_{i}^{\text{lower}} } \right) $$

  (18)

  where,

  i :

  1–8

  N _i :

  standardized coefficient

  X _i :

  model coefficient

  X ^upper _i , X ^lower _i :

  the upper and lower limits for searching standardized coefficient

  C:

  coefficient of penalty function

Finally, the object function could be summarized as,

$$ \begin{aligned} & {\text{obj}}\_f = f \hfill \; {\text{Limitation}}\,{\text{ satisfied}} \\ & {\text{obj}}\_f = f + f_{{{\text{P}}1}} + f_{\text{P2}} + f_{\text{P3}} + f_{\text{P4}} \hfill \; {\text{Limitation}}\,{\text{unsatisfied}} \\ &{\text{obj}}\_f \to { \min } \\ \end{aligned} $$

Based on the collected rainfall and flow rate data, the rainfall event in July 18th, 2008 (Typhoon Kalmaegi) was chosen to calibrate the parameters of the revised tank model. Figure 6 and Table 3 shows the calibrated results of the revised tank model, while Table 4 shows the evaluation index. According to Table 4, the RMSE of the revised tank model calibration result is 0.0011, the CE is 0.98, the EQ_p is 4.29%, the ET_p is 20 min, and the EV is −6.76%. When the CE is 0.98 very close to 1, the simulated hydrograph approaches the observation values. Therefore, this study uses this set of parameters to verify the following rainfall events.

Fig. 6

Calibrated results of the revised tank model (KALMAEGI: July 18–19, 2008)

Table 3 Parameter values of the revised tank model

Table 4 Rainfall event values evaluated with the revised tank model

Simulation results

To confirm the revised tank model used in terraced paddy field, the four rainfall events with the best simulation performance were selected from the collected rainfall flow rate data and used in rainfall-runoff simulations with the revised tank model.

The first rainfall event is Typhoon SINLAKU (Sep 12, 2008), with a total rainfall of 301 mm. Figure 7 depicts the simulation results. The overall shape of the simulated runoff hydrograph shows good performance. With less than 5 mm rainfall in the simulation, calculation of peak discharge and the actual value rather, that EP_p is 0 min, rainfall more than 5 mm, the calculated flow than the measured flow largest. This rainfall event has a RMSE of 0.0035, CE of 0.75, EQ_p of 52.06%, and EV of 45.5%.

Fig. 7

The simulation results of the revised tank model (SINLAKU: Sep 12–16, 2008)

The second rainfall event is Typhoon JANGMI (Sep 27, 2008), with a total rainfall of 669 mm. Figure 8 shows the simulation results. The overall shape of the simulated hydrograph also indicates good performance. Simulated peak flows and their actual values are almost the same. EP_p is 5 min, but in the recession section of the hydrograph and the actual value have some errors. The RMSE of this rainfall event is 0.0016, while its CE is 0.76, EQ_p is 13.4%, and EV is 37%.

Fig. 8

The simulation results of the revised tank model (JANGMI: Sep 27, 2008–Oct 1, 2008)

The third rainfall event is LIGHT RAIN (June 13, 2005), with a total rainfall of 44 mm. Figure 9 presents these simulation results. In this case, the calculated peak flow is close to the actual value, but the simulated recession section is less than the actual flow. From the rainfall events that the rain stopped and then began recession, recession hydrograph is still a reasonable performance. Hydrological evaluation of this simulation shows a RMSE of 0.0011, CE of 0.91, EQ_p of 6.3%, EV of −11.6%, and ET_p of −70 min.

Fig. 9

The simulation results of the revised tank model (LIGHT RAIN: June 13–14, 2005)

The fourth rainfall event is PLUM RAIN (May 5, 2005), with a total rainfall of 464.5 mm. Figure 10 shows these simulation results. This rainfall event occurred for a long time in the rainfall-runoff simulation—as long as 17 days. The overall shape of the simulated runoff hydrograph exhibited good performance. Before May 12, the simulated peak discharge of was almost the same as the actual value. After May 12, the simulated calculations of continuous rainfall were greater than the actual flow peak discharge. This simulation had an RMSE of 0.0018, CE of 0.67, EQ_p of 55.93%, EV of 3.4%, and ET_p of 10 min.

Fig. 10

The simulation results of the revised tank model (PLUM RAIN: May 5–22, 2005)

Table 5 shows that the largest RMSE of the revised tank model simulation result is 0.0035, the smallest CE is 0.91, the largest EQ_p is 55.93%, the largest ET_p is −70 min, and the largest EV is 45.5%.

Table 5 Values of each rainfall event evaluated with the rainfall-runoff model

These results indicate that the overall performance of the revised tank model is very good. Although EV and ET_p are somewhat high, the estimation of the actual flow rate in the hydrograph is very accurate.

Discussion and conclusion

Discussion

• 1. The simulation results of the revised tank model indicate that its overall performance is very good. This model simulates the changes in outflow accurately. Its smallest RMSE is 0.0011, and its RMSE maximum is 0.0035, which are both close to 0. The CE values range from 0.67 to 0.91, showing that the simulated and observed values are very close. EQ_p ranges from 6.3 to 55.93%, showing a small difference between the simulated and observed peak discharge rates. EV ranges from −11.6 to 45.5%, show a small difference between the simulated and observed discharge rates.

• 2. Figures 6, 7, 8, 9, and 10 show that rainfall, light rain, a single peak rainfall, more peak rainfall, and rainy season conditions all achieve good simulation results. Thus, the proposed model accurately simulates flow rate changes in terraced paddy fields.

• 3. It is possible to increase the accuracy of the revised tank model simulation results using parameters calibrated by the Multi-start Powell method.

• 4. Figures 7, 8, and 10 show that simulated peak flow values are greater than the actual flow. This may be due to heavy rainfall, which makes the ridges break near the weir, causing outflow from the weir side. Since the weir cannot completely collect the actual flow in this case, the simulated peak flow is greater than the actual flow.

• 5. The tank model calibration parameter method is use of one rainfall event to the rate set its parameters, and use has been completion calibration of the parameters into the tank model. This study uses several different rainfall events to verify the tank model of rainfall-runoff mechanism. If the evaluation indicators are good, this set of parameters can control the hydrological and physiographic conditions in the test area, and can simulate the variations in flow in rice paddies. If the evaluation index is unsatisfactory, it is necessary to re-calibrate the parameters. The parameters used in this study accurately represent the rainfall-runoff mechanism in terraced paddy fields.

• 6. Table 3 (PS1, PS2) shows the initial values, with changes in rainfall intensity at different times (PS1, PS2) leading to changes in these values.

Conclusion

This study presents the following conclusions regarding the rainfall-runoff mechanism in terraced paddy fields:

• (1) Evaluated the simulation results of the revised tank model in terraced paddy fields with five commonly used indicators in statistics and hydrology confirms that the overall performance of the revised tank model is great. Simulation results prove that the model is applicable to the rainfall-runoff simulation of terraced paddy fields.

• (2) Previous complex tank models use long-term rainfall-runoff simulations (a day), while this study successfully conducts short-term simulations. The ideal simulation results prove that the model is applicable to both long- and short-term simulations.

• (3) The reason for the high accuracy in this hydrological model is that it is based on strong physical concepts uses the Multi-start Powell method for parameter calibration. The overall performance of the revised tank model is great, and it precisely predicts runoff changes. The evaluation values of both RMSE and CE show that this model achieves good simulation results.

• (4) Selected rainfall events, including rainfall, light rain, a single peak rainfall, more peak rainfall, and the rainy season, all achieve good simulation results. The proposed model can simulate flow rate changes in terraced paddy fields.