Introduction

The role of permanent Global Navigation Satellite System (GNSS) networks is constantly evolving. However, their main application is still the same: providing the highest-quality geodetic reference for scientific, governmental and commercial users. Long time series of GNSS-derived parameters have many new practical and scientific applications, like the definition of global reference frames, geodynamics and atmosphere analysis, climate and sea level research, etc. The millimeter accuracy of the reference station positions is required to satisfy the needs of the tasks mentioned above. Additionally, these applications require a stable and consistent series of GNSS estimates. Eckl et al. (2001) proved that sub-centimeter accuracy could be achieved based on GPS-only measurements. A similar analysis performed by Firuzabadi and King (2012) showed that with sessions six hours or longer and four or more reference stations, the precision of 1–2 mm in horizontal and about 3–5 mm in vertical is achievable. On the other hand, any changes in hardware configuration and antenna vicinity can introduce shifts or outliers to the station coordinate time series. Such hardware changes and the resulting discontinuities in station coordinates prove to be a major challenge for utilizing the continuously operating reference stations for various precise applications. Neglecting such effects can introduce notable errors into the analysis results (Kenyeres and Bruyninx 2004).

An example of a network where the mentioned issues are fundamental can be the EUREF Permanent Network (EPN). One of the most important tasks done under the EPN is the European Terrestrial Reference System (ETRS89) development, based on the continuous GNSS observations conducted on evenly distributed European stations. Torres et al. (2009) presented an overview of the status and development of EUREF core projects. In Bruyninx et al. (2012) the efforts made to monitor and improve the quality of the EPN products and services were described. The ETRS89 features designated high-precision reference station coordinates as well as velocities that describe a movement of a station, and therefore, a change in its coordinates over time (Altamimi et al. 2012). Investigations of apparent position shifts caused by equipment replacement at EPN stations can be found in the study made by Kenyeres and Bruyninx (2004). For example, in the case of the KARL station (Karlsruhe, Germany), the replacement of TRM22020.00 + GP antenna with radome to TRM29659.00 without radome caused a significant height offset of 4 cm. More examples concerning reference stations like EUSK, HOFN, KELY, MOPI can be found at the EPN CB website (https://www.epncb.oma.be/). Wanniger (2009) suggests that the shift of coordinates due to a change of antenna may be due to a difference in the multipath signal sensitivity or the effect of using antennas and radomes without calibration information. The carrier phase multipath effect is caused by signal reflectors in the vicinity of the antenna. Elósegui et al. (1995) analyzed near-field multipath. They found that the concrete and the metal plate embedded in the pillar were significant scattering sources. The observed scattering could be reduced greatly by using microwave absorbing materials. Dilssner et al. (2008) concluded that an antenna calibration accounting for the near-field multipath was imperative for precise height determination. In most cases, the change of the antenna does not apply to changes in its environment; thus, the change in the reflection characteristics applies to differences in physical dimensions of the antennas or different heights of mounting the new antenna. Even marginal geometrical changes may be a source of modulation of the multipath signals. Additionally, antennas and receivers have different sensitivity to multipath signals, which can be a reason for apparent position shifts after their replacement. A solution to the problem can be in situ calibrations (Böder et al. 2001). For example, Park et al. (2004a, b) designed and constructed a prototype Antenna and Multipath Calibration System (AMCS) to obtain in situ corrections for antenna phase center variations and multipath. However, despite their constant development, such systems still seem to be of little practical use. The GNSS antenna calibration technology development is also manifested through new calibration centers (Willi et al. 2020; Wübbena et al. 2019; Dawidowicz et al. 2021) or the inclusion of new GNSS signals in the calibration process (Kröger et al. 2021; Wanninger et al. 2022).

Antennas play an important role in GNSS measurement and strongly contribute to the overall achievable performance (Caizzone et al. 2021). Hence position components discontinuities can also be caused by the errors in antenna phase center corrections (PCC) used in the data processing. Description of antenna calibration methodology and its challenges can be found in Menge et al. (1998) or Mader (1999). Since PCC of the same antenna obtained from various calibrations may differ up to several millimeters (Kallio et al. 2019; Krzan et al. 2020), this may indicate a possible imperfection in the GNSS antenna calibration models. Therefore, this paper addresses the offset within the EPN station coordinate time series caused by antenna/radome changes. These changes were also analyzed in the context of variations in multipath effects as well as differences dependent on PCC model type.

Methodology

Several currently active EPN stations were selected for our analyses. The main criterion of selection was accessibility to three types of PCC models (type mean, individual robot-derived, individual chamber-derived) for the station, during the analyzed period. Twelve stations, all located in Germany, were found to meet this condition. All chamber-derived individual PCC models used in this study were developed by the Institute of Geodesy and Geoinformation at the University of Bonn (Görres et al. 2006). Geo +  + company (Garbsen, Germany) is the developer of PCC using the absolute field method (individual and type mean) (Schmitz et al. 2006; Wübbena et al. 2019). Antenna calibration based on similar technology is also conducted by the National Geodetic Survey (NGS) (Bilich and Mader 2010; Bilich et al. 2018). The individual PCC models are accessible at the EPN website. We also used type mean PCC models, resulting from averaging the corrections for a given antenna type from several calibrations of the same model, included in igs14.atx file (2132 version). The details of hardware changes at the test stations can be found in stations logs files (Table 1).

Table 1 Selected EPN stations logs files (status on April 1, 2022)
Full size table

The Precise Point Positioning (PPP) technique, applying the Ionosphere-Free (IF) combination of GNSS signals, was chosen in the study to derive station position components. PPP provides autonomous, absolute positioning not affected by any observation errors in surrounding GNSS reference stations. The NAvigation Package for Earth Observation Satellites (NAPEOS) software (Springer 2009) was used for data processing. Main NAPEOS processing parameters are presented in Table 2.

Table 2 NAPEOS processing parameters
Full size table

Six solutions were processed using two different constellation setups and three different PCC models. GPS-only and GPS + Galileo observations were processed using three types of the PCC models: type mean, individual field and individual chamber-derived. As a result, we obtained station coordinates in the IGS14 reference frame, which were subsequently transformed into ETRF2014 (Altamimi 2018). The transformation to ETRF was to ensure that the coordinates would remain constant over time. As the elaboration period is 3 years, the station coordinates in the ITRF would have changed by up to a few centimeters over this period. At the same time, the annual velocities of the stations used in the study, in the ETRF system, are usually well below 1 mm/yr. Finally, obtained results were compared to the reference coordinates from EPN C2085 (March 8, 2019) cumulative solution (Detailed information can be found in the Supplement). In the case of the chamber calibrations, PCCs for Galileo are determined and available. However, for the individual robot-derived and type mean PCCs, corrections for Galileo are not available. Therefore, GPS corrections were adopted as it is done in the Multi-GNSS Experiment (MGEX) (Montenbruck et al. 2017). This fact is important due to the difference in frequencies between the Galileo E5 (1191.795 MHz) and GPS L2 (1227.600 MHz) signals, which may introduce some inaccuracies in the solutions. This does not directly apply to Galileo E1 and GPS L1 bands, where both frequencies are identical (1575.420 MHz). Proposed two solutions allow us to analyze a case where all calibrations are directly available (GPS-only) and where for some signals, PCCs are adopted from another system (GPS + Galileo). All other processing options were kept the same for each solution.

Antenna characteristic

During the test period, only two types of antennas were mounted at the analyzed stations: LEIAR25.R3 LEIT and LEIAR25.R4 LEIT (Fig. 1). It should be noted that only in four cases there was a change between LEIAR25.R3 LEIT and LEIAR25.R4 LEIT (stations: BORJ, HEL2, LEIJ, WARN); otherwise, LEIAR25.R4 LEIT antenna was replaced by the same model of antenna.

Fig. 1
figure 1

Scheme of Leica AR25 (LEIAR25) antenna

Full size image

Figure 1 presents the scheme of Leica AR25 (LEIAR25) antenna. Both types (R3 LEIT and R4 LEIT) have the same construction and technical specification (Table 3). These antenna switching, with identical physical dimensions and mounting types, was the only factor that changed in local conditions. So potential multipath change noticed in results, according to Dilßner et al. (2008), can be related to the impact of reflecting objects located in the near-field region on the overall electromagnetic properties of the antenna (which can be different for different antenna units).

Table 3 Main technical properties of Leica AR25 antenna (https://leica-geosystems.com/)
Full size table

To have an insight on the potential impact of PCC models on the analyzed shifts in position parameters, PCC differences for antenna before and after replacement were calculated. Due to the lack of PCC for Galileo signals from robot calibrations, we decided to analyze PCC differences for GPS signals only. These comparisons were made mainly for individual PCCs (robot- and camber-derived), because in most cases LEIAR25.R3 LEIT antenna was replaced by the same model, which results in the same type mean PCC characteristic and zero differences during comparison. For station HEL2, where LEIAR25.R3 LEIT antenna was replaced by LEIAR25.R4 LEIT, PCC differences derived from type mean PCC models were also presented.

The PCC comparison was based on the approach proposed by Schön and Kersten (2014). Phase Center Variations (PCV), as well as PCC, are expressed in antenna body frame with \(\alpha {\text{and}} z\) as the horizontal and zenithal angle. To achieve a common datum, at the first step, PCV should be shifted to reach 0 for zero zenith angle direction: PCV(α, 0) = 0. This step is required for individual chamber-derived models’ comparison, and it can be done by adding a constant shift \(\delta\) equal to:

$$\delta = - {\text{PCV}}\left( {a,0} \right)$$
(1)

The first step is unnecessary if both compared PCC models have a common datum (PCV(α, 0) = 0). This situation occurs in the case of all robot-derived (type mean or individual) model comparisons. At the second step, we used formula (2) for reducing PCC obtained for newly established antenna to the PCO obtained for former (replaced) antenna (Schön and Kersten 2014):

$${\text{PCC}}_{N} \left( {\alpha ,z} \right) = s^{T} {\text{PCO}}_{{\text{O}}} + \left( {{\text{PCV}}_{{\text{N}}} \left( {\alpha ,z} \right) + s^{T} \left( {{\text{PCO}}_{{\text{N}}} - {\text{PCO}}_{{\text{O}}} } \right)} \right)$$
(2)

where s denotes the line-of-sight unit vector, PCCN is the new antenna PCC reduced to former antenna PCO, \({\text{PCO}}_{{\text{O}}}\) denotes former antenna PCO, \({\text{PCV}}_{{\text{N}}}\) denotes new antenna PCV, \({\text{PCO}}_{{\text{N }}}\) is the new antenna PCO.

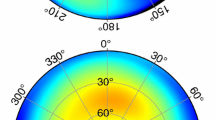
The final step was the computation of former and new antenna PCC differences (dPCC) for L1, L2 and IF frequencies. Figures 2 , 3, 4 present full PCC comparison for the three selected stations. Table 4 presents the maximum values of PCC differences obtained during the full PCC comparison for the analyzed stations.

Fig. 2
figure 2

Full PCC comparison (dPCC, station AUBG, LEIAR25.R4 LEIT to LEIAR25.R4 LEIT antenna changing). The top row compares individual robot-derived PCC and the bottom row to individual chamber-derived PCC

Full size image
Fig. 3
figure 3

Full PCC comparison (dPCC, station DILL: a first, b second LEIAR25.R4 LEIT to LEIAR25.R4 LEIT antenna changing). Top rows refer to a comparison of individual robot-derived PCC and bottom rows to individual chamber-derived PCC

Full size image
Fig. 4
figure 4

Full PCC comparison (dPCC, station HEL2, LEIAR25.R3 LEIT to LEIAR25.R4 LEIT antenna changing). The top row refers to a comparison of individual robot-derived PCC, the middle row to individual chamber-derived PCC, and the bottom row to type mean robot-derived PCC

Full size image
Table 4 Maximum PCC differences for AUBG, DILL and HEL2 stations
Full size table

Generally, the most significant differences were obtained comparing the chamber-derived models, reaching up to 8 mm in the case of IF combination (HEL2 station). The only exception is the second replacement of antenna at DILL station (DILL 2) where larger differences were obtained in the case of comparison of robot-derived PCC models. The change of antenna type that occurred at the HEL2 station caused type mean PCC differences not exceeding 3 mm, regardless of the analyzed frequency.

Figure 5 shows dPCC in the zenith angle-only function based on NO AZI corrections from ANTEX files. Stations where the antenna was changed more than once during the analyzed period were indicated by adding the appropriate index to the name, e.g., DILL 1, DILL 2.

Fig. 5
figure 5

Zenith-only angle-dependent PCC comparison

Full size image

Generally, for L1 frequency, differences do not exceed 2 mm. Exceptions are stations HEL2 and BORJ, where the differences reach up to 3 mm for chamber-derived models, and station LEIJ where for both types of individual PCC models, the differences reach up to 6 mm. For L2, the differences are visibly larger and, in some cases, reach up to 5 mm (especially for chamber-derived PCC models). There are a few cases (e.g., DILL 2, HELG, RANT 2, SAS2) where the dPCC do not exceed 2 mm, regardless of frequency and calibration method. As at most stations, the same antenna model (LEIAR25.R4 LEIT) was used after replacement; the type mean PCC comparison generated zero differences.

Position component time series analysis

Position component time series of daily solutions were studied, covering the period from 01.01.2017 to 31.12.2019. At this stage, we analyze the stability of coordinates as well as the effects of hardware changes. Since the analysis of time series generally applies to North, East and Up (NEU) position components, the time series of the Cartesian XYZ coordinates were converted to the topocentric system. Time series of the NEU differences relative to the EPN cumulative solution, for one example, station DILL, are presented in Fig. 6. Analogous figures for stations AUBG and HEL2 can be found in the Supplement.

Fig. 6
figure 6

Time series of the NEU differences to EPN cumulative solution for DILL station. The cyan vertical line indicates the moment of the receiver, and the dashed red vertical line the moment of the antenna change

Full size image

Differences for NE position components, presented in Fig. 6, rarely exceed the threshold of ± 5 mm; this is true for GPS-only as well as for GPS + Galileo solutions. For the Up component, the inconsistencies throughout 3 years are much higher and reach up to ± 20 mm for both analyzed solutions. Position time series clearly reveals shifts in topocentric coordinates resulting from the antenna change. For more detailed insight, box whisker plots (BWP), based on 30-day period data before (1) and after (2) antenna replacement, for all tested stations were calculated.

The results obtained using GPS-only signals presented in Figs. 7, 8 , 9 reveal that the antenna change effect is visible in all position components as a difference of mean value. For some stations (e.g., BORJ), jumps in position components appeared for both solutions and all used PCC models. On the other hand, there are stations (e.g., HEL2) where position offset is not so evident, and it is visible only in certain cases. Analogous analyses for the GPS + Galileo processing variant can be found in the Supplement. In the next step, we assume that position component jumps are relevant if the mean value of the second period is out of the interquartile range value of the first period (statistical meaning). Their respective statistics are presented in Table 5.

Fig. 7
figure 7

Box whisker plot for North component, depending on used PCC model type, based on GPS-only solution

Full size image
Fig. 8
figure 8

Box whisker plot for East component, depending on used PCC model type, based on GPS-only solution

Full size image
Fig. 9
figure 9

Box whisker plot for Up component, depending on used PCC model type, based on GPS-only solution

Full size image
Table 5 Summary of solutions with relevant position component jumps
Full size table

Table 6 summarizes jumps of position components caused by antenna replacements. Jumps were calculated as a difference between component mean positions based on 30-day period of data before and after the antenna replacement. The names of stations at which the LEIAR25.R3 LEIT antenna was replaced by LEIAR25.R4 LEIT are marked in bold.

Table 6 Summary of position component jumps
Full size table

Next, we investigate selected cases with the most noticeable position component jumps. For this purpose, we marked in bold (Table 6) the most significant offsets which, equal or exceed ± 2 mm for horizontal coordinates and ± 4 mm for vertical ones. First of all, it can be observed that significant position component shifts occurred both at stations where antenna type was and was not changed during replacement. Keeping the same antenna model does not guarantee the continuity of position time series. Furthermore, higher differences were generally obtained for the solution where GPS + Galileo observations were used. This can be explained by adopting GPS corrections for Galileo signals in the case of individual robot-derived and type mean PCCs. In the case of individual chamber-derived PCCs, this may also indicate that multi-frequency calibration can be more challenging.

We also focused on differences in observed coordinate jumps depending on the PCC model. Significant jumps occurred in all cases. The biggest difference obtained for the type mean model is equal to 8.1 mm (WARN station, GPS + Galileo solution). In the case of the individual robot-derived PCC model, it is equal to − 9.8 mm (BORJ station, GPS-only solution). Finally, for the individual chamber-derived PCC model it is equal to − 7.3 mm (BORJ station, GPS + Galileo solution). All these cases are associated with the change of antenna type at the station. In most cases, it is also observed that higher differences were obtained for solutions using type mean models. The most notable examples include AUBG North and East, SAS2 North, KARL North, RANT 1 and HELG UP. This proves the advantage of individual models over type mean. On the other hand, the high differences obtained for individual models may reflect cases with a deficiency in such types of PCCs.

Site multipath analysis

To have an insight on the potential impact of multipath on the observed position shifts, multipath for GPS L1 and L2 signals was calculated and analyzed. Multipath was derived using the following equations (Vázquez et al. 2012):

$${\text{MP1}} = p_{1} - \left( {1 + \frac{2}{\alpha - 1}} \right){\Phi }_{1} + \left( {\frac{2}{\alpha - 1}} \right){\Phi }_{2}$$
(3)
$${\text{MP2}} = p_{2} - \left( {\frac{2\alpha }{{\alpha - 1}}} \right){\Phi }_{1} + \left( {\frac{2\alpha }{{\alpha - 1}} - 1} \right){\Phi }_{2}$$
(4)

where \(p_{i}\) is the pseudorange observation,\({\Phi }_{i}\) is the carrier phase observation,\(\alpha = \left( {\frac{{f_{1} }}{{f_{2} }}} \right)^{2}\), \(f_{1}\) is the frequency of L1, and \(f_{2}\)—frequency of L2.

As results obtained for MP1 and MP2 were similar, in the context of the offsets resulting from antenna/radome changes, MP1 results are presented in the following section. This is because this frequency proved to be the most frequently used as it is the same or close to the first signal from all systems (Galileo E1, Beidou B1C, GLONASS L1 etc.), and moreover, it is always used in any single or dual-frequency solutions.

RMS of daily MP1 throughout 2017–2019 presented in Fig. 10 varies in the range from 0.2 to 0.5 m: for AUBG station within the range from 0.2 to 0.4 m, for other stations from 0.3 to 0.5 m. The jumps in MP1RMS are also visible. In some cases, these jumps appear to be related to the timing of the antenna change, for example, the first replacement on stations DILL and HEL2. However, such a correlation is difficult to be found in the case of station AUBG or the second replacement at station DILL. Additionally, noticeable offsets in the analyzed time series occur at moments unrelated to a change of equipment, like from days 950 to 1000 in the case of DILL station or from days 450 to 550 in the case of HEL2 station.

Fig. 10
figure 10

Time series of the RMS of daily GPS MP1. The cyan vertical line indicates the replacement of the receiver and the dashed red vertical line the replacement of the antenna change. The winter days (from December 1 to February 28) are shaded

Full size image

For more detailed analyses, box whisker plots based on 30 days period data before (Period 1) and after (Period 2) antenna replacement for all tested stations were calculated and presented in Fig. 11. The BWP for daily MP1 RMS also revealed the effect of changing the antenna. For some cases, like station HELG, second replacement on stations RANT and WARN, the displacement is clearly visible. Only in one case of the aforementioned (station WARN) is this related to changing the antenna type. On the other hand, there are cases (e.g., AUBG, HOFJ, LDB2 stations) where the analyzed offset is unnoticeable. In contrast, the LEIAR25.R4 LEIT antenna was replaced by the same antenna model at these stations. If we assume that jumps of RMS of daily GPS MP1 are relevant if the mean value of the second period is out of the interquartile range value of the first period (statistical meaning), 50% of solutions are characterized by relevant jumps. Table 7 summarizes the offset of MP1 RMS caused by the antenna replacement. Similarly, to the position components, jumps were calculated as a difference between the mean RMS values, which were obtained based on the data from 30 days before and after the antenna replacement.

Fig. 11
figure 11

Box whisker plot for RMS of daily GPS MP1

Full size image
Table 7 Discontinuity of mean RMS of GPS MP1
Full size table

The absolute values of the detected MP1 offsets at the analyzed stations vary from 0.01 cm (LEIJ station) to even 15.28 cm (WARN station). If we focus on stations with the most significant jumps, reaching up to 10 cm, we can observe that they occurred at WARN station, where LEIAR25.R3 LEIT antenna was replaced by LEIAR25.R4 LEIT and HELG and RANT stations (second replacement of antenna), where the antenna type during replacement was not changed.

Discussion and summary

Tables 8 and 9 summarize the obtained results. We marked by “x” those stations for which the zenith-only PCC differences reach or exceed 2 mm for L1 frequency and 3 mm for L2 for at least two PCC models. In the “NEU” columns, cases where the position component jumps were relevant from the statistical point of view have been marked by “x”. Finally, in the “MP1” column, all cases where the mean RMS of GPS MP1 was relevant from the statistical point of view were marked by “x”.

Table 8 Summary of the results for GPS-only solution
Full size table
Table 9 Summary of the results for GPS + Galileo solution
Full size table

Analyzing the column with Zenith-only PCC difference in Table 8, it can be seen, as expected, that a change to a different model of antenna generated more considerable differences than a change of antenna within the same model. In the case of stations where the LEIAR25.R4 LEIT antenna replaced the LEIAR25.R3 LEIT one, significant differences occurred in the case of all PCC model types. Additionally, for two stations AUBG and HOFJ, where the LEIAR25.R3 LEIT antenna was replaced by the same antenna type, the differences exceed the adopted criteria in the case of chamber-derived PCC models. Larger differences in PCC models coincide quite well with the position components jumps, which are relevant from the statistical point of view (marked by “x” in “NEU” columns). Furthermore, in the case of GPS-only processing, changing antenna type from LEIAR25.R3 LEIT to LEIAR25.R4 LEIT does not mean that significant position component jumps will occur. Only for station BORJ, significant jumps occur for all position components in the case of using all three PCC models. For the other three stations where such a replacement took place, discontinuities occurred only for some position components and some PCC models. Analyzing the frequency of the occurrence of relevant jumps depending on the PCC model type, it can be seen that the most stable results were achieved using the robot-derived individual PCC model (48% of relevant jump). In the case of type mean and chamber-derived individual PCC 57% of jumps were relevant from the statistical point of view.

Regarding RMS of daily GPS MP1, seven stations (50%) are characterized by offset relevant from the statistical point of view. For the solution using robot-derived PCC, the relevant jumps discovered in the coordinate time series for stations DILL 1, HOFJ and RANT 1, agree quite well with the relevant jumps discovered in RMS of the MP1 time series. For solutions using chamber-derived PCC such agreement can be observed for stations DILL 1, HEL2, HOFJ, LEIJ, and RANT 1. In these cases, it can be assumed that the MP1 change may also have been the reason for detected position components’ shifts.

In the case of GPS + Galileo processing (Table 9), changing antenna type resulted in significant position component jumps in almost all cases. Only for LEIJ station significant jumps were not present in the case of using all types of PCC models. For the other three stations, where the LEIAR25.R3 LEIT antenna was replaced by the LEIAR25.R4 LEIT one, such offsets occurred for all position components in the case of all PCC models. This proves that in the case of changing the antenna model for multi-GNSS processing purposes, it is more likely to obtain discontinuities in the position component time series, as the risk of inaccuracies in the PCC model is greater. This is due to more frequencies to model, incomplete Galileo constellation during the robot calibration process, and the adaptation of GPS corrections for Galileo signals.

Analyzing the frequency of occurrence of relevant jumps depending on the PCC model type, we can see that, in the case of GPS + Galileo processing, most stable results were achieved using the chamber-derived PCC model (relevant jump for 55% of solutions). In case of type mean and individual robot-derived PCC, relevant jumps occurred in 64% and 62% of solutions, respectively. This means that using a Galileo-dedicated PCC model can guarantee higher stability of position component time series. Furthermore, GPS + Galileo processing mode generated more relevant position component discontinuities from a statistical point of view than the GPS-only solution. The reason may be the use of more GNSS signals compared to the GPS-only case and the more challenging estimation of accurate PCC models. In the case of robot-derived PCCs, the reason could also be the adaptation of GPS corrections for Galileo signals.

Analyzing the correlation between the relevant jumps discovered in coordinates and appropriate jumps discovered in MP1 time series for robot-derived PCC models, we found in GPS + Galileo solution an agreement for two times more cases than in GPS-only solution. Such correlation was found for DILL 1, HOFJ, RANT 1, as well as for HEL2, RANT 2 and WARN. These three new cases result from the higher number of significant jumps noted in GPS + Galileo solution for this type of PCC model. On the other hand, correlation was found in four cases (AUBG, DILL 1, HEL2, WARN) for the solution using chamber-derived PCC. This is one less case than in GPS-only results and is connected to a lesser number of significant position jumps noted in GPS + Galileo solution for the chamber-derived PCC model.

Conclusions

The study addresses the offset within the EPN station coordinate time series caused by antenna/radome changes. We analyze the shift magnitude as well as its PCC model and multipath dependency. Analyzing the obtained results, it can be seen that the antenna change effect is visible in all position components. In the case of the horizontal position components, the position differences reach up to 5 mm. For the Up component, the differences are visibly larger and, in certain cases, exceed 5 mm.

Our analyses prove that changing antenna type does not mean significant position component jumps will occur in the case of GPS-only processing. Only for one station, out of four where the LEIAR25.R3 LEIT antenna was replaced by the LEIAR25.R4 LEIT one, significant jumps occur for all position components in the case of using all three types of PCC models. For the other three stations, discontinuity occurred only for some position components and some PCC models. A more significant role plays the accuracy of the PCC models and possible MP changes after antenna replacement. In the case of GPS + Galileo processing, changing antenna type almost always means that significant position component jumps will occur. Only for one station significant jump did not occur (in the case of using any PCC models). For the other three stations, the offsets occurred for all position components in the case of all PCC models. This means that in case of changing the antenna model for multi-GNSS processing purposes, it is more likely to obtain significant jumps in the position component time series, as the risk of inaccuracies in the PCC model is greater. Note that currently, multi-GNSS processing is a standard approach.

Considering the frequency of occurrence of relevant jumps depending on the PCC model type for GPS-only solutions, the most stable results were achieved using robot-derived individual PCC models. In such type of solution (GPS-only) robot-derived individual PCC models usually guarantee higher stability of position component time series. On the other hand, in the case of GPS + Galileo processing, the most stable results were obtained using chamber-derived individual PCC models. This proves that using PCC models where Galileo signals were directly calibrated guarantees higher stability of position component time series in comparison to solutions where Galileo PCC corrections were adopted from GPS.

The correlation between position component and RMS of GPS MP1 discontinuities for GPS-only solutions occurs on average in about 29% of cases. In 36% of cases, relevant jumps were noticed in position components, but there were no such offsets in the RMS of MP1. In the case of GPS + Galileo processing mode, the correlation between position component and RMS of GPS MP1 discontinuities occurred on average at about 41% of cases. As in GPS-only solutions, there are also cases (29%) where relevant jumps were noticed in position components, but there were no such offsets in RMS of MP1.