Introduction

GNSS signals are refracted by the troposphere along their path to the receiver. This part of the atmosphere is neutral and non-dispersive for radio frequencies up to 15 GHz. This refraction is called tropospheric delay, and it is a function of the refractive index (N). The tropospheric refractivity is characterized by pressure (P), temperature (T), and water vapor pressure (e). Roughly 90% of the tropospheric delay is related to the hydrostatic component and can be estimated with high precision using empirical models (Hopfield 1969, Saastamoinen 1973). Conversely, the tropospheric wet part cannot be simply modeled with sufficient accuracy due to the significant variation of water vapor with time and space (Rohm and Bosy 2011). Water vapor plays an essential role in the earth's water cycle, and therefore, it is a crucial factor for weather research and climate studies (Kačmařík and Rapant 2012, Lutz 2008, Troller 2004). Traditional methods like radiosondes, remote sensing satellites, water vapor radiometer, and lidar can be used for measuring the distribution of this parameter in the troposphere (Bai 2004; Nicholson et al. 2005; Troller 2004). However, these techniques have some limitations and drawbacks, like low spatial–temporal resolution or high cost (Bai 2004; Kačmařík and Rapant 2012, Troller 2004). Nowadays, GNSS data can solve these disadvantages and provide continuous scans of the troposphere at very low costs (e.g., Bevis et al. 1992, Priego et al.2017)).Typically, only the Zenith Wet Delay (ZWD) above the GNSS receiver is estimated at any time. As these ZWDs denote integral quantities deduced from data of a usually sparse site network, they do not provide the requested 3D spatial resolution of wet refractivity. For this reason, in recent decades, GNSS tropospheric tomography has been developed to resolve the tempo-spatial wet refractivity (\({N}_{\mathrm{w}}\)) field. For example, Flores et al. (2000) applied horizontal and vertical constraints to reconstruct the tomography field using a Kalman filter. Champollion et al. (2005) considered the standard atmosphere and meteorological observations as a priori constraint to improve the tomography accuracy. Rohm and Bosy (2011) used a set of parameters, which had been extracted from the analysis of airflow to the tomography equations. Adavi and Mashhadi-Hossainali (2014) proposed the model space resolution matrix to determine the optimum horizontal resolution for the tomography model. This method is based on the dependency of the resolution matrix on the property of the tomography design matrix. Guo et al. (2016) suggested the optimal method to define the optimum weights for tomography equations and constraint equations in the tomography problem. In 2018, Zhao et al (2018). investigated the impact of multi-GNSS on the GNSS tomography solution by considering moderate weights for the observation equations derived from multi-GNSS and the different constraints. Experiments on the combination of GNSS data and Interferometric Synthetic Aperture Radar (InSAR) data as input observation information for the tomographic system were carried out by Heublein et al. (2019). Shehaj et al. (2020) presented a new technique based on the collocation approach to retrieve the refractivity field from GNSS measurements, comparable to typical tomography.

In this method, the area of interest is discretized into 3D elements (voxels) in the vertical and horizontal directions. In order to reconstruct the wet refractivity field in different epochs, the measurements of the Slant Wet Delay (SWD) are integrated in the desired period. Therefore, this parameter is assumed to be constant in this time window (Rohm and Bosy 2011; Troller 2004). The resolution of the reconstructed wet refractivity is highly dependent on the GNSS network density. Consequently, an existing dense GNSS network is one of the essential pre-requirements in this approach. However, the use of dual-frequency (DF) receivers is not economically practicable in this regard, as the cost of each receiver is remarkably expensive. As an alternative, single-frequency (SF) receivers can be considered to achieve a sufficient spatial resolution for GNSS meteorology (Bai 2004, Deng et al. 2009, Krietemeyer et al. 2018). Therefore, in this study, we examine the potential of SF observations in comparison to DF observations for reconstructing the wet refractivity field in an Austrian GNSS network with twenty-one stations. To quantify the ionospheric delay in the SF processing in precise point positioning (PPP) mode, we use the Satellite-specific and Epoch-differenced Ionospheric Delay (SEID) model (Deng et al. 2009).

Aside from the impact of SF and DF observations on the accuracy of ZTD and the wet refractivity field, a second essential component in GNSS tomography is investigated in this research. This second element concerns the effect of various regularization techniques, including ART methods and TV, by considering SF and DF observations. Therefore, we first introduce the concept of GNSS tropospheric tomography. Then, the estimation of the ZTD using SF observations in PPP mode and DF observations in double-difference mode are defined. The accuracy of estimated ZTD using SF and DF modes is discussed in comparison to ZTD derived from the Numerical Weather Models (NWM). In this study, we have used the AROME (Applications of Research to Operations at MEsoscale) model, which is one of the regional NWM models in Europe. After that, iterative regularization methods, as well as TV techniques, are described in order to reconstruct the wet refractivity field. The reconstructed wet refractivity using different regularization methods on two different observation types (SF and DF) is compared to radiosonde observations. In the end, the conclusions about the obtained results are stated.

Methodology

First, the concept of GNSS tropospheric tomography by considering horizontal and vertical constraints is introduced. Next, estimation of ZTD using PPP strategy and network strategy is described, followed by the presentation of the iterative techniques and direct technique to retrieve the tomography solution. Figure 1 presents the studied schemes in this research. As shown in this figure, the impact of using SF and DF observations on the ZTD accuracy is investigated as a first step. Then, the wet refractivity field is reconstructed by considering these two different datasets using the mentioned processing strategies.

Fig. 1
figure 1

Overview of schemes studied in this research

Full size image

Table 1 demonstrates various regularization methods in order to retrieve the wet refractivity structure. According to this table, iterative regularization methods have been compared to the TV technique. In addition, the outputs of the TV method have been applied as an a priori field for iterative methods.

Table 1 Various regularization methods to reconstruct the wet refractivity field in this research
Full size table

Overall, the wet refractivity outcome of seven different regularization methods has been compared to the radiosonde wet refractivity on basis of SF and DF observations in this research, which are: (1) Landweber + AROME, (2) MART + AROME, (3) ART + AROME, (4) TV, (5) Landweber + TV, (6) MART + TV, and (7) ART + TV.

GNSS tropospheric tomography

Using the following definition, the method of tomography is applied to reconstruct the spatial structure of the wet refractivity Nw in the troposphere (Troller et al. 2006):

$${\mathrm{SWD}}_{j}={10}^{-6 } \sum_{i=1}^{m}{{N}_{\mathrm{w}}}_{i} {d}_{ij}$$
(1)

where \({d}_{ij}\) represents the path length of signal j in model element i. In matrix form, Equation 1 reads as:

$$\mathbf{S}\mathbf{W}\mathbf{D}={\varvec{A}} {{\varvec{N}}}_{\mathbf{w}}$$
(2)

here \({\varvec{A}}\) is a structure matrix which links the observation vector (\(\mathbf{S}\mathbf{W}\mathbf{D}\)) to the unknown vector (\({{\varvec{N}}}_{\mathbf{w}}\)). The elements of the observation vector \(\left(SWD\right)\) are computed as follows:

$$\mathrm{SWD}=\left(\mathrm{ZTD}-\mathrm{ZHD}\right) \mathrm{VMF}\left(\mathrm{elv}\right)+{\mathrm{mf}}_{\mathrm{g}}\left(\mathrm{elv}\right) \left[{G}_{\mathrm{NS}}\mathrm{ cosaz}+ {G}_{\mathrm{EW}}\mathrm{ sinaz}\right]$$
(3)

where ZTD is the zenith total delay estimated from GNSS data processing. Furthermore, ZHD, \({G}_{\mathrm{NS}}\), and \({G}_{\mathrm{EW}}\) are the zenith hydrostatic delay, north–south, and east–west horizontal gradients, respectively. In addition, elv and az are elevation and azimuth angles of the individual signal paths. \(VMF\) and \({mf}_{g}\) are the corresponding mapping functions to convert the ZWD (which is ZTD-ZHD) and the horizontal gradients to Slant Wet Delays (SWDs). It should be indicated that this research applies the Vienna Mapping Function-1 (VMF1) and Chen-Herring mapping functions (Böhm et al. 2006; Chen and Herring 1997). Moreover, the Saastamoinen model is used for computing ZHD (Saastamoinen 1973).

In (2), the design matrix \({\varvec{A}}\) depends on the resolution of the model, the satellite constellation, the distribution of the GNSS receivers, and the time window of observation integration (Bender and Raabe 2007; Troller 2004). Due to the incomplete spatial coverage of GNSS signals in the model voxels, some of the voxels are under-determined. Therefore, the tomographic reconstruction Equation (2) is mixed-determined (Menke 2012). Consequently, the formation of a regular normal equation matrix that can be inverted is impossible due to the ill-posedness of (2). To solve this issue, constraints have to be added. In this study, we consider horizontal and vertical constraints as noted below (Rohm and Bosy 2011, Troller 2004, Yang et al. 2018):

$$0={\varvec{H}} {{\varvec{N}}}_{\mathbf{w}}$$
(4)
$$0={\varvec{V}} {{\varvec{N}}}_{\mathbf{w}}$$
(5)

where \({\varvec{H}}\) and \({\varvec{V}}\) denote coefficient matrices of horizontal and vertical constraints, respectively. By combination of (2), (4), and (5), the total observation equation of the tomography model is given by:

$$\left[\begin{array}{c}\mathbf{S}\mathbf{W}\mathbf{D}\\ 0\\ 0\end{array}\right]=\left[\begin{array}{c}{\varvec{A}}\\ {\varvec{H}}\\ {\varvec{V}}\end{array}\right] \left[\begin{array}{c}{{N}_{w}}_{1}\\ \vdots \\ {{N}_{\mathrm{w}}}_{m}\end{array}\right]$$
(6)

which is used to retrieve the wet refractivity field.

ZTD estimation using GNSS data processing

This section introduces two different strategies for estimating the ZTD. In the first strategy, the undifferenced PPP mode is applied for tropospheric modeling in goGPS software using SF observation data (Herrera et al. 2016). The ZTD is derived by processing dual-frequency (DF) observations with the Bernese GNSS software in the second one.

PPP strategy using SEID algorithm

The ionospheric delay is one of the major error sources in GNSS based positioning. For that reason, the ionospheric-free linear combination (IF LC) built of dual-frequency observations is normally used in PPP. Unfortunately, cheap SF receivers do not track observations on a second frequency. In addition, the accuracy of the ionospheric model should be a few tens of TECU in order to achieve promising results using SF observations. This quality can neither be provided at the moment by well-known broadcast models like Klobuchar or NeQuick nor by IGS-GIMs. To overcome these difficulties, Deng et al. (2009) have developed a technique that derives a synthetic second frequency from multi-frequency receivers located close to the SF receiver using the geometry-free linear combination. They call this approach the Satellite-specific and Epoch-differenced Ionospheric Delay (SEID) model (see Fig. 2). Hence, with the generated synthetic second frequency, it is possible to calculate a PPP solution using the ionospheric-free linear combination. By exerting this method, Deng et al. (2009) have reached an RMS of 3 mm of the ZTD estimates in comparison to ZTD estimates based on PPP solutions using real observations on two frequencies. The generated synthetic frequency data have been derived from reference stations within a distance of 52–75 km.

Fig. 2
figure 2

Building L2 observations used in goGPS software (Scheme 1)

Full size image

In this study, data of the four nearby IGS stations GRAZ, MEDI, WTZR, and ZIMM were applied together with the SEID model to generate the synthetic second frequency for the case study stations from which only SF observations were used. Due to the fact that goGPS supports SEID only for GPS, no other GNSS was included in the analysis. For the PPP solution, CNES (Centre National d’Etudes Spatiales) final products available from (Crustal Dynamics Data Information System) were used for satellite orbits and clock solutions. In this case study, the ZTD was estimated with an update rate of 30 s. Then, the estimated ZTD values were averaged over every 1 h in order to provide better consistency with the processing of the tomography model.

Network strategy

Generally, the process of ZTD determination by means of the Bernese GNSS software in baseline mode is illustrated by the flow diagram in Fig. 3 (Dach R et al. 2015). According to this figure, phase and code observations are preprocessed, and single-difference observations are created. After that, produced data are applied in the GPSEST step. Finally, station coordinates and ZTD are estimated.

Fig. 3
figure 3

Flowchart of tropospheric parameter estimation using the Bernese GNSS software (Scheme 2)

Full size image

Final precise orbits and earth rotation parameters provided from CNES are applied to achieve high precision. Ephemeris data are parameterized via the collocation method in module ORBGEN and interpolated to the desired GNSS observations epochs (here 30 s). For datum definition, the coordinates of the IGS stations, GRAZ, MEDI, WTZR, and ZIMM, were tightly constrained. Besides, the relative and absolute a priori ZTD sigmas for all stations were set to 5 m and 1 m, respectively. In contrast to the float PPP scheme, the phase ambiguities were fixed in the DF scheme. In this strategy, ZTD was estimated every 15 min over the investigated period. Finally, hourly mean values of the estimated DF ZTDs were calculated to establish better consistency with the tomography model.

Regularization methods

First, some of the iterative regularization techniques (ART, MART, and Landweber) are defined. These methods have been particularly developed for the tomography reconstruction problems and are mostly applicable to such approaches (Aster et al. 2013; Landweber 1951). Then, the total variation (TV) regularization method is described. This method was first proposed by Rudin et al. (1992) for image denoising problems. TV is a nonlinear technique that effectively preserves discontinuities in the model and resists noise (Aster et al. 2013, Karl, 2005, Lee et al. 2007, Vogel and Oman, 1996).

Iterative regularization methods

The iterative regularization techniques have been denoted as one of the most popular and successful methodologies to reconstruct the ionosphere's total electron content and, recently, the wet refractivity of the troposphere. In these techniques, there is no need to invert the design matrix \({\varvec{A}}\) during the reconstruction procedure (Bender et al. 2011). The main form of the iterative regularization technique is represented as below (Kaltenbacher et al. 2008):

$${{\varvec{N}}}_{\mathrm{w}}^{k+1}={\mathbf{N}}_{\mathrm{w}}^{\mathrm{k}}+{G}_{k}\left({{\varvec{N}}}_{\mathrm{w}}^{k},\mathbf{S}\mathbf{W}\mathbf{D}\right)$$
(7)

where \({G}_{k}\) and k are a correction term and iteration number, respectively. \({G}_{k}\) can be defined differently according to the desired methodology. This algorithm is a kind of closed-loop process and it starts with an initial guess for the unknown parameters field (Lohvithee 2019), which could be estimated from the Numerical Weather Model (NWM). Then, to correct the estimated wet refractivity field for the next iteration, the inconsistency between the estimated wet refractivity field and the prior field is computed using (Bender et al. 2011, Gordon, 1974; Lohvithee, 2019).

ART—The algebraic reconstruction technique (ART) is one of the most popular and frequently used algorithms among the different types of iterative methods (Gordon et al. 1970). This algorithm can be formulated as shown below (Gordon, 1974, Kak and Slaney, 1999):

$${{\varvec{N}}}_{w}^{k+1}={{\varvec{N}}}_{w}^{k}+ \lambda \left({SWD}_{i}-\langle {{\varvec{A}}}^{i}, {{\varvec{N}}}_{w}^{k}\rangle /\langle {{\varvec{A}}}^{i},{{\varvec{A}}}^{i}\rangle \right) {{\varvec{A}}}^{i}$$
(8)

The ART method covers two loops: The inner loop (index i) processes observation by observation. The outer loop (index k) is started after applying all SWDs in (8) (Bender et al. 2011; Xiaoying et al. 2014). \(\lambda\) is a regularization parameter from \((\mathrm{0,1}]\) and provides the weight of the correction term with respect to the initial wet refractivity field (Bender et al. 2011; Turonova 2011).

MART—In the multiplicative algebraic reconstruction technique (MART), the proceeding value of the corresponding voxel is corrected by multiplication with \({G}_{k}\) which corresponds to the second factor in (7) (Subbarao et al. 1997). In principle, this increases the convergence speed compared to additive techniques like ART (Bender et al. 2011; Subbarao et al. 1997). This method can be accomplished using (Subbarao et al. 1997):

$${{\varvec{N}}}_{wj}^{k+1}={{\varvec{N}}}_{wj}^{k} \lambda {\left({\mathrm{SWD}}_{i}/\langle {{\varvec{A}}}^{i}, {{\varvec{N}}}_{w}^{k}\rangle \right)}^{\left(\lambda {{\varvec{A}}}_{j}^{i}/\langle {{\varvec{A}}}^{i},{{\varvec{A}}}^{i}\rangle \right)}$$
(9)

where j is the column number of the voxel. In this method, the regularization parameter \(\lambda\) is defined within the range of \((\mathrm{0,2}]\) (Bender et al. 2011).

Landweber—Landweber is one of the most popular iterative regularization methods from the Simultaneous Iterative Reconstruction Technique (SIRT) group (Hansen 1998; Kaltenbacher et al. 2008). In this technique, the system of observation equations is solved simultaneously, and it is defined as follows (Landweber 1951):

$${{\varvec{N}}}_{w}^{k+1}={{\varvec{N}}}_{w}^{k}+ {\lambda }_{k} {{\varvec{A}}}^{\mathbf{T}}(\mathbf{S}\mathbf{W}\mathbf{D}-{\varvec{A}}{\boldsymbol{ }{\varvec{N}}}_{w}^{k})$$
(10)

In this algorithm, \({\lambda }_{k}\) is selected to range between \(0<\lambda <2/{s}_{\mathrm{max}}^{2}\) where \({s}_{\mathrm{max}}\) is the largest eigenvalue of matrix \({{\varvec{A}}}^{\mathrm{T}}{\varvec{A}}\) (Aster et al. 2013).

Total variation method

The TV regularization method has been used in different kinds of inverse problems such as CT (computed tomography) reconstruction with low signal-to-noise ratio with promising results (Defrise et al. 2011; Persson et al. 2001; Sidky et al. 2006; Tang et al. 2009). In recent years, the TV method has also been applied in ionospheric tomography (IED) as well.

The objective function in the TV regularization method is given as (Jensen et al. 2012; Lohvithee, 2019; Persson et al. 2001; Rudin et al. 1992):

$$J\left({{\varvec{N}}}_{\mathrm{w}}\right)=\mathrm{argmin}\left({\tau \Vert {{\varvec{N}}}_{\mathrm{w}}\Vert }_{\mathrm{TV}}+\frac{1}{2} {\Vert {\varvec{A}} {{\varvec{N}}}_{\mathrm{w}}-\mathbf{S}\mathbf{W}\mathbf{D}\Vert }_{2}^{2}\right)$$
(11)

where \(\tau >0\) is the regularization parameter and the TV norm (\({\Vert {{\varvec{N}}}_{\mathrm{w}}\Vert }_{\mathrm{TV}}\)) in (11) can be calculated as follows (Persson et al. 2001):

$${\Vert {{\varvec{N}}}_{\mathrm{w}}\Vert }_{\mathrm{TV}}= {\Vert \overrightarrow{D} {{\varvec{N}}}_{\mathrm{w}}\Vert }_{1}= \sum_{i,j,k}\Vert {D}_{i,j,k} {{N}_{w}}_{i,j,k}\Vert$$
(12)

where \({D}_{i,j,k} {{N}_{w}}_{i,j,k}\) is the discrete gradient of \({N}_{w}\) at voxel i, j, k. Here, the augmented Lagrangian algorithm for TV minimization is used (Li, 2009):

$${\mathcal{L}}_{A}\left({w}_{i,j,k},{N}_{\mathrm{w}}\right)=\sum_{i,j,k}\left(\Vert {w}_{i,j,k}\Vert -{\mathcal{V}}_{i,j,k}^{\mathrm{T}}\left({D}_{i,j,k}{{\varvec{N}}}_{w}-{w}_{i,j,k}\right)+\frac{{\beta }_{i,j,k}}{2} {\Vert {D}_{i,j,k}{{\varvec{N}}}_{\mathrm{w}}-{w}_{i,j,k}\Vert }_{2}^{2}\right)-{\lambda }^{T}\left({\varvec{A}} {{\varvec{N}}}_{\mathrm{w}}-\mathbf{S}\mathbf{W}\mathbf{D}\right)+ \frac{\mu }{2} {\Vert {\varvec{A}} {{\varvec{N}}}_{\mathrm{w}}-\mathbf{S}\mathbf{W}\mathbf{D}\Vert }_{2}^{2}$$
(13)

where \({w}_{i}\) can be obtained as below(Li 2009):

$${w}_{i}=\mathrm{max} \left\{\Vert {D}_{i,j,k}{{\varvec{N}}}_{w}-\frac{{\upsilon }_{i,j,k}}{{\beta }_{i,j,k}}\Vert -\frac{1}{{\beta }_{i,j,k}},0\right\} \frac{\left({D}_{i,j,k}{N}_{w}-{\upsilon }_{i,j,k}/{\beta }_{i,j,k}\right)}{\Vert {D}_{i,j,k}{N}_{w}-{\upsilon }_{i,j,k}/{\beta }_{i,j,k}\Vert }$$
(14)

\({\upsilon }_{i,j,k}\) and λ are continuously updated during the minimization of (13) at each iteration.

(Li 2009; Li et al. 2010):

$${{\stackrel{\sim }{\upsilon }}_{i,j,k}}^{\mathrm{iter}+1}={{\upsilon }_{i,j,k}}^{\mathrm{iter}}-{\beta }_{i,j,k} \left({D}_{i,j,k}{{{\varvec{N}}}_{\mathrm{w}}}^{*}-{{w}_{i,j,k}}^{*}\right) \mathrm{for all} i,j,k$$
(15)
$${\stackrel{\sim }{\lambda }}^{\mathrm{iter}+1}={\lambda }^{\mathrm{iter}}-\mu \left({\varvec{A}} {{{\varvec{N}}}_{\mathrm{w}}}^{*}-\mathbf{S}\mathbf{W}\mathbf{D}\right)$$
(16)

In (15) and (16), \({{{\varvec{N}}}_{\mathrm{w}}}^{*}\) and \({{w}_{i,j,k}}^{*}\) indicate approximate values for (13) (Li 2009). Moreover, the barrier parameter \(\mu\) should be defined based on the sparsity level of the true solution and the noise level in the observation (Li et al. 2010). However, the determination of the noise level without accessing the exact solution is challenging. According to experience, \(\mu\) varies from \({2}^{4}\) to \({2}^{13}\), and the best value is chosen subject to the RMSE of the recovered field (Li, 2009; Li et al. 2010). The value of \({\beta }_{i,j,k}\) should also been chosen between \({2}^{4}\) and \({2}^{13}\) (Li et al. 2010).

Case study

To analyze schemes SF and DF by applying different regularization techniques, 21 multi-GNSS stations from the EPOSA (Echtzeit Positionierung Austria) GNSS network, which mostly covers Austria's eastern part, have been selected. The mean inter-station distance is about 60 km, with height differences varying from 220 to 860 m. The distribution of the EPOSA GNSS stations and a radiosonde station is shown in Fig. 4.

Fig. 4
figure 4

Distribution of GNSS stations of the EPOSA network for the case study

Full size image

Observations on days 232–245 in August 2019 have been chosen due to the unstable weather conditions with high and low amounts of precipitation in the period of interest. Figure 5 shows variations of precipitation revealed by the AROME model and the observed relative humidity calculated from radiosonde data.

Fig. 5
figure 5

Variations of relative humidity up to 4 km height (top) and average of precipitation within the whole area (bottom) during the time of interest

Full size image

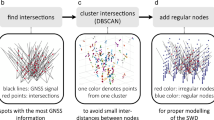
For the tomographic model, the model space resolution matrix has been applied in order to choose the optimum horizontal resolution (more details in (Adavi and Weber 2019)). According to the obtained results, a horizontal resolution (voxel side length) of 60 km has been chosen. The exponential model has been used to define the vertical resolution (Manning 2013, Möller 2017, Perler 2011) up to a height of 15 km with 9 layers. Moreover, the topography of the case study was also taken into account. For this purpose, the height of the grid point should be computed based on the elevation model of the case study area (see (Adavi et al. 2020) for more details). Here, the shuttle radar topography mission (SRTM) image has been utilized. Table 2 shows the selected parameters and corresponding heights in the center of voxels in this study. The designed tomography model with 60 km horizontal resolution and layers according to the table is shown in Fig. 6. In this table, \(\mathrm{d}h\left(0\right)\) is the height difference between the lowest two layers and \({q}_{h}\) is the growth factor (please see (Perler 2011) for more details).

Table 2 Vertical tomography models and corresponding vertical voxel boundaries
Full size table
Fig. 6
figure 6

Designed tomography model for the area of interest

Full size image

Furthermore, the time resolution of the designed tomographic model is selected to be 1 h, which means 24 time bins each day. To ensure that the contribution of low elevation rays (tracked mostly by reference sites at the border of our model area) which leave the tomographic model via lateral surfaces is accounted for correctly, the tomography area was extended by a sparse outer voxels model. The horizontal size of these boundary zones was chosen \(5^\circ\) in this research.

Numerical results

In this section, the accuracy of the reconstructed refractivity field is evaluated in comparison with the type of observations (SF and DF) in varieties of the regularization techniques. Therefore, the following schemes were considered (Fig. 7).

Fig. 7
figure 7

Studied schemes in this research

Full size image

According to Fig. 7, the first step of all schemes is to select the type of observation, which could affect the accuracy and precision of ZTD and SWD. To illustrate the mentioned impact, the estimated ZTD from SF and DF observations has been compared to the ZTD derived by ray-tracing through the AROME model. As shown in Fig. 8, the consistency of the derived ZTDs by the DF algorithm is higher compared to ZTDs calculated from SF data both at midnight and noontime. However, the performance of both strategies with respect to AROME at noontime is slightly superior compared to midnight. However, the inconsistency between the SF ZTDs and AROME ZTDs is much more visible in comparison to DF ZTDs and AROME ZTDs. This could be explained by considering the float solution of the PPP ZTD estimation process. Moreover, remaining mismodeling of ionospheric variation by the SEID algorithm could affect the ZTD solution (Aichinger-Rosenberger 2021). Nevertheless, the obtained results show the potential of the SF observations to estimate ZTD with an average RMSE of less than 0.075 m with respect to AROME ZTD.

Fig. 8
figure 8

Average RMSE of ZTD difference at 00:00 UTC (top) and hour 12:00 UTC (bottom) determined for days 232–245 for single-frequency and dual-frequency observations with respect to AROME

Full size image

Table 3 summarizes the average RMSE for both SF and DF strategies at midnight and noontime during the period of interest. The numbers in brackets denote the minimum and maximum RMSE among all GNSS stations.

Table 3 Mean RMSE over all stations with respect to AROME ZTDs for SF and DF schemes during the period of interest
Full size table

Moreover, Table 4 reports the mean bias during the period of interest for SF and DF schemes at midnight and noontime. According to this table, the range of bias variations in the DF scheme is smaller than that in the SF scheme. Again the numbers in brackets denote the minimum and maximum bias among all GNSS stations.

Table 4 Mean bias over all stations for SF and DF schemes during the period of interest
Full size table

Figure 9 represents the time series of SF ZTD and DF ZTD for two example stations, GRAZ (height approx. 538 m) and TRAI (height approx. 407 m) compared to AROME ZTD during the period of interest at midnight and noontime. As shown in this figure, the behavior of DF ZTD shows considerable similarity with the AROME ZTD. The similarity between the time series of SF ZTD and AROME ZTD is also appreciable but not as high as for DF ZTD.

Fig. 9
figure 9

Time series of average ZTD using SF and DF schemes for GRAZ and TRAI stations at midnight (top) and noontime (bottom)

Full size image

In order to gain a better representation of the similarity of GNSS ZTD in both schemes and AROME ZTD, Pearson correlation has been calculated during the period of interest at midnight and noontime for all GNSS stations. Indeed, the correlation was estimated per hour between the ZTD series of GNSS stations. Table 5 summarizes the mean correlation for both schemes during the period of interest. Same as Tables 3 and 4, the numbers in brackets show the minimum and maximum correlation among all studied GNSS stations. According to these results, DF ZTD is highly similar to AROME ZTD for both midnight and noontime. For SF ZTD, there is only one day with a correlation lower than 50 percent, and for the rest of the days, this amount is higher than 50 percent. Therefore, also the SF ZTD and AROME ZTD time series show a reasonable correlation. The correlation is slightly higher at noontime in comparison to midnight.

Table 5 Mean Correlation over all stations for SF and DF schemes during the period of interest
Full size table

It has to be highlighted that not only the GNSS ZTDs but also deficiencies in the AROME model can cause inconsistency between ZTDs time series. Figure 10 shows the differences between relative humidity (RH) and temperature (T) of the AROME model and RS measurements on DoY 235. As can be seen in Fig. 10, the difference between temperature profiles of AROME and RS are varying from \(-2 K\) to \(4 K\). For RH profiles, the difference range is changing between 40% and 60%. Table 6 summarizes mean RMSE of temperature and relative humidity in comparison to RS11035 profiles (red star in Fig. 4) during the period of interest.

Fig. 10
figure 10

Difference of T (left) and RH (right) of the AROME model in comparison to radiosonde (RS) observations on DoY 235 at midnight (hour 00:00 UTC) at RS11035 location

Full size image
Table 6 Daily RMSE of AROME meteorological profiles in comparison to RS measurements
Full size table

In a next step, the accuracy of the reconstructed wet refractivity profiles using different strategies has been evaluated by reference radiosonde observations located at Vienna airport (RS11035) at hours 00:00 and 12:00 UTC. Figure 11 demonstrates the average of the mean absolute error (MAE) in wet refractivity over the period of interest for the SF and DF schemes that apply to different regularization methods in order to reconstruct the wet refractivity field. According to Fig. 11 (top), the performance of the SF scheme is comparable with the DF scheme especially when the AROME model is applied as an initial field at midnight. However, the differences between SF and DF schemes for the ART method were increased in the noontime, and this may return to the sensitivity of the ART method to the existing noise in SF ZTD. Moreover, the TV regularization method provides promising results mainly for the DF scheme. Therefore, we could achieve an acceptable reconstructed wet refractivity field without the existence of an initial field using this algorithm. In addition, the output of the TV method was applied in the ART techniques as an initial guess, which could also lead to acceptable results.

Fig. 11
figure 11

MAE of the reconstructed wet refractivity profiles for heights up to 2 km at 00:00 UTC (top left), 2 to 6 km at 00:00 UTC (top right), up to 2 km at 12:00 UTC (bottom left), and 2 to 6 km at 12:00 UTC (bottom right) at RS11035 location

Full size image

In order to discover the overall accuracy of the retrieved wet refractivity using the tomography method, the dispersion of the different schemes in comparison to the radiosonde profile at RS11035 was calculated for the period of interest and the studied hours (00:00 UTC and 12:00 UTC). Figure 12 shows the scatter plot of wet refractivity for the DF scheme (left panel) and for the SF scheme (right panel). The y-axis denotes wet refractivity (in ppm) calculated from the RS measurements, while the x-axis shows wet refractivity of the tomographic approach. Each graphic covers 252 data points evaluated within the 14-day period investigated here times the 9 voxels (height layers) above the RS launch site times 2 launches per day (14*9*2 = 252). According to Fig. 12, the spreading of the reconstructed tomography field in the DF scheme is generally smaller than that in the SF scheme. The TV algorithm for both the DF and SF schemes shows a comparable dispersion to the least-square line. The match between RS and reconstructed wet refractivity by applying the AROME model as a priori field is closer than for other schemes for both the SF and DF strategies. Moreover, as shown in Fig. 12, applying TV output as an initial field for ART regularization techniques provides reasonable results in both schemes.

Fig. 12
figure 12

Comparison of reconstructed wet refractivity of DF schemes (left panel) and SF schemes (right panel) to RS11035 wet refractivity during the period of interest

Full size image

To better interpret the obtained results, the slope of the least-square line is reported in Table 7. According to this table and also Fig. 12, it could be concluded that the performance of all ART techniques (ART, MART, and Landweber) + AROME for the SF scheme is as good as for the DF scheme since the slope of the corresponding least-square lines is almost close to 1:1. The TV method and ART techniques + TV for both schemes slightly underestimate the wet refractivity field. However, the obtained results from these methods are also reasonable.

Table 7 The slope of the least-square line for all regularization methods in SF and DF schemes
Full size table

According to the reported values in Table 8, the correlation for different regularization techniques in SF and DF schemes is almost higher than 95% except for MART + TV in the SF scheme, which is about 93%. Therefore, the retrieved wet refractivity for SF and DF schemes using all regularization techniques correlates considerably with the RS profile.

Table 8 Correlation coefficient [%] between the reconstructed wet refractivity profile and RS profile using different regularization methods for SF and DF schemes during the period of interest
Full size table

The average RMSE of wet refractivity for all days considered for the location of RS11035 is listed in Table 9. It can be concluded that the differences of the reconstructed refractivity profiles by applying the AROME model as an initial field (obtained from both the SF and DF schemes) with respect to refractivity calculated from RS data are almost small at midnight and noontime. In addition, the performance of the TV method and TV + ART techniques for SF and DF schemes is roughly comparable during the studied epochs. In general, as expected, the DF method shows a lower RMSE almost for all regularization techniques compared to the SF scheme. Nevertheless, even in the SF scheme, the TV method and TV + ART techniques could provide reasonable results in tropospheric tomography.

Table 9 Average RMSE [ppm] over 14 days for different schemes of SF and DF modes at the location of RS11035
Full size table

The average of bias was also calculated over the study period to assess further the accuracy of the reconstructed wet refractivity field, using different regularization methods in SF and DF schemes. Table 10 summarizes the average bias for the location of RS11035 during the whole experimental period. According to that, the bias of the reconstructed tomography profile using different regularization techniques is almost similar for SF and DF schemes at midnight and noontime. Same as MAE, the bias for ART + AROM and ART + TV during noontime in the SF scheme is significant. This could be due to higher solar activities during the noontime, which causes noise in SF ZTD and consequently SWD observations, since the ART technique is especially sensitive to the existing noise in the observations. Moreover, it should be highlighted that the correlation between reconstructed profiles and RS profiles obtained by various regularization schemes in the SF scheme is almost higher than for the DF scheme, while bias and RMSE demonstrate different results. This may return to the fact that correlation is not sensitive to any shift in the reconstructed wet refractivity profile with respect to the RS profile. Nevertheless, all statistical results show promising results using TV and ART techniques + TV for DF and SF schemes to reconstruct wet refractivity in the troposphere.

Table 10 Average bias [ppm] over 14 days for different schemes of SF and DF modes at the location of RS11035
Full size table

Conclusions

In this article, the potential use of SF observations for GNSS tomography was studied. In addition, the impact of different regularization methods was investigated by applying an initial field or not. In this regard, a part of the EPOSA GNSS network located in the east of Austria was utilized to analyze the accuracy of the reconstructed refractivity field using different strategies. For this purpose, two different strategies were applied to estimate ZTDs and use the SWDs as an input for the tomography. In the first strategy, single-frequency (SF) observations were processed using PPP in goGPS software. In the second strategy, dual-frequency (DF) observations were processed in double-difference mode with the Bernese software. Subsequently, we have solved the tomography problem using the different regularization methods: ART, MART, Landweber, and TV. The AROME model and the TV method provided the required initial field for the iterative techniques to analyze the impact of this input on the retrieved accuracy of the wet refractivity field. The results showed that the AROME ZTD correlate with DF ZTD and SF ZTD on average at 97% and 66%, correspondingly. However, the reported correlation is not sensitive to a bias between the data sets. Analyzing RMSE of the estimated ZTDs using SF and DF observations showed that the DF scheme provides better results (avg. RMSE 0.019 m) in comparison to the SF scheme (avg. RMSE 0.075 m). Furthermore, the bias of SF ZTD was slightly larger during noontime which can be explained by the daily solar radiation and consequential complexity to describe the ionospheric delay with SEID. Moreover, there might also be artifacts from model deficiencies, e.g., satellite clocks in PPP processing. As expected, a successful integer fixing of the ambiguities improves the results and leads to a much more accurate estimation of the ZTD.

The accuracy of retrieved refractivity fields using various regularization methods in SF and DF schemes was assessed by RS observations. According to the obtained results, the performance of ART techniques (ART, MART, and Landweber) by applying the AROME model as an initial field was comparable for both SF and DF schemes. In addition, the accuracy of the reconstructed wet refractivity field using the TV method and ART techniques + TV for SF schemes was almost as good as for the DF scheme. Moreover, the correlation between retrieved wet refractivity and RS wet refractivity for all regularization techniques in SF and DF schemes was almost higher than 95%. However, a considerable MAE and bias for ART + AROM and ART + TV in the SF scheme has been detected during noontime. This study showed that entering ZTDs calculated from SF data instead of DF data yields degradation of the RMSE of the reconstructed profiles between 10% and 40% over all investigated regularization techniques. In the presence of a reasonable initial field, an acceptable reconstruction of the wet refractivity at the level of 4–7 ppm wet refractivity field with respect to radiosonde profile could be achieved, but also TV + Landweber and TV + MART techniques can retrieve wet refractivity profiles at 6–8 ppm-level.

In future studies, PPP AR (ambiguity resolution) techniques have to be further investigated to improve ZTD estimates derived from DF or even SF data in future studies. Moreover, the tomography approach based on the TV regularization method should be investigated in more extended periods and under different weather conditions to prove the potential of this method for reconstructing the wet refractivity field without using any initial field.