An open-source low-cost sensor for SNR-based GNSS reflectometry: design and long-term validation towards sea-level altimetry

Abstract

Monitoring sea level is critical due to climate change observed over the years. Global Navigation Satellite System Reflectometry (GNSS-R) has been widely demonstrated for coastal sea-level monitoring. The use of signal-to-noise ratio (SNR) observations from ground-based stations has been especially productive for altimetry applications. SNR records an interference pattern whose oscillation frequency allows retrieving the unknown reflector height. Here we report the development and validation of a complete hardware and software system for SNR-based GNSS-R. We make it available as open source based on the Arduino platform. It costs about US$200 (including solar power supply) and requires minimal assembly of commercial off-the-shelf components. As an initial validation towards applications in coastal regions, we have evaluated the system over approximately 1 year by the Guaíba Lake in Brazil. We have compared water-level altimetry retrievals with independent measurements from a co-located radar tide gauge (within 10 m). The GNSS-R device ran practically uninterruptedly, while the reference radar gauge suffered two malfunctioning periods, resulting in gaps lasting for 44 and 38 days. The stability of GNSS-R altimetry results enabled the detection of miscalibration steps (10 cm and 15 cm) inadvertently introduced in the radar gauge after it underwent maintenance. Excluding the radar gaps and its malfunctioning periods (reducing the time series duration from 317 to 147 days), we have found a correlation of 0.989 and RMSE of 2.9 cm in daily means. To foster open science and lower the barriers for entry in SNR-based GNSS-R research and applications, we make a complete bill of materials and build tutorials freely available on the Internet so that interested researchers can  replicate the system.

Introduction

Monitoring sea level is fundamental to assess climate change observed over the years. Sea-level changes can be caused by multiple phenomena, of oceanic or crustal origin, and having anthropic influence or not (Cazenave and Nerem 2004). Oceanography and geodesy thus have become of great importance for monitoring sea level (Tamisiea et al. 2014), to help to predict future situations and in planning for mitigation and adaptation (Nicholls 2011; Elsharouny 2016). The determination of mean sea level and its temporal evolution remains a challenge due to the many variables involved. There is still a need for observations covering larger areas during longer periods, particularly along the coastlines. Unfortunately, observational gaps persist both in time and in space (Cazenave and Nerem 2004).

Devices with different working principles have been used to measure sea level (Cipollini et al. 2017). Monostatic satellite altimeters are the main instrument in the open oceans. In coastal regions, though, satellite altimetry confounds land and ocean, and tide gauges remain the instrument of choice. We are close to almost two centuries of experience with automatic tide gauges (Matthäus 1972); the traditional mechanical float with shaft encoder has been replaced over time by acoustic, pressure, or radar sensors. Each has its own limitations: acoustic sensors might be affected by the temperature, pressure sensors need corrections for atmospheric pressure and water density, and radar has errors proportional to wave height (Martín Míguez et al. 2012; Boon et al. 2012). Yet problems persist in ensuring that there is no spurious vertical movement resulting in erroneous sea-level change interpretations. The standard recommendation has recently become that satellite geodesy instrumentation should be installed as close as possible to tide gauges to measure coastal crustal deformation and put relative sea-level records into a geocentric frame (Larson 2016).

Global Navigation Satellite System Reflectometry (GNSS-R) is a remote sensing technique following the principle of bistatic radar (Zavorotny et al. 2014). The sensor can operate basically as an altimeter or a scatterometer. One particular GNSS-R configuration is based on the simultaneous reception of multiple paths—direct or line-of-sight propagation and indirect reflections—which are tracked using a single signal replica. This mode may be called GNSS multipath reflectometry (GNSS-MR), and it involves the constructive/destructive interference between at least two coherent paths. Such an interference pattern can be recorded in carrier-phase or pseudorange observables, although it is most readily recognized in signal-to-noise ratio (SNR) observations (Garrison et al. 2019). In that case, SNR-based GNSS-MR technique is also known as GNSS interferometric reflectometry (GNSS-IR) or GNSS interference pattern technique (GNSS-IPT). Several studies have shown how GNSS-IR/IPT can monitor a variety of surface targets and estimate geophysical parameters such as sea surface height, ocean winds, and soil moisture (Larson 2016). A particularly productive application has been the proximal sensing of sea level from coastal stations. In that application, a single continuously tracking device can ensure both conventional GNSS positioning control and sea-level sensing via GNSS-R (Larson et al. 2013b). For sea-level measurements, coastal GNSS-R complements monostatic satellite altimeters and has unique advantages over conventional tide gauges.

Most GNSS-R studies applied to sea-level monitoring used geodetic-quality receivers and antennas. This is because, at several coastal locations, there are continuously operating reference stations (CORS). However, geodetic GNSS equipment is relatively expensive and may be targeted for theft and vandalism. Lower-cost devices can provide an alternative solution (Biagi et al. 2016), especially attractive for unattended sites. They also enable major densification in the sensing networks, as the cost of individual stations is a fraction of high-end instrumentation. Particularly open-source hardware platforms, such as Arduino, have received much attention for environmental sensing applications and prototyping (Chen et al. 2017; Rainville et al. 2019; Rodrigues and Moraes 2019). We report the design of a complete hardware and software system for a SNR-based GNSS-R sensor and demonstrate its validation for measuring water level.

Previous work

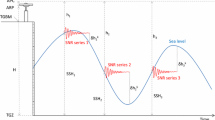
In the present section, we briefly review the background and previous work about SNR-based GNSS-R for sea-level monitoring. For ground-based installations, GNSS-R coverage can be adjusted by changing the antenna height $H$, as the horizontal distance to reflection points is given by $H/\mathrm{tan}e$, in terms of the satellite elevation angle $e$. The detection range and location can be planned in terms of specular points and first Fresnel zones, the approximate sensing points and areas (Geremia-Nievinski et al. 2016).

Previous studies include Nievinski and Larson (2014b) on the theoretical side, who described a physically based model for GNSS multipath observables. A critical aspect is a dependence on the phase of reflections, making inapplicable much of GNSS-R studies developed for incoherent scattering. On the experimental side, about forty existing GNSS stations have been demonstrated for sea-level altimetry (Geremia-Nievinski et al. 2020), from which we highlight the first ones and those with the longest duration, as follows. The pioneer was Anderson (2000), after which there was a decade long hiatus, followed by two other demonstrations (Rodriguez-Alvarez et al. 2011a; Hongguang et al. 2012). These initial proofs-of-concept had all a duration of less than a week. Longer time series were presented first by Larson et al. (2013a), with 3-4 months at Onsala (Sweden) and Friday Harbor (Washington state), followed by Larson et al. (2013b), with 1-year observations obtained at Peterson Bay (Alaska). Their results showed that it is possible to measure sea level using geodetic receivers with a precision of 5–10 cm RMSE for raw retrievals (depending on the tidal range), with improved statistics (~ 2 cm) when forming daily means and neglecting longer-term variations. Finally, Larson et al. (2017) revisited Friday Harbor station for a much longer, 10-year period. Compared to a co-located tide gauge (300 m distance), it confirmed 12 cm and 2 cm RMS for raw retrievals and daily means, respectively. Modernized GPS signals, such L2C and L5, have superior performance in producing cleaner multipath signatures (Tabibi et al. 2015), although the legacy L1 C/A signal is also feasible for GNSS-R altimetry (Larson and Small 2016).

Previous hardware and software developments

Most studies on GNSS-R for coastal sea-level sensing used geodetic-quality commercial off-the-shelf (COTS) receivers and antennas, as reviewed by Geremia-Nievinski et al. (2020). Geodetic GNSS antennas are nearly hemispherical, thus less sensitive to reception from negative elevation angles. Despite their design, such antennas are still usable for GNSS-R, as they are unable to reject multipath at grazing incidence. This is because, away from zenith and nadir, there is little separation in direction of arrival and in polarization state between reflections and line-of-sight radio propagation (Nievinski and Larson 2014b). Unfortunately, these devices are relatively expensive, which limits the wider use of GNSS-R for environmental monitoring as the primary application, not just as a secondary role for GNSS CORS networks. Here we review hardware and software developed for SNR-based GNSS-R, with a focus on open-source and low-cost alternatives. A similar demonstration has been published recently (Williams et al. 2020), although the developed hardware and software system is not available as open source.

One of the pioneers in hardware alternatives for SNR-based GNSS-R was Rodriguez-Alvarez et al. (2011b), who named their device “Soil Moisture IPT Observations at L-band” (SMIGOL). Although developed originally for monitoring soil moisture and other terrestrial variables such as vegetation, SMIGOL was also demonstrated for water-level sensing in a reservoir (Rodriguez-Alvarez et al. 2011b) and later for sea level (Alonso-Arroyo et al. 2015). It employs a commercial receiver module (Trimble Lassen iQ) that offers 12 simultaneous tracking channels at L1 frequency and C/A code modulations in a 26 mm x 26 mm form factor (Rodríguez Álvarez 2011). The module is connected to an SD-card data logger (Sparkfun Logomatic and, later, Sparkfun Openlog) and a PIC microcontroller via a custom board. The antenna was most notably designed to be linearly (vertically) polarized for improved soil moisture sensing and manufactured from scratch as a microstrip patch. Although SMIGOL was highly successful for the intended use and its components had low cost, its custom manufacture seems labour intensive and the embedded code is not publicly available, which unfortunately hinders its replication by other researchers.

Another alternative of low-cost hardware for SNR-based GNSS-R was called “Free-Standing Receiver of Snow Depth” (FROS-D), developed by Adams et al. (2013) based on prototypes of, and for use by, Chen et al. (2017). The intended application was snow depth measurement, which is a type of altimetry, so the device would presumably be equally applicable for sea-level measurement. The GPS receiver used was a commercial module (GlobalTop Gmm-u2P) based on a chipset (MediaTek MT3339) that offers 22 tracking channels at L1 frequency and C/A modulation in a small form factor (9 mm x 13 mm module and 4.3 cm x 4.3 mm chip). A Raspberry Pi microprocessor provided control and storage. Finally, the antenna was custom designed (Chen 2016), based on a half-wavelength dipole; it is linearly polarized, normally vertical in upright installations, which authors have experimented changing to horizontal polarization by tipping the antenna sideways. The cost of the system, including autonomous power supply and supporting structure, was US$1200, which is lower than comparable COTS devices. Unfortunately, FROS-D had the same fate as SMIGOL: successful use by the developers involved but little  replication by external researchers. Finally, we should mention that the same GPS chip (MediaTek MT3339) has found other environmental applications beyond GNSS-R. Rodrigues and Moraes (2019) employed it for ionospheric scintillation monitoring, and Rainville et al. (2019) used it for volcanic ash detection.

We should note that the antenna designed and manufactured by Chen (2016) has also been used with a custom software-defined receiver (SDR) for GNSS-R applications (Chen et al. 2014). Other open-source SDR was used for GNSS-R by Lestarquit et al. (2016) and Hobiger et al. (2016). Such GNSS-R applications are not instances of GNSS-IR/IPT, let alone of the more general GNSS-MR, because of the way that reflections are tracked; there is not a single replica for the composite, i.e. direct plus reflected signals. SDR is highly versatile, especially useful for prototyping, but it is still not practical for field applications because it requires storing extremely large datasets for post-processing or demanding higher power consumption in real-time processing.

Other related efforts are that of Rodrigues and Kasser (2014), who used low-cost equipment (LEA-6T u-blox receiver and Tallysman TW3430 antenna) for tracking the GPS L1 C/A signal. Although it is an instance of GNSS-R for water-level altimetry, it is not an instance of GNSS-IR/IPT, as they have relied on carrier phase observables instead of SNR. The main drawbacks are the need for a second receiver serving as a base station and also the vulnerability to incoherence of reflections due to surface roughness. Similar difficulties with wind-driven water waves in carrier-phase GNSS-R (despite using geodetic-quality equipment) were experienced by  Löfgren et al. (2011), although in that case, the base station antenna was co-located on top of the GNSS-R antenna.

Low-cost single-frequency COTS GPS/GNSS antennas have the potential for improved performance in GNSS-MR in general and GNSS-IR/IPT in particular, because of their high susceptibility to multipath reception, even at high elevation angles. For example, Rover and Vitti (2019) evaluated two types of low-cost antennas (u-blox ANN-MS and Tallysman TW4721) to measure snow height in three 90-min campaigns. More recently, Strandberg and Haas (2020) assessed the antenna embedded in a mobile tablet device (Samsung Galaxy Tab A), for water-level monitoring in a 36-h session. However, the short duration of evaluation in the limited periods reported above raises questions about the long-term stability and durability of low-cost hardware options for continuous operation in harsh weather conditions.

Now turning to software, open-source options include WAVPY (Fabra et al. 2017), an object-oriented library developed in Python language for simulations in GNSS-R. Although aimed at more advanced observables, such as delay-Doppler maps, it could presumably be used for simulating multipath SNR as well. Nievinski and Larson (2014c) developed an open-source GNSS-R simulator in MATLAB/Octave capable of providing SNR, carrier phase and pseudorange under multipath reception conditions. The tool allows one to investigate the behaviour of observations at a user-specified case, which is useful for site planning. The simulator is also used as the physically based forward modelling step embedded in the statistical inversion of SNR measurements collected in the field (Tabibi et al. 2017). An open-source software package for processing SNR measurements is MATLAB is described by Roesler and Larson (2018), including the translation of RINEX files, mapping of reflection zones and reflector height estimation. It allows researchers interested in getting to know SNR-based GNSS-R to get started without implementing code from scratch Martin et al. (2020; Zhang et al. (2021).

System design

It is possible to leverage simpler consumer-grade GPS/GNSS receivers that output only SNR. This contrasts with professional equipment that outputs pseudorange and carrier-phase measurements. So, for our purpose, raw data in RINEX format are not necessary and the simpler NMEA format suffices. The fact that the interferometric propagation delay (the difference across reflection and direct radio waves) is mostly unaffected by the antenna gain pattern enables the utilization of lower-cost antennas. The major cancellation of ionospheric delays, inherent in ground-based interferometry, also makes dual-frequency data less necessary, as single-frequency GNSS devices are nearly equally as precise in that regard.

To foster open science, we provide a 30-page tutorial with step-by-step instructions for users to replicate our sensor, posted publicly (as per code availability statement below). To facilitate the entry for researchers interested in SNR-based GNSS-R, we gave preference to do-it-yourself kits available commercially. The main electronic components employed are: an Arduino board integrated with secure digital (SD) card reader/writer (Adafruit Feather Adalogger), a single-frequency GPS L1 C/A add-on (Adafruit GPS FeatherWing) and an external GPS patch antenna (28-dB active, Chang Hong GPS-01-174-1M-0102). The GPS add-on was specifically selected because it is based on the chipset (MediaTek MT3339) used in FROS-D, although the GPS module is slightly different (GlobalTop FGPMMOPA6H). Additionally, a complete solar power supply system was designed, consisting of a 6-W solar panel, a charger/regulator and 3.7-V 4400-mAh battery. Other minor components include connectors and adapters. A complete bill of materials is made available online; the total cost of materials was US$200 as of January 2020. Adafruit's printed circuit board (PCB) design files are openly available in EagleCAD file format and licensed under Creative Commons Attribution-ShareAlike 3.0 terms.

For testing purposes, we have assembled multiple sensor units, keeping the devices operating outdoors over extended periods for quality control and checking daily power consumption. The solar system was designed to keep the cost as low as possible while guaranteeing uninterrupted service (assuming a minimum of 5 h of solar illumination per day). A simple bent metal plate can be used for securing the solar panel at the ideal angle for a given geographical latitude. The mechanical supporting structure was sourced locally and consisted of a metal base, mast and a service box.

We have developed two pieces of software, both available as open source. The first one was written in the "Processing" programming language and runs embedded in the Arduino device. It is responsible for logging the GPS/GNSS data and battery level to the SD card at a user-specified sampling rate (normally 1 Hz) and file duration (hourly or daily). The source code is loaded as a “sketch” in the Arduino integrated development environment to be uploaded to the board, after which it runs continuously in loop mode.

The second software program was developed to load the data in a desktop computer for post-processing. We employed the MATLAB environment for convenience, but the source code should be compatible with the GNU Octave free/libre environment. The NMEA 0183 data format is not tabular, so each 1-Hz data block needs to be parsed to organize the SNR readings for each satellite at each new epoch (date and time). Only the recommended minimum common (RMC) and satellites in view (GSV) NMEA messages are decoded for faster processing. The data files are manually transferred from the SD card to the computer. For 1 Hz sampling rate, the file size is 30 MB per day, which results in approximately 1 GB per month. Therefore, a 32 GB card (maximum capacity for FAT32 filesystem) can store data for more than 2.5 years. The data files are ASCII encoded and highly compressible (10x ratio with zip compression).

Demonstration and validation

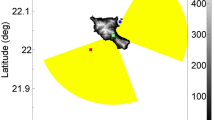
On 26 October 2018 a GNSS-R unit was installed at the Mauá Wharf by the Guaíba Lake in the city of Porto Alegre, Southern Brazil (latitude −30.0277° S, longitude −51.2287° W). The GNSS antenna is about 3.5 m above the water level. For validation, there is a water-level sensor within 10-m distance, operated by the State Secretary for the Environment (SEMA). The gauge is a vertical radar (Campbell Scientific’s CS475A), with a 15-min update interval and centimeter numerical resolution. We have applied a daily moving average to smooth out random noise. Figure 1 shows the installation site in a panoramic view. Fresnel zones in Fig. 2 indicate that azimuths due north, west and southwest can be used for water-level sensing. There is a gap due south as a consequence of the orbital inclination of the GPS satellite constellation.

Fig. 1

GNSS-R sensor (left), experimental station site (middle) and radar gauge (right)

Fig. 2

First Fresnel zones around the site installation; the lowest satellite elevation was set to 5°, and the reflector height was 2 m. Credit of background image: Google Earth

SNR modelling

The data processing necessary for estimating water level is based on previously developed forward and inverse models (Nievinski and Larson 2014a, 2014d). Only minor adaptations were necessary to account for the composition of the target surface (water instead of snow). The altimetric retrieval algorithm starts with a first approximation to SNR field measurements, essentially a polynomial fitting followed by spectral analysis (e.g. Lomb-Scargle periodogram) of detrended SNR:

$${\text{SNR}} \approx \left(c_{0} + c_{1} \sin e + c_{2} \sin^{2} e \right) + A \cdot \cos ( 2{\pi \lambda }^{ - 1} \cdot 2H\sin e + \varphi )$$

(1)

The unknown of interest is the reflector height H, while the amplitude A and the phase shift $\varphi$ are just nuisance parameters to improve the fit; the satellite elevation angle e is known from ephemeris and the carrier wavelength λ is predetermined in GNSS. Second, the polynomial/spectral fitting is applied to synthetic SNR observations, producing another set of parameter estimates (${H}^{{\prime}},{A}^{{\prime}},\varphi {{\prime}}$):

$${\text{SNR}} = P_{n}^{ - 1} P_{d} \left( {1 + P_{i} + 2\sqrt {P_{i} } \cos \phi_{i} } \right)$$

(2)

where ${P}_{i}={P}_{r}/{P}_{d}$ is the interferometric power and ${\phi }_{i}={\phi }_{r}-{\phi }_{d}$ is the interferometric phase, in terms of direct and reflected quantities, as per subscripts; ${P}_{n}$ is the noise power. These quantities are all obtained with a physically based simulator (Nievinski and Larson 2014c), based on user-specified surface type (freshwater), a first guess for reflector height, etc. In a third step, we define empirical corrections based on the difference or ratio between the two previous parameter sets: ${H}_{B}=H-H^{{\prime}}$, ${\varphi }_{B}=\varphi -\varphi^{{\prime}}$, $B=A/A^{{\prime}}$. Fourth, we define a corrected or augmented physical model,

$${\text{SNR}} = P_{n}^{ - 1} P_{d} \left( {1 + P_{i} /B^{2} + 2\sqrt {P_{i} /B^{2} } \cos \left( {\phi_{i} - \varphi_{B} - 2\pi \lambda^{ - 1} 2H_{B} \sin e} \right)} \right)$$

(3)

which is finally used in a nonlinear least squares fit. The description above is just a summary of the methodology fully described in Nievinski and Larson (2014a, d).

Figure 3 shows the behaviour of the inversion over the SNR data obtained with the GNSS-R device. The grey curve showing raw SNR measurements (in decibels) has a typical interference pattern with deep fades and little distortion. The red curve represents the inversion, with the model fitting the data reasonably well. In blue at the bottom, we show the residuals, which have a much smaller variance than the raw data. The procedure above is performed independently for each rising or setting satellite track. We applied a visibility mask between 15 and 35 degrees for satellite elevation angles and 190 and 10 degrees in azimuth (in clockwise order) for better tuning of results. We have applied a daily moving average to GNSS-R water-level retrievals for consistency with the radar gauge record.

Fig. 3

Inversion results for a single satellite tracks: measurements are in grey and model fit in red (top panel); residuals are in blue (bottom panel)

Water-level results

We analysed a time series of 10 months (317 days) to validate the GNSS-R device. Figure 4 shows the GNSS-R and radar gauge time series during the period from 28 October 2018 to 09 September 2019. A mean difference was removed as we did not have reliable levelling information about the vertical offset between the two sensors. The GNSS-R sensor has been operating autonomously and without interruptions, checked in monthly visits, having withstood severe weather conditions such as thunderstorms. By contrast, the radar gauge suffered two malfunctioning periods, resulting in gaps lasting for 44 and 38 days. We contacted the station operator (SEMA) to understand the reason for the gaps, and we were informed that the device went through maintenance and recalibration. We were able to detect two miscalibration steps (about 10 cm and 15 cm, bottom panel of Fig. 4), inadvertently introduced in the radar gauge (at 2019.4 and 2019.6), which attests the good stability of the GNSS-R sensor. We reduced the time series to the period from 27 October 2018 to 23 March 2019, to exclude the radar gauge malfunctioning periods (Figs. 5 and 6). Figure 6 shows the reduced time series scatterplot. The resulting correlation found was 0.989, and the root-mean-square error (RMSE) is equal to 2.9 cm.

Fig. 4

Top: water-level time series (GNSS-R and radar gauge in black and red, respectively); bottom: height error time series (blue) for the full period

Fig. 5

Top: water-level time series (GNSS-R and radar gauge in black and red, respectively); bottom: height error (blue) during reduced period

Fig. 6

Scatterplot of the radar gauge data and the GNSS-R device in reduced period

Discussion

The lake conditions are relatively benign compared to the sea, which is the intended target. Reduced surface roughness (diminished water waves) and negligible tidal range imply that the statistics above represent a best-case condition. The differences include a small error contribution from the radar gauge, whose nominal accuracy is 0.2 cm for the instantaneous water level, under ideal laboratory conditions. However, field deployment introduces new error sources for the radar, such as wind waves, antenna misalignment (which is assumed to point vertically) and the mechanical stability of the large arm needed to support the antenna over the water (we have witnessed vibration under heavy wind loads). Martín Míguez et al. (2012) quantified the radar performance in the field and concluded that its precision is closer to 0.3 cm, after correcting for various systematic effects (datum, scale, timing, etc.). Boon et al. (2012) compared four radar sensors and found that their precision varied from 0.6 cm to 1.5 cm, depending on the wave height; they could avoid datum errors, as the sensors were co-located in a levelled platform. So, the 2.9 cm RMSE statistic found in the present study is a bit higher than that of state of art in water-level sensing, although it is comparable to previous GNSS-R studies, reporting centimeter-level RMSE. Improved results are expected in the future, as systematic errors are better characterized and corrected for in GNSS-R estimates.

Given that every water-level sensor has its own pros and cons, here we summarize the main features of GNSS-R. Its main disadvantages are (1) little control over the reflection area, as it depends on the moving satellite and the height of the receiving antenna—there is no possibility of pointing the antenna to the area of interest; (2) altimetry retrievals have a low temporal resolution, as it depends on the number and duration of satellite overpasses; (3) as a relatively new technique, its systematic errors are still not fully characterized; and (4) it may be hampered by the loss of electromagnetic coherence due to surface roughness, which limits the range of usable satellite elevation angles for given wind speed or wave height. On the other hand, SNR-based GNSS-R offers several unique benefits for water-level sensing: (1) sensing occurs at slant or oblique incidence, instead of being perpendicular to the surface; this allows a greater horizontal and vertical separation between sensor and sea, which shelters the sensor from extreme events and enables measuring sea level where it might not be feasible to have a conventional tide gauge; (2) it operates in open air, which implies easier installation and lower maintenance, compared to stilling wells and waveguides; (3) the bistatic configuration permits low energy consumption, as the sensor only receives the radio waves transmitted by GNSS satellites, which means that a small solar panel can keep the system operating continuously; (4) its low cost allows spatial densification of the monitoring network and permits a greater tolerance for theft and vandalism; (5) it has a large sampling area, for each satellite (the Fresnel zone around each specular reflection) and for a site-wide average among all satellites; (6) it can control for vertical land movement (i.e. subsidence or uplift), with possible connection to the geocenter via GNSS positioning (assuming carrier-phase observations are available); and (7) its zero or datum origin is more clearly defined (at the antenna phase centre), alleviating the need for empirical calibration.

Conclusions and Future Work

Monitoring sea level is essential due to climate change and the resulting social and economic losses. GNSS Reflectometry (GNSS-R) has been demonstrated in the literature as a promising alternative for coastal sea-level monitoring. Most ground-based GNSS-R experiments rely on expensive geodetic-quality instrumentation, which limits its mass adoption. Towards that goal, we report the development of an open-source low-cost sensor for SNR-based GNSS-R aimed towards sea-level sensing applications.

We have evaluated the system for almost 1 year (317 days) by the Guaíba Lake in Brazil. We have compared the water level altimetry retrievals with independent measurements from a co-located radar tide gauge (within 10 m). The GNSS-R device ran practically uninterruptedly. Thanks to its stability, we were able to detect miscalibration steps introduced when the radar gauge underwent maintenance. Statistics during the regular period (correlation of 0.989 and RMSE of 2.9 cm in daily means) are promising and confirm that the designed GNSS-R device can retrieve water height with centimetric accuracy.

More work is necessary to assess sensor performance under more challenging conditions. For example, we have recently set up a permanent installation located on the coast, at the Port of Imbituba, Brazil. We are also seeking to integrate the antenna gain patterns, which might improve the observation fitting and possibly the precision of retrievals. We hope this open science effort will lower the barriers for entry in SNR-based GNSS-R.