Abstract
We contribute to the debate on the identification of phase scintillation induced by the ionosphere on the global navigation satellite system (GNSS) by introducing a phase detrending method able to provide realistic values of the phase scintillation index at high latitude. It is based on the fast iterative filtering signal decomposition technique, which is a recently developed fast implementation of the well-established adaptive local iterative filtering algorithm. FIF has been conceived to decompose nonstationary signals efficiently and provide a discrete set of oscillating functions, each of them having its frequency. It overcomes most of the problems that arise when using traditional time–frequency analysis techniques and relies on a consolidated mathematical basis since its a priori convergence and stability have been proved. By relying on the capability of FIF to efficiently identify the frequencies embedded in the GNSS raw phase, we define a method based on the FIF-derived spectral features to identify the proper cutoff frequency for phase detrending. To test such a method, we analyze the data acquired from GPS and Galileo signals over Antarctica during the September 2017 storm by the ionospheric scintillation monitor receiver (ISMR) located in Concordia Station (75.10° S, 123.33° E). Different cases of diffraction and refraction effects are provided, showing the capability of the method in deriving a more accurate determination of the \(\sigma_{\phi }\) index. We found values of cutoff frequency in the range of 0.73–0.83 Hz, providing further evidence of the inadequacy of the choice of 0.1 Hz, which is often used when dealing with ionospheric scintillation monitoring at high latitudes.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Irregularities in ionospheric plasma density give rise to perturbations on Global Navigation Satellite System (GNSS) signals in space. Such irregularities are variations of the plasma density with respect to the ambient ionosphere that may vary on a large range of scale sizes: from centimeters up to a few hundreds of kilometers. The nature of the perturbation depends on the typical scale of the irregularities and on their dynamics. The threshold separating small from large-scale irregularities is given by the Fresnel scale that is of the order of a few hundreds of meters for L-band signals. Irregularities having scale sizes above the Fresnel scale cause a refractive effect of the trans-ionospheric signals, because of the variation of the refractive index of the ionosphere. Below the Fresnel scale, refractive and diffractive effects concur. The latter is because, when crossed by the plane-wave, small-scale irregularities act as a new wave source, resulting in an interference pattern when received at the ground (Wernik et al. 2003). Neglecting the effect of the ionospheric turbulence, the refractive effects can be considered deterministic in nature (Rino 2011, chapter 3). On the other hand, diffractive effects are stochastic (McCaffrey and Jayachandran 2019 and references therein). The following represents the ionospheric refractive contribution to the carrier phase equation:
\(r_{L}\) is the phase advance induced by the refractive contribution of the ionosphere, \(N_{e}\) is the electron density of the ray path x from the receiver \(r_{x}\) to the satellite \(s_{x}\), and \(f_{L}\) is the frequency of the carrier L.
Deterministic effects are less impacting high-accuracy positioning as they can be accounted through standard techniques, like ionosphere-free linear combination (IFLC). Stochastic effects pose the real ionospheric threat on GNSS positioning and must be faced with dedicated techniques (Conker et al. 2003; Aquino et al. 2005; Tinin, 2015; Park et al. 2016) that may also be based on the use of the multi-frequency capability of modern receivers (Gherm et al. 2011).
The diffraction of the GNSS signal leads to sudden and rapid fluctuations of both phase and amplitude, while refraction triggers phase fluctuations only. The most recent literature suggests naming “scintillation” only the fluctuations due to stochastic effects (De Franceschi et al. 2019; McCaffrey and Jayachandran 2019). We follow such definition of scintillation. The scintillation phenomenon is more likely to occur at high and low equatorial latitudes (Basu et al. 2002), even if the two geographical sectors are characterized by significant differences in terms of formation mechanisms of the small-scale irregularities and of dependence on parameters, such as season, phase of the solar cycle and geo-space conditions (Spogli et al. 2013 and references therein).
Problem of phase detrending
We consider as input data the raw accumulated phase Φ in radians and the signal intensity (SI). The SI is computed according to the formula:
where I and Q are the post-correlation in-phase and quadrature components recorded by a GNSS receiver, respectively.
To quantify scintillation, one commonly uses phase and amplitude indices (Fremouw et al. 1978). They are denoted \(\sigma_{\phi }\) and \(S_{4}\), respectively, and they are defined as:
where \(\phi _{\text{detr}}\) is the detrended phase and < … > denotes an ensemble average.
The total \(S_{4 }\) also includes a correction term to compensate for the thermal noise impact (Van Dierendonck et al. 1993, Eq. 13). Typically, in Ionospheric Scintillation Monitor Receivers (ISMRs), scintillation indices are evaluated every minute and for every satellite in view (Bougard et al. 2011).
Phase detrending arises from the need to include in the phase scintillation index only the high-frequency fluctuations due to diffraction. To calculate the detrended phase, a sixth-order Butterworth filter with a fixed 0.1 Hz cutoff frequency (\(\nu_{\text{c}}\)) is commonly used (Van Dierendonk and Arbesser-Rastburg 2004). Such a choice derives from early scintillation studies conducted in the 70s on VHF and L/S-band scintillation with a fixed or slowly varying receiver–transmitter geometry (Fremouw et al. 1978). In addition, this detrending scheme inherits from the first widely used ISMR developed in the 90s: the NovAtel OEM4 dual-frequency receiver with a low-noise OCXO oscillator and a special firmware able to make it act as a GPS Ionospheric Scintillation and TEC Monitor Receiver (GISTM) (Van Dierendonck et al. 1993).
However, the perils of using a fixed cutoff frequency at 0.1 Hz for phase detrending at high latitude have been highlighted by the pioneering works by Forte (2005) and Beach (2006). After some years of almost silence about the topic, only in the recent past, the 0.1 Hz cutoff issue has been raised again by several authors from different groups worldwide (Mushini et al. 2012; Carrano and Rino 2016; Wang et al. 2018; McCaffrey and Jayachandran 2019; De Franceschi et al. 2019). This problem leads to the issue commonly known as “phase without amplitude scintillation at high latitude” (Forte and Radicella 2002).
A detailed description of the issue can be found in the aforementioned references; here, we recall the main concept underlying the 0.1 Hz cutoff limitations. If no irregularities are present, a value of \(\nu_{\text{c}}\) = 0.1 Hz is appropriate to remove the low-frequency effect, mainly the Doppler shift affecting the phase due to the satellite motion. When an irregularity layer is present, the ideal value of \(\nu_{\text{c}}\) would coincide with the Fresnel frequency \(\nu_{\text{F}}\). In fact, when single-irregularity-layer approximation stands, irregularities of the order of the first Fresnel zone (dF) or below trigger scintillation (Yeh and Liu 1982). Hence, the value of dF separates small to large scales embedded in the ionospheric irregularities.
Under far-field approximation, which is always satisfied for GNSS signals received at the ground, and single-thin-irregularity-layer approximation, which may not always be satisfied, the first Fresnel zone is given by the following formula:
where λ is the signal wavelength and hirr is the distance between the receiver and the irregularity layer. In the case of Galileo E1 signal (λ = 19 cm) and irregularity layer at the peak of the ionospheric F-layer (for instance, 350 km), dF ≈ 365 m. The Fresnel frequency \(\nu_{\text{F}}\) is linked to dF by the following relationship:
where vrel is the relative velocity between irregularity velocity and ionospheric penetration point velocity (Forte and Radicella 2004).
By adopting \(\nu_{\text{c}}\) = \(\nu_{\text{F}}\) = 0.1 Hz and by considering hirr = 350 km, the relative velocity is vrel = 36.5 m/s. As demonstrated by Forte and Radicella (2004), such values are suitable for plasma dynamics and corresponding observational geometry in the low-latitude ionosphere (Muella et al. 2014) but are significantly low when dealing with high latitudes. At high latitudes, plasma convection velocity is reasonably between 100 and 1000 m/s (Moen et al. 2013), resulting in a shifting of the amplitude and phase fluctuations to higher frequencies with respect to low-latitude irregularities (Carrano and Rino 2016). In other words, the power spectral density (PSD) of the phase (PSDpha) and amplitude (PSDamp) is shifted, as sketched in Figs. 2 and 3 of Forte and Radicella (2004). This was also thoroughly discussed in the pioneering work by Yeh and Liu (1982), in which the influence of the ionosphere on a different part of the spectrum is studied. In addition, high-latitude ionosphere may be affected by the presence of ionospheric E region irregularities (Keskinen and Ossakow 1983), leading again to the change of dF (because of the change in hirr) and, consequently, \(\nu_{\text{F}}\). Therefore, at high latitude the use of \(\nu_{\text{c}}\) = 0.1 Hz is far from the ideal \(\nu_{\text{c}}\) = \(\nu_{\text{F}}\) conditions and, if adopted, leads to a significant overestimation of the phase scintillation index and to a significant difference with respect to the amplitude scintillation index. This is because PSDpha increases linearly as \(\nu\) decreases, while PSDamp is flat below the Fresnel frequency. Since scintillation indices are proportional to the integral of the PSD in the considered frequency range, i.e.,
where \(\nu_{\text{Nyq}}\) is the Nyquist frequency, a “wrong” \(\nu_{\text{c}}\) = \(\nu_{\text{F}}\) makes \(\sigma_{\phi }\) larger and larger (see Figs. 1, 2, 3 of Forte and Radicella 2002).
Several attempts have been made to get a step ahead of the filtering procedure and find then a proper detrending scheme able to identify \(\nu_{\text{c}}\) correctly: polynomial fitting (Zhang et al. 2010), cascaded Butterworth (Ghafoori and Skone 2015), continuous wavelet transform (CWT) (Materassi and Mitchell 2007; Mushini et al. 2012), discrete wavelet transform (DWT) (Niu et al. 2012), mixed approach (McCaffrey and Jayachandran 2019).
Proposed solution
We introduce a method based on the fast iterative filtering (FIF) technique (Cicone and Zhou 2020) for the time–frequency analysis of a nonstationary signal. The FIF technique is a recently developed fast implementation of the adaptive local iterative filtering (ALIF) algorithm (Lin et al. 2009; Piersanti et al. 2018), which is based on the idea of using, nontrivially, the fast Fourier transform to speed up the convolution evaluations required in the iterations of the algorithm (Cicone 2019). FIF produces the very same results as ALIF, but in one-hundredth of the time, on the average. We recall here that ALIF is a well-recognized technique for the time–frequency analysis of signals (Cicone et al. 2016). ALIF inherits from the (ensemble) empirical mode decomposition (EMD/EEMD), (Yen et al. 1998; Wu and Huang 2009) the ability to decompose a given signal into functions oscillating around zero, called Intrinsic Mode Functions (IMFs) or Intrinsic Mode Components (IMCs), each of them characterized by its frequency \(\nu\) (Cicone 2019). We adopt the notation IMCs, in order to avoid confusion with the interplanetary magnetic field. Regarding the computation of the frequency of each IMC, we refer the interested reader to Huang et al. (2009).
Iterative filtering (IF)-based techniques have been recently introduced in the field of ionospheric physics to study spectral and multi-scale properties of nonlinear nonstationary signals (Piersanti et al. 2017; Bertello et al. 2018; Materassi et al. 2019), and in particular, they have been used to study the spectral properties of amplitude scintillation at low latitudes (Piersanti et al. 2018; Spogli et al. 2019). We adopt FIF because it provides the best performance of the IF family techniques thanks to its formulation based, nontrivially, on the fast calculation of convolutions via fast Fourier transform (Cicone 2020; Cicone and Zhou 2020). According to such features, we provide a time–frequency analysis able to exactly identify the frequency components embedded in GNSS raw phase measurements and then enable an accurate determination of \(\nu_{\text{c}}\). Basic principles of FIF are recalled in the next section.
Leveraging on this capability of FIF to act as a modal technique and then to provide a discrete set of functions and frequencies, we are able to exactly identify the frequency components embedded in GNSS raw phase and amplitude measurements. This allows strongly relying on the physical meaning of the modes/frequencies found by FIF. In fact, as phase and amplitude spectra are related to that of the ionospheric irregularities, the identified modes are expected to draw exactly the multi-scale properties of the ionospheric medium, especially in the high-frequency range as slopes of the high-frequency asymptotes of the irregularity and scintillation spectra tend to coincide (Wernik et al. 2003 and its Fig. 1, in particular).
To do this exercise, we analyze GNSS data as recorded by the multi-constellation multi-frequency ISMR receiver managed by INGV (Istituto Nazionale di Geofisica e Vulcanologia) in Antarctica, at Concordia station (75.10° S, 123.33° E, geomagnetic 88.02° S, 225.55° E). We concentrate on 4 case events, characterized by different scintillation conditions on GPS and Galileo signals. According to our knowledge, this is the first attempt of proper phase detrending by using Galileo signals in the southern polar cap. The importance of using the Galileo signals in is due to the fact that Galileo came available quite recently, and its contribution in terms of increasing coverage and additional information provided for positioning needs to be tested extensively. The test is even more challenging because it is done over measurements taken inside the polar cap, a region quite poorly covered by similar observations and characterized by harsh environmental conditions. The testing of the Galileo signal performance in Antarctica has been first reported by Alfonsi et al. (2016), based on the data acquired by the same receiver considered here. Initial results of the FIF-based phases detrending for cutoff optimization have been presented at AGU Fall Meeting 2019 in Romano et al. (2019), while the complete analysis is provided here.
Data
The receiver in Concordia Station is a Septentrio PolaRxS, that is a multi-frequency multi-constellation receiver able to track GPS L1CA, L1P, L2C, L2P, L5; GLONASS L1CA, L2CA; Galileo E1, E5a, E5b, E5AltBoc; COMPASS B1, B2; SBAS L1 (Bougard et al. 2011). It is equipped with a low-noise OCXO oscillator and stores, for every satellite in view and for every available frequency, the raw phase (in cycles) and post-correlation I and Q samples acquired at a sampling rate of 50/100 Hz. For this study, 50 Hz data are available.
The receiver also provides ionospheric scintillation indices, \(\sigma_{\phi }\) and \(S_{4 }\) every minute by leveraging on raw phase and on I and Q samples. To calculate the 1-minute indices, the receiver is equipped with a firmware able to apply a Butterworth filter on phase measurements with a selectable cutoff frequency. The monitoring station in Concordia routinely provides indices by using the standard \(\nu_{\text{c}}\) = 0.1 Hz. Hereafter, we refer to “parsed scintillation indices” as \(S_{4}\) and \(\sigma_{\phi }\) values provided by the receiver firmware with fixed 0.1 Hz cutoff frequency.
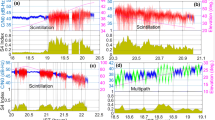
We analyze the data acquired during the geomagnetic storm that occurred between September 6–10, 2017, being one of the largest of the current solar cycle (Linty et al. 2018; Zhang et al. 2019). It was characterized by several flare events and by the impact of a coronal mass ejection (CME) on the earth, which caused a G4 level storm, having its peak between September 7–8 (max Kp = 8 and minimum Dst = – 142 nT).
The black dots in Fig. 1 depict the time profile of the parsed \(\sigma_{\phi }\) (top panel) and \(S_{4}\) (bottom panel) for all the GPS and Galileo satellites in view during September 8, 2017. The increase in both indices in the (UT) afternoon sector indicates the presence of both small- and large-scale irregularities, while the peaking of the parsed \(\sigma_{\phi }\) alone in the (UT) morning sector indicates the presence of large-scale irregularities producing phase fluctuations. The favorable conditions of irregularities formation of different scale sizes allow selecting four different scintillation events, according to the different levels of the parsed indices. Such events refer to four satellites, as summarized in Table 1. The parsed scintillation indices of the selected satellites are reported as colored dots in Fig. 1. To produce these time profiles, we considered an elevation mask of 30° to avoid multipath effects mimicking scintillation.
It is noteworthy that the selected case events are not affected by cycle slips, whose treating is out of the scope of the current study. The time series of Φ and SI are used to feed the FIF technique, as described in the following section.
Fast iterative filtering
Classical time–frequency analysis techniques based on Fourier and wavelet transforms require a priori assumption, and our study deals with nonstationary signals. The uncertainty principle representation is another obstacle for time–frequency analysis. ALIF (Cicone et al. 2016, Piersanti et al. 2018) and its fast implementation, FIF (Cicone and Zhou 2020, Cicone 2020), allow decomposing a nonstationary nonlinear signal s into functions oscillating around zero, IMCs, each of them characterized by its frequency \(\nu\), according to the following equation:
where NIMC is the total number of IMCs and res is the residual, which is neglected in the analysis. ALIF and FIF inherit their algorithmic structure from the EEMD technique but with a stronger mathematical basis that ensures the convergence and stability of these algorithms (Cicone et al. 2016; Cicone and Zhou 2020). A comparison among time–frequency analysis techniques is reported in Table 2. See also Piersanti et al. (2018, Table 1). In this technique, uncertainty is not an issue since the time–frequencies plots are computed after the signal decomposition. This table allows us to quickly summarize the advantages of FIF versus other signal processing methods, which have already been presented and detailed in Piersanti et al. (2018).
Figure 2 shows an example of 4 IMCs obtained by decomposing the raw phase measurements of E01 satellite (E1 frequency) in the considered time range. The IMC numbers are 1, 25, 50 and 75, characterized by the frequencies 25 Hz, 1.32 Hz, 0.12 Hz and 0.01 Hz, respectively.
An important remark concerns the boundaries: As any signal processing technique, also in FIF they shall be carefully handled (Cicone and Dell’Acqua 2019; Stallone et al. 2020). In particular, the FIF method assumes periodicity of the signal at the boundaries. This may produce apparent jumps at the boundaries, which will determine unwanted oscillations nearby the edges of a signal, as explained in (Stallone et al. 2020).
We adopt a simple approach to reduce this effect. To make the raw phase measurements periodic, we consider a slightly longer time window than the reference one on both sides of the signal. In addition, we extend the signal on both sides, following what is suggested in Stallone et al. (2020). We feed FIF with this extended signal. After we run the decomposition, we simply drop the results obtained outside the time window of interest. This has been proven to reduce drastically the spurious frequencies injected in the IMCs by the boundary jumps (Cicone and Dell’Acqua 2019; Stallone et al. 2020).
Retrieval of the cutoff frequency
The novelty of this research is the adoption of FIF to derive the spectra from which we derive the value of \(\nu_{\text{c}}\). To be specific, in order to compute the value of \(\nu_{\text{c}}\), we leverage on the PSD obtained by considering the relative energy (Erel) of all IMCs. For the kth IMC, having frequency \(\nu^{ *}\), \(E_{\text{rel}} {\underline{\underline{\text{def}}}} E_{\text{rel}}^{k} \left( {\nu^{*} } \right)\) is defined as (Spogli et al. 2019):
where < … > indicates the time average. The PSD is then obtained by plotting the set of NIMC values of \(E_{\text{rel}}^{k} \left( \nu \right)\) as a function of \({{\nu }}\).
To differentiate refractive from diffractive variations (McCaffrey and Jayachandran 2019), we also decompose through FIF technique the IFLC of GNSS observables, defined as:
where \(\Phi_1\) and \(\Phi_2\) are the phase measurements of two GNSS carrier signals, and f1 and f2 are their relative central frequencies. For case events related to GPS satellites, we use the L1 and L2 bands, while for the Galileo case, we use the E1 and E5a ones. IFLC uses the 1/f2 dependence of the refractive effects on the ionosphere. Stochastic effects do not follow such dependence (Carrano et al. 2013). From the decomposed IFLC, the PSD is also derived according to what already described for the raw phase.
Then, to compute the cutoff frequency, we rely on the comparison between the PSDs of the phases of L1/L2 and E1/E5a bands and of the corresponding IFLC. As the cutoff frequency is expected to lie above 0.1 Hz, we consider only the range between 0.1 and 25 Hz, being this the Nyquist interval of the considered sampling rate. The PSD of IFLC is expected to be lower than those of the phases in the frequency range in which the bulk of the refraction is cut away by the IFLC.
Thus, the point at which the PSD of the IFLC goes below the phase PSD can be reasonably assumed to be the cutoff frequency. The strength of FIF in doing this task is that it provides the actual set of frequencies embedded in the phase measurements (and in the IFLC). Therefore, such a crossing point is pretty easy to identify. To further confirm the goodness of the \(\nu_{\text{c}}\) selection, we also compare the already described PSDs with the PSDs of the corresponding amplitudes, derived again by using FIF to decompose the amplitude. The peak of the amplitude PSD provides a measure of the Fresnel frequency (Wernik et al. 2003).
Once the optimized cutoff frequency is achieved, it can be used to recalculate the ionospheric scintillation indices. The value of \(\Phi {_\text{detr}}\) in the interval Δt between t0 and t0 + 1 min is then computed using (3) in the following equation:
in which the sum is made only on the IMCs having a frequency above \(\nu_{\text{c}}\). The value of \(\sigma_{\phi }\) calculated by the new cutoff frequency theoretically should better correlate with the values of \(S_{4}\) (Beach 2006), as both tend to account for the sole stochastic effects. Theoretically, their relative behavior should differ just because \(\sigma_{\phi }\) accounts also for the stochastic effects triggered by refractive effects due to turbulent processes occurring at small-scale level, that is not the case for S4. Besides, for each case event, more discussion is given to this aspect. For the remainder, we refer to the new value of \(\sigma_{\phi }\) calculated through FIF as \(\sigma_{\phi }^{\text{FIF}}\).
In addition, to verify that FIF provides reliable \(\sigma_{\phi }\) values, a consistency check is also done by setting \(\nu_{\text{c}}\) = 0.1 Hz and by comparing the phase scintillation indices computed by means of (11), hereafter denoted \(\sigma_{\phi }^{{{\text{FIF}},0.1}}\), with the parsed ones.
Results
The results comprise four case events in which we consider large/small/large and small irregularities and a case characterized by no scintillation (Table 1). For each case event, a cutoff frequency has been adapted based on PSD calculation. By the dedicated cutoff frequency for each case, \(\sigma_{\phi }\) is calculated and the results have been shown as follows.
Case 1: satellite G05
The PSDs of phase, amplitude and IFLC for L1 and L2 bands of G05 from 02:45 to 03:15 UT are shown in Fig. 3. The intersection of phase PSDs (black for L1 and green for L2 band) and IFLC PSD (red) is indicated by the blue dashed line and identifies the value \(\nu_{\text{c}}\) = 0.83 Hz. We recall here that Case 1 is characterized by the absence of small-scale irregularities, as the parsed \(S_{4}\) is low. The amplitude PSDs (gray for L1 and pale green for L2 band) show a peak in the high-frequency range, indicating the presence of small-scale irregularities but such as not resulting in \(S_{4}\) above a weak scintillation activity (Table 1 and Fig. 1).
The top panel of Fig. 4 shows the time profile of the parsed \(\sigma_{\phi }\) (blue), of \(\sigma_{\phi }^{{{\text{FIF}},0.1}}\)(black) and of \(\sigma_{\phi }^{\text{FIF}}\) (\(\nu_{\text{c}}\) = 0.83 Hz) for G05 L1 band. As expected, the values of \(\sigma_{\phi }^{\text{FIF}}\) (red) are significantly smaller with respect to the parsed ones (blue). As a consistency check, the comparison between \(\sigma_{\phi }^{{{\text{FIF}},0.1}}\) (black) and parsed \(\sigma_{\phi }\) (blue) shows the behavior of the two quantities is in agreement. Here, we remind that different detrending schemes, even with the same cutoff frequency, may lead to different values of \(\sigma_{\phi }\) (Najmafshar et al. 2014). In addition, another source of difference between \(\sigma_{\phi }^{{{\text{FIF}},0.1}}\) and parsed \(\sigma_{\phi }\) is related to the fact that FIF provides a discrete spectrum; thus, the cutoff frequency is not exactly 0.1 Hz, but slightly more as we just consider IMCs having frequencies strictly larger than 0.1 Hz.
The bottom panel of Fig. 4 shows the time profiles of \(\sigma_{\phi }^{\text{FIF}}\) (red) and of the parsed \(S_{4}\) (blue) to compare the behavior of the newly computed indices with respect to the amplitude scintillation behavior. As already mentioned, because they both account mainly for stochastic effects only, the scintillation indices should present good correlation. Further comments about this are provided below in Conclusion and remarks section.
Case 2: satellite G31
The PSDs of phase, amplitude and IFLC for L1 and L2 bands of G31 from 11:45 to 12:15 UT are shown in Fig. 5. We recall here that Case 2 was characterized by the absence of phase and amplitude fluctuations (low values of parsed indices). In this case, the phase PSDs (black for L1 and green for L2 band) are above IFLC PSD (red) for all frequencies, and then, no cutoff frequency is identified by our method. This is expected since no ionospheric irregularities are present. Likewise, no peaks are found in the amplitude PSDs. FIF is able to identify the case in which neither phase fluctuations nor scintillation happens. In this case, the scintillation indices computation is negligibly affected by the cutoff frequency selection and the standard choice at 0.1 Hz can be adopted.
Case 3: satellite G26
The PSDs of phase, amplitude and IFLC for L1 and L2 bands of G26 from 15:00 to 15:30 UT are shown in Fig. 6. The intersection of phase PSDs (black for L1 and green for L2 band) and IFLC PSD (red) is indicated by the blue dashed line and identifies the value \(\nu_{\text{c}}\) = 0.73 Hz. We recall here that Case 3 is characterized by the presence of small-scale irregularities, as proved by large values of the parsed \(S_{4}\). This is also confirmed by amplitude PSDs (gray for L1 and pale green for L2 band), which presents a clear peak in the high-frequency range and a significant decrease in correspondence with the identified cutoff frequency.
The top panel of Fig. 7 shows the time profile of the parsed \(\sigma_{\phi }\) (blue), of \(\sigma_{\phi }^{{{\text{FIF}},0.1}}\)(black) and of \(\sigma_{\phi }^{\text{FIF}}\) (\(\nu_{\text{c}}\) = 0.73 Hz) for G26 L1 band. As already noticed for Case 1, once again as expected the values of \(\sigma_{\phi }^{\text{FIF}}\) (red) are significantly smaller with respect to the parsed ones (blue). Also, in this case, we provided a consistency check by comparing \(\sigma_{\phi }^{{{\text{FIF}},0.1}}\) (black) and the parsed \(\sigma_{\phi }\) (blue) and again, the agreement between the two quantities is confirmed.
The bottom panel of Fig. 7 shows the time profiles of \(\sigma_{\phi }^{\text{FIF}}\) (red) and of the parsed \(S_{4}\) to compare the behavior of the newly computed indices with respect to the amplitude scintillation behavior. As already found in case #1, because they both account mainly for stochastic effects only, the scintillation indices should present good correlation.
Case 4: satellite E01
The PSDs of phase, amplitude and IFLC for E1 and E5a bands of E01 from 14:45 to 15:15 UT are shown in Fig. 8. The intersection of phase PSDs (black for E1 and green for E5a band) and IFLC PSD (red) is indicated by the blue dashed line and identifies the value \(\nu_{\text{c}}\) = 0.73 Hz. Case 4 is similar to Case 3 and is characterized by the presence of small-scale irregularities. This is again confirmed by amplitude PSDs (gray for E1 and pale green for E5a band), which presents a clear peak in the high-frequency range and a significant decrease in correspondence with the identified cutoff frequency.
The top panel of Fig. 9 shows the time profile of the parsed \(\sigma_{\phi }\) (blue), of \(\sigma_{\phi }^{{{\text{FIF}},0.1}}\)(black) and of \(\sigma_{\phi }^{\text{FIF}}\) (\(\nu_{\text{c}}\) = 0.73 Hz) for G26 L1. As already noticed for both Cases 1 and 3, as expected, the values of \(\sigma_{\phi }^{\text{FIF}}\) (red) are significantly smaller with respect to the parsed ones (blue). Even in this case, we made a comparison between \(\sigma_{\phi }^{{{\text{FIF}},0.1}}\) (black) and the parsed \(\sigma_{\phi }\) (blue) and again, the agreement between the two quantities is confirmed.
The bottom panel of Fig. 9 shows the time profiles of \(\sigma_{\phi }^{\text{FIF}}\) (red) and of the parsed \(S_{4}\) to compare the behavior of the newly computed indices with respect to the amplitude scintillation behavior. As already found for cases #1 and #3, because they both account mainly for stochastic effects only, the scintillation indices should present good correlation.
Conclusion and remarks
We addressed the problem of the proper identification of the cutoff frequency for phase detrending and design a detrending scheme able to provide a more realistic determination of the phase scintillation index. This is required to avoid including phase fluctuations in \(\sigma_{\phi }\) computation that are not due to stochastic effects. This is crucial to correctly identify scintillation on L-band signals in the high-latitude regions, where the adoption of the cutoff frequency at 0.1 Hz (standard) value has been demonstrated to be inappropriate. The significance of the study is inspired by previous works (Mushini et al. 2012; McCaffrey and Jayachandran 2019) aimed at disentangling ionospheric effects (refractive and diffractive) and improving the computation of the scintillation indices on a case-by-case basis.
For this purpose, we adopt a new detrending scheme based on the decomposition provided by the FIF (Cicone and Zhou 2020; Cicone 2020). The strength of using FIF as band-pass filtering is twofold: (i) FIF is able to provide a small and discrete set of functions and frequencies characterizing the spectrum of the raw phase (and amplitude, for comparison reasons) measurements and (ii) the convergence and stability of the algorithm (Cicone et al. 2016; Cicone 2020) ensure that the frequencies are uniquely identified and they correspond, as shown in the proposed examples, to the embedded components of the raw phase measurements.
The raw phase and amplitude data acquired by the scintillation receiver located in the Concordia station are here used. Then, 4 case studies (30 min each) are analyzed during the geomagnetic storm occurred on September 8, 2017:
-
One case characterized by the presence of only deterministic effects due to the refraction induced by large-scale irregularities.
-
Two cases characterized by the presence of both refractive and diffractive effects due to the presence of small to large-scale irregularities.
-
One case in which no irregularities affect the signal propagation.
FIF is able to reproduce the expected spectral features of the phase, amplitude and IFLC from which we derive our method for the cutoff frequency calculation. The Fresnel frequency, and then the selected cutoff frequency, is assumed to be the frequency at which the spectrum of the IFLC goes below those of the phases. In the 3 cases events characterized by the presence of ionospheric irregularities, we compute the new values of cutoff frequency that are found to range from 0.73 to 0.83 Hz (see Table 3). Such values are significantly larger than 0.1 Hz, providing further evidence that the standard choice is not suitable. The found cutoff frequencies correspond to the plasma drift velocity of the order of 300 m/s, reasonable at high latitudes and under storm conditions. It is worth noticing that the cutoff frequency found with the above-mentioned criterion also corresponds to a local minimum of the IFLC spectrum. Such a minimum at the Fresnel frequency may be justified by the fact the frequencies lower than that are also influenced by the satellite motion, as proven by the fact that at lower frequencies, all the spectra tend to coincide. Above Fresnel frequency, the stochastic noise induced by the ionosphere on both first and second carrier phase tends to sum up in IFLC, resulting in increased values of the IFLC spectra with respect to one of the phases. In other words, the stochastic effects on signal propagation seem to worsen on IFLC than on the single phases.
To corroborate the fact that the refined \(\sigma_{\phi }\), as it better accounts mainly for the diffractive effects, behaves in a similar way to \(S_{4}\), we further verified the correlation between indices. Figure 10 shows the correlation between \(S_{4}\) and \(\sigma_{\phi }\) calculated by FIF with 0.1 Hz cutoff frequency (black dots) and with the refined cutoff (red dots) by merging all data from cases 1, 3 and 4. The solid lines indicate the linear fits whose coefficients of determination R2 are also reported. The value of R2 indicates a significantly improved degree of correlation when considering the refined determination of the phase scintillation, as it tends to better account for the diffractive effects. Table 4 summarizes the values of R2 for each case event separately and shows that what found considering the whole dataset is valid also on a case-by-case basis. The deviation from the ideal situation R2 = 1 is likely because the refined \(\sigma_{\phi }\) also includes stochastic effects triggered by refractive effects due to turbulent processes occurring at small-scale levels (Rino 2011).
These results not only stress out the importance of introducing an adaptive cutoff frequency for receivers located at high latitudes but also suggest and motivate further studies on how accurate scintillation indices determination impacts GNSS positioning. Further studies will also include a trade-off analysis about the optimal number of raw measurements to cover a single ionospheric sector and to provide sufficient input to FIF. This is because the ionospheric variability at high latitudes is high in both space and time. Besides, a statistical assessment is needed under different geospatial conditions. This may open the door to a possible real-time implementation of FIF-based filtering in dedicated infrastructures (Ghobadi et al. 2019). To this end, also a thorough assessment of the computing time performance is needed, while a preliminary assessment is given by Cicone (2020).
Data availability
Scintillation data are available through the eSWua website (eswua.ingv.it).
References
Alfonsi L, Cilliers PJ, Romano V, Hunstad I, Correia E, Linty N, Riley P (2016) First observations of GNSS ionospheric scintillations from DemoGRAPE project. Space Weather 14(10):704–709
Aquino M, Moore T, Dodson A, Waugh S, Souter J, Rodrigues FS (2005) Implications of ionospheric scintillation for GNSS users in Northern Europe. J Navig 58(2):241–256
Basu S, Groves KM, Basu S, Sultan PJ (2002) Specification and forecasting of scintillations in communication/navigation links: current status and future plans. J Atmos Solar Terr Phys 64(16):1745–1754
Beach TL (2006) Perils of the GPS phase scintillation index (φ). Radio Sci 41(5):1–7
Bertello I, Piersanti M, Candidi M, Diego P, Ubertini P (2018) Electromagnetic field observations by the DEMETER satellite in connection with the 2009 L’Aquila earthquake. Ann Geophys 36(5):1483–1493
Bougard B, Sleewaegen J-M, Spogli L, Veettil SV, Monico JF (2011) CIGALA: challenging the solar maximum in brazil with PolaRxS. In: Proceedings of the. ION GNSS 2011, Institute of Navigation, Portland, OR, September 20–23, pp 2572–2579
Carrano CS, Rino CL (2016) A theory of scintillation for two-component power law irregularity spectra: overview and numerical results. Radio Sci 51(6):789–813
Carrano CS, Groves KM, McNeil WJ, Doherty PH (2013) Direct measurement of the residual in the ionosphere-free linear combination during scintillation. In: Proceedings of the ION NTM 2013, Institute of Navigation, San Diego, CA, January 27–29, pp 585–596
Cicone A (2019) Nonstationary signal decomposition for dummies. In: Advances in mathematical methods and high performance computing, Springer, Cham, 2019, pp 69–82
Cicone A (2020) Iterative filtering as a direct method for the decomposition of nonstationary signals. Numer Algorith 2020:1–17
Cicone A, Dell’Acqua P (2019) Study of boundary conditions in the iterative filtering method for the decomposition of nonstationary signals. J Comput Appl Math 2020(373):112248
Cicone A, Zhou H (2020) Iterative filtering algorithm numerical analysis with new efficient implementations based on FFT. Submitted. ArXiv: 1802.01359
Cicone A, Liu J, Zhou H (2016) Adaptive local iterative filtering for signal decomposition and instantaneous frequency analysis. Appl Comput Harm Anal 41(2):384–411
Conker RS, El-Arini MB, Hegarty CJ, Hsiao T (2003) Modeling the effects of ionospheric scintillation on GPS/Satellite-Based Augmentation System availability. Radio Sci 38(1):1–1
De Franceschi G, Spogli L, Alfonsi L, Romano V, Cesaroni C, Hunstad I (2019) The ionospheric irregularities climatology over Svalbard from solar cycle 23. Sci Rep 9(1):1–14
Forte B (2005) Optimum detrending of raw GPS data for scintillation measurements at auroral latitudes. J Atmos Solar Terr Phys 67(12):1100–1109
Forte B, Radicella SM (2002) Problems in data treatment for ionospheric scintillation measurements. Radio Sci 37(6):1–8
Forte B, Radicella SM (2004) Geometrical control of scintillation indices: what happens for GPS satellites. Radio Sci 39(5):1–13
Fremouw EJ, Leadabrand RL, Livingston RC, Cousins MD, Rino CL, Fair BC, Long RA (1978) Early results from the DNA Wideband satellite experiment—Complex-signal scintillation. Radio Sci 13(1):167–187
Ghafoori F, Skone S (2015) Impact of equatorial ionospheric irregularities on GNSS receivers using real and synthetic scintillation signals. Radio Sci 50(4):294–317
Gherm VE, Zernov NN, Strangeways HJ (2011) Effects of diffraction by ionospheric electron density irregularities on the range error in GNSS dual-frequency positioning and phase decorrelation. Radio Sci 46(3):1–10
Ghobadi H, Testa P, Spogli L, Cafaro M, Alfonsi L, Romano V, Bru R (2019) User-oriented ICT cloud architecture for high-accuracy GNSS-based services. Sensors 19(11):2635
Huang NE, Wu Z, Long SR, Arnold KC, Chen X, Blank K (2009) On instantaneous frequency. Adv Adap Data Anal 1(2):177–229
Keskinen MJ, Ossakow SL (1983) Theories of high-latitude ionospheric irregularities: a review. Radio Sci 18(6):1077–1091
Lin L, Wang Y, Zhou H (2009) Iterative filtering as an alternative algorithm for empirical mode decomposition. Adv Adap Data Anal 1(4):543–560
Linty N, Minetto A, Dovis F, Spogli L (2018) Effects of phase scintillation on the GNSS positioning error during the September 2017 storm at Svalbard. Space Weather 16(9):1317–1329
Materassi M, Mitchell CN (2007) Wavelet analysis of GPS amplitude scintillation: a case study. Radio Sci 42(1):1–10
Materassi M, Piersanti M, Consolini G, Diego P, D’Angelo G, Bertello I, Cicone A (2019) Stepping into the equatorward boundary of the auroral oval: preliminary results of multi scale statistical analysis. Ann Geophys 62(4):455
McCaffrey AM, Jayachandran PT (2019) Determination of the refractive contribution to GPS phase “Scintillation”. J Geophys Res Space Phys 124(2):1454–1469
Moen J, Oksavik K, Alfonsi L, Daabakk Y, Romano V, Spogli L (2013) Space weather challenges of the polar cap ionosphere. J Space Weather Space Clim 2013(3):A02
Muella MT, de Paula ER, Jonah OF (2014) GPS L1-frequency observations of equatorial scintillations and irregularity zonal velocities. Surv Geophys 35(2):335–357
Mushini SC, Jayachandran PT, Langley RB, MacDougall JW, Pokhotelov D (2012) Improved amplitude-and phase-scintillation indices derived from wavelet detrended high-latitude GPS data. GPS Sol 16(3):363–373
Najmafshar M, Skone S, Ghafoori F (2014) GNSS data processing investigations for characterizing ionospheric scintillation. In: ION GNSS, 2014, Institute of Navigation, Tampa, FL, September 8–12, pp 1190–1202
Niu F, Morton Y, Wang J, Pelgrum W (2012) GPS carrier phase detrending methods and performances for ionosphere scintillation studies. In: Proceedings of the ION GNSS, 2012, Institute of Navigation, Nashville, TN, September 17–21, pp 1462–1467
Park J, Sreeja V, Aquino M, Cesaroni C, Spogli L, Dodson A, De Franceschi G (2016) Performance of ionospheric maps in support of long baseline GNSS kinematic positioning at low latitudes. Radio Sci 51(5):429–442
Piersanti M, Cesaroni C, Spogli L, Alberti T (2017) Does TEC react to a sudden impulse as a whole? The 2015 Saint Patrick’s Day storm event. Adv Space Res 60(8):1807–1816
Piersanti M, Materassi M, Cicone A, Spogli L, Zhou H, Ezquer RG (2018) Adaptive local iterative filtering: a promising technique for the analysis of nonstationary signals. J Geophys Res Space Phys 123(1):1031–1046
Rino C (2011) The theory of scintillation with applications in remote sensing. Wiley, New York
Romano V, Ghobadi H, Spogli L, Cafaro M, Alfonsi L, Cicone A, Linty N (2019) Disentangling ionospheric refraction and diffraction effects in GNSS raw phase through fast iterative filtering technique. In: AGU fall meeting 2019. AGU
Spogli L, Alfonsi L, Cilliers PJ, Correia E, De Franceschi G, Mitchell CN, Romano V, Kinrade J, Cabrera MA (2013) GPS scintillations and total electron content climatology in the southern low, middle and high latitude regions. Ann Geophys 56(2):0220
Spogli L, Piersanti M, Cesaroni C, Materassi M, Cicone A, Alfonsi L, Romano V, Ezquer RG (2019) Role of the external drivers in the occurrence of low-latitude ionospheric scintillation revealed by multi-scale analysis. J Space Weather Space Clim 2019(9):A35
Stallone A, Cicone A, Materassi M, Zhou H (2020) New insights and best practices for the successful use of Empirical Mode Decomposition. Iterative Filtering and derived algorithms, Submitted
Tinin MV (2015) Eliminating diffraction effects during multi-frequency correction in global navigation satellite systems. J Geodesy 89(5):491–503
Van Dierendonck AJ, Arbesser-Rastburg B (2004) Measuring Ionospheric scintillation in the equatorial region over Africa, including measurements from SBAS geostationary satellite signals. In: Proceedings of the ION GNSS 2004, Institute of Navigation, Long Beach, CA, September 21–24, pp 316–324
Van Dierendonck AJ, Klobuchar J, Quyen H (1993) Ionospheric Scintillation monitoring using commercial single frequency C/A code receivers. In: Proceedings of the ION GPS 1993, Institute of Navigation, Salt Lake City, UT, September 22–24, pp 1333–1342
Wang Y, Zhang QH, Jayachandran PT, Moen J, Xing ZY, Chadwick R, Ma YZ, Ruohoniemi JM, Lester M (2018) Experimental evidence on the dependence of the standard GPS phase scintillation index on the ionospheric plasma drift around noon sector of the polar ionosphere. J Geophys Res Space Phys 123(3):2370–2378
Wernik AW, Secan JA, Fremouw EJ (2003) Ionospheric irregularities and scintillation. Adv Space Res 31(4):971–981
Wu Z, Huang NE (2009) Ensemble empirical mode decomposition: a noise-assisted data analysis method. Adv Adap Data Anal 1(1):1–41
Yeh KC, Liu CH (1982) Radio wave scintillations in the ionosphere. Proc IEEE 70(4):324–360
Yen NC, Tung CC, Liu HH (1998) The empirical mode decomposition and the Hilbert spectrum for nonlinear and nonstationary time series analysis. Proc R Soc Lond A 454:903–995
Zhang L, Morton Y, van Graas F, Beach T (2010) Characterization of GNSS signal parameters under ionosphere scintillation conditions using software-based tracking algorithms. In: IEEE/ION position, location and navigation symposium, Indian Wells, CA, pp 264–275
Zhang K, Li X, Xiong C, Meng X, Li X, Yuan Y, Zhang X (2019) The Influence of Geomagnetic Storm of 7‐8 September 2017 on the Swarm Precise Orbit Determination. J Geophys Res Space Phys 124(8):6971–6984
Acknowledgements
This research is supported by TREASURE, a project funded by the European Union’s Horizon 2020 research and innovation program under the Marie Skłodowska-Curie Actions Grant Agreement No. 722023 (http://ww.treasure-gnss.eu). The authors thank PNRA (Programma Nazionale di Ricerche in Antartide) for supporting the upper atmosphere observations at Concordia Station (Antarctica). The FIF algorithm, available for the public at https://github.com/Acicone/FIF, was developed by Dr. Antonio Cicone, who is a member of the Italian “Gruppo Nazionale di Calcolo Scientifico” (GNCS) of the Istituto Nazionale di Alta Matematica “Francesco Severi” (INdAM). His work was partially supported through the Progetto Premiale FOE 2014 “Strategic Initiatives for the Environment and Security—SIES” of the INdAM and the CSES-Limadou project of the Istituto di Astrofisica e Planetologia Spaziali (IAPS) of the Istituto Nazionale di Astrofisica (INAF). A special thanks to Dr. Giorgiana De Franceschi for her kind support, which inspired our work.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Ghobadi, H., Spogli, L., Alfonsi, L. et al. Disentangling ionospheric refraction and diffraction effects in GNSS raw phase through fast iterative filtering technique. GPS Solut 24, 85 (2020). https://doi.org/10.1007/s10291-020-01001-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10291-020-01001-1