Abstract
The velocity estimates and their uncertainties derived from position time series of Global Navigation Satellite System stations are affected by seasonal signals and their harmonics, and the statistical properties, i.e., the stochastic noise, contained in the series. If the deterministic model in the form of linear trend and periodic terms is not accurate enough to describe the time series, it will alter the stochastic model, and the resulting effect on the velocity uncertainties can be perceived as a result of a misfit of the deterministic model. The effects of insufficiently modeled seasonal signals will propagate into the stochastic model and falsify the results of the noise analysis, in addition to velocity estimates and their uncertainties. We provide the general dilution of precision (GDP) of velocity uncertainties as the ratio of uncertainties of velocities determined from to two different deterministic models while accounting for stochastic noise at the same time. In this newly defined GDP, the first deterministic model includes a linear trend, while the second one includes a linear trend and seasonal signals. These two are tested with the assumption of white noise only as well as the combinations of power-law and white noise in the data. The more seasonal terms are added to the series, the more biased the velocity uncertainties become. With increasing time span of observations, the assumption of seasonal signals becomes less important, and the power-law character of the residuals starts to play a crucial role in the determined velocity uncertainties. With reference frame and sea level applications in mind, we argue that 7 and 9 years of continuous observations is the threshold for white and flicker noise, respectively, while 17 years are required for random-walk to decrease GDP below 5% and to omit periodic oscillations in the GNSS-derived time series taking only the noise model into consideration.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Today, Global Navigation Satellite System (GNSS) measurements, in particular those from the Global Positioning System (GPS), are fundamental to many geodetic and geophysical investigations (Kreemer et al. 2014; Métivier et al. 2014) and are frequently used during the construction of kinematic reference frames, such as, for example, the International Terrestrial Reference Frame 2014 (ITRF2014) (Altamimi et al. 2016). From the processing or re-processing of the observables of permanently installed GNSS stations, daily or weekly geocentric coordinate solutions are obtained, from which position time series are formed. The primary product from the analysis of these time series is often the linear rate of change, or velocity, and the associated uncertainty (Zhang et al. 1997).
The velocities are assumed to represent the linear movement of the earth’s crust due to tectonic plate motions (Larson et al. 1997; Drewes 2009; Altamimi et al. 2012) or the viscoelastic relaxation associated with glacial isostatic adjustment (Johansson et al. 2002; Bradley et al. 2009). In addition, almost all sites within the global network of GPS stations also show nonlinear periodic motions, which have been associated primarily with the seasonal effects on earth. However, some stations may also exhibit nonlinear and non-periodic character motions (Shih et al. 2008; Bogusz 2015). This may be due to the elastic response of the earth’s crust from the rapid ice mass loss at the polar ice sheets or mountain glaciers (Wahr et al. 2013), being located in the deforming zones near plate boundaries (Wdowinski et al. 2004) or areas of oil, gas, or groundwater extraction (Munekane et al. 2004). In this study, we will not deal with cases showing such nonlinear and non-periodic behavior.
Blewitt and Lavallée (2002) were one of the first to investigate the effect of periodic signals on GPS time series, and today it is widely acknowledged that such seasonal terms affect GPS and other geodetic time series (Bos et al. 2010; Davis et al. 2012; Bogusz and Figurski 2014). The causes are almost completely understood and can be grouped into categories suggested by Dong et al. (2002): real geophysical effects of atmospheric (Tregoning and van Dam 2005), hydrological (van Dam et al. 2001) or ocean loadings (van Dam et al. 2012) with thermal expansion (Romagnoli et al. 2003; Xu et al. 2017) and numerical artifacts of navigation satellite systems. Penna and Stewart (2003) described aliased periodic signals in the coordinate time series due to under-sampling of residual diurnal and semidiurnal tidal signatures. Griffiths and Ray (2013) extended this analysis for the largest waves in the International Earth Rotation and Reference Frame Service (IERS) Conventions 2010 diurnal and semi-diurnal tidal polar motion model, assuming 24-h sampling. The second technique-related error is associated with satellite orbits (draconitics). Agnew and Larson (2007) found that for daily sampling rates in GPS-derived coordinates this period will alias to a frequency of 1.04333 cpy (cycles per year). Ray et al. (2008) compared harmonics obtained using techniques such as GPS, Very Long Baseline Interferometry, and Satellite Laser Ranging when they discovered an anomalous peak in the GPS-derived time series, which was not present in other series. They explained it to be related to the interval required for the constellation to repeat its inertial orientation with respect to the sun (GPS year). Amiri-Simkooei (2013), analyzing Jet Propulsion Laboratory (JPL) data, obtained a period of 351.6 ± 0.2 days. Abraha et al. (2017) proved that most of the power in draconitic period is satellite induced. Finally, multipath (King et al. 2012), insufficient modeling of antennas (Sidorov 2016), errors in the network, the adjustment that transfers from fiducial stations, or the inclusion of the scale (Tregoning and van Dam 2005) contributes to constellation-specific periodic signals in the time series.
From the above, it is clear that the deterministic model of a GNSS position time series needs to include parameters for both the linear and periodic motions at a given station (Bevis and Brown 2014). Furthermore, in a true geodetic approach, the model must provide means to obtain the most realistic uncertainties associated with the parameter estimates in order to provide confidence limits at a given significance level. In this respect, we model the time series, which have been pre-processed for outliers, offsets, and gaps, with least squares estimation (LSE) as:
where x 0, v, ACi, ASi, n are the intercept, velocity, cosine, and sine terms of ith harmonic and the number of harmonics of the angular velocity ω of period T, respectively. The term ε(t) contains the residuals and all variations not explicitly modeled and, therefore, disregarded by this station motion model. It is now commonly known that the residuals do not follow a strict random behavior, i.e., a white noise with spectral index κ = 0, but follow that of a combination of colored and white noise, with the latter often being modeled as a power-law process (Agnew 1992). This temporally correlated noise is of a form of flicker noise with spectral index κ = − 1 or of random-walk process with spectral index κ = − 2. Flicker noise is present in the GPS position time series due to mismodeling in GNSS satellites orbits, Earth Orientation Parameters, large-scale atmospheric or hydrospheric effects. It has been already described by Williams et al. (2004) or Amiri-Simkooei et al. (2007) who stated that a combination of flicker and white noise is the preferred noise model for GPS data. Teferle et al. (2008) emphasized that their time series showed evidence of power-law noise close to the flicker. Caporali (2003) stated that the power spectral densities of time series prove that flicker noise is preferred for most stations to represent the data at frequencies below 6 cpy. For frequencies higher than 6 cpy, the spectrum tends to become a white noise. Santamaria-Gomez et al. (2011) concluded that a combination of power-law and white noise is the preferred one for a global data set. Klos et al. (2015) stated that this combination is valid also for weekly data. A random-walk process might be present in GPS position time series due to local environment and monumentation. Johnson and Agnew (1995) were the first to state that the type of monument may have an impact on the long-term correlation present in GPS data. Beavan (2005) compared two monuments: a concrete pillar and a deep drilled braced monument and stated that there is no significant difference in the stochastic part of GPS position time series collected. However, the analysis was only performed for 4.5 years of data. Even when a perfect monument is considered with the environment being transparent to the signal, the noise would be flicker and arise from low-frequency fluctuations of the satellite clocks (Dutta and Horn 1981). Beyond these features, there are also some seasonal features that add more correlated noise to GNSS data. As stated by Johnson and Agnew (1995), if time series were too short, it is more difficult to detect any change due to correlation than it is for long data. As is now widely acknowledged, the stochastic properties of the residuals significantly influence the magnitude of the uncertainties associated with the parameters (Zhang et al. 1997; Langbein and Johnson 1997; Mao et al. 1999; Williams 2003), and the whiter the noise, the faster the velocity uncertainty decays with increasing time series length. Therefore, the noise character has the greatest impact on velocity uncertainty and errors of the deterministic model estimated at the same time.
We provide a general dilution of precision (GDP) of the velocity uncertainties being the ratio of uncertainties of velocities arising from two different assumptions of the deterministic model. The first of them assumes a linear velocity only, while the second is a combination of linear velocity and periodic components. Each of the assumptions is presented with certain noise models starting from white, moving on to flicker and end up with random-walk, the most extreme case for GNSS position time series. The determined errors of the velocities are being discussed along the two previous papers of Blewitt and Lavallée (2002) and Bos et al. (2010) which provided the first overview of this topic. Using simulated data we show that our approach has additional advantages to GNSS time series analysis in comparison to the ones mentioned before. We deliver the estimates of a combined effect of periodic signals and noise model assumed in residuals, to show how much one may underestimate the uncertainties of velocities when inappropriate assumptions were made prior to the analysis. Finally, we apply the newly developed formulae to real GNSS time series of selected ITRF2014 stations. Beyond the GNSS position time series, our conclusions are also valid for any other type of position time series, as those collected by Very Long Baseline Interferometry (VLBI), Doppler Orbitography and Radiopositioning Integrated by Satellite (DORIS), Satellite Laser Ranging (SLR), or tide gauges.
Dilution of precision
Blewitt and Lavallée (2002) developed a model to calculate the bias level when one does not account for periodic signals of annual frequency. The velocity bias expressed in mm/year introduced by them was a zero-crossing oscillatory function of data span, tending to zero for infinitely long time series. According to this function they discovered the “zero-bias theorem” for unbiased velocity near integer-plus-half years and introduced the ratio of uncertainties of velocities v 1 and v 2. They called it the dilution of precision (DP) and estimated its value as (Blewitt and Lavallée 2002):
where τ is the time span and f denotes the frequency of the periodic terms. Figure 1 shows the DP value which increases toward infinity when the time span is shorter than 1 year. A number of maxima of oscillations in DP can be noticed for integer years. These come from periodic terms in (1) defined by f. The time span of observations is given by τ. For certain epochs starting from 1.5 years with a step of 1-year the DP = 1. It results from the fact that the velocity uncertainties for a model with linear velocity and a model with seasonal terms added are equal to each other. Also, for a time span longer than 3.5 years, the DP < 1.05, which means that the difference between both variances is below 5%. However, Blewitt and Lavallée (2002) inputted only white noise, and as a consequence assumed that the character of a stochastic part ε has a little impact on the estimated uncertainties.

(recomputed from Blewitt and Lavallée 2002)
Dilution of precision for models: with linear velocity and linear velocity plus annual term.
It is expected that when we add a power-law noise, the difference between both variances will need more time to fall below 5%, while the power-law noise process adds temporal correlation to the time series. That is why Bos et al. (2010) discussed the results of Blewitt and Lavallée (2002) by empirically analyzing the effect of periodic signals using six stations, but assumed a combination of colored and white noise. They noticed that the way the stochastic part is described might be of greater importance than that of the seasonal part in the deterministic model. This is due to the fact that velocity uncertainty depends mostly on the spectral index and amplitude of the power-law process. They concluded that the knowledge of the noise characteristics of GNSS time series is crucial when velocities and their uncertainties are determined. Furthermore, they observed a shift in the minimum of the DP from the integer-plus-half years toward integer-plus-a-quarter years position. We confirm the results found by Bos et al. (2010) and also deliver the mathematic formulae of DP for time series with power-law noise combined with white one.
In order to estimate the DP, it is first necessary to obtain an expression for the covariance of the estimates in terms of the noise covariance. For this, let us consider the vector of residuals ε defined as the difference between the model parameters and the data fitted into (1):
where A is the model or design matrix, \( {\varvec{\uptheta}} \) is a vector with parameters of the model, x stands for the observational data or measurements, and ε is the vector of residuals.
When the parameters of the model are determined by means of maximum likelihood estimation (MLE; Langbein 2012) and assuming a Gauss distribution for such estimates, they are computed as:
with C εε being the covariance matrix for the residuals ε.
Then, using (3) to replace x in (4), and rearranging terms, it yields:
which can be used to compute the second moment or covariance of the residuals in terms of the covariance noise as follows:
In general, the vector of the residuals ε is a linear combination of colored and white noise:
where the first term on the right side is a convolution of white noise, \( w_{i} \in {\rm N}\left( {0,\sigma_{pl} } \right) \), and the second term is a white noise process, \( v_{i} \in {\rm N}\left( {0,\sigma_{wn} } \right) \), with σ pl and σ wn standing for the amplitude parameters of the colored and white noise processes, respectively. N is the number of data, while h is defined by the recursive formula (Bos et al. 2008):
with κ being the spectral index ranging from −3 to 1, which, when appropriately assigned, may characterize the stochastic part of the time series (Mandelbrot and Van Ness 1968).
From (7) the covariance of the residuals is:
or, in matrix notation:
L is a lower triangular Toeplitz matrix with coefficients defined as follows:
where \( h_{i - j} \) are the same coefficients as in (8) that depend on the spectral index κ. Finally, by inserting (10) in (6), we get the following expression for the covariance matrix of the estimated parameters, \( {\hat{\mathbf{\theta }}} \):
where E is the part of the covariance matrix from the power-law process that depends on the spectral index \( \kappa \):
Thus, the covariance of the estimates is expressed in terms of the spectral index \( \kappa \) and the amplitudes of the colored and white noise processes, σ pl and σ wn , respectively.
Finally, note that the process defined by (7) and (8) is a fractionally differenced Gaussian noise process with spectral density (Hosking 1981):
which, as \( f \to 0 \), yields a power-law:
Henceforth, we will refer to the color noise process as power-law throughout the paper.
Models
If we assume that the deterministic model of GNSS time series follows a linear trend with a vector of parameters built as:
where v is the slope or velocity and x 0 is the intercept, the model matrix A is created as:
Then, the variance of velocity estimate can be computed by inserting (17) into (12).
The proper modeling of the seasonal terms may directly influence on the reliability of determined parameters, such as the velocity. Indeed, as Blewitt and Lavallée (2002) already showed, the seasonal terms may influence the uncertainty of velocity. However, they did not consider the power-law character of residuals but assumed them to follow a white noise process. Bos et al. (2010) noticed that not only do the seasonal terms affect the linear velocity when being improperly removed, but the noise properties are much more important for a reliable estimation of the velocity error. These directly affect the uncertainty of velocity due to different shapes of the covariance matrix, as in (9–10).
Let us assume now a deterministic model with linear velocity and annual term:
The vector of parameters is built here as:
where AC and AS are the annual cosine and sine terms, respectively. Similar to the previous model, substitution of (18) in (12) yields the covariance for the estimates in (19).
Simulated series
In order to test the general dilution of precision formulas derived above, we carried out a number of evaluations. For these, we simulated time series of up to a maximum length of 25 years, which is at the time of writing the longest term of available GNSS time series. Synthetic data were created based on two approaches for the deterministic part: The first included annual and semiannual terms, and the second included all significant periods, i.e., all tropical and draconitic terms up to ninth harmonic, plus fortnightly and the Chandlerian period since the latter may be present at some stations at island and coastal sites (Richard Gross, private communication, 2015); see Bogusz and Klos (2016) for more details. Then, we added temporal correlation in the form of a combination of power-law and white noise, built a noise covariance matrix as in (9) and transferred it to estimate the variances of the estimated parameters as in (12). We assumed four different spectral indices equal to 0, − 1, − 1.5, and − 2 that indicate pure white, pure flicker, fractional Brownian motion, and pure random-walk noise, respectively, with \( \sigma_{pl}^{2} = 1 \) and \( \sigma_{wn}^{2} = 1 \). White noise was added to flicker, fractional Brownian motion, and random-walk when assumed.
Figure 2 shows the error of the velocity for white, flicker and random-walk noise. For time series shorter than 70 days, the error of velocity is much higher for white and flicker noise assumptions than for random-walk noise. This situation changes when the data becomes longer than 70 days. The error of velocity is the smallest for the white noise assumption. Random-walk noise delivers the greatest errors of parameters. The longer the data is, the greater is the difference between errors delivered for random-walk noise and flicker or white noise assumptions. Having assumed white, flicker and random-walk noises, for 20 years of data one will obtain an error of velocity equal to 10−3, 10−2, and 10−1 mm/year, respectively.
We estimated the relative differences in velocity variances for two deterministic models: with linear velocity denoted as \( \sigma_{v1}^{2} \) and with linear velocity plus seasonal terms denoted as \( \sigma_{v2}^{2} \), as
Adding seasonal terms results in oscillations in the estimated velocity error when the length of time series changes. The velocity variances are computed from the diagonal terms of the covariance matrix (12). These oscillations, of course, are not so obvious any more when the spectral index of power-law dependencies increases, as was also noticed in Bos et al. (2010). The largest differences between two models are being observed for the random-walk noise assumption. As the spectral index was shifted from 0 toward − 2, the differences between velocity uncertainties will, of course, enlarge much more. Due to the above, the largest differences between two models are being expected for badly monumented stations (Langbein and Johnson 1997; Beavan 2005; Klos et al. 2016).
The uncertainties estimated will differ when seasonal terms are included or are not included. This difference is computed as a ratio between both values. We called it the general dilution of precision (GDP) in accordance with Blewitt and Lavallée (2002) and as in (2), but taking into consideration a power-law noise in the stochastic part, as was underlined in (15). We have adopted two approaches to estimate the seasonal part. First, the widely used annual and semiannual terms were subtracted from the GPS position time series. Then, the approach, which is consistent with Bogusz and Klos (2016), was assumed: tropical and draconitics up to their ninth harmonics, plus Chandlerian and fortnightly terms were modeled. Figures 3 and 4 show a GDP for white, flicker, random-walk and fractional Brownian motion of spectral indices equal to 0, − 1, − 2, and − 1.5, respectively.
General dilution of precision (GDP) for white noise (blue), flicker noise (red), fractional Brownian motion of spectral index equal to − 1.5 (orange), and random walk (black) plotted for a deterministic model containing a linear velocity plus extended model of periodicities of all tropical and draconitic terms up to ninth harmonic plus fortnightly and the Chandlerian period, according to Bogusz and Klos (2016)
We computed the GDP values for harmonics of 1 year. They increased the local maxima in the GDP plot. It can be noticed that in comparison to Blewitt and Lavallée (2002) who considered the annual term, the semiannual signal also increases the local minimum of GDP with a white noise assumption. It means that adding the power-law noise to the annual curve or adding a semiannual term to white noise causes an increase in the velocity uncertainty even at those points where the estimated velocity should not be biased. The more seasonal terms are added to the series, the more biased is the velocity uncertainty, especially for short time scales. Having compared Figs. 3, 4, and 5, it is clear that the type of deterministic model affects the velocity uncertainty and makes GDP to reach the value of 5% (we adopted this number following Blewitt and Lavallée 2002) after 9 years, rather than 4, as was expected for annual plus semiannual terms (a case of white and flicker noise). The value of 5% means an increase in velocity uncertainty of 0.025 mm/year when a typical error of velocity of 0.5 mm/year is considered (Bruyninx et al. 2013). However, with the increasing demand on velocities from reference frame (0.1 mm/year, Plag and Pearlman 2009) and sea level applications, we argue that even lower changes than 5% of GDP could be considered as significant. All the above shows is that periodic terms affect the velocity uncertainty much more at short timescales than they do for long-term data, leaving the values of velocity unbiased at the same time. With the increasing time span of observations, the assumption of seasonal signals becoming less important is validated. Here, the power-law character of the residuals plays a crucial role in determining the velocity uncertainty. In this way, 7, 9, and 17 years are enough for white, flicker, and random-walk noise, respectively, to decrease GDP below 5%, to omit periodic oscillations in the GNSS-derived time series and to take only noise model into consideration. So, providing a long time series, the periodicities we assumed will not influence the velocity uncertainty as much as noise would. This is why we should focus on obtaining the best estimate for the spectral index of each geodetic time series such as position, sea level, or zenith total delay.
Comparison between GDPs estimated for white noise (blue), flicker noise (red), fractional Brownian motion of spectral index equal to − 1.5 (orange) and random walk (black) plotted for deterministic model containing (1) linear velocity plus annual and semiannual oscillations (dashed lines) and (2) linear velocity plus extended model of periodicities from Bogusz and Klos (2016) (solid lines)
Real GNSS time series
In order to confirm our theoretical approach with real data, we used position time series of continuous GPS stations. The time series we chose contributed to the newest International Terrestrial Reference Frame (ITRF2014). The GPS measurements were processed in the network solution named “repro2” by the International GNSS Service (IGS) (Rebischung et al. 2016, http://acc.igs.org/reprocess2.html). In this study, we picked 898 stations with time series of different lengths from 3 to 23 years that showed no specific or unusual behavior regarding long-term nonlinearity or earthquakes. This is to ensure that our results are not compromised by stations, which, for example, did not follow the assumption of a linear evolution in the coordinates. The station distribution is indicated in Fig. 6. The daily time series of the North, East, and Up components were pre-processed for outliers, offsets, and gaps if necessary and then analyzed with the reformulated maximum likelihood estimation (MLE) as implemented in the Hector software (Bos et al. 2013). We generated two different models to be fitted to GPS position time series. In the first case, the stochastic model was assumed to be a pure white noise with just linear velocity in the deterministic part. In the second case, a combination of power-law and white process with the full deterministic model was employed. To generate the GDP values, we estimated the ratio between (a) and (b), meaning that we fit (a) the appropriate noise model which has been already found to be preferred for GPS data and the most proper deterministic model taking all periodicities into account against (b) which is a simple linear fit with white noise assumption. The above exercise shows a clear combined effect of periodicities and power-law noise on the uncertainties of linear velocities.
The median amplitudes of the annual term are at the level of 1.65, 1.78, and 4.22 ± 0.20 mm for the North, East, and Up components, respectively. Almost all median amplitudes of the second, third, and fourth harmonics of the annual term fall below 1 mm with errors varying between 0.10 and 0.25 mm for horizontal and vertical changes.
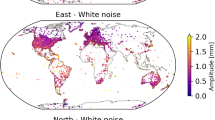
Figure 6 presents a stochastic character: a power-law spectral index of examined stations. A clear spatial dependence may be noticed for few areas. In general, spectral indices estimated for ITRF2014 stations vary between − 1.6 and − 0.3, meaning we deal with different spectral characters of residuals. Spectral indices higher than − 0.5 were found for the shortest time series examined, confirming the findings of Williams et al. (2004) who emphasized, that white noise may cover a power-law character of residuals when time series are not long enough. For the North and East components, no spatial dependencies were found, expect for the area of Europe, for which the spectral indices we found are much more consistent than for any other part of the world. For the Up component, a clear spatial dependence may be found for Europe, indicating a strong impact of a Baltic Sea on the residuals of GPS position time series. That has been already also noticed by Klos and Bogusz (2017), explaining lower indices found for the coastal areas of the Baltic Sea by the impact of the sea. Also, stations situated within the areas of tundra and tropics are characterized by lower spectral indices than the rest of the stations. However, the detailed description of possible causes of such a character falls outside the scopes of this study.
Figure 7 presents GDP values for a globally distributed set of stations of series of different lengths from 3 to 23 years. From these figures, we can easily notice, that the GDPs for all components remain between 1 and 10 for a majority of stations with medians of 3.1, 3.2, and 2.8, respectively, for the North, East, and Up components. For 20, 17, and 19 North, East, and Up components, respectively, the GDP fall within 5%, as indicated by Blewitt and Lavallée (2002). For 5, 8, and 2 North, East, and Up components, respectively, the GDP values are equal to 1, meaning that there was no difference in velocity uncertainty when only white noise with a linear velocity was assumed and when a full deterministic model was employed along with the preferred noise model. The GDP estimates vary between 1 and 10 for a set of 756, 739 and 696 stations for the North, East, and Up components, respectively, of the ITRF2014 GPS position time series.
General Dilution of precision (GDP) for the North, East, and Up components. GDP means here a ratio between two assumptions of models being fitted into position time series: (1) a linear velocity plus a pure white noise, (2) a linear velocity, all seasonal terms and a combination of power-law and white noise model
The results delivered for real GPS position time series are in good agreement with the theoretical formulae derived above. No spatial dependencies were found for the North and East components. The greatest deviations from 1 were observed for stations with large gaps within the data or significant variations in the amplitudes of seasonal signals, which were not modeled and therefore transferred to the stochastic part and also, for those, where the noise character was estimated to vary between flicker and random-walk noise. This means that the character of the noise, which affects the residuals of GPS data, influences the value of GDP for time series of sufficient length. For short series, the seasonal signals which were added to the deterministic model affect the GDP more than the character of the residuals, as was shown for the synthetic dataset. For a few stations, the GDP estimates are higher than 10. This was noticed for stations with large gaps inside the time span of observations. A clear influence of the Baltic Sea was noticed for the GDPs estimated for the Up component. All values are higher than 10, meaning that the uncertainties of estimates are highly affected by the type of noise by which time series are characterized.
Conclusions and discussion
Not accounting for the seasonal signals results in an increase in the autocorrelation or temporally correlated noise within the time series. This, in turn, influences the stochastic model when the periodic signals are not properly modeled. In this way, if we were certain about the presence of seasonal signals in the GNSS time series and did not model them, the residuals would resemble more a flicker noise. This would lead to increased uncertainties for all parameter estimates. Again, when the seasonal signals are properly modeled, another issue that may cause an artificial increase in the velocity uncertainty is an improperly assumed noise model itself. When flicker and random walk are being compared to a fractional Brownian motion, there may be an underestimation of the error bounds by a factor of two.
Some points can be easily noticed and raised for deeper discussion from the presented results. As long as the spectral index increases, the amplitudes of oscillations also increase. This arises from the fact that any power-law process with κ < 0 brings a correlation between amplitudes of seasonal terms and velocity. In this way, the GDP value is much higher for any time series length considered. The strong peaks of oscillations as seen in the GDP are indicated for short time scales, especially for the random-walk case. The applied oscillations play a significant role, even much more important than the a priori assumed noise character. The noise character starts to become important for time series longer than 9 years. The local minima and maxima of GDP are also being enlarged together with a change of the spectral index from 0 to − 2. This shows that the GDP may differ from integer-plus-half years as found by Blewitt and Lavallée (2002), who considered only white noise. This is clearly noticed in the case of random walk and has already been empirically confirmed by Bos et al. (2010). In this research, we provided mathematic formulas for the findings of Bos et al. (2010) and confirmed their correctness with synthetic and real GPS data and focused on power-law plus white noise, which is generally regarded as the best estimate for the stochastic model of GNSS time series. We showed that periodic signals are more important for short time scales, whereas the stochastic noise plays a significant role when the length of the time series increases. Also, with increasing spectral indices, the GDP decreases more slowly. We discussed a previously published approach, which indicated that 3.5 years of data are enough for the GDP to fall below 5%. When more seasonal signals and their harmonics were added to the deterministic model that include periodicities of all tropical and draconitic terms up to ninth harmonic plus fortnightly and the Chandlerian period, the GDP requires 9 years to fall below 5% for a white and flicker noise model. We have also discovered that the noise character starts to become more important than the periodic signals for time series longer than 9 years. And finally, Blewitt and Lavallée (2002) used the value of 5% to calculate the minimum velocity bias. However, this value is disputable. With the increasing demand on velocities, we argue that even smaller change in GDP could be considered as significant. This means that 7 and 9 years of continuous observations could be considered as the threshold for white and flicker noise, while 17 years for random walk to make the GDP to decrease to below 5% and to omit periodic signals in the GNSS-derived time series, taking only the noise model into consideration.
For real GPS data, the GDP values vary between 0 and 20, when a full deterministic model plus a proper noise model are considered against the assumption of linear velocity plus a white noise model. This clearly shows the combined effect which different assumptions for the mathematical model have on the uncertainties of the estimates. When the more realistic model is used, the closer to the truth and proper uncertainties are obtained.
Naturally, these assumptions are also valid for other kinds of data, such as VLBI, SLR, DORIS, or tide gauges. VLBI and SLR position time series are both characterized by the stochastic part being quite close to white noise (Feissel-Vernier et al. 2007; Botai et al. 2011), meaning that the type of noise would not have much impact on the uncertainties of the estimates. In these cases, a number of seasonals being fitted into position time series play a crucial role in the GDP estimates. As was shown by Collilieux et al. (2007) that the VLBI and SLR position time series are characterized by a number of significant oscillations, which have to be taken into account when a realistic model is to be employed. Riddell et al. (2017) found that the uncertainties of X, Y, and Z translations increase of 0.10 mm/year at a minimum, when a power-law noise is employed to describe them. The uncertainties of parameters delivered from DORIS series with the preferred noise model described as white plus flicker noise (Williams and Willis 2006; Khelifa et al. 2012) will be influenced much more by the character of noise than VLBI and SLR position series.
References
Abraha KE, Teferle FN, Hunegnaw A, Dach R (2017) GNSS related periodic signals in coordinate time-series from precise point positioning. Geophys J Int 208(3):1449–1464. https://doi.org/10.1093/gji/ggw467
Agnew DC (1992) The time-domain behaviour of power-law noises. Geophys Res Lett 19(4):333–336
Agnew DC, Larson KM (2007) Finding the repeat times of the GPS constellation. GPS Solut 11(1):71–76. https://doi.org/10.1007/s10291-006-0038-4
Altamimi Z, Métivier L, Collilieux X (2012) ITRF2008 plate motion model. J Geophys Res Solid Earth 117(B7):B07402. https://doi.org/10.1029/2011JB008930
Altamimi Z, Rebischung P, Métivier L, Collilieux X (2016) ITRF2014: a new release of the International Terrestrial Reference Frame modeling nonlinear station motions. J Geophys Res Solid Earth 121:6109–6131. https://doi.org/10.1002/2016JB013098
Amiri-Simkooei AR (2013) On the nature of GPS draconitic year periodic pattern in multivariate position time series. J Geophys Res Solid Earth 118(5):2500–2511. https://doi.org/10.1002/jgrb.50199
Amiri-Simkooei AR, Tiberius CCJM, Teunissen PJG (2007) Assessment of noise in GPS coordinate time series: methodology and results. J Geophys Res. https://doi.org/10.1029/2006JB004913
Beavan J (2005) Noise properties of continuous GPS data from concrete pillar geodetic monuments in New Zealand and comparison with data from U.S. deep drilled braced monuments. J Geophys Res. https://doi.org/10.1029/2005JB003642
Bevis M, Brown A (2014) Trajectory models and reference frames for crustal motion geodesy. J Geod 88:283–311. https://doi.org/10.1007/s00190-013-0685-5
Blewitt G, Lavallée D (2002) Effect of annual signals on geodetic velocity. J Geophys Res 107(B7):ETG 9-1–ETG 9-11. https://doi.org/10.1029/2001JB000570
Bogusz J (2015) Geodetic aspects of GPS permanent station non-linearity studies. Acta Geodyn Geomater 12(4):323–333. https://doi.org/10.13168/AGG.2015.0033
Bogusz J, Figurski M (2014) Annual signals observed in regional GPS networks. Acta Geodyn Geomater 11(2):125–131. https://doi.org/10.13168/AGG.2014.0003
Bogusz J, Klos A (2016) On the significance of periodic signals in noise analysis of GPS station coordinates time series. GPS Solut 20(4):655–664. https://doi.org/10.1007/s10291-015-0478-9
Bos MS, Fernandes RMS, Williams SDP, Bastos L (2008) Fast error analysis of continuous GPS observations. J Geod 82(3):157–166. https://doi.org/10.1007/s00190-007-0165-x
Bos M, Bastos L, Fernandes RMS (2010) The influence of seasonal signals on the estimation of the tectonic motion in short continuous GPS time-series. J Geodyn 49(3–4):205–209. https://doi.org/10.1016/j.jog.2009.10.005
Bos MS, Fernandes RMS, Williams SDP, Bastos L (2013) Fast error analysis of continuous GNSS observations with missing data. J Geod 87(4):351–360. https://doi.org/10.1007/s00190-012-0605-0
Botai OJ, Combrinck L, Sivakumar V (2011) Inferences of a-stable distribution of the underlying noise components in geodetic data. S Afr J Geol 114(3–4):541–548. https://doi.org/10.2113/gssajg.114.3-4.541
Bradley SL, Milne GA, Teferle FN, Bingley RM, Orliac EJ (2009) Glacial isostatic adjustment of the British Isles: new constraints from GPS measurements of crustal motion. Geophys J Int 178(1):14–22. https://doi.org/10.1111/j.1365-246X.2008.04033.x
Bruyninx C, Altamimi Z, Caporali A, Kenyeres A, Lidberg M, Stangl G, Torres JA (2013) Guidelines for EUREF Densifications. http://www.epncb.oma.be/_documentation/guidelines/
Caporali A (2003) Average strain rate in the Italian crust inferred from a permanent GPS network—I. Statistical analysis of the time-series of permanent GPS stations. Geophys J Int 155(1):241–253. https://doi.org/10.1046/j.1365-246X.2003.02034.x
Collilieux X, Altamimi Z, Coulot D, Ray J, Sillard P (2007) Comparison of very long baseline interferometry, GPS, and satellite laser ranging height residuals from ITRF2005 using spectral and correlation methods. J Geophys Res. https://doi.org/10.1029/2007JB004933
Davis JL, Wernicke BP, Tamisiea ME (2012) On seasonal signals in geodetic time series. J Geophys Res. https://doi.org/10.1029/2011JB008690
Dong D, Fang P, Bock Y, Cheng MK, Miyazaki S (2002) Anatomy of apparent seasonal variations from GPS-derived site position time series. J Geophys Res. https://doi.org/10.1029/2001JB000573
Drewes H (2009) The actual plate kinematic and crustal deformation model APKIM2005 as basis for a non-rotating ITRF. In: International association of geodesy symposia, vol 134. pp 95–99. https://doi.org/10.1007/978-3-642-00860-3_15
Dutta P, Horn PM (1981) Low-frequency fluctuations in solids: 1/f noise. Rev Mod Phys 53:497
Feissel-Vernier M, de Viron O, Le Bail K (2007) Stability of VLBI, SLR, DORIS and GPS positioning. Earth Planets Space 59:475–497
Griffiths J, Ray JR (2013) Sub-daily alias and draconitic errors in the IGS orbits. GPS Solut 17(3):413–422. https://doi.org/10.1007/s10291-012-0289-1
Hosking JRM (1981) Fractional differencing. Biometrika 68(1):165–176
Johansson JM, Davis JL, Scherneck HG, Milne GA, Vermeer M, Mitrovica JX, Bennett RA, Jonsson B, Elgered G, Elósegui P, Koivula H, Poutanen M, Rönnäng BO, Shapiro II (2002) Continuous GPS measurements of postglacial adjustment in Fennoscandia 1. Geodetic results. J Geophys Res Solid Earth 107(B8):ETG 3-1–ETG 3-27
Johnson HO, Agnew DC (1995) Monument motion and measurements of crustal velocities. Geophys Res Lett 22(21):2905–2908. https://doi.org/10.1029/95GL02661
Khelifa S, Kahlouche S, Belbachir MF (2012) Signal and noise separation in time series of DORIS station coordinates using wavelet and singular spectrum analysis. C R Geosci 344:334–348. https://doi.org/10.1016/j.crte.2012.05.003
King M, Bevis M, Wilson T, Johns B, Blume F (2012) Monument-antenna effects on GPS coordinate time series with application to vertical rates in Antarctica. J Geod 86(1):53–63. https://doi.org/10.1007/s00190-011-0491-x
Klos A, Bogusz J (2017) An evaluation of velocity estimates with a correlated noise: case study of IGS ITRF2014 European stations. Acta Geodyn Geomater 14(3):255–265. https://doi.org/10.13168/AGG.2017.0009
Klos A, Bogusz J, Figurski M, Gruszczynska M, Gruszczynski M (2015) Investigation of noises in the EPN weekly time series. Acta Geodyn Geomater 2(178):117–126. https://doi.org/10.13168/AGG.2015.0010
Klos A, Bogusz J, Figurski M, Kosek W (2016) Noise analysis of continuous GPS time series of selected EPN stations to investigate variations in stability of monument types. In: Proceedings of the VIII Hotine Marussi symposium, Springer IAG symposium series, vol 142, pp 19–26. https://doi.org/10.1007/1345_2015_62
Kreemer C, Blewitt G, Klein EC (2014) A geodetic plate motion and Global Strain Rate Model. Geochem Geophys 15:3849–3889. https://doi.org/10.1002/2014GC005407
Langbein J (2012) Estimating rate uncertainty with maximum likelihood: differences between power-law and flicker-random-walk models. J Geod 86(9):775–783. https://doi.org/10.1007/s00190-012-0556-5
Langbein J, Johnson H (1997) Correlated errors in geodetic time series: implications for time-dependent deformation. J Geophys Res 102(B1):591–603
Larson KM, Freymueller JT, Philipsen S (1997) Global plate velocities from the Global Positioning system. J Geophys Res 102(B5):9961–9981
Mandelbrot B, Van Ness J (1968) Fractional Brownian motions, fractional noises, and applications. SIAM Rev 10:422–439
Mao A, Harrison C, Dixon TH (1999) Noise in GPS coordinate time series. J Geophys Res 104(B2):2797–2816
Métivier L, Collilieux X, Lercier D, Altamimi Z, Beauducel F (2014) Global coseismic deformations, GNSS time series analysis, and earthquake scaling laws. J Geophys Res Solid Earth 119:9095–9109. https://doi.org/10.1002/2014JB011280
Munekane H, Tobita M, Takashima K (2004) Groundwater-induced vertical movements observed in Tsukuba, Japan. Geophys Res Lett 31(12):L12608. https://doi.org/10.11029/12004GL020158
Penna NT, Stewart MP (2003) Aliased tidal signatures in continuous GPS height time series. Geophys Res Lett 30(23):2184. https://doi.org/10.1029/2003GL018828
Plag H-P, Pearlman M (eds) (2009) Global Geodetic Observing System. Meeting the requirements of a global society on a changing planet in 2020. 10.1007/978-3-642-02687-4
Ray J, Altamimi Z, Collilieux X, van Dam T (2008) Anomalous harmonics in the spectra of GPS position estimates. GPS Solut 12(1):55–64. https://doi.org/10.1007/s10291-007-0067-7
Rebischung P, Altamimi Z, Ray J, Garayt B (2016) The IGS contribution to ITRF2014. J Geod 90(7):611–630. https://doi.org/10.1007/s00190-016-0897-6
Riddell AR, King MA, Watson CS, Sun Y, Riva REM, Rietbroek R (2017) Uncertainty in geocenter estimates in the context of ITRF2014. J Geophys Res Solid Earth 122(5):2016JB013698. https://doi.org/10.1002/2016JB013698
Romagnoli C, Zerbini S, Lago L, Richter B, Simon D, Domenichini F, Elmi C, Ghirotti M (2003) Influence of soil consolidation and thermal expansion effects on height and gravity variations. J Geodyn 35(4–5):521–539. https://doi.org/10.1016/S0264-3707(03)00012-7
Santamaria-Gomez A, Bouin MN, Collilieux X, Woppelmann G (2011) Correlated errors in GPS position time series: implications for velocity estimates. J Geophys Res 116(B1):B01405. https://doi.org/10.1029/2010JB007701
Shih DCF, Wu YM, Lin GF, Hu JC, Chen YG, Chang CH (2008) Assessment of long-term variation in displacement for a GPS site adjacent to a transition zone between collision and subduction. Stoch Environ Res Risk Assess 22(3):401–410. https://doi.org/10.1007/s00477-007-0128-z
Sidorov D (2016) Receiver antenna and empirical multipath correction models for GNSS solutions. Ph.D., University of Luxembourg
Teferle FN, Williams SDP, Kierulf KP, Bingley RM, Plag HP (2008) A continuous GPS coordinate time series analysis strategy for high-accuracy vertical land movements. Phys Chem Earth 33(3–4):205–216. https://doi.org/10.1016/j.pce.2006.11.002
Tregoning P, van Dam T (2005) Atmospheric pressure loading corrections applied to GPS data at the observation level. Geophys Res Lett 32(22):L22310. https://doi.org/10.1029/2005GL024104
van Dam T, Wahr J, Milly PCD, Shmakin AB, Blewitt G, Lavallée D, Larson KM (2001) Crustal displacements due to continental water loading. Geophys Res Lett 28(4):651–654
van Dam T, Collilieux X, Wuite J, Altamimi Z, Ray J (2012) Nontidal ocean loading: amplitudes and potential effects in GPS height time series. J Geod 86(11):1043–1057. https://doi.org/10.1007/s00190-012-0564-5
Wahr J, Khan SA, van Dam T, Liu L, van Angelen JH, van den Broeke MR, Meertens CM (2013) The use of GPS horizontals for loading studies, with applications to northern California and southeast Greenland. J Geophys Res Solid Earth 118(4):1795–1806. https://doi.org/10.1002/jgrb.50104
Wdowinski S, Bock Y, Baer G, Prawirodirdjo L, Bechor N, Naaman S, Knafo R, Forrai Y, Melzer Y (2004) GPS measurements of current crustal movements along the Dead Sea Fault. J Geophys Res 109(B05403):1–16. https://doi.org/10.1029/2003JB002640
Wessel P, Smith WHF, Scharroo R, Luis J, Wobbe F (2013) Generic mapping tools: improved version released. Eos Trans Am Geophys Union 94(45):409–410. https://doi.org/10.1002/2013EO450001
Williams SDP (2003) Offsets in Global Positioning System time series. J Geophys Res 108(B6):2310. https://doi.org/10.1029/2002JB002156
Williams SDP, Willis P (2006) Error analysis of weekly station coordinates in the DORIS network. J Geod 80:525–539. https://doi.org/10.1007/s00190-006-0056-6
Williams SDP, Bock Y, Fang P, Jamason P, Nikolaidis RM, Prawirodirdjo L, Miller M, Johnson D (2004) Error analysis of continuous GPS position time series. J Geophys Res 109(B3):B03412. https://doi.org/10.1029/2003jb002741
Xu XQ, Dong D, Fang M, Zhou Y, Wei N, Zhou F (2017) Contributions of thermoelastic deformation to seasonal variations in GPS station position. GPS Solut. https://doi.org/10.1007/s10291-017-0609-6
Zhang J, Bock Y, Johnson H, Fang P, Williams S, Genrich J, Wdowinski S, Behr J (1997) Southern California permanent GPS geodetic array: error analysis of daily position estimates and site velocities. J Geophys Res 102(B8):18035–18055
Acknowledgements
The maps were prepared with GMT software (Wessel et al. 2013). Anna Klos and Janusz Bogusz are supported by the Faculty of Civil Engineering and Geodesy of the MUT statutory research funds. Addisu Hunegnaw is financed by the University of Luxembourg projects GSCG & SGSL.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Klos, A., Olivares, G., Teferle, F.N. et al. On the combined effect of periodic signals and colored noise on velocity uncertainties. GPS Solut 22, 1 (2018). https://doi.org/10.1007/s10291-017-0674-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10291-017-0674-x