Introduction

Scientists who study the solid earth are increasingly using the GPS system. It offers a wide range of applications that allow the determination of not only long-term changes, like tectonic or glacial isostatic adjustment studies with daily or weekly solutions, but also to investigate either long-term geophysical signals or sub-daily changes, including seismic and volcanic deformations, or ice sheet flow. When creating a subsequent kinematic reference frame, the most important issue is to ensure its optimum definition and stability or reliability as a function of time. While the origin and scale of reference frames with their physical characteristics are the main parameters used for numerous applications related to the earth sciences, the knowledge on earth’s orientation and its changes over time is necessary to ensure the continuity of the observation of earth rotation. Any, even a small change in the aforementioned is transferred to all geophysical results based on the International Terrestrial Reference Frame (ITRF), for example the average sea level.

For all those tasks mentioned, the proper determination of velocity of a permanent station and its uncertainties is essential. Therefore, the knowledge of seasonal changes is also crucial. Among all the oscillations with a period close to 1 year, these should be distinguished: a tropical year (365.2421 days), i.e., time within when the earth returns to the same position with respect to the sun, and a draconitic year (~351 days), i.e., time within when the constellation of GPS satellites return to the same position with respect to the sun.

The first periodic variations with a period of tropical year may reflect a common physical basis, such as seasonal mass redistribution (van Dam et al. 1994; Blewitt and Lavallée 2002; Wu et al. 2006), or mismodelling in short periods (Dong et al. 2002, Penna and Stewart 2003). However, all these seasonal variations can be modelled by the set of the harmonic functions as shown in Amiri-Simkooei et al. (2007). Moreover, they showed that the more the harmonic components of seasonal oscillation assumed to be present in GPS time series, the closer the stochastic part is to white noise. Bos et al. (2010) noticed that under equal noise conditions, the worst accuracy of linear velocity was obtained from the time series biased with seasonal signals. They also stated that omitting noise properties causes significant variations in the parameters estimated from the GPS data.

The second periodic variation with frequency of a draconitic year is an effect of a systematic, technique-related error associated with satellite orbits. It has already been discovered in GPS time series by several researchers. Agnew and Larsson (2007) used broadcast ephemerides of all GPS satellites operating between 1996 and 2006 to find orbital repeat times. They stated that for daily sampling rates, this period will alias to a frequency of 1.04333 cpy. Ray et al. (2008) examined spectra of more than 160 IGS permanent stations. Having the length of them equal to 200 weeks, they analyzed the 6th harmonics. They calculated 1.040 ± 0.008 cpy (351.2 year) frequency with a linear overtone assumed and called it the “GPS year.” They found no confirmation of such harmonics either in VLBI or SLR, or in geophysical fluids. Collilieux et al. (2007) investigated height residual time series of VLBI, SLR and GPS submitted to the ITRF2005. Apart from significant power near 1 and 2 cpy, they also found 3.12 and 4.16 cpy, being detectable in the individual time series. Santamaría-Gómez et al. (2011) analyzed time series from a homogeneously reprocessed solution of 275 globally distributed stations in terms of noise content and velocity uncertainty assessment. Before velocity estimation, they subtracted annual and semi-annual signals from the data of a minimum length of 2.5 years. They verified the presence of the residual periodicities by the nonlinear iterative least squares (LS) method and found substantial amplitudes in the periods from 1st to 4th harmonics, while very little significance from the 5th harmonic onward. Amiri-Simkooei (2013) analyzed JPL data processed at the GPS Analysis Center to obtain a significant signal with a period of 351.6 ± 0.2 days and its higher harmonics in North, East and Up time series. He used the least squares harmonic estimation (LS-HE) for detecting and including a set of harmonic functions for the periodicities in the considered time series. He obtained the variation range of this periodic pattern of about 3.0, 3.2 and 6.5 mm amplitude for all three components, respectively, and found the white and flicker noise to be prevailing in the position time series with a relatively small contribution of random walk noise. Griffiths and Ray (2013) discovered harmonic signals (draconitic and overtones up to at least sixth) in the power spectra of nearly all IGS products by reconsidering how errors in the conventional model fit into GPS orbit and EOP (Earth Orientation Parameters) products. They suggested two main driving mechanisms: bias due to mismodelling of orbit dynamics and local multipath effects. Rodriguez-Solano et al. (2012) investigated global network (CODE solutions) and explained the 6th overtone of the draconitic year in GPS station positions estimates (at the mm level) by the earth radiation pressure, arising from wrong modelling over large regions.

Using GPS in combination with some other techniques, one can successfully isolate the cause of the polar motion wobble. Gross et al. (2004) using GPS data collected between 1997 and 2000 predicted how the position of the North Pole would vary given changes in earth’s mass distribution and then compared the predicted wobble to the direct observations of the axis made during the same period by satellites and very long baseline interferometry. Kouba (2005) used polar motion combined series produced by the International GPS Service (IGS) using only GPS data and compared with the combined excitations of atmosphere and oceans at all intervals, showing high overall correlation of 0.8–0.9. The effect of mismodelling of the Chandler period and its overtones can be observed in GPS-derived coordinates. Collilieux et al. (2007) found a wide range of frequencies detected between 0.75 and 0.9 cpy in GPS, VLBI and SLR height residuals from ITRF2005 solution. We would expect a signal at the Chandler period to be present at some stations, where the change in sea surface heights loads the crust, causing a loading signal at the Chandler period that would be largest at island and coastal sites (Richard Gross, personal communication). The oceanic pole tide is the response of the oceans to the wobble of the underlying solid earth. This also introduces a small signal at the Chandler period in sea surface height measurements (Desai 2005).

Time series

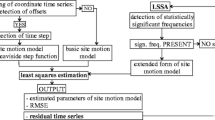
We used here the position time series obtained at the Jet Propulsion Laboratory (JPL) using the GIPSY-OASIS software in a Precise Point Positioning (PPP) mode, available at the ftp://sideshow.jpl.nasa.gov/. The details concerning processing of GNSS observations can be found at https://gipsy-oasis.jpl.nasa.gov. At the pre-analysis stage, the outliers and offsets were detected using median absolute deviation (MAD) criterion and sequential t test analysis of regime shifts (STARS) algorithm (Rodionov and Overland 2005). Detecting discontinuities with STARS is divided into two steps: In the first one, it is checked whether the distance of each point from the local mean is significant according to a t test. In second one, the jump candidates are accepted using inequality with some empirical parameters. A more detailed description about implementing STARS in geodetic time series can be found in Bruni et al. (2014). Although this is self-acting procedure, we used it only for indicating possible steps, after that we removed them manually as recommended in Gazeaux et al. (2013) or described in Williams (2003a). The missing data (gaps no longer than 40 days) were filled with a white noise. Even though adding white noise will weaken the real signals, such an interpolation was done, because maximum-likelihood estimation (MLE) gives more realistic results when performed on continuous data (Bos et al. 2008).

To separate the tropical and draconitic curves of 365.2 and 351.6 days with spectral analysis, one will need at least 25.5 years of continuous data. This length comes from the Rayleigh criterion—minimum length of series required to resolve two constituents (Godin 1972). The sinusoidal model of the least squares estimation which determines all periodicities simultaneously will allow us to determine the amplitudes and phases of both the tropical and the draconitic years and its harmonics for data shorter than 25.5 years, being completely sure of their presence in the data (Tom Herring, personal communication). However, we introduced here a threshold of 12.8 years in the length of the data in order to be sure that the 2nd tropical and draconitic harmonics were resolved in spectral estimation, which resulted in the number of globally distributed stations limited to 180 out of the whole IGS network (Fig. 1). The longest series contained 22.1 years of GPS daily solutions.

Fig. 1
figure 1

The 180 IGS stations analyzed. Different colors dots indicate various lengths of the time series in years

Full size image

It is widely acknowledged that any periodic signal consists of the principal frequency as well as its higher harmonics. Due to this, we assumed that the IGS time series contains both the deterministic part by means of functional model that includes trend and seasonality as well as background noise (stochastic part). Additionally, we incorporated oscillations of 13.66 days corresponding to Mf body tide (Melchior 1983), 14.6 days reported in Amiri-Simkooei (2013), 14.19 and 14.76 days which are the GPS aliasing periods pointed out in Griffiths and Ray (2013), into our functional model. The final form of the equation describing the time series is:

$$\begin{aligned} x(t)& = x_{0} + v_{x} \cdot t + A^{13.66} \cdot \sin (\omega^{13.66} \cdot t + \phi^{13.66} ) + A^{14.6} \cdot \sin (\omega^{14.6} \cdot t + \phi^{14.6} ) \\ &\quad + A^{14.19} \cdot \sin (\omega^{14.19} \cdot t + \phi^{14.19} ) + A^{14.76} \cdot \sin (\omega^{14.76} \cdot t + \phi^{14.76} ) \\& \quad + \sum\limits_{i = 1}^{9} {\left[ {A_{i}^{\text{CH}} \cdot \sin \left( {\omega_{i}^{\text{CH}} \cdot t + \phi_{i}^{\text{CH}} } \right)} \right]} + \sum\limits_{i = 1}^{9} {\left[ {A_{i}^{T} \cdot \sin \left( {\omega_{i}^{\text{T}} \cdot t + \phi_{i}^{\text{T}} } \right)} \right]} \\& \quad + \sum\limits_{i = 1}^{9} {\left[ {A_{i}^{\text{D}} \cdot \sin \left( {\omega_{i}^{\text{D}} \cdot t + \phi_{i}^{\text{D}} } \right)} \right]} + \varepsilon_{x} (t) \\ \end{aligned}$$
(1)

where the superscripts CH, T and D denote Chandler, tropical and draconitic oscillations, respectively. At the next stage of the analysis, this equation is linearized by introducing in-phase (AS) and out-of-phase (AC) terms, providing LS-based estimation of the unknowns:

$$\begin{aligned} A \cdot \sin \left( {\omega \cdot t + \varphi } \right) & = A \cdot \cos \varphi \cdot \sin \left( {\omega \cdot t} \right) + A \cdot \sin \varphi \cdot \cos \left( {\omega \cdot t} \right) \\ & = {\text{AS}} \cdot \sin \left( {\omega \cdot t} \right) + {\text{AC}} \cdot \cos \left( {\omega \cdot t} \right) \\ \end{aligned}$$
(2)

where AS = A · cos φ and AC = A · sin φ. In this research, we quantified overtones of basic oscillation up to 9th, which will be proven to be significant in the next chapter. We assumed that the Chandler period is equal to 433.0 days and the draconitic period is equal to 351.6 days following Amiri-Simkooei (2013).

The deterministic part (trend plus seasonal signals) was modelled with the weighted least squares method:

$${\mathbf{y}} = \left[ {{\mathbf{A}}^{{\mathbf{T}}} {\mathbf{C}}_{{\mathbf{x}}}^{{ - {\mathbf{1}}}} {\mathbf{A}}} \right]^{{ - {\mathbf{1}}}} {\mathbf{A}}^{{\mathbf{T}}} {\mathbf{C}}_{{\mathbf{x}}}^{{ - {\mathbf{1}}}} {\mathbf{x}}$$
(3)

where y is the 70 × 1 vector of unknowns: interception, linear trend as well as in-phase and out-of-phase seasonal terms combining residual Chandler oscillation, the tropical annual curve and terms with draconitic period up to their 9th harmonic with fortnightly and quasi-fortnightly oscillations, x is the n × 1 vector of observations (n—number of data in North, East or Up components), C x is the weight matrix, containing RMSs, and A is the n × 70 matrix of coefficients. The covariance matrix is then defined as follows:

$${\mathbf{C}}_{{\mathbf{y}}} = \left[ {{\mathbf{A}}^{{\mathbf{T}}} {\mathbf{C}}_{{\mathbf{x}}}^{{ - {\mathbf{1}}}} {\mathbf{A}}} \right]^{{ - {\mathbf{1}}}}$$
(4)

and contains uncertainties of the unknowns.

Periodicities in IGS data

Periodic signals will naturally make the data appear to be autocorrelated in the same way that a linear trend would if it is not properly removed. Davis et al.’s (2012) research on seasonal signals in GNSS and GRACE basically attempts to prove that the flicker noise is simply the non-periodic part of the seasonal signal. While it is a reasonable argument, it would mean that the flicker noise would be visible in the spectrum for periods longer than 1 year, which it clearly is. They concluded that noise in the GNSS time series reported by others may be associated with neglecting the stochastic component of the seasonal signal. On the basis of that, the more the seasonal components is assumed in the deterministic model, the less the autocorrelated are the residuals. We propose here that the deterministic part includes all periodicities from 1st to 9th harmonics of residual Chandler, tropical and draconitic periods and compare it with commonly used calculations of the annual and semi-annual tropical curve. Figure 2 (top) presents the daily changes from KUNM station (Kunming, China) with deterministic model containing harmonics proposed here fitted with the weighted least squares approach. The residua are given in bottom panel. Figure 3 presents an exemplary Lomb–Scargle periodogram (Lomb 1976; Scargle 1982) of Up component from the KUNM (Kunming, China) permanent station. The KUNM series is 15 years long, which means that all oscillations starting from the 2nd harmonics of tropical and draconitic periods and higher ones can be reliably separated with spectral analysis. Here, the 2nd harmonics are equal to 4.0 and 4.1 mm for tropical and draconitic year. Significant peak is noticed for 3rd harmonic of draconitic year (3.12 cpy) with the amplitude of 2.7 mm.

Fig. 2
figure 2

Fifteen-year time series of Up component (black) given in (mm) from KUNM (Kunming, China). Top panel contains original time series along with the deterministic model (red) consisting of the best fitted straight line plus all considered sinusoids up to 9th harmonic. Bottom panel contains residuals of the deterministic model

Full size image
Fig. 3
figure 3

Lomb–Scargle periodogram in a log–log scale for Up component of station KUNM (Kunming, China). Vertical lines denote Chandlerian, tropical and draconitic harmonics. The horizontal axis was limited to include periods 1–10 cpy

Full size image

The dominant oscillations for the IGS stations were found in the stacked spectra (Fig. 4) for frequencies close to 1 cpy, though no conclusions are to be drawn about the complexity of the spectrum. An evident comb of 2 cpy (2nd tropical and draconitic harmonics) was noticed with the predominating tropical oscillation. Although the tropical year prevails in the 1st and 2nd harmonics, the draconitic oscillations overweigh others for 3rd, 4th and up to the 10th. Then, again prominent peaks were noticed in draconitics around 3–7 cpy, or as it is for North component, where the 9th draconitic harmonic is still significant (9.35 cpy, 3.1 mm). In addition, the following is noteworthy: extremely high peaks for 6th harmonic of draconitic oscillation for North (6.26 cpy, 1.6 mm), 7th draconitic for East (7.27 cpy, 1.7 mm), whereas tropical oscillations can be noticed only for first three harmonics (up to 3 cpy). In the Up component, no prominent oscillations were found for periods lower than 5 cpy. The stacked spectra reveal nothing about Chandlerian oscillations, though they are seen up to 9th harmonics (7.59 cpy) with the amplitude of up to 1 mm for several of IGS stations.

Fig. 4
figure 4

Stacked spectra averaged with 0.05 cpy window in a log–log scale of North, East and Up components from 180 globally distributed IGS stations (top). The vertical lines denote Chandlerian, tropical and draconitic harmonics. The PSD’s of Up and East were artificially shifted in a vertical direction for better interpretation purposes. On bottom the stacked spectra of Up component are given from 3 to 10 cpy with 95 % significance level in a linear scale, for which significant peaks are easy to notice

Full size image

The largest tropical amplitude (determined using LSE) is 8.5 ± 0.3 at station KUNM (Kunming, China) in Up component (1st harmonic), while the largest draconitic amplitude is 2.8 ± 0.2 at station FAIR (Fairbanks, USA) in Up component (1st harmonic). As expected, all stations with the highest Chandlerian amplitudes (1st harmonic) are located at the Pacific coasts. They are HOLP (Hollydale, USA—1.3 ± 0.1 mm amplitude in Up direction) and UCLU (Ucluelet, Canada—1.1 ± 0.1 mm amplitude in Up). However, these numbers are greater than expected from the ocean pole tide loading model by a factor of about 3 (Shailen Desai, personal communication). Details concerning magnitudes of oscillations and their overtones are presented in Fig. 5.

Fig. 5
figure 5

Amplitudes of tropical, draconitic and Chandlerian residual oscillations in Up component for IGS stations determined using LSE (mm). Tropical amplitudes are presented in blue, draconitic in red and Chandlerian in green

Full size image

The largest oscillations were observed in the periods corresponding to 1 tropical year, but their presence due to mismodelling in the short periods (Penna et al. 2007; King et al. 2008; Bogusz and Figurski 2012) is what has to be kept in mind. Moreover, Tregoning and Watson (2009) remarked that omitting diurnal and semi-diurnal atmospheric tidal effects can introduce an artificial signal close to the draconitic period and its first harmonics. In the data analyzed, neither tidal nor non-tidal atmospheric models were introduced. Moreover, there are some influences such as multipath which are not able to be modelled in the GNSS data processing and therefore induce a systematic error in the position estimate that appears as correlated noise in the time series (King and Watson 2010).

Noise analysis

In this section, we address the issues of whether all residual periodicities, as proposed here, need to be taken into consideration when performing noise analysis. All non-modelled geophysical processes or non-included artificial effects in time series lead to an underestimation of errors of velocities, and also to changes in the velocity values themselves. On the other hand, an improper removal of seasonals may result in autocorrelation of residuals. We also must face the fact that there are still some correlations despite subtraction of seasonals, the possible explanation of which was given by Agnew and Larsson (2007). They found another important property of GPS system: The time when satellites return to their initial position varies among the satellites of GPS constellation due to singular changes in the mean motion. This in turn means that the draconitic effect in the time series could not be exactly harmonic (Santamaría-Gómez et al. 2011). Other effects related to mismodelling are associated with the Chandler wobble, whose amplitude varies highly in time and its approximation with sine may leave some residual oscillations.

In this study, we subtracted all periodicities for Chandlerian, tropical and draconitic oscillations starting from 1st to 9th harmonic to avoid autocorrelation in the data. These were modelled with the least squares estimation in station-by-station procedure, as described in the previous section. Despite finding the effects of harmonics of a higher order to be insignificant for several stations, we decided to model all of them. We expect this approach to be completely free of any, real or spurious, periods of interest.

The time series of geophysical processes follow the power-law noise character (Agnew 1992; Davis et al. 1994; Langbein and Johnson 1997; Mao et al. 1999; Vasseur and Yodzis 2004). Williams (2003b) investigated power-law dependencies in geodetic time series. He examined the effect of colored noise with non-integer spectral indices (κ) and provided equations for rate uncertainties while taking into consideration the noise amplitude (A PL), sampling frequency and length of time series. Williams et al. (2004) analyzed time series from 414 permanent stations in nine different solutions for noise content using MLE. The analysis was performed with two noise models. In the first approach, they calculated white noise (WN) only, a combination of WN plus flicker noise (FN), or WN plus random walk (RW). The second approach contained a combination of WN plus power-law (PL). They found that WN + FN is clearly the dominant one, and the maximum log-likelihood values confirmed it to be preferential. Amiri-Simkooei (2009) analyzed GPS position time series by using the least squares variance component estimation (LS-VCE), which gives, in contrast to MLE, unbiased and minimum variance estimators.

In this study, we used the Hector software to undertake the research on time series. All coordinate components were analyzed with pre-assumed power-law plus white noise model, aimed at determining the velocities and their formal errors. Hector uses reformulated MLE with missing data in the observations and maximizes the logarithm of the likelihood function (Bos et al. 2012):

$$\ln \left[ {p\left( {\mathbf{r}} \right)} \right] = - \frac{1}{2}\left[ {\left( {n - m} \right)\ln 2\pi + \ln \det \left( {{\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{C} }}} \right) + {\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{r} }}^{T} {\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{C} }}^{ - 1} {\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{r} }}} \right]$$
(5)

where n is the total number of continuous data, m is the number of missing data, \({\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{C} }}\) is the newly formed covariance matrix of (n − m) × (n − m) size, and \({\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{r} }}\) are the residuals.

The parameters that describe different noise models (as, e.g., Equation (6) discussed in Langbein 2004), and thus far the covariance matrix \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{C}\) are being changed as far as the greatest value of (5) is found (Bos et al. 2012). In this way, the optimum noise model for the analyzed data is being estimated.

The median percentage of gaps in our time series equalled 0.8 %, with a maximum of 12.8 %. There were 84 continuous time series out of 180. Concerning the spectral indices of residuals estimated after substraction of the deterministic part with the method proposed here, it was not noticed that the spectral index of Up component was “less white” than North and East components (Fig. 6). The spectral indices ranged from –0.12 (Up component of BAKO (Cibinong, Indonesia), 20 years of observations) to –0.92 (North component of MATE (Matera, Italy), 22.1 years of observations). We obtained median values of “global” spectral indices equal to: –0.41 ± 0.15, –0.38 ± 0.12 and –0.33 ± 0.18 for North, East and Up components, respectively. The shift of spectral indices toward flicker noise, κ = –1, is probably due to the large-scale processes of atmospheric or hydrospheric origin with spatial correlation to some extent.

Fig. 6
figure 6

Histograms of spectral indices of topocentric components

Full size image

The thus far commonly used approach of GPS seasonal modelling as the sum of annual and semi-annual tropical curves was adopted here as the reference solution. As was expected, the power-law amplitudes decrease when all periodicities are subtracted from the time series of topocentric components. Moreover, the spectral indices are much “whiter” in comparison with the reference solution (Fig. 7). The largest shift toward white noise was noticed for horizontal components, whereas noise character changed for Up only for about 25 % of considered IGS stations.

Fig. 7
figure 7

Histogram of differences in spectral indices between the reference solution and the one proposed here. The negative values mean that residua shifted toward white noise when the proposed subtraction of the seasonal changes was used

Full size image

The power-law noise amplitude decreased between both solutions of 0.7 mm/year−κ/4 (Fig. 8). The combination of seasonals proposed here resulted in a decrease in noise amplitudes for the vast majority of IGS stations in East and Up. The North component showed odd results on noise amplitudes that were higher after looking at the seasonals in a more complex way. However, the significance of these changes is questionable, since the averaged uncertainty of power-law amplitude in North and East direction is equal to about ± 0.1, while in Up it is ± 0.3 mm/year−κ/4.

Fig. 8
figure 8

Histogram of differences in power-law noise amplitudes [mm/year−κ/4] between the described and reference approaches. The positive values mean that series residua have a smaller power-law noise amplitude for the proposed approach

Full size image

The Akaike information criterion (AIC) was used here for a qualitative description of our results. The preferred model, i.e., the one that minimizes the Kullback–Leibler distance between the model and the truth, is the one with the minimum AIC value. The AIC values were estimated for both seasonal approaches. The proposed assumption of seasonals caused the AIC values to show a decrease in the median value of 30 % (Fig. 9), which in fact means that all the seasonals mentioned here have to be taken into account when analyzing noises.

Fig. 9
figure 9

Comparison of how the proposed solution fits the data based on the AIC values, shown as percentage of improvement. No negative values/worsening have been noticed

Full size image

In order to characterize the geodetically important properties of these two solutions, comparing the reference with the one proposed here, we implemented two types of differences in velocity values determined with linear regression and in the accuracy of the velocity estimated with (Bos et al. 2008):

$$m_{v} \approx \pm \sqrt {\frac{{A_{\text{PL}}^{2} }}{{\Delta T^{{2 - \frac{\kappa }{2}}} }} \cdot \frac{{\varGamma \left( {3 - \kappa } \right) \cdot \varGamma \left( {4 - \kappa } \right) \cdot \left( {N - 1} \right)^{\kappa - 3} }}{{\left[ {\varGamma \left( {2 - \frac{\kappa }{2}} \right)} \right]^{2} }}}$$
(6)

where N is the data length, κ means the estimated spectral index, ΔT is the sampling rate, A PL represents the amplitude of noise, and Γ is the gamma function.

The velocities of permanent stations showed a change in values for several of IGS stations when comparing the reference solution with the one proposed. It seems that even the removal of seasonals with a few millimeters of amplitude results in a change in the velocity value (Bogusz and Figurski 2014) of even 0.20 mm/year. The majority of changes in velocity values were equal to 0.05 mm/year for the Up component, while the vast majority of velocities remained almost unchanged for North and East (Fig. 10).

Fig. 10
figure 10

Histogram of differences in velocity values in (mm/year) of reference solution that removes the annual and semi-annual tropical periods with the one proposed in this research

Full size image

Finally, when it comes to the velocity uncertainty, the differences in their values were calculated according to (6) for 180 of analyzed stations. It was noticed that for the majority of stations, the velocity uncertainty decreased after removal of seasonals as proposed here from −0.03 to 0.10 mm/year in the most extreme cases. With such long time series, the velocity uncertainties are small, even taking the color noise into consideration, so it is better to use the percentages of those changes. From Fig. 11, we noticed that there are some of the GPS stations that improved their velocity RMS even up to 56 %.

Fig. 11
figure 11

Histogram of differences in the velocity uncertainties estimates (%). The positive values mean a decrease in velocity uncertainties after the proposed method

Full size image

Summary and conclusions

Linear regression is the most common method used today in geophysics to study, e.g., plate tectonic motion. Therefore, the proper interpretation of velocities of permanent GNSS stations in terms of geodynamics requires taking account of the correct deterministic model and the numerous studies on the stochastic character part. It is well known that there is an equivalence between functional and stochastic models (Blewitt 1998) and therefore any unmodelled functional part will show up in the stochastic model and vice versa (Klos et al. 2014b). The removal of all known periodicities causes a significant shift of spectral index toward white noise. Each of the non-subtracted periodicities will naturally cause data to be autocorrelated. Simulations we made prior to this research prove that changing the assumption concerning seasonals from the tropical annual and semi-annual year into Chandler plus tropical annual and its three harmonics, causes a decrease in median spectral indices estimated for IGS stations, processed in network solution mode, from −0.7 up to −0.3 along with a decrease in median amplitude of the power-law noise of even 2 mm/year−κ/4. The assumption of seasonals as a combination of the Chandlerian, tropical and draconitic year with their harmonics up to 9th, as proposed here, resulted in 100 % of stations to fall into the fractional Gaussian motion (0 < κ < –1) area. The maximum and median values of spectral indices and power-law noise amplitudes were contrasted in Table 1. The medians of spectral indices of power-law noises are, respectively, at the level of −0.41, −0.37 and −0.33 for North, East and Up with the median amplitudes of 1.75, 1.55 and 4.68 mm/year−κ/4. These results estimated for PPP GPS processing mode are closer to the white noise with spectral index equal to zero and have lower amplitudes than the ones estimated for network solutions (Williams et al. 2004; Teferle et al. 2008; Klos et al. 2014a).

Table 1 Minimum, maximum and median values of spectral indices and amplitudes of power-law noise obtained
Full size table

Moreover, in contrast to other researches (Teferle et al. 2008; Williams et al. 2004) it was not noticed that the vertical magnitudes are larger than the horizontal ones. The ratio of spectral indices in the vertical and horizontal direction was calculated as:

$$r = \frac{{\kappa_{\text{U}} }}{{\frac{1}{2}\left( {\kappa_{\text{N}} + \kappa_{\text{E}} } \right)}}$$
(7)

with κ N , κ E and κ U being spectral indices of North, East and Up, respectively. The results show that a minimum ratio of r = 0.30, a maximum ratio of r = 2.11 and a median of r = 0.92. Of analyzed stations, 56.1 % had a ratio of r < 1, which means that the spectral indices for Up are closer to zero and so closer to white noise at the same time than for North and East components.

The AIC criterion was estimated here for two seasonal approaches. The reference solution being the sum of tropical annual and semi-annual periods showed worse AIC characteristic than the new approach proposed here being the sum of Chandlerian, tropical and draconitic curves up to their 9th harmonics. These three conclusions show the correctness of our approach.

The source of noises in GPS-derived time series may be a combination of global, regional and local site-dependent effects. The regional effects named common-mode errors that influence the whole network of stations may be removed from the data with a range of spatiotemporal filtering methods. This problem has already been raised by several authors (Williams et al. 2004; Amiri-Simkooei 2013; Bogusz et al. 2015). This kind of filtering that takes into account other noise sources than mis- or unmodelled seasonals would improve the noise results in a similar way as our approach did.