Carrier phase wind-up in GPS reflectometry

Abstract

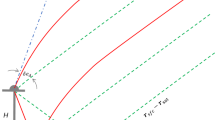
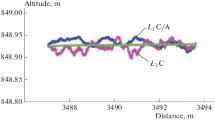
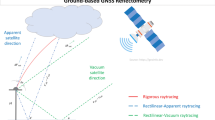
Changes in GPS transmitter and receiver antenna orientations induce variations in observed carrier phase values. An analytic formula for this well-known carrier phase wind-up correction is derived which generalizes a previous result. In addition, it is shown that in GPS reflectometry the wind-up values of direct and coherently reflected rays may differ by up to several centimeters. The results are discussed on the basis of simulated measurements.

Appendix

In the following we first show that the phase wind-up value derived from Eq. 10 is identical to the value derived using Eq. 14 provided that the transmitter and receiver antenna boresight vectors $\hat{t}^{b}$ and $\hat{r}^{b}$ lie in one plane. We then derive Eq. 8.

The unit wave vector $\hat{k}$ can then be written as a linear combination of $\hat{t}^{b}$ and $\hat{r}^{b}$

$$ \hat{k} = \alpha \hat{t}^{b} + \beta \hat{r}^{b} $$

(26)

where it is assumed that $\hat{t}^{b}$ and $\hat{r}^{b}$ are not collinear. We define nine parameters a, b, c, d, A, B, C, D and Δ by

$$ R \equiv \left( {\begin{array}{*{20}c} {\hat{t}^{a} \cdot \hat{r}^{a} } & {\hat{t}^{a} \cdot \hat{r}^{t} } & {\hat{t}^{a} \cdot \hat{r}^{b} } \\ {\hat{t}^{t} \cdot \hat{r}^{a} } & {\hat{t}^{t} \cdot \hat{r}^{t} } & {\hat{t}^{t} \cdot \hat{r}^{b} } \\ {\hat{t}^{b} \cdot \hat{r}^{a} } & {\hat{t}^{b} \cdot \hat{r}^{t} } & {\hat{t}^{b} \cdot \hat{r}^{b} } \\ \end{array} } \right) \equiv \left( {\begin{array}{*{20}c} a & c & A \\ b & d & B \\ C & D & \Updelta \\ \end{array} } \right) $$

(27)

noting that

$$ \begin{aligned} \Updelta & = \left( {\hat{t}^{a} \times \hat{t}^{t} } \right) \cdot \left( {\hat{r}^{a} \times \hat{r}^{t} } \right) \\ & = \left( {\hat{t}^{a} \cdot \hat{r}^{a} } \right)\left( {\hat{t}^{t} \cdot \hat{r}^{t} } \right) - \left( {\hat{t}^{t} \cdot \hat{r}^{a} } \right)\left( {\hat{t}^{a} \cdot \hat{r}^{t} } \right) \\ & = ad - bc. \\ \end{aligned} $$

(28)

Since the vectors $\left[ {\hat{t}^{a} ,\hat{t}^{t} ,\hat{t}^{b} } \right]$ and $\left[ {\hat{r}^{a} ,\hat{r}^{t} ,\hat{r}^{b} } \right]$ can be regarded as bases of cartesian coordinate systems, the matrix R is orthonormal, i.e.,

$$ \begin{gathered} \sum\limits_{k = 1}^{3} {R_{ik} R_{jk} = \delta_{ij} } \\ \sum\limits_{k = 1}^{3} {R_{ki} R_{kj} = \delta_{ij} } \\ \end{gathered} $$

(29)

with the Kronecker delta defined by

$$ \delta_{ij} \equiv \left\{ {\begin{array}{*{20}c} 0 & : & {i \ne j} \\ 1 & : & {i = j} \\ \end{array} } \right. $$

(30)

For example, Eq. 29 translates into the following relations which will be used later

$$ cA + dB + D\Updelta = 0 $$

(31)

$$ a^{2} + b^{2} + C^{2} = 1 $$

(32)

$$ c^{2} + d^{2} + D^{2} = 1 $$

(33)

$$ a^{2} + c^{2} + A^{2} = 1 $$

(34)

$$ b^{2} + d^{2} + B^{2} = 1 $$

(35)

$$ C^{2} + D^{2} + \Updelta^{2} = 1 $$

(36)

From Eq. 26 and $\left| {\hat{k}} \right| = 1$ it follows that

$$ \alpha^{2} + \beta^{2} + 2\alpha \beta \Updelta = 1 $$

(37)

and Eqs. 32, 33 and 36 yield

$$ a^{2} + b^{2} + c^{2} + d^{2} = 1 + \Updelta^{2} $$

(38)

Equation 10 can now be re-written in terms of the parameters defined in Eq. 27,

$$ \begin{aligned} \vec{T}^{t} (\hat{k}) \cdot \hat{r}^{a} & = \left( {\left( {\hat{k} \times \hat{t}^{t} } \right) \times \hat{k}} \right) \cdot \hat{r}^{a} \\ & = \left( {\hat{t}^{t} - \hat{k}\left( {\hat{k} \cdot \hat{t}^{t} } \right)} \right) \cdot \hat{r}^{a} \\ & = b - \alpha \beta BC \\ \end{aligned} $$

(39)

Similarly, one obtains

$$ \begin{aligned} \vec{T}^{a} (\hat{k}) \cdot \hat{r}^{t} & = c - \alpha \beta AD \\ \vec{T}^{a} (\hat{k}) \cdot \hat{r}^{a} & = a - \alpha \beta AC \\ \vec{T}^{t} (\hat{k}) \cdot \hat{r}^{t} & = d - \alpha \beta BD \\ \end{aligned} $$

(40)

In the next step, the products AD, BC, AC and BD are expressed in terms of a, b, c and d. For example, by squaring Eq. 31, inserting Eqs. 35, 34 and 33 and using Eq. 38 one obtains

$$ \begin{aligned} AD & = \frac{1}{2c\Updelta }\left( {d^{2} (1 - b^{2} - d^{2} ) - c^{2} (1 - a^{2} - c^{2} ) - \Updelta^{2} (1 - c^{2} - d^{2} )} \right) \\ & = \frac{1}{2c\Updelta }\left( {d^{2} (a^{2} + c^{2} - \Updelta^{2} ) - c^{2} (b^{2} + d^{2} - \Updelta^{2} ) - \Updelta^{2} (1 - c^{2} - d^{2} )} \right) \\ & = \frac{1}{2c\Updelta }\left( {\Updelta (ad + bc) - \Updelta^{2} + 2c^{2} \Updelta^{2} )} \right) \\ & = b + c\Updelta \\ \end{aligned} $$

(41)

Similarly, for the remaining products one finds

$$ \begin{aligned} BC & = c + b\Updelta \\ AC & = - d + a\Updelta \\ BD & = - a + d\Updelta \\ \end{aligned} $$

(42)

and Eq. 10 becomes

$$ \Upphi = \arctan\!2(b + c,a - d). $$

The corresponding expressions for Eq. 15 are

$$ \begin{aligned} \vec{D} \cdot \vec{D}' & = a - d + \alpha \beta (BD - AC) + (\alpha - \beta )(a - d) \\ & = (a - d)(1 + \alpha - \beta - \alpha \beta (1 + \Updelta )) \\ \left| {\vec{D}} \right|^{2} & = \vec{D} \cdot \vec{D} = 2 - \alpha^{2} (C^{2} + D^{2} ) - 2\alpha \Updelta - 2\beta \\ & = (1 - \alpha \Updelta - \beta )^{2} \\ \left| {\vec{D}'} \right|^{2} & = \vec{D}' \cdot \vec{D}' = 2 - \beta^{2} (A^{2} + B^{2} ) + 2\beta \Updelta + 2\alpha \\ & = (1 + \alpha + \beta \Updelta )^{2} \\ \varsigma & = \frac{1}{2}(b + c)(1 + \alpha - \beta )^{2} \\ \end{aligned} $$

(43)

using Eqs. 26 and 37. Note that Eqs. 14 and 43 imply

$$ \left| {\vec{D}} \right| = 1 - \alpha \Updelta - \beta \ne 0\quad {\text{and}}\quad \left| {\vec{D}^{\prime}} \right| = 1 + \alpha + \beta \Updelta \ne 0. $$

(44)

Using Eqs. 43 and 37, $\tilde{\Upphi }$ is given by

$$ \begin{aligned} \tilde{\Upphi } & = \text{sgn} (\varsigma )\arccos \left( {\frac{(a - d)(1 + \alpha - \beta - \alpha \beta (1 + \Updelta ))}{(1 - \alpha \Updelta - \beta )(1 + \alpha + \beta \Updelta )}} \right) \\ & = \text{sgn} (b + c)\arccos \left( {\frac{a - d}{1 - \Updelta }} \right) \\ \end{aligned} $$

(45)

since

$$ (1 - \alpha \Updelta - \beta )(1 + \alpha + \beta \Updelta ) = (1 - \Updelta )(1 + \alpha - \beta - \alpha \beta (1 + \Updelta )) $$

(46)

In Eq. 45 sgn(ζ) has been replaced by sgn(b + c) which is only admissible for 1 + α − β ≠ 0. However, if 1 + α − β = 0 the rhs of Eq. 46 was identically zero (see Eq. 37) contradicting Eq. 44.

With $\arctan\!2(\sqrt {1 - x^{2} } ,x) = \arccos x,$ where −1≤ x ≤ +1, one finds for x ≡ (a − d)/(1 − Δ) that $\sqrt {1 - x^{2} } = \left| {b + c} \right|/(1 - \Updelta ).$ Thus,

$$ \begin{aligned} \tilde{\Upphi } & = \text{sgn} (b + c)\arccos \left( {\frac{a - d}{1 - \Updelta }} \right) \\ & = \text{sgn} (b + c)\arctan\!2\left( {\frac{|b + c|}{1 - \Updelta },\frac{a - d}{1 - \Updelta }} \right) \\ & = \arctan\!2(b + c,a - d) \\ & = \Upphi \\ \end{aligned} $$

(47)

concluding the proof that $\tilde{\Upphi } = \Upphi$ provided the transmitter and receiver antenna bore sight vectors $\hat{t}^{b}$ and $\hat{r}^{b}$ lie in one plane.

Equation 8 is derived in the following way: with sin Ω = (e ^iΩ − e ^−iΩ)/(2i) and cos Ω = (e ^iΩ + e ^−iΩ)/2 we find

$$ \begin{aligned} a\sin \Upomega + b\cos \Upomega & = \left( {\frac{a}{2i} + \frac{b}{2}} \right)e^{i\Upomega } + \left( { - \frac{a}{2i} + \frac{b}{2}} \right)e^{ - i\Upomega } \\ & = \frac{1}{2}\sqrt {a^{2} + b^{2} } e^{ - i\arctan\!2(a,b)} e^{i\Upomega } + \frac{1}{2}\sqrt {a^{2} + b^{2} } e^{i\arctan\!2(a,b)} e^{ - i\Upomega } \\ & = \sqrt {a^{2} + b^{2} } \cos (\Upomega - \arctan\!2(a,b)) \\ \end{aligned} $$

(48)