Abstract
A linearization technique for binary quadratic programs (BQPs) that comprise linear constraints is presented. The technique, called “inductive linearization”, extends concepts for BQPs with particular equation constraints, that have been referred to as “compact linearization” before, to the general case. Quadratic terms may occur in the objective function, in the set of constraints, or in both. For several relevant applications, the linear programming relaxations obtained from applying the technique are proven to be at least as strong as the one obtained with a well-known classical linearization. It is also shown how to obtain an inductive linearization automatically. This might be used, e.g., by general-purpose mixed-integer programming solvers.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In this paper, we present a linearization technique for binary quadratic programs (BQPs) that comprise linear and possibly also quadratic constraints. A general form of the problems addressed could be written as follows:

Here, \(x \in \{0,1\}^n\) are the binary variables whose index set is denoted with \(N :=\{ 1, \ldots , n\}\) in the sequel. The set of products P occurring in the BQP is established by the matrices \({Q_k \in \mathbb {R}^{n \times n}}\), \(k \in \{0, \ldots , m_Q\}\), in the objective function and the \(m_Q \in \mathbb {N}_0\) quadratic restrictions as follows:
Despite using the term “binary quadratic program”, the case where \(m_Q > 0\) and \(Q_0\) is all zero, i.e. the problem is rather a quadratically-constrained binary linear program, is explicitly permitted. Moreover, since \(x_i x_j = x_j x_i\) for \(i, j \in N\), \(i \ne j\), and \(x_i = x_i^2\) for all \(i \in N\), we may assume the matrices \(Q_k\), \(k \in \{0, \ldots , m_Q\}\), to be strictly upper triangular, and thus \(i < j\) for \({(i,j) \in P}\).
While quadratic constraints may or may not exist, the linear constraints \({Ax \le b}\) are in the center of the linearization technique proposed in this paper, and their presence is hence necessary to apply it. More precisely, we will require that each variable \(x_i\), \(i \in N\), that is a factor of a product in P (to be linearized with the technique proposed), arises in at least one linear constraint (with a non-zero coefficient). In a binary program, this can be assumed (or established) without of loss of generality (see also the appendix). Moreover, if this requirement is neither fulfilled in the original problem nor established for some factors, this does not affect a successful inductive linearization of all the products whose factors do fulfill the requirement.
The inductive linearization technique generalizes on a method by Liberti (2007) that exploits the special case of equations with right hand side and left hand side coefficients equal to one, and on its later revision (cf. Mallach 2018). In his original article, Liberti coined the name “compact linearization” because it typically adds fewer constraints to such problems than the “standard linearization” (to be addressed in Sect. 2). Moreover, a more compact linearization than the ones proposed by Frieze and Yadegar (1983) and Adams and Johnson (1994) can be obtained for the quadratic assignment problem, and one that is as compact as the one proposed by Billionnet and Elloumi (2001) for the quadratic semi-assignment problem.
The generalized approach now achieves constraint-side compactness for several differently structured BQPs as well. Some of these are addressed in Sect. 6. However, constraint-side compactness cannot be guaranteed for any kind of BQP with linear constraints. Moreover, depending on how the method is applied, it may also induce more than \(|P |\) linearization variables (although this can, in principle, always be circumvented as described in the appendix). For these reasons, and since other techniques have been called “compact linearization” in the literature as well (see e.g. Hansen and Meyer 2009), a different naming is indicated. In particular, “inductive linearization” appears to be a good fit, since – as we will see – the approach aims at “inducing” the products of the set P by multiplying original constraints with original variables. Not only in this fashion, it relates to the reformulation-linearization technique (RLT, cf. Adams and Sherali 1999), but has the appealing advantage that its generated constraints linearize implicitly.
The outline of this paper is as follows: In Sect. 2, we briefly review related techniques to linearize BQPs. The generalized inductive linearization technique is presented in Sect. 3, and it is shown in Sect. 4 how it can be applied automatically, e.g., as part of a general-purpose mixed-integer programming solver. In Sect. 5, it is thoroughly investigated under which circumstances the linear programming relaxation of the obtained formulation is provably strong. Prominent combinatorial optimization problems where previously proposed mixed-integer programming formulations now appear as particular inductive linearizations are highlighted in Sect. 6. Finally, a conclusion and outlook is given in Sect. 7.
2 Linearization methods for BQPs
As linearizations of quadratic and, more generally, polynomial programming problems, enable the application of well-studied mixed-integer linear programming techniques, they have been an active field of research since the 1960s.
The seminal idea to model binary conjunctions \(x_i \cdot x_j\) using additional (binary) variables \(y_{ij}\) and the two inequalities \(x_i + x_j - 2y_{ij} \ge 0\) and \(x_{i} + x_{j} - y_{ij} \le 1\) is attributed to Fortet (1959, 1960), and discussed in several succeeding books and papers, e.g. by Balas (1964), Zangwill (1965), Watters (1967), Hammer and Rudeanu (1968), and Glover and Woolsey (1973). Shortly thereafter, Glover and Woolsey (1974) found that an integrality requirement on \(y_{ij}\) becomes obsolete when replacing the first inequality by the pair \(y_{ij} - x_i \le 0\) and \(y_{ij} - x_j \le 0\). The resulting system of inequalities, usually written down as
and that also appears as a special case of the convex envelopes for general nonlinear programming problems as proposed by McCormick (1976), is until today regarded as “the standard linearization”, especially as it is always applicable. Moreover, Padberg (1989) proved the four inequalities to be facet-defining for the polytope associated to unconstrained binary quadratic optimization problems:
Since, nevertheless, the “standard linearization” often provides rather weak linear relaxations in practice while it considerably increases their size, refined techniques that exploit additional structure of a particular problem, smartly couple product variables, or construct linear over- or underestimators for certain expressions are of high demand. However, such refinements are often tailored to (the objective functions of) BQPs, i.e., consider only linear constraints or none at all. Examples are the posiform-based techniques by Hansen and Meyer (2009), the “Clique-Edge Linearization” by Gueye and Michelon (2009), as well as earlier ones by Oral and Kettani (1992a, 1992b). The “Extended Linear Formulation” by Furini and Traversi (2013) could be applied to arbitrary products but counteracts compactness compared to a “standard linearization” in general. Another exception is the well-known transformation between binary quadratic optimization and the maximum cut problem (cf. Hammer 1965; Barahona et al. 1989; De Simone 1990). It allows for a direct translation of a (possibly quadratic) constraint set, but it necessitates a sophisticated branch-and-cut implementation to be solved. More involved are as well the linearizations by Chaovalitwongse et al. (2004) and Sherali and Smith (2007), especially in the presence of quadratic constraints. There is also no emphasis on the possibly sparse set of truly appearing products P. The RLT can as well be applied to BQPs even if these involve quadratic constraints. However, in general, it rather counteracts compactness, and it is not a linearization technique as such but rather requires a linearization technique to be employed for its second step. As an exception, an implicit linearization takes place in the case of products of variables from a set \(N' \subseteq N\) if there are constraints that imply \(0 \le x_i \le 1\) for all \(i \in N'\) (cf. Adams and Sherali 1986). Even in this case, however, the set of products induced still need not have any relation to the set P. In contrast to that, the technique proposed in this paper can be interpreted as a usually incomplete or “sparse” first level application of the RLT’s reformulation phase that is tailored to induce only (a minimum cardinality superset of) the set of products P that is implicitly linearized employing as few constraints as possible.
3 Inductive linearization
Consider a given problem in the form denoted in the introduction, and with the associated set P of products. Let us assume w.l.o.g. that the linear constraints \(Ax \le b\) are given as equations and less-or-equal inequalities. Suppose further that we identify a working (sub-)set of these that we denote with \(K_E\) and \(K_I\), respectively. Let these constraints be
where \(I_k :=\{ i \in N \mid a_k^i \ne 0\}\) denotes the support index set of the respective constraint with index \(k \in K_E\) or \(k \in K_I\).
As already indicated in the introduction, we require w.l.o.g. a choice of \(K :=K_E \cup K_I\) such that there exist indices \(k, \ell \in K\) with \(i \in I_k\) and \(j \in I_\ell \) for all \((i,j) \in P\). If there are factors lacking such a constraint in the original problem formulation, in principle any equation or less-or-equal inequality may be employed that is valid for its feasible set. Alternatively, the corresponding products may be linearized by other means without affecting the validity of the inductive approach for all other products that fulfill the requirement. We thus assume from now on that P only contains products that do so.
As also mentioned already in the introduction, Liberti (2007) initially covered the case of equations \(K_E\) with \(b_k = 1\) and \(a_k^i = 1\) for all \(k \in K_E\) and \(i \in I_k\). A revised description of the technique tailored to this special case is described in Mallach (2018).
In the first step of the generalized approach, each equation \(k \in K_E\) is associated another index set \(M^{E}_k \subseteq N\) that is supposed to specify original variables used as multipliers. To each inequality \(k \in K_I\), two such index sets \(M^{+}_k, M^{-}_k \subseteq N\) are associated. The corresponding interpretation is as follows: If \(j \in M^{E}_k\) (\(j \in M^{+}_k\)) the equation \(k \in K_E\) (inequality \(k \in K_I\)) is multiplied by \(x_j\), and if \(j \in M^{-}_k\), the inequality \(k \in K_I\) is multiplied by \((1 - x_j)\).
This leads to the following subset of the first level RLT constraints:
Let \(M_k :=M^{E}_k\) if \(k \in K_E\), and \(M_k :=M^{+}_k \cup M^{-}_k\) if \(k \in K_I\). Then
is the index set of the products induced by (6)–(8).
If we now rewrite (6)–(8) by substituting for each \((i,j) \in Q\) the product \(x_i x_j\) by a continuous linearization variable that has explicit lower and upper bounds, i.e., \(0 \le y_{ij} \le 1\), we obtain the linearization constraints:
The constraints (6)–(8) are valid for the original problem and so are the constraints (9)–(11) whenever \(y_{ij} = x_i x_j\) holds for all \((i, j) \in Q\). We will show in the following that this is “automatically” the case for binary \(x_i\), \(x_j\) if three handy consistency conditions are satisfied. Since this facilitates the readability of the proofs considerably, let us assume for the moment that we have \(a_k \ge 0\) and \(b_k \ge 0\) for all \(k \in K\). As expounded in the appendix, the general case can be handled without loss of generality either by establishing these properties explicitly or by imposing the implications of the three consistency conditions in an adapted fashion.
As a consequence, if we choose the sets \(M_k\) consistently and such that Q is a superset of P, we obtain a linearization for our original problem. In fact, at the potential expense of losing some relaxation strength, it is always possible to have \(Q=P\) as described in the appendix. More generally, we will strive to obtain a set \(Q \supseteq P\) as small as possible without the respective modifications. As can be observed e.g. in Sect. 6, the ideal sets \(M_k\) for this goal can typically be determined by inspection if a structured problem is given. The general case of their derivation is covered in Sect. 4.
The three consistency conditions to be met when choosing the sets \(M_k\) are, for all \((i,j) \in Q\):
Condition 1
There is a \(k \in K\) such that \(i \in I_k\) and \(j \in M^{E}_k\) or \(j \in M^{+}_k\), respectively.
Condition 2
There is a \(k \in K\) such that \(j \in I_k\) and \(i \in M^{E}_k\) or \(i \in M^{+}_k\), respectively.
Condition 3
There is a \(k \in K\) such that \(i \in I_k\) and \(j \in M^{E}_k\) or \(j \in M^{-}_k\), respectively, or such that \(j \in I_k\) and \(i \in M^{E}_k\) or \(i \in M^{-}_k\), respectively.
For clarification before we proceed to the proof, three comments are in order. Firstly, of course the pairs contained in Q depend on the choice of the sets \(M_k\), and due to the consistency conditions, this also holds vice versa. Secondly, it is a valid choice to employ the same index k (if \(i,j\in I_k\)) for satisfying Conditions 1 and 2. Thirdly, if Condition 1or Condition 2 is established using an equation, then Condition 3 is implied (it only needs to be considered in the presence of inequalities in the set K).
Theorem 4
For any integer solution \(x \in \{0,1\}^n\), the linearization constraints (9)–(11) imply \(y_{ij} = x_i x_j\) for all \((i,j) \in Q\) if and only if Conditions 1–3 are satisfied.
Proof
Let \((i,j) \in Q\). By Condition 1, at least one of the two constraints


exists, any of which has \(y_{ij}\) on its left hand side. Since \(a_k^h > 0\) for all \(h \in I_k\) and \(y_{ij} \ge 0\), each of them establishes that \(y_{ij} = 0\) whenever \(x_j = 0\).
Similarly, by Condition 2, at least one of the two constraints


exists, any of which has \(y_{ij}\) on its left hand side. Since \(a_k^h > 0\) for all \(h \in I_k\) and \(y_{ij} \ge 0\), each of them establishes that \(y_{ij} = 0\) whenever \(x_i = 0\).
Let now \(x_i = x_j = 1\). By Condition 3, we either have at least one equation or at least one inequality of type (11) that relates \(y_{ij}\) to either \(x_i\) or \(x_j\).
Suppose first that (\(*_{{E}_j}\)) exists (the case with (\(*_{{E}_i}\)) is analogous) and that \(y_{ij} <1\) as otherwise there is nothing to show. We are then in the following situation:

At the same time, we also have \(\sum _{h \in I_k, h \ne i} a_k^h x_h = b_k - a_k^i\) with \(x_h \in \{0,1\}\) for each \(h \in I_k\). In other words, the left hand side of (\(*'_{{E}_j}\)) is larger by an amount of \(a_k^i (1 - y_{ij}) > 0\). This implies, however, that there must be some \(h \in I_k\), \(h \ne i\), such that \(y_{hj} > 0\) (or \(y_{jh} > 0\)) while \(x_h = 0\). But this is impossible since Conditions 1 and 2 are established for these variables as well.
Finally, we consider the case that Condition 3 is satisfied by the existence of at least one of the two following inequalities (with possibly different \(k \in K_I\)):


Since \(x_i = x_j = 1\), the right hand sides of both of these inequalities evaluate to zero. Looking at the left hand side of (\(*_{{I}_j-}\)), for any \(h \in I_k\) (including i) the terms \((x_h - y_{hj})\) respectively \((x_h - y_{jh})\) cannot be negative since \(y_{hj}\) (\(y_{jh}\)) must be equal to zero if \(x_h\) is (by the arguments above) and since the upper bounds assure \(y_{hj} \le 1\) (\(y_{jh} \le 1\)) if \(x_h\) is equal to one. Moreover, since the right hand side evaluates to zero and \(a_k^h > 0\) for all \(h \in I_k\), the terms cannot be positive as well. It follows that \(x_h = y_{hj}\) for all \(h \in I_k\) (including i) and thus \(y_{ij} = 1\) as desired. The arguments for inequality (\(*_{{I}_i-}\)) are once more analogous.
We have just shown the sufficiency of the constraints induced by satisfying Conditions 1–3. For necessity: Any \(y_{ij}\) inevitably needs to be related at least once to \(x_i\) and at least once to \(x_j\). Within a framework that constructs a linearization only by means of constraints of type (9)–(11), this is equivalent to satisfying Conditions 1 and 2. As has been shown, if these are satisfied using equations, Condition 3 is implied. Otherwise, i.e., if two inequalities of type (11) are used, it is easy to see that the case \(x_i = x_j = 1\) does not imply \(y_{ij} = 1\) without an inequality of type (11). \(\square \)
Remark 1
The induced set Q may contain tuples that correspond to squares. Eliminating them is a simple and worthwhile optimization (see also Theorem 8 in Sect. 5). Recognition is already possible when squares are (or rather would be) induced: If \(x_j\) is used as a multiplier for a constraint with \(j \in I_k\), the result may be instantly strengthened to:
If the structure of the present linear constraints is more specific, satisfying Conditions 1–3 has more implications, and may even lead to linear programming relaxations that are provably at least as tight as the one obtained with the “standard linearization”. This will be discussed in more detail in Sect. 5. Beforehand, we strive to clarify how to determine a compact inductive linearization.
4 Obtaining a compact inductive linearization (automatically)
Especially for combinatorial optimization problems, inductive linearizations (i.e., multiplier sets that induce a set \(Q \supseteq P\) and satisfy the consistency conditions) are derived almost naturally, and have been derived in the literature even without any notice of the more general concept presented here. Section 6 gives three prominent examples. Moreover, if a particular BQP has some structure and a (sub-)set of constraints suitable to be employed, an inductive linearization can often be found by inspection once the necessary way of combining constraints with multipliers dictated by Conditions 1–3 is understood.
In any case, an inductive linearization that is as compact as possible (in terms of additional variables and constraints) can be computed. On the negative side, the associated optimization problem is NP-hard in its general form as we will prove below. On the positive side, it can be modeled and solved in practice using a mixed-integer program, and there are polynomial time algorithms for more specifically structured BQPs. Further potential for quick computations in practice stems from the possibility to carefully preselect the set K of original constraints considered for inductions, and from the fact that the number of candidate constraints to induce a certain product is typically not too large.
Before we discuss this in some more detail, we first present the hardness proof. To this end, the problem to determine a most compact inductive linearization is now defined more formally.
Problem 1
(Most Compact Inductive Linearization Problem (MCILP)) Let a BQP with variable index set N, products P, and a selection of constraints \(K = K_E \cup K_I\) with left hand side index sets \(I_k\) for all \(k \in K\) be given. If \(k \in K_E\), let \(w_{kj}^E \in \mathbb {R}\) be a given cost for multiplying the equation with \(x_j\). If \(k \in K_I\), let \(w_{kj}^+ \in \mathbb {R}\) be a given cost for multiplying the inequality with \(x_j\), and let \(w_{kj}^- \in \mathbb {R}\) be a given scalar cost for multiplying the inequality with \((1 - x_j)\). Moreover, let \(w_{ij} \in \mathbb {R}\) be a given scalar cost for inducing the product associated to the tuple \((i,j) \in N \times N\), \(i < j\). Then the Most Compact Inductive Linearization Problem (MCILP) is to compute a multiplier multiset \(M :=\bigcup _{k \in K} M_k\) of an inductive linearization such that a set \(Q \supseteq P\) is induced minimizing the expression
among all possible choices of M satisfying the consistency conditions.
Theorem 5
The MCILP is NP-hard (even in the equation-only case).
Proof
We show a polynomial time and space transformation of the minimum set covering problem, that was shown to be NP-hard by Karp (1972), to the MCILP.
For this purpose, consider a given finite set S together with a given collection \(C = \{ S_j \mid S_j \subseteq S,\; j \in \{1, \ldots , m\} \}\) of m subsets of S whose union gives S. The set covering problem is then to find a minimum cardinality selection \(C^* \subseteq C\) of these subsets that still covers S. An instance of this problem will subsequently be denoted by (S, C) and the elements of S will be identified by their indices. For technical reasons and w.l.o.g., we let these indices start at 2, i.e., we assume that \(1 \not \in S\).
Given an instance (S, C) of the set covering problem as just defined, create a corresponding instance of the MCILP as follows: First, set \(N = S \cup \{1\}\) and \(P = \{ (1,i) \mid i \in S\}\). Then, for each subset \(S_k \in C\), \(k \in \{1, \ldots , m\}\), define a corresponding equation with index set \(I_k = S_k\), and append a single equation with index set \(I_{m+1} = \{ 1 \}\). All the resulting \(\vert K\vert = \vert C\vert + 1 = m + 1\) linear equations may have arbitrary positive coefficients on the left hand side and an arbitrary positive right hand side. Finally, we choose \(w_{kj}^E = 1\) for all \(k \in K = K_E\) and all \(j \in N\), \(w_{ij} = 1\) for all \((i,j) \in N \times N\), \(i < j\), and all other costs (they do not apply) to be zero.
Due to this construction, a collection \(C^* \subseteq C\) covers S if and only if P can be induced by multiplying the left hand sides of the equations associated to the sets \(S_j \in C^*\) plus the finally appended one with variables from the set N in a way satisfying Conditions 1–3. To see that, observe first that P can always be induced by choosing \(M^{E}_{m+1} = S\) which is also the only way to satisfy Condition 1 (and thus Condition 3) for all \((1,i) \in P\). However, satisfying Condition 2 for all \((1,i) \in P\) requires to use variable \(1 \in N\) as a multiplier for a selection of the first \(\vert C|= m\) equations such that the union of their index sets contains all elements of S.
Moreover, in any optimal solution (M, Q) of the corresponding MCILP, each set \(M^{E}_k\) associated to some \(S_k \in C\) will either be empty or contain only the variable \(1 \in N\), while \(M^{E}_{m+1} = S\). This is true, since by construction, using any other \(j \in N\), \(j \ne 1\), as a multiplier for the first \(\vert C|= m\) equations would not further contribute to cover P but result in a higher objective value. The same is true if \(M^{E}_{m+1}\) would be appended by \(1 \in N\). As a consequence, any optimal solution (M, Q) has \(Q=P\). Moreover, the restriction of M to the sets that contain the variable \(1 \in N\) is a minimum cardinality selection of constraints whose left hand sides are, by the construction of the sets \(I_k\), \(k \in K\), in one-to-one correspondence to a minimum cardinality (sub-)collection \(C^* \subseteq C\) covering S. \(\square \)
As a remark, under the assumption made that each factor of a product arises with a non-zero coefficient in at least one linear constraint in K, a feasible solution to the MCILP (and also a solution to the theoretical case with all-negative cost coefficients) is trivially obtained by multiplying each constraint in K with every variable in N.
For a general BQP, a “most compact” inductive linearization can be computed by solving the following mixed-integer program:
The formulation involves binary variables \(z_{kj}^E\) supposed to be equal to one if \({j \in M^{E}_k}\) for \(k \in K_E\) and equal to zero otherwise, and binary variables \(z^{+}_{kj}\) and \(z^{-}_{kj}\) supposed to express whether \(j \in M^{+}_k\) and \(j \in M^{-}_k\) for \(k \in K_I\). To account for whether \((i,j) \in Q\), there is a further continuous variable \(f_{ij}\) for all \(i,j \in N, i \le j\) that will be equal to one in this case and equal to zero otherwise. Constraints (12) fix those \(f_{ij}\) to one where the corresponding pair (i, j) is contained in P. Whenever some \(j \in N\) is assigned to some set \(M_k\), then the corresponding products \((i,j) \in Q\) or \((j,i) \in Q\) for all \(i \in I_k\) are induced by the inequalities (13)–(18). Finally, if \((i,j) \in Q\), then Conditions 1–3 are enforced by the inequalities (19)–(21), respectively.
The Conditions 1–3 impose a certain minimum number of constraints required for a consistent linearization of any set \(Q \supseteq P\) that naturally depends on P, the cardinalities of the sets \(I_k\), \(k \in K\), and the distribution of the variables \(x_i\), \(i \in N\), across them. To obtain a solution with this minimum number of constraints that, among all of these solutions, also induces a minimum number of variables, one may e.g. set \(w_{ij} = 1\) for all \(i,j \in N, i \le j\), and all other cost coefficients to a value larger than \(\max _{k \in K} \vert I_k|\), or solve two MIPs where the number of constraints is fixed within the second one. In general, a more fine grained preference of certain constraints (e.g., with few non-zeroes, or rather equations than inequalities) is possible.
Finally, the mixed-integer program significantly simplifies if only equations are considered. If in addition, the constraints comprising each \(x_i\), \(i \in N\), are unique, i.e., \(I_k \cap I_\ell = \emptyset \), for all \(k,\ell \in K\), \(\ell \ne k\), its constraint matrix becomes totally unimodular. Thus, it may then be solved as a linear program or, alternatively, using a simple combinatorial algorithm as described in Mallach (2018). This algorithm might also be altered to a heuristic for the general case of non-disjoint sets \(I_k\), \(k \in K\).
5 Linear relaxation strength of inductive linearizations
5.1 Implication of the “standard linearization”
We first elaborate on particular settings where the inequalities (1)–(3) are implied by (part of) an inductive linearization.
The case when only equations with right hand sides and coefficients equal to one are employed has already been covered in Mallach (2018). However, accidentally, the proof there did not verify that inequalities (3) hold [in addition to inequalities (1) and (2)] in case of non-integral solutions x. This is caught up on now by giving a complete proof of the following theorem. Moreover, across all the proofs that follow, emphasis is given to precisely identify the subsets of products affected by the respective setting.
Theorem 6
Consider a (sub-)set \(K'_{E}\) of Eq. (4) with \(b_k = 1\) for all \(k \in K'_{E}\), and \(a_k^i = 1\) for each \(i \in I_k\), \(k \in K'_{E}\). Let \(Q' \subseteq Q\) be the set of tuples induced by the multipliers \(M^{E}_k\), \(k \in K'_{E}\), and suppose that these multipliers satisfy the Conditions 1 and 2 for all \((i,j) \in Q'\). Then, for any \(0 \le x \le 1\), we have \(y_{ij} \le x_i\), \(y_{ij} \le x_j\) and \(y_{ij} \ge x_i + x_j - 1\) for all \((i,j) \in Q'\).
Proof
Let \((i,j) \in Q'\). By Condition 1 and the assumption on the multipliers, there is a \(k \in K'_{E}\) such that \(i \in I_k\), \(j \in M^{E}_k\) and such that the associated equation is:
Since it has \(y_{ij}\) on its left hand side, it establishes that \(y_{ij} \le x_j\).
Similarly, by Condition 2 and the assumption on the multipliers, there is a \(k \in K'_{E}\) such that \(j \in I_k\), \(i \in M^{E}_k\) and such that the associated equation is:
Since it has \(y_{ij}\) on its left hand side, it establishes that \(y_{ij} \le x_i\).
To show that \(y_{ij} \ge x_i + x_j - 1\), consider Eq. (22) in combination with its original counterpart \(\sum _{h \in I_k} x_h = 1\). For any \(y_{hj}\) (or \(y_{jh}\)) in (22), the Conditions 1 and 2 and the assumption on the multipliers assure that there is an equation establishing \(y_{hj} \le x_h\) (\(y_{jh} \le x_h\)). Thus we have:
Applying this upper bound within Eq. (22), we obtain:
\(\square \)
The same result can be obtained, if only inequalities are employed.
Theorem 7
Consider a (sub-)set \(K'_{I}\) of inequalities (5) with \(b_k = 1\) for all \(k \in K'_{I}\), and \(a_k^i = 1\) for each \(i \in I_k\), \(k \in K'_{I}\). Let \(Q' \subseteq Q\) be the set of tuples induced by the multipliers \(M^{+}_k\) and \(M^{-}_k\), \(k \in K'_{I}\), and suppose that these multipliers satisfy the Conditions 1–3 for all \((i,j) \in Q'\). Then, for any \(0 \le x \le 1\), we have \(y_{ij} \le x_i\), \(y_{ij} \le x_j\) and \(y_{ij} \ge x_i + x_j - 1\) for all \((i,j) \in Q'\).
Proof
Let \((i,j) \in Q'\). Conditions 1 and 2 and the assumption on the multipliers imply \(y_{ij} \le x_j\) and \(y_{ij} \le x_i\) in the same way as in the proof of Theorem 6. Moreover, by Condition 3, there is, w.l.o.g., some \(k \in K'_{I}\) with \(i \in I_k\) and \(j \in M^{-}_k\), i.e., such that there is an inequality of the form:
Due to Conditions 1 and 2 and the assumptions made, we have that \(x_h \ge y_{jh}\) for each \(h \in I_k, (j,h) \in Q'\) and \(x_h \ge y_{hj}\) for each \(h \in I_k, (h,j) \in Q'\) in (24). By reordering the inequality to
we obtain the desired result. \(\square \)
There is another special case where a provably strong inductive linearization can be obtained and that arises in the context of the example application in Sect. 6.2. It covers equations with a right hand side of two and coefficients one that are multiplied by all variables on their left hand sides (i.e., \(M_k = I_k\)).
Theorem 8
Consider a (sub-)set \(K'_{E}\) of Eq. (4) with \(b_k = 2\) for all \(k \in K'_{E}\), \(a_k^i = 1\) for each \(i \in I_k\), \(k \in K'_{E}\), and suppose that \(M^{E}_k = I_k\) for all \(k \in K'_{E}\). Let \(Q' \subseteq Q\) be the set of tuples induced by these multipliers after eliminating squares. Then, for any \(0 \le x \le 1\), we have \(y_{ij} \le x_i\), \(y_{ij} \le x_j\) and \(y_{ij} \ge x_i + x_j - 1\) for all \((i,j) \in Q'\).
Proof
In the case assumed in the theorem, the induced Eq. (9) first look like
and satisfy Conditions 1 and 2 for all products on the left hand side.
Since \(y_{jj}\) shall take on the same value as \(x_j\), we may eliminate \(y_{jj}\) on the left and once subtract \(x_j\) on the right (cf. Remark 1). We obtain:
As before, these equations imply inequalities (1) and (2) for all the products on the left hand side. Combining them with the original equations \(\sum _{a \in I_k} x_a = 2\) yields the following identities:
As an immediate consequence, it follows that
For any pair \(\{i,j\} \subseteq I_k\) we obtain a subtotal of (26) if we sum the Eq. (25) expressed for i and for j (which both contain \(y_{ij}\) on their left hand sides). We can exploit this as follows (cf. Fischer (2013)) in order to show that \(y_{ij} \ge x_i + x_j - 1\):
\(\square \)
Remark 2
In Theorem 8, if \(M_k \ne I_k\), then it is impossible to conclude \(y_{ij} \ge x_i + x_j - 1\) from Eq. (26). Moreover, if \(b_k > 2\) or squares are not eliminated then one cannot conclude \(y_{ij} \le x_i\) and \(y_{ij} \le x_j\) from Eq. (9) for arbitrary non-integral x. The latter is also true if \(b_k \ge 2\) in the general setting where the non-zero left hand side coefficients are all equal to one. It is thus apparent that the strength of the relaxations of inductively linearized BQPs relates to the ratio between the right hand side and the left hand side coefficients.
5.2 A scenario with a strictly stronger linear relaxation
A particular case where an inductive linearization can be shown to have a linear relaxation that is even strictly stronger than the one obtained with the “standard linearization”, is the following one.
Theorem 9
Consider an inductive linearization that has \({Q=P}\) and that contains the equation
for some fixed \(i \in N\). Suppose further there is a feasible solution \(x^*\) for the linear relaxation of the respective problem where \(x^*_i > 0\), \(x^*_h > 0\), and \(x^*_i + x^*_h \le 1\), for all \(h \in I_k\). Then the linear relaxation of the “standard linearization” contains points that are infeasible to the one obtained by the inductive linearization.
Proof
For any solution \(x^*\) as in the theorem, the inequalities (3) of the “standard linearization” for each \(y_{ih}\), \(h \in I_k\), are dominated by \(y_{ih} \ge 0\), and thus there is a feasible point in the corresponding relaxation where \(y_{ih} = 0\) for all \(h \in I_k\). Any such point is readily seen to be infeasible for the equation of the inductive linearization displayed in the theorem, as its right hand side is non-zero for \(x^*\). \(\square \)
Remark 3
The assumption \(Q=P\) is important to facilitate a formal proof of a superior strength case, as a “standard linearization” only linearizes the products in P. Also, without assuming \(Q=P\), the value \(b_k x_{i}\) could be entirely complemented by \(a_k^h y_{hi}\) or \(a_k^h y_{ih}\) for some \(h \in I_k\) where (h, i) respectively (i, h) is in \(Q {\setminus } P\). By the way, for the same reason, it is also necessary to satisfy Conditions 1–3 for all products in Q rather than just for those in P in order to obtain a truly consistent linearization of the latter (which is one of the corrections to the initial approach for assignment constraints made in Mallach (2018)).
6 Example applications and computational aspects
In the following, we highlight some prominent combinatorial optimization problems where formulations found earlier appear now as inductive linearizations, and provide some pointers to early computational evidence for successful applications of the proposed method.
6.1 The quadratic assignment problem
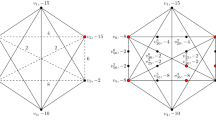
A canonical integer programming formulation for the quadratic assignment problem (QAP) in the form by Koopmans and Beckmann (1957), has variables \(x_{ip} \in \{0,1\}\) for “facilities” i and “locations” p, both indexed by \(\{1, \ldots , n\}\). As already mentioned by Liberti (2007), the following formulation by Frieze and Yadegar (1983) may then be obtained by applying the inductive linearization technique (and ignoring commutativity in the first place).
For each linearization variable \(y_{ipjq}\) representing the product \(x_{ip} x_{jq}\), \(i,p,j,q \in \{1, \ldots , n\}\), the displayed formulation however satisfies each of the Conditions 1 and 2twice, i.e., it is not a “most compact” inductive linearization. There is also an equivalent formulation by Adams and Johnson (1994) that cannot, at least not directly, be generated from the approach proposed. It comprises only (29) and (30), and thus satisfies Conditions 1 twice while Conditions 2 are “indirectly” enforced by means of additional constraints \(y_{ipjq} = y_{jqip}\) for all \(i,p,j,q \in \{1, \ldots , n\}\).
To characterize a “most compact” inductive QAP linearization, observe first that each of the variables \(X :=\{ x_{ip} \mid i,p \in \{1, \ldots , n\} \}\) occurs exactly once in the set of constraints (27) and exactly once in the set of constraints (28). Thus, in order to induce all products and to satisfy Conditions 1 and 2 for them, it suffices to either multiply all of constraints (27) with X – which induces (29) and (31), or to multiply all of constraints (28) with X – which induces (30) and (32). Moreover, since the identities (33) and the variables \(y_{ipiq}\) for all \(p,q \in \{1, \ldots , n\}\) as well as all variables \(y_{ipjp}\) for all \(i,j \in \{1, \ldots , n\}\) can be eliminated, it suffices to formulate (30) and (32) only for \(i \ne j\), and (29) and (31) only for \(p \ne q\). If one further identifies \(y_{jqip}\) with \(y_{ipjq}\) whenever \(i < j\), it even suffices to have only exactly one of these four equation sets in order to satisfy Conditions 1 and 2. The total number of additional equations then reduces to \(n^3 - n^2\) compared to \(3 \cdot \big ( \frac{1}{2} (n^2 - n) (n^2 -n) \big ) = \frac{3}{2} (n^4 - 2n^3 + n^2)\) inequalities when using the “standard linearization” and creating \(y_{ipjq}\) only for \(i < j\) and \(p \ne q\) as well. However, these most compact formulations have a considerably weaker linear programming relaxation than the ones by Frieze and Yadegar (1983) and Adams and Johnson (1994).
6.2 The symmetric quadratic traveling salesman problem
The symmetric quadratic traveling salesman problem asks for a tour \(T \subseteq E\) in a complete undirected graph \(G=(V,E)\) such that the objective \(\sum _{\{i,j,k\} \subseteq V, j \ne i < k \ne j } c_{ijk} x_{ij} x_{jk}\) (where \(x_{ij} = 1\) if \(\{i,j\} \in T\) and \(x_{ij} = 0\) otherwise) is minimized.
Consider the following mixed-integer programming formulation for this problem as presented by Fischer and Helmberg (2013) and based on the integer programming formulation for the classical traveling salesman problem with linear objective by Dantzig et al. (1954).
Here, we restrict the set K of constraints considered for inductions to the Eq. (34). To induce the products as in (35), i.e. each pair of edges with common index j, we need to multiply the left hand sides of the Eq. (34) exactly with all the variables occurring there, i.e., we have to set \(M_k = I_k\) for all \(k \in K\). This choice satisfies both Conditions 1 and 2 for all these pairs. Since \(a_k^i = 1\) for all \(i \in I_k\) and \(b_k = 2\) for all \(k \in K\), we comply to the requirements of the special case addressed in Theorem 8 (Sect. 5.1) and obtain the equations:
After introducing linearization variables with indices ordered as desired, these are rewritten as:
Each of these equations induces one variable more than truly desired, namely \(y_{kjk}\) as the linearized substitute for the square term \(x_{jk} x_{jk}\). Thus we may safely subtract \(y_{kjk}\) from the left and \(x_{jk}\) from the right hand side and obtain
which are exactly the linearization constraints as presented by Fischer and Helmberg (2013). For the here assumed complete undirected graph on \(\vert V\vert = n\) vertices, the number of these equations amounts to only \(n^2\) compared to \(\frac{3}{2}(n^3 - 3n^2 + 2n)\) inequalities that would result from a “standard linearization”.
6.3 The quadratic 0-1 knapsack problem
A very simple inequality-only application for the inductive linearization technique is the quadratic 0-1 knapsack problem. Here, items from a ground set J are to be selected while each item \(j \in J\) has a size \(a_j \in \mathbb {R}\), and there is a capacity limit \(b \in \mathbb {R}\). The goal is to maximize a quadratic profit function associated to single items and pairs of items selected.
Billionnet and Calmels (1996) as well as many succeeding authors employed inequalites of type (7) in combination with the “standard linearization”. A few years later, Helmberg et al. (2000) considered the further addition of inequalities of type (8) in the context of semidefinite relaxations and showed that they can help to obtain better dual bounds.
A corresponding square-reduced (cf. Remark 1) inductive linearization is the following mixed-integer program:
Once more, the formulation is more compact than a “standard linearization”: Assuming \(\vert J \vert = n\), the \(\left( {\begin{array}{c}n\\ 2\end{array}}\right) \) products are linearized using only 2n instead of \(3\left( {\begin{array}{c}n\\ 2\end{array}}\right) \) inequalities. However, in the general case of arbitrary \(a_j\), \(j \in J\), and b, an implication of the “standard linearization” inequalities (1)–(3) cannot be expected.
6.4 Computational aspects
Sections 6.1 and 6.2 exemplified two favorable situations where one obtains an inductive linearization that is at least as strong as the “standard linearization” and that is considerably smaller in size at the same time. Although this does not necessarily lead to faster solution times of the entire mixed-integer programs, it generally improves the applicability to somewhat larger instances as one can solve smaller linear relaxations without any trade-off regarding the bounds obtained.
For some particular combinatorial optimization problems, there is also already computational evidence that the inductive linearization approach is superior to the “standard linearization”. One example is the graph partitioning problem as addressed in Mallach (2018). Another one is the multiprocessor scheduling problem with communication delays addressed in Davidović et al. (2007), Liberti (2007), and Mallach (2017).
Since the inductive approach is applicable to any BQP with linear constraints, many more well-suited applications can be expected, but also limitations concerning the relaxation strength (e.g., because of large ratios between right hand sides and left hand side coefficients) and compactness (e.g., if the support of the constraints at hand relates undesirably to the set P) are indicated. A meaningful impression of the corresponding effects for the practical solution of various kinds of BQPs can thus be provided only by a broad computational study that is beyond the scope of this paper.
7 Conclusion and outlook
The inductive (previously termed “compact”) linearization technique has been extended to binary quadratic problems with arbitrary linear constraints. While such a linearization can often be derived by inspection for combinatorial optimization problems, it can also be computed by solving a mixed-integer program or using a polynomial-time combinatorial algorithm for specially structured BQPs. Several cases where the linear relaxation of an inductively linearized binary quadratic problem is provably at least as strong as or even strictly stronger than the one obtained with the “standard linearization” have been identified. Moreover, previously found formulations for the quadratic assignment, the symmetric quadratic traveling salesman, and the quadratic 0-1 knapsack problem were highlighted that can also be derived by applying the proposed technique. A few examples from the literature already provide computational evidence that the inductive linearization can be superior to the “standard linearization” in practice. A thorough and broad computational study across the vast field of potential applications is in order.
Change history
07 October 2021
A Correction to this paper has been published: https://doi.org/10.1007/s10288-021-00494-x
References
Adams WP, Johnson TA (1994) Improved linear programming-based lower bounds for the quadratic assignment problem. In: Pardalos PM, Wolkowicz H (eds) Quadratic assignment and related problems, DIMACS series on discrete mathematics and computer science, vol 16. AMS, Providence, pp 43–75
Adams WP, Sherali HD (1986) A tight linearization and an algorithm for zero-one quadratic programming problems. Manag Sci 32(10):1274–1290. https://doi.org/10.1287/mnsc.32.10.1274
Adams WP, Sherali HD (1999) A Reformulation-Linearization technique for solving discrete and continuous nonconvex problems, nonconvex optimization and its applications, vol 31. Springer, Berlin. https://doi.org/10.1007/978-1-4757-4388-3
Balas E (1964) Extension de l’algorithme additif à la programmation en nombres entiers et à la programmation non linéaire. Comptes rendus de l’Académie des Sciences Paris 258:5136–5139
Barahona F, Jünger M, Reinelt G (1989) Experiments in quadratic 0–1 programming. Math Programm 44(1):127–137. https://doi.org/10.1007/BF01587084
Billionnet A, Calmels F (1996) Linear programming for the 0–1 quadratic knapsack problem. Eur J Oper Res 92(2):310–325. https://doi.org/10.1016/0377-2217(94)00229-0
Billionnet A, Elloumi S (2001) Best reduction of the quadratic semi-assignment problem. Discrete Appl Math 109(3):197–213. https://doi.org/10.1016/S0166-218X(00)00257-2
Chaovalitwongse W, Pardalos PM, Prokopyev OA (2004) A new linearization technique for multi-quadratic 0–1 programming problems. Oper Res Lett 32(6):517–522. https://doi.org/10.1016/j.orl.2004.03.005
Dantzig G, Fulkerson R, Johnson S (1954) Solution of a large-scale traveling-salesman problem. J Oper Res Soc Am 2(4):393–410. https://doi.org/10.1287/opre.2.4.393
Davidović T, Liberti L, Maculan N, Mladenović N (2007) Towards the optimal solution of the multiprocessor scheduling problem with communication delays. In: Baptiste P, Kendall G, Munier-Kordon A, Sourd F (eds) Proc. 3rd Multidisciplinary Int. Conf. on Scheduling: Theory and Application, École Polytechnique, Paris, France, pp 128–135
De Simone C (1990) The cut polytope and the boolean quadric polytope. Discrete Math 79(1):71–75. https://doi.org/10.1016/0012-365X(90)90056-N
Fischer A (2013) A polyhedral study of quadratic traveling salesman problems. PhD thesis, Chemnitz University of Technology
Fischer A, Helmberg C (2013) The symmetric quadratic traveling salesman problem. Math Program 142(1–2):205–254. https://doi.org/10.1007/s10107-012-0568-1
Fortet R (1959) L’algèbre de boole et ses applications en recherche opérationnelle. Cahiers du Centre d’Etudes de Recherche Opérationnelle 1:5–36
Fortet R (1960) Applications de l’algèbre de boole en recherche opérationnelle. Revue de la Société Française de Recherche Opérationnelle 4:17–26
Frieze AM, Yadegar J (1983) On the quadratic assignment problem. Discrete Appl Math 5(1):89–98. https://doi.org/10.1016/0166-218X(83)90018-5
Furini F, Traversi E (2013) Extended linear formulation for binary quadratic problems. Optimization Online
Glover F, Woolsey E (1973) Further reduction of zero-one polynomial programming problems to zero-one linear programming problems. Oper Res 21(1):156–161
Glover F, Woolsey E (1974) Converting the 0–1 polynomial programming problem to a 0–1 linear program. Oper Res 22(1):180–182. https://doi.org/10.1287/opre.22.1.180
Gueye S, Michelon P (2009) A linearization framework for unconstrained quadratic (0–1) problems. Discrete Appl Math 157(6):1255–1266. https://doi.org/10.1016/j.dam.2008.01.028
Hammer PL (1965) Some network flow problems solved with pseudo-boolean programming. Oper Res 13(3):388–399
Hammer PL, Rudeanu S (1968) Boolean Methods in Operations Research and Related Areas, Ökonometrie und Unternehmensforschung/Econometrics and Operations Research, vol 7. Springer, Berlin. https://doi.org/10.1007/978-3-642-85823-9
Hansen P, Meyer C (2009) Improved compact linearizations for the unconstrained quadratic 0–1 minimization problem. Discrete Appl Math 157(6):1267–1290. https://doi.org/10.1016/j.dam.2007.12.008
Helmberg C, Rendl F, Weismantel R (2000) A semidefinite programming approach to the quadratic knapsack problem. J Comb Optim 4(2):197–215. https://doi.org/10.1023/A:1009898604624
Karp RM (1972) Reducibility among combinatorial problems. In: Miller RE, Thatcher JW, Bohlinger JD (eds) Complexity of computer computations. Plenum Press, New York, pp 85–103. https://doi.org/10.1007/978-1-4684-2001-2_9
Koopmans TC, Beckmann M (1957) Assignment problems and the location of economic activities. Econometrica 25(1):53–76
Liberti L (2007) Compact linearization for binary quadratic problems. 4OR 5(3):231–245. https://doi.org/10.1007/s10288-006-0015-3
Mallach S (2017) Improved mixed-integer programming models for the multiprocessor scheduling problem with communication delays. J Comb Optim. https://doi.org/10.1007/s10878-017-0199-9
Mallach S (2018) Compact linearization for binary quadratic problems subject to assignment constraints. 4OR 16:295–309. https://doi.org/10.1007/s10288-017-0364-0
McCormick GP (1976) Computability of global solutions to factorable nonconvex programs: part I—convex underestimating problems. Math Program 10(1):147–175. https://doi.org/10.1007/BF01580665
Oral M, Kettani O (1992a) A linearization procedure for quadratic and cubic mixed-integer problems. Oper Res 40(1–supplement–1):S109–S116. https://doi.org/10.1287/opre.40.1.S109
Oral M, Kettani O (1992b) Reformulating nonlinear combinatorial optimization problems for higher computational efficiency. Eur J Oper Res 58(2):236–249. https://doi.org/10.1016/0377-2217(92)90210-Z
Padberg M (1989) The boolean quadric polytope: some characteristics, facets and relatives. Math Program 45(1):139–172. https://doi.org/10.1007/BF01589101
Sherali HD, Smith JC (2007) An improved linearization strategy for zero-one quadratic programming problems. Optim Lett 1(1):33–47. https://doi.org/10.1007/s11590-006-0019-0
Watters LJ (1967) Reduction of integer polynomial programming problems to zero-one linear programming problems. Oper Res 15:1171–1174
Zangwill WI (1965) Media selection by decision programming. J Adv Res 5:23–37
Acknowledgements
I would like to thank Anja Fischer for bringing up the question whether the original approach for assignment constraints might be possibly generalized to arbitrary right hand sides and pointing me to her research about the symmetric quadratic traveling salesman problem. Just as well I thank Sourour Elloumi for encouraging me to consider the inequality cases in more detail.
Funding
Open Access funding provided by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The author declares that there is no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Most of this work was done while the author was at the University of Cologne, Germany.
The original online version of this article was revised: the incorrect texts have been correctly replaced in the original article.
Appendix: normalization of linear constraints in binary optimization
Appendix: normalization of linear constraints in binary optimization
Let \(Ax \le b\) be a system of linear equations and less-or-equal inequalities with \(A \in \mathbb {R}^{m \times n}\) and \(b \in \mathbb {R}^m\) for some \(m > 0\). It is clear that any linear constraint system can be cast in this way, as any greater-or-equal inequality can be turned into a less-or-equal one by simply negating its left and right hand sides. In the case of a binary (quadratic) program, we may even restrict A to be non-negative, and b to be non-negative or even positive, although this might seem counter-intuitive in the first place. The “proof” (no originality is claimed) is as follows.
Let
be an equation of the system (the following also holds for a \(\le \)-inequality), and let \(I_k^- \subseteq I_k\) be the set of variable indices such that \(a_k^i < 0\) for each \(i \in I_k^-\). For ease of notation, define also \(I_k^+ = I_k {\setminus } I_k^-\).
Now define a new complement variable \(\bar{x}_i\) for each \(i \in I_k^-\) along with the corresponding equation
that apparently has only positive coefficients on the left hand side and a positive right hand side. Moreover, we may now replace the initial original equation with
where now the term \(-\sum _{i \in I_k^-} a_k^i\) on the left and on the right hand side is non-negative as well.
Carrying out this procedure for every equation or inequality with negative coefficients on the left hand side clearly gives a system with only non-negative coefficients on the left.
Now suppose that any of the (resulting) constraints has a negative right hand side. Then, since each \(a_k^i \ge 0\) and \(x_i \ge 0\) (\(\bar{x}_i \ge 0\)), the system is infeasible. Since this could be detected this way, we may assume w.l.o.g. that \(b_k \ge 0\). Furthermore, if \(b_k = 0\), then all the variables on the left hand side can be fixed (original ones to zero, complemented ones to one) and thus be removed from the formulation.
While the above approach introducing complement variables turns any BQP with linear constraints into one that is suitable for an inductive linearization, it is not necessary to (explicitly) apply it in practice. In general, it is also not advisable to do so. For instance, because it may add up to n variables and equations. Moreover, because each multiplication of the Eq. (36) with an original variable induces two rather undesirable linearization equations (to satisfy Conditions 1 and 2) that even inevitably result if a factor \(x_i\) appears only with negative support in the original constraints (and thus multiplication would be with \(\bar{x}_i\) instead of with \(x_i\) in its modified counterpart). Finally, complementing variables in original constraints “beforehand” may also incur avoidable overhead if it is not a priori clear that the respective constraints will be at all employed for multiplications.
A more advisable strategy is thus to keep the original constraints as they are, and to consider them for multiplication with each \(x_j\) and \(\bar{x}_j\) without ever really introducing the latter (as one can directly use \((1 - x_j)\) instead). Thereby, one may keep track for each \(x_i\) with a non-zero coefficient on the left hand side which of the four possible combinations \(x_i x_j\), \(\bar{x}_i x_j\), \(x_i \bar{x}_j\), and \(\bar{x}_i \bar{x}_j\) has to be induced (respectively, which of these is to be represented by a linearization variable) such that the respective linearization constraint imposes the necessary implications on their value. Then, with the relaxed condition that not necessarily a linearization variable for \(x_i x_j\) is induced but a variable with Conditions 1–3 satisfied for (at least) one of the four combinations, we are already done for all products not appearing in the objective function. For those appearing in the objective function, the value of \(x_i x_j\) can, if necessary, always be deduced by (one of) the three equations
and substituting for the respective linearization variables. Instead of adding any of these to the formulation along with \(y_{ij}\), one may also exploit the relations by substituting for \(x_i x_j\) directly in the objective function. This way no additional equations are caused at all, and the handling of constraints with negative coefficients thus becomes almost completely oblivious.
As a further postprocessing option, one may eliminate all variables in \(Q {\setminus } P\) from the linearization constraints if all of these have been generated from inequalities (possibly due to a splitting of equations). Due to their less-or-equal sense and their positive left hand side coefficients, such an elimination does neither affect their validity nor their implications w.r.t. the consistency of the linearization. However, the feasible set of the relaxation is, in general, relaxed by this procedure.
As a very final remark, even for a BQP without any (non-trivial) linear constraints one could employ the inductive linearization technique using the upper bound inequalities \(x_i \le 1\). However, not surprisingly, multiplying these with some \(x_j\) and \(1 - x_j\) (and multiplying \(x_j \le 1\) with \(x_i\) and \((1-x_i)\)) induces the respective “standard linearization” inequalities (1)–(3). So while this is pointless in principle, it may nevertheless be a convenient way to deal with single “unconstrained” variables (if these appear as factors) within the approach presented, respectively without implementing a special handling. More appropriate artificial valid constraints should however be employed instead whenever this is possible.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Mallach, S. Inductive linearization for binary quadratic programs with linear constraints. 4OR-Q J Oper Res 19, 549–570 (2021). https://doi.org/10.1007/s10288-020-00460-z
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10288-020-00460-z