1 Introduction

From the architectural system design perspective, an interaction system can be seen as an economic (or general physical) agents interacting pairwise, but not necessarily in a cooperative manner to achieve a common functional goal (Vissers et al. 2016; Faigle and Grabisch 2017). This abstract viewing of a system is a natural generalization of game theoretic models in which strategic interaction among rational decision-makers is studied. The same concept in the context of supply chain policy design is the classical capacity allocation games whereby a capped capacity/resource should be distributed to multiple buyers where total demand is higher than available capacity. In addition to manufacturing sector, these games are vastly popular in service supply chain, such as allocating an airport’s terminal gates to the airlines, renting terminal cranes to career ships in ports, and allocation of berth space capacity to vessels in a container terminal (Jahani et al. 2021). Several studies have proposed various policies to either equitably allocate capacity/stock to buyers, or to minimize/maximize the penalty/award associated with the Service Level Agreement (SLA) between product/service provider and clients (e.g., Cachon and Lariviere 1999b; Benjaafar et al. 2007; Chen et al. 2013; Qing et al. 2017; Chen and Thomas 2018). However, limited number of studies could model the strategic reasoning of players in capacity allocation games (e.g., Cachon and Lariviere 1999c; Liu and Ryzin 2011; Cui and Zhang 2018).

For example, assume that buyers’ orders exceed supplier capacity. In this case, a proportional rationing rule applies to capacity allocation among buyers. In other words, an optimal allocation policy may be able to minimize supplier’s penalty cost or to maximize the buyers’ perceived service level; however, when buyers are aware of supplier’s capped capacity, in order to maximize their profit, they are induced to adopt early or excess purchasing strategies based on their different levels of strategic-reasoning capabilities. In fact, limited stock of supplier is a strong incentive for buyers to strategize over order quantities (Liu and Ryzin 2008). It is obvious that ignoring the strategic thinking and behavior model of buyers undermines any attempt to develop an effective capacity allocation policy. That is the reason why classical game theory has been less successful to model capacity allocation decisions under strategic reasoning.

The shortcoming of classical allocation games can be overcome through employing quantum game theory principals. In a quantum version of a game, a bit is replaced by the qubit, which is a quantum superposition of two or more base states. Furthermore, in a quantum game, the set of qubits representing players’ choice of strategy may be entangled. In essence, an entangled pair of strategies implies that an operation performed on one of the qubits, influences the other qubit as well, thus changing the expected pay-offs of the game. The Superposition and Entanglement are the two powerful concepts that bring the field of game theory to the quantum world. In this study, quantum game theory is used to model the reasoning capabilities of clients in the form of entangled strategies. In the next section, the literature base around the identified gap is reviewed.

2 Background

To highlight the significance of the identified knowledge gap, first, the proposed mechanisms to allocate limited capacity to a number of clients is investigated. Then, from what have been outlined in the literature, we delineate how strategic reasoning of clients may influence the output of various allocation policies. Finally, recent developments in capacity games are reviewed to understand how the arrangement between the supplier and buyers can be improved to achieve higher pay-offs.

2.1 Capacity allocation

A basic application of the capacity allocation problem can be observed in a supply chain in which a single supplier sells a product to several downstream buyers (Cachon and Lariviere 1999c). The capacity of supplier is limited and the information regarding the buyers’ optimal stocking levels is private for each buyer. If total orders’ quantities for all buyers would be greater than the available capacity, the supplier employs a publicly known allocation mechanism –a mapping from buyer orders to capacity assignments– to allocate capacity. This field of research on capacity allocation models started from the well-known article under the tile The Optimum Distribution of Effort by Koopman (1953) in the twentieth century (Luss 2012, p. xi). From that point of time onward, various allocation policies have been proposed to mainly fulfill one of the two following objectives: (i) maximizing the fairness (equity) in allocating limited resources among competing orders or activities. We may consider the following examples under this category: allocation of bandwidth in telecommunication networks or clouds (Xu and Yu 2014; Nezarat and Dastghaibifard 2015), allocation of water resources (Roozbahani et al. 2020), and allocation of takeoff and landing ’slots’ at airports. (ii) minimizing penalty cost of not meeting the target performance measure (e.g. fill rate), or maximizing the award for constantly meeting the target performance measure as per the terms of a performance based contract (e.g. service level agreement) (Durango-Cohen and Li 2017; Abbasi et al. 2018, 2020; Jahani et al. 2021).

To define allocation models, the following notations are used. There are M buyers in a supply chain with a single supplier that has a finite capacity (\({\mathcal {K}}\)). Let \(q_m\) be the buyer m’s order quantity, and \(\omega \) be a function representing the allocation mechanism that assigns a feasible allocation to each vector of orders. It is obvious that the supplier never allocates to a buyer more than the buyer’s order, i.e. \(\omega _m(q) \le q_m\). In addition, total allocated capacity to all buyers does not exceed the capacity of supplier, i.e., \(\sum _{m=1}^{M} \omega _m(q) \le {\mathcal {K}}\).

As outlined by Cachon and Lariviere (1999b) and Chen et al. (2013), the most intuitive allocation mechanism is Proportional Allocation (P). In this mechanism (Eq. 1), each buyer receives the same fraction of her order on condition that the capacity of the supplier binds.

$$\begin{aligned} \omega _{m} (q) = \min \left\{ {q_{m} ,\;\frac{{ q_{m} }}{{\sum \nolimits _{{j = 1}}^{M} {q_{j} } }}} \right\} \end{aligned}$$
(1)

The second policy is the Linear Allocation (L) whereby each buyer receives her order minus a common deduction (Eq. 2). In the operational level, buyers’ indexes are ranked in a decreasing order based on order quantity (\(q_1 \ge q_2 \ge \dots \ge q_M\)). Suppose \(\tilde{n}\) is the largest integer less than or equal to M where \(\omega _{\tilde{n}}(q,\tilde{n}) \ge 0\). Then, the allocation function can be defined as:

$$\begin{aligned} \omega _m(q,\tilde{n}) = {\left\{ \begin{array}{ll} q_m - \frac{\displaystyle 1}{\displaystyle \tilde{n}} \max \left( 0, \sum \limits _{j=1}^{\tilde{n}} q_j - {\mathcal {K}}\right) &{} m\le \tilde{n}\\ 0 &{} m > \tilde{n} \end{array}\right. } \end{aligned}$$
(2)

Relaxed Linear Allocation (RL), as shown in (Eq. 3), is a derivative of L which has been used in some studies (e.g., Cachon and Lariviere 1999b). We have excluded this allocation mechanism from our study as it may produce infeasible allocations, i.e., \(\omega _m(q) < 0\) is possible.

$$\begin{aligned} \omega _m(q) = \min \left\{ q_m, q_m - \frac{\displaystyle 1}{\displaystyle N} \sum \limits _{j=1}^{M} q_j - {\mathcal {K}}\right\} \end{aligned}$$
(3)

Another well-known allocation mechanism is Uniform Allocation (U) which favors the small orders (Eq. 4). Similar to L policy, index of buyers are ranked in decreasing order as per the order quantity (\(q_1 \ge q_2 \ge \dots \ge q_M\)). Given that \(\tilde{n}\) is the largest integer less than or equal to M where \(\omega _{{\hat{n}}}(q,{\hat{n}}) \le q_{{\hat{n}}}\). Then, the function of U allocation policy can be expressed as:

$$\begin{aligned} \omega _m(q,{\hat{n}}) = {\left\{ \begin{array}{ll} \frac{\displaystyle 1}{\displaystyle {\hat{n}}} \left( {\mathcal {K}}- \sum \limits _{j={\hat{n}}+1}^{M} q_j \right) &{} m\le {\hat{n}}\\ q_m &{} m > {\hat{n}} \end{array}\right. } \end{aligned}$$
(4)

The final allocation policy which is investigated in this study is the Lexicographic Allocation (\(L_x\)) mechanism. First, despite order quantities, a sequence in which the buyers’ orders are to be satisfied is prepared. The decision rule for sequencing the buyers can be as simple as alphabetical order. Alternatively, the specific relationship or commitment to a buyer determines its priority. Assume that for a supply chain with two buyers, the order of buyer 1 should be satisfied first. Then, we have:

$$\begin{aligned} \begin{aligned} \omega _1(q)&= \min \{q_1, {\mathcal {K}}\} \quad \text {and} \\ \omega _2(q)&= \min \{q_2, {\mathcal {K}}- \omega _1(q)\} \end{aligned} \end{aligned}$$
(5)

otherwise,

$$\begin{aligned} \begin{aligned} \omega _2(q)&= \min \{q_2, {\mathcal {K}}\} \quad \text {and} \\ \omega _1(q)&= \min \{q_1, {\mathcal {K}}- \omega _2(q)\} \end{aligned} \end{aligned}$$

In a general format, the \(L_x\) is presented in Eq. 6 given that priority of serving buyers is considered as \(m=1, 2, \dots , M\).

$$\begin{aligned} \omega _m(q) = \min \left\{ q_m, \left( {\mathcal {K}}- \sum \limits _{j=1}^{i-1} \omega _j \right) \right\} , \quad m=1, 2, \dots , M \end{aligned}$$
(6)

2.2 Strategic reasoning in capacity allocation

Several classes of allocation mechanisms are prone to manipulation (Furuhata and Zhang 2006). In fact, buyers will order more than they need to achieve a more favorable allocation. This category is known as manipulative mechanism. On the contrary, the second class of mechanisms refers to policies that induces the buyers to order exactly their needs. This class is referred to as truth-inducing mechanism in the literature (e.g., Hall and Liu 2008; Spiliotopoulou et al. 2019). When a supplier is using a truth-inducing mechanism, buyers freely reveal their private information. For example, suppose a supplier employs the Lexicographic allocation mechanism and the sequence of buyers is determined in alphabetical order. In this case, a buyer is unable to get more benefit by ordering more that what she requires.

Since it is inevitable that buyers may strategize over order quantities when a manipulative mechanism is in practice, an effective allocation policy should consider the potential influence of strategic reasoning on performance indicator of the existing arrangement. Several studies have investigated the impact of strategic reasoning in allocation policies and provided interesting results. For example, Cachon and Lariviere (1999b) show that there is no truth-inducing mechanism that maximizes the total profits of buyers. Therefore, it is expected that in real business world, truth-inducing mechanisms would be less practical. In addition, they concluded that a manipulable mechanism may encourage the supplier to choose a higher level of capacity compared to the situation where a truth-inducing mechanism would be selected. Further, the profit of total supply chain, suppliers, and even buyers may be reduced by switching to a truth-inducing mechanism. Therefore, it is difficult to consider the truth-telling as a universally desirable goal. In the same vein, Chen et al. (2013) show that the non-manipulative mechanisms such as Lexicographic could dampen the competition at the retail level, which results in improved profits for both supplier and the entire supply chain. Mallik (2007) also shows that a large class of allocation rules are manipulable; however, a bonus/incentive contract is mostly required for elicitation of truthful information from the buyers.

A new term as service-maximizing allocation function is coined by Elahi et al. (2012) which refers to the policy that induces suppliers to provide the maximum feasible service level for the amount of demand allocated. They identify a family of Proportional allocation functions that are service-maximizing.

Strategic reasoning has also been experimentally studied by a number of researchers including Chen et al. (2012) under the Proportional allocation capacity where subjects are motivated by financial incentives. They conclude that the Nash Equilibrium, which assumes that players are perfectly rational, substantially exaggerates buyers’ tendency to strategically order more than they need. They suggested a model of bounded rationality based on the Quantal Response Equilibrium, in which players are not perfect optimizer and they face uncertainty in their opponents’ actions.

As an inevitable consequence of strategic reasoning, buyers receive too much if capacity does not bind (Cachon and Lariviere 1999a). They highlight that in the capacity allocation game, each buyer would form expectations on how much other buyers actually need (which is uncertain) and how much each will actually order, knowing that all buyers are dealing with the same issue. They also show that buyers’ behavior in this game facing either Proportional or Linear allocation policies can be very unpredictable as there may not exist a Nash equilibrium. In that case, any order quantity more than a buyer’s desired quantity can be justified, no matter how large. As a result, a buyer with a high need may be allocated less than a buyer with a low demand leading to an ex post inefficient allocation.

2.3 Game theoretic approach and quantum games

Developing an effective allocation policy is in the field of mechanism design that takes the game theory approach to designing economic incentives or framework, toward desired objectives in strategic settings, where players act rationally. That is why in almost all attempts to design a mechanism for allocating limited capacity, game theory is employed (for example, see Dai et al. 2005, 2006; Hall and Liu 2008; Elahi et al. 2012; Elahi 2013; Huang et al. 2013; Durango-Cohen and Li 2017; Qing et al. 2017). However, classical game theory is pushed to its limits when players are not acting rationally and/or they manipulate their decisions for achieving higher economic gains. This issue drives this study to explore the capabilities of quantum game theory for modeling the strategic reasoning of players in capacity allocation games.

As defined by Figueiredo (2004), “any quantum system which can be manipulated by two parties or more and where the utility of the moves can be reasonably quantified, may be conceived as a quantum game”. At the most abstract level, while game theorist is only looking into the actions and strategies to deliver the best outcome, a quantum physicist is thinking how the results of a game can be generalized into the quantum domain when linear superposition of these actions is allowed (Eisert et al. 1999).

Although it is more than two decades that Meyer (1999) merged game theory with quantum computing and proposed the first quantized game, the application of quantum games in supply chain management is scarce. As an example, Zhang et al. (2015) studied the service quality preference behaviors of service integrator and a service provider in service supply chain (SSC) with stochastic demand. Nash equilibrium and quantum game were used to optimize the models and it was identified that values of service quality and utilities under the quantum game equilibrium were superior compared to solutions under the Nash equilibrium, if players were preference-neutral for service qualities.

In this study, the capacity allocation policies are investigated when the strategic rationing of buyers is assumed to be entangled in a quantum game setting.

3 Notations

The notations employed in the model are as follows:

M

Number of buyers.

\({\mathcal {K}}\)

The base capacity level of supplier in a base stock policy.

\(d_{mt}\)

Demand of buyer m in time t.

\(q_{mt}\)

Order quantity of buyer m in time t.

\(p_s\)

Supplier’s selling price.

\(p_b\)

Buyer’s selling price.

h

Buyer’s holding cost for a single period.

s

Buyer’s shortage cost for a single period.

\(\pi _{mt}\)

Profit of buyer m in time t.

\(\omega (.)\)

Allocation mechanism function that assigns a feasible allocation to each vector of orders.

\({\mathcal {P}}\)

The set of allocation policies, \(P=\{\mathrm {P, L, }\) \(\mathrm { U, Lx}\}\), \(p \in {\mathcal {P}}\).

\({\mathcal {F}}_{m,\infty }(p)\)

The long run fill rate of buyer m under service policy \(p\in {{\mathcal {P}}}\).

\({\widehat{J}}\)

Unitary operator that entangles the players’ qubits.

\({\widehat{J}}^\dagger \)

Unitary operator that disentangles the players’ qubits.

\(\gamma \)

Squeezing parameter (measure of entanglement).

i

Imaginary number, \(i^2=-1\).

\({\widehat{X}}_m\)

Position operators of buyer m.

\({\widehat{P}}_m\)

Momentum operators of buyer m.

\({\widehat{a}}^\dagger _m ({\widehat{a}}_m)\)

Creation (Annihilation) operator of buyer m’s electromagnetic field.

\({\widehat{D}}_m\)

Unitary operators expressing buyer m’s strategic moves.

\({\mathcal {S}}_m\)

Strategy set of buyer m.

4 Model

To model an allocation game, we assume that supplier utilizes the base stock policy whereby replenishment order is placed to restore the base-stock \({\mathcal {K}}\), whenever the inventory position is below \({\mathcal {K}}\). This assumption is in congruence with many practices in the service supply chains in which a limited capacity (e.g., gates in airports, parking lots, and cranes in ports) is replenished to the base-level on a timely basis. The other general assumptions are: (i) time is discrete and is organized in a numerable and infinite succession of equally spaced instants; (ii) demands are non-negative; (iii) demand during a period is fulfilled with the on-hand stock at the beginning of that period; (iv) the available inventory is pooled to fulfill the demand of all buyers; (v) lead time is also assumed to be zero, similar to mentioned literature, for the sake of simplicity; (vi) excess inventory is carried to the next period; and (vii) without loss of generality and for the exposition simplicity, two buyers are considered in the allocation model (i.e., \(M=2\)).

We use fill rate to assess the performance of allocation policies over an infinite horizon for each buyer (Eq. 7). In the simulation model, allocation decisions are iterated for large number of times to obtain an acceptable estimate of infinite horizon.

$$\begin{aligned} \mathcal {F}_{{m,\infty }} (p): = \frac{{\sum \nolimits _{{t = 1}}^{\infty } {\omega _{m} } (q_{{mt}} )}}{{\sum \nolimits _{{t = 1}}^{\infty } {q_{{mt}} } }} \end{aligned}$$
(7)

If the effect of strategic reasoning is disregarded, each buyer m receives the demand of \(d_{mt}\) in time t and places an order with the amount of \(q_{mt}\) to the supplier, where \(q_{mt} = d_{mt}\). Then, buyer m receives the allocated capacity of \(\omega _m(q_{mt})\) and then the corresponding fill rate \({\mathcal {F}}_{m,\infty }\), holding and shortage costs, and profit are computed for sufficiently large number of iterations. The simplest format of capacity allocation game from buyer’s perspective is presented in Eq. 8, where the supplier’s price is \(p_s\), buyer’s price for selling to the next-tier buyers is \(p_b\), and h and s are buyer’s holding and shortage costs, respectively. In this game, profit of buyer m in time t depends on the allocated capacity (\(\omega _{mt}\)) which in turn relies on the order quantities of all buyers (\(q_{mt}, q_{-mt}\)). Note that allocation functions, in majority of cases, are not differentiable, thereby the buyer’s profit function is not differentiable. Therefore, simulation seems to be the proper method of analysis for this game.

$$\begin{aligned} \max \pi _{mt}(q_{mt},q_{-mt} )= \omega _{mt} \, p_b - \omega _{mt} \, p_s - s \left[ \sum _{c=0}^t (d_{mc} - \omega _{mc})\right] ^+ \end{aligned}$$
(8)

When buyers do not strategize over order quantities in the classical format of allocation games, allocated capacity never exceeds the demands, (i.e., \(\omega _m \le q_m\); \(q_m=d_m\)). This implies that the system does not get into a holding position. and thus the term of holding cost is removed from Eq. 8. However, buyers’ strategic reasoning may cause a discrepancy between the actual needs and order quantities (i.e., \(q_{mt} \ge d_{mt}\)), and thus allocated stock may be less than or greater than the actual demand. Hence, the profit function of buyer is modified to capture the scenarios that the allocated stock may be greater than the buyer’s demand (Eq. 9).

$$\begin{aligned} \max \pi _{mt}(q_{mt},q_{-mt} )&=\min \left( \omega _{mt}+\left[ \sum _{c=0}^{t-1} (\omega _{mc}-d_{mc})\right] ^+ , \, d_{mt} \right. \nonumber \\&\left. \quad + \left[ \sum _{c=0}^{t-1} (d_{mc} - \omega _{mc})\right] ^+\right) \, p_b - \omega _{mt} \, p_s \nonumber \\&\quad -h \left[ \sum _{c=0}^t (\omega _{mc}-d_{mc})\right] ^+ -s \left[ \sum _{c=0}^t (d_{mc} - \omega _{mc})\right] ^+ \end{aligned}$$
(9)

To investigate the relationship between the demand and order quantities, behavior of buyers on strategizing over order quantities is modeled using the quantum game framework. To extend a classical game into the quantum counterpart, a Hilbert space is generally set up whereby the possible outcomes of each classical strategy are assigned to certain quantum states. This leads to quantum strategies which are operations on the quantum states. At the end, final measurement determines the game’s payoffs. Since the strategic space of allocation games is a continuum, we use a Hilbert space with a continuous set of orthogonal bases, i.e., the Hilbert space of a continuous-variable quantum system.

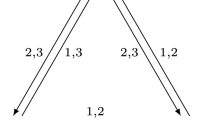
The quantum structure of an allocation game is presented in the Fig. 1. The game starts from the vacuum state \(\vert vac\rangle _1 \otimes \, \vert vac\rangle _2\) which is the tensor product of single-mode vacuum states of two electromagnetic fields. First, the state passes through a unitary operator \({\widehat{J}}(\gamma )\) which is known to both buyers. Note that for an unitary operator, \({\widehat{J}} {\widehat{J}}^\dagger = 1\) where \({\widehat{J}}^\dagger \) is the adjoint operator of \({\widehat{J}}\). \(\gamma \) is a non-negative real number that is known as the squeezing parameter of the pair and can be reasonably perceived as a measure of entanglement. When \(\gamma \rightarrow \infty \) which is the infinite squeezing limit, the relevant pair will be approximate to the Einstein-Podolsky-Rosen (EPR) state. At this stage, the state of the game is \(\vert \psi _0\rangle = {\widehat{J}}(\gamma ) \vert vac\rangle _1 \, \vert vac\rangle _2\).

Fig. 1
figure 1

Quantization of allocation model under strategic reasoning

Full size image

\({\widehat{D}}_1\) and \({\widehat{D}}_2\) are unitary operators expressing the decision-making and strategic moves of buyers 1 and 2, respectively. In the next step, the disentangling operator (\({\widehat{J}}^\dagger \)) is applied to the state before the final measurement. Hence, the final state before measurement is presented in Eq. 10.

$$\begin{aligned} \vert \psi _f\rangle = {\widehat{J}}^\dagger (\gamma ) \, ({\widehat{D}}_1 \otimes {\widehat{D}}_2) \, {\widehat{J}}(\gamma ) \, \vert vac\rangle _1 \, \vert vac\rangle _2 \end{aligned}$$
(10)

The quantum capacity allocation game should be formulated in a way that the classical version of this game can be deducted as a subset of the quantum structure (Eisert et al. 1999). In other words, the classical game is a subset of this minimal extension in the sense that the quantum game turns back to the original classical form when the initial state is not entangled, i.e., no strategic reasoning. Therefore, the entangling operator (\({\widehat{J}}\)) and the strategy set (\(S_m\)) should be defined such that when \({\widehat{J}}(\gamma ) = {\widehat{J}}^\dagger (\gamma ) = {\mathcal {I}}\) (the identity operator), the classical game is faithfully obtained. Let \({\widehat{X}}_m = ({\widehat{a}}^\dagger _m + {\widehat{a}}_m) / \sqrt{2}\) and \({\widehat{P}}_m = i \, ({\widehat{a}}^\dagger _m - {\widehat{a}}_m) / \sqrt{2}\) be the position and momentum operators of buyer m, where \({\widehat{a}}^\dagger _m ({\widehat{a}}_m)\) is the creation (annihilation) operator of buyer m’s electromagnetic field. As suggested by the Li et al. (2002), if the players are limited to select their strategies from the sets shown as below,

$$\begin{aligned} S_m = \left\{ {\widehat{D}}_m(x_m) = \text {exp}(-i \, x_m \, {\widehat{P}}_m) \, | \, x_m \in [0,\infty ) \right\} , \; m=1,2 \end{aligned}$$
(11)

the final state would be obtained as presented in Eq. 12.

$$\begin{aligned} \vert \psi _f\rangle = \left( \text {exp}(-i \, x_1 \, {\widehat{P}}_1) \vert vac\rangle _1 \right) \otimes \left( \text {exp}(-i \, x_2 \, {\widehat{P}}_2) \vert vac\rangle _2 \right) \end{aligned}$$
(12)

Accordingly, the results of \(q_1=x_1\) and \(q_2=x_2\) are obtained from the consequent final measurement which indicates that the original classical game is re-established. It can be therefore concluded that the strategic set \(S_m\) is the quantum equivalent of the classical strategic space.

We use the basic form of entanglement operator (Eq. 13) as suggested by several studies (e.g., Li et al. 2002; Zhou et al. 2005; Zhang et al. 2015; Frackiewicz and Sładkowski 2016; Yang and Zhang 2019).

$$\begin{aligned} {\widehat{J}}(\gamma )&= \text {exp} \left\{ -\gamma ({\widehat{a}}^\dagger _1 {\widehat{a}}^\dagger _2 - {\widehat{a}}_1 {\widehat{a}}_2) \right\} \nonumber \\&= \text {exp} \left\{ i \, \gamma ({\widehat{X}}_1 {\widehat{P}}_2 + {\widehat{X}}_2 {\widehat{P}}_1) \right\} \end{aligned}$$
(13)

Considering the formula of Baker-Campbell-Hausdoff and the procedure which is presented in the study of Wang et al. (2020), the following results are achieved:

$$\begin{aligned} {\widehat{J}}^\dagger (\gamma ) \, \widehat{D_1}(x_1) \, {\widehat{J}}(\gamma )&= \text {exp} \left\{ -ix_1 \left( {\widehat{P}}_1 \frac{1}{2} (e^\gamma + e^{-\gamma }) + {\widehat{P}}_2 \frac{1}{2} (e^\gamma - e^{-\gamma }) \right) \right\} \nonumber \\ {\widehat{J}}^\dagger (\gamma ) \, \widehat{D_2}(x_2) \, {\widehat{J}}(\gamma )&= \text {exp} \left\{ -ix_2 \left( {\widehat{P}}_1 \frac{1}{2} (e^\gamma - e^{-\gamma }) + {\widehat{P}}_2 \frac{1}{2} (e^\gamma + e^{-\gamma }) \right) \right\} \end{aligned}$$
(14)

This leads to the final state to be formulated as:

$$\begin{aligned} \vert \psi _f\rangle = \; \text {exp} \left\{ -i \left( x_1 \, \frac{1}{2} (e^\gamma + e^{-\gamma }) + x_2 \, \frac{1}{2} (e^\gamma - e^{-\gamma }) \right) {\widehat{P}}_1 \right\} \, \vert vac\rangle _1 \nonumber \\ \otimes \; \text {exp} \left\{ -i \left( x_1 \, \frac{1}{2} (e^\gamma - e^{-\gamma }) + x_2 \, \frac{1}{2} (e^\gamma + e^{-\gamma }) \right) {\widehat{P}}_2 \right\} \, \vert vac\rangle _2 \end{aligned}$$
(15)

Finally, given that \(x_m\) in the quantum model is representing the order quantities without presenting the strategic reasoning (i.e., \(q_m = d_m\)), order quantities of players under strategic reasoning –there is an entanglement between the order quantities of the buyers– are measured as follows:

$$\begin{aligned} q_1&= d_1 \; \frac{1}{2} (e^\gamma + e^{-\gamma }) + d_2 \; \frac{1}{2} (e^\gamma - e^{-\gamma }) \nonumber \\&= d_1 \; \cosh {\gamma } + d_2 \; \sinh {\gamma } \nonumber \\ q_2&= d_1 \; \frac{1}{2} (e^\gamma - e^{-\gamma }) + d_2 \; \frac{1}{2} (e^\gamma + e^{-\gamma }) \nonumber \\&= d_2 \; \cosh {\gamma } + d_1 \; \sinh {\gamma } \end{aligned}$$
(16)

Equation 16 shows how order quantities of buyers are related to initial demand values when they are entangled with the degree of \(\gamma \). In the next section, we compare performance of various capacity allocation policies with/without strategic reasoning over order quantities.

5 Computational results

In the Background section, it was highlighted that majority of capacity allocation policies were manipulative. However, it is still unclear as what a buyer could expect from each policy when behaving strategically. To further investigate this matter, first, performance of capacity allocation policies is probed under no strategic reasoning scenarios. Then, we compare the efficiency of policies when buyers strategize over order quantities.

To assess the allocation policies the following general settings are common to all designed scenarios. The base capacity level of supplier is \({\mathcal {K}}=100\). There are two buyers in the system \(M=2\). The selling price of supplier is \(p_s=10\$\) and buyers sell the product to the next-tier buyers with a price of \(p_b = 0.6 \times p_s = \$6\). Holding and shortage costs of buyers are \(h=\$0.005\) and \(s=\$0.005\), respectively. Demand of buyers follows a Uniform distribution \({\mathcal {U}}\)(0,1.2\({\mathcal {K}}\)). This selection ensures that in some periods the capacity binds. Each designed experiment is iterated for 1000 periods to ensure that reliable results are obtained. We assume that there is no lost sales and the unused capacities are carried over to the following periods. In the next section, a number of experiments are designed to assess effectiveness of the allocation policies with/without strategic reasoning of buyers.

How do allocation policies perform when buyers truthfully select order quantities?

To address this question, demands of buyers are sampled from \({\mathcal {U}}\)(0,120) and allocation policies are evaluated for supplier’s base capacity levels in the range of 50 to 140. Regarding the \(L_x\) policy, it is assumed that buyer 1 has the first priority for her order to be fulfilled. Figure 2 shows a comparison among performance of allocation policies when buyers do not strategize over order quantities.

Fig. 2
figure 2

Performance of allocation policies when buyers do not strategize over order quantities

Full size image

Figure 2\(a_1\) and \(b_1\) depict variations of fill rate for buyers 1 and 2 when the base capacity of supplier changes in the range of 50 to 140. Although it is intuitive to observe that fill rate increases for higher levels of supplier’s capacity, two other insights can be gleaned. First, \(L_x\) is a truth-inducing mechanism whereby no buyer has the intensive to inflate the orders. Obviously, this leads to higher fill rate for buyer 1 since she has the priority to be served and the mechanism is robust against manipulation. It is however no doubt that despite some special cases that favoring a buyer is necessary, in a free competitive market, the application of this policy is limited. The second observation is that performance of P, L, and U allocation policies are similar. This shows that irrespective of supplier’s selected allocation policy to be either P, L, or U, buyers experience the same long term fill rate for the entire range of supplier’s base capacity levels. Reviewing the mean shortage costs (Fig. 2\(a_2\) and \(b_2\)), and mean profits (Fig. 2\(a_3\) and \(b_3\)) confirms that P, L, and U allocation policies deliver the same outputs when no strategic reasoning is involved in buyers’ ordering decisions. Note that no graph for the mean holding costs of buyers is presented as holding cost is zero when buyers do not strategize over order quantities, where \(q_{mt} = d_{mt}\) and thus \(\omega _m(q) \le q_m\).

As outlined earlier, \(L_x\) is a truth-inducing allocation mechanism. Therefore, in the next sections where performance of allocation policies under strategic reasoning is investigated, \(L_x\) is excluded from the analysis.

How do allocation policies perform when one of the buyers strategizes over order quantities?

Consider a scenario that a player adopts quantum strategy while the other player still uses the classical counterpart. In the context of capacity allocation, it means that the quantum buyer may inflate the order quantity based on the entanglement level hoping to gain more profit by securing bigger slice of the limited capacity (\({\mathcal {K}}=100\)). The classical player however truthfully submits order quantities which are equal to the received demands. The entanglement level (\(\gamma \)) of the quantum buyer is considered to be in range of (0, \(\frac{\pi }{3}\)). Zero entanglement reverts the problem to its classical counterpart where order quantities are just driven by demands.

We use Eq. 16 to compute order quantities of the quantum buyer which indicates that higher entanglement values result in more inflation in order quantities. From the practical perspective, quantum buyer is unlikely to order significantly higher than what is required. Therefore, assuming high values for the entanglement level undermines practicality of the proposed experiment. Nonetheless, in this study, a wider range of entanglement level is examined to portrait potential trends.

Figure 3\(a_1\) and \(a_2\) show how fill rate of buyers using various allocation policies is impacted when buyer 1 adopts quantum strategies. It is necessary to mention that fill rate is investigated from the buyers’ perspective. To compute the value of fill rate, the total allocated capacities can be divided by either order quantities or demand values. For the buyers however it is important to realize that what proportion of the received demands are satisfied. This is also in congruence with managing service level agreements between the buyers and their own buyers in the next tier if minimizing the penalty cost of not meeting the target fill rate is the objective and fill rate is employed as the performance measure. Consequently, the quotient of total allocated capacities divided by total demands is used for computing the fill rate to investigate this performance measure from the buyers’ angle.

Fig. 3
figure 3

Performance of allocation policies when buyer 1 strategizes over order quantities

Full size image

Two import insights can be gleaned by reviewing the fill rate of buyers. First, quantum buyer outperforms the classical player in achieving higher fill rates for the entire range of entanglement levels. Thus, all three policies (P, L, U) are manipulative. Second, allocation policies do not analogously react to the inflated orders. In other words, in addition to categorizing allocation policies into truth-inducing and manipulative types, it seems crucial to understand the degree that each allocation policy can be manipulated.

While Uniform allocation policy is less sensitive to inflated demands, strategizing over order quantities by the quantum buyer where the Linear allocation policy is selected can result in significant improvement in the fill rate. From the model’s perspective, it was earlier explained that Uniform policy somehow advantages the buyer with the least order quantity. This is the reason that the Uniform policy is less influenced by the quantum buyer’s inflated orders. If the supplier’s intention is to discourage the strategic behaviors of buyers, Uniform policy seems to be the best option as fill rate of the classical buyer remains in the range of 66.0% to 73.5% while the quantum buyer can reach to 100% fill rate in very high entanglement levels. It can be also observed that degree of being manipulative for the Proportional policy is between the Uniform and Linear policies.

Reviewing the shortage cost of buyers 1 and 2 in Fig. 3\(b_1\) and \(b_2\) reveals that strategic reasoning helps the quantum buyer to secure higher fill rate and thus less shortage cost is realized. The only allocation policy that relatively protects the classical buyer from exponential growth of the shortage cost is the Uniform policy. It can be also noted that when entanglement level is greater than 0.4 for the Linear policy and 0.6 for the Proportional policy, no shortage is expected for the quantum buyer.

With respect to the holding cost, Fig. 3\(c_2\) confirms what was initially realized for the previous experiment where both players used classical strategies. In this case, holding cost is zero as buyer’s order quantity to the supplier is equal to the received order from the next-tier buyer and thus the awarded capacity never exceeds the demand. For the quantum buyer though, excessive order quantities lead to exponential rise of the holding cost when the entanglement level is higher than 0.4 and 0.6 for Linear and Proportional allocation policies, respectively. In addition, quantum buyer does not experience any holding cost for the Uniform policy as Fig. 3\(b_1\) confirms that shortages are realized for the entire range of the examined entanglement levels.

In Fig. 3\(d_1\) and \(d_2\), profit of buyers 1 and 2 is presented, respectively. When buyer 1 adopts quantum strategy, buyer 2 experiences a decline in profit. This decline is severe for Linear mechanism whereas Uniform is the the most robust policy against inflated orders of the quantum buyer. Under the Uniform policy, up to the entanglement level of approximately 0.6, quantum buyer has a slight increase in the profit which is proportionate to what the classical buyer is losing. Above 0.6, the impact of strategic reasoning is insignificant.

The most interesting observation in Fig. 3\(d_1\) is the pattern of profit for quantum buyer under Linear and Proportional policies. It is obvious that there is a trade-off between the boosted profit from higher value of allocated capacity and holding cost of the excess allocated capacity as a result of inflated orders. This trade-off justifies the existence of a local maximum in the profit of quantum buyer. The maximum profits of quantum buyer in the Proportional and Linear policies are 240 (\(\gamma =0.55\)) and 240 (\(\gamma =0.4\)), respectively. We can also notice that profit of quantum buyer for Uniform policy reaches to maximum of 115 in very high values of entanglement level which is less expected in the real business environment. When \(\gamma =0.5\), the quantum buyer can achieve a profit of 220 which is apparently less than both Proportional and Linear policies.

To understand the pattern of profit for the quantum buyer, we need to review fill rate (Fig. 3\(a_1\)), shortage cost (Fig. 3\(b_1\)), and holding cost (Fig. 3\(c_1\)). Higher level of entanglement results is higher fill rate for the quantum player. This finding makes the Uniform policy less desirable for the quantum buyer as using other two policies and strategizing over order quantities lead to higher available items and thus higher profit. Although the most growth in quantum buyer’s allocated capacities is obtained when the Linear policy is exercised, the advantage of using this policy vanishes when holding cost shows a big jump for values of \(\gamma > 0.4\). We can observe that profit of the quantum buyer using the Proportional policy reaches to the same maximum of Linear policy when \(\gamma = 0.55\). This is due to the fact that although shortage cost of Linear mechanism is less than Proportional policy when \(\gamma > 0.4\), the rate of increasing the holding cost for the Linear mechanism is higher than the Proportional policy as a result of higher fill rate for the quantum buyer.

We observe that allocation policies deliver different performances when a buyer strategizing over order quantities. However, in general, both fill rate and the cumulative profit indicate that the quantum buyer outperforms the classical one in achieving higher fill rate as well as profit for the entire range of entanglement levels. This finding however may be absent for special cases where the ratio of holding cost to the selling price is extremely high which rarely occurs in the real business world. The recommendation derived from this finding should be however taken with some reservations. Note that quantum player is never placed in the position of negative profit for the Uniform policy. Whereas, both Linear and Proportional policies may result to losing money for higher entanglement levels, i.e. \(\gamma > 0.6\) and \(\gamma > 1.1\), respectively.

How do allocation policies perform when both buyers strategize over order quantities?

Any buyer may seize an opportunity of strategic reasoning for achieving higher profit when a manipulative allocation policy is used by a supplier. Therefore, it is prudent to examine a scenario where both buyers adopt quantum strategies. Settings are the same as the previous experiment but both buyers strategize over order quantities.

Similar to the case that both buyers are classical, when both buyers are quantum, fill rate and profit for all three allocation policies are identical. In other words, when both buyers are quantum, using any of Proportional, Linear, and Uniform allocation policies leads to the same fill rate and profit for a particular value of supplier’s capacity. Accordingly, in Fig. 4 where the performance of case 1 (both buyers are classical) and case 3 (both buyers are quantum) is compared, results are independent of type of allocation policy to be either Proportional, Linear, or Uniform. The entanglement level of \(\frac{\pi }{6}\) is considered for this experiment as it was earlier shown that both Linear and Proportional policies delivered a high profit using this setting.

Fig. 4
figure 4

Comparing fill rate and profit of quantum and classical buyers over various supplier’s capacity levels

Full size image

Figure 4\(a_1\) shows the changes in fill rate of buyers when both are classical compared to the scenario that both are quantum. It can be observed that for the entire range of supplier’s capacity levels, both buyers can achieve higher fill rate if they strategize over order quantities. However, strategic reasoning reaches to it’s limitation if it is abused by the buyers. As depicted in Fig. 4\(a_2\), when the capacity is sufficiently large, strategizing over the order quantities has an adverse effect on the profit. The reason is that for this case the capacity is unlikely to bind and both players generally receive what they order. Therefore, inflating orders results in higher holding cost and also higher cost of purchasing higher number of items from the supplier. Therefore, inflating or over-inflating orders is effective for improving the fill rate but not necessarily for the profit of quantum buyers. It is crucial to note that the turning point of profit depends on the settings ruling the arrangement between the supplier and buyers and also the demand of buyers. This is a valuable insight for the quantum buyers to understand strategizing over order quantities must be taken using data-driven practices.

How do allocation policies perform when one of the buyers adopts quantum strategies with adaptive entanglement level?

It is hard to imagine that a rational decision maker with reasonable cognitive abilities sticks to a single entanglement level whereas there is an opportunity to adjust the entanglement level in any period based on the past transactions. In the previous sections, we showed how each allocation policy performed given the strategic reasoning of decision makers. In this section, it is assumed that buyer 2 remains as a quantum buyer with a fixed entanglement level (\(\gamma \)) while buyer 1 as an adaptive quantum buyer adjusts the entanglement level (\(\gamma _{adaptive}\)) based on the past allocated stock.

As delineated in the Algorithm 1, for the first thirty transitions, both buyers uses the fixed entanglement level. Afterwards, in each period (t), buyer 1 computes the Coefficient of Adjusting the Entanglement level (CAE) as per the ratio of mean shortage cost and mean holding cost incurred over the previous periods (from 0 to \(t-1\)). When this ratio is greater than one, it indicates that the adaptive quantum buyer should select higher entanglement levels whereas when CAE is less than one, the buyer needs to choose smaller value for \(\gamma \).

Note that in Eq. 16, values of demand \(d_m\) are not time dependent and the order quantities can be estimated for any combination of demands. However, since we measure the cumulative profit of buyers over multiple periods in Algorithm 1, we have adjusted the notation of demand to \(d_{mt}\) to reflect the fact that demands of buyers in each period may be non-identical.

figure a

Figure 5 illustrates the fill rate of buyers 1 and 2 for (\(a_1\)) Proportional, (\(a_2\)) Linear, and (\(a_3\)) Uniform allocation policies as well as the obtained profit (\(b_1\), \(b_2\), and \(b_3\)) for the same settings over the entanglement levels starting from zero to \(\frac{\pi }{3}\). For all allocation policies, it is obvious that the adaptive quantum buyer (buyer 1) outperforms the quantum buyer (buyer 2) from both fill rate and profit perspectives. Therefore, it is beneficial for a buyer to adopt the quantum strategies with adaptive entanglement level. In the same vein, we can observe that using the adaptive approach is more effective in smaller values of entanglement level. This is a useful insight as the likelihood of using the smaller values of entanglement level is higher.

We can notice that performance of the selected three policies is not identical when a buyer adopts quantum strategies with adaptive entanglement level. Using the Proportional and Linear mechanisms provides higher fill rate as well as higher profit for the quantum adaptive buyer (buyer 1) compared to the Uniform policy. Linear Policy however is more robust in higher entanglement levels to deliver the aforementioned advantages versus the Proportional policy. The maximum benefits of using the adaptive quantum approach remain fairly constant up to the value of \(\gamma < 0.5\) for the Proportional policy while the same benefits can be realized for higher values under Linear policy (\(\gamma < 0.9\)).

Fig. 5
figure 5

Performance of allocation policies for an adaptive quantum buyer and a quantum buyer

Full size image

6 Discussion and concluding remarks

From the first glance, psychology and quantum physics may seem entirely unrelated. However, from an interesting angle, both fields try to foresee how unruly systems might behave in the future. Whilst psychology aims to predict human behaviors, quantum physics attempts to demystify the probabilistic behavior of physical particles. Subatomic particles are in an ambiguous state known as superposition where two opposite states are simultaneously exist, e.g., putting a coin on its side. Likewise, an individual’s choices are superimposed before the measurement as the final choice is unknown and unpredictable. In addition, subatomic particles can become entangled and affect each other’s behavior even when separated by great distances. From the decision making angle of cognitive science, a similar analogy can be drawn between behaviors and beliefs. The interaction or state of entanglement between decision makers’ minds, influences the measurement outcome which is nothing but the final choice an individual makes. Therefore, considering the quantum game theory framework provides an opportunity to incorporate the entangled mind of decision makers which are in a superposition state.

There have been proliferate number of studies using game theory to solve general capacity allocation problem. When capacity binds, supplicants compete to secure higher capacity in order to maximize their profit. It is the reason various capacity allocation mechanisms have been proposed in the literature. Although some studies have attempted to investigate as whether an allocation policy is truth-inducing or manipulative, to the best of authors’ knowledge, it is still unclear to what extent an allocation policy can be manipulated.

In this study, we use the quantum game framework to probe how strategic reasoning of buyers may impact the performance of five capacity allocation policies: Proportional, Linear, Relaxed Linear, Uniform, and Lexicographic. Four experiments have been designed and the following insights have been gleaned: (i) despite using the Relaxed Linear policy in various literature, as it sometimes deliver negative allocations, we have removed this policy from the analysis. (ii) \(L_x\) is a truth-inducing mechanism whereby no buyer has an intensive to inflate the orders. It delivers higher performance to the buyer with the predetermined priority. (iii) When buyers truthfully submit their order quantities, performance (fill rate and profit) of P, L, and U mechanisms is identical. (iv) When one of the buyers adopts quantum strategies and strategizes over order quantities, P, L, and U are manipulative. In this case, the quantum buyer receives higher fill rate than the classical buyer for the entire range of examined entanglement levels. Uniform mechanism though is the least manipulative policy compared to the P and L. The highest fill rate can be achieved under Linear policy; however, profit of the quantum buyer gets to a maximum point for L and P policies and then it decreases to even negative values for higher entanglement levels. The growth in profit of the quantum buyer under U policy is minimal for increasing values of entanglement levels; however, it never leads to a loss situation. (v) When both buyers are quantum and using strategic reasoning to adjust their order quantities, higher fill rate is achieved for the entire range of examined supplier’s capacity levels. On the other hand, profit of quantum buyers gets to its topmost point for a certain value of supplier’s capacity and it decreases to even less than the classical buyers for very high values of supplier’s capacity. When demand distribution of buyers are considered, in a reasonable range of supplier’s capacity, profit resulting from quantum strategies outperforms the classical counterparts. (vi) Profit and fill rate of an adaptive quantum buyer are always higher than the quantum buyer for all examined allocation policies (P, L, and U). In addition, the influence of using the adaptive approach is the least under the Uniform policy. Moreover, the range of entanglement level for which a policy approximately delivers the maximum profit is wider for the Linear policy.

From the theoretical perspective, this study contributes to understanding how strategic reasoning of decision makers may influence the allocation decisions using the quantum game framework. We have shown how entangled minds of buyers who are strategizing over order quantities impact the outcome of the game including the fill rate and profit. As practical contributions, this research provides a guideline for supplier as to what degree an allocation policy could be manipulative. Similarly, it suggests the buyers on how to maximize their profit when dealing with various allocation mechanisms.

This study also portraits four avenues for the future research in this domain. First, empirical studies may attempt to determine the entanglement level between two decision makers as it has a profound impact on the outcome of the game. Second, in computing quantum order quantities, demand of competitor is assumed to be known. Given a known market share for each player in industry, estimating the demand of competitor is not an error-free process. Therefore, future studies may investigate how forecasting errors regarding the competitors’ demands may influence the game outcomes. Third, we encourage the researchers to assess other allocation policies which have not been covered in this study. Fourth, we have examined the allocation policies in the case that the inventory is carried over to the future periods. Future studies may overcome this limitation by testing the allocation mechanisms under the lost sales scenario. Finally, as allocation policies are frequently employed in service level agreements with linear and non-linear penalties/incentives, we suggest to investigate how penalty cost of not meeting the agreed service level may influence the provided insights.