Abstract
We introduce Spectra, a new specification language for reactive systems, specifically tailored for the context of reactive synthesis. The meaning of Spectra is defined by a translation to a kernel language. Spectra comes with the Spectra Tools, a set of analyses, including a synthesizer to obtain a correct-by-construction implementation, several means for executing the resulting controller, and additional analyses aimed at helping engineers write higher-quality specifications. We present the language in detail and give an overview of its tool set. Together with the language and its tool set, we present four collections of many, non-trivial, large specifications, written by undergraduate computer science students for the development of autonomous Lego robots and additional example reactive systems. The collected specifications can serve as benchmarks for future studies on reactive synthesis. We present the specifications, with observations and lessons learned about the potential use of reactive synthesis by software engineers.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Reactive synthesis is an automated procedure to obtain a correct-by-construction reactive system from its temporal logic specification [66]. Rather than manually constructing an implementation and using model-checking or testing to verify it against a specification, see Fig. 1 top, synthesis offers an approach where a correct implementation of the system is automatically obtained for a given specification, see Fig. 1 bottom, if such an implementation exists.
As the correct-by-construction promise is attractive, much research effort has been invested and much progress has been achieved over the last two decades on reactive synthesis theory, algorithms, and tools. These include, e.g., the identification of expressive fragments of temporal logics that have efficient, symbolic synthesis solutions [10, 41, 42], various kinds of compositional synthesis [46], controller synthesis for probabilistic systems [20, 44], support for the addition of quantitative criteria [5], bounded synthesis [26], and tools such as RATSY [6], and Slugs [22], to list a few. Still, major challenges remain on the way to bringing the correct-by-construction promise to software engineering practice.
Some of these challenges are at the level of the specification language, i.e., the syntax, semantics, and expressiveness of reactive specifications. First, the language should have features that are specific to its use in the context of reactive synthesis, such as the explicit distinction between system and environment variables, and the explicit distinction between guarantees and assumptions. Second, careful balance should be found between the language’s usability to engineers, in writing and reading, on the one hand, and its formal expressive power, on the other hand. Finally, the language alone may not be enough to address all challenges. Rather, a set of analyses and tools, beyond synthesis itself, specifically tailored for the new language and its use in an end-to-end reactive synthesis environment, is required, for example, in debugging specifications and in executing the synthesized controllers. In this paper we describe the results of our research efforts over the last five years, to start developing such language and tool set.
We introduce Spectra, a new specification language for reactive systems, specifically tailored for the context of reactive synthesis. The meaning of Spectra is defined by a translation to a kernel language. Importantly, beyond the kernel, Spectra includes advanced language features like parametric predicates, monitors, bounded integers and arithmetic operations, a library of patterns and means to define new patterns, bounded counters, and quantified arrays. These advanced language features, some of which are unique to Spectra, are meant to enable and encourage reuse and support specifications’ readability and maintainability by engineers.
Spectra comes with the Spectra Tools, a set of analyses, including not only a synthesizer to obtain a correct-by-construction implementation, but also several means for executing the resulting controller. It further includes additional analyses aimed at helping engineers write higher-quality specifications, including, e.g., several means to dealing with unrealizable and non-well-separated specifications.
To date, Spectra has been used by small teams of undergraduate computer science students for the development of autonomous Lego robots and additional example reactive systems in four-semester long project classes we have taught at Tel Aviv University, in 2015, 2017, 2019, and 2020. From these classes, we have collected over 320 versions of specifications of about 10 different Lego robots and 14 additional systems, all written by these students as they worked on their projects for several months. Thus, together with the language and the tool set, we present four collections of many, non-trivial, large specifications. The collections can serve as benchmarks for future studies on reactive synthesis. We present the specifications the students wrote, with observations and lessons learned about the potential use of reactive synthesis by software engineers.
It is important to note that Spectra is designed for general purpose reactive systems specifications rather than for the particular domain of robotics (as, e.g., in the case of LTLMop [27]). Spectra is also not to be confused for an architecture modeling language for robotic systems (as, e.g., RoboChart [60] or MontiArcAutomaton [69]). Spectra can and has been used in combination with C&C modeling languages for code generation and the deployment of synthesized controller on robots [50, 52], but, as already demonstrated in the SYNTECH collection of specifications, this is only one of the use cases of Spectra.
Finally, currently, Spectra is not about specifications that cover probabilistic, timed, or other quantitative requirements. Many other works, including some by the authors of the present paper, have discussed various extensions of synthesis to handle specifications with these objectives [2, 5, 11, 16, 36, 48]. We believe that adding language elements for expressing these and similar objectives, and extending Spectra Tools to support them, is possible; however, it is outside the scope of our current work.
A number of logics and languages exist for the specification of reactive systems. These include linear temporal logic (LTL) [65], Property Specification Language (PSL) [23], SMV—the input language of the NuSMV tool [15], TLA\(^+\) [45] (Temporal Logic of Actions), and the Temporal Logic Synthesis Format (TLSF) [35]. Moreover, a number of specification languages for reactive synthesis have been developed on top of GR(1), with related synthesis tools, including ApsectLTL [54], LTLMop (Linear Temporal Logic MissiOn Planning) [27], SGR(1) [12, 17], Slugs (SmalL bUt Complete GROne Synthesizer) [22], Open Promela [25], Tulip [24, 76], and RATSY [6]. As we show, Spectra has unique language features, unique supporting analyses and execution mechanisms, and a large set of benchmark specifications, not available for these other languages and tools. We discuss the above languages and tools and compare them to Spectra in Sect. 8.
The contributions of this paper are as follows:
-
We present the Spectra language definition, including formal syntax and semantics of its unique constructs. While a few previous papers have already used small example specifications written in Spectra, in the limited context of presenting a specific new analysis (e.g., for non-well-separation [51], for unrealizability [43, 53], for vacuity [57]), the syntax and semantics of the language were not presented before. Moreover, several of the unique and powerful constructs of the language, beyond the kernel, including monitors, PastLTL operators, bounded counters, and quantified arrays, did not appear in any previous publication.
-
We present an overview of Spectra Tools. While specific tools have been individually presented in previous publications (e.g., for dealing with unrealizability [43]), an overview of the Spectra Tools architecture and tool set did not appear before. All tools we report on in our overview have been implemented and already used by the undergraduate students who participated in our project classes and created the specifications in the four collections.
-
We present four collections of specifications, all written by undergraduate students in project classes we have taught. Together, the collections include over 320 versions of specifications of about 10 different Lego robots and 14 additional systems. The collections are larger and more complex than all previous collections of reactive systems specifications published in the context of synthesis, and can thus serve as new benchmarks for future studies in the field.
-
We present a discussion of design decisions, observations, and lessons we have learned from the development of Spectra and Spectra Tools and from our experience with it so far. The discussion covers topics such as the difficulty of writing specifications, the necessity of internal symbolic representations, the fundamental design decision of choosing GR(1) as kernel for Spectra, the decision to implement our own synthesizer, and the decision to make Spectra domain agnostic.
Spectra and Spectra Tools aim to advance the state of the art in reactive synthesis. For engineers who develop reactive systems, they provide a novel and friendly language and environment to experience writing formal specifications, examine the idea of reactive synthesis, and start considering whether and how it may be applicable to the systems they develop. For researchers, they provide a testbed and benchmark data for future research on specification languages and reactive synthesis development environments. We make Spectra, Spectra Tools, and all specifications we report about publicly available for inspection and further use by engineers and researchers.
1.1 Paper structure
The paper is structured as follows. Section 2 provides necessary background on linear temporal logic and its GR(1) fragment, which are required for the formal definition of Spectra semantics. Section 3 introduces a small language kernel of Spectra and defines the semantics of a specification as a GR(1) synthesis problem. This section also introduces an example specification that serves as a running example throughout the paper. Section 4 covers the language elements Spectra provides and defines their semantics via translations to the kernel. In Sect. 5 we give an overview of Spectra Tools. We describe our preliminary experience with Spectra in Sect. 6, which is mainly based on observations from the project classes we have taught over the five years where students have used Spectra and Spectra Tools to develop about 10 different autonomous Lego robots and several additional systems. In Sect. 7 we discuss lessons learned about Spectra, Spectra Tools, and our design decisions. We discuss related work in Sect. 8 and conclude in Sect. 9.
2 Background
We provide background on linear temporal logic and synthesis, which is required for the definition of Spectra syntax and semantics. We continue with the notation that we use to define the grammar of Spectra.
2.1 Linear temporal logic and synthesis
We repeat some of the standard definitions of linear temporal logic (LTL), e.g., as found in [10], a modal temporal logic with modalities referring to time [65]. The syntax of LTL formulas is typically defined over a set of atomic propositions \( AP \) with the future temporal operators
 (next) and
(next) and  (until). Intuitively, an atomic proposition is similar to a Boolean variable. If the variable is true, the atomic proposition is present; if the variable is false, the atomic proposition is absent.
(until). Intuitively, an atomic proposition is similar to a Boolean variable. If the variable is true, the atomic proposition is present; if the variable is false, the atomic proposition is absent.
Definition 1
The syntax of LTL formulas over \( AP \) is
 for \(p \in AP \).
for \(p \in AP \).
For \(\Sigma = 2^ AP \), a computation \(u=u_0u_1..\in \Sigma ^\omega \) is a sequence where \(u_i\) is the set of atomic propositions that hold at the i-th position. For position i we use \(u,i\models \varphi \) to denote that \(\varphi \) holds at position i, inductively defined as:
-
\(u,i\models p\) iff \(p \in u_i\);
-
\(u,i\models \lnot \varphi \) iff \(u, i \not \models \varphi \);
-
\(u,i\models \varphi _1 \vee \varphi _2\) iff \(u,i\models \varphi _1\) or \(u,i\models \varphi _2\);
-
 iff \(u, i{+}1\models \varphi \);
iff \(u, i{+}1\models \varphi \); -
 iff \(\exists k\ge i{:~} u,k\models \varphi _2\) and \(\forall j, i\le j < k{:~} u,j\models \varphi _1.\)
iff \(\exists k\ge i{:~} u,k\models \varphi _2\) and \(\forall j, i\le j < k{:~} u,j\models \varphi _1.\)
We denote \(u,0\models \varphi \) by \(u \models \varphi \). We use additional LTL operators
 (finally) where
(finally) where  and
and
 (globally), where
(globally), where  .
.
Finally, we also use PastLTL [29] operators
 (previously, dual of
(previously, dual of
 ) and
) and  (since, dual of
(since, dual of  ):
):
-
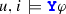 iff \(i> 0 \wedge u,(i-1) \models \varphi \);
iff \(i> 0 \wedge u,(i-1) \models \varphi \); -
 iff \(\exists k \le i{:~} u,k\models \varphi _2\) and \(\forall j, k < j \le i{:~} u,j\models \varphi _1.\)
iff \(\exists k \le i{:~} u,k\models \varphi _2\) and \(\forall j, k < j \le i{:~} u,j\models \varphi _1.\)
We use additional PastLTL operators
 (once), where
(once), where  , and
, and
 (historically), where
(historically), where  .
.
LTL formulas can be used as specifications of reactive systems where atomic propositions are represented by Boolean variables. The set of variables representing atomic propositions is partitioned into Boolean environment (input) and system (output) variables. An assignment to all variables is called a state.
A strategy for an LTL specification \(\varphi \) prescribes the outputs of a system that from its winning states for all environment choices lead to computations that satisfy \(\varphi \). A specification \(\varphi \) is called realizable if a strategy exists such that for all initial environment choices the initial states are winning states. The goal of LTL synthesis is, given an LTL specification, to find a strategy that realizes it, if one exists.
To illustrate the difference between LTL model-checking and LTL synthesis in Fig. 1, we could replace specification by LTL formula and implementation by controller (a formalization of a strategy).
2.2 Generalized reactivity of rank 1 (GR(1))
LTL synthesis is computationally expensive. Thus, authors have suggested fragments of LTL that have efficient synthesis algorithms.
GR(1) is a fragment of LTL that has an efficient symbolic synthesis algorithm [10, 64] and whose expressive power covers most of the well-known LTL specification patterns of Dwyer et al. [21, 49]. GR(1) specifications include assumptions and guarantees about what needs to hold on all initial states, on all states and transitions (safety), and infinitely often on every run (justice). A GR(1) synthesis problem consists of the following elements [10]:
-
\({\mathcal {X}}\) is a set of Boolean input variables controlled by the environment;
-
\({\mathcal {Y}}\) is a set of Boolean output variables controlled by the system;
-
\(\theta ^e\) is an assertion, i.e., a propositional logic formula, over \({\mathcal {X}}\) characterizing initial environment states;
-
\(\theta ^s\) is an assertion over \({\mathcal {X}} \cup {\mathcal {Y}}\) characterizing initial system states;
-
\(\rho ^e({\mathcal {X}}, {\mathcal {Y}}, {\mathcal {X}}')\) represents constraints on the transition relation of the environment, where \({\mathcal {X}}'\) denotes a primed copy of variables \({\mathcal {X}}\), i.e., given a current state, \(\rho ^e\) restricts the next input;
-
\(\rho ^s({\mathcal {X}}, {\mathcal {Y}}, {\mathcal {X}}', {\mathcal {Y}}')\) represents constraints on the transition relation of the system, where \({\mathcal {X}}'\) and \({\mathcal {Y}}'\) denote primed copies of variables \({\mathcal {X}}\) and \({\mathcal {Y}}\), i.e., given a current state and next input, \(\rho ^s\) restricts the next output;
-
\(J^e_{i \in 1..n}\) is a set of assertions over \({\mathcal {X}} \cup {\mathcal {Y}}\) for the environment to satisfy infinitely often (called justice assumptions);
-
\(J^s_{j \in 1..m}\) is a set of assertions over \({\mathcal {X}} \cup {\mathcal {Y}}\) for the system to satisfy infinitely often (called justice guarantees).
A GR(1) synthesis problem is strictly realizableFootnote 1 iff the following LTL formula is realizable:

Specifications for GR(1) synthesis have to be expressible in the above structure and thus do not cover the complete LTL. Efficient symbolic algorithms for GR(1) realizability checking and controller synthesis have been presented in [10, 64].
As an example, consider a GR(1) synthesis problem to synthesize the controller for the traffic light of a simple junction with a main street and a side street (this example is illustrated in Fig. 3 and further explained in Sect. 3.1):
-
\({\mathcal {X}} = \{cm, cs\}\) represents information about a car on the main street (cm) and on the side street (cs);
-
\({\mathcal {Y}} = \{gm, gs\}\) represents control over a green light on the main street (gm) and on the side street (gs);
-
\(\theta ^e={\lnot }cm \wedge {\lnot }cs\), i.e., initially there is no car on the main street nor the side street;
-
\(\theta ^s=\top \), i.e., no restriction on initial outputs;
-
\(\rho ^e=\top \), i.e., no safety assumptions;
-
\(\rho ^s=\lnot (gm \wedge gs)\), i.e., the main street and side street never have a green light at the same time;
-
\(J^e=\{cm, cs\}\), i.e., cars are always eventually appearing on the main street and on the side street;
-
\(J^s=\{gm, gs\}\), i.e., the light must always eventually turn green on the main street and on the side street.
This example GR(1) synthesis problem is realizable iff this LTL formula is realizable:

An example strategy that satisfies this GR(1) synthesis problem could alternate between output \(gs \wedge {\lnot }gm\) and output \({\lnot }gs \wedge gm\), which ensures that the lights are never green at the same time and that always eventually each light will turn green. The goal of reactive synthesis is to compute such strategies automatically.
GR(1) synthesis has been used and extended in different contexts and for different application domains, including robotics [40, 47, 52], scenario-based specifications [55], aspect languages [54], event-based behavior models [18], hybrid systems [24], and device drivers [74], to name a few.
2.3 Extended notation for context-free grammars
The Spectra language is defined by a context-free grammar. We now describe the grammar notation that we use throughout this paper. Our notation is based on common concepts known from language workbenches, e.g., MontiCore [33] and XText [77]. An excerpt of the Spectra grammar is shown in Fig. 2.
Production rules are enclosed in brackets and printed bold. As an example, the production rule for symbol
 is defined in Fig. 2, l. 5 and referenced in l. 3 inside the definition of the production rule for symbol
is defined in Fig. 2, l. 5 and referenced in l. 3 inside the definition of the production rule for symbol
 . We use common multiplicity symbols for defining the number of repetitions of elements, where \(*\) denotes zero or more repetitions, \(+\) denotes at least one repetition, and ? denotes zero or one repetitions, i.e., the element is optional. As an example, the declaration of specification elements (
. We use common multiplicity symbols for defining the number of repetitions of elements, where \(*\) denotes zero or more repetitions, \(+\) denotes at least one repetition, and ? denotes zero or one repetitions, i.e., the element is optional. As an example, the declaration of specification elements (
 , l. 3) is repeated at least once. Terminals of the grammar that are also keywords of Spectra are printed in blue, e.g., the keywords
, l. 3) is repeated at least once. Terminals of the grammar that are also keywords of Spectra are printed in blue, e.g., the keywords
 ,
,  , and
, and  . Other terminals are printed in gray, e.g., the semicolon (
. Other terminals are printed in gray, e.g., the semicolon (
 , l. 7) after a variable declaration.
, l. 7) after a variable declaration.
Grammar extensions For readability and modular language definition, we introduce two extensions to the grammar notation. First, we introduce internal names for produced symbols, e.g., the name elems for the list of
 in Fig. 2, l. 3. We refer to these internal names when we describe well-formedness rules of Spectra documents. Second, we introduce the grammar-level keyword
in Fig. 2, l. 3. We refer to these internal names when we describe well-formedness rules of Spectra documents. Second, we introduce the grammar-level keyword
 to denote the extension of production rules. As an example, the production
to denote the extension of production rules. As an example, the production
 extends
extends  in Fig. 2, l. 9. As a result of the extension, the symbol
in Fig. 2, l. 9. As a result of the extension, the symbol
 can replace any occurrence of the symbol
can replace any occurrence of the symbol
 . Note the difference between
. Note the difference between
 and
and  which are both alternatives for
which are both alternatives for  . The difference is that production rule
. The difference is that production rule
 was included in the definition of
was included in the definition of  , while the production rule
, while the production rule
 was added later. We use this extension mechanism when we add new language features. Finally, we introduce the grammar-level keyword
was added later. We use this extension mechanism when we add new language features. Finally, we introduce the grammar-level keyword
 to denote that a new production rule replaces an existing production rule. As an example, the production
to denote that a new production rule replaces an existing production rule. As an example, the production
 replaces
replaces  in Sect. 4.10, Fig. 13, l. 1. As a result of the replacement, the symbol
in Sect. 4.10, Fig. 13, l. 1. As a result of the replacement, the symbol
 replaces any occurrence of the symbol
replaces any occurrence of the symbol
 .
.
Special productions We make use of three standard, primitive productions that we do not define in any production rule. These are
 for file names,
for file names,  for names of elements, and
for names of elements, and
 for integers.
for integers.
Simplification The parts of the Spectra grammar we show in Sects. 3 and 4, present a simplified version of the grammar that we use in the implementation of Spectra Tools, described in Sect. 5. For the purpose of presentation, we have simplified the production rules. As an example, it is common to encode operator precedence directly into production rules in order to simplify the parsing of specifications. This implementation related formulation blows up the grammar of expressions as every operator might require a separate production rule. We present a simplified version of the grammar and define operator precedence when we describe each language element.
3 Spectra kernel
Spectra is based on a small kernel language for writing specifications. The Spectra kernel contains only the essential elements to formulate GR(1) synthesis problems. Specifically, these language elements are Boolean environment variable declarations, Boolean system variable declarations, assumptions, and guarantees. We now introduce the syntax of the Spectra kernel and then give the semantics of specifications as GR(1) synthesis problems. We will extend and modify the example as we introduce new language elements throughout Sect. 4.
3.1 Example
Consider a traffic light on a simple junction as shown in Fig. 3. A team of engineers specified this system in Lst. 1 using only language elements of the Spectra kernel.
As a first step, the engineers identify the environment and system controlled variables by determining the inputs and outputs of the system. Two Boolean environment variables carMain and carSide (Lst. 1, ll. 3–4) model sensors to notify whether there is traffic on the main street or on the side street, respectively. The system controls two traffic lights through the Boolean variables greenMain and greenSide (Lst. 1, ll. 6–7).
Next, the engineers define assumptions, which characterize environment behavior, and guarantees, which express the required system behavior. The team assumes that initially there is no traffic and that always eventually there is traffic on each of the streets (Lst. 1, ll. 9–11). The system has to guarantee that traffic passage at the same time on both streets never occurs (Lst. 1, l. 13). In addition, the system has to guarantee to always eventually allow traffic passage on each of the streets (Lst. 1, ll. 14–15).
Finally, the engineers check whether the specification is realizable and synthesize an implementation. In case an implementation cannot be found, the engineers update the specification by weakening guarantees or strengthening assumptions. The Spectra specification shown in Lst. 1 is realizable. A simple, possible implementation keeps one traffic light green until a car arrives and passes, and then repeats the same for the other street.

3.2 Syntax
A grammar of the Spectra kernel is shown in Fig. 4. Every valid specification can be produced from the production rule
 of the kernel grammar (and its extensions we present in Sect. 4).
of the kernel grammar (and its extensions we present in Sect. 4).
Every specification starts with the keyword
 and a name. The name of a specification is only informative and has no technical meaning. A specification contains one or more specification elements
and a name. The name of a specification is only informative and has no technical meaning. A specification contains one or more specification elements
 . Specification elements of the Spectra kernel are variable declarations (Fig. 4, l. 7), assumptions (Fig. 4, l. 11), and guarantees (Fig. 4, l. 16).
. Specification elements of the Spectra kernel are variable declarations (Fig. 4, l. 7), assumptions (Fig. 4, l. 11), and guarantees (Fig. 4, l. 16).
Variable declarations introduce variables controlled by the environment (keyword
 ) or by the system (keyword
) or by the system (keyword
 ). Variables have a type and a name. The only type available in the kernel is
). Variables have a type and a name. The only type available in the kernel is
 (Fig. 4, l. 9).
(Fig. 4, l. 9).
Assumptions have an optional name and can be of three kinds. They are either initial assumptions (keyword
 ), safety assumptions (keyword
), safety assumptions (keyword
 ), or justice assumptions (keyword
), or justice assumptions (keyword
 ).Footnote 2 All assumption kinds are formulated by expressions
).Footnote 2 All assumption kinds are formulated by expressions
 (Fig. 4, l. 21). Expressions follow standard definitions of propositional expressions. The unary operators of expressions are negation and
(Fig. 4, l. 21). Expressions follow standard definitions of propositional expressions. The unary operators of expressions are negation and
 , the binary operators are standard Boolean operators and equality, and the primary expressions are
, the binary operators are standard Boolean operators and equality, and the primary expressions are
 ,
,  , and references to variables (Fig. 4, l. 30). The precedence of operators in expressions from strongest binding to weakest is
, and references to variables (Fig. 4, l. 30). The precedence of operators in expressions from strongest binding to weakest is
 ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  . As usual, binary operators associate from left to right.
. As usual, binary operators associate from left to right.
Guarantees are defined analogously to assumptions, with the exceptions of the keyword
 instead of
instead of  and differences in well-formedness rules.
and differences in well-formedness rules.
Well-formedness rules The names of variables, assumptions, and guarantees have to be unique. An initial assumption cannot reference system variables. A safety assumption cannot nest references to system variables in the scope of the
 operator. A
operator. A  operator cannot be (transitively) nested inside a
operator cannot be (transitively) nested inside a
 operator.
operator.
Scopes The Spectra kernel contains three kinds of named elements: variables, assumptions, and guarantees. The scope of variable names is global, i.e., the names of variables have to be unique and variables can be referenced from anywhere in the specification. The scope of names of assumptions and guarantees is also global but they cannot be referenced from anywhere inside the specification.
3.3 Semantics
The semantic domain of the Spectra kernel language is GR(1) synthesis problems. We define the semantics of the Spectra kernel by translating every well-formed specification to a GR(1) synthesis problem.
Given a Spectra specification m, its semantics is defined by the following GR(1) synthesis problem:
-
\({\mathcal {X}}\) is the set of all variables declared in m with the keyword
 ;
; -
\({\mathcal {Y}}\) is the set of all variables declared in m with the keyword
 ;
; -
\(\theta ^e\) is the conjunction of the semantics of all initial assumptions (with keyword
 );
); -
\(\theta ^s\) is the conjunction of the semantics of all initial guarantees (with keyword
 );
); -
\(\rho ^e({\mathcal {X}} \cup {\mathcal {Y}}, {\mathcal {X}}')\) is the conjunction of the semantics of all safety assumptions (with keyword
 );
); -
\(\rho ^s({\mathcal {X}} \cup {\mathcal {Y}}, {\mathcal {X}}' \cup {\mathcal {Y}}')\) is the conjunction of the semantics of all safety guarantees (with keyword
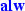 );
); -
\(J^e_{i \in 1..n}\) is the set of the semantics of all justice assumptions (with keyword
 );
); -
\(J^s_{j \in 1..m}\) is the set of the semantics of all justice guarantees (with keyword
 ).
).
To obtain the semantics of assumptions and guarantees, we translate their expression
 to assertions in the GR(1) synthesis problem. This translation is straightforward on the structures of
to assertions in the GR(1) synthesis problem. This translation is straightforward on the structures of
 . The symbols of Boolean operators of
. The symbols of Boolean operators of
 and
and  are translated to their counterparts in assertions. The keywords
are translated to their counterparts in assertions. The keywords
 and
and  of
of  are translated to a contradiction and a tautology, respectively. A variable reference of
are translated to a contradiction and a tautology, respectively. A variable reference of
 is translated to an assertion over a Boolean variable from \({\mathcal {X}}\) and \({\mathcal {Y}}\) with the referenced name. Finally, the unary operator
is translated to an assertion over a Boolean variable from \({\mathcal {X}}\) and \({\mathcal {Y}}\) with the referenced name. Finally, the unary operator
 substitutes all variables from \({\mathcal {X}}\) and \({\mathcal {Y}}\) in its scope with corresponding primed variables from \({\mathcal {X}}'\) and \({\mathcal {Y}}'\).
substitutes all variables from \({\mathcal {X}}\) and \({\mathcal {Y}}\) in its scope with corresponding primed variables from \({\mathcal {X}}'\) and \({\mathcal {Y}}'\).
To illustrate the semantics, note that the specification shown in Lst. 1 corresponds to the GR(1) synthesis problem example presented at the end of Sect. 2.2. The environment variables carMain and carSide correspond to atomic propositions cm and cs. The assumption
 from Lst. 1, l. 9 is translated to \(\theta ^e={\lnot }cm \wedge {\lnot }cs\) in Sect. 2.2.
from Lst. 1, l. 9 is translated to \(\theta ^e={\lnot }cm \wedge {\lnot }cs\) in Sect. 2.2.
4 Spectra language elements
We now present the Spectra language elements beyond the kernel language. The language elements we present include enumerations and bounded integers (Sect. 4.1), defines and type definitions with arrays (Sect. 4.2), state invariants (Sect. 4.3), PastLTL operators (Sect. 4.4), predicates (Sect. 4.5), monitors (Sect. 4.6), counters (Sect. 4.7), patterns (Sect. 4.8), quantification (Sect. 4.9), and imports (Sect. 4.10).
For each language element we (1) discuss the motivation to have it in the language (including an example in the context of the junction from Lst. 1 – a complete example of most language elements in one specification is shown in App. B), (2) present its syntax as a grammar that extends the Spectra kernel, (3) list well-formedness rules of the extended language, (4) discuss the scope of newly introduced named elements, and finally (5) present the semantics of new elements.
Note that we define the semantics of Spectra language elements by a translation to Spectra without the new language element. A direct translation to the Spectra kernel would be possible but often more complicated because all combinations of language elements would have to be considered in the translation, e.g., references to defines can appear in parameters of predicates. Instead, we present modular translations that allow for the combination of any subset of Spectra language elements. The application of all semantics defining translations will result in a specification in the Spectra kernel language. This design also ensures that extensions of the Spectra kernel beyond GR(1) will directly support the new Spectra language elements.Footnote 3
4.1 Enumerations and bounded integers
4.1.1 Motivation
The Spectra kernel contains only Boolean variables. However, in many cases it is more convenient to use enumerations of values to define the type of a multi-valued variable. As an example, system variable go in Lst. 2, l. 6 has values MAIN, SIDE, and NONE. In expressions, these values can be used and compared to each other and to variables of the same type.
Similarly, some values are best modeled using integers. Spectra supports a bounded integer type with lower and upper bounds. An example appears in Lst. 2 where the variables carsMain and carsSide are of integer type with values from 0 to 10 and 0 to 6, respectively. Bounded integers can be compared to integer literals, arithmetic expressions, and other integer variables (see Lst. 2, ll. 9-11) even when their bounds are different.

4.1.2 Syntax
The syntax of enumerations and bounded integers is shown in Fig. 5. Enumerations are defined by production rule
 and consist of a list of names enclosed in curly brackets
and consist of a list of names enclosed in curly brackets  ,
,  . Names of enumeration values can be referenced as primary expressions (Fig. 5, ll. 5–6), e.g., they can also be used in expressions.
. Names of enumeration values can be referenced as primary expressions (Fig. 5, ll. 5–6), e.g., they can also be used in expressions.
Bounded integer types in Spectra start with
 , followed by lower and upper bounds in parenthesis (Fig. 5, ll. 9–10). We also add arithmetic operators for addition, subtraction, multiplication, division, and modulo to Spectra, together with inequalities in Fig. 5, l. 12–13. The inequalities bind with the same priority as equality, and the arithmetic operators bind stronger than all previously introduced operators. Finally, we add arithmetic negation as a unary operator and integer constants as primary expressions in Fig. 5, ll. 15–19.
, followed by lower and upper bounds in parenthesis (Fig. 5, ll. 9–10). We also add arithmetic operators for addition, subtraction, multiplication, division, and modulo to Spectra, together with inequalities in Fig. 5, l. 12–13. The inequalities bind with the same priority as equality, and the arithmetic operators bind stronger than all previously introduced operators. Finally, we add arithmetic negation as a unary operator and integer constants as primary expressions in Fig. 5, ll. 15–19.
Well-formedness rules The names of enumeration values must be unique and different from variable names. Equality is the only comparison allowed for enumeration values and variables of enumeration type and Boolean type. The upper bound upper of a bounded integer must be strictly greater than its lower bound lower. The new operators
 and
and  can only be used in arithmetic expressions constructed from these operators, primitive values
can only be used in arithmetic expressions constructed from these operators, primitive values
 , and references to integer variables (alternative varRef of
, and references to integer variables (alternative varRef of
 ).
).
4.1.3 Semantics
We define the semantics of enumerations and bounded integers by a translation into Spectra without enumerations and bounded integers. We translate every variable of an enumeration type with \(n=|vals|\) values to \(\lceil \log _2(n)\rceil \) Boolean variables. To every value in vals, we assign one combination of values of the new variables. We add initial and safety constraints to the specification so that the new variables represent one of the defined values (important for \(2^{\lceil \log _2(n)}\rceil > n\)). We translate every equality expression involving enumerations to equivalent expressions over the Boolean variables that encode them.
Similarly, we translate every bounded integer variable to \(\lceil \log _2(upper-lower)\rceil \) Boolean variables. For the translation of bounded arithmetic expressions, we employ an encoding inspired by Bartzis and Bultan [4].
4.2 Defines and type definitions with arrays
4.2.1 Motivation
Specifications often contain sub-expressions that reoccur multiple times. In the example of the traffic light, one might expect that many constraints refer to empty streets, formally carSide=false & carMain=false. If these reoccurring expressions get longer and more complicated, the overall specification becomes harder to read and difficult to maintain, e.g., when updating a condition. To support more concise specifications and to simplify the maintenance of reoccurring sub-expressions, Spectra introduces defines. In the traffic light example, we might introduce the name streetsEmpty for the expression carSide=false & carMain=false shown in Lst. 3, ll. 1-2. Assumptions and guarantees may then use streetsEmpty as a reference to the define (ll. 4-6).

Similarly, several variables in a specification may be of the same type. Here, to support more concise specifications and to simplify the maintenance of reoccurring types, Spectra introduces type definitions. In Lst. 4, the enumeration type Item is defined by a type definition in l. 1 and referenced as the type of a system variable in l. 4.
Finally, the readability of some specifications benefits from using array types rather than many individual variables. As an example, we define a two-dimensional array of type Item in Lst. 4, l. 4 with both dimensions of size 10, i.e., an array with 100 fields. The initial guarantee in Lst. 4, l. 6 references a field of the array and states that its value is ROBOT of the array’s type Item.

4.2.2 Syntax
The syntax of defines and type definitions is shown in Fig. 6. Defines are specification elements and thus appear as top level elements inside specifications. Defines have a name and an expression. References to defines
 are primary expressions (Fig. 6, l. 4).
are primary expressions (Fig. 6, l. 4).
Type definitions (Fig. 6, l. 8) are also specification elements and thus appear as top level elements inside specifications. Type definitions have a name and a type.
References to type definitions
 are treated as types (Fig. 6, l. 13). We introduce array declarations in the same rule as references to type definitions. Array declarations reference a type definition and define any number of dimensions of the array. Array fields are accessed in the same way as any other variable (Fig. 6, l. 17): a variable reference is followed by the coordinates of the specific field.
are treated as types (Fig. 6, l. 13). We introduce array declarations in the same rule as references to type definitions. Array declarations reference a type definition and define any number of dimensions of the array. Array fields are accessed in the same way as any other variable (Fig. 6, l. 17): a variable reference is followed by the coordinates of the specific field.
Well-formedness rules The names of defines and type definitions must be unique names of elements of the specification. Defines with the operator
 may not be used in expressions where
may not be used in expressions where
 is not allowed, e.g., defines with the operator
is not allowed, e.g., defines with the operator
 may not be nested inside the operator
may not be nested inside the operator
 . Note that the expression of a define is not required to evaluate to a Boolean value. However, the semantics of a specification with defines and type definitions has to be a well-formed specification.
. Note that the expression of a define is not required to evaluate to a Boolean value. However, the semantics of a specification with defines and type definitions has to be a well-formed specification.
Finally, each dimension of an array needs to be positive. All references to array fields need to have the same number of coordinates as the referenced array has dimensions.Footnote 4 All coordinates in a field reference need to be smaller than the corresponding dimension of that array.
Scopes The names of defines and type definitions have the same scope as the names of environment and system variables defined in the Spectra kernel. The names of defines are visible to other defines.
4.2.3 Semantics
We define the semantics of defines and type definitions with arrays by a translation into Spectra without defines and type definitions. Every reference to a define is replaced by the expression of the define. Then, we expand any variable or parameter declarations that include array declarations into multiple variable or parameter declarations that still include references to type definitions but no further array declarations, e.g., the array-type variable declaration in Lst. 4, l. 4 is translated into 100 variable declarations of type Item with fresh names (one for each field of the array). All references to array fields are replaced by a reference to the corresponding, expanded variable or parameter. Finally, every reference to a type definition is replaced by the type of the type definition.
4.3 State invariants
4.3.1 Motivation
Some constraints should hold in all states, e.g., the guarantee that green lights on the side and main street never occur together (Lst. 1, l. 13). These assumptions and guarantees could be expressed as combinations of initial and safety constraints; however, we chose to introduce a special handling for state invariants to make specifications easier to read and write.Footnote 5
4.3.2 Syntax
The syntax of state invariants is a subset of safety constraints from the kernel, specifically, the subset of
 with keyword
with keyword  where the following expression does not contain the operator
where the following expression does not contain the operator
 . If the following expression includes the operator
. If the following expression includes the operator
 , then the safety constraint is not a state invariant and will directly be interpreted as part of the GR(1) kernel.
, then the safety constraint is not a state invariant and will directly be interpreted as part of the GR(1) kernel.
Note that this language extension does not add new syntax to Spectra and is implemented on the level of the semantics of operator
 , see Sect. 7.3.
, see Sect. 7.3.
Well-formedness rules The expression
 of a state invariant may not contain the operator
of a state invariant may not contain the operator
 . A state invariant of the environment, i.e., used in an assumption, may not contain system variables.
. A state invariant of the environment, i.e., used in an assumption, may not contain system variables.
4.3.3 Semantics
We define the semantics of state invariants by a translation of state invariants to Spectra without state invariants. Every state invariant is translated into an initial constraint with the same expression
 and a safety constraint (with keyword
and a safety constraint (with keyword
 ) with the expression
) with the expression
 nested inside the operator
nested inside the operator  . Together, the two constraints ensure that the invariant holds in the initial state and in every successor state.
. Together, the two constraints ensure that the invariant holds in the initial state and in every successor state.
4.4 PastLTL
4.4.1 Motivation
Assumptions and guarantees define constraints on reactive behavior by relating the inputs and outputs of the current state to those of the next state. However, in some situations the restriction to only current and next inputs and outputs becomes limiting. As an example, consider the assumption that a car appears on the side street at least once in every run. This assumption cannot directly be expressed in terms of current and next inputs and outputs, and also not directly as a justice assumption that would have to hold infinitely often. However, this assumption is easily formalized using PastLTL operators supported by Spectra inside a justice assumption:  .
.
4.4.2 Syntax
We show the syntax of PastLTL expressions in Fig. 7. Spectra supports three unary PastLTL operators and one binary PastLTL operator. For all operators Spectra also provides a one letter abbreviation (preceding the operator name in Fig. 7).
Well-formedness rules All operands of PastLTL operators must evaluate to Boolean values (all PastLTL expressions evaluate to Boolean values).
4.4.3 Semantics
We define the semantics of PastLTL by a translation of PastLTL to Spectra without PastLTL. Recall from the preliminaries that the two operators
 and
and  provide full expressiveness of PastLTL; all other PastLTL operators can be defined in terms of these two, e.g., the operator
provide full expressiveness of PastLTL; all other PastLTL operators can be defined in terms of these two, e.g., the operator
 \(\varphi \) used in our example is defined as
\(\varphi \) used in our example is defined as

 \(\varphi \). We will show the translation for the operators
\(\varphi \). We will show the translation for the operators
 and
and  .
.
Given the PastLTL expression
 \(\varphi \), we create a Boolean system variable aux with a fresh name. We then add the initial guarantee
\(\varphi \), we create a Boolean system variable aux with a fresh name. We then add the initial guarantee
 !aux and the safety guarantee
!aux and the safety guarantee

 \(\varphi \). Technically, the variable aux stores the previous valuation of \(\varphi \). Finally, we replace all occurrences of
\(\varphi \). Technically, the variable aux stores the previous valuation of \(\varphi \). Finally, we replace all occurrences of
 \(\varphi \) with a reference to the new variable aux.
\(\varphi \) with a reference to the new variable aux.
Given a PastLTL expression \(\varphi \)
 \(\psi \), we create a Boolean system variable aux with a fresh name. We then add the initial guarantee
\(\psi \), we create a Boolean system variable aux with a fresh name. We then add the initial guarantee
 \(\psi \) and the safety guarantee
\(\psi \) and the safety guarantee

 (aux&
(aux&
 (\(\varphi \)) |
(\(\varphi \)) |
 (\(\psi \))). The variable aux is true if \(\psi \) holds or if aux was true before and \(\varphi \) holds, i.e., if \(\varphi \) holds since \(\psi \) was true in the past. Finally, we replace all occurrences of \(\varphi \)
(\(\psi \))). The variable aux is true if \(\psi \) holds or if aux was true before and \(\varphi \) holds, i.e., if \(\varphi \) holds since \(\psi \) was true in the past. Finally, we replace all occurrences of \(\varphi \)
 \(\psi \) with a reference to the new variable aux.
\(\psi \) with a reference to the new variable aux.
4.5 Predicates
4.5.1 Motivation
Sometimes, repeating parts that appear in specifications differ in sub-expressions. In these cases, defines from Sect. 4.2 cannot be used to avoid repetition. Instead, for these cases, we introduce predicates, which can instantiate sub-expressions with their parameters.
As an example, consider an extension of the traffic light with pedestrian crossing, as shown in Lst. 5. Similar to a green light on the main street, a green light for pedestrians should also mutually exclude a green light on the side street. To avoid repetition and manual errors, we can extract the expression for mutual exclusion into a predicate with two parameters as shown in Lst. 5, ll. 5-6. The predicate can then be instantiated, e.g., in a guarantee as shown in l. 8.

4.5.2 Syntax
We show the syntax of predicate definitions and predicate instantiations in Fig. 8. The grammar starts with the syntax for predicate definitions
 , which are specification elements and thus appear as top level elements inside specifications. Predicate definitions have a name, followed by a list of typed parameters
, which are specification elements and thus appear as top level elements inside specifications. Predicate definitions have a name, followed by a list of typed parameters
 . The body of a predicate definition is an expression.
. The body of a predicate definition is an expression.
Predicate instances
 (Fig. 8, ll. 11–12) are primary expressions. Instances reference the name of a predicate and provide expressions for each parameter of the predicate.
(Fig. 8, ll. 11–12) are primary expressions. Instances reference the name of a predicate and provide expressions for each parameter of the predicate.
Well-formedness rules All parameters of predicate instances must be expressions that evaluate to the type declared in the predicate definition. The body of the predicate must be an expression that evaluates to Boolean. The body of a predicate cannot (also not transitively, e.g., through predicate instances or defines) contain an instance of the predicate itself.
Scopes The names of predicates have the same scope as the names of environment and system variables defined in the Spectra kernel. As a result, the names of predicates are visible to other predicates. The names of parameters of the predicate are only visible inside the body of the predicate.
4.5.3 Semantics
We define the semantics of predicate instantiations and predicates by a translation into Spectra without predicates. Every predicate instance is translated into a Boolean expression. Technically, we replace a predicate instance by a copy of the body of the predicate. In the copy, we replace references to predicate parameters by the expressions provided for each parameter.
4.6 Monitors
4.6.1 Motivation
Assumptions and guarantees define constraints on reactive behavior by relating the inputs and outputs of the current state to those of the next state. However, in some situations, the restriction of referencing only inputs and outputs becomes limiting. As an example, consider an extension of the traffic light with a button for pedestrians to press. The system should guarantee that all button presses eventually lead to a green light for pedestrians. Yet, in our example, there is no variable indicating whether a request has already been served. As a solution, Spectra introduces monitors, which come with a definition of how their value is updated at every execution step. As an example, the monitor needGreenMain (Lst. 6, l. 6–12) is of type boolean and its value is updated on button presses not followed by green lights. This monitor is used in a guarantee (Lst. 6, l. 4) to ensure that requests are always eventually handled.

4.6.2 Syntax
The syntax of monitors is shown in Fig. 9. Monitors are specification elements and thus appear as top level elements inside specifications. Monitors have a type and a name. The body of a monitor consists of initial and safety constraints.
References to monitors
 are primary expressions (Fig. 9, l. 8), i.e., monitors can be referenced in the same way as variables.
are primary expressions (Fig. 9, l. 8), i.e., monitors can be referenced in the same way as variables.
Well-formedness rules The names of monitors must be unique names of elements of the specification. The body of a monitor may not contain justice constraints. The expression
 of an initial constraint may not include the unary operator
of an initial constraint may not include the unary operator
 . The semantics of the constraints in the body of the monitor must assign a unique value to the monitor in any step, and it must not restrict any other variable (when seen as an automaton with the monitor variable as states and all other variables as input, the defined automaton has to be deterministic and complete).Footnote 6
. The semantics of the constraints in the body of the monitor must assign a unique value to the monitor in any step, and it must not restrict any other variable (when seen as an automaton with the monitor variable as states and all other variables as input, the defined automaton has to be deterministic and complete).Footnote 6
Scopes The names of monitors have the same scope as the names of environment and system variables defined in the Spectra kernel. Importantly, the name of a monitor is visible in the constraints of the monitor.
4.6.3 Semantics
We define the semantics of monitors by a translation of monitors to Spectra without monitors. For every monitor definition, we create a system variable with the name and type of the monitor. All monitor constraints become guarantees. All references to the monitor become references to the new system variable with the same name and type.
4.7 Counters
4.7.1 Motivation
Some constraints require to keep track of number of occurrences of cases, events, or actions, e.g., for the traffic light we might want to limit the number of steps that an ambulance on the main street has to wait before the light turns green. Spectra provides bounded integers and arithmetic operations (see Sect. 4.1), which in principle allow one to formulate counting. However, using them for expressing counting, based on explicit safety constraints, may be tedious and error prone.
As a solution, Spectra introduces counters, which come with a definition of how their value is increased, decreased, or reset at an execution step. For example, Lst. 7 shows a bounded counter ambulanceWait from 0 to 5 that increases when an ambulance waits on the main street (Lst. 7, l. 2). The counter is reset once the main street light is green. In case of overflows the counter’s current value is kept (Lst. 7, l. 4). The counter in the example is referenced in a guarantee that asserts that the number of steps that an ambulance waits is below 5.
Using a counter, counting is encapsulated in a dedicated specification element, tailored to counting related definitions. This hides the complexity of using safety constraints to define counting, and makes it easier to correctly define and use variables that serve as counters.

4.7.2 Syntax
The syntax of counters is shown in Fig. 10. Counters are specification elements and thus appear as top level elements inside specifications. Counters have a range and a name. The body of a counter contains optional initial (
 ), increment (
), increment (
 ), decrement (
), decrement ( ), and reset (
), and reset ( ) constraints. As all counters are bounded, a counter may declare overflow and underflow methods, where
) constraints. As all counters are bounded, a counter may declare overflow and underflow methods, where
 means that an over-/underflow may not happen,
means that an over-/underflow may not happen,
 preserves current counter values, and
preserves current counter values, and
 sets the counter to the opposite bound.
sets the counter to the opposite bound.
References to counters
 are primary expressions (Fig. 10, l. 8), i.e., counters can be referenced in the same way as variables.
are primary expressions (Fig. 10, l. 8), i.e., counters can be referenced in the same way as variables.
Well-formedness rules The names of counters must be unique names of elements of the specification. The body of a counter may not contain justice constraints. The expression
 of an initial constraint (
of an initial constraint ( ) may not include the unary operator
) may not include the unary operator
 . The semantics of any
. The semantics of any  ,
,  , or
, or  constraints of the counter must be exclusive, i.e., a counter cannot be increased, decreased, or reset at the same time. (Spectra Tools checks this and reports relevant problems if found.) Counters may only be referenced in arithmetic expressions.
constraints of the counter must be exclusive, i.e., a counter cannot be increased, decreased, or reset at the same time. (Spectra Tools checks this and reports relevant problems if found.) Counters may only be referenced in arithmetic expressions.
Scopes The names of counters have the same scope as the names of environment and system variables defined in the Spectra kernel. Importantly, the name of a counter is visible in the constraints of the counter.
4.7.3 Semantics
We define the semantics of counters by a translation of counters to Spectra without counters. For every counter definition, we create a system variable of integer type with the size and the name of the counter. The initial counter constraint becomes an initial guarantee. Any  ,
,  , or
, or  constraint of the counter becomes a safety guarantee that implies correct increase, decrease, or reset (to lower bound) of the counter variable value with respect to the chosen overflow semantics. The default
constraint of the counter becomes a safety guarantee that implies correct increase, decrease, or reset (to lower bound) of the counter variable value with respect to the chosen overflow semantics. The default
 and
and  methods are
methods are  .
.
-
For overflow type
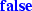 , the guarantees for
, the guarantees for  and
and 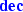 constraints are expressed without checking over- or underflows, i.e., these would lead to safety guarantee violations.
constraints are expressed without checking over- or underflows, i.e., these would lead to safety guarantee violations. -
For overflow type
 , we add a case distinction to the guarantees for
, we add a case distinction to the guarantees for
 and
and  constraints to handle overflows and underflows by preserving the current counter values.
constraints to handle overflows and underflows by preserving the current counter values. -
For overflow type
 , we add a case distinction to the guarantees for
, we add a case distinction to the guarantees for
 constraints to set the counter at the upper bound to its lower bound. Respectively, for
constraints to set the counter at the upper bound to its lower bound. Respectively, for
 constraints we set a counter at the lower bound to its upper bound.
constraints we set a counter at the lower bound to its upper bound.
Finally, we add a safety guarantee where the conjunction of the negations of all  ,
,  , and
, and  constraints implies that the counter variable does not change its value. All references to the counter become references to the new system variable with the same name and bounded integer type.
constraints implies that the counter variable does not change its value. All references to the counter become references to the new system variable with the same name and bounded integer type.
4.8 Patterns
4.8.1 Motivation
Specifications of reactive systems require engineers to express complex temporal relations between environment and system variables. LTL provides great expressiveness for temporal relations. However, some relations, if expressed directly in LTL, lead to long formulas, which might be complicated to read, challenging to write, or simply not within the restricted syntax of GR(1). As an example, consider the popular response pattern that a car on the main street eventually leads to a green light. This guarantee can be expressed in LTL as followsFootnote 7:

Note that even this simple LTL formula is not in the GR(1) fragment.
Dwyer et al. [21] have identified 55 LTL specification patterns that are common in industrial specifications. They have suggested a classification and natural language descriptions for the identified patterns. The example above is one of their patterns and would be transcribed as:

We have investigated patterns for GR(1) synthesis in [49]. We have shown that 52 of these 55 LTL specification patterns can be supported as assumptions and guarantees for GR(1) synthesis.Footnote 8 In Spectra, the example guarantee is formulated as a pattern definition (Spectra comes with a catalog of pattern definitions for all 52 supported LTL specification patterns, e.g., the one shown in Lst. 8) and the pattern instantiation shown in Lst. 9, l. 1.


Note that the response pattern expresses the requirement of letting cars pass much better than the justice guarantee used in Lst. 1, l. 14, as the latter required the now unnecessary assumption in Lst. 1, l. 10, that always eventually cars will be on the main street.
Note that Spectra patterns are not limited to the 52 patterns defined in the catalog. Spectra provides engineers with means to define and reference their own patterns.
4.8.2 Syntax
The syntax of patterns is shown in Fig. 11. The grammar starts with the syntax for pattern definitions
 , which are specification elements and thus appear as top level elements inside specifications. Pattern definitions have a name, followed by a list of parameter names. The body of a pattern definition can declare variables local to the pattern and temporal constraints. A pattern may contain any number of initial and safety constraints, but it must contain exactly one justice constraint.
, which are specification elements and thus appear as top level elements inside specifications. Pattern definitions have a name, followed by a list of parameter names. The body of a pattern definition can declare variables local to the pattern and temporal constraints. A pattern may contain any number of initial and safety constraints, but it must contain exactly one justice constraint.
Pattern instances
 (Fig. 11, ll. 12–13) are temporal constraints. Instances reference the name of a pattern and provide expressions for each parameter of the pattern.
(Fig. 11, ll. 12–13) are temporal constraints. Instances reference the name of a pattern and provide expressions for each parameter of the pattern.
Well-formedness rules The body of a pattern contains exactly one justice constraint. The expression
 of an initial or justice constraint may not include the unary operator
of an initial or justice constraint may not include the unary operator
 . The expression
. The expression
 of a safety constraint may only include references to pattern variables vars in the scope of the operator
of a safety constraint may only include references to pattern variables vars in the scope of the operator
 . The semantics of the initial and the safety constraints must assign a unique value to all pattern variables in any step and must not restrict any other variable (when seen as an automaton with the pattern variables as states and all other variables as input, the defined automaton has to be deterministic and complete).Footnote 9
. The semantics of the initial and the safety constraints must assign a unique value to all pattern variables in any step and must not restrict any other variable (when seen as an automaton with the pattern variables as states and all other variables as input, the defined automaton has to be deterministic and complete).Footnote 9
The production
 may only appear exclusively as a temporal constraint in assumptions or guarantees, i.e., it can appear neither inside another expression nor in any other place in a specification.
may only appear exclusively as a temporal constraint in assumptions or guarantees, i.e., it can appear neither inside another expression nor in any other place in a specification.
Scopes The names of pattern parameters params, and the names of pattern variables vars, are only visible inside the body of the pattern, delimited by  , The names of patterns are visible beyond specification files and thus can be imported, Sect. 4.10. This is important for the ability to reuse patterns across specifications.
, The names of patterns are visible beyond specification files and thus can be imported, Sect. 4.10. This is important for the ability to reuse patterns across specifications.
4.8.3 Semantics
We define the semantics of patterns by a translation of pattern instances and patterns to Spectra without patterns. For every pattern instance, we create a copy of all pattern variables as system variables with a fresh name and the same type. We instantiate pattern constraints by replacing references to pattern variables with references to the fresh names and by replacing references to variable names with copies of the corresponding expression of the parameter values from pVals.
Instantiated initial pattern constraints become initial guarantees; instantiated safety pattern constraints become safety guarantees; the instantiated justice constraint becomes a justice assumption if the pattern instance is contained inside an assumption; and the instantiated justice constraint becomes a justice guarantee if the pattern instance is contained inside a guarantee (the formal translation appears in [49]).
4.9 Quantification
4.9.1 Motivation
Arrays, integers, and counters allow for very succinct specifications. However, some constraints apply to fields of arrays or for specific values of integer variables. Writing these constraints could become very repetitive. To ensure that this kind of repetitive constraints can be written succinctly in Spectra, we introduce universal and existential quantification. Consider the example shown in Lst. 10. The universal quantification in l. 5 states that either the current value of pos is p or active pickup requests at position p stay active.

4.9.2 Syntax
The syntax for quantification is shown in Fig. 12. A quantified expression
 starts either with the universal quantifier
starts either with the universal quantifier
 or with the existential quantifier
or with the existential quantifier
 . The quantifier is followed by a variable name and its domain. Finally, a quantified expression contains an expression
. The quantifier is followed by a variable name and its domain. Finally, a quantified expression contains an expression
 .
.
We also extend the syntax of references to array fields. Array fields can be indexed by names of quantified variables in addition to integer literals (as shown in Fig. 6).
Well-formedness rules Replacing the quantified variable by any literal from its domain makes the quantified expression well-formed. Only quantified variables of integer types may index fields of arrays.
Scopes The names of quantified variables are visible inside the quantified expression.
4.9.3 Semantics
We define the semantics of quantification by a translation of quantification to Spectra without quantification. Starting from inner-most quantified expressions, every universal quantification is replaced by a conjunction of copies of the quantified expression, where every occurrence of the quantified variable is replaced by a different value from its domain. Similarly, every existential quantification is replaced by a disjunction.
4.10 Imports
4.10.1 Motivation
We have motivated many language features of Spectra based on reuse. In all cases, a reuse within a single specification makes sense. In some cases, a reuse across specifications is also desirable. As an example, patterns, e.g., from the catalog of Dwyer et al. [21] or domain-specific pattern collections for mobile robots [59], are general and should be useful for many different specifications. Thus, to support reuse across specifications, we have added an import mechanism to Spectra. A specification can import other specifications and thus use their patterns and predicate definitions (see Sect. 4.5 and Sect. 4.8).
4.10.2 Syntax
The syntax of imports is shown in Fig. 13. We extend specifications with import statements. Each import statement starts with the keyword
 , contains a filename in quotation marks, and ends with a semicolon.
, contains a filename in quotation marks, and ends with a semicolon.
Well-formedness rules The names of patterns and predicates in all imported and in the current Spectra files must be unique. The bodies of all (transitively) imported predicates may only contain references to other predicates and their parameters (e.g., they may not reference system or environment variables or defines from other specificationsFootnote 10).
4.10.3 Semantics
We define the semantics of imports by a translation of imports to Spectra without imports. Given a Spectra file with imports, we copy all (transitively) referenced patterns of the imported files into the current file. We also copy all (transitively) referenced predicates into the current file and remove the import statements.
5 Spectra Tools
Spectra comes with Spectra Tools, a set of analyses and tools packaged as an extensible set of Eclipse plug-ins. A rich Eclipse editor for Spectra is implemented using XText [77]. All symbolic representations and operations are carried out using a BDD library (several libraries can be used, including, e.g., CUDD [72]).
Spectra Tools is available from [73], together with a user guide and many example specifications. Beyond the SYNTECH specifications we describe in Sect. 6, the examples on the Spectra website include specifications and simulations for some classic problems, such as the Towers of Hanoi, Cinderella and her stepmother, moving obstacle evasion, etc. We encourage the interested reader to try them out.
We now give an overview of the architecture of Spectra Tools and how it supports language extensions, including the ones presented in Sect. 4.
5.1 Spectra Tools Architecture
We have built Spectra Tools in a modular way that supports separation of concerns and reduces technological dependencies. The main concerns of Spectra Tools are the input language syntax, the definition of semantics of language constructs in terms of the Spectra kernel, a representation of the semantics of Spectra at the BDD level, analyses and tools that operate on this BDD-based representation, and a UI layer. These concerns (shown as gray, rounded boxes) are reflected in a set of components shown in Fig. 14.
Spectra Tools defines a rich abstract syntax representation of Spectra including its kernel and all language elements inside component GameInput. The semantics of all language elements as presented in Sect. 4 is defined by transformations of the abstract syntax. All these transformations are implemented in component GameInputTrans, e.g., the component contains a class CounterTranslator, which implements the translation described in Sect. 4.7.3, a class QuantifierTranslator, which implements the translation described in Sect. 4.9.3, etc.Footnote 11
Component BddGenerator takes the abstract syntax of the Spectra kernel and translates it into a BDD-based representation defined by component GameModel. Importantly, this representation is completely independent of any concrete or abstract syntax of Spectra. Together with component Games, a structure that encodes the Spectra kernel semantics as described in Sect. 3.3 is provided.
GR(1) synthesis, implemented in component GR1, and additional more advanced analyses, e.g., component WellSeparation (see Sect. 5.6), rely on the representation provided by component GameModel. We describe some of the different analyses and tools in the following subsections below.
Finally, Spectra Tools provides a UI integrated into Eclipse that enables engineers to apply analyses to specifications. The component SpectraToolsUI in Fig. 14 implements the UI. It has dependencies that go all the way up to the level of the input language, as the UI orchestrates the execution of the parser, the translations, and the analyses chosen by the engineer.
Two main advantages of the Spectra Tools architecture, as we show in Fig. 14, are (1) its separation of technological and representation concerns and (2) its modularity. As an example, the separation of technological concerns allows for replacing XText by other language workbenches or an API-based use of Spectra Tools (indeed, in addition to the Eclipse-based plug-ins, we provide a command line interface that is independent of Eclipse). As another example, the modular semantics definition per language element inside component GameInputTrans leads to small and easily testable translations implementing the semantics of each of the language elements described Sect. 4.
We now give an overview of the different analyses and tools. All the features described below are implemented in Spectra Tools.
5.2 Realizability checking
First and foremost, Spectra Tools provides means to check whether a specification is realizable, i.e., whether there exists a controller that can ensure all guarantees given that all assumptions hold. The check is implemented as part of components GR1 and made available through component SpectraToolsUI shown in Fig. 14.
As an example, Spectra tools returns a positive result when checking realizability for the specification from Lst. 1. The value of checking realizability without construction a controller is that this check is usually much faster than controller construction.
The algorithm for realizability checking follows [10], but, importantly, incorporates a number of performance heuristics from [28]. We have implemented heuristics in two levels. At the BDD and controlled predecessors computation level, we use grouping of variables and their primed copies, combined conjunction and existential abstraction, and the use of a partitioned transition relation. At the algorithmic level, we use early detection of fixed-point, early detection of unrealizability, and fixed-point recycling.
As empirically shown in [28], the combination of all these heuristics provides improvements in realizability checking running times. Moreover, the greatest improvement is for specifications that have slower original running times. This is a positive result, as these specifications are the ones it is most important to address in order to make reactive synthesis more useful and applicable in practice.
Finally, the evaluation in [28] also shows that thanks to these heuristics, Spectra outperforms two previously published tools, RATSY [6] and Slugs [22], on large specifications. While for small specifications, the other tools running times for realizability checking are better than Spectra’s, the larger the specification, the faster Spectra becomes relative to the two other tools.
For details about these heuristics and their evaluation, including the details of the comparison against RATSY and Slugs on specifications from the literature, we refer the reader to [28].
5.3 Synthesis of concrete and symbolic controllers
Beyond realizability checking, Spectra Tools includes two synthesis features, which take the specification as input and output a correct-by-construction controller, if one exists. After a series of basic checks and translations, synthesis is performed symbolically following the algorithms described in [10], with performance heuristics adapted from [28] (see above in Sect. 5.2).
As an example, for the specification from Lst. 1 Spectra Tools computes a controller that waits for a car to appear on the side street, gives a green light to that car, waits for a car to appear on the main street, gives a green light to that car, and repeats this process indefinitely.
The engineer can choose the form of the synthesis output. First, the output may be a concrete controller, which is further presented in the console or used for application-specific code generation. As the concrete controller is complete for the environment and deterministic for the system, i.e., in every state it accepts all inputs from the environment and deterministically responds with an assignment to the system variables, it allows for straightforward application-specific code generation.
Second, the output may be a symbolic controller, following ideas from [10]. Roughly, the symbolic controller consists of two functions, represented using BDDs. The first BDD describes the set of allowed initial states, while the second describes the controller’s allowed transitions. The engineer can save it and execute it, see below in Sect. 5.4.
One advantage of the concrete controller output is that it enables direct code generation. When it is very small, it is also simple to read and inspect. In our experience however, the concrete representation does not even scale to systems like the autonomous Lego robots we describe in Sect. 6. Its generation is slow, due to the need to enumerate all states, and its size is beyond what any engineer can manually inspect. Moreover, sometimes the size of straightforward generated code prohibits compilation.Footnote 12 All these disadvantages motivated us to design and implement the symbolic controller.
Finally, we have recently presented just-in-time reactive synthesis (JITS) [58], and implemented it in Spectra Tools. JITS accelerates synthesis time significantly, as it skips the symbolic controller construction all together. Instead, next states are computed at the controller’s execution time, only when they are required. JITS itself is symbolic, and takes advantage of the symbolic representation of the results of realizability checking.
5.4 Controller execution
Spectra Tools provides several different means to execute and simulate the synthesized controller, concrete or symbolic. This functionality is implemented as part of components GR1 and ControllerRunner shown in Fig. 14.
First is code generation from concrete controllers. The concrete controller is directly translated to a simple implementation of a state machine. We currently have application-specific Java code generation tailored to run on Lego NXT robots.
Second is an execution API for symbolic controllers. The symbolic controller is loaded and iteratively called, at runtime, with the current inputs from the environment, to provide the next outputs (assignment to system variables). This runtime environment requires a BDD library; however, its use is limited to single calls to extract a satisfying assignment. Our students have used this API to execute their Lego robots (where the actual execution runs on a Raspberry Pi) and to develop some small example standalone Java applications.
Third is a simulation environment, inside Eclipse, we call Controller Walker. The Walker uses the execution API for symbolic controllers. It shows the engineer the current state of the controller (values of environment and system variables) and allows her to ‘walk’, step by step, forward and backward, on its transition system. It serves as the main tool for closely inspecting the behavior of the synthesized controller.
5.5 Analyses of unrealizability
One of the challenges of writing specifications for synthesis is unrealizability. Spectra Tools provides several means to deal with unrealizable specifications.
As an example for an unrealizable specification, consider the specification from Lst. 1 where the two assumptions
 carSide and
carSide and
 carMain are replaced by a single, similar assumption:
carMain are replaced by a single, similar assumption:

Identifying unrealizability and computing an unrealizable core When synthesis fails due to unrealizability, the engineer receives an appropriate message. Then, she can ask to compute an unrealizable core, i.e., a locally minimal subset of the specification’s guarantees, which already makes it unrealizable. Spectra Tools computes the core using DDmin [79], following ideas described in [39] and with heuristics investigated in [28]. The core guarantees are highlighted on the specification (using Eclipse standard editor markers). The user guide in [73] includes example screenshots.
In the example above, Spectra Tools highlights the guarantee
 carMain
carMain
 greenMain as an unrealizable core (the other justice guarantee in Lst. 1 equally constitutes another unrealizable core).
greenMain as an unrealizable core (the other justice guarantee in Lst. 1 equally constitutes another unrealizable core).
Computing a concrete counter-strategy Given an unrealizable specification, the engineer can generate a concrete counter-strategy, which specifies one strategy for the environment to force any system to violate the specification. The counter-strategy is computed by playing a Rabin game, following the algorithm from [39, 56]. The counter-strategy can be presented in simple textual format on the console. It can also be interactively simulated, together with the JVTS, see next.
In the example above, Spectra Tools computes a strategy for the environment that satisfies the modified justice assumption always by setting carSide to true but constantly setting carMain to false. This makes it impossible for any controller to satisfy the justice guarantee
 carMain
carMain
 greenMain.
greenMain.
Computing a JVTS As concrete counter-strategies may be very large and difficult to understand, we have recently presented the Justice Violations Transition System (JVTS), a symbolic representation of a counter-strategy [43]. The JVTS is much smaller and simpler than its corresponding concrete counter-strategy. Moreover, it is annotated with invariants that explain how the counter-strategy forces the system to violate the specification. We compute the JVTS symbolically, and thus more efficiently, without the expensive enumeration of concrete states. We provide the JVTS with an on-demand interactive concrete and symbolic play. See [43]. The JVTS computation is implemented as part of component JVTS shown in Fig. 14.
Suggestions of repairs for unrealizable specifications Given an unrealizable specification, a repair is a set of assumptions that one may add to the original specification in order to make it realizable. Spectra Tools implements two symbolic algorithms for computing repairs, one based on the JVTS, which may suggest many possible repairs but is incomplete, and a second algorithm, which is sound and complete but only computes a single repair, if one exists. See [53]. This repair functionality is implemented as part of components Repair and RepairUI shown in Fig. 14, and depends on component JVTS.
In the example above, Spectra Tools suggests the interesting repair
 carMain
carMain
 carSide.
carSide.
5.6 Analyses of non-well-separation
One way a controller may satisfy a specification is by preventing the environment from satisfying the assumptions, without satisfying the guarantees. Although valid, this solution is usually undesired. Specifications that allow it are called non-well-separated [38]. In [51] we have shown that non-well-separation is a common problem in specifications. The well-separation check is implemented as part of component WellSeparation shown in Fig. 14, which depends on component GR1.
As an example, consider the specification from Lst. 1 with the additional assumption
 carSide
carSide
 greenSide. While Spectra Tools confirms that the original specification is well-separated, it finds that the modified version is not. The reason for non-well-separation is that the system could always set greenSide to false and thus force the environment to violate the new assumption.Footnote 13
greenSide. While Spectra Tools confirms that the original specification is well-separated, it finds that the modified version is not. The reason for non-well-separation is that the system could always set greenSide to false and thus force the environment to violate the new assumption.Footnote 13
Spectra Tools provides means to identify and investigate non-well-separation. The engineer can check her specification for well-separation. If the specification is not well-separated, information about the specific type of non-well-separation found is displayed. Furthermore, the engineer can ask to compute a strategy that shows how the environment can be forced to violate its assumptions. Finally, a non-well-separation core, a minimal set of assumptions that leads to non-well-separation, can be computed (again, using DDmin [79]), and highlighted on the specification (using Eclipse standard editor markers). See [51].
5.7 Additional analyses
Spectra Tools provides several additional analyses that aim at helping engineers write higher-quality specifications. We give some examples below.
First, some assumptions and guarantees may be trivially false or trivially true. Clearly, such assumptions or guarantees point to a problem in the quality of the specification, even when they are just redundant. We provide a basic analysis that looks for such trivial assumptions and guarantees and highlights them to the engineer. Furthermore, we have recently presented a more general and comprehensive work on detecting inherent vacuities [57]. Intuitively, a specification is inherently vacuous if one or more of its elements is logically redundant, i.e., removing it will not change the semantics of the specification. We define and detect several kinds of vacuities, as well as a vacuity core, which localizes the cause of vacuity. All these analyses are implemented in Spectra Tools.
Second, some Spectra language elements are not easy to write correctly. For example, monitors contain constraints inside their body that should only restrict the monitor variable itself. However, it is easy to mistakenly write constraints that are contradicting or constraining other variables. These malformed monitors might lead to unrealizability of the whole specification. Spectra Tools implements checks and highlighting for monitors to rule out this reason for unrealizability.
Finally, as one would expect from an engineer-friendly editor for writing and reading specifications, Spectra Tools editor provides an outline, syntax coloring, type checks, and specification completion. These are implemented by taking advantage of the rich XText [77] APIs.
6 Collections of Spectra specifications
Over the last five years (in 2015, 2017, 2019, and 2020), small teams of 3rd year Computer Science undergraduate students from Tel Aviv University, have used Spectra and Spectra Tools in four-semester long project classes we have taught. In the first two project classes, in 2015 and in 2017, the students have developed about 10 different autonomous Lego robots, which they wrote the specifications for, and actually built and run.Footnote 14 In the third and fourth project classes, in 2019 and 2020, the students have developed several example systems with a PC-based simulation. From these classes, we have collected over 320 versions of specifications, all written by these students as they worked on their projects for several months.
In the first two instances of the class, our choice of Lego as the underlying robotics technology for initial experience with Spectra was motivated by its relatively low cost and its modularity, allowing us to gain experience from several different robots, e.g., a robot sorting Lego pieces by color, an elevator servicing different floors, a self-parking Lego car, each performing very different tasks. Furthermore, although different in detail and scale, the use of the Lego robots provided us with concrete examples of some of the challenges one expects to encounter with real-world robotic technologies, such as the inaccuracy of sensor readings, and the limitations in terms of battery, memory, and computation power. In the 2019 and 2020 classes we have decided to extend our experience with systems outside the autonomous robots domain, and therefore suggested other target systems for the students to specify and develop simulations for.
From this experience, we have learned a lot about the challenges of writing specifications for synthesis and using it in practice. We developed some of the tools described above as a result of what we learned when guiding the students through the projects in the four classes.
Thus, the SYNTECH15, SYNTECH17, SYNTECH19, and SYNTECH20 collections of specifications we describe below, (SYNTECH for short), were not created specifically for the evaluation in our paper but as part of the ordinary work of the students in the project class. In total, we have collected 327 (\(=78+149+27+73\)) specifications. We consider these specifications to be the most realistic and relevant examples one could find for the purpose of learning about the challenges of using reactive synthesis in practice. We made them available for download in [73].
It is important to note the background of the students and what we have taught them. All students were third-year computer science undergrads at Tel Aviv University. All had learned Python, Java, and C++ in other classes. All have completed basic classes on data structures, computer architecture, and algorithms. Some had limited industry experience as software developers. None had knowledge of formal methods or any experience with formal verification tools. We taught them the syntax and semantics of Spectra, while covering only the very basic syntax and semantics of LTL required, i.e., we taught them the semantics of
 and
and  , but did not teach the syntax and semantics of the LTL
, but did not teach the syntax and semantics of the LTL
 (until) operator and the fact that temporal operators can be nested. We showed them a few example systems that we have created. We did not teach them anything about the inner workings of GR(1) synthesis, BDDs, fixed-point algorithms, etc.
(until) operator and the fact that temporal operators can be nested. We showed them a few example systems that we have created. We did not teach them anything about the inner workings of GR(1) synthesis, BDDs, fixed-point algorithms, etc.
Thus, it is also important to discuss the quality of the specifications in the four collections. All specifications were written by teams of 2-5 third-year students. They wrote the specifications in order to get their robots and systems running and working correctly—as they did eventually, satisfying an initial set of high-level requirements one may expect from such robots and systems. They wrote them neither in order to make best use of the language features of Spectra, nor to look for its advantages or challenges, nor to create high-quality examples of great specifications. One team gave up in the middle of the project, not for any reason related to the project itself (Elevator project in SYNTECH15 collection). We still include the specifications they wrote in the collection.
We consider the above characteristics to be both a strength and a weakness of these specifications. A weakness, because they cannot be used to demonstrate Spectra best-practices, reusable solutions, etc., they may include all kinds of redundancies, use of inconsistent or misleading variable and value names, partial or inaccurate documentation, etc. A strength, because they provide a first example of specifications, software engineers may write when given a synthesis-based development environment for reactive systems in order to make the systems they develop work.
In the remainder of this section, we present the SYNTECH collections with an overview of each collection. We conclude with aggregated statistics that give a rough idea about the size and complexity of the specifications that the students wrote.
6.1 Collection SYNTECH15
In the class we taught in 2015, the students have created the following robots: ColorSort—a robot sorting Lego bricks by color; Elevator—an elevator servicing different floors (incomplete); Humanoid—a mobile robot of humanoid shape; PCar—a self-parking car; Gyro—a robot with self-balancing capabilities; and SPCar—a second project of a self-parking car.
We call this set of specifications SYNTECH15. The set consists of 78 specifications of which 61 are realizable and 17 are unrealizable.
6.2 Collection SYNTECH17
We have re-taught a similar project class two years later with an improved set of tools that implemented some of the analyses described in Sect. 5 (i.e., including analysis of non-well-separation, but excluding JVTS and repair). In this class, the students have created the following robots: APShuttle—a shuttle car that moves passengers between several stations and returns to a designated station for maintenance; ConvoyCar—a robot car driving in a convoy following a line and evading obstacles; Elevator—an elevator with automatic doors and several modes of operation; RobotArm—a robotic arm that moves objects; and SimpleCar—a self-parking car.
We call this set of specifications SYNTECH17. The set consists of 149 specifications of which 123 are realizable and 26 are unrealizable.
6.3 Collection SYNTECH19
We have re-taught a similar project class in 2019, in which the students were able to use an improved set of tools that implemented all of the analyses described in Sect. 5 (except repairing of unrealizable specifications, which we made available in Spectra Tools only after the class ended) as well as new language features including arrays and counter definitions. Spectra Tools was also, by then, more stable (with less bugs), faster (already employing some of the heuristics presented in [28]), and better documented for its users.
In this class, the students were divided into 6 teams. Two teams developed a controller for the traffic lights of a 4-way junction. Three teams developed a controller for an automatic teller machine (ATM). One team developed a controller for an irrigation system. All wrote a specification and a corresponding Java simulation with interactive GUI that allows one to execute and play with the synthesized (symbolic) controller.
We call this set of specifications SYNTECH19. The set consists of a total of 27 specifications, including the final version that the students have submitted, some additional variants that the students have submitted, and other specifications from the version control of the projects.
6.4 Collection SYNTECH20
Finally, we have re-taught a similar project class in 2020, in which the students were able to use an improved documentation and improved set of tools that implemented all of the analyses described in Sect. 5.
In this class, the students were divided into 8 teams. Three teams chose to develop a smarthome system. The other teams developed a controller for a smart neighborhood simulation, for an airport control tower, for a parking lot management system, and for an elevator. All wrote a specification and a corresponding Java simulation with interactive GUI that allows one to execute and play with the synthesized (symbolic) controller.
We call this set of specifications SYNTECH20. The set consists of a total of 73 specifications, including the final version that the students have submitted, some additional variants that the students have submitted, and other specifications from the version control of the projects.
6.5 Statistics for SYNTECH collections
Table 1 presents statistics about the specifications in the SYNTECH15, SYNTECH17, SYNTECH19, and SYNTECH20 collections. The data give a rough idea about the size and complexity of the specifications that the students wrote and actually used to run their systems. While in all collections we have several versions of specifications for each system (between 4 and 45 versions per specification, most realizable, some unrealizable), we show here only the statistics for the last specification submitted by each students team, which is, as one would expect, realizable.
For each specification, the table shows the number of lines of specification including comments (lines of spec); number of environment (# env var decls) and system (# sys var decls) variable declarations—of variables of any type, e.g., integer or enumeration types (also, an array of any size is counted as one variable declaration); number of environment (# bool env vars), system (# bool sys vars), auxiliary (# bool aux vars) variables, as well as total number of variables (# bool total vars)—these numbers refer to Boolean variables, i.e., the variable count after the translation to the Spectra kernel; number of initial assumptions and guarantees (# ini asm/gar), number of safety assumptions and guarantees (# safety asm/gar), number of justice assumptions and guarantees (# justice asm/gar)—excluding any assumptions or guarantees created by translations; number of pattern instances (# pattern inst), as well as total number of assumptions and guarantees (# total asm/gar)—including pattern instances; number of PastLTL operators (# past operators), number of defines (# defines), number of predicate definitions that are used at least once (# predicates), number of monitors (# monitors), number of pattern definitions beyond the Dwyer et al. patterns (# pattern defs), number of counter definitions (# counter defs), and number of array definitions (# array defs).
We provide the following preliminary observations from the data in the table. First, note that the specifications are not very small and are not trivial. For example, in SYNTECH15 to SYNTECH20, number of lines of specification (including comments) ranges from 32 to 602 (medians 201, 414, 169, 216.5 resp.). The total number of Boolean variables, i.e., the variable count after the translation to the Spectra kernel, ranges from 4 to 87 (medians 29.5, 45, 36, and 39 resp.). The total number of assumptions and guarantees, excluding any assumptions or guarantees created by translations, ranges from 5 to 105 (medians 42.5, 48, 31.5, 60.5 resp.).
Second, note some use of advanced language features beyond pure GR(1), e.g., PastLTL, monitors, patterns, counters, or arrays; however, the use of these advanced features varies much between specifications and is not pervasive. A possible explanation for this phenomenon is that the students had not enough documentation and examples available to them (as they were using our language and tool set while we were developing and documenting it, i.e., they did not have the complete version of the user guide we now made available), resulting in problems in understanding, leading to lack of confidence in using the more advanced language feature.
Finally, note larger and more complex specifications from SYNTECH17 to SYNTECH20 compared to SYNTECH15. We believe this is due to the additional language constructs and better tool set available to the students. Predicates, monitors, and pattern definitions, were not available to the students of the SYNTECH15. Moreover, starting from SYNTECH17 our students had faster realizability checking (due in part to the heuristics we described in [28]), faster synthesis (due to ability to output a symbolic rather than a concrete controller), and ability to execute the symbolic controller (and not the generated code from the concrete one) on the robots. The slight drop in sizes of specifications from SYNTECH17 to SYNTECH19 and SYNTECH20 might be due to the different target of the latter. While specifications of SYNTECH15 and SYNTECH17 capture the behavior of robotic systems, specifications of SYNTECH19 and SYNTECH20 capture behavior integrated in a software system or simulation. Moreover, naturally, the use of defines, predicates, and arrays makes it easier to write more concise specifications.
7 Discussion
We now discuss more general design decisions, observations, and lessons we have learned from the development of Spectra and Spectra Tools and from our experience with it so far.Footnote 15 The discussion covers the following topics: the difficulty of writing specifications, the necessity of internal symbolic representations, the use of
 vs.
vs.  , the fundamental design decision of choosing GR(1) as kernel for Spectra, the decision to implement our own synthesizer, the decision to make Spectra domain agnostic, and the use of the SYNTECH collections as benchmarks.
, the fundamental design decision of choosing GR(1) as kernel for Spectra, the decision to implement our own synthesizer, the decision to make Spectra domain agnostic, and the use of the SYNTECH collections as benchmarks.
7.1 Difficulty of writing specifications
Many authors have discussed the difficulty of writing formal specifications, in particular in LTL, see, e.g., [70]. Indeed, one important lesson we have learned from our preliminary experience with Spectra is the difficulty of writing specifications.
Each assumption and guarantee alone, thanks to the intentionally limited syntax (e.g., no nesting of LTL operators), is relatively easy to write and read. The use of enumerations, defines, and arrays, further makes it easier to write and read specifications.
Yet, at the level of a complete specification, consisting of many assumptions and guarantees, writing and reading is difficult. It is very easy to unintentionally write unrealizable or non-well-separated specifications, and fixing these problems is difficult. Spectra Tools support for dealing with these problems and others, as we described in Sect. 5, helps, but there is still much room for improvement in this regard.
Moreover, some students tended to translate an imperative way of thinking, which they are used to from traditional programming languages they know, into too-detailed safety guarantees, rather than writing higher-level assumptions and guarantees, and letting the synthesizer solve the dependencies and complete the details.
Consider the following as a negative example for the use of an imperative style inspired by the forklift example from [50]. An engineer could specify that a forklift should go forward to find cargo, e.g.,
 !cargo ->
!cargo ->
 (forward). To ensure that the forklift does not hit obstacles, the engineer might add
(forward). To ensure that the forklift does not hit obstacles, the engineer might add
 obstacle ->
obstacle ->
 (turn), but would also have to add an exception to the previous guarantee, e.g., change it to
(turn), but would also have to add an exception to the previous guarantee, e.g., change it to
 !cargo & !obstacle ->
!cargo & !obstacle ->
 (forward). Finally, adding an emergency stop feature would again require updating both guarantees with exceptions. In contrast, our example specification in [50] shows a declarative way of expressing similar behavior in the guarantees. In our experience, the imperative style is more natural to students but often leads to unrealizability, while a declarative style is less natural to students but is easier to maintain and evolve.
(forward). Finally, adding an emergency stop feature would again require updating both guarantees with exceptions. In contrast, our example specification in [50] shows a declarative way of expressing similar behavior in the guarantees. In our experience, the imperative style is more natural to students but often leads to unrealizability, while a declarative style is less natural to students but is easier to maintain and evolve.
7.2 Necessity of symbolic controller and execution mechanism
Another lesson one can learn from our experience is the necessity to use a symbolic representation for execution.
Very soon after the students started writing the specifications for SYNTECH15, the size of the generated concrete controllers we saw prohibited their use for straightforward code generation. Specifically, synthesis often produced controllers with thousands of states, which prohibits straightforward code generation due to size limits of the Java compiler. Thus, we were forced to quickly implement and let the students use the symbolic execution mechanism described in Sect. 5. With the symbolic execution mechanism, the students were able to execute controllers with up to \(2^{70}\) states.Footnote 16 Based on our experience in the SYNTECH projects, with the use of the symbolic mechanism, execution of large controllers becomes feasible.
7.3 Always versus G
Spectra, as most other GR(1) tools, has previously used the keyword
 instead of
instead of  for safety constraints in assumptions and guarantees. However, this use of the keyword
for safety constraints in assumptions and guarantees. However, this use of the keyword
 instead of
instead of  is different than LTL-
is different than LTL- in most GR(1) tools. This has lead to some cases of confusion (for ourselves, our students, and users of other tools, see below), specifically in the context of non-well-separation and for the execution of controllers.
in most GR(1) tools. This has lead to some cases of confusion (for ourselves, our students, and users of other tools, see below), specifically in the context of non-well-separation and for the execution of controllers.
As an example, consider the simple specification in Lst. 11 where the environment maintains a counter of loaded packages from 0 to 3. If the system sets variable load to true when loadedPackages=3, the environment has to violate its assumption as it cannot further increase the bounded integer. An engineer intended to fix this problem by adding the guarantee
 (loadedPackages = 3 -> !load). However, this intended fix does not workFootnote 17: Although it uses the confusing operator
(loadedPackages = 3 -> !load). However, this intended fix does not workFootnote 17: Although it uses the confusing operator
 , the guarantee is an assertion over current and next state, and so a transition to a state with loadedPackages = 3 and load is allowed. The guarantee only asserts that such a state would not have any possible successors (but at that point the environment already had to violate its assumption).
, the guarantee is an assertion over current and next state, and so a transition to a state with loadedPackages = 3 and load is allowed. The guarantee only asserts that such a state would not have any possible successors (but at that point the environment already had to violate its assumption).

As an example from another GR(1) synthesis tool, a bug/issueFootnote 18 has been reported for Slugs [22], where
 has the syntax
has the syntax  . In the report, a user writes “the environment is seemingly allowed to falsify one of its own safety requirements, specifically the mutex statement:
. In the report, a user writes “the environment is seemingly allowed to falsify one of its own safety requirements, specifically the mutex statement:
 ”. The user further notes that “The issue is resolved if the env safety is written in the “next” tense:
”. The user further notes that “The issue is resolved if the env safety is written in the “next” tense:
 .
.
An informal discussion with one the authors of RATSY [6] reveals an implementation of the same semantics of
 in GR(1), which they, however, reported had not led to problems so far.
in GR(1), which they, however, reported had not led to problems so far.
We have decided to address this confusion at the language level and avoid it by replacing the GR(1)-
 by the new keyword
by the new keyword
 .Footnote 19
.Footnote 19
7.4 Choice of GR(1) as kernel
A fundamental language design decision we have made early on was to use GR(1) as a kernel for Spectra. Our choice of GR(1) was motivated by its performance and expressive power. In retrospect, five years into the development and use of Spectra, we believe that we have made the right decision.
From the synthesis performance perspective, given our efficient symbolic implementation following [10], with some of the additional heuristics investigated in [28], our experience shows that synthesis computation time is not negligible but at the same time not necessarily the main challenge for engineers’ effective use of reactive synthesis. In our four project classes, the students used their own ordinary laptop computers for synthesis, from within Eclipse. While we did not systematically collect synthesis performance data, we have experienced synthesis times ranging from less than five seconds to up to a minute. We did not hear complaints or much negative feedback from the students about the performance of checking realizability or synthesizing a symbolic controller.
From the expressive power perspective, on the one hand, we have shown that the expressive power of GR(1) synthesis is enough to support most LTL specification patterns [21, 49]. On the other hand, our experience shows that writing specifications is difficult and using more expressive languages, e.g., full LTL, with nested temporal operators, might anyways be very challenging for engineers. Thus, the expressive power of GR(1) seems well suited for our purpose.
Still, we have work in progress toward enriching Spectra with additional language constructs and expressiveness, beyond LTL. As an example, we have work in progress on adding regular expressions and a variant of the rich triggers operator of PSL [23]. As another example, we have work in progress on adding a quantitative aspect to Spectra synthesis using the notion of energy, which corresponds with the accumulation and consumption of a finite resource such as power or memory. There, synthesis becomes the problem of generating an implementation that not only meets the pure GR(1) specification but also guarantees that the resource is never over consumed, if such an implementation exists. Finally, on this front of enriching Spectra, we have recently presented GR(1)* [3], a fragment of CTL* that extends GR(1) with existential guarantees that are not expressible in LTL. Importantly, yet, in comparison to GR(1), GR(1)* remains efficient, and induces only a minor additional cost in terms of time complexity, proportional to the extended length of the formula.
7.5 Implementing our own synthesizer
Given the above fundamental choice to use GR(1) as a kernel for Spectra, one may suggest that we could have implemented Spectra Tools on top of an existing GR(1) synthesizer. Indeed, several open-source GR(1) synthesizers are available, e.g., RATSY [6] and Slugs [22]. Why should we make the investment and implement yet another one?
The decision to implement our own new synthesizer was due to two main reasons. The first reason is performance. Our early experience showed that existing synthesizers (then, only RATSY), may not give us the performance required for the size of specifications we aimed to handle. Building our own synthesizer allowed us to optimize the code, use encoding inspired by Bartzis and Bultan [4] for arithmetic operations, and further integrate performance heuristics at the BDD level as well as at the fixed-point algorithms level [28]. As we show in [28], these proved to be very effective in improving the performance of GR(1) realizability checking compared to RATSY and Slugs, specifically for large specifications.
The second reason is flexibility in developing analyses beyond realizability checking and synthesis. Implementing our own synthesizer allowed us the complete flexibility to choose an architecture that will enable the independent implementation of related algorithms, e.g., for dealing with non-well-separation and unrealizability (core, counter-strategy, JVTS, repair), see Sect. 5.1. We continue to take advantage of this flexibility for additional new analyses that we are currently developing.
Finally, note that while we have implemented our own synthesizer, we did not start the implementation from nothing. Our implementation started from infrastructure provided by JTLV [67]. Moreover, we did not implement our own BDD library but rely on existing ones. Currently, the user of Spectra Tools can choose between (our own slightly modified versions of) CUDD [72] library and JTLV’s pure Java library.
7.6 Decision to make Spectra domain agnostic
Another design decision we have made early on was to define Spectra as a general purpose specification language, not limited or tied to a specific application domain of reactive systems. Thus, we kept the language and the analyses domain agnostic, completely separated from the application-specific implementation required for the execution of the synthesized controller in specific environments.
We have already taken advantage of this separation, in that we have implemented two independent execution environments, for Lego NXT robots and for stand-alone Java applications, as demonstrated in the SYNTECH collections. Thanks to this separation and based on our experience, we expect that in the future one can relatively easily extend the execution end of Spectra Tools to additional domains and execution environments.
7.7 The SYNTECH collections as benchmarks
Finally, in Sect. 6 we gave an overview of the four SYNTECH collections of Spectra specifications. We described how we obtained these collections, and presented an overview of the specifications and various metrics in Table 1, such as the number of assumptions and guarantees in each specification, etc. Finally, we have also discussed their quality characteristics, their strengths and weaknesses. All these are relevant when considering the use of these collections as benchmarks.
Sim et al. [71] formulated a theory of benchmarking within scientific disciplines and challenge software engineering research to become more scientific and cohesive by working as a community to define benchmarks. To date, benchmark specifications for GR(1) synthesis have been very limited. Most if not all works used only a handful of specifications, mainly the ARM AMBA AHB Arbiter (AMBA) [8] and a Generalized Buffer from an IBM tutorial (GenBuf) [9], which were created by researchers for the specific purpose of evaluating the performance of GR(1) synthesis tools. One advantage of these two specifications, is that they are parametric. This makes them suitable for evaluating scalability. They are, however, very systematic and very carefully designed. They may not adequately represent specifications that engineers may write in practice.
We made Spectra versions of AMBA and GenBuf, as well as of additional parametric specifications of some classic problems (e.g., Towers of Hanoi, Dining Philosophers, Cinderella and her stepmother) available on the Spectra website. Since all are parametric, they are indeed suitable for evaluating scalability, but, as argued above, may not adequately represent specifications that engineers may write in practice.
As described in Sect. 6, the SYNTECH specifications are different. In this sense, we believe they provide new valuable benchmarks for reactive synthesis related research. Indeed, we have already used SYNTECH15 and SYNTECH17 as benchmarks to examine the motivation for and the efficiency and effectiveness of various analyses, e.g., [28, 43, 51, 53]. Others have also already used them, e.g., [14, 59]. As we make these collections publicly available, we hope they will serve to advance reactive synthesis research and its future use in practice.
8 Related work
We review work related to Spectra and Spectra Tools from different perspectives. First, we discuss related specification languages. Second, we discuss GR(1) specification languages and synthesis tools.
8.1 Related specification languages
A number of logics and languages exist for the specification of reactive systems. Most fundamental, linear temporal logic (LTL) [65], a modal temporal logic with modalities referring to time, was introduced for the specification of reactive behavior and is probably the most commonly used specification language for model-checking today. The time complexity of synthesis from LTL is double-exponential in the length of the formula [66]. Nevertheless, some tools provide implementations of LTL synthesis (see an overview in [34]). These tools either suffer from scalability problems or provide only bounded solutions. We are not aware of any larger LTL specifications successfully used for reactive synthesis. Spectra is based on GR(1), a fragment of LTL with more efficient synthesis algorithms. When teaching Spectra to the undergraduate students who participated in our four project classes, we have deliberately avoided teaching LTL, so that the students use Spectra based on the intuitions of
 and
and
 , instead of the sometimes complicated semantics of LTL formulas with nested temporal operators.
, instead of the sometimes complicated semantics of LTL formulas with nested temporal operators.
Property Specification Language (PSL) [23] is an extension of LTL with many operators that were introduced to help engineers write specifications more concisely. PSL has become an IEEE standard in 2005. While the expressiveness of PSL extends the one of LTL (and GR(1)), we believe that some of its language constructs, e.g., the trigger operator, are interesting language features with which to extend Spectra in the future. The main use of PSL specifications is verification of reactive systems. PSL has been suggested for reactive synthesis in [8], with a case study of synthesizing an AMBA AHB bus controller. Importantly, however, despite its title, the PSL language constructs appearing in [8] are limited to those directly expressible in GR(1), and it is unclear whether their translation has been automated. Moreover, support for the trigger operator is not discussed in [8]. PSL includes neither a distinction between environment and system variables, nor any operators similar to Spectra’s advanced constructs of monitors, patterns, and counters.
SMV is the input language of the NuSMV tool [15] for symbolic model-checking [13]. The SMV language consists of a part for declaratively describing finite-state machines from variables and transitions, and of another part for specifications written in LTL or CTL. SMV has influenced the input languages of JTLV [67] and the design of Spectra. The declaration of variables, types, and definitions in Spectra is similar to that of SMV. A major difference between Spectra and SMV is, however, Spectra’s built-in distinction between environment and system variables. In addition, the advanced language constructs of parametric predicates, monitors, patterns, counters, and quantified arrays are also unique to Spectra.
TLA\(^+\) [45] (Temporal Logic of Actions) is a versatile specification language for software systems. TLA\(^+\) includes language constructs for the structural definition of closed and open (reactive) systems. Behavior in TLA\(^+\) can be specified using temporal operators. Analyses of TLA\(^+\) specifications are supported by the TLC model-checker [78]. The TLA\(^+\) language is too expressive for model-checking to be fully automated and only subsets of the language are supported. TLA\(^+\) has been successfully applied in industrial settings [61]. We believe that in the future, Spectra could benefit from composition mechanisms for specifications, similar to the ones provided by TLA\(^+\).
The Temporal Logic Synthesis Format (TLSF) [35] has been designed as a high-level description language for LTL synthesis problems. TLSF is used as an exchange format for LTL specifications in the SYNTCOMP competition [34]. TLSF is not specific to GR(1) and incorporates some features similar to the ones of PSL [23] for quantification and parametrization for the purpose of compact expression of repetitive constraints. TLSF does not provide advanced language features like monitors, counters, or patterns. To the best of our knowledge, existing specifications written in TLSF have been translated from other languages and thus the experience of developing specifications directly in TLSF is limited.
8.2 Related GR(1) specification languages and tools
A number of specification languages and tools for reactive synthesis have been developed on top of GR(1).
ApsectLTL [54] is an aspect-oriented specification language for reactive synthesis where specifications consist of a base and a set of aspects. An AspectLTL base consists of variable declarations and guarantees. AspectLTL aspects define new variables and advice in terms of additional guarantees over variables of aspects and the base. The AspectLTL language provides support for bounded integers, arrays, enumeration types, defines, and PastLTL. However, it lacks support for assumptions and does not include advanced language features like monitors, patterns, parametrized predicates, and counters. AspectLTL comes with rich Eclipse editors and tools for debugging and tracing of specifications [56]. The available body of AspectLTL specifications is limited to small examples created by the authors. It might be interesting to consider an aspect language based on Spectra. However, this would require the identification of suitable pointcuts for the new language constructs.
LTLMop (Linear Temporal Logic MissiOn Planning) [27] is a software for specifying and synthesizing robot missions on 2D maps. The tool comes with a graphical map editor and allows specifications to be expressed in the GR(1) subset of LTL or structured English [37]. LTLMop supports different GR(1) synthesizers (including JTLV [67] and Slugs [22]) and various output formats of synthesized controllers with support for deployment on the ROS middleware [75]. The tool supports various analyses of unrealizable specifications [68]. Some specifications created by the authors are available for examples presented in LTLMop’s research papers. Compared to Spectra, LTLMop has a very specialized focus for mission planning on a 2D map. To the best of our knowledge, the specification language does not provide advanced language features beyond those contained in the Spectra kernel.
A version of the Modal Transition System Analyzer (MTSA) [19] has been extended with synthesis for SGR(1) [12, 17], which is a variant of GR(1) that is specialized to the context of event-based models. MTSA models systems as Finite State Processes (FSP), a language for the compositional definition of Labeled Transition Systems (LTS) [19], and expresses specifications in Fluent Linear Temporal Logic (FLTL) [30]. An SGR(1) synthesis problem consists of an LTS modeled in FSP, and justice assumptions and guarantees specified as assertions over fluents [17]. A major difference between MTSA and SGR(1), and all other GR(1) languages and tools that we review in this section, including Spectra, is that MTSA and SGR(1) are event-based, i.e., the system and environment communicate via a single event per step, instead of by assigning values to multiple variables. MTSA has been extended with a check for non-well-separation: D’Ippolito et al. [18] (indirectly) refer to non-well-separation by characterizing the possible controllers that force assumption violations as anomalous. To the best of our knowledge, non-well-separation is only checked but unlike in Spectra Tools, no additional well-separation analyses (strategies or cores as in [51], see Sect. 5.6), are provided by MTSA. Moreover, to the best of our knowledge, analyses related to unrealizability have not been applied to SGR(1), unlike Spectra Tools, which provides various means to deal with unrealizable specifications, see Sect. 5.5. Finally, synthesis of SGR(1) follows a concrete rather than a symbolic algorithm, and has been applied only to very small example systems designed by the authors of [12, 17].
Slugs (SmalL bUt Complete GROne Synthesizer) [22] is an implementation and extensible tool for GR(1) synthesis. Slugs comes with plug-ins that implement analyses of unrealizability [68], synthesis for weighted specifications [36], and various modifications of the original GR(1) algorithm (see Sect. 3 in [22]). The input format of Slugs is limited to Boolean variables and GR(1) constraints. Note that the input of Slugs corresponds to the Spectra kernel, and thus it does not include advanced constructs corresponding to Spectra’s monitors, parametrized predicates, counters, etc. Structured Slugs is an alternative format that provides support for bounded non-negative integers with comparison and addition. In contrast, Spectra supports bounded integers (not only non-negative) with more arithmetic operations, including addition, subtraction, multiplication, division, and modulo (see Sect. 4.1). Structured Slugs can automatically be translated to Slugs input format. Note, however, that the arithmetic translation from Structured Slugs to Slugs input is done at the syntax level, while our translation in Spectra is implemented at the BDD level with potential performance benefits related to variable order [4]. Slugs has been used as a platform for various research papers. However, we are not aware of documented experience of using Slugs for synthesis except for small examples in research papers. Finally, in [28], the performance of realizability checking in Slugs is systematically compared against the performance of realizability checking in Spectra, using two well-known families of specifications from the literature. The comparison shows that Spectra, with all the heuristics of [28] employed, outperforms Slugs on large specifications. While for small specifications Slugs running times for realizability checking are better than Spectra’s, the larger the specification, the faster Spectra becomes relative to Slugs.
Open Promela [25] is a multi-paradigm specification language for synthesis defined as an extension of the syntax of Promela. The semantics of Open Promela is different from Promela and is defined by a translation to GR(1). The term “multi-paradigm” refers to the mix of imperative and declarative language elements. In addition to declarative assertions, the language introduces imperative variables and processes. Intuitively, the value of an imperative variable remains unchanged unless it appears in an assignment. Processes control assignments to variables, e.g., for describing possible transitions. Synthesis from Open Promela specifications is supported by a translation to the input format of Slugs [22]. Imperative language elements are expressed by adding constraints to variables. The language of Open Promela is demonstrated on a variant of the GR(1) AMBA specification [8]. We are not aware of tools for analyzing Open Promela specifications, their unrealizability, or their non-well-separation. To the best of our knowledge, the body of available Open Promela specifications is limited to few examples.
Tulip [24, 76] is a toolbox for the synthesis of hybrid systems. It combines GR(1) synthesis with automated abstractions of continuous dynamics. The syntax of Tulip expressions and operators is inspired by TLA\(^+\) [45] while specifications appear to be built programmatically.Footnote 20 We are not aware of Tulip’s support beyond synthesis itself, for analyzing specifications, unrealizability, or non-well-separation. Its input language does not include advanced constructs similar to Spectra’s monitors, counters, and patterns. To the best of our knowledge, the collected experience of writing specifications in Tulip is limited to few examples.
RATSY [6] has been developed as a requirement analysis tool that includes GR(1) synthesis. The tool has a graphical user interface to draw Buchi automata that serve as GR(1) assumptions or guarantees. Execution traces are visualized and RATSY implements algorithms for exploring counter-strategies in case of unrealizability [39]. RATSY does not support constructs similar to Spectra’s advanced language constructs such as monitors, patterns, and counters. Interestingly, RATSY’s user-manual presents an example of how to use RATSY to specify a bounded counter, by listing the different (safety) requirements one needs to specify.Footnote 21 One may contrast this with the simplicity of Spectra’s counter construct, which hides the complexity and encapsulates the concept of counting into a single specification element. The focus of RATSY on requirements and its graphical user interface differs from that of Spectra where the syntax of specifications is text-based. However, we believe that some analyses may benefit from visualizations of transition systems and we have integrated some of these into Spectra Tools, specifically visualizing both concrete and symbolic representations of counter-strategies [43]. Finally, in [28], the performance of realizability checking in RATSY is systematically compared against the performance of realizability checking in Spectra, using two well-known families of specifications from the literature. The comparison shows that Spectra, with all the heuristics of [28] employed, outperforms RATSY on large specifications. While for small specifications, RATSY running times for realizability checking are better than Spectra’s, the larger the specification, the faster Spectra becomes relative to RATSY (similarly to Slugs, see above).
Finally, some scenario-based specification languages and tools, as well as event-based modeling tools, make use of a translation to GR(1) or variants thereof. These include, e.g., PlayGo [32], which uses the translation described in [55], ScenarioTools [31], and SGR(1) [18] (discussed above). Some of these use a visual language while others use a textual language. Some of these provide tools for execution and debugging. None includes support for language features such as Spectra’s monitors, parametrized predicates, quantified arrays, patterns, and counters. It may be interesting to extend Spectra with an event-based idiom and scenario-like language constructs.
9 Conclusion and future work
The definition and development of Spectra and Spectra Tools are part of the SYNTECH project,Footnote 22 which aims at bridging the gap between the theory and algorithms of reactive synthesis, on the one hand, and software engineering practice, on the other. We use the language and tool set to learn about the challenges in bridging this gap and to develop and evaluate possible means to address them. An overview of the SYNTECH project was recently presented in an invited keynote by the first listed author at FormaliSE’20.Footnote 23
In this paper we presented the Spectra language. Spectra provides means to specify assumptions and guarantees for a reactive system, using high-level constructs such as patterns, monitors, and counters. We further presented an overview of Spectra Tools, a set of analyses and tools providing synthesis into correct-by-construction controllers, means to execute and simulate the synthesized controllers, and additional analyses aimed at helping engineers write higher-quality specifications. Finally, we presented statistics and observations based on four collections of specifications and on our early experience with Spectra.
We consider future work on different fronts. First, on the language front, we are working on enriching Spectra with additional language constructs, e.g., powerful temporal constructs, such as the triggers operator of PSL [23]. We further consider the development of additional pattern libraries, beyond the one covering the patterns of Dwyer et al., which already comes with the language. For example, a set of specification patterns for robotic missions was presented in [59]; we have work in progress on adding a library of these patterns to Spectra.
Second, on the tools front, we have work in progress on an improved simulation, testing, and debugging environment for the synthesized controller. This includes, for example, the ability to set breakpoints using propositions, to check whether a state that satisfies a certain proposition is reachable from the current state, etc.
Third, on the application domain front, we are looking to expand to other domains beyond autonomous Lego robots and the example systems we had so far. We are specifically examining case studies in the medical devices and network protocols domains, together with two industry partner companies.
Finally, we are looking into performing broader and more systematic evaluations of Spectra and Spectra Tools. We have already shared it with colleagues in other universities who may use it in teaching. We have also shared it with potential industrial collaborators. To broaden the evaluation, we plan to collect data about the experience in using Spectra in additional application domains. To make it more systematic, we will consider controlled experiments where, for example, different teams of students are instructed to do the same project with and without the availability of specific language constructs or analyses. We hope all these will generate additional data and insights into the potential applicability of reactive synthesis to software engineering.
Notes
Note that many authors, including us, sometime present the simpler and more intuitive formula for implication realizability rather than the one for strict realizability. For a comparison of strict realizability and implication realizability and a reduction between the two, see [10, 38]. Spectra supports strict realizability.
Other GR(1)-based specification languages use the LTL operator
 for
for  and
and  for
for  . This leads to confusion as their semantics usually does not match the LTL semantics. We discuss this further in Sect. 7.3.
. This leads to confusion as their semantics usually does not match the LTL semantics. We discuss this further in Sect. 7.3.Note that this does not allow for partial evaluation of a multi-dimensional array to a lower-dimensional array. For this task and other use cases Spectra provides quantification, see Sect. 4.9.
Note that the common keyword
 used for
used for
 in other GR(1) specification languages is often confused for defining state invariants (as the LTL semantics would suggest), leading to problems we discuss in Sect. 7.3.
in other GR(1) specification languages is often confused for defining state invariants (as the LTL semantics would suggest), leading to problems we discuss in Sect. 7.3.This property is difficult to check or ensure syntactically. See also Sect. 7.
LTL formula taken from the patterns catalog of Dwyer et al. [21]. There might be multiple ways to express an equivalent guarantee.
The three patterns that cannot be supported, number 23, 50, and 55, are among the least frequently used patterns according to the survey reported in [21].
This property is difficult to check syntactically. See also Sect. 7.
Note that these references from predicates are allowed in general (see Sect. 4.5) and are very convenient to use.
A single exception is translation of bounded integers and arithmetic operations, which is implemented in component BddGenerator for performance considerations following [4].
As an example, a code generator for Java generating if-statements to check all inputs easily creates methods larger than 64kB, which is the size limit for the Java compiler.
Note though, that in many cases, Spectra Tools does not exploit non-well-separation, e.g., in our example, it again computes the controller described in Sect. 5.3.
More information including short videos are available from http://smlab.cs.tau.ac.il/syntech/lego.
In a recent short workshop paper, we listed software engineering challenges of applying reactive synthesis to robotics [52]. The discussion here is broader and is not limited to the robotics domain.
The size of the state-space is estimated based on the number of Boolean variables after translation to the kernel, as we are not able to enumerate the reachable states of controllers this size.
It works neither in the strict nor in the implication semantics of GR(1) [10].
See the report and discussion at https://github.com/VerifiableRobotics/slugs/issues/5.
For backward compatibility, we still allow the use of
 , and interpret it as the GR(1)-
, and interpret it as the GR(1)-
 .
.See examples available from https://github.com/tulip-control/tulip-control/tree/master/examples.
http://rat.fbk.eu/ratsy/uploads/Main/RatsyManual_v2.1.pdf, downloaded July 2019, pages 9 to 13.
SYNTECH: http://smlab.cs.tau.ac.il/syntech/.
FormaliSE’20 keynote about SYNTECH: https://youtu.be/ig8_PbkGito.
References
2013 IEEE/RSJ International Conference on Intelligent Robots and Systems, Tokyo, Japan, November 3–7, 2013, IEEE (2013)
Almagor, S., Kupferman, O., Ringert, J.O., Velner, Y.: Quantitative assume guarantee synthesis. In: Majumdar, R., Kuncak, V. (eds.) Computer Aided Verification—29th International Conference, CAV 2017, Heidelberg, Germany, July 24–28, 2017, Proceedings, Part II, volume 10427 of Lecture Notes in Computer Science, pp. 353–374, Springer (2017)
Amram, G., Maoz, S., Pistiner, O.: GR(1)*: GR(1) specifications extended with existential guarantees. In: ter Beek, M.H., McIver, A., Oliveira, J.N. (eds.) Formal Methods—The Next 30 Years—Third World Congress, FM 2019, Porto, Portugal, October 7–11, 2019, Proceedings, volume 11800 of Lecture Notes in Computer Science, pp. 83–100, Springer (2019)
Bartzis, C., Bultan, T.: Efficient BDDs for bounded arithmetic constraints. STTT 8(1), 26–36 (2006)
Bloem, R., Chatterjee, K., Henzinger, T.A., Jobstmann, B.: Better quality in synthesis through quantitative objectives. In: Bouajjani, A., Maler, O., (eds.) Computer Aided Verification, 21st International Conference, CAV 2009, Grenoble, France, June 26–July 2, 2009. Proceedings, volume 5643 of Lecture Notes in Computer Science, pp. 140–156. Springer (2009)
Bloem, R., Cimatti, A., Greimel, K., Hofferek, G., Könighofer, R., Roveri, M., Schuppan, V., Seeber, R.: RATSY—a new requirements analysis tool with synthesis. In: CAV, volume 6174 of LNCS, pp. 425–429. Springer (2010)
Bloem, R., Ehlers, R., Könighofer, R.: Cooperative reactive synthesis. In: Finkbeiner, B., Pu, G., Zhang, L. (eds.) Automated Technology for Verification and Analysis—13th International Symposium, ATVA 2015, Shanghai, China, October 12–15, 2015, Proceedings, volume 9364 of Lecture Notes in Computer Science, pp. 394–410. Springer (2015)
Bloem, R., Galler, S.J., Jobstmann, B., Piterman, N., Pnueli, A., Weiglhofer, M.: Interactive presentation: Automatic hardware synthesis from specifications: a case study. In: Lauwereins, R., Madsen, J. (eds.) 2007 Design. Automation and Test in Europe Conference and Exposition, DATE 2007, Nice, France, April 16–20, 2007, pp. 1188–1193. EDA Consortium, San Jose, CA, USA (2007)
Bloem, R., Galler, S.J., Jobstmann, B., Piterman, N., Pnueli, A., Weiglhofer, M.: Specify, compile, run: hardware from PSL. Electr. Notes Theor. Comput. Sci. 190(4), 3–16 (2007)
Bloem, R., Jobstmann, B., Piterman, N., Pnueli, A., Sa’ar, Y.: Synthesis of Reactive(1) Designs. J. Comput. Syst. Sci. 78(3), 911–938 (2012)
Bohy, A., Bruyère, V., Filiot, E., Raskin, J.: Synthesis from LTL specifications with mean-payoff objectives. In: Piterman, N., Smolka, S.A. (eds.) Tools and Algorithms for the Construction and Analysis of Systems—19th International Conference, TACAS 2013, Held as Part of the European Joint Conferences on Theory and Practice of Software, ETAPS 2013, Rome, Italy, March 16–24, 2013. Proceedings, volume 7795 of Lecture Notes in Computer Science, pp. 169–184. Springer (2013)
Braberman, V.A., D’Ippolito, N., Piterman, N., Sykes, D., Uchitel, S.: Controller synthesis: from modelling to enactment. In: Notkin, D., Cheng, B.H.C., Pohl, K. (eds.) 35th International Conference on Software Engineering, ICSE ’13, San Francisco, CA, USA, May 18–26, 2013, pp. 1347–1350. IEEE Computer Society (2013)
Burch, J.R., Clarke, E.M., McMillan, K.L., Dill, D.L., Hwang, L.J.: Symbolic model checking: 10\(\hat{\,}\)20 states and beyond. In: Proceedings of the Fifth Annual Symposium on Logic in Computer Science (LICS ’90), Philadelphia, Pennsylvania, USA, June 4–7, 1990, pp. 428–439. IEEE Computer Society (1990)
Cavezza, D.G., Alrajeh, D., György, A.: Minimal assumptions refinement for GR(1) specifications. CoRR, arXiv:1910.05558 (2019)
Cimatti, A., Clarke, E.M., Giunchiglia, E., Giunchiglia, F., Pistore, M., Roveri, M., Sebastiani, R., Tacchella, A.: NuSMV 2: An OpenSource Tool for Symbolic Model Checking. In: CAV, volume 2404 of LNCS, pp. 359–364. Springer (2002)
David, A., Jensen, P.G., Larsen, K.G., Mikucionis, M., Taankvist, J.H.: Uppaal stratego. In: Baier, C., Tinelli, C. (eds.) Tools and Algorithms for the Construction and Analysis of Systems - 21st International Conference, TACAS 2015, Held as Part of the European Joint Conferences on Theory and Practice of Software, ETAPS 2015, London, UK, April 11–18, 2015. Proceedings, volume 9035 of Lecture Notes in Computer Science, pp. 206–211. Springer (2015)
D’Ippolito, N., Braberman, V.A., Piterman, N., Uchitel, S.: Synthesis of live behaviour models for fallible domains. In: ICSE, pp. 211–220 (2011)
D’Ippolito, N., Braberman, V.A., Piterman, N., Uchitel, S.: Synthesizing nonanomalous event-based controllers for liveness goals. ACM Trans. Softw. Eng. Methodol. 22(1), 9 (2013)
D’Ippolito, N., Fischbein, D., Chechik, M., Uchitel, S.: MTSA: the modal transition system analyser. In: 23rd IEEE/ACM International Conference on Automated Software Engineering (ASE 2008), 15–19 September 2008, L’Aquila, Italy, pp. 475–476. IEEE Computer Society (2008)
Dräger, K., Forejt, V., Kwiatkowska, M.Z., Parker, D., Ujma, M.: Permissive controller synthesis for probabilistic systems. In: TACAS, volume 8413 of LNCS, pp. 531–546. Springer (2014)
Dwyer, M.B., Avrunin, G.S., Corbett, J.C.: Patterns in property specifications for finite-state verification. In: ICSE, pp. 411–420. ACM (1999)
Ehlers, R., Raman, V.: Slugs: Extensible GR(1) synthesis. In: CAV, volume 9780 of LNCS, pp. 333–339. Springer (2016)
Eisner, C., Fisman, D.: A Practical Introduction to PSL. Springer, Series on Integrated Circuits and Systems (2006)
Filippidis, I., Dathathri, S., Livingston, S.C., Ozay, N., Murray, R.M.: Control design for hybrid systems with tulip: the temporal logic planning toolbox. In: 2016 IEEE Conference on Control Applications, CCA 2016, Buenos Aires, Argentina, September 19–22, 2016, pp. 1030–1041. IEEE (2016)
Filippidis, I., Murray, R.M., Holzmann, G.J.: A multi-paradigm language for reactive synthesis. In: P. Cerný, V. Kuncak, and P. Madhusudan, editors, Proceedings Fourth Workshop on Synthesis, SYNT 2015, San Francisco, CA, USA, 18th July 2015., volume 202 of EPTCS, pp. 73–97 (2015)
Finkbeiner, B., Schewe, S.: Bounded synthesis. STTT 15(5–6), 519–539 (2013)
Finucane, C., Jing, G., Kress-Gazit, H.: Ltlmop: Experimenting with language, temporal logic and robot control. In: 2010 IEEE/RSJ International Conference on Intelligent Robots and Systems, October 18–22, 2010, Taipei, Taiwan, pp. 1988–1993. IEEE (2010)
Firman, E., Maoz, S., Ringert, J.O.: Performance heuristics for GR(1) synthesis and related algorithms. Acta Inform. 57(1–2), 37–79 (2020)
Gabbay, D.M.: The declarative past and imperative future: Executable temporal logic for interactive systems. In: Banieqbal, B., Barringer, H., Pnueli, A. (eds.) Temporal Logic in Specification, Altrincham, UK, April 8–10, 1987, Proceedings, volume 398 of Lecture Notes in Computer Science, pp. 409–448. Springer (1987)
Giannakopoulou, D., Magee, J.: Fluent model checking for event-based systems. In: Paakki, J., Inverardi, P., (eds.) Proceedings of the 11th ACM SIGSOFT Symposium on Foundations of Software Engineering 2003 held jointly with 9th European Software Engineering Conference, ESEC/FSE 2003, Helsinki, Finland, September 1–5, 2003, pp. 257–266. ACM (2003)
Greenyer, J., Gritzner, D., Gutjahr, T., König, F., Glade, N., Marron, A., Katz, G.: Scenariotools—a tool suite for the scenario-based modeling and analysis of reactive systems. Sci. Comput. Program. 149, 15–27 (2017)
Harel, D., Maoz, S., Szekely, S., Barkan, D.: Playgo: towards a comprehensive tool for scenario based programming. In: Pecheur, C., Andrews, J., Nitto, E.D. (eds.) ASE 2010, 25th IEEE/ACM International Conference on Automated Software Engineering, Antwerp, Belgium, September 20–24, 2010, pp. 359–360. ACM (2010)
Hölldobler, K., Rumpe, B.: MontiCore 5 Language Workbench Edition 2017. Aachener Informatik-Berichte, Software Engineering, Band 32. Shaker Verlag, December (2017)
Jacobs, S., Basset, N., Bloem, R., Brenguier, R., Colange, M., Faymonville, P., Finkbeiner, B., Khalimov, A., Klein, F., Michaud, T., Pérez, G.A., Raskin, J., Sankur, O., Tentrup, L.: The 4th reactive synthesis competition (SYNTCOMP 2017): Benchmarks, participants & results. In: Fisman, D., Jacobs, S. (eds.) Proceedings Sixth Workshop on Synthesis, SYNT@CAV 2017, Heidelberg, Germany, 22nd July 2017., volume 260 of EPTCS, pp. 116–143 (2017)
Jacobs, S., Klein, F., Schirmer, S.: A high-level LTL synthesis format: TLSF v1.1. In: Piskac and Dimitrova [62], pp. 112–132
Jing, G., Ehlers, R., Kress-Gazit, H.: Shortcut through an evil door: optimality of correct-by-construction controllers in adversarial environments. In: 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems, Tokyo, Japan, November 3–7, [1], pp. 4796–4802 (2013)
Jing, G., Finucane, C., Raman, V., Kress-Gazit, H.: Correct high-level robot control from structured english. In: IEEE International Conference on Robotics and Automation, ICRA 2012, 14-18 May, 2012, St. Paul, Minnesota, USA, pp. 3543–3544. IEEE (2012)
Klein, U., Pnueli, A.: Revisiting synthesis of GR(1) specifications. In: Haifa Verification Conference (HVC), volume 6504 of LNCS, pp. 161–181. Springer (2010)
Könighofer, R., Hofferek, G., Bloem, R.: Debugging formal specifications: a practical approach using model-based diagnosis and counterstrategies. STTT 15(5–6), 563–583 (2013)
Kress-Gazit, H., Fainekos, G.E., Pappas, G.J.: Temporal-logic-based reactive mission and motion planning. IEEE Trans. Robot. 25(6), 1370–1381 (2009)
Kupferman, O., Lustig, Y., Vardi, M.Y., Yannakakis, M.: Temporal synthesis for bounded systems and environments. In: Schwentick, T., Dürr, C. (eds.) 28th International Symposium on Theoretical Aspects of Computer Science, STACS 2011, March 10–12, 2011, Dortmund, Germany, volume 9 of LIPIcs, pp. 615–626. Schloss Dagstuhl-Leibniz-Zentrum fuer Informatik (2011)
Kupferman, O., Vardi, M.Y.: Synthesis of trigger properties. In: LPAR, volume 6355 of LNCS, pp. 312–331. Springer (2010)
Kuvent, A., Maoz, S., Ringert, J.O.: A symbolic justice violations transition system for unrealizable GR(1) specifications. In: Bodden, E., Schäfer, W., van Deursen, A., Zisman, A. (eds.), Proceedings of the 2017 11th Joint Meeting on Foundations of Software Engineering, ESEC/FSE 2017, Paderborn, Germany, September 4–8, 2017, pp. 362–372. ACM (2017)
Kwiatkowska, M.Z., Parker, D.: Automated verification and strategy synthesis for probabilistic systems. In: Hung D.V., Ogawa, M. (eds.), Automated Technology for Verification and Analysis—11th International Symposium, ATVA 2013, Hanoi, Vietnam, October 15-18, 2013. Proceedings, volume 8172 of Lecture Notes in Computer Science, pp. 5–22. Springer (2013)
Lamport, L.: Specifying Systems. Addison–Wesley, The TLA+ Language and Tools for Hardware and Software Engineers (2002)
Lustig, Y., Vardi, M.Y.: Synthesis from component libraries. STTT 15(5–6), 603–618 (2013)
Maniatopoulos, S., Schillinger, P., Pong, V., Conner, D.C., Kress-Gazit, H.: Reactive high-level behavior synthesis for an atlas humanoid robot. In: Kragic, D., Bicchi, A., Luca, A.D. (eds.) 2016 IEEE International Conference on Robotics and Automation, ICRA 2016, Stockholm, Sweden, May 16–21, 2016, pp. 4192–4199. IEEE (2016)
Maoz, S., Pistiner, O., Ringert, J.O.: Symbolic BDD and ADD algorithms for energy games. In: Piskac and Dimitrova [62], pp. 35–54
Maoz, S., Ringert, J.O.: GR(1) synthesis for LTL specification patterns. In: ESEC/FSE, pp. 96–106. ACM (2015)
Maoz, S., Ringert, J.O.: Synthesizing a Lego Forklift Controller in GR(1): A Case Study. In: Proceedings of the 4th Workshop on Synthesis, SYNT 2015 colocated with CAV 2015, volume 202 of EPTCS, pp. 58–72 (2015)
Maoz, S., Ringert, J.O.: On well-separation of GR(1) specifications. In: FSE, pp. 362–372. ACM (2016)
Maoz, S., Ringert, J.O.: On the Software Engineering Challenges of Applying Reactive Synthesis to Robotics. In: Proceedings of the 1st Int. Workshop on Robotics Software Engineering, RoSE 2018 colocated with ICSE 2018 (2018)
Maoz, S., Ringert, J.O., Shalom, R.: Symbolic repairs for GR(1) specifications. In: Mussbacher, G., Atlee, J.M., Bultan, T. (eds.) Proceedings of the 41st International Conference on Software Engineering, ICSE 2019, Montreal, QC, Canada, May 25–31, 2019, pp. 1016–1026. IEEE/ACM (2019)
Maoz, S., Sa’ar, Y.: AspectLTL: an aspect language for LTL specifications. In: AOSD, pp. 19–30. ACM (2011)
Maoz, S., Sa’ar, Y.: Assume-guarantee scenarios: Semantics and synthesis. In: MODELS, volume 7590 of LNCS, pp. 335–351. Springer (2012)
Maoz, S., Sa’ar, Y.: Two-way traceability and conflict debugging for aspectltl programs. Trans. Aspect-Oriented Softw. Dev. 10, 39–72 (2013)
Maoz, S., Shalom, R.: Inherent vacuity for GR(1) specifications. In: ESEC/FSE, pp. 99–110. ACM (2020)
Maoz, S., Shevrin, I.: Just-in-time reactive synthesis. In: ASE, pp. 635–646. IEEE (2020)
Menghi, C., Tsigkanos, C., Pelliccione, P., Ghezzi, C., Berger, T.: Specification patterns for robotic missions. CoRR, arXiv:1901.02077 (2019)
Miyazawa, A., Ribeiro, P., Li, W., Cavalcanti, A., Timmis, J., Woodcock, J.: Robochart: modelling and verification of the functional behaviour of robotic applications. Softw. Syst. Model. 18(5), 3097–3149 (2019)
Newcombe, C., Rath, T., Zhang, F., Munteanu, B., Brooker, M., Deardeuff, M.: How amazon web services uses formal methods. Commun. ACM 58(4), 66–73 (2015)
Piskac, R., Dimitrova, R., (eds.): Proceedings Fifth Workshop on Synthesis, SYNT@CAV 2016, Toronto, Canada, July 17–18, 2016, volume 229 of EPTCS (2016)
Piterman, N., Pnueli, A.: Faster solutions of rabin and streett games. In: 21th IEEE Symposium on Logic in Computer Science (LICS 2006), 12–15 August 2006, Seattle, WA, USA, Proceedings, pp. 275–284. IEEE Computer Society (2006)
Piterman, N., Pnueli, A., Sa’ar, Y.: Synthesis of reactive(1) designs. In: VMCAI, volume 3855 of LNCS, pp. 364–380. Springer (2006)
Pnueli, A.: The temporal logic of programs. In: 18th Annual Symposium on Foundations of Computer Science, Providence, Rhode Island, USA, 31 October–1 November 1977, pp. 46–57. IEEE Computer Society (1977)
Pnueli, A., Rosner, R.: On the Synthesis of a Reactive Module. In: POPL, pp. 179–190. ACM Press (1989)
Pnueli, A., Sa’ar, Y., Zuck, L.D.: JTLV: a framework for developing verification algorithms. In: CAV, volume 6174 of LNCS, pp. 171–174. Springer (2010)
Raman, V.: Kress-Gazit, H.: Analyzing unsynthesizable specifications for high-level robot behavior using ltlmop. In: Gopalakrishnan G., Qadeer, S. (eds.) Computer Aided Verification—23rd International Conference, CAV 2011, Snowbird, UT, USA, July 14–20, 2011. Proceedings, volume 6806 of Lecture Notes in Computer Science, pp. 663–668. Springer (2011)
Ringert, J.O., Roth, A., Rumpe, B., Wortmann, A.: Language and code generator composition for model-driven engineering of robotics component & connector systems. J. Softw. Eng. Robot. 6, 33–57 (2015)
Rozier, K.Y.: Specification: the biggest bottleneck in formal methods and autonomy. In: VSTTE, volume 9971 of LNCS, pp. 8–26 (2016)
Sim, S.E., Easterbrook, S.M., Holt, R.C.: Using benchmarking to advance research: a challenge to software engineering. In: Clarke, L.A., Dillon, L., Tichy, W.F. (eds.) Proceedings of the 25th International Conference on Software Engineering, May 3–10, 2003, Portland, Oregon, USA, pp. 74–83. IEEE Computer Society (2003)
Somenzi, F.: CUDD: BDD package, University of Colorado, Boulder. http://vlsi.colorado.edu/~fabio/CUDD/cudd.pdf
Spectra Website. http://smlab.cs.tau.ac.il/syntech/spectra/
Walker, A., Ryzhyk, L.: Predicate abstraction for reactive synthesis. In: Formal Methods in Computer-Aided Design, FMCAD 2014, Lausanne, Switzerland, October 21–24, 2014, pp. 219–226. IEEE (2014)
Wong, K.W., Finucane, C., Kress-Gazit, H.: Provably-correct robot control with ltlmop, OMPL and ROS. In: 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems, Tokyo, Japan, November 3–7 [1], p. 2073 (2013)
Wongpiromsarn, T., Topcu, U., Ozay, N., Xu, H., Murray, R.M.: TuLiP: A Software Toolbox for Receding Horizon Temporal Logic Planning. In: Proceedings of the 14th International Conference on Hybrid Systems: Computation and Control, HSCC ’11, pp. 313–314. New York, NY, USA, ACM (2011)
Xtext. Xtext. https://www.eclipse.org/Xtext/
Yu, Y., Manolios, P., Lamport, L.: Model checking tla\(^{+}\) specifications. In: L. Pierre and T. Kropf, editors, Correct Hardware Design and Verification Methods, 10th IFIP WG 10.5 Advanced Research Working Conference, CHARME ’99, Bad Herrenalb, Germany, September 27–29, 1999, Proceedings, volume 1703 of Lecture Notes in Computer Science, pp. 54–66. Springer (1999)
Zeller, A.: Yesterday, my program worked. today, it does not. why? In: ESEC/FSE, volume 1687 of LNCS, pp. 253–267. Springer (1999)
Acknowledgements
We thank the 67 undergraduate students who participated in our four project classes. We thank Elizabeth Firman, Aviv Kuvent, Or Pistiner, Rafi Shalom, Ilia Shevrin, Keren Solodkin, and Yoni Wolbe for their contribution to the implementation of Spectra Tools.
This project has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation program (grant agreement No 638049, SYNTECH).
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Antonio Vallecillo.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
A Spectra grammar
We show a combination of the grammars of the Spectra kernel from Fig. 4 and of all extensions from Sect. 4 in Fig. 15. As mentioned in Sect. 2.3, this grammar includes simplifications for readability and in order to fit it on a single page.
Spectra provides more verbose alternative to most keywords shown in Table 2. We have decided to use the shorter keywords in Sects. 3 and 4 as they seem to be preferred when writing specifications.
B Complete extended example
Listing 12 shows our initial example from Lst. 1 and all its extensions mentioned in Sect. 4. The extensions include enumerations and integer variables from Lst. 2, the define and its use from Lst. 3, state invariants as described in Sect. 4.3, the PastLTL example from Sect. 4.4, the predicate from Lst. 5, the monitor from Lst. 6, the counter from Lst. 7, the pattern instances from Lst. 9, and an import as described in Sect. 4.10 to import the pattern definition shown in Lst. 8.
The lines of the different listings are rearranged in Lst. 12 to define all system and environment variables at the top of the specification. The body of the define from Lst. 3 has been extended to include variable ambulanceMain. With this inclusion the complete specification as shown in Lst. 12 is realizable.

Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Maoz, S., Ringert, J.O. Spectra: a specification language for reactive systems. Softw Syst Model 20, 1553–1586 (2021). https://doi.org/10.1007/s10270-021-00868-z
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10270-021-00868-z


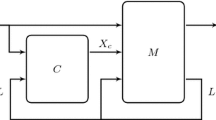



 iff
iff  iff
iff 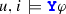 iff
iff  iff
iff 


 ;
; ;
; );
); );
); );
); );
); );
); ).
).





 , the guarantees for
, the guarantees for  and
and  constraints are expressed without checking over- or underflows, i.e., these would lead to safety guarantee violations.
constraints are expressed without checking over- or underflows, i.e., these would lead to safety guarantee violations. , we add a case distinction to the guarantees for
, we add a case distinction to the guarantees for
 and
and  constraints to handle overflows and underflows by preserving the current counter values.
constraints to handle overflows and underflows by preserving the current counter values. , we add a case distinction to the guarantees for
, we add a case distinction to the guarantees for
 constraints to set the counter at the upper bound to its lower bound. Respectively, for
constraints to set the counter at the upper bound to its lower bound. Respectively, for
 constraints we set a counter at the lower bound to its upper bound.
constraints we set a counter at the lower bound to its upper bound.



 for
for  and
and  for
for  . This leads to confusion as their semantics usually does not match the LTL semantics. We discuss this further in Sect.
. This leads to confusion as their semantics usually does not match the LTL semantics. We discuss this further in Sect.  used for
used for
 in other GR(1) specification languages is often confused for defining state invariants (as the LTL semantics would suggest), leading to problems we discuss in Sect.
in other GR(1) specification languages is often confused for defining state invariants (as the LTL semantics would suggest), leading to problems we discuss in Sect.  , and interpret it as the GR(1)-
, and interpret it as the GR(1)-
 .
.