A dynamic network model to measure exposure concentration in the Austrian interbank market

Abstract

Motivated by an original financial network dataset, we develop a statistical methodology to study non-negatively weighted temporal networks. We focus on the characterization of how nodes (i.e. financial institutions) concentrate or diversify the weights of their connections (i.e. exposures) among neighbors. The approach takes into account temporal trends and nodes’ random effects. We consider a family of nested models on which we define and validate a model-selection procedure that can identify those models that are relevant for the analysis. We apply the methodology to an original dataset describing the mutual claims and exposures of Austrian financial institutions between 2008 and 2011. This period allows us to study the results in the context of the financial crisis in 2008 as well as the European sovereign debt crisis in 2011. Our results highlight that the network is very heterogeneous with regard to how nodes send, and in particular receive edges. Also, our results show that this heterogeneity does not follow a significant temporal trend, and so it remains approximately stable over the time span considered.

1 Motivation

Recently, the EU was hit by two major financial crises. In 2008, the problems started initially in the US subprime mortgage market and were partially caused by lax regulation and overly confident debt ratings. The source of the European sovereign debt crisis in 2011, however, was most likely private debt arising from property bubble and resulting in government bailouts. The lack of a common fiscal union in the EU did not help with the situation, which resulted in the European central bank providing cheap loans to maintain a steady cash flow between EU banks. During these turbulent times, European banks were facing high levels of uncertainty. It was not clear which counter party would remain solvent in the foreseeable future and even sovereign bonds were no longer considered a safe option. In the face of these unfavorable conditions, the banks were forced to reconsider their interbank investments and re-adjust their portfolios in order to account for the change in the economic situation.

With the goal of contributing to the discussion on diversification and concentration of interbank exposures, we focus our attention on an original dataset of the Austrian interbank market between the spring of 2008 and autumn of 2011. Namely, we introduce a dynamic network model to quantify exposure concentration of individual banks and of the market overall. We accomplish this by extending the current literature on latent variable network models to a framework for compositional data that evolve over time. This framework can potentially provide bank-dependent measures of systemic risk, as well as a global measure of the overall level of systemic risk in the market. We resort to an intuitive modeling of a single network homogeneity (drift) parameter which we use to capture the homogeneity over time, as well as node random effects parameters that capture exposure concentration and attractiveness of banks, individually. Our model is specifically designed for instances where a network needs to be characterized by a single evolving variable, or when one is interested in obtaining a model-based quantitative measurement of the inter-temporal development of network homogeneity. While our approach is strongly motivated by our original financial application, it also provides a new methodology extension that can be used to analyze any temporal and compositional network data, where the main interest lies in studying the concentration/diversification of edge weights. This contributes to the literature on the statistical analysis of weighted networks, and in particular to the literature on networks indicating proportions, which is a rather unexplored topic. The code associated to our methodology is available from the public repository (Rastelli and Hledik 2021).

1.1 Motivating example

In a financial context, a change in a financial network structure can have far-reaching and non-trivial consequences. To illustrate this fact further, consider a hypothetical financial network of four institutions (banks) represented by nodes and their mutual financial exposures (debt) represented by edges. In this simple example, connections are symmetric and every bank splits its investment among its neighbors equally. Furthermore, banks are required by a regulator to always keep a capital buffer to account for unexpected withdrawals, unfavorable economic conditions and other factors. Therefore, we assume that an institution remains safe unless it loses at least half of its investments in other institutions. If that happens, the institution gets bankrupt and it might further negatively affect other banks in the network. To see how network structure affects the overall stability, consider a case where one of these four banks gets affected by an exogenous shock such that it has to declare bankruptcy. In such case, its neighbors will not get their respective investment and might suffer the same fate, putting their own neighbors in danger. This contagious behavior is dependent on how the banks are linked together, which illustrates the importance of structure when addressing questions on systemic importance and financial stability.

Fig. 1

Different loan network structures on a set of four banks

For the hypothetical case of four banks, there are up to 11 topologically different network structures that can possibly occur: a subset of these are shown in Fig. 1. In the case shown in Fig. 1a, there is no danger of contagion since there are no edges to propagate shocks. An analogical result follows from the network shown in Fig. 1c, where a failure of one node is not sufficient to take down the rest because every other institution only loses one third of its investment. Problems arise in intermediately connected systems such as Fig. 1b, where an initial shock may wipe out the whole system.

This basic example hints at a much more complex issue of network stability that has been extensively studied by financial regulators in the past two decades. It highlights that the level of exposure concentration in a system plays a crucial role in determining its stability and that assessment of this trait for observed networks can prove challenging. In this paper, we address this impasse, introducing a statistical model specifically designed to measure the concentration of exposures for every bank in the system, hence obtaining a measure for one of the facets of systemic risk.

2 Related literature

This paper is connected to two important strands of research. On the one hand, we contribute to the literature on statistical analysis of networks, since we extend the current available methodologies, based on latent variables, that can be used to analyze non-negatively weighted temporal networks. On the other hand, we contribute to the established literature on systemic risk and financial networks. This area of research has often focused on the stability of financial systems as well as the possibility of contagious bankruptcies similar to our simple example above. Research papers on this subject have been published by both academics in finance as well as market regulators.¹ Our proposed research borrows from and contributes to both fields, ultimately creating a novel perspective on financial systemic risk.

Within the statistics literature, our paper contributes to the research on latent variable network modeling. Prominent contributions include the foundational paper on latent space models by Hoff et al. (2002), later extended to the dynamic framework by Sarkar and Moore (2006), and the latent stochastic blockmodels (Nowicki and Snijders 2001) extended to a dynamic framework by Yang et al. (2011), Xu and Hero (2014) and Matias and Miele (2017), among others. These latent variable models possess a number of desirable theoretical features, as illustrated in Rastelli et al. (2016) and Daudin et al. (2008) for the latent space model and stochastic blockmodel, respectively.

Our approach also shares a number of similarities with other recent papers that apply a latent variable framework on various types of dynamic network data. These include, among others, Friel et al. (2016), where the authors introduce a dynamic latent space model to measure the financial stability of the Irish Stock Exchange; Sewell and Chen (2016), who introduce a latent space model for dynamic weighted networks; and Matias et al. (2018), where the authors propose a dynamic extension of the stochastic blockmodel. Our model could be seen as a variant of the works by Westveld and Hoff (2011) and Sewell (2018), which deal with temporal latent variable weighted networks, to the context of compositional data. Differently from all these works using latent variable frameworks, our approach relies on a new model which is designed to measure and study the systemic risk associated to a financial system. We point out that our approach also has similarities to Dirichlet regression models for compositional data, as per Minka (2000), van der Merwe (2019) and references therein; however, differently from these works, we apply compositional data analysis to the context of network analysis.

Within the finance literature, one of the earliest papers on the topic of systemic risk was the work of Allen and Gale (2000), who have shown that the structure of the interbank market is important for the evaluation of possible contagious bankruptcies. Later on, Gai and Kapadia (2010) extended their work from a simple model of four institutions to a financial network of an arbitrary size. Other notable papers on systemic risk include, for example, Glasserman and Young (2016) or Acemoglu et al. (2015), while Upper (2011) provides an excellent survey of regulatory-published scientific reports on the subject. With respect to the questions on diversification, we refer the reader to Elliott et al. (2014) and Frey and Hledik (2018), where a nontrivial relationship between diversification, exposure concentration and contagious defaults is presented, or to Goncharenko et al. (2018), where banks endogenously choose their level of diversification given the network structure in an equilibrium setting.

For a better understanding of the topic of systemic risk and financial networks and of its apparent interdisciplinary nature, see the literature review of Caccioli et al. (2018). For a better picture of how these tools can potentially be used for a macroprudential risk assessment, see Gai and Kapadia (2019) or Battiston and Martinez-Jaramillo (2018). The role of diversification and exposure concentration and its intricate effect on financial stability is addressed in Bardoscia et al. (2017). This paper also underlines the importance of network topology and its effects on overall stability of the financial system.

Our paper shares similar goals with these works, and we further add to these papers by introducing a new generative mechanism and a modeling framework where exposure concentration and homogeneity of the system can be studied inter-temporally.

Lastly, we also contribute to the literature on the stability of the Austrian interbank market. Related works in this area include Elsinger et al. (2006), Puhr et al. (2012) and Boss et al. (2004) who have looked at possible contagious effects and descriptive statistics of the Austrian financial network. Compared to these contributions, one novelty of our work is that we are able to consider the temporal dependency of the network, thus providing an appreciation of the changes in the structure of the network over time.

3 Data and exploratory analysis

We use an original dataset obtained by the Austrian National Bank which contains quarterly observations of the Austrian interbank market for a period of four years (from spring of 2008 until autumn of 2011). More precisely, the dataset contains aggregated mutual claims between any two of $N=800$ Austrian banks for all relevant quarters (2008Q1–2011Q4), resulting in 16 observations of the financial network. All of the banks considered exist throughout the whole period.

In order to comply with the privacy rules of the Austrian National Bank, the data is anonymized such that the true identities of banks in the system are hidden and replaced by non-descriptive IDs. Moreover, we are unable to observe the absolute values of banks’ mutual claims, only their scaled equivalents (relative to the highest exposure value, independently for each time frame). As a consequence, as per privacy protection, the magnitude of claims is effectively not comparable across time. This motivated us to seek an approach that could bypass this limitation: for the purposes of our model, the true values of the claims are not required, since our framework only uses their relative size. In addition, we illustrate in Appendix A a procedure that allows us to approximate the true values of the claims up to a proportionality constant: we do not use these estimated quantities in our model, but we use them to reconstruct and approximate a value representing the importance of each institution. In order to better clarify these concepts, we now give a sequence of definitions to set our notation.

3.1 Definitions

A dynamic network of interbank exposures is a sequence of graphs where, for each time frame, the nodes correspond to banks and the edges correspond to the connections between them. In particular, the edges are directed and carry positive values indicating the claim on one bank from another. We note that an observed network of interbank exposures between N banks over T time frames may be represented as a collection of T interaction matrices of the same size $N\times N$, as in the following definition:

Definition 3.1

A sequence of true exposures ${\mathcal {E}}=\{{{\textbf {E}}}^{(t)}\}_{t\in {\mathcal {T}}}$ defined on the set of nodes ${\mathcal {V}}$ over the timespan ${\mathcal {T}}$ consists of a collection of interaction matrices ${{\textbf {E}}}^{(t)} \ \ \forall t \in {\mathcal {T}}$ with elements $e^{(t)}_{ij}$ for $t\in {\mathcal {T}}$, $i\in {\mathcal {V}}$, $j\in {\mathcal {V}}$, where $e^{(t)}_{ij}$ corresponds to the financial exposure of bank i towards bank j in period t.

We focus on the case where ${\mathcal {V}}=\left\{ 1,\dots ,N\right\}$ and ${\mathcal {T}}=\left\{ 1,\dots ,T\right\}$. In the Austrian interbank market context, the adjacency matrix ${{\textbf {E}}}^{(t)}$ contains the true values of all mutual claims between any two of $N=800$ Austrian banks at the corresponding time frame. However, as explained earlier, we are unable to observe the true exposures ${\mathcal {E}}$ due to privacy policy of the Austrian National Bank. By contrast, we adopt a procedure (see Appendix A for full details) that allows us to estimate the following quantities:

Definition 3.2

A sequence of absolute exposures ${\mathcal {X}}=\{{{\textbf {X}}}^{(t)}\}_{t\in {\mathcal {T}}}$ on the set of nodes ${\mathcal {V}}$ over the timespan ${\mathcal {T}}$ has elements defined as follows:

$$\begin{aligned} x_{ij}^{(t)}{\mathop {=}\limits ^{def}}\frac{e_{ij}^{(t)}}{\max _{\{k,l\}} e_{kl}^{(1)}} \ \ \ \forall i,j \in {\mathcal {V}}, \forall t \in {\mathcal {T}} \end{aligned}$$

(1)

In other words, the sequence of absolute exposures is simply a scaled version of the non-observable sequence of the true exposures, where every exposure is divided by the value of the first period’s largest exposure. Lastly, we define the sequence of relative exposures that our statistical model uses as observed data:

Definition 3.3

A sequence of relative exposures ${\mathcal {Y}}=\{{{\textbf {Y}}}^{(t)}\}_{t\in {\mathcal {T}}}$ on the set of nodes ${\mathcal {V}}$ over the time span ${\mathcal {T}}$ has elements defined as follows:

$$\begin{aligned} y_{ij}^{(t)}{\mathop {=}\limits ^{def}}\frac{x_{ij}^{(t)}}{\sum _{k=1}^{N} x_{ik}^{(t)}} \ \ \ \forall i,j \in {\mathcal {V}}, \forall t \in {\mathcal {T}} \end{aligned}$$

(2)

This transformation constricts the edge weights in our networks to a [0, 1] interval, making it easier to work with from the network homogeneity viewpoint. In this network, every nodes’ outgoing edge values always sum up to 1. Differently from ${\mathcal {X}}$, the data ${\mathcal {Y}}$ is not estimated and available to us in exact form, regardless of the transformations and anonymizations.

To summarize, ${\mathcal {E}}$ corresponds to the non-observed real value of interbank connections, ${\mathcal {X}}$ to their estimated scaled version and ${\mathcal {Y}}$ to the relative interbank connections. Our model only uses ${\mathcal {Y}}$ as observed data, which in fact corresponds to the only quantities that are available to us in an exact form. We use ${\mathcal {X}}$ as a proxy to derive a measure of importance of banks. In order to do so, we introduce the bank’s relevance:

Definition 3.4

The relevance of bank i in time period t is defined as:

$$\begin{aligned} r_i^{(t)} = \sum _{k\in {\mathcal {V}}} x_{ik}^{(t)} + \sum _{k\in {\mathcal {V}}} x_{ki}^{(t)}. \end{aligned}$$

(3)

Thus, the relevance simply corresponds to the bank’s overall sum of its interbank assets and liabilities. Again, the relevance variable is not used in the modeling, instead it is only used to contextualize the results.

With a clear measure of systemic importance, we can now select a subsample of banks with the highest aggregated relevance $r_i = \sum _{t=1}^{T} r_i^{(t)}$. This allows us to focus on the interactions of systemically important banks and observe emergence of unique patterns. We use the aggregated relevance measure to create a smaller dataset consisting of the 200 systemically most relevant institutions and their mutual connections. From now on, we shall refer to the full dataset and the reduced dataset as OeNB 800 and OeNB 200, respectively.²

3.2 Exploratory data analysis

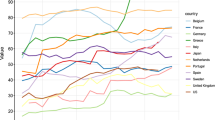
In order to have a better overview of the data, we have conducted an exploratory analysis. We plot the evolution of the average bank relevance in Fig. 2. As expected from its definition, we see a sharp drop in the second half of 2008 as a direct effect of the financial crisis.

Fig. 2

Bank relevance for the full sample (a) and the sample containing only the 200 most relevant banks (b), recalculated after the exclusion of the 600 banks

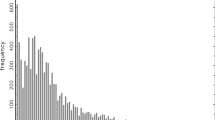
Table 1 and Fig. 3 contain brief descriptive statistics, where one can see the number as well as magnitude of connections as a function of time. The number of connections ($2{\text {nd}}$ column) shows the number of edges in the network as of time t, while the relative size ($3{\text {rd}}$ column) is proportional to the overall total exposure, calculated as the ratio between the average absolute exposure in each year, and the highest absolute exposure in the first time observation. We would like to highlight the second and third quarter of 2008, where a drop in the overall total exposure in the economy can be observed. This period corresponds to the financial crisis associated with the failure of Lehman Brothers in the US and the problems stemming from the housing market. Interestingly, in the Austrian interbank market, the overall number of connections does not seem to be affected by these events as much as their size. This shows that, albeit Austrian banks have reduced their mutual exposures significantly, they were rarely completely cut off. Another important period is during the second and third quarter of 2011, which is roughly when the European sovereign debt crisis started. At a first glance, there does not seem to be much in relation to this event in our data.

Fig. 3

Number of connections and their relative size in time, for OeNB 800

Table 1 Number of connections and their relative size in time, for OeNB 800

Interbank markets are commonly disassortative, i.e. nodes with a low number of neighbors are mostly connected to nodes with high number of neighbors and vice versa, see Hurd (2016). This property in financial networks is quite common and is generally referred to as “core-periphery” structure. Social networks tend to be fundamentally different, since a high number of “hubs” in the network does not necessarily imply a low number of triangles, see for instance (Li et al. 2014; Watts and Strogatz 1998). Financial systems also tend to be very sparse. These same patterns are confirmed in the Austrian interbank market, as shown in Fig. 4.

Fig. 4

Adjacency matrix for the first time period, for OeNB 800, consisting of 2952 edges represented as dots (a) and a graphical representation of the network snapshot for the nodes with at least one connection (b)

3.3 Entropy as a measure of concentration

We have observed several interesting patterns in the data which suggest that using a more complex model could produce new insights regarding the evolution of bank exposure concentration. Since the main interest of our research lies in the connectivity patterns of agents in an interbank market, we have also looked at the evolution of an entropy index for this system. For this purpose, we use a standard definition of entropy as follows:

Definition 3.5

The entropy $S_i^{(t)}$ of node $i\in {\mathcal {V}}$ at time $t \in {\mathcal {T}}$ is defined as:

$$\begin{aligned} S_i^{(t)}{\mathop {=}\limits ^{def}}-\sum _{k=1}^{N}y_{ik}^{(t)}\log {y_{ik}^{(t)}} \end{aligned}$$

(4)

with the convention that $y\log y = 0$ when $y=0$.

Speaking more plainly, this quantity describes how an institution distributes its assets among counterparties. A bank with a single debtor would have zero entropy, since its relative exposure is trivially one for that one debtor and zero for all the other banks. With an increased number of debtors with equal exposures, a node’s entropy increases and, for a fixed number of debtors, the entropy of a node is maximized when its assets are distributed evenly among neighbors. Ergo, if two nodes have the same number of outgoing connections, one may view the one with a higher entropy as better diversified. We will refer to “better diversified” nodes as ones with lower exposure concentration or, alternatively, as the ones with higher exposure spread.

Fig. 5

Distribution of entropy change in time, for OeNB 800

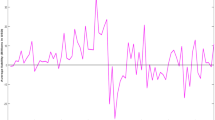
In Fig. 5, we plot the change in nodes’ entropies in consecutive periods ($S_i^{(t+1)} - S_i^{(t)}$). One can observe an increase in both mean and variance during the second and third quarter of 2011, which corresponds to the sovereign crisis in Europe. At that point, future bailouts of several EU countries were uncertain which might have added to the volatility in the market. Interestingly, no similar effect can be seen during the 2008 crisis. We point out that there are other ways of assessing the temporal evolution of node exposure homogeneity. We have chosen the entropy index for our exploratory analysis, as it constitutes a simple, clean and easily tractable approach, but one could easily turn to other measures, e.g. the Herfindahl index as is common practice in economics literature.

4 The model

4.1 The full model

The observed data are the relative interbank exposures $y_{ij}^{(t)}$ from Definition 3.3. We assume that there are no self-connections, i.e., when not stated otherwise, we always work with $t\in {\mathcal {T}}$, $i,\ j \in {\mathcal {V}}$ and $i\ne j$. Since these exposures are relative, it follows from definition that they satisfy (for all i and t):

$$\begin{aligned} y_{ij}^{(t)} \in [0,1] \text{ and } \sum _{j\in {\mathcal {V}}: j\ne i}y_{ij}^{(t)} = 1. \end{aligned}$$

(5)

We propose to model the vector ${{\textbf {y}}}_{i\cdot }^{(t)} = \left( y_{i1}^{(t)}, \dots , y_{iN}^{(t)} \right)$ as a Dirichlet random vector characterized by the parameters $\varvec{\alpha }_{i\cdot }^{(t)} = \left( \alpha _{i1}^{(t)}, \dots , \alpha _{iN}^{(t)} \right)$, where $\alpha _{ij}^{(t)}>0$. The values $y_{ii}^{(t)}$ are excluded from the analysis for all $i \in {\mathcal {V}}$ and $t \in {\mathcal {T}}$. Following the established standard in latent variable models, the data are assumed to be conditionally independent given the latent parameters $\varvec{\alpha } = \left\{ \alpha _{ij}^{(t)}\right\} _{i,j,t}$. Hence, the model likelihood reads as follows:

$$\begin{aligned} {\mathcal {L}}_{{\mathcal {Y}}}\left( \varvec{\alpha } \right) = \prod _{t=1}^{T}\prod _{i=1}^{N}\left\{ \frac{\Gamma \left( \sum _{j}\alpha _{ij}^{(t)} \right) }{\prod _{j}\Gamma \left( \alpha _{ij}^{(t)} \right) } \prod _j \left[ y_{ij}^{(t)}\right] ^{\alpha _{ij}^{(t)}-1} \right\} \end{aligned}$$

(6)

where, again, j varies in ${\mathcal {V}}$ and is different from i, and $\Gamma \left( \cdot \right)$ denotes the gamma function.

As concerns the $\varvec{\alpha }$ parameters, we separate a trend component from the sender and receiver random effects through the following deterministic representation:

$$\begin{aligned} \log \left( \alpha _{ij}^{(t)}\right) = \mu ^{(t)} + \theta _i + \gamma _j \end{aligned}$$

(7)

With this formulation, the model parameters $\varvec{\mu } = \left\{ \mu ^{(t)}\right\} _{t\in {\mathcal {T}}}$, $\varvec{\theta } = \left\{ \theta _i\right\} _{i\in {\mathcal {V}}}$ and $\varvec{\gamma } = \left\{ \gamma _j\right\} _{j\in {\mathcal {V}}}$ possess a straightforward interpretation, which we illustrate in the next section. Note that the relation between the model parameters and $\varvec{\alpha }$ is deterministic, meaning that $\varvec{\alpha }$ is used only to clarify the notation, and it may be omitted from the model specification.

4.2 Interpretation of model parameters

Before we move to parameter interpretation, we would like to highlight how a symmetric parameter vector $\varvec{\alpha } = \left\{ \alpha ,\dots ,\alpha \right\}$ can affect the realizations of the random vector ${{\textbf {y}}}\sim Dir\left( \varvec{\alpha } \right)$. If the value of $\alpha$ increases, then the variance of the components of the random vector ${{\textbf {y}}}$ tend to decrease. Since the values generated from a Dirichlet distribution lie in an N-dimensional simplex, low variance translates to $y_i \approx 1/N, \forall i \in {\mathcal {V}}$, e.g. the values are more or less equally distributed (as per their marginal distributions). High variance, however, is obtained when the value of $\alpha$ is small, and it implies that one of the components turns out to be close to one while all the others are close to zero. These two examples closely mimic the high-entropy homogeneous regime and the low-entropy heterogeneous regime introduced in Sect. 3, respectively. Similarly, when the Dirichlet parameter is a non-symmetric random vector ${{\textbf {y}}}\sim Dir\left( \alpha _1,\dots ,\alpha _N \right)$, an increase in a single parameter component $\alpha _j$ determines a higher expected value in $y_j$, at the expense of the other elements in ${{\textbf {y}}}$.

In our formulation, the log-additive structure in Eq. (7) decomposes $\varvec{\alpha }$ in three parts. The contribution given by $\mu ^{(t)} + \theta _i$ affects all of the components of $\varvec{\alpha }_{i\cdot }^{(t)}$ in a symmetric fashion. Hence, in accordance with our explanation above, these parameters capture the level of homogeneity in the network through a homogeneity trend parameter $\mu ^{(t)}$ and a node specific homogeneity random effect $\theta _i$. In financial terms, an increase in either $\mu ^{(t)}$ or $\theta _i$ corresponds to lower concentration of exposures for bank i at time t, resulting in a more homogeneous network structure. Vice versa, a decrease in $\mu ^{(t)}$ or $\theta _i$ is linked with an increase in exposure concentration which in turn results in a more heterogeneous network structure.

The interpretation of $\gamma _j$ is similar. In our context, an increase in $\gamma _j$ tends to increase the weight of all edges that j receives from its counter parties. Equivalently, one can say that in such case the bank j becomes more attractive, in the spirit of other banks concentrating their exposures more towards j.

To summarize, there is a clear way to interpret the main parameters of our model. The parameter $\mu ^{(t)}$ indicates the global homogeneity level at time frame $t\in {\mathcal {T}}$, the parameter $\theta _i$ characterizes the individual bank i homogeneity level as a sender random effect (its exposure diversification), and the parameter $\gamma _j$ represents the bank j’s attractiveness as a receiver random effect.

4.3 Nested models

We consider simpler versions of our full model, where some of the elements that compose the $\varvec{\alpha }$s are removed. The models that we consider are defined by different versions of Eq. (7), as follows:

full:	$\log \left( \alpha _{ij}^{(t)}\right) = \mu ^{(t)} + \theta _i + \gamma _j$
sender-receiver:	$\log \left( \alpha _{ij}^{(t)}\right) = c + \theta _i + \gamma _j$
trend-receiver:	$\log \left( \alpha _{ij}^{(t)}\right) = \mu ^{(t)} + \gamma _j$
trend-sender:	$\log \left( \alpha _{ij}^{(t)}\right) = \mu ^{(t)} + \theta _i$
trend:	$\log \left( \alpha _{ij}^{(t)}\right) = \mu ^{(t)}$
sender:	$\log \left( \alpha _{ij}^{(t)}\right) = c + \theta _i$
receiver:	$\log \left( \alpha _{ij}^{(t)}\right) = c + \gamma _j$
null:	$\log \left( \alpha _{ij}^{(t)}\right) = c$

Here, the value c is a parameter that replaces $\mu$ when $\mu$ is not included in the model, thus absorbing any effect that is homogeneous across all nodes and time frames. The models above represent simpler frameworks whereby each of the elements of our model (exposure diversification trend $\mu$, exposure diversification random effect $\theta$, attractiveness $\gamma$) can be removed.

4.4 Bayesian hierarchical structure

We complete our models by introducing the following Bayesian hierarchical structure on the parameters that we have mentioned earlier.

Whenever the drift parameters $\varvec{\mu }$ are present in the model, we assume a random walk process prior on them:

$$\begin{aligned} \mu _1 \sim {\mathcal {N}}(0,1/\tau _{\mu }),{} & {} \mu _t=\mu _{t-1} + \eta _t, \ \ \forall t>1, \end{aligned}$$

where $\eta _t\sim {\mathcal {N}}(0,1/\tau _\eta )$ and $\tau _\eta \sim Gamma(a_\eta ,b_\eta )$. The model parameter c follows the same distribution of $\mu _1$. The hyperparameter $\tau _{\mu }$ is user-defined and set to a small value to support a wide range of initial conditions. The hyperparameters $a_\eta$ and $b_\eta$ are also user-defined and set to small values (0.01) to allow a flexible prior structure.

Whenever the parameters $\varvec{\theta }$ and $\varvec{\gamma }$ are present in the model, they are assumed to be i.i.d. Gaussian variables with:

$$\begin{aligned} \theta _i \sim {\mathcal {N}}\left( 0,1/\tau _\theta \right) ,{} & {} \tau _\theta \sim \text {Gamma}(a_\theta ,b_\theta ),\\ \gamma _j \sim {\mathcal {N}}\left( 0,1/\tau _\gamma \right) ,{} & {} \tau _\gamma \sim \text {Gamma}(a_\gamma ,b_\gamma ) \end{aligned}$$

Similarly to the other hyperparameters, $a_\theta$, $b_\theta$, $a_\gamma$ and $b_\gamma$ are also set to small values (0.01). The arrangement of parameters in Fig. 6 summarizes the dependencies in the full model graphically.

Fig. 6

Graphical representation of model dependencies

5 Parameter estimation

In this section, we focus on the estimation procedure for the full model only, noting that the estimation of the nested models follows analogous procedures, whereby the removed parameters are set to zero and are not updated.

Our proposed model has T drift parameters (denoted by $\varvec{\mu }$), N exposure diversification parameters (denoted by $\varvec{\theta }$), N attractiveness parameters (denoted by $\varvec{\gamma }$), and three precision parameters (denoted by $\varvec{\tau }$). We describe in this section a procedure to jointly estimate all of these model parameters.

5.1 Identifiability

The additive structure in Eq. (7) yields a non-identifiable likelihood model. For example, one could define ${\tilde{\theta }}_i = \theta _i + d$ and ${\tilde{\gamma }}_j = \gamma _j - d$ for some $d\in {\mathbb {R}}$ and the likelihood value would be the same for the two configurations, i.e. ${\mathcal {L}}_{{\mathcal {Y}}}\left( \varvec{\mu },\tilde{\varvec{\theta }},\tilde{\varvec{\gamma }} \right) = {\mathcal {L}}_{{\mathcal {Y}}}\left( \varvec{\mu },\varvec{\theta },\varvec{\gamma } \right)$. One way to deal with such identifiability problem would be to include a penalization through the priors on $\varvec{\theta }$ and $\varvec{\gamma }$. One could specify more informative Gaussian priors centered in zero, which would in turn shrink the parameters to be distributed around zero.

However, such approach may also interfere with the results, since the model would not be able to capture the presence of outliers. Hence, we opt for a more commonly used method, and impose the $\varvec{\gamma }$s to sum to zero as expressed through the following constraint:

$$\begin{aligned} \gamma _1 = -\sum _{j=2}^N\gamma _j. \end{aligned}$$

(8)

This new model, characterized by $T+2N-1$ parameters, is now identifiable with respect to its posterior distribution.

5.2 Markov chain Monte Carlo

The posterior distribution associated to our model factorizes as follows:

$$\begin{aligned} \begin{aligned} \pi \left( \varvec{\mu },\varvec{\theta },\varvec{\gamma },\varvec{\tau } \vert {\mathcal {Y}} \right)&\propto {\mathcal {L}}_{{\mathcal {Y}}}\left( \varvec{\mu },\varvec{\theta },\varvec{\gamma } \right) \pi \left( \varvec{\mu }\vert \tau _{\eta }\right) \pi \left( \varvec{\theta }\vert \tau _{\theta }\right) \pi \left( \varvec{\gamma }\vert \tau _{\gamma }\right) \times \\&\times \pi \left( \tau _{\eta }\vert a_\eta ,b_\eta \right) \pi \left( \tau _{\theta }\vert a_\theta ,b_\theta \right) \pi \left( \tau _{\gamma }\vert a_\gamma ,b_\gamma \right) \end{aligned} \end{aligned}$$

(9)

We adopt a fully Bayesian approach, relying on a Markov chain Monte Carlo algorithm to obtain a random sample from the posterior distribution (9). We use a Metropolis-within-Gibbs sampler that alternates the following steps³:

• 1. Sample $\mu _s$ for all $s\in {\mathcal {T}}$ from the following full-conditional using Metropolis-Hastings with a Gaussian proposal:

  $$\begin{aligned} \begin{aligned} \pi \left( \mu _{s}\vert \dots \right)&\propto \left\{ \prod _{i} \Gamma \left( e^{\mu _{s}}e^{\theta _i}\sum _je^{\gamma _j} \right) \right\} \left\{ \prod _{i,j} \frac{ \left[ y_{ij}^{(s)}\right] ^{\alpha _{ij}^{(s)}-1} }{ \Gamma \left( \alpha _{ij}^{(s)}\right) }\right\} \\&\quad \cdot \left\{ \exp \left\{ -\frac{\tau _{\mu }\left[ \mu _{s}\right] ^2}{2}\right\} \right\} ^{\mathbbm {1}_{\left\{ s=1\right\} }} \\&\quad \cdot \left\{ \exp \left\{ -\frac{\tau _{\eta }\left[ \mu _{s}-\mu _{s-1}\right] ^2}{2}\right\} \right\} ^{\mathbbm {1}_{\left\{ s>1\right\} }} \\&\quad \cdot \left\{ \exp \left\{ -\frac{\tau _{\eta }\left[ \mu _{s+1}-\mu _{s}\right] ^2}{2}\right\} \right\} ^{\mathbbm {1}_{\left\{ s<T\right\} }}. \end{aligned} \end{aligned}$$

  (10)

• 2. Sample $\theta _k$ for all $k\in {\mathcal {V}}$ from the following full-conditional using Metropolis-Hastings with a Gaussian proposal:

  $$\begin{aligned} \pi \left( \theta _k\vert \dots \right) \propto \left\{ \prod _{t} \Gamma \left( e^{\mu _{t}}e^{\theta _k}\sum _je^{\gamma _j} \right) \right\} \left\{ \prod _{t,j} \frac{ \left[ y_{kj}^{(t)}\right] ^{\alpha _{kj}^{(t)}-1} }{ \Gamma \left( \alpha _{kj}^{(t)} \right) }\right\} \exp \left\{ -\frac{\tau _{\theta }}{2}\theta _k^2\right\} . \end{aligned}$$

  (11)

• 3. Sample $\gamma _\ell$ for all $\ell \in {\mathcal {V}}\setminus \{1\}$ from the following full-conditional using Metropolis-Hastings with a Gaussian proposal:

  $$\begin{aligned} \begin{aligned} \pi \left( \gamma _{\ell }\vert \dots \right)&\propto \left\{ \prod _{t,i} \Gamma \left( e^{\mu _{t}}e^{\theta _i}\sum _je^{\gamma _j} \right) \right\} \left\{ \prod _{t,i} \frac{ \left[ y_{i\ell }^{(t)}\right] ^{\alpha _{i\ell }^{(t)}-1} }{ \Gamma \left( \alpha _{i\ell }^{(t)} \right) }\right\} \\&\quad \cdot \left\{ \prod _{t,i} \frac{ \left[ y_{i1}^{(t)}\right] ^{\alpha _{i1}^{(t)}-1} }{ \Gamma \left( \alpha _{i1}^{(t)} \right) }\right\} \exp \left\{ -\frac{\tau _{\gamma }}{2}\gamma _{\ell }^2\right\} . \end{aligned} \end{aligned}$$

  (12)

• 4. Sample $\tau _{\eta }$ from the following conjugate full-conditional:

  $$\begin{aligned} \pi \left( \tau _{\eta } \vert \dots \right) \sim Gamma\left( a_{\eta } + \frac{T-1}{2}, b_{\eta } + \sum _{t>1}\left( \mu _{t}-\mu _{t-1} \right) ^2/2 \right) . \end{aligned}$$

  (13)

• 5. Sample $\tau _{\theta }$ from the following conjugate full-conditional:

  $$\begin{aligned} \pi \left( \tau _{\theta } \vert \dots \right) \sim Gamma\left( a_{\theta } + N/2, b_{\theta } + \sum _{i}\theta _i^2/2 \right) . \end{aligned}$$

  (14)

• 6. Sample $\tau _{\gamma }$ from the following conjugate full-conditional:

  $$\begin{aligned} \pi \left( \tau _{\gamma } \vert \dots \right) \sim Gamma\left( a_{\gamma } + \frac{N-1}{2}, b_{\gamma } + \sum _{j>1}\gamma _j^2/2 \right) . \end{aligned}$$

  (15)

In output, the algorithm returns a collection of sampled observations for each model parameter, which are then used to empirically characterize the targeted posterior distribution.

6 Model selection

In our analysis, we have 8 competing models, so we need to define an optimality criterion to select the best model for each dataset.

Some of the most commonly used criteria for model selection, especially in nested generalized regression models, are the AIC, or Akaike information criterion from Akaike (1974), and the BIC, or Bayesian information criterion from Schwarz (1978). In practice, these two criteria correspond to a penalised log-likelihood, where the penalization term grows with the number of parameters in the model considered, so that parsimony is promoted. These criteria define a quantitative framework to characterize the trade-off between model complexity and how good the model fit is.

In this paper, we adopt both the AIC and BIC as model choice criteria, and derive our optimal models using these approaches.

7 Simulation study

In this section, we illustrate our methodology on artificial data, to demonstrate its correctness and efficiency in estimating parameters and choosing the correct model. We consider artificial networks with $T = 10$ and $N = 40$, and model parameters generated as follows:

$$\begin{aligned} \mu ^{(1)} \sim {\mathcal {N}}\left( 0, \sigma ^2_0 \right) ; \quad \quad \quad \mu ^{(t+1)} \sim {\mathcal {N}}\left( \mu ^{(t)}, \sigma _0^2 \right) ; \quad \quad \quad \theta _i \sim {\mathcal {N}}\left( 0, \sigma _0^2 \right) ; \quad \quad \quad \gamma _j \sim {\mathcal {N}}\left( 0, \sigma _0^2 \right) ; \end{aligned}$$

for all is, js and ts. In order to create an agreement with the constraint in Eq. (8), we apply a translation to $\gamma _1,\dots , \gamma _N$ by subtracting $\sum _{j=1}^N\gamma _j/N$. We consider values of $\sigma _0$ in the set $\left\{ 0.25,\ 0.5,\ 1 \right\}$, reflecting different levels of difficulty in estimating the model. This is due to the fact that the effect of each parameter diminishes with $\sigma _0$, since they all get closer to zero in our additive model. Vice versa, a larger $\sigma _0$ creates stronger effects which are easier to infer.

In addition, we generate data from four different models, as follows:

Model 1, sender-receiver:	$\log \left( \alpha _{ij}^{(t)}\right) = c + \theta _i + \gamma _j$
Model 2, trend-receiver:	$\log \left( \alpha _{ij}^{(t)}\right) = \mu ^{(t)} + \gamma _j$
Model 3, trend-sender:	$\log \left( \alpha _{ij}^{(t)}\right) = \mu ^{(t)} + \theta _i$
Model 4, full:	$\log \left( \alpha _{ij}^{(t)}\right) = \mu ^{(t)} + \theta _i + \gamma _j$

Under each model, and under each value of $\sigma _0$, we generate 200 networks using our likelihood model, and then use our procedure to select the model and estimate all parameters. To do so, we run the full sampling procedure using the same four models as candidates, for each dataset. We use 1000 iterations as burn-in, and then save one sample every tenth, until a posterior sample of 100 values is obtained for each parameter. The proposal variances are all set to 1. Clearly, these sampling parameters are arbitrary, however, we show in the results that they work very well for the datasets considered.

Once we have run the sampling procedure for every $\sigma _0$, for every true model, for every candidate model, and for every network, we compare our candidate fitted models using the two model choice criteria: AIC and BIC.

The accuracy of the two model-choice criteria (expressed as the number of correctly identified models, out of 200) is shown in Table 2.

Table 2 Confusion tables indicating the number of datasets (out of 200) for every combination of true model vs. estimated model, for three model selection criteria (over three rows of tables) and three values of $\sigma _0$ (over three columns of tables)

Here, we see that, generally, both criteria perform reasonably well under a variety of settings. This is a very positive result, considering that the real model parameters are generated with a fairly small standard deviation. In particular, AIC achieves the best results in recovering the correct model from the data, whereas BIC tends to infer a wrong model when $\sigma _0 = 2$. However, as expected, results generally improve when $\sigma _0$ increases. It is important to note that BIC tends to select Model 2 very often. This happens because Model 2 is the one containing the smallest number of parameters (T and $N-1$, for $\varvec{\mu }$ and $\varvec{\gamma }$, respectively), so this is the model where the heavier penalization of the BIC has the least effect.

In Fig. 7, we show the estimation error for the best AIC models, for each of the model parameters and $\sigma _0 \in \left\{ 0.2,\ 0.4\right\}$.

Fig. 7

True value of model parameters vs. estimated values. The top row corresponds to $\sigma _0 = 0.2$ and the bottom row corresponds to $\sigma _0 = 0.4$. Colors indicate the true underlying model number. The plots include only parameter estimates corresponding to correctly identified models

This figure illustrates that, although the datasets are fairly small, the errors are very contained and there is little to no evidence of bias, regardless of the model considered. For the parameter $\varvec{\theta }$, we notice some bias which is justifiable by the near-non-identifiability of the additive model (see Sect. 5.1). This bias seems to be compensated by the parameter $\varvec{\mu }$. In both cases, points are still distributed on a line roughly parallel to the bisector line, indicating no errors up to a translations of the parameters.

8 OeNB 200 and OeNB 800 results

8.1 Technical details

We ran our Metropolis-within-Gibbs sampler on both datasets OeNB 200 and OeNB 800, and for all models, for a total of 100, 000 iterations. For all runs, the first 75, 000 iterations were discarded as burn-in. For the remaining sample, every 5-th draw was saved to produce the final results. In summary, we used samples of 5000 observations to characterize the posterior distribution of each model parameter.

The first 75, 000 iterations of the burn-in period were also used to adaptively tune the Gaussian proposal variance individually for each parameter, to make sure that all of the acceptance rates were approximately $33\%$. The proposal variances were hence fixed to these ideal values for the rest of the process. The trace plots and convergence diagnostic tests all showed very good mixing of the Markov chains, suggesting a satisfactory convergence.

Similarly to many other latent variable models for networks, the computational cost required by our sampler grows as $TN^2$. We implemented the algorithm in C++ to speed up the procedure, and then wrapped the functions into an R package which is available from our public repository (Rastelli and Hledik 2021).

8.2 Model comparisons

We calculate the AIC and BIC for all 8 models and for both datasets; the results are shown in Tables 3 and 4, which give more numerical details regarding the ranking of the models according to the criteria.

Table 3 OeNB_200: Ranking of the models according to AIC

Table 4 OeNB_800: Ranking of the models according to AIC

We discuss the results according to the AIC and BIC optimal models in the following subsections.

8.3 OeNB 200 dataset

In OeNB 200, the AIC-optimal model is sender-receiver, whereas the BIC-optimal model is receiver, which essentially corresponds to the same model where also $\varvec{\theta }$ has been removed. We further note that all models that include $\varvec{\mu }$ are worse than their simpler counterparts that do not include $\varvec{\mu }$. This highlights very strong evidence that the global exposure diversification trend parameter $\varvec{\mu }$ is not relevant for this dataset, and thus it should not be included in the analysis.

In the context of our application, our procedure selects a model without the trend component, meaning that the exposure concentration level depends only on the bank’s individual value and it does not depend on time. Thus, our method indicates that the most relevant banks did not uniformly change their exposure concentration between 2018 and 2012, rather they adopted different strategies and reacted in different ways to the crises.

Fig. 8

Empirical distribution of posterior expectations of $\varvec{\theta }$ (left panel) and $\varvec{\gamma }$ (right panel) for the 200 most relevant banks

The AIC-optimal model sender-receiver characterizes the exposures of these banks using the attractiveness parameter of each bank ($\varvec{\gamma }$), and the individual exposure diversification of each bank ($\varvec{\theta }$). We show the estimated posterior expectations of these parameters in Fig. 8. In both histograms we see that the distributions are skewed, in that there are some banks that have very large values of either exposure spread or attractiveness. In fact, from the left panel of Fig. 9, we see that those banks that have high exposure spread (low concentration) also tend to have high attractiveness, and vice versa. This figure highlights that large relevant banks tend to have higher exposure spread while simultaneously also being more attractive, and, vice versa, small banks often play a more peripheral role in the network, usually as offspring of some larger bank. A similar observation of heavy tailed degree distribution has also been reported by Boss et al. (2004).

Fig. 9

Left panel: posterior expectations of $\varvec{\theta }$ vs. the posterior expectations of $\varvec{\gamma }$, for the OeNB 200 dataset (sender-receiver model). Both size and color of the points indicate the relevance. Right panel: posterior expectations of $\varvec{\theta }$ vs. the aggregated relevance of banks, for OeNB 200 (sender-receiver model)

The right panel of Fig. 9 focuses more directly on the relation between the estimates of $\varvec{\theta }$ and the aggregated relevance of banks. This scatter-plot indicates that more relevant banks tend to have a more pronounced exposure spread, whereas small banks concentrate their exposures more. This observation further confirms our ideas about a stylized financial network where the disassortative behavior is very common.

The left panel of Fig. 10 highlights instead a different aspect of our analysis: we show that the parameter estimates for $\varvec{\gamma }$ are essentially the same for the two optimal models, indicating that the parameters $\varvec{\theta }$ and $\varvec{\gamma }$ capture different aspects and patterns in the data.

Fig. 10

Left panel: posterior expectations of $\varvec{\gamma }$ in the sender-receiver model vs. posterior expectations of $\varvec{\gamma }$ in the receiver model, for OeNB 200. Right panel: posterior variance of $\varvec{\theta }$ vs. posterior variance of $\varvec{\gamma }$, with nodes’ sizes and colors representing aggregated relevance for OeNB 200 (sender-receiver model)

This means that it is important to investigate the effect of both of these parameters through the model choice framework, since they give relevant and rather independent contributions in explaining the data. The reason why the $\varvec{\theta }$s are removed from one model is purely because of the penalization value which inevitably must lead to a model with fewer parameters.

The Bayesian approach employed for the inferential procedure permits a full characterization of the posterior distribution of each of the parameters. We take advantage of this to investigate whether there is any pattern in the quantified uncertainty around each parameter estimate. For this purpose, the right panel of Fig. 10 shows the relation between the posterior variances of the $\varvec{\theta }$ vs. $\varvec{\gamma }$. We note that there seems to be no explicit pattern between the parameters, and no apparent relation with the relevance of the corresponding banks. The posterior variances of $\varvec{\theta }$s tend to be higher than the posterior variances of $\varvec{\gamma }$s.

8.4 OeNB 800 dataset

In OeNB 800, the model receiver is optimal according to the AIC, whereas the null model is optimal according to BIC. This is primarily determined by the fact that the full dataset involves a very large number of parameters, and thus the penalization term becomes substantial.

The null model is the simplest and it describes a homogeneous network structure, whereby all the banks exhibit the same behaviour at all time frames. While the expectation for all edge weights is the same, the variance associated to the Dirichlet distribution makes it possible that a variety of different values and patterns are observed. So, according to this model, it is still perfectly reasonable that some banks will be exposed to very few counterparts whereas others will distribute their risks on a more wide set of partners. Still, the most fundamental message that we extract from either of the optimal models is that there is no evidence of a relevant change over time, at a global level, for the connectivity patterns.

The optimal receiver model characterizes the exposures using only the attractiveness parameter for each bank. This is essentially equivalent to a fitness model, whereby banks with higher “fitness” are more often receiving edges than those with lower fitness. In our context, highly attractive banks tend to borrow from more partners, so they are key institutions to monitor since they can put pressure on a large number of other institutions.

Fig. 11

Left panel: empirical distribution of the posterior means of $\varvec{\gamma }$ under the receiver model. Right panel: empirical distribution of the posterior means of $\varvec{\gamma }$ plotted against the total incoming weights for each node, under the receiver model. The color of points indicates the relevance

In the left panel of Fig. 11, we see that the distribution of the $\varvec{\gamma }$ posterior means is very heavy tailed, in that a number of institutions exhibit very high attractiveness values (histogram bins become very thin for values larger than 0.2). This highlights the heterogeneous structure of this network where the nodes can exhibit very diverse patterns of connections. The right panel of Fig. 11 underlines more clearly the connection to a fitness model, in that it essentially shows that the $\varvec{\gamma }$ parameters clearly capture the in-degrees of the nodes. We also highlight the relation between $\varvec{\gamma }$ and the relevance of the banks in the left panel of Fig. 12, where we notice that high relevance tends to translate into a high attractiveness.

Fig. 12

Left panel: posterior means of $\varvec{\gamma }$ plotted against the log-relevance of each bank, for the receiver model. Right panel: empirical posterior density for the only parameter c in the null model

For completeness, we show the posterior density for the only parameter c under the null model, in the right panel of Fig. 12.

9 Conclusions

This paper contributes to the literature on networks by extending the current available network frameworks to model temporal non-negatively weighted interactions, and to capture systematic parts of their development. Our original application to the Austrian interbank market gives a new perspective on the recent crises and demonstrates how our model can be used as a means to measure exposure concentration and bank’s attractiveness as drivers of systemic risk. Differently from Friel et al. (2016), our measure is not affected by banks entering or leaving the system, since our available data only contains banks which are active throughout the whole period.

In our analysis we have shown that, for the Austrian market, the financial institutions did not change substantially their connectivity patterns over time, regardless of the financial instabilities experienced in 2008 and 2011. Our results are fairly in agreement with the exploratory data analysis, which highlighted some substantial changes with regard to the overall exposure sizes, but only one noticeable change in terms of concentration of exposures, during the second quarter of 2011. Our model-based approach showed that no change of patterns were significant, however we point out that our models that included the temporal dependency would capture a major change in that same time period (results not shown). A critical reason why our approach does not consider the time trend significant is that the trend is assumed to be the same across all network participants. Clearly this can be a rather strong assumption, in that if time trends are present, then they would likely differ across participants. This strongly suggests a very interesting future development of this work whereby one can extend the model to include node-specific time trends.

The findings of our analysis may be of a particular use to regulators and central banks to assess and design future policy measures. In addition, our results showed that the roles played by the different banks can be vastly different, particularly in the context of exposure concentration. This emphasizes that larger banks, which are generally more susceptible to systemic risk, tend to use more conservative strategies and to spread out evenly their credit risks.

One limitation of our modeling framework is that it only focuses on the relative exposures, hence discarding the real magnitudes of the claims. Future extensions of this work may consider a joint modeling of the exposure values and how they are diversified among neighbors. Another possible extension of our framework would include a more sophisticated modeling structure, to account for transitivity or reciprocity. Also, one could easily resort to clustering, where, for example, different clusters are characterized by different network homogeneity drifts $\varvec{\mu }$. Finally, we would like to remark that in our dataset all nodes are present at all time frames, however, this assumption is unlikely to hold in a more general setting. As a consequence, a relevant extension of our work would introduce mechanisms to let nodes join or exit the study at any point in time, perhaps in reflection of potential financial defaults.

Appendices

Appendices

A. Data transformation

The source data from the Austrian National Bank is in the form of four variables: a timestamp, an ID of a lender bank, an ID of a borrower, and the relative exposure from one towards the other. We use the term relative since the largest exposure in each time period is assumed to be of size 1, and all other exposures in that time period are scaled accordingly to keep their relative size unchanged. As a result, in each time-period, all exposures are located in a $\left( 0,1\right]$ interval with the highest exposure attaining a value of 1. Formally, making use of Definition 3.2, the observable data in our sample can be viewed as a dynamic adjacency matrix D:

Definition A.1

A sequence of observable exposures ${\mathcal {D}}=\{{D}^{(t)}\}_{t\in {\mathcal {T}}}$ on the set of nodes ${\mathcal {V}}$ over the time span ${\mathcal {T}}$ is defined as follows:

$$\begin{aligned} d_{ij}^{(t)}{\mathop {=}\limits ^{def}}\frac{e_{ij}^{(t)}}{\max _{\begin{array}{c} k,l \end{array}} e_{kl}^{(t)}} \ \ \ \forall i,j,k,l \in {\mathcal {V}}, \forall t \in {\mathcal {T}} \end{aligned}$$

(16)

It is not possible to make inter-temporal analysis of changes in exposures by using the sequence ${\mathcal {D}}$, because every exposure is scaled against the highest exposure in its time period. In order to circumvent this issue and obtain information which is comparable in time, we have devised the following procedure.

We make an assumption about the stability of the Austrian market. Namely, when looking at the change of a particular edge value between two consecutive periods, say from $d_{ij}^{(t)}$ to $d_{ij}^{(t+1)}$, the ratio $\frac{d_{ij}^{(t)}}{d_{ij}^{(t+1)}}$ with highest likelihood of occurrence in the sample corresponds to banks keeping the absolute value of their exposures unchanged. Indeed, after examining this ratio in all consecutive periods, we observe that the most frequent value is situated in the middle of the sample and is always a clear outlier in terms of likelihood of occurrence.⁴

It is straightforward to re-scale the whole dataset using this procedure. Despite the fact that we still cannot observe the actual levels of exposures between banks in our sample, we are now able to approximate these values up to a proportionality constant. We denote the values that we obtain with this procedure with ${\mathcal {X}}$ throughout the paper, and use these to calculate the relevance of the banks. We point out that these values are not used in the statistical model that we introduce.

To summarize, there are four different types of dynamic adjacency matrices used in our paper: ${\mathcal {E}}$ corresponds to the true data with the actual connection values (exact values not available), ${\mathcal {D}}$ represents the scaled data where edge weights are normalized with respect to the highest value in each period (exact values are available), ${\mathcal {X}}$ contains the scaled data where all edge weights are normalizes with respect to the highest value in the first period (available in approximate form), and ${\mathcal {Y}}$ contains the relative exposures of banks (exact values are available) which are derived from ${\mathcal {X}}$ or equivalently from ${\mathcal {D}}$.