Kernel regression for errors-in-variables problems in the circular domain

Abstract

We study the problem of estimating a regression function when the predictor and/or the response are circular random variables in the presence of measurement errors. We propose estimators whose weight functions are deconvolution kernels defined according to the nature of the involved variables. We derive the asymptotic properties of the proposed estimators and consider possible generalizations and extensions. We provide some simulation results and a real data case study to illustrate and compare the proposed methods.

1 Introduction

Circular, or angular, data are observations consisting of directions or angles, and, as such, are defined on a circle—with unit radius—after the origin and orientation are established. Such data occur in many fields, for example: meteorology (wind and marine current directions), biology (directions of animal species migration), bioinformatics (conformational angles of a protein), geology (directions of rock fracture), social science and economics (clock or calendar effects). The fact that maximum and minimum of the measure scale are the same makes classical methods of statistics generally inappropriate for addressing circular data. However, circular statistics is a very active research field, and there are counterparts for most inferential techniques. For a recent comprehensive account about circular statistics, see Ley and Verdebout (2017) and Ley and Verdebout (2018).

Statistical regression models are generally based on the assumption that predictors have been measured exactly. However, sometimes they are, for some reason, not directly observable or are measured with errors, for instance due to imperfect measurement devices (deterioration or miscalibration), or the impossibility of directly accessing the variables of interest. When this is the case, specific models, known as errors-in-variables or measurement error models, have to be considered. A key to solving many errors-in-variables problems is often to take the Fourier transform of the various functions involved, because, in the Fourier domain, equations generally become much simpler to solve. For a review of the extensive literature about the so-called deconvolution problem see, e.g., Carroll and Hall (1988); Liu and Taylor (1989); Carroll et al. (1995).

In the regression setting the kernel deconvolution estimator has been shown to reach the optimal rate of convergence by Fan and Truong (1993). The generalization of the higher order version of the local constant estimator, along with the derivation of the asymptotic normality, has been proposed by Delaigle et al. (2009). Carroll et al. (1999) introduced two new approaches to nonparametric regression in the presence of measurement error based on the simulation-extrapolation method and regression splines. Also, estimators involving kernel and orthogonal series methods based on a low order approximation approach have been proposed by Carroll and Hall (2004). The estimation of a nonparametric regression function with a covariate contaminated by a mixture of Berkson and classical measurement has been treated by Carroll et al. (2007).

The problem of estimating the density of an unobserved circular variable measured with error has been recently addressed by Di Marzio et al. (2021). Also, nonparametric regression for circular responses has been introduced by Di Marzio et al. (2012a) and Di Marzio et al. (2012b).

In this paper we introduce a nonparametric regression estimator that is consistent in the presence of measurement error when the data can be represented as points on the circumference of the unit circle. Specifically, we present a deconvolution estimator, showing resulting rates of asymptotic accuracy measures comparable to Euclidean deconvolution ones. The finite-sample properties of the estimator are investigated through Monte Carlo experiments.

We collect some basic concepts about the characteristic functions in Sect. 2, and recall the Nadaraya-Watson estimators involving circular variables in Sect. 3. Estimators which take into account of the presence of the measurement error are proposed in Sect. 4, along with some asymptotics. In Sect. 5 we present some simulation results, and we conclude with a real data case study exploring the relation between levels of carbon monoxide and wind direction in Sect. 6.

2 Some preliminaries

Given a real random variable X with distribution function $F_X$, its characteristic function is defined as $\varphi _X(t) ={{\,\mathrm{\textsf{E}}\,}}[\exp (i t X)]=\int _{-\infty }^\infty \exp (i t x) dF_X(x)$, where $i^2=-1$. Since there is a one-to-one correspondence between characteristic functions and distribution functions, if $\varphi _X$ is absolutely integrable, it is possible to recover the density function $f_X$ of X, for every $x \in {\mathbb {R}}$, from the characteristic one by using the well known inversion formula

$$\begin{aligned} f_X(x)=\frac{1}{2\pi }\int \varphi _X(t)\exp (-i t X)dt. \end{aligned}$$

(1)

Now consider the random variable $\Theta$ taking values on the unit circle. In this case, the density of $\Theta$, say $f_\Theta$, is a $2\pi$-periodic density function, i.e. $f_\Theta (\theta )=f_\Theta (\theta +2r\pi )$ for any integer r; then its characteristic function, say $\varphi _\Theta$, is just defined for integer $\ell$, and satisfies $\varphi _\Theta (\ell )=\varphi _{\Theta +2\pi }(\ell ), \ell \in {\mathbb {Z}}$. Notice that $\varphi _\Theta (\ell )$ corresponds to the $\ell$th trigonometric moment of $\Theta$

$$\begin{aligned} \varphi _\Theta (\ell ) = \alpha _{\ell } +i \beta _{\ell }, \;\; \alpha _\ell = {{\,\mathrm{\textsf{E}}\,}}[\cos (\ell \Theta )],\;\; \beta _\ell ={{\,\mathrm{\textsf{E}}\,}}[\sin (\ell \Theta )], \end{aligned}$$

and that $\beta _\ell =0$ when $f_\Theta$ is symmetric. It is interesting to note that $\alpha _\ell$ and $\beta _\ell$ are the $\ell$th order Fourier coefficients of the density $f_\Theta$. Analogously to the inversion formula for characteristic functions of real-valued random variables, if $f_\Theta$ is square integrable on $[0,2\pi )$, one can represent $f_\Theta (\theta )$, $\theta \in [0,2\pi )$, through the Fourier series

$$\begin{aligned} f_\Theta (\theta )=\frac{1}{2\pi }\sum _{\ell =-\infty }^\infty \varphi _\Theta (\ell ) \exp (-i \ell \theta )=\frac{1}{2\pi }\left\{ 1+2\sum _{\ell =1}^\infty \left( \alpha _\ell \cos (\ell \theta )+\beta _\ell \sin (\ell \theta )\right) \right\} .\end{aligned}$$

(2)

The smoothness of a generic density function can be determined by the rate of decay of the characteristic function: a polynomial decay characterizes ordinary smooth functions, while an exponential decay characterizes supersmooth ones. When the random variable is real-valued, examples of ordinary smooth densities include the Laplace and Gamma, while the Normal and Cauchy ones are supersmooth. In the circular case, examples for these two classes of functions are obtained by considering the wrapped version of the aforementioned densities. The von Mises density belongs to the class of the supersmooth ones.

3 Circular kernel regression in the error-free case

In this section we briefly recall the local constant regression estimators, also known as kernel regression or Nadaraya-Watson estimators, proposed by Di Marzio et al. (2009) and Di Marzio et al. (2012a) when the predictor and/or the response variables have circular nature.

3.1 Circular response

Consider a pair of $(\mathbb {\Psi } \times \mathbb {\Delta })$-valued random variables $(\Psi ,\Delta )$, where $\mathbb {\Psi }$ is a generic domain and $\mathbb {\Delta }= [0,2\pi )$. We are interested in the dependence of the response $\Delta$ on the predictor $\Psi$. Given the random sample $(\Psi _1,\Delta _1), \ldots , (\Psi _n, \Delta _n)$, assume the regression model

$$\begin{aligned} \Delta _i=(m(\Psi _i)+\epsilon _i) \textsf{mod}(2\pi ), \end{aligned}$$

(3)

where the $\epsilon _i$s are i.i.d. random angles with zero mean direction and non-zero concentration (so we do not allow a $U(0,2\pi )$ distribution for $\epsilon _i$), which are independent of the $\Psi _i$s. Now, for $\psi \in \mathbb {\Psi }$, let

$$\begin{aligned} m(\psi )=\textsf{atan2}(g_1(\psi ), g_2(\psi )), \end{aligned}$$

(4)

with $g_j=m_j f$, for $j \in (1,2)$, where f is the design density, i.e. the density of the covariate, which may be linear or circular, $m_1(\psi )=\textsf{E}[\sin (\Delta )\mid \Psi =\psi ]$, $m_2(\psi )=\textsf{E}[\cos (\Delta )\mid \Psi =\psi ]$ and the function $\textsf{atan2}(y, x)$ returns the angle between the x-axis and the vector from the origin to (x, y). A kernel estimator for the regression function m at $\psi$ has been proposed by Di Marzio et al. (2012a) as

$$\begin{aligned} {\hat{m}}(\psi ; \nu )=\textsf{atan2}\left( {\hat{g}}_1(\psi ; \nu ),{\hat{g}}_2(\psi ; \nu )\right) , \end{aligned}$$

(5)

where

$$\begin{aligned} {\hat{g}}_1(\psi ; \nu ) =\frac{1}{n}\sum _{i=1}^{n}\sin (\Delta _i)W_\nu (\Psi _i-\psi ) \;\; \text {and} \;\; {\hat{g}}_2(\psi ; \nu ) =\frac{1}{n}\sum _{i=1}^{n}\cos (\Delta _i)W_\nu (\Psi _i-\psi ), \end{aligned}$$

(6)

with $W_\nu$ being a weight function, which may be linear or circular according to the nature of $\Psi$, having $\nu >0$ as its smoothing parameter, whose role is to emphasize the contribution of the observations close to the estimation point $\psi$. Noting that $m_1(\psi )$ and $m_2(\psi )$ are the components of the conditional first trigonometric moment of $\Delta$, we can write $m_1(\psi )=C(\psi ) f_s(\psi )$ and $m_2(\psi )=C(\psi ) f_c(\psi )$, where $C(\psi )=\{m_1^2(\psi )+m_2^2(\psi )\}^{1/2}$ and $f_s^2(\psi )+f_c^2(\psi )=1$. We also define $s_1^2(\psi )=\textsf{E}[\sin ^2(\Delta )\mid \Psi =\psi ]$, $s_2^2(\psi )=\textsf{E}[\cos ^2(\Delta )\mid \Psi =\psi ]$ and $c(\psi )=\textsf{E}[\sin (\Delta )\cos (\Delta )\mid \Psi =\psi ]$, which describe the conditional second trigonometric moments of $\Delta$.

In what follows, we recall both the cases where ${\Psi }$ is a random angle, i.e. $\mathbb {\Psi }=[0,2\pi )$, or ${\Psi }$ is a linear random variable, i.e. $\mathbb {\Psi }={\mathbb {R}}$.

3.1.1 Circular predictor

Consider the case where both $\mathbb {\Psi }$ and $\mathbb {\Delta }$ are $[0,2\pi )$, and denote the predictor variable as $\Theta$. For $\theta \in [0,2\pi )$, a local constant estimator for $m(\theta )$ is defined as in Eq. (5) where the functions ${\hat{g}}_j$, $j \in (1,2)$, involve a circular kernel $K_\kappa$ with a smoothing parameter $\kappa >0$ called the concentration.

We recall that a circular kernel of order r, defined by Di Marzio et al. (2009) as rth sin-order kernel, is a function symmetric around the null mean direction, with $\kappa$ increasing with n in such a way that, as $\kappa$ increases, $\int _{-\xi }^\xi K_\kappa (\theta ) d\theta$ tends to 1, for $\xi \in (0,\pi )$, and, denoting $\eta _j(K_\kappa )=\int _0^{2\pi } \sin ^j(\theta )K_\kappa (\theta )d\theta$, it holds

$$\begin{aligned} \eta _0(K_\kappa )=1, \quad \eta _j(K_\kappa )=0 \;\; \text {for} \;\; 0<j<r, \quad \text {and} \;\; \eta _r(K_\kappa )\ne 0. \end{aligned}$$

Some asymptotic properties for the local constant estimator ${\hat{m}}(\theta )$ are collected in the following

Result 1

Given the $[0,2\pi )\times [0,2\pi )$-valued random sample $(\Theta _1,\Delta _1),\ldots ,(\Theta _n,\Delta _n)$, consider estimator (5) equipped with a circular kernel $K_\kappa$ as the weight function. If

• (i) $K_\kappa$ is a second sin-order kernel admitting a convergent Fourier series representation $1/(2\pi )\{1+2\sum _{\ell =1}^{\infty }\gamma _\ell (\kappa )\cos (\ell \theta )\}$, with $\kappa$ increasing with n in such a way that, for $\ell \in {\mathbb {Z}}^+$, $\lim _{n\rightarrow \infty }\frac{1- \gamma _\ell (\kappa )}{1-\gamma _2(\kappa )}=\frac{\ell ^2}{4},$ $\lim _{n\rightarrow \infty }\gamma _\ell (\kappa )=1 \;\;\; \text {and} \;\;\; \lim _{n\rightarrow \infty } \frac{1}{n} \sum _{\ell =1}^\infty \gamma _\ell ^2(\kappa )=0,$

• (ii) the design density $f_\Theta$ and the conditional expectations $m_1$ and $m_2$ are twice continuously differentiable in a neighbourhood of $\theta$,

then, at $\theta \in [0,2\pi )$,

$$\begin{aligned} \textsf{E}[{\hat{m}}(\theta ; \kappa )]- m(\theta )= \frac{(1-\gamma _2(\kappa ))}{4} \left\{ m''(\theta )+\frac{2m'(\theta )\{C(\theta )f_{\Theta }(\theta )\}'}{C(\theta )f_{\Theta }(\theta )}\right\} +o(1-\gamma _2(\kappa )), \end{aligned}$$

and

$$\begin{aligned} \textsf{Var}[{\hat{m}}(\theta ;\kappa )]&=\frac{\left( 1+2\sum _{\ell =1}^\infty \gamma _\ell ^2(\kappa )\right) }{2\pi n C^2(\theta ) f_{\Theta }(\theta )} \left\{ f_c^2(\theta )s_1^2(\theta )+f_s^2(\theta )s_2^2(\theta )-2 f_c(\theta )f_s(\theta )c(\theta )\right\} \\&+o\left( \frac{ \sum _{\ell =1}^\infty \gamma _\ell ^2(\kappa )}{n}\right) . \end{aligned}$$

Remark 1

Condition i) of Result 1 is very mild because most of the usual circular densities, which are symmetric about the null mean direction, are included in the class of second sin-order kernels. Among these, an uncommon case is the uniform kernel on $[-\pi /(\kappa +1),\pi /(\kappa +1)]$, which has a smaller support than the circle, where $\kappa \in {\mathbb {N}}$. A kernel satisfying above conditions, without being a density is instead the Dirichlet kernel $(2\pi \sin (\theta /2))^{-1} \sin ((\kappa +1/2)\theta )$. It can be negative, and its order depends on the value of $\kappa$, being $\kappa +1$ if $\kappa$ is odd, and $\kappa +2$ otherwise.

A local linear version of estimator ${\hat{m}}$ can be obtained using the circular analogue of a local linear weight in defining the sample statistics ${\hat{g}}_1$ and ${\hat{g}}_2$, see Di Marzio et al. (2012a) for details.

3.1.2 Linear predictor

Now we consider the case where $\mathbb {\Psi }={\mathbb {R}}$, and denote the predictor variable as X. Here the functions ${\hat{g}}_j$, $j \in (1,2)$, of the local constant estimator (5) use a linear kernel

$$\begin{aligned} K_h(x)=\frac{1}{h} K\left( \frac{x}{h}\right) , \end{aligned}$$

(7)

which is a symmetric density function, with maximum at 0 and a smoothing parameter $h>0$ called the bandwidth. Also define the quantities $\mu _j(K)=\int x^j K(x)dx$ and $v(K)=\int K^2(x)dx$, and recall that K is a kth-order kernel if $\mu _0(K)=1$, $\mu _j(K)=0$ for $j=(1,\ldots ,k-1)$, and $\mu _k(K)\ne 0$.

The asymptotic properties are collected in the following

Result 2

Given the ${\mathbb {R}} \times [0,2\pi )$-valued random sample $(X_1,\Delta _1),\ldots ,(X_n,\Delta _n)$, consider the estimator given by (5), equipped with a linear kernel $K_h$ as the weight function. If

• (i) $K_h$ is a second order kernel such that $h\rightarrow 0$ and $nh\rightarrow \infty$ as $n\rightarrow \infty$;

• (ii) the design density $f_X$ and the conditional expectations $m_1$ and $m_2$ are twice continuously differentiable in a neighbourhood of x,

then, for any interior point x of the support of $f_X$,

$$\begin{aligned} \textsf{E}[{\hat{m}}(x;h)]- m(x)=\frac{h^2\mu _2(K)}{2} \left( m''(x)+ \frac{2 m'(x)\{C(x)f(x)\}'}{C(x)f(x)}\right) +o(h^2), \end{aligned}$$

and

$$\begin{aligned}{} & {} \textsf{Var}[{\hat{m}}(x;h)]= \frac{v(K)}{C^2(x)f(x)nh}\\{} & {} \quad \{f_s^2(x)s_2^2(x)+f_c^2(x)s_1^2(x)-2f_s(x)f_c(x)c(x)\}+ o\left( \frac{1}{nh}\right) . \end{aligned}$$

Remark 2

Condition i) of Result 2 is a basic requirement and is satisfied by common second order kernels such as the Uniform, Epanechnikov, Biweight, Triweight, Gaussian ones.

Analogously to the previous case, a local linear version of estimator ${\hat{m}}$ can be obtained using a local linear weight in defining the sample statistics ${\hat{g}}_j$, $j \in (1,2)$ as detailed in Di Marzio et al. (2012a).

3.2 Linear response

Consider the case where $\mathbb {\Psi }= [0,2\pi )$ and $\mathbb {\Delta }={\mathbb {R}}$, and denote, respectively, the predictor and the response variables as $\Psi$ and Y. Given the random sample $(\Psi _1,Y_1), \ldots , (\Psi _n, Y_n)$, assume the regression model

$$\begin{aligned} Y_i=m(\Psi _i)+\sigma (\Psi _i)\epsilon _i, \end{aligned}$$

(8)

where the $\epsilon _i$s are i.i.d. real-random variables with zero mean and unit variance, and $\sigma ^2(\cdot )$ is the conditional variance of Y.

A kernel regression estimator for m at $\psi \in [0,2\pi )$ is defined as

$$\begin{aligned} {\hat{m}}(\psi ;\kappa )=\frac{\sum _{i=1}^{n} K_\kappa (\Psi _i-\psi )Y_i}{\sum _{i=1}^{n} K_\kappa (\Psi _i-\psi )}, \end{aligned}$$

(9)

with $K_\kappa$ being a circular kernel.

Some asymptotic properties are collected in the following

Result 3

Given the $[0,2\pi ) \times {\mathbb {R}}$-valued random sample $(\Psi _1,Y_1),\ldots ,(\Psi _n,Y_n)$, consider the estimator given by (9). If assumption i) of Result 1 holds, and

• (i) the second derivative of the regression function m is continuous,

• (ii) the conditional variance $\sigma ^2(\cdot )$ is continuous, and the density $f_\Psi$ is continuously differentiable,

then

$$\begin{aligned} \textsf{E}[{\hat{m}}(\psi ; \kappa )]- m(\psi )= \frac{(1-\gamma _2(\kappa ))}{4} \left\{ {m''(\psi )}+\frac{2m'(\psi )f_{\Psi }'(\psi )}{f_{\Psi }(\psi )}\right\} +o(1-\gamma _2(\kappa )), \end{aligned}$$

and

$$\begin{aligned} \textsf{Var}[{\hat{m}}(\psi ;\kappa )]=\frac{\left( 1+2\sum _{\ell =1}^\infty \gamma _\ell ^2(\kappa )\right) }{2\pi n f_{\Psi }(\psi )} \sigma ^2(\psi ) +o\left( \frac{ \sum _{\ell =1}^\infty \gamma _\ell ^2(\kappa )}{n}\right) . \end{aligned}$$

More generally, a class of nonparametric regression estimators outlined for the case of a linear response and circular predictor has been described in detail by Di Marzio et al. (2009).

4 Circular kernel regression with errors-in-variables

Now we consider the errors-in-variables context, where the predictor variable is observed with errors. Specifically, suppose that we are interested in estimating nonparametrically the regression of Y on X, denoted as m, and that our data are realizations from variables $Z=X+\varepsilon$ and Y, say $(z_1, y_1), \ldots , (z_n, y_n)$. A general model for this case could be

$$\begin{aligned} y_i= m(x_i)+\epsilon _i \\ z_i=x_i+\varepsilon _i \nonumber \end{aligned}$$

for $i=1,\ldots ,n$, where X and Y respectively refer to the predictor and response variable, $\epsilon _i$s are realizations of the random error term $\epsilon$, and $\varepsilon _i$s are realizations of the random measurement error $\varepsilon$. The unobserved variable X is always referred to as the latent or true variable. The usual assumptions include that $\epsilon$ is independent from both X and $\varepsilon$, and that the distribution of $\epsilon$ is unknown but has mean 0 and constant variance, while the distribution of $\varepsilon$ is known. Let $f_Z$, $f_{X}$ and $f_\varepsilon$ respectively denote the probability density function of Z, X and $\varepsilon$. Basic theoretical considerations suggest that $f_Z$ is obtained from the convolution between $f_{X}$ and $f_\varepsilon$, i.e.

$$\begin{aligned} f_Z (z) = \int _{-\infty }^{\infty } f_{X} (z-\upsilon ) dF_\varepsilon (\upsilon ), \end{aligned}$$

where $F_\varepsilon$ denotes the distribution function of $\varepsilon$. As a consequence, the estimators of the error-free model are clearly not consistent.

A deconvolution approach can be used to obtain accurate estimators for m. We start by expressing the above relationship using the characteristic functions

$$\begin{aligned} \varphi _{Z}=\varphi _{X}\varphi _{\varepsilon }, \end{aligned}$$

where $\varphi _{Z}$, $\varphi _{X}$ and $\varphi _{\varepsilon }$ denote the characteristic functions of Z, X and $\varepsilon$, respectively. Assuming that $\varphi _{\varepsilon }$ is known, and $\varphi _{Z}$ can be estimated on the basis of sample data, the quantity of interest can be identified by the ratio

$$\begin{aligned} \varphi _{X}=\frac{\varphi _{Z}}{\varphi _{\varepsilon }}. \end{aligned}$$

(10)

The problem arises from the fact that $\varphi _{\varepsilon }(t)$ vanishes as $t\rightarrow \infty$. Hence, plugging the estimate ${\hat{\varphi }}_{Z}$ in Eq. (10) may not yield a consistent estimate of $\varphi _{X}$, because even very small overestimates of $\mid \varphi _{Z}\mid$ are magnified by the arbitrarily large factor $1/\varphi _{\varepsilon }$. This is the well-known ill-defined inverse problem. The scenario is exacerbated if the error density is supersmooth because this makes the characteristic function tend to zero very fast as $t \rightarrow \infty$. The solution is represented by the so-called kernel deconvolution estimator proposed by Stefanski and Carroll (1990), which uses a kernel whose Fourier transform has a compact domain. This yields a compactly supported estimate ${\hat{\varphi }}_{Z}$, and, consequently, ${\hat{\varphi }}_{Z}$ will vanish before small values of $\varphi _{\varepsilon }(t)$ cause the ratio to diverge. A more general perspective suggests to use a damping factor, i.e. to multiply ${\hat{\varphi }}_{Z}$ by a function that steadily goes to zero. Usually this function is the Fourier transform of an ordinary kernel $W_\nu$. Consequently, using the inversion theorem (1), the deconvolution kernel will be

$$\begin{aligned} {\tilde{W}}_\nu (x)=\frac{1}{2\pi } \int \exp (-itx) \frac{\varphi _W(t)}{\varphi _\varepsilon (t/\nu )}dt, \end{aligned}$$

(11)

where $\varphi _W$ is the Fourier transform of the kernel $W_\nu$.

The description of our strategy will be implemented in the next sections to obtain errors-in-variables estimators for the cases when the predictor and/or response have a circular nature.

4.1 Circular response

We are interested in estimating a regression function m as in Eq. (4), but now we only observe the sample $(\Phi _1, \Delta _1), \ldots , (\Phi _n, \Delta _n)$ of i.i.d. observations,

with $\Delta _i$s obtained according to model (3), and $\Phi _i$s being independent copies of the random variable

$$\begin{aligned} \Phi =(\Psi +\varepsilon )\textsf {mod}(2\pi ), \end{aligned}$$

(12)

where $\Psi _i$s are independent copies of the latent variable $\Psi$ whose density function $f_\Psi$ is defined on a generic domain $\mathbb {\Psi }$, and $\varepsilon$ is a random measurement error assumed to be independent of $(\Psi ,\epsilon )$, with a known density function $f_{\varepsilon }$ which is symmetric around zero. We also assume that $f_{\varepsilon }$, $f_{\Psi }$ and $f_{\Phi }$ are square integrable densities.

On the basis of the deconvolution approach, a local estimator for m at $\psi \in \mathbb {\Psi }$ can be defined as

$$\begin{aligned} {\tilde{m}}(\psi ;\nu )=\textsf{atan2}({\tilde{g}}_1(\psi ;\nu ), {\tilde{g}}_2(\psi ;\nu )), \end{aligned}$$

(13)

where the functions ${\tilde{g}}_j$, $j \in (1,2),$ have the same structure as ${\hat{g}}_j$ in Eq. (6),

but employ the deconvolution kernel (11) in place of the weight function $W_\nu$.

4.1.1 Circular predictor

Consider the case where $\mathbb \Psi =[0,2\pi )$ and denote the predictor as $\Theta$. Also, let $f_{\varepsilon }$ be a circular density admitting an absolutely convergent Fourier series representation. A nonparametric estimator for m at $\theta \in [0,2\pi )$, denoted by ${\tilde{m}}(\theta ; \kappa )$, can be obtained by employing circular deconvolution kernels in formula (13). Therefore, recalling that the characteristic function of a periodic density takes values only for integer numbers, using the inversion formula (2), and considering that for a symmetric function $\beta _\ell =0$ for any $\ell$, we have

$$\begin{aligned} {\tilde{K}}_{\kappa }(\theta )= \frac{1}{2\pi }\left\{ 1+2\sum _{\ell =1}^\infty \frac{\gamma _\ell (\kappa )}{\lambda _\ell (\kappa _{\varepsilon })} \cos (\ell \theta )\right\} , \end{aligned}$$

(14)

with smoothing parameter $\kappa >0$, where $\gamma _\ell (\kappa )$ and $\lambda _\ell (\kappa _\varepsilon )$, for $\ell \in {\mathbb {Z}}$, respectively are the $\ell$th Fourier coefficient of the periodic weight function $K_\kappa$ and the error density $f_\varepsilon$ whose concentration is $\kappa _\varepsilon$. The estimator is well defined when the error density has nonvanishing Fourier coefficients, $\gamma _\ell (\kappa )$ is not identically zero and $\sum _{\ell =1}^\infty \mid {\gamma _\ell (\kappa )}/ {\lambda _\ell (\kappa _{\varepsilon })}\mid <\infty$ for all $(\kappa ,\kappa _\varepsilon ) \in {\mathbb {R}}^2_{+}$, which imply that both $K_\kappa$ and ${\tilde{K}}_\kappa$ are square integrable functions.

Some asymptotic properties are collected in the following

Result 4

Given the $[0,2\pi ) \times [0,2\pi )$-valued random sample $(\Phi _1,\Delta _1),\ldots ,(\Phi _n,\Delta _n)$, consider the estimator ${\tilde{m}}(\theta ;\kappa )$, $\theta \in [0,2\pi )$. If the assumptions of Result 1 hold, then

$$\begin{aligned} \textsf{E}[{\tilde{m}}(\theta ; \kappa )]- m(\theta )= \frac{(1-\gamma _2(\kappa ))}{4} \left\{ m''(\theta )+\frac{2m'(\theta )\{C(\theta )f_{\Theta }(\theta )\}'}{C(\theta )f_{\Theta }(\theta )}\right\} +o(1-\gamma _2(\kappa )), \end{aligned}$$

and

$$\begin{aligned} \textsf{Var}[{\tilde{m}}(\theta ;\kappa )]&=\frac{\left( 1+2\sum _{\ell =1}^\infty \gamma _\ell ^2(\kappa )/\lambda ^2_\ell (\kappa _{\varepsilon })\right) }{2\pi n C^2(\theta ) f_{\Theta }(\theta )} \\&\left\{ f_c^2(\theta )s_1^2(\theta )+f_s^2(\theta )s_2^2(\theta )-2 f_c(\theta )f_s(\theta )c(\theta )\right\} +\\&+o\left( \frac{ \sum _{\ell =1}^\infty \gamma _\ell ^2(\kappa )/\lambda ^2_\ell (\kappa _{\varepsilon })}{n}\right) . \end{aligned}$$

Proof

See Appendix. $\square$

We notice that the measurement error does not affect the bias of estimator ${\tilde{m}}$, which is identical to the error-free case, while the variance is considerably larger. This result will hold for the deconvolution estimators described in the next sections too.

Remark 3

Estimator (13) can also be obtained by using the unbiased score approach, which is based on the idea that it suffices to impose the constraint that ${\tilde{g}}_j$, for $j\in (1,2)$, employ an unknown weight function $L_k$ such that

$$\begin{aligned} \textsf{E}[{\tilde{g}}_j(\theta ;\kappa )\mid \Theta _1,\ldots ,\Theta _n, \Delta _1,\ldots ,\Delta _n]= {\hat{g}}_j(\theta ;\kappa ), \end{aligned}$$

i.e.

$$\begin{aligned} \textsf{E}[L_\kappa (\Phi _i-\theta )\mid \Theta _i]= K_\kappa (\Theta _i-\theta ). \end{aligned}$$

By working in the Fourier domain, it can be seen that $L_\kappa (\theta )={\tilde{K}}_\kappa (\theta )$.

4.1.2 Linear predictor

Now, we consider the case where $\mathbb {\Psi }={\mathbb {R}}$, and denote the predictor variable as X. We assume that the measurement errors come from a known, symmetric density $f_{\varepsilon }$ with variance $\varsigma ^2$, and the characteristic function $\varphi _\varepsilon (t)\ne 0$ for all t.

A kernel regression estimator for m at $x \in {\mathbb {R}}$, denoted by ${\tilde{m}}(x; h)$, is defined by employing in estimator (13) a linear deconvolution kernel

$$\begin{aligned} {\tilde{K}}_h(x)=\frac{1}{2\pi }\int \exp ({-itx}) \frac{\varphi _K(t)}{\varphi _\varepsilon (t/h)}dt, \end{aligned}$$

(15)

with a smoothing parameter $h>0$, where $\varphi _K(t)=\int \exp ({itx})K(x)dx$ is the Fourier transform of the kernel $K_h$ defined in formula (7). In this case we assume that $\varphi _K$ is not identically zero and $\int \mid \varphi _K(t)/\varphi _\varepsilon (t/h)\mid dt <\infty$ for all $h>0$, which imply that $\mid \varphi _K\mid$, $\varphi _K^2$ and $\varphi _K^2/\mid \varphi _\varepsilon (\cdot /h)\mid$ are all integrable.

As for the asymptotic properties we have the following

Result 5

Given the ${\mathbb {R}} \times [0,2\pi )$-valued random sample $(X_1,\Delta _1),\ldots ,(X_n,\Delta _n)$, consider the estimator ${\tilde{m}}(x;h)$, $x\in {\mathbb {R}}$. If the assumptions of Result 2 hold, then, for any interior point x of the support of $f_X$,

$$\begin{aligned} \textsf{E}[{\tilde{m}}(x;h)]- m(x)=\frac{h^2\mu _2(K)}{2} \left( m''(x)+ \frac{2 m'(x)\{C(x)f(x)\}'}{C(x)f(x)}\right) +o(h^2), \end{aligned}$$

and

$$\begin{aligned}&\textsf{Var}[{\tilde{m}}(x;h)] = \frac{\int \mid \varphi _K(t)\mid ^2 \mid \varphi _\varepsilon (\varsigma t/h)\mid ^{-2} dt}{2\pi n h C^2(x)f_X(x)}\\&\quad \{f_s^2(x)s_2^2(x)+f_c^2(x)s_1^2(x)-2f_s(x)f_c(x)c(x)\}\\&\quad +o\left( \frac{1}{nh}\right) . \end{aligned}$$

Proof

See Appendix. $\square$

Remark 4

If $f_X$ is assumed to have a limited support, say [a, b], where $-\infty<a<b<+\infty$, then a different bias and variance hold when $x \in [a,a+h]\cup [b-h,b]$. For this special case we need to adapt the boundary theory described in Di Marzio et al. (2012a) by employing a deconvolution kernel (15).

4.2 Linear response

We are now interested in the dependence of the real-valued response Y on the circular predictor $\Psi$, when the random sample $(\Phi _1,Y_1), \ldots , (\Phi _n, Y_n)$, modelled according Eqs. (8) and (12) is available. Here the $\varepsilon _i$s are i.i.d. circular random variables with zero mean direction and finite concentration, and are independent of the $(\Psi _i,\epsilon _i)$’s.

The local constant estimator for m is defined by

$$\begin{aligned} {\tilde{m}}(\psi ; \kappa )=\frac{\sum _{i=1}^{n} {\tilde{K}}_\kappa (\Phi _i-\psi )Y_i}{\sum _{i=1}^{n}{\tilde{K}}_\kappa (\Phi _i-\psi )}, \end{aligned}$$

(16)

where ${\tilde{K}}_\kappa$ is a circular deconvolution kernel defined in formula (14).

As for the asymptotic properties we have the following

Result 6

Given the $[0,2\pi )\times {\mathbb {R}}$-valued random sample $(\Phi _1,Y_1),\ldots ,(\Phi _n,Y_n)$, consider the estimator ${\tilde{m}}(\psi ;\kappa )$, $\psi \in [0,2\pi )$. If assumption i) of Result 1, and assumptions i) and ii) of Result 3 hold, then

$$\begin{aligned} \textsf{E}[{\tilde{m}}(\psi ; \kappa )]- m(\psi )= \frac{(1-\gamma _2(\kappa ))}{4} \left\{ {m''(\psi )}+\frac{2m'(\psi )f_{\Psi }'(\psi )}{f_{\Psi }(\psi )}\right\} +o(1-\gamma _2(\kappa )), \end{aligned}$$

and

$$\begin{aligned} \textsf{Var}[{\tilde{m}}(\psi ;\kappa )]=\frac{\left( 1+2\sum _{\ell =1}^\infty \gamma _\ell ^2(\kappa )/\lambda ^2_\ell (\kappa _{\varepsilon })\right) }{2\pi n f_{\Psi }(\psi )} \sigma ^2(\psi ) +o\left( \frac{ \sum _{\ell =1}^\infty \gamma _\ell ^2(\kappa )/\lambda ^2_\ell (\kappa _{\varepsilon })}{n}\right) . \end{aligned}$$

Proof

See Appendix. $\square$

Remark 5

We notice that, as in the Euclidean setting, the measurement error has no effect on the asymptotic bias of the estimator, which, when the predictor observed with error is circular (linear respectively), depends only on the second moment of the classical kernel $K_\kappa$ ($K_h$ resp.). The asymptotic variance, similarly to the Euclidean setting, depends on the Fourier coefficients (characteristic function resp.) of the error density appearing in roughness of the deconvolution kernel ${\tilde{K}}_\kappa$ (${\tilde{K}}_h$ resp.).

Concerning the distribution of the estimators, asymptotic results can be obtained following the same approach of Delaigle et al. (2009), where some regularity conditions, directly applicable for our linear predictor case, are provided. In particular, using their assumptions about the kernel, the design density, the moments of the response and the error density – with the adaptations for the circular predictor case – the asymptotic normality of the estimators could be established following the same lines of theorems 1 and 2 of Delaigle et al. (2009). In fact, in the simulations of the next section we observed that the distribution of the estimates in correspondence of high design density is bell-shaped, closely recalling a Gaussian one.

5 Simulations

Our overall goal is to compare the performance of the standard Nadaraya-Watson regression estimator (SNW) with the proposed deconvolution one (DNW). Note that we will use “local constant” estimators only in these examples. We choose to avoid the task of smoothing degree selection in the estimates, consequently our results illustrate the potential of each method, with the caveat that the best performance is obtained conditional on an optimally selected smoothing degree. Our motivation for this is that we have not presented any data driven rule for smoothing selection, and so it appears preferable to avoid the situation in which the adoption of a sub-optimal rule then hides the strict merits of the estimators.

We consider these three simulation scenarios:

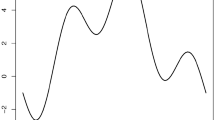
• (i) the circular-circular (C–C) case where the regression function m is modelled as

  $$\begin{aligned} m(\theta )=(1+2\cos (\theta +3\sin (\theta )))\textsf {mod}(2\pi ), \qquad \theta \in [0,2\pi ), \end{aligned}$$

  the measurement and regression errors are assumed to follow, respectively, a wrapped Laplace (wL) and von Mises (vM) distribution, i.e., for $i=1,\ldots ,n$, $\varepsilon _i\sim wL(0,0.2)$ and $\epsilon _i\sim vM(0,5)$, $\Theta _i$ come from a von Mises density with mean $\pi$ and concentration parameter 0.01, and a von Mises density is used as the kernel;

• (ii) the circular-linear (C–L) case where we assume that

  $$\begin{aligned} m(\theta )=1+2\cos (\theta +3\sin (\theta )), \qquad \theta \in [0,2\pi ), \end{aligned}$$

  the measurement and regression errors follow, respectively, a wrapped Laplace and Normal distribution, i.e. $\varepsilon _i\sim wL(0,0.2)$ and $\epsilon _i\sim N(0,0.2^2)$, for $i=1,\ldots ,n$, $\Theta _i\sim vM(\pi ,0.01)$, and the employed weight function is the von Mises density;

• (iii) the linear-circular (L–C) case where we use for m the model

  $$\begin{aligned} m(x)=(10+0.05 x^2)\textsf {mod}(2\pi ), \qquad x \in {\mathbb {R}}, \end{aligned}$$

  the measurement and regression errors follow, respectively, a Laplace and von Mises distribution, i.e. $\varepsilon _i\sim L(0,0.2)$ and $\epsilon _i\sim vM(0,4)$, for $i=1,\ldots ,n$, $X_i\sim N(6,2^2)$, and the standard Normal distribution is employed as the weight function.

An illustration of above regression models is shown in Fig. 1. In both the scenarios i) and ii) in the summation of Eq. (14) we used a truncation at $\ell =10$. Here $\ell$ does not play the role of a smoothing parameter, but it is necessary to set it in order to ensure a perfect description of the chosen kernel through its Fourier coefficients. We have prudentially chosen $\ell =10$ because this value largely guarantees an adequate representation of the deconvolution kernel in all of our simulation case studies.

Fig. 1

From left: C–C, C–L and L–C regression models

Obviously, to study the effect of the measurement errors, it’s possible to consider additional scenarios with different concentration (dispersion) parameters for the error model. However, we notice that when this latter goes to infinity (zero) we can ignore the error in the analysis, therefore the errors-in-variables estimator gives the same results as the standard kernel regression estimator. This is easily seen considering that in this case $\alpha _\ell \rightarrow 1$ for any $\ell$. In contrast, when it approaches zero (infinity), the target regression model becomes particularly hard to estimate because the error makes it unidentifiable. Additional simulative results are reported in the Supplementary Material.

In a first experiment we use the best possible smoothing degree for each sample, obtained as minimizer of the averaged squared error (ASE) along a grid of size M describing the design density support. Due to the nature of response variables, ASE has two definitions. For the bth sample, $b \in 1,\ldots ,B$, in the L–C and C–C cases it is defined as

$$\begin{aligned} \text {ASE}_b(\nu )=\frac{1}{M} \sum _{j=1}^M (1-\cos (m(s_j)-{\tilde{m}}_b(s_j; \nu ))), \end{aligned}$$

where $\nu \in \{h, \kappa \}$, with $s_j \in \{x_j, \theta _j\}$ being a grid element, and $(1-\cos (\rho -\tau ))$ is the usual angular distance between circular locations $\rho$ and $\tau$. While, for the C–L case ASE is defined as

$$\begin{aligned} \text {ASE}_b(\kappa )=\frac{1}{M} \sum _{j=1}^M(m(\theta _j)-{\tilde{m}}_b(\theta _j; \kappa ))^2, \end{aligned}$$

where $\theta _j$ is a grid element. For both $n=200$ and $n=500$ we have drawn $B=500$ samples. Averaging over samples leads to the following global performance index (see, for example, Hart (1997), p. 86)

$$\begin{aligned} \text {MASE}(\nu )=\frac{1}{B} \sum _{b=1}^B \text {ASE}_b(\nu ), \end{aligned}$$

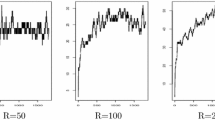
where $\nu \in \{h, \kappa \}$. We show $\text {MASE}$ as a function of $\nu$, and the corresponding minima in Fig. 2 and Table 1, respectively. We note that the deconvolution estimator gives a clear advantage, while both methods improve as the sample size increases.

Table 1 Minimum values of $\text {MASE}$s over 500 samples of size n for SNW and DNW estimators

Interestingly, the figure shows that deconvolution method tends to be uniformly superior for large n and the same choice of smoothing parameter, and this appears to be reassuring if we consider that a proper data driven smoothing selector still does not exist. However, the $\text {MASE}$ curves allow also a kind of sensibility analysis, meaning that the curvatures of the deconvolution $\text {MASE}$s are generally much more pronounced than in the naive case. This suggests that an hypothetical selection method would be doomed to high variability.

Fig. 2

$\text {MASE}$ curves of SNW (continuous) and DNW (dashed) estimators over a grid of smoothing values for the C–C (top), C–L (middle), and L–C (bottom) scenarios. Empty circles indicate the minima of the curves

5.1 Mis-specification of the measurement error

In this section we consider the case of a wrongly imposed measurement error model. In a first experiment data are corrupted by adding a supersmooth error and an ordinary smooth model is assumed, while in a second experiment we consider the opposite scenario. We have ensured that the concentration (or variability) of the error sample is very similar to that one of the assumed model in order to isolate the misspecification effect. Results are reported in Table 2. In panel A (B), in the C–C and C–L cases data are corrupted by a von Mises (wrapped Laplace) measurement error, while it is assumed a wrapped Laplace (von Mises) noise model. In the L–C case data are corrupted by a Normal (Laplace) error where a Laplace (Normal) distribution is assumed.

Table 2 Minimum values of $\text {MASE}$s over 500 samples of size n for SNW and DNW estimators when the error is wrongly imposed

From Panel A we see that, if we wrongly assume a (wrapped) Laplace model, results are still reasonable, because we obtain positively biased estimates of the higher order coefficients, and this does not strongly affect the stability of DNW estimator, once considered that such estimates appear in the denominators of the deconvolution kernels. The opposite scenario clearly yields poorer performance, as seen in Panel B, because assuming a supersmooth error density leads to negatively biased estimates of the higher order coefficients hampering the stability of DNW estimator. As a result, an advice arises of, if in doubt, assume a smooth error model.

6 Pollution and surface wind data

The amount of pollution faced by a particular location will depend on a variety of factors. In this section we consider the response variable to be the amount of carbon monoxide (CO), and the explanatory variable to be the wind direction. In this case if the source of the pollution is upwind of the sensor, then a higher amount of pollution is likely and vice versa. The data were obtained from the Texas Commission on Environmental Quality who have many monitoring sites. Figure 3 shows the locations of sites which are close to Houston.

Fig. 3

Active monitoring sites close to Houston, Texas. Data from Houston North Loop is selected for our illustration. Extracted using the GeoTAM Map Viewer at https://www.tceq.texas.gov/airquality/monops/sites/air-mon-sites

We have selected a site near Houston (“North Loop”) in Harris County at Latitude: $29.81^o$ North and Longitude: $-95.39^o$ West using data from 2018.¹ The data is collected hourly, but we have calculated the average daily wind direction (using the directional average), and the average daily CO (in parts per million). We note that on 6 (out of 365) days the wind direction had two peaks, and in such cases the average is not so meaningful. But this is a small proportion (less than 2%) of the days and is unlikely to change our conclusions. These daily averages were “thinned” to reduce serial correlation resulting in 183 observations from alternate days. A technical treatment of correlation in circular data has been done by Di Marzio et al. (2012b). It is argued that, for a fixed sample size, the variance of an estimator increases with the correlation and it is often the case that the autocorrelation structure determines the optimal smoothing degree.

As a first benchmark we initially fit a parametric model in which CO (y) is related to wind direction ($\theta$) using a sine-cosine model

$$\begin{aligned} y_i=\beta _0+\beta _1\sin \theta _i+\beta _2\cos \theta _i+\varepsilon _i,\qquad i=1,\ldots ,n. \end{aligned}$$

This gives fitted values ${\hat{\beta }}_0=0.568, {\hat{\beta }}_1= -0.173, {\hat{\beta }}_2=0.074$, with the prediction curve plotted with the data in Fig. 4. It is clear that the CO pollution is highest when the wind is coming from the south (2.73 radians).

As a second benchmark, we fit a standard circular-linear nonparametric regression, in which the measurements are treated as error free. The smoothing parameter (chosen by leave-one-out cross-validation) was selected as $\kappa = 7.77$ for a von Mises kernel, and the resulting curve is shown is also shown in Fig. 4. For this model, the maximum CO occurs at 2.11 radians.

In this circular-linear case, we use a measurement error model for the observed wind direction which can be approximated by a wrapped Normal error with zero mean and concentration equal to 0.9. This choice was motivated, in part, by Di Marzio et al. (2021) when dealing with surface wind data, but also influenced by a desire to note a difference from the error-free case (which is equivalent to taking $\rho =1$). As suggested by simulation results, in the summation of Eq. (14) we used a truncation at $\ell =10$. This function depends only on $\kappa$, since $\kappa _\varepsilon$ is determined by the wrapped Normal concentration parameter. The estimated CO is then given using Eq. (16), in which $\kappa$ was found by leave-one-out cross-validation to be 3.35. Naive cross-validation is sometimes used in practice although it does not have a sound theoretical foundation. The resulting curve is shown in Fig. 4, and is seen to be somewhat less smooth than the error-free model estimate. The nonparametric errors-in-variables model has residual sum of squares equal to 1.91, whereas the parametric model is slightly larger (2.40) and the error-free model very similar (1.99). The maximum estimated CO occurs at $\theta =2.17$ for the errors-in-variables model.

Fig. 4

Carbon monoxide vs wind direction at Houston North Loop monitoring station—alternate daily averages for 2018. Parametric sin/cos model (red), fitted nonparametric errors in variables model (black) and standard circular-linear (no error model) kernel regression (dashed)

7 Discussion

In the paper we introduce a local constant fit for circular data when the sample is affected by a measurement error. Future research work will deal with the generalization of the proposed methodology to higher order interpolating polynomials, the specification of more suitable smoothing degree selectors and the treatment of the circular errors-in-variables regression problem with other methods, such as the low-order approximation or equivalence ones.

Appendix A

Proof of Result 4. By following the same lines as in the proof of Lemma 1 in Di Marzio et al. (2012a), and noting that, for a circular kernel $K_\kappa$, its second sin-moment $\eta _2(K_\kappa )=\int \sin ^2(\theta ) K_\kappa (\theta ) d\theta$ and roughness $R(K_\kappa )=\int K^2_\kappa (\theta ) d\theta$ are equal to $(1-\gamma _2(\kappa ))/2$ and $\sum _{\ell =1}^\infty \gamma _\ell ^2(\kappa )$, respectively, we obtain

$$\begin{aligned}{} & {} \textsf{E}[{\tilde{g}}_j(\theta ; \kappa )]= g_j(\theta )+ \frac{(1-\gamma _2(\kappa ))}{4} g_j''(\theta )+o(1-\gamma _2(\kappa )), \\{} & {} \quad \textsf{Var}[{\tilde{g}}_j(\theta ;\kappa )] =\frac{\left( 1+2\sum _{\ell =1}^\infty \gamma _\ell ^2(\kappa )/\lambda ^2_\ell (\kappa _{\varepsilon })\right) f_{\Theta }(\theta )s_j^2(\theta )}{2\pi n } \\{} & {} \quad +o\left( \frac{ \sum _{\ell =1}^\infty \gamma _\ell ^2(\kappa )/\lambda ^2_\ell (\kappa _{\varepsilon })}{n}\right) , \end{aligned}$$

for $j \in (1,2)$, and

$$\begin{aligned} \textsf{Cov}[{\tilde{g}}_1(\theta ;\kappa ),{\tilde{g}}_2(\theta ;\kappa )]&=\frac{\left( 1+2\sum _{\ell =1}^\infty \gamma _\ell ^2(\kappa )/\lambda ^2_\ell (\kappa _{\varepsilon })\right) f_{\Theta }(\theta ) c(\theta )}{2\pi n } \\&\quad +o\left( \frac{ \sum _{\ell =1}^\infty \gamma _\ell ^2(\kappa )/\lambda ^2_\ell (\kappa _{\varepsilon })}{n}\right) . \end{aligned}$$

Then by applying the same arguments in the proof of Theorem 1 in Di Marzio et al. (2012a) gives the asymptotic bias and the asymptotic variance results. $\Box$

Proof of Result 5. By reasoning as in the proof of Lemma 3 in Di Marzio et al. (2012a), and considering that $x \in {\mathbb {R}}$ is an interior point of the support of $f_X$, we obtain

$$\begin{aligned}{} & {} \textsf{E}[{\tilde{g}}_j(x; h)]= g_j(x)+ \frac{h^2}{2}\mu _2(K) g_j''(x)+o(h^2), \\{} & {} \quad \textsf{Var}[{\tilde{g}}_j(x;h)]=\frac{\int \mid \varphi _K(t)\mid ^2 \mid \varphi _\varepsilon (\varsigma t/h)\mid ^{-2} dt f_{X}(x)s_j^2(x)}{ 2\pi nh } +o\left( \frac{1}{nh}\right) , \end{aligned}$$

for $j \in (1,2)$, and

$$\begin{aligned} \textsf{Cov}[{\tilde{g}}_1(x;h),{\tilde{g}}_2(x;h)]=\frac{\int \mid \varphi _K(t)\mid ^2 \mid \varphi _\varepsilon (\varsigma t/h)\mid ^{-2} dt f_{X}(x) c(x)}{2\pi nh } +o\left( \frac{ 1}{nh}\right) . \end{aligned}$$

Then by applying the same arguments in the proof of Theorem 3 in Di Marzio et al. (2012a) gives the asymptotic bias and the asymptotic variance results. $\Box$

Proof of Result 6. We obtain the asymptotic bias by reasoning as in the proof of Result 4. This result can be, additionally, derived by employing the unbiased score approach. The asymptotic variance follows from the same arguments as in the proof of Theorem 3 in Di Marzio et al. (2009), when considering the roughness of a deconvolution kernel. $\Box$