Abstract
Causal mediation analysis is used to decompose the total effect of an exposure on an outcome into an indirect effect, taking the path through an intermediate variable, and a direct effect. To estimate these effects, strong assumptions are made about unconfoundedness of the relationships between the exposure, mediator and outcome. These assumptions are difficult to verify in a given situation and therefore a mediation analysis should be complemented with a sensitivity analysis to assess the possible impact of violations. In this paper we present a method for sensitivity analysis to not only unobserved mediator-outcome confounding, which has largely been the focus of previous literature, but also unobserved confounding involving the exposure. The setting is estimation of natural direct and indirect effects based on parametric regression models. We present results for combinations of binary and continuous mediators and outcomes and extend the sensitivity analysis for mediator-outcome confounding to cases where the continuous outcome variable is censored or truncated. The proposed methods perform well also in the presence of interactions between the exposure, mediator and observed confounders, allowing for modeling flexibility as well as exploration of effect modification. The performance of the method is illustrated through simulations and an empirical example.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
To estimate causal direct and indirect effects of an exposure on an outcome a key assumption is unconfoundedness of the relationships between exposure, mediator, and outcome. Since unconfoundedness is difficult to verify in a given situation results should be accompanied by a sensitivity analysis to gauge the impact of violations on the estimated effects (Rosenbaum 2010, Chap. 14).
In mediation analysis the focus has been predominantly on sensitivity against violations of no unobserved mediator-outcome confounding. The argument used is that confounding related to the exposure could be handled by randomization or by adjusting for a “sufficiently rich” set of pre-exposure confounders, while confounding related to the mediator is more difficult to design or adjust away. However, in many applications the exposure cannot be randomized and it is often difficult to guarantee that a sufficiently rich set of pre-exposure confounders has been adjusted for.
Different approaches have been suggested for sensitivity analysis to unobserved mediator-outcome confounding. Among these are methods based on correcting estimates and confidence intervals (CIs) using a bias factor based on the specification of the relationships between the unobserved confounder and the mediator, outcome and/or exposure (VanderWeele 2010; Hafeman 2011; le Cessie 2016). An alternative approach using the correlation between the error terms in the parametric regression models for the mediator and outcome as the sensitivity parameter was suggested by Imai et al. (2010a) and implemented in the R (R Core Team 2017) package mediation (Tingley et al. 2014, 2019). This approach involves deriving expressions for the direct and indirect effects that take this correlation into account. It offers sensitivity analysis to unobserved mediator-outcome confounding for continuous mediators and outcomes as well as when either the mediator or the outcome is binary, with the caveat that the binary outcome model cannot include any exposure-mediator interactions.
A similar approach was suggested by Lindmark et al. (2018) for cases when both the mediator and outcome are binary and probit models are used for estimation. Instead of deriving expressions for the direct and indirect effects this approach incorporates correlations between error terms of the mediator, outcome and exposure assignment models into the estimation of the model parameters upon which the direct and indirect effects estimates are based. This approach is able to take into account not only mediator-outcome confounding but also exposure-mediator and exposure-outcome confounding. It is also flexible in that a sensitivity analysis can be performed also in the presence of interactions involving the exposure, mediator and observed confounders. The latter allows richer model specification and also enables performing sensitivity analyses in situations where the investigation of effect heterogeneity in different subpopulations is of interest.
Estimation of direct and indirect effects is further complicated when there is censoring or truncation of the data. In the context of structural equation models for estimation of mediation effects Wang and Zhang (2011) showed that censoring leads to both reduced accuracy and precision, especially when it is the outcome variable that is censored. They suggested a tobit mediational model to account for censored data in the estimation of effects. However, as their approach was not in the context of causal mediation analysis no attention was given to assumptions about unconfoundedness or related sensitivity analyses. The mediation package (Tingley et al. 2014, 2019) allows estimation of causal mediation effects when the outcome is censored based on a tobit model but does not provide an accompanying sensitivity analysis method. Aside from these examples, most research into methods for mediation analysis in the presence of censoring of the outcome has taken place in the context of time-to-event outcomes (see e.g. Lange and Hansen (2011); VanderWeele (2011) and VanderWeele (2015), Chap. 4) including suggestions for sensitivity analyses to unobserved mediator-outcome confounding (Tchetgen Tchetgen 2011; VanderWeele 2013). The related but more severe issue of truncation, i.e. when the outcome is not recorded at all for certain values has to our knowledge not been examined within the mediation literature.
In this paper we extend the sensitivity analysis method to unobserved mediator-outcome confounding and confounding involving the exposure for parametric estimation of direct and indirect effects introduced in Lindmark et al. (2018) to include cases with continuous mediators and/or outcomes. We also suggest sensitivity analysis methods for unobserved mediator-outcome confounding for the more complicated settings when the outcome is censored or truncated, building on the tobit model for censored outcomes (Tobin 1958) and its equivalent for truncated outcomes (Hausman and Wise 1977). We illustrate the performance of the method through simulations and present an empirical example. The approach is implemented in the R package sensmediation (Lindmark 2019) with the exception of the suggested methods for censored or truncated outcomes where we provide R code for the analyses performed in this paper.
The paper is structured as follows. In Sect. 2.1 direct and indirect effects are defined using the counterfactual framework for mediation (Robins and Greenland 1992; Pearl 2001) and the assumptions required for identification are presented. In Sect. 2.2 the general idea behind the sensitivity analysis method is presented and parametric estimators of direct and indirect effects with accompanying sensitivity analyses for different combinations of continuous and binary mediators and outcomes are suggested. In Sect. 2.3 corresponding results are presented for cases where the outcome is censored or truncated. The simulation scenarios are outlined in Sect. 3.1 with simulation results in Sect. 3.2 and an empirical example in Sect. 3.3. Finally, we summarize the findings and discuss limitations and further developments in Sect. 4.
2 Methods
2.1 Identification and assumptions
Let Z be an exposure, Y an outcome, and M a mediator of the exposure-outcome relationship (see Fig. 1).
Let \(M_{i}(z)\) denote the potential value of the mediator for individual i under exposure level z, \(Y_{i}(z, m)\), the potential outcome for individual i under exposure level z and mediator level m and \(Y_{i}(z,M_i(z'))\), the composite potential outcome if the exposure \(Z_i\) were set to the value z and the mediator \(M_i\) were set to its value under exposure level \(Z_i=z'\).
We define the natural direct effect contrasting two exposure levels \(z_1\) and \(z_0\), as
the effect on Y of changing Z from \(z_0\) to \(z_1\) if the mediator were allowed to vary as it would naturally if all individuals in the population were under exposure level z.
The natural indirect effect is defined as
the effect on Y when, keeping the exposure fixed at z in the population, allowing the mediator to change from its potential value when \(z_0\) to its potential value when \(z_1\).
If we make a composition assumption, i.e. that \(Y_i(z)=Y_i(z,M_i(z))\) (VanderWeele and Vansteelandt 2009), the total effect \(TE_{z_1,z_0}=\mathbb {E}\left[ Y_i(z_1)-Y_i(z_0)\right]\) can be decomposed as either \(TE_{z_1,z_0}=NDE_{z_1,z_0}(z_0)+NIE_{z_1,z_0}(z_1)\) or \(TE_{z_1,z_0}=NDE_{z_1,z_0}(z_1)+NIE_{z_1,z_0}(z_0)\). Using terminology introduced by Robins and Greenland (1992) the former decomposition is into the pure natural direct and total natural indirect effect and the latter decomposition into the total natural direct and pure natural indirect effects.
Often we have a binary exposure taking the values \(Z = 1\) if exposed and \(Z = 0\) if unexposed. The most common decomposition is then \(TE_{1,0}= NDE_{1,0}(0)+NIE_{1,0}(1)\).
To identify natural direct and indirect effects from observed data, we assume consistency, so that for an individual i with observed exposure \(Z_i=z\) we have that \(M_i=M_i(z)\) and \(Y_i=Y_i(z)\), and for an individual i with observed exposure \(Z_i=z\) and observed mediator \(M_i=m\) we have that \(Y_i=Y_i(z,m)\) (VanderWeele and Vansteelandt 2009). Together with the composition assumption this implies \(Y_i=Y_i(z,M_i(z))\).
We also assume no interference, i.e. that the exposure level of one individual does not have an effect on the mediator or the outcome of another individual (De Stavola et al. 2015). Finally, we make crucial assumptions about unconfoundedness:
Assumption 1
Sequential ignorability (Imai et al. 2010a)
-
1.
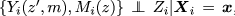 i.e., there is no unobserved confounding of the exposure-mediator and exposure-outcome relationship given the observed pre-exposure covariates \(\varvec{X}_i\).
i.e., there is no unobserved confounding of the exposure-mediator and exposure-outcome relationship given the observed pre-exposure covariates \(\varvec{X}_i\). -
2.
 i.e., given \(\varvec{X}_i\) and the observed exposure \(Z_i\) there is no confounding of the mediator-outcome relationship.
i.e., given \(\varvec{X}_i\) and the observed exposure \(Z_i\) there is no confounding of the mediator-outcome relationship.
where \(0<P\left( Z_i=z|\varvec{X}_i=\varvec{x} \right)\) and \(0<P\left( M_{i}(z)=m|Z_i=z,\varvec{X}_i=\varvec{x} \right)\) for \(z\in \mathcal {Z}\) (the support of Z), and all \(\varvec{x}\in \mathcal {X}\) (the support of \(\varvec{X}\)) and \(m\in \mathcal {M}\) (the support of M).
Note that Assumption 1 implies a so-called cross-world independence assumption (see e.g. VanderWeele et al. 2014), i.e. independence between the counterfactual outcome under exposure level \(Z=z'\) and mediator level \(M=m\) and the counterfactual mediator under exposure level \(Z=z\), where \(z'\) and z are possibly different values. Since in reality different values of the exposure cannot be observed simultaneously this assumption is difficult to verify empirically. The cross-world independence assumption is violated in cases where there is intermediate confounding, i.e. mediator-outcome confounders affected by the exposure.
If these assumptions are fulfilled the natural direct and indirect effects conditional on the covariates are identified by (Pearl 2001)
For continuous mediators we replace the sums and probabilities in (1) and (2) with integrals and densities. By marginalizing (1) and (2) over \(\varvec{x}\) we obtain the \(NDE_{z_1,z_0}\left( z\right)\) and \(NIE_{z_1,z_0}\left( z\right)\), the natural direct and indirect effects at the population level.
Here we use a parametric approach where the natural direct and indirect effects are estimated by specifying parametric regression models for the outcome and mediator and rewriting (1) and (2) as functions of the regression parameters. The resulting estimators are consistent given that the previously outlined assumptions are fulfilled and the regression models are correctly specified. In the following section we derive estimators of the natural direct and indirect effects for combinations of binary and continuous mediators and outcomes (for the combination binary mediator and outcome, see Lindmark et al. (2018)).
2.2 Estimators and sensitivity analysis in the absence of censoring or truncation of the outcome
We specify a parametric regression model for the mediator conditional on the exposure and observed covariates. For a continuous mediator we specify a linear regression model
where the \(\eta _i\) are i.i.d. (independent and identically distributed) with zero mean and standard deviation \(\sigma _{\eta }\).
For a binary mediator we specify a probit regression model with \(M_i = I(M_i^*>0)\), where
where \(\eta ^*_i{\mathop {\sim }\limits ^{i.i.d.}} N(0,1)\).
We also specify a parametric regression model for the outcome conditional on the exposure, mediator and observed covariates. For a continuous outcome we specify
where the \(\xi _i\) are i.i.d.with zero mean and standard deviation \(\sigma _{\xi }\). For a binary outcome we specify \(Y_i = I(Y_i^*>0)\), where
with \(\xi ^*_i{\mathop {\sim }\limits ^{i.i.d.}} N(0,1)\).
In Table 1 expressions for the natural direct and indirect effects are presented for different model combinations, first when both mediator and outcome are continuous, then when the mediator is binary and the outcome continuous and lastly when the mediator is continuous and the outcome binary. Note that these are more general versions of previously derived expressions, see Imai et al. (2010a), adding interactions between the covariates and exposure and mediator to the regression models used to allow for moderated mediation, i.e. different direct and indirect effects for different covariate levels. The natural direct and indirect effects are estimated by fitting the mediator and outcome models using maximum likelihood (ML) and plugging the estimated parameters into the appropriate expressions in Table 1. Approximate standard errors of the effects can be obtained using the delta method (Oehlert 1992).
2.2.1 Sensitivity analysis
The sensitivity analysis is presented for mediator-outcome confounding (\(\mathbf{U} _2\) in Fig. 2) but can be modified to exposure-mediator (\(\mathbf{U} _1\)) or exposure-outcome (\(\mathbf{U} _3\)) confounding by replacing the mediator model with a model for the exposure assignment conditional on the covariates and the outcome model with the mediator model, or by replacing the mediator model with an exposure model, respectively. For details see Lindmark et al. (2018).
We assume that the error terms in the mediator and outcome models are bivariate normal with correlation \(\rho\). If there is unobserved mediator-outcome confounding then \(\rho \ne 0\), otherwise \(\rho =0\). The sensitivity analysis is performed by deriving the joint likelihood for M and Y as a function of the regression parameters and \(\rho\). In Table 2 the log-likelihoods for a sample of n units (\(i=1,...,n\)) derived for different model combinations are presented. We cannot estimate \(\rho\) from the observed data without further assumptions (Imai et al. 2010b) and instead proceed with a modified maximum likelihood (ML) procedure, where the log-likelihood is maximized with regards to the regression parameters for a fixed value of the correlation, \(\rho =\tilde{\rho }\). The sensmediation package (Lindmark 2019) uses functions from the maxLik (Henningsen and Toomet 2011; Toomet and Henningsen 2015) package for the maximization. The default maximization method is the Newton-Raphson algorithm which utilizes analytical gradients and Hessians of the log-likelihood functions.
The resulting parameter estimates \({{{\hat{\beta }}}}\left( \tilde{\rho }\right)\) or \({\hat{\beta }}^*\left( \tilde{\rho }\right)\) and \({\hat{\theta }}\left( \tilde{\rho }\right)\) or \({\hat{\theta }}^*\left( \tilde{\rho }\right)\) (plus \(\hat{\sigma }_{\eta }\left( \tilde{\rho }\right)\) for a continuous mediator and binary outcome) are then plugged into the expressions for the \(NDE_{z_1,z_0}(z,\varvec{x})\) and \(NIE_{z_1,z_0}(z,\varvec{x})\) (Table 1). This gives estimates of the conditional natural direct and indirect effects under a given level of unobserved mediator-outcome confounding, \(\widehat{NDE}_{z_1,z_0}(z,\varvec{x},\tilde{\rho })\) and \(\widehat{NIE}_{z_1,z_0}(z,\varvec{x},\tilde{\rho })\). Estimates of the marginal natural direct and indirect effects under given levels of confounding are given by averaging these estimated conditional effects over the study population. Approximate standard errors of the effects under a given level of confounding can be obtained through the delta method.
The results of the sensitivity analysis can be presented in different ways. One is to report the results over a range of the sensitivity parameter. This range can be defined using subject matter knowledge about the probable nature of the unobserved confounding, e.g. whether or not an unobserved confounder is expected to affect both the mediator and the outcome in the same directions and thus induce a positive error term correlation. In the absence of such prior knowledge a wide range encompassing both negative and positive correlations can be used. The results can be summarized through plots of point estimates and CIs and/or so called uncertainty intervals (UIs) (Vansteelandt et al. 2006; Genbäck et al. 2015, 2018), the union of all \(100\times (1-\alpha )\)% CIs over the range of the sensitivity parameter. An alternative, or complement, to these is to report the values of the sensitivity parameter where the \(100\times (1-\alpha )\)% CIs include 0, i.e. where the effect is no longer significant at an \(\alpha\) level of significance.
2.3 Estimation and sensitivity analysis in the presence of censoring or truncation of the outcome
Here we present estimation methods and sensitivity analyses to mediator-outcome confounding when we have a continuous mediator and the outcome is either left censored or left truncated, i.e. where censoring/truncation occurs for values of the outcome variable that are below a certain point. The methods presented here can be used also for right censoring/truncation, i.e. where censoring/truncation occurs for values of the outcome variable that are above a certain point. This can be accomplished by multiplying the right censored/truncated outcome variable by − 1, thus transforming it into a left censored/truncated variable.
These methods are not currently implemented in the sensmediation package but analytic gradients of the log-likelihoods are provided in appendices to facilitate implementation of the optimization to obtain ML estimates. We also provide the code used to perform the analyses in the simulation study which may be adapted to other applications. Here, the optimization was performed using the Broyden-Fletcher-Goldfarb-Shanno (BFGS) method implemented in the maxLik (Henningsen and Toomet 2011; Toomet and Henningsen 2015) package, as no analytic Hessian was derived.
For comments on adapting the methods presented to sensitivity analyses of unobserved confounding involving the exposure, see Sect. 4.
2.3.1 Sensitivity analysis unobserved mediator-outcome confounding, censored outcome
Assume that we have a continuous mediator and outcome that follow models (3) and (5), but that we observe \(Y_i=\max (Y_i,t)\), i.e. left censoring at t. To estimate direct and indirect effects the mediator model could be fitted using e.g. OLS or ML while the regression parameters in the outcome model could be estimated using e.g. tobit regression (Tobin 1958). To assess the sensitivity of the estimated effects to mediator-outcome confounding we again assume that the error terms \(\eta _i\) and \(\xi _i\) are bivariate normal with correlation \(\rho\). The joint distribution of the mediator and outcome is then given by
That is, for observations that are not censored the joint distribution is simply a bivariate normal distribution while for observations that are censored we have: \(f(y_i,m_i)=f(y_i<t,m_i)=f(\xi _i<t-\varvec{\theta }'\varvec{C}_{2i},\eta _i=m_i-\varvec{\beta }'\varvec{C}_{1i}),\) with the resulting density derived as in Appendix A. The joint log-likelihood is
To obtain \({\hat{\theta }}\left( \tilde{\rho }\right)\) and \({\hat{\beta }}\left( \tilde{\rho }\right)\), (7) is maximized for a fixed \(\rho =\tilde{\rho }\) (gradients are provided in Appendix B). These estimates are then plugged into the expressions for the natural direct and indirect effects in Table 1, model combination (3) and (5) to obtain estimates under a given level of unobserved mediator-outcome confounding and censoring.
2.3.2 Sensitivity analysis unobserved mediator-outcome confounding, truncated outcome
Truncation is a more complicated problem than censoring as observations are completely missing, meaning that truncation of the outcome also leads to missing mediator values. To reduce the complexity here we simplify the models (3) and (5) for M and Y to only include main effects but the results can be extended to models including interactions. The mediator and outcome models used here are:
The expressions for the natural direct and indirect effects under these simpler models are given by
Now assume that we only observe \(Y_i > t\), i.e. truncation at t. Since truncation of the outcome also leads to missing mediator values we simultaneously estimate the parameters in the mediator and outcome regression models. Assume that \(\eta ^{\dagger }_i\) and \(\xi ^{\dagger }_i\) are bivariate normal with correlation \(\rho\). Then,
where \(\varvec{C}_{3i}=(1,z_i,\varvec{x}_i)'\), \(\varvec{C}_{4i}=(1,z_i,m_i,\varvec{x}_i)'\) and
(See Appendix C for derivation). The joint log-likelihood for the mediator and outcome is given by
By maximizing (12) (for gradients see Appendix D) for \(\rho =0\) we obtain \({\hat{\theta }}^{\dagger }\) and \({\hat{\beta }}^{\dagger }\) under truncation. The relevant parameters can then be plugged into (10) and (11) to obtain estimates of the natural direct and indirect effects. For sensitivity analysis we maximize (12) for non-zero \(\rho =\tilde{\rho }\) to obtain \({\hat{\theta }}^{\dagger }\left( \tilde{\rho }\right)\) and \({\hat{\beta }}^{\dagger }\left( \tilde{\rho }\right)\) and in turn \(\widehat{NDE}_{z_1,z_0}(z,\tilde{\rho })\) and \(\widehat{NIE}_{z_1,z_0}(z,\tilde{\rho })\).
3 Results
3.1 Simulation scenarios and data generation
To demonstrate the performance of the proposed approach a simulation study was performed. For each replicate, observations of an exposure, an outcome, a mediator and an observed confounder affecting the exposure, mediator and outcome were generated (R code is found at by https://github.com/anitalindmark/Sensitivity_analysis).
Five scenarios were investigated (see Table 3 for a summary). In scenarios a, b, d and e the data generating mediator and outcome models contained all interactions involving the exposure and (for the outcome model) mediator. In scenario c where the outcome was truncated data were generated from models containing only main effects.
The regression coefficients used to generate the mediators and outcomes were selected to yield approximately equal effects within each scenario for comparability. For scenarios a, b, d and e the true effects were obtained by using the data generating regression coefficients in the expressions in Table 1. To obtain marginal effects Monte Carlo integration was performed by generating a very large number (\(n = 1\times 10^9\)) of values of the observed covariate, calculating the effects conditional on these values, and averaging the effects. For scenario c the true effects were given by (10) and (11), i.e. by the true regression coefficient for the exposure in the outcome model and the product of the true regression coefficient for the exposure in the mediator model and the true coefficient for the mediator in the outcome model, respectively. True values in all scenarios were \(NIE_{1,0}(1)\approx 0.041\) and \(NDE_{1,0}(0)\approx 0.038\).
In each scenario a–e mediator-outcome confounding was induced by correlating the error terms of the data generating models, with \(\rho =0.5\). For scenarios a, d and e separate simulations with exposure-mediator and exposure-outcome confounding were performed. For these simulations confounding was induced by correlating the error terms in the model used to generate the exposure and the model to generate the mediator and outcome, respectively.
Samples of size \(n_{obs} = 500, 1000, 5000\) were generated 2000 times from each scenario. In each of the 2000 replicates effects and standard errors were estimated based on two values of the sensitivity parameter: \(\tilde{\rho }=0\) (assuming no unobserved confounding) and \(\tilde{\rho }=0.5\) (the true value). The sensmediation package was used for estimation. For censoring and truncation separate functions for the optimization, log-likelihoods and gradients were implemented (code for these are found at https://github.com/anitalindmark/Sensitivity_analysis). Functions from the sensmediation package were then used to calculate the effects and standard errors. The input outcome model for scenario b (censored outcome) was estimated using the tobit function from the AER package (Kleiber and Zeileis 2008, 2020).
3.2 Simulation results
Results were summarized using the rsimsum package (Gasparini 2018) and are presented according to recommendations in Morris et al. (2019). The performance measures used are the bias and empirical coverage rate of 95% CIs over the 2000 replicates. In addition, the SEs of the effects estimated using the delta method are compared to empirical SEs over the 2000 replicates using the relative % error:
where \(\widehat{\text {DeltaSE}}\) is the square root of the average squared delta method SEs over the 2000 replicates and \(\widehat{\text {EmpSE}}\) is the empirical standard error for the 2000 replicates.
As the performance measures from the 2000 replicates are estimates of the true performance measures, simulation uncertainty is taken into account by presenting 95% CIs for the performance measures based on Monte Carlo SEs (Morris et al. 2019). We present the results graphically in lollipop plots (Figs. 3, 4, 5, 67, 8, 9, 10, 11 and 12 in Appendix E), where dots represent the estimated performance measure, with a line from the dot to the target value of that performance measure. The 95% CIs are represented by parentheses and thus parentheses not enclosing the target value indicate evidence that the performance measure does not meet the target.
Results for mediator-outcome confounding and scenarios a-e are summarized in Figs. 3, 4 and 5. For all scenarios, not taking into account unobserved confounding (i.e. using \(\tilde{\rho }=0\)) led to substantial bias (Fig. 3a). Note that since the total effect is not affected by mediator-outcome confounding and is given by summing the natural direct and indirect effects the biases of the \(\widehat{NDE}_{1,0}(0)\) and \(\widehat{NIE}_{1,0}(1)\) arising from unobserved mediator-outcome confounding are of similar sizes but opposite signs, i.e. cancel each other out. The delta method SEs appeared to target the empirical SEs (Fig. 4a) but the large bias resulted in very poor coverage of the 95% CIs (Fig. 5a).
Bias for simulations with mediator-outcome confounding based on 2000 replicates for effects estimated using A: \(\tilde{\rho }=0\) and B: \(\tilde{\rho }=0.5\) . The dotted vertical lines indicate no bias. Black dots indicate bias for \(\widehat{NDE}_{1,0}(0, \tilde{\rho })\) and gray dots bias for \(\widehat{NIE}_{1,0}(1,\tilde{\rho })\). Parentheses represent Monte Carlo 95% CIs. The range of the scale in panel B has been shaded light gray in panel A to facilitate comparisons
Relative % error for simulations with mediator-outcome confounding. Relative % error in delta method standard errors compared to empirical standard errors based on 2000 replicates for effects estimated using A: \(\tilde{\rho }=0\) and B: \(\tilde{\rho }=0.5\). The dotted vertical lines indicate 0% error. Black dots indicate relative % error in delta method SE for \(\widehat{NDE}_{1,0}(0,\tilde{\rho })\) and gray dots relative % error for \(\widehat{NIE}_{1,0}(1,\tilde{\rho })\). Parentheses represent Monte Carlo 95% CIs
Empirical coverage of 95% CIs for simulations with mediator-outcome confounding based on 2000 replicates for effects estimated using A: \(\tilde{\rho }=0\) and B: \(\tilde{\rho }=0.5\). The dotted vertical lines indicate 95% coverage. Black dots indicate coverage for \(\widehat{NDE}_{1,0}(0, \tilde{\rho })\) and gray dots coverage for \(\widehat{NIE}_{1,0}(1, \tilde{\rho })\). Parentheses represent Monte Carlo 95% CIs. The range of the scale in panel B has been shaded light gray in panel A to facilitate comparisons
Bias over the 2000 replicates for scenarios a–e when using the true value \(\tilde{\rho }=0.5\) for estimation of effects is illustrated in Fig. 3b. The bias is generally small, especially for the larger sample sizes, although a slightly larger bias was observed for \(\widehat{NDE}_{1,0}(0,\tilde{\rho }=0.5)\) in scenario c with a sample size of 500. The relative % error in delta method SE shown in Fig. 4b indicates that the delta method SEs generally appear to target empirical SEs. There is a tendency for a slight overestimation by the delta method SE of the \(\widehat{NIE}_{1,0}(1, \tilde{\rho }=0.5)\) for sample sizes \(n_{obs}=500,5000\) in scenario c, truncated outcome. Values of the empirical and delta method SEs are found in Tables S1 and S2 of Online Resource 1. Looking at the empirical coverage of 95% CIs in all scenarios (Fig. 5b) these are generally close to the nominal level.
Results for scenarios a, d and e with unobserved exposure-mediator confounding are found in Figs. 8, 9 and 10 in Appendix E and Tables S3 and S4 in Online Resource 1. Here the sensitivity parameter is the correlation between error terms in the exposure and mediator models, \(\tilde{\rho }_{zm}\). Corresponding results for unobserved exposure-outcome confounding are found in Figs. 11, 12 and 13 in Appendix E and Tables S5 and S6 in Online Resource 1. Here the sensitivity parameter is the correlation between error terms in the exposure and outcome models, \(\tilde{\rho }_{zy}\). We see similar results as in the simulations with unobserved mediator-outcome confounding, with small bias when using the correct correlation value (Figs. 8b and 11b) and empirical coverage of 95% CIs generally close to the nominal level (Figs. 10b and 13b). A notable difference is that unobserved exposure-mediator confounding leads to large bias for \(\widehat{NIE}_{1,0}(1,\tilde{\rho }_{zm}=0)\) but small bias for \(\widehat{NDE}_{1,0}(0, \tilde{\rho }_{zm}=0)\) and conversely unobserved exposure-outcome confounding leads to large bias for \(\widehat{NDE}_{1,0}(0,\tilde{\rho }_{zy}=0)\) but small bias for \(\widehat{NIE}_{1,0}(1,\tilde{\rho }_{zy}=0)\).
3.3 Empirical example
To illustrate the method we use the publicly available data set UPBdata from the R package medflex (Steen et al. 2020). The data were used to illustrate functions in the medflex package in Steen et al. (2017) and are a subsample of 385 individuals that participated in a survey study as part of the Interdisciplinary Project for the Optimization of Separation trajectories (Ghent University and Catholic University of Louvain 2010). The individuals had divorced between March 2008 and March 2009 and were asked to respond to various questionnaires related to romantic relationship and breakup characteristics (De Smet et al. 2012).
Following the example in Steen et al. (2017) we look at the relationship between attachment style towards the ex-partner prior to the breakup and unwanted pursuit behaviors (UPBs) towards the ex-partner after the breakup and the extent to which this is mediated by level of emotional distress experienced during the breakup. A binary exposure is used, indicating whether or not the individual’s self-reported anxious attachment level was higher than the sample mean. The outcome is whether or not the individual reported that they had displayed UPBs towards their ex-partner after the breakup. The mediator is standardized self-reported experienced level of negative affectivity (emotional distress) during the breakup, a continuous variable. We adjust for age, highest attained education level (high, intermediate, low) and gender (male, female). The hypothesized relationships between the variables are illustrated in Fig. 6. All analyses are performed using the sensmediation package (Lindmark 2019), code found at https://github.com/anitalindmark/Sensitivity_analysis.
We begin with estimation of the natural direct and indirect effects assuming no unmeasured confounding and then proceed with sensitivity analyses to the three types of unmeasured confounding.
Since we have a continuous mediator and a binary outcome the analyses are based on models (3) and (6) and the corresponding estimators from Table 1. In this example we investigate effect modification (moderation) by gender. To this end we include an interaction between the exposure and gender in the model for the mediator (Table S7 of Online Resource 1) as well as interactions between gender and both exposure and mediator in the outcome model (Table S8 of Online Resource 1). An interaction term between exposure and mediator is also included in the outcome model, as recommended by VanderWeele (2015) to fully capture the dynamics of mediation.
Estimated effects averaged over all observed confounders (marginal effects) as well as conditional on male and female gender are presented in Table 4. Looking at the estimated total effects we see that anxious attachment increases the risk of UPBs both marginally and conditional on gender, with a larger effect for men than for women. Over half of this total effect is an indirect effect of anxious attachment on UPBs operating through negative affectivity, with a slightly larger proportion for males than for females.
To gauge the effect of possible unobserved confounding on the results we perform sensitivity analyses. Here we choose to focus on the natural indirect effect, which was statistically significant in the original analysis. We present results for all three types of confounding, with sensitivity parameters ranging from − 0.9 to 0.9 in increments of 0.1. Plots of point estimates of the marginal natural indirect effect with corresponding CIs over the range of the sensitivity parameters are presented in Fig. 7. For both mediator-outcome confounding (Fig. 7a) and exposure-mediator confounding (Fig. 7b) the overall pattern is that the natural indirect effect decreases over the range of the sensitivity parameter. If additional adjustment were made for a confounder inducing an error term correlation (\(\tilde{\rho }\) or \(\tilde{\rho }_{zm}\)) of 0.3 or higher the CIs of the effect would include 0 and additional adjustment for a confounder inducing a \(\tilde{\rho }\) of at least 0.6 or a \(\tilde{\rho }_{zm}\) of at least 0.5 would lead to CIs entirely below 0. The natural indirect effect is not sensitive to unobserved exposure-outcome confounding (Fig. 7c). Note that as the exposure and outcome are both binary the sensitivity analyses to exposure-outcome confounding were performed using methods presented in Lindmark et al. (2018).
Results of sensitivity analyses. A: Unobserved negative affectivity (mediator)-UPBs (outcome) confounding. B: Unobserved anxious attachment (exposure)-negative affectivity (mediator) confounding. C: Unobserved anxious attachment (exposure)-UPBs (outcome) confounding. Solid lines correspond to point estimates and shaded areas to 95% CIs
The results in Fig. 7 are summarized in Table 5 which also shows the 95% UIs over the range of the sensitivity parameter. Corresponding results for men and women are also shown, indicating similar results as those seen for the marginal effect. For exposure-outcome confounding the lower bounds of the 95% UIs over the range of the sensitivity parameter all lie above 0, indicating that the effects are not sensitive to unobserved exposure-outcome confounding.
4 Discussion
In this paper we have extended results from Lindmark et al. (2018) to provide methods for sensitivity analysis of unobserved confounding in mediation analysis for combinations of continuous and binary mediators and outcomes, as well as for censored or truncated outcomes. Where previous methods focus exclusively on mediator-outcome confounding (VanderWeele 2010; Imai et al. 2010a; Hafeman 2011; le Cessie 2016), this approach is flexible due to the ability to take into account not only mediator-outcome confounding but also exposure-mediator and exposure-outcome confounding. The latter two are of particular importance in observational studies, where the exposure has not been randomized, due to the difficulty in guaranteeing that all relevant confounders have been adjusted for. It also has the advantage that sensitivity analyses can be performed also in the presence of interactions involving the exposure, mediator and covariates, allowing more complicated models and facilitating sensitivity analyses also when the interest lies in exploration of effect modification.
We performed simulations that showed that the method targets the true effects when the error term correlation induced by unobserved confounding is taken into account in the estimation. Generally this illustrates that the method does indeed capture the effect that would have been observed under a given level of correlation. In reality this correlation will be unknown to the researcher and therefore further simulation studies investigating, e.g. the performance of UIs based on a range of correlation levels is of interest.
The method has some limitations that should be subjects for future development. One such limitation is the reliance on the specification of parametric regression models with distributional assumptions on the error terms. The results may therefore be sensitive to model misspecification and the nature of this sensitivity should be subject to further study. On the other hand, since the method allows inclusion of interactions involving the exposure, mediator and covariates, rich parametric models can be specified which can reduce the risk of model misspecification bias. This under the condition that the data allow such a specification and are large enough to lessen the impact of the increase in variance. In any case, further developments utilizing either semi-parametric techniques (Tchetgen Tchetgen and Shpitser 2012; Huber 2014) or retaining parametric regression models but relaxing the multivariate normality assumption of the error terms upon which the method introduced here relies are warranted.
The issue of model misspecification is even more important for the proposed methods for censoring or truncation since maximum likelihood estimators for regression parameters when the outcome is censored or truncated have been shown to be sensitive to violations of distributional assumptions (Vijverberg 1987). Semi-parametric estimators that impose fewer assumptions on the error term have been developed both for censoring, e.g. Powell (1986), and truncation, e.g. Powell (1986); Lee (1993); Laitila (2001). Further research into the usefulness of such models in the context of mediation is of interest.
For the cases with a censored/truncated outcome and a continuous mediator we have presented results for sensitivity analyses to mediator-outcome confounding only. Since we assume that only the outcome is censored, not the exposure or mediator, a sensitivity analysis to exposure-mediator confounding is straight-forward and can be performed using the methods presented in Sect. 2.2.1. For a truncated outcome this would be more complicated since truncation of the outcome means that values will be missing for the exposure and mediator as well, which would need to be taken into account. For exposure-outcome confounding and a censored outcome, if the exposure is continuous and can be modeled with a linear regression model a sensitivity analysis could be performed by replacing the mediator model with the exposure model in the joint log-likelihood. The situation is again less straight-forward for truncation where the joint exposure-outcome distribution would need to be derived.
The methods presented in this paper evaluate sensitivity to each type of unobserved confounding separately, assuming that the other two kinds are not present. Extending the method to investigate sensitivity to all three types of confounding simultaneously is therefore of interest.
In this paper we present results for natural direct and indirect effects on the mean difference scale. Adapting the methods to other scales is of interest, in particular for cases with a binary outcome where the researchers may be interested in effects on the risk ratio or odds ratio scales (VanderWeele and Vansteelandt 2010; Valeri and VanderWeele 2013; Doretti et al. 2021).
Finally, it is important to note that the natural direct and indirect effects are not identified when the cross-world assumption introduced in Sect. 2.1 is violated. Such violations include the presence of mediator-outcome confounders that are affected by the exposure, regardless of whether these are observed or not. In such cases we either need to make additional parametric assumptions (Robins and Greenland 1992; Petersen et al. 2006; De Stavola et al. 2015) or use different effect definitions, e.g. so called interventional direct and indirect effects (see e.g. VanderWeele et al. 2014; Lok 2016).
To summarize, we have provided sensitivity analysis methods for unobserved confounding that are useful when performing parametric estimation of natural direct and indirect effects even when more complex models including interactions involving the exposure and/or mediator are used. With further developments these methods can be made even more flexible.
Data availability
The empirical example is based on the publicly available dataset UPBdata available through the R package medflex (https://cran.r-project.org/package=medflex).
Code availability
R code for the simulations and the analyses in the empirical example is available from https://github.com/anitalindmark/Sensitivity_analysis.
References
De Smet O, Loeys T, Buysse A (2012) Post-breakup unwanted pursuit: a refined analysis of the role of romantic relationship characteristics. J Fam Violence 27(5):437–452
De Stavola BL, Daniel RM, Ploubidis GB, Micali N (2015) Mediation analysis with intermediate confounding: structural equation modeling viewed through the causal inference lens. Am J Epidemiol 181(1):64–80
Doretti M, Raggi M, Stanghellini E (2021) Exact parametric causal mediation analysis for a binary outcome with a binary mediator. Stat Methods Appt. https://doi.org/10.1007/s10260-021-00562-w
Gasparini A (2018) Rsimsum: Summarise results from monte carlo simulation studies. J Open Source Softw 3(26):739. https://doi.org/10.21105/joss.00739
Genbäck M, Stanghellini E, de Luna X (2015) Uncertainty intervals for regression parameters with non-ignorable missingness in the outcome. Stat Pap 56(3):829–847
Genbäck M, Ng N, Stanghellini E, de Luna X (2018) Predictors of decline in self-reported health: addressing non-ignorable dropout in longitudinal studies of aging. Eur J Ageing 15(2):211–220. https://doi.org/10.1007/s10433-017-0448-x
Ghent University and Catholic University of Louvain (2010) Interdisciplinary project for the optimisation of separation trajectories - divorce and separation in Flanders. http://www.scheidingsonderzoek.ugent.be/index-eng.html
Hafeman D (2011) Confounding of indirect effects: a sensitivity analysis exploring the range of bias due to a cause common to both the mediator and the outcome. Am J Epidemiol 174(6):710–717
Hausman JA, Wise DA (1977) Social experimentation, truncated distributions, and efficient estimation. Econometrica 45(4):919–938
Henningsen A, Toomet O (2011) maxlik: a package for maximum likelihood estimation in R. Comput Stat 26(3):443–458. https://doi.org/10.1007/s00180-010-0217-1
Huber M (2014) Identifying causal mechanisms (primarily) based on inverse probability weighting. J Appl Econ (Chichester Engl) 29(6):920–943
Imai K, Keele L, Tingley D (2010a) A general approach to causal mediation analysis. Psychol Methods 15(4):309–334
Imai K, Keele L, Yamamoto T (2010b) Identification, inference and sensitivity analysis for causal mediation effects. Stat Sci 25(1):51–71
Kleiber C, Zeileis A (2008) Applied econometrics with R. Springer, New York
Kleiber C, Zeileis A (2020) AER: applied econometrics with R. https://cran.r-project.org/package=AER, R package version 1.2-9
Laitila T (2001) Properties of the QME under asymmetrically distributed disturbances. Stat Probab Lett 52(4):347–352
Lange T, Hansen JV (2011) Direct and indirect effects in a survival context. Epidemiology 22(4):575–581. https://doi.org/10.1097/ede.0b013e31821c680c
le Cessie S (2016) Bias formulas for estimating direct and indirect effects when unmeasured confounding is present. Epidemiology 27(1):125–132
Lee M (1993) Quadratic mode regression. J Econom 57(1):1–19
Lindmark A (2019) sensmediation: Parametric estimation and sensitivity analysis of direct and indirect effects. http://cran.R-project.org/package=sensmediation, R package version 0.3.0
Lindmark A, de Luna X, Eriksson M (2018) Sensitivity analysis for unobserved confounding of direct and indirect effects using uncertainty intervals. Stat Med 37(10):1744–1762. https://doi.org/10.1002/sim.7620
Lok JJ (2016) Defining and estimating causal direct and indirect effects when setting the mediator to specific values is not feasible. Stat Med 35(22):4008–4020. https://doi.org/10.1002/sim.6990
Morris TP, White IR, Crowther MJ (2019) Using simulation studies to evaluate statistical methods. Stat Med 38(11):2074–2102. https://doi.org/10.1002/sim.8086
Oehlert GW (1992) A note on the delta method. Am Stat 46:27–29. https://doi.org/10.2307/2684406
Pearl J (2001) Direct and indirect effects. In: Proceedings of the 17th conference in uncertainty in artificial intelligence. Morgan Kaufmann Publishers Inc., San Francisco, CA, pp 411–420
Petersen ML, Sinisi SE, van der Laan MJ (2006) Estimation of direct causal effects. Epidemiology 17(3):276–284
Powell J (1986) Symmetrically trimmed least squares estimation for tobit models. Econometrica 54(6):1435–1460
R Core Team (2017) R: a language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria https://www.R-project.org
Robins JM, Greenland S (1992) Identifiability and exchangeability for direct and indirect effects. Epidemiology 3(2):143–155
Rosenbaum PR (2010) Design of observational studies, 1st edn. Springer, New York
Steen J, Loeys T, Moerkerke B, Vansteelandt S (2017) medflex: an R package for flexible mediation analysis using natural effect models. J Stat Softw 76(11)
Steen J, Loeys T, Moerkerke B, Vansteelandt S (2020) medflex: flexible mediation analysis using natural effect models. R package version 0.6-7. http://CRAN.R-project.org/package=medflex
Tchetgen Tchetgen EJ (2011) On causal mediation analysis with a survival outcome. Int J Biostat 7(1):1–38. https://doi.org/10.2202/1557-4679.1351
Tchetgen Tchetgen EJ, Shpitser I (2012) Semiparametric theory for causal mediation analysis: efficiency bounds, multiple robustness and sensitivity analysis. Ann Stat 40(3):1816–1845
Tingley D, Yamamoto T, Hirose K, Keele L, Imai K (2014) mediation: R package for causal mediation analysis. J Stat Softw 59(5):1–38
Tingley D, Yamamoto T, Hirose K, Keele L, Imai K (2019) mediation: R package for causal mediation analysis. http://CRAN.R-project.org/package=mediation, R package version 4.5.0\
Tobin J (1958) Estimation of relationships for limited dependent variables. Econometrica 26(1):24–36
Toomet O, Henningsen A (2015) maxlik: maximum likelihood estimation and related tools. R package version. http://CRAN.R-project.org/package=maxLik, R package version 1.3–4
Valeri L, VanderWeele TJ (2013) Mediation analysis allowing for exposure-mediator interactions and causal interpretation: theoretical assumptions and implementation with SAS and SPSS macros. Psychol Methods 18(2):137–150
VanderWeele TJ (2010) Bias formulas for sensitivity analysis for direct and indirect effects. Epidemiology 21(4):540–551
VanderWeele TJ (2011) Causal mediation analysis with survival data. Epidemiology 22(4):582–585. https://doi.org/10.1097/ede.0b013e31821db37e
VanderWeele TJ (2013) Unmeasured confounding and hazard scales: sensitivity analysis for total, direct, and indirect effects. Eur J Epidemiol 28(2):113–117. https://doi.org/10.1007/s10654-013-9770-6
VanderWeele TJ (2015) Explanation in causal inference: methods for mediation and interaction, 1st edn. Oxford University Press, New York
VanderWeele TJ, Vansteelandt S (2009) Conceptual issues concerning mediation, interventions and composition. Stat Interface 2(4):457–468
VanderWeele TJ, Vansteelandt S (2010) Odds ratios for mediation analysis for a dichotomous outcome. Am J Epidemiol 172(12):1339–1348
VanderWeele TJ, Vansteelandt S, Robins JM (2014) Effect decomposition in the presence of an exposure-induced mediator-outcome confounder. Epidemiology 25(2):300–306. https://doi.org/10.1097/ede.0000000000000034
Vansteelandt S, Goetghebeur E, Kenward MG, Molenberghs G (2006) Ignorance and uncertainty regions as inferential tools in a sensitivity analysis. Stat Sin 16(3):953–979
Vijverberg WPM (1987) Non-normality as distributional misspecification in single-equation limited dependent variable models. Oxf Bull Econ Stat 49(4):417–430
Wang L, Zhang Z (2011) Estimating and testing mediation effects with censored data. Struct Equ Modeling 18(1):18–34. https://doi.org/10.1080/10705511.2011.534324
Acknowledgements
The author is grateful to Xavier de Luna for input on earlier versions of the paper and to the two anonymous referees for their helpful comments and suggestions. This research was supported by FORTE (Swedish Research Council for Health, Working Life and Welfare, Grant 2018-00852) and the Swedish Research Council (Grant 2018-02670).
Funding
Open access funding provided by Umea University. The study was funded by FORTE (Swedish Research Council for Health, Working Life and Welfare, grant 2018-00852) and the Swedish Research Council (grant 2018-02670).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
None declared.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A Derivation of the joint distribution of \(\mathbf{M}\) and \(\mathbf{Y}\) under a binary probit mediator model (4) and a linear outcome model (5)
To obtain the joint distribution of \(M_i, Y_i\) given \(Z_i,\varvec{X}_i\), with \(M_i\) following model (4) and \(Y_i\) following model (5) we see that:
where the final equality follows from \((\eta ^*_i,\xi _{i})'\sim N\left( \left[ \begin{array}{c} 0 \\ 0 \end{array}\right] ,\left[ \begin{array}{cc} 1 &{} \rho \sigma _{\xi }\\ \rho \sigma _{\xi }&{} \sigma _{\xi }^2 \end{array}\right] \right)\), so that
\(\eta ^*_i|\left( \xi _{i}=y_i-\varvec{\theta }'\varvec{C}_{2i}\right) \sim N\left( \dfrac{\rho }{\sigma _{\xi }}(y_i-\varvec{\theta }'\varvec{C}_{2i}),1-\rho ^2\right)\).
Using the same reasoning we have
and finally the joint distribution
Appendix B Gradients of the joint log-likelihood, censored outcome (7)
Let \(C=\frac{t-\varvec{\theta }'\varvec{C}_{2i}-\frac{\sigma _{\xi }}{\sigma _{\eta }}\rho (m_i-\varvec{\beta }'\varvec{C}_{1i})}{\sigma _{\xi }\sqrt{1-\rho ^2}}\). Then,
Appendix C Derivation of \(\mathbf{P} \left( \mathbf{Y} _\mathbf{i} > \mathbf{t} \right)\), the probability of being included in the sample
Assume that \(M_i\) and \(Y_i\) can be modeled with (8) and (9) and that only \(Y_i > t\) are observed. We have that \(P\left( Y_i> t\right) =1-P\left( Y_i\leqslant t\right) =1-P\left( \xi _i\leqslant t-\varvec{\theta }^{\dagger \prime }\varvec{C}_{4i}\right)\), and
where in the second equality we replace \(M_i\) with \(\varvec{\beta }^{\dagger \prime }\varvec{C}_{3i}+\eta ^{\dagger }_i\), thus incorporating the regression parameters of the mediator model in the part of the distribution that takes truncation into account (similarly to the suggestion of Hausman and Wise (1977) for a two equation model). Since \(\xi ^{\dagger }_i+\theta ^{\dagger }_2\eta ^{\dagger }_i{\mathop {\sim }\limits ^{i.i.d.}} N(0,\sigma _{\xi ^{\dagger }}^2+\theta _2^{\dagger 2}\sigma _{\eta ^{\dagger }}^2+2\theta ^{\dagger }_2\rho \sigma _{\xi ^{\dagger }}\sigma _{\eta ^{\dagger }})\) we have that
Appendix D Gradients of the joint log-likelihood, truncated outcome (12)
Let \(\varvec{\theta }^{\dagger }_{\backslash 2}=(\theta ^{\dagger }_0,\theta ^{\dagger }_1,\varvec{\theta }^{\dagger \prime }_4)'\), and \(D=\frac{t-\left( \theta ^{\dagger }_0+\theta ^{\dagger }_1z_i + \theta ^{\dagger }_2\varvec{\beta }^{\dagger \prime }\varvec{C}_{3i} + \varvec{\theta }^{\dagger \prime }_4\varvec{x}_i\right) }{\sqrt{\sigma _{\xi ^{\dagger }}^2+\theta _2^{\dagger 2}\sigma _{\eta ^{\dagger }}^2+2\theta ^{\dagger }_2\rho \sigma _{\xi ^{\dagger }}\sigma _{\eta ^{\dagger }}}}\). Then,
Appendix E Simulation results exposure-mediator and exposure outcome confounding
Bias for simulations with exposure-mediator confounding based on 2000 replicates for effects estimated using A: \(\tilde{\rho }_{zm}=0\) and B: \(\tilde{\rho }_{zm}=0.5\). The dotted vertical lines indicate no bias. Black dots indicate bias for \(\widehat{NDE}_{1,0}(0,\tilde{\rho }_{zm})\) and gray dots bias for \(\widehat{NIE}_{1,0}(1,\tilde{\rho }_{zm})\). Parentheses represent Monte Carlo 95% CIs. The range of the scale in panel B has been shaded light gray in panel A to facilitate comparisons
Relative % error for simulations with exposure-mediator confounding. Relative % error in delta method standard errors compared to empirical standard errors based on 2000 replicates for effects estimated using A: \(\tilde{\rho }_{zm}=0\) and B: \(\tilde{\rho }_{zm}=0.5\). The dotted vertical lines indicate 0% error. Black dots indicate relative % error in delta method SE for \(\widehat{NDE}_{1,0}(0, \tilde{\rho }_{zm})\) and gray dots relative % error for \(\widehat{NIE}_{1,0}(1, \tilde{\rho }_{zm})\). Parentheses represent Monte Carlo 95% CIs
Empirical coverage of 95% CIs for simulations with exposure-mediator confounding based on 2000 replicates for effects estimated using A: \(\tilde{\rho }_{zm}=0\) and B: \(\tilde{\rho }_{zm}=0.5\). The dotted vertical lines indicate 95% coverage. Black dots indicate coverage for \(\widehat{NDE}_{1,0}(0, \tilde{\rho }_{zm})\) and gray dots coverage for \(\widehat{NIE}_{1,0}(1, \tilde{\rho }_{zm})\). Parentheses represent Monte Carlo 95% CIs. The range of the scale in panel B has been shaded light gray in panel A to facilitate comparisons
Bias for simulations with exposure-outcome confounding based on 2000 replicates for effects estimated using A: \(\tilde{\rho }_{zy}=0\) and B: \(\tilde{\rho }_{zy}=0.5\). The dotted vertical lines indicate no bias. Black dots indicate bias for \(\widehat{NDE}_{1,0}(0,\tilde{\rho }_{zy})\) and gray dots bias for \(\widehat{NIE}_{1,0}(1,\tilde{\rho }_{zy})\). Parentheses represent Monte Carlo 95% CIs. The range of the scale in panel B has been shaded light gray in panel A to facilitate comparisons
Relative % error for simulations with exposure-outcome confounding. Relative % error in delta method standard errors compared to empirical standard errors based on 2000 replicates for effects estimated using A: \(\tilde{\rho }_{zy}=0\) and B: \(\tilde{\rho }_{zy}=0.5\). The dotted vertical lines indicate 0% error. Black dots indicate relative % error in delta method SE for \(\widehat{NDE}_{1,0}(0,\tilde{\rho }_{zy})\) and gray dots relative % error for \(\widehat{NIE}_{1,0}(1,\tilde{\rho }_{zy})\). Parentheses represent Monte Carlo 95% CIs
Empirical coverage of 95% CIs for simulations with exposure-outcome confounding based on 2000 replicates for effects estimated using A: \(\tilde{\rho }_{zy}=0\) and B: \(\tilde{\rho }_{zy}=0.5\). The dotted vertical lines indicate 95% coverage. Black dots indicate coverage for \(\widehat{NDE}_{1,0}(0,\tilde{\rho }_{zy})\) and gray dots coverage for \(\widehat{NIE}_{1,0}(1,\tilde{\rho }_{zy})\). Parentheses represent Monte Carlo 95% CIs. The range of the scale in panel B has been shaded light gray in panel A to facilitate comparisons
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Lindmark, A. Sensitivity analysis for unobserved confounding in causal mediation analysis allowing for effect modification, censoring and truncation. Stat Methods Appl 31, 785–814 (2022). https://doi.org/10.1007/s10260-021-00611-4
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10260-021-00611-4






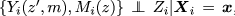 i.e., there is no unobserved confounding of the exposure-mediator and exposure-outcome relationship given the observed pre-exposure covariates
i.e., there is no unobserved confounding of the exposure-mediator and exposure-outcome relationship given the observed pre-exposure covariates  i.e., given
i.e., given 










