Nonlinear large deformation of a spherical red blood cell induced by ultrasonic standing wave

Abstract

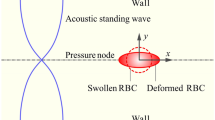
A computational model is developed to investigate the nonlinear static deformation of a spherical (osmotically swollen) red blood cell (RBC) induced by ultrasonic standing wave. The ultrasonic standing wave can generate steady acoustic radiation stress to deform the cell, and in turn, the deformed cell reshapes the acoustic field. This is a real-time coupling problem between the acoustic field and the mechanical field. In the computational model, the acoustic radiation stress acting on the RBC membrane is modeled by adopting the nonviscous momentum flux theory. The RBC membrane is modeled as a hyperelastic shell considering the in-plane elasticity, bending elasticity, and surface tension of the membrane. The volume conservation constraint of the membrane sealing fluid is applied to ensure the osmotic balance of the membrane. To address this real-time coupling problem, the computational model is implemented by a finite element method algorithm. The numerical results are compared with the existing theoretical model and experimental data, and the strain hardening trend of the experimental data is successfully predicted, which verifies the accuracy and effectiveness of the computational model. The computational model can accurately extract the mechanical properties of cells from acoustic deformation experiments, which is helpful for the diagnosis of some human diseases.

Appendix: Numerical model for calculating the energy minimization shape of lipid membrane

According to Sect. 3, the weak form equations for the evolution velocity and curvature tensor, $\left( {{\mathbf{v}},{\mathbf{b}}} \right)$, of the lipid membrane are given by

$$ \oint_{S\left( \tau \right)} {\left[ { - \gamma {\mathbf{v}} \cdot \delta {\mathbf{v}} - 2E_{b} \left( {h^{2} {\mathbf{i}}_{s} - h{\mathbf{b}} - {\mathbf{n}} \otimes \nabla_{s} h} \right):\nabla_{s} \delta {\mathbf{v}} - \sigma {\mathbf{i}}_{s} :\nabla_{s} \delta {\mathbf{v}} + \Delta p{\mathbf{n}} \cdot \delta {\mathbf{v}}} \right]{\text{d}}a} = 0 $$

(41)

$$ \oint_{S\left( \tau \right)} {\left[ {{\mathbf{b}}:\delta {\mathbf{b}} - \left( {\nabla_{s} \delta {\mathbf{b}}:{\mathbf{i}}_{s} } \right) \cdot {\mathbf{n}} - \left( {{\mathbf{b}}:{\mathbf{i}}_{s} } \right){\mathbf{n}} \otimes {\mathbf{n}}:\delta {\mathbf{b}}} \right]{\text{d}}a} = 0 $$

(42)

Here, $\left( {\delta {\mathbf{v}},\delta {\mathbf{b}}} \right)$ are the test functions of $\left( {{\mathbf{v}},{\mathbf{b}}} \right)$. $\left( {\sigma ,\Delta p} \right)$ are two Lagrange multipliers to enforce the following area and volume constraints. The surface tension $\sigma$ is now used as a Lagrange multiplier to enforce the surface area retention constraint

$$ \overline{A} - A = 0 $$

(43)

Here, $\overline{A}$ is the desired surface area, which is considered to be consistent with the reference surface area, and $A$ is the current surface area. Formally, they are given by

$$ \overline{A} = \oint_{{S_{0} }} {1{\text{d}}A} \;{\text{and}}\;A = \oint_{S\left( \tau \right)} {1{\text{d}}a} $$

(44)

The pressure jump $\Delta p$ is now used as a Lagrange multiplier to enforce the volume controller

$$ \frac{{{\text{d}}V}}{{{\text{d}}\tau }} = \frac{{\overline{V} - V}}{{\tau_{V} }} $$

(45)

The controller drives the current volume $V$ to the desired volume $\overline{V}$ in a characteristic time $\tau_{V}$. $\overline{V}$ is derived from $\overline{A}$ according to the reduced volume $v$ as

$$ \overline{V} = \frac{{v\overline{A}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-\nulldelimiterspace} 2}}} }}{{6{\uppi }^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}} }} $$

(46)

$V$ and its time derivative ${{{\text{d}}V} \mathord{\left/ {\vphantom {{{\text{d}}V} {{\text{d}}\tau }}} \right. \kern-\nulldelimiterspace} {{\text{d}}\tau }}$ are given by

$$ V = \frac{1}{3}\oint_{S} {{\mathbf{x}} \cdot {\mathbf{n}}{\text{d}}v} \;{\text{and}}\;\frac{{{\text{d}}V}}{{{\text{d}}\tau }} = \oint_{S\left( \tau \right)} {{\mathbf{v}} \cdot {\mathbf{n}}{\text{d}}a} $$

(47)

The parameters are set as: $E_{b} = 1\;{\text{N/m}}$, $\tau_{V} = 1{\text{s}}$, $a_{0} = 1\;{\text{m}}$ and $\gamma = 1\;{\text{Pa}} \cdot {\text{s}} \cdot {\text{m}}^{ - 1}$. The overall computational algorithm is similar to that described in Sect. 3 and Fig. 6: the acoustic module is de-activated, and the mechanical module is replaced with weak form equations (41)–(47) to solve the unknown field variables $\left( {{\mathbf{v}},{\mathbf{b}}} \right)$ and global variables $\left( {\sigma ,\Delta p} \right)$, while maintaining the moving mesh module. Taking reduced volume $v = 0.58$ as an example, Fig. 

Fig. 15

The energy minimum shapes calculated from different initial shapes at reduce volume $v = 0.58$: a the oblate spheroid with a/b = 1.5 and b the prolate spheroid with a/b = 0.44. For both cases, the membrane surface is discretized by 96 line elements. Note that the “moving mesh” module in COMSOL is not only supported in the boundary, so the computational domain of the moving mesh is extended to the internal domain defined by the membrane

15 shows the energy minimum shapes calculated from different initial shapes: (a) an oblate spheroid with three semi-axes $\left( {1.5a_{0} ,1.5a_{0} ,a_{0} } \right)$ and (b) a prolate spheroid with three semi-axes $\left( {2.25a_{0} ,a_{0} ,a_{0} } \right)$. It is observed that the initial oblate shape leads to a biconcave energy minimum shape, while the initial prolate shape leads to a peanut-shaped one.