Coupled acoustic-shell model for experimental study of cell stiffness under acoustophoresis

Abstract

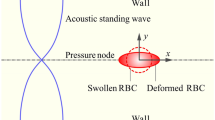
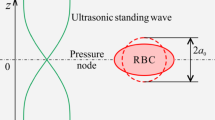
Under the influence of acoustic radiation force, particles can be trapped and deformed at the pressure node in a microfluidic channel. Based on this principle, the elastic modulus of biological cells can be estimated. In this study, a numerical framework, consisting of a boundary element model for acoustic field and an axisymmetric shell model, is developed to simulate the cell deformation under acoustic radiation force. The boundary element model is used to calculate the radiation traction exerted on the cell surface. The cell membrane deformation due to this traction is simulated by using the axisymmetric shell model. The Young’s moduli of algae and red blood cell membranes are then estimated by comparing the experimental observation with the simulated membrane deformation. It is found that the value of Young’s modulus of the red blood cell membrane is lower than that of algae cell membrane. Furthermore, for both cells, the estimated Young’s moduli are negligible compared to the bulk moduli of the cells reported in the previous studies.

Appendix

As discussed in Sect. 2.1, for each acoustic domain, a system of equations that is similar to Eq. (6) can be formulated. For the exterior domain, the system of equations is given by

$$\begin{aligned} ({\mathbf C} ^-+\,{\mathbf H} ^-_{0})\left\{ \phi _{\mathrm{sc}}\right\} = {\mathbf G} _{0}\left\{ \dfrac{\partial \phi _{\mathrm{sc}}}{\partial n^-}\right\} \end{aligned}$$

(35)

It is noted that ${\mathbf H} ^-_{0}$ and ${\mathbf G} _{0}$ are evaluated by using Eqs. (7) and (8) based on $k_0$ and ${\mathbf n} ^-$. Matrix ${\mathbf C} ^-$ is a diagonal matrix that contains the solid angles of the surface elements with respect to the exterior domain. Similarly, for the interior domain, the system of equations is given by

$$\begin{aligned} ({\mathbf C} ^++\,{\mathbf H} ^+_{i})\left\{ \phi _{i}\right\} = {\mathbf G} _{i}\left\{ \dfrac{\partial \phi _{i}}{\partial n^+}\right\} \end{aligned}$$

(36)

where ${\mathbf C} ^+$ is the diagonal matrix that contains the solid angles of the surface elements with respect to the interior domain. It is noted that the incident wave potential $\phi _{\mathrm{in}}$ satisfies the boundary integral equation for the interior domain if $k_i = k_0$. Hence, the following system of equations can be formulated.

$$\begin{aligned} ({\mathbf C} ^++\,{\mathbf H} ^+_{0})\left\{ \phi _{\mathrm{in}}\right\} = {\mathbf G} _{0}\left\{ \dfrac{\partial \phi _{\mathrm{in}}}{\partial n^+} \right\} \end{aligned}$$

(37)

By substituting Eqs. (9), (37) and (10)–(36), we obtain

$$\begin{aligned} \left( \dfrac{\rho _{0}}{\rho _{i}}\right) ({\mathbf C} ^++\,{\mathbf H} ^+_{i}) \lbrace \phi _{\mathrm{sc}}\rbrace + {\mathbf G} _{i}\left\{ \dfrac{\partial \phi _{\mathrm{sc}}}{\partial n^-}\right\} = \left( \dfrac{\rho _{0}}{\rho _{i}}\right) \left( {\mathbf H} ^+_{0}-{\mathbf H} ^+_{i}\right) \lbrace \phi _{\mathrm{in}}\rbrace + \left( {\mathbf G} _{i} - \left( \dfrac{\rho _{0}}{\rho _{i}}\right) {\mathbf G} _{0}\right) \left\{ \dfrac{\partial \phi _{\mathrm{in}}}{\partial n^+}\right\} \end{aligned}$$

(38)

In the limit of $\dfrac{\rho _{0}}{\rho _{i}}\rightarrow 0$, Eq. (38) reduces to

$$\begin{aligned} \dfrac{\partial \phi _{\mathrm{in}}}{\partial n^+}+\dfrac{\partial \phi _{\mathrm{sc}}}{\partial n^+}=0 \end{aligned}$$

(39)

which is the boundary condition for a rigid immovable particle. The final system of equations, Eq. (11), is given by the combination of Eqs. (35) and (38).