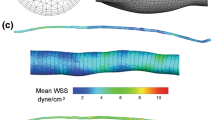
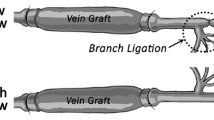
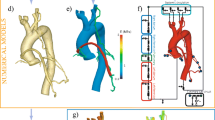
Abstract
Although vein bypass grafting is one of the primary options for the treatment of arterial occlusive disease and provides satisfactory results at an early stage of the treatment, the patency is limited to a few months in many patients. When the vein is implanted in the arterial system, it adapts to the high flow rate and high pressure of the arterial environment by changing the sizes of its layers, and this remodeling is believed to be a precursor of future graft failure. Hemodynamic forces, such as wall shear stress (WSS) and wall tension, have been recognized as major factors impacting vein graft remodeling. Although a wide range of experimental evidence relating hemodynamic forces to vein graft remodeling has been reported, a comprehensive mathematical model describing the relationship among WSS, wall tension, and the structural adaptation of each individual layer of the vein graft wall is lacking. The current manuscript presents a comprehensive and robust framework for treating the complex interaction between the WSS, wall tension, and the structural adaptation of each individual layer of the vein graft wall. We modeled the intimal and medial area and the radius of external elastic lamina, which in combination dictate luminal narrowing and the propensity for graft occlusion. Central to our model is a logistic relationship between independent and dependent variables to describe the initial increase and later decrease in the growth rate. The detailed understanding of the temporal changes in vein graft morphology that can be extracted from the current model is critical in identifying the dominant contributions to vein graft failure and the further development of strategies to improve their longevity.
Article PDF
Similar content being viewed by others
Avoid common mistakes on your manuscript.
References
Alford PW, Humphrey JD, Taber LA (2008) Growth and remodeling in a thick-walled artery model: effects of spatial variations in wall constituents. Biomech Model Mechanobiol 7: 245–262
Berguer R, Higgins RF, Reddy DJ (1980) Intimal hyperplasia. Arch Surg 115: 332–335
Bhardwaj S, Roy H, Ylä-Herttuala S (2008) Gene therapy to prevent occlusion of venous bypass grafts. Expert Rev Cardiovasc Ther 6: 641–652
Britton NF (2003) Essential mathematical biology. Springer, London
Budu-Grajdeanu P, Schugart RC, Friedman A, Valentine C, Agarwal AK, Rovin BH (2008) A mathematical model of venous neointimal hyperplasia formation. Theor Biol Med Model 5: 2
Conte MS, Bandyk DF, Clowes AW, Moneta GL, Seely L, Lorenz TJ, Namini H, Hamdan AD, Roddy SP, Belkin M, Berceli SA, DeMasi RJ, Samson RH, Berman SS, P. I. Investigators (2006) Results of PREVENT III: a multicenter, randomized trial of edifoligide for the prevention of vein graft failure in lower extremity bypass surgery. J Vasc Surg 43: 742–751
Dobrin PB, Littooy FN, Endean ED (1989) Mechanical factors predisposing to intimal hyperplasia and medial thickening in autogenous vein grafts. Surgery 105: 393–400
Fernandez CM, Goldman DR, Jiang Z, Ozaki CK, Tran-Son-Tay R, Berceli SA (2004) Impact of shear stress on early vein graft remodeling: a biomechanical analysis. Ann Biomed Eng 32: 1484–1493
Figueroa CA, Baek S, Taylor CA, Humphrey JD (2009) A computational framework for fluid-solid-growth modeling in cardiovascular simulations. Comput Methods Appl Mech Eng 198: 3583–3602
Fillinger MF, Cronenwett JL, Besso S, Walsh DB, Zwolak RM (1994) Vein adaptation to the hemodynamic environment of infrainguinal grafts. J Vasc Surg 19: 970–979
Friedman MH, Deters OJ, Bargeron CB, Hutchins GM, Mark FF (1986) Shear-dependent thickening of the human arterial intima. Atherosclerosis 60: 161–171
Fujikawa H, Kai A, Morozumi S (2004) A new logistic model for Escherichia coli growth at constant and dynamic temperatures. Food Microbiol 21: 501–509
Galt SW, Zwolak RM, Wagner RJ, Gilbertson JJ (1993) Differential response of arteries and vein grafts to blood flow reduction. J Vasc Surg 17: 563–570
Goudar CT, Joeris K, Konstantinov KB, Piret JM (2005) Logistic equations effectively model mammalian cell batch and fed-batch kinetics by logically constraining the fit. Biotechnol Prog 21: 1109–1118
Grondin CM, Lepage G, Castonguay YR, Meere C, Grondin P (1971) Aortocoronary bypass graft: initial blood flow through the graft, and early postoperative patency. Circulation 44: 815–819
Hwang M, Garbey M, Berceli SA, Tran-Son-Tay R (2009) Rule-based simulation of multi-cellular biological systems—a review of modeling techniques. Cell Mol Bioeng 2: 285–294
Jiang Z, Wu L, Miller BL, Goldman DR, Fernandez CM, Abouhamze ZS, Ozaki CK, Berceli SA (2004) A novel vein graft model: adaptation to differential flow environment. Am J Physiol Heart Circ Physiol 286: H240–H245
Jiang Z, Tao M, Omalley KA, Wang D, Ozaki CK, Berceli SA (2009) Established neointimal hyperplasia in vein grafts expands via TGF-b-mediated progressive fibrosis. Am J Physiol Heart Circ Physiol 297: H1200–H1207
Mai J, Sameni M, Mikkelsen T, Sloane BF (2002) Degradation of extracellular matrix protein tenascin-C by cathepsin B: an interaction involved in the progression of gliomas. Biol Chem 383: 1407–1413
Mann MJ (2004) Novel strategies for the prevention of bypass graft failure. BioDrugs 18: 1–8
Meyerson SL, Skelly CL, Curi MA, Shakur UM, Vosicky JE, Glagov S, Schwartz LB (2001) The effects of extremely low shear stress on cellular proliferation and neointimal thickening in the failing bypass graft. J Vasc Surg 34: 90–97
Morinaga K, Eguchi H, Miyazaki T, Okadome K, Sugimachi K (1987) Development and regression of intimal thickening of arterially transplanted autologous vein grafts in dogs. J Vasc Surg 5: 719–730
Owens CD, Wake N, Jacot JG, Gerhard-Herman M, Gaccione P, Belkin M, Creager MA, Conte MS (2006) Early biomechanical changes in lower extremity vein grafts—distinct temporal phases of remodeling and wall stiffness. J Vasc Surg 44: 740–746
Schwartz LB, O’Donohoe MK, Purut CM, Mikat EM, Hagen PO, McCann RL (1992) Myointimal thickening in experimental vein grafts is dependent on wall tension. J Vasc Surg 15: 176–186
Schwartz SM (1999) The intima: a new soil. Circ Res 85: 877–879
Sumpio BE, Banes AJ (1988) Response of porcine aortic smooth muscle cells to cyclic tensional deformation in culture. J Surg Res 44: 696–701
Tran-Son-Tay R, Hwang M, Garbey M, Jiang Z, Ozaki CK, Berceli SA (2008) An experiment-based model of vein graft remodeling induced by shear stress. Ann Biomed Eng 36: 1083–1091
Valentín A, Humphrey JD (2009) Evaluation of fundamental hypotheses underlying constrained mixture models of arterial growth and remodeling. Phil Trans R Soc A 367: 3585–3606
Zohdi TI (2005) A simple model for shear stress mediated lumen reduction in blood vessels. Biomech Model Mechanobiol 4: 57–61
Zwolak RM, Adams MC, Clowes AW (1987) Kinetics of vein graft hyperplasia: association with tangential stress. J Vasc Surg 5: 126–136
Acknowledgments
This work was supported by the National Institutes of Health (R01-HL095508-01).
Open Access
This article is distributed under the terms of the Creative Commons Attribution Noncommercial License which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This is an open access article distributed under the terms of the Creative Commons Attribution Noncommercial License (https://creativecommons.org/licenses/by-nc/2.0), which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
About this article
Cite this article
Hwang, M., Berceli, S.A., Garbey, M. et al. The dynamics of vein graft remodeling induced by hemodynamic forces: a mathematical model. Biomech Model Mechanobiol 11, 411–423 (2012). https://doi.org/10.1007/s10237-011-0321-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10237-011-0321-3