Initial formation of channel–shoal patterns in double–inlet systems

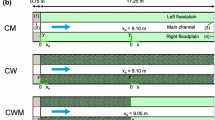
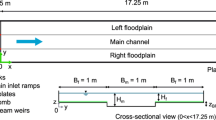
Abstract

Channel–shoal patterns are often observed in the back–barrier basins of inlet systems and are important from both an economical and ecological point of view. Focussing on double–inlet systems, the initial formation of these patterns is investigated using an idealized model. The model is governed by the depth–averaged shallow water equations, a depth–integrated concentration equation and a tidally–averaged bottom evolution equation. Focussing on rectangular basins and neglecting the effects of earth rotation, it is found that laterally uniform morphodynamic equilibria can become linearly unstable, resulting in initial patterns that resemble channels and shoals. When the water motion is only forced by an M₂ tidal constituent, the existence of (laterally uniform) morphodynamic equilibria for which both inlets are connected strongly depends on the relative phase and amplitudes of the tidal forcing. If such equilibria exist, they can be either stable against small perturbations or linearly unstable. If these equilibria are linearly unstable, two instability mechanisms can be identified, the first related to the convergences and divergences of diffusive transports, the second mechanism related to a combination of advective and diffusive transports. In the former case, all eigenvalues are real and the bedforms grow exponentially in time. In the latter case, the eigenvalues are complex, resulting in bedforms that both migrate and grow in time. In case external overtides and a time–independent discharge are included, no diffusive instabilities are found anymore for the parameters considered in this paper. This implies that all instabilities are migrating in time. In all cases considered, the bed perturbations have only an appreciable amplitude at locations where the underlying laterally uniform equilibrium has a local minimum in water depth. This is consistent with observations from numerical models and laboratory experiments.

Appendix A: Diffusively dominated transport

The influence of the relative M₂ phase, ${\Delta }\phi _{M_{2}}$, on the diffusively dominated morphodynamic equilibria is investigated. For simplicity, the undisturbed water depth at inlet I I is taken to be equal to 11.7 m, the same water depth as inlet I. All other parameter values are taken from Table 2. When the sediment transport is dominated by diffusion, the morphodynamic equilibrium condition reduces to

$$ \begin{array}{@{}rcl@{}} \nabla\cdot\left( <\!\!{\mathbf{F}^{00}_{\text{diff}}}\!\!> + <\!\!{\mathbf{F}^{00}_{\text{topo}}}\!\!>+<\!\!{\mathbf{F}_{\text{bed}}}\!\!> \right) = 0. \end{array} $$

(A1)

In a rectangular geometry, morphodynamic equilibria which are laterally uniform can be found using the bifurcation approach discussed in Deng et al. (2021). As an example, Fig. 10a shows the minimum water depths WD$_{{\min \limits }}$ of these morphodynamic equilibria as a function of ${\Delta }\phi _{M_{2}}$ varying from − 60^∘ to 60^∘. It demonstrates that the existence of morphodynamic equilibria depends on the relative M₂ phase: for ${\Delta }\phi _{M_{2}}$ between 10^∘ to 16^∘, no morphodynamic equilibrium is found for which both inlets are connected. For other relative M₂ phases considered, there is always a 1D–stable equilibrium.

Fig. 10

Laterally uniform morphodynamic equilibria for diffusively dominated transport. Panel (a) shows WD$_{{\min \limits }}$ the minimum water depth of equilibrium bed profiles, with its location coded with color. Panel (b) shows the equilibrium bed profiles for three different values of ${\Delta }\phi _{M_{2}}$. The minimum water depths in the cases shown in panel(b) are indicated by cross-shaped markers in panel (a)

To investigate the linear stability of these 1D–stable morphodynamic equilibria to the perturbations with lateral structure, morphodynamic equilibria obtained with ${\Delta }\phi _{M_{2}}={19}^{\circ }$ (orange), ${\Delta }\phi _{M_{2}}={20}^{\circ }$ (green) and ${\Delta }\phi _{M_{2}}={25}^{\circ }$ (red) are examined. Their bed profiles are shown in Fig. 10b. These three equilibrium bed profiles correspond to WD$_{{\min \limits }}$ indicated by crosses (with colors associated to their bed profiles) in Fig. 10a. The largest dimensionless growth rate R(ω) of these three morphodynamic equilibria as a function of dimensionless wave number l_n is shown in Fig. 11a. It shows that at l_n = 0 the largest dimensionless growth rate R(ω) is negative for all three selected ${\Delta }\phi _{M_{2}}$, which shows these three morphodynamic equilibria are 1D–stable. Increasing the dimensionless wave number l_n from 0 to 1200, the largest dimensionless growth rate R(ω) for ${\Delta }\phi _{M_{2}}={19}^{\circ }$ first increases, till a maximum is obtained at approximately l_n = 560, and then decreases to become negative for $l_{n}\sim 1200$. Positive R(ω) indicates that the laterally uniform morphodynamic equilibrium for ${\Delta }\phi _{M_{2}}={19}^{\circ }$ is unstable against perturbations with a lateral structure. Unlike ${\Delta }\phi _{M_{2}}={19}^{\circ }$, the largest dimensionless growth rate R(ω) for ${\Delta }\phi _{M_{2}}={25}^{\circ }$ is negative for all l_n considered, which indicates the corresponding equilibrium is stable against perturbations with lateral structure. The critical value of the relative M₂ phase, ${\Delta }\phi _{M_{2}}$, that seperates stable and unstable morphodynamic equilibrium against perturbations with lateral structure, is ${\Delta }\phi _{M_{2}}={20}^{\circ }$ (see also Fig. 14).

Fig. 11

The dimensionless growth rate R(ω) for three different ${\Delta }\phi _{M_{2}}$ (Panel (a)). The corresponding bottom patterns h_n for mode number n = 0 (l_n = 0) are shown in panel (b), while those for mode number n = 18 (l_n = 555.9) are shown in panel (c)

When using width B = 6 km, the dimensionless wave number l_n = 555.9, at which R(ω) for ${\Delta }\phi _{M_{2}}={19}^{\circ }$ reaching a maximum, corresponds to a mode number n = 18. The bed patterns h_n for n = 18 (l_n = 555.9) are shown in Fig. 11c. Compared with the bed patterns for n = 0 shown in Fig. 11b, the bed patterns for n = 18 are more localized, i.e., the bed patterns for n = 18 are nonzero within a region of approximately 15km, while the bed patterns for n = 0 are nonzero everywhere between the two inlets. Figure 11c also shows that the bed patterns for n = 18 are close to where WD$_{{\min \limits }}$ is found. The morphodynamic equilibrium for ${\Delta }\phi _{M_{2}}={19}^{\circ }$ is called diffusively unstable, since only diffusive transport plays a role.

To study the instability mechanism in detail, the classical diffusive transport $<\!\!{\mathbf {F}^{00}_{\text {diff}}}\!\!>$, the topographically induced diffusive transport $<\!\!{\mathbf {F}^{00}_{\text {topo}}}\!\!>$ and the total transport < F > of the first 1 km in lateral direction for ${\Delta }\phi _{M_{2}}={19}^{\circ }$ and mode number n = 0 are shown in Fig. 12a, c and e, while those for ${\Delta }\phi _{M_{2}}={19}^{\circ }$ and mode number n = 18 are shown in Fig. 12b, d and f, respectively. These figures show that the topographically induced diffusive transport $<\!\!{\mathbf {F}^{00}_{\text {topo}}}\!\!>$ is directed from crests to troughs and stablizes the bottom pattern, while the classical diffusive transport $<\!\!{\mathbf {F}^{00}_{\text {diff}}}\!\!>$ is generally directed from troughs to crests and destablizes the bottom patterns. These two diffusive transport result in a total transport < F >, which can be either directed from crests to troughs (n = 0) or from troughs to crests (n = 18), depending on the mode number n, as well as the relative M₂ phase. When mode number n = 0, these three sediment transports flow in a longitudinal direction, since there is no lateral structure, while these transports flow laterally when mode number n = 18.

Fig. 12

Bottom patterns of laterally uniform morphodynamic equilibria for diffusively dominated transport. Panels (a), (c) and (e) show the bottom patterns for ${\Delta }\phi _{M_{2}}={19}^{\circ }$ and n = 0, with white areas representing crests and dark areas representing troughs. The arrows indicate the direction and relative magnitude of classical diffusive flux $<\!\!{\mathbf {F}^{00}_{\text {diff}}}\!\!>$, the topographically induced diffusive flux $<\!\!{\mathbf {F}^{00}_{\text {topo}}}\!\!>$ and the total flux < F >. Panels (b), (d) and (f) show the same but for ${\Delta }\phi _{M_{2}}={19}^{\circ }$ and n = 18

The instability mechanism can also be studied using the divergences of these three sediment fluxes, which have the same lateral structure as their corresponding bottom pattern. Figure 13a shows these divergences in the longitudinal direction at y = 0 for ${\Delta }\phi _{M_{2}}={19}^{\circ }$ and mode number n = 0, together with the corresponding bottom pattern, while the ones for ${\Delta }\phi _{M_{2}}={19}^{\circ }$ and mode number n = 18 are shown in Fig. 13b. From these figures it follows that the divergence of the classical diffusive transport $<\!\!{\mathbf {F}^{00}_{\text {diff}}}\!\!>$ enhances perturbations of bottom patterns, and the divergence of topographically induced diffusive transport $<\!\!{\mathbf {F}^{00}_{\text {topo}}}\!\!>$ reduces the amplitudes of the perturbations. These two sediment transports almost balance each other, resulting in a divergence of the total transport < F > with smaller magnitude. When mode number n = 0 is considered, < F > transports sediment from troughs to crests, while for mode number n = 18, < F > transports sediment from crests to troughs.

Fig. 13

Divergences of sediment fluxes. Panel (a) shows the divergences of the sediment fluxes for ${\Delta }\phi _{M_{2}}={19}^{\circ }$ and mode number n = 0 at y = 0, together with the corresponding bottom pattern. Panel (b) shows the same but for ${\Delta }\phi _{M_{2}}={19}^{\circ }$ and mode number n = 18

The existence and stability of laterally uniform morphodynamic equilibria depends not only on the relative M₂ phase but also on the M₂ amplitude at inlet I I, which is shown in Fig. 14. In this figure, the region in parameter space where no laterally uniform morphodynamic equilibrium exists, is indicated by the white color. Linearly stable equilibria are found in the black colored area, while linearly unstable equilibria (resulting from the diffusive mechanism) in the light gray colored area.

Fig. 14

Existence and linear stability of stable laterally uniform morphodynamic as a function of the M₂ tidal amplitude at inlet II and the raltive phases when dominated by diffusive transport. The white, black, dark region indicate where no, linearly stable, diffusively unstable morphodynamic equilibria are found. If the underlying equilibrium is unstable, the mechanism resulting in the largest positive growth rate is used as indicateive of the instability mechanism. The crosses indicate the experiments discussed in detail in this Appendix A