Modeling equilibrium bed profiles of short tidal embayments

Abstract

In many tidal embayments, bottom patterns, such as the channel-shoal systems of the Wadden Sea, are observed. To gain understanding of the mechanisms that result in these bottom patterns, an idealized model is developed and analyzed for short tidal embayments. In this model, the water motion is described by the depth- and width-averaged shallow water equations and forced by a prescribed sea surface elevation at the entrance of the embayment. The bed evolves due to the divergence and convergence of suspended sediment fluxes. To model this suspended-load sediment transport, the three-dimensional advection–diffusion equation is integrated over depth and averaged over the width. One of the sediment fluxes in the resulting one-dimensional advection–diffusion equation is proportional to the gradient of the local water depth. In most models, this topographically induced flux is not present. Using standard continuation techniques, morphodynamic equilibria are obtained for different parameter values and forcing conditions. The bathymetry of the resulting equilibrium bed profiles and their dependency on parameters, such as the phase difference between the externally prescribed M₂ and M₄ tide and the sediment fall velocity, are explained physically. With this model, it is then shown that for embayments that are dominated by a net import of sediment, morphodynamic equilibria only exist up to a maximum embayment length. Furthermore, the sensitivity of the model to different morphological boundary conditions at the entrance of the embayment is investigated and it is demonstrated how this strongly influences the shape and number of possible equilibrium bottom profiles. This paper ends with a comparison between the developed model and field data for the Wadden Sea’s Ameland and Frisian inlets. When the model is forced with the observed M₂ and M₄ tidal constituents, morphodynamic equilibria can be found with embayment lengths similar to those observed in these inlets. However, this is only possible when the topographically induced suspended sediment flux is included. Without this flux, the maximum embayment length for which morphodynamic equilibria can be found is approximately a third of the observed length. The sensitivity of the model to the topographically induced sediment flux is discussed in detail.

1 Introduction

Chains of barrier islands are found in many coastal areas all over the world, for example, along the Dutch, German, and Danish Wadden coast, see Ehlers (1988), Davis (1996), and FitzGerald (1996). Tidal embayments, which are a dynamic part of these barrier systems, are important from both an economic and an ecological point of view. When the seabed of these tidal embayments consists of sand and/or mud, channels and shoals develop due to the interaction of the currents generated by tides, wind, and density differences with the erodible bed (De Swart and Zimmerman 2009). This morphodynamic development has a significant effect on the general tendency of the tidal embayment to import or export sediment. External conditions, such as mean sea level rise and human interferences, can also strongly influence the morphologic behavior. Taking into account these complex dynamics and the importance of these areas, it is crucial to accurately model, simulate, and predict the morphodynamic development.

For this purpose, various types of models can be used (see De Vriend 1996). Restricting our attention to process-based models, we discern numerical and idealized models. In the past few decades, complex process-based numerical models have been developed (Wang et al. 1995; Cayocca 2001; Roelvink 2006), which are able to simulate intriguing morphodynamic developments. These process-based models contain state-of-the-art physical descriptions and parameterizations. A disadvantage is that, in general, these morphodynamic models can only be used to simulate the morphodynamic development over a time scale of the order of decades, unless numerical implementations are used that are not, from a mathematical point of view, proven to be correct (see Roelvink 2006). Furthermore, because of their complexity, the results are, in general, difficult to analyze and interpret. The other type of process-based models is idealized models. These models focus on specific morphodynamic phenomena by simplifying the equations in an appropriate way, retaining only processes that appear to be important. By comparing the model results to field data, the validity of these assumptions has to be assessed. This results in highly schematized models that can be analyzed using standard mathematical tools. The advantage of this approach is that long-term morphodynamic behavior can be simulated, analyzed, and interpreted. Therefore, idealized models are useful tools to investigate model formulations and assumptions and, if necessary, improve these formulations and assumptions.

To study the morphodynamics in short tidal embayments, one-dimensional models have been developed to study the feedback between water motion, sediment transport, and bed evolution. Schuttelaars and De Swart (1996) considered a short rectangular embayment with fixed coastlines and an erodible bed. The water motion was modeled by the shallow-water equations and driven by a prescribed tidal elevation at the entrance of the embayment. The sediment transport was described by a width-averaged, depth-integrated concentration equation. The bed evolved due to convergence and divergence of the sediment fluxes. Considering only a prescribed M₂ tidal elevation at the entrance of the embayment, a unique morphodynamic equilibrium was found, characterized by a constant sloping bed towards the coast.

In order to compare the model results with observations in the Dutch Wadden coast, the external tidal forcing should include both the M₂ and the M₄ tidal constituents. Schuttelaars and De Swart (1996) and Van Leeuwen et al. (2000) both investigated the influence of the external M₄ tide on the morphodynamic equilibria. However, when using realistic parameter values, Van Leeuwen et al. (2000) obtained equilibrium profiles that are strongly convex. A maximum length for which equilibria could be found was only about 40% of the observed length (see De Swart and Blaas 1998). Contrary to the model presented in this paper, both Schuttelaars and De Swart (1996) and Van Leeuwen et al. (2000) described the sediment transport by an advection–diffusion equation, where sediment fluxes induced by spatial variations of the water depth (directed towards deeper water) were assumed to be compensated by fluxes induced by waves and secondary circulations in the vertical plane. One of the aims of this paper is to demonstrate that inclusion of these topographically induced fluxes is necessary to obtain morphodynamic equilibria with observed embayment lengths for realistic parameter values, including an external forcing of the water motion by both the M₂ and M₄ tidal constituents.

Van Leeuwen et al. (2000) extended the model of Schuttelaars and De Swart (1996) by considering funnel-shaped estuaries and by using a depth-dependent formulation for erosion and deposition. They found that the influence of the width convergence and the tidal flats on the properties of the morphodynamic equilibrium was minor as long as the convergence was not too strong. Similar results were found by Lanzoni and Seminara (2002), who used a more sophisticated description of the water motion and a transport formula proposed by Van Rijn (1984). Using a model similar to those of Van Leeuwen et al. (2000) and Schuttelaars and De Swart (1996), Todeschini et al. (2008) found that the maximum length of the embayment strongly depends on the convergence of the estuary. In the above-mentioned models, different boundary conditions where used. In Hibma et al. (2003), it is concluded that the morphological boundary condition at the entrance of the embayment strongly influences the behavior of morphodynamic models. The second aim of this paper is to clarify the effect of these boundary conditions on the characteristics of the equilibrium bed profiles.

The paper is organized as follows: In Section 2 we describe the model equations and assumptions together with the method used to solve the resulting system of equations. Section 3 presents the effect of different sediment flux contribution on the morphodynamic equilibria. For all the flux contributions, a parameter sensitivity analysis is performed and extensively discussed. Furthermore, different morphologic boundary conditions are considered. In Section 4, a comparison with observations is presented. Conclusions based on the results are given in Section 5.

2 Model formulation

2.1 Geometry

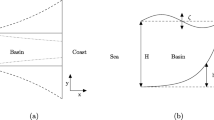
The embayment considered is of rectangular shape with width B and a fixed length L. As the typical length of the embayment L, we take the tidally averaged position of the moving landward boundary. This length L is assumed to be small compared to the frictionless tidal wavelength $L_g=T\sqrt{gH}$, with T the tidal period of the M ₂-tidal constituent, g the gravitational constant, and H the undisturbed water depth. Tidal resonance is not considered. The coastlines of the embayment are fixed and the bed (described by z = h) is erodible, see Fig. 1. The sediment of the bed consists of very fine sand (d∼130 μm); hence, bedload transport is negligible compared to suspended load transport. The basin has an open connection to the adjacent sea. In morphodynamic equilibrium, H is the water depth at the entrance of the embayment, and the local water depth is given by H − h + ζ, with ζ the sea surface elevation.

Fig. 1

Left, top view; right, cross-sectional view of the embayment

2.2 Hydrodynamics

The water motion is described by the cross-sectionally averaged shallow-water equations for a homogeneous fluid. Assuming a narrow (B ≪ L and B ≪ R, with R the Rossby deformation radius), short (L ≪ L _g ) channel, the shallow-water equations reduce to (see Appendix D)

$$\zeta_t+\left[\left(\zeta +H-h \right)u \right]_x=0,$$

(1)

$$ \zeta_x=0,$$

(2)

where u is the depth-averaged velocity. A subscript denotes differentiation with respect to that variable unless stated otherwise. The momentum Eq. 2 models a spatially uniform variation of the free surface, which is fully determined by the boundary condition at the entrance. At the landward side, the kinematic boundary condition is used. The boundary conditions read

$$\zeta\!=\!\rm{A}_{\rm{M}_2}\cos\!\big(\sigma t\!-\!\phi_{\rm{A}_{\rm{M}_2}}\big)\!+\!\rm{A}_{\rm{M}_4}\cos\!\big(2\sigma t\!-\! \phi_{\rm{A}_{\rm{M}_4}}\big)\; \; \; \mathrm{at}\; x=0,$$

(3)

$$u=\frac{d\hat x}{d t}\,\, \mathrm{at}\; x=\hat x,$$

(4)

where $\rm{A}_{\rm{M}_2}$ ($\phi_{\rm{A}_{\rm{M}_2}}$) and $\rm{A}_{\rm{M}_4}$ ($\phi_{\rm{A}_{\rm{M}_4}}$) are the tidal amplitudes (phases) of, respectively, the M₂ and M₄ tidal constituents. The frequency of the first harmonic constituent (M₂) is denoted by σ. Hence, at the open boundary, the system is forced with a basic tide and its first overtide. In Eq. 4, x is the position of the moving water front (see Section 3.2 for a discussion of this boundary condition). Note that $\left< \hat x \right>=L$, where $\left\langle \cdot \right\rangle$ stands for averaging over the tidal period.

2.3 Sediment transport and bed evolution

The sediment transport equation is obtained by integrating the three-dimensional advection diffusion equation over depth and averaging over width (for a derivation, see Appendix A). Using ζ _x  = 0, the resulting depth-integrated concentration equation reads

$$ C_t+\left( uC\right)_x-\tilde\kappa C_{xx}-\left[\tilde\kappa\frac{\omega_s}{\kappa_v}\beta h_xC\right]_x=\alpha u^2 -\frac{\omega_s^2}{\kappa_v}\beta C.$$

(5)

The depth-integrated and width-averaged sediment concentration C with dimension (kg m^− 2) refers to the total amount of sediment stored in a water column with unit horizontal area. The first contribution on the right-hand side models the whirling up of sediment from the bed. Here, we have assumed a linear dependency on the bed shear stress, although the erosion generally depends nonlinearly on this parameter (see Dyer 1986; Dyer and Soulsby 1988). As we only consider transport of fine sand in this paper, the critical velocity of motion is small compared to the tidal velocity during the largest part of a tidal cycle. Therefore, as a first approximation, we set the critical velocity for erosion to zero. The second contribution on the right-hand side of Eq. 5 models the deposition of sediment.

The second term on the left-hand side is the divergence of the advective sediment flux; the third and fourth terms model the diffusive contributions. Here, $\tilde \kappa$ is the horizontal diffusivity (∼10² m²/s), ω _s is a constant settling velocity of sediment (∼0.015 m/s), and κ _v is a vertical diffusion coefficient (∼0.1 m²/s). The last term on the left-hand side is often neglected or assumed to be balanced by wave action in depth-averaged modeling of suspended sediment transport. This term represents the convergence and divergence of the horizontal diffusive sediment flux induced by topographic variations. The occurrence of this sediment flux can be easily understood if one considers the vertical distribution of sediment in the water. The concentration is highest near the bed and reduces with decreasing depth, as illustrated in Fig. 2. Therefore, at a fixed depth, the sediment concentration is higher in the shallower areas than in the deeper areas. Hence, there is a horizontal concentration gradient between these regions. In a three-dimensional model for the suspended sediment concentration, this would result in a diffusive sediment flux directed towards the deeper water area. When integrating over depth, this sediment flux is still present and is given by the fourth term on the left-hand side of Eq. 5 (for a derivation, see Appendix A).

Fig. 2

Conceptual picture of a 3D physical process, which is described in the model by the topographically induced diffusive sediment flux F _vd. The colors represent the concentration of sediment. Black represents the seabed. The more red (blue), the higher (lower) the suspended sediment concentration. Consider two adjacent water columns in the estuary. As the concentration is highest near the bottom and decreases with decreasing depth in the water column, there is a horizontal concentration gradient between the adjacent water columns. This results in a diffusive sediment flux towards deeper areas

The deposition parameter β depends exponentially on local depth and reads

$$\beta=\frac{1}{1-e^{-\frac{\omega_s}{\kappa_v}\left(\zeta+H-h \right)}}. $$

(6)

The influence of this parameter strongly depends on the grain size. This formulation favors deposition in shallower areas.

The erosion parameter α is defined as

$$ \alpha=\rho_s(1-p)\frac{\Gamma \omega_s}{u^2_{\ast,\rm{c}}}c_d, $$

(7)

with p∼0.4 the bed porosity, ρ _s∼2650 kg m³ the density of the sand, u _∗ ,c∼0.03 m/s the critical friction velocity for erosion, c _d ∼0.0025 the drag coefficient, and Γ∼7.8·10^− 5 an empirical constant; see Dyer (1986). The sediment is assumed to be non-cohesive and has a uniform grain size (d = 130 μm).

The bed evolution equation is derived from continuity of mass in the sediment layer. The bed evolution takes place on a much longer time scale than the water motion and the sediment transport. This implies that we can consider the bathymetry to be constant on the fast hydrodynamic time scale. The bed only changes due to tidally averaged erosion and deposition of sediment. Assuming suspended load transport to be dominant (neglecting the bedload transport mechanism) and using the fact that the bed evolves on a much larger time scale than the time scale of the hydrodynamics (this will be substantiated after Eq. 12d), the bed evolution equation reads

$$ \rho_{\rm{s}}\left( 1-p\right) h_t=-\left\langle \alpha u^2-\frac{\omega_s^2}{\kappa_v} \beta C\right\rangle,$$

(8)

where $\left\langle \cdot \right\rangle$ denoted tidal averaging.

Since there is no consensus on the boundary condition to use at the entrance, the sensitivity of model results to different boundary conditions at the seaward side will be investigated. The default condition used in this paper (see also Schuttelaars and De Swart 1996; Van Leeuwen 2002) fixes the bed level at the entrance (h|_x = 0 = 0). In case of exporting boundaries, De Jong (1998) required h _x |_x = 0 = 0, thus allowing the model to choose its own equilibrium depth at the entrance. An even less restrictive condition would be to require h _xx |_x = 0 = 0, the boundary condition used in De Jong (1995) and in the numerical implementation of the model of, for example, Lanzoni and Seminara (2002). Using this boundary condition, the system will again try to find its own equilibrium depth at the entrance. The sensitivity of model results to the different boundary conditions at the seaward side is discussed in Section 3.2. On the landward side, $x=\hat x$, the boundary condition for the time-averaged concentration reads

$$ \left\langle-\tilde\kappa C_{x}-\left[\tilde\kappa\frac{\omega_s}{\kappa_v}\beta h_xC\right]\right\rangle =0.$$

(9)

Physically, this means that no net sediment flux is allowed through this boundary.

The time-dependent boundary condition for the concentration at the entrance and the coast are

$$C'(x,t,\kappa)=C'(x,t,\kappa=0),$$

(10)

with $C'=C-\left\langle C\right\rangle$ the time-fluctuating part of the concentration. This condition implies that no diffusive boundary layer develops in the fluctuating part of the concentration C′ at these boundaries.

2.4 Scaling and derivation of the short embayment model

The governing equations are made dimensionless by introducing characteristic scales for the variables:

$$\begin{array}{lll} x=Lx^\ast,& t=\sigma^{-1}t^\ast,&u=Uu^\ast,\\[5pt] \zeta=A_{\rm{M}_2}\zeta^\ast=\frac{HU}{\sigma L}\zeta^\ast,&C=\displaystyle\frac{\alpha U^2 \kappa_{\rm{v}}}{\omega_{\rm{s}}^2}C^\ast,&h=Hh^\ast, \end{array} $$

(11)

where $U=\sigma A_{\rm{M}_2} L/H$ is the velocity scale related to the tidal forcing at the entrance of the embayment. The scale for the concentration is obtained by requiring an approximate balance between erosion and deposition. After suppressing the asterisk, the dimensionless model equations read (see Appendix D)

$$ \zeta_t+\left[\left(\varepsilon\zeta +1-h \right)u \right]_x=0,$$

(12a)

$$ \zeta_x=0,$$

(12b)

$$ aC_t+ a \varepsilon\left( uC\right)_x-a\kappa\left[ C_x+\lambda \beta h_xC\right]_x =u^2-\beta C,$$

(12c)

$$ h_t=-\delta\left\langle u^2-\beta C\right\rangle , $$

(12d)

where the parameter δ (see Table 1) is the ratio of the tidal period T and the morphodynamic time scale $T_{\rm{m}}=2\pi\rho_{\rm{s}}(1-p)H/(\alpha U^2)$ ∼ 20 years, and ε is the ratio of the tidal excursion (i.e., the distance traveled by a fluid particle in a tidal period) and the tidal inlet length. Furthermore, a is the ratio of the time scale of the deposition process and the tidal period and κ is the ratio of the diffusive time scale and the tidal period. The sediment Péclet number λ is the ratio of the typical time it takes a particle to settle in the water column, and the typical time needed to mix particles through the water column. The dimensionless deposition parameter β reads

$$ \beta=\frac{1}{\left( 1-e^{-\lambda\left(\varepsilon\zeta+1-h \right)}\right)}. $$

(13)

Table 1 Characteristic values for the Ameland Inlet system

Since δ is small (∼10^− 4), it follows that the morphodynamic time scale is much larger than the tidal time scale and the bed evolves on a long time scale. Hence, to a good approximation, the bottom can be considered steady on the fast hydrodynamic time scale, and averaging over the tidal period is allowed (see also Krol 1990). The tidally averaged bed evolution Eq. 12d can be written as

$$ h_{\tau}=-\left\langle F\right\rangle _x, $$

(14)

with τ = δt is the long time scale at which the bed evolves. The sediment flux F is given by

$$ F=a \varepsilon uC-a\kappa\left[ C_x+\lambda \beta h_xC\right]. $$

(15)

The bed evolution Eq. 14 shows that the bed changes due to the convergence and divergence of the tidally averaged sediment flux. This flux consists of an advective contribution F _adv = aε uC, a diffusive contribution F _diff = − aκ C _x , and a diffusive flux induced by the spatial variations in the water depth F _vd = − aκ λβ h _x C.

The scaled boundary conditions at x = 0 read

$$ \zeta=\cos(t)+\frac{\gamma}{2}\cos(2t-\phi), $$

(16a)

$$ h_{\rm{n}x}=0\;\;\;\rm{with}\;\;n=0,1\;\rm{or}\;2,$$

(16b)

$$ C'(x,t,\kappa)=C'(x,t,\kappa=0), $$

(16c)

and at $x=\hat x$

$$\varepsilon u={\hat x}_t,$$

(17a)

$$ -a\kappa\left\langle C_x+\lambda \beta h_xC\right\rangle =0,$$

(17b)

$$ C'(x,t,\kappa)=C'(x,t,\kappa=0), $$

(17c)

where γ is the ratio of the M₄ and the M₂ tidal amplitudes and ϕ is the relative phase (i.e., $\phi_{\rm{M}_4}-2\phi_{\rm{M}_2}$). In the boundary condition Eq. 16b, the subscript n denotes the n ^th derivative of h with respect to x. The intersection point of bottom and water level $\hat x$ is determined by solving the relation

$$ 1-h(x)+\varepsilon \zeta(x,t)=0. $$

(18)

Using the fact that, on average, the scaled embayment length is 1, $\hat x$ can be expanded in the parameter ε, which is usually much smaller than one (see Table 1). Introducing this expansion in Eq. 18, it follows that h = 1 at x = 1 in leading order. After substitution of this condition in the continuity equation, the boundary condition at the end of the embayment can be reformulated as a boundary condition at x = 1 and is given by

$$ u_x\;\,\rm{ is\;finite}$$

(19a)

$$ \left\langle F\right\rangle =0,$$

(19b)

$$ C'(x,t,\kappa)=C'(x,t,\kappa=0). $$

(19c)

2.5 Solution method

From observations in the Dutch Wadden Sea (see Table 1), it is reasonable to assume that ε ≪ 1 and γ ≪ 1. The model equations are solved by making a regular expansion in these small parameters:

$$ \Psi=\Psi^{0,0}+\varepsilon\Psi^{1,0}+\gamma\Psi^{0,1}+\rm{h.o.t.}, $$

(20)

where $\Psi \in \left\lbrace \zeta, u, C, \beta\right\rbrace$. The first superscript, on the right-hand side in Eq. 20, stands for the order of ε, the second one for the order of γ. Any term on the right-hand side of Eq. 20 can be decomposed in its tidal constituents (M₂, M₄, M₆, etc.), and a residual component:

$$\Psi^{i,j}=\left\langle \Psi^{i,j}(x)\right\rangle +\sum\limits_{\rm{k}}\Psi_{\rm{sk}}^{i,j}(x)\sin(\rm{k}t)+ \sum\limits_{\rm{k}}\Psi_{\rm{ck}}^{i,j}(x)\cos(\rm{k}t), $$

(21)

where $\left\langle \Psi^{i,j}(x)\right\rangle$, $\Psi_{\rm{sk}}^{i,j}(x)$, and $\Psi_{\rm{ck}}^{i,j}(x)$ give, respectively, the spatial dependency for the time residual, temporal sine (denoted by the subscript sk), and cosine components (denoted by ck) with frequency k of Ψ^i,j.

Substituting these expansions in the system of equations, collecting terms of equal order in ε and γ, and equal temporal behavior, we obtain a set of equations with unknown spatial variables. For the model described in this paper, expressions for the spatial dependency of ζ, u, C, β can be calculated explicitly, see Appendix C.

To calculate the morphodynamic equilibria, the tidally averaged sediment fluxes need to be investigated. Inspection of the time dependency of u and C and the expression for the sediment flux (see Appendix C) reveals that the leading-order tidally averaged advective sediment fluxes are of the order ε ² and εγ and the diffusive sediment fluxes are of the order 1:

$$ \left\langle F\right\rangle = \left\langle F_{\rm{adv}}^{2,0}\right\rangle +\left\langle F_{\rm{adv}}^{1,1}\right\rangle +\left\langle F_{\rm{diff}}^{0,0}\right\rangle +\left\langle F_{\rm{vd}}^{0,0}\right\rangle. $$

(22)

The residual advective flux, due to the correlation of velocity and concentration components and induced by internal nonlinear interaction, is given by

$$ \left\langle F_{\rm{adv}}^{2,0}\right\rangle =a^2\varepsilon^2\frac{1}{2}\left[ u_{\rm{s}}^{0,0} C_{\rm{s}}^{1,0}+ u_{\rm{2s}}^{1,0} C_{\rm{2s}}^{0,0}\right], $$

(23)

the advective flux caused by the presence of the external overtide M₄ reads

$$ \left\langle F_{\rm{adv}}^{1,1}\right\rangle=a\varepsilon\gamma\frac{1}{2}\left[u_{\rm{s}}^{0,0}C_{\rm{s}}^{0,1}+ u_{\rm{s2}}^{0,1}C_{\rm{s2}}^{0,0}+u_{\rm{c2}}^{0,1} C_{\rm{c2}}^{0,0}\right]. $$

(24)

The residual concentration results in a diffusive flux

$$ \left\langle F_{\rm{diff}}^{0,0}\right\rangle = -a\kappa\left\langle C^{0,0} \right\rangle_x, $$

(25)

and the residual diffusive sediment flux related to the topographic variations is given by

$$ \left\langle F_{\rm{vd}}^{0,0}\right\rangle =-a\kappa\lambda \beta^{0,0} h_x \left\langle C^{0,0} \right\rangle. $$

(26)

Using realistic parameter values, it turns out that all fluxes can be of the same order and, hence, must be taken into account.

In this contribution, we will not study the time evolution of the bed, but focus on morphodynamic equilibrium solutions for embayments with a prescribed length and a prescribed depth. In case the depth is fixed at the entrance (i.e., n = 0 in boundary condition 16b), the required morphodynamic equilibrium will be found directly by prescribing this depth at the entrance. If either n = 1 or n = 2 is chosen as boundary condition at the entrance (i.e., either the first or the second derivative of the bed is prescribed), we calculate the morphodynamic equilibria for a range of prescribed depths but only select those bed profiles as morphodynamic equilibrium profiles that satisfy the required boundary condition Eq. 16b with n = 1 or n = 2. The influence of this boundary condition will be discussed in more detail in Section 3.2. Using the boundary condition $\left\langle F\right\rangle |_{x=1}=0$, the bed evolution Eq. 14 reduces to the following nonlinear ordinary differential equation:

$$ \left\langle F\right\rangle =0. $$

(27)

In case of diffusively dominated transport, including both diffusive fluxes and taking a depth-independent deposition parameter, the exact solution is known; see Appendix B. In general, this equation cannot be solved analytically. Therefore, the spatial variables are expanded in Chebyshev polynomials, and the resulting (nonlinear) system of equations is solved using a (standard) collocation method. In general, this nonlinear system of equations has to be solved numerically using a Newton–Rapshon method.

For this method to converge, a good initial guess is needed. Fortunately, the exact solution of the diffusively dominated transport case is known. We use this solution (or the constantly sloping profile obtained by Schuttelaars and De Swart 1996) as an initial guess in the Newton–Raphson procedure, and we slowly change the sediment flux (either by introducing additional physical processes or by changing parameter values) to get a numerical solution for parameter ranges and/or formulations for which no analytic solution can be found.

3 Model results

The results shown in this section are obtained with parameter values that characterize the Ameland Inlet system, see Table 1. The tidal basin, which is relatively undisturbed by human interferences, is located between the barrier islands Terschelling and Ameland in the Dutch Wadden Sea. The semi-diurnal tidal amplitude at the Ameland Inlet is ∼0.84 m. The M₄ tidal constituent has an amplitude of ∼0.08 m and a phase difference ϕ with the M₂ tide (i.e., $\phi_{\rm{M}_4}-2\phi_{\rm{M}_2}$) of ∼195°. The typical depth at the entrance of the basin is about 12 m, and its length is approximately 20 km.

In the following sections, we will investigate the existence and characteristics of morphodynamic equilibria obtained with these parameter values and investigate the sensitivity of these findings for varying embayment length, sediment Péclet number λ, and phase difference ϕ. Since we only consider short embayments, embayment lengths of 3 to 30 km are considered. We define the maximum embayment length for which a morphodynamic equilibrium equation still exists by L _max if this length is smaller than 30 km. Otherwise, we say that no maximum embayment length can be found within this model, as the embayment length is assumed to be small compared to the frictionless tidal wavelength. The settling velocity is taken over the range of very fine to coarse sand, and the depth of the inlet is varied between 5 and 30 m. The resulting Péclet number varies between 0.2 and 15. The phase difference ϕ is varied in a range that is representative for the Wadden Sea, namely between 150° and 230°. The morphodynamic equilibria are characterized by a no-flux condition (i.e., the sediment flux is zero, see Eq. 27).

To physically explain these equilibrium profiles, we will examine the sediment fluxes. It turns out that investigation of the leading-order contribution in the small parameter a∼0.0622 of the sediment fluxes suffices to explain the observed equilibria. These leading-order flux contributions read

$$ F_{\rm{diff}}^{0,0}= -a \kappa \left[ \frac{u^{0,0}_{\rm{s}}\left( u^{0,0}_{\rm{s}}\right) _x}{\beta^{0,0}} - \frac{1}{2}\frac{\left( u_{\rm{s}}^{0,0}\right) ^2\left( \beta^{0,0}\right) _x}{\left( \beta^{0,0}\right) ^2} \right], $$

(28a)

$$ \begin{array}{rll} F_{\rm{adv}}^{2,0}&=&-a^2\varepsilon^2 \frac{ \left(u^{0,0}_{\rm{s}}\right) ^2}{ 8\beta^{0,0}}\left[ 9\frac{u^{0,0}_{\rm{s}}\left( u^{0,0}_{\rm{s}}\right) _x}{\beta^{0,0}}+\right.\nonumber\\[2pt] &&\left.-3 \frac{\left( u^{0,0}_{\rm{s}}\right)^2 \left( \beta^{0,0}\right) _x}{\left( \beta^{0,0}\right)^2 } +\lambda u^{0,0}_{\rm{s}} e^{-\lambda(1-h)}\!\! \right] \!+\! O(a^4) ,\end{array}$$

(28b)

$$ F_{\rm{adv}}^{1,1}=a\varepsilon\gamma\frac{3\left(u^{0,0}_{\rm{s}}\right) ^3}{4 \beta^{0,0}}\sin(\phi)+O(a^3),$$

(28c)

$$ F_{\rm{vd}}^{0,0}=-a\kappa \frac{\lambda}{2} h_x \left( u^{0,0}_{\rm{s}}\right) ^2. $$

(28d)

In Section 3.1, we will focus on the influence of different flux contributions to the morphodynamic equilibria. In Section 3.2, the influence of the boundary conditions on the morphodynamic equilibria will be discussed.

3.1 Sediment transport mechanisms

In Sections 3.1.1 and 3.1.2, the water motion is only forced by a prescribed external M₂ tide, in Section 3.1.1, we focus on the diffusive sediment flux $F_{\rm{diff}}^{0,0}$, and in Section 3.1.2, the advective flux $F_{\rm{adv}}^{2,1}$ is added. In Sections 3.1.3 and 3.1.4, both M₂ and M₄ tidal constituents force the water motion. First, the influence of the advective flux due to the externally prescribed M₄ forcing $F_{\rm{adv}}^{1,1}$ is studied. Finally, in Section 3.1.4, the influence of the topographically induced sediment flux $F_{\rm{vd}}^{0,0}$ on the morphodynamic equilibrium is investigated.

3.1.1 Diffusively dominated transport

Results

As a first step, we only consider sediment transport due to the diffusive sediment flux $F_{\rm{diff}}^{0,0}$, given in Eq. 25. The equilibrium bed profile h _eq is determined by requiring that this tidally averaged sediment flux vanishes everywhere:

$$ \left\langle F_{\rm{diff}}^{0,0}\right\rangle =0. $$

(29)

The resulting bed profile is convex; see the dashed–dotted line in Fig. 3. A similar solution is obtained by Van Leeuwen et al. (2000), using a slightly different landward boundary condition. The convexity of the bed profile depends on the depth dependency of the deposition parameter β in the deposition term and its dependence on the Péclet number λ. Due to the depth dependency, deposition is stronger in shallower areas than in deeper parts of the basin. If the Péclet number is decreased relative to the reference case (e.g., taking finer sand), the obtained profile becomes more convex at first. However, there is a maximum in convexity for Péclet number λ∼0.3 (e.g., a sediment diameter d∼70 μm, for default vertical diffusion κ _v and depth H). When the Péclet number is decreased even more (e.g., for even finer sand), the profile becomes less convex and, finally, for extremely small Péclet numbers (e.g., very fine sediments), constantly sloping. For a Péclet number larger than that used in the reference case (e.g., medium sand), the profile tends to the constantly sloping profile. For a constant deposition parameter, β = 1 (i.e., large Péclet number), the constantly sloping bed is found, a result also obtained in Schuttelaars and De Swart (1996), who took β = 1. The dashed–dotted blue profile shown in Fig. 3 is obtained for a length of 20 km. Changing the (scaled) inlet length but keeping other parameters fixed results in the same morphodynamic equilibrium solution.

Fig. 3

Equilibrium bed profiles in case of only diffusively dominated transport (dashed–dotted blue line), for only advective (M₂) transport (dashed green line), and for both diffusive and advective transport (solid black line). These profiles are obtained using the default parameters (see Table 1) with a depth-dependent deposition parameter β. The dotted gray line (linearly sloping profile) is obtained for diffusively dominated transport with a constant deposition parameter (β∼1). (In this case (β = 1), the same profile can be found for advectively dominated or combined transport)

Discussion

The leading-order contribution to the diffusive sediment flux Eq. 25, given in Eq. 28a, consists of two parts. The first part is related to the spatial variations of the M₂ tidal amplitude and the second part is related to the spatial variations of the depth-dependent deposition parameter β.

First, consider the case that deposition is depth-independent (β = 1). In this case, the second term is zero. From the condition of morphodynamic equilibrium, it follows that $u^{0,0}_{\rm{s}}$ must be spatially constant. Using the analytic expression for $u^{0,0}_{\rm{s}}$ (Eq. 67a, Appendix C), the equilibrium bed profile has to be constantly sloping. Next, consider deposition depending on the local water depth. In case the bed profile is approximately a constantly sloping profile, the second contribution to $F_{\rm{diff}}^{0,0}$ is proportional to $\lambda h_x e^{-\lambda(1-h)}$. Since h _x is always positive, this flux is always importing. To get an equilibrium, the first term of $F_{\rm{diff}}^{0,0}$ must be exporting. Hence, $u^{0,0}_{\rm{s}}$ must increase towards the end of the embayment. Using Eq. 67a, it is clear that $u^{0,0}_{\rm{s}}$ increases if h becomes convex ($u^{0,0}_{\rm{s}}$ decreases for a concave bed). Hence, to get a morphodynamic equilibrium, h has to be convex. The more convex the bed profile, the larger the export due to the spatial variations in $u^{0,0}_{\rm{s}}$.

The magnitude of the importing flux depends on the Péclet number. This flux vanishes both for small and large Péclet number λ, resulting in a constantly sloping profile. For λ∼0.3, the import is maximal and, hence, the convexity is maximal. No maximum length exists, as the two fluxes that are part of $F_{\rm{diff}}^{0,0}$ can balance for any length.

3.1.2 Combined transport, introducing M₂ advective processes

Results

In this paragraph, we consider sediment transport due to both advective and diffusive processes. Since the water motion is only forced by an externally prescribed M₂ tidal constituent, overtides are only generated internally. This implies that the advective sediment flux only consists of $F_{\rm{adv}}^{2,0}$. Furthermore, we neglect the sediment transport due to topographic variations. The morphodynamic equilibrium condition reads

$$ \left\langle F_{\rm{diff}}^{0,0} + F_{\rm{adv}}^{2,0}\right\rangle =0, $$

(30)

where $F_{\rm{adv}}^{2,0}$ is defined in Eq. 23. The corresponding equilibrium bed profile is slightly less convex than the one obtained without advection; see the solid line in Fig. 3. The dashed–dotted line shows the equilibrium bed profile for diffusive transport only. The embayment becomes even less convex when only advective transport is considered (dashed line in Fig. 3). If the length of the embayment is increased, the solution becomes less convex. The same holds for a smaller horizontal diffusion parameter $\tilde \kappa$. The sensitivity to the Péclet number is the same as in the previous case: For large Péclet numbers, the profile becomes less convex; for smaller Péclet numbers, the profile becomes more convex, although, again, there is a maximum convexity.

Discussion

The leading order contribution to the advective sediment flux Eq. 23, given in Eq. 28b, consists of three parts. The first contribution is related to the spatial variations of the M₂ tidal amplitude and the second to the depth-dependent deposition parameter. These two contributions are very similar to those of the diffusive flux discussed above. The third term is always importing and is related to the Péclet number λ and strongly depends on the grain size.

When only the advective flux is considered, a slightly less convex profile was found, compared to the diffusively dominated case (see Fig. 3). Using that the third contribution of Eq. 28b is, in general, smaller than the first two terms, the convexity can be explained using the same arguments as for the diffusively dominated case: the second term is importing, so the first contribution has to be exporting, resulting in a convex bed. The bed is less convex compared to the diffusively dominated case as the ratio of the magnitude of the exporting flux and the importing flux is in case of the advectively dominated transport larger than in case of diffusively dominated transport (this ratio is three in case of the advective flux, while, for the diffusive case, the ratio is two). Hence, the bed must be less convex in the advectively dominated case to balance the import of sediment. This also explains why inclusion of diffusion results in a slightly more convex profile.

Using that the advective flux only depends on the length of the embayment by its dependency on the velocity, and that the diffusive flux scales with the length as 1/L ², it is evident that, if the length of the embayment is increased, the relative importance of the advective flux increases. Hence, slightly less convex profiles are found if the length is increased. Using the same argument as in the previous section, it is clear that no limitation for the length of the embayment exists. The sensitivity of the bed profile to the Péclet number can be understood using the arguments from the previous section.

3.1.3 Combined transport, introducing an overtide

Results

In the previous two paragraphs, the water motion was only forced by the leading order tide. In this paragraph, the water motion is forced by both an externally prescribed M₂ and M₄ tidal constituent. Neglecting the sediment transport due to the variations in topography, the condition for morphological equilibrium now becomes

$$ \left\langle F_{\rm{diff}}^{0,0} + F_{\rm{adv}}^{2,0} + F_{\rm{adv}}^{1,1} \right\rangle =0, $$

(31)

where $F_{\rm{adv}}^{1,1}$ is the flux due to the presence of the externally prescribed overtide, given in Eq. 24. It turns out that no equilibrium exists for embayment lengths of 20 km; the maximum embayment length (L _max) for which an equilibrium can be found is 8 km. The corresponding equilibrium bed profile is shown in Fig. 4. Decreasing the diffusion coefficient results in a decrease of the maximum length for which solutions can be found (i.e., $\tilde\kappa\simeq 10$ gives L _max∼3 km). When a larger Péclet number (e.g., coarser grains) is considered, the equilibrium profile becomes less convex (and eventually almost constantly sloping, if λ is large enough), and a slightly larger maximum length of the embayment can be found. For smaller Péclet numbers (e.g., finer sediment), the profile becomes more convex and the maximum embayment length decreases.

Fig. 4

Equilibrium profile for the default parameters is given by the solid line, the other profiles are obtained for different phase differences between the externally prescribed M₂ and M₄ tidal constituents

The advective sediment flux exports sediment out of the embayment when the relative phase difference lies between 150° and 180°. For a phase difference of 180° to 230°, this flux is importing. A phase difference of 150° to 156° results in an equilibrium profile (with L = 8 km) that is concave (see Fig. 4). The maximum length of the embayment is also related to the phase difference. For a phase difference between 180° and 230°, the maximum embayment length will increase with decreasing ϕ. For a phase difference such that $F_{\rm{adv}}^{1,1}$ is exporting, morphodynamic equilibrium profiles exist for all embayment lengths considered.

Discussion

The sign of the leading order contributions to the advective sediment flux due to an external forcing with an M₄ tidal current (Eq. 24), given in Eq. 28c, strongly depends on the phase difference ϕ between the M₂ and M₄ tidal constituents. For the default phase difference (195°), this flux is always importing; see the dotted line in Fig. 5a. In the range of ϕ values we consider, the import of sediment is largest when ϕ is close to 230°. For ϕ = 150°, the export of sediment is largest. For ϕ = 180°, the net sediment transport due to the external overtide is negligible. When the M₄ amplitude is increased (and, therefore, γ is larger), the effect of the advective flux $F_{\rm{adv}}^{1,1}$ will be larger.

Fig. 5

Equilibrium bottom profile (blue) and the corresponding sediment flux contributions obtained when the system is forces by both the M₂ and M₄ tidal constituents. a The reference case. b Here, ϕ = 156° and L = 25 km

To get a morphodynamic equilibrium for the reference phase difference ϕ = 195°, there has to be an exporting flux as well. The flux related to internally generated overtides is of the order a ² ε ²∼1.9·10^− 5, and turns out to be one order of magnitude smaller than $F_{\rm{adv}}^{1,1}=O(a\varepsilon\gamma)\sim 0.83\cdot 10^{-3}$. Hence, only the diffusive fluxes can balance the import due to the externally prescribed overtides. This is illustrated in Fig. 5a, where the sediment fluxes are shown. It is evident that the main balance is between the advective flux due to the externally generated overtide and the diffusive contribution. To get such a balance, the magnitude of the diffusive $F_{\rm{diff}}^{0,0}$ and advective $F_{\rm{adv}}^{1,1}$ contribution must be of the same order. Using Eqs. 28a and 28c, it is found that

$$ \frac{3}{4}\varepsilon \gamma \sin \phi \sim \kappa\;\;\;\;\;\;\;\;\;\; \Rightarrow \;\;\;\;\;\;\;\;\;\;L^{2}\sim \frac{4\tilde \kappa}{3\varepsilon \gamma \sigma\sin\phi }.\label{maxlength} $$

(32)

Physically, this means that the diffusive fluxes can only balance the advective fluxes for a not-too-long embayment, since this diffusive flux becomes too weak for longer embayments. In case of the parameter values of Table 1, Eq. 32 predicts a maximum embayment length of the order of 15 km; the precise value of L _max∼8 km follows from an exact consideration of the flux balance.

When the phase difference is chosen larger than its default value, the maximum embayment length decreases. If ϕ is decreased, the maximum embayment length increases. Note that Eq. 32 can only be used if the main balance is between the diffusive $F_{\rm{diff}}^{0,0}$ and advective $F_{\rm{adv}}^{1,1}$ fluxes. This is not the case anymore for ϕ ≃ 180°. In that case, the balance from the previous section must be considered.

If ϕ is such that the sediment flux is exporting, there is no restriction to the maximum length as the exporting effect of $F_{\rm{adv}}^{1,1}$ is balanced by both the diffusive and the advective fluxes, see Fig. 5b. If $F^{1,1}_{\rm{adv}}$ is importing, the diffusive flux must be exporting, which is only possible for convex profiles (see discussion in Section 3.1.1). This means that the convexity has to increase if the import due to $F^{1,1}_{\rm{adv}}$ increases, resulting in a maximum embayment length.

The advective flux $F^{1,1}_{\rm{adv}}$ only weakly depends on the settling velocity, and no qualitatively different results are found when varying ω _s , compared to the previous section.

3.1.4 Total combined transport, introducing the topographically induced sediment flux

Results

As in the previous paragraph, we consider an embayment forced with both the M₂ and M₄ tides, but now, the topographically induced sediment flux is included. Therefore, the morphodynamic equilibrium condition reads

$$ \left\langle F_{\rm{diff}}^{0,0} + F_{\rm{vd}}^{0,0} + F_{\rm{adv}}^{2,0} + F_{\rm{adv}}^{1,1}\right\rangle =0. $$

(33)

The expression for the topographically induced sediment flux $F_{\rm{vd}}^{0,0}$ is given in Eq. 26. This equilibrium profile is shown in Fig. 6 (solid line), which is an equilibrium for an embayment length of 20 km. The maximum embayment length for which a solution exists is L _max ≃ 21 km.

Fig. 6

Equilibrium profiles obtained when both diffusive and both M₂ and M₄ advective sediment fluxes are considered. The reference case, solid line; small diffusion parameter, dashed line; and for a coarser grainsize, dashed–dotted line

If the diffusion parameter κ is decreased, the maximum embayment length is reduced. In Fig. 6, the equilibrium bed profile (dashed line) is shown for $\tilde \kappa$=10, resulting in L _max ≃ 6 km. The morphodynamic equilibria are quite sensitive to the Péclet number λ. In the previous sections, changing λ only affected the convexity of the bed profiles. However, as a result of the topographically induced sediment flux, changing λ can result in concave profiles. In Fig. 6, the dashed–dotted line represents the profile obtained for λ = 3.6 (i.e., ω _s  = 0.03 m/s, with κ _v and H as given in Table 1).

The advective sediment flux still causes import of sediment for a phase difference between 150° and 180°, and export for a phase difference between 180° and 230°. For a phase difference of ϕ < 187°, the equilibrium (with L = 20 km) becomes concave. Again, there is no maximum embayment length when the advective flux $F_{\rm{adv}}^{1,1}$ results in export of sediment. For a phase difference ϕ that results in more import of sediment, the maximum embayment length becomes smaller.

Discussion

The diffusive sediment flux $F_{\rm{vd}}^{0,0}$, given by Eq. 26 and rewritten in Eq. 28d, strongly depends on the topography of the bed h through its spatial derivative. This means that this flux will be directed toward the deeper areas. Considering an embayment length of 20 km, the flux balance for the equilibrium solution is given in Fig. 7. At the entrance, the importing advective flux $F_{\rm{adv}}^{1,1}$ and diffusive flux due to variations in topography $F_{\rm{vd}}^{0,0}$ balance; at the landward boundary there is a balance between the importing fluxes $F_{\rm{adv}}^{1,1}$ and $F_{\rm{diff}}^{0,0}$ on the one hand, and the exporting flux $F_{\rm{vd}}^{0,0}$ on the other hand.

Fig. 7

Equilibrium bottom profile (blue line) and the corresponding sediment contributions obtained when the system is forced by both the M₂ and M₄ tidal constituent and both diffusive sediment fluxes are accounted for

Contrary to the previous case, an equilibrium exists for L = 20 km. This is due to the fact that $F_{\rm{vd}}^{0,0}$ results in an export of sediment. Hence, even for embayment lengths where the diffusive flux $F_{\rm{diff}}^{0,0}$ is not effective enough, the import of sediment due to $F_{\rm{adv}}^{1,1}$ can still be balanced.

The existence of a maximum embayment length can be understood as well: the magnitude of the sediment flux of the externally prescribed overtide only weakly depends on the embayment length; the diffusive fluxes strongly depend on the length. Both diffusive fluxes scale with 1/L ², resulting in a weaker flux when L is increased. If L is increased too much, the export of sediment decreases until it becomes too weak to balance the importing $F_{\rm{adv}}^{1,1}$, resulting in a maximum embayment length. This maximum embayment length will be larger than that found in Section 3.1.3 since the flux $F_{\rm{vd}}^{0,0}$ adds to the export of sediment.

The topographically induced sediment flux $F_{\rm{vd}}^{0,0}$ is proportional to the Péclet number λ. A small value of λ results in sediment being well mixed through the water column, and the effect of $F_{\rm{vd}}^{0,0}$ is rather small, while a larger value of λ results in a larger concentration gradient in the horizontal direction, resulting in a stronger flux due to topographic variations.

The convexity or concavity of the equilibrium profile depends on the length of the embayment, on the phase difference between the M₂ and M₄ tide, and on the Péclet number and can be understood by a detailed analysis of the various fluxes.

3.1.5 Depth-dependent erosion and deposition

Up till now, we considered the erosion and deposition parameter to be constant. Van Leeuwen et al. (2000) investigated the influence of a depth-dependent erosion and deposition, neglecting the topographically induced sediment fluxes and the externally prescribed overtides. They found that the equilibrium profiles are more convex, due to the introduction of the depth-dependent erosion and deposition. We also investigated this influence including all sediment fluxes, and it turns out that the conclusions of Van Leeuwen et al. (2000) are still valid: when considering depth-dependent deposition, the profile is slightly more convex, and a depth-dependent erosion results in a slightly less convex profile, see, respectively, the dashed and dashed/dotted profiles in Fig. 8. The combination of both depth-dependent erosion and deposition only slightly differs from the depth-independent profile; compare the solid and dotted profiles in this figure, respectively. We therefore use the simpler, depth-independent formulation in the remainder of this paper.

Fig. 8

Sensitivity of the morphology to depth-dependent formulations of the erosion and deposition

3.2 Influence of boundary conditions

In the literature, different boundary conditions at the landward and seaward boundaries are used. Therefore, we investigate the influence of these boundary conditions on the equilibrium bed profiles.

3.2.1 Inlet boundary conditions

Results

In De Jong (1995) and Hibma et al. (2003), it has been noted that the crucial difference in the evolution to equilibrium of various one-dimensional morphodynamic inlet models is a result of the boundary condition used at the seaward side; see also De Swart and Zimmerman (2009). We want to stress that the continuation method we use in this paper to obtain morphodynamic equilibria has nothing to do with time integration: this method tries to find a morphodynamic equilibrium, given the length of the embayment and the depth at the entrance (i.e., n = 0 in Eq. 16b). To investigate the influence of the boundary condition h _x  = 0 (i.e., n = 1) or h _xx  = 0 (i.e., n = 2) at x = 0 on the resulting morphodynamic equilibria, we vary the depth at the entrance in the range of 3 to 30 m and calculate the solutions for all depths. However, when considering h _x  = 0 as boundary condition at the entrance, we only accept those solutions that satisfy this condition as morphodynamic equilibria. This procedure works since we are looking for equilibrium profiles, i.e., profiles with a fixed depth at the entrance. The condition h _x  = 0 can be seen as an extra constraint the morphodynamic solution has to satisfy. A similar procedure is followed for the requirement that h _xx  = 0 at x = 0.

Fixing the length of the embayment and using the method described in Section 2.5, this procedure is visualized in Fig. 9a, where we plot the values of h _x |_x = 0 and h _xx |_x = 0 as a function of depth at the entrance for a fixed embayment length of L = 20 km. From this figure, it is clear that no equilibria are found when n = 1 is chosen in Eq. 16b, i.e., when h _x  = 0. This is the case for all embayment lengths between 3 and 30 km, and water depths between 5 and 30 m, with all other parameters having their default values, see Table 1. If n = 2, we observe that two morphodynamic equilibria exist (see the two zero crossings of the dashed–dotted line in Fig. 9a): one that is relatively shallow at the entrance, and one that is much deeper, see Fig. 9b. In Fig. 10, the dependence of these two equilibrium solutions on the length of the embayment is plotted. Decreasing the embayment length results in shallower basins, the entrance depth of the shallow solution changes faster with changing length of the embayment.

Fig. 9

Influence of inlet boundary conditions for reference case, varying the entrance depth H. a Values of the first and second derivatives of h at the entrance, for different entrance depths. b Two equilibrium bed profiles satisfying the seaward boundary condition h _xx |_x = 0 = 0

Fig. 10

Two equilibrium solutions satisfying the boundary condition h _xx |_x = 0 = 0 for every realistic (fixed) length of the embayment. The corresponding depths at the entrance are plotted

Next, we investigate the dependence of the possible solutions to the phase difference ϕ. As an example, we take a phase difference ϕ = 165°. In Fig. 11a, h _x |_x = 0 and h _xx |_x = 0 are plotted as a function of depth at the entrance. Here, we see h _xx |_x = 0 (dashed–dotted line again) crosses the zero axes two times. In this case, the value of h _x (solid line) crosses the zero axis as well. The corresponding equilibrium bed profiles are given in Fig. 11b. Here, the dotted (green) and dashed–dotted (blue) profiles are the shallow and deep solutions, corresponding to the condition h _xx |_x = 0 = 0, and the solid profile satisfies h _x |_x = 0 = 0.

Fig. 11

Influence of inlet boundary conditions in case the phase difference ϕ = 165°, varying the entrance depth H. a Values of the first and second derivatives of h at the entrance, for different entrance depths. b Two equilibrium bed profiles satisfying the seaward boundary condition h _xx |_x = 0 = 0 and one that satisfies h _x |_x = 0 = 0

In Fig. 12, the resulting morphodynamic equilibrium as a function of ϕ and the applied boundary condition is summarized. In this figure, the solid black line shows the water depth at the entrance as a function of φ, for which h _x |_x = 0 = 0 and L = 20 km, the dashed green line shows the shallow solution for which h _xx |_x = 0 = 0, the dashed–dotted blue line shows the deep solution for this boundary condition. The gray lines show the result for L = 25 km. From this figure, it is clear that, for a ϕ of 150° to 175°, three equilibrium solutions exist (including one satisfying the boundary condition with n=1), for a ϕ of 175° to 180°, only one solution exists, and for a ϕ of 180° to 230°, two solutions exist.

Fig. 12

Two equilibrium solutions satisfying the boundary condition h _xx |_x = 0 = 0, and one equilibrium solution satisfies the boundary condition h _x |_x = 0 = 0 for a range of phase differences. The corresponding depths at the entrance are plotted in color for an embayment length of L = 20 km and in gray for an embayment length of L = 25 km. Note that the assumption that bottom friction is negligible is not valid for the solutions with a depth less than 5 m

An interesting finding here is that the number of possible equilibrium solutions strongly depends on the chosen seaward boundary condition. For n = 0, for every depth at the entrance, one unique equilibrium profile can be found. When n = 1, there is only an equilibrium solution for a phase difference between 150° and 175°; no equilibrium exists for other values of ϕ. For n = 2, multiple equilibrium solutions can be found for a phase difference between 180° and 230°; only one unique equilibrium is found for ϕ between 150° and 175°

Discussion

When considering h _xx |_x = 0 = 0 for the reference case considering the range of ϕ and L values, we obtained one relatively shallow equilibrium, and one equilibrium that was much deeper for all embayment lengths we considered. Considering an embayment length of 10 km, the main flux balance is between $F_{\rm{adv}}^{1,1}$ and $F_{\rm{vd}}^{0,0}$ in case of a shallow basin (see Fig. 13a). For the deep solution, the flux balance is dominated by a balance between both diffusive fluxes over the total length, see Fig. 13b. Hence, we may characterize the shallow equilibrium as an advective–diffusive balance and the deep equilibrium as a diffusive balance.

Fig. 13

Equilibrium bottom profile (blue line) and the corresponding sediment flux contributions for both equilibrium solutions satisfying h _xx |_x = 0, for a length of 10 km. a Shallow-water solution, H = 7.60 m. b Deep-water solution, H = 29.30 m

When increasing the length of the embayment, $F^{0,0}_{\rm{diff}}$ becomes more important for the shallow solution, see Fig. 14a. For the deep solution, the advective flux, $F^{2,0}_{\rm{adv}}$, becomes more important at the entrance, see Fig. 14b. The main balance for the two solutions, however, is still quite different and has the characteristics as mentioned above.

Fig. 14

Equilibrium bottom profile (blue line) and the corresponding sediment flux contributions for both equilibrium solutions satisfying h _xx |_x = 0, for a length of 20 km. a Shallow-water solution, H = 14.8 m. b Deep-water solution, H = 32.5 m

When considering h _x |_x = 0 = 0 for phase differences corresponding to an exporting sediment flux, we obtained one possible solution. In Fig. 15, this morphodynamic equilibrium with the corresponding flux contributions is shown in case of a phase difference of ϕ = 165°. Obviously, the $F_{\rm{vd}}^{0,0}$ is zero at the entrance, where the flux balance is mainly between the diffusive flux $F_{\rm{diff}}^{0,0}$ and the flux due to the first overtide $F_{\rm{adv}}^{2,0}$. At the landward side of the basin, there is mainly a diffusively dominated balance.

Fig. 15

Sediment flux contributions for the equilibrium solutions satisfying h _x |_x = 0, where ϕ = 165° and H = 15.6 m

3.2.2 Landward boundary conditions

Until now, we required the water flux to vanish at the moving landward boundary. Another boundary condition often used at the landward end (Schuttelaars and De Swart 1996; Van Leeuwen et al. 2000) reads

$$ \left(1-h+\varepsilon\zeta \right) u=0\; \;\;\;\;\;\mathrm{at}\; x=1,$$

(34)

This condition assumes no net water flux through the boundary fixed at the landward side. There is hardly any effect on the equilibrium bed profile, but this boundary condition does strongly affect the velocities at this boundary. In case of a fixed boundary, velocities and concentration become singular at this fixed boundary, even though the water fluxes go to zero.

4 Observed bed profiles

The model results are compared with observations in the Ameland Inlet system and the Frisian Inlet system in the Dutch Wadden Sea. Here, we assume the basins are in morphodynamic equilibrium. Hence, their depth at the entrance and the length of the embayment follows from observations. In Fig. 16a, the dotted line indicates the depth profile obtained from the observation of the depth in the Ameland Inlet system that are averaged over the width of the basin. The model results are obtained using the moving landward boundary condition and a fixed depth at the entrance. When the topographically induced sediment flux is neglected, no equilibrium bed profiles can be found for the observed embayment length of 20 km (a maximum length of 8 km is found, see dashed–dotted profile). Including the topographically induced sediment flux results in a good comparison with the data. We also compared our model results for parameter values of the Frisian Inlet, resulting in similar conclusions, see Fig. 16b.

Fig. 16

A comparison of model results with observations. For the standard characteristics of the Ameland Inlet, see Table 1. The standard characteristics of the Frisian Inlet are A_M2  =  0.93, A_M4  =  0.08, ϕ  =  207°, w_s = 0.015 ms^− 1, H = 10 m, L = 15 km. a Ameland Inlet. b Frisian Inlet

5 Conclusion

In this paper, we investigate the existence of morphodynamic equilibria in a short, tidally dominated embayment of rectangular shape using the width- and depth-averaged shallow-water equations. The water motion in the embayment is driven by prescribed surface elevations at the seaward boundary, existing in a leading order tide and its first overtide. The sediment transport is described by the depth-integrated and width-averaged advection diffusion equation, and the bed changes due to convergence and divergence of sediment fluxes. To solve the resulting set of equations, we averaged these equations over a tidal period to separate the short tidal time scale and the longer morphodynamic time scale.

A topographically induced sediment flux, found by integrating the three-dimensional advection diffusion equation over the depth and averaging over the width is shown to be essential to obtain solutions that resemble observed morphodynamic equilibria when the system is forced by both the main tidal constituent and its first overtide. In many models, this term is neglected or assumed to be balanced by wind- or density-driven currents, see Schuttelaars (1997) and Van Leeuwen (2002). Furthermore, the influence of the morphological seaward boundary condition is investigated. We find that the bottom boundary condition at the seaward side has a considerable effect on the shape of the bottom profile and on the number of possible equilibrium solutions.

By prescribing the length of the embayment and its depth at the entrance, morphodynamic equilibria can be obtained using a continuation method. The resulting equilibria and their sensitivity to parameters can be explained in detail by considering the sediment fluxes in separation. If no overtide is present and only the diffusive sediment flux is considered, we find convex profiles that exist for every embayment length. After introducing the advective sediment flux resulting from internally generated overtides, similar profiles are found. In case that an external overtide is introduced that results in import of sediment, convex profiles are found for embayments up to a maximum length. When this overtide is exporting, both convex and concave profiles are found, and there is no restriction to the embayment length for which equilibria exist. Finally, the topographically induced sediment flux is introduced as well. For the case of the importing overtide, both concave and convex profiles are found, with a much larger maximum length than when compared to the case without this diffusive flux. The concavity of the profiles depends on the sediment properties and the length of the embayment. Again, in case the external overtide results in import of sediment, a maximum embayment length is found. In case this overtide results in export of sediment, there is no maximum for the embayment length. Comparing these solutions with observations of the Ameland inlet and the Frisian inlet systems in the Dutch Wadden sea, the profiles obtained when the topographically induced sediment flux is taken into account, compare much better than when the profiles are obtained without this flux.

The sensitivity to both the seaward and landward boundary conditions was considered in case all the sediment fluxes are included. At the seaward side, instead of prescribing the depth, we require its first or second derivative to vanish. It turns out that, in general, there are two morphodynamic equilibrium solutions when the latter condition is used. One solution is deep and concave, the other solution is shallow and almost constantly sloping. These solutions are found for most parameter settings considered in this paper. In case the external overtide results in little export of sediment, only the deep solution is found. Solutions satisfying a zero first derivative of the bottom at the entrance only exist if the overtide is exporting. These solutions are concave. Changing the boundary condition at the landward side did not result in qualitatively different results. We also considered the fixed landward boundary condition as used by Schuttelaars and De Swart (1996) and Van Leeuwen et al. (2000), but this affected neither the shape of the bottom profile, nor the number of possible solutions. It only affected the velocity and concentration at this boundary.

Finally, we want to stress that, in deriving the morphodynamic model, quite a few assumptions have been made. Here, we shortly discuss a number of processes and parameterizations that might affect the results. First, we assume the embayment to have a constant width. From literature (Todeschini et al. 2008), it is known that a strongly varying width can influence the morphodynamic equilibria. Second, we assume that bottom friction is negligible in the embayment. From a scaling analysis, it follows that this is not true in the shallow parts of the estuary. Third, we neglect the critical velocity for motion in the erosion formulation we used. Fourth, we neglect wind and density flows. Although the influence of these assumptions on the resulting morphodynamic equilibria is of interest and can be investigated by extending the model in the appropriate way, this is beyond the scope of the present paper.

Appendices

Appendix A: Derivation of the general 1D concentration equation

The conservation equation that describes the suspended sediment concentration (C ₃) in three dimensions is derived from the conservation of mass and reads

$$ \frac{\partial C_3}{\partial t}+\bigtriangledown\cdot\overrightarrow{F}=0, $$

(35)

where the sediment flux $\overrightarrow{F}=\overrightarrow{F}_a+\overrightarrow{F}_s+\overrightarrow{F}_d$, with

$$ \begin{array}{llll} \overrightarrow{F}_a&=&C_3\overrightarrow{u}+C_3w\overrightarrow{e}_z\;\;\;\;&\mathrm{Advective\;flux},\\ \overrightarrow{F}_s&=&-C_3\omega_s\overrightarrow{e}_z\;\;\;&\mathrm{Settling\;flux},\\ \overrightarrow{F}_d&=&-\kappa_h\bigtriangledown_hC_3-\kappa_v\displaystyle\frac{\partial C_3}{\partial z} \overrightarrow{e}_z \;\;\;\;&\mathrm{Diffusive\;flux}. \end{array} $$

(36)

Here, $\overrightarrow{u}$ is the horizontal velocity field, w is the vertical velocity component, ω _s is the settling velocity, $\overrightarrow{e}_z$ is a unit vector in the vertical direction, and κ _h and κ _v are horizontal and vertical diffusion coefficients, respectively. This leads to the following three-dimensional advection–diffusion equation for the suspended sediment concentration:

$$\begin{array}{rll} \frac{\partial C_3}{\partial t}&+&\bigtriangledown\left(C_3\overrightarrow{u}-\kappa_h\bigtriangledown_hC_3 \right)\\ &+& \frac{\partial}{\partial z}\left(C_3\left( w-\omega_s\right) - \kappa_v\frac{\partial C_3}{\partial z}\right) =0. \end{array}$$

(37)

As boundary conditions, the normal components of the combined diffusive and settling flux equal a specified erosion-deposition flux S _∗ (unit kg m^− 3),

$$ -\left(\overrightarrow{F}_s+\overrightarrow{F}_d \right)\cdot \overrightarrow{n}=S_\ast, $$

(38)

where $\overrightarrow{n}$ is a normal vector at the boundary, which is directed out of the fluid domain. At the non-erodible boundary (e.g., the free surface of the flow) the erosion–deposition flux S _∗ = 0; at the erodible bottom, the erosion-deposition flux is given by S _∗ = E − D, with E = ω _s c _a as the erosion flux and D = ω _s c _b as the deposition flux. Here, c _a is the reference concentration and has to be parameterized in terms of the flow conditions, whilst c _b is the concentration near the bottom and follows from the solution of the concentration equation. The erosion flux can be written as

$$ E=\omega_s\rho_s\left( 1-p\right)\Gamma \frac{|\tau_b|}{\tau_c}, $$

(39)

where ρ _s is the sediment density, p is the bed porosity, τ _b is the actual bed shear-stress, Γ is an empirical constant, and τ _c is the critical shear-stress for erosion. Note that we neglect the minimum threshold velocity below which no erosion occurs, as it usually has little effect in strong tidal conditions, see, for example, Prandle (2009, page 126–127). Furthermore, the linear relation between erosion and bed shear stress we adopt here is an approximation of the formulation proposed by Smith and McLean (1977). Note that, in fact, we assume that 1/γ ₀ ≫ τ _b /τ _c  ≫ 1 with $\gamma_0 \sim 10^{-5}$, see Dyer and Soulsby (1988).

To get an expression for the depth-integrated concentration, Eq. 37 is integrated over the depth:

$$\begin{array}{lll} && \int_h^{H+\zeta}\frac{\partial C_3}{\partial t}dz+\int_h^{H+\zeta}\bigtriangledown\left(C_3\overrightarrow{u}-\kappa_h\bigtriangledown_hC_3 \right)dz+\nonumber\\ &&\quad\int_h^{H+\zeta}\frac{\partial}{\partial z}\left(C_3\left( w-\omega_s\right) - \kappa_v\frac{\partial C_3}{\partial z}\right) dz=0. \end{array}$$

(40)

Using Leibniz’s rule for differentiation under the integral sign, this results in

$$\begin{array}{lll} &&\displaystyle\frac{\partial}{\partial t}\int_h^{H+\zeta}C_3dz+\bigtriangledown\cdot\int_h^{H+\zeta}C_3\overrightarrow{u}dz-\kappa_h\bigtriangledown_h \nonumber\\ &&\quad\cdot \displaystyle\int_h^{H+\zeta}\!\!\bigtriangledown_hC_3dz+\!\left[ -\displaystyle\frac{\partial }{\partial t}\left( H\!+\!\zeta\right)C_3-\bigtriangledown\left( H\!+\!\zeta\right) \cdot uC_3\right.\nonumber\\ [3pt] &&\qquad\qquad\qquad\qquad\qquad+\kappa_h \bigtriangledown_h\left(H+\zeta \right)\cdot \bigtriangledown_hC_3\Bigg] \mid_{z=H+\zeta}+\nonumber\\ [3pt] &&\left[ \displaystyle\frac{\partial}{\partial t}\left(h \right) C_3+\bigtriangledown(h)\cdot uC_3-\kappa_h\bigtriangledown_h\left( h\right)\cdot C_3\right] \mid_{z=h}+\nonumber\\ [3pt] &&\left[ C_3\left( w-\omega_s\right) - \kappa_v\displaystyle\frac{\partial C_3}{\partial z}\right]^{H+\zeta}_{h}=0. \end{array}$$

(41)

This expression can be simplified by using the kinematic boundary conditions, at the top and bottom, resulting in

$$ \begin{array}{lll} &&\left[ \displaystyle\frac{\partial \zeta}{\partial t}+u\frac{\partial \zeta}{\partial x}+v\frac{\partial \zeta}{\partial y}\right]_{z=H+\zeta}=w\mid_{z=H+\zeta},\\[14pt] &&\left[ \displaystyle\frac{\partial h}{\partial t}+u\frac{\partial h}{\partial x}+v\frac{\partial h}{\partial y}\right]_{z=h}\;\;\;\; =w\mid_{z=h}, \end{array}$$

(42)

Equation 41 is reduced to

$$\begin{array}{lll} &&\frac{\partial}{\partial t}\int_h^{H+\zeta}C_3dz+\bigtriangledown\cdot\int_h^{H+\zeta}C_3\overrightarrow{u}dz+-\kappa_h\bigtriangledown_h\nonumber\\ [3pt] &&\quad\cdot \int_h^{H+\zeta}\bigtriangledown_hC_3dz+\kappa_h \bigtriangledown_h\left(H+\zeta \right)\cdot \bigtriangledown_hC_3\mid_{z=H+\zeta}+\nonumber \\ [3pt] &&\quad-\kappa_h\bigtriangledown_h\left( h\right)\cdot C_3\mid_{z=h}+\left[ -C_3\omega_s - \kappa_v\frac{\partial C_3}{\partial z}\right]^{H+\zeta}_{h}=0.\nonumber\\ \end{array}$$

(43)

As a next step, we use the boundary conditions for the erosion flux S _∗ to further simplify this equation. First, we rewrite Eq. 38,

$$ -\left( -C_3\omega_s\overrightarrow{e}_z-\kappa_h\bigtriangledown_hC_3-\kappa_v\frac{\partial C_3}{\partial z} \overrightarrow{e}_z\right)\cdot \overrightarrow{n} =S_\ast. $$

(44)

The normal vectors at z = H + ζ and at z = h, which point out of the fluid domain, are given by

$$ \overrightarrow{n}_{\mathrm{top}}=\left(-\frac{\partial }{\partial x}\left(H+\zeta \right) ,-\frac{\partial}{\partial y}\left(H+\zeta \right),1 \right), $$

(45)

and

$$ \overrightarrow{n}_{\mathrm{bot}}=\left(\frac{\partial h}{\partial x} ,\frac{\partial h}{\partial y},-1 \right). $$

(46)

Introducing the vectors into Eq. 44, the boundary conditions for the erosion flux S _∗ become

$$ \omega_sC_3+\kappa_v\frac{\partial C_3}{\partial z}-\kappa_h \bigtriangledown_h\left(H+\zeta \right)\cdot \bigtriangledown_hC_3=0. $$

(47)

$$ -\omega_sC_3-\kappa_v\frac{\partial C_3}{\partial z}+\kappa_h \bigtriangledown_h\left(h \right)\cdot \bigtriangledown_hc=E-D. $$

(48)

When Eqs. 47 and 48 are introduced into Eq. 43, we find

$$\begin{array}{rll} \frac{\partial C_2}{\partial t}&+&\bigtriangledown\cdot\int_h^{H+\zeta}C_3\overrightarrow{u}dz-\kappa_h\bigtriangledown_h\cdot \int_h^{H+\zeta}\bigtriangledown_hC_3dz \\ &&=E-D, \end{array}$$

(49)

where $C_2=\int_h^{H+\zeta}C_3dz$ is the depth-integrated concentration with dimensions in kilograms per square meter. Now, the velocity and the concentration are decomposed in a depth-averaged part and a depth-dependent part, respectively. Hence, $\overrightarrow{u}=\overline{u}+u'$, where $\overline{u}$ is the depth-averaged velocity and u′ is the deviation of the depth-averaged velocity. This is done for C ₃ as well, i.e., $C_3=\overline{C}_3+C_3'$, where $\overline{C}_3=\frac{C_2}{\zeta+H-h}$. Substituting this in the along-channel advective part of Eq. 49 gives

$$\begin{array}{rll} \int_h^{H+\zeta}C_3\overrightarrow{u}dz&=& \int_h^{H+\zeta}C_3(\overline{u}+u')dz\nonumber\\ &=&\overline{u}C_2+\overline{C_3}\int_h^{H+\zeta}u'dz+\overline{u}\int_h^{H+\zeta}C_3'dz\notag\\ &&+\int_h^{H+\zeta}C_3'u'dz\nonumber\\ &=&\overline{u}C_2+\int_h^{H+\zeta}C_3'u'dz\\ &=&\overline{u}C_2+\int_h^{H+\zeta}-\kappa_d\frac{\partial C_3}{\partial x}dz, \end{array}$$

(50)

where the assumption was made that $C_3'u'=-\kappa_d\frac{\partial C_3}{\partial x}$ (in case of an estuary of constant depth, this assumption reduces to the shear dispersion as discussed by Fischer et al. 1979). Introducing Eq. 50 into Eq. 49 leads to the two-dimensional concentration equation

$$ \frac{\partial}{\partial t}C_2+\bigtriangledown\cdot C_2\overline{u} -\kappa\bigtriangledown_h\cdot \int_h^{H+\zeta}\bigtriangledown_hC_3dz=E-D,$$

(51)

where $\tilde\kappa=\kappa_d+\kappa_h$.

The erosion flux E is given by Eq. 39 and the deposition flux is defined by D = ω _s c _b , where c _b is the concentration at the bottom. In order to express c _b in the depth-integrated concentration C ₂, an approximate balance is assumed between the dominant terms in the 3D concentration Eq. 37, the vertical turbulent mixing and downward settling. Hence, the balance reads

$$ \omega_sC_3=-\kappa_v\frac{\partial C_3}{\partial z}. $$

(52)

The vertical dispersion coefficient is assumed to be independent of z. Using the boundary condition at the bottom C ₃|_z = h = c _b , the solution to this equation is

$$C_3=c_be^{-\frac{\omega_s}{\kappa_v}\left( z-h\right) }. $$

(53)

Integration over depth gives the concentration near the bottom expressed in the depth-integrated concentration. This results in

$$ c_b=\frac{\omega_s}{\kappa_v}\beta_bC_2,\;\;\;\mathrm{where}\;\;\beta_b=\frac{1}{1-e^{-\frac{\omega_s}{\kappa_v}\left(\zeta+H-h \right) }}. $$

(54)

Using this expression for the bottom concentration, the deposition flux D can be expressed as

$$ D=\frac{\omega_s^2}{\kappa_v}\beta_b C_2. $$

(55)

Expressing the bed shear stress as $\tau_b=\rho c_d|\overline{u}|\overline{u}$ (Soulsby 1997, page 53) and the critical bed shear stress as $\tau_c=\rho u^2_{\ast\rm{c}}$ (where ρ is the water density and u _∗ c is the critical friction velocity), the erosion flux reads

$$ E=\left[ \rho_s\left( 1-p\right)\frac{\Gamma \omega_s} {u^2_{\ast\rm{c}}}c_d\right]u^2=\alpha u^2. $$

(56)

Substituting the expression for the deposition flux D, Eq. 55 and erosion Eq. 56 in Eq. 51 give

$$\begin{array}{rll} \frac{\partial}{\partial t}C_2&+&\bigtriangledown\cdot C_2\overline{u} -\tilde\kappa\bigtriangledown_h\cdot \int_h^{H+\zeta}\bigtriangledown_hC_3dz\nonumber\\ &&=\alpha \overline{u}^2-\frac{\omega_s^2}{\kappa_v}\beta_b C_2, \end{array}$$

(57)

where α is a coefficient related to sediment properties (erosion, grain size, shape, etc.) In the concentration Eq. 57, only the diffusion term still needs to be expressed in terms of C ₂. Using Leibniz’s rule, the diffusion term becomes

$$\begin{array}{rll} \tilde\kappa\bigtriangledown_h\cdot \int_h^{H+\zeta}\!\bigtriangledown_hC_3dz&=&-\tilde\kappa \bigtriangledown_h\cdot\Big[ \bigtriangledown_h\int_h^{H+\zeta}C_3dz+\nonumber\\ &&-\bigtriangledown_h\left(H+\zeta \right) C_3\mid_{z=H+\zeta}\notag\\ &&+\bigtriangledown_h\left(h \right) C_3\mid_{z=h}\Big]\\ &=&-\tilde\kappa \bigtriangledown_h\cdot\Big[\!\bigtriangledown_hC_2\!-\!\bigtriangledown_h\left(H\!+\!\zeta \right)c_t\\&&+\bigtriangledown_hh c_b\Big], \end{array}$$

(58)

where c _t  = C ₃|_{z = H + ζ}. According to Eq. 53, $c_t=c_be^{-\frac{\omega_s}{\kappa_v}\left(H+\zeta-h \right) }$, with c _b defined in Eq. 54. This results in

$$ c_t=\frac{\omega_s}{\kappa_v}\beta_tC_2,\;\;\;\;\;\;\mathrm{with}\;\;\beta_t=\frac{1}{e^{\frac{\omega_s}{\kappa_v}\left(\zeta+H-h \right) }-1}. $$

(59)

Substituting these expressions in Eq. 58, the concentration equation reads

$$\begin{array}{rll} \frac{\partial}{\partial t}C_2&+&\bigtriangledown\cdot C_2\overline{u}\\&-&\tilde\kappa\bigtriangledown_h\cdot \left[ \bigtriangledown_hC_2-\bigtriangledown_h\left(H+\zeta \right)\cdot \left( \frac{\omega_s}{\kappa_v}\beta_tC_2\right) \right.\notag\\ &&\left. + \bigtriangledown_h\left(h \right)\cdot \left( \frac{\omega_s}{\kappa_v}\beta_bC_2\right) \right]=\alpha \overline{u}^2-\frac{\omega_s^2}{\kappa_v}\beta_b C_2.\nonumber\end{array}$$

(60)

Taking a constant width, the two-dimensional concentration equation directly reduces to the one-dimensional concentration equation, which we use in the main text.

$$\begin{array}{rll} \frac{\partial}{\partial t}C&+&\left( uC\right)_x-\tilde\kappa C_{xx}+\tilde\kappa\frac{\omega_s}{\kappa_v}\left[ \left(H+\zeta \right)_x \beta_tC\right]_x \\ &-&\tilde\kappa\frac{\omega_s}{\kappa_v}\left[\beta_bh_xC\right]_x =\alpha u^2-\frac{\omega_s^2}{\kappa_v}\beta_b C. \end{array}$$

(61)

Appendix B: Analytical solution of the bed evolution equation (diffusively dominated transport)

The bed evolution equation for diffusively dominated transport, including both the diffusive and the topographically induced sediment fluxes, leads to the following differential equation:

$$ \frac{x-1}{\left({1-h_{eq}}\right)^2}+\frac{(x-1)^2h_{eq,x}}{(1-h_{eq})^3}+\lambda\frac{h_{eq,x}(x-1)^2}{2(1-h_{eq})^2}=0, $$

with h _eq (x = 0) = 0. Define

$$ h_{eq}(x)=1-\frac{2}{\lambda}f(b(x-1)), $$

(62)

and substitute this expression in Eq. 62. After substituting Z = (x − 1) in the resulting expression, one finds the following equation:

$$ Z\left(1+f(bZ) \right)f_Z(bZ)=f(bZ). $$

(63)

This equation can be solved in terms of the LambertW function. Using the boundary condition, the resulting expression for h _eq reads

$$ h_{eq}(x)=1-\frac{2}{\lambda}W\left( -\frac{\lambda}{2}(x-1)e^{\left( \frac{\lambda}{2}\right) }\right) . $$

(64)

Appendix C: Model solutions

1.1 Water motion

According to the momentum Eq. 12b, the elevation of the sea surface is independent of the position in the basin. This means that the sea-surface excursions are determined by the tidal excursion at the open end and are uniform in the embayment.

$$ \zeta(t)=\cos(t)+\frac{\gamma}{2}\cos(2t-\phi). $$

(65)

Given expressions 20 and 21, it follows that

$$ \zeta_{\rm{c}}^{0,0}=1, \;\;\;\;\;\;\;\;\; \zeta_{\rm{s2}}^{0,1}=\frac{1}{2}\sin(\phi),\;\;\;\;\;\;\;\;\; \zeta_{\rm{c2}}^{0,1}=\frac{1}{2}\cos(\phi). $$

(66)

Using the continuity Eq. 12a, boundary condition h _eq |(x = 0) = 0, and expressions 20 and 21, the velocity can be solved explicitly and reads

$$ u_{\rm{s}}^{0,0}(x)=\frac{x-1}{1-h}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;u_{\rm{s2}}^{1,0}(x)=\frac{-\zeta_{\rm{c}}^{0,0}u^{0,0}_{\rm{s}}+c_{I1} } {2\left( 1-h\right) }$$

(67a)

$$ u_{\rm{s2}}^{0,1}(x)=\frac{2\zeta^{0,1}_{\rm{c2}}x+c_{I2}}{\left( 1-h\right) } \;\;\;\;\;\;\;\;\;u_{\rm{c2}}^{0,1}(x)=\frac{-2\zeta^{0,1}_{\rm{s2}}x+c_{I3}}{\left(1-h\right) }, $$

(67b)

where

$$ c_{I1}=\frac{\zeta_\text{c}^{0,0}{u^{0,0}_\text{s}}_x|_{x=1}}{h_x|_{x=1}}(1-h)|_{x=1}+\zeta^{0,0}_\text{c}u^{0,0}_s|_{x=1},$$

(68)

$$ c_{I2}= -\frac{2\zeta^{0,0}_\text{c2}\left( 1- h\right)|_{x=1} }{h_x|_{x=1}}-2\zeta^{01}_\text{c2}$$

(69)

$$ c_{I3}=\frac{2\zeta^{0,0}_\text{s2}\left( 1- h\right)|_{x=1} }{h_x|_{x=1}}+2\zeta^{01}_\text{s2}.$$

(70)

1.2 Sediment transport

To solve for the concentrations, the deposition parameter β is expanded in the small parameter ε, as explained in Section 2.5. The leading-order contributions read

$$ \beta^{0,0}=\frac{1}{1-e^{-\lambda(1-h)}}, \;\;\;\;\;\;\;\;\; \beta_{\rm{c}}^{1,0}=-\frac{e^{-\lambda(1-h)}\lambda}{(1-e^{-\lambda(1-h)})^2}.$$

(71)

Note that there is no contribution of first order in γ.

According to the main balance of the concentration equation, the first-order non-zero amplitudes are

$$\begin{array}{rll} \left\langle C^{0,0}\right\rangle&=&\frac{1}{2}\frac{{u_{\rm{s}}^{0,0}}^{2}}{{\beta^{0,0}}}, C^{0,0}_{\rm{c2}}=\frac{1}{2}\frac{-\beta^{0,0}{u_{\rm{s}}^{0,0}}^{2}}{\left( {\beta^{0,0}}^2+4a^2 \right)}, \\ C^{0,0}_{\rm{s2}}&=&\frac{-a{u_{\rm{s}}^{0,0}}^{2}}{{\beta^{0,0}}^2+4a^2}, \end{array}$$

(72)

$$\begin{array}{rll} C^{1,0}_{\rm{s}}&=&\left\{-2a\beta^{0,0}\left[u^{0,0}_{\rm{s}}\left\langle C^{0,0}\right\rangle\right]_x +a\beta^{0,0}\left[ u^{0,0}_{\rm{s}}C^{0,0}_{\rm{c2}}\right]_x\right. \\&&{\kern4pt}-a^2\left[ u^{0,0}_{\rm{s}}C^{0,0}_{\rm{s2}}\right]_x + 2au^{0,0}_{\rm{s}}u^{1,0}_{\rm{2s}}-\beta^{0,0}\beta^{1,0}_{\rm{c}}C^{0,0}_{\rm{s2}} \notag\\ [3pt]&&{\kern4pt}-\left.a\beta^{1,0}_{\rm{c}}C^{0,0}_{\rm{c2}}- 2a\beta^{1,0}_{\rm{c}}\left\langle C^{0,0}\right\rangle\right\}\frac{1}{2\left(a^2+{\beta^{0,0}}^2 \right)},\nonumber\end{array}$$

(73)

$$ C^{0,1}_{\rm{s}}=\frac{au^{0,0}_{\rm{s}}u^{0,1}_{\rm{s2}}-\beta^{0,0}u^{0,0}_{\rm{s}}u^{0,1}_{\rm{c2}}}{{\beta^{0,0}}^2+a^2}. $$

(74)

Only the amplitudes necessary to calculate the tidally averaged sediment flux are given here.

The leading-order and order-ε terms are generated by the external M₂ forcing and the internally generated overtides. The terms of order γ are generated by the interaction of the M₂ tide and the externally prescribed M₄ tidal forcing.

Appendix D: Scaling the equations of motion

Using scaling analysis, this supplement shows how the morphodynamic equations are obtained (Eqs. 12a–12d). As a starting point, we take the width-averaged shallow-water equations, the width- and depth-averaged concentration equation, and the bed evolution equation. Considering a rectangular embayment:

$$\zeta_t-h_t+\left[(\zeta+H-h)u \right]_x=0,$$

(75)

$$u_t+uu_x+\frac{ru}{(\zeta+H-h)}=-g\zeta_x,$$

(76)

$$\begin{array}{rll} C_t&+&\left( uC\right)_x-\tilde\kappa C_{xx}+\tilde\kappa\frac{\omega_s}{\kappa_v}\left[ \left(H+\zeta \right)_x \beta_tC\right]_x+\\ &&-\tilde\kappa\frac{\omega_s}{\kappa_v}\left[\beta_bh_xC\right]_x =\alpha u^2-\frac{\omega_s^2}{\kappa_v}\beta_b C,\end{array}$$

(77)

$$\rho_{\rm{s}}\left( 1-p\right)\left( h_t+\left\langle S_{\rm{b}}\right\rangle_x \right) =-\left\langle \alpha u^2-\frac{\omega_s^2}{\kappa_{\rm{v}}} \beta C\right\rangle,$$

(78)

where S _b is the volumetric sediment flux in the active layer (bed load). A parameterization of the bed load transport presented in (Dyer 1986; Van Rijn 1993) is used:

$$ S_\text{b}=\hat{s}\frac{|u|^\text{b}}{u_\text{c}^\text{b}}\left(\frac{u}{|u|}-\mu_* h_{x} \right) $$

(79)

Here, u _c is the critical velocity for erosion which, for fine sand, is of the order of 0.3 m s^− 1. Typical values for b and κ _* are b∼3 and κ _*∼2, see Van Rijn (1993). The parameter $\hat{s}$ is a function of the sediment properties. According to Dyer (1986); Fredsoe and Deigaard (1992); Van Rijn (1993), a typical value of $\hat s$ is O(10^− 6) m² s^− 1 for fine sand.

These equations are made dimensionless by scaling the variables as

$$ \begin{array}{lll} x=Lx^\ast,&t=t^\ast\sigma^{-1},&u=Uu^\ast,\\[4pt] \zeta=A_{\text{M}_\text{2}}\zeta^\ast=\displaystyle\frac{HU}{\sigma L}\zeta^\ast,&C=\displaystyle\frac{\alpha U^2 \kappa_\text{v}}{\omega_\text{s}^2}C^\ast,&h=Hh^\ast. \end{array}$$

(80)

Typical values for these quantities are given in Table 1. Substituting the scaled variables in Eq. 75 results in

$$ \frac{\sigma H U}{\sigma L}\zeta^*_{t^*}\!-\!\sigma H h^*_{t^*}\!+\!\frac{U}{L}\left[\left( \frac{H U}{\sigma L}\zeta^*\!+\!H\!-\!H h^*\right)u^* \right]_{x^*}\!=\!0. $$

(81)

Dividing by σH U/(σL) and introducing $\varepsilon=\frac{U}{\sigma L}\sim0.07$ leads to

$$ \zeta^*_{t^*}-\frac{1}{\varepsilon} h^*_{\tau^*}+\left[\left(\varepsilon\zeta^*+1-h^*\right)u^* \right]_{x^*}=0. $$

(82)

In a similar way Eq. 76 reduces to

$$ u^*_{t^*}+\varepsilon u^* u^*_{x^*}+\frac{\hat{r}u^*}{(\varepsilon\zeta^*+1-h^*)}=-\Lambda^2 \zeta^*_{x^*}. $$

(83)

Considering the characteristics of the Ameland inlet system, $\hat{r}=\frac{r}{\sigma H }\sim0.25$ and $\Lambda^2=\frac{gH}{\sigma^2 L^2}\sim 15$. Therefore, the left-hand side of the equation is negligible, except for the shallow region at the end of the embayment. Therefore, the momentum equation can be approximated by Eq. 12b. The simplification of the momentum equation only holds for embayments with a length that is small compared with the tidal wave length (Λ² ≪ 1) and when the frictional time scale is at least of the same order as the tidal period.

The concentration equation in dimensionless form reads

$$ a\left[ C_t+ \varepsilon\left( uC\right)_x-\kappa\left[ C_x+\lambda \beta h_xC\right]_x\right] =u^2-\beta C, $$

(84)

where a = σκ _v /ω _s .

Dividing Eq. 78 by $\rho_{\rm{s}}\left( 1-p\right)\sigma H$ gives

$$ h^*_{t^*}+\delta_{\rm{b}}\left\langle \left( |u^*|^\text{b}\left(\frac{u^*}{|u^*|}-\mu h^*_{x^*} \right)\right)_{x^*} \right\rangle =-\delta\left\langle {u^*}^2-\beta C^*\right\rangle,$$

(85)

where $\mu=\frac{\kappa_*H}{L}$, $\delta=\frac{\alpha U^2}{\rho_{\rm{s}}\left( 1-p\right)\sigma H}$, and $\delta_{\rm{b}}=\frac{\hat{s}}{\sigma H L}\left( \frac{U}{u_\text{c}}\right) ^\text{b}$. Using the typical values corresponding to fine sand and the characteristics of the Ameland inlet, δ∼7.2·10^− 5 and $\delta_{\rm{b}}\sim8.3\cdot10^{-9}$. The bed load contribution is considerably smaller than the suspended load contribution, when considering fine sand, and, hence, has been neglected in Eq. 12d. Furthermore, it follows that the bed changes on a much larger time scale than the hydrodynamic time scale. Using this in Eq. 82 implies that 1/εh _t is negligible (δ/ε∼10^− 3) compared to the first terms, resulting in Eq. 12a.