1 Introduction

An accurate description of the oceanic state is essential for understanding the climate system, particularly at lower frequencies, since the ocean serves as a large reservoir and conveyor of heat and water. Furthermore, a continuous monitoring of the oceanic state is of paramount importance for socioeconomic activities, such as fisheries, weather forecasting, ship navigation, and marine rescue. For the above cited reasons, one of the key goals in operational oceanography is to obtain a dynamically consistent oceanic state and forecast its future evolution. A wide range of assimilation methods have been proposed to effectively incorporate information derived from in situ and satellite observations into ocean general circulation models (OGCMs). Recent advances in observational techniques, increase in computational power, and development of elaborated numerical schemes for OGCM and data assimilation have enabled us to routinely monitor the state of world oceans. Various ocean reanalysis products are also available, both at a global (Balmaseda et al. 2008, 2013; Carton and Giese 2008; Chassignet et al. 2009; Toyoda et al. 2013; Zuo et al. 2017; Carton et al. 2018; Lellouche et al. 2021) and a regional (Usui et al. 2006, 2017; Miyazawa et al. 2009; Oke et al. 2013) scale: these products have been extensively used for studies of physical oceanography and climate sciences, and contributed to a deeper understanding of the role played by the ocean.

Recently, a growing body of evidence demonstrated that frontal-scale oceanic variability, such as mesoscale eddies, and associated modulations of current fields, plays important roles in water mass formation, air-sea interaction, and transports of heat/freshwater/biogeochemical tracers (Dong et al. 2014; Zhang et al. 2014; Ma et al. 2016). As a source of stochasticity, mesoscale variability interacts with large-scale circulation through nonlinear processes (Pierini 2006; Taguchi et al. 2007; Arbic et al. 2014; Sérazin et al. 2015, 2016). Indeed, recent modelling studies with high-resolution OGCMs have pointed out that characteristics of spatiotemporal variability in sea surface height (SSH) fields are remarkably different depending on the horizontal resolution of OGCMs (Sérazin et al. 2015; Penduff et al. 2018; Close et al. 2020), due to the emergence of intrinsic variability at mesoscales (from 10 to 100 km). More in detail, the intrinsic oceanic variability has been demonstrated to not only affect the characteristics and predictability of mesoscale eddy fields, but also to alter that of large-scale circulation in the global ocean (Nonaka et al. 2016, 2020; Sérazin et al. 2016; Leroux et al. 2018). Growing interests into mesoscale variability and its roles in the global ocean motivated us to expand the model domain of the Japan Coastal Ocean Predictability Experiments (JCOPE) system, which is a regional ocean monitoring and forecasting system for the western North Pacific, to the global ocean. Even with the current generation of supercomputers, constructing an eddy-resolving ocean reanalysis product for the global ocean is still a challenging task in terms of computational requirements. Indeed, most of the state-of-the-art products are still at eddy-permitting resolution (with horizontal resolutions of 1/3°–1/4°) (Balmaseda et al. 2015), although several operational centers have started to provide eddy-resolving (~ 1/10°) regional (Miyazawa et al. 2009; Oke et al. 2013; Usui et al. 2017) and global products (Chassignet et al. 2009; Metzger et al. 2014; Lellouche et al. 2018, 2021).

The JCOPE system is a dynamical ocean monitoring and forecasting system configured for the western North Pacific at eddy-resolving resolutions: it has been continuously developed by the Japan Agency for Marine-Earth Sciences and Technology (JAMSTEC), with several versions released with different horizontal resolutions and data assimilation schemes (Miyazawa et al. 2009, 2017). The JCOPE system has been routinely used for nowcasting and forecasting of ocean state around Japan on a daily basis to provide information for social communities: it can realistically capture temperature, salinity, and current fields within the western North Pacific (Miyazawa et al. 2009) and has been widely used to investigate various aspects of the upper ocean circulations in the area (Soeyanto et al. 2014; Mitsudera et al. 2018; Aoki et al. 2020). Furthermore, the JCOPE system has been used for socio-economic application studies, such as the dispersion of radionuclide around Japan (Miyazawa et al. 2012a, 2013), and the migration of Japanese eel (Chang et al. 2015). Given the promising skills of the JCOPE system in the western North Pacific, we have extended its model domain to the global ocean, by developing a new eddy-resolving quasi-global ocean reanalysis product, the JCOPE Forecasting Global Ocean (JCOPE-FGO). In the present manuscript, we provide an overview of its basic formulation, as well as the validation of its analyzed fields from 1993 to 2021.

One key novel aspect of our newly developed product is the use of an updated river forcing: the JCOPE-FGO incorporates river runoff forcing with a daily resolution into the OGCM, whereas climatological or monthly mean forcing have been adopted in most of other existing products. River forcing used in our system are based on the JRA55-do, which is a state-of-the art dataset of historical river discharge rates and is used for the coordinated Ocean Model Intercomparison Project (OMIP) (Suzuki et al. 2018; Tsujino et al. 2018). Inclusions of refined river forcing may be important for an accurate representation of near-surface salinity and other related fields especially in coastal regions. Indeed, several regional and global studies have examined the impact of continental river runoff by comparing two sets of OGCM experiments with and without river runoff, pointing out that near-surface salinity is strongly affected by the intrusion of freshwater from large rivers, such as the Amazon and Ganges/Brahmaputra (Han et al. 2001; Masson and Delecluse 2001; Yaremchuk et al. 2005; Huang and Mehta 2010; Gévaudan et al. 2022). However, these studies are mostly based on OGCMs with relatively coarse resolutions; thus, several important factors, such as continental shelves around the coast and dispersions of coastal freshwater by mesoscale eddies, may not be accurately represented. To assess the impact of river discharge on the representation of the analyzed oceanic fields, we have conducted an additional reanalysis experiment that does not incorporate river runoff into the OGCM. By comparing it with the reference reanalysis product, here we evaluate the impact of river runoff upon the analyzed oceanic fields, with a specific focus on coastal salinity.

This paper is organized as follows. In Sect. 2, we describe basic formulations of the OGCM (Sect. 2.1), the three-dimensional variational (3DVAR) method (Sect. 2.2), and procedures for the assimilation cycle (Sect. 2.3) used in the present version of the JCOPE-FGO. Section 3 presents validations of the analyzed fields in the JCOPE-FGO against assimilated and independent observations. The impact of river runoff is discussed in Sect. 4 using an additional reanalysis product that does not include river discharge forcing. Summary and perspective for future development and applications are provided in Sect. 5.

2 Data and methods

2.1 Ocean model configuration

The OGCM used in this system is the third-generation model of JCOPE (JCOPE-T; Varlamov and Miyazawa 2021), which has been developed based on the Princeton Ocean Model with a generalized coordinate of sigma (POMgcs) (Mellor et al. 2002). The source code of this model is optimized for massive parallel calculation with Message Passing Interface. As shown in Fig. 1, the model covers the global ocean from 75°S to 75°N except for the Arctic Ocean, with a horizontal resolution of 0.1° × 0.1°. No sea ice model and tidal forcing are included in the present version. The model has 44 sigma levels for the vertical direction, while bottom topography (color shading in Fig. 1) is taken from the bathymetry dataset of ETOPO5, after a spatial smoothing is applied to mitigate errors in the calculation of the pressure gradient force (Mellor et al. 1994). The northern and southern boundaries are closed, and a non-slip condition is imposed along continental boundaries. In regions near the northern and southern artificial boundaries, temperature and salinity fields of the whole water column are restored to the monthly climatological values of the World Ocean Atlas 2013 (WOA13). The restoring timescale along these boundaries are set to 1 day, and it gradually increases to infinity at a latitudinal distance of 5° from the boundaries. Similar temperature and salinity restoring with a nudging timescale of 30 days are also applied to the following marginal seas to avoid spurious model drift: the Mediterranean, Black, Baltic, and Red Sea, as well as the Persian Gulf and Okhotsk Sea, as in several other ocean reanalysis products (Usui et al. 2006; Miyazawa et al. 2009). This restoring of temperature and salinity leads to a better representation of water masses spreading from Arctic regions and marginal seas such as the Okhotsk water (Mitsudera et al. 2004); however, it acts to suppress their temporal variations that may potentially alter density stratification and circulation. We have adopted the flux-corrected transport scheme (Boris and Book 1973) to calculate the tracer advection term, while the fourth order scheme (McCalpin 1994) is used for the baroclinic pressure gradient. A biharmonic viscosity of 1.0 × 109 m4 s−1 and a diffusivity of 1.0 × 108 m4 s−1 are added to suppress computational noise. In addition, the turbulent closure scheme of Furuichi et al. (2012), a modified version of the Mellor-Yamada scheme, is used to calculate vertical viscosity and diffusion coefficients.

Fig. 1
figure 1

The model domain of the JCOPE-FGO. The bottom topography used in the model (from ETOPO5 data) is represented by color shading. Locations of river mouths incorporated into the model are indicated by red dots, and the size of each dot represents the value of annual mean discharge rate (in m.3/s; see legends)

Full size image

Surface-forcing fields are taken from hourly meteorological fields from the National Centers for Environmental Prediction Climate Forecast System (NCEP-CFS) (Saha et al. 2010, 2014); its first version (CFSv1) has been used from January 1993 to December 2010, while the second version (CFSv2) has been employed from January 2011. These forcing fields include downward longwave radiation, surface wind/air temperature/humidity, cloudiness, and precipitation. The turbulent heat and freshwater fluxes at the sea surface, as well as the wind stress, are computed by these meteorological fields, and modelled sea surface temperature (SST) and surface currents using the bulk formulae of Li et al. (2010). In addition, the daily river discharge obtained from the JRA55-do dataset (Suzuki et al. 2018; Tsujino et al. 2018) is used to represent the freshwater input from rivers to the open ocean. In the present system, only large rivers with their annual mean discharge rates exceeding 1.0 × 103 [m3 s−1] are incorporated; locations of individual river mouths are depicted by red dots in Fig. 1. Here the freshwater flux at the sea surface is represented as the virtual salt flux, and river runoff is added to precipitation values at the grid points adjacent to each river mouth, following methodology adopted in other studies (Huang and Mehta 2010).

2.2 3DVAR

To smoothly assimilate satellite and in situ observations into the OGCM, we apply the same 3DVAR scheme of the original JCOPE2 system (Miyazawa et al. 2009) to obtain the analysis value. The state vector \(\mathbf{X}\) represents temperature and salinity from the sea surface to 1500 m depth at each grid point; the 3DVAR scheme seeks to minimize the cost function J, which can be defined as:

$$J\left(\mathbf{X}\right)={\left(\mathbf{X}-{\mathbf{X}}^{\mathbf{f}}\right)}^{\mathbf{t}}{\mathbf{B}}^{-1}\left(\mathbf{X}-{\mathbf{X}}^{\mathbf{f}}\right)+{\left({\mathbf{y}}_{\mathbf{T}}^{\mathbf{o}}-{\mathbf{H}}_{\mathbf{T}}\mathbf{X}\right)}^{\mathbf{t}}{\mathbf{R}}_{\mathbf{T}}^{-1}\left({\mathbf{y}}_{\mathbf{T}}^{\mathbf{o}}-{\mathbf{H}}_{\mathbf{T}}\mathbf{X}\right)+{\left({\mathbf{y}}_{\mathbf{S}}^{\mathbf{o}}-{\mathbf{H}}_{\mathbf{S}}\mathbf{X}\right)}^{\mathbf{t}}{\mathbf{R}}_{\mathbf{S}}^{-1}\left({\mathbf{y}}_{\mathbf{S}}^{\mathbf{o}}-{\mathbf{H}}_{\mathbf{S}}\mathbf{X}\right)+{\left({\mathbf{y}}_{\mathbf{S}\mathbf{S}\mathbf{H}\mathbf{A}}^{\mathbf{o}}-{\mathbf{H}}_{\mathbf{S}\mathbf{S}\mathbf{H}\mathbf{A}}\mathbf{X}\right)}^{\mathbf{t}}{\mathbf{R}}_{\mathbf{S}\mathbf{S}\mathbf{H}\mathbf{A}}^{-1}\left({\mathbf{y}}_{\mathbf{S}\mathbf{S}\mathbf{H}\mathbf{A}}^{\mathbf{o}}-{\mathbf{H}}_{\mathbf{S}\mathbf{S}\mathbf{H}\mathbf{A}}\mathbf{X}\right)+{\left({\mathbf{y}}_{\mathbf{S}\mathbf{S}\mathbf{T}}^{\mathbf{o}}-{\mathbf{H}}_{\mathbf{S}\mathbf{S}\mathbf{T}}\mathbf{X}\right)}^{\mathbf{t}}{\mathbf{R}}_{\mathbf{S}\mathbf{S}\mathbf{T}}^{-1}\left({\mathbf{y}}_{\mathbf{S}\mathbf{S}\mathbf{T}}^{\mathbf{o}}-{\mathbf{H}}_{\mathbf{S}\mathbf{S}\mathbf{T}}\mathbf{X}\right),$$
(1)

where \({\mathbf{X}}^{\mathbf{f}}\) denotes the first guess value; \(\mathbf{B}\) is the background error covariance matrix; \({\mathbf{y}}_{\mathbf{T}}^{\mathbf{o}}, {\mathbf{y}}_{\mathbf{S}}^{\mathbf{o}},{\mathbf{y}}_{\mathbf{S}\mathbf{S}\mathbf{H}\mathbf{A}}^{\mathbf{o}},\) and \({\mathbf{y}}_{\mathbf{S}\mathbf{S}\mathbf{T}}^{\mathbf{o}}\) are column vectors representing observed in situ temperature, salinity, satellite sea surface height anomaly (SSHA), and SST, respectively; and \({\mathbf{H}}_{\mathbf{T}},{\mathbf{H}}_{\mathbf{S}},{\mathbf{H}}_{\mathbf{S}\mathbf{S}\mathbf{H}\mathbf{A}}\), and \({\mathbf{H}}_{\mathbf{S}\mathbf{S}\mathbf{T}}\) are the corresponding operators that project the model state to observations (see below for details). In addition, \({\mathbf{R}}_{\mathbf{T}},{\mathbf{R}}_{\mathbf{S}},{\mathbf{R}}_{\mathbf{S}\mathbf{S}\mathbf{H}\mathbf{A}}\), and \({\mathbf{R}}_{\mathbf{S}\mathbf{S}\mathbf{T}}\), denote respective observation error covariance matrices. Based on the first guess and observed values, the analysis value that minimized the cost function (1) is obtained by a conjugate gradient method.

Due to computational constraints, analysis is made on a 1/3° × 1/3° horizontal grid that covers the OGCM domain, and the 3DVAR analysis is separately conducted for 23 subdomains shown in Fig. 2. There are overlapping areas around borders of subdomains, and values over overlapping domains are linearly weighted to ensure smooth transitions across borders following Fujii and Kamachi (2003a). Furthermore, to efficiently represent hydrographic properties, the state vector is expressed in terms of the temperature-salinity coupling empirical orthogonal function (T-S coupling EOF; Fujii and Kamachi 2003b). After normalizing temperature and salinity at each vertical level, T-S coupling EOFs are separately calculated for each subdomain, based on historical archives of temperature and salinity profiles from the World Ocean Database 2013 (WOD13) (Levitus et al. 2013). Here, the first 12 EOFs are retained in the present configuration, which explain more than 90% of the total observed temperature and salinity variability over individual subregions. The T-S coupling EOF scheme has been adopted by several operational ocean reanalysis systems (Usui et al. 2006; Miyazawa et al. 2009; Toyoda et al. 2013) and is shown to successfully represent various water mass properties of the global ocean (Fujii and Kamachi 2003b, a).

Fig. 2
figure 2

a Allocation of model subdomains used for 3DVAR analysis of JCOPE-FGO. Areas with more than two subregions overlap are indicated by purple shading. b, c Spatial distribution of b zonal and c meridional scales (in km) used for the background error covariance matrix

Full size image

To project the modelled fields to three-dimensional temperature \({\mathbf{H}}_{\mathbf{T}}\) (and salinity \({\mathbf{H}}_{\mathbf{S}}\) as well as SST \({\mathbf{H}}_{\mathbf{S}\mathbf{S}\mathbf{T}}\), we adopt the bilinear interpolation scheme. The projection of SSHA (\({\mathbf{H}}_{\mathbf{S}\mathbf{S}\mathbf{H}\mathbf{A}}\)) is nonlinear, and it consists of two steps. First, we compute the dynamic height from model’s temperature and salinity fields assuming the reference depth of 2000 m. Second, satellite SSHAs are added to the climatological dynamic height field computed from the temperature and salinity of the WOA13. Then, they are compared in terms of cost function to estimate the analysis values of temperature and salinity; thus, the model’s SSH field is not directly incremented in our scheme.

Formulations of error covariance matrices are also basically similar to those adopted in the JCOPE2. The background error covariance matrix represented in the normalized T-S EOF subspace is specified as a Gaussian function:

$$\mathrm{exp}\left(-\frac{{d}_{x}^{2}}{{S}_{x}^{2}}\right)\bullet \mathrm{exp}\left(-\frac{{d}_{y}^{2}}{{S}_{y}^{2}}\right),$$
(2)

where \({d}_{x}\) and \({d}_{y}\) represent zonal and meridional distances between the grid points, and \({S}_{x}\) (\({S}_{y}\)) denotes zonal (meridional) scale. In our system, \({S}_{x}\) and \({S}_{y}\) are specified as shown in Fig. 2b, c, respectively, based on statistical results by Kuragano and Kamachi (2000). The observation covariance matrices of in situ temperature and salinity, satellite SSHA, and SST are assumed to be diagonal matrices, as in Miyazawa et al. (2009). The first guess value, \({\mathbf{X}}^{\mathbf{f}}\), is obtained by blending temperature and salinity calculated by OGCM and climatological values. For more detailed settings and formulations of the 3DVAR scheme, readers are referred to Miyazawa et al. (2009).

Data sources for in situ and satellite observations are as follows: temperature and salinity profiles are obtained from the delayed-mode archive of the Global Temperature-Salinity Profile Program (GTSPP; see http://www.nodc.noaa.gov/GTSPP/index.html). The SSHA satellite is acquired from along-track SSHA data of the Ssalto/Duacs altimeter products, released by CMEMS; the satellite SST is from the Merged satellite and in situ data Global Daily Sea Surface Temperatures (MGDSST) (Kurihara et al. 2006) provided by the Japan Meteorological Agency.

2.3 Assimilation cycle

The assimilation cycle interval corresponds to 7 days: procedures archived during one cycle of assimilation are schematically summarized in Fig. 3. First, the OGCM is initialized from the end of the previous assimilation cycle and integrated forward for 4 days to obtain the first guess value located at the midpoint of the assimilation window. Then, the 3DVAR scheme is used to synthesize the model’s state, as well as observed and yield analysis values of temperature and salinity at the midpoint. Considering the fact that typical repeat cycles of satellite altimeters are around 10 days, the time windows of satellites SSHA and SST are set to 9 days (− 4 day to + 4 day), whereas that of the GTSPP temperature and salinity are 19 days (− 9 day to + 9 day) due to limited number of profiles particularly at earlier periods of the reanalysis. Finally, the model is again restarted from the final state of the previous assimilation cycle and integrated forward for 7 days with incremental corrections for every time step. Here, incremental corrections are applied following the incremental analysis update (IAU) methodology by Bloom et al. (1996), in which the difference between the first guess and analysis values divided by 7 days is smoothly added to tendency equations of temperature and salinity during integrations. The reanalysis of JCOPE-FGO has been made from January 1993 to present, and all outputs are available as daily-averaged values. We present reanalysis results performed between January 1993 and December 2021.

Fig. 3
figure 3

Schematic diagram illustrating assimilation cycles of JCOPE-FGO (see the main text for details (Sects. 2.2 and 2.3))

Full size image

In addition to this reference reanalysis product, we have constructed an additional product that has the same configuration as the original one, except that it does not include river runoff forcing: this additional experiment spanning from January 1993 to December 2018 is referred to as “NoRIV” reanalysis and will be used to assess the impact of river runoff in Sect. 4.

3 Validation of reanalysis product

3.1 Temperature and salinity

As a first step to validate JCOPE-FGO, climatological views of analyzed sea surface temperature (SST) and salinity (SSS) are shown in Fig. 4. Gross features of the climatological SST pattern, such as the cold tongue in the eastern equatorial Pacific, the warm pool extending from the western equatorial Pacific to the Indian Ocean, and the sharp SST fronts in the western boundary current regions, are adequately analyzed with JCOPE-FGO (Fig. 4a). Similarly, the large-scale patterns of climatological SSS fields, including their subtropical maxima, fresh pools around the tropical rain bands and Bay of Bengal, and the distinct interbasin contrast between the Atlantic and Pacific (with higher SSS in the Atlantic than in the Indo-Pacific sectors), are also well analyzed. In addition, JCOPE-FGO reasonably represents the general features of the observed upper ocean circulation and mesoscale eddy fields (Fig. 4c, d), as we will discuss in detail in Sect. 3.2.

Fig. 4
figure 4

Climatology of sea surface temperature (a: in °C), salinity (b: in psu), height (SSH) (c: in m), and eddy kinetic energy (EKE) (d: in m2/s2) at the sea surface from JCOPE-FGO, averaged over January 1993–December 2021. Note that EKE is calculated from surface geostrophic currents derived from SSH fields; thus, regions near the equator are masked out in d

Full size image

To quantitatively assess how and to which extent our product can reproduce observed temperature and salinity fields, the mean bias, correlation, and root mean square errors (RMSE) of SST and SSS with respect to profiles in the GTSPP archive are presented in Fig. 5. Note that these reference observations are assimilated in JCOPE-FGO; thus, they are not totally independent from each other. However, a good agreement between analyzed and assimilated fields is a necessary condition to demonstrate the skills of the reanalysis product; thus, we perform this comparison as a benchmark test. To construct the global maps of statistical metrics described above, individual profiles in the GTSPP archive within the analysis period (January 1993 to December 2021) are binned into a 1° × 1° grid covering the model domain, while corresponding reanalysis fields for each location and date of observations are interpolated using daily outputs of JCOPE-FGO. Due to inhomogeneous distributions of observational platforms, the number of observations is not spatially uniform: relatively large numbers are found near the coastlines of the northern hemisphere and along major ship tracks (Fig. 5a, b).

Fig. 5
figure 5

Comparison of SST and SSS between the GTSPP and JCOPE-FGO. The number of temperature and salinity profiles from January 1993 to December 2021 per 1° × 1° grid is shown in a and b, respectively. Mean bias (i.e., JCOPE-FGO minus GTSPP) of SST and SSS are shown in c and d, respectively, whereas correlations (e, f) and root mean squared errors (g, h) are displayed in the lower two panels. In e and f, only correlation coefficients statistically significant at the 99% confidence level are plotted

Full size image

The mean bias of SST (Fig. 5c) is less than 0.5 °C in most part of the global ocean except for several regions near the coast (e.g., south of Japan, east coast of the USA). The correlation between observed and analyzed SST is also close to unity in most regions (Fig. 5e), suggesting that our product can adequately capture the mean fields and temporal variability of SST. The RMSEs of SST between the observation and JCOPE-FGO are relatively large around the western boundary current regions (Fig. 5g): this may reflect strong intrinsic variability associated with strong mesoscale eddy activities (see Fig. 4d) (Bishop et al. 2017; Small et al. 2020).

Compared to SST, relatively large SSS biases of JCOPE-FGO are found in several locations (Fig. 5d): specifically, fresher biases are seen in the eastern equatorial Pacific, Bay of Bengal, and eastern tropical Atlantic, whereas saltier biases are found in the Gulf Stream and Kuroshio Extension regions. The correlation coefficients between SSS of JCOPE-FGO and that of observations are also lower than SST, although they are still statistically significant in most part of the global ocean, and are especially high in the tropics (Fig. 5f). RMSEs of SSS are less than 0.3 psu in most part of the global ocean, but regions with prominent bias (e.g., eastern tropical Pacific, the Bay of Bengal) and strong mesoscale eddy activities (e.g., Gulf stream regions) tend to have large values of RMSEs (Fig. 5h). These results suggest that the product broadly captures the observed spatiotemporal variations in SSS, even though there are several regions with relatively large biases. Such disagreement between JCOPE-FGO and observed fields are likely to be caused by multiple factors, such as limited numbers of salinity observations used to constrain the model (Fig. 5a, b), weaker dependence of salinity upon atmospheric forcing compared to temperature (Mignot and Frankignoul 2003; Kido et al. 2021), and deficiencies in OGCM and 3DVAR schemes. Although a detailed investigation on the origin of model bias for each region is beyond the scope of the present study, a careful and coordinated assessment of the aforementioned factors will be helpful for possible improvements in representation of SSS fields of the future versions.

To assess the reliability of the analyzed subsurface temperature and salinity fields, we have carried out similar validation procedures with the GTSPP for each vertical level from the surface to 1500 m depth (Fig. 6). Results for all profiles in the global ocean (Fig. 6a, b) show that the vertical structures of mean temperature and salinity analyzed in JCOPE-FGO are broadly consistent with those of the GTSPP (Fig. 6a, b, represented by black and red curves). This can be confirmed from the fact that globally averaged temperature biases are lower than 1 °C (Fig. 6a, blue curve), while those that regard salinity are lower than 0.1 psu (Fig. 6b, blue curve). The RMSE of temperature is relatively large (~ 1.5 °C) between 100 and 200 m depth, compared to other depths, presumably due to large temperature variations associated with vertical displacements of thermocline (Fig. 6a, green curve). The RMSE of salinity is large (~ 0.7 psu) near the surface: this may be due to relatively large errors in SSS as discussed above (Fig. 6b; see also Fig. 5). These results demonstrate that JCOPE-FGO can reasonably reproduce thermohaline structures in the global ocean.

Fig. 6
figure 6

Comparison of temperature and salinity vertical profiles from JCOPE-FGO and GTSPP archives. a and b represent temperature and salinity for the whole domain, with black (red) curves representing the mean values of GTSPP (JCOPE-FGO) (bottom axis). Mean biases of JCOPE-FGO (blue curves) and root mean square errors between JCOPE-FGO and GTSPP (green curves) (top axis) are also shown. c, d Same as in a and b, but for the equatorial Pacific (120°E–80°W, 5°S–5°N). e, f Same as in c and d, but for the western North Pacific (135°–180°E, 20°–40°N). g, h Same as in c and d, but for the western North Atlantic (80°W–40°W, 20°–40°N). i, j Same as in c and d, but for the eastern South Pacific (120°W–80°W, 32°–20°S)

Full size image

To better delineate regional features, similar comparisons between analyzed temperature and salinity and GTSPP archives have been conducted regarding several key regions that exhibit characteristic water mass structures (Fig. 6c-j). In the equatorial Pacific, JCOPE-FGO has positive (negative) temperature biases near 100 to 200 m (400 to 500 m) depth (Fig. 6c), which correspond to the lower part of the thermocline, suggesting that the analyzed thermocline in the JCOPE-FGO is too shallow compared to observations. Such thermocline bias is a common problem for other OGCMs and ocean reanalysis products (Usui et al. 2006; Balmaseda et al. 2008): a too low vertical resolution and misrepresentations of vertical mixing processes in OGCMs are most the likely factors at the origin of this problem. Furthermore, thermohaline properties of water masses found in subtropical oceans, such as the Subtropical Mode Water in the western North Pacific (Fig. 6e, f) and Atlantic oceans (Fig. 6g, h) (Hanawa and Talley 2001), are analyzed in detail within the JCOPE-FGO, although temperature in the upper (lower) part of the thermocline are too warm (cold) compared to in situ observation. In addition, JCOPE-FGO reasonably captures hydrographic structures of subtropical salinity maximum regions (Fig. 6i, j). In the present research, we have carefully checked hydrographic structures in other parts of the global ocean and found that qualitative features seen in GTSPP observations are reasonably represented in JCOPE-FGO throughout the analysis period (both before and after the launch of the Argo network around 2004). The overall agreement of mean temperature and salinity fields between JCOPE-FGO and GTSPP demonstrates that our product can realistically represent spatiotemporal patterns of upper ocean thermohaline structures in most part of the global ocean, although some quantitative biases, possibly due to deficiencies of OGCMs and the 3DVAR scheme, have been found in several regions. A more comprehensive assessment using independent in situ observations (e.g., intensive observation campaigns) would be helpful to understand regional features.

3.2 Sea level and velocity fields

In order to assess dynamical fields analyzed in JCOPE-FGO, we have constructed climatologies of sea surface height (SSH) and eddy kinetic energy (EKE), as for SST and SSS. Here, EKE is calculated from surface geostrophic currents obtained from SSH fields, as follows:

$$EKE=\frac{1}{2}\left({u}_{g}^{\mathrm{^{\prime}}2}+{v}_{g}^{\mathrm{^{\prime}}2}\right)=\frac{1}{2}\left[{\left(-\frac{g}{f}\frac{{\partial h}^{\mathrm{^{\prime}}}}{\partial y}\right)}^{2}+{\left(\frac{g}{f}\frac{{\partial h}_{\mathrm{^{\prime}}}}{\partial x}\right)}^{2}\right],$$
(3)

where \(f\) is the Coriolis parameter, \(g\) is the gravitational acceleration, and \({h}^{^{\prime}}\) represents SSH anomaly (obtained by subtracting climatological values) (Qiu and Chen 2013). Several important signatures of the upper ocean circulation, such as swift zonal currents near the equator, the western boundary currents (e.g., the Kuroshio, Gulf Stream, and Agulhas current), and the Antarctic Circumpolar Current (ACC), can be qualitatively inferred from the climatological map of SSH fields (Fig. 4c). In addition, our product reasonably captures the distribution of mesoscale eddies in the global ocean, with large values in the western boundary current regions, such as the Kuroshio and Gulf stream (Fig. 4d). Generally, the amplitude of EKE in JCOPE-FGO is comparable to that derived from satellite altimetry data and other eddy-resolving ocean reanalysis products: indeed, the globally averaged EKE from JCOPE-FGO is 0.0084 m2/s2, while that calculated from the observed SSHA with the same method is 0.010 m2/s2. However, some quantitative discrepancies between JCOPE-FGO and observation do exist at regional scales, and this could be due to implicit spatial smoothing applied in the 3DVAR scheme (note that analysis grid of 3DVAR is 1/3° × 1/3°) as well as misrepresentations of related dynamical fields (e.g., horizontal and vertical shear of large-scale currents).

Next, climatology of surface velocity is similarly constructed from JCOPE-FGO (Fig. 7) to better describe the upper-ocean circulation. The global map of horizontal current fields (Fig. 7a) demonstrates that the major currents in the world oceans have been reasonably analyzed. Seasonal changes in surface currents, such as the Somali Current in the western Indian Ocean and the Wyrtki Jet in the equatorial Indian Ocean, are also correctly analyzed in the JCOPE-FGO (figures not shown). Since our model has a horizontal resolution of 0.1°, fine structures of jets flowing in the western boundary current regions are adequately represented, as inferred from magnified plots of current fields (Fig. 7b-e).

Fig. 7
figure 7

a Surface velocity from JCOPE-FGO averaged over January 1993–December 2021. The current speed is represented by color shading, whereas zonal and meridional velocities are shown by vectors. b–e As in a, but with magnified views in the western North Pacific (b), North Atlantic (c), South Indian Ocean (d), and South Atlantic (e). Locations of passages used to estimate volume transports (Table 1) are indicated by green lines

Full size image

To understand how our reanalysis product can realistically track the temporal variation in SSHA, we have calculated correlation coefficients and RMSEs between SSHAs from JCOPE-FGO and those derived from the CMEMS gridded product (Fig. 8). We note that the CMEMS SSHA is used to correct analyzed temperature and salinity fields via 3DVAR scheme, but the SSH field is not directly incremated in our configuration (see Sect. 2.2). Since the OGCM employed in this system is a volume-conserving model with the Boussinesq approximation, a globally uniform steric effect due to thermal expansion of seawater is not explicitly included in terms of sea level fields (Greatbatch 1994; Griffies et al. 2014). Indeed, the globally averaged SSH is almost constant in time in JCOPE-FGO, while it increases steadily in time in the satellite altimeter. Thus, we removed linear trends of SSHAs both from JCOPE-FGO and satellite altimeter prior to calculation of skill metrics.

Fig. 8
figure 8

a Correlation and b RMSE of sea-level anomalies between FGO and the CMEMS gridded SLA. In a, only correlation coefficients statistically significant at the 99% confidence level are plotted

Full size image

The globally averaged value of correlation coefficients is 0.71, and their values are especially high in the tropical Pacific and Indian Ocean (Fig. 8a). High correlations in the Indo-Pacific region may reflect the fact that SSHA variability in these regions is predominantly caused by wind-driven baroclinic waves (Timmermann et al. 2010; Roberts et al. 2016). Correspondingly, RMSEs are very small at lower latitudes (Fig. 8b). Our product is also skillful at representing time evolution of SSHA in midlatitude oceans; statistically significant correlation coefficients are found even near the western boundary current regions (Fig. 8a), despite the presence of strong intrinsic variability (Fig. 8b, see also Fig. 1a by Nonaka et al. 2020). These results suggest that corrections of temperature and salinity fields via assimilation of satellite SSHA actually lead to correct representations of SSHA. The spatial pattern of correlation map of SSHA fields (Fig. 8a) is broadly similar to other ocean reanalysis products with eddy-permitting OGCMs (for example, see Fig. 2b by Balmaseda et al. 2015), but our product seems to better track variability in the extratropical oceans (e.g., the Kuroshio Extension and Agulhas Current regions) possibility, owing to higher horizontal resolution of the OGCM.

However, several regions with relatively low correlations of SSHA have also been detected, such as the eastern North Pacific (around 150°–120°W, 30°–45°N), the southern part of tropical Atlantic Ocean (around 40°W–20°E, 15°–5°S), and the southeastern tropical Pacific (120°–80°W, 30–15°S). These regions are characterized by relatively weak temporal variability of SSHA; thus, the signal-to-noise ratio is smaller than in other regions. More detailed investigations are required to understand the origin of these discrepancies. Possible remedies are more elaborated domain decompositions for the 3DVAR scheme (Fig. 2a), adjustment of spatial-scale parameters (Fig. 2b, c), and use of ensemble technique to better utilize information provided by the satellite altimetry data.

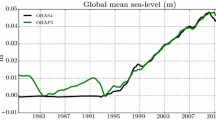
While the model’s SSHA fields do not explicitly include the increasing trend associated with the thermal expansion of water column, it is possible to diagnostically calculate the steric sea level height from three-dimensional density fields (Greatbatch 1994; Griffies et al. 2014). To demonstrate this point, we have computed the steric sea level height at each grid point by vertically integrating density anomalies from the bottom to the surface, and their long-term trends are compared with those from satellite observation (Fig. 9a-c). The overall increasing trends of the observed SLA, as well as some regional features (e.g., enhanced sea level rising in the Kuroshio regions and weaker sea level rise in the eastern equatorial Pacific), are also captured in the steric sea level height fields of the JCOPE-FGO. The temporal evolution of globally averaged sea level anomalies in the observation also agrees well with that of steric height of the JCOPE-FGO (Fig. 9c), apart from some quantitative discrepancies. This again confirms that the JCOPE-FGO can reasonably analyze three-dimensional temperature and salinity fields both at regional and global scales.

Fig. 9
figure 9

a Spatial pattern of linear trends of sea-level anomalies during the period of January 1993–December 2021 calculated from the CMEMS. b As in a, but for that of steric sea-level height of JCOPE-FGO. c Time series of globally averaged sea-level anomalies from CMEMS (red line) and steric sea level of JCOPE-FGO

Full size image

The dynamical fields of JCOPE-FGO have been further evaluated by comparing surface current fields with independent observations obtained by drifting buoys. For this purpose, we have adopted the quality-controlled 6-h interpolated surface drifting buoys provided by the NOAA Global Drifter Program (NOAA GDP data) (Lumpkin and Centurioni 2019) as reference data. Similar to the validation of temperature and salinity fields, all drifter data from January 1993 to December 2021 are binned into a 1° × 1° horizontal grid; comparisons are made on a daily basis at each grid point and corresponding location to calculate statistical metrics (i.e., mean bias, correlation, and RMSE).

The mean bias of surface current fields of JCOPE-FGO with respect to the NOAA GDP drifter data are generally negligibly small in most part of the global ocean, except for its zonal component in the equatorial Pacific. To the west of the dateline in the equatorial Pacific, JCOPE FGO produces a too strong westward current compared to the drifter observation, whereas the westward current is weaker than the observation to the east (Fig. 10a). Such biases in the equatorial currents may be due to inaccuracies in wind forcing and misrepresentation of vertical stratification. Other regional features in surface current biases, such as slight southward shift of Gulf Stream to the east of the Cape Hatteras, and weaker southwestward current off the Brazilian coast around 30°S have also been detected, but the overall patterns of the mean surface current fields in JCOPE-FGO compare well with those obtained from observation.

Fig. 10
figure 10

a, b Mean errors of surface zonal (a) and meridional (b) currents from JCOPE-FGO relative to the NOAA drifter data (i.e., the JCOPE-FGO minus observation). c, d As in a and b, but for correlations between JCOPE-FGO and NOAA drifter data. e, f As in c and d, but for root mean square errors (RMSE)

Full size image

Additionally, the correlation coefficients of zonal and meridional currents between the JCOPE-FGO and NOAA-GDP drifters are reasonably high and statistically significant in many areas of the global ocean, further demonstrating the skill of our product in representing surface current fields. The correlation coefficients of zonal currents are generally larger than that of meridional currents, especially in the tropics: this is presumably due to the larger magnitude (and hence larger signal-to-noise ratio) of the zonal than that of the meridional component. RMSEs between JCOPE-FGO and NOAA-GDP are large over regions with strong currents and mesoscale eddies, such as the western boundary current regions and equatorial Pacific. The spatial patterns of metrics of current fields (Fig. 10) largely agree with those of SSHA fields (Fig. 8), implying that both validations against assimilated (i.e., satellite SSHA) and independent (i.e., drifter data) observation give consistent results.

Due to the scarcity of available observations, it is not possible for us to validate spatiotemporal variability of subsurface current fields on a global scale. Instead, we calculated vertically integrated volume transports across several major sections using JCOPE-FGO and compared these values with historical estimates (Table 1). First, the time-averaged volume transport of the Indonesian throughflow agree well with direct estimates (15.7 Sv in the JCOPE-FGO, whereas it corresponds to 15 Sv according to Sprintall et al. 2009). Furthermore, we have checked volume transports across each section (e.g., the Lombok strait), which also match well with observations. Values of volume transports of major western boundary currents (here we compared Kuroshio, Gulf Stream, and Agulhas Currents) are consistent with historical estimates by direct observation (Fig. 7b-d, Table 1). In addition, the mean northward volume transport across 26.5°N in the upper 1000 m, which is a measure of the strength of the Atlantic Meridional Overturning Circulation (AMOC), is 13.6 Sv; this is close to the observational estimates of about 17 Sv (Cunningham et al. 2007; Karspeck et al. 2017). The vertical structure of the time-mean AMOC stream function at that latitude seen in the observation, with a northward flow in the upper 1000 m and southward return flow in the deeper layer, is also correctly captured in the JCOPE-FGO (figure not shown). However, the Kuroshio Current flowing south of Japan (31.3 Sv) seems to be somehow underestimated compared to the direct observation (42 Sv; Imawaki et al. 2001). Volume transport of ACC across the Drake passage exceeds 100 Sv in JCOPE-FGO (109 Sv), but it is lower than the estimate from direct observation (141 Sv; Koenig et al. 2014) (Table 1). It is not easy to articulate the reason responsible for the underestimations, but differences in estimation periods, contributions from small-scale features not adequately captured in the observation, and implicit spatial smoothing made by the 3DVAR scheme are possible factors. Further validations of our product against directly observed three-dimensional current fields will be helpful for a more comprehensive evaluation.

Table 1 Time-mean volume transport through several major passages (in Sv = 1.0 × 106 [m3/s]) (see Fig. 7 for locations of each passage)
Full size table

4 Impact of river runoff forcing

4.1 Global impact

To assess the impact of river discharge on representations of upper ocean fields, we have constructed a twin reanalysis product that does not include river forcing in the OGCM (referred to as the NoRIV product), as described in Sect. 2.3. Using outputs from both products, we firstly compare global maps of climatological SSS and SSH fields in Fig. 11: interestingly, both the original JCOPE-FGO and NoRIV runs exhibit a broadly similar spatial pattern of mean SSS fields, and their differences are not evident in a global-scale view (Fig. 11a, c). Indeed, differences in SSS between the two runs are mostly confined to narrow coastal regions near river mouths of large rivers (see Fig. 1 for their specific locations); as expected, the original JCOPE-FGO has lower SSS compared to the NoRIV run. SSS differences between the two runs are less than 1.0 psu in open ocean areas with depth greater than 1000 m, but they reach more than 3.0 psu over continental shelves adjacent to river mouths (Fig. 11e). Similar salinity differences have been found below the sea surface, but they rapidly get weaker as depth increases and become negligibly small at depths greater than 100 m. Differences in climatological SSH between the two runs are also not clear for most areas (Fig. 11b, d), but there are several regions with systematically higher SSH in the original run than the NoRIV run, such as the East China Sea and Southeast coasts of the USA (Fig. 11f). These changes in salinity and SSH associated with river forcing may alter the evolution of temperature by modifying density stratification and currents; however, differences in temperature between the two runs were rather limited (less than 1.0 °C for most part of the ocean), since the same information on thermal fields are incorporated and used to correct the model’s temperature. Therefore, impacts of large rivers are mostly found in near-surface salinity fields of narrow coastal regions adjacent to river mouths, and their influence do not effectively spread out to open ocean areas.

Fig. 11
figure 11

a, b Climatology of a sea surface salinity (SSS; in psu) and b sea surface height (SSH; in m) from the original JCOPE-FGO. c, d As in a and b, but for the run without river forcing (NoRIV run). e, f Differences in climatological e SSS and f SSH between the original JCOPE-FGO and the NORIV reanalysis product

Full size image

The association between regions with large SSS differences between the two runs and coastal shelves can be seen from magnified views of SSS and bottom topography around river mouths of major rivers (Fig. 12). For example, the signature of low-salinity water along the Mississippi-Alabama coast, associated with freshwater inputs from the Mississippi River, is clearly seen in the original JCOPE-FGO (Fig. 12a), whereas it is completely absent in the NoRIV run (Fig. 12b). The low-salinity water found in the original JCOPE-FGO is mostly confined to areas with depths shallower than 400 m, as inferred from the map of bottom topography (Fig. 12c, d). Such features are also captured by satellite observation and high-resolution regional ocean model simulations (Schiller et al. 2011; Fournier et al. 2016), as we will discuss in detail in the next subsection. Furthermore, the original JCOPE-FGO captures similar spreading of low-salinity waters over shallow areas for other rivers. For example, freshwater from the Amazon River is advected northwestward along the coast of South America by the North Brazilian Current (Fig. 12e-h), whereas low-salinity water flowing into the Bay of Bengal is transported along the east coast of India by the East India Coastal Current (Fig. 12i-l). On the other hand, the low-salinity water originating from the Yangtze River spreads to broader regions of continental shelf of the Yellow Sea (Fig. 12m-p). Such offshore spreading of freshwater is particularly evident during few months after the corresponding river runoff reaches its seasonal maximum; however, low-salinity water is mostly confined to coastal area for other seasons. These distinct imprints of large rivers in the world ocean have been detected by satellite SSS observations (Fournier et al. 2017; Fournier and Lee 2021); results from our sensitivity experiments suggest that an explicit incorporation of river forcing into the OGCM is essential for an accurate representation of these features.

Fig. 12
figure 12

a–c Magnified view of climatology of SSS from the original JCOPE-FGO (a), the NoRIV run (b), and differences between the original and NoRIV run (c) near the river mouth of the Mississippi River. The OGCM bathymetry used in both configurations is shown in d. e–h As in a–d, but for the Amazon River. i–l As in a–d, but for the Bay of Bengal. m–p As in a–d, but for the Yangtze River

Full size image

Our results demonstrating localized natures of riverine fresh water is in a stark contrast with previous modelling studies that have stressed the importance of their non-local effect (Huang and Mehta 2010). Nevertheless, these results were primarily based on non-eddy-resolving or eddy-permitting OGCMs that are not able to properly resolve mesoscale eddies and detailed topographical features, such as continental shelves. For this reason, the effect of freshwater inputs from rivers may be artificially exaggerated in these studies with respect to the actual ocean. However, as a counterclaim of our statement, one may argue that relatively small differences in SSS between the two reanalysis runs over offshore regions are due to implicit corrections of SSS by the data assimilation process, and true impacts of river forcing may potentially be underestimated in the present sensitivity experiments. That is, if some portions of low-salinity signals associated with river runoff are captured by in situ observations, their information will be used to correct the model’s SSS to produce river-induced low-salinity signals, regardless of with and without an explicit inclusion of river discharge into the OGCM.

To explore this alternative possibility, we have compared analysis increments (i.e., the analysis value minus first-guess value) that are added to correct the model’s SSS for both runs (Fig. 13). The spatial pattern of the analysis increments for the SSS from the original JCOPE-FGO (Fig. 13a) is very similar to that from the NoRIV run (Fig. 13b), with relatively large values (0.2–0.3 psu) in the tropical Atlantic and western North Pacific. If signatures of rivers captured by observations are used to correct the analysis fields, the analysis increments added in the NoRIV run should be more negative compared to that of the original JCOPE-FGO, since the former would require more corrections to implicitly represent unresolved effects of freshwater inputs from rivers. However, differences in analysis increments between the two runs are considerably smaller than their total values for most areas (lower than 0.02 psu), suggesting that corrections associated with observationally captured riverine waters seem to be of secondary importance (Fig. 13c). Few exceptions are narrow regions with positive differences (i.e., corrections applied to the NoRIV run are more negative compared to the original JCOPE-FGO), such as the eastern part of the tropical Atlantic and northwestern part of the Bay of Bengal. In these areas, low-salinity waters associated with river plumes captured by observations may be used to correct model’s salinity fields both in the original and NoRIV runs. It is difficult to quantitatively discuss how such implicit SSS corrections in both runs affect our estimations of impacts of river discharge upon salinity fields, but they are limited to small areas near the coast. We have also tested a limited number of experiments with and without river forcing using the same OGCM without data assimilation and found that impacts of data assimilation are minor at least in our model. Based on the above results, we conclude that the small magnitude of SSS differences between the two runs over areas away from the coast is not solely an artifact arising from data assimilation, although the total influence of river discharge may be potentially underestimated in some regions where low-salinity signals associated with river runoff are partly captured by the observation. Further assessments with different eddy-resolving OGCMs (both with and without data assimilations) are necessary to assess the validity of our findings presented above.

Fig. 13
figure 13

a Long-term mean differences between the analyzed and first-guess sea surface salinity (SSS; in psu) from the original JCOPE-FGO. b As in a, but for the run without river forcing (NoRIV run). Differences between a and b are shown in c

Full size image

4.2 An illustrative example: offshore spreading of Mississippi River plume

As a typical example showing the significant impact of river discharge, we focus on the spreading of low-salinity water from the Mississippi River to the Gulf of Mexico. Due to its physical and biological importance, dynamics of the Mississippi River plume and its interaction with large-scale ocean circulation in the bay have been extensively investigated, both by observational and modelling approaches (Morey 2003; Morey et al. 2003; Schiller et al. 2011; Fournier et al. 2016; Brokaw et al. 2019).

To illustrate how realistically the original JCOPE-FGO can reproduce the observed low-salinity signals associated with riverine fresh water, we compared the analyzed SSS fields of the two runs with the observed state derived from the Soil Moisture and Ocean Salinity (SMOS) satellite. Here, we use the Level-3 debiased version 5 gridded product released by LOCEAN and ACRI-st work, as Ocean Salinity Center of Expertise for CATDS (CATDS CEC-OS) (Boutin et al. 2018) as the reference field. As a typical example showing the dispersal of freshwater from the Mississippi River to the bay, snapshots of SSS and SSH from satellite observations and original/NoRIV runs of JCOPE-FGO in June 2014 are shown in Fig. 14. From the SMOS SSS fields, distinct low-salinity water (with salinity lower than 32 psu) associated with the Mississippi River plume is clearly found along the Louisiana-Mississippi-Alabama coast (Fig. 14a). Such signatures are also well captured by JCOPE-FGO, but they are totally missing in the NoRIV run (Fig. 14c, e). During this period, the Loop Current flowing from the Yucatan Peninsula extend northward to reach the continental shelf of around 28°N (Fig. 14b), and associated anticyclonic circulation transports low-salinity water southward along the West Florida Shelf (Fig. 14a) (Brokaw et al. 2019). Such southward spreading of low-salinity water is again well captured in the original JCOPE-FGO, but not present in the NoRIV run, as also seen from the map of SSS differences between the two runs (Fig. 14g). Interestingly, the detachment of anticyclonic eddy at the edge of the Loop Current (88°W, 27°N) detected in the CMEMS observation (Fig. 14b) is more pronounced in the original JCOPE-FGO (Fig. 14d) compared to the NoRIV run (Fig. 14f). This implies a possibility of mutual interactions between river plume waters and the Loop Current system (Schiller et al. 2011). However, due to strong intrinsic variability arising from the nonlinear nature of the current, differences in SSH between the two experiments are not limited to the region (Fig. 14h); thus, it is difficult to draw robust conclusions on the origins of differences in dynamical fields of the two runs. Further sensitivity experiments using increased ensemble members with perturbed initial conditions will be helpful to elucidate their detailed dynamics, which will be an interesting application of the newly developed system.

Fig. 14
figure 14

a, b Spatial distributions of SSS (a) and SLA (b) in June 2004 derived from satellite observation. SSS data is from SMOS, whereas SLA is from CMEMS gridded product. c, d As in a and b, but those derived from the JCOPE-FGO. Surface horizontal current fields are also shown in d by vectors. e, f As in c and d, but from the JCOPE-FGO NoRIV. Differences between the original FGO and NoRIV reanalysis are shown in g and h. The red box shown in c represents the region used for area averaging to make time series in Fig. 15

Full size image

Remarkable SSS differences between the original and NoRIV runs are evident for other periods: the former compares well with the SMOS observation. To illustrate this point, Fig. 15 shows the time series of SSS averaged over the northern part of the Gulf of Mexico (89°–83°W, 28°–29.5°N, see Fig. 14c for its geographical location) (Fig. 15b), as well as the discharge rate of Mississippi River (Fig. 15a) from JRA55-do. The observed SSS exhibits a pronounced seasonal cycle, with the highest (lowest) peak around boreal winter (summer) (Fig. 15b). This can be naturally understood as a delayed response to seasonal changes in river discharge rate, which reaches its seasonal maximum (minimum) around May (October) (Fig. 15b). The distinct seasonal cycle of SSS is correctly analyzed in the original JCOPE-FGO, although its amplitude is slightly underestimated compared to the SMOS (Fig. 15b, black curve). In contrast, SSS averaged over the same region in the NoRIV run exceeds 36.0 psu throughout the period, and no well-defined seasonal variation is observed (Fig. 15b, red curve). This can be confirmed from the fact that the correlation coefficient between the SMOS SSS and JCOPE-FGO is 0.88, whereas it declines to 0.32 in the case of NoRIV run. These results clearly demonstrate that an explicit incorporation of river discharge forcing is essential for better simulation of coastal salinity and related oceanic fields even for data-assimilated ocean reanalysis product.

Fig. 15
figure 15

a Time series of volume transport of Mississippi River derived from the JRA55-do dataset (in [m3/s]). b Time series of area-averaged SSS (in psu) over the region near the river mouth of Mississippi River (89°–83°W, 28°–29.5°N) from SMOS satellite observation (gray curve), the original JCOPE-FGO (black curve), and JCOPE-FGO_NoRIV (red curve). Correlation coefficients between SMOS and JCOPE-FGO/FGO_NoRIV are shown in the lower left

Full size image

5 Summary and discussion

We have developed a new ocean reanalysis product, the JCOPE-FGO, that covers the global ocean from 75°S to 75°N with a horizontal resolution of 0.1° × 0.1°. In the JCOPE-FGO system, information obtained from in situ temperature/salinity profiles and satellite observations of SST and SSHA are dynamically incorporated into an eddy-resolving OGCM with the 3DVAR scheme, as well as estimates of three-dimensional oceanic states from January 1993 to December 2021 are provided. Through comprehensive validations of analyzed oceanic fields of the JCOPE-FGO against various types of available observations, we find that the product can realistically represent spatial distributions of water mass structures and dynamical fields in most part of the global ocean, although some quantitative discrepancies are also identified over several specific regions. The temporal variations in these fields are also correctly captured both in the tropical and extratropical oceans. This indicates that the product serves as a useful tool for monitoring changes in oceanic state and understanding their physical origins.

A unique feature of this product is the use of a refined global river discharge dataset; its impact upon the representation of oceanic fields is investigated in detail by conducting a twin experiment that does not include river forcing (NoRIV run). A comparison of SSS between the original and NoRIV runs reveals that impacts of large rivers upon salinity are mostly confined to narrow coastal regions near river mouths. Such limited offshore spreading of freshwater from rivers is somewhat different from results based on OGCMs with relatively coarse resolution: this may reflect the fact that an accurate representation of topographical features near the coast with higher resolution is crucial for better representation of low-salinity signals associated with river discharge. The importance of river forcing is further demonstrated by an example focusing on the spreading of freshwater from the Mississippi River to the Gulf of Mexico. Comparisons of analyzed fields from the two reanalysis runs with satellite observations reveal that the complex interplay between the low-salinity water and the Loop Current is realistically represented in the original JCOPE-FGO compared to the NoRIV run. Thus, an explicit incorporation of river forcing in the present system is beneficial for better representations of coastal salinity and related fields.

Although JCOPE-FGO can reasonably capture the observed oceanic variability both at large and small spatial scales in the global ocean, several notable biases do exist in several regions. There are several remedies that may potentially lead to better representations of observed oceanic fields. In terms of the OGCM, an increased number of vertical layers, adoption of refined vertical mixing schemes, and use of different atmospheric forcing fields would be helpful to mitigate the model biases found in the present version. In addition, an explicit incorporation of tidal forcing as well as sea ice processes may also be advantageous for better representation of regional-scale variability. Incorporation of Arctic regions in the model domain and use of an explicit sea ice model may lead to a better representation of temporal variations in water mass structures over the polar region and their spreading to lower latitudes, such as the “Great Salinity Anomaly” (Dickson et al. 1988; Belkin et al. 1998) and related processes. Regarding data assimilation, tuning of tilling allocations and assimilation parameters, use of the spatial scale-dependent 3DVAR algorithm (Miyazawa et al. 2017, 2021), and assimilations of additional variables, such as satellite SSS data (Martin et al. 2019), may boost the skill of this system. Implementations of more advanced data assimilation schemes, such as the ensemble Kalman filter (EnKF) (Miyazawa et al. 2012b) and four-dimensional variational method (4DVAR) (Usui et al. 2015), will also be a possible direction for future development. Similar ocean reanalysis products with eddy-resolving resolution have also been developed by several research groups (Chassignet et al. 2009; Metzger et al. 2014; Lellouche et al. 2018, 2021), and a multi-product intercomparison approach may also be helpful for understanding the origins of biases (Balmaseda et al. 2015).

Since the JCOPE-FGO covers quasi-global ocean with an eddy-resolving resolution, it can be used to investigate a wide range of oceanic phenomena from regional to global scales, such as dynamics of river plumes, variability of mesoscale eddies, and basin-scale circulations. It may also be utilized as a boundary forcing of nested regional ocean models and biogeochemical tracer models. Furthermore, as in other regional JCOPE products, the JCOPE-FGO can be used as an ocean forecasting system by initializing the OGCM with analyzed fields obtained by assimilation cycles. Indeed, we are planning to conduct a series of retrospective forecast experiments and explore the potential predictability of various oceanic fields from a global perspective. It is hoped that this product and its updated versions will be widely used for a variety of studies on physical oceanography, climate dynamics, and other related fields.