Abstract
During polar nights in January 2012 and 2017, significantly higher bioluminescence (BL) potential emissions in the upper 50 m were observed in the fjord Rijpfjorden (Svalbard, Norway) in comparison to offshore stations (located on the shelf-break, shelf-slope areas and in the deeper water). The objective of this paper is to better understand why, during two polar nights (separated by 5 years), the values of BL potential in the northern Svalbard fjord are higher than at offshore stations, and what the role of advection is in observed elevated BL potential values in the top 50 m of the fjord. To address the above objective, we applied the same BL potential modeling approach and strategies during polar nights for both 2012 and 2017. For both years, advection of BL potential from offshore (including upwelling along the shelf, shelf-slope) produced an increase of BL potential in the fjord area, in spite of the introduction of mortality in bioluminescent organisms. Observations of BL potential indicated high emissions at depths below 100 m at offshore stations for both polar nights. Our modeling studies demonstrated that these high values of BL potential below 100 m are upwelled and advected to the top 50 m of the fjord. We demonstrated that upwelling and advection of these deep high BL potential values (and therefore, upwelling and advection of corresponding bioluminescent taxa) from offshore areas are dominant factors in observed BL potential dynamics in the top 50 m in the fjord.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Bioluminescence is light produced by organisms through chemical reactions, which structure ecological interactions in dim habitats, particularly in the marine environment (Haddock et al. 2010). At high latitudes, polar night is a prolonged period of seasonal darkness with the sun remaining below the horizon throughout the diel cycle for up to 177 days at the North Pole (Cohen et al. 2020). Accordingly, bioluminescence, rather than sunlight, represents a significant portion of the photons available for pelagic organism interactions during the Polar Night (Cronin et al. 2016; Cohen et al. 2015).
During the last decade, field studies have provided snapshots of bioluminescence and the distribution of bioluminescent organisms during the Polar Night (Berge et al. 2012, 2020; Cronin et al. 2016). Because most bioluminescent organisms in the marine environment generate light in response to mechanical stimulation, bioluminescence is commonly measured as bathyphotometer bioluminescence potential (BL potential), defined as mechanically stimulated light measured inside of a chambered pump-through bathyphotometer (Herren et al. 2005; Moline et al. 2005; Latz and Rohr 2013). The bathyphotometer pumps water into its detection chamber and mechanically stimulates marine organisms to produce light inside the detection chamber.
During the polar night of January, 2012, BL potential observations were significantly higher in the top 50 m in the area of a northern Arctic fjord (Rijpfjorden, Svalbard, Norway) in comparison to offshore stations located on the shelf-break, shelf-slope areas and in the deeper water (Shulman et al. 2020). In our previous studies, we demonstrated that the advection, upwelling and mixing of BL potential (representing bioluminescent taxa) from offshore were dominant factors in explaining the observed high BL potential values in the top 50 m of the fjord area in comparison to offshore stations (Shulman et al. 2020). The interpretation of our previous results is that during the Polar Night, the fjord represents an area where bioluminescent organisms from offshore aggregate through advection and mixing. These conclusions were based on observations and modeling during only one polar night (January 2012), and we were concerned that they might be too specific to that particular polar night of 2012. How typical are these conclusions with respect to conditions during other years? It is a challenging question to address because of the paucity of observations, especially during polar nights in the Arctic.
In the present paper, we compare observations of BL potential during January of 2012 and 2017, and deploy the same modeling strategies for both polar night periods in order to compare dynamics of BL potential during two polar nights, separated by five years. As we will demonstrate below, observed BL potential emissions in the top 50 m in the fjord are higher than that in offshore areas for both years, indicating a higher presence of bioluminescent organisms in the top 50 m in the fjord area than offshore during both polar nights. Can physical processes explain why the values of BL potential in the top 50 m of the fjord would be higher than those at offshore stations for both years, and specifically, what is the role of advection in the observed elevation of BL potential values in the fjord in comparison to offshore stations?
To address the questions above, we deploy the modeling approach used in Shulman et al. (2020). Changes in BL potential are modeled with the advection–diffusion-source (ADS) model, and the focus is on modeling and predictions of changes in averaged values of BL potential over a specific domain of interest (in the present paper the domain of interest is the area around a sampling station near the fjord mouth). As we demonstrated in Shulman et al. (2020), the estimation of the ensemble of possible averaged values of BL potential in the area of interest requires: 1) estimation of the adjoint (by backward in time integration of the adjoint model); 2) generation of ensembles of possible distributions of the BL potential initial conditions and source minus sink terms; and 3) estimation of two integrals over the modeling domain: the integration of the adjoint with the BL potential initial conditions, and the integration of the adjoint with the BL potential source minus sink terms.
The structure of the paper is as follows: BL potential observations for Polar Nights of 2012 and 2017 are described in Sect. 2; BL potential modeling is briefly presented in Sect. 3; Sect. 4 is devoted to the results, and Sect. 5 is discussion and conclusions.
2 Bioluminescence potential observations during polar nights of 2012 and 2017
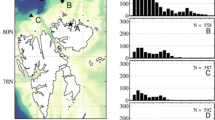
Bathymetry around Svalbard (Spitsbergen and Nordaustlandet, Norway), situated between the Barents Sea and the Arctic Ocean and locations of four observational stations sampled during the polar night in January 12–16 of 2012 and four observational stations sampled during the polar night in January 10–14 of 2017 are shown on Fig. 1. Stations A2012 and A2017 are located at the mouth of the fjord Rijpfjorden; stations B2012 and B2017 are to the north of the fjord and in the shelf-break, shelf-slope area; stations C2012 and C2017 are also located in the shelf-break, shelf-slope area, but are to the west-south of the fjord, and finally stations D2012 and D2017 are fur most offshore and in the Arctic basin.
Surveys of BL potential were conducted using a bathyphotometer called the Underwater Bioluminescence Assessment Tool (UBAT; WetLabs, Inc., Philomath, OR). For both years, the UBAT was mounted on the profiling cage. Downcasts from 2012 surveys down to 500 m depth were used in the present study. In 2017, each profile consisted of 4 min stops at 20 m depth intervals down to 120 m depth. The UBAT outputs 60 Hz as well as one second averaged data. The BL potential measured by the bathyphotometer represents a sum of light emitted by different organisms in the detection chamber. Usually zooplankton emit bright flashes (larger than 1010 ph/s), while most dinoflagellate species only emit flashes less than 109 ph/s. Figure 2 shows that during both polar nights there were higher BL potential emissions in the top 50 m in the fjord (at stations A2012 ad A2017) in comparison to other stations located offshore (60 Hz data are plotted). This is well-supported by statistical properties of observed values of BL potential (60 Hz data) in Table 1 for 2012 and Table 2 for 2017. Johnsen et al. (2014) and Cronin et al. (2016) used 108 ph/s as a threshold value, below which the BL potential values were not considered. This value is about 100 times larger than the BL potential for filtered sea water. Here, we also considered only BL potential values, which are larger or equal to 108 ph/s (i. e. larger or equal 8 in log10 transformed sense).
Observed BL potential emissions (log10 transformed) at stations shown on Fig. 1
The tables present a number of emissions recorded (NOtotal) in the top 50 m, a number of non-zero emissions recorded in the top 50 m (NOO), a number of emissions with log10 transformed values larger or equal 8 in the top 50 m (NO), fractions NO/NOtotal and NO/NOO, and maximum values of log10 transformed emissions in the top 50 m for the considered stations.
In accord with Table 1, fractions of emissions with log10 transformed values larger or equal 8 to total emissions (NO/NOtotal) and to non-zero emissions (NO/NOO) are larger at A2012 station ( in the fjord) than at offshore stations (B2017, C2017 and D2017). Table 1 shows that 31% of total emissions (fraction NO/NOtotal) and 56% of non-zero emissions (fraction NO/NOO) at station A2012 are larger or equal to 8 (in log10 transformed sense). While these fractions are 7% of the total and 15% of non-zero emissions at B2012; 3.5% and 22% at C2012, and 6.6% and 15% for D2012. Table 2 shows similar results for the Polar Night of 2017. About 14% of total emissions and 39% of non-zero emissions at station A2017 are larger or equal to 8 (in log10 transformed sense). While these fractions are 3% of total and 16% of non-zero emissions at B2017; 3.7% and 20% at C2017, and 1.9% and 5.4% for offshore station D2017.
In the fjord, fractions NO/NOtotal and NO/NOO are larger at A2012 station (31% and 56% correspondingly) than at A2017 (14% and 39% correspondingly). At the same time, absolute values of NOtotal, NOO and NO are smaller at A2012 than at A2017. This is due to more extended sampling durations at particular depths during 2017, which resulted in registering more emissions in comparison to 2012 sampling. Note, that like for fjord stations, values of NOtotal, NOO, NO are also smaller for other 2012 stations in comparison to corresponding 2017 stations (Tables 1 and 2), while fractions NO/NOtotal and NO/NOO are mostly larger for 2012 stations in comparison to corresponding 2017 stations.
Histogram plots of log10 transformed BL potential emissions in the top 50 m for 2012 and 2017 stations are shown on Fig. 3 (only log10 transformed BL potential emissions, which are larger or equal to 8, are considered). During both polar nights there were higher BL potential observed values in the top 50 m in the fjord (at stations A2012 ad A2017) in comparison to other stations located offshore.
Histograms of log10 transformed BL potential emissions in top 50 m at 2012 stations (left) and 2017 stations (right) presented on the Fig. 1. Only log10 transformed emissions, which are larger or equal 8, are considered
Figures 2–3 and Tables 1–2 strongly demonstrate that observed BL potential emissions in the top 50 m in the fjord are higher than that in offshore areas for both years, indicating a higher presence of bioluminescent organisms in the top 50 m in the fjord area than offshore during both Polar Nights.
3 BL potential modeling
We suppose that changes in BL potential can be described with the advection–diffusion-source (ADS) model (Shulman and Anderson 2019, Shulman et al. 2020). In accord with derivations presented in Shulman et al. (2020), the average value of BL potential in the particular area of interest Ω (representing a subdomain of the modeling domain D) has the following representation at evaluation time T:
where C is BL potential normalized by a constant normalization coefficient μ = 108ph/s, \(\tau (x,y,z) \in D\), dτ is element of volume in the integral, VΩ is the volume of the domain Ω, C0(τ) is initial condition at t = t0, λ is an adjoint variable that equal 1 in the domain Ω at the verification time T and integrated backward in time to t0 in accord with the adjoint equation to the ADS model (Shulman et al. 2020), S(τ, t)—represents local sources minus sink of C.
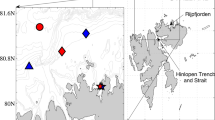
For the area of interest Ω, we selected the top 50 m of 6 × 6 grid cells of the circulation model (see Appendix) around stations A2012 and A2017 in the fjord (Fig. 1). This translates into an approximately 12 km x 26 km x 50 m box (marked by red box on Fig. 4a). In this case, J in (1) represents the average value of BL potential in the top 50 m of the area around stations A2012 and A2017 in the fjord at evaluation time T. For polar night of 2012, we selected the evaluation time T as January 14th 12Z of 2012 (Shulman et al. 2020). For Polar Night of 2017, we selected the evaluation time also January 14th 12Z but of 2017.
(a) Red box is the area of interest Ω in the fjord; (b) distribution of adjoint after 4 days of integration of the adjoint equation (vertically integrated adjoint for each model grid (normalized by the volume of the area of interest Ω)); (c) as in (b) but after 10 days of integration of the adjoint equation. Locations of stations B2012 and B2017 are marked by blue and red diamonds, C2012 and C2017—blue and red triangles, and D2012 and D2017—blue and red circles
Based on an ensemble of initial conditions C0,n(τ) and an ensemble of sources minus sink of BL potential Sn(τ, t), Eq. (2) estimates an ensemble of possible distributions of mean values of BL potential \(J_{n}^{T-{t_0}}\) depending on the value of T-t0:
The ensemble of initial values of (2) has the following representation:
Properties of the ensemble \({J}_{n}^{T-{t}_{0}}\) (2) can be evaluated by estimating the fraction of ensemble members with averaged values of BL potential larger or equal to 108 ph/s (our chosen threshold for BL potential) to the total ensemble size N:
where \({N}_{8}^{T-{t}_{0}}\) is a number of ensemble members \({J}_{n}^{T-{t}_{0}}\) (2) with values of log10 (\({J}_{n}^{T-{t}_{0}}\)) larger or equal 8, N is chosen to be equal 10,000. Corresponding initial value of fractions (4) is:
where \({N}_{8}^{0}\) is a number of ensemble members \({J}_{n}^{0}\) (3) with values of log10 (\({J}_{n}^{0}\)) larger or equal to 8.
Comparisons of fractions \({\lambda }_{8}^{T-{t}_{0}}\) and \({\lambda }_{8}^{0}\) provide the insight into dynamics of BL potential in the fjord area over time (T-t0). We considered values of T-t0ranging from 2 to 10 days in one day increments.
Figure 4a shows the distribution of the adjoint at time evaluation T for 2017 (January 14th 12Z of 2017), when the adjoint equals 1 in the area of interest Ω (the red box on Fig. 4a) and equals 0 everywhere outside of Ω. From these initial values at t = T, the adjoint equation is integrated backward in time (Shulman et al. 2020). The circulation model physical fields (Appendix A) were averaged over the sampling period of Jan. 11–14, 2017. This is equivalent to an assumption that changes in BL potential can be described with the advection–diffusion-source (ADS) model with averaged over sampling period (4 days) physical fields. Vertically integrated adjoint distributions (normalized by the volume of the area of interest Ω) after T-t0 = 4 days of backward in time integration (at time t0 equals Jan. 10th 12Z of 2017) and after T-t0 = 10 days of backward integration (at time t0 equals Jan 4th 12Z) are shown on Fig. 4b and c. Over 10 days of integration, the adjoint’s non zero values reached the location of station B2012 (Fig. 4c) but not areas around other stations. Adjoint distributions for 2012 (Fig. 2 of Shulman et al. 2020) are similar to adjoint distributions for 2017 (Fig. 4), when after 10 days of backward integration, the adjoint’s non zero values for 2012 reached also the location of station B2012 but not areas around other stations (Fig. 2 of Shulman et al. 2020). Following the approach outlined in Shulman et al (2020), BL potential observations at station B2012 were used to generate an ensemble of possible initial BL potential distributions (C0,n(τ)) and an ensemble of possible sources minus sink term of BL potential (Sn(τ,t)).
4 Results
First, we present runs 2012GR1 for 2012 and 2017GR1 for 2017 when the same ensemble of initial conditions C0,n(τ)was used for both years, and the local sources of changes in BL potential (Sn(τ,t)) equal to zero. In this case, changes in \({J}_{n}^{T-{t}_{0}}\) (2) are determined by the initial distribution of BL potential C0,n(τ) at time t0 and by physical processes (represented by the adjoint). In accord with Table 3, for runs 2012GR1 values of \({\lambda }_{8}^{T-{t}_{0}}\) are increasing from the initial value \({\lambda }_{8}^{0}\) = 0.03 to 0.17 for T-t0 = 2 days, then to 0.3 for T-t0 = 4 days (one order of increase in comparison to initial value \({\lambda }_{8}^{0}\)), and up to 0.45 for T-t0 = 10 days. For 2017 (runs 2017GR1) values of \({\lambda }_{8}^{T-{t}_{0}}\) increase from the same initial values \({\lambda }_{8}^{0}\)= 0.03 to 0.09 for T-t0 = 2 days, then to 0.15 for T-t0 = 4 days, and up to 0.31 for T-t0 = 10 days (one order of increase in comparison to initial value \({\lambda }_{8}^{0}\)). This is well illustrated on Fig. 5, showing histograms of log10 (\({J}_{n}^{T-{t}_{0}}\)) values for 2012GR1 and 2017GR1 runs after T-t0 equal to 2, 4 and 10 days together with a histogram for the ensemble of initial values log10 (\({J}_{n}^{0}\)). There is an increase in frequencies of histograms with increasing time. Because 2012GR1 and 2017GR1 runs were done with Sn(τ,t) equal to zero (no local sources of BL potential to increase or decrease local BL potential values), all increases in fractions \({\lambda }_{8}^{T-{t}_{0}}\) (Table 3) and in histograms frequencies (Fig. 5) should be attributed to advection and mixing of BL potential (representing bioluminescent organisms) into the area of interest.
Histograms of log10 (\({J}_{n}^{T-{t}_{0}}\)) (2) for 2012GR1 (left) and 2017GR1 (right): (a) initial values log10 (\({J}_{n}^{0}\)) (3); (b) for 2012GR1 after T-t0 = 2 days; (c) for 2012GR1 after T-t0 = 4 days; (d) for 2012GR1 after T-t0 = 10 days; (e) for 2017GR1 after T-t0 = 2 days; (f) for 2017GR1 after T-t0 = 4 days and (g) for 2017GR1 after T-t0 = 10 days. Only histograms for values larger or equal 8 are shown
Those increases in modeled BL potential values are due to the horizontal advection into the area of interest and vertical advection from below 50 m to the top 50 m of the area of interest. In order to quantify relative contributions of horizontal and vertical advection to the increase of BL potential values in the top 50 m in the fjord, we estimated the following ensemble of ratios \({\zeta_n}\) for 2012GR1 and 2017GR1:
where
and
In (7) and (8), D1 and D2 are subdomains of the modeling domain D: D1 covers the offshore area to the north of the red box on Fig. 4a and D2 is the domain below the 50 m of the red box. In this case, \(J_{1,n}^{T-{t_0}}\) (7) represents the contribution of offshore horizontal advection to the BL potential mean values in the area of interest for 2012GR1 and 2017GR1 runs. While, \({J}_{2,n}^{T-{t}_{0}}\) (8) represents the contribution of vertical advection to the BL potential mean values in the area of interest. In this case, the ensemble of ratios \(\zeta_n^{T - {t_0}}\) (6) represents the relative contribution of vertical advection versus horizontal advection to the total change in mean BL potential values in the area of interest. Ensemble members of \(\zeta_n^{T - {t_0}}\) larger than one indicate that vertical advection contributes more to the increase in BL potential than horizontal advection for those ensemble members, and vice versa. Table 4 shows statistics for ensembles of \(\zeta_n^{T - {t_0}}\), estimated for runs 2012GR1 and 2017GR1. It shows that the mean value for ensembles \(\zeta_n^{T - {t_0}}\) decreases over time for both years. It is below 1 after 2 days of integration for 2017GR1, and after 6 days of integration for 2012GR1. This means that for both years, horizontal advection is the more dominant factor to the increase of BL potential than vertical advection. After T-t0 = 3 days for 2017GR1 and T-t0 = 7 days for 2012GR1, minimum and maximum values of all ensemble members of \(\zeta_n^{T - {t_0}}\) are less than one for both years. This means that all ensemble members of \(\zeta_n^{T - {t_0}}\) have a contribution of horizontal advection that is larger than the contribution from the vertical advection. All of this demonstrates that the horizontal advection from offshore (including upwelling of BL potential from offshore along the shelf, shelf-slope) is the dominant factor increasing BL potential in the fjord for both years.
In our next group of experiments 2012GR2 and 2017GR2, we assumed that there is no reproduction during the polar night but mortality rates were uniformly distributed between 0.1 and 0.2 day−1. Table 3 shows fractions \(\lambda _{8}^{T-{t_0}}\) (4) for 2012GR2 and 2017GR2. For T-t0 = 2 days, fractions \({\lambda }_{8}^{T-{t}_{0}}\) increase from the initial value 0.03 to 0.15 for 2012GR2 and from the same initial value 0.03 to 0.08 for 2017GR2. Then for T-t0 = 4 days, fractions increase to 0.25 for 2012GR2 and to 0.13 for 2017GR2. For 2012GR2, fractions \({\lambda }_{8}^{T-{t}_{0}}\) reach a maximum value around 0.29 for T-t0 = 6–7 days, and then slightly drop to 0.27 for T-t0 = 10 days, while for runs 2017GR2, fractions \({\lambda }_{8}^{T-{t}_{0}}\) steadily increase over 10 days to a 0.2 value. This indicates that without new reproduction and with mortality rates from 0.1 to 0.2 day−1, there is an increase in BL potential values in the fjord over time in comparison to offshore values. For both considered years, the advection and upwelling of BL potential from offshore to the fjord produce an increase of BL potential in the fjord area, in spite of the introduction of mortality of bioluminescent organisms in runs 2012GR2 and 2017GR2. Figure 6 shows histograms of predicted log10 (\(J_{n}^{T-{t_0}}\)) values for 2012GR2 and 2017GR2 runs. As for 2012GR1 and 2017GR1 runs (Fig. 5), there is an increase over time in frequencies of histograms. For both years, these histograms again support the conclusion that our modeling studies have demonstrated that higher values of BL potential in the fjord are the result of the advection of BL potential from offshore, irrespective of mortality.
As on Fig. 5 but for runs 2012GR2 (left) and 2017GR2 (right)
The offshore station B2012 (used to build the ensemble of initial distribution C0,n(τ)) has values of log10 (BL) higher than 8 at depths deeper than 50 m, with a prominent maximum value larger than 11 between 100 and 125 m depth (Fig. 2). Therefore, the ensemble of initial distributions C0,n(τ) has the similar high BL potential values in the modeling domain (including the fjord area). As a result, those high BL potential values from the depths below100m are advected into the top 50 m of the fjord, which resulted in the increase of mean BL potential values. In accord with Fig. 2, at depths100-130 m, there are observed BL potential emissions reaching value 11 and higher at stations A2012 and A2017 in the fjord, and at stations B2017, B2012, C2012, and D2017 offshore. Finally, there are emissions larger than 11 at depths below 300 m at offshore stations C2012 and D2012, but note that these deeper depths were not sampled in 2017. This demonstrates that high BL potential emissions observed below 100 m are a typical phenomenon both offshore and in the fjord during both Polar Nights in the Arctic.
To further evaluate the impact of high BL potential values below 100 m on the BL potential dynamics in the top 50 m in the fjord, we conducted runs 2012GR3 and 2017GR3 when high values of BL potential below 100 m were replaced with threshold values equal to 8 (in log10 sense) in the ensemble of initial conditions C0,n(τ) (see Supplementary Material (SM) for details). Due to a lack of subsurface high values of BL potential in the initial conditions in the entire modeling domain, histograms for runs 2012GR3 and 2017GR3 (Figure SM1) show BL potential values not larger than 9.5 in the top 50 m of the fjord. For both polar nights, this demonstrates that high values of BL potential in the top 50 m in the fjord are a result of advection of subsurface (below 100 m) high values of BL potential (and therefore, advection of subsurface bioluminescent organisms). In our next runs 2012GR4 and 2017GR4, we removed high values of BL potential below 100 m in the ensemble of initial conditions C0,n(τ) only in the area outside of the fjord, while for runs 2012GR5 and 2017GR5, we removed high values of BL potential below 100 m only in the area inside of the fjord (see SM for details). Comparisons of above runs with 2012GR1 and 2017GR1 provide the impact of offshore versus inshore subsurface high values of BL potential on the BL potential dynamics in the top 50 m in the fjord.
For both considered years, the differences between runs YEARGR1 (where YEAR means 2012 or 2017) and corresponding runs YEARGR4 (with subsurface high values of BL potential in the initial conditions only in the fjord) are growing over time (Tables SM1 and SM2). This increase in differences is a result of an increased impact of offshore advection and upwelling of high BL potential values from below 100 m in YEARGR1 runs, and the lack of this advection and upwelling in YEARGR4. In opposite dynamics, the difference between runs YEARGR1 and corresponding runs YEARGR5 (with subsurface high values of BL potential in the initial conditions in the offshore area) are decreasing over time (Tables SM1 and SM2). This indicates that with time progressing, the advection and upwelling of high values of BL potential from below 100 m offshore, which is present in both YEARGR1 and YEARGR5 runs, becomes the dominant factor in the BL potential dynamics in the top 50 m in the fjord. Finally, differences between runs YEARGR5 and YEARGR4 (see SM for details) also demonstrate that advection and upwelling from offshore is becoming the dominant factor in the BL potential dynamics in the top 50 m of the fjord over time.
5 Discussions and conclusions
During Polar Nights of January 2012 and 2017, significantly higher BL potential emissions in the top 50 m were observed in the northern Svalbard fjord (Rijpfjorden) in comparison to offshore stations (located on the shelf-break, shelf-slope areas and in the Arctic basin). Around 56% of BL potential non-zero emissions were larger or equal to 108 ph/s in the fjord area in 2012 and 39% in 2017, while no more than 22% in 2012 and 20% in 2017 were observed at offshore stations located on the shelf-break, shelf-slope areas and in the Arctic basin. The objective of this paper was to better understand why, during two polar nights (separated by 5 years), the values of BL potential in Rijpfjorden are higher than at offshore stations, and what role advection plays in the observed elevated BL potential values in the top 50 m of the fjord. This is important for biological studies because bioluminescence, rather than sunlight, represents a significant portion of the photons available for pelagic organism interactions during the Polar Night (Cohen et al. 2020, 2015; Cronin et al. 2016).
To address the above objective, we applied the same BL potential modeling approach (developed in Shulman et al. 2020) during both polar nights. The approach is based on estimation of the ensemble of possible averaged values of BL potential over a specific domain of interest (in the present paper the domain of interest is the area around a sampling station near the fjord mouth). Numerical experiments were conducted when the local sources of changes in BL potential were equal to zero–this means that all changes in mean values of BL potential in the area of the fjord were determined by advection and mixing of BL potential. Results of those simulations demonstrated increases in ensemble members with BL potential values larger or equal to 108 ph/s in comparison to corresponding ensemble members in the initial distribution for both years. After 4 days of simulations, the increase in the number of ensemble members with BL potential values larger than or equal to 108 ph/s was ten times in comparison to the initial distribution for 2012 and five times for 2017. After 10 days of simulations, the increase was fifteen times in comparison to the ensemble of initial BL potential values in 2012 and around ten times for 2017. In our next numerical experiments, we introduced mortality of bioluminescent organisms (from 0.1 to 0.2 day−1). For both considered polar nights, advection and upwelling of BL potential from offshore to the fjord produced an increase of BL potential in the fjord area, in spite of the introduction of mortality for bioluminescent organisms. These modeling results indicate that the advection and mixing of BL potential from offshore are dominant factors in increases of BL potential in the fjord area in the top 50 m in comparison to offshore areas.
Observations of BL potential indicated high emissions (larger than 1011 ph/s), at depths below 100 m at the fjord as well as at offshore stations for both polar nights. As the result of this, the ensemble of initial conditions (which was derived from BL observations at the offshore station located in the area of shelf-break and was closest to the fjord) had a subsurface maximum of BL potential at depths between 100 and 125 m. Our modeling studies demonstrated that these high values of BL potential below 100 m are upwelled and advected to the top 50 m of the fjord. We demonstrated that upwelling and advection of these deep high BL potential values (and therefore, upwelling and advection of corresponding bioluminescent taxa) from offshore areas are dominant factors in observed BL potential dynamics in the top 50 m in the fjord.
The question remains regarding sources of bioluminescent taxa responsible for the high values of observed BL potential in offshore waters to the north of Rijpfjorden. It is well-known that the North Atlantic water enters the northern Svalbard area from the west-south of Svalbard (Falk-Petersen et al. 2015; Beszczynska-Moller et al. 2012; Basedow et al. 2018; Wassmann et al. 2019; Vernet et al. 2019), and that there is “Atlantification” of the Arctic including some Svalbard fjords which in turn influences plankton communities (Csapó et al. 2021, Lind et al. 2018). Basedow et al. (2018) observed that the transport of North Atlantic Water into the Arctic is larger during the Polar Night (January) than in May and August, and that there is a strong influx of zooplankton with North Atlantic Water during the Polar Night. They observed an influx of the bioluminescent copepod Metridia longa, which remains active during the Polar Night, and it has a relatively deep distribution (> 150 m; Blachowiak-Samolyk et al. 2015, 2017). Indeed, Hop et al. 2019 reported similar processes contributed to higher abundance of Metridia longa and ostracods (known to be bioluminescent, e.g. Cronin et al. 2016) on the slope and shelf outside of Rijpfjorden during summer across several years. Therefore, this indicates that the advection of zooplankton by the North Atlantic Water is one possible source of bioluminescent organisms offshore of the northern Svalbard during the Polar Night.
Another question remaining is why are bioluminescent taxa observed predominantly below 100 m in offshore waters? In accord with Webster et al (2015), “the moon was full during the sampling period” in January 2012. The full moon was also present on January 12 of 2017, right in the middle of the considered sampling period during January of 2017. Therefore, we can suspect that full moon or near full moon conditions were present during both sampling periods of the two Polar Nights under consideration. As stated in Cohen et al. 2020, marine organisms are sensitive to light, and numerous recent studies demonstrated that the position of zooplankton is vertically controlled by light (Båtnes et al. 2015, Cohen et al. 2015) and closely related to specific isolumes (Webster et al. 2015, Berge et al. 2012, 2020, Hobbs et al. 2021). Last et al. (2016) established that moonlight extends the depth of zooplankton vertical migrations in Svalbard fjords and across the Arctic during winter, while Båtnes et al. (2015) suggested copepods can migrate down to 120–170 m during moonlight under attenuation of light corresponding to the ambient (winter) conditions. Therefore, the vertical migration of the bioluminescent organisms (due to behavioral sensitivity to the light conditions) might be one of the reasons why high values of BL potential were observed below 100 m during both Polar Nights under consideration. Another source might be a weak reproduction and different survivial strategies of the zooplankton during Polar Night in the Arctic (Berge et al. 2020). Research and modeling of possible sources of bioluminescent taxa presence below 100 m will be a topic of our future studies.
Data availability
The datasets generated during the current study are available from the corresponding author on reasonable request.
References
Basedow SL, Sundfjord A, von Appen W-J, Halvorsen E, Kwasniewski S, Reigstad M (2018) Seasonal variation in transport of zooplankton into the arctic basin through the atlantic gateway, fram strait. Front Mar Sci 5:194. https://doi.org/10.3389/fmars.2018.00194
Båtnes AS, Miljeteig C, Berge J, Greenacre M, Johnsen G (2015) Quantifying the light sensitivity of Calanus spp. during the polar night: potential for orchestrated migrations conducted by ambient light from the sun, moon, or aurora borealis? Polar Biol 38:51–65. https://doi.org/10.1007/s00300-013-1415-4
Berge J, Båtnes AS, Johnsen G, Blackwell SM, Moline MA (2012) Bioluminescence in the high Arctic during the polar night. Mar Biol 159:231–237. https://doi.org/10.1007/s00227-011-1798-0
Berge J, Daase M, Hobbs L, Falk-Petersen S, Darnis G, Søreide J (2020) Zooplankton in the Polar Night. In: J Berge, G Johnsen, JH Cohen (Eds) Polar Night Marine Ecology: Life and Light in the Dead of Night. Springer Nature, Switzerland AG, pp 116–130
Beszczynska-Moller A, Fahrbach E, Schauer U, Hansen E (2012) Variability in Atlantic water temperature and transport at the entrance to the Arctic Ocean, 1997–2010. ICES J Mar Sci 69(5):852–863. https://doi.org/10.1093/icesjms/fss056
Blachowiak-Samolyk K, Wiktor JM, Hegseth EN, Wold A, Falk-Petersen S, Kubiszyn AM (2015) Winter Tales: the dark side of planktonic life. Polar Biol 38:23–36. https://doi.org/10.1007/s00300-014-1597-4
Blachowiak-Samolyk K, Zwolicki A, Webster CN, Boehnke R, Wichorowski M, Wold A, Bielecka L (2017) Characterisation of large zooplankton sampled with two different gears during midwinter in Rijpfjorden, Svalbard. Pol Polar Res 38:459–484. https://doi.org/10.1515/popore-2017-0023
Bleck R (2002) An oceanic general circulation model framed in hybrid isopycnic-Cartesian coordinates. Ocean Model 4:55–88. https://doi.org/10.1016/S1463-5003(01)00012-9
Cohen JH, Berge J, Moline MA, SørensenAJ LK, Falk-Petersen S et al (2015) Is Ambient Light during the High Arctic Polar Night Sufficient to Act as a Visual Cue for Zooplankton? PLoS ONE 10(6):e0126247. https://doi.org/10.1371/journal.pone.0126247
Cohen JH, Berge J, Moline MA, Johnsen G, Zolich AP (2020) Light in the Polar Night. In: J. Berge, G. Johnsen, J.H. Cohen (Eds.) Polar Night Marine Ecology: Life and Light in the Dead of Night. Springer Nature, Switzerland AG, pp 37–66
Cronin HA, Cohen JH, Berge J, Johnsen G, Moline MA (2016) Bioluminescence as an ecological factor during high Arctic polar night. Sci Rep 6:36374. https://doi.org/10.1038/srep36374
Csapó HK, Grabowski M, Węsławski JM (2021) Coming home - Boreal ecosystem claims Atlantic sector of the Arctic. Sci Total Environ 771:144817. https://doi.org/10.1016/j.scitotenv.2020.144817
Cummings J, Bertino L, Brasseur P, Fukumori I, Kamachi M, Martin MJ, Mogensen K, Oke P, Testud CE, Verron J, Weaver A (2009) Ocean data assimilation systems for GODAE. Oceanography 22(3):96–109
Falk-Petersen S, Pavlov V, Berge J, Cottier F, Kovacs KM, Lydersen C (2015) At the rainbow’s end: high productivity fueled by winter upwelling along an Arctic shelf. Polar Biol 38:5–11. https://doi.org/10.1007/s00300-014-1482-1
Haddock SHD, Moline MA, Case JF (2010) Bioluminescence in the sea. Annu Rev Mar Sci 2:443–493. https://doi.org/10.1146/annurev-marine-120308-081028
Herren CM, Haddock SHD, Johnson C, Orrico CM, Moline MA, Case JF (2005) A multi-platform bathyphotometer for fine-scale, coastal bioluminescence research, Limnol Oceanogr. Methods 3:247–262. https://doi.org/10.4319/lom.2005.3.247
Hobbs L, Banas NS, Cohen JH, Cottier FR, Berge J, Varpe Ø (2021) A marine zooplankton community vertically structured by light across diel to interannual timescales. Biol Let 20200810.https://doi.org/10.1098/rsbl.2020.0810
Hop H, Assmy P, Wold A, Sundfjord A, Daase M, Duarte P, Kwasniewski S, Gluchowska M, Wiktor JM, Tatarek A, Wiktor J Jr, Kristiansen S, Fransson A, Chierici M, Vihtakari M (2019) Pelagic Ecosystem Characteristics Across the Atlantic Water Boundary Current From Rijpfjorden, Svalbard, to the Arctic Ocean During Summer (2010–2014). Front Mar Sci 6:181. https://doi.org/10.3389/fmars.2019.00181
Huenerlage K, Graeve M, Buchholz F (2016) Lipid composition and trophic relationships of krill species in a high Arctic fjord. Polar Biol 39:1803–1817. https://doi.org/10.1007/s00300-014-1607-6
Hunke EC, Lipscomb W (2008) CICE: The Los Alamos sea ice model, documentation and software user’s manual, version 4.0. Tech. Rep. LA-CC-06–012 Los Alamos National Laboratory, Los Alamos, NM. http://climate.lanl.gov/models/cice/index.htm
Johnsen G, Candeloro M, Berge J, Moline M (2014) Glowing in the dark: discriminating patterns of bioluminescence from different taxa during the Arctic polar night. Polar Biol 37(5):707–713. https://doi.org/10.1007/s00300-014-1471-4
Last KS, Hobbs L, Berge J, Brierley AS, Cottier F (2016) Moonlight Drives Ocean-Scale Mass Vertical Migration of Zooplankton during the Arctic Winter. Curr Biol 26:244–251. https://doi.org/10.1016/j.cub.2015.11.038
Latz MI, Rohr J (2013) Bathyphotometer bioluminescence potential measurements: A framework for characterizing flow agitators and predicting flow-stimulated bioluminescence intensity. Cont Shelf Res 61–62:71–84. https://doi.org/10.1016/j.csr.2013.04.033
Lind S, Ingvaldsen RB, Furevik T (2018) Arctic warming hotspot in the northern Barents Sea linked to declining sea-ice import. Nat Clim Chang 8:634–639. https://doi.org/10.1038/s41558-018-0205-y
Metzger EJ, Smedstad OM, Thoppil PG, Hurlburt HE, Cummings JA, Wallcraft AJ, Zamudio L, Franklin DS, Posey PG, Phelps MW, Hogan PJ, Bub FL, DeHaan CJ (2014) US Navy operational global ocean and Arctic ice prediction systems. Oceanography 27(3):32–43. https://doi.org/10.5670/oceanog.2014.66
Moline MA, Blackwell SM, Allen B, Austin T, Forrester N, Goldsborogh R, Purcell M, Stokey R, von Alt C (2005) Remote Environmental Monitoring UnitS: an autonomous vehicle for characterizing coastal environments. J Atmos Ocean Technol 22:1798–1809. https://doi.org/10.1175/JTECH1809.1
Saha S et al (2010) The NCEP Climate Forecast System Reanalysis. Bull Amer Meteor Soc 91:1015–1057. https://doi.org/10.1175/2010BAMS3001.1
Shulman I, Anderson S (2019) Bioluminescence potential modeling with an ensemble approach. Ocean Dyn 69:599. https://doi.org/10.1007/s10236-019-01264-4
Shulman I, Moline MA, Cohen JH, Anderson S, Metzger EJ, Rowley C (2020) Bioluminescence potential modeling during polar night in the Arctic: impact of advection versus local sources. Ocean Dyn 70(9):1211–1223. https://doi.org/10.1007/s10236-020-01392-2
Vernet M, Ellingsen IH, Seuthe L, Slagstad D, Cape MR, Matrai PA (2019) Influence of Phytoplankton Advection on the Productivity Along the Atlantic Water Inflow to the Arctic Ocean. Front Mar Sci 6:583. https://doi.org/10.3389/fmars.2019.00583
Wassmann P, Slagstad D, Ellingsen I (2019) Advection of Mesozooplankton Into the Northern Svalbard Shelf Region. Front Mar Sci 6:458. https://doi.org/10.3389/fmars.2019.00458
Webster CN, Varpe Ø, Falk-Petersen S et al (2015) Moonlit swimming: vertical distributions of macrozooplankton and nekton during the polar night. Polar Biol 38:75–85. https://doi.org/10.1007/s00300-013-1422-5
Acknowledgements
This research was funded through the US Naval Research Laboratory under program element 61153N. Support for JHC and MAM for observational work came from the Norwegian Research Council (NFR) projects ArcticABC and DeepImpact (NFR grants 244319 and 300333). Computer time for the numerical simulations was provided through a grant from the Department of Defense High Performance Computing Initiative. This manuscript is US NRL contribution JA-7330-21-5107.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare no competing interests.
Electronic supplementary material
Below is the link to the electronic supplementary material.
Appendix. The circulation model
Appendix. The circulation model
The ocean reanalysis used here is similar to the operational Global Ocean Forecast System (GOFS) 3.1 (Metzger et al. 2014) with the ocean model based on the HYbrid Coordinate Ocean Model (HYCOM) (Bleck 2002) that is two-way coupled to the Community Ice CodE (CICE) (Hunke and Lipscomb 2008). The model has ~ 1/12° (~ 9 km) horizontal resolution at the equator (~ 4.5 km resolution in the study area) and 41 vertical hybrid coordinate layers. It uses the Navy Coupled Ocean Data Assimilation (NCODA) system for assimilation of satellite surface height anomalies, temperature, and sea ice concentration as well as available in-situ vertical temperature and salinity profiles from XBTs, CTDs, Argo floats, moored buoys, gliders and marine mammals (Cummings et al. 2009). Observations are assimilated on a 24-h update cycle. The system is forced with atmospheric momentum and heat fluxes from the 0.3125° 1-hourly NCEP Climate Forecast System Reanalysis (CFSR) (Saha et al. 2010).
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Shulman, I., Cohen, J.H., Moline, M.A. et al. Modeling studies of the bioluminescence potential dynamics in a high Arctic fjord during polar night. Ocean Dynamics 72, 37–48 (2022). https://doi.org/10.1007/s10236-021-01491-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10236-021-01491-8