Quantifying wave measurement differences in historical and present wave buoy systems

Abstract

An intra-measurement evaluation was undertaken, deploying a NOMAD buoy equipped with three National Data Buoy Center and two Environment and Climate Change Canada-AXYS sensor/payload packages off Monterey, California; a Datawell Directional Waverider buoy was deployed within 19 km of the NOMAD site. The six independent wave measurement systems reported hourly estimates of the frequency spectra, and when applicable, the four Fourier directional components. The integral wave parameters showed general agreement among the five sensors compared to the neighboring Datawell Directional Waverider, with the Inclinometer and the Watchman performing similarly to the more sophisticated 3DMG, HIPPY, and Triaxys sensor packages. As the H_m0 increased, all but the Inclinometer were biased low; however, even the Watchman reported reasonable wave measurements up to about 6–7 m, after which the H_m0 becomes negatively biased up to about a meter, comparable to previous studies. The parabolic fit peak spectral wave period, T_pp, results showed a large scatter, resulting from the complex nature of multiple swell wave systems compounded by local wind-sea development, exacerbated by a variable that can be considered as temporally unstable. The three directional sensors demonstrated that NOMAD buoys are capable of measuring directional wave properties along the western US coast, with biases of about 6 to 9 deg, and rms errors of approximately 30 deg. Frequency spectral evaluations found similarities in the shape, but a significant under estimation in the high frequency range. The results from slope analyses also revealed a positive bias in the rear face of the spectra, and a lack of invariance in frequency as suggested by theory.

1 Introduction

Wind-generated surface gravity waves have been measured by various systems for more than six decades (Cavaleri et al. 2018). These include surface-piercing instruments; acoustic profilers; pressure sensors from single units to arrays (e.g., slope arrays and linear arrays); downward-looking lasers; and HF- and X-band radar systems (Young et al. 1985; Neito Borge et al. 2004). Many of the radar systems have been deployed on fixed platforms for some time, and over the past decade, stereo-imaging systems estimate the free surface (Benetazzo et al. 2012). Over the last decade, small mini-drifter buoys capable of returning non- and directional wave measurements (Thomson 2012; Collins III et al. 2014; Centurioni et al. 2017) have been incorporated into operations, adding to the spatial coverage of the world’s oceans. These assets complement the long-term use of satellite-based remote sensing systems (including aircraft) used to map estimates of the significant wave height, or estimate the directional wave properties (Synthetic Aperture Radars) spatially over the ocean surface (Ardhuin et al. 2019).

Historically, wave measurements have and continue to be monitored by point source, moored wave buoys deployed in the ocean. Point source measurements provide the temporal variation in the wave conditions at a designated location but not the spatial variability, unless sampled at multiple sites. Due to operational concerns, most of the buoys are located along the world’s coastlines, extending to about 200 km from shore. Data recovered have been used for data assimilation, to investigate wind-wave growth, to calibrate and validate operational wave models used by Numerical Weather Prediction (NWP) centers (e.g., European Centre for Medium Range Forecasts, National Centers for Environment Prediction), to drive nearshore wave modeling technologies, and to track long-term wave climate trends.

The buoys come in a variety of shapes, sizes, composition, super- and substructures, and mooring configurations. Housed in every buoy is a sensor that measures the buoy’s motion relative to the water surface and then converts it to an estimate of the free surface. More recently, if the sensor is designed to measure the three-dimensional axial components, directional estimates of the free surface can be computed. As long as the motion sensor used can accurately measure the attributes of the carrier frequencies contained in surface gravity wind-generated waves (from about 0.03 to 0.5 Hz), it should not matter what the sensor actually is. A similar argument can be used for the buoy itself. As long as the transfer function of the buoy’s motion to the free surface accurately defines all of the characteristics of that particular buoy (e.g., size, shape, composition, super- and substructure, mooring), then all data derived from all buoys should be the same. Lastly, and as noted, the motion of the buoy is usually measured in terms of acceleration. Onboard algorithms are used to convert the acceleration to displacement, and the time series to spectra. Differences in methods exist. For example, Datawell takes the raw acceleration time series and doubly integrates into a displacement. Fast Fourier Transfers are then used to generate frequency spectra and the four directional variables. NOAA-National Data Buoy Center (NOAA-NDBC) takes the raw acceleration time series and uses a Fast Fourier Transfer to generate acceleration spectra and then from linear wave theory converts the acceleration spectra to displacement spectra, and the four directional variables. In principle, there are differences; however, in the end, the estimates should technically be the same.

Over the period of record, there have been modifications to the sensor and payload (onboard analysis package) that can affect long-term records (Gemmrich et al. 2011) that have been used to assess the trends in the wave climate (e.g., Ruggiero et al. 2010; and Menendez et al. 2008). Using altimeter data as a common reference, Durrant et al. (2009) compared Environment and Climate Change Canada (ECCC) and NOAA-NDBC wave height data and found a systematic difference of 10% between the two data sources. Large portions of the point source measurements from both sources were derived from 6-m Navy Oceanographic and Meteorological Automatic Device, or NOMAD buoy (6N) systems. With these results, and with NDBC planning to decommission all of their NOMAD buoys, it became a necessity to construct a meaningful experiment in hopes of answering some of the questions regarding these long-standing data records.

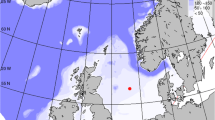
In 2012, a plan for an experiment—Field Laboratory for Ocean Sea State Investigation and Experimentation (FLOSSIE¹)—was developed, whereby a 6N hull would be configured with all historical sensor and payload packages used by NDBC during the past four decades. In July 2015, FLOSSIE was deployed and continued to operate until August 2020, although only two of the original five sensors were transmitting data at the end of the deployment period. A Pacific coast site was selected south of San Francisco in Monterey Canyon (Fig. 1), approximately 36 to 54 km from shore in a water depth of 2400 m. Three NDBC sensors (Inclinometer, a Datawell HIPPY sensor, and a tri-axial motion sensor) and two Environment and Climate Change Canada (ECCC) sensor/payload packages (strapped down accelerometer AXYS-Watchman payload and an AXYS-Triaxys system) were placed in the hull of the 6N buoy. The configuration and results would provide the means to evaluate similarities and differences between ECCC and NDBC 6N buoy records, substantiating or refuting the results documented by Durrant et al. (2009). Two additional wave buoys were deployed in close proximity to FLOSSIE (about 13 to 19 km): a 3-m NDBC discus buoy (the same tri-axial motion sensor and a HIPPY sensor) and a Datawell Directional Waverider (DWR) buoy used as a relative reference in the evaluation. The mooring configuration for the three buoys used standard systems for the depth of deployments. FLOSSIE is part of the continued effort of the US Army Corps of Engineer (USACE) Engineer Research and Development Center’s Coastal and Hydraulics Laboratory (CHL) to test and evaluate wave measurements, as identified in the IOOS Waves Plan (IOOS 2009), consistent with the recommendations of Swail et al. (2010) from OceanObs’09.

Fig. 1

FLOSSIE, NDBC 3-m discus buoy (46042, two deployments), DWR-Datawell Directional Waverider (46114), deployment site, Monterey Canyon, CA. Bathymetry color contoured in meters

Over the past decade, NOMAD buoys continue to be decommissioned and replaced by newer assets, as was the case previously for the family of large 12- and 10-m discus buoys. To date, NDBC no longer supports any NOMAD buoys and ECCC decommissioned its last one in 2019. So why investigate the accuracy in a buoy that is no longer in operation? Despite the loss of these assets, archived data records from these buoys continue to be used in climate trend analyses, altimeter algorithm assessments, and long-term wave hindcast evaluations. It is vital to understand the characteristics of these measurements and their performance with respect to a suitable relative reference, in this case the Datawell Directional Waverider, and to emerging measurement systems.

In the following sections, we give a historical account and intra-measurement evaluations of NOMAD buoys (Section 2). In Section 3, we describe the data attributes of the FLOSSIE buoy and the other components of the field program. Section 4 contains the results of our comparison of the integral wave parameters (height, period, and direction), while Section 5 describes the comparison of the frequency spectral analyses, slope spectra, and touching on the directional characteristics derived from a non-symmetrical buoy. A discussion section is provided in Section 6, and summary of the findings and concluding remarks are given in Section 7.

2 NOMAD history and applications

The NOMAD buoy is a boat-shaped hull designed to withstand extreme sea states when moored in deep water (Timpe and Rainnie Jr 1982; Timpe and Van de Voorde 1995). NOMADs are 6 m long (hence the designator “6N”), 3 m wide and about 2 m deep, weighing about 5200 kg (not including ballast which may add up to 4000 kg). NOAA-NDBC had experienced their large 10-m discus buoys capsizing in extreme storms and were looking for alternatives to alleviate the problem. In 1979, a NOMAD was moored to a 10-m discus buoy (45.9 deg N/131.1 deg W) to test for survivability of the buoy and instrumentation and to check for data quality. A mooring failure cut short the experiment; however, sufficient data were recovered to satisfy the goals of the experiment to indicate that NOMADs could replace existing large 12-and 10-m discus buoys. Over the next two decades, NOAA-NDBC expanded its use of NOMAD buoys and new buoy systems (3-m discus buoys) populating the ocean/meteorological network

of operational sites surrounding the US coastline and provided guidance to the total system accuracies of the measurements taken (Meindl and Hamilton 1992). A historical account of the NOAA-NDBC NOMAD buoys is provided in Fig. 2. Use of 6Ns increased first in the earlier years, peaking in the mid-1980s, decreasing slightly to about 20 in a given year, and then increasing again in the early through the mid to late 2000s. The noticeable increase is a result of two new buoy networks: Alaska (Aleutian Island, Bering Sea) and a second in the tropical cyclone (hurricane storm track path) located in the southern Caribbean Sea, extending into the Atlantic Ocean covering the southern portion of the USA. Around 2008, the number of NOMADs decreased significantly to the present, where in 2019, the remaining two buoys were decommissioned and replaced with 3-m discus buoys. If one were to total the number of US operational buoys over the duration of their deployments, there are 707 buoy-years (1-year deployment for one buoy is equal to 1 buoy-year) of NOMAD data stored and used by the waves community in various fashions. The Canadian buoy network, operating similar NOMAD buoys, has a similar history, with at its maximum eight operational NOMAD buoys spanning more than three decades. The last remaining 6N buoy was decommissioned in 2019, replaced with a 3-m discus buoy. In light of the sheer number of existing wave measurements from 6N NOMAD buoys, it seemed timely to evaluate the accuracy of the estimates. That fostered the Field Laboratory for Ocean Sea State Investigation and Experimentation (FLOSSIE, Jensen et al. 2015).

Fig. 2

NDBC NOMAD buoy count per year identified by domain (Pac, Pacific; Atl, Atlantic; GoM, Gulf of Mexico; GtL, Great Lakes)

3 FLOSSIE and the buoy farm

The primary efforts in this investigation were:

• 1. To study the similarities and differences in NDBC’s 6N historical configurations defined by the payload, sensor, and processor

• 2. To study the similarities and differences between NDBC and ECCC 6N sensor/payload configurations

• 3. To compare the integral wave parameters and frequency spectra from the NDBC and ECCC configurations to a common reference (Datawell DWR) and an operational NDBC 3-m discus buoy.

• 4. To investigate the accuracy in estimating directional properties derived from non-symmetric hull configurations, i.e., a boat-shaped hull

In order to address these objectives, the FLOSSIE buoy was configured with multiple sensor and payload systems housed in the hull, combined with a standard suite of NDBC meteorological sensors (anemometers, barometric pressure, air and water temperature sensors). This is illustrated in Fig. 3 where there are four primary compartments in a 6N buoy. Compartments 1 and 4 (Fig. 4) are empty except for cable pass-through. Compartment 2 contains the NDBC-HIPPY, Axys-Triaxys sensor and payloads, Axys-Watchman and Wave Module, batteries, and internal temperature sensor. Compartment 3 houses NDBC’s motion sensor (NDBC-3DMG), the inclinometer, compass, and payload analysis packages (DACT, ARES, DWPM, and DDWM).

Fig. 3

Schematic of a NDBC 6N buoy configuration, from Timpe and Van de Voorde 1995. Anemometers are positioned differently (see Fig. 4) from this diagram

Fig. 4

FLOSSIE dockside at NDBC (provided by R. Riley, NDBC)

There are five different data sets recovered from FLOSSIE:

• 1. NDBC: NDBC-Inclinometer/DACT (non-directional) – hereafter Inclinometer

• 2. NDBC: NDBC-HIPPY/magnetometer (original sensor/payload package to estimate directional waves) – hereafter HIPPY

• 3. NDBC: Motion sensor (NDBC-3DMG/payload package) standard directional wave buoy system – hereafter 3DMG

• 4. AXYS: Axys-Triaxys Next Wave II Directional Wave Sensor/Wave Module (new payload package used for directional wave measurements, e.g., TRIAXYS buoys) – hereafter Triaxys

• 5. ECCC: Axys-Watchman (strapped down accelerometer used by ECCC) – hereafter Watchman

FLOSSIE is the focal point of this paper; however, there is much more to the intra-measurement evaluation that is part of the buoy farm located in Monterey Bay Canyon (Fig. 1). Besides FLOSSIE, two other wave measurement systems have been deployed: an NDBC 3-m discus buoy containing two sensor/payload packages (HIPPY/3DMG-MicroStrain, Riley et al. 2011) and a Datawell Directional Waverider buoy operated by the Coastal Data Information Program (CDIP, http://cdip.ucsd.edu/).

• 6. CDIP/USACE: Datawell Directional Waverider – hereafter DWR

The Datawell Directional Waverider buoy was selected as the relative reference to be used in all wave intra-measurements evaluations, following Swail et al. (2010) and IOOS (2009). A Datawell buoy is not a universally accepted standard for wave measurements; it was selected because these systems have been used operationally for more than 40 years, with a large degree of understanding of the data characteristics and quality.

All real-time NDBC and ECCC data are transmitted separately on a 60- or 30-min interval via IRIDIUM communications. All data (original time series and processed data sets) are also stored to disks onboard. These disks were recovered during scheduled maintenance runs to the buoy on a yearly basis. The Datawell transmits the raw time series directly to the CDIP operational center at a 30-min interval.

In general, there are two primary data files for each of the eight wave measurement systems. The integral wave parameters (significant wave height (H_mo) and wave period (period of the peak spectral energy, T_p, and/or a mean wave period T_mean)) are computed from the defined frequency spectra. AXYS systems provide additional integral wave parameters derived from the raw time series that are not used in the analysis. Meteorological instrumentation onboard NDBC 46042 and FLOSSIE provides measurements of:

• Wind speed measured at an elevation of 5m, U₅/wind gust (measured at 5m), U_G

• Wind direction, θ_wind

• Barometric pressure, B_p

• Air and water temperature, T_air, T_water

The second data set consists of spectral and directional estimates derived from the time series of the buoy motion. These parameters are defined by:

$$ S\left(f,\theta \right)=E(f)\left[{a}_1\cdotp \cos\ \theta +{b}_1\cdotp \sin\ \theta +{a}_2\cdotp \cos\ 2\theta +{b}_2\cdotp \sin\ 2\theta +{a}_3\cdotp \cos\ 3\theta +{b}_3\cdotp \sin\ 3\theta +{a}_4\cdotp \cos\ 4\theta +{b}_4\cdotp \sin\ 4\theta +\cdots \right] $$

(1)

where S(f,θ) is the two-dimensional wave spectra defined by the range in frequencies (f) and direction (θ). E(f) is the frequency spectra and sometimes defined by a₀ where ${\mathrm{a}}_0=\raisebox{1ex}{$E(f)$}\!\left/ \!\raisebox{-1ex}{$\pi $}\right.$. The terms defined by a₁, b₁, a₂, and b₂ are the Fourier coefficients. Directional buoy measurements return the First-5 components in the infinite Fourier series (a₀, a₁, b₁, a₂, b₂) defined in Eq. 1. The Datawell and AXYS systems’ spectral estimates are defined by the First-5 Fourier coefficients at each frequency band. The directional parameters (mean wave direction at the peak frequency θ_mean(f_m), spread, σ(f_m), where f_m is equal to 1/T_p) are computed from the four directional Fourier components or a₁, b₁, a₂, and b₂, provided directly from the data sets or:

$$ {\theta}_{\mathrm{m}\mathrm{ean}}\left({f}_m\right)={\tan}^{-1}\left\{\frac{b_1\left({f}_{\mathrm{m}}\right)}{a_1\left({f}_{\mathrm{m}}\right)}\right\} $$

(2)

$$ \sigma \left({f}_{\mathrm{m}}\right)=\sqrt{2\left\{\Big(1-{\left({a}_1^2\left({f}_{\mathrm{m}}\right)+{b}_1^2\left({f}_{\mathrm{m}}\right)\right)}^{1/2}\right\}} $$

(3)

The NDBC returns a slightly different form defined by:

$$ S\left(f,\theta \right)\approx {C}_{11}\cdotp \left\{\frac{\left[\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.+{r}_1\cdotp \cos \left(\theta -{\theta}_1\right)+{r}_2\cos \left(2\left(\theta -{\theta}_2\right)\right)\right]}{\pi}\right\} $$

(4)

C11 is equivalent to E(f) in Eq. 1. The directional Fourier coefficients r₁ and r₂ are related to the a₁, b₁, a₂, and b₂ values as:

$$ {r}_1=\raisebox{1ex}{$\sqrt{a_1^2+{b}_1^2}$}\!\left/ \!\raisebox{-1ex}{${a}_0$}\right. $$

(5)

$$ {r}_2=\raisebox{1ex}{$\sqrt{a_2^2+{b}_2^2}$}\!\left/ \!\raisebox{-1ex}{${a}_0$}\right. $$

(6)

$$ {\theta}_1={\tan}^{-1}\left(\raisebox{1ex}{${b}_1$}\!\left/ \!\raisebox{-1ex}{${a}_1$}\right.\right) $$

(7)

$$ {\theta}_2=\left(\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.\right){\tan}^{-1}\left(\raisebox{1ex}{${b}_2$}\!\left/ \!\raisebox{-1ex}{${a}_2$}\right.\right) $$

(8)

NDBC represents the mean directional components (θ₁ and θ₂) by α₁ and α₂ where:

$$ \alpha =\left(\raisebox{1ex}{$3\pi $}\!\left/ \!\raisebox{-1ex}{$2$}\right.\right)-\theta $$

(9)

The NDBC directional estimates are converted to the First-5 Fourier coefficients so that all data are equivalent.

FLOSSIE was deployed on 28 July 2015 for 59 months, transmitting the meteorological and wave data displayed in Fig. 5 for the five sensors onboard and the DWR. General information regarding the various buoy platforms is provided in Table 1, including the 3-m NDBC buoy containing the dual directional sensors. All sites are stationed in deep water, roughly 36 to 54 km from the nearest coastline. Return on the data from various sensor/payloads was exceptional where the number of dropouts or flagged (not passing quality control) data were less than 1% for the three NDBC sensors, until mid-May 2020 when the HIPPY sensor failed. The ECCC sensors—Strapped Down Accelerometer (Axys-Watchman payload)—failed during routine buoy maintenance in August 2017. The Axys-Triaxys operated until the transmitter failed in October 2018. The DWR experienced bio-fouling that would contaminate the high frequency energies, from April to August 2016, and again from June to September 2017. The relative magnitude in the error for the two periods of record was less than a percent of the total uncontaminated wave energy. Other less obtrusive data dropouts did exist from all records but were limited to intermittent hours.

Fig. 5

Data return of the five sensors onboard FLOSSIE and the DWR. The solid vertical lines represent the failure of a given sensor. The dashed and dotted vertical lines indicate maintenance of the DWR and FLOSSIE, respectively

Table 1 General characteristics of buoy platforms

As noted in Table 2, of the five sensor/payload packages, two provided non-directional wave estimates, NDBC-SM133 (NDBC-Inclinometer) and ECCC-SDA (Axys-Watchman, strapped down accelerometer). Two data sets provided wave estimates on a 30-min interval (3DMG and DWR). For this analysis, the time stamp for any data not reporting at 00 or 30 min was shifted 6 or 10 min to be consistent with the other records. The analysis assumed all data obtained were quality controlled by the various data providers passing their standard operational testing procedures.

Table 2 Sensor/payload characteristics

We limit the evaluation for the period of record from August 2015 through July 2019. Data from the sensors are calculated from analysis packages used by each respective organization: NDBC, ECCC, and CDIP. The evaluation is based on the data reported to the Global Telecommunication System directly to the user community and that found in various data archives. One may consider this as an impediment and will not provide an in-depth study of individual sensor differences, as there are differences in analysis methods that would affect the evaluation. However, the goal here is to isolate the differences from end-to-end, that one faces using transmitted wave measurements and specific to a NOMAD hull. The discussion is also limited to the data obtained from FLOSSIE and the Datawell Directional Waverider. Intra-measurement evaluations of data recovered from 46042 (NDBC dual sensor: HIPPY/3DMG-MicroStrain) are summarized in Bouchard et al. (2015).

The wave parameters defined in the analysis are assumed to be the zeroth moment wave height (H_mo), the period of the peak spectral energy (T_p), and the vector mean wave direction at the peak spectral energy frequency (θ_mean(f_m)). Triaxys mean wave direction is defined by the “weighted average over the entire frequency spectrum,” dependent on the wave state, rather than translated from the corresponding three-dimensional displacement time series used by CDIP and NDBC (3DMG and HIPPY). If multiple wave systems occur (i.e., low-frequency swell energy and locally generated wind seas), the reported Triaxys mean wave direction may differ. In addition, the Triaxys returns directional parameters based on magnetic north and not true north. Based on FLOSSIE’s site, the magnetic declination is 14 deg. The rotation was not included; however, when the directional wave evaluation is summarized, the difference is noted. The difference in the wave direction will be dependent on the energy contained in the frequency range defining the two peaks. The DWR reports its measurements in magnetic north, however, is adjusted to true north prior to dissemination. This is also true for the NDBC sensor directional data. The original Watchman frequency spectra contained what appeared to be noise in the low frequency range of (< 0.03 Hz). A filter scheme developed by AXYS, used operationally by ECCC for wave data processing, was provided and applied to the frequency spectra eliminating the noise. The spectra were then processed recovering the integral wave parameters and used in subsequent analyses.

Use of the T_p and θ_mean(f_m) will have a dependency on the frequency range and intervals used by the various data providers, specific to the wave measurement system and processing routines used. To reduce the inconsistencies, we have selected the parabolic fit peak period (T_pp). The definition of T_pp is a weighted average based on the energy levels for the neighboring discrete frequency bands on each side of the peak frequency. The averaging is a result of fitting a parabola to the three points. This removes the dependency on dissimilar discrete frequency bands and minimizes large changes in the parameter over time, especially in the low frequency range of the energy spectrum, E(f). The parabolic fit peak wave period better represents the wave conditions, while the T_mean tends to generalize the dominant wave system, which is the reason why T_pp was selected as a metric for evaluation; however, in mixed seas of similar energy, it can tend to alternate between two different values.

4 FLOSSIE integral wave parameter analysis

As noted above, the field experiment operated over a period of 59 months. During that time, the local winds measured on FLOSSIE showed the expected seasonal variation where the higher winds are found in the winter (Dec–Feb) months. Superimposed on the seasonal variation, the wind speed fluctuated during storm events. Overall, the mean wind speed was about 6.3 m/s (standard deviation 3.1 m/s), with a maximum value of 20.9 m/s. The wind direction during the period of record is predominantly north to northwesterly. As storm events with increasing wind speeds move through the area, the wind direction changes from the northwesterly direction to southerly directions. These winds would contribute to local wind sea development adding to the energy derived from background and active swells derived from the North and South Pacific Ocean.

Over the period of record for the intra-measurement evaluation, the wave conditions were highly variable on an inter-annual, seasonal, and storm event scale (see Fig. 6). The time series shows the expected seasonal variation, with significant wave heights of 6–10 m in the winter months (Dec–Feb), while during the summer (Jun–Aug), the wave climate is reduced to about 2.5 m, with transitional periods in autumn (Sep–Nov) and spring (Mar–May). Figure 6 also shows good general agreement among the six sensors over the period of record.

Fig. 6

Time plot of the significant wave heights from the five sensors onboard FLOSSIE and the DWR. Each panel (a–e) represents a year, from 2015 through 2019

Peak and mean wave periods (not shown) for all sensors are similar over time. As FLOSSIE is stationed along the US Pacific coast, the wave climate is dominated by swells from the northwest (10 to 18 s) in the winter, with intervals during storms where the peak period is dictated by local wind seas (5 to 8 s). In the summer months, swells from the south dominate, although at lower energy levels, with occasional local wind seas. Due to the proximity and orientation of the California coast, very little wave energy comes from any easterly direction.

The evaluation of the multiple sensor/payload packages in FLOSSIE is based on a relative reference. That reference is the DWR located about 19.3 km from FLOSSIE (Fig. 1). We assume the waves measured at both sites are derived from similar meteorological systems existing in the Pacific Ocean (for the low frequency swell), and locally generated wind seas. Local conditions most likely are not exactly the same for two sites (FLOSSIE and 46042) separated by nearly 20 km, however were considered negligible.

To investigate the similarities and differences between the DWR as the relative reference and each of the five sensors onboard FLOSSIE, the DWR is time-paired to each data set independent of the other four. This could introduce a bias in the results, as each time-paired data set may differ based on the total number of observations. With the exception of the Watchman, the difference in the number of pairs and their temporal distribution were inconsequential; even the Watchman contained more than 10,000 pairs of data so the results should be relatively robust.

4.1 Evaluation of significant wave height (H _m0)

Figure 7 shows the results of the comparisons of the significant wave height measured by the five sensors onboard FLOSSIE versus the DWR, in a scatter plot in the left panel and the quantile-quantile (QQ) analysis on the right. Statistical results of the analysis are provided in Table 3.

Fig. 7

Scatter of the H_m0 data for the five FLOSSIE sensors versus the DWR (left panel), and QQ analysis (right panel). Each sensor is color-coded identified in the legend and the total number of observations used in the analysis. Dashed and dotted lines in the QQ plot reflect ±0.25 and ±0.5 m

Table 3 FLOSSIE wave parameter statistical results compared to the DWR for analysis period Jul 2015–Jul 2019

The scatter plot results distinctly show the similarities in the five sensors from FLOSSIE, generally symmetrical in the distribution following the line of perfect fit. In general, the data differences are within about ±1.0 m until the 6-m threshold is reached, after which the spread increases as the number of observations decreases. Analyses were also performed which showed that there were no leading or trailing time shifts between the DWR and FLOSSIE due to the 19.2-km separation distance and 30- or 60-min data return interval.

The QQ analysis (right panel, Fig. 7) shows that all five FLOSSIE sensors are positively biased with respect to the DWR up to about 5 m, with the Inclinometer showing the greatest deviation (0.21 m) from the line of perfect fit. Above 5 m, the 3DMG (NDBC’s motion sensor), the HIPPY (a Datawell, tri-axial gimbaled sensor), the Triaxys, and Watchman (strapped down accelerometer used operational by ECCC) fall close to the line of perfect fit, while the Inclinometer remains high. Above about 7 m, the lines diverge, with the 3DMG, HIPPY, and Watchman reporting increasingly low values compared to the DWR, while the Inclinometer remains above the line of equality until the 9-m level. The Triaxys shows some variability above the 6-m level, with biases first about 0.5 m positive then about 0.5 m negative. The more limited number of data points for H_m0 conditions greater than 6 m will contribute to the variability in the results, especially the limited data records from the Watchman (about one-third of the other records), but this does, however, reflect the real differences in the sensor systems.

Due to the extremely large number of observation pairs (more than 168,000), the scatter plot in Fig. 7 is difficult to interpret for each individual sensor. Figure 8 (a–e) shows the scatterplot results separately for each FLOSSIE sensor compared to the DWR, with the accompanying regression line. This shows that three of the sensors (HIPPY, 3DMG, Triaxys) perform very similarly in terms of scatter and slope of the regression line, with the Triaxys being slightly better. The Inclinometer has a similar scatter, but the slope is 1.00, i.e., matches the DWR exactly. The Watchman, the basis of the Canadian buoy network, tends to have a higher scatter and is more affected at the higher wave heights, above about 7 m. The regression coefficients—bias of 0.23 m and slope of 0.93—are identical in slope but are a factor of four higher in bias compared to those reported by Swail et al. (2011) from a parallel Canadian investigation on the Grand Banks for a DWR compared to a Watchman on a NOMAD buoy (0.05 m, 0.93)

Fig. 8

Scatter of the H_m0 data for the five FLOSSIE sensors versus the DWR. a NDBC-Inclinometer. b NDBC-3DMG. c NDBC-HIPPY. d Axys-Triaxys. e Axys-Watchman. Symbols (blue) define time-paired observations; gray line represents line of perfect fit; black dash and dotted lines indicate ±0.25 m and ± 0.5 m; solid red line is linear fit to data (equation identified in top left corner)

Two additional analyses were conducted to investigate the scatter identified in the five sensors of FLOSSIE versus the DWR. First, rather than using the DWR as the independent variable versus the FLOSSIE sensors, now the Inclinometer is used in its place, comparing to the remaining four FLOSSIE sensor data sets. The Inclinometer had been the only sensor/payload system used by NDBC in all 6N buoys; therefore, it was selected as the independent variable to complement the preceding analysis. This removes the consideration of the different hulls and the spatial separation, and compares only the differences in the sensors and processors. Figure 9 shows the collective comparisons of the other four FLOSSIE sensors to the Inclinometer, the left panel showing the scatter and the right panel the QQ analysis. Figure 10 (a–d) shows the individual regression analysis for each sensor versus the Inclinometer.

Fig. 9

Scatter of the H_m0 data for the four FLOSSIE sensors (NDBC-3DMG, NDBC-HIPPY, Axys-Triaxys, and Axys-Watchman) versus the NDBC-Inclinometer (left panel). Each sensor is color-coded identified in the legend and the total number of observations used in the analysis. Quantile-quantile analysis (right panel) where dashed and dotted lines in the QQ plot reflect ±0.25 and ±0.5 m

Fig. 10

Scatter of the H_m0 data for the four FLOSSIE sensors versus the NDBC-Inclinometer. a NDBC-3DMG. b NDBC-HIPPY. c Axys-Triaxys. d Axys-Watchman. Gray line represents line of perfect fit; black dash and dotted lines identify ±0.25- and ±0.5-m ranges; solid red line defines the linear fit

The results from the Inclinometer versus the four alternate sensors in FLOSSIE show a substantial decrease in the scatter of the data, now confined to +0.5 to −1.0 m compared to slightly more than ±1.0 m using the DWR. The rms errors (root-mean-square error) were less than half those of the comparisons with the DWR, and the 3DMG matched the Inclinometer closely with an rms error of 0.079 m and a correlation of 0.998. The slopes of the regression lines were nearly identical to those of the DWR comparisons for those four sensors, suggesting that the differences for the main part of the population were due to sensor processing differences rather than the hull.

The second analysis investigated a co-deployment of two identical DWRs deployed near the Harvest Platform located approximately 29 km west of Point Conception, CA, in a water depth of 560 m, from July 2015 to July 2017, separated by 2 km with a watch circle of about 750 m. The two buoys used in the analysis were operated and maintained by CDIP (http://cdip.ucsd.edu/), as the DWR used in the FLOSSIE study. The data processing is identical, the time stamps for the majority of the data were identical, and those that varied were approximately a 9-min temporal difference, having little or no impact on scatter for sampling differences. Hence, the data records and processing would be the most consistent set of conditions available for a co-located, intra-measurement evaluation.

The scatter plot results for the co-located Harvest DWRs are shown in Fig. 11. The range of the scatter for the two DWR’s is similar in magnitude to that found in the evaluation of the five FLOSSIE sensors versus the DWR depicted in Fig. 7, although the rms error is about half as large, which is to be expected since the separation distance is eight times smaller than FLOSSIE and the DWR in Monterey Canyon. Since this represents nearly a perfect inter-comparison (identical buoys, 2-km separation), it is reasonable to assume that the agreement shown between them (3-cm difference in the mean wave height, rms error 0.17 m, scatter index 6%) represents the maximum achievable for two co-located measurements.

Fig. 11

Scatter of the H_m0 data (left panel) and T_pp (right panel, parabolic fit peak wave period, see below) for the two DWRs deployed at Harvest Platform. Line of perfect fit (gray line), linear regression (red line), quantile-quantile (green line), and ±0.25- and ±0.5-m ranges in significant wave height (left panel) or peak spectral wave period (right panel) defined in legend

In light of these limitations on agreement between any two co-deployments, the agreement between the DWR and the FLOSSIE sensors is found to be relatively good, with the primary cause being the sensor processing.

4.2 Evaluation of parabolic fit peak wave period (T _pp)

There are many different wave period definitions; however, we have selected the parabolic fit peak period (T_pp) to reduce the frequency binning used in the processing of the various sensors if T_p were adopted as the wave period metric. In addition, as the wave conditions during the study were a mixture of multiple wave systems derived from North and South Pacific storm events and interspersed with local wind seas using T_mean would return values that would be a weighted average, and not a true representation of the wave conditions present.

Using the same data sets as in the H_m0 evaluation, the T_pp time-paired data results for scatter and QQ are shown in Fig. 12, where the DWR is the independent variable and the five FLOSSIE sensors the dependent variable.

Fig. 12

Scatter of the T_pp data for the five FLOSSIE sensors versus the DWR (left panel), and QQ analysis (right panel). Each sensor is color-coded identified in the legend and the total number of observations used in the analysis. Dashed and dotted lines in the QQ plot reflect ±1.0 and ±2.0 s

It is obvious there is a substantial amount of scatter in the reported data from the FLOSSIE sensors compared to the DWR. The main lobe of differences is below the line of perfect fit where all sensors are reporting lower values compared to the DWR. A portion of the scatter is a result of a mixed locally generated wind sea, and swell, where the peak energy alternates between low frequencies (swell) and high frequencies (wind sea) as in the case of frontal passages, and/or during low wave energy conditions.

Evaluation of the FLOSSIE sensors using the Inclinometer as the independent variable showed similar results to those in Fig. 12. The primary cluster of data fell within ±1.0 s, the scatter above and below 2.0 s was reduced, and more observations were positively biased compared to negatively biased. The rms errors were reduced compared to the DWR comparisons. The 3DMG showed an rms error of 1.71 s compared to the Inclinometer on FLOSSIE compared to the 2.33 s for the DWR; all of the other sensors showed similar reductions.

The second cause for the large number of deviations in T_pp results can be attributed to defining the peak energy in the spectrum for low wave height conditions. The temporal variation in T_pp under the low energy conditions can oscillate from low to high discrete frequency bands caused by changes in the local wind speed or direction and possible phase differences collecting the data. Given all of the subtleties in the collection procedure, the inherent unstable nature defining the peak wave period over time, results from FLOSSIE are relatively consistent with the DWR. Comparisons with the values from the Harvest Platforms showed absolute (rms) errors of 1.13 s (2.17 s) for Harvest versus 1.29 s (2.39 s) for the FLOSSIE HIPPY sensor.

One last attribute found in Fig. 12 is the presence of vertical data clusters that are found in the DWR results. Using T_pp over a peak wave period (T_p, defined by the frequency band containing the maximum energy in E(f)) was to remove the dependency resulting from differences in discrete frequency bands, as well as produce somewhat smoother variations in the wave period over time. However, it appears a frequency banding dependency exists in the data to some degree. The center of each vertical distribution is consistent with the discrete frequency bands reported by the DWR. From the results, the DWR frequency spectra are symmetrical about the peak frequency, whereas in most all cases for the five FLOSSIE sensors, the energy levels on either side of the peak frequency differ.

Analyses comparing the mean wave period (T_mean) of the DWR and FLOSSIE sensors (Appendix Fig. 18), show that the scatter is greatly reduced, with absolute (rms) errors of 0.45 s (0.55 s).

A clearer representation of the deviation or similarity between the FLOSSIE sensor T_pp estimates compared to the DWR is shown in the QQ analysis (of Fig. 12, right panel). Despite the apparent discrepancies (more data below the line of perfect fit) found in the scatter plot, the QQ analysis reveals the FLOSSIE sensors follow a similar trend and a negative bias of about 1 s over the range of wave periods measured. The oscillations apparent in all results are caused by the DWR and its propensity to center about each discrete frequency band as previously discussed. As the T_pp increases, the Inclinometer diverges from the remaining four sensors, producing a large positive bias indicating added energy in the lower frequency range of its spectra. This trend is also evident in the Watchman data where the divergence occurs around 22 s and is most likely caused by the filter scheme used on the frequency spectra.

4.3 Evaluation of mean wave direction ((θ _mean(f _m))

The final integral wave parameter to be evaluated is the vector mean wave direction defined at the spectral peak (θ_mean(f_m)). Originally, the intent of FLOSSIE was to evaluate various sensor systems focusing on the historical sensor packages of NDBC (Inclinometer) and ECCC (Watchman). However, NDBC and ECCC, with the support of AXYS, wanted to examine if more precise (e.g., Teng and Bouchard 2005) sensor packages would provide an increase in performance and accuracy in all wave measurement properties. Introducing 3DMG and HIPPY sensors and the Triaxys Directional Wave Sensor II to FLOSSIE provided an opportunity to determine if accurate directional wave estimates could be obtained from a 6N, non-symmetrical buoy hull. Figure 13 (left panel) displays the θ_mean(f_m), a real measurement using the time series from the three displacements, and a computed vector mean wave direction. The overall vector mean wave direction (θ_mean, Fig. 13, right panel) is computed from the four directional parameters (a₁, b₁, a₂, and b₂ or from NDBC, α₁, α₂, r₁, and r₂) defining the directional distribution at a 1 deg directional resolution (Eq. 1) using a maximum entropy method (MEM, Benoit et al. 1997). The results from θ_mean are estimates of the wave direction, whereas θ_mean(f_m) is based on a direct measurement. Calculations to estimate θ_MEAN are identical across the sensors, and therefore, conclusions can be drawn from the results.

Fig. 13

Scatter of the measured θ_mean(f_m) data for the three FLOSSIE directional sensors versus the DWR (left panel), and the computed θ_mean (right panel). Each sensor is color-coded identified in the legend and the total number of observations used in the analysis. The line of perfect fit is defined by the solid gray line; dashed and dotted lines in the graphics reflect ±22.5 and ±45.0 deg thresholds. Lobes identified as P1 and P2 and L1 and L2 refer to consistencies between TEST observations and inconsistencies in TEST observations, respectively

The θ_mean(f_m) scatter plot (Fig. 13, left panel) shows four distinct clusters of data. Two primary lobes (P1, P2) are centered about 270 (P1) and 180 deg, respectively. The directions are consistent with a US Pacific coast dominant swell wave climate. During the winter season, coastal swell conditions are derived from North Pacific Ocean storms translating from west to east; during the summer season, the swell climate is a result of storms from the South Pacific Ocean. The swell dominance in the wave climate is also supported by the complete lack of directional data in the range from 0 to 150 deg. That directional arch is consistent with the outline of the Monterey Canyon coastline (Fig. 1). Wind measurements from FLOSSIE for the period of record were analyzed and showed that 12.2% of the total observed winds were within the 0 to 150 deg directional window. For that population, the mean wind speed was 4 m/s with a maximum of more than 20 m/s. Thus, it is possible for waves to exist in that directional window. It appears from the θ_mean(f_m) that the energy level for the local wind sea never exceeds the energy level of the swell. The results show a gap containing limited data returns for wave directions centered about 225 deg extending about 25 deg on either side in the records. This is most likely the transitional region from North to South Pacific swells. The less populated region is consistent with the wind directional distribution and is not confined to the FLOSSIE (three sensors) and DWR. Similar directional results were observed at 46042 (Fig. 1) using the DWR as the BASE reference, is evident when the θ_mean(f_m) from 46042’s HIPPY sensor was used and also when the HIPPY on FLOSSIE (compared to the remaining two sensors) was selected as the independent variable. The remaining two lobes (L1, L2) are mirror images and polar opposites of the independent value where large differences in the wave direction are evident and are discussed below.

Focusing on the two primary lobes (P1 and P2), it is evident that the 3DMG and HIPPY sensors fall within the 45 deg difference limits and are positively biased (clockwise in direction space) but in general show good agreement to the DWR. The Triaxys sensor compares more favorably (distribution falling closer to the line of perfect fit) and is negatively (counterclockwise) biased compared to the DWR; this agreement is even better when you consider that Triaxys reports directions with respect to magnetic north, so applying the magnetic declination value of 14 degrees to those results brings them close to the line. In general, however, the three directional wave results do quite well, despite the expected limitations of a non-symmetrical buoy hull.

The side lobes (L1, L2), centered about 180 and 320 deg (top lobe), with the smaller data cluster centered at 320 and 180 deg (bottom lobe), are interesting and require additional analysis. L1 and L2 represent 6% and 2% of the total population, respectively. There is more than a 140 deg difference between the DWR and FLOSSIE sensors. The easiest explanation is as follows. L1 (6% of the total population) is represented by the data where the FLOSSIE sensors select the North Pacific Ocean swells as the primary wave system while the DWR selects the South Pacific Ocean swells. L2 (2% of the total population) contains data opposite, where FLOSSIE sensors select South Pacific Ocean swells and the DWR now defines the primary wave system from the North Pacific Ocean. The two lobes represent the transition period from northerly to southerly wave events or vice versa. We find the data from L1 maps directly into the T_pp cluster below the line of perfect fit in Fig. 11 while L2 maps into the cluster above the line of perfect fit in Fig. 12. Similar clusters are also evident in the data from 46042 using the DWR as the base (independent variable), using the HIPPY sensor as the base compared to the directional sensors on FLOSSIE and the intra-measurement evaluation of θ_mean(f_m) exclusive to the onboard sensors of FLOSSIE. Given the results from four independent analyses, the large differences in the wave directions found in L1 and L2 are caused by multiple wave systems containing similar energies in different frequency bands. The differences could, albeit unlikely, be a bi-product of different discrete frequency bands defining the spectra, or other subtle components in the onboard algorithms used in the Triaxys, 3DMG, and HIPPY. However, in general, the two NDBC sensor packages (FLOSSIE and 46042) contain the identical frequency banding, but their analysis packages are slightly different and would not alter the results to a large degree. Differences in frequency bands do, however, contribute to a certain degree as the peak frequency especially under low energy conditions can change over time and θ_mean(f_m) as well. Those differences will result in different values defining the direction. We have established (Fig. 12) the differences that can be as much as 10 s in the extreme case.

One remaining factor is general characteristics of the wave conditions along the western US coastline, defined by long period swell arriving within a directional window centered at 290 deg and contained in a ±20 to ±40 deg range. Even with strong local winds creating wind seas that fall outside the swell directional window, moving the peak frequency to the wind sea portion of the spectrum would require the wind speed to be on the order of 10 m/s, a sustained direction for at least 12 h, and during low swell energy conditions. Over the FLOSSIE period of record, the number of occurrences meeting these criteria was extremely small. For the clusters defined by L1 and L2 in Fig. 13, the wind speed on average was between 5.5 and 6.3 m/s with a maximum of 16 m/s; however, the wind direction was rotating during frontal or low pressure system passages. Further evaluations of the mean wave direction defined at each frequency (θ_mean(f)) over time would be required to isolate the details of the wave environment but are beyond the scope of the paper. The variability in θ_mean(f_m) is significantly reduced using the overall mean wave direction, θ_MEAN, and comparable to using T_p versus T_mean.

The mean wave direction (Fig. 13, right panel) for the three FLOSSIE directional sensors agrees relatively well with that for the DWR. The range of the sensor data is consistent with the DWR, from about 160 deg to 330 deg. The distribution and differences between the FLOSSIE sensors and DWR become wider for wave directions in the range between 270 and 360 deg. Similar to θ_mean(f_m), there is a greater number of wave directions from the North Pacific Ocean compared to the South Pacific. It is evident in all sensor results that the Triaxys is more aligned to the line of perfect fit if the magnetic to true north adjustment is applied; however, there is a slight negative bias in the range of directions from 250 to 320 deg. That particular data set has the lowest population size and is about 30% lower than the HIPPY and 65% lower than the 3DMG (30-min sample rate). The 3DMG is negatively biased in the range of wave directions derived from the South Pacific Ocean, becomes consistent with the DWR in the mid-angle range, and then is positively biased for wave directions above about 250 deg. Data from 3DMG is more positively biased, exceeding the +45 deg threshold more often than the remaining two sensors. The HIPPY mean wave direction estimates are slightly better than the 3DMG. The spread of the data is positively biased, but the extent of the positive bias remains slightly below the +45 deg threshold for directions greater than 250 deg. In the case of the lower directional values (derived from the South Pacific Ocean), there is a slight negative bias remaining above −22.5 deg line. Collins III et al. (2014), based primarily on single peaked spectra (around 50 to 350 observations for each data set), found biases in direction between −11.5 and +17.3 deg. The results from FLOSSIE indicate a much greater bias; however, the results for what has become a complex directional wave climate, all three sensors manage to estimate the vector mean wave direction within ±45 deg.

5 FLOSSIE frequency spectral analysis

It has been shown thus far that there are similarities and differences found in the integral wave properties derived from the FLOSSIE sensors. To investigate further, analysis of the frequency spectra obtained from the FLOSSIE sensors relative to the DWR is presented. The analysis is based on the time-paired observations of the frequency spectra as performed for the integral wave properties. Figure 14 displays the mean frequency spectra for each sensor, and the mean of the 90th quantile. All sensors show similarities in the energy spectra defined in the forward and rear face, with some deviations at the spectral peak for the overall mean and the 90th percentile populations. For the overall mean spectral results (left panel, Fig. 13), the Watchman data contains the lowest energy, although very similar to the DWR results, while the Inclinometer tends to be the highest and the other three sensors fall between. For the 90th percentile conditions (right panel, Fig. 14), there is a strong similarity of the spectral results in the forward face, while the Watchman now contains more energy defining the rear face and also is elevated at the spectral peak. The DWR mean spectra for the 90th percentile are found to contain the lowest energy level, as noted in the H_m0 results. The strong similarity in peak energy values (excluding the Watchman, elevated because of its population size) and location in frequency space somewhat contradicts the T_pp results found in Fig. 14. Further analysis (not presented) of the spectra using the Watchman period of record showed a consistency in the peak energy compared to the four FLOSSIE sensors and the DWR.

Fig. 14

Mean wave frequency spectra based on the period of record Jul 2015–Jul 2019 (left panel) and 90th percentile (right panel) from the five FLOSSIE sensors time-paired to the DWR, identified in the legend for the period of record. The mean H_m0 values for the spectra are identified in the secondary legend

As the energy spectral estimates are contained in a range of at least five orders of magnitude, a linear plot does not reveal the details that are found especially for the mean spectral results. Figure 15 contains the same analyses displayed in Fig. 14, plotted on logarithmic scales. This presentation also provides a means to determine if the spectral tail follows the well-established theoretical slope of f⁻⁴ (e.g., Phillips 1985). In the low frequency range, all sensors exhibit low frequency energy, attributed to noise common to all sensor systems. The magnitude of the presumed noise is between two and three orders of magnitude lower than that contained in the spectral peak. There are measurable differences between sensors in the forward face of the spectra that would impart differences found in, for example, the T_pp estimates, contrary to the results from Fig. 14 (left panel). In the rear face, four sensors (Inclinometer, 3DMG, HIPPY, and Triaxys) exhibit a slight rise in energy at 0.1 Hz, while the Watchman and DWR follow a consistent trend downward. The slope of the rear face is shallower than an f⁻⁴ depicted by the solid black line, as the results are over the entire period of record, reflecting non-saturated conditions typical in a high wave energy environment. At approximately 0.4 Hz, all FLOSSIE sensors show a marked change in slope approaching an f⁻¹⁰, whereas the DWR continues to follow a consistent slope. It could be assumed the change in slope is caused by FLOSSIE’s hull and overall weight (5200 kg) suggesting a 6N buoy would be incapable of accurately measuring waves of 2.5 s or shorter. This artifact was also evident in the 3-m discus buoy (46042, not presented) and has been documented by Rogers (2017). The DWR is a spherical 0.9-m buoy and about 225 kg or about 23 times lighter than FLOSSIE; thus, it would be expected that a DWR could measure into the high frequency range more accurately. The results for the 90th percentile show similar trends; however, the slope of the rear face tends to follow the f⁻⁴ slope above 0.4 Hz, whereas all FLOSSIE sensors follow an f⁻¹⁰ slope, similar to that found in the overall mean results. In either case, the energy level found in frequencies above 0.4 Hz is about two orders of magnitude lower than the energy peak but within the same order of magnitude measured by the DWR and would, once integrated, influence the H_m0 results.

Fig. 15

Logarithmic plot of the mean wave frequency spectra based on the period of record Jul 2015–Jul 2019 (left panel) and 90th percentile (right panel) from the five FLOSSIE sensors time-paired to the DWR, identified in the legend for the period of record. The mean H_m0 values for the spectra are identified in the secondary legend

Application of buoy measurements for radar altimeter estimates has relied on accurate estimates of the slope spectra (Wang and Ichikawa 2016; Hwang and Fan 2018; Chen et al. 2016). Bragg resonance is critical to scatterometry and is dependent on the surface roughness elements in a narrow spectral region satisfying resonance conditions. The length scales of these resonance surface wave components (Bragg waves) are much shorter than the dominant surface waves near the spectral peak (Hwang and Fan 2018). In other words, scatterometry is dependent on high-quality estimates in the rear face (high frequency range) of a spectrum. NOMAD buoys have been used (along with other hull types) in studies of this nature. It would seem reasonable to investigate spectra from FLOSSIE in the context of slope spectra defined as:

$$ \zeta (f)=\left[\frac{{\left(2\pi f\right)}^4}{g^2}\right]\ E(f) $$

(10)

where f is the frequency, g is the gravitational acceleration, and E(f) is the frequency spectra, and the slope spectra (ζ(f)) have units of time. The equational form of the slope spectra is similar to multiplying the frequency spectra by f⁻⁴ (e.g., Donelan et al. 1985), to determine if the spectra follow the theory of wind-generated waves. The slope, according to theory, should become independent of frequency and follow a horizontal line.

Data from FLOSSIE (Fig. 14) are used along with the above equation to compute slope spectra for the five FLOSSIE sensors and the DWR. Results of the analysis are shown in Fig. 16, where the mean slope spectra are plotted in the left panel and the 90th percentile of the H_m0 population are plotted in the right panel. We find the slope spectra derived from the FLOSSIE sensors do not follow a constant in the rear face of the spectrum; however, the DWR is relatively constant in frequency. Results for the forward face show divergence between sensors up to their relative peak conditions. The shape of the mean slopes are similar, with a peak slightly less than 0.3 Hz, and abruptly fall in the high frequency range. The Triaxys is the outlier in the group, where its peak is displaced about 0.1 Hz toward the right. It is clear, over the mean slope spectra, that there is a difference in the FLOSSIE sensors, especially the Triaxys compared to the DWR, and do not compare favorably to the theoretical limit.

Fig. 16

Mean slope spectra based on the period of record Jul 2015–Jul 2019 (left panel) and 90th percentile (right panel) from the five FLOSSIE sensors time-paired to the DWR, identified in the legend for the period of record. The mean H_m0 values for the spectra are identified in the secondary legend. Note approximate f_m for period of record and 90th percentile are 0.072 Hz and 0.069 Hz, respectively

Results for the 90th percentile slope spectra (right panel, Fig. 16) show similarities in the forward face of the slope spectra. The divergence in the results found in the mean (left panel) now occurs at lower frequencies, while the Triaxys abruptly follows a shallower slope between the four FLOSSIE sensors and the DWR. The peak magnitudes vary from about 0.024 s for the DWR to a high of about 0.037 s for the Triaxys. The location in frequency space is about 0.24 s to 0.35 Hz (Triaxys). In general, the slope spectra for the five FLOSSIE sensors are about 20% greater than the DWR and again do not follow a horizontal trend such as that found in the DWR results.

The logarithmic plot of the slope spectra (Fig. 17) shows more details of the results compared to the linear plot of Fig. 16. First, the results of the mean conditions (left panel, Fig. 17) show consistency between sensors and the DWR defined by the forward face with exception of the Watchman. At about 0.1 Hz, the FLOSSIE sensor slope spectra rise above the DWR and remain there until 0.32 s to 0.42 Hz. From that point, all FLOSSIE sensors fall well below the DWR. The Inclinometer is the highest in magnitude followed by HIPPY, 3DMG, and Watchman, and then Triaxys. None of the FLOSSIE sensors shows independence from the frequency as in the case of the DWR. The slope spectral rear face (Fig. 17) occupies the range from about 0.07 (peak energy) to 0.35 Hz (just before the change in slope), and in that range of the slope spectra, all five FLOSSIE sensors overestimate the slope (and energy) by about 20%. In the high frequency range (greater than 0.35 Hz, or about 6f/f_m), it is obvious the FLOSSIE sensors significantly underestimate the slope compared to the DWR. The results from the 90th percentile (right panel, Fig. 17) show that the trends are consistent compared to the overall mean spectral slope results. The DWR slope independence range is expanded now starting from 0.15 Hz (2f/f_m) and extending to its frequency maximum. The FLOSSIE sensors show very little signs of frequency independence, as in the case of the DWR, and overestimates the slope relative to the DWR.

Fig. 17

Logarithmic mean slope spectra based on the period of record Jul 2015–Jul 2019 (left panel) and 90th percentile (right panel) from the five FLOSSIE sensors time-paired to the DWR, identified in the legend for the period of record. The mean H_m0 values for the spectra are identified in the secondary legend. Note approximate f_m for period of record and 90th percentile are 0.072 Hz and 0.069 Hz, respectively

6 Discussion

6.1 Integral wave properties

A NOMAD buoy is roughly 23 times the weight of a DWR, non-symmetric in shape, and 3.3 to 6.7 times larger. Given the physical attributes of FLOSSIE, one might consider these types of buoys as a poor platform to provide quality wave measurements. It is, in general, not the case.

While there are differences found as defined by statistical testing and graphical presentations of the data for the selected integral wave properties: H_m0, T_pp, T_mean, and θ_mean(f_m), the results from the five FLOSSIE sensors are consistent with the neighboring DWR. Scatter does exist but is contained in a range of ±1.0 m and in the QQ analysis at about ±0.25 m until approximately 7.0 m, where all except the Inclinometer underestimate the extreme events by more than a meter. Statistical results demonstrate similarities over the large data sets where the rms errors are about 0.30 m, while four out of the five sensors report biases of about 0.10 m. The Inclinometer reports a slightly higher bias of 0.20 m. Overall, no one sensor/payload system was substantially more accurate, even the more sophisticated systems (3DMG, HIPPY, and Triaxys) compared to long-standing sensor/payloads used by NDBC and ECCC in the form of the Inclinometer and Watchman.

Focusing only on the FLOSSIE sensors using the Inclinometer as the independent variable, the results are very similar to comparisons with the DWR, with less scatter and improved statistical measures (absolute error, rms error); however, the regression lines are virtually unchanged. The reduction in the scatter and error statistics is of the same magnitude as the dual DWRs at Harvest, suggesting that much of the difference is due to the natural variability of the sea state, even over a 2-km separation (Harvest). The scatter found in the dual DWR deployment, with common hull, sensor, and processing systems, would suggest that those statistics (3-cm difference in the mean wave height, rms error of 0.17 m, scatter index of 6%) represent the maximum achievable agreement for any two co-located measurements.

The Watchman, the basis of the Canadian buoy network, tends to have a higher scatter and is more affected at the higher wave heights, above about 7 m. The regression coefficients—bias of 0.23 m and slope of 0.93—are virtually identical to those reported by Swail et al. (2011) from a parallel Canadian investigation on the Grand Banks for a DWR compared to a Watchman on a NOMAD buoy (0.05, 0.93).

These results are similar to that of Durrant et al. (2009), who found that the ECCC buoys (principally the Watchman with a strapped down accelerometer) were underestimating H_m0 relative to the NDBC buoys (Inclinometer, 3DMG, and HIPPY) by about 10%, using altimeter data as a common reference.

The integral wave properties and differences found in the H_m0 and T_mean are less sensitive to temporally changing wave conditions. For T_pp and θ_mean(f_m), multiple wave systems existing at or near the same frequency but different wave directions resulted in elevated errors.

While all FLOSSIE sensors for T_pp show up to 0.5 s biases, rms errors of more than 2 s, correlations around 0.7 and a slope of 0.7, the FLOSSIE sensor results for these parameters were very similar to the co-located DWR data set. The T_mean evaluations were similar to the T_pp, although about a factor of two less than the T_pp in terms of absolute and rms error. As for the wave height, analysis of the FLOSSIE sensors using the Inclinometer as the independent variable showed similar results to the DWR comparison, with lower scatter and error, consistent with the error levels in the dual DWR analysis. The apparent large scatter, and corresponding statistics, is likely due mostly to a mismatch in the reported T_pp, occurring during the transition of South and North Pacific storm event systems, compounded at times by the development of local wind seas. Any slight deviation in the energy level from one frequency band to another will result in poor agreement. The extensive scatter found in the FLOSSIE results was also evident in the dual DWR (Harvest) data, confirming that T_pp can be very unstable parameter to use in evaluations without exploring the frequency spectra and the directional moments. Further investigations of the full directional spectrum comparisons are warranted and are beyond the scope of the paper.

For the sensors capable of estimating wave directional properties onboard FLOSSIE (3DMG, HIPPY, and Triaxys), the results for θ_mean(f_m) demonstrated that NOMAD buoys are capable of measuring directional wave properties along the western US coast. Comparisons to the DWR revealed circular biases on the order 6 to 9 deg (after adjusting the Triaxys magnetic to true north), and circular rms errors approximately 30 deg. When the wave climate becomes complex, e.g., a mixture of North and South Pacific swell systems exacerbated by local wind sea development, the agreement in the measurements decreases. The large differences found in the θ_mean(f_m) are dependent on f_m, and thus, a mismatch occurs. As noted above, further investigations of the full directional spectrum comparisons are warranted.

6.2 Frequency and slope spectra

Despite statistical consistency in the H_m0 results, the spectra from FLOSSIE sensors differ especially in the rear face of the spectra. The higher energy values would contribute to the positive biases found in the statistical results. Although the west coast is dominated by swell (derived from North and South Pacific storm events), the differences found could be the cause of large discrepancies in the T_pp (mismatch) results when the wave environment is complex containing multiple wave systems. This would also be the reason for the differences found in the θ_mean(f_m). The high frequency tail (greater than 0.35 Hz) for all FLOSSIE transition to an f⁻¹⁰. This will only have a slight impact on H_m0, as the magnitudes are generally two orders of magnitude less than that of the spectral peak energy. The cause of the differences in the DWR is attributed to the differences in size and weight of a NOMAD buoy relative to the DWR, the differences in processing algorithms (response amplitude operator or filtering) used by NDBC or ECCC. Similar results were also found in the frequency spectra from the neighboring 3-m discus buoy 46042 (Fig. 1), but to a lesser extent.

It seems likely that the existence of low frequency noise in all sensors will have a limited impact on the integral wave properties, as the magnitudes are far below the energy level of the measured wave spectra. Under low energy conditions, however, the noise would contribute to differences in the significant wave height and the T_pp results. As an example, the Inclinometer spectra are the highest in noise levels compared to the other sensors and could be the reason for the large differences found in the T_pp scatter and quantile-quantile results (Fig. 12).

The analysis of the FLOSSIE sensors investigated the slope spectra, as the results should follow theoretical grounds where the rear face of the spectrum would become independent in frequency space. We found there is no consistency in the results from all five FLOSSIE sensors supporting an f⁻⁴ tail whereas the DWR does. The results also demonstrated all FLOSSIE sensors contained higher energy levels, about 20%, compared to the DWR. This would contribute to the positive biases found in the H_m0 results. The implication of the elevated slope values and a lack of invariance in frequency would contaminate any use of these data products applied to altimetry analyses. The high frequency range (greater than 0.35 Hz, about 6f/f_m) a substantial reduction in the energy level would also lead to uncertainty in the slope spectra from NOMAD buoys. As in the case of the frequency spectra, future analyses must be performed to determine the extent and cause of these uncertainties, and whether they are a result of the hull, sensor, or processing algorithms used.

7 Summary

A 6-m NOMAD buoy called FLOSSIE was deployed offshore in a water depth of 2400 m in Monterey Canyon for nearly 5 years, incorporating five sensor-payload systems used by NOAA-NDBC and ECCC operational centers to measure waves and distribute to various user communities around the world. Despite the success of NOMAD buoys for the past four decades, the increased cost for operation and maintenance has led to the replacement of these assets with smaller, cheaper buoys. The departure of these systems has caused concern, as the data obtained over the lifespan of each asset continues to be used in wind-generated surface gravity wave–related applications, from wave model evaluation, research in air-sea interaction, altimeter assessment, and mapping climate trends, without a true understanding of the quality of the data or comparability to the new systems.

The intra-measurement investigation described here was intended to evaluate the quality of the operational wave measurements compared to an internationally agreed relative reference; in this case, a DWR deployed approximately 19.3 km from FLOSSIE. Since three of the five sensors were capable of estimating the first four Fourier directional parameters, it seemed timely to determine if a non-symmetrical ship-hull buoy could estimate wave directions. In addition, since a DWR would be used as the relative reference, an independent analysis of a dual DWR deployment was carried out using identical buoys, processing procedures, anchored with a separation distance of 2 km, to provide a benchmark for the agreement between co-deployed sensors.

There were more than 168,000 time-paired observations used in the FLOSSIE sensor integral and spectral analysis. Unfortunately the Watchman’s early failure precluded more extensive evaluations; however, there were sufficient data (more than 10,000 observations) covering multiple seasonal and inter-annual variability to properly assess its quality relative to the other four sensors, especially the Inclinometer. FLOSSIE evaluations for the integral wave parameters (height, period, and direction) showed general agreement among the five sensors compared to the neighboring DWR, with the Inclinometer and the Watchman performing similarly to the more sophisticated 3DMG, HIPPY, and Triaxys sensor packages. As the H_m0 increased, all but the Inclinometer were biased low from 0.5 to 1.0 m (Watchman); however, even the Watchman seems to report reasonable wave measurements up to about 6–7 m, after which the H_m0 becomes negatively biased up to about a meter, comparable to the Canadian experiment. The Inclinometer-Watchman comparison supported the results of Durrant et al. (2009).

The T_pp results showed a large scatter, with the reduced agreement in the FLOSSIE sensors resulting from the complex nature of multiple swell wave systems compounded by local wind sea development, exacerbated by a variable that can be considered as temporally unstable. Results from the T_mean definition showed a dramatic improvement. It was also demonstrated that NOMAD buoys operating with directional sensors could measure wave directions with a fair degree of accuracy, although when the wave conditions become complex, deviations will result.

The spectral evaluation of the five FLOSSIE sensors clearly showed a strong similarity to the DWR for the mean and the 90th percentile. However, there was significant reduction in the wave energy above about 0.35 Hz. Considering the size and weight of a NOMAD buoy relative to a DWR, this is probably not surprising, although sensor-related processing may also be a factor; in either case, the results would require future evaluation of the full directional spectra. The most revealing analysis was based on the slope spectra. Based on theoretical considerations, the slope should be invariant in frequency beyond the peak frequency, as in the case of the DWR. However, all five FLOSSIE sensors show substantial deviations across the frequency range compared to the DWR, which suggests that there are issues in either the sensor themselves or processing algorithms (e.g., response amplitude operator or filtering) that are causing these differences. Again, future examination of the frequency spectra is required.

The FLOSSIE field study has uncovered many of the attributes of the various sensor-analysis packages commonly used, as well as those of the NOMAD hull itself, giving a basis to use wave data derived from these buoys. The results cannot be assumed to be universal, i.e., completely applicable beyond the specific wave climate of offshore California. However, the results found in this study are similar to those found in the completely different wave environment of the northwest Atlantic for the NOMAD-Watchman compared to the Datawell. The FLOSSIE experiment does provide an excellent basis for continued intra-measurement evaluations that need to carry on into the future as new buoy systems equipped with new wave measurement sensors are developed and ultimately migrated into operations, where the wave data community uses the data for various applications, from modeling to real-time forecasting to climate change.

Appendices

Appendix 1. List of metrics and equational formulations

Table 3 refers to a series of statistical parameters used in the evaluation of the various FLOSSIE sensor/payload systems summarized in the paper. The following summarizes the definitions used for those variables. The statistical tests are defined by the BASE (DWR) and the TEST (all other inboard sensors of FLOSSIE, NDBC-Inclinometer, NDBC-3DMG, NDBC-HIPPY, Axys-TRIAXYS, and Axys-Watchman). The statistical tests used time-paired observations between the BASE and TEST data sets. All directional metric results were derived from the CircStat toolbox of Berens (2009).

Mean is defined by either BASE or TEST wave parameter (H_m0, T_pp, T_mean, θ_mean) based on:

$$ \mathrm{Mean}=\sum \limits_{i=1}^{i=\mathrm{TotObs}}\mathrm{Variable}/\mathrm{TotObs} $$

Bias is defined as:

$$ \mathrm{Bias}=\sum \limits_{i=1}^{i=\mathrm{TOtObs}}\left({\mathrm{TEST}}_i-{\mathrm{BASE}}_i\right)/\mathrm{TotObs} $$

Abs error, Absolute Error:

$$ \mathrm{Abs}\ \mathrm{error}=\sum \limits_{i=1}^{i=\mathrm{TotObs}}\mid \left({\mathrm{TEST}}_i-{\mathrm{BASE}}_i\right)\mid /\mathrm{TotObs} $$

RMSE, root-mean-square error (bias adjusted):

$$ \mathrm{RMSE}=\sqrt{\sum \limits_{i=1}^{i=\mathrm{TotObs}}{\left({\mathrm{TEST}}_i-{\mathrm{BASE}}_i-\mathrm{Bias}\right)}^2/\mathrm{TotObs}} $$

SI, scatter index:

$$ \mathrm{SI}=100\cdotp \left(\mathrm{RMSE}/\mathrm{Mean}\left(\mathrm{BASE}\right)\right) $$

Corr, correlation coefficient:

$$ \mathrm{Corr}=\frac{\sum \limits_{i=1}^{i=\mathrm{TotObs}}\left({\mathrm{BASE}}_i-\mathrm{Mean}\Big(\mathrm{BASE}\right)\Big)\cdotp \left({\mathrm{TEST}}_i-\mathrm{Mean}\left(\mathrm{TEST}\right)\right)}{\sum \limits_{i=1}^{i=\mathrm{TotObs}}{\left({\mathrm{BASE}}_i-\mathrm{Mean}\left(\mathrm{BASE}\right)\right)}^2\cdotp {\left({\mathrm{TEST}}_i-\mathrm{Mean}\left(\mathrm{TEST}\right)\right)}^2} $$

Lin Slp, linear slope:

$$ \mathrm{Lin}\ \mathrm{Slp}=\frac{\sum \limits_{i=1}^{i=\mathrm{TotObs}}\left({\mathrm{BASE}}_i-\mathrm{Mean}\left(\mathrm{BASE}\right)\right)\cdotp \left({\mathrm{TEST}}_i-\mathrm{Mean}\left(\mathrm{TEST}\right)\right)}{\sum \limits_{i=1}^{i=\mathrm{TotObs}}{\left({\mathrm{BASE}}_i-\mathrm{Mean}\left(\mathrm{BASE}\right)\right)}^2} $$

Lin Intcp, linear intercept:

$$ \mathrm{Lin}\ \mathrm{Intcp}=\mathrm{Mean}\left(\mathrm{TEST}\right)-\mathrm{Lin}\ \mathrm{Slp}\cdotp \mathrm{Mean}\left(\mathrm{BASE}\right) $$

Sym Slp, symmetric slope:

$$ \mathrm{Sym}\ \mathrm{Slp}=\sum \limits_{i=1}^{i=\mathrm{TotObs}}\left({\mathrm{BASE}}_i\cdotp {\mathrm{TEST}}_i\right)/\sum \limits_{i=1}^{i=\mathrm{TotObs}}{\left({\mathrm{BASE}}_i\right)}^2 $$

Appendix 2. T _mean scatter and QQ results

Figure 18 contains the T_mean time-paired observations for the period of record (Jul 2015–Jul 2019), where the DWR is the independent variable and the five FLOSSIE sensors are the dependent variable. As indicated in the body of the text, the results using T_mean as the metric reduces the scatter about the line of perfect fit ((a), left panel) for all sensors, and display an improved consistency of QQ ((b), right panel) with the DWR compared to the T_pp metric found in Fig. 12.

Fig. 18

Scatter of the T_mean data for the five FLOSSIE sensors versus the DWR (left panel), and QQ analysis (right panel). Each sensor is color-coded identified in the legend and the total number of observations used in the analysis. Dashed and dotted lines in the QQ plot reflect ±1.0 and ±2.0 s