Abstract
A multi-scale three-dimensional variational (MS-3DVAR) scheme is developed to assimilate high-resolution Himawari-8 sea surface temperature (SST) data for the first time into an operational ocean nowcast/forecast system targeting the North Western Pacific, JCOPE2. MS-3DVAR improves representation of the Kuroshio path south of Japan, its associated sea level variations, and temperature/salinity profiles south of Japan, the Kuroshio/Oyashio mixed water region, and the Japan Sea as compared to those of the products by the traditional single-scale 3DVAR. Validation results demonstrate that MS-3DVAR well assimilates the sparsely distributed in situ temperature and salinity profiles data by spreading the information over the large scale and by representing the detailed information near the measurement points. MS-3DVAR succeeds to assimilate the Himawari-8 SST product without noisy features caused by the cloud effects. We also find that MS-3DVAR is more effective for estimating oceanic conditions in regions with smaller mesoscale variability including the mixed water region and Japan Sea than in south of Japan.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The operational ocean forecasting based on numerical ocean modeling and data assimilation is advancing toward operating the products with higher spatial resolution and temporal frequency (Varlamov et al. 2015). Increasing computational resources based on evolving high-performance computing technology facilitates developments of numerical ocean models with higher resolution. Skillful nowcast/forecast with high-resolution models requires enough amounts of the observation data well constraining the model state through data assimilation.
Coverage and density of the current satellite altimeters for monitoring the sea surface height anomaly (SSHA) have a limitation of the minimum observable spatial scale of 100 km (Fu and Ferrari 2008). To capture whole activity of the mesoscale and submesoscale eddies ranging from O (100 km) to O (1 km) scales, we need to fully utilize the current available observation data together with developing new observation facilities including the wide-swath radar interferometry satellites (Fu and Ubelmann 2014; Ichikawa 2014).
The satellite sea surface temperature (SST) is another important data source for monitoring oceanic condition. The high-resolution SST products obtained from the infrared radiometers well detect the front variability if cloud masking contaminates signals included in the data. A SST product obtained from the infrared sensor of the recent launched Japanese geostationary satellite “Himawari-8” allows relatively high-frequency measurement of SST in a wide area of Western Pacific every 10 min with horizontal resolution 0.02° (Kurihara et al. 2016). Temporal composite of the high-frequency snapshot measurements removes the missing and contaminated regions caused by the cloud noise more effectively than the previous infrared SST products including the Advanced Very High-Resolution Radiometer (AVHRR). In the present study, we develop an assimilation scheme suitable for the Himawari-8 SST data on an operational ocean nowcast/forecast system in North Western Pacific ocean: JCOPE2 (the real-time nowcast/forecast information is available from the website http://www.jamstec.go.jp/jcope/; also see Miyazawa et al. 2009 for a detailed description), which originally assimilates SSHA, Multi-Channel SST resampled with coarse resolution from AVHRR (May et al. 1998), and in situ temperature and salinity profile (T/S) data. This is the first application of the Himawari-8 SST product to operational ocean nowcast/forecast systems.
The current version of JCOPE2 adopts the three-dimensional variational (3DVAR) data assimilation scheme assuming a horizontal single scale of approximately 100 km in the background error covariance (Miyazawa et al. 2009), which significantly affects the spatial scale of the target phenomena represented by the data assimilation. We compare the skills of a single-scale (SS-) and multi-scale (MS-) 3DVAR implementations on JCOPE2. Li et al. (2015a) describe an algorithm of the MS-3DVAR scheme, and they demonstrate that it reasonably assimilates the observation data with both dense and coarse distributions in the coastal oceans off Alaska (Li et al. 2013) and California (Li et al. 2015b) coasts. Muscarella et al. (2014) briefly report that both the dense satellite and coarse in situ data are well assimilated into their ocean model in the Kuroshio Extension region. Here, we examine in detail the effects of MS-3DVAR on the skill of JCOPE2 south of Japan, in the Kuroshio/Oyashio mixed water region (the mixed water region), and in the Japan Sea.
Given that the high-resolution data are available with uniform distribution without any data missing regions, SS-3DVAR with a horizontal scale comparable to the data resolution effectively extracts fine-scale information from the data. In this case, skills of MS-3DVARs and SS-3DVARs are comparable to each other (Li et al. 2015a). In real situations, however, the distributions of the available data are not uniform; in particular, the high-resolution infrared SST including the Himawari-8 product involves the data missing areas due to the cloud noise (e.g., Miyazawa et al. 2013), and in situ temperature and salinity data are obtained with quite coarse resolution (e.g., Miyazawa et al. 2012). The MS-3DVAR scheme effectively assimilates the localized and patchy dense-distributed observation data without unrealistic smoothing and well spreads the information of the sparse-distributed data (Li et al. 2015a). In terms of this viewpoint, we investigate skills in SS-3DVAR cases with different horizontal scales and compare their skills with that of MS-3DVAR.
The paper is organized as follows. The model and observation data used in this study are described in Sect. 2. Model skills for the SST reproducibility, the Kuroshio path and its related sea level variations, and the temperature/salinity profiles are shown in Sect. 3. We examine differences in the skills between the SS-3DVAR and MS-3DVAR schemes by checking the fitting to the assimilated SST data (Sect. 3.1), by validating the results using independent observation data (Sect. 3.2), and by diagnosing the results in terms of intercomparison among sensitivity experiments (Sect. 3.3). We also examine sensitivity of choices of three SST products: Himawari-8, Merged Satellite and In situ Data Global Daily SST (MGDSST; Kurihara et al. 2006), and Moderate Resolution Imaging Spectroradiometer (MODIS)-SST (Hosoda et al. 2007) in Sect. 3.4. Final section is devoted for summary and discussion.
2 Methods and data
The forward ocean model of JCOPE2 driven by the NCEP/NCAR reanalysis data (Miyazawa et al. 2009), based on the Princeton Ocean Model with generalized coordinate of sigma (Mellor et al. 2002), covers the Western North Pacific (10.5–62° N, 108–180° E; Fig. 1), and has a horizontal resolution of 1/12° and 46 vertical active levels. For this study, the model is modified to involve some recent advances in the ocean modeling as follows: (1) replacement of the baroclinic pressure gradient scheme from the fourth order (McCalpin 1994) to the rotated schemes (Thiem and Berntsen 2006), (2) replacement of the turbulent closure model from Mellor and Yamada (1982)’s level 2.5 model with surface wave breaking parameterization (Mellor and Blumberg 2004) to the Nakanishi and Niino (2009)’s model with a modification for oceanic applications by Furuichi et al. (2012), (3) input of surface wind relative to ocean current into the bulk formulae (Griffies et al. 2009), (4) use of MGDSST (Kurihara et al. 2006) for correction of the surface heat flux, (5) addition of precipitation and evaporation data from the NCEP/NCAR reanalysis into the surface freshwater flux with correction to the monthly climatological salinity, (6) the enhanced precipitation along the coasts caused by the coastal precipitation over a strip of land 80 km wide, which represents the freshwater flux from small rivers (Hirose 2011), and (7) the additional horizontal viscosity (1000 m2 s−1) around the Tsugaru Strait controlling the volume transport of the Tsugaru warm current (Uchimoto et al. 2007) and enhancement of the vertical viscosity/diffusivity (a lower bound value of 0.02 m2 s−1) around the Bussol Strait representing the tidal mixing effect (Fujisaki et al. 2010).
The 3DVAR scheme on JCOPE2 implemented by Miyazawa et al. (2009) is modified to extract the information on shorter temporal and smaller spatial-scale phenomena from the high-resolution observation data. The data assimilation cycle period and horizontal grid interval of the analysis are shortened from 7 to 2 days and from 0.25° to 0.125°, respectively. SSHA, SST, and T/S data are assimilated into the model with time window parameters: 5, 1, and 5 days before and after the analysis time, respectively. The temperature-salinity coupling empirical orthogonal mode functions (Fujii and Kamachi 2003) for each subregion (Fig. 1) have been recalculated using the World Ocean Database 2013 and Marine Information Research Center Data Set 2001. To accelerate the whole assimilation process, each cost function minimization is separately conducted for each subregion (Fig. 1) using different processors on multi-core workstations.
The most critical change in the data assimilation process is use of multi-scale cost functions inspired by series of the recent MS-3DVAR studies (Li et al. 2013, 2015a, 2015b; Muscarella et al. 2014). Here, we introduce large-scale and small-scale components of the analysis increments, δX L and δX S , respectively, for estimation of the analysis temperature/salinity X a from the first guess ones X f,
The first guess X f from the model is also decomposed into large-scale and small-scale ones,
which are related to the decomposition of the dense observation data,
MS-3DVAR separately minimizes two types of cost functions for the large-scale and small-scale components,
where B L and B S are the large-scale and small-scale background error covariance matrices, respectively; y d and y c are the observation data with spatially dense and coarse distributions, respectively; H d and H c are operators projecting the model variables to the dense and coarse observation variables, respectively. \( {R}_L^d \), \( {R}_S^d \), and R c are the observational error covariance matrices associated with \( {y}_L^d \), \( {y}_S^d \), and y c, respectively. Additional terms H c B L H cT and H c B S H cT to the conventional 3DVAR cost function are the large-scale and small-scale representativeness error matrices. Practically, H c B L H cT could be negligible (Li et al. 2015a) compared to R c due to relatively weak correlation among variables represented by B L . Note that the formulation of MS-3DVAR (2) and (3) is slightly different from the original one represented by the cost function in an incremental form (e.g., see equations 34 and 35 in Li et al. 2015a).
The background error covariance matrix B in the 3DVAR scheme of JCOPE2 is characterized by a horizontal-scale parameter (approximately 100 km) representing the decorrelation scale in the Gaussian function (Miyazawa et al. 2009). Considering the typical horizontal scale of the mesoscale eddies in North Western Pacific O (100 km) (Kuragano and Kamachi 2000) and the detectable minimum scale on the analysis grid with 0.125° (~14 km), we define the large (for B L ) and small (for B S ) scale parameters as 100 and 30 km, respectively.
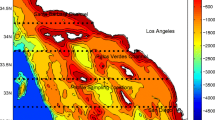
The high-resolution SST data from Himawari-8 (Fig. 2a), MGDSST, and Aqua/Terra MODIS are considered as the dense observation data in the present study. Gaussian smoothing filter with a spatial scale of 1.5° (approximately 170 km) is utilized for the decomposition of the model (4) and dense observation (5) variables as in the previous studies (Li et al. 2015a, 2015b). T/S profile data are categorized as the coarse observation containing the information on the various phenomena over the broad horizontal-scale range and are included in both the large-scale and small-scale cost functions (2) and (3). SSHA may also contain rich information on the various scale phenomena; however, the maximum spatial interval of the satellite tracks exceeds 100 km at the present time, and the observable spatial scale has a minimum limit of 100 km (Fu and Ferrari 2008). We thus include SSHA only in the coarse observation term of the large-scale cost function. In the present study, MS-3DVAR is applied to the subregions 2, 3, 4, 10, and 11 (Fig. 1) because of our particular interest to the ocean current variability there.
The observation error covariance matrix is supposed as the diagonal form. We assume that the error standard deviation values of SSHA are 0.05–0.1 m (Table 1). The observation error standard deviation of temperature \( {T}_{err}^o \) including both in situ and satellite SST and salinity \( {S}_{err}^o \) is specified as follows:
where \( {T}_{std}^o\left( n, z\right) \) and \( {S}_{std}^o\left( n, z\right) \) are the standard deviation values of observed temperature and salinity, respectively, and depend on the 11 subregions (n) and 24 vertical levels (z) from 0 to 1500 m. σ denotes the normalized first guess error parameter as represented in
where \( {T}_{err}^f \) and \( {S}_{err}^f \) are the error standard deviation values of the first guess temperature and salinity, respectively. Table 1 indicates σ values applied to the subregions (Fig. 1), which are generally similar to those used in the previous studies (Usui et al. 2006; Miyazawa et al. 2009).
After checking a preliminary assimilation result, we have decided to enhance constraint to the SST observation in the regions 1, 5, 6, 7, 8, and 9: \( {\left.{T}_{err}^o\right|}_{z=0}={SST}_{err n}\sqrt{1-\sigma}{T}_{std}^o \) (SST errn = 0.5; Table 1). The large-scale representativeness error matrix (H c B L H cT) is simply ignored in the MS-3DVAR implementation by following the discussion by Li et al. (2015a). Effects of small-scale one H c B S H cT included in the large-scale cost function (2) are simply parameterized by slightly decreasing σ from 0.7 to 0.6 (Table 1).
The modified JCOPE2 system is tested for both SS-3DVAR and MS-3DVAR schemes assimilating the following observation data: along-track SSHA data of the Ssalto/Duacs altimeter products (Jason-2, Cryosat-2, Saral, HaiYang-2), Himawari-8 SST data, and the Global Temperature-Salinity Profile Program (GTSPP) temperature and salinity profiles (see Fig. 3a for the locations). To validate the products by using the temperature and salinity data independent from the assimilation, we randomly extract 10% amount of the data from the GTSPP archive and do not assimilate them (Fig. 3b).
Numbers of in situ temperature profiles within the grids with 1/4° distance in the GTSPP archive for the period from 1 August 2015 to 1 May 2016 for the data used in the data assimilation experiments (a) and for the data not used in them (b). Squares shown in a indicate the regions for validation of the modeled temperature/salinity. Labels shown in a denote locations of the regions (south of Japan (SOJ), mixed water region (MWR), the Japan Sea southern region (JSS)). Labels shown in b denote locations of the tide gauge stations (Aburatsu (AB), Tosashimizu (TS), Muroto (MU), Kurshimoto (KU), Uragami (UR), Miyakejima (MJ), Hachijojima (HJ), Saigo (SA), Sado (SD), Fukaura (FK))
Several choices of the horizontal error covariance scale for SS-3DVAR 100, 50, and 30 km are applied in the target regions 2, 3, 4, 10, and 11 for comparison to the result of MS-3DVAR (“multi”) with a combination of 100 and 30-km scales (Table 2). In other regions 1, 5, 6, 7, 8, and 9, zonal and meridional horizontal scales are specified as 150 and 100 km, respectively, for SS-3DVAR according to a scale estimate based on Kuragano and Kamachi (2000). Example snapshots of SST on 18 January 2016 are shown in Fig. 2b (100 km), c (multi), and d (30 km).
In addition, other SST products MODIS-SST and MGDSST are used in place of Himawari-8 SST for MS-3DVAR (Table 2). The original SST products of Himawari-8 and MODIS have horizontal resolutions of 2 and 1 km, respectively. The assimilation of them is performed after regridding to a 0.1° grid (e.g., see Fig. 2a for Himawari-8). It is found that the MODIS data requires relatively rigorous quality check (Miyazawa et al. 2013) and additional horizontal Gaussian smoothing with a 0.25° scale because they sometimes show serious noisy features. The assimilation of MGDSST with horizontal resolution of 0.25° is performed without regridding.
All experiments are started without data assimilation from the initial condition same as the FRA-JCOPE2 reanalysis data (Soeyanto et al. 2014) on 1 June 2015, and data assimilation is applied from 1 August 2015. The daily mean assimilation (analysis) products for a period from 3 August 2015 to 1 May 2016 are analyzed.
3 Results and discussion
3.1 Fitting to the assimilated sea surface temperature data
Figure 4a, d, g indicates that root mean square difference (RMSD) between the modeled and assimilated Himawari-8 SST data is relatively low in the three target regions for a period from August to October 2015. Coverage rate of the SST data affected by the cloud condition is negatively correlated with RMSD owing to possible deterioration of the SST data quality through the cloud effects (Kurihara et al. 2016). In the mixed water and Japan Sea southern regions, the coverage rate frequently drops and RMSD also frequently increases in winter season. Mean RMSD values of the MS-3DVAR case (green-colored curves) are less than 1 °C (0.55, 0.98, and 0.75 (°C) averaged for south of Japan, the mixed water region, and the Japan Sea southern region, respectively), which is comparable to RMSD between Himawari-8 (daily composite in 0.1° grid) and in situ observation (GTSPP) SST data, 0.83 °C in the JCOPE2 region (see Fig. 1 for the region), and RMSD of 0.59 K evaluated from the rigorous validation using the buoy data by Kurihara et al. (2016). Mean absolute difference (BIAS) values of the MS-3DVAR case are +0.16, +0.12, and +0.02 (°C) for south of Japan, the mixed water region, and the Japan Sea southern region, respectively, and they are also similar to the estimate using in situ data obtained by Kurihara et al. (2016), +0.16 K, and our estimate in the JCOPE2 region between the gridded Himawari-8 and in situ data, +0.18 °C.
Daily sequences showing RMSD between the modeled and Himawari-8 SST data averaged south of Japan (a, b, c), in the mixed water region (d, e, f), and in the Japan Sea southern region (g, h, i). a, d, g Total RMSD sequences. b, e, f, c, f, i Larger scale and smaller scale RMSD sequences (colored thick curves), respectively. A scale of 150 km is specified as a criterion of scale decomposition using Gaussian smoothing filter. Thin black curves denote coverage rate of Himawari-8 SST data in the three subregions
Sensitivity to horizontal single scales is not evident south of Japan (Fig. 4a). In particular, RMSD for larger scale features is not sensitive to the choices of the horizontal scales there (Fig. 4b). The SS-3DVAR case with 100-km scale shows largest deviation for smaller scale features among all the cases (Fig. 4c). RMSD of the MS-3DVAR case is basically similar to that of the SS-3DVAR case with 30 km for the total (Fig. 4a), larger scale (Fig. 4b), and smaller scale (Fig. 4c) variations.
In the mixed water region, applying smaller horizontal scales to SS-3DVAR leads to further reduction in total RMSD (Fig. 4d) and small-scale RMSD (Fig. 4f), though large-scale RMSD is not much different among all the experiments (Fig. 4e). The MS-3DVAR case shows the skill comparable to that of SS-3DVAR with 30 km (Fig. 4d–f). Applying single 100 and 50-km scales results in larger amplitude of small-scale RMSD in winter season as compared to the 30-km case and MS-3DVAR (Fig. 4f), suggesting insufficient capture of the observed features as indicated by comparison of Fig. 2a, b.
Total RMSD values in the Japan Sea southern region of all the SS-3DVAR cases increase more than that of the MS-3DVAR case during a period from October 2015 to January 2016 (Fig. 4g). Both large (Fig. 4h) and small (Fig. 4i) scale RMSD values of the SS-3DVAR cases also show similar increase, but the increase of the small-scale RMSD values (Fig. 4i) is more evident than that of the large-scale RMSD values (Fig. 4h).
We find that relatively small-scale patches of anomalous temperature and salinity sometimes appear under the cloudy conditions in the cases of 50 and 30 km. Examples of the SST patches in the Japan Sea in the case of 30 km are shown in Fig. 2d (around 37° N, 133° E, and 39° N, 139° E) when the clouds contaminate the Himawari-8 SST distribution in the Japan Sea (Fig. 2a). The cloudy conditions in the Japan Sea frequently appear especially in winter season, which is related to the winter monsoon. SS-3DVAR with smaller scales of 30–50 km results in overfitting to the SSHA data (residual of approximately 0.02 m under the prescribed error standard deviation estimate of 0.05 m) in the Japan Sea, and the anomalous temperature/salinity patches are sometimes created owing to the overfitting to SSHA and relatively weak constraint by the other data including Himawari-8 SST, depending on amount of the available data affected by the cloud condition. A sensitivity experiment of SS-3DVAR with 30-km scale without SSHA assimilation in the Japan Sea (the regions 10 and 11; see Fig. 1 for the locations) reduces all the RMSD indices (Fig. 4g–i), demonstrating the overfitting to SSHA in the SS-3DVAR with 30-km scale.
3.2 Validation of the products using independent observation data
We examine the Kuroshio path variation south of Japan by comparing the modeled Kuroshio path positions defined as the strongest gradient positions of SSH with the Kuroshio path positions reported by the Japan Coast Guard. Time sequences of RMSD in the latitudinal positions averaged from 133 to 139 E (Fig. 5) indicate that all the cases show similar variations, implying that reproducibility of the Kuroshio path positions is not much sensitive to the choice of the horizontal scales. This is not surprising because the reference Kuroshio path positions mainly represent the smoothed large-scale information (e.g., see Fig. 9 in Miyazawa et al. 2013). Temporally and spatially averaged RMSD values shown in Table 3 suggest a best skill in the MS-3DVAR case among all the cases. Figure 5 displays that the MS-3DVAR case results in more stable RMSD variation than the SS-3DVAR cases as also indicated in standard deviation results (Table 3).
Daily sequences showing RMSD averaged from 133° E to 139° E in latitudes between the modeled and observed Kuroshio path positions. The modeled Kuroshio path positions are defined as positions of the strongest geostrophic current calculated from SSH gradient with minimum kinetic energy amplitude of 0.4 m2 s−2
Daily tide gauge data (see Fig. 3b for the locations of the tide gauge stations) are compared with the modeled sea level variations (Tables 4 and 5) after the barometric correction (Kawabe 1989) and the tide killer filtering (Hanawa and Mitsudera 1985). The corrected sea level variations along the southern coasts of Japan are closely related with the Kuroshio path variations with various timescales (Kawabe 1989). All the cases show similar good skills (Table 4) except for the sea level difference (SLD) between Kushimoto and Uragami (KSUR), which is a useful indicator of the Kuroshio path variation around these places (Kawabe 1989). MS-3DVAR well reproduces two events of passing of the Kuroshio small meander off Kushimoto and Uragami in August 2015 and February–March 2016 (not shown), resulting in smaller RMSD (Fig. 5) and better reproducibility in SLD (not shown) during the two periods than the SS-3DVAR cases.
In the Japan Sea, sea level variability after barometric and tidal corrections is affected by the path variations of the Tsushima Warm Current (Choi et al. 2004). Skills for reproducing the sea level variations at three points in the Japan Sea (see Fig. 3b for the locations) are generally similar among all the cases (Table 5). Note that RMSD at the Saigo station (SA) increases in the SS-3DVAR cases with 50 and 30-km scales and exclusion of SSHA assimilation in the 30-km case reduces RMSD, suggesting that the overfitting to SSHA causes the relatively large deviation from the observed sea level variation there. Around SA, the mesoscale eddy activity is relatively high as compared to around the other two stations, and the overfitting to SSHA tends to be pronounced around there (also see Fig. 9).
Figure 6 compares fitting to in situ temperature and salinity profiles independent from the assimilation among the MS-3DVAR and SS-3DVAR cases. In south of Japan, a temperature RMSD profile in the upper 400-m depth for the MS-3DVAR case is smaller than all the other cases (Fig. 6a); even the mean absolute difference (BIAS) in temperature and salinity shows no considerable difference among all the cases (Fig. 6a, b), and salinity RMSD of MS-3DVAR is slightly worse than SS-3DVAR with 100-km scale for a depth range from 200 to 500 m.
Profiles of RMSD (curves) and BIAS (points) in temperature (a, c, e) and salinity (b, d, f) between the assimilation products and independent observation data (see Fig. 3b for data locations). a, b South of Japan. c, d Mixed water region. e, f The Japan Sea southern region
In the mixed water region (Fig. 6c, d), the MS-3DVAR case results in reduced RMSD and BIAS of temperature and salinity in the upper 200 m as compared to those in the SS-3DVAR cases. Comparison of temperature and salinity snapshots indicates that decreasing horizontal scale in the SS-3DVAR cases tends to represent small-scale patches in the Oyashio water region (not shown) and intensity of the patches are more enhanced in salinity than that in temperature, as demonstrated by significant increase in salinity RMSD for the 30-km case shown in Fig. 6d.
Dependence of the skill on the single horizontal scales used in the SS-3DVAR cases is not simple in the Japan Sea southern region (Fig. 6e, f). The use of the 100-km scale leads to RMSD exceeding 3 °C owing to less ability to capture detailed structures of the observed phenomena by use of the horizontal larger scale as compared to the observable horizontal scale (cf. Fig. 2a, b). Decreasing the horizontal scale to 50 km reduces RMSD in temperature but increases that in salinity. Further reduction of the scale to 30 km slightly changes the skill in salinity but considerably deteriorates the skill in temperature in association with the unrealistic patchy phenomena (e.g., Fig. 2d) caused by overfitting to the SSHA observation, which is demonstrated by the improved skill in the sensitivity experiment excluding SSHA assimilation. Both RMSD and BIAS of MS-3DVAR are generally smallest among all the cases.
3.3 Diagnosis of the SS-3DVAR and MS-3DVAR results
MS-3DVAR spreads the information contained in the coarse observation data over the broad area through the optimization of the large-scale cost function, while it extracts the detailed information from the observation through the small-scale cost function optimization (Li et al. 2015a). To confirm the effects of the multi-scale optimization, we plot in Fig. 7 temperature RMSD at 100-m depth between the analysis and assimilated in situ observation data, which are evaluated from the third terms of (4) and (5) in the MS-3DVAR cases and from the corresponding term in the SS-3DVAR cases, in optimization results for the regions 4 (Fig. 7a), 2 (Fig. 7b), and 11 (Fig. 7c), which roughly correspond to SOJ, MWR, and JSS, respectively. In the region 4 including south of Japan (see Fig. 1 for the location), the large-scale cost function in MS-3DVAR is well optimized as done in the 100-km scale SS-3DVAR cost function, and moreover, the small-scale cost function in MS-3DVAR is optimized more effectively than done in the SS-3DVAR cost function with 30-km scale (Fig. 7a). In both the region 2 including the mixed water region (Fig. 7b) and region 11 including the Japan Sea southern region (Fig. 7c), the analysis temperatures in both large and small scales are fitted to the observation data more than those in the SS-3DVAR cases with 100 and 30-km scales, respectively. Figure 7 demonstrates that the MS-3DVAR case achieves the estimation of the temperature simultaneously in both large and small scales. Although the SS-3DVAR cases with the smaller scales allow the fitting to the data confined near the measurement location, it does not confirm the fitting over larger scales. The deterioration of the skill in the fitting to the independent data (Fig. 6) could occur as a result of the enhanced fitting with the single smaller scales.
Time sequences of RMSD between the analysis and assimilated observation temperature data at 100-m depth in the optimized cost functions of the regions 4 (a), 2 (b), and 11 (c). See Fig. 1 for the locations. Note that “multi.large” and “multi.small” correspond to the third terms of (4) and (5), respectively
Temperature (Fig. 8a) and salinity (Fig. 8b) RMSDs at 100-m depth between the MS-3DVAR and SS-3DVAR with 100 km clearly indicate that the modification by MS-3DVAR appears confined around the oceanic fronts including the Kuroshio, Kuroshio Extension, the Japan Sea Subpolar Fronts, and Subarctic Frontal Zone (Kida et al. 2015), which is quite consistent with the expected effect of MS-3DVAR allowing representation of the fine-scale structures associated with the front variability by use of a smaller horizontal scale, 30 km. SS-3DVAR with 30-km scale also results in the changes around the oceanic fronts as compared to SS-3DVAR with 100-km scale (Fig. 8c). The magnitude of RMSD in the mixed water region and the Japan Sea is larger than that of the MS-3DVAR case (Fig. 8a), and it is related with the patchy features shown in SS-3DVAR with 30-km scale (e.g., Fig. 2b) and the enhanced deviation from the independent data (Fig. 6c, e). RMSD between MS-3DVAR and SS-3DVAR with 30-km scale (Fig. 8d) also suggests the overmodification around the fronts caused by the use of 30-km single scale.
Since the typical horizontal scale of mesoscale eddy in the Japan Sea is 100–150 km (Morimoto et al. 2000) and observable minimum scale of the present altimeter satellites is 100 km (Fu and Ferrari 2008), the horizontal scales of 30 and 50 km are not suitable for the assimilation of SSHA for capturing the mesoscale eddies in the Japan Sea. The overfitting often arises owing to the weak constraint to the SST data with large part of missing when the clouds associated with the winter monsoon cover the large area of the Japan Sea.
Figure 9 compares RMS variability of temperature at 100-m depth among SS-3DVAR with 100-km scale (Fig. 9a), with 50-km scale (Fig. 9b), with 30-km scale (Fig. 9c), with 30-km scale but without SSHA data assimilation (Fig. 9d), and MS-3DVAR (Fig. 9e). The use of smaller horizontal scales (50 and 30 km) results in wrongly enhanced variability especially around the SA station (see Fig. 3b for the location), leading to worse skills in the sea level variation (Table 5). Excluding SSHA assimilation in SS-3DVAR with 30-km scale (Fig. 9d) effectively removes the overfitting effect but it causes the underestimation of the variability as compared to those in the other cases with SSHA assimilation. MS-3DVAR (Fig. 9e) seems to represent a well-organized feature of the variability mainly related to the mesoscale Tsushima Warm Current variations (Morimoto and Yanagi 2001).
MS-3DVAR is able to avoid the mismatch between the observable minimum sampling scale and dominant horizontal scale of the target phenomena, like aliasing. Note that the use of multi-scales is more effective in the mixed water region and Japan Sea than south of Japan (Figs. 8 and 9). This is reasonably consistent with smaller horizontal scales of oceanic phenomena characterized by the first mode internal Rossby radius in the former two regions than in the latter one region (Oh et al. 2000).
3.4 SST sensitivity experiments
Other high-resolution SST products of MGDSST and MODIS-SST are assimilated into the model using MS-3DVAR. Even with coarser resolution (0.25°) of MGDSST than Himawari-8 (0.1° in this implementation), RMSD and BIAS of the MGDSST case in comparison with the T/S data are almost similar to those in the case assimilating Himawari-8 SST (Fig. 10 for south of Japan and also in the other regions including the mixed water region and the Japan Sea; not shown). The skill reproducing the Kuroshio path positions is also similar to the Himawari-8 case (Table 3).
a As in Fig. 6a except for validation of the assimilation products with three products of sea surface temperature data: Himawari-8 (multi), MGDSST, and MODIS-SST. b As in a except for the salinity profiles
The assimilation of MODIS-SST causes increase of both RMSD and BIAS in subsurface layer (Fig. 10, also in the other regions; not shown), suggesting that the noise in MODIS-SST remaining after the quality check and horizontal smoothing still affects the representation of temperature/salinity profiles of the assimilation products. The recent degradation of the MODIS sensor (Polachenski et al. 2015) possibly enhances the noise. Reproducibility of the Kuroshio path positions in the MODIS-SST case is worse and more unstable than in the other cases (Table 3), which could be also affected by the noise.
The sea level variations south of Japan are well reproduced in both MGDSST and MODIS cases (not shown) as in the Himawari-8 case (multi in Fig. 5b) except for SLD between Kushimoto and Uragami. For this SLD, correlation coefficients are 0.61 and 0.50 for the MGDSST and MODIS-SST cases, respectively, while it is 0.70 for the Himawari-8 case, suggesting a better skill for representing the Kuroshio path variation east of Kushimoto and Uragami by assimilating the Himawari-8 SST as compared to the assimilation of the other SST products.
4 Summary
We implement the MS-3DVAR (Li et al. 2015a) with a combination of 100 and 30-km scales on an operational North Western Pacific ocean nowcast/forecast system JCOPE2, which originally uses a SS-3DVAR scheme with approximately 100-km scale (Miyazawa et al. 2009). The present study is the first application of MS-3DVAR and Himawari-8 SST assimilation to operational ocean nowcast/forecast systems. MS-3DVAR effectively assimilates the sparse-distributed T/S profile data by spreading the information over the large scale and representing the detailed information near the measurement points, as noticed by the original theoretical study (Li et al. 2015a). In addition, we find that JCOPE2 with MS-3DVAR reasonably assimilates the Himawari-8 SST product without noisy features caused by the cloud effects that are involved in the infrared-type SST data. We also find that MS-3DVAR is more effective for estimating oceanic conditions in regions with smaller mesoscale variability including the mixed water region and Japan Sea as compared to in south of Japan because it safely avoids aliasing-like phenomena that are induced by coarse density sampling of SSHA.
The Himawari-8 SST product is assimilated by MS-3DVAR without any additional quality check and smoothing, while the assimilation of the MODIS-SST product results in the worse skill of the water mass distribution even with the relatively rigorous quality check and additional smoothing, indicating requirement of more enhanced calibration for the current MODIS-SST product. The skills of the MGDSST assimilation product for the indices used in the present study are almost comparable to those of the Himawari-8 SST assimilation. The assimilation of MGDSST with 0.25° resolution could be useful for the current target scale range: 100–30 km. Although the Himawari-8 SST data are available from August 2015, MGDSST and AVHRR SST data are available from 1980s. We are planning to update the JCOPE2 reanalysis data (Miyazawa et al. 2009) by the use of the modified JCOPE2 with MS-3DVAR utilizing MGDSST and/or AVHRR SST.
Note that temperature/salinity RMSD between the MGDSST and Himawari-8 SST assimilation cases (not shown) shows considerable deviation from each other similar to those shown in Fig. 8a, b but with smaller magnitude around the oceanic fronts than indicated in Fig. 8a, b, suggesting possible impacts of utilizing the higher resolution Himawari-8 SST data under the current model setting (cf. Kawai et al. 2015). Full utilization of the high-resolution Himawari-8 SST may require applying it to higher resolution ocean models with smaller target scales and/or more advanced data assimilation methods (e.g., the ensemble Kalman filter with 1/36° resolution by Hihara et al. 2017, in preparation).
MS-3DVAR provides an intermediate option for further improvement of the 3DVAR prior to switching over to the advanced but expensive methods including the ensemble Kalman filter (e.g., Miyazawa et al. 2013) and 4DVAR (e.g., Usui et al. 2015). It is interesting to carefully compare cost and benefit depending on possible choices of the forward models with higher resolution and the data assimilation methods with various levels of the implementation and computational costs.
References
Choi B-J, Haidvogel DB, Cho Y-K (2004) Nonseasonal sea level variations in the Japan/East Sea from satellite altimeter data. J Geophys Res 109(C12). doi:10.1029/2004JC002387
Fu LL, Ferrari R (2008) Observing oceanic submesoscale processes from space. EOS Transactions American Geophysical Union 89:488
Fu LL, Ubelmann C (2014) On the transition from profile altimeter to swath altimeter for observing global ocean surface topography. J Atmos Ocean Tech 31:560–568
Fujii Y, Kamachi M (2003) A reconstruction of observed profiles in the sea east of Japan using vertical coupled temperature-salinity EOF modes. J Oceanogr 59:173–186
Fujisaki A, Yamaguchi H, Mitsudera H (2010) Numerical experiments of air–ice drag coefficient and its impact on ice–ocean coupled system in the Sea of Okhotsk. Ocean Dyn 60:377–394
Furuichi N, Hibiya T, Niwa Y (2012) Assessment of turbulence closure models for resonant inertial response in the oceanic mixed layer using a large eddy simulation model. J Oceanogr 68:285–294
Griffies SM, Biastoch A, Boning C, Bryan F, Danabasoglu G, Chassignet EP, England MH, Gerdes R, Haak H, Hallberg RW, Hazeleger W, Jungclaus J, Large WG, Madec G, Pirani A, Samuels BL, Scheinert M, Sen Gupta A, Severijns CA, Simmons HL, Treguier AM, Winton M, Yeager S, Yin J (2009) Coordinated ocean-ice reference experiments (COREs). Ocean Model 26:1–46
Hanawa K, Mitsudera H (1985) About the daily averaging method of oceanic data (in Japanese). Bull on Coastal Oceanogr 23:79–87
Hirose N (2011) Inverse estimation of empirical parameters used in a regional ocean circulation model. J Oceanogr 67:323–336
Hosoda K, Murakami H, Sakaida F, Kawamura H (2007) Algorithm and validation of sea surace temperature observation using MODIS sensors aboard Terra and Aqua in the western north Pacific. J Oceanogr 63:267–280
Ichikawa K (2014) Satellite altimeters in the early 21th century (in Japanese with English abstract and figure captions). Oceanog in Jpn 23:13–27
Kawabe M (1989) Sea level changes south of Japan associated with the non-large-meander path of the Kuroshio. J Oceanogr Sco Jpn 45:181–189
Kawai Y, Miyama T, Iizuka S, Manda A, Yoshioka MK, Katagiri S, Tachibana Y, Nakamura H (2015) Marine atmospheric boundary layer and low-level cloud responses to the Kuroshio Extension front in the early summer of 2012: three-vessel simultaneous observations and numerical simulations. J Oceanogr 71:511–526
Kida S, Mitsudera H, Aoki S, Guo X, Ito S, Kobashi F, Komori N, Kubokawa A, Miyama T, Morie R, Nakamura H, Nakamura T, Nakano H, Nishigaki H, Nonaka M, Sasaki H, Sasaki YN, Suga T, Sugimoto S, Taguchi B, Takaya K, Tozuka T, Tsujino H, Usui N (2015) Oceanic fronts and jets around Japan: a review. J Oceanogr 71:469–497
Kuragano T, Kamachi M (2000) Global statistical space-time scales of oceanic variability estimated from the TOPEX/POSEIDON altimeter data. J Geophys Res 105:955–974
Kurihara Y, Sakurai T, Kuragano T (2006) Global daily sea surface temperature analysis using data from satellite microwave radiometer, satellite infrared radiometer and in-situ observations (in Japanese). Weather Bull 73:s1–s18
Kurihara Y, Murakami H, Kachi M (2016) Sea surface temperature from the new Japanese geostationary meteorological Himawari-8 satellite. Geophys Res Let 43:1234–1240
Li Z, Chao Y, Farara JD, McWilliams JC (2013) Impacts of distinct observations during the 2009 Prince William sound field experiment: a data assimilation study. Cont Shelf Res 63:S209–S222
Li Z, McWilliams JC, Ide K, Farrara JD (2015a) A multi-scale variational data assimilation scheme: formulation and illustration. Mon Wea Rev 143:3804–3822
Li Z, McWilliams JC, Ide K, Farrara JD (2015b) Coastal ocean data assimilation using a multi-scale three-dimensional variational scheme. Ocean Dyn 65:1001–1015
May DA, Parmeter MM, Olszewski DS, McKenzie BD (1998) Operational processing of satellite sea surface temperature retrievals at the Naval Oceanographic Office. Bull Amer Meteor Soc 79:397–407
McCalpin JD (1994) A comparison of second-order and fourth-order pressure gradient algorithms in a sigma coordinate ocean model. Int Num Methods Fluids 18:361–383
Mellor GL, Blumberg A (2004) Wave breaking and ocean surface layer thermal response. J Phys Oceanogr 34:693–698
Mellor GL, Yamada T (1982) Development of a turbulence closure model for geophysical fluid problems. Rev Geophys Space Phys 20:851–875
Mellor GL, Hakkinen S, Ezer T, Patchen R (2002) A generalization of a sigma coordinate ocean model and an inter comparison of model vertical grids. In: Pinardi N, Woods JD (eds) Ocean Forecasting: Conceptual Basis and Applications. Springer, New York, pp 55–72
Miyazawa Y, Zhang RC, Guo X, Tamura H, Ambe D, Lee JS, Okuno A, Yoshinari H, Setou T, Komatsu K (2009) Water mass variability in the Western North Pacific detected in a 15-year eddy resolving ocean reanalysis. J Oceanogr 65:737–756
Miyazawa Y, Miyama T, Varlamov SM, Guo X, Waseda T (2012) Open and coastal seas interactions south of Japan represented by an ensemble Kalman Filter. Ocean Dyn 62:645–659
Miyazawa Y, Murakami H, Miyama T, Varlamov SM, Guo X, Waseda T, Sil S (2013) Data assimilation of the high-resolution sea surface temperature obtained from the Aqua-Terra satellites (MODIS-SST) using an ensemble Kalman filter. Remote Sens 5:3123–3139
Morimoto A, Yanagi T (2001) Variability of sea surface circulation in the Japan Sea. J Oceanogr 57:1–13
Morimoto A, Yanagi T, Kaneko A (2000) Eddy field in the the Japan Sea derived from satellite altimetric data. J Oceanogr 56:449–462
Muscarella PA, Carrier MJ, Ngodock HE (2014) An example of a multi-scale three-dimensional variational data assimilation scheme in the Kuroshio Extension using the naval coastal ocean model. Cont Shel Res 73:41–48
Nakanishi M, Niino H (2009) Development of an improved turbulence closure model for the atmospheric boundary layer. J Metorol Soc Jpn 87:895–912
Oh IS, Zhurbas V, Park W, (2000) Estimating horizontal diffusivity in the East Sea (Sea of Japan) and the northwest Pacific from satellite-tracked drifter data. J Geophys Res: Oceans 105(C3):6483–6492
Polachenski CM, Dibb JE, Flanner MG, Chen JY, Courville ZR, Lai AM, Schauer JJ, Shafer MM, Bergin M (2015) Neither dust nor black carbon causing apparent albedo decline in Greenland's dry snow zone: implications for MODIS C5 surface reflectance. Geophys Res Let 42:9319–9327
Soeyanto E, Guo X, Ono J, Miyazawa Y (2014) Interannual variations of Kuroshio transport in the East China Sea and its relation to the Pacific Decadal Oscillation and mesoscale eddies. J Geophys Oceans 119:3595–3616
Thiem O, Berntsen J (2006) Internal pressure errors in sigma coordinate ocean models due to anisotropy. Ocean Model 12:140–156
Uchimoto K, Mitsudera H, Ebuchi N, Miyazawa Y (2007) Anticyclonic eddy caused by the Soya Warm Current in an Okhotsk OGCM. J Oceanogr 63:379–391
Usui N, Tsujino H, Fujii Y, Kamachi M (2006) Short-range prediction experiments of the Kuroshio path variabilities south of Japan. Ocean Dyn 56:607–623
Usui N, Fujii Y, Sakamoto K, Kamachi M (2015) Development of a four-dimensional variational assimilation system for coastal data assimilation around Japan. Mon Wea Rev 143:3874–3892
Varlamov SM, Guo X, Miyama T, Ichikawa K, Waseda T, Miyazawa Y (2015) M2 baroclinic tide variability modulated by the ocean circulation south of Japan. J Geophys Res Oceans 120:3681–3710
Acknowledgements
Comments from two anonymous reviewers are quite useful for improving the earlier versions of the manuscript. This work is part of the Japan Coastal Ocean Predictability Experiment (JCOPE) promoted by the Japan Agency for Marine-Earth Science and Technology (JAMSTEC). A source code of the rotated baroclinic pressure gradient scheme was provided by Takashi Kagimoto. The multi-core workstations based on the Intel Xeon processors were prepared by Hidehiro Fujio. The research product of sea surface temperature produced from Himawari-8, Version 1.1, was supplied by the P-Tree System, Japan Aerospace Exploration Agency (JAXA). The Moderate Resolution Imaging Spectroradiometer (MODIS) SST produced from Aqua/Terra was also provided from JAXA. Merged Satellite and In situ Data Global Daily SST (MGDSST) was obtained from the NEAR-GOOS regional real-time database. The Ssalto/Duacs altimeter products were produced and distributed by the Copernicus Marine and Environment Monitoring Service (CMEMS) (http://www.marine.copernicus.eu). The Naval Oceanographic Office (NAVOCEANO)-Multi-Channel SST (MCSST) were downloaded from Physical Oceanography Distributed Active Archive Center (PODAAC) ftp site: ftp://podaac.jpl.nasa.gov. In situ temperature and salinity profiles were obtained from the Global Temperature-Salinity Profile Program (GTSPP) website: http://www.nodc.noaa.gov/GTSPP/. Tide gauge data were provided from the Japan Meteorological Agency (JMA) and the Japan Coast Guard. The atmospheric pressure data for the barometric correction of the tide gauge data were provided from JMA.
Author information
Authors and Affiliations
Corresponding author
Additional information
Responsible Editor: Emil Vassilev Stanev
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Miyazawa, Y., Varlamov, S.M., Miyama, T. et al. Assimilation of high-resolution sea surface temperature data into an operational nowcast/forecast system around Japan using a multi-scale three-dimensional variational scheme. Ocean Dynamics 67, 713–728 (2017). https://doi.org/10.1007/s10236-017-1056-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10236-017-1056-1