An idealized model of tidal dynamics in the North Sea: resonance properties and response to large-scale changes

Abstract

An idealized process-based model is developed to investigate tidal dynamics in the North Sea. The model geometry consists of a sequence of different rectangular compartments of uniform depth, thus, accounting for width and depth variations in a stepwise manner. This schematization allows for a quick and transparent solution procedure. The solution, forced by incoming Kelvin waves at the open boundaries and satisfying the linear shallow water equations on the f plane with bottom friction, is in each compartment written as a superposition of eigenmodes, i.e. Kelvin and Poincaré waves. A collocation method is employed to satisfy boundary and matching conditions. First, the general resonance properties of a strongly simplified geometry with two compartments, representing the Northern North Sea and Southern Bight, are studied. Varying the forcing frequency while neglecting bottom friction reveals Kelvin and Poincaré resonance. These resonances continue to exist (but with lower amplification and a modified spatial structure) when adding the Dover Strait as a third compartment and separating the solutions due to forcing from either the north or the south only. Including bottom friction dampens the peaks. Next, comparison with tide observations along the North Sea coast shows remarkable agreement for both semi-diurnal and diurnal tides. This result is achieved with a more detailed geometry consisting of 12 compartments fitted to the coastline of the North Sea. Further simulations emphasize the importance of Dover Strait and bottom friction. Finally, it is found that a sea level rise of 1 m, uniformly applied to the entire North Sea, amplifies the M2-elevation amplitudes almost everywhere along the coast, with an increase of up to 8 cm in Dover Strait. Bed level changes of ±1 m, uniformly applied to the Southern Bight only, imply weaker changes, with changes in coastal M2-elevation amplitudes below 5 cm.

1 Introduction

Understanding tidal dynamics in the North Sea is important for navigation, coastal safety and ecology. This link is both direct, through fluctuating water levels and oscillatory currents, and indirect, through the dynamics of tide-induced bed forms (Dyer and Huntley 1999). Of particular interest is the tide’s response to large-scale changes due to human intervention (de Boer et al 2011) and sea level rise.

Tide observations in the North Sea indicate a predominant semi-diurnal character (Otto et al 1990; Huthnance 1991). Semi-diurnal lunar (M2) elevation amplitudes are of the order of 1 m. Diurnal components are weaker, with coastal elevation amplitudes of K1 and O1 of about 10 cm. Figure 1 shows the locations of coastal tide stations where harmonic constants, i.e. tidal range and phase of the four most important constituents (M2, S2, K1 and O1) are available (Bristish Admiralty2009a, b).

Fig. 1

Bathymetric chart of the North Sea, with depth below MSL in m (data source: Amante and Eakins 2009). White lines indicate the idealized model geometry consisting of 12 rectangular compartments to be used in this study (points A to F introduced are for convenience). Open circles denote the coastal tide stations involved in the comparison between model results and observations. Small dots indicate other tide stations not considered in this study (British Admiralty 2009a, b)

North Sea tides result primarily from co-oscillation with the Atlantic (Defant 1961). Their complexity is due to several factors (see Fig. 1):

• Significant variations in depth, ranging roughly from 20–150 m from south to north, dissipation through bottom friction being important in the shallower parts. The Norwegian Trench in the northeast has depths of up to 700 m.

• Significant basin width, relative to the Rossby deformation radius, emphasizing the importance of rotation.

• Significant variations in basin width, ranging from over 500 km in the north to about 200 km in the Southern Bight (points BCD) and less than 40 km in the Dover Strait (point C). In combination with the preceding point, this explains the profound two-dimensional spatial structure of the tide.

• The presence of two open boundaries to the Atlantic: east of Scotland and Dover Strait.¹

Detailed numerical model studies have been carried out to reproduce the tide observations mentioned above (Sinha and Pingree 1997; Davies and Kwong 2000, see Fig. 2). Such numerical tide simulations are a key factor in the water level forecasts for a storm surge warning system; e.g. in the Dutch Continental Shelf model (Gerritsen et al 1995; Verlaan et al 2005). Numerical models are generally computationally expensive and not aimed at obtaining insight in the physics, which limits their suitability for a systematic study of the resonance properties of the North Sea.

Fig. 2

Co-tidal charts of M2-tide (left) and K1-tide (right), with elevation amplitudes in cm (solid) and phases in degrees (dashed), as obtained with a numerical model (Davies and Kwong 2000, reprinted with permission from the American Geophysical Union)

On the other hand, idealized process-based models are specifically designed to obtain insight in tidal dynamics. Taylor’s (1922) classical solution to the problem of Kelvin wave reflection in a rectangular rotating basin of uniform depth and width explains elevation amphidromic points (no surface fluctuations) and current amphidromic points (no velocities) occurring alternately on the centerline of the basin. Incorporating dissipation causes the amphidromes to shift in the cross-basin direction (Rienecker and Teubner 1980; Rizal 2002; Roos and Schuttelaars 2009). To mimic Dover Strait, Brown (1987, 1989) imposed an oscillating free surface elevation at the head, which causes an along-basin shift of the amphidromes. We note that also complex numerical models have been run with simplified geometries, to study the frictional and wind effects with a three-dimensional model (Davies and Jones 1995, 1996), the influence of basin geometry on the current amphidromic system (Xia et al 1995) and sandbank formation (Carbajal et al 2005). Table 1 summarizes the tidal basins around the world that have been studied using (extensions of) Taylor’s (1922) idealized model. Although the idealized studies mentioned above provide qualitative insight, the rather strong geometrical schematizations preclude a more specific understanding of the North Sea tides.

Table 1 Overview of studies extending Taylor’s (1922) approach and applying it to basins other than the North Sea

A third class of studies specifically focused on the resonance properties of tidal basins, which is indicative of their response to large-scale changes. A classical result for semi-enclosed bays co-oscillating with a larger sea/ocean states that resonance occurs when basin length equals one quarter of the shallow water wavelength (or an odd multiple; see e.g. Defant 1961). This theory, however, ignores radiative damping into the adjacent sea/ocean (Garrett 1975) and is only valid for narrow rectangular bays of uniform depth and width. Rotation complicates the resonance properties of wider basins, which also allow for a cross-bay half-wave² resonance (Huthnance 1980).³ This type of resonance, associated with amplification of Poincaré modes, is also possible in wide embayments of uniform width with a shallow zone near the head (Webb 1976; Roos and Schuttelaars 2011). Alternatively, the resonant frequencies of various basins around the world have been estimated by fitting analytical frequency-response curves to tide observations (Garrett 1972; Godin 1993; Sutherland et al 2005; Arbic et al 2007). The curves are derived from e.g. the rectangular bay model mentioned above (or a Helmholtz oscillator for smaller basins), whereas the observations comprise amplitude gains and phase shifts over the basin for various tidal constituents. This method relies on the availability of observations at different tidal frequencies, their proximity to resonance and the validity of the model underlying the adopted frequency-response curve.

The present study is aimed at understanding tidal dynamics in the North Sea, particularly its resonance properties and its response to large-scale changes. Motivated by the lack of geometrical detail in existing idealized model studies and the limited suitability of numerical models for this purpose, we present a new idealized model (Fig. 1). Innovative aspects of our work are the model geometry (many compartments, depth and width variations, two open boundaries), the focus on resonance properties, and the detailed comparison with semi-diurnal and diurnal tide observations along the North Sea coast. Our approach largely follows that of Roos and Schuttelaars (2011) but involves the necessary extensions to make it suitable for the North Sea.

This paper is organized as follows. The model set-up and solution method are presented in Section 2. In Section 3, we investigate the general resonance properties of a relatively shallow compartment connected to a wider and deeper compartment and to a narrow strait. A crucial next step is then to show that our model is quantitatively capable of reproducing tidal dynamics as observed in the North Sea (tide stations in Fig. 1). As shown in Section 4, good agreement with semi-diurnal and diurnal tide observations is achieved with a geometry consisting of 12 compartments. This result gives confidence in the model’s reliability in situations for which no observational data are available. Further simulations, presented in Section 5, then provide insight into:

• The importance of the tidal energy fluxes from the north (east of Scotland) and the south (through Dover Strait) as well as the effects of closure of Dover Strait

• The role of bottom friction

• The effects of sea level rise, simulated by an overall increase in water depth

• The system’s sensitivity to bed level variations in the Southern Bight

Finally, Sections 6 and 7 contain the discussion and conclusions, respectively.

2 Model

2.1 Model formulation

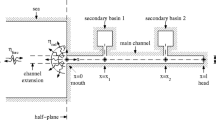
Consider a tidal wave of angular frequency ω and typical elevation amplitude Z. The model geometry consists of a sequence of J rectangular compartments of length l _j , width b _j and (uniform) depth h _j (Fig. 3). The geometries in Fig. 3a, b will be used in Section 3 to investigate general resonance properties. The more detailed geometry in Fig. 3c will be used in Section 4 to reproduce tide observations in the North Sea and forms the basis of further simulations in Section 5. Details of these configurations are given in Table 3, where δ _j denotes the displacement of compartment j’s centerline with respect to that of compartment j − 1.

Fig. 3

Definition sketch of the model geometry, showing a a simple set-up with two compartments, b extension with strait and c the North Sea fit with 12 compartments also shown in Figs. 1 and 6. Shaded compartments represent the Southern Bight; details in Table 3

The compartment widths are not small compared with the (local) Rossby deformation radius, which shows the importance of adopting a horizontally two-dimensional approach including rotation. Assuming that Z/h _j  ≪ 1, conservation of momentum and mass is expressed by the depth-averaged linear shallow water equations on the f plane:⁴

$$ \frac{\partial u_j}{\partial t} - f_jv_j + \frac{r_ju_j}{h_j} = -g \frac{\partial \eta_j}{\partial x} , $$

(1)

$$ \frac{\partial v_j}{\partial t} + f_ju_j + \frac{r_jv_j}{h_j} = -g \frac{\partial \eta_j}{\partial y} , $$

(2)

$$ \frac{\partial \eta_j}{\partial t} + h_j \left[ \frac{\partial u_j}{\partial x} + \frac{\partial v_j}{\partial y}\right] = 0 . $$

(3)

For compartment j, u _j and v _j are the depth-averaged flow velocity components in along-basin x and cross-basin y-direction, respectively, and η _j is the free surface elevation (j = 1, ⋯ ,J). Furthermore, f _j  = 2Ωsinϑ _j is a Coriolis parameter (with Ω = 7.292×10^− 5 rad s^− 1 the angular frequency of the Earth’s rotation and ϑ _j the central latitude of compartment j) and g = 9.81 m s^− 2 the gravitational acceleration. Finally, we have introduced a bottom friction coefficient

$$ r_j = \frac{8c_\mathrm{D}\langle U_j\rangle}{3\pi} , \qquad \langle U_j \rangle = \alpha F U_j , $$

(4)

based on linearization of a quadratic friction law while accounting for the simultaneous presence of several tidal components. In Eq. 4, $c_\mathrm{D}=2.5\times10^{-3}$ is a standard drag coefficient. Furthermore, the velocity scale $\langle U_j \rangle$ is a correction of the coastal current amplitude U _j of a classical Kelvin wave without bottom friction (Gill 1982):

$$ U_j = Z_\mathrm{M2} \sqrt{\frac{g}{h_j}} . $$

(5)

Here, the coastal elevation amplitude Z _M2 = 1.40 m is typical for the dominant M2-tide, obtained by averaging over all coastal tide stations under consideration.

Turning back to Eq. 4, the following corrections are made to U _j to obtain a proper velocity scale $\langle U_j \rangle$. Firstly, the coefficient α accounts for the fact that current amplitudes throughout the domain are typically smaller than the tidal current amplitudes near the coast (α < 1). In Section 4, α will be used as a tuning parameter that is assumed identical for all constituents. Secondly, the coefficient F accounts for the fact that the simultaneous presence of several tidal components enhances friction (F > 1), particularly for the weaker components (Jeffreys 1970; Pingree 1983; Inoue and Garrett 2007). Properly incorporating this mechanism is important when we use our model to reproduce tide observations in Section 4. To calculate the F values for M2, S2, K1 and O1 in the North Sea, we follow the procedure by Inoue and Garrett (2007); see Table 2 and Appendix A. As it turns out, the ratios F/F _M2 are close to the theoretical maximum of 1.5 obtained in the ϵ ↓ 0-limit with ϵ = Z/Z _M2 (Jeffreys 1970). In Section 3, where we investigate the model’s frequency response by varying ω in a broad range surrounding the tidal bands, we will ignore the presence of other components and take F = 1.

Table 2 Amplitudes Z and friction coefficients F, as used in Eq. 4, of four tidal components in the North Sea

Our model geometry displays different types of boundaries. At the closed boundaries $\mathcal{B}_{u,j}$ and $\mathcal{B}_{v,j}$ orthogonal to the along-basin and cross-basin direction, respectively, we impose a no-normal flow condition, i.e.

$$ u_j = 0 , \qquad \mbox{for $(x,y) \in \mathcal{B}_{u,j}$,} $$

(6)

$$ v_j = 0 , \qquad \mbox{for $(x,y) \in \mathcal{B}_{v,j}$.} $$

(7)

Next, continuity of elevation and normal flux is required across the topographic steps $\mathcal{I}_{j,j+1}$ between the adjacent compartments:

$$ h_ju_j = h_{j+1}u_{j+1} , \quad \eta_j=\eta_{j+1} , \qquad \mbox{for $(x,y) \in \mathcal{I}_{j,j+1}$.} $$

(8)

Finally, the system is forced by a single Kelvin wave coming in through the open boundary for the geometry in Fig. 3a, or by two Kelvin waves coming in through the two open boundaries for the geometries in Fig. 3b, c. In either case, other waves are allowed to radiate outward. In the case of two incoming Kelvin waves, the solution will also depend on their relative amplitudes and phase lag, which complicates the interpretation of the model results.

2.2 Solution method

Let ϕ ≡ (u, v, η) symbolically denote the solution. In each compartment we seek time-periodic solutions of the form

$$ \phi_j \equiv (u_j,v_j,\eta_j) = \Re \left\{ ( \hat{u}_j,\hat{v}_j,\hat{\eta}_j ) \exp(i\omega t) \right\} , $$

(9)

with $\Re$ denoting the real part, ω the angular frequency and $( \hat{u}_j,\hat{v}_j,\hat{\eta}_j )$ the complex amplitudes of flow and elevation, which depend on x and y. These amplitudes are then written as a truncated superposition of fundamental wave solutions in an open channel, i.e. Kelvin and Poincaré modes, propagating or exponentially decaying in the positive and negative x-direction (see Appendix B). Since these individual waves satisfy the lateral boundary condition in Eq. 7, so does their superposition in the solution.

A collocation technique is then employed to also satisfy the other no-normal flow condition in Eq. 6 and the matching conditions in Eq. 8. We, thus, extend earlier studies to account for width variations (Webb 1976; Jung et al 2005; Roos and Schuttelaars 2011). Collocation points are defined with an equidistant spacing along the interfaces and the adjacent closed longitudinal boundaries.⁵ At each collocation point, we require either zero normal flow (if located on a closed boundary) or matching of elevation and normal flux (if located on an interface). The truncation numbers mentioned previously are chosen such to balance the distribution of collocation points. The coefficients of the individual modes then follow from a linear system, which is solved using standard techniques.

In the remainder of this study we adopt an average spacing between collocation points of about 6 km. In Section 3, where we investigate the resonance properties of the simple geometries in Fig. 3a, b, this leads to a total number of about 170 Kelvin and Poincaré modes. In reproducing the tide observations from the North Sea (Section 4; geometry of Fig. 3c), the same spacing implies a total number of about 1700 Kelvin and Poincaré modes in the complete domain.

3 Results: general resonance properties

3.1 Indicators of amplitude gain in the Southern Bight

To investigate resonance properties, we consider the frequency-response of our model. To this end, we analyze the solution for different values of the forcing frequency ω in a range that includes the diurnal and semi-diurnal tidal bands. This analysis will be carried out for the simple geometries shown in Fig. 3a, b. The first consists of two compartments, representing the relatively wide and deep northern part of the North Sea and the narrower and shallower Southern Bight. This geometry is extended in Fig. 3b by including a third compartment, representing Dover Strait as a second opening to the Atlantic. For simplicity, all compartments have been symmetrically aligned about the basin’s central axis, i.e. δ _j  = 0. See Table 3 for the dimensions and latitudes.

Table 3 Compartment properties of the basin geometries in Fig. 3

To quantify the ‘response’, we introduce the amplitude gain A _head. This indicator is defined as the elevation amplitude, scaled against the input amplitude Z _inc and averaged over the head of the bight (thick solid line in Fig. 3a):

$$ A_\mathrm{head} = \frac{1}{b_2Z_\mathrm{inc}} \int |\hat{\eta}_2| \mathrm{d}y . $$

(10)

Although A _head is commonly used to quantify the amplitude gain (e.g. Huthnance 1980), it is less meaningful for the case with a strait, because part of the bay head is then an open boundary (Fig. 3b). We, therefore, introduce a second indicator A _bight, averaging the elevation amplitude over the complete bight (shaded area in Fig. 3a, b):

$$ A_\mathrm{bight} = \frac{1}{b_2l_2Z_\mathrm{inc}} \iint |\hat{\eta}_2| \mathrm{d}x \; \mathrm{d}y . $$

(11)

3.2 Results for two compartments

Figure 4a shows the amplitude gains A _head and A _bight as a function of forcing frequency for the two-compartment geometry (Fig. 3a), both without and with bottom friction. It is seen that both amplitude gains show qualitatively similar behaviour, with, as one may expect, the bight-averaged indicator A _bight (red line) being somewhat lower than the head-averaged A _head (black line).

Fig. 4

Amplitude gain versus forcing frequency ω for the model geometries in Fig. 3a, b: a two compartments, b three compartments (including strait). Solid lines without bottom friction, dashed lines with bottom friction. In (a), the black and red lines indicate A _head and A _bight, respectively. In (b), the red and blue lines indicate A _bight(N) and A _bight(S), respectively, i.e. separately forcing the system from the north and south only. The co-tidal charts of the cases denoted by the lowercase letters a–l are depicted in Fig. 5

The curves without bottom friction (solid lines) display a peak between the diurnal band (ω ≈ 1 cpd) and semi-diurnal band (ω ≈ 2 cpd), a weaker response at ω = 2.5 − 3 cpd and two further peaks at higher values of the forcing frequency. As can be seen from the co- tidal chart in Fig. 5a, the first peak is associated with a quarter wavelength resonance of the Kelvin mode in the Southern Bight. Next, Fig. 5b shows an example of weaker amplification in the bight, which is accompanied by higher amplitudes in the corners of the deep and wide compartment (e.g. the German Bight, region near point E in Fig. 1). The second peak in the frequency-response curve represents resonance of the first Poincaré mode (Fig. 5c), whereas the third peak is a three quarter wavelength resonance of the Kelvin mode. We note that adjusting the dimensions of the model geometry may affect the order in which the Kelvin and Poincaré resonances appear as a function of ω.

Fig. 5

Co-tidal charts of the twelve cases a-l highlighted in the frequency-response curves in Fig. 4 (without bottom friction). The top row pertains to the two-compartment geometry (Fig. 3a); the middle and bottom rows to the three-compartment geometry (Fig. 3b) if forced from the north or south only, respectively. Please note the different colourbars used in each row

As shown by the dashed lines in Fig. 4a, including bottom friction causes the peaks to nearly disappear. The amplitude gain becomes nearly monotonically decreasing function of ω. It should be noted that, in the simulation with bottom friction, we assume Z = 1 m, ignore the enhancement of friction due to the simultaneous presence of other constituents (F = 1) and maintain α = 0.6; see Eqs. 4–5.

3.3 Results for three compartments (including strait)

Now let us proceed with the three-compartment geometry of Fig. 3b. Justified by the linearity of the problem, we may write the solution as

$$ \phi = \phi_\mathrm{(N)} + \phi_\mathrm{(S)} , $$

(12)

where ϕ ₍N) is the solution if forced from the north only and ϕ ₍S) the solution if forced from the south only (while maintaining the other boundary as an open boundary). Accordingly, we define A _bight(N) and A _bight(S) as the amplitude gains of these separate solutions. It should be noted that, due to phase differences, the amplitude gain of the complete solution does not equal the sum of the individual amplitude gains, i.e. in general $A_\mathrm{bight} \ne A_\mathrm{bight(N)}+A_\mathrm{bight(S)}$.

Figure 4b shows the frequency-response curves if the three-compartment-system is forced from the north only (A _bight(N), red) and south only (A _bight(S), blue). For the case without bottom friction (solid lines), the curves are qualitatively similar to the case with two compartments (Fig. 4a), i.e. showing similar peaks at similar ω values, regardless whether the system is forced from the north or south. Restricting our attention first to the case with forcing from the north only, it is seen that the amplitude gain is roughly a factor 2 smaller than in the two-compartment-case, which is due to radiation of energy from the bight into the strait. The lowest values are obtained if the system is forced from the south only, which is due to (1) radiation of energy from the bight into the northern compartment and (2) the absence of a shoaling effect, because the depth in bight and strait is identical (h ₂ = h ₃ = 20 m; see Table 3). The co-tidal charts in Fig. 5e–l show that the resonance mechanisms identified in Section 3.2 continue to exist after the introduction of a strait and the distinction in forcing from either the north or south. It is seen that they occur at nearly the same frequencies, yet in a somewhat modified spatial form.

Finally, analogous to the case with two compartments, it is found that including bottom friction dampens the peaks of the frequency-response curves (dashed curves in Fig. 4b). Analogous to Section 3.2, our simulations with bottom friction use Z = 1 m, F = 1 and α = 0.6 in Eqs. 4–5.

4 Reproducing tide observations in the North Sea

In this section, our model will be tested against tide observations from the coastal tide stations shown in Fig. 1 (British Admiralty 2009a, b). The tide observations comprise elevation amplitudes and phases of the four dominant constituents: M2, S2 (semi-diurnal), K1 and O1 (diurnal). The procedure, roughly similar to that presented in Roos and Schuttelaars’ (2011) study of the Adriatic Sea, Gulf of California and Persian Gulf, consists of four steps.

• 1. Choose the basin geometry by specifying the compartment dimensions l _j and b _j (j = 1,...,J), the position of the first and the centerline displacements δ _j of all other compartments. This step is carried out manually leading to a configuration with J = 12 compartments and an orientation aligned with the Southern Bight (positive x-axis directed 13° East from North). See Figs. 1, 3c and Table 3. We note that an accurate representation of the northeastern part (Norwegian Trench, Skagerrak) is not our main interest.

• 2. Specify h _j as the compartment-averaged depth and ϑ _j as the compartment’s central latitude (j = 1,...,J). Bathymetric data are taken from (Amante and Eakins 2009). In calculating the compartment-averaged depth, the parts on land are ignored.

• 3. Project the available coastal tide stations orthogonally onto the nearest coastal boundary. This projection allows us to visualize the observations as a function of the coastal coordinate and compare them to model results. Tide stations located up-river, up-estuary, at offshore locations or otherwise more than 50 km away from the model boundaries are discarded.

• 4. Perform simulations using the basin set-up, depth values and latitudes as above. The amplitudes and phases (Z ₍N),ϕ ₍N),Z ₍S),ϕ ₍S)) of the two incoming Kelvin waves and the overall correction factor α serve as tuning parameters. The friction coefficients r _j are calculated from Eqs. 4–5, using the typical elevation amplitude Z _M2 and the F values from Table 2. The simulations mentioned above are carried out for each of the four tidal constituents: M2, S2, K1 and O1 (all using the same α-value).

The results are presented in Fig. 6. The corresponding amplitudes and phases of the incoming Kelvin waves are shown in Table 4. The best agreement between model results and coastal tide observations is obtained by setting the overall correction factor for the velocity scale in Eq. 4 at α = 0.6. The plots in Fig. 6a–d show remarkable agreement between model results and observations, regarding the coastal amplitudes and phases of all four constituents. This qualitative and quantitative agreement applies to nearly the entire North Sea (coastal coordinate A to E), except the region in the north-east (EF) where the bathymetry is less accurately represented than elsewhere in the model domain. However, because of the counterclockwise propagation direction of the tidal wave in the North Sea, errors in this part of the domain do not adversely affect the model results elsewhere.

Table 4 Amplitudes and phases of the incoming Kelvin waves for the simulations in Fig. 6

The qualitative features of the M2 and K1 co-tidal charts from our idealized model in Fig. 6a, c show good agreement with those obtained using numerical models (e.g., Davies and Kwong 2000, see Fig. 2). The M2-amphidrome in Fig. 6a is located too far away from the German Bight and the K1-amphidrome near Norway in Fig. 6c should be virtual. Furthermore, the virtual nature of the K1-amphidrome in the Dover Strait is not reproduced by our model. Note that in conducting the simulations, we tuned to obtain agreement with coastal tide observations, rather than to obtain agreement with the positions of amphidromic points from numerical models.

Fig. 6

Modelled amphidromic chart (top) and comparison of model results (solid lines) and observations (open circles) as a function of the coastal coordinate along A–F, i.e. elevation amplitudes (middle) and phases (bottom) for four constituents: a M2, b S2 and, on the next page, c K1, d O1. Note the differences in scales of the colourbars and the amplitude axes

5 Further results

5.1 Forcing from north and south, Dover Strait, dissipation

In this section, we will perform further simulations to unravel and better understand tidal dynamics in the North Sea. To this end, we continue to use the basin geometry of Fig. 3c, which was already used in Section 4 to reproduce the North Sea tides. For brevity, we focus on the dominant tidal constituent only: M2.

Firstly, we investigate the M2-tidal elevation amplitudes in the cases of tidal forcing from the north only (Z ₍N) from Table 4 and Z ₍S) = 0) and, alternatively, from the south only (Z ₍N) = 0 and Z ₍S) from Table 4). The corresponding coastal amplitudes, as a function of the coastal coordinate, are plotted in Fig. 7a. It is seen that the forcing through Dover Strait hardly affects the elevation amplitude along the UK coast. Furthermore, the plot alternately displays coastal stretches of constructive interference (e.g. around C and along DE) and destructive interference (e.g. at point B).

Fig. 7

M2-tidal elevation amplitudes as function of the coastal coordinate for the following cases. a Forcing from the north only (red, dotted), forcing from the south only (blue, dashed). b Simulation without bottom friction (blue, dashed); simulation after closure of Dover Strait (red, dotted; with bottom friction). In both plots, the black solid line denotes the reference case already shown in Fig. 6a

Secondly, the importance of Dover Strait is studied by performing a simulation in which the Dover Strait is closed off. To this end, compartment j = 12 is removed and the southern boundary of compartment j = 11 is treated as a closed boundary, where according to Eq. 6, u _j  = 0 is imposed (and, consequently, no tidal energy enters or leaves the domain). Analogous to the simulations above, the characteristics of the incoming Kelvin wave from the north are as in Table 4. As shown in Fig. 7b, the resulting curve is slightly higher than the red dotted curve in Fig. 7a. Due to reflection in the Southern Bight, amplitudes are higher than in the case with an open Dover Strait and forcing from the North only, particularly in the eastern part of the domain. These results emphasize the importance of including Dover Strait as an open boundary with appropriate forcing (Brown 1987), and the strait’s influence extending to the German Bight contrasts earlier beliefs (Defant 1961).

Thirdly, the importance of dissipation is assessed by performing a simulation for the M2-tide without bottom friction, i.e. for r _j  = 0 for all j. In doing so, we retain the input characteristics of the incoming Kelvin waves as given in Table 4. As shown in Fig. 7b, without bottom friction, amplitudes in the eastern part would be much higher, by a factor of more than two (blue dashed line). The increasing difference along ABCDEF with the frictional case (black solid line) furthermore emphasizes the counterclockwise propagation direction of the tidal wave.

5.2 Sea level rise

To mimic sea level rise, we now perform simulations with an overall increase in water depth Δh of 0–2 m. This range surrounds the value of 1 m, which corresponds to a high-end projection for local sea level rise along the Dutch coast onto the year 2100 (Katsman et al 2011). The chosen Δh value is applied uniformly to all compartments in Fig. 3c and Table 3. In our analysis, we assume that the horizontal boundaries of our basin are maintained, e.g. by coastal defence works. According to the depth dependency of the bottom friction formulation in Eqs. 4–5, the friction coefficients experience a slight decrease. Furthermore, the tidal wave speed will increase slightly as the result of the increased water depth. As before, the amplitudes and phases of the incoming Kelvin waves are assumed to be unaffected. To assess whether this assumption is justified, one would require a larger model domain which is beyond the scope of the present study.

Fig. 8a shows the difference in coastal elevation amplitudes induced by Δh = 1 m. The overall qualitative picture of coastal amplitudes is unaffected. Hardly any changes occur along the UK coast, whereas in the Dover Strait and the eastern part of the domain amplitudes increase up to 8 and 5 cm, respectively.

Fig. 8

Changes in coastal M2-elevation amplitudes, due to sea level rise, as a function of the coastal coordinate. a Line plot for an overall sea level rise of Δh = 1 m, b colour plot for an overall sea level rise in the range 0–2 m. The dashed black line in the colour plot denotes the reference value used in the line plot

To get an impression of the sensitivity around this reference case, the colour plot in Fig. 8b shows the effects of sea level rise in a range of 0 − 2 m. It is seen that the qualitative picture, e.g. the locations where an increase or decrease is obtained, hardly depends on the value of Δh. From a quantitative point of view, the response turns out to be roughly linear in Δh.

5.3 Bed level changes in the Southern Bight

Finally, we investigate the sensitivity of the M2-tide to changes in bed level in the Southern Bight. To this end, we varied the water depth in the Southern Bight uniformly in a range from Δh _SB = − 2 m (depth decrease) to Δh _SB = + 2 m (depth increase). These changes are applied to the compartments 9, 10 and 11 in Fig. 3c and Table 3. The adopted range includes the reference values Δh _SB = ±1 m, which we will discuss separately below. We then perform simulations as described in Section 5.2 for the case of sea level rise.

The results for the reference values are plotted in Fig. 9a, showing changes in coastal M2-elevation amplitudes that are less than 5 cm in magnitude, alternately showing zones of increase and decrease. It is seen that deepening of the Southern Bight produces a curve qualitatively resembling but showing smaller changes than the sea level rise simulation in Fig. 8. Roughly the inverse of this curve is obtained when making the Southern Bight 1 m shallower instead of deeper, suggesting a linear dependency on Δh _SB. The colour plot in Fig. 9b shows the variation around the reference values of ±1 m. Again, the qualitative picture is insensitive to Δh _SB and the quantitative response is roughly linear in Δh _SB.

Fig. 9

Changes in coastal M2-elevation amplitudes, due to a uniform bed level change in the Southern Bight, as a function of the coastal coordinate. a Line plots for a uniform depth increase of Δh _SB = 1 m (black) and a uniform depth decrease of Δh _SB = 1 m (red), b colour plot for a uniform depth change in the range − 2 to + 2 m. The dashed lines in the colour plot denote the reference values used in the line plots

6 Discussion

6.1 Model properties

The solution procedure is quick, a typical North Sea simulation taking less than a second on a personal computer. This allows us to conduct many simulations (as required e.g. in Figs. 4, 5, 8b and 9b). In our simulations to reproduce the tides in the North Sea, we have considered all aspects of basin geometry (dimensions, positioning, depth, latitude) and the friction coefficients as fixed, except for the parameter α. We then used the amplitudes Z ₍N) and Z ₍S) and phases φ ₍N) and φ ₍S) of the incoming Kelvin waves along with the correction factor α as tuning parameters. We remark that the dynamics of the system is effectively controlled by three dimensionless quantities: the correction factor α (assumed the same for all constituents to minimize the degrees of freedom), the amplitude ratio Z ₍S)/Z ₍N) and the phase lag ϕ ₍S) − ϕ ₍N). This is true for amplitudes for which the Z and F values in Table 2 remain representative; such that the friction coefficients r _j in Eq. 4 remain unaffected. The remaining 2 degrees of freedom then merely provide an overall multiplication factor and an overall phase shift, used to improve the agreement with observations.

There is a degree of arbitrariness in choosing the basin geometry, particularly its orientation, the number of compartments as well as their dimensions and relative position. Because of our interest in the Southern Bight, we have chosen the orientation of the Southern Bight. Other simulations, not reported here, show that aligning the geometry with the deeper northern part leads to similar results (although fitting the direction of Dover Strait is somewhat awkward). Alternatively, simulations with fewer compartments, also not reported here, lack the more precise quantitative agreement with observations. The inaccuracies in the basin geometry induce (quantitative) inaccuracies in both the physics and the projection procedure.

On the other hand, increasing the number of compartments does not further improve the agreement, merely increasing the computational time. The absence of lateral depth variations then becomes a crucial limitation. Allowing for a lateral topographic step in each compartment, effectively creating two subcompartments of uniform depths h _j and h _j ′, would improve our representation of bathymetry and, hence, the agreement between model results and observations (especially if additional compartments would be added to represent the Skagerrak). The fundamental wave solutions can then no longer be found fully analytically; a relatively straight-forward search routine for the wave numbers is required (Roos and Schuttelaars 2011). Alternatively, one may also adopt an arbitrary, smooth transverse depth profile in each compartment. However, the transverse structure of the fundamental wave solutions must then be found numerically, which is computationally relatively expensive (de Boer et al 2011).

6.2 Resonance properties

Now let us interpret the resonance properties against the background of previous studies. The two- compartment geometry studied in Section 3.2 (Fig. 3a), consisting of a relatively shallow and narrow bight (j = 2) connected to a deeper and wider compartment (j = 1), can be interpreted as an intermediate geometry between two extremes studied previously in different contexts: a shallow rectangular gulf opening to a deeper semi-infinite ocean (Garrett 1975; Huthnance 1980) and the channel model without width variations and with a longitudinal depth step (Webb 1976; Roos and Schuttelaars 2011). These geometries are approximated by our model in the limits of b ₁/b ₂ → ∞ and b ₁/b ₂ ↓ 1, respectively.

A further complication is encountered by our inclusion of a third compartment representing a strait as a second connection with the ocean (see Section 3.3 and Fig. 3b). Due to the linearity of the problem, the solution can be conveniently written as the superposition of two solutions: one forced at the open boundary of the deep and wide compartment only, the other forced through the strait only. However, since these solutions may locally interfere in a constructive, destructive or neutral manner, the final amplification strongly depends on the relative amplitude and phase of the two types of boundary forcing. The presence of two open boundaries thus complicates the interpretation of resonance mechanisms.

By varying the forcing frequency in the two- and three-compartment model, we identified the following resonance mechanisms:

• Kelvin resonance, i.e. the generalization of the classical quarter wavelength resonance to the case including rotation, radiation damping and bay width (Garrett 1975; Webb 1976; Huthnance 1980; Roos and Schuttelaars 2011).

• Poincaré resonance, i.e. the amplification of cross-bay modes in the shallow and narrow compartment (Huthnance 1980; Roos and Schuttelaars 2011). This mode was not found by (Garrett 1975) due to the narrow-gulf assumption. The cases with an amplified response in the corners of the wide compartment (e.g. the German Bight) show that this type of amplification may also occur in the deep and wide compartment. In our example, this phenomenon is accompanied by a rather weak response in the bight.

After including a strait and separately forcing the system from the north and south, these resonances continue to occur. The response is weaker, particularly in the case of forcing through the strait, and the spatial structure modified. Clearly, the frequency-response curves shown in Fig. 4 are much more complex than those of a rectangular bay or a Helmholtz model.

7 Conclusions

We have developed an idealized process-based model to gain insight in the tidal dynamics of the North Sea. By accounting for bottom friction, changes in depth and width and the presence of two open boundaries, our model extends and combines earlier work (Taylor 1922; Godin 1965; Rienecker and Teubner 1980; Roos and Schuttelaars 2011). The solution method combines a superposition of wave solutions per compartment with a collocation method, thus accounting for no-normal flow at the longitudinal closed boundaries and the matching conditions between adjacent compartments. The resulting model is quick to run and allows inclusion of sufficient level of geometrical detail for a comparison with observations.

First, we studied the general resonance properties of a highly simplified geometry with two compartments, representing the deep and wide Northern North Sea and the shallow and narrow Southern North Sea. By varying the tidal frequency while neglecting bottom friction, we identified both Kelvin and Poincaré resonance. These resonances continue to exist when adding a third compartment that accounts for the Dover Strait and subsequently forcing the system from the North and South only. However, resonance peaks are lower than in the two-compartment case. The response when being simultaneously forced from the North and South, as in the tidal case, strongly depends on the relative amplitude and phase. Incorporating bottom friction further reduces the resonance peaks. Due to the differences in geometry, our findings add to results from earlier studies on basins connected to deeper and in some cases also wider bodies of water (Garrett 1975; Webb 1976; Huthnance 1980; Roos and Schuttelaars 2011).

Next, we adopted a more detailed geometry with 12 compartments fitted to the coastline of the North Sea. Comparison with tide observations along the North Sea coast, i.e. tidal range and phase of the principal semi-diurnal (M2 and S2) and diurnal constituents (K1 and O1), shows good agreement. These results give confidence in applying our idealized model to situations for which no data are available. This leads to the following results:

• The solutions due to the tidal energy coming in from north and south create alternating patterns of constructive and destructive interference along the coast. Closure of Dover Strait would imply significant decreases in M2-tidal range along the German coast.

• Without bottom friction, coastal amplitudes would be larger, particularly in the eastern part of the North Sea (roughly a factor 2 for M2).

• To mimic sea level rise, a simulation with a 1 m increase in water depth, while leaving the horizontal boundaries of the system and the amplitudes/ phases of the incoming Kelvin waves unaffected, leads to an increase in coastal M2-elevation amplitudes up to 8 cm, particularly in the eastern part of the North Sea.

• Bed level variations of ±1 m uniformly applied to the Southern Bight lead to changes in coastal M2-elevation amplitudes of the order of cm, particularly in the Southern Bight itself and in the German Bight.

Appendices

Appendix

A Calculation of friction coefficients

To calculate the friction coefficient F in Eq. 4 for each of the tidal constituents in Table 2, we follow the procedure proposed by (Inoue and Garrett 2007). We consider a (unidirectional) tidal signal with a dominant M2-component and three smaller components (S2, K1 and O1) of relative amplitude ϵ _S2, ϵ _K1 and ϵ _O1, respectively.

The fourth order approximations of the friction coefficients of the dominant M2-component and the weaker S2-component are given by

$$ \begin{array}{rll} F_\mathrm{M2} &=& 1 + \frac{3}{4} \left( \epsilon_\mathrm{S2}^2 +\epsilon_\mathrm{K1}^2+\epsilon_\mathrm{O1}^2 \right) - \frac{3}{64} \left( \epsilon_\mathrm{S2}^4 +\epsilon_\mathrm{K1}^4+\epsilon_\mathrm{O1}^4 \right) \\ &&- \frac{3}{16} \left( \epsilon_\mathrm{S2}^2\epsilon_\mathrm{K1}^2 + \epsilon_\mathrm{S2}^2\epsilon_\mathrm{O1}^2 + \epsilon_\mathrm{K1}^2\epsilon_\mathrm{O1}^2 \right) , \end{array}$$

(13)

$$ \begin{array}{rll} F_\mathrm{S2} &=& \frac{3}{2} \left[ 1 + \frac{1}{4} \left( \frac{\epsilon_\mathrm{S2}^2}{2} + \epsilon_\mathrm{K1}^2 + \epsilon_\mathrm{O1}^2 \right) \right. \\ && \qquad + \frac{1}{64} \left(\frac{\epsilon_\mathrm{S2}^4}{3} + \epsilon_\mathrm{K1}^4 + \epsilon_\mathrm{O1}^4 \right) \\ && \left.\qquad+ \frac{1}{16} \left( \frac{\epsilon_\mathrm{S2}^2\epsilon_\mathrm{K1}^2}{2} + \frac{\epsilon_\mathrm{S2}^2\epsilon_\mathrm{O1}^2}{2} + \epsilon_\mathrm{K1}^2\epsilon_\mathrm{O1}^2 \right) \right] , \end{array} $$

(14)

respectively. (Eq. 13 is given by (Inoue and Garrett 2007); Eq. 14 provides the fourth order terms not specified in their study.)

Note that the dependencies of F _S2 on the terms involving ϵ _S2 differ from the dependencies on terms not involving ϵ _S2. Expressions for F _K1 and F _O1 follow directly from Eq. 14 by interchanging the roles of ϵ _S2, ϵ _K1 and ϵ _O1. Table 2 in the main text shows the ϵ- and F values.

B Wave solutions in a channel of uniform depth

This appendix contains analytical expressions of the wave solutions in an infinitely long channel of uniform width b _j (lateral boundaries at y = 0 and y = b _j ) and uniform depth h _j (with j = 1, 2), including bottom friction:

$$ \left( \begin{array}{c} \eta_{j,m}^\oplus \\ u_{j,m}^\oplus \\ v_{j,m}^\oplus \\ \end{array} \right) = Z^{\prime} \left( \begin{array}{c} \tilde{\eta}_{j,m}^\oplus(y) \\ \tilde{u}_{j,m}^\oplus(y) \\ \tilde{v}^\oplus_{j,m}(y) \end{array} \right) \exp(i[\omega t-k_{j,m}^\oplus x]) , $$

(15)

with amplitude factor Z′ (in m), wave number $k_{j,m}^\oplus$ and lateral structures $\tilde{\eta}_{j,m}^\oplus(y)$, $\tilde{u}_{j,m}^\oplus(y)$ and $\tilde{v}_{j,m}^\oplus(y)$. For the Kelvin mode (m = 0) propagating in the positive x-direction, we obtain

$$ k_{j,0}^\oplus = \gamma_j K_j , $$

(16)

$$ \left( \begin{array}{c} \tilde{\eta}_{j,m}^\oplus(y) \\ \tilde{u}_{j,m}^\oplus(y) \\ \tilde{v}_{j,m}^\oplus(y) \end{array} \right) = \left( \begin{array}{c} 1 \\ \gamma_j^{-1}\sqrt{g/h_j} \\ 0 \end{array} \right) \exp \left( \frac{-y}{\gamma_j R_j} \right), $$

(17)

respectively. Here, we have used the reference wave number K _j , the Rossby deformation radius R _j (both typical for a classical Kelvin wave without friction) and a frictional correction factor, given by

$$ K_j = \frac{\omega}{\sqrt{gh_j}} , \qquad R_j = \frac{\sqrt{gh_j}}{f} , \qquad \gamma_j = \sqrt{ 1 - \frac{ir_j}{\omega h_j} } , $$

(18)

respectively.

The wave number and lateral structures of the mth Poincaré mode (m > 0) propagating (if free) or decaying (if evanescent) in the positive x-direction are given by

$$ k_{j,m}^\oplus = \sqrt{ \gamma_j^2K_j^2 - \gamma_j^{-2}R_j^{-2} - \beta_m^2 } , $$

(19)

$$ \tilde{\eta}_{j,m}^\oplus(y) = \cos(\beta_m y) - \frac{fk_{j,m}^\oplus}{\beta_m\gamma_j^2\omega}\sin(\beta_m y) , $$

(20)

$$ \tilde{u}_{j,m}^\oplus(y) = \frac{gk_{j,m}^\oplus}{\gamma_j^2\omega}\cos(\beta_m y) - \frac{f}{\beta_m\gamma_j^2h_j} \sin(\beta_m y) , $$

(21)

$$ \tilde{\nu}_{j,m}^\oplus(y) = \frac{-i\omega}{\beta_m\gamma_j^2h_j} \left[ \gamma_j^2 - \frac{k_{j,m}^{\oplus2}}{K_j^2} \right] \sin(\beta_m y) , $$

(22)

respectively, with β _m  = mπ/b _j .

The modes propagating or decaying in the negative x-direction are defined analogous to Eq. 15, but now using a superscript ^⊝ instead of a superscript ^⊕. By symmetry, the two type of modes $\tilde{\phi}_{j,m}^\oplus$ and $\tilde{\phi}_{j,m}^\ominus$ satisfy the following relationships:

$$ \tilde{\phi}_{j,m}^\ominus(y) = \left( \begin{array}{c} \tilde{\eta}_{j,m}^\oplus(b_j-y) \\ -\tilde{u}_{j,m}^\oplus(b_j-y) \\ -\tilde{v}_{j,m}^\oplus(b_j-y) \\ \end{array} \right) , \qquad k_{j,m}^\ominus = -k_{j,m}^\oplus . $$

(23)

Finally, dealing with the lateral displacements of the compartments relative to one another requires suitable translations of the y-coordinate in the above solutions.