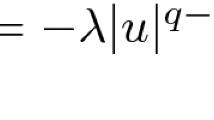A multiplicity result for a (p, q)-Schrödinger–Kirchhoff type equation

Abstract

In this paper, we study a class of (p, q)-Schrödinger–Kirchhoff type equations involving a continuous positive potential satisfying del Pino–Felmer type conditions and a continuous nonlinearity with subcritical growth at infinity. By applying variational methods, penalization techniques and Lusternik–Schnirelman category theory, we relate the number of positive solutions with the topology of the set where the potential attains its minimum values.

1 Introduction

1.1 Background and motivations

In this paper, we consider the following class of (p, q)-Schrödinger–Kirchhoff type problems:

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle -\left( 1+a \int _{{\mathbb {R}}^{N}}|\nabla u|^{p}\, {\text {d}}x\right) \Delta _{p}u-\left( 1+b \int _{{\mathbb {R}}^{N}}|\nabla u|^{q}\, {\text {d}}x\right) \Delta _{q}u + V(\varepsilon x) (u^{p-1} + u^{q-1})= f(u) {\text { in }} {\mathbb {R}}^{N}, \\ u\in W^{1, p}({\mathbb {R}}^{N})\cap W^{1,q}({\mathbb {R}}^{N}), \quad u>0 {\text { in }} {\mathbb {R}}^{N}, \end{array} \right. \end{aligned}$$

(1)

where $\varepsilon >0$ is a small parameter, $a, b>0$, $1< p<q<N<2q$, $\Delta _{r}u={{\,\mathrm{div}\,}}(|\nabla u|^{r-2}\nabla u)$, with $r\in \{p, q\}$, is the r-Laplacian operator, the potential $V:{\mathbb {R}}^{N}\rightarrow {\mathbb {R}}$ and the nonlinearity $f:{\mathbb {R}}\rightarrow {\mathbb {R}}$ are continuous functions.

When $a=b=0$, the equation in (1) becomes a (p, q)-Schrödinger equation of the form

$$\begin{aligned} \displaystyle -\Delta _{p}u-\Delta _{q}u + V(x) (u^{p-1} + u^{q-1})= f(x, u)\quad {\text { in }} {\mathbb {R}}^{N}, \end{aligned}$$

(2)

whose study is motivated by the general reaction diffusion system

$$\begin{aligned} u_{t}= {{\,\mathrm{div}\,}}[D(u) \nabla u] + c(x, u) \end{aligned}$$

where $D(u)= |\nabla u|^{p-2} + |\nabla u|^{q-2}$. This system has a wide range of applications in physics and related sciences such as biophysics, plasma physics and chemical reaction design. In these applications, the function u describes a concentration; the first term on the right-hand side of (2) corresponds to the diffusion with a diffusion coefficient Du, whereas the second one is the reaction and relates to source and loss processes. Typically, in chemical and biological applications, the reaction term c(x, u) has a polynomial form with respect to the concentration u; see [14] for more details about the applications.

We point out that several existence, multiplicity and regularity results for (2) have been established in these last years by several authors. In [28], the authors established some regularity results for (2). By combining concentration-compactness principle and mountain pass theorem, an existence result has been obtained in [29]. The author in [22] proved the existence of a ground-state positive solution for a (p, q)-Schrödinger equation with critical growth. The multiplicity and concentration of nontrivial solutions for (2) have been established in [3]. The authors in [39] combined refined variational methods based on critical point theory with Morse theory and truncation techniques to obtain a multiplicity result for a (p, q)-Laplacian problem in bounded domains. For other interesting results, one can consult [2, 7, 8, 34, 40, 44] and references therein.

When $p=q$, (2) boils down a p-Schrödinger equation of the type

$$\begin{aligned} -\Delta _{p} u + V(x) u^{p-1}= f(x, u)\quad {\text { in }} {\mathbb {R}}^{N}, \end{aligned}$$

(3)

for which different and interesting results have been obtained in the literature; see for instance [3, 4, 19, 23, 52]. Note that, in the case $p=q=2$, Eq. (3) reduces to the well-known Schrödinger equation which has been widely studied in the last three decades; see for example [18, 25, 43, 48, 50].

When $a=b\ne 0$, $p=q=2$ and $N=3$, problem (1) becomes a Kirchhoff equation of the form

$$\begin{aligned} -\left( 1+a \int _{{\mathbb {R}}^{3}} |\nabla u|^{2} \, {\text {d}}x\right) \Delta u + V(x) u = f(x, u) \quad {\text { in }} {\mathbb {R}}^{3}. \end{aligned}$$

(4)

Equation (4) is related to the stationary analog of the Kirchhoff equation [32]

$$\begin{aligned} u_{tt}- \left( \alpha +\beta \int _{\Omega } |\nabla u|^{2}\, {\text {d}}x \right) \Delta u = f(x, u) \quad {\text { in }} \Omega , \end{aligned}$$

where $\Omega \subset {\mathbb {R}}^{N}$ is a smooth bounded domain, $\alpha >0$, $\beta \ge 0$, and u satisfies some boundary conditions, which was proposed by Kirchhoff in 1883 as a nonlinear extension of D’Alembert’s wave equation for free vibration of elastic strings

$$\begin{aligned} \rho u_{tt} - \left( \frac{p_{0}}{h} + \frac{E}{2L} \int _{0}^{L} \left| u_{x}\right| ^{2} {\text {d}}x \right) u_{xx} =0. \end{aligned}$$

(5)

Here, $u=u(x, t)$ is the transverse string displacement at the space coordinate x and the time t, L is the length of the string, h is the area of the cross section, E is the Young’s modulus of the material, $\rho$ is the mass density and $p_{0}$ is the initial axial tension.

From a purely mathematical point of view, it is important to mention that the early studies dedicated to the Kirchhoff equation (5) were given by Bernstein [10] and Pohozaev [42]. However, the Kirchhoff equation (5) began to attract the attention of more researchers only after the paper by Lions [36], in which a functional analysis approach was proposed to attack it. For some interesting results on Kirchhoff problems, we refer to [13, 24, 30, 41, 49].

Finally, if $a=b \ne 0$, $p=q>1$ and $N=3$ in (1), we have the following p-Laplacian Kirchhoff type equation

$$\begin{aligned} -\left( 1+a \int _{{\mathbb {R}}^{3}} |\nabla u|^{p} \, {\text {d}}x\right) \Delta _{p} u + V(x) |u|^{p-2}u = f(x, u) \quad {\text { in }} {\mathbb {R}}^{3}, \end{aligned}$$

(6)

which has been investigated in several works; see for instance [15, 16, 27, 35, 51].

Due to the interest shared by the mathematical community toward quasilinear problems and Kirchhoff type equations, in [12, 31], the authors studied Kirchhoff type equations involving the (p, q)-Laplacian operator with $p\ne q$, in a bounded domain and in the whole of ${\mathbb {R}}^3$, respectively.

Motivated by the above works, the purpose of this paper is to study the multiplicity and the concentration of solutions for (1).

1.2 Assumptions and main result

For simplicity, we assume that $a=b=1$ in (1). Let us now introduce the hypotheses on the potential V and the nonlinearity f that we are going to consider throughout the paper.

Let $V:{\mathbb {R}}^{N}\rightarrow {\mathbb {R}}$ be a continuous function that satisfies the following assumptions due to del Pino–Felmer [18]:

$(V_1)$:

there exists $V_{0}>0$ such that $\displaystyle {V_{0}=\inf _{x\in {\mathbb {R}}^{N}} V(x)}$;

$(V_2)$:

there exists an open bounded set $\Lambda \subset {\mathbb {R}}^{N}$ such that

$$\begin{aligned} V_{0}< \min _{\partial \Lambda } V \quad {\text { and }} \quad 0\in M=\{x\in \Lambda : V(x)=V_{0}\}. \end{aligned}$$

Assume that $f: {\mathbb {R}}\rightarrow {\mathbb {R}}$ is a continuous function such that $f(t)=0$ for $t\le 0$ and fulfills the following hypotheses:

$(f_{1})$:

$\displaystyle {\lim _{|t|\rightarrow 0} \frac{|f(t)|}{|t|^{2p-1}}=0}$;

$(f_{2})$:

there exists $\nu \in (2q, q^{*})$ such that $\displaystyle {\lim _{|t|\rightarrow \infty } \frac{|f(t)|}{|t|^{\nu -1}}=0}$, where $q^{*}= \frac{Nq}{N-q}$;

$(f_{3})$:

there exists $\mu \in (2q, \nu )$ such that $\displaystyle {0<\mu F(t)= \mu \int _{0}^{t} f(\tau ) \, {\text {d}}\tau \le t f(t)}$ for all $t>0$;

$(f_{4})$:

the map $t\mapsto \displaystyle {\frac{f(t)}{t^{2q-1}}}$ is increasing for $t>0$.

In order to give the precise statement of our main theorem, let us recall that, for any closed subset Y of a topological space X, the Lusternik–Schnirelman category of Y in X, $cat_{X}(Y)$, stands for the least number of closed and contractible sets in X which cover Y; see [50]. Then, we can state the following result.

Theorem 1

Let V satisfy $(V_{1})$ and $(V_{2})$, and let f be a continuous function such that the hypotheses $(f_{0})$–$(f_{4})$ hold. Then, for any $\delta >0$ such that

$$\begin{aligned} M_{\delta }=\left\{ x\in {\mathbb {R}}^{N}: {\text{dist}}(x, M)\le \delta \right\} \subset \Lambda , \end{aligned}$$

there exists $\varepsilon _{\delta }>0$ such that, for any $\varepsilon \in (0, \varepsilon _{\delta })$, problem (1) has at least $cat_{M_{\delta }}(M)$ positive solutions. Moreover, if $u_{\varepsilon }$ denotes one of these solutions and $x_{\varepsilon }\in {\mathbb {R}}^{N}$ is a global maximum point of $u_{\varepsilon }$, then

$$\begin{aligned} \lim _{\varepsilon \rightarrow 0} V(\varepsilon x_{\varepsilon })=V_{0}. \end{aligned}$$

1.3 Main difficulties and ideas

Due to the lack of information about the behavior of the potential V at infinity and the fact that our problem is set in an unbounded domain, we adapt the local mountain pass argument introduced by del Pino and Felmer [18]. It consists in making a suitable modification on f, solving a modified problem, whose corresponding energy functional has a nice geometric structure, and then checking that, for $\varepsilon >0$ small enough, the solutions of the new problem are indeed solutions of the original one. We note that, because of the presence of the (p, q)-Laplacian operators and Kirchhoff terms, even for the corresponding modified energy functional, it is hard to obtain compactness, and an accurate analysis will be done to prove a first existence result for the modified problem; see Lemmas 5, 6 and 7. Secondly, we make use of a technique given by Benci and Cerami [9] to establish a relationship between the category of the set M and the number of solutions for the modified problem. We underline that, since f is merely continuous, standard ${\mathcal {C}}^{1}$-Nehari manifold arguments as in [2,3,4,5, 30, 50] do not work in our setting, and so we take advantage of some abstract results due to Szulkin and Weth [46]. Note that, this type of approach has been also used in [24] where a Schrödinger–Kirchhoff elliptic equation was considered. Clearly, with respect to [24], a more careful analysis will be needed and some refined estimates will be used to overcome some technical difficulties. Finally, to obtain a uniform $L^{\infty }$-estimate for an appropriate translated sequence of solutions to the modified problem, we do not use the classical Moser iteration argument [38] as in [3, 19, 23, 24, 30], because such technique does not seem to work well in our situation, but we follow some arguments found in [2, 21, 26, 33] which are inspired by the well-known method pioneered by De Giorgi [17]; see Lemma 15.

As far as we know, all results presented in this work are new in the literature. Moreover, we believe that the ideas developed here can be applied in other situation to study (p, q)-Schrödinger–Kirchhoff type problems involving potentials satisfying local conditions and continuous nonlinearities.

The outline of the paper is the following. In Sect. 2, we introduce the modified problem. Section 3 is devoted to the study of the autonomous problem associated with (1). In Sect. 4, we prove a multiplicity result for the modified problem. The proof of Theorem 1 is given in Sect. 5.

2 The modified problem

2.1 Notations and preliminary results

In order to simplify the presentation, we denote by C a generic positive constant, which may change from line to line, but does not depend on crucial quantities. Let A be a measurable subset of ${\mathbb {R}}^{N}$. By $A^{c},$ we denote the complement of A. Let $1\le r\le \infty$. We will use the notation $|\cdot |_{L^{r}(A)}$ for the norm in $L^{r}(A)$, and when $A={\mathbb {R}}^{N},$ we simply write $|\cdot |_{r}$. By ${\mathcal {B}}_{r}(x_{0}),$ we indicate the open ball in ${\mathbb {R}}^{N}$ centered at $x_{0}\in {\mathbb {R}}^{N}$ and radius $r>0$. In the case $x_{0}=0,$ we simply write ${\mathcal {B}}_{r}$.

Let $1<r<\infty$ and $N>r$. By ${\mathcal {D}}^{1, r}({\mathbb {R}}^{N}),$ we mean the closure of ${\mathcal {C}}^{\infty }_{c}({\mathbb {R}}^{N})$ functions with respect to the norm

$$\begin{aligned} |\nabla u|_{r}^{r}= \int _{{\mathbb {R}}^{N}} |\nabla u|^{r} {\text {d}}x. \end{aligned}$$

By $W^{1, r}({\mathbb {R}}^{N}),$ we denote the Sobolev space equipped with the norm

$$\begin{aligned} \Vert u\Vert _{W^{1,r}({\mathbb {R}}^{N})}=\left( |u|^{r}_{r}+|\nabla u|^{r}_{r} \right) ^{\frac{1}{r}}. \end{aligned}$$

The following embeddings are well known.

Theorem 2

[1] Let $p\in (1, \infty )$ and $N>p$. Then, there exists a constant $S_{*}>0$ such that, for any $u\in {\mathcal {D}}^{1, p}({\mathbb {R}}^{N})$,

$$\begin{aligned} |u|^{p}_{p^{*}} \le S_{*}^{-1} |\nabla u|^{p}_{p}. \end{aligned}$$

Moreover, $W^{1, p}({\mathbb {R}}^{N})$ is continuously embedded in $L^{t}({\mathbb {R}}^{N})$ for any $t\in [p, p^{*}]$ and compactly in $L^{t}({\mathcal {B}}_{R})$, for all $R>0$ and any $t\in [1, p^{*})$.

For the reader’s convenience, we also recall the following vanishing lemma.

Lemma 1

[37] Let $p\in (1, \infty )$, $N>p$ and $r\in [p, p^{*})$. If $\{u_{n}\}_{n\in {\mathbb {N}}}$ is a bounded sequence in $W^{1, p}({\mathbb {R}}^{N})$ and if

$$\begin{aligned} \lim _{n\rightarrow \infty } \sup _{y\in {\mathbb {R}}^{N}} \int _{{\mathcal {B}}_{R}(y)} |u_{n}|^{r} {\text {d}}x=0, \end{aligned}$$

where $R>0$, then $u_{n}\rightarrow 0$ in $L^{t}({\mathbb {R}}^{N})$ for all $t\in (p, p^{*})$.

Let $p, q\in (1, \infty )$ and set

$$\begin{aligned} {W}^{p, q}=W^{1, p}({\mathbb {R}}^{N})\cap W^{1, q}({\mathbb {R}}^{N}) \end{aligned}$$

endowed with the norm

$$\begin{aligned} \Vert u\Vert _{{W}^{p, q}}=\Vert u\Vert _{W^{1,p}({\mathbb {R}}^{N})}+\Vert u\Vert _{W^{1,q}({\mathbb {R}}^{N})}. \end{aligned}$$

For any $\varepsilon >0$, we introduce the space

$$\begin{aligned} {\mathbb {W}}_{\varepsilon }=\left\{ u\in {W}^{p, q}: \int _{{\mathbb {R}}^{N}} V(\varepsilon x) \left( |u|^{p}+|u|^{q}\right) \,{\text {d}}x<\infty \right\} \end{aligned}$$

endowed with the norm

$$\begin{aligned} \Vert u\Vert _{{\mathbb {W}}_{\varepsilon }}= \Vert u\Vert _{V_{\varepsilon }, p} + \Vert u\Vert _{V_{\varepsilon }, q}, \end{aligned}$$

where

$$\begin{aligned} \Vert u\Vert _{V_{\varepsilon }, r}= \left( |\nabla u|_{r}^{r} + \int _{{\mathbb {R}}^{N}} V(\varepsilon x) |u|^{r}\, {\text {d}}x\right) ^{\frac{1}{r}} \quad {\text { for all }} r\in (1, \infty ). \end{aligned}$$

Finally, we recall the following well-known elementary inequalities [45] which will be used in the sequel: for any $\xi , \eta \in {\mathbb {R}}^{N},$ we have

$$\begin{aligned}&(|\xi |^{r-2}\xi - |\eta |^{r-2}\eta ) \cdot (\xi - \eta ) \ge c_{1} |\xi -\eta |^{r} \quad {\text { for }} r\ge 2, \end{aligned}$$

(7)

$$\begin{aligned}&( |\xi |^{r-2}\xi - |\eta |^{r-2}\eta )\cdot (\xi - \eta ) \ge c_{2} \frac{|\xi -\eta |^{2}}{(|\xi |+ |\eta |)^{2-r}} \quad {\text { for }} 1<r<2, \end{aligned}$$

(8)

for some $c_{1}, c_{2}>0$ constants. In particular,

$$\begin{aligned} (|\xi |^{r-2}\xi - |\eta |^{r-2}\eta ) \cdot (\xi - \eta )>0\quad {\text { for all }}\xi \ne \eta . \end{aligned}$$

(9)

Note that, when $1<r<2$ using (8) and the following elementary inequality

$$\begin{aligned} ( |\xi | + |\eta |)^{r} \le 2^{r-1} (|\xi |^{r} + |\eta |^{r}) \quad {\text { for all }} \xi ,\eta \in {\mathbb {R}}^{N}, \end{aligned}$$

we deduce that there exists $c_{3}>0$ such that for any $\xi , \eta \in {\mathbb {R}}^{N},$ the following relation satisfies

$$\begin{aligned} {[} ( |\xi |^{r-2}\xi - |\eta |^{r-2}\eta )\cdot (\xi - \eta ) ]^{\frac{r}{2}} \ge c_{3} \frac{|\xi -\eta |^{r}}{(|\xi |^{r}+ |\eta |^{r})^{\frac{2-r}{2}}} \quad {\text { for }} 1<r<2. \end{aligned}$$

(10)

2.2 The penalization approach

To deal with (1), we use a del Pino–Felmer penalization type approach [18]. Firstly, we note that the map $t\mapsto \frac{f(t)}{t^{p-1}+t^{q-1}}$ is increasing in $(0, \infty )$. Indeed, once we write

$$\begin{aligned} \frac{f(t)}{t^{p-1}+t^{q-1}}=\frac{f(t)}{t^{2q-1}} \frac{t^{2q-1}}{t^{p-1}+t^{q-1}} \end{aligned}$$

then, by $(f_{4}),$ we know that $t\mapsto \frac{f(t)}{t^{2q-1}}$ is increasing in $(0, \infty )$, and since $2q>p,$ we deduce that $t\mapsto \frac{t^{2q-1}}{t^{p-1}+t^{q-1}}$ is increasing in $(0, \infty )$.

Take

$$\begin{aligned} {{K}}>\frac{q}{p}\left( \frac{\mu -p}{\mu -q}\right) >1, \end{aligned}$$

and let $a>0$ be such that

$$\begin{aligned} f(a)=\frac{V_{0}}{{K}}(a^{p-1}+a^{q-1}). \end{aligned}$$

Consider the function ${\tilde{f}}: {\mathbb {R}}\rightarrow {\mathbb {R}}$ given by

$$\begin{aligned} {\tilde{f}}(t)=\left\{ \begin{array}{ll} f(t) &{}{\text { if }} t\le a,\\ \displaystyle \frac{V_{0}}{{K}} (t^{p-1}+t^{q-1}) &{}{\text { if }} t>a. \end{array} \right. \end{aligned}$$

Denote by $\chi _{A}$ the characteristic function of $A\subset {\mathbb {R}}^{N}$, and define the function $g: {\mathbb {R}}^{N}\times {\mathbb {R}}\rightarrow {\mathbb {R}}$ as

$$\begin{aligned} g(x, t)= \left\{ \begin{array}{ll} \chi _{\Lambda }(x)f(t)+(1-\chi _{\Lambda }(x)){\tilde{f}}(t) &{}{\text { if }} t>0, \\ 0 &{}{\text { if }} t\le 0. \end{array} \right. \end{aligned}$$

Using the hypotheses on f, we infer that g is a Carathéodory function such that

$(g_1)$:

$\displaystyle \lim _{t\rightarrow 0} \frac{g(x,t)}{t^{2p-1}}=0$ uniformly with respect to $x\in {\mathbb {R}}^{N}$,

$(g_2)$:

$g(x,t)\le f(t)$ for all $x\in {\mathbb {R}}^{N}$ and $t>0$,

$(g_3)$:

(i) $\displaystyle 0< \mu G(x,t) \le g(x,t)t$ for all $x\in \Lambda$ and $t>0$, where $\displaystyle G(x, t)= \int _{0}^{t} g(x, \tau )\, {\text {d}}\tau$,

(ii) $\displaystyle 0\le pG(x,t) \le g(x,t)t\le \frac{V_{0}}{{\mathrm{K}}} (t^{p}+t^{q})$ for all $x\in \Lambda ^{c}$ and $t>0$,

$(g_4)$:

for each $x\in \Lambda,$ the function $t\mapsto \displaystyle \frac{g(x,t)}{(t^{p-1}+t^{q-1})}$ is increasing in $(0, \infty )$, and for each $x\in \Lambda ^{c},$ the function $t\mapsto \displaystyle \frac{g(x,t)}{(t^{p-1}+t^{q-1})}$ is increasing in (0, a).

We point that, from $(g_{1})$, $(g_{2})$, $(f_{1})$ and $(f_{2})$, for any $\zeta >0,$ there exists $C_{\zeta }>0$ such that

$$\begin{aligned} |g(x, t)|\le \zeta |t|^{p-1}+ C_{\zeta }|t|^{\nu -1} \quad {\text { for all }} (x,t)\in {\mathbb {R}}^{N}\times {\mathbb {R}}. \end{aligned}$$

(11)

Let us introduce the following auxiliary problem:

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle -\left( 1+\int _{{\mathbb {R}}^{N}}|\nabla u|^{p}\, {\text {d}}x\right) \Delta _{p}u-\left( 1+\int _{{\mathbb {R}}^{N}}|\nabla u|^{q}\, {\text {d}}x\right) \Delta _{q}u+V(\varepsilon x)(u^{p-1}+u^{q-1})=g(\varepsilon x, u) {\text { in }} {\mathbb {R}}^{N}, \\ u\in {W}^{p, q}, \quad u>0 {\text { in }} {\mathbb {R}}^{N}. \end{array} \right. \end{aligned}$$

(12)

Define the set $\Lambda _{\varepsilon }=\{x\in {\mathbb {R}}^{N} \, : \, \varepsilon x\in \Lambda \}$. We underline that if $u_{\varepsilon }$ is a solution to (12) satisfying $u_{\varepsilon }(x)\le a$ for all $x\in \Lambda _{\varepsilon }^{c}$, then $u_{\varepsilon }$ is also a solution to (1).

Let us introduce the functional ${L}_{\varepsilon }: {\mathbb {W}}_{\varepsilon }\rightarrow {\mathbb {R}}$ associated with (12), that is

$$\begin{aligned} {L}_{\varepsilon }(u)= \frac{1}{p}\Vert u\Vert _{V_{\varepsilon },p}^{p}+\frac{1}{2p}|\nabla u|^{2p}_{p}+\frac{1}{q}\Vert u\Vert _{V_{\varepsilon },q}^{q}+\frac{1}{2q}|\nabla u|^{2q}_{q}-\int _{{\mathbb {R}}^{N}} G(\varepsilon x, u)\, {\text {d}}x. \end{aligned}$$

We note that ${L}_{\varepsilon }\in {\mathcal {C}}^{1}({\mathbb {W}}_{\varepsilon }, {\mathbb {R}})$ and

$$\begin{aligned} \langle {L}'_{\varepsilon }(u), \varphi \rangle&=(1+|\nabla u|_{p}^{p})\int _{{\mathbb {R}}^{N}} |\nabla u|^{p-2}\nabla u\cdot \nabla \varphi \, {\text {d}}x+(1+|\nabla u|_{q}^{q})\int _{{\mathbb {R}}^{N}} |\nabla u|^{q-2}\nabla u\cdot \nabla \varphi \, {\text {d}}x\\&\quad +\int _{{\mathbb {R}}^{N}}V(\varepsilon x) |u|^{p-2}u\,\varphi \, {\text {d}}x+ \int _{{\mathbb {R}}^{N}} V(\varepsilon x)|u|^{q-2}u\,\varphi \, {\text {d}}x - \int _{{\mathbb {R}}^{N}} g(\varepsilon x, u)\varphi \, {\text {d}}x \end{aligned}$$

for any $u, \varphi \in {\mathbb {W}}_{\varepsilon }$.

The Nehari manifold associated with ${L}_{\varepsilon }$ is given by

$$\begin{aligned} {\mathcal {N}}_{\varepsilon }=\left\{ u\in {\mathbb {W}}_{\varepsilon }: \langle {L}'_{\varepsilon }(u), u\rangle =0 \right\} , \end{aligned}$$

and let

$$\begin{aligned} c_{\varepsilon }=\inf _{u\in {\mathcal {N}}_{\varepsilon }} {L}_{\varepsilon }(u). \end{aligned}$$

Let ${\mathbb {S}}_{\varepsilon }=\left\{ u\in {\mathbb {W}}_{\varepsilon }: \Vert u\Vert _{{\mathbb {W}}_{\varepsilon }}=1 \right\}$ be the unit sphere in ${\mathbb {W}}_{\varepsilon }$, and set ${\mathbb {S}}_{\varepsilon }^{+}={\mathbb {S}}_{\varepsilon }\cap {\mathbb {W}}_{\varepsilon }^{+}$, where ${\mathbb {W}}_{\varepsilon }^{+}$ stands for the open set

$$\begin{aligned} {\mathbb {W}}_{\varepsilon }^{+}=\{u\in {\mathbb {W}}_{\varepsilon }: |\mathrm{supp}(u^{+})\cap \Lambda _{\varepsilon }|>0\}. \end{aligned}$$

Note that, ${\mathbb {S}}_{\varepsilon }^{+}$ is an incomplete ${\mathcal {C}}^{1,1}$-manifold of codimension one. Hence, for all $u\in {\mathbb {S}}_{\varepsilon }^{+}$, ${\mathbb {W}}_{\varepsilon }=T_{u}{\mathbb {S}}_{\varepsilon }^{+}\oplus {\mathbb {R}}u$, where

$$\begin{aligned} T_{u}{\mathbb {S}}_{\varepsilon }^{+}&=\left\{ v\in {\mathbb {W}}_{\varepsilon }: (1+|\nabla u|_{p}^{p})\int _{{\mathbb {R}}^{N}} |\nabla u|^{p-2} \nabla u \cdot \nabla v\, {\text {d}}x\right. \\&\quad +(1+|\nabla u|_{q}^{q})\int _{{\mathbb {R}}^{N}} |\nabla u|^{q-2} \nabla u \cdot \nabla v\, {\text {d}}x \\&\quad \left. +\int _{{\mathbb {R}}^{N}} V(\varepsilon x)(|u|^{p-2}uv+|u|^{q-2}uv) \, {\text {d}}x=0 \right\} . \end{aligned}$$

First, we show that ${L}_{\varepsilon }$ has a mountain pass geometry [6].

Lemma 2

The functional ${L}_{\varepsilon }$ has the following properties:

• (i) There exist $\alpha , \rho >0$ such that ${L}_{\varepsilon }(u) \ge \alpha$ for $\Vert u\Vert _{{\mathbb {W}}_{\varepsilon }}= \rho$.

• (ii) There exists $e\in {\mathbb {W}}_{\varepsilon }$ with $\Vert e\Vert _{{\mathbb {W}}_{\varepsilon }}>\rho$ and ${L}_{\varepsilon }(e)<0$.

Proof

(i) Fix $\zeta \in (0, V_{0})$. From (11), we have

$$\begin{aligned} {L}_{\varepsilon }(u)\ge C_{1} \Vert u\Vert _{V_{\varepsilon }, p}^{p} + \frac{1}{q} \Vert u\Vert _{V_{\varepsilon }, q}^{q} - \frac{C_{\zeta }}{\nu } |u|_{\nu }^{\nu }. \end{aligned}$$

Choosing $\Vert u\Vert _{{\mathbb {W}}_{\varepsilon }}=\rho \in (0, 1)$ and using $1<p<q$, we have $\Vert u\Vert _{V_{\varepsilon },p}<1$ and thus $\Vert u\Vert ^{p}_{V_{\varepsilon },p}\ge \Vert u\Vert ^{q}_{V_{\varepsilon },p}$. Recalling that

$$\begin{aligned} a^{t}+b^{t}\ge C_{t} (a+b)^{t} \quad {\text { for all }} a, b\ge 0, t>1, \end{aligned}$$

and using Theorem 2, we find

$$\begin{aligned} {L}_{\varepsilon }(u)\ge C_{2} \Vert u\Vert ^{q}_{{\mathbb {W}}_{\varepsilon }}-\frac{C_{\zeta }}{\nu } |u|_{\nu }^{\nu }\ge C_{2} \Vert u\Vert ^{q}_{{\mathbb {W}}_{\varepsilon }}-C_{3} \Vert u\Vert _{{\mathbb {W}}_{\varepsilon }}^{\nu }. \end{aligned}$$

Since $\nu >q$, there exists $\alpha >0$ such that ${L}_{\varepsilon }(u)\ge \alpha$ for $\Vert u\Vert _{{\mathbb {W}}_{\varepsilon }}= \rho$.

(ii) By $(f_{3}),$ we deduce that

$$\begin{aligned} F(t)\ge A t^{\mu }-B \quad {\text { for all }} t>0. \end{aligned}$$

Then, for all $u\in {\mathbb {W}}^{+}_{\varepsilon }$ and $t>0$, we have

$$\begin{aligned} {L}_{\varepsilon }(t u)&\le \frac{t^{p}}{p} \Vert u\Vert _{\varepsilon ,p}^{p} +\frac{t^{2p}}{2p}|\nabla u|_{p}^{2p}+\frac{t^{q}}{q} \Vert u\Vert _{\varepsilon ,q}^{q}+\frac{t^{2q}}{2q}|\nabla u|_{q}^{2q}\\&\quad - A t^{\mu } \int _{\Lambda _{\varepsilon }} (u^{+})^{\mu } \, {\text {d}}x +B|\mathrm{supp}(u^{+})\cap \Lambda _{\varepsilon }|, \end{aligned}$$

and observing that $\mu>2q>2p$ we deduce that ${L}_{\varepsilon }(tu) \rightarrow -\infty$ as $t\rightarrow \infty$. $\square$

In order to overcome the non-differentiability of ${\mathcal {N}}_{\varepsilon }$ and the incompleteness of ${\mathbb {S}}_{\varepsilon }^{+}$, we prove the following results.

Lemma 3

Under the assumptions $(V_1)$–$(V_2)$ and $(f_1)$–$(f_4)$, the following properties hold:

• (i) For each $u\in {\mathbb {W}}_{\varepsilon }^{+}$, there exists a unique $t_{u}>0$ such that if $\alpha _{u}(t)={L}_{\varepsilon }(tu)$, then $\alpha '_{u}(t)>0$ for $0<t<t_{u}$ and $\alpha '_{u}(t)<0$ for $t>t_{u}$.

• (ii) There exists $\tau >0$ independent of u such that $t_{u}\ge \tau$ for any $u\in {\mathbb {S}}_{\varepsilon }^{+}$ and for each compact set ${\mathcal {W}}\subset {\mathbb {S}}_{\varepsilon }^{+}$, there is a positive constant $C_{{\mathcal {W}}}$ such that $t_{u}\le C_{{\mathcal {W}}}$ for any $u\in {\mathcal {W}}$.

• (iii) The map ${\hat{m}}_{\varepsilon }: {\mathbb {W}}_{\varepsilon }^{+}\rightarrow {\mathcal {N}}_{\varepsilon }$ given by ${\hat{m}}_{\varepsilon }(u)= t_{u}u$ is continuous and $m_{\varepsilon }= {\hat{m}}_{\varepsilon }|_{{\mathbb {S}}_{\varepsilon }^{+}}$ is a homeomorphism between ${\mathbb {S}}_{\varepsilon }^{+}$ and ${\mathcal {N}}_{\varepsilon }$. Moreover, $m_{\varepsilon }^{-1}(u)=\frac{u}{\Vert u\Vert _{{\mathbb {W}}_{\varepsilon }}}$.

• (iv) If there is a sequence $\{u_{n}\}_{n\in {\mathbb {N}}}\subset {\mathbb {S}}_{\varepsilon }^{+}$ such that ${\mathrm{dist}}(u_{n}, \partial {\mathbb {S}}_{\varepsilon }^{+})\rightarrow 0,$ then $\Vert m_{\varepsilon }(u_{n})\Vert _{{\mathbb {W}}_{\varepsilon }}\rightarrow \infty$ and ${L}_{\varepsilon }(m_{\varepsilon }(u_{n}))\rightarrow \infty$.

Proof

(i) Similar to the proof of Lemma 2, we can see that $\alpha _{u}(0)=0$, $\alpha _{u}(t)>0$ for $t>0$ small enough and $\alpha _{u}(t)<0$ for $t>0$ sufficiently large. Then, there exists a global maximum point $t_{u}>0$ for $\alpha _{u}$ in $[0, \infty )$ such that $\alpha _{u}'(t_{u})=0$ and $t_{u}u \in {\mathcal {N}}_{\varepsilon }$. We claim that $t_{u}>0$ is unique. We argue by contradiction and suppose that there exist $t_{1}> t_{2}>0$ such that $\alpha _{u}'(t_{1})=\alpha _{u}'(t_{2})=0$. Therefore,

$$\begin{aligned} \frac{\Vert u\Vert ^{p}_{V_{\varepsilon },p}}{t_{1}^{2q-p}}+\frac{\Vert u\Vert _{V_{\varepsilon },q}^{q}}{t_{1}^{q}}+\frac{|\nabla u|_{p}^{2p}}{t_{1}^{2q-2p}}+|\nabla u|_{q}^{2q}=\int _{{\mathbb {R}}^{N}} \frac{g(\varepsilon x, t_{1}u)}{(t_{1}u)^{2q-1}} u^{2q} {\text {d}}x, \end{aligned}$$

and

$$\begin{aligned} \frac{\Vert u\Vert ^{p}_{V_{\varepsilon },p}}{t_{2}^{2q-p}}+\frac{\Vert u\Vert _{V_{\varepsilon },q}^{q}}{t_{2}^{q}}+\frac{|\nabla u|_{p}^{2p}}{t_{2}^{2q-2p}}+|\nabla u|_{q}^{2q}=\int _{{\mathbb {R}}^{N}} \frac{g(\varepsilon x, t_{2}u)}{(t_{2}u)^{2q-1}} u^{2q} {\text {d}}x. \end{aligned}$$

From the definition of g, $(g_4)$ and $(f_4)$, we get

$$\begin{aligned}&\left( \frac{1}{t_{1}^{2q-p}}-\frac{1}{t_{2}^{2q-p}}\right) \Vert u\Vert _{V_{\varepsilon },p}^{p}+\left( \frac{1}{t_{1}^{q}}-\frac{1}{t_{2}^{q}} \right) \Vert u\Vert _{V_{\varepsilon },q}^{q}+\left( \frac{1}{t_{1}^{2q-2p}}-\frac{1}{t_{2}^{2q-2p}} \right) |\nabla u|_{p}^{2p}\\&\quad =\int _{{\mathbb {R}}^{N}} \left[ \frac{g(\varepsilon x, t_{1}u)}{(t_{1}u)^{2q-1}} - \frac{g(\varepsilon x, t_{2}u)}{(t_{2}u)^{2q-1}}\right] u^{2q} {\text {d}}x\\&\quad \ge \int _{\Lambda _{\varepsilon }^{c}\cap \{t_{2}u>a\}} \left[ \frac{g(\varepsilon x, t_{1}u)}{(t_{1}u)^{2q-1}} - \frac{g(\varepsilon x, t_{2}u)}{(t_{2}u)^{2q-1}}\right] u^{2q} {\text {d}}x \\&\quad \quad + \int _{\Lambda _{\varepsilon }^{c}\cap \{t_{2}u\le a<t_{1}u\}} \left[ \frac{g(\varepsilon x, t_{1}u)}{(t_{1}u)^{2q-1}} - \frac{g(\varepsilon x, t_{2}u)}{(t_{2}u)^{2q-1}}\right] u^{2q} {\text {d}}x \\&\quad \quad +\int _{\Lambda _{\varepsilon }^{c}\cap \{t_{1}u<a\}} \left[ \frac{g(\varepsilon x, t_{1}u)}{(t_{1}u)^{2q-1}} - \frac{g(\varepsilon x, t_{2}u)}{(t_{2}u)^{2q-1}}\right] u^{2q} {\text {d}}x \\&\quad \ge \frac{V_{0}}{{K}} \int _{\Lambda _{\varepsilon }^{c}\cap \{t_{2}u>a\}} \left[ \left( \frac{1}{(t_{1}u)^{2q-p}}-\frac{1}{(t_{2}u)^{2q-p}}\right) +\left( \frac{1}{(t_{1}u)^{q}}-\frac{1}{(t_{2}u)^{q}}\right) \right] u^{2q} {\text {d}}x\\&\quad \quad +\int _{\Lambda _{\varepsilon }^{c}\cap \{t_{2}u\le a <t_{1}u\}} \left[ \frac{V_{0}}{{K}}\left( \frac{1}{(t_{1}u)^{2q-p}}+\frac{1}{(t_{1}u)^{q}}\right) - \frac{f(t_{2}u)}{(t_{2}u)^{2q-1}}\right] u^{2q} {\text {d}}x. \end{aligned}$$

Multiplying both sides by $\frac{(t_{1}t_{2})^{2q-p}}{t_{2}^{2q-p}- t_{1}^{2q-p}}<0$ (since $t_{1}>t_{2}$), we have

$$\begin{aligned}&\Vert u\Vert _{V_{\varepsilon },p}^{p}+ \frac{(t_{1}t_{2})^{q-p}}{t_{2}^{2q-p}- t_{1}^{2q-p}} (t_{2}^{q}-t_{1}^{q}) \Vert u\Vert _{V_{\varepsilon },q}^{q}\\&\quad =\Vert u\Vert _{V_{\varepsilon },p}^{p}+ \frac{(t_{1}t_{2})^{2q-p}}{t_{2}^{2q-p}- t_{1}^{2q-p}} \frac{t_{2}^{q}-t_{1}^{q}}{(t_{1}t_{2})^{q}} \Vert u\Vert _{V_{\varepsilon },q}^{q}\\&\quad \le \frac{V_{0}}{{K}} \int _{\Lambda _{\varepsilon }^{c}\cap \{t_{2}u>a\}} u^{p} {\text {d}}x +\frac{V_{0}}{{K}} \frac{(t_{1}t_{2})^{2q-p}}{t_{2}^{2q-p}- t_{1}^{2q-p}} \frac{t_{2}^{q}-t_{1}^{q}}{(t_{2}t_{1})^{q}} \int _{\Lambda _{\varepsilon }^{c}\cap \{t_{2}u>a\}} u^{q} {\text {d}}x\\&\quad \quad +\frac{(t_{1}t_{2})^{2q-p}}{t_{2}^{2q-p}- t_{1}^{2q-p}} \int _{\Lambda _{\varepsilon }^{c}\cap \{t_{2}u\le a<t_{1}u\}} \left[ \frac{V_{0}}{{K}}\left( \frac{1}{(t_{1}u)^{2q-p}}+\frac{1}{(t_{1}u)^{q}}\right) - \frac{f(t_{2}u)}{(t_{2}u)^{2q-1}}\right] u^{2q} {\text {d}}x \\&\quad \le \frac{V_{0}}{{K}} \int _{\Lambda _{\varepsilon }^{c}\cap \{t_{2}u>a\}} u^{p} {\text {d}}x +\frac{V_{0}}{{K}} \frac{(t_{1}t_{2})^{q-p}}{t_{2}^{2q-p}- t_{1}^{2q-p}} (t_{2}^{q}-t_{1}^{q}) \int _{\Lambda _{\varepsilon }^{c}\cap \{t_{2}u>a\}} u^{q} {\text {d}}x \\&\quad \quad + \frac{V_{0}}{{K}} \frac{t_{2}^{2q-p}}{t_{2}^{2q-p}- t_{1}^{2q-p}}\int _{\Lambda _{\varepsilon }^{c}\cap \{t_{2}u\le a<t_{1}u\}} u^{p}\, {\text {d}}x+\frac{V_{0}}{{K}}\frac{t^{q-p}_{1}t_{2}^{2q-p}}{t_{2}^{2q-p}- t_{1}^{2q-p}}\int _{\Lambda _{\varepsilon }^{c}\cap \{t_{2}u\le a<t_{1}u\}} u^{q}\, {\text {d}}x\\&\quad \quad -\frac{(t_{1}t_{2})^{2q-p}}{t_{2}^{2q-p}- t_{1}^{2q-p}} \int _{\Lambda _{\varepsilon }^{c}\cap \{t_{2}u\le a<t_{1}u\}} \frac{f(t_{2}u)}{(t_{2}u)^{2q-1}} u^{2q} {\text {d}}x\\&\quad \le \frac{V_{0}}{{K}} \int _{\Lambda _{\varepsilon }^{c}\cap \{t_{2}u>a\}} u^{p} {\text {d}}x +\frac{V_{0}}{{K}} \frac{(t_{1}t_{2})^{q-p}}{t_{2}^{2q-p}- t_{1}^{2q-p}} (t_{2}^{q}-t_{1}^{q}) \int _{\Lambda _{\varepsilon }^{c}\cap \{t_{2}u>a\}} u^{q} {\text {d}}x \\&\quad \quad + \frac{V_{0}}{{K}}\frac{t_{2}^{2q-p}}{t_{2}^{2q-p}- t_{1}^{2q-p}}\int _{\Lambda _{\varepsilon }^{c}\cap \{t_{2}u\le a<t_{1}u\}} u^{p}\, {\text {d}}x+\frac{V_{0}}{{K}}\frac{t^{q-p}_{1}t_{2}^{2q-p}}{t_{2}^{2q-p}- t_{1}^{2q-p}}\int _{\Lambda _{\varepsilon }^{c}\cap \{t_{2}u\le a<t_{1}u\}} u^{q}\, {\text {d}}x\\&\quad \quad -\frac{V_{0}}{{K}}\frac{t_{1}^{2q-p}}{t_{2}^{2q-p}- t_{1}^{2q-p}}\int _{\Lambda _{\varepsilon }^{c}\cap \{t_{2}u\le a<t_{1}u\}} u^{p}\, {\text {d}}x- \frac{V_{0}}{{K}}\frac{t_{1}^{2q-p}t_{2}^{q-p}}{t_{2}^{2q-p}- t_{1}^{2q-p}}\int _{\Lambda _{\varepsilon }^{c}\cap \{t_{2}u\le a<t_{1}u\}} u^{q}\, {\text {d}}x\\&\quad =\frac{V_{0}}{{K}} \int _{\Lambda _{\varepsilon }^{c}\cap \{t_{2}u>a\}} u^{p} {\text {d}}x +\frac{V_{0}}{{K}} \frac{(t_{1}t_{2})^{q-p}}{t_{2}^{2q-p}- t_{1}^{2q-p}} (t_{2}^{q}-t_{1}^{q}) \int _{\Lambda _{\varepsilon }^{c}\cap \{t_{2}u>a\}} u^{q} {\text {d}}x \\&\quad \quad + \frac{V_{0}}{{K}}\frac{t_{2}^{2q-p}}{t_{2}^{2q-p}- t_{1}^{2q-p}}\int _{\Lambda _{\varepsilon }^{c}\cap \{t_{2}u\le a<t_{1}u\}} u^{p}\, {\text {d}}x+\frac{V_{0}}{{K}}\frac{t^{q-p}_{1}t_{2}^{2q-p}}{t_{2}^{2q-p}- t_{1}^{2q-p}}\int _{\Lambda _{\varepsilon }^{c}\cap \{t_{2}u\le a<t_{1}u\}} u^{q}\, {\text {d}}x\\&\quad \quad -\frac{V_{0}}{{K}}\frac{t_{1}^{2q-p}}{t_{2}^{2q-p}- t_{1}^{2q-p}}\int _{\Lambda _{\varepsilon }^{c}\cap \{t_{2}u\le a<t_{1}u\}} u^{p}\, {\text {d}}x- \frac{V_{0}}{{K}}\frac{t_{1}^{2q-p}t_{2}^{q-p}}{t_{2}^{2q-p}- t_{1}^{2q-p}}\int _{\Lambda _{\varepsilon }^{c}\cap \{t_{2}u\le a <t_{1}u\}} u^{q}\, {\text {d}}x\\&\quad \le \frac{V_{0}}{{K}} \int _{\Lambda ^{c}_{\varepsilon }} u^{p}\, {\text {d}}x+\frac{V_{0}}{{K}} \frac{(t_{1}t_{2})^{q-p}}{t_{2}^{2q-p}- t_{1}^{2q-p}} (t_{2}^{q}-t_{1}^{q}) \int _{\Lambda _{\varepsilon }^{c}} u^{q} {\text {d}}x\\&\quad \le \frac{1}{{K}}\Vert u\Vert ^{p}_{V_{\varepsilon },p}+\frac{1}{{K}} \frac{(t_{1}t_{2})^{q-p}}{t_{2}^{2q-p}- t_{1}^{2q-p}} (t_{2}^{q}-t_{1}^{q}) \Vert u\Vert _{V_{\varepsilon },q}^{q}, \end{aligned}$$

where we used the fact that $(f_4)$ and our choice of the constant a give

$$\begin{aligned} \frac{f(t_{2}u)}{(t_{2}u)^{2q-1}}&=\frac{f(t_{2}u)}{(t_{2}u)^{p-1}+(t_{2}u)^{q-1}} \, \frac{(t_{2}u)^{p-1}+(t_{2}u)^{q-1}}{(t_{2}u)^{2q-1}}\\&\le \frac{f(a)}{a^{p-1}+a^{q-1}} \frac{(t_{2}u)^{p-1}+(t_{2}u)^{q-1}}{(t_{2}u)^{2q-1}}\\&= \frac{V_{0}}{K}\left( \frac{1}{(t_{2}u)^{2q-p}}+\frac{1}{(t_{2}u)^{q}}\right) \quad {\text { in } }\Lambda _{\varepsilon }^{c}\cap \{t_{2}u\le a <t_{1}u\}. \end{aligned}$$

Since $u\ne 0$ and ${K}>1$, we get a contradiction.

(ii) Let $u\in {\mathbb {S}}_{\varepsilon }^{+}$. Using (i), we can find $t_{u}>0$ such that $\alpha _{u}'(t_{u})=0$, that is

$$\begin{aligned} t_{u}^{p-1} \Vert u\Vert _{V_{\varepsilon },p}^{p}+t_{u}^{q-1} \Vert u\Vert _{V_{\varepsilon },q}^{q}+t_{u}^{2p-1}|\nabla u|_{p}^{2p}+t_{u}^{2q-1}|\nabla u|_{q}^{2q}= \int _{{\mathbb {R}}^{N}} g(\varepsilon x, t_{u}u) \,u \,{\text {d}}x. \end{aligned}$$

Fix $\zeta >0$. By (11) and Theorem 2, we have

$$\begin{aligned} t_{u}^{p-1} \Vert u\Vert _{V_{\varepsilon },p}^{p}+t_{u}^{q-1} \Vert u\Vert _{V_{\varepsilon },q}^{q}&\le \int _{{\mathbb {R}}^{3}} g(\varepsilon x, t_{u}u)\, u\, {\text {d}}x\le \zeta t_{u}^{p-1}\Vert u\Vert ^{p}_{V_{\varepsilon },p} + C_{\zeta } t_{u}^{\nu -1}\Vert u\Vert _{V_{\varepsilon },q}^{\nu }. \end{aligned}$$

Taking $\zeta >0$ sufficiently small, we find

$$\begin{aligned} Ct^{p-1}_{u}\Vert u\Vert _{V_{\varepsilon },p}^{p}+t_{u}^{q-1} \Vert u\Vert _{V_{\varepsilon },q}^{q}\le Ct_{u}^{\nu -1}\Vert u\Vert _{V_{\varepsilon },q}^{\nu }\le Ct_{u}^{\nu -1}. \end{aligned}$$

Now, if $t_{u}\le 1$, then $t_{u}^{q-1}\le t_{u}^{p-1}$, and using the facts that $1=\Vert u\Vert _{{\mathbb {W}}_{\varepsilon }}\ge \Vert u\Vert _{V_{\varepsilon },p}$ and $q>p$ imply that $\Vert u\Vert _{V_{\varepsilon },p}^{p}\ge \Vert u\Vert ^{q}_{V_{\varepsilon },p}$, we can see that

$$\begin{aligned} Ct_{u}^{q-1} =Ct_{u}^{q-1} \Vert u\Vert ^{q}_{{\mathbb {W}}_{\varepsilon }} \le t_{u}^{q-1} (C\Vert u\Vert _{V_{\varepsilon },p}^{q}+\Vert u\Vert _{V_{\varepsilon },q}^{q})\le t_{u}^{q-1}(C\Vert u\Vert _{V_{\varepsilon },p}^{p}+\Vert u\Vert _{V_{\varepsilon },q}^{q}) \le Ct_{u}^{\nu -1}. \end{aligned}$$

Thanks to $\nu >q$, we can find $\tau >0$, independent of u, such that $t_{u}\ge \tau$.

When $t_{u}>1$, then $t_{u}^{q-1}>t_{u}^{p-1}$, and noting that $1=\Vert u\Vert _{{\mathbb {W}}_{\varepsilon }}\ge \Vert u\Vert _{V_{\varepsilon },p}$ and $q>p$ imply $\Vert u\Vert _{V_{\varepsilon },p}^{p}\ge \Vert u\Vert ^{q}_{V_{\varepsilon },p}$, we obtain

$$\begin{aligned} Ct_{u}^{p-1} =Ct_{u}^{p-1} \Vert u\Vert ^{q}_{{\mathbb {W}}_{\varepsilon }} \le t_{u}^{p-1} (C\Vert u\Vert _{V_{\varepsilon },p}^{q}+\Vert u\Vert _{V_{\varepsilon },q}^{q})\le t_{u}^{p-1}(C\Vert u\Vert _{V_{\varepsilon },p}^{p}+\Vert u\Vert _{V_{\varepsilon },q}^{q}) \le Ct_{u}^{\nu -1}. \end{aligned}$$

Since $\nu>q>p$, there exists $\tau >0$, independent of u, such that $t_{u}\ge \tau$.

Now, let ${\mathcal {W}}\subset {\mathbb {S}}_{\varepsilon }^{+}$ be a compact set and assume by contradiction that there exists a sequence $\{u_{n}\}_{n\in {\mathbb {N}}}\subset {\mathcal {W}}$ such that $t_{n}=t_{u_{n}}\rightarrow \infty$. Then, there exists $u\in {\mathcal {W}}$ such that $u_{n}\rightarrow u$ in ${\mathbb {W}}_{\varepsilon }$. From (ii) of Lemma 2, we have that

$$\begin{aligned} {L}_{\varepsilon }(t_{n}u_{n})\rightarrow -\infty . \end{aligned}$$

(13)

On the other hand, if $v\in {\mathcal {N}}_{\varepsilon }$, by $\langle {L}_{\varepsilon }'(v), v \rangle =0$ and $(g_{3})$, we have that

$$\begin{aligned} {L}_{\varepsilon }(v)= {L}_{\varepsilon }(v)- \frac{1}{\mu } \langle {L}_{\varepsilon }'(v), v \rangle \ge {\tilde{C}} (\Vert v\Vert _{V_{\varepsilon },p}^{p}+\Vert v\Vert _{V_{\varepsilon },q}^{q}). \end{aligned}$$

Taking $v_{n}=t_{u_{n}}u_{n}\in {\mathcal {N}}_{\varepsilon }$ in the above inequality, we find

$$\begin{aligned} {L}_{\varepsilon }(t_{n}u_{n})\ge {\tilde{C}} (\Vert v_{n}\Vert _{V_{\varepsilon },p}^{p}+\Vert v_{n}\Vert _{V_{\varepsilon },q}^{q}). \end{aligned}$$

Since $\Vert v_{n}\Vert _{{\mathbb {W}}_{\varepsilon }}=t_{n}\rightarrow \infty$ and $\Vert v_{n}\Vert _{{\mathbb {W}}_{\varepsilon }}=\Vert v_{n}\Vert _{\varepsilon ,p}+\Vert v_{n}\Vert _{\varepsilon ,q}$, we can use (13) to get a contradiction.

(iii) Let us observe that ${\hat{m}}_{\varepsilon }$, $m_{\varepsilon }$ and $m_{\varepsilon }^{-1}$ are well defined. Indeed, by (i), for each $u\in {\mathbb {W}}_{\varepsilon }^{+},$ there is a unique $m_{\varepsilon }(u)\in {\mathcal {N}}_{\varepsilon }$. On the other hand, if $u\in {\mathcal {N}}_{\varepsilon },$ then $u\in {\mathbb {W}}^{+}_{\varepsilon }$. Otherwise, we have

$$\begin{aligned} |{{\,\mathrm{supp}\,}}(u^{+}) \cap \Lambda _{\varepsilon }|=0, \end{aligned}$$

and by $(g_3)$-(ii), we deduce that

$$\begin{aligned} \Vert u\Vert _{V_{\varepsilon },p}^{p}+\Vert u\Vert ^{q}_{V_{\varepsilon },q}&\le \int _{{\mathbb {R}}^{N}} g(\varepsilon x, u)\, u \, {\text {d}}x= \int _{\Lambda _{\varepsilon }^{c}} g(\varepsilon x, u)\, u \, {\text {d}}x + \int _{\Lambda _{\varepsilon }} g(\varepsilon x, u)\, u \, {\text {d}}x \\&= \int _{\Lambda _{\varepsilon }^{c}} g(\varepsilon x, u^{+})\, u^{+} \, {\text {d}}x \\&\le \frac{1}{{K}} \int _{\Lambda _{\varepsilon }^{c}} V(\varepsilon x) (|u|^{p}+|u|^{q}) {\text {d}}x \\&\le \frac{1}{{K}} \left( \Vert u\Vert _{V_{\varepsilon },p}^{p}+\Vert u\Vert ^{q}_{V_{\varepsilon },q} \right) \end{aligned}$$

which is impossible due to ${K}>1$ and $u\ne 0$. Therefore, $m_{\varepsilon }^{-1}(u)= \frac{u}{\Vert u\Vert _{{\mathbb {W}}_{\varepsilon }}}\in {\mathbb {S}}_{\varepsilon }^{+}$ is well defined and continuous. From

$$\begin{aligned} m_{\varepsilon }^{-1}(m_{\varepsilon }(u))= m_{\varepsilon }^{-1}(t_{u}u)= \frac{t_{u}u}{\Vert t_{u}u\Vert _{{\mathbb {W}}_{\varepsilon }}}= \frac{u}{\Vert u\Vert _{{\mathbb {W}}_{\varepsilon }}}=u \quad {\text { for all }} u\in {\mathbb {S}}_{\varepsilon }^{+}, \end{aligned}$$

we infer that $m_{\varepsilon }$ is a bijection. To prove that ${\hat{m}}_{\varepsilon }: {\mathbb {W}}_{\varepsilon }^{+}\rightarrow {\mathcal {N}}_{\varepsilon }$ is continuous, let $\{u_{n}\}_{n\in {\mathbb {N}}}\subset {\mathbb {W}}_{\varepsilon }^{+}$ and $u\in {\mathbb {W}}^{+}_{\varepsilon }$ be such that $u_{n}\rightarrow u$ in ${\mathbb {W}}_{\varepsilon }$. Since ${\hat{m}}(tu)={\hat{m}}(u)$ for all $t>0$, we may assume that $\Vert u_{n}\Vert _{{\mathbb {W}}_{\varepsilon }}=\Vert u\Vert _{{\mathbb {W}}_{\varepsilon }}=1$ for all $n\in {\mathbb {N}}$. By (ii), there exists $t_{0}>0$ such that $t_{n}=t_{u_{n}}\rightarrow t_{0}$. Since $t_{n}u_{n}\in {\mathcal {N}}_{\varepsilon }$,

$$\begin{aligned} t_{n}^{p}\Vert u_{n}\Vert ^{p}_{V_{\varepsilon },p}+t_{n}^{q}\Vert u_{n}\Vert _{V_{\varepsilon },q}^{q}+t^{2p}_{n}|\nabla u_{n}|_{p}^{2p}+t^{2q}_{n}|\nabla u_{n}|_{q}^{2q}= \int _{{\mathbb {R}}^{N}} g(\varepsilon x, t_{n}u_{n})\, t_{n}u_{n} \, {\text {d}}x, \end{aligned}$$

and passing to the limit as $n\rightarrow \infty,$ we obtain

$$\begin{aligned} t_{0}^{p}\Vert u\Vert ^{p}_{V_{\varepsilon },p}+t_{0}^{q}\Vert u\Vert ^{q}_{V_{\varepsilon },q}+t^{2p}_{0}|\nabla u|_{p}^{2p}+t^{2q}_{0}|\nabla u|_{q}^{2q}= \int _{{\mathbb {R}}^{N}} g(\varepsilon x, t_{0}u) \, t_{0}u\, {\text {d}}x, \end{aligned}$$

which yields $t_{0}u\in {\mathcal {N}}_{\varepsilon }$. From (i), $t_{u}= t_{0}$, and this means that ${\hat{m}}_{\varepsilon }(u_{n})\rightarrow {\hat{m}}_{\varepsilon }(u)$ in ${\mathbb {W}}_{\varepsilon }^{+}$. Thus, ${\hat{m}}_{\varepsilon }$ and $m_{\varepsilon }$ are continuous functions.

(iv) Let $\{u_{n}\}_{n\in {\mathbb {N}}}\subset {\mathbb {S}}_{\varepsilon }^{+}$ be a sequence such that ${\mathrm{dist}}(u_{n}, \partial {\mathbb {S}}_{\varepsilon }^{+})\rightarrow 0$. Then, for each $v\in \partial {\mathbb {S}}_{\varepsilon }^{+}$ and $n\in {\mathbb {N}}$, we have $u_{n}^{+}\le |u_{n}-v|$ a.e. in $\Lambda _{\varepsilon }$. Therefore, by $(V_1)$, $(V_2)$ and Theorem 2, we can see that for each $r\in [p, q^{*}_{s}],$ there exists $C_{r}>0$ such that

$$\begin{aligned} |u_{n}^{+}|_{L^{r}(\Lambda _{\varepsilon })} \le \inf _{v\in \partial {\mathbb {S}}_{\varepsilon }^{+}} |u_{n}- v|_{L^{r}(\Lambda _{\varepsilon })} \le C_{r} \inf _{v\in \partial {\mathbb {S}}_{\varepsilon }^{+}} \Vert u_{n}- v\Vert _{{\mathbb {W}}_{\varepsilon }} \quad {\text { for all }} n\in {\mathbb {N}}. \end{aligned}$$

By virtue of $(g_{1})$, $(g_{2})$, $(g_{3})$-(ii) and $q>p$, we get, for all $t>0$,

$$\begin{aligned} \int _{{\mathbb {R}}^{N}} G(\varepsilon x, tu_{n})\, {\text {d}}x&= \int _{\Lambda _{\varepsilon }^{c}} G(\varepsilon x, tu_{n})\, {\text {d}}x + \int _{\Lambda _{\varepsilon }} G(\varepsilon x, tu_{n})\, {\text {d}}x\\&\le \frac{V_{0}}{{K}p} \int _{\Lambda _{\varepsilon }^{c}} (t^{p}|u_{n}|^{p}+t^{q}|u_{n}|^{q}) {\text {d}}x+ \int _{\Lambda _{\varepsilon }} F(tu_{n})\, {\text {d}}x\\&\le \frac{t^{p}}{{K}p} \int _{{\mathbb {R}}^{N}} V(\varepsilon x)|u_{n}|^{p}\, {\text {d}}x+\frac{t^{q}}{{K}p} \int _{{\mathbb {R}}^{N}} V(\varepsilon x)|u_{n}|^{q}\, {\text {d}}x\\&\quad + C_{1}t^{p} \int _{\Lambda _{\varepsilon }} (u_{n}^{+})^{p} {\text {d}}x+ C_{2} t^{\nu } \int _{\Lambda _{\varepsilon }} (u_{n}^{+})^{\nu } {\text {d}}x\\&\le \frac{t^{p}}{{K}p} \int _{{\mathbb {R}}^{N}} V(\varepsilon x)|u_{n}|^{p}\, {\text {d}}x+\frac{t^{q}}{{K}p} \int _{{\mathbb {R}}^{N}} V(\varepsilon x)|u_{n}|^{q}\, {\text {d}}x \\&\quad + C_{p}' t^{p} {\mathrm{dist}}(u_{n}, \partial {\mathbb {S}}_{\varepsilon }^{+})^{p} + C_{\nu }' t^{\nu }{\mathrm{dist}}(u_{n}, \partial {\mathbb {S}}_{\varepsilon }^{+})^{\nu }. \end{aligned}$$

Therefore,

$$\begin{aligned} \int _{{\mathbb {R}}^{N}} G(\varepsilon x, tu_{n})\, {\text {d}}x \le \frac{t^{p}}{{K}p} \int _{{\mathbb {R}}^{N}} V(\varepsilon x)|u_{n}|^{p}\, {\text {d}}x+\frac{t^q}{{K}p} \int _{{\mathbb {R}}^{N}} V(\varepsilon x)|u_{n}|^{q}\, {\text {d}}x+o_{n}(1). \end{aligned}$$

(14)

Now, we note that ${K}>1$, and that $1=\Vert u_{n}\Vert _{{\mathbb {W}}_{\varepsilon }}\ge \Vert u_{n}\Vert _{V_{\varepsilon },p}$ implies that $\Vert u_{n}\Vert ^{p}_{V_{\varepsilon },p}\ge \Vert u_{n}\Vert ^{q}_{V_{\varepsilon },p}$. Then, for all $t>1$, we obtain that

$$\begin{aligned} \begin{aligned}&\frac{t^{p}}{p} \Vert u_{n}\Vert ^{p}_{V_{\varepsilon },p}+\frac{t^{q}}{q} \Vert u_{n}\Vert ^{q}_{V_{\varepsilon },q}-\frac{t^{p}}{{K}p} \int _{{\mathbb {R}}^{N}} V(\varepsilon x)|u_{n}|^{p}\, {\text {d}}x-\frac{t^{q}}{{K}p} \int _{{\mathbb {R}}^{N}} V(\varepsilon x)|u_{n}|^{q}\, {\text {d}}x \\&\quad = \frac{t^{p}}{p} |\nabla u_{n}|^{p}_{p}+t^{p} \left( \frac{1}{p}-\frac{1}{{K}p}\right) \int _{{\mathbb {R}}^{N}} V(\varepsilon x) |u_{n}|^{p}\, {\text {d}}x+\frac{t^{q}}{q} |\nabla u_{n}|^{q}_{q}\\&\qquad +t^{q} \left( \frac{1}{q}-\frac{1}{{K}p}\right) \int _{{\mathbb {R}}^{N}} V(\varepsilon x) |u_{n}|^{q}\, {\text {d}}x \\&\quad \ge C_{1} t^{p} \Vert u_{n}\Vert _{V_{\varepsilon },p}^{p}+C_{2} t^{q} \Vert u_{n}\Vert _{V_{\varepsilon },q}^{q} \\&\quad \ge C_{1} t^{p} \Vert u_{n}\Vert _{V_{\varepsilon },p}^{q}+C_{2} t^{q} \Vert u_{n}\Vert _{V_{\varepsilon },q}^{q} \\&\quad \ge C_{1} t^{p} \Vert u_{n}\Vert _{V_{\varepsilon },p}^{q}+C_{2} t^{p} \Vert u_{n}\Vert _{V_{\varepsilon },q}^{q} \\&\quad \ge C_{3} t^{p} (\Vert u_{n}\Vert _{V_{\varepsilon },p}+\Vert u_{n}\Vert _{V_{\varepsilon },q})^{q}=C_{3}t^{p}. \end{aligned} \end{aligned}$$

(15)

Bearing in mind the definition of $m_{\varepsilon }(u_{n})$ and using (14), (15), we find

$$\begin{aligned}&\liminf _{n\rightarrow \infty } {L}_{\varepsilon }(m_{\varepsilon }(u_{n}))\\&\quad \ge \liminf _{n\rightarrow \infty } {L}_{\varepsilon }(t u_{n})\\&\quad \ge \liminf _{n\rightarrow \infty }\left[ \frac{t^{p}}{p} \Vert u_{n}\Vert ^{p}_{V_{\varepsilon },p}+\frac{t^{q}}{q} \Vert u_{n}\Vert ^{q}_{V_{\varepsilon },q}-\int _{{\mathbb {R}}^{N}} G(\varepsilon x, tu_{n})\, {\text {d}}x\right] \ge C_{3} t^{p} \quad {\text { for all }} t>1. \end{aligned}$$

By sending $t\rightarrow \infty$, we get ${L}_{\varepsilon }(m_{\varepsilon }(u_{n}))\rightarrow \infty$ as $n\rightarrow \infty$. On the other hand, by the definition of ${L}_{\varepsilon }$, we see that for all $n\in {\mathbb {N}}$

$$\begin{aligned}&\frac{1}{p}\Vert m_{\varepsilon }(u_{n})\Vert _{V_{\varepsilon },p}^{p}(1+\Vert m_{\varepsilon }(u_{n})\Vert _{V_{\varepsilon },p}^{p})+\frac{1}{q}\Vert m_{\varepsilon }(u_{n})\Vert _{V_{\varepsilon },q}^{q}(1+\Vert m_{\varepsilon }(u_{n})\Vert ^{q}_{V_{\varepsilon , q}})\\&\quad \ge \frac{1}{p}\Vert m_{\varepsilon }(u_{n})\Vert _{V_{\varepsilon },p}^{p}+\frac{1}{2p}|\nabla m_{\varepsilon }(u_{n})|_{p}^{2p}+\frac{1}{q} \Vert m_{\varepsilon }(u_{n})\Vert _{V_{\varepsilon },q}^{q}+\frac{1}{2q}|\nabla m_{\varepsilon }(u_{n})|_{q}^{2q} \ge {L}_{\varepsilon }(m_{\varepsilon }(u_{n})) \end{aligned}$$

which implies that $\Vert m_{\varepsilon }(u_{n})\Vert _{{\mathbb {W}}_{\varepsilon }}\rightarrow \infty$ as $n\rightarrow \infty$. $\square$

Remark 1

If $u\in {\mathcal {N}}_{\varepsilon }$, it follows from (11) and Theorem 2 that

$$\begin{aligned} \Vert u\Vert _{V_{\varepsilon },p}^{p}+\Vert u\Vert ^{q}_{V_{\varepsilon },q}&\le \int _{{\mathbb {R}}^{N}} g(\varepsilon x, u)\, u \, {\text {d}}x\le \zeta |u|_{p}^{p}+C_{\zeta }|u|_{q^{*}}^{q^{*}}\le \frac{\zeta }{V_{0}}\Vert u\Vert _{V_{\varepsilon },p}^{p}+C'_{\zeta } \Vert u\Vert ^{q^{*}}_{V_{\varepsilon },q}. \end{aligned}$$

Choosing $\zeta \in (0, V_{0})$ we find $\Vert u\Vert _{V_{\varepsilon },q}\ge \kappa =(C'_{\zeta })^{-\frac{1}{q^{*}-q}}$ which implies that $\Vert u\Vert _{\varepsilon }\ge \Vert u\Vert _{V_{\varepsilon },q}\ge \kappa$.

Define the maps

$$\begin{aligned} {\hat{\psi }}_{\varepsilon }: {\mathbb {W}}_{\varepsilon }^{+} \rightarrow {\mathbb {R}}\quad {\text { and }} \quad \psi _{\varepsilon }: {\mathbb {S}}_{\varepsilon }^{+}\rightarrow {\mathbb {R}}, \end{aligned}$$

by ${\hat{\psi }}_{\varepsilon }(u)= {L}_{\varepsilon }({\hat{m}}_{\varepsilon }(u))$ and $\psi _{\varepsilon }={\hat{\psi }}_{\varepsilon }|_{{\mathbb {S}}_{\varepsilon }^{+}}$. From Lemma 3 and arguing as in the proofs of Proposition 9 and Corollary 10 in [46], we may obtain the following result.

Proposition 1

Assume that $(V_{1})$–$(V_{2})$ and $(f_{1})$–$(f_{4})$ are satisfied. Then,

• (a) ${\hat{\psi }}_{\varepsilon } \in {\mathcal {C}}^{1}({\mathbb {W}}_{\varepsilon }^{+}, {\mathbb {R}})$ and

  $$\begin{aligned} \langle {\hat{\psi }}_{\varepsilon }'(u), v\rangle = \frac{\Vert {\hat{m}}_{\varepsilon }(u)\Vert _{{\mathbb {W}}_{\varepsilon }}}{\Vert u\Vert _{{\mathbb {W}}_{\varepsilon }}} \langle {L}_{\varepsilon }'({\hat{m}}_{\varepsilon }(u)), v\rangle \quad {\text { for all }} u\in {\mathbb {W}}_{\varepsilon }^{+}, v\in {\mathbb {W}}_{\varepsilon }. \end{aligned}$$

• (b) $\psi _{\varepsilon } \in {\mathcal {C}}^{1}({\mathbb {S}}_{\varepsilon }^{+}, {\mathbb {R}})$ and

  $$\begin{aligned} \langle \psi _{\varepsilon }'(u), v \rangle = \Vert m_{\varepsilon }(u)\Vert _{{\mathbb {W}}_{\varepsilon }} \langle {L}_{\varepsilon }'(m_{\varepsilon }(u)), v\rangle , \quad {\text { for all }} v\in T_{u}{\mathbb {S}}_{\varepsilon }^{+}. \end{aligned}$$

• (c) If $\{u_{n}\}_{n\in {\mathbb {N}}}$ is a ${\text {(PS)}}_{c}$ sequence for $\psi _{\varepsilon }$, then $\{m_{\varepsilon }(u_{n})\}_{n\in {\mathbb {N}}}$ is a ${\text {(PS)}}_{c}$ sequence for ${L}_{\varepsilon }$. If $\{u_{n}\}_{n\in {\mathbb {N}}}\subset {\mathcal {N}}_{\varepsilon }$ is a bounded ${\text {(PS)}}_{c}$ sequence for ${L}_{\varepsilon }$, then $\{m_{\varepsilon }^{-1}(u_{n})\}_{n\in {\mathbb {N}}}$ is a ${\text {(PS)}}_{c}$ sequence for $\psi _{\varepsilon }$.

• (d) u is a critical point of $\psi _{\varepsilon }$ if, and only if, $m_{\varepsilon }(u)$ is a critical point for ${L}_{\varepsilon }$. Moreover, the corresponding critical values coincide and

  $$\begin{aligned} \inf _{u\in {\mathbb {S}}_{\varepsilon }^{+}} \psi _{\varepsilon }(u)= \inf _{u\in {\mathcal {N}}_{\varepsilon }} {L}_{\varepsilon }(u). \end{aligned}$$

Remark 2

As in [46], we have the following variational characterization of the infimum of ${L}_{\varepsilon }$ over ${\mathcal {N}}_{\varepsilon }$:

$$\begin{aligned} c_{\varepsilon }=\inf _{u\in {\mathcal {N}}_{\varepsilon }} {L}_{\varepsilon }(u)=\inf _{u\in {\mathbb {W}}_{\varepsilon }^{+}} \max _{t>0} {L}_{\varepsilon }(tu)=\inf _{u\in {\mathbb {S}}_{\varepsilon }^{+}} \max _{t>0} {L}_{\varepsilon }(tu). \end{aligned}$$

Next, we claim that ${L}_{\varepsilon }$ satisfies the Palais–Smale condition. First of all, we have the following result.

Lemma 4

Let $\{u_{n}\}_{n\in {\mathbb {N}}}\subset {\mathbb {W}}_{\varepsilon }$ be a ${\text {(PS)}}_{c}$ sequence for ${L}_{\varepsilon }$. Then, $\{u_{n}\}_{n\in {\mathbb {N}}}$ is bounded in ${\mathbb {W}}_{\varepsilon }$.

Proof

From $(g_{3})$, $q>p$ and $\mu >2q$, we have that

$$\begin{aligned} C(1+\Vert u_{n}\Vert _{\varepsilon })&\ge {L}_{\varepsilon }(u_{n})- \frac{1}{\mu } \langle {L}'_{\varepsilon }(u_{n}), u_{n}\rangle \\&=\left( \frac{1}{p}- \frac{1}{\mu }\right) \Vert u_{n}\Vert _{V_{\varepsilon },p}^{p} +\left( \frac{1}{2p}- \frac{1}{\mu }\right) |\nabla u_{n}|_{p}^{2p} +\left( \frac{1}{q}- \frac{1}{\mu }\right) \Vert u_{n}\Vert _{V_{\varepsilon },q}^{q}\\&\quad +\left( \frac{1}{2q}- \frac{1}{\mu }\right) |\nabla u_{n}|_{q}^{2q} \\&\quad + \frac{1}{\mu } \int _{\Lambda _{\varepsilon }^{c}} [g(\varepsilon x, u_{n})u_{n}- \mu G(\varepsilon x, u_{n})] \, {\text {d}}x + \frac{1}{\mu } \int _{\Lambda _{\varepsilon }} [g(\varepsilon x, u_{n})u_{n}- \mu G(\varepsilon x, u_{n})] \, {\text {d}}x \\&\ge \left( \frac{1}{q}- \frac{1}{\mu }\right) [\Vert u_{n}\Vert _{V_{\varepsilon },p}^{p} + \Vert u_{n}\Vert _{V_{\varepsilon },q}^{q}]-\left( \frac{1}{p}- \frac{1}{\mu }\right) \frac{1}{{K}} \int _{\Lambda _{\varepsilon }^{c}} V(\varepsilon x) (|u_{n}|^{p}+|u_{n}|^{q})\, {\text {d}}x\\&\ge \left[ \left( \frac{1}{q}- \frac{1}{\mu }\right) - \left( \frac{1}{p}- \frac{1}{\mu }\right) \frac{1}{{K}} \right] (\Vert u_{n}\Vert _{V_{\varepsilon },p}^{p}+\Vert u_{n}\Vert _{V_{\varepsilon },q}^{q})\\&= {\tilde{C}} (\Vert u_{n}\Vert _{V_{\varepsilon },p}^{p}+\Vert u_{n}\Vert _{V_{\varepsilon },q}^{q}), \end{aligned}$$

where ${\tilde{C}}=\left( \frac{1}{q}- \frac{1}{\mu }\right) - \left( \frac{1}{p}- \frac{1}{\mu }\right) \frac{1}{{K}}>0$ since ${K}>\left( \frac{\mu -p}{\mu -q}\right) \frac{q}{p}$.

Now, we assume by contradiction that $\Vert u_{n}\Vert _{{\mathbb {W}}_{\varepsilon }}\rightarrow \infty$ and consider the following cases:

• (1) $\Vert u_{n}\Vert _{V_{\varepsilon },p}\rightarrow \infty$ and $\Vert u_{n}\Vert _{V_{\varepsilon }, q}\rightarrow \infty$;

• (2) $\Vert u_{n}\Vert _{V_{\varepsilon },p}\rightarrow \infty$ and $\Vert u_{n}\Vert _{V_{\varepsilon }, q}$ is bounded;

• (3) $\Vert u_{n}\Vert _{V_{\varepsilon },q}\rightarrow \infty$ and $\Vert u_{n}\Vert _{V_{\varepsilon }, p}$ is bounded.

In case (1), for n large, we have $\Vert u_{n}\Vert _{V_{\varepsilon }, q}^{q-p}\ge 1$, that is $\Vert u_{n}\Vert _{V_{\varepsilon }, q}^{q}\ge \Vert u_{n}\Vert _{V_{\varepsilon }, q}^{p}$. Therefore,

$$\begin{aligned} C_{0}(1+ \Vert u_{n}\Vert _{{\mathbb {W}}_{\varepsilon }}) \ge {\tilde{C}} (\Vert u_{n}\Vert _{V_{\varepsilon },p}^{p}+\Vert u_{n}\Vert _{V_{\varepsilon }, q}^{p})\ge C_{1} (\Vert u_{n}\Vert _{V_{\varepsilon },p}+\Vert u_{n}\Vert _{V_{\varepsilon },q})^{p}=C_{1}\Vert u_{n}\Vert _{{\mathbb {W}}_{\varepsilon }}^{p} \end{aligned}$$

that is an absurd. In case (2), we have

$$\begin{aligned} C_{0}(1+\Vert u_{n}\Vert _{V_{\varepsilon },p}+\Vert u_{n}\Vert _{V_{\varepsilon },q})=C_{0}(1+\Vert u_{n}\Vert _{{\mathbb {W}}_{\varepsilon }})\ge {\tilde{C}} \Vert u_{n}\Vert _{V_{\varepsilon },p}^{p} \end{aligned}$$

and consequently

$$\begin{aligned} C_{0}\left( \frac{1}{\Vert u_{n}\Vert _{V_{\varepsilon },p}^{p}}+\frac{1}{\Vert u_{n}\Vert _{V_{\varepsilon },p}^{p-1}}+\frac{\Vert u_{n}\Vert _{V_{\varepsilon },q}}{\Vert u_{n}\Vert ^{p}_{V_{\varepsilon },p}}\right) \ge {\tilde{C}}. \end{aligned}$$

Since $p>1$ and passing to the limit as $n\rightarrow \infty$, we obtain $0< {\tilde{C}}\le 0$ which is impossible. The last case is similar to the case (2), so we omit the details. Consequently, $\{u_{n}\}_{n\in {\mathbb {N}}}$ is bounded in ${\mathbb {W}}_{\varepsilon }$. $\square$

Lemma 5

Let $\{u_{n}\}_{n\in {\mathbb {N}}}\subset {\mathbb {W}}_{\varepsilon }$ be a ${\text {(PS)}}_{c}$ sequence for ${L}_{\varepsilon }$. Then, for any $\eta >0,$ there exists $R=R(\eta )>0$ such that

$$\begin{aligned} \limsup _{n\rightarrow \infty } \int _{{\mathcal {B}}_{R}^{c}} |\nabla u_{n}|^{p}+|\nabla u_{n}|^{q}+ V(\varepsilon x) (|u_{n}|^{p}+|u_{n}|^{q}) \, {\text {d}}x <\eta . \end{aligned}$$

(16)

Proof

For $R>0$, let $\psi _{R}\in {\mathcal {C}}^{\infty }({\mathbb {R}}^{N})$ be such that $0\le \psi _{R}\le 1$, $\psi _{R}=0$ in ${\mathcal {B}}_{\frac{R}{2}}$, $\psi _{R}=1$ in ${\mathcal {B}}_{R}^{c}$, and $|\nabla \psi _{R}|\le \frac{C}{R}$, for some constant $C>0$ independent of R. From the boundedness of $\{\psi _{R}u_{n}\}_{n\in {\mathbb {N}}}$ in ${\mathbb {W}}_{\varepsilon }$, it follows that $\langle {L}_{\varepsilon }'(u_{n}), \psi _{R}u_{n}\rangle =o_{n}(1)$, namely

$$\begin{aligned}&(1+|\nabla u_{n}|_{p}^{p})\int _{{\mathbb {R}}^{N}} |\nabla u_{n}|^{p}\psi _{R}\, {\text {d}}x+(1+|\nabla u_{n}|_{q}^{q}) \int _{{\mathbb {R}}^{N}} |\nabla u_{n}|^{q}\psi _{R}\, {\text {d}}x \\&\quad \quad +\int _{{\mathbb {R}}^{N}} V(\varepsilon x) |u_{n}|^{p} \psi _{R} \, {\text {d}}x+\int _{{\mathbb {R}}^{N}} V(\varepsilon x) |u_{n}|^{q} \psi _{R} \, {\text {d}}x\\&\quad =o_{n}(1) + \int _{{\mathbb {R}}^{N}} g(\varepsilon x, u_{n}) \psi _{R} u_{n}\, {\text {d}}x - (1+|\nabla u_{n}|_{p}^{p})\int _{{\mathbb {R}}^{N}} |\nabla u_{n}|^{p-2}\nabla u_{n} \cdot \nabla \psi _{R} u_{n}\, {\text {d}}x \\&\quad \quad - (1+|\nabla u_{n}|_{q}^{q})\int _{{\mathbb {R}}^{N}} |\nabla u_{n}|^{q-2}\nabla u_{n} \cdot \nabla \psi _{R} u_{n}\, {\text {d}}x. \end{aligned}$$

Take $R>0$ such that $\Lambda _{\varepsilon }\subset {\mathcal {B}}_{\frac{R}{2}}$. From the definition of $\psi _{R}$ and $(g_{3})$-(ii), we see that

$$\begin{aligned} \begin{aligned}&\int _{{\mathcal {B}}_{R}^{c}} |\nabla u_{n}|^{p}\, {\text {d}}x+ \int _{{\mathcal {B}}_{R}^{c}} |\nabla u_{n}|^{q}\, {\text {d}}x+ \left( 1- \frac{1}{K}\right) \int _{{\mathcal {B}}_{R}^{c}} V(\varepsilon x) (|u_{n}|^{p}+|u_{n}|^{q}) \, {\text {d}}x \\&\quad \le o_{n}(1)- (1+|\nabla u_{n}|_{p}^{p})\int _{{\mathbb {R}}^{N}} |\nabla u_{n}|^{p-2}\nabla u_{n} \cdot \nabla \psi _{R} u_{n}\, {\text {d}}x \\&\quad \quad - (1+|\nabla u_{n}|_{q}^{q})\int _{{\mathbb {R}}^{N}} |\nabla u_{n}|^{q-2}\nabla u_{n} \cdot \nabla \psi _{R} u_{n}\, {\text {d}}x. \end{aligned} \end{aligned}$$

(17)

Now, using the Hölder inequality and the boundedness of $\{u_{n}\}_{n\in {\mathbb {N}}}$ in ${\mathbb {W}}_{\varepsilon }$, we have, for $t\in \{p, q\}$,

$$\begin{aligned} \left| \int _{{\mathbb {R}}^{N}} |\nabla u_{n}|^{t-2}\nabla u_{n} \cdot \nabla \psi _{R} u_{n}\, {\text {d}}x\right| \le \frac{C}{R}|\nabla u_{n}|^{t-1}_{t} |u_{n}|_{t}\le \frac{C}{R} \end{aligned}$$

which implies that

$$\begin{aligned} \lim _{R\rightarrow \infty }\limsup _{n\rightarrow \infty }\left| \int _{{\mathbb {R}}^{N}} |\nabla u_{n}|^{t-2}\nabla u_{n} \cdot \nabla \psi _{R} u_{n}\, {\text {d}}x\right| =0. \end{aligned}$$

(18)

Thanks to (17) and (18), we deduce that (16) holds true. $\square$

Due to the presence of the Kirchhoff terms, the following lemma plays a crucial role to get the strong convergence of bounded Palais–Smale sequences.

Lemma 6

Let $\{u_{n}\}_{n\in {\mathbb {N}}}\subset {\mathbb {W}}_{\varepsilon }$ be a ${\text {(PS)}}_{c}$ sequence for ${L}_{\varepsilon }$, and let $R>0$. Then,

$$\begin{aligned} \begin{aligned}&\lim _{n\rightarrow \infty } \int _{{\mathcal {B}}_{R}} |\nabla u_{n}|^{p}+|\nabla u_{n}|^{q}+ V(\varepsilon x) (|u_{n}|^{p}+|u_{n}|^{q}) \, {\text {d}}x \\&\quad = \int _{{\mathcal {B}}_{R}} |\nabla u|^{p}+|\nabla u|^{q}+ V(\varepsilon x) (|u|^{p}+|u|^{q}) \, {\text {d}}x. \end{aligned} \end{aligned}$$

(19)

Proof

Take $\eta _{\rho }\in {\mathcal {C}}^{\infty }({\mathbb {R}}^{N})$ such that

$$\begin{aligned} \eta _{\rho }(x)= \left\{ \begin{array}{ll} 1 &{}{\text { for }} x\in {\mathcal {B}}_{\rho }, \\ 0 &{}{\text { for }} x\notin {\mathcal {B}}_{2\rho }, \end{array} \right. \end{aligned}$$

with $0\le \eta _{\rho }(x)\le 1$ and $|\nabla \eta _{\rho }|\le \frac{2}{\rho }$. Since $\{u_{n}\}_{n\in {\mathbb {N}}}$ is bounded in ${\mathbb {W}}_{\varepsilon }$ (by Lemma 4), we may assume that

$$\begin{aligned} |\nabla u_{n}|_{p}^{p}\rightarrow T_{p} \quad {\text { and }} \quad |\nabla u_{n}|_{q}^{q}\rightarrow T_{q} \quad {\text { as }} n\rightarrow \infty . \end{aligned}$$

(20)

Fix $R>0$ and take $\rho >R$. For $t\in \{p, q\}$ and $n\in {\mathbb {N}}$, define

$$\begin{aligned} A_{n}^{t}&= \left( 1+ |\nabla u_{n}|_{t}^{t} \right) \int _{{\mathcal {B}}_{R}} \left( |\nabla u_{n}|^{t-2}\nabla u_{n} - |\nabla u|^{t-2} \nabla u\right) \cdot \left( \nabla u_{n}- \nabla u\right) \, {\text {d}}x \\&\quad + \int _{{\mathcal {B}}_{R}} V(\varepsilon x) \left( |u_{n}|^{t-2}u_{n} - |u|^{t-2} u\right) \left( u_{n}- u\right) \, {\text {d}}x. \end{aligned}$$

By (9), we note that $A_{n}^{t}\ge 0$. Moreover, we see that

$$\begin{aligned} 0\le A_{n}^{t}&=\left( 1+ |\nabla u_{n}|_{t}^{t} \right) \int _{{\mathcal {B}}_{R}} \left( |\nabla u_{n}|^{t-2}\nabla u_{n} - |\nabla u|^{t-2} \nabla u\right) \cdot \left( \nabla u_{n}- \nabla u\right) \eta _{\rho }\, {\text {d}}x \\&\quad + \int _{{\mathcal {B}}_{R}} V(\varepsilon x) \left( |u_{n}|^{t-2}u_{n} - |u|^{t-2} u\right) \left( u_{n}- u\right) \eta _{\rho }\, {\text {d}}x\\&\le \left( 1+ |\nabla u_{n}|_{t}^{t} \right) \int _{{\mathbb {R}}^{N}} \left( |\nabla u_{n}|^{t-2}\nabla u_{n} - |\nabla u|^{t-2} \nabla u\right) \cdot \left( \nabla u_{n}- \nabla u\right) \eta _{\rho }\, {\text {d}}x \\&\quad + \int _{{\mathbb {R}}^{N}} V(\varepsilon x) \left( |u_{n}|^{t-2}u_{n} - |u|^{t-2} u\right) \left( u_{n}- u\right) \eta _{\rho }\, {\text {d}}x\\&=\left( 1+ |\nabla u_{n}|_{t}^{t} \right) \int _{{\mathbb {R}}^{N}} |\nabla u_{n}|^{t} \eta _{\rho }\, {\text {d}}x + \int _{{\mathbb {R}}^{N}} V(\varepsilon x) |u_{n}|^{t}\eta _{\rho }\, {\text {d}}x \\&\quad + \left( 1+ |\nabla u_{n}|_{t}^{t} \right) \int _{{\mathbb {R}}^{N}} |\nabla u|^{t}\eta _{\rho }\, {\text {d}}x +\int _{{\mathbb {R}}^{N}} V(\varepsilon x) |u|^{t}\eta _{\rho }\, {\text {d}}x \\&\quad - \left[ \left( 1+ |\nabla u_{n}|_{t}^{t} \right) \int _{{\mathbb {R}}^{N}} |\nabla u_{n}|^{t-2}\nabla u_{n} \cdot \nabla u \eta _{\rho }\, {\text {d}}x + \int _{{\mathbb {R}}^{N}} V(\varepsilon x) |u_{n}|^{t-2} u_{n}u\eta _{\rho }\, {\text {d}}x \right] \\&\quad - \left[ \left( 1+ |\nabla u_{n}|_{t}^{t} \right) \int _{{\mathbb {R}}^{N}} |\nabla u|^{t-2}\nabla u \cdot \nabla u_{n} \eta _{\rho }\, {\text {d}}x + \int _{{\mathbb {R}}^{N}} V(\varepsilon x) |u|^{t-2} u u_{n}\eta _{\rho }\, {\text {d}}x \right] . \end{aligned}$$

Set

$$\begin{aligned} I_{n, \rho }^{1}&= \left( 1+ |\nabla u_{n}|_{p}^{p} \right) \int _{{\mathbb {R}}^{N}} |\nabla u_{n}|^{p} \eta _{\rho }\, {\text {d}}x + \int _{{\mathbb {R}}^{N}} V(\varepsilon x) |u_{n}|^{p}\eta _{\rho }\, {\text {d}}x \\&\quad +\left( 1+ |\nabla u_{n}|_{q}^{q} \right) \int _{{\mathbb {R}}^{N}} |\nabla u_{n}|^{q} \eta _{\rho }\, {\text {d}}x + \int _{{\mathbb {R}}^{N}} V(\varepsilon x) |u_{n}|^{q}\eta _{\rho }\, {\text {d}}x -\int _{{\mathbb {R}}^{N}} g(\varepsilon x, u_{n})u_{n}\eta _{\rho }\, {\text {d}}x, \\ I_{n, \rho }^{2}&=\left( 1+ |\nabla u_{n}|_{p}^{p} \right) \int _{{\mathbb {R}}^{N}} |\nabla u|^{p}\eta _{\rho }\, {\text {d}}x +\int _{{\mathbb {R}}^{N}} V(\varepsilon x) |u|^{p}\eta _{\rho }\, {\text {d}}x \\&\quad - \left( 1+ |\nabla u_{n}|_{p}^{p} \right) \int _{{\mathbb {R}}^{N}} |\nabla u|^{p-2}\nabla u \cdot \nabla u_{n} \eta _{\rho }\, {\text {d}}x + \int _{{\mathbb {R}}^{N}} V(\varepsilon x) |u|^{p-2} u u_{n}\eta _{\rho }\, {\text {d}}x\\&\quad +\left( 1+ |\nabla u_{n}|_{q}^{q} \right) \int _{{\mathbb {R}}^{N}} |\nabla u|^{q}\eta _{\rho }\, {\text {d}}x +\int _{{\mathbb {R}}^{N}} V(\varepsilon x) |u|^{q}\eta _{\rho }\, {\text {d}}x \\&\quad - \left( 1+ |\nabla u_{n}|_{q}^{q} \right) \int _{{\mathbb {R}}^{N}} |\nabla u|^{q-2}\nabla u \cdot \nabla u_{n} \eta _{\rho }\, {\text {d}}x + \int _{{\mathbb {R}}^{N}} V(\varepsilon x) |u|^{q-2} u u_{n}\eta _{\rho }\, {\text {d}}x, \\ I_{n, \rho }^{3}&= \left( 1+ |\nabla u_{n}|_{p}^{p} \right) \int _{{\mathbb {R}}^{N}} |\nabla u_{n}|^{p-2}\nabla u_{n} \cdot \nabla u \eta _{\rho }\, {\text {d}}x + \int _{{\mathbb {R}}^{N}} V(\varepsilon x) |u_{n}|^{p-2} u_{n}u\eta _{\rho }\, {\text {d}}x \\&\quad + \left( 1+ |\nabla u_{n}|_{q}^{q} \right) \int _{{\mathbb {R}}^{N}} |\nabla u_{n}|^{q-2}\nabla u_{n} \cdot \nabla u \eta _{\rho }\, {\text {d}}x + \int _{{\mathbb {R}}^{N}} V(\varepsilon x) |u_{n}|^{q-2} u_{n}u\eta _{\rho }\, {\text {d}}x\\&\quad -\int _{{\mathbb {R}}^{N}} g(\varepsilon x, u_{n})u \eta _{\rho }\, {\text {d}}x \end{aligned}$$

and

$$\begin{aligned} I_{n, \rho }^{4}= \int _{{\mathbb {R}}^{N}} g(\varepsilon x, u_{n})(u_{n}-u)\eta _{\rho }\, {\text {d}}x. \end{aligned}$$

Then, we have

$$\begin{aligned} 0\le A_{n}^{p}+ A_{n}^{q} \le |I_{n, \rho }^{1}|+ |I_{n, \rho }^{2}|+ |I_{n, \rho }^{3}|+ |I_{n, \rho }^{4}|. \end{aligned}$$

(21)

We note that

$$\begin{aligned} I_{n, \rho }^{1}=&\langle {L}'_{\varepsilon }(u_{n}), u_{n}\eta _{\rho }\rangle - \left[ \left( 1+ |\nabla u_{n}|_{p}^{p} \right) \int _{{\mathbb {R}}^{N}} |\nabla u_{n}|^{p-2}\nabla u_{n} u_{n} \nabla \eta _{\rho }\, {\text {d}}x \right. \\&\left. + \left( 1+ |\nabla u_{n}|_{q}^{q} \right) \int _{{\mathbb {R}}^{N}} |\nabla u_{n}|^{q-2}\nabla u_{n} u_{n} \nabla \eta _{\rho }\, {\text {d}}x\right] \end{aligned}$$

and since $\{u_{n}\eta _{\rho }\}_{n\in {\mathbb {N}}}$ is bounded in ${\mathbb {W}}_{\varepsilon }$, we have $\langle {L}'_{\varepsilon }(u_{n}), u_{n}\eta _{\rho }\rangle =o_{n}(1)$. A direct computation and (20) yield

$$\begin{aligned} \lim _{\rho \rightarrow \infty } \left[ \limsup _{n\rightarrow \infty } \left| \left( 1+ |\nabla u_{n}|_{t}^{t} \right) \int _{{\mathbb {R}}^{N}} |\nabla u_{n}|^{t-2}\nabla u_{n} u_{n} \nabla \eta _{\rho }\, {\text {d}}x\right| \right] =0 \quad {\text { for }} t\in \{p, q\}, \end{aligned}$$

(22)

and so

$$\begin{aligned} \lim _{\rho \rightarrow \infty } \left[ \limsup _{n\rightarrow \infty } \left| I_{n, \rho }^{1}\right| \right] =0. \end{aligned}$$

(23)

On the other hand, the weak convergence and (20) imply

$$\begin{aligned} \lim _{n\rightarrow \infty } |I_{n, \rho }^{2}|&= \lim _{n \rightarrow \infty } \left| \left( 1+ |\nabla u_{n}|_{p}^{p} \right) \int _{{\mathbb {R}}^{N}} |\nabla u|^{p-2} \nabla u \cdot (\nabla u_{n}-\nabla u)\eta _{\rho }\, {\text {d}}x \right. \\&\quad + \int _{{\mathbb {R}}^{N}} V(\varepsilon x)|u|^{p-2} u(u_{n}-u)\eta _{\rho }\, {\text {d}}x \\&\quad + \left( 1+ |\nabla u_{n}|_{q}^{q} \right) \int _{{\mathbb {R}}^{N}} |\nabla u|^{q-2} \nabla u \cdot (\nabla u_{n}-\nabla u)\eta _{\rho }\, {\text {d}}x \\&\left. \quad + \int _{{\mathbb {R}}^{N}} V(\varepsilon x)|u|^{q-2} u(u_{n}-u)\eta _{\rho }\, {\text {d}}x \right| =0. \end{aligned}$$

Furthermore,

$$\begin{aligned} I_{n, \rho }^{3}=&\langle {L}'_{\varepsilon }(u_{n}), u\eta _{\rho }\rangle - \left[ \left( 1+ |\nabla u_{n}|_{p}^{p} \right) \int _{{\mathbb {R}}^{N}} |\nabla u_{n}|^{p-2} \nabla u_{n} u \nabla \eta _{\rho }\, {\text {d}}x \right. \\&\left. + \left( 1+ |\nabla u_{n}|_{q}^{q} \right) \int _{{\mathbb {R}}^{N}} |\nabla u_{n}|^{q-2} \nabla u_{n} u \nabla \eta _{\rho }\, {\text {d}}x \right] , \end{aligned}$$

and by (20), (22) and $\langle {L}'_{\varepsilon }(u_{n}), u\eta _{\rho }\rangle =o_{n}(1)$, we deduce

$$\begin{aligned} \lim _{\rho \rightarrow \infty } \left[ \limsup _{n\rightarrow \infty } |I_{n, \rho }^{3}|\right] =0. \end{aligned}$$

Finally, from the growth assumptions on g and Theorem 2, we see that

$$\begin{aligned} \lim _{n\rightarrow \infty } |I_{n, \rho }^{4}|=0 \quad {\text { for any }} \rho >R. \end{aligned}$$

(24)

Combining (21), (23), (24), we get

$$\begin{aligned} 0\le \limsup _{n\rightarrow \infty } \left( A_{n}^{p}+ A_{n}^{q}\right) \le 0. \end{aligned}$$

Consequently,

$$\begin{aligned}&\lim _{n\rightarrow \infty } \left[ \int _{{\mathcal {B}}_{R}} \left( |\nabla u_{n}|^{t-2}\nabla u_{n} - |\nabla u|^{t-2} \nabla u\right) \cdot \left( \nabla u_{n}- \nabla u\right) \, {\text {d}}x \right. \\&\qquad \left. + \int _{{\mathcal {B}}_{R}} V(\varepsilon x) \left( |u_{n}|^{t-2}u_{n} - |u|^{t-2} u\right) \left( u_{n}- u\right) \, {\text {d}}x\right] =0 \quad {\text { for }} t\in \{p, q\}. \end{aligned}$$

In particular, if $t\ge 2$, from (7), we have

$$\begin{aligned} \int _{{\mathcal {B}}_{R}} |\nabla u_{n}- \nabla u|^{t}\, {\text {d}}x \le C \int _{{\mathcal {B}}_{R}} \left( |\nabla u_{n}|^{t-2}\nabla u_{n} - |\nabla u|^{t-2} \nabla u\right) \cdot \left( \nabla u_{n}- \nabla u\right) \, {\text {d}}x\rightarrow 0. \end{aligned}$$

When $1<t<2$, by (10) and Hölder inequality, we obtain

$$\begin{aligned}&\int _{{\mathcal {B}}_{R}} |\nabla u_{n}- \nabla u|^{t}\, {\text {d}}x \\&\quad \le C\left[ \int _{{\mathcal {B}}_{R}} \left( |\nabla u_{n}|^{t-2}\nabla u_{n} - |\nabla u|^{t-2} \nabla u\right) \cdot \left( \nabla u_{n}- \nabla u\right) \, {\text {d}}x\right] ^{\frac{t}{2}} \left[ |\nabla u_{n}|_{t}^{t}+|\nabla u|_{t}^{t} \right] ^{\frac{2-t}{2}} \\&\quad \le C \left[ \int _{{\mathcal {B}}_{R}} \left( |\nabla u_{n}|^{t-2}\nabla u_{n} - |\nabla u|^{t-2} \nabla u\right) \cdot \left( \nabla u_{n}- \nabla u\right) \, {\text {d}}x\right] ^{\frac{t}{2}}\rightarrow 0. \end{aligned}$$

Arguing as before, we deduce that for $t\in \{p, q\}$

$$\begin{aligned} \int _{{\mathcal {B}}_{R}} V(\varepsilon x) |u_{n}-u|^{t} \, {\text {d}}x \rightarrow 0 {\text { as }} n\rightarrow \infty . \end{aligned}$$

Accordingly, for $t\in \{p, q\}$, we get

$$\begin{aligned} \lim _{n\rightarrow \infty } \int _{{\mathcal {B}}_{R}} \left[ |\nabla u_{n}|^{t}+ V(\varepsilon x) |u_{n}|^{t}\right] \, {\text {d}}x = \int _{{\mathcal {B}}_{R}} \left[ |\nabla u|^{t}+ V(\varepsilon x) |u|^{t}\right] \, {\text {d}}x, \end{aligned}$$

which gives (19). $\square$

Now, we show that ${L}_{\varepsilon }$ verifies the Palais–Smale compactness condition.

Lemma 7

${L}_{\varepsilon }$ satisfies the Palais–Smale condition at any level $c\in {\mathbb {R}}$.

Proof

Let $\{u_{n}\}_{n\in {\mathbb {N}}}\subset {\mathbb {W}}_{\varepsilon }$ be a ${\text {(PS)}}_{c}$ sequence for ${L}_{\varepsilon }$. From Lemma 4, we know that $\{u_{n}\}_{n\in {\mathbb {N}}}$ is bounded in ${\mathbb {W}}_{\varepsilon }$. Up to a subsequence, we may assume that $u_{n}\rightharpoonup u$ in ${\mathbb {W}}_{\varepsilon }$ and $u_{n}\rightarrow u$ in $L^{r}_{loc}({\mathbb {R}}^{N})$ for all $r\in [1, q^{*})$. By Lemma 5, for each $\eta >0,$ there exists $R=R(\eta )>\frac{C}{\eta }$, with $C>0$ independent of $\eta$, such that (19) is satisfied. This together with Lemma 6 implies that

$$\begin{aligned} \Vert u\Vert _{V_{\varepsilon }, p}^{p}+\Vert u\Vert _{V_{\varepsilon }, q}^{q}&\le \liminf _{n\rightarrow \infty } \,(\Vert u_{n}\Vert _{V_{\varepsilon }, p}^{p}+\Vert u_{n}\Vert _{V_{\varepsilon }, q}^{q})\\&\le \limsup _{n\rightarrow \infty } \, (\Vert u_{n}\Vert _{V_{\varepsilon }, p}^{p}+\Vert u_{n}\Vert _{V_{\varepsilon }, q}^{q})\\&=\limsup _{n\rightarrow \infty } \left[ \int _{{\mathcal {B}}_{R}} |\nabla u_{n}|^{p}+|\nabla u_{n}|^{q}+ V(\varepsilon x) (|u_{n}|^{p}+|u_{n}|^{q}) \, {\text {d}}x \right. \\&\quad \left. +\int _{{\mathcal {B}}^{c}_{R}} |\nabla u_{n}|^{p}+|\nabla u_{n}|^{q}+ V(\varepsilon x) (|u_{n}|^{p}+|u_{n}|^{q}) \, {\text {d}}x\right] \\&= \int _{{\mathcal {B}}_{R}} |\nabla u|^{p}+|\nabla u|^{q}+ V(\varepsilon x) (|u|^{p}+|u|^{q}) \, {\text {d}}x\\&\quad +\limsup _{n\rightarrow \infty }\left[ \int _{{\mathcal {B}}^{c}_{R}} |\nabla u_{n}|^{p}+|\nabla u_{n}|^{q}+ V(\varepsilon x) (|u_{n}|^{p}+|u_{n}|^{q}) \, {\text {d}}x\right] \\&<\int _{{\mathcal {B}}_{R}} |\nabla u|^{p}+|\nabla u|^{q}+ V(\varepsilon x) (|u|^{p}+|u|^{q}) \, {\text {d}}x+\eta . \end{aligned}$$

Since $R\rightarrow \infty$ when $\eta \rightarrow 0$, it follows that

$$\begin{aligned} \Vert u\Vert _{V_{\varepsilon }, p}^{p}+\Vert u\Vert _{V_{\varepsilon }, q}^{q}&\le \liminf _{n\rightarrow \infty } (\Vert u_{n}\Vert _{V_{\varepsilon }, p}^{p}+\Vert u_{n}\Vert _{V_{\varepsilon }, q}^{q})\\&\le \limsup _{n\rightarrow \infty } (\Vert u_{n}\Vert _{V_{\varepsilon }, p}^{p}+\Vert u_{n}\Vert _{V_{\varepsilon }, q}^{q})\\&\le \Vert u\Vert _{V_{\varepsilon }, p}^{p}+\Vert u\Vert _{V_{\varepsilon }, q}^{q} \end{aligned}$$

and thus

$$\begin{aligned} \Vert u_{n}\Vert _{V_{\varepsilon }, p}^{p}+\Vert u_{n}\Vert _{V_{\varepsilon }, q}^{q}=\Vert u\Vert _{V_{\varepsilon }, p}^{p}+\Vert u\Vert _{V_{\varepsilon }, q}^{q}+o_{n}(1). \end{aligned}$$

From the Brezis–Lieb lemma [11], we have

$$\begin{aligned} \Vert u_{n}-u\Vert ^{p}_{V_{\varepsilon },p}=\Vert u_{n}\Vert ^{p}_{V_{\varepsilon },p}-\Vert u\Vert _{V_{\varepsilon },p}^{p}+o_{n}(1) \end{aligned}$$

and

$$\begin{aligned} \Vert u_{n}-u\Vert ^{q}_{V_{\varepsilon },q}=\Vert u_{n}\Vert ^{q}_{V_{\varepsilon },q}-\Vert u\Vert _{V_{\varepsilon },q}^{q}+o_{n}(1). \end{aligned}$$

Therefore,

$$\begin{aligned} \Vert u_{n}-u\Vert ^{p}_{V_{\varepsilon },p}+\Vert u_{n}-u\Vert ^{q}_{V_{\varepsilon },q}=o_{n}(1) \end{aligned}$$

which yields $u_{n}\rightarrow u$ in ${\mathbb {W}}_{\varepsilon }$ as $n\rightarrow \infty$. $\square$

Remark 3

We can assume that any ${\text {(PS)}}$ sequence $\{u_{n}\}_{n\in {\mathbb {N}}}$ of ${L}_{\varepsilon }$ is nonnegative. To see this, from $\langle {L}'_{\varepsilon }(u_{n}), u_{n}^{-}\rangle =o_{n}(1)$ and $g(\varepsilon x, t)=0$ for $t\le 0$, we have

$$\begin{aligned}&(1+|\nabla u_{n}|_{p}^{p})\int _{{\mathbb {R}}^{N}} |\nabla u_{n}|^{p-2}\nabla u_{n}\cdot \nabla u^{-}_{n}\,{\text {d}}x +(1+|\nabla u_{n}|_{q}^{q}) \int _{{\mathbb {R}}^{N}} |\nabla u_{n}|^{q-2}\nabla u_{n}\cdot \nabla u^{-}_{n}\,{\text {d}}x \\&\quad \quad + \int _{{\mathbb {R}}^{N}} V(\varepsilon x) (|u_{n}|^{p-2} u_{n}\, +|u_{n}|^{q-2} u_{n})\, u_{n}^{-} \,{\text {d}}x=o_{n}(1), \end{aligned}$$

where $u_{n}^{-}=\min \{u_{n}, 0\}$, and then

$$\begin{aligned} \Vert u_{n}^{-}\Vert _{V_{\varepsilon }, p}^{p}+\Vert u_{n}^{-}\Vert _{V_{\varepsilon }, q}^{q}= o_{n}(1), \end{aligned}$$

namely $u_{n}^{-}\rightarrow 0$ in ${\mathbb {W}}_{\varepsilon }$. In particular, $\{u_{n}^{+}\}_{n\in {\mathbb {N}}}$ is bounded in ${\mathbb {W}}_{\varepsilon }$. Since $|\nabla u_{n}|_{t}^{t}=|\nabla u^{+}_{n}|_{t}^{t}+o_{n}(1)$ and $\Vert u_{n}\Vert _{V_{\varepsilon }, t}=\Vert u_{n}^{+}\Vert _{V_{\varepsilon }, t}+o_{n}(1)$ for $t\in \{p, q\}$, we deduce that ${L}_{\varepsilon }(u_{n})={L}_{\varepsilon }(u^{+}_{n})+o_{n}(1)$ and ${L}'_{\varepsilon }(u_{n})={L}'_{\varepsilon }(u^{+}_{n})+o_{n}(1)$. Hence, ${L}_{\varepsilon }(u^{+}_{n})\rightarrow c$ and ${L}'_{\varepsilon }(u^{+}_{n})\rightarrow 0$ as $n\rightarrow \infty$.

Corollary 1

The functional $\psi _{\varepsilon }$ satisfies the Palais–Smale condition on ${\mathbb {S}}_{\varepsilon }^{+}$ at any level $c\in {\mathbb {R}}$.

Proof

Let $\{u_{n}\}_{n\in {\mathbb {N}}}\subset {\mathbb {S}}^{+}_{\varepsilon }$ be a Palais–Smale sequence for $\psi _{\varepsilon }$ at the level c. Then,

$$\begin{aligned} \psi _{\varepsilon }(u_{n})\rightarrow c \quad {\text { and }} \quad \psi _{\varepsilon }'(u_{n})\rightarrow 0 {\text { in }} (T_{u_{n}} {\mathbb {S}}_{\varepsilon }^{+})'. \end{aligned}$$

By Proposition 1-(c), we see that $\{m_{\varepsilon }(u_{n})\}_{n\in {\mathbb {N}}}\subset {\mathbb {W}}_{\varepsilon }$ is a Palais–Smale sequence for ${L}_{\varepsilon }$ at the level c. From Lemma 7, we deduce that ${L}_{\varepsilon }$ satisfies the ${\text {(PS)}}_{c}$ condition in ${\mathbb {W}}_{\varepsilon }$. Then, up to a subsequence, we can find $u\in {\mathbb {S}}_{\varepsilon }^{+}$ such that

$$\begin{aligned} m_{\varepsilon }(u_{n})\rightarrow m_{\varepsilon }(u) {\text { in }} {\mathbb {W}}_{\varepsilon }. \end{aligned}$$

In view of Lemma 3-(iii), we conclude that $u_{n}\rightarrow u$ in ${\mathbb {S}}_{\varepsilon }^{+}$. $\square$

3 The autonomous problem

In this section, we consider the following autonomous problem related to (1):

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle -\left( 1+ \int _{{\mathbb {R}}^{N}} |\nabla u|^{p}\, {\text {d}}x \right) \Delta _{p}u -\left( 1+ \int _{{\mathbb {R}}^{N}} |\nabla u|^{q}\, {\text {d}}x \right) \Delta _{q}u + V_{0} (u^{p-1}+u^{q-1})=f(u) {\text { in }} {\mathbb {R}}^{N},\\ u\in W^{1, p}({\mathbb {R}}^{N})\cap W^{1, q}({\mathbb {R}}^{N}), \quad u>0 {\text { in }} {\mathbb {R}}^{N}. \end{array} \right. \end{aligned}$$

(25)

Set ${\mathbb {Y}}_{V_{0}}=W^{1, p}({\mathbb {R}}^{N})\cap W^{1, q}({\mathbb {R}}^{N})$ endowed with the norm

$$\begin{aligned} \Vert u\Vert _{{\mathbb {Y}}_{V_{0}}}= \Vert u\Vert _{1, p}+ \Vert u\Vert _{1, q}, \end{aligned}$$

where

$$\begin{aligned} \Vert u\Vert _{1, t}= \left( |\nabla u|_{t}^{t}+V_{0} |u|_{t}^{t} \,\right) ^{\frac{1}{t}} \quad {\text { for all }} t\in \{p, q\}. \end{aligned}$$

Let ${\mathcal {L}}_{V_{0}}: {\mathbb {Y}}_{V_{0}}\rightarrow {\mathbb {R}}$ be the energy functional associated with (25), then

$$\begin{aligned} {\mathcal {L}}_{V_{0}}(u)= \frac{1}{p}\Vert u\Vert _{1, p}^{p}+\frac{1}{2p}|\nabla u|^{2p}_{p}+ \frac{1}{q}\Vert u\Vert _{1, q}^{q}+\frac{1}{2q}|\nabla u|^{2q}_{q}-\int _{{\mathbb {R}}^{N}} F(u) \, {\text {d}}x. \end{aligned}$$

It is easy to check that ${\mathcal {L}}_{V_{0}}\in {\mathcal {C}}^{1}({\mathbb {Y}}_{V_{0}}, {\mathbb {R}})$ and that

$$\begin{aligned} \langle {\mathcal {L}}'_{V_{0}}(u), \varphi \rangle&=(1+|\nabla u|_{p}^{p}) \int _{{\mathbb {R}}^{N}} |\nabla u|^{p-2} \nabla u \cdot \nabla \varphi \, {\text {d}}x+(1+|\nabla u|_{q}^{q})\int _{{\mathbb {R}}^{N}} |\nabla u|^{q-2} \nabla u \cdot \nabla \varphi \, {\text {d}}x\\&\quad +V_{0} \left[ \int _{{\mathbb {R}}^{N}} |u|^{p-2}u\,\varphi \, {\text {d}}x+ \int _{{\mathbb {R}}^{N}} |u|^{q-2}u\,\varphi \, {\text {d}}x \right] - \int _{{\mathbb {R}}^{N}} f(u)\varphi \, {\text {d}}x \end{aligned}$$

for any $u, \varphi \in {\mathbb {Y}}_{V_{0}}$.

The Nehari manifold ${\mathcal {M}}_{V_{0}}$ associated with ${\mathcal {L}}_{V_{0}}$ is

$$\begin{aligned} {\mathcal {M}}_{V_{0}} = \left\{ u\in {\mathbb {Y}}_{V_{0}}\setminus \{0\} : \langle {\mathcal {L}}'_{V_{0}}(u), u\rangle =0 \right\} , \end{aligned}$$

and we set

$$\begin{aligned} d_{V_{0}}=\inf _{u\in {\mathcal {M}}_{V_{0}}} {\mathcal {L}}_{V_{0}}(u). \end{aligned}$$

Denote by ${\mathbb {S}}_{V_{0}}$ the unit sphere of ${\mathbb {Y}}_{V_{0}}$ and set ${\mathbb {S}}_{V_{0}}^{+}= {\mathbb {S}}_{V_{0}}\cap {\mathbb {Y}}_{V_{0}}^{+}$, where

$$\begin{aligned} {\mathbb {Y}}_{V_{0}}^{+}=\left\{ u\in {\mathbb {Y}}_{V_{0}}: |{{\,\mathrm{supp}\,}}(u^{+})|>0 \right\} . \end{aligned}$$

Note that, ${\mathbb {S}}_{V_{0}}^{+}$ is an incomplete ${\mathcal {C}}^{1,1}$-manifold of codimension one contained in ${\mathbb {Y}}_{V_{0}}^{+}$. Thus, ${\mathbb {Y}}_{V_{0}}= T_{u}{\mathbb {S}}_{V_{0}}^{+}\oplus {\mathbb {R}}u$ for each $u\in {\mathbb {S}}_{V_{0}}^{+}$, where

$$\begin{aligned} T_{u}{\mathbb {S}}_{V_{0}}^{+}&=\left\{ v\in {\mathbb {Y}}_{V_{0}} : (1+|\nabla u|_{p}^{p})\int _{{\mathbb {R}}^{N}} |\nabla u|^{p-2} \nabla u \cdot \nabla v\, {\text {d}}x+(1+|\nabla u|_{q}^{q})\int _{{\mathbb {R}}^{N}} |\nabla u|^{q-2} \nabla u \cdot \nabla v\, {\text {d}}x \right. \\&\left. \qquad +V_{0} \int _{{\mathbb {R}}^{N}} (|u|^{p-2}u+|u|^{q-2}u)v\, {\text {d}}x=0\right\} . \end{aligned}$$

Arguing as in Sect. 2, we can see that the following results hold.

Lemma 8

Under the assumptions $(f_1)$-$(f_4)$, the following properties hold:

• (i) For each $u\in {\mathbb {Y}}_{V_{0}}^{+}$, there exists a unique $t_{u}>0$ such that if $\alpha _{u}(t)= {\mathcal {L}}_{V_{0}}(tu)$, then $\alpha '_{u}(t)>0$ for $0<t<t_{u}$ and $\alpha '_{u}(t)<0$ for $t>t_{u}$.

• (ii) There exists $\tau >0$ independent of u such that $t_{u}\ge \tau$ for any $u\in {\mathbb {S}}_{V_{0}}^{+}$ and for each compact set ${\mathcal {W}}\subset {\mathbb {S}}_{V_{0}}^{+},$ there is a positive constant $C_{{\mathcal {W}}}$ such that $t_{u}\le C_{{\mathcal {W}}}$ for any $u\in {\mathcal {W}}$.

• (iii) The map ${\hat{m}}_{V_{0}}: {\mathbb {Y}}_{V_{0}}^{+}\rightarrow {\mathcal {M}}_{V_{0}}$ given by ${\hat{m}}_{V_{0}}(u)= t_{u}u$ is continuous and $m_{V_{0}}= {\hat{m}}_{V_{0}}|_{{\mathbb {S}}_{V_{0}}^{+}}$ is a homeomorphism between ${\mathbb {S}}_{V_{0}}^{+}$ and ${\mathcal {M}}_{V_{0}}$. Moreover, $m_{V_{0}}^{-1}(u)=\frac{u}{\Vert u\Vert _{{\mathbb {Y}}_{V_{0}}}}$.

• (iv) If there is a sequence $\{u_{n}\}_{n\in {\mathbb {N}}}\subset {\mathbb {S}}_{V_{0}}^{+}$ such that ${\mathrm{dist}}(u_{n}, \partial {\mathbb {S}}_{V_{0}}^{+})\rightarrow 0,$ then $\Vert m_{V_{0}}(u_{n})\Vert _{{\mathbb {Y}}_{V_{0}}}\rightarrow \infty$ and ${\mathcal {L}}_{V_{0}}(m_{V_{0}}(u_{n}))\rightarrow \infty$.

Let us consider the maps

$$\begin{aligned} {\hat{\psi }}_{V_{0}}: {\mathbb {Y}}_{V_{0}}^{+} \rightarrow {\mathbb {R}}\quad {\text { and }} \quad \psi _{V_{0}}: {\mathbb {S}}_{V_{0}}^{+}\rightarrow {\mathbb {R}}, \end{aligned}$$

defined as ${\hat{\psi }}_{V_{0}}(u)= {\mathcal {L}}_{V_{0}}({\hat{m}}_{V_{0}}(u))$ and $\psi _{V_{0}}={\hat{\psi }}_{V_{0}}|_{{\mathbb {S}}_{V_{0}}^{+}}$.

Proposition 2

Assume that $(f_{1})$-$(f_{4})$ are satisfied. Then,

• (a) ${\hat{\psi }}_{V_{0}} \in {\mathcal {C}}^{1}({\mathbb {Y}}_{V_{0}}^{+}, {\mathbb {R}})$ and

  $$\begin{aligned} \langle {\hat{\psi }}_{V_{0}}'(u), v\rangle = \frac{\Vert {\hat{m}}_{V_{0}}(u)\Vert _{{\mathbb {Y}}_{V_{0}}}}{\Vert u\Vert _{{\mathbb {Y}}_{V_{0}}}} \langle {\mathcal {L}}_{V_{0}}'({\hat{m}}_{V_{0}}(u)), v\rangle \quad \forall u\in {\mathbb {Y}}_{V_{0}}^{+}, \forall v\in {\mathbb {Y}}_{V_{0}}. \end{aligned}$$

• (b) $\psi _{V_{0}} \in {\mathcal {C}}^{1}({\mathbb {S}}_{V_{0}}^{+}, {\mathbb {R}})$ and

  $$\begin{aligned} \langle \psi _{V_{0}}'(u), v \rangle = \Vert m_{V_{0}}(u)\Vert _{{\mathbb {Y}}_{V_{0}}} \langle {\mathcal {L}}_{V_{0}}'(m_{V_{0}}(u)), v\rangle , \quad \forall v\in T_{u}{\mathbb {S}}_{V_{0}}^{+}. \end{aligned}$$

• (c) If $\{u_{n}\}_{n\in {\mathbb {N}}}$ is a ${\text {(PS)}}_{d}$ sequence for $\psi _{V_{0}}$, then $\{m_{V_{0}}(u_{n})\}_{n\in {\mathbb {N}}}$ is a ${\text {(PS)}}_{d}$ sequence for ${\mathcal {L}}_{V_{0}}$. If $\{u_{n}\}_{n\in {\mathbb {N}}}\subset {\mathcal {M}}_{V_{0}}$ is a bounded ${\text {(PS)}}_{d}$ sequence for ${\mathcal {L}}_{V_{0}}$, then $\{m_{V_{0}}^{-1}(u_{n})\}_{n\in {\mathbb {N}}}$ is a ${\text {(PS)}}_{d}$ sequence for $\psi _{V_{0}}$.

• (d) u is a critical point of $\psi _{V_{0}}$ if, and only if, $m_{V_{0}}(u)$ is a nontrivial critical point for ${\mathcal {L}}_{V_{0}}$. Moreover, the corresponding critical values coincide and

  $$\begin{aligned} \inf _{u\in {\mathbb {S}}_{V_{0}}^{+}} \psi _{V_{0}}(u)= \inf _{u\in {\mathcal {M}}_{V_{0}}} {\mathcal {L}}_{V_{0}}(u). \end{aligned}$$

Remark 4

As in [46], we have the following characterization of the infimum of ${\mathcal {L}}_{V_{0}}$ over ${\mathcal {M}}_{V_{0}}$:

$$\begin{aligned} 0<d_{V_{0}}&=\inf _{u\in {\mathcal {M}}_{V_{0}}} {\mathcal {L}}_{V_{0}}(u)=\inf _{u\in {\mathbb {Y}}_{V_{0}}^{+}} \max _{t>0} {\mathcal {L}}_{V_{0}}(tu)=\inf _{u\in {\mathbb {S}}_{V_{0}}^{+}} \max _{t>0} {\mathcal {L}}_{V_{0}}(tu). \end{aligned}$$

The next lemma allows us to assume that the weak limit of a ${\text {(PS)}}_{d_{V_{0}}}$ sequence of ${\mathcal {L}}_{V_{0}}$ is nontrivial.

Lemma 9

Let $\{u_{n}\}_{n\in {\mathbb {N}}}\subset {\mathbb {Y}}_{V_{0}}$ be a ${\text {(PS)}}_{d_{V_{0}}}$ sequence for ${\mathcal {L}}_{V_{0}}$ such that $u_{n}\rightharpoonup 0$ in ${\mathbb {Y}}_{V_{0}}$. Then, one and only one of the following alternatives occurs:

• (a) $u_{n}\rightarrow 0$ in ${\mathbb {Y}}_{V_{0}}$, or

• (b) there is a sequence $\{y_{n}\}_{n\in {\mathbb {N}}}\subset {\mathbb {R}}^{N}$ and constants $R, \beta >0$ such that

  $$\begin{aligned} \liminf _{n\rightarrow \infty }\int _{{\mathcal {B}}_{R}(y_{n})} |u_{n}|^{q} \, {\text {d}}x \ge \beta . \end{aligned}$$

Proof

Assume that (b) does not hold. Since $\{u_{n}\}_{n\in {\mathbb {N}}}$ is bounded in ${\mathbb {Y}}_{V_{0}}$, we can apply Lemma 1 to see that

$$\begin{aligned} u_{n}\rightarrow 0 \quad {\text { in }} L^{r}({\mathbb {R}}^{N}) {\text { for all }} r \in (p, q^{*}). \end{aligned}$$

In particular, by $(f_{1})$–$(f_{2})$, it follows that

$$\begin{aligned} \int _{{\mathbb {R}}^{N}} f(u_{n})u_{n}\, {\text {d}}x =o_{n}(1) \quad {\text { as }} n\rightarrow \infty . \end{aligned}$$

Recalling that $\langle {\mathcal {L}}'_{V_{0}}(u_{n}), u_{n}\rangle =o_{n}(1)$, we have

$$\begin{aligned} \Vert u_{n}\Vert _{1,p}^{p}+\Vert u_{n}\Vert _{1,q}^{q}\le \int _{{\mathbb {R}}^{N}} f(u_{n}) u_{n}\, {\text {d}}x=o_{n}(1), \end{aligned}$$

that is $\Vert u_{n}\Vert _{{\mathbb {Y}}_{V_{0}}}\rightarrow 0$ as $n\rightarrow \infty$ and the item (a) holds true. $\square$

Remark 5

From the above result, we deduce that if u is the weak limit of a ${\text {(PS)}}_{d_{V_{0}}}$ sequence for ${\mathcal {L}}_{V_{0}}$, then we can assume $u\ne 0$. In fact, if $u_{n}\rightharpoonup 0$ in ${\mathbb {Y}}_{V_{0}}$ and, if $u_{n}\nrightarrow 0$ in ${\mathbb {Y}}_{V_{0}}$, by Lemma 9, we can find $\{y_{n}\}_{n\in {\mathbb {N}}}\subset {\mathbb {R}}^{N}$ and $R, \beta >0$ such that

$$\begin{aligned} \liminf _{n\rightarrow \infty }\int _{{\mathcal {B}}_{R}(y_{n})} |u_{n}|^{q} \, {\text {d}}x \ge \beta . \end{aligned}$$

Set $v_{n}(x)=u_{n}(x+y_{n})$. Then, using the invariance of ${\mathbb {R}}^N$ by translation, we see that $\{v_{n}\}_{n\in {\mathbb {N}}}$ is a bounded ${\text {(PS)}}_{d_{V_{0}}}$ sequence for ${\mathcal {L}}_{V_{0}}$ such that $v_{n}\rightharpoonup v$ in ${\mathbb {Y}}_{V_{0}}$ for some $v\ne 0$.

In what follows, we prove the existence of a positive ground-state solution for (25).

Theorem 3

Let $\{u_{n}\}_{n\in {\mathbb {N}}}\subset {\mathbb {Y}}_{V_{0}}$ be a Palais–Smale sequence of ${\mathcal {L}}_{V_{0}}$ at the level $d_{V_{0}}$. Then, there exists $u\in {\mathbb {Y}}_{V_{0}}\setminus \{0\}$ with $u\ge 0$ such that, up to a subsequence, $u_{n}\rightarrow u$ in ${\mathbb {Y}}_{V_{0}}$. Moreover, u is a positive ground-state solution to (25).

Proof

As in the proof of Lemma 7, we can see that $\{u_{n}\}_{n\in {\mathbb {N}}}$ is a bounded sequence in ${\mathbb {Y}}_{V_{0}}$ so, going if necessary to a subsequence, we may assume that

$$\begin{aligned} \begin{aligned} \begin{array}{ll} u_{n}\rightharpoonup u &{}{\text { in }} {\mathbb {Y}}_{V_{0}}, \\ u_{n}\rightarrow u &{}{\text { in }} L^{r}_{loc}({\mathbb {R}}^{N}) {\text { for all }} r\in [1, p^{*}). \end{array} \end{aligned} \end{aligned}$$

(26)

From Remark 5, we may suppose that $u\ne 0$. Moreover, we may assume that

$$\begin{aligned} |\nabla u_{n}|^{p}_{p}\rightarrow t_{1} \quad {\text { and }} \quad |\nabla u_{n}|^{q}_{q}\rightarrow t_{2}. \end{aligned}$$

Step 1 $\nabla u_{n}\rightarrow \nabla u$ a.e. in ${\mathbb {R}}^{N}$.

Fix $\varphi \in {\mathcal {C}}^{\infty }_{c}({\mathbb {R}}^{N})$. Since $u_{n}\rightharpoonup u$ in ${\mathbb {Y}}_{V_{0}}$ and ${\mathcal {L}}'_{V_{0}}(u_{n})\rightarrow 0$, we have that $\langle {\mathcal {L}}'_{V_{0}}(u_{n})-{\mathcal {L}}'_{V_{0}}(u), (u_{n}-u)\varphi \rangle =o_{n}(1)$. Therefore,

$$\begin{aligned} o_{n}(1)&=\langle {\mathcal {L}}'_{V_{0}}(u_{n})-{\mathcal {L}}'_{V_{0}}(u), (u_{n}-u)\varphi \rangle \nonumber \\&=(1+|\nabla u_{n}|_{p}^{p}) \int _{{\mathbb {R}}^{N}} (|\nabla u_{n}|^{p-2}\nabla u_{n}-|\nabla u|^{p-2}\nabla u)\cdot \nabla [(u_{n}-u)\varphi ] \,{\text {d}}x \nonumber \\&\quad +(1+|\nabla u_{n}|_{q}^{q}) \int _{{\mathbb {R}}^{N}} (|\nabla u_{n}|^{q-2}\nabla u_{n}-|\nabla u|^{q-2}\nabla u)\cdot \nabla [(u_{n}-u)\varphi ] \,{\text {d}}x \nonumber \\&\quad +[(1+|\nabla u_{n}|_{p}^{p})-(1+|\nabla u|_{p}^{p})]\int _{{\mathbb {R}}^{N}} |\nabla u|^{p-2} \nabla u \cdot \nabla [(u_{n}-u)\varphi ]\,{\text {d}}x \nonumber \\&\quad +[(1+|\nabla u_{n}|_{q}^{q})-(1+|\nabla u|_{q}^{q})]\int _{{\mathbb {R}}^{N}} |\nabla u|^{q-2} \nabla u \cdot \nabla [(u_{n}-u)\varphi ] \,{\text {d}}x \nonumber \\&\quad +\int _{{\mathbb {R}}^{N}} V_{0}|u_{n}|^{p-2}u_{n}(u_{n}-u)\varphi \,{\text {d}}x+\int _{{\mathbb {R}}^{N}} V_{0}|u_{n}|^{q-2}u_{n}(u_{n}-u)\varphi \,{\text {d}}x\nonumber \\&\quad -\int _{{\mathbb {R}}^{N}} f(u_{n})(u_{n}-u)\varphi \,{\text {d}}x \nonumber \\&\quad +(1+|\nabla u|_{p}^{p}) \int _{{\mathbb {R}}^{N}} |\nabla u|^{p-2}\nabla u\cdot \nabla [(u_{n}-u)\varphi ]\,{\text {d}}x \nonumber \\&\quad +(1+|\nabla u|_{q}^{q}) \int _{{\mathbb {R}}^{N}} |\nabla u|^{q-2}\nabla u\cdot \nabla [(u_{n}-u)\varphi ]\,{\text {d}}x+o_{n}(1) \nonumber \\&= (1+|\nabla u_{n}|_{p}^{p}) \int _{{\mathbb {R}}^{N}} (|\nabla u_{n}|^{p-2}\nabla u_{n}-|\nabla u|^{p-2}\nabla u)\cdot \nabla [(u_{n}-u)\varphi ] \,{\text {d}}x \nonumber \\&\quad +(1+|\nabla u_{n}|_{q}^{q}) \int _{{\mathbb {R}}^{N}} (|\nabla u_{n}|^{q-2}\nabla u_{n}-|\nabla u|^{q-2}\nabla u)\cdot \nabla [(u_{n}-u)\varphi ] \,{\text {d}}x \nonumber \\&\quad +(1+|\nabla u_{n}|_{p}^{p})\int _{{\mathbb {R}}^{N}} |\nabla u|^{p-2} \nabla u \cdot \nabla [(u_{n}-u)\varphi ] \,{\text {d}}x \nonumber \\&\quad +(1+|\nabla u_{n}|_{q}^{q})\int _{{\mathbb {R}}^{N}} |\nabla u|^{q-2} \nabla u \cdot \nabla [(u_{n}-u)\varphi ] \,{\text {d}}x \nonumber \\&\quad +\int _{{\mathbb {R}}^{N}} V_{0}|u_{n}|^{p-2}u_{n}(u_{n}-u)\varphi \,{\text {d}}x+\int _{{\mathbb {R}}^{N}} V_{0}|u_{n}|^{q-2}u_{n}(u_{n}-u)\varphi \,{\text {d}}x \nonumber \\&\quad -\int _{{\mathbb {R}}^{N}} f(u_{n})(u_{n}-u)\varphi \,{\text {d}}x+o_{n}(1) \nonumber \\&={\mathcal {A}}_{n}^{p}+ {\mathcal {A}}_{n}^{q}+ {\mathcal {B}}_{n}^{p}+ {\mathcal {B}}_{n}^{q}+ {\mathcal {C}}_{n}^{p}+ {\mathcal {C}}_{n}^{q}- {\mathcal {D}}_{n}+o_{n}(1). \end{aligned}$$

(27)

By using (26) and the boundedness of $\{u_{n}\}_{n\in {\mathbb {N}}}$ in ${\mathbb {Y}}_{V_{0}}$, it is easy to check that, for $t\in \{p, q\}$,

$$\begin{aligned}&\int _{{\mathbb {R}}^{N}} |\nabla u|^{t-2}\nabla u\cdot (\nabla u_{n}-\nabla u)\varphi \,{\text {d}}x\rightarrow 0, \end{aligned}$$

(28)

$$\begin{aligned}&\int _{{\mathbb {R}}^{N}} |\nabla u|^{t-2}\nabla u\cdot \nabla \varphi (u_{n}-u) \,{\text {d}}x\rightarrow 0, \end{aligned}$$

(29)

$$\begin{aligned}&\int _{{\mathbb {R}}^{N}} (|\nabla u_{n}|^{t-2}\nabla u_{n}-|\nabla u|^{t-2}\nabla u)\cdot \nabla \varphi (u_{n}-u)\,{\text {d}}x\rightarrow 0, \end{aligned}$$

(30)

$$\begin{aligned}&{\mathcal {C}}_{n}^{t}=\int _{{\mathbb {R}}^{N}} V_{0}|u_{n}|^{t-2}u_{n}(u_{n}-u)\varphi \,{\text {d}}x\rightarrow 0, \end{aligned}$$

(31)

$$\begin{aligned}&{\mathcal {D}}_{n}=\int _{{\mathbb {R}}^{N}} f(u_{n})(u_{n}-u)\varphi \,{\text {d}}x\rightarrow 0. \end{aligned}$$

(32)

In particular, from the boundedness of $\{|\nabla u_{n}|_{t}\}_{n\in {\mathbb {N}}}$ in ${\mathbb {R}}$ together with (28) and (29), we deduce that

$$\begin{aligned} \begin{aligned}&(1+|\nabla u_{n}|_{t}^{t})\int _{{\mathbb {R}}^{N}} |\nabla u|^{t-2}\nabla u\cdot (\nabla [(u_{n}-u)\varphi ])\,{\text {d}}x \\&\quad =(1+|\nabla u_{n}|_{t}^{t}) \left[ \int _{{\mathbb {R}}^{N}} |\nabla u|^{t-2}\nabla u\cdot (\nabla u_{n}-\nabla u)\varphi \,{\text {d}}x+\int _{{\mathbb {R}}^{N}} |\nabla u|^{t-2}\nabla u\cdot \nabla \varphi (u_{n}-u) \,{\text {d}}x \right] \rightarrow 0. \end{aligned} \end{aligned}$$

(33)

Hence, by combining (27)–(33), we have

$$\begin{aligned} o_{n}(1)= {\mathcal {A}}_{n}^{p}+{\mathcal {A}}_{n}^{q}+o_{n}(1), \end{aligned}$$

from which

$$\begin{aligned} \int _{{\mathbb {R}}^{N}} (|\nabla u_{n}|^{t-2}\nabla u_{n}-|\nabla u|^{t-2}\nabla u)\cdot (\nabla u_{n}-\nabla u)\varphi \,{\text {d}}x\rightarrow 0 \end{aligned}$$

for $t\in \{p, q\}$. Now, if $t\ge 2$, from (7), we get

$$\begin{aligned} \int _{{\mathbb {R}}^{N}} |\nabla u_{n}-\nabla u|^{t}\varphi \,{\text {d}}x\le C\int _{{\mathbb {R}}^{N}} (|\nabla u_{n}|^{t-2}\nabla u_{n}-|\nabla u|^{t-2}\nabla u)\cdot (\nabla u_{n}-\nabla u)\varphi \,{\text {d}}x\rightarrow 0. \end{aligned}$$

When $1<t<2$, from (7), we obtain

$$\begin{aligned} \left( \int _{{\mathbb {R}}^{N}} |\nabla u_{n}- \nabla u|^{t}\varphi \, {\text {d}}x\right) ^{\frac{2}{t}}&\le \left( \int _{{\mathbb {R}}^N} \frac{|\nabla u_{n}-\nabla u|^{2}}{(|\nabla u_{n}| + |\nabla u|)^{2-t}}\varphi \, {\text {d}}x \right) \left( \int _{{\mathbb {R}}^N} (|\nabla u_{n}| + |\nabla u|^{t})\varphi \, {\text {d}}x \right) ^{\frac{2-t}{t}} \\&\le C \int _{{\mathbb {R}}^{N}} \left( |\nabla u_{n}|^{t-2}\nabla u_{n} - |\nabla u|^{t-2} \nabla u\right) \cdot \left( \nabla u_{n}- \nabla u\right) \varphi \, {\text {d}}x\rightarrow 0. \end{aligned}$$

Therefore, for $t\in \{p, q\}$, we have

$$\begin{aligned} \int _{{\mathbb {R}}^{N}} |\nabla u_{n}-\nabla u|^{t}\varphi \,{\text {d}}x\rightarrow 0. \end{aligned}$$

Then, for some subsequence of $\{u_{n}\}_{n\in {\mathbb {N}}}$, we have $\nabla u_{n}\rightarrow \nabla u$ a.e. in ${\mathbb {R}}^{N}$.

Step 2 $|\nabla u_{n}|_{t}\rightarrow |\nabla u|_{t}$ for $t\in \{p, q\}$.

By Step 1 and Fatou’s lemma, we know that $|\nabla u|_{p}^{p}\le t_{1}$ and $|\nabla u|_{q}^{q}\le t_{2}$. Now, we show that

$$\begin{aligned} |\nabla u|_{p}^{p}= t_{1} \quad {\text { and }} \quad |\nabla u|_{q}^{q}= t_{2}. \end{aligned}$$

Assume by contradiction that $|\nabla u|_{p}^{p}<t_{1}$ and $|\nabla u|_{q}^{q}\le t_{2}$. Since $\langle {\mathcal {L}}'_{V_{0}}(u_{n}), \varphi \rangle \rightarrow 0$ for all $\varphi \in {\mathcal {C}}^{\infty }_{c}({\mathbb {R}}^{N})$ and ${\mathcal {C}}^{\infty }_{c}({\mathbb {R}}^{N})$ is dense in ${\mathbb {Y}}_{V_{0}}$, we see that

$$\begin{aligned} (1+t_{1})|\nabla u|_{p}^{p}+(1+t_{2})|\nabla u|_{q}^{q}+V_{0}(|u|_{p}^{p}+|u|_{q}^{q})=\int _{{\mathbb {R}}^{N}} f(u)u\, {\text {d}}x. \end{aligned}$$

Hence,

$$\begin{aligned}&(1+|\nabla u|_{p}^{p})|\nabla u|_{p}^{p}+(1+|\nabla u|_{q}^{q})|\nabla u|_{q}^{q}+V_{0}(|u|_{p}^{p}+|u|_{q}^{q})-\int _{{\mathbb {R}}^{N}} f(u)u\, {\text {d}}x\\&\quad <(1+t_{1})|\nabla u|_{p}^{p}+(1+t_{2})|\nabla u|_{q}^{q}+V_{0}(|u|_{p}^{p}+|u|_{q}^{q})-\int _{{\mathbb {R}}^{N}} f(u)u\, {\text {d}}x=0, \end{aligned}$$

which implies that $\langle {\mathcal {L}}'_{V_{0}}(u), u\rangle <0$. Using $(f_{1})$ and $(f_{2})$, we see that $\langle {\mathcal {L}}'_{V_{0}}(t_{0}u), t_{0}u\rangle >0$ for some $0<t_{0}\ll 1$. Then, we can find $\tau \in (t_{0}, 1)$ such that $\langle {\mathcal {L}}'_{V_{0}}(\tau u), \tau u\rangle =0$. This fact together with the characterization of $d_{V_{0}}$, $t\mapsto \frac{1}{2q} f(t)t-F(t)$ is increasing (by $(f_3)$ and $(f_4)$), the Fatou’s lemma gives

$$\begin{aligned} d_{V_{0}}\le {\mathcal {L}}_{V_{0}}(\tau u)&= {\mathcal {L}}_{V_{0}}(\tau u)- \frac{1}{2q}\langle {\mathcal {L}}_{V_{0}}'(\tau u), \tau u\rangle \\&<{\mathcal {L}}_{V_{0}}(u)- \frac{1}{2q}\langle {\mathcal {L}}_{V_{0}}'(u), u\rangle \\&\le \liminf _{n\rightarrow \infty } \left[ {\mathcal {L}}_{V_{0}}(u_{n})- \frac{1}{2q}\langle {\mathcal {L}}_{V_{0}}'(u_{n}), u_{n}\rangle \right] = d_{V_{0}}, \end{aligned}$$

and this is an absurd. Consequently, $|\nabla u_{n}|_{t}\rightarrow |\nabla u|_{t}$ for $t\in \{p, q\}$ and we have ${\mathcal {L}}'_{V_{0}}(u)=0$.

Step 3 u is positive.

Using $\langle {\mathcal {L}}'_{V_{0}}(u), u^{-}\rangle =0$, where $u^{-}=\min \{u, 0\}$, and $f(t)=0$ for $t\le 0$, we have

$$\begin{aligned} \Vert u^{-}\Vert _{1, p}^{p} + \Vert u^{-}\Vert _{1, q}^{q}\le 0 \end{aligned}$$

which gives $u^{-}=0$, that is $u\ge 0$ in ${\mathbb {R}}^{N}$. Therefore, $u\ge 0$ and $u\not \equiv 0$ in ${\mathbb {R}}^{N}$. Arguing as in [28], we deduce that $u\in L^{\infty }({\mathbb {R}}^{N})\cap {\mathcal {C}}^{1, \alpha }_{loc}({\mathbb {R}}^{N})$ and $|u(x)|\rightarrow 0$ as $|x|\rightarrow \infty$. By means of the Harnack inequality [47], we conclude that $u>0$ in ${\mathbb {R}}^{N}$. $\square$

The next compactness result will be used in the sequel.

Lemma 10

Let $\{u_{n}\}_{n\in {\mathbb {N}}}\subset {\mathcal {M}}_{V_{0}}$ be a sequence such that ${\mathcal {L}}_{V_{0}}(u_{n})\rightarrow d_{V_{0}}$. Then, $\{u_{n}\}_{n\in {\mathbb {N}}}$ has a convergent subsequence in ${\mathbb {Y}}_{V_{0}}$.

Proof

By Lemma 8-(iii), Proposition 2-(d) and the definition of $d_{V_{0}}$ we have that

$$\begin{aligned} v_{n}=m^{-1}_{V_{0}}(u_{n})=\frac{u_{n}}{\Vert u_{n}\Vert _{{\mathbb {Y}}_{V_{0}}}}\in {\mathbb {S}}_{V_{0}}^{+} \quad {\text { for all }} n\in {\mathbb {N}} \end{aligned}$$

and

$$\begin{aligned} \psi _{V_{0}}(v_{n})={\mathcal {L}}_{V_{0}}(u_{n})\rightarrow d_{V_{0}}=\inf _{v\in {\mathbb {S}}_{V_{0}}^{+}}\psi _{V_{0}}(v). \end{aligned}$$

Note that, $(\overline{{\mathbb {S}}}_{V_{0}}^{+}, \delta _{V_{0}})$, where $\delta _{V_{0}}(u, v)=\Vert u-v\Vert _{{\mathbb {Y}}_{V_{0}}}$, is a complete metric space. Consider the map ${\mathcal {G}}: \overline{{\mathbb {S}}}_{V_{0}}^{+}\rightarrow {\mathbb {R}}\cup \{\infty \}$ given by

$$\begin{aligned} {\mathcal {G}}(u)= {\left\{ \begin{array}{ll} \psi _{V_{0}}(u)&{} \text { if }u\in {\mathbb {S}}_{V_{0}}^{+}, \\ \infty &{} \text { if }u\in \partial {\mathbb {S}}_{V_{0}}^{+}. \end{array}\right. } \end{aligned}$$

By Lemma 8-(iv), ${\mathcal {G}}\in {\mathcal {C}}(\overline{{\mathbb {S}}}_{V_{0}}^{+}, {\mathbb {R}}\cup \{\infty \})$, and by Proposition 2-(d), we have that ${\mathcal {G}}$ is bounded below. Then, we can apply Ekeland’s variational principle [20] to deduce that there exists a sequence $\{{\hat{v}}_{n}\}_{n\in {\mathbb {N}}}\subset {\mathbb {S}}_{V_{0}}^{+}$ such that $\{{\hat{v}}_{n}\}_{n\in {\mathbb {N}}}$ is a ${\text {(PS)}}_{d_{V_{0}}}$ sequence for $\psi _{V_{0}}$ at the level $d_{V_{0}}$ and $\Vert {\hat{v}}_{n}-v_{n}\Vert _{{\mathbb {Y}}_{V_{0}}}=o_{n}(1)$. At this point, the proof follows from Proposition 2, Theorem 3, and arguing as in the proof of Corollary 1. $\square$

For the minimax levels $c_{\varepsilon }$ and $d_{V_{0}}$, we have the following relation.

Lemma 11

$\lim _{\varepsilon \rightarrow 0} c_{\varepsilon }=d_{V_{0}}$.

Proof

By Theorem 3, we know that there exists a positive ground-state $\omega$ of (25). Define $\omega _{\varepsilon }(x)= \psi _{\varepsilon }(x)\omega (x)$, where $\psi _{\varepsilon }(x)= \psi (\varepsilon x)$ with $\psi \in {\mathcal {C}}^{\infty }_{c}({\mathbb {R}}^{N})$ such that $0\le \psi \le 1$, $\psi (x)=1$ if $|x|\le 1$ and $\psi (x)=0$ if $|x|\ge 2$. We also assume that $\mathrm{supp}( \psi )\subset {\mathcal {B}}_{2}\subset \Lambda$. By the dominated convergence theorem, it follows that

$$\begin{aligned} \omega _{\varepsilon }\rightarrow \omega {\text { in }} {W}^{p, q}\quad {\text { and }} \quad {\mathcal {L}}_{V_{0}}(\omega _{\varepsilon }) \rightarrow {\mathcal {L}}_{V_{0}}(\omega )= d_{V_{0}} \quad {\text { as }} \varepsilon \rightarrow 0. \end{aligned}$$

(34)

Now, for each $\varepsilon >0,$ there exists $t_{\varepsilon }>0$ such that

$$\begin{aligned} {L}_{\varepsilon }(t_{\varepsilon } \omega _{\varepsilon })=\max _{t\ge 0}\, {L}_{\varepsilon }(t \omega _{\varepsilon }). \end{aligned}$$

Consequently, $\langle {L}_{\varepsilon }'(t_{\varepsilon } \omega _{\varepsilon }), \omega _{\varepsilon }\rangle =0$, that is

$$\begin{aligned}&t^{p}_{\varepsilon }|\nabla \omega _{\varepsilon }|_{p}^{p}+t^{2p}_{\varepsilon }|\nabla \omega _{\varepsilon }|_{p}^{2p}+t^{q}_{\varepsilon }|\nabla \omega _{\varepsilon }|_{q}^{q}+t^{2q}_{\varepsilon }|\nabla \omega _{\varepsilon }|_{q}^{2q} \\&\quad +t^{p}_{\varepsilon }\int _{{\mathbb {R}}^{N}} V(\varepsilon x)\omega ^{p}_{\varepsilon } \,{\text {d}}x+t^{q}_{\varepsilon }\int _{{\mathbb {R}}^{N}} V(\varepsilon x)\omega ^{q}_{\varepsilon } \,{\text {d}}x=\int _{{\mathbb {R}}^{N}} f(t_{\varepsilon } \omega _{\varepsilon })t_{\varepsilon }\omega _{\varepsilon }\, {\text {d}}x. \end{aligned}$$

Let us prove that $t_{\varepsilon }\rightarrow t_{0}\in (0, \infty )$. Assume by contradiction that $t_{\varepsilon }\rightarrow \infty$. Since

$$\begin{aligned} \begin{aligned}&t^{p-2q}_{\varepsilon }|\nabla \omega _{\varepsilon }|_{p}^{p}+t^{2p-2q}_{\varepsilon }|\nabla \omega _{\varepsilon }|_{p}^{2p}+t^{-q}|\nabla \omega _{\varepsilon }|_{q}^{q}+ |\nabla \omega _{\varepsilon }|_{q}^{2q}\\&\quad +t^{p-2q}_{\varepsilon }\int _{{\mathbb {R}}^{N}} V(\varepsilon x)\omega ^{p}_{\varepsilon } \,{\text {d}}x+t^{-q}\int _{{\mathbb {R}}^{N}} V(\varepsilon x)\omega ^{q}_{\varepsilon } \,{\text {d}}x=\int _{{\mathbb {R}}^{N}} \frac{f(t_{\varepsilon } \omega _{\varepsilon })}{(t_{\varepsilon } \omega _{\varepsilon })^{2q-1}}\omega _{\varepsilon }^{2q}\, {\text {d}}x, \end{aligned} \end{aligned}$$

(35)

using (34), $p<2q$ and $(f_3)$, we deduce that $|\nabla \omega |^{2q}_{q}=\infty$ which is impossible. Hence, $t_{0}\in [0, \infty )$. If by contradiction $t_{0}=0$, from $(f_1)$ and $(f_2)$, we see that, for $\zeta \in (0, V_{0})$ fixed, we have

$$\begin{aligned} \left( 1-\frac{\zeta }{V_{0}}\right) \Vert \omega _{\varepsilon }\Vert ^{p}_{V_{\varepsilon , p}}+t^{q-p}_{\varepsilon } \Vert \omega _{\varepsilon }\Vert ^{q}_{V_{\varepsilon , q}}\le C_{\zeta }t^{q-p}_{\varepsilon } \Vert \omega _{\varepsilon }\Vert ^{q^{*}}_{V_{\varepsilon , q}}. \end{aligned}$$

This combined with $q>p$ gives $\Vert \omega \Vert ^{p}_{1, p}=0$, that is a contradiction.

Now, letting $\varepsilon \rightarrow 0$ in (35), we obtain

$$\begin{aligned}&t^{p-2q}_{0}|\nabla \omega |^{p}_{p}+t_{0}^{2p-2q}|\nabla \omega |_{p}^{2p}+t^{-q}_{0}|\nabla \omega |^{q}_{q}+|\nabla \omega |_{q}^{2q}\\&\quad +t^{p-2q}_{0}\int _{{\mathbb {R}}^{N}} V_{0} \omega ^{p} \,{\text {d}}x+t^{-q}_{0}\int _{{\mathbb {R}}^{N}} V_{0} \omega ^{q} \,{\text {d}}x=\int _{{\mathbb {R}}^{N}} \frac{f(t_{0}\omega )}{(t_{0}\omega )^{2q-1}}\omega ^{2q}\,{\text {d}}x. \end{aligned}$$

Using $2q>q>p$, $(f_{4})$ and $\omega \in {\mathcal {M}}_{V_{0}},$ we conclude that $t_{0}=1$.

Finally, we observe that

$$\begin{aligned} c_{\varepsilon }\le \max _{t\ge 0} {L}_{\varepsilon }(t \omega _{\varepsilon })= & {} {L}_{\varepsilon }(t_{\varepsilon } \omega _{\varepsilon })= \mathcal {{\mathcal {L}}}_{V_{0}}(t_{\varepsilon } \omega _{\varepsilon }) + \frac{t_{\varepsilon }^{p}}{p} \int _{{\mathbb {R}}^{N}} (V_{\varepsilon }(x) - V_{0} ) \omega _{\varepsilon }^{p} \, {\text {d}}x\\&+\frac{t_{\varepsilon }^{q}}{q} \int _{{\mathbb {R}}^{N}} (V_{\varepsilon }(x) - V_{0} ) \omega _{\varepsilon }^{q} \, {\text {d}}x. \end{aligned}$$

Since $V(\varepsilon \cdot )$ is bounded on the support of $\omega _{\varepsilon }$, we use the dominated convergence theorem, (34) and the above inequality to see that $\limsup _{\varepsilon \rightarrow 0}c_{\varepsilon }\le d_{V_{0}}$. On the other hand, it follows from $(V_1)$ that $\liminf _{\varepsilon \rightarrow 0}c_{\varepsilon }\ge d_{V_{0}}$. In conclusion, $\lim _{\varepsilon \rightarrow 0}c_{\varepsilon }= d_{V_{0}}$. $\square$

4 Multiplicity of solutions to (12)

In this section, we collect some technical results which will be used to implement the barycenter machinery below. Take $\delta >0$ such that

$$\begin{aligned} M_{\delta }=\left\{ x\in {\mathbb {R}}^{N}: {\mathrm{dist}}(x, M)\le \delta \right\} \subset \Lambda , \end{aligned}$$

and choose a non-increasing function $\eta \in {\mathcal {C}}^{\infty }([0, \infty ), [0, 1])$ such that $\eta (t)=1$ if $0\le t\le \frac{\delta }{2}$, $\eta (t)=0$ if $t\ge \delta$ and $|\eta '(t)|\le c$ for some $c>0$. For any $y\in M$, we define

$$\begin{aligned} \Psi _{\varepsilon , y}(x)=\eta (|\varepsilon x-y|) w\left( \frac{\varepsilon x-y}{\varepsilon }\right) , \end{aligned}$$

and take $t_{\varepsilon }>0$ satisfying

$$\begin{aligned} \max _{t\ge 0} {L}_{\varepsilon }(t \Psi _{\varepsilon , y})={L}_{\varepsilon }(t_{\varepsilon } \Psi _{\varepsilon , y}), \end{aligned}$$

where $w\in {\mathbb {Y}}_{V_{0}}$ is a positive ground-state solution to (25) whose existence is guaranteed by Theorem 3.

Let $\Phi _{\varepsilon }: M\rightarrow {\mathcal {N}}_{\varepsilon }$ be given by

$$\begin{aligned} \Phi _{\varepsilon }(y)= t_{\varepsilon } \Psi _{\varepsilon , y}. \end{aligned}$$

By construction, $\Phi _{\varepsilon }(y)$ has compact support for any $y\in M$.

Lemma 12

The functional $\Phi _{\varepsilon }$ verifies the following limit:

$$\begin{aligned} \lim _{\varepsilon \rightarrow 0} {L}_{\varepsilon }(\Phi _{\varepsilon }(y))=d_{V_0} {\text { uniformly in }} y\in M. \end{aligned}$$

Proof

Suppose that the thesis of the lemma is false. Then, we can find $\delta _{0}>0$, $\{y_{n}\}_{n\in {\mathbb {N}}}\subset M$ and $\varepsilon _{n}\rightarrow 0$ such that

$$\begin{aligned} |{L}_{\varepsilon _{n}}(\Phi _{\varepsilon _{n}}(y_{n}))-d_{V_0}|\ge \delta _{0}. \end{aligned}$$

(36)

Now, for each $n\in {\mathbb {N}}$ and for all $z\in {\mathcal {B}}_{\frac{\delta }{\varepsilon _{n}}}$, we have $\varepsilon _{n} z\in {\mathcal {B}}_{\delta }$, and so

$$\begin{aligned} \varepsilon _{n} z+y_{n}\in {\mathcal {B}}_{\delta }(y_{n})\subset M_{\delta }\subset \Lambda . \end{aligned}$$

Using the definition of $\Phi _{\varepsilon _{n}}(y_{n})$, that $G=F$ in $\Lambda \times {\mathbb {R}}$ and taking the change of variable $z=\frac{\varepsilon _{n}x-y_{n}}{\varepsilon _{n}}$, we have

$$\begin{aligned} {L}_{\varepsilon _{n}}(\Phi _{\varepsilon _{n}}(y_{n}))&=\frac{t^{p}_{\varepsilon _{n}}}{p} \Vert \Psi _{\varepsilon _{n}, y_{n}} \Vert ^{p}_{V_{\varepsilon _{n}},p}+\frac{t^{2p}_{\varepsilon _{n}}}{2p} |\nabla \Psi _{\varepsilon _{n}, y_{n}}|^{2p}_{p}+\frac{t^{q}_{\varepsilon _{n}}}{q} \Vert \Psi _{\varepsilon _{n}, y_{n}} \Vert ^{q}_{V_{\varepsilon _{n}},q}+\frac{t^{2p}_{\varepsilon _{n}}}{2q} |\nabla \Psi _{\varepsilon _{n}, y_{n}}|^{2q}_{q} \nonumber \\&\quad -\int _{{\mathbb {R}}^{N}} G(\varepsilon _{n} x, t_{\varepsilon _{n}} \Psi _{\varepsilon _{n}, y_{n}}) \, {\text {d}}x \nonumber \\&=\frac{t^{p}_{\varepsilon _{n}}}{p} \left( |\nabla (\eta (|\varepsilon _{n}\cdot |) w)|^{p}_{p}+\int _{{\mathbb {R}}^{N}} V(\varepsilon _{n} z+y_{n}) (\eta (|\varepsilon _{n} z|) w(z))^{p} \, {\text {d}}z\right) \nonumber \\&\quad + \frac{t^{2p}_{\varepsilon _{n}}}{2p}|\nabla (\eta (|\varepsilon _{n}\cdot |) w)|^{2p}_{p} \nonumber \\&\quad +\frac{t^{q}_{\varepsilon _{n}}}{q} \left( |\nabla (\eta (|\varepsilon _{n}\cdot |) w)|^{q}_{q}+\int _{{\mathbb {R}}^{N}} V(\varepsilon _{n} z+y_{n}) (\eta (|\varepsilon _{n} z|) w(z))^{q} \, {\text {d}}z\right) \nonumber \\&\quad + \frac{t^{2q}_{\varepsilon _{n}}}{2q}|\nabla (\eta (|\varepsilon _{n}\cdot |) w)|^{2q}_{q} \nonumber \\&\quad -\int _{{\mathbb {R}}^{N}} F(t_{\varepsilon _{n}} \eta (|\varepsilon _{n} z|) w(z)) \, {\text {d}}z. \end{aligned}$$

(37)

Our purpose is to show that $t_{\varepsilon _{n}}\rightarrow 1$ as $n\rightarrow \infty$. First, we prove that $t_{\varepsilon _{n}}\rightarrow t_{0}\in [0, \infty )$. Note that, $\langle {L}'_{\varepsilon _{n}}(\Phi _{\varepsilon _{n}}(y_{n})),\Phi _{\varepsilon _{n}}(y_{n})\rangle =0$ and $g=f$ on $\Lambda \times {\mathbb {R}}$ yield

$$\begin{aligned} \begin{aligned}&\frac{1}{t_{\varepsilon _{n}}^{2q-p}} \Vert \Psi _{\varepsilon _{n}, y_{n}}\Vert _{V_{\varepsilon _{n}},p}^{p} +\frac{1}{t_{\varepsilon }^{2q-2p}} |\nabla \Psi _{\varepsilon _{n}, y_{n}}|^{2p}_{p}+\frac{1}{t_{\varepsilon }^{q}}\Vert \Psi _{\varepsilon _{n}, y_{n}}\Vert _{V_{\varepsilon _{n}},q}^{q}+|\nabla \Psi _{\varepsilon _{n}, y_{n}}|^{2q}_{q}\\&\quad =\int _{{\mathbb {R}}^{N}} \Bigl [ \frac{f(t_{\varepsilon _{n}} \eta (|\varepsilon _{n} z|) w(z))}{(t_{\varepsilon _{n}} \eta (|\varepsilon _{n} z|) w(z))^{2q-1}}\Bigr ] (\eta (|\varepsilon _{n} z|) w(z))^{2q} \, {\text {d}}z. \end{aligned} \end{aligned}$$

(38)

Since $\eta (|x|)=1$ for $x\in {\mathcal {B}}_{\frac{\delta }{2}}$ and ${\mathcal {B}}_{\frac{\delta }{2}}\subset {\mathcal {B}}_{\frac{\delta }{\varepsilon _{n}}}$ for all n large enough, from (38) we deduce that

$$\begin{aligned}&\frac{1}{t_{\varepsilon _{n}}^{2q-p}} \Vert \Psi _{\varepsilon _{n}, y_{n}}\Vert _{V_{\varepsilon _{n}},p}^{p}+\frac{1}{t_{\varepsilon }^{2q-2p}} |\nabla \Psi _{\varepsilon _{n}, y_{n}}|^{2p}_{p}+\frac{1}{t_{\varepsilon }^{q}}\Vert \Psi _{\varepsilon _{n}, y_{n}}\Vert _{V_{\varepsilon _{n}},q}^{q}+|\nabla \Psi _{\varepsilon _{n}, y_{n}}|^{2q}_{q}\\&\quad \ge \int _{{\mathcal {B}}_{\frac{\delta }{2}}} \left[ \frac{f(t_{\varepsilon _{n}} w(z))}{(t_{\varepsilon _{n}} w(z))^{2q-1}}\right] |w(z)|^{2q} \, {\text {d}}z. \end{aligned}$$

Then, using $(f_4)$, we obtain

$$\begin{aligned} \begin{aligned}&\frac{1}{t_{\varepsilon _{n}}^{2q-p}} \Vert \Psi _{\varepsilon _{n}, y_{n}}\Vert _{V_{\varepsilon _{n}},p}^{p} +\frac{1}{t_{\varepsilon }^{2q-2p}} |\nabla \Psi _{\varepsilon _{n}, y_{n}}|^{2p}_{p}+\frac{1}{t_{\varepsilon }^{q}}\Vert \Psi _{\varepsilon _{n}, y_{n}}\Vert _{V_{\varepsilon _{n}},q}^{q}+|\nabla \Psi _{\varepsilon _{n}, y_{n}}|^{2q}_{q}\\&\quad \ge \Bigl [ \frac{f(t_{\varepsilon _{n}} w({\hat{z}}))}{(t_{\varepsilon _{n}} w({\hat{z}}))^{2q-1}}\Bigr ] |w({\hat{z}})|^{2q} |{\mathcal {B}}_{\frac{\delta }{2}}|, \end{aligned} \end{aligned}$$

(39)

where $w({\hat{z}})=\min _{z\in {\overline{{\mathcal {B}}}}_{\frac{\delta }{2}}} w(z)>0$ (w is continuous and positive in ${\mathbb {R}}^N$). If, by contradiction, $t_{\varepsilon _{n}}\rightarrow \infty$, using $2q>q>p$ and the dominated convergence theorem, we have

$$\begin{aligned} \Vert \Psi _{\varepsilon _{n}, y_{n}} \Vert _{V_{\varepsilon _{n}},r}\rightarrow \Vert w\Vert _{1,r}\in (0, \infty ) \quad \forall r\in \{p,q\}, \end{aligned}$$

(40)

and

$$\begin{aligned} \frac{1}{t_{\varepsilon _{n}}^{2q-p}} \Vert \Psi _{\varepsilon _{n}, y_{n}}\Vert _{V_{\varepsilon _{n}},p}^{p}+\frac{1}{t_{\varepsilon }^{2q-2p}} |\nabla \Psi _{\varepsilon _{n}, y_{n}}|^{2p}_{p}+\frac{1}{t_{\varepsilon }^{q}}\Vert \Psi _{\varepsilon _{n}, y_{n}}\Vert _{V_{\varepsilon _{n}},q}^{q}+|\nabla \Psi _{\varepsilon _{n}, y_{n}}|^{2q}_{q}\rightarrow |\nabla \omega |_{q}^{2q}. \end{aligned}$$

(41)

On the other hand, condition $(f_3)$ gives

$$\begin{aligned} \lim _{n\rightarrow \infty } \frac{f(t_{\varepsilon _{n}} w({\hat{z}}))}{(t_{\varepsilon _{n}} w({\hat{z}}))^{2q-1}}=\infty . \end{aligned}$$

(42)

In view of (39), (41) and (42), we obtain an absurd. Therefore, $\{t_{\varepsilon _{n}}\}_{n\in {\mathbb {N}}}$ is bounded, and we may suppose that $t_{\varepsilon _{n}}\rightarrow t_{0}$ for some $t_{0}\ge 0$. Taking into account (38), (40), $(f_1)$–$(f_2)$, we deduce that $t_{0}\in (0, \infty )$. Now, letting $n\rightarrow \infty$ in (38), and using (40) and the dominated convergence theorem, we obtain that

$$\begin{aligned} t_{0}^{p-2q} \Vert w\Vert ^{p}_{1,p}+t_{0}^{2p-2q}|\nabla w|_{p}^{2p}+t_{0}^{-q}\Vert w\Vert _{1,q}^{q}+|\nabla w|_{q}^{2q}=\int _{{\mathbb {R}}^{N}} \frac{f(t_{0} w)}{(t_{0}w)^{2q-1}} \,w^{2q} \, {\text {d}}x. \end{aligned}$$

Since $w\in {\mathcal {M}}_{V_0}$, then

$$\begin{aligned} \Vert w\Vert ^{p}_{1,p}+|\nabla w|_{p}^{2p}+\Vert w\Vert _{1,q}^{q}+|\nabla w|_{q}^{2q}=\int _{{\mathbb {R}}^{N}} f(w) w\, {\text {d}}x, \end{aligned}$$

Combining the above identities, we find

$$\begin{aligned}&(t_{0}^{p-2q}-1)\Vert w\Vert ^{p}_{1,p}+(t_{0}^{2p-2q}-1)|\nabla w|_{p}^{2p}+(t_{0}^{-q}-1)|\nabla w|_{q}^{2q}\\&\quad =\int _{{\mathbb {R}}^{N}} \left[ \frac{f(t_{0} w)}{(t_{0}w)^{2q-1}} -\frac{f(w)}{w^{2q-1}} \right] \,w^{2q} \, {\text {d}}x, \end{aligned}$$

and using $2q>q>p$ and $(f_4)$, we deduce that $t_{0}=1$ and the claim is proved.

By sending $n\rightarrow \infty$ in (37), we have that

$$\begin{aligned} \lim _{n\rightarrow \infty } {L}_{\varepsilon _{n}}(\Phi _{\varepsilon _{n}, y_{n}})={\mathcal {L}}_{V_0}(w)=d_{V_0}, \end{aligned}$$

which is in contrast with (36). This completes the proof of the lemma. $\square$

Let $\rho =\rho (\delta )>0$ be such that $M_{\delta }\subset {\mathcal {B}}_{\rho }$. Define $\varUpsilon : {\mathbb {R}}^{N}\rightarrow {\mathbb {R}}^{N}$ as $\varUpsilon (x)=x$ for $|x|<\rho$ and $\varUpsilon (x)=\frac{\rho x}{|x|}$ for $|x|> \rho$. Finally, we introduce the barycenter map $\beta _{\varepsilon }: {\mathcal {N}}_{\varepsilon }\rightarrow {\mathbb {R}}^{N}$ given by

$$\begin{aligned} \beta _{\varepsilon }(u)=\frac{\displaystyle {\int _{{\mathbb {R}}^{N}} \varUpsilon (\varepsilon x)(|u(x)|^{p}+|u(x)|^{q}) \,{\text {d}}x}}{\displaystyle {\int _{{\mathbb {R}}^{N}} |u(x)|^{p}+|u(x)|^{q} \,{\text {d}}x}}. \end{aligned}$$

Since $M\subset {\mathcal {B}}_{\rho }$, by the definition of $\varUpsilon$ and applying the dominated convergence theorem, we conclude that

$$\begin{aligned} \lim _{\varepsilon \rightarrow 0} \beta _{\varepsilon }(\Phi _{\varepsilon }(y))=y {\text { uniformly in }} y\in M. \end{aligned}$$

(43)

The next compactness result is fundamental for showing that the solutions of (12) are solutions of (1).

Lemma 13

Let $\varepsilon _{n}\rightarrow 0$ and $\{u_{n}\}_{n\in {\mathbb {N}}}\subset {\mathcal {N}}_{\varepsilon _{n}}$ be such that ${L}_{\varepsilon _{n}}(u_{n})\rightarrow d_{V_0}$. Then, there exists $\{{\tilde{y}}_{n}\}_{n\in {\mathbb {N}}}\subset {\mathbb {R}}^{N}$ such that $v_{n}(x)=u_{n}(x+ {\tilde{y}}_{n})$ has a convergent subsequence in ${\mathbb {Y}}_{V_0}$. Moreover, up to a subsequence, $\{y_{n}\}_{n\in {\mathbb {N}}}=\{\varepsilon _{n}{\tilde{y}}_{n}\}_{n\in {\mathbb {N}}}$ is such that $y_{n}\rightarrow y_{0}\in M$.

Proof

As in the proof of Lemma 7, we can prove that $\{u_{n}\}_{n\in {\mathbb {N}}}$ is bounded in ${\mathbb {Y}}_{V_{0}}$. In view of $d_{V_0}>0$, we have that $\Vert u_{n}\Vert _{{\mathbb {W}}_{\varepsilon _{n}}}\nrightarrow 0$. Arguing as in the proof of Lemma 9 and Remark 5, we can find $\{{\tilde{y}}_{n}\}_{n\in {\mathbb {N}}}\subset {\mathbb {R}}^{N}$ and $R, \beta >0$ such that

$$\begin{aligned} \liminf _{n\rightarrow \infty }\int _{{\mathcal {B}}_{R}({\tilde{y}}_{n})} |u_{n}|^{q} {\text {d}}x\ge \beta . \end{aligned}$$

Putting $v_{n}(x)=u_{n}(x+ {\tilde{y}}_{n})$, we see that $\{v_{n}\}_{n\in {\mathbb {N}}}$ is bounded in ${\mathbb {Y}}_{V_0}$, and, up to a subsequence, we may suppose that $v_{n}\rightharpoonup v\not \equiv 0$ in ${\mathbb {Y}}_{V_0}$. Take $t_{n}>0$ such that ${\tilde{v}}_{n}=t_{n}v_{n} \in {\mathcal {M}}_{V_0}$ and set $y_{n}=\varepsilon _{n}{\tilde{y}}_{n}$. Using $u_{n}\in {\mathcal {N}}_{\varepsilon _{n}}$ and $(g_2)$, we get

$$\begin{aligned} d_{V_0}&\le {\mathcal {L}}_{V_0}({\tilde{v}}_{n})\\&\le \frac{1}{p} |\nabla {\tilde{v}}_{n}|_{p}^{p}+\frac{1}{2p} |\nabla {\tilde{v}}_{n}|_{p}^{2p}+\frac{1}{q}|\nabla {\tilde{v}}_{n}|_{q}^{q}+\frac{1}{2q} |\nabla {\tilde{v}}_{n}|_{q}^{2q}+\int _{{\mathbb {R}}^{N}}V(\varepsilon _{n} x+y_{n}) \left( \frac{1}{p}|{\tilde{v}}_{n}|^{p}+\frac{1}{q}|{\tilde{v}}_{n}|^{q}\right) \, {\text {d}}x \\&\quad -\int _{{\mathbb {R}}^{N}} F({\tilde{v}}_{n})\, {\text {d}}x \\&\le \frac{t_{n}^{p}}{p} |\nabla u_{n}|_{p}^{p}+\frac{t_{n}^{2p}}{2p} |\nabla u_{n}|_{p}^{2p}+\frac{t_{n}^{q}}{q} |\nabla u_{n}|_{q}^{q}+\frac{t_{n}^{2q}}{2q} |\nabla u_{n}|_{q}^{2q}+\int _{{\mathbb {R}}^{N}}V(\varepsilon _{n} x) \left( \frac{t_{n}^{p}}{p}|u_{n}|^{p}+\frac{t_{n}^{q}}{q}|u_{n}|^{q}\right) \, {\text {d}}x \\&\quad -\int _{{\mathbb {R}}^{N}} G(\varepsilon _{n} x, t_{n}u_{n})\, {\text {d}}x \\&={L}_{\varepsilon _{n}}(t_{n}u_{n}) \le {L}_{\varepsilon _{n}}(u_{n})= d_{V_0}+ o_{n}(1). \end{aligned}$$

Hence,

$$\begin{aligned} {\mathcal {L}}_{V_0}({\tilde{v}}_{n})\rightarrow d_{V_0} \,{\text { and }} \,\{{\tilde{v}}_{n}\}_{n\in {\mathbb {N}}}\subset {\mathcal {M}}_{V_0}. \end{aligned}$$

(44)

Moreover, $\{{\tilde{v}}_{n}\}_{n\in {\mathbb {N}}}$ is bounded in ${\mathbb {Y}}_{V_0}$ and we may suppose that ${\tilde{v}}_{n}\rightharpoonup {\tilde{v}}$. We may assume that $t_{n}\rightarrow t_{0}\in (0, \infty )$. From the uniqueness of the weak limit, we have that ${\tilde{v}}=t_{0} v\not \equiv 0$. By (44) and Lemma 10, ${\tilde{v}}_{n}\rightarrow {\tilde{v}}$ in ${\mathbb {Y}}_{V_0}$ and thus $\displaystyle {v_{n}\rightarrow v}$ in ${\mathbb {Y}}_{V_0}$. In particular,

$$\begin{aligned} {\mathcal {L}}_{V_0}({\tilde{v}})=d_{V_0} \, {\text { and }} \, \langle {\mathcal {L}}'_{V_0}({\tilde{v}}), {\tilde{v}}\rangle =0. \end{aligned}$$

Next, we prove that $\{y_{n}\}_{n\in {\mathbb {N}}}$ admits a bounded subsequence. Assume, by contradiction, that there exists a subsequence of $\{y_{n}\}_{n\in {\mathbb {N}}}$, still denoted by itself, such that $|y_{n}|\rightarrow \infty$. Let $R>0$ be such that $\Lambda \subset {\mathcal {B}}_{R}$. Then, for n large enough, we have $|y_{n}|>2R$, and for each $x\in {\mathcal {B}}_{\frac{R}{\varepsilon _{n}}}$ we obtain

$$\begin{aligned} |\varepsilon _{n} x+y_{n}|\ge |y_{n}|-|\varepsilon _{n} x|>R. \end{aligned}$$

Then, taking into account that $v_{n}\rightarrow v$ in ${\mathbb {Y}}_{V_0}$, the definition of g, and the dominated convergence theorem, we deduce that

$$\begin{aligned} \Vert v_{n}\Vert _{1,p}^{p}+\Vert v_{n}\Vert _{1,q}^{q}&\le \int _{{\mathbb {R}}^{N}} g(\varepsilon _{n}x+y_{n}, v_{n}) v_{n} \, {\text {d}}x \\&\le \int _{{\mathcal {B}}_{\frac{R}{\varepsilon _{n}}}} {\tilde{f}}(v_{n}) v_{n} \,{\text {d}}x+\int _{{\mathcal {B}}^{c}_{\frac{R}{\varepsilon _{n}}}} f(v_{n}) v_{n} \, {\text {d}}x \\&\le \frac{1}{{K}} \int _{{\mathcal {B}}_{\frac{R}{\varepsilon _{n}}}} V_{0} (|v_{n}|^{p}+|v_{n}|^{q}) \,{\text {d}}x+o_{n}(1) \end{aligned}$$

which implies that

$$\begin{aligned} \left( 1-\frac{1}{{K}}\right) \left( \Vert v_{n}\Vert ^{p}_{1,p}+\Vert v_{n}\Vert ^{q}_{1,q} \right) \le o_{n}(1), \end{aligned}$$

and this gives a contradiction because of $v_{n}\rightarrow v\not \equiv 0$ in ${\mathbb {Y}}_{V_0}$. Therefore, $\{y_{n}\}_{n\in {\mathbb {N}}}$ is bounded in ${\mathbb {R}}^{N}$ and, up to a subsequence, we may assume that $y_{n}\rightarrow y_{0}$. If $y_{0}\notin {\overline{\Lambda }}$, we can proceed as above to conclude $v_{n}\rightarrow 0$ in ${\mathbb {Y}}_{V_0}$. Hence, $y\in {\overline{\Lambda }}$. In order to prove that $V(y_{0})=V_{0}$, we suppose, by contradiction, that $V(y_{0})>V_{0}$. Then, using ${\tilde{v}}_{n}\rightarrow {\tilde{v}}$ in ${\mathbb {Y}}_{V_0}$, Fatou’s lemma and the invariance of ${\mathbb {R}}^{N}$ by translations, we deduce that

$$\begin{aligned} d_{V_0}&={\mathcal {L}}_{V_{0}}({\tilde{v}})\\&< \liminf _{n\rightarrow \infty } \left[ \frac{1}{p} |\nabla {\tilde{v}}_{n}|_{p}^{p}+\frac{1}{2p} |\nabla {\tilde{v}}_{n}|_{p}^{2p}+\frac{1}{q} |\nabla {\tilde{v}}_{n}|_{q}^{q}+\frac{1}{2q} |\nabla {\tilde{v}}_{n}|_{q}^{2q} \right. \\&\quad \left. +\int _{{\mathbb {R}}^{N}}V(\varepsilon _{n} x+y_{n}) \left( \frac{1}{p}|{\tilde{v}}_{n}|^{p}+\frac{1}{q}|{\tilde{v}}_{n}|^{q}\right) \, {\text {d}}x- \int _{{\mathbb {R}}^{N}} F({\tilde{v}}_{n})\, {\text {d}}x \right] \\&\le \liminf _{n\rightarrow \infty } {L}_{\varepsilon _{n}}(t_{n}u_{n}) \le \liminf _{n\rightarrow \infty } {L}_{\varepsilon _{n}} (u_{n})=d_{V_0} \end{aligned}$$

which yields a contradiction. Thus, $V(y_{0})=V_{0}$ and $y_{0}\in {\overline{M}}$. From $(V_2),$ we get that $y_{0}\notin \partial M$ and so $y_{0}\in M$. $\square$

We now define the following subset of the Nehari manifold

$$\begin{aligned} {\widetilde{{\mathcal {N}}}}_{\varepsilon }=\left\{ u\in {\mathcal {N}}_{\varepsilon }: {L}_{\varepsilon }(u)\le d_{V_0}+\pi (\varepsilon )\right\} , \end{aligned}$$

where $\pi (\varepsilon )=\sup _{y\in M}|{L}_{\varepsilon }(\Phi _{\varepsilon }(y))-d_{V_0}|$. By Lemma 12, we deduce that $\pi (\varepsilon )\rightarrow 0$ as $\varepsilon \rightarrow 0$. By the definition of $\pi (\varepsilon )$, we have that, for all $y\in M$ and $\varepsilon >0$, $\Phi _{\varepsilon }(y)\in {\widetilde{{\mathcal {N}}}}_{\varepsilon }$ and ${\widetilde{{\mathcal {N}}}}_{\varepsilon }\ne \emptyset$.

In what follows, we provide an interesting relation between $\widetilde{{\mathcal {N}}}_{\varepsilon }$ and the barycenter map.

Lemma 14

For any $\delta >0$, there holds that

$$\begin{aligned} \lim _{\varepsilon \rightarrow 0} \sup _{u\in \widetilde{{\mathcal {N}}}_{\varepsilon }} {\mathrm{dist}}(\beta _{\varepsilon }(u), M_{\delta })=0. \end{aligned}$$

Proof

Let $\varepsilon _{n}\rightarrow 0$ as $n\rightarrow \infty$. By definition, there exists $\{u_{n}\}_{n\in {\mathbb {N}}}\subset {\widetilde{{\mathcal {N}}}}_{\varepsilon _{n}}$ be such that

$$\begin{aligned} {\mathrm{dist}}(\beta _{\varepsilon _{n}}(u_{n}), M_{\delta })=\sup _{u\in {\widetilde{{\mathcal {N}}}}_{\varepsilon _{n}}} {\mathrm{dist}}(\beta _{\varepsilon _{n}}(u), M_{\delta })+o_{n}(1). \end{aligned}$$

Then, it is enough to find a sequence $\{y_{n}\}_{n\in {\mathbb {N}}}\subset M_{\delta }$ such that

$$\begin{aligned} \lim _{n\rightarrow \infty } |\beta _{\varepsilon _{n}}(u_{n})-y_{n}|=0. \end{aligned}$$

Since ${\mathcal {L}}_{V_{0}}(tu_{n})\le {L}_{\varepsilon _{n}}(tu_{n})$ and $\{u_{n}\}_{n\in {\mathbb {N}}}\subset {\widetilde{{\mathcal {N}}}}_{\varepsilon _{n}}\subset {\mathcal {N}}_{\varepsilon _{n}}$, we have that

$$\begin{aligned} d_{V_{0}}\le c_{\varepsilon _{n}}\le {L}_{\varepsilon _{n}}(u_{n})\le d_{V_{0}}+h(\varepsilon _{n}) \end{aligned}$$

from which ${L}_{\varepsilon _{n}}(u_{n})\rightarrow d_{V_{0}}$. Then, we can apply Lemma 13 to find $\{{\tilde{y}}_{n}\}\subset {\mathbb {R}}^{N}$ such that $y_{n}=\varepsilon _{n}{\tilde{y}}_{n}\in M_{\delta }$ for n large enough. Hence,

$$\begin{aligned} \beta _{\varepsilon _{n}}(u_{n})=y_{n}+\frac{\displaystyle {\int _{{\mathbb {R}}^{N}}[\varUpsilon (\varepsilon _{n}z+y_{n})-y_{n}] (|u_{n}(z+{\tilde{y}}_{n})|^{p}+ |u_{n}(z+{\tilde{y}}_{n})|^{q}) \, {\text {d}}z}}{\displaystyle {\int _{{\mathbb {R}}^{N}} (|u_{n}(z+{\tilde{y}}_{n})|^{p}+|u_{n}(z+{\tilde{y}}_{n})|^{q}) \, {\text {d}}z}}. \end{aligned}$$

Since $u_{n}(\cdot +{\tilde{y}}_{n})$ strongly converges in ${\mathbb {Y}}_{V_{0}}$ and $\varepsilon _{n}z+y_{n}\rightarrow y\in M_{\delta }$ for all $z\in {\mathbb {R}}^N$, we deduce that $\beta _{\varepsilon _{n}}(u_{n})=y_{n}+o_{n}(1)$. Therefore, $\{y_{n}\}_{n\in {\mathbb {N}}}$ satisfies the required property and the lemma is proved. $\square$

5 Proof of the main result

In this section, we give the proof of the main result of this work. We start by proving a multiplicity result for (12). Note that, since ${\mathbb {S}}^{+}_{\varepsilon }$ is not a complete metric space, we cannot use directly an abstract result as in [2,3,4,5, 23]. However, we can apply the abstract category result in [46] to deduce the following result.

Theorem 4

Assume that $(V_1)$–$(V_2)$ and $(f_1)$–$(f_4)$ hold. Then, for any given $\delta >0$ such that $M_{\delta }\subset \Lambda$, there exists ${\bar{\varepsilon }}_\delta >0$ such that, for any $\varepsilon \in (0, {\bar{\varepsilon }}_\delta )$, problem (12) has at least $cat_{M_{\delta }}(M)$ positive solutions.

Proof

For each $\varepsilon >0$, we consider $\gamma _{\varepsilon } : M \rightarrow {\mathbb {S}}_{\varepsilon }^{+}$ given by

$$\begin{aligned} \gamma _{\varepsilon }(y)= m_{\varepsilon }^{-1}(\Phi _{\varepsilon }(y)). \end{aligned}$$

By Lemma 12, we get

$$\begin{aligned} \lim _{\varepsilon \rightarrow 0} \psi _{\varepsilon }(\gamma _{\varepsilon }(y)) = \lim _{\varepsilon \rightarrow 0} {L}_{\varepsilon }(\Phi _{\varepsilon }(y))= d_{V_0} {\text { uniformly in }} y\in M. \end{aligned}$$

Hence, there exists ${\hat{\varepsilon }}>0$ such that

$$\begin{aligned} \widetilde{{\mathcal {S}}}^{+}_{\varepsilon }=\{ w\in {\mathbb {S}}_{\varepsilon }^{+} : \psi _{\varepsilon }(w) \le d_{V_0} + \pi (\varepsilon )\}\ne \emptyset \end{aligned}$$

for all $\varepsilon \in (0, {\hat{\varepsilon }})$, in view of $\psi _{\varepsilon }(M)\subset \widetilde{{\mathcal {S}}}^{+}_{\varepsilon }$. Here, $\pi (\varepsilon )=\sup _{y\in M}|\psi _{\varepsilon }(\gamma _{\varepsilon }(y))-d_{V_0}|\rightarrow 0$ as $\varepsilon \rightarrow 0$.

From the above considerations, and using Lemma 12, Lemma 3-(iii), Lemma 14 and (43), we can find ${\bar{\varepsilon }}= {\bar{\varepsilon }}_{\delta }>0$ such that the diagram of continuous mappings below is well defined for $\varepsilon \in (0, {\bar{\varepsilon }})$:

$$\begin{aligned} M{\mathop {\rightarrow }\limits ^{\Phi _{\varepsilon }}} \Phi _{\varepsilon }(M) {\mathop {\rightarrow }\limits ^{m_{\varepsilon }^{-1}}} \gamma _{\varepsilon }(M){\mathop {\rightarrow }\limits ^{m_{\varepsilon }}} \Phi _{\varepsilon }(M) {\mathop {\rightarrow }\limits ^{\beta _{\varepsilon }}} M_{\delta }. \end{aligned}$$

From (43), we can choose a function $\varsigma (\varepsilon , y)$ with $|\varsigma (\varepsilon , y)|<\frac{\delta }{2}$ uniformly in $y\in M$ and for all $\varepsilon \in (0, {\bar{\varepsilon }})$, such that $\beta _{\varepsilon }(\Phi _{\varepsilon }(y))= y+ \varsigma (\varepsilon , y)$ for all $y\in M$. Therefore, the map ${\mathcal {H}}: [0,1]\times M\rightarrow M_{\delta }$ given by ${\mathcal {H}}(t, y)= y+ (1-t)\varsigma (\varepsilon , y), {\text { with }} (t, y)\in [0,1]\times M$ is a homotopy between $\beta _{\varepsilon } \circ \Phi _{\varepsilon } = (\beta _{\varepsilon } \circ m_{\varepsilon }) \circ (m_{\varepsilon }^{-1}\circ \Phi _{\varepsilon })$ and the inclusion map $id: M \rightarrow M_{\delta }$. Consequently,

$$\begin{aligned} cat_{\gamma _{\varepsilon }(M)} \gamma _{\varepsilon }(M)\ge cat_{M_{\delta }}(M). \end{aligned}$$

(45)

Applying Corollary 1, Lemma 11, and Theorem 27 in [46], with $c= c_{\varepsilon }\le d_{V_0}+\pi (\varepsilon ) =d$ and $K= \gamma _{\varepsilon }(M)$, we deduce that $\Psi _{\varepsilon }$ has at least $cat_{\gamma _{\varepsilon }(M)} \gamma _{\varepsilon }(M)$ critical points on $\widetilde{{\mathcal {S}}}^{+}_{\varepsilon }$. Then, by Proposition 1-(d) and (45), we can infer that ${L}_{\varepsilon }$ admits at least $cat_{M_{\delta }}(M)$ critical points in $\widetilde{{\mathcal {N}}}_{\varepsilon }$. $\square$

The next result will be crucial to study the behavior of the maximum points of the solutions. The proof is based on some arguments found in [2, 21, 26, 33].

Lemma 15

Let $\varepsilon _{n}\rightarrow 0$ and $u_{n}\in \widetilde{{\mathcal {N}}}_{\varepsilon _{n}}$ be a solution to (12). Then, ${L}_{\varepsilon _{n}}(u_{n})\rightarrow d_{V_{0}}$, and there exists $\{{\tilde{y}}_{n}\}_{n\in {\mathbb {N}}}\subset {\mathbb {R}}^{N}$ such that $v_{n}=u_{n}(\cdot +{\tilde{y}}_{n})\in L^{\infty }({\mathbb {R}}^{N})$ and for some ${\bar{C}}>0$ it holds

$$\begin{aligned} |v_{n}|_{\infty }\le {\bar{C}} \quad {\text { for all }} n\in {\mathbb {N}}. \end{aligned}$$

Moreover,

$$\begin{aligned} v_{n}(x)\rightarrow 0 {\text { as }} |x|\rightarrow \infty {\text { uniformly in }} n\in {\mathbb {N}}. \end{aligned}$$

(46)

Proof

Observing that ${L}_{\varepsilon _{n}}(u_{n})\le d_{V_{0}}+\pi (\varepsilon _{n})$ with $\pi (\varepsilon _{n})\rightarrow 0$ as $n\rightarrow \infty$, we can repeat the same arguments used at the beginning of the proof of Lemma 13 to show that ${L}_{\varepsilon _{n}}(u_{n})\rightarrow d_{V_{0}}$. Then, applying Lemma 13, there exists $\{{\tilde{y}}_{n}\}_{n\in {\mathbb {N}}}\subset {\mathbb {R}}^{N}$ such that $v_{n}=u_{n}(\cdot +{\tilde{y}}_{n})\rightarrow v$ in ${\mathbb {Y}}_{V_{0}}$ for some $v\in {\mathbb {Y}}_{V_{0}}\setminus \{0\}$ and $\varepsilon _{n}{\tilde{y}}_{n}\rightarrow y_{0}\in M$.

Let $x_{0}\in {\mathbb {R}}^{N}$, $R_{0}>1$, $0<t<s<1<R_{0}$ and $\xi \in {\mathcal {C}}^{\infty }_{c}({\mathbb {R}}^{N})$ such that

$$\begin{aligned} 0\le \xi \le 1, \quad {{\,\mathrm{supp}\,}}\xi \subset {\mathcal {B}}_{s}(x_{0}), \quad \xi \equiv 1 {\text { on }} {\mathcal {B}}_{t}(x_{0}), \quad |\nabla \xi |\le \frac{2}{s-t}. \end{aligned}$$

For $\zeta \ge 1$, set $A_{n, \zeta , \rho }= \{x\in {\mathcal {B}}_{\rho }(x_{0})\,: \, v_{n}(x)>\zeta \}$ and

$$\begin{aligned} Q_{n}= \int _{A_{n, \zeta , s}} \left( |\nabla v_{n}|^{p}+ |\nabla v_{n}|^{q}\right) \xi ^{q}\, {\text {d}}x. \end{aligned}$$

Note that, $v_{n}$ satisfies

$$\begin{aligned}&A_{n}\int _{{\mathbb {R}}^{N}} |\nabla v_{n}|^{p-2} \nabla v_{n}\cdot \nabla \eta \, {\text {d}}x+B_{n}\int _{{\mathbb {R}}^{N}} |\nabla v_{n}|^{q-2} \nabla v_{n}\cdot \nabla \eta \, {\text {d}}x\\&\qquad +\int _{{\mathbb {R}}^{N}}V_{n} (x)(v^{p-1}_{n}+v^{q-1}_{n}) \eta \, {\text {d}}x = \int _{{\mathbb {R}}^{N}} g_{n}(x, v_{n}) \eta \, {\text {d}}x, \end{aligned}$$

for all $\eta \in {\mathbb {X}}_{\varepsilon }$, where $A_{n}= 1+|\nabla v_{n}|_{p}^{p}$ and $B_{n}=1+|\nabla v_{n}|_{q}^{q}$. Taking $\eta _{n}= \xi^{q} (v_{n} - \zeta)^{+}$ as test function, we obtain

$$\begin{aligned}&A_{n} \left[ q \int _{A_{n, \zeta , s}} \xi ^{q-1} (v_{n}-\zeta )^{+} |\nabla v_{n}|^{p-2}\nabla v_{n} \cdot \nabla \xi \, {\text {d}}x + \int _{A_{n, \zeta , s}} \xi ^{q} |\nabla v_{n}|^{p}\, {\text {d}}x \right] \\&\quad \quad +B_{n} \left[ q \int _{A_{n, \zeta , s}} \xi ^{q-1} (v_{n}-\zeta )^{+} |\nabla v_{n}|^{q-2}\nabla v_{n} \cdot \nabla \xi \, {\text {d}}x + \int _{A_{n, \zeta , s}} \xi ^{q} |\nabla v_{n}|^{q}\, {\text {d}}x \right] \\&\quad \quad + \int _{A_{n, \zeta , s}} V_{n}(v_{n}^{p-1}+ v_{n}^{q-1})\xi ^{q} (v_{n}-\zeta )^{+}\, {\text {d}}x \\&\quad = \int _{A_{n, \zeta , s}} g_{n}(x, v_{n})\xi ^{q} (v_{n}-\zeta )^{+}\, {\text {d}}x. \end{aligned}$$

Let us observe that $v_{n}\rightarrow v\not \equiv 0$ in ${\mathbb {Y}}_{V_{0}}$ so that $1\le A_{n}\le C_{1}$ and $1\le B_{n}\le C_{2}$ for some $C_{1}, C_{2}>0$. Therefore, by $(V_{1})$, we get

$$\begin{aligned} Q_{n}&\le C \int _{A_{n, \zeta , s}} \xi ^{q-1} (v_{n}-\zeta )^{+} |\nabla \xi | \left( |\nabla v_{n}|^{p-1}+ |\nabla v_{n}|^{q-1}\right) \, {\text {d}}x \\&\quad - \int _{A_{n, \zeta , s}} V_{0} \xi ^{q-1} (v_{n}-\zeta )^{+} (v_{n}^{p-1}+ v_{n}^{q-1}) \, {\text {d}}x + \int _{A_{n, \zeta , s}} g_{n}(x, v_{n}) \xi ^{q} (v_{n}-\zeta )^{+}\, {\text {d}}x. \end{aligned}$$

Using the growth assumptions on g, for any $\alpha >0$ there exists $C_{\alpha }>0$ such that

$$\begin{aligned} |g(x, t)|\le \alpha |t|^{p-1}+C_{\alpha }|t|^{q^{*}-1} \quad {\text { for all }} (x, t)\in {\mathbb {R}}^{N}\times {\mathbb {R}}. \end{aligned}$$

Then, choosing $\alpha >0$ sufficiently small, we find

$$\begin{aligned} Q_{n}&\le C \int _{A_{n, \zeta , s}} \xi ^{q-1} (v_{n}-\zeta )^{+} |\nabla \xi | \left( |\nabla v_{n}|^{p-1}+ |\nabla v_{n}|^{q-1}\right) \, {\text {d}}x + \int _{A_{n, \zeta , s}} v_{n}^{q^{*}-1} \xi ^{q} (v_{n}-\zeta )^{+}\, {\text {d}}x. \end{aligned}$$

Proceeding similarly to the proof of Lemma 3.4 in [2], we get

$$\begin{aligned} Q_{n}\le C \left( \int _{A_{n, \zeta , s}} \left| \frac{v_{n}-\zeta }{s-t}\right| ^{q^{*}} \, {\text {d}}x + (\zeta ^{q^{*}} +1)|A_{n, \zeta , s}| \right) . \end{aligned}$$

Exploiting the definition of $\xi$, we can infer that

$$\begin{aligned} \int _{A_{n, \zeta , t}} |\nabla v_{n}|^{q} \, {\text {d}}x \le C \left( \int _{A_{n, \zeta , s}} \left| \frac{v_{n}-\zeta }{s-t}\right| ^{q^{*}} \, {\text {d}}x + (\zeta ^{q^{*}} +1)|A_{n, \zeta , s}| \right) \end{aligned}$$

where C does not depend on $\zeta$ and $\zeta \ge \zeta _{0}\ge 1$, for some constant $\zeta _{0}$.

Now, fix $R_{1}>0$ and define

$$\begin{aligned}&\sigma _{j}= \frac{R_{1}}{2}\left( 1+ \frac{1}{2^{j}}\right) , \\&{\bar{\sigma }}_{j}=\frac{1}{2}\left( \sigma _{j}+\sigma _{j+1}\right) ,\\&\zeta _{j}=\frac{\zeta _{0}}{2} \left( 1- \frac{1}{2^{j+1}}\right) , \\&Q_{j, n}= \int _{A_{n, \zeta _{j}, \sigma _{j}}} \left( (v_{n}-\zeta _{j})^{+}\right) ^{q^{*}}\, {\text {d}}x. \end{aligned}$$

Then, arguing as in Step 1 in Lemma 3.5 in [2], we can see that for each $n\in {\mathbb {N}}$

$$\begin{aligned} Q_{j, n} \le C A^{\tau } Q_{j, n}^{1+\tau } \quad {\text { for all }} j\in {\mathbb {N}}\cup \{0\}, \end{aligned}$$

where $C, \tau >0$ are independent of n and $A>1$. Since $v_{n}\rightarrow v$ in ${\mathbb {Y}}_{V_{0}}$, we see that

$$\begin{aligned} \limsup _{\zeta _{0}\rightarrow \infty } \left( \limsup _{n\rightarrow \infty } Q_{0, n}\right) = \limsup _{\zeta _{0}\rightarrow \infty } \left( \limsup _{n\rightarrow \infty } \int _{A_{n, \zeta _{0}\sigma _{0}}} \left( \left( v_{n} - \frac{\zeta_{0}}{4} \right)^{+} \right)^{q^{*}}\, {\text {d}}x \right) =0. \end{aligned}$$

Then, there exists $n_{0}\in {\mathbb {N}}$ and $\zeta _{0}^{*}>0$ such that

$$\begin{aligned} Q_{0, n} \le C^{\frac{1}{\tau }} A^{-\frac{1}{\tau ^{2}}} \quad {\text { for }} n\ge n_{0} {\text { and }} \zeta _{0}\ge \zeta _{0}^{*}. \end{aligned}$$

Exploiting Lemma 4.7 in [33], we have that $\lim _{j\rightarrow \infty } Q_{j, n}=0$ for $n\ge n_{0}$. On the other hand,

$$\begin{aligned} \lim _{j\rightarrow \infty } Q_{j, n}= \lim _{j\rightarrow \infty } \int _{A_{n, K_{n}, \sigma _{n}}} \left( (v_{n}-\zeta _{j})^{+}\right) ^{q^{*}}\, {\text {d}}x = \int _{A_{n, \frac{\zeta }{2}, \frac{R_{1}}{2}}} \left( \left( v_{n} - \frac{\zeta_{0}}{2} \right)^{+}\right) ^{q^{*}}\, {\text {d}}x. \end{aligned}$$

Hence,

$$\begin{aligned} \int _{A_{n, \frac{\zeta _{0}}{2}, \frac{R_{1}}{2}}} \left( \left( v_{n} - \frac{\zeta_{0}}{2} \right)^{+}\right) ^{q^{*}}\, {\text {d}}x=0 \quad {\text { for all }} n\ge n_{0}, \end{aligned}$$

and so, for all $n\ge n_{0}$,

$$\begin{aligned} v_{n}(x)\le \frac{\zeta _{0}}{2} \quad {\text { for a.e. }} x\in {\mathcal {B}}_{\frac{R_{1}}{2}}(x_{0}). \end{aligned}$$

From the arbitrariness of $x_{0}\in {\mathbb {R}}^{N}$, we deduce that $v_{n}(x)\le \frac{\zeta _{0}}{2}$ for a.e. $x\in {\mathbb {R}}^{N}$ and for all $n\ge n_{0}$, that is

$$\begin{aligned} |v_{n}|_{\infty }\le \frac{\zeta _{0}}{2}, \quad {\text { for all }} n\ge n_{0}. \end{aligned}$$

Setting ${\bar{C}}=\max \left\{ \frac{\zeta _{0}}{2}, |v_{1}|_{\infty }, \dots , |v_{n_{0}-1}|_{\infty } \right\}$, we find that $|v_{n}|_{\infty }\le {\bar{C}}$ for all $n\in {\mathbb {N}}$. Combining this estimate with the regularity results in [28], we can see that $\{v_{n}\}_{n\in {\mathbb {N}}}\subset {\mathcal {C}}^{1, \alpha }_{loc}({\mathbb {R}}^{N})$.

Finally, we show that $v_{n}(x)\rightarrow 0$ as $|x|\rightarrow \infty$ uniformly in $n\in {\mathbb {N}}$. Arguing as before, we can see that for each $\delta >0,$ we have that

$$\begin{aligned} \limsup _{|x_{0}|\rightarrow \infty } \left( \limsup _{n\rightarrow \infty } Q_{0, n}\right) =\limsup _{|x_{0}|\rightarrow \infty } \left( \limsup _{n\rightarrow \infty } \int _{A_{n, K_{0}, \sigma _{0}}} \left( \left( v_{n} - \frac{\delta}{4} \right)^{+}\right) ^{q^{*}}\, {\text {d}}x\right) =0. \end{aligned}$$

Therefore, applying lemma Lemma 4.7 in [33], there exist $R_{*}>0$ and $n_{0}\in {\mathbb {N}}$ such that

$$\begin{aligned} \lim _{j\rightarrow \infty } Q_{j, n}=0 \quad {\text { if }} |x_{0}|>R_{*}, \, {\text { for }} n\ge n_{0}, \end{aligned}$$

which yields

$$\begin{aligned} v_{n}(x)\le \frac{\delta }{4} \quad {\text { for }} x\in {\mathcal {B}}_{\frac{R_{1}}{2}}(x_{0})\, {\text { and }} \, |x_{0}|>R_{*}, {\text { for all }} n\ge n_{0}. \end{aligned}$$

Now, increasing $R_{*}$ if necessary, it holds

$$\begin{aligned} v_{n}(x)\le \frac{\delta }{4} \quad {\text { for }} |x|>R_{*}, {\text { for all }} n\ge n_{0}. \end{aligned}$$

This completes the proof of the lemma. $\square$

We are now ready to provide the main result of this section.

Proof of Theorem 1

Fix $\delta >0$ such that $M_\delta \subset \Lambda$. We first claim that there exists ${\tilde{\varepsilon }}_{\delta }>0$ such that for any $\varepsilon \in (0, {\tilde{\varepsilon }}_{\delta })$ and any solution $u_{\varepsilon } \in \widetilde{{\mathcal {N}}}_{\varepsilon }$ of (12), it holds

$$\begin{aligned} |u_{\varepsilon }|_{L^{\infty }(\Lambda _{\varepsilon }^{c})}<a. \end{aligned}$$

(47)

Suppose, by contradiction, that for some sequence $\varepsilon _{n}\rightarrow 0$ we can find $u_{n}=u_{\varepsilon _{n}}\in \widetilde{{\mathcal {N}}}_{\varepsilon _{n}}$ such that ${L}'_{\varepsilon _{n}}(u_{\varepsilon _{n}})=0$ and

$$\begin{aligned} |u_{n}|_{L^{\infty }(\Lambda _{\varepsilon _{n}}^{c})}\ge a. \end{aligned}$$

(48)

As in Lemma 13, we have that ${L}_{\varepsilon _{n}}(u_{n}) \rightarrow d_{V_0}$ and therefore we can use Lemma 13 to find a sequence $\{{\tilde{y}}_{n}\}_{n\in {\mathbb {N}}}\subset {\mathbb {R}}^{N}$ such that $v_{n}=u_{n}(\cdot +{\tilde{y}}_{n})\rightarrow v$ in ${\mathbb {Y}}_{V_{0}}$ and $\varepsilon _{n}{\tilde{y}}_{n}\rightarrow y_{0} \in M$.

Take $r>0$ such that ${\mathcal {B}}_{r}(y_{0})\subset {\mathcal {B}}_{2r}(y_{0})\subset \Lambda$, and so ${\mathcal {B}}_{\frac{r}{\varepsilon _{n}}}(\frac{y_{0}}{\varepsilon _{n}})\subset \Lambda _{\varepsilon _{n}}$. Then, for any $y\in {\mathcal {B}}_{\frac{r}{\varepsilon _{n}}}({\tilde{y}}_{n})$, it holds

$$\begin{aligned} \left| y - \frac{y_{0}}{\varepsilon _{n}}\right| \le |y- {\tilde{y}}_{n}|+ \left| {\tilde{y}}_{n} - \frac{y_{0}}{\varepsilon _{n}}\right|<\frac{1}{\varepsilon _{n}}(r+o_{n}(1))<\frac{2r}{\varepsilon _{n}}\quad {\text { for }} n {\text { sufficiently large. }} \end{aligned}$$

For these values of n, we have that $\Lambda _{\varepsilon _{n}}^{c}\subset {\mathcal {B}}_{\frac{r}{\varepsilon _{n}}}^{c}({\tilde{y}}_{n})$. In view of (46), there exists $R>0$ such that

$$\begin{aligned} v_{n}(x)<a \quad {\text { for any }} |x|\ge R \, , n\in {\mathbb {N}}, \end{aligned}$$

from which

$$\begin{aligned} u_{n}(x)<a \quad {\text { for any }} x\in {\mathcal {B}}_{R}^{c}({\tilde{y}}_{n})\, , n\in {\mathbb {N}}. \end{aligned}$$

On the other hand, there exists $\nu \in {\mathbb {N}}$ such that for any $n\ge \nu$ it holds

$$\begin{aligned} \Lambda ^{c}_{\varepsilon _{n}}\subset {\mathcal {B}}^{c}_{\frac{r}{\varepsilon _{n}}}({\tilde{y}}_{n})\subset {\mathcal {B}}^{c}_{R}({\tilde{y}}_{n}). \end{aligned}$$

Consequently, $u_{n}(x)<a$ for any $x\in \Lambda ^{c}_{\varepsilon _{n}}$ and $n\ge \nu$, which contradicts (48).

Let ${\bar{\varepsilon }}_{\delta }>0$ be given by Theorem 4 and set $\varepsilon _{\delta }= \min \{{\tilde{\varepsilon }}_{\delta }, {\bar{\varepsilon }}_{\delta }\}$. Take $\varepsilon \in (0, \varepsilon _{\delta })$. By Theorem 4, we obtain at least $cat_{M_{\delta }}(M)$ positive solutions to (12). If $u_{\varepsilon }$ is one of these solutions, we have that $u_{\varepsilon }\in \widetilde{{\mathcal {N}}}_{\varepsilon }$, and we can use (47) and the definition of g to deduce that $g(\varepsilon x, u_{\varepsilon })=f(u_{\varepsilon })$. This means that $u_{\varepsilon }$ is also a solution of (1). Therefore, (1) has at least $cat_{M_{\delta }}(M)$ solutions.

Now, we consider $\varepsilon _{n}\rightarrow 0$ and take a sequence $\{u_{n}\}_{n\in {\mathbb {N}}}\subset {\mathbb {W}}_{\varepsilon _{n}}$ of solutions to (12) as above. In order to study the behavior of the maximum points of $u_{n}$, we first note that, by the definition of g and $(g_{1})$, there exists $\sigma \in (0, a)$ sufficiently small such that

$$\begin{aligned} g(\varepsilon x, t)t\le \frac{V_{0}}{{K}} (t^{p}+t^{q}) \quad {\text { for any }} x\in {\mathbb {R}}^{N}, 0\le t\le \sigma . \end{aligned}$$

(49)

As before, we can take $R>0$ such that

$$\begin{aligned} |u_{n}|_{L^{\infty }({\mathcal {B}}^{c}_{R}({\tilde{y}}_{n}))}<\sigma . \end{aligned}$$

(50)

Up to a subsequence, we may also assume that

$$\begin{aligned} |u_{n}|_{L^{\infty }({\mathcal {B}}_{R}({\tilde{y}}_{n}))}\ge \sigma . \end{aligned}$$

(51)

Otherwise, if this is not the case, we see that $|u_{n}|_{\infty }<\sigma$. Then, it follows from $\langle {L}'_{\varepsilon _{n}}(u_{n}), u_{n}\rangle =0$ and (49) that

$$\begin{aligned} \Vert u_{n}\Vert _{V_{\varepsilon _{n}},p}^{p}+\Vert u_{n}\Vert _{V_{\varepsilon _{n}},q}^{q}\le \int _{{\mathbb {R}}^{N}} g(\varepsilon _{n} x, u_{n}) u_{n} \,{\text {d}}x\le \frac{V_{0}}{{K}} \int _{{\mathbb {R}}^{N}} (|u_{n}|^{p}+|u_{n}|^{q}) \, {\text {d}}x \end{aligned}$$

which implies that $\Vert u_{n}\Vert _{V_{\varepsilon _{n}},p}^{p}, \Vert u_{n}\Vert _{V_{\varepsilon _{n}},q}^{q}\rightarrow 0$, and thus ${L}_{\varepsilon }(u_{n})\rightarrow 0$. This last fact is impossible because ${L}_{\varepsilon }(u_{n})\rightarrow d_{V_{0}}>0$. Hence, (51) holds.

By virtue of (50) and (51), we can see that if $p_{n}$ is a global maximum point of $u_{n}$, then $p_{n}={\tilde{y}}_{n}+q_{n}$ for some $q_{n}\in {\mathcal {B}}_{R}$. Recalling that $\varepsilon _{n}{\tilde{y}}_{n}\rightarrow y_{0}\in M$ and using the fact that $\{q_{n}\}_{n\in {\mathbb {N}}}\subset {\mathcal {B}}_{R}$, we obtain that $\varepsilon _{n}p_{n}\rightarrow y_{0}$. Since V is a continuous function, we deduce that

$$\begin{aligned} \lim _{n\rightarrow \infty }V(\varepsilon _{n}p_{n})= V(y_{0})=V_{0}. \end{aligned}$$

This completes the proof of Theorem 1. $\square$