Halfspaces minimise nonlocal perimeter: a proof via calibrations

Abstract

We consider a nonlocal functional $J_K$ that may be regarded as a nonlocal version of the total variation. More precisely, for any measurable function $u:\mathbb {R}^d\rightarrow \mathbb {R}$, we define $J_K(u)$ as the integral of weighted differences of u. The weight is encoded by a positive kernel K, possibly singular in the origin. We study the minimisation of this energy under prescribed boundary conditions, and we introduce a notion of calibration suited for this nonlocal problem. Our first result shows that the existence of a calibration is a sufficient condition for a function to be a minimiser. As an application of this criterion, we prove that halfspaces are the unique minimisers of $J_K$ in a ball, provided they are admissible competitors. Finally, we outline how to exploit the optimality of hyperplanes to recover a $\varGamma$-convergence result concerning the scaling limit of $J_K$.

1 Introduction

We consider the d-dimensional vector space $\mathbb {R}^d$ equipped with the Euclidean inner product $\cdot$. In this note, we show that halfspaces are the unique local minimisers of the nonlocal functional

$$\begin{aligned} \begin{aligned} J_K(u;\varOmega )&:=\frac{1}{2}\int _{\varOmega }\int _{\varOmega }K(y-x)\left|u(y)-u(x)\right|{\mathrm {d}}y {\mathrm {d}}x \\&\quad +\,\int _{\varOmega }\int _{\varOmega ^c}K(y-x)\left|u(y)-u(x)\right|{\mathrm {d}}y {\mathrm {d}}x, \end{aligned} \end{aligned}$$

(1)

where $\varOmega \subset \mathbb {R}^d$ is a Lebesgue measurable set and $\varOmega ^c$ is its complement, while u and K are positive Lebesgue measurable functions on $\mathbb {R}^d$. Further hypotheses on the reference set $\varOmega$ and on the kernel K are stated below, see Sect. 1.1.

We recall that when $u=\chi _E$ is the characteristic function of the Lebesgue measurable set $E\subset \mathbb {R}^d$, that is $\chi _{E}(x)=1$ if $x\in E$ and $\chi _{E}(x)=0$ otherwise, then $J_K$ can be understood as a nonlocal perimeter of the set E in $\varOmega$. More generally, $J_K(u;\varOmega )$ may be understood as a nonlocal total variation of u in $\varOmega$.

Nonlocal perimeters were firstly introduced by Caffarelli et al. [8] to the purpose of modelling phase field models that feature long-range space interactions. In their work, $K(x) = \left| x \right| ^{-d-s}$, with $s\in (0,1)$. Subsequently, many authors have extended the analysis in several directions, and by now the literature has become vast; as a narrow list of papers that are more closely related to ours, we suggest that the interested reader may consult [3, 7, 9, 12, 19] and the references therein.

Let B be the open unit ball in $\mathbb {R}^d$ with centre in the origin, put $\mathbb {S}^{d-1}:=\partial B$, and let $\mathscr {L}^d$ be the d-dimensional Lebesgue measure. Our aim is to prove the following:

Theorem 1

For all ${\hat{n}}\in \mathbb {S}^{d-1}$, we define $H:=\left\{ x\in \mathbb {R}^d: x\cdot {\hat{n}} > 0\right\}$. Then,

$$\begin{aligned} J_K( \chi _H; B ) \le J_K( v; B ) \end{aligned}$$

for all $\mathscr {L}^d$-measurable $v:\mathbb {R}^d\rightarrow [0,1]$ such that $v(x)=\chi _H(x)$ for $\mathscr {L}^d$-a.e. $x\in B^c$.

When $K>0$$\mathscr {L}^d$-a.e., for any other minimiser u satisfying the same constraint, it holds $u(x)=\chi _H(x)$$\mathscr {L}^d$-a.e. $x\in \mathbb {R}^d$.

The proof that we propose relies on a general criterion for minimality, see Theorem 2, which in turn involves a notion of calibration fitted for the nonlocal problem at stake, see Definition 1.

Let us outline the structure of this note. In the next subsection, we make the mathematical framework of this paper precise and we set the notations in use. Section 2 contains the definition of nonlocal calibration and the Proof of Theorem 1. Lastly, in Sect. 3, as a possible application of our main result, we discuss its role in the analysis of the scaling limit of the functional $J_K$.

1.1 Set-up and notations

We remind that we work in $\mathbb {R}^d$, the d-dimensional Euclidean space, endowed with the inner product $\cdot$ and the associated norm $\left| \, \cdot \, \right|$. We let $\mathscr {L}^d$ and $\mathscr {H}^{d-1}$ be, respectively, the d-dimensional Lebesgue and the $(d-1)$-dimensional Hausdorff measure on $\mathbb {R}^d$. We shall henceforth omit to specify the measure w.r.t. which a set or a function is measurable, when the measure is $\mathscr {L}^d$ or the product $\mathscr {L}^d\otimes \mathscr {L}^d$ on $\mathbb {R}^d\times \mathbb {R}^d$; analogously, we shall use the expression “a.e.” in place of “$\mathscr {L}^d$-a.e.” and of “$\mathscr {L}^d\otimes \mathscr {L}^d$-a.e.”. If u and v are measurable functions, we shall also write “$u=v$ in E” as a shorthand for “$u(x)=v(x)$ for a.e. $x\in E$”.

In this note, $\varOmega \subset \mathbb {R}^d$ is an open and connected reference set such that $\mathscr {L}^d(\varOmega )\in (0,+\infty )$. Later on, in Sect. 3, some regularity on the boundary $\partial \varOmega$ will be required.

For what concerns the kernel $K:\mathbb {R}^d\rightarrow [0,+\infty ]$, it is not restrictive to assume that is even, i.e.

$$\begin{aligned} K(x) = K(-x) \quad \text {a.e. } x\in \mathbb {R}^d. \end{aligned}$$

Besides, we suppose that

$$\begin{aligned} \int _{\mathbb {R}^d} \left( 1 \wedge \left| x \right| \right) K(x) {\mathrm {d}}x < +\infty , \end{aligned}$$

(2)

where if $t,s\in \mathbb {R}$, $t \wedge s$ equals the minimum between t and s. This condition entails that $K \in L^1(B(0,r)^c)$ for all balls B(0, r) with centre in the origin and radius $r>0$; in particular, K might have a non-$L^1$ singularity in 0. The main example of functions that fulfil (2) is given by fractional kernels [8, 17], i.e. kernels of the form

$$\begin{aligned} K(x) = \frac{a(x)}{ \left|x\right|^{d+s} }, \end{aligned}$$

where $a:\mathbb {R}^d\rightarrow \mathbb {R}$ is an even function such that $0<\lambda \le a(x) \le \varLambda$ for some $\lambda ,\varLambda \in \mathbb {R}$ and $s\in (0,1)$.

A faster decay at infinity for K will be needed in Sect. 3, see (15).

We are interested in a variational problem concerning $J_K$, to which we shall informally refer as Plateau’s problem. Precisely, given a Lebesgue measurable set $E_0 \subset \mathbb {R}^d$ such that $J_K( \chi _{E_0}; \varOmega )<+\infty$, we define the family

$$\begin{aligned} \mathscr {F}:=\left\{ v:\mathbb {R}^d\rightarrow [0,1] : v \text { is measurable and } v = \chi _{E_0} \text { in } \varOmega ^c\right\} , \end{aligned}$$

(3)

and we address the minimisation of $J_K(\,\cdot \,;\varOmega )$ in the class $\mathscr {F}$; namely, we consider

$$\begin{aligned} \inf \left\{ J_K(v;\varOmega ) : v\in \mathscr {F}\right\} . \end{aligned}$$

(4)

Remark 1

(Truncation) For $s\in \mathbb {R}$, let us set $T(s) :=\big ( (0 \vee s) \wedge 1\big )$ ($t \vee s$ is the maximum between the real numbers t and s). Observe that $T \circ \chi _{E_0} = \chi _{E_0}$ and $J_K( T \circ u; \varOmega ) \le J_K( u; \varOmega )$, so the infimum in (4) equals

$$\begin{aligned} \inf \left\{ J_K(v;\varOmega ) : v:\mathbb {R}^d\rightarrow \mathbb {R}\text { is measurable and } v = \chi _{E_0} \text { in } \varOmega ^c \right\} . \end{aligned}$$

We therefore see that choice of $\mathscr {F}$ as the class of competitors is not restrictive.

Remark 2

(The class of competitors is nonempty) Standing our assumptions on $\varOmega$, any set E that has finite perimeter satisfies $J_K( \chi _E; \varOmega ) <+\infty$, see [4, 19] We shall recall the definition of finite perimeter set later in this subsection.

As the functional $J_K(\,\cdot \,; \varOmega )$ is convex, when $\varOmega$ has finite measure, existence of solutions to (4) can be established by the direct method of calculus of variations (see [4]; see also [12] for an approach via approximation by smooth sets). In particular, as consequence of the following coarea-type formula:

$$\begin{aligned} J_K(u;\varOmega ) = \int _{0}^{1}{{\,\mathrm{Per}\,}}_K(\left\{ u>t\right\} ;\varOmega ){\mathrm {d}}t, \end{aligned}$$

(5)

there always exists a minimiser which is a characteristic function. Indeed, for any $u:\mathbb {R}^d\rightarrow [0,1]$, there exists $t^*\in \mathbb {R}$ such that ${{\,\mathrm{Per}\,}}_K(\left\{ u>t^*\right\} ; \varOmega )\le J_K(u; \varOmega )$; otherwise, (5) would be contradicted. Thus, if u is a minimiser of (4), then $\chi _{\left\{ u>t^*\right\} }$ is minimising as well.

Formula (5) can be easily validated, see for instance [9, 12]. The family of functionals on $L^1(\varOmega )$ such that a generalised coarea formula holds was firstly introduced by Visintin [22].

It is well known that existence of solutions to the classical counterpart of (4) may be proved in the framework of geometric measure theory. We remind here some basic facts, while we refer to the monographs [2, 18] for a thorough treatment of the subject.

We say that $u:\varOmega \rightarrow \mathbb {R}$ is a function of bounded variation in $\varOmega$, and we write $u\in {\mathrm {BV}}(\varOmega )$, if $u\in L^1(\varOmega )$ and

$$\begin{aligned} \left|\mathrm {D}u\right|(\varOmega ) :=\sup \left\{ \int _{\varOmega } u(x){\mathrm {div}}\zeta (x) {\mathrm {d}}x : \zeta \in C^{\infty }_c (\mathbb {R}^d;\mathbb {R}^d), \left\| \zeta \right\| _{L^\infty }\le 1\right\} < + \infty . \end{aligned}$$

We dub $\left|\mathrm {D}u\right|(\varOmega )$ the total variation of u in $\varOmega$. We also say that a measurable set E is a set of finite perimeter in $\varOmega$ when its characteristic function $\chi _E$ is a function of bounded variation in $\varOmega$, and, in this case, we refer to ${{\,\mathrm{Per}\,}}(E;\varOmega ) :=\left|\mathrm {D}\chi _E\right|(\varOmega )$ as perimeter of E in $\varOmega$. In this framework, the result that parallels the existence of solutions to (4) reads as follows: there is a set E with finite perimeter in $\varOmega$ such that ${{\,\mathrm{Per}\,}}(E;\varOmega )$ attains

$$\begin{aligned} \inf \left\{ \left|\mathrm {D}u\right|(\varOmega ) : u:\mathbb {R}^d\rightarrow [0,1] \text { is measurable and } u = \chi _{E_0} \text { in } \varOmega ^c\right\} . \end{aligned}$$

(6)

Finite perimeter sets stand as measure-theoretic counterparts of smooth hypersurfaces. For example, we may equip them with an inner normal: for any $x\in {\mathrm {supp}}\left|\mathrm {D}\chi _E\right|$, we define

$$\begin{aligned} {{\hat{n}}}(x):=\lim _{r\rightarrow 0^+}\frac{\mathrm {D}\chi _E(B(x,r))}{\left|\mathrm {D}\chi _E\right|(B(x,r))}, \end{aligned}$$

(7)

where $\mathrm {D}\chi _E$ is the distributional gradient of $\chi _E$ and B(x, r) is the open ball of centre x and radius $r>0$. A fundamental result by De Giorgi [13] states that

$$\begin{aligned} {{\,\mathrm{Per}\,}}(E;\varOmega )=\mathscr {H}^{d-1}(\partial ^*E\cap \varOmega ), \end{aligned}$$

where

$$\begin{aligned} \partial ^*E :=\left\{ x\in \mathbb {R}^d: {{\hat{n}}}(x) \text{ exists } \text{ and } \left|{{\hat{n}}}(x)\right|=1\right\} \end{aligned}$$

is the so-called reduced boundary of E. In addition, for any $x\in \partial ^*E$,

$$\begin{aligned} \frac{E-x}{r} \rightarrow \left\{ y\in \mathbb {R}^d: y\cdot {{\hat{n}}}(x) > 0\right\} \quad \text{ as } r\rightarrow 0^+ \text{ in } L^1_{\mathrm {loc}}(\mathbb {R}^d) . \end{aligned}$$

(8)

Once existence of solutions to (6) is on hand, a useful criterion to verify the minimality of a given competitor is provided by means of calibrations. The notion of calibration may be expressed in very general terms (see [16, 20] and references therein); as far as we are concerned, we say that a (classical) calibration for the finite perimeter set E is a divergence-free vector field $\zeta :\mathbb {R}^d\rightarrow \mathbb {R}^d$ such that $\left| \zeta (x) \right| \le 1$ a.e. and $\zeta (x) = {\hat{n}}(x)$ for $\mathscr {H}^{d-1}$-a.e. $x\in \partial ^*E$. It can be shown that if the set E admits a calibration, then its perimeter equals the infimum in (6). The goal of the next section is to establish a nonlocal analogue of this principle.

2 Minimality via calibrations

In this section, we propose a notion of calibration adapted to the current nonlocal setting, and we show that the existence of a calibration is a sufficient condition for a function u to minimise the energy $J_K$ w.r.t compact perturbations. Then, we show that halfspaces admit calibrations, and thus we infer their minimality.

We remind that we assume that $\mathbb {R}^d\times \mathbb {R}^d$ is equipped with the product measure $\mathscr {L}^d\otimes \mathscr {L}^d$.

Definition 1

Let $u:\mathbb {R}^d\rightarrow [0,1]$ and $\zeta :\mathbb {R}^d\times \mathbb {R}^d\rightarrow \mathbb {R}$ be measurable functions. We say that $\zeta$ is a nonlocal calibration for u if the following hold:

• 1. $\left|\zeta (x,y)\right|\le 1$ for a.e. $(x,y)\in \mathbb {R}^d\times \mathbb {R}^d$;

• 2. for a.e. $x\in \mathbb {R}^d$,

  $$\begin{aligned} \lim _{r\rightarrow 0^+}\int _{B(x,r)^c} K(y-x)\left( \zeta (y,x)-\zeta (x,y)\right) {\mathrm {d}}y = 0; \end{aligned}$$

  (9)

• 3. for a.e. $(x,y)\in \mathbb {R}^d\times \mathbb {R}^d$ such that $u(x)\ne u(y)$,

  $$\begin{aligned} \zeta (x,y)(u(y)-u(x))=\left|u(y)-u(x)\right|. \end{aligned}$$

  (10)

Remark 3

In a very recent, independent work [6], Cabré has proposed a notion of nonlocal calibration akin to ours. Given an open bounded set $\varOmega \subset \mathbb {R}^d$ and a measurable $E\subset \mathbb {R}^d$ such that $E = \left\{ f_E >0\right\}$ for some measurable $f_E:\mathbb {R}^d\rightarrow \mathbb {R}$, he introduces the set functional

$$\begin{aligned} \mathscr {C}_\varOmega (F) :=\int \int _{(\varOmega ^c \times \varOmega ^c)^c} K(y-x)(\chi _F(y)-\chi _F(x)) \mathrm {sign}(f_E(y)-f_E(x)) {\mathrm {d}}y {\mathrm {d}}x, \end{aligned}$$

where $F\subset \mathbb {R}^d$ satisfies $F\cap \varOmega ^c=E\cap \varOmega ^c$, and, in [6, Theorem 2.4], he provides sufficient conditions for the set E to be a minimiser for Plateau’s problem, as well as conditions to grant uniqueness. As applications, the author establishes the local minimality of graphs with 0 nonlocal curvature and, very interestingly, re-proves a result in [8] stating that minimisers have null nonlocal curvature in a viscosity sense.

The next remark collects some comments about the definition above.

Remark 4

Let $\zeta :\mathbb {R}^d\times \mathbb {R}^d\rightarrow \mathbb {R}$ be a calibration for $u:\mathbb {R}^d\rightarrow [0,1]$.

• 1. It is not restrictive to assume that $\zeta$ is antisymmetric: indeed, ${\tilde{\zeta }}(x,y):=( \zeta (x,y)-\zeta (y,x) )/2$ is a calibration for u as well.

• 2. In view of (2), the integral in (9) is convergent for each $r>0$. We can regard (9) as a nonlocal counterpart of the vanishing divergence condition that is prescribed for classical calibrations. Such nonlocal gradient and divergence operators were introduced in [15], and they have already been exploited to study nonlocal perimeters by Mazón et al. [19], where the authors propose a notion of K-calibrable set in relation to a nonlocal Cheeger energy.

• 3. Suppose that $u=\chi _E$ for some measurable $E\subset \mathbb {R}^d$. By (10), $\zeta$ must satisfy

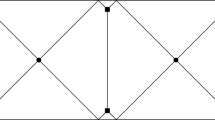
  $$\begin{aligned} \zeta (x,y) = {\left\{ \begin{array}{ll} -1 &{} \quad \text {if } x\in E, y\in E^c \\ 1 &{} \quad \text {if } x\in E^c, y\in E. \end{array}\right. } \end{aligned}$$

  Heuristically, this means that the calibration gives the sign of the inner product between the vector $y-x$ and the inner normal to E at the “crossing point”, provided the boundary of E is sufficiently regular (see Fig. 1). Indeed, if we imagine to displace a particle from to x and y, $\zeta$ equals $-1$ when the particle exits E, and it equals 1 if the particle enters E.

Fig. 1

If $\zeta$ is a calibration for the set E (i.e. for $\chi _E$) and x, y are as in the picture, then $\zeta (x,y)=-1$

Our criterion reads as follows:

Theorem 2

Let $E_0\subset \mathbb {R}^d$ be a measurable set such that $J_K(\chi _{E_0};\varOmega ) <+\infty$, and let $\mathscr {F}$ be the family in (3). If for some $u\in \mathscr {F}$ there exists a calibration $\zeta$, then

$$\begin{aligned} J_K(u;\varOmega )\le J_K(v;\varOmega )\quad {\mathrm{for~all}}~v\in \mathscr {F}. \end{aligned}$$

Moreover, if $K>0$ a.e. and ${\tilde{u}}\in \mathscr {F}$ is another minimiser, then $\zeta$ is a calibration for ${\tilde{u}}$ as well.

Proof

By the definitions of $J_K(\,\cdot \,;\varOmega )$, $\zeta$, and $\mathscr {F}$, for any $v\in \mathscr {F}$,

$$\begin{aligned} J_K(v;\varOmega )\ge a(v) + b_1(v) + b_0, \end{aligned}$$

(11)

where

$$\begin{aligned} a(v):= & {} \frac{1}{2}\int _{\varOmega }\int _{\varOmega }K(y-x)\zeta (x,y)(v(y)-v(x)){\mathrm {d}}y{\mathrm {d}}x,\\ b_1(v):= & {} - \int _{\varOmega }\int _{\varOmega ^c} K(y-x) \zeta (x,y) v(x){\mathrm {d}}y {\mathrm {d}}x, \\ b_0:= & {} \int _{\varOmega }\int _{\varOmega ^c} K(y-x) \zeta (x,y) \chi _{E_0}(y){\mathrm {d}}y {\mathrm {d}}x. \end{aligned}$$

Since it is not restrictive to assume that $J_K(v;\varOmega )$ is finite, we can suppose that a(v), $b_1(v)$, and $b_0$ are finite as well.

We claim that it suffices to prove that $a(v)=-b_1(v)$ to grant the minimality of u. Indeed, $a(v)=-b_1(v)$ yields

$$\begin{aligned} J_K(v;\varOmega )\ge b_0 \quad \text {for all } v\in \mathscr {F}, \end{aligned}$$

(12)

and we remark that the lower bound $b_0$ is attained by u, because equality holds in (11) for this function. Therefore, u is a minimiser.

Now, we prove that $a(v)=-b_1(v)$ for all $v\in \mathscr {F}$. Recalling that we can assume $\zeta$ to be antisymmetric, we have

$$\begin{aligned} a(v)=-\int _{\varOmega }\int _{\varOmega }K(y-x)\zeta (x,y)v(x){\mathrm {d}}y{\mathrm {d}}x. \end{aligned}$$

Also, (9) yields

$$\begin{aligned} \begin{aligned} 0&= -2\lim _{r\rightarrow 0^+}\int _{B(x,r)^c} K(y-x) \zeta (x,y){\mathrm {d}}y \\&= -2\lim _{r\rightarrow 0^+}\int _{B(x,r)^c \cap \varOmega } K(y-x) \zeta (x,y){\mathrm {d}}y -2\int _{\varOmega ^c} K(y-x) \zeta (x,y){\mathrm {d}}y, \end{aligned} \end{aligned}$$

whence

$$\begin{aligned} a(v) = -\lim _{r\rightarrow 0^+} \int _\varOmega \int _{B(x,r)^c \cap \varOmega } K(y-x) \zeta (x,y) v(x){\mathrm {d}}y {\mathrm {d}}x = -b_1(v). \end{aligned}$$

Next, let ${\tilde{u}}\in \mathscr {F}$ be another minimiser of $J_K(\,\cdot \,;\varOmega )$, that is $J_K({\tilde{u}};\varOmega )=b_0$. Our purpose is proving that for a.e. $(x,y)\in \mathbb {R}^d\times \mathbb {R}^d$ such that ${\tilde{u}}(x)\ne {\tilde{u}}(y)$ it holds

$$\begin{aligned} \zeta (x,y)\left( {\tilde{u}}(y)-{\tilde{u}}(x)\right) = \left|\tilde{u}(y)-{\tilde{u}}(x)\right|. \end{aligned}$$

(13)

First of all, note the equality holds for a.e. $(x,y)\in \varOmega ^c \times \varOmega ^c$, because $u={\tilde{u}}$ in $\varOmega ^c$. Furthermore, from (11) we have

$$\begin{aligned} b_0=J_K({\tilde{u}};\varOmega )\ge a({\tilde{u}})+b_1({\tilde{u}})+b_0 =b_0, \end{aligned}$$

thus

$$\begin{aligned}&\frac{1}{2}\int _{\varOmega }\int _{\varOmega }K(y-x) \left[ \left|{\tilde{u}}(y)-{\tilde{u}}(x)\right|-\zeta (x,y)({\tilde{u}}(y)-\tilde{u}(x))\right] {\mathrm {d}}y {\mathrm {d}}x \\&\quad +\,\int _{\varOmega }\int _{\varOmega ^c}K(y-x) \left[ \left|{\tilde{u}}(y)-{\tilde{u}}(x)\right|-\zeta (x,y)({\tilde{u}}(y)-\tilde{u}(x))\right] {\mathrm {d}}y {\mathrm {d}}x = 0. \end{aligned}$$

The integrand appearing in the previous identity is positive; therefore, when $K>0$, we deduce that (13) is satisfied for a.e. $x\in \varOmega$ and $y\in \mathbb {R}^d$. Eventually, in the case $x\in \varOmega ^c$ and $y\in \varOmega$, we achieve the conclusion by exploiting the antisymmetry of $\zeta$. $\square$

We take advantage of the previous theorem to prove that halfspaces are the unique local minimisers of $J_K(\,\cdot \,;B)$. This property has already been shown for fractional kernels in [3, 8] by means of a reflection argument, which in fact turns out to be effective whenever K is radial and strictly decreasing [4]. Here, we are able to deal with the case when the kernel is neither monotone nor radial.

We start with the following lemma, whose proof is a simple verification:

Lemma 1

Given ${\hat{n}}\in \mathbb {S}^{d-1}$, let us set

$$\begin{aligned} \zeta (x,y):=\mathrm {sign}((y-x)\cdot {\hat{n}}) \quad {{\mathrm{and}}}\quad H:=\left\{ x\in \mathbb {R}^d: x\cdot {\hat{n}} > 0\right\} . \end{aligned}$$

Then, $\zeta$ is a calibration for $\chi _H$.

Now, we prove Theorem 1.

Proof of Theorem 1

In view of Theorem 2 and of the lemma above, we deduce that $\chi _H$ is a minimiser of the problem under consideration. Hence, we are left to prove uniqueness.

Let $u:\mathbb {R}^d\rightarrow [0,1]$ be another minimiser. The second assertion in Theorem 2 grants that $\zeta (x,y):=\mathrm {sign}((y-x)\cdot {\hat{n}})$ is a calibration for u as well, so we get

$$\begin{aligned} \mathrm {sign}((y-x)\cdot {\hat{n}})(u(y)-u(x))=\left|u(y)-u(x)\right|\quad \text {for a.e. } x,y \in \mathbb {R}^d, \end{aligned}$$

whence

$$\begin{aligned} u(x) \le u(y) \quad \text {for a.e. } x,y \in \mathbb {R}^d\text { such that } x\cdot {\hat{n}}<y\cdot {\hat{n}}. \end{aligned}$$

(14)

Next, we focus on the superlevel sets of u: for $t\in (0,1)$, we define

$$\begin{aligned} E_t :=\left\{ x : u(x) > t\right\} , \end{aligned}$$

and we observe that if $(x,y)\in E_t \times E_t^c$, it must be $x\cdot {{\hat{n}}} \ge y \cdot {{\hat{n}}}$ for a.e. $x\in E_t$ and a.e. $y \in E_t^c$; otherwise, by (14) we would have $u(x) \le u(y)$ on some nonnegligible subsets of $E_t$ and $E_t^c$. Therefore, there exists $\lambda _t \in \mathbb {R}$ such that (up to negligible sets) $E_t \subset \left\{ x : x\cdot {\hat{n}} \ge \lambda _t\right\}$ and $E_t^c \subset \left\{ y : y\cdot {\hat{n}} \le \lambda _t\right\}$, whence $\mathscr {L}^d( E_t\, \!\bigtriangleup \!\, \left\{ x : x\cdot {\hat{n}} \ge \lambda _t\right\} ) = 0$ for all $t\in (0,1)$. Recalling that it holds $u = \chi _H$ in $B^c$, we infer that $\lambda _t = 0$ and this gets

$$\begin{aligned} \mathscr {L}^d( E_t \!\bigtriangleup \!H ) = 0 \qquad \text {for all }t\in (0,1). \end{aligned}$$

Summing up, we proved that $u:\mathbb {R}^d\rightarrow [0,1]$ is a function such that, for all $t\in (0,1)$, the superlevel set $E_t$ coincides with the halfspace H, up to a negligible set. To reach the conclusion, we let $\left\{ t_k\right\} _{k\in \mathbb {N}}\subset (0,1)$ be a sequence that converges to 0 when $k\rightarrow +\infty$. Because it holds

$$\begin{aligned} \left\{ x : u(x) = 0\right\} = \bigcap _{k\in \mathbb {N}} E_{t_k}^c \quad \text {and}\quad \left\{ x : u(x) = 1\right\} = \bigcap _{k\in \mathbb {N}} E_{1 - t_k}, \end{aligned}$$

we see that $\mathscr {L}^d( \left\{ x : u(x) = 0\right\} \!\bigtriangleup \!H^c ) = 0$ and $\mathscr {L}^d( \left\{ x : u(x) = 1\right\} \!\bigtriangleup \!H) = 0$. Thus, $u = \chi _H$ in $\mathbb {R}^d$. $\square$

3 $\varGamma$-limit of the rescaled energy

In this section, we outline how to exploit Theorem 1 to study the limiting behaviour of certain rescalings of the energy $J_K$. In precise terms, we are interested in the $\varGamma$-convergence as $\varepsilon \rightarrow 0^+$ of $\left\{ J_{K_\varepsilon }(\,\cdot \,;\varOmega ) \right\}$ with respect to the $L^1_{{\mathrm {loc}}}(\mathbb {R}^d)$-convergence, where for $\varepsilon >0$, we let

$$\begin{aligned} K_\varepsilon (x) :=\frac{1}{\varepsilon ^d} K\left( \frac{x}{\varepsilon } \right) . \end{aligned}$$

In [4], the analysis has already been carried out by Berendsen and the author of this note when K is radial and strictly decreasing, but, as we concisely explain in the remainder of this note, the same arguments may be conveniently adapted to the current more general setting. We shall not deal with all the computations in depth, because our main interest here is how to take advantage of the minimality of halfspaces. This will be apparent in Lemma 2. We refer to the works in the bibliography for the technical details.

For the sake of completeness, we recall the following definition:

Definition 2

($\varGamma$-convergence) Let X be a set endowed with a notion of convergence, and for $\varepsilon >0$, let $f_\varepsilon :X\rightarrow [-\infty ,+\infty ]$ be a function. We say that the family $\left\{ f_\varepsilon \right\}$$\varGamma$-converges as $\varepsilon \rightarrow 0^+$ to the function $f_0:X\rightarrow [-\infty ,+\infty ]$ w.r.t. the convergence in X if

• 1. for any $x_0\in X$ and for any $\left\{ x_\varepsilon \right\} \subset X$ that converges to $x_0$, it holds

  $$\begin{aligned} f_0(x_0)\le \liminf _{\varepsilon \rightarrow 0}f_\varepsilon (x_\varepsilon ); \end{aligned}$$

• 2. for any $x_0\in X$ there exists $\left\{ x_\varepsilon \right\} \subset X$ that converges to $x_0$ with the property that

  $$\begin{aligned} \limsup _{\varepsilon \rightarrow 0}f_\varepsilon (x_\varepsilon )\le f_0(x_0). \end{aligned}$$

When $u:\mathbb {R}^d\rightarrow [0,1]$ is a measurable function, let us define

$$\begin{aligned} J_\varepsilon ^1(u; \varOmega ):= & {} \frac{1}{2}\int _\varOmega \int _\varOmega K_\varepsilon (y-x)\left|u(y)-u(x)\right|{\mathrm {d}}y{\mathrm {d}}x, \\ J_\varepsilon ^2(u; \varOmega ):= & {} \int _{\varOmega }\int _{\varOmega ^c}K_\varepsilon (y-x)\left|u(y)-u(x)\right|{\mathrm {d}}y {\mathrm {d}}x,\\ J_\varepsilon (u; \varOmega ):= & {} J_\varepsilon ^1(u; \varOmega ) + J_\varepsilon ^2(u; \varOmega ). \end{aligned}$$

Observe that, according to the notation in (1), $J_\varepsilon = J_{K_\varepsilon }$. We also introduce the limit functional

$$\begin{aligned} J_0(u;\varOmega ) :={\left\{ \begin{array}{ll} \frac{1}{2}\int _{\mathbb {R}^d} K(z) \left( \int _\varOmega \left| z \cdot \mathrm {D}u\right| \right) {\mathrm {d}}z&{}\quad \text {if } u\in {\mathrm {BV}}(\varOmega ), \\ +\infty &{}\quad \text {otherwise}. \end{array}\right. } \end{aligned}$$

Our goal is proving the following:

Theorem 3

($\varGamma$-convergence of the rescaled energy) Let $\varOmega \subset \mathbb {R}^d$ be an open, connected, and bounded set with Lipschitz boundary. Let also $K:\mathbb {R}^d\rightarrow (0,+\infty )$ be an even function such that

$$\begin{aligned} \int _{\mathbb {R}^d} K(x)\left|x\right| dx < +\infty . \end{aligned}$$

(15)

Then, for any measurable $u:\mathbb {R}^d\rightarrow [0,1]$ the following hold:

• 1. For any family $\left\{ u_\varepsilon \right\}$ that converges to u in $L^1_{\mathrm {loc}}(\mathbb {R}^d)$, we have

  $$\begin{aligned} J_0(u;\varOmega ) \le \liminf _{\varepsilon \rightarrow 0^+} \frac{1}{\varepsilon } J^1_\varepsilon (u_\varepsilon ;\varOmega ). \end{aligned}$$

• 2. There exists a family $\left\{ u_\varepsilon \right\}$ that converges to u in $L^1_{\mathrm {loc}}(\mathbb {R}^d)$ such that

  $$\begin{aligned} \limsup _{\varepsilon \rightarrow 0^+} \frac{1}{\varepsilon } J_\varepsilon (u_\varepsilon ;\varOmega ) \le J_0(u;\varOmega ). \end{aligned}$$

We remark that, being $J_\varepsilon ^2(\,\cdot \,;\varOmega )$ positive, Theorem 3 entails the $\varGamma$-convergence of $\left\{ J_\varepsilon (\,\cdot \,;\varOmega )\right\}$ to $J_0(\,\cdot \,;\varOmega )$ w.r.t. the $L^1_{\mathrm {loc}}(\mathbb {R}^d)$-convergence. Also, note that (15) prescribes a condition that is more stringent than (2).

Several results about the asymptotics of functionals akin to $J_\varepsilon$ have been considered in the literature [1, 5, 13, 19, 21]; in particular, we wish to mention the following one by Ponce:

Theorem 4

(Corollary 2 and Theorem 8 in [21]) Let $\varOmega \subset \mathbb {R}^d$ be an open bounded set with Lipschitz boundary and let $u\in {\mathrm {BV}}(\varOmega )$. If (15) holds, then

$$\begin{aligned} \lim _{\varepsilon \rightarrow 0^+} \frac{1}{\varepsilon } J^1_\varepsilon (u;\varOmega ) = J_0(u;\varOmega ) \end{aligned}$$

(16)

Moreover, $J_0(\,\cdot \,;\varOmega )$ is the $\varGamma$-limit as $\varepsilon \rightarrow 0^+$ of $\left\{ \varepsilon ^{-1} J_\varepsilon (\,\cdot \,;\varOmega )\right\}$ w.r.t. the $L^1(\varOmega )$-topology.

We discuss separately the proofs of statements 1 and 2 in Theorem 3. Preliminarily, we remark that we only need to study the $\varGamma$-convergence of $J_\varepsilon$ regarded as a functional on measurable sets, namely, for $E\subset \mathbb {R}^d$ measurable, we consider

$$\begin{aligned}&J^i_\varepsilon (E;\varOmega ) :=J^i_\varepsilon (\chi _E;\varOmega ) \quad \text {for } i=1,2, \\&J_\varepsilon (E;\varOmega ) :=J_\varepsilon (\chi _E;\varOmega ), \end{aligned}$$

and the limit functional

$$\begin{aligned} J_0(E;\varOmega ) :=J_0(\chi _E;\varOmega ). \end{aligned}$$

Indeed, by appealing to results by Chambolle et al. [10, Propositions 3.4 and 3.5], it is possible to recover the $\varGamma$-convergence of $J_\varepsilon$ as a functional on measurable functions from the analysis of the restrictions; this is mainly due to convexity and to the validity of coarea formulas.

So, as for the $\varGamma$-upper limit inequality, we need to show that, for any given measurable $E\subset \mathbb {R}^d$, there exists a family $\left\{ E_\varepsilon \right\}$ that converges to E in $L^1_{\mathrm {loc}}(\mathbb {R}^d)$ as $\varepsilon \rightarrow 0^+$ such that

$$\begin{aligned} \limsup _{\varepsilon \rightarrow 0^+} \frac{1}{\varepsilon } J_\varepsilon ^1(E_\varepsilon ;\varOmega ) \le J_0(E;\varOmega ). \end{aligned}$$

Hereafter, by saying that the family of sets $\left\{ E_\varepsilon \right\}$ converges to E in $L^1_{\mathrm {loc}}(\mathbb {R}^d)$, we mean that $\chi _{E_\varepsilon } \rightarrow \chi _E$ in $L^1_{\mathrm {loc}}(\mathbb {R}^d)$.

The desired inequality may be achieved as in [4] by reasoning on a class of sets $\mathscr {D}$ which is dense w.r.t. the energy $J_0$ among all measurable sets. We omit the details, since Theorem 1 plays no role in this step.

Now we turn to the proof of the $\varGamma$-lower limit inequality. Our task is proving that, for any given measurable $E\subset \mathbb {R}^d$ and for any family $\left\{ E_\varepsilon \right\}$ that converges to E in $L^1_{\mathrm {loc}}(\mathbb {R}^d)$ as $\varepsilon \rightarrow 0^+$, it holds

$$\begin{aligned} J_0(E;\varOmega ) \le \liminf _{\varepsilon \rightarrow 0^+} \frac{1}{\varepsilon } J_\varepsilon ^1(E_\varepsilon ;\varOmega ). \end{aligned}$$

(17)

In [21], the approach to the $\varGamma$-lower limit inequality relies on representation formulas for the relaxations of a certain class of integral functionals. Here, following [4], we propose a strategy which combines pointwise limit (16) and Theorem 1.

Observe that we can write

$$\begin{aligned} J_0(E;\varOmega ) :={\left\{ \begin{array}{ll} \int _{\partial ^*E \cap \varOmega } \sigma _K({\hat{n}}(x)) {\mathrm {d}}\mathscr {H}^{d-1}(x) &{}\quad \text {if }E\text { is a finite perimeter set in }\varOmega , \\ +\infty &{} \quad \text {otherwise}, \end{array}\right. } \end{aligned}$$

where ${\hat{n}}:\partial ^*E \rightarrow \mathbb {S}^{d-1}$ is the measure-theoretic inner normal of E (recall (7)) and $\sigma _K:\mathbb {R}^d\rightarrow [0,+\infty )$ is the anisotropic norm

$$\begin{aligned} \sigma _K(p) :=\frac{1}{2}\int _{\mathbb {R}^d} K(z)\left|z\cdot p\right|{\mathrm {d}}z, \quad \text {for } p\in \mathbb {R}^d. \end{aligned}$$

(18)

Remark 5

(The radial case [4]) When K is radial, $J_0$ coincides with De Giorgi’s perimeter, up to a multiplicative constant that depends on K and on d. Indeed, if $K(x) = {\bar{K}} (\left|x\right|)$ for some ${\bar{K}}:[0,+\infty ) \rightarrow [0,+\infty )$, for any ${{\hat{p}}}\in \mathbb {S}^{d-1}$, we have that

where $e_d :=(0,\ldots ,0,1)$ is the last element of the canonical basis.

By a blow-up argument à la Fonseca-Müller [14] that has already been applied to similar problems [1, 3], it turns out that $\varGamma$-lower limit inequality (17) holds as soon as one characterises the norm $\sigma _K$ in terms of the evaluation on halfspaces of the $\varGamma$-inferior limit of $\varepsilon ^{-1} J_\varepsilon (\,\cdot \,;B)$. Precisely, we need to validate the following:

Lemma 2

For any ${\hat{p}}\in \mathbb {S}^{d-1}$,

$$\begin{aligned} \sigma _K ({\hat{p}}) = \inf \left\{ \liminf _{\varepsilon \rightarrow 0^+} \frac{1}{\omega _{d-1} \varepsilon } J^1_\varepsilon (E_\varepsilon ;B) : E_\varepsilon \rightarrow H_{{\hat{p}}} \text { in } L^1(B) \right\} , \end{aligned}$$

where $\omega _{d-1}$ is the $(d-1)$-dimensional Lebesgue measure of the unit ball in $\mathbb {R}^{d-1}$, and $H_{{\hat{p}}} :=\left\{ x\in \mathbb {R}^d: x\cdot {\hat{p}} > 0 \right\}$.

It is in the proof of this lemma that Theorem 1 comes into play.

Proof of Lemma 2

For ${\hat{p}}\in \mathbb {S}^{d-1}$, let us set

$$\begin{aligned} \sigma '_K({\hat{p}}) :=\inf \left\{ \liminf _{\varepsilon \rightarrow 0^+} \frac{1}{\omega _{d-1} \varepsilon } J^1_\varepsilon (E_\varepsilon ;B) : E_\varepsilon \rightarrow H_{{\hat{p}}} \text { in } L^1(B) \right\} . \end{aligned}$$

(19)

By (16), we know that

$$\begin{aligned} \sigma _K({\hat{p}}) = \lim _{\varepsilon \rightarrow 0^+} \frac{1}{\omega _{d-1}\varepsilon } J^1_\varepsilon (H_{{\hat{p}}};B), \end{aligned}$$

(20)

hence $\sigma _K ({\hat{p}}) \ge \sigma '_K({\hat{p}})$.

To the purpose of proving the reverse inequality, we introduce a third function $\sigma ''_K$ and we show that $\sigma _K \le \sigma ''_K \le \sigma '_K$. So, for ${\hat{p}}\in \mathbb {S}^{d-1}$ and $\delta \in (0,1)$, we let

$$\begin{aligned} \sigma ''_K({\hat{p}}) :=\inf \left\{ \liminf _{\varepsilon \rightarrow 0^+} \frac{1}{ \omega _{d-1} \varepsilon } J^1_\varepsilon (E_\varepsilon ;B) : E_\varepsilon \rightarrow H_{{\hat{p}}} \text { in } L^1(B) \text { and } E_\varepsilon \!\bigtriangleup \!H_{{\hat{p}}} \subset B_{1-\delta } \right\} , \end{aligned}$$

where $B_{1-\delta } :=B(0,1-\delta )$ and $E_\varepsilon \!\bigtriangleup \!H_{{\hat{p}}}$ is the symmetric difference between $E_\varepsilon$ and $H_{{\hat{p}}}$. We decide not to use a notation that exhibits the dependence of $\sigma ''_K$ on the parameter $\delta$ because a posteriori the values of $\sigma ''_K$ are not influenced by it.

We firstly show that $\sigma _K \le \sigma ''_K$. Let ${E_\varepsilon }$ be a family of measurable subsets of $\mathbb {R}^d$ such that $E_\varepsilon \cap B^c = H_{{\hat{p}}}\cap B^c$ and that $E_\varepsilon \rightarrow H_{{\hat{p}}}$ in $L^1(B)$. By Theorem 1, we have that

$$\begin{aligned} 0&\le J_\varepsilon (E_\varepsilon ; B) - J_\varepsilon (H_{{\hat{p}}}; B) \\&= J^1_\varepsilon (E_\varepsilon ; B) - J^1_\varepsilon (H_{{\hat{p}}}; B) - \left[ J^2_\varepsilon (E_\varepsilon ; B) - J^2_\varepsilon (H_{{\hat{p}}}; B) \right] . \end{aligned}$$

If we also assume that $E_\varepsilon \!\bigtriangleup \!H_{{\hat{p}}} \subset B_{1-\delta }$, we see that

$$\begin{aligned}&J^2_\varepsilon (E_\varepsilon ; B) - J^2_\varepsilon (H_{{\hat{p}}}; B)\\&\quad = \int _{E_\varepsilon \cap B_{1-\delta }}\int _{H_{{\hat{p}}} \cap B^c} K_\varepsilon (y-x) {\mathrm {d}}y {\mathrm {d}}x - \int _{H_{{\hat{p}}} \cap B_{1-\delta }}\int _{H_{{\hat{p}}} \cap B^c} K_\varepsilon (y-x) {\mathrm {d}}y {\mathrm {d}}x \end{aligned}$$

and hence, noticing that $\left|y-x\right|\ge \delta$ if $x\in B^c$ and $y\in B_{1-\delta }$,

$$\begin{aligned} \left| J^2_\varepsilon (E_\varepsilon ; B) - J^2_\varepsilon (H_{{\hat{p}}}; B) \right|&\le \frac{2}{\delta } \int _{ E_\varepsilon \!\bigtriangleup \!H _{{\hat{p}}}} \int _{ B^c } K_\varepsilon (y-x) \frac{\left|y-x\right|}{\varepsilon }{\mathrm {d}}y {\mathrm {d}}x \\&\le \frac{2}{\delta } \mathscr {L}^d(E_\varepsilon \!\bigtriangleup \!H _{{\hat{p}}}) \int _{ \mathbb {R}^d} K(z) \left|z\right| {\mathrm {d}}z. \end{aligned}$$

By our choice of $\left\{ E_\varepsilon \right\}$ and (15), this yields

$$\begin{aligned} \lim _{\varepsilon \rightarrow 0^+} \left| J^2_\varepsilon (E_\varepsilon ; B) - J^2_\varepsilon (H_{{\hat{p}}}; B) \right| = 0, \end{aligned}$$

whence

$$\begin{aligned} 0&\le \liminf _{\varepsilon \rightarrow 0^+} \left[ J_\varepsilon (E_\varepsilon ; B) - J_\varepsilon (H_{{\hat{p}}}; B) \right] \\&= \liminf _{\varepsilon \rightarrow 0^+} \left[ J^1_\varepsilon (E_\varepsilon ; B) - J^1_\varepsilon (H_{{\hat{p}}}; B) \right] . \end{aligned}$$

Recalling (20) and the definition of $\sigma ''_K$, we deduce $\sigma _K({\hat{p}}) \le \sigma ''_K({\hat{p}})$.

To conclude, we are left to show that $\sigma ''_K \le \sigma '_K$. This may be done as in the proof of [4, Lemma 3.11] by means of a suitable “gluing” lemma (see also [3]). $\square$