The elliptic modular surface of level 4 and its reduction modulo 3

Abstract

The elliptic modular surface of level 4 is a complex K3 surface with Picard number 20. This surface has a model over a number field such that its reduction modulo 3 yields a surface isomorphic to the Fermat quartic surface in characteristic 3, which is supersingular. The specialization induces an embedding of the Néron–Severi lattices. Using this embedding, we determine the automorphism group of this K3 surface over a discrete valuation ring of mixed characteristic whose residue field is of characteristic 3. The elliptic modular surface of level 4 has a fixed-point-free involution that gives rise to the Enriques surface of type IV in Nikulin–Kondo–Martin’s classification of Enriques surfaces with finite automorphism group. We investigate the specialization of this involution to characteristic 3.

1 Introduction

Let R be a discrete valuation ring, and let ${{\mathcal {X}}}\rightarrow {\text {Spec}}R$ be a smooth proper family of varieties over R. We denote by $X_{{\bar{\eta }}}$ the geometric generic fiber and by $X_{{\bar{s}}}$ the geometric special fiber. Let ${\text {Aut}}({{\mathcal {X}}}/R)$ denote the group of automorphisms of ${{\mathcal {X}}}$ over ${\text {Spec}}R$. Then we have natural homomorphisms

$$\begin{aligned} {\text {Aut}}(X_{{\bar{s}}})\leftarrow {\text {Aut}}({{\mathcal {X}}}/R)\rightarrow {\text {Aut}}(X_{{\bar{\eta }}}). \end{aligned}$$

In this paper, we calculate the group ${\text {Aut}}({{\mathcal {X}}}/R)$ in the case where ${{\mathcal {X}}}$ is a certain natural model of the elliptic modular surface of level 4, and the special fiber $X_{{\bar{s}}}$ is its reduction modulo 3. In this case, the surfaces $X_{{\bar{\eta }}}$ and $X_{{\bar{s}}}$ are K3 surfaces, and their automorphism groups have been calculated in [1, 2], respectively, by Borcherds’ method [3, 4]. This paper gives the first application of Borcherds’ method to the calculation of the automorphism group of a family of K3 surfaces.

1.1 Elliptic modular surface of level 4

The elliptic modular surface of levelN is a natural compactification of the total space of the universal family over $\varGamma (N)\backslash {{\mathbb {H}}}$ of complex elliptic curves with level N structure, where ${{\mathbb {H}}}\subset {{\mathbb {C}}}$ is the upper-half plane and $\varGamma (N)\subset {\mathrm {PSL}}_2({{\mathbb {Z}}})$ is the congruence subgroup of level N. This important class of surfaces was introduced and studied by Shioda [5].

The elliptic modular surface of level 4 is a K3 surface birational to the surface defined by the Weierstrass equation

$$\begin{aligned} Y^2=X(X-1)\left( X-\left( \frac{1}{2}\left( \sigma +\frac{1}{\sigma }\right) \right) ^2\right) , \end{aligned}$$

(1.1)

where $\sigma$ is an affine parameter of the base curve ${{\mathbb {P}}}^1=\overline{\varGamma (4)\backslash {{\mathbb {H}}}}$ (see Section 3 in [6]). Shioda [5, 6] studied the reduction of this surface in odd characteristics. On the other hand, Keum and Kondo [1] calculated the automorphism group of the elliptic modular surface of level 4.

To describe the results of Shioda [5, 6] and Keum–Kondo [1], we fix some notation. A lattice is a free ${{\mathbb {Z}}}$-module L of finite rank with a non-degenerate symmetric bilinear form $\langle \,, \,\rangle :L\times L\rightarrow {{\mathbb {Z}}}$. The group of isometries of a lattice L is denoted by ${\mathrm {O}}(L)$, which we let act on L from the right. A lattice L of rank n is said to be hyperbolic (resp. negative-definite) if the signature of $L\otimes {{\mathbb {R}}}$ is $(1, n-1)$ (resp. (0, n)). For a hyperbolic lattice L, we denote by ${\mathrm {O}}^+(L)$ the stabilizer subgroup of a connected component of $\{ {x\in L\otimes {{\mathbb {R}}}} \mid {\langle x, x\rangle >0} \}$ in ${\mathrm {O}}(L)$. Let Z be a smooth projective surface defined over an algebraically closed field. We denote by $S_{Z}$ the lattice of numerical equivalence classes [D] of divisors D on Z and call it the Néron–Severi lattice of Z. Then $S_{Z}$ is hyperbolic by the Hodge index theorem. We denote by ${{\mathcal {P}}}_{Z}$ the connected component of $\{ {x\in S_{Z}\otimes {{\mathbb {R}}}} \mid {\langle x, x\rangle >0} \}$ that contains an ample class. We then put

$$\begin{aligned} N_{Z}:=\{\, {x\in {{\mathcal {P}}}_{Z}} \mid {\langle x, [C]\rangle \ge 0\;\; \text {for all curves }C\text { on }Z} \, \}. \end{aligned}$$

We let the automorphism group ${\text {Aut}}(Z)$ of Z act on $S_{Z}$ from the right by pullback of divisors. Then we have a natural homomorphism

$$\begin{aligned} {\text {Aut}}(Z)\rightarrow {\text {Aut}}(N_{Z}):=\{\, {g\in {\mathrm {O}}^+(S_{Z})} \mid {N_{Z}^g=N_{Z}} \, \}. \end{aligned}$$

For an ample class $h\in S_{Z}$, we put

$$\begin{aligned} {\text {Aut}}(Z, h):=\{\, {g\in {\text {Aut}}(Z)} \mid {h^g=h} \, \}, \end{aligned}$$

and call it the projective automorphism group of the polarized surface (Z, h).

Let $k_p$ be an algebraically closed field of characteristic $p\ge 0$. From now on, we assume that $p\ne 2$. Let $\sigma :X_p\rightarrow {{\mathbb {P}}}^1$ be the smooth minimal elliptic surface defined over $k_p$ by (1.1). Then $X_p$ is a K3 surface. For simplicity, we use the following notation throughout this paper:

$$\begin{aligned} S_{p}:=S_{X_p}, \quad {{\mathcal {P}}}_p:={{\mathcal {P}}}_{X_p}, \quad N_{p}:=N_{X_p}. \end{aligned}$$

Shioda [5, 6] proved the following:

Theorem 1.1

(Shioda [5, 6]) Suppose that $p\ne 2$.

• (1) The elliptic surface $\sigma :X_p\rightarrow {{\mathbb {P}}}^1$ has exactly six singular fibers. These singular fibers are located over $\sigma =0, \pm 1, \pm i, \infty$, and each of them is of type $\mathrm{I}_4$. The torsion part of the Mordell–Weil group of $\sigma :X_p\rightarrow {{\mathbb {P}}}^1$ is isomorphic to $({{\mathbb {Z}}}/4{{\mathbb {Z}}})^2$.

• (2) The Picard number ${\text {rank}}(S_{p})$ of $X_p$ is

  $$\begin{aligned} {\left\{ \begin{array}{ll} 20 &{}\quad \hbox {if }p=0\hbox { or }p\equiv 1\bmod 4, \\ 22 &{}\quad \hbox {if }p\equiv 3 \bmod 4. \end{array}\right. } \end{aligned}$$

• (3) If $k_0={{\mathbb {C}}}$, the transcendental lattice of the complex K3 surface $X_0$ is

  $$\begin{aligned} \left( \begin{array}{cc} 4 &{}\quad 0 \\ 0 &{}\quad 4 \end{array}\right) . \end{aligned}$$

• (4) The K3 surface $X_3$ is isomorphic to the Fermat quartic surface

  $$\begin{aligned} F_3 \;:\;x_1^4+x_2^4+x_3^4+x_4^4=0 \end{aligned}$$

  in characteristic 3.

It follows from Theorem 1.1 (3) and the theorem of Shioda–Inose [7] that, over the complex number field, $X_0$ is isomorphic to the Kummer surface associated with $E_{\sqrt{-1}}\times E_{\sqrt{-1}}$, where $E_{\sqrt{-1}}$ is the elliptic curve ${{\mathbb {C}}}/({{\mathbb {Z}}}\oplus {{\mathbb {Z}}}{\sqrt{-1}})$. (See also Proposition 15 of Barth–Hulek [8].) Therefore the result of Keum–Kondo [1] contains the calculation of ${\text {Aut}}(X_0)$.

Definition 1.2

Let Z be a K3 surface defined over $k_p$. A double-plane polarization is a vector $b=[H]\in N_{Z}\cap S_{Z}$ with $\langle b, b\rangle =2$ such that the corresponding complete linear system |H| is base-point-free, so that |H| induces a surjective morphism $\varPhi _b:Z\rightarrow {{\mathbb {P}}}^2$. Let $b$ be a double-plane polarization, and let $Z\rightarrow Z_b\rightarrow {{\mathbb {P}}}^2$ be the Stein factorization of $\varPhi _b$. Then we have a double-plane involution$g(b)\in {\text {Aut}}(Z)$ associated with the finite double covering $Z_b\rightarrow {{\mathbb {P}}}^2$. Let ${\text {Sing}}(b)$ denote the singularities of the normal K3 surface $Z_b$. Since $Z_b$ has only rational double points as its singularities, we have the ADE-type of ${\text {Sing}}(b)$.

Remark 1.3

Suppose that an ample class $a\in S_{Z}$ and a vector $b\in S_{Z}$ with $\langle b, b\rangle =2$ are given. Then we can determine whether b is a double-plane polarization or not, and if b is a double-plane polarization, we can calculate the set of classes of smooth rational curves contracted by $\varPhi _b:Z\rightarrow {{\mathbb {P}}}^2$ and compute the matrix representation of the double-plane involution $g(b):Z\rightarrow Z$ on $S_{Z}$. These algorithms are described in detail in [9] (and also in [10]). They are the key tools of this paper.

We re-calculated ${\text {Aut}}(X_0)$ by using these algorithms and obtained a generating set of ${\text {Aut}}(X_0)$ different from the one given in [1].

Theorem 1.4

(Keum–Kondo [1]) There exist an ample class $h_0\in S_{0}$ of degree $\langle h_0, h_0\rangle =40$ and four double-plane polarizations $b_{80}, b_{112}, b_{296}, b_{688}\in S_{0}$ such that ${\text {Aut}}(X_0)$ is generated by the projective automorphism group ${\text {Aut}}(X_0, h_0)\cong ({{\mathbb {Z}}}/2{{\mathbb {Z}}})^5 {\,:\,} {{\mathfrak {S}}}_5$ and the double-plane involutions $g(b_{80}), g(b_{112}), g(b_{296}), g(b_{688})$.

Table 1 Four double-plane involutions on $X_0$

See Table 1 for the properties of the double-plane polarizations $b_d$. See Proposition 4.2 for the geometric meaning of these generators of ${\text {Aut}}(X_0)$ with respect to the action of ${\text {Aut}}(X_0)$ on $N_{0}$. In Sect. 4.3, we also give a detailed description of the finite group ${\text {Aut}}(X_0, h_0)$ in terms of a certain graph ${{\mathcal {L}}}_{40}$.

Remark 1.5

In [2], the automorphism group ${\text {Aut}}(X_3)\cong {\text {Aut}}(F_3)$ of the Fermat quartic surface $F_3$ in characteristic 3 was calculated (see Theorem 4.1). This calculation also plays an important role in the proof of our main results.

1.2 Main results

In [1, 2], the following was proved, and hence, from now on, we regard ${\text {Aut}}(X_0)$ as a subgroup of ${\mathrm {O}}^+(S_{0})$ and ${\text {Aut}}(X_3)$ as a subgroup of ${\mathrm {O}}^+(S_{3})$.

Proposition 1.6

In each case of $X_0$ and $X_3$, the action of the automorphism group on the Néron–Severi lattice is faithful. $\square$

Let R be a discrete valuation ring whose fraction field K is of characteristic 0 and whose residue field k is of characteristic 3. Suppose that $\sqrt{-1}\in R$. In Sect. 2.5, we construct explicitly a smooth family of K3 surfaces ${{\mathcal {X}}}\rightarrow {\text {Spec}}R$ over R such that the geometric generic fiber ${{\mathcal {X}}}\otimes _{R}{\bar{K}}$ is isomorphic to $X_0$ and the geometric special fiber ${{\mathcal {X}}}\otimes _{R}{\bar{k}}$ is isomorphic to $X_3$. The construction of this model ${{\mathcal {X}}}$ is natural in the sense that it uses the inherent elliptic fibration of $X_0$. Note that the model of $X_0$ over R is not unique and that the main results on ${\text {Aut}}({{\mathcal {X}}}/R)$ below may depend on the choice of the model.

By Proposition 3.3 of Maulik and Poonen [11], the specialization from ${{\mathcal {X}}}\otimes _{R} K$ to ${{\mathcal {X}}}\otimes _{R}k$ gives rise to a homomorphism

$$\begin{aligned} \rho :S_{0}\rightarrow S_{3}. \end{aligned}$$

In Sect. 2.3, we give an explicit description of $\rho$. It turns out that $\rho$ is a primitive embedding of lattices. We regard $S_{0}$ as a sublattice of $S_{3}$ by $\rho$ and put

$$\begin{aligned} {\mathrm {O}}^+(S_{3}, S_{0}):=\{\, {g\in {\mathrm {O}}^+(S_{3})} \mid {S_{0}^g=S_{0}} \, \}. \end{aligned}$$

Then we have a natural restriction homomorphism

$$\begin{aligned} {\tilde{\rho }}:{\mathrm {O}}^+(S_{3}, S_{0})\rightarrow {\mathrm {O}}^+(S_{0}). \end{aligned}$$

The main results of this paper are as follows:

Theorem 1.7

The restriction of ${\tilde{\rho }}$ to ${\mathrm {O}}^+(S_{3}, S_{0})\cap {\text {Aut}}(X_3)$ induces an injective homomorphism

$$\begin{aligned} {\tilde{\rho }}|_{{\text {Aut}}}:{\mathrm {O}}^+(S_{3}, S_{0})\cap {\text {Aut}}(X_3) \hookrightarrow {\text {Aut}}(X_0). \end{aligned}$$

The image of ${\tilde{\rho }}|_{{\text {Aut}}}$ is generated by the finite subgroup ${\text {Aut}}(X_0, h_0)$ and the two double-plane involutions $g(b_{112}), g(b_{688})$. The other double-plane involutions $g(b_{80})$ and $g(b_{296})$ do not belong to the image of ${\tilde{\rho }}|_{{\text {Aut}}}$.

Let $R^\prime$ be a finite extension of R, and let ${{\mathcal {X}}}^\prime :={{\mathcal {X}}}\otimes _R R^\prime \rightarrow {\text {Spec}}R^\prime$ be the pullback of ${{\mathcal {X}}}\rightarrow {\text {Spec}}R$. We have a natural embedding ${\text {Aut}}({{\mathcal {X}}}/R)\hookrightarrow {\text {Aut}}({{\mathcal {X}}}^\prime /R^\prime )$. We put

$$\begin{aligned} {\text {Aut}}(\overline{{{\mathcal {X}}}/R}):=\mathrm{colim}_{R^\prime } {\text {Aut}}({{\mathcal {X}}}^\prime /R^\prime ). \end{aligned}$$

Let $\mathrm{res}_3:{\text {Aut}}(\overline{{{\mathcal {X}}}/R})\rightarrow {\text {Aut}}(X_3)$ and $\mathrm{res}_0:{\text {Aut}}(\overline{{{\mathcal {X}}}/R})\rightarrow {\text {Aut}}(X_0)$ denote the restriction homomorphisms. It is obvious that $\mathrm{res}_0$ is injective and that the following diagram commutes.

(1.2)

Theorem 1.8

The image of $\mathrm{res}_0$ is equal to the image of ${\tilde{\rho }}|_{{\text {Aut}}}$.

Thus we have obtained a set of generators of ${\text {Aut}}(\overline{{{\mathcal {X}}}/R})$.

1.3 Enriques surfaces

By Nikulin [12] and Kondo [13], the complex Enriques surfaces with finite automorphism group are classified, and this classification is extended to Enriques surfaces in odd characteristics by Martin [14]. The Enriques surfaces in characteristic $\ne 2$ with finite automorphism group are divided into seven classes $\mathrm{I}$–$\mathrm{VII}$. In this paper, we concentrate on the Enriques surface of type $\mathrm{IV}$.

Definition 1.9

A fixed-point-free involution of a K3 surface in characteristic $\ne 2$ is called an Enriques involution. An Enriques surface Y in characteristic $\ne 2$ is of type $\mathrm{IV}$ if ${\text {Aut}}(Y)$ is of order 320. An Enriques involution of a K3 surface is of type $\mathrm{IV}$ if the quotient Enriques surface is of type $\mathrm{IV}$.

Proposition 1.10

(Kondo [13], Martin [14]) In each characteristic $\ne 2$, an Enriques surface of type $\mathrm{IV}$ exists and is unique up to isomorphism. There exist exactly 20 smooth rational curves on an Enriques surface of type $\mathrm{IV}$. $\square$

Let $Y_{{\mathrm{IV}}, p}$ denote an Enriques surface of type $\mathrm{IV}$ in characteristic $p\ne 2$. Kondo [13] showed that the covering K3 surface of $Y_{{\mathrm{IV}}, 0}$ is isomorphic to $X_0$.

Proposition 1.11

There exist exactly six Enriques involutions in the projective automorphism group ${\text {Aut}}(X_0, h_0)$. These six Enriques involutions are conjugate in ${\text {Aut}}(X_0, h_0)$, and hence, the corresponding Enriques surfaces are isomorphic to each other. All of them are of type $\mathrm{IV}$.

By Theorem 1.7, these six Enriques involutions in ${\text {Aut}}(X_0, h_0)$ specialize to involutions of $X_3$.

Theorem 1.12

Let $\varepsilon _3\in {\text {Aut}}(X_3)$ be an involution that is mapped to an Enriques involution in ${\text {Aut}}(X_0, h_0)$ by ${\tilde{\rho }}|_{{\text {Aut}}}$. Then $\varepsilon _3$ is an Enriques involution of type $\mathrm{IV}$, and the pullbacks of the 20 smooth rational curves on $X_3/\langle {\varepsilon _3} \rangle \cong Y_{{\mathrm{IV}}, 3}$ by the quotient morphism $X_3\rightarrow X_3/\langle {\varepsilon _3} \rangle$ are lines of the Fermat quartic surface $F_3\cong X_3$.

Fig. 1

Petersen graph

During the investigation, we have come to notice that the geometry of $X_p$ and $Y_{{\mathrm{IV}}, p}$ is closely related to the Petersen graph (Fig. 1). See Sect. 2 for this relation. As a by-product, we see that the dual graph of the 20 smooth rational curves on $Y_{{\mathrm{IV}}, p}$ is as in Fig. 2. Compare Fig. 2 with the picturesque but complicated figure of Kondo (Figure 4.4 of [13]).

It has been observed that the Petersen graph is related to various K3/Enriques surfaces. See, for example, Vinberg [15] for the relation with the singular K3 surface with the transcendental lattice of discriminant 4. See also Dolgachev–Keum [16] and Dolgachev [17] for the relation with Hessian quartic surfaces and associated Enriques surfaces.

Fig. 2

Smooth rational curves on $Y_{{\mathrm{IV}}, p}$

1.4 Plan of the paper

In Sect. 2, we present a precise description of the embedding $\rho :S_{0}\hookrightarrow S_{3}$. First we introduce the notion of $\mathrm{QP}$-graphs. Then, using an isomorphism $X_3\cong F_3$ given by Shioda [6], we show that $S_{0}$ is a lattice obtained from a $\mathrm{QP}$-graph and calculate the embedding $\rho :S_{0}\hookrightarrow S_{3}$ explicitly. An elliptic modular surface of level 4 over a discrete valuation ring is constructed, and the relation with the Petersen graph is explained geometrically. In Sect. 3, we review the method of Borcherds [3, 4] to calculate the orthogonal group of an even hyperbolic lattice and fix terminologies about chambers. The application of this method to K3 surfaces is also explained. In Sect. 4, we review the results of [1] for ${\text {Aut}}(X_0)$ and of [2] for ${\text {Aut}}(X_3)$. Using the chamber tessellations of $N_{0}$ and $N_{3}$ obtained in these works, we give a proof of Theorems 1.7 and 1.8 in Sect. 5. In Sect. 6, we investigate Enriques involutions of $X_0$ and $X_3$.

In this paper, we fix bases of lattices and reduce proofs of our results to simple computations of vectors and matrices. Unfortunately, these vectors and matrices are too large to be presented in the paper. We refer the reader to the author’s web site [18] for this data. In the computation, we used GAP [19].

Thanks are due to Professors I. Dolgachev, G. van der Geer, S. Kondo, Y. Matsumoto, S. Mukai, H. Ohashi, T. Shioda, and T. Terasoma. In particular, the contents of Sect. 2.5 are obtained through discussions with S. Mukai and T. Terasoma. Thanks are also due to the referees of the first and second version of this paper for their many comments and suggestions. In particular, the contents of Sect. 2.6 are suggested by one of the referees.

2 The lattices $S_{0}$ and $S_{3}$

2.1 Graphs and lattices

First we fix terminologies and notation about graphs and lattices.

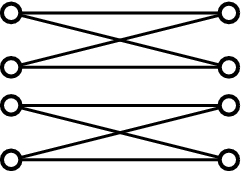
A graph (or more precisely, a weighted graph) is a pair $(V, \eta )$, where V is a set of vertices and $\eta$ is a map from the set $V \atopwithdelims ()2$ of non-ordered pairs of distinct elements of V to ${{\mathbb {Z}}}_{\ge 0}$. When the image of $\eta$ is contained in $\{0, 1\}$, we say that $(V, \eta )$ is simple and denote it by (V, E), where $E=\eta ^{-1}(1)$ is the set of edges. Let $\varGamma =(V, E)$ and $\varGamma ^\prime =(V^\prime , E^\prime )$ be simple graphs. A map$\gamma :\varGamma \rightarrow \varGamma ^\prime$of simple graphs is a pair of maps $\gamma _{V}:V\rightarrow V^\prime$ and $\gamma _E:E\rightarrow E^\prime$ such that, for all $\{v, v^\prime \}\in E$, we have $\gamma _E(\{v, v^\prime \})=\{\gamma _V(v), \gamma _V(v^\prime )\}\in E^\prime$. A graph is depicted by indicating each vertex by and $\eta (\{v, v^\prime \})$ by the number of line segments connecting v and $v^\prime$. The Petersen graph${{\mathcal {P}}}=(V_{{{\mathcal {P}}}}, E_{{{\mathcal {P}}}})$ is the simple graph given in Fig. 1. It is well known that the automorphism group ${\text {Aut}}({{\mathcal {P}}})$ of ${{\mathcal {P}}}$ is isomorphic to the symmetric group ${{\mathfrak {S}}}_5$.

A submodule M of a free ${{\mathbb {Z}}}$-module L is primitive if L / M is torsion-free. A nonzero vector v of L is primitive if ${{\mathbb {Z}}}v\subset L$ is primitive.

Let L be a lattice. We say that L is even if $\langle x, x\rangle \in 2{{\mathbb {Z}}}$ for all $x\in L$. The dual lattice of L is the free ${{\mathbb {Z}}}$-module $L^{\vee }:={\mathrm {Hom}}(L,{{\mathbb {Z}}})$, into which L is embedded by $\langle \,, \,\rangle$. Hence we have $L^{\vee }\subset L\otimes {{{\mathbb {Q}}}}$. The discriminant group$A(L)$ is the finite abelian group $L^{\vee }/L$. We say that L is unimodular if A(L) is trivial.

With a graph $\varGamma =(V, \eta )$ with $|V|<\infty$, we associate an even lattice $\langle {\varGamma } \rangle$ as follows. Let ${{\mathbb {Z}}}^V$ be the ${{\mathbb {Z}}}$-module freely generated by the elements of V. We define a symmetric bilinear form $\langle \,, \,\rangle$ on ${{\mathbb {Z}}}^V$ by

$$\begin{aligned} \langle v, v^\prime \rangle ={\left\{ \begin{array}{ll} -2 &{}\quad \hbox {if }v= v^\prime , \\ \eta (\{v, v^\prime \}) &{}\quad \hbox {if }v\ne v^\prime . \end{array}\right. } \end{aligned}$$

Let ${\text {Ker}}\langle \,, \,\rangle \subset {{\mathbb {Z}}}^V$ denote the submodule $\{ {x\in {{\mathbb {Z}}}^V} \mid {\langle x, y\rangle =0\;\text {for all}\; y\in {{\mathbb {Z}}}^V} \}$. Then the quotient module $\langle {\varGamma } \rangle :={{\mathbb {Z}}}^V/{\text {Ker}}\langle \,, \,\rangle$ has a natural structure of an even lattice.

Suppose that Z is a K3 surface or an Enriques surface defined over an algebraically closed field. Let ${{\mathcal {L}}}$ be a set of smooth rational curves on Z. Then the mapping $C\mapsto [C]$ embeds ${{\mathcal {L}}}$ into the Néron–Severi lattice $S_{Z}$ of Z. The dual graph of ${{\mathcal {L}}}$ is the graph $({{\mathcal {L}}}, \eta )$, where $\eta (\{C_1, C_2\})$ is the intersection number of two distinct curves $C_1, C_2\in {{\mathcal {L}}}$. By abuse of notation, we sometimes use ${{\mathcal {L}}}$ to denote the dual graph $({{\mathcal {L}}}, \eta )$ or the image of the embedding ${{\mathcal {L}}}\hookrightarrow S_{Z}$. Then the even lattice $\langle {{{\mathcal {L}}}} \rangle$ constructed from the dual graph of ${{\mathcal {L}}}$ is canonically identified with the sublattice of $S_{Z}$ generated by ${{\mathcal {L}}}\subset S_{Z}$, because every smooth rational curve on Z has self-intersection number $-2$.

Example 2.1

Let $\varGamma$ be the graph given in Fig. 2. Then $\langle {\varGamma } \rangle$ is an even hyperbolic lattice of rank 10 with $A(\langle {\varGamma } \rangle )\cong ({{\mathbb {Z}}}/2{{\mathbb {Z}}})^2$. Since the Néron–Severi lattice of an Enriques surface is unimodular of rank 10, the classes of 20 smooth rational curves on $Y_{{\mathrm{IV}}, p}$ generate a sublattice of index 2 in the Néron–Severi lattice.

2.2 $\mathrm{QP}$-graph

We introduce the notion of $\mathrm{QP}$-graphs, where $\mathrm{QP}$ stands for a quadruple covering of the Petersen graph. In the following, a quadrangle means the simple graph .

Definition 2.2

A $\mathrm{QP}$-graph is a pair $({{\mathcal {Q}}}, \gamma )$ of a simple graph ${{\mathcal {Q}}}=(V_{{{\mathcal {Q}}}}, E_{{{\mathcal {Q}}}})$ and a map $\gamma :{{\mathcal {Q}}}\rightarrow {{\mathcal {P}}}$ to the Petersen graph with the following properties.

• (i) The map $\gamma _{V}:V_{{{\mathcal {Q}}}}\rightarrow V_{{{\mathcal {P}}}}$ is surjective, and every fiber of $\gamma _{V}$ is of size 4.

• (ii) For any edge e of ${{\mathcal {P}}}$, the subgraph $(\gamma _V^{-1}(e), \gamma _E^{-1}(\{e\}))$ of ${{\mathcal {Q}}}$ is isomorphic to the disjoint union of two quadrangles.

  

• (iii) Any two distinct quadrangles in ${{\mathcal {Q}}}$ have at most one common vertex.

A map $\gamma :{{\mathcal {Q}}}\rightarrow {{\mathcal {P}}}$ satisfying conditions (i)–(iii) is called a $\mathrm{QP}$-covering map. Two $\mathrm{QP}$-graphs $({{\mathcal {Q}}}, \gamma )$ and $({{\mathcal {Q}}}^\prime , \gamma ^\prime )$ are said to be isomorphic if there exists an isomorphism $h:{{\mathcal {Q}}}\rightarrow {{\mathcal {Q}}}^\prime$ such that $\gamma ^\prime \circ h=\gamma$.

Proposition 2.3

Up to isomorphism, there exist exactly two $\mathrm{QP}$-graphs $({{\mathcal {Q}}}_0, \gamma _0)$ and $({{\mathcal {Q}}}_1, \gamma _1)$. The even lattices $\langle {{{\mathcal {Q}}}_0} \rangle$ and $\langle {{{\mathcal {Q}}}_1} \rangle$ are hyperbolic of rank 20. The discriminant group $A(\langle {{{\mathcal {Q}}}_0} \rangle )$ of $\langle {{{\mathcal {Q}}}_0} \rangle$ is isomorphic to $({{\mathbb {Z}}}/2{{\mathbb {Z}}})^2$, whereas $A(\langle {{{\mathcal {Q}}}_1} \rangle )$ is isomorphic to $({{\mathbb {Z}}}/4{{\mathbb {Z}}})^2$.

Proof

We enumerate all isomorphism classes of $\mathrm{QP}$-graphs. Let $\Delta$ be the set of ordered pairs $[\{i_1, i_2\}, \{i_3, i_4\}]$ of non-ordered pairs of elements of $\{1,2,3,4\}$ such that $\{i_1, i_2, i_3, i_4\}=\{1,2,3,4\}$. We have $|\Delta |=6$. Let ${{\mathcal {T}}}(\Delta )$ be the set of ordered triples $[\delta _1, \delta _2, \delta _3]$ of elements of $\Delta$ such that, if $\mu \ne \nu$, then $\delta _{\mu }=[\{i_1, i_2\}, \{i_3, i_4\}]$ and $\delta _{\nu }=[\{i^\prime _1, i^\prime _2\}, \{i^\prime _3, i^\prime _4\}]$ satisfy $|\{i_1, i_2\}\cap \{i_1^\prime , i_2^\prime \}|=1$. Then we have $|{{\mathcal {T}}}(\Delta )|=48$. The following facts can be easily verified.

• (a) The natural action on ${{\mathcal {T}}}(\Delta )$ of the full permutation group ${{\mathfrak {S}}}_4$ of $\{1,2,3,4\}$ decomposes ${{\mathcal {T}}}(\Delta )$ into two orbits $o_1$ and $o_2$ of size 24.

• (b) For any triple $[\delta _1, \delta _2, \delta _3]\in {{\mathcal {T}}}(\Delta )$ and any permutation $\mu , \nu , \rho$ of 1, 2, 3, the triple $[\delta _{\mu }, \delta _{\nu }, \delta _{\rho }]$ belongs to the same orbit as $[\delta _1, \delta _2, \delta _3]$.

• (c) For $\delta =[\{i_1, i_2\}, \{i_3, i_4\}]\in \Delta$, we put ${\bar{\delta }}:=[\{i_3, i_4\}, \{i_1, i_2\}]\in \Delta$. Then $[\delta _1, \delta _2, \delta _3]\in {{\mathcal {T}}}(\Delta )$ and $[\delta _1, \delta _2, {\bar{\delta }}_3]\in {{\mathcal {T}}}(\Delta )$ belong to different orbits.

Let $\psi$ be a map from the set $V_{{{\mathcal {P}}}}$ of vertices of ${{\mathcal {P}}}$ to the set $\{o_1, o_2\}$ of the orbits. We construct a $\mathrm{QP}$-graph $({{\mathcal {Q}}}_{\psi }, \gamma _{\psi })$ with the set of vertices

$$\begin{aligned} V_{{{\mathcal {Q}}}}:=V_{{{\mathcal {P}}}}\times \{1,2,3,4\} \end{aligned}$$

as follows. For each vertex $v\in V_{{{\mathcal {P}}}}$, we choose an element $[\delta _1, \delta _2, \delta _3]$ from the orbit $\psi (v)$, choose an ordering $e_1, e_2, e_3$ on the three edges of ${{\mathcal {P}}}$ emitting from v, and assign $\delta _i$ to the pair $(v, e_i)$ for $i=1,2,3$. Let $e=\{v, v^\prime \}$ be an edge of ${{\mathcal {P}}}$. Suppose that $\delta =[\{i_1, i_2\}, \{i_3, i_4\}]$ is assigned to (v, e) and $\delta ^\prime =[\{i^\prime _1, i^\prime _2\}, \{i^\prime _3, i^\prime _4\}]$ is assigned to $(v^\prime , e)$. Then the edges of ${{\mathcal {Q}}}_{\psi }$ lying over the edge e of ${{\mathcal {P}}}$ are the following eight edges.

Let $\gamma _{\psi }:{{\mathcal {Q}}}_{\psi }\rightarrow {{\mathcal {P}}}$ be obtained from the first projection $V_{{{\mathcal {Q}}}}\rightarrow V_{{{\mathcal {P}}}}$. Then $({{\mathcal {Q}}}_{\psi }, \gamma _{\psi })$ is a $\mathrm{QP}$-graph. The isomorphism class of $({{\mathcal {Q}}}_{\psi }, \gamma _{\psi })$ is independent of the choice of a representative $[\delta _1, \delta _2,\delta _3]$ of each orbit $\psi (v)$ and the choice of the ordering of the edges emitting from each vertex of ${{\mathcal {P}}}$. Indeed, changing these choices merely amounts to relabeling the vertices in each fiber of the first projection $V_{{{\mathcal {Q}}}}\rightarrow V_{{{\mathcal {P}}}}$ (see fact (b)). It is also obvious that every $\mathrm{QP}$-graph is isomorphic to $({{\mathcal {Q}}}_{\psi }, \gamma _{\psi })$ for some $\psi :V_{{{\mathcal {P}}}}\rightarrow \{o_1, o_2\}$.

For an orbit $o\in \{o_1, o_2\}$, let ${\bar{o}}$ denote the other orbit; $\{o_1, o_2\}=\{o, {\bar{o}}\}$. Let $\psi :V_{{{\mathcal {P}}}}\rightarrow \{o_1, o_2\}$ be a map, and let $e=\{v, v^\prime \}$ be an edge of ${{\mathcal {P}}}$. We define $\psi ^\prime :V_{{{\mathcal {P}}}}\rightarrow \{o_1, o_2\}$ by $\psi ^\prime (v):=\overline{\psi (v)}, \psi ^\prime (v^\prime ):=\overline{\psi (v^\prime )}$ and $\psi ^\prime (v^{\prime \prime }):=\psi (v^{\prime \prime })$ for all $v^{\prime \prime }\in V_{{{\mathcal {P}}}}{\setminus }\{v, v^\prime \}$. Then $({{\mathcal {Q}}}_{\psi }, \gamma _{\psi })$ and $({{\mathcal {Q}}}_{\psi ^\prime }, \gamma _{\psi ^\prime })$ are isomorphic. (See the picture below and fact (c).)

Hence the isomorphism class of $({{\mathcal {Q}}}_{\psi }, \gamma _{\psi })$ depends only on $|\psi ^{-1}(o_1)|\bmod 2$. We denote by $({{\mathcal {Q}}}_0, \gamma _0)$ the $\mathrm{QP}$-graph $({{\mathcal {Q}}}_{\psi }, \gamma _{\psi })$ with $|\psi ^{-1}(o_1)|\equiv 0\bmod 2$ and by $({{\mathcal {Q}}}_1, \gamma _1)$ the $\mathrm{QP}$-graph $({{\mathcal {Q}}}_{\psi }, \gamma _{\psi })$ with $|\psi ^{-1}(o_1)|\equiv 1\bmod 2$. Since we have constructed ${{\mathcal {Q}}}_0$ and ${{\mathcal {Q}}}_1$ explicitly, the assertions on $\langle {{{\mathcal {Q}}}_0} \rangle$ and $\langle {{{\mathcal {Q}}}_1} \rangle$ can be proved by direct computation. $\square$

Proposition 2.4

Let $({{\mathcal {Q}}}, \gamma )$ be a $\mathrm{QP}$-graph. Each automorphism $g\in {\text {Aut}}({{\mathcal {Q}}})$ maps every fiber of $\gamma _V:V_{{{\mathcal {Q}}}}\rightarrow V_{{{\mathcal {P}}}}$ to a fiber of $\gamma _V$, and hence induces ${\bar{g}}\in {\text {Aut}}({{\mathcal {P}}})$ such that ${\bar{g}}\circ \gamma =\gamma \circ g$. The mapping $g\mapsto {\bar{g}}$ gives a surjective homomorphism

$$\begin{aligned} {\text {Aut}}({{\mathcal {Q}}})\rightarrow {\text {Aut}}({{\mathcal {P}}})\cong {{\mathfrak {S}}}_5, \end{aligned}$$

and its kernel is isomorphic to $({{\mathbb {Z}}}/2{{\mathbb {Z}}})^6$.

Proof

Since ${{\mathcal {P}}}$ does not contain a quadrangle, every quadrangle of ${{\mathcal {Q}}}$ is mapped to an edge of ${{\mathcal {P}}}$ by $\gamma$. Hence two distinct vertices $v, v^\prime$ of ${{\mathcal {Q}}}$ are mapped to the same vertex of ${{\mathcal {P}}}$ by $\gamma$ if and only if $\{v, v^\prime \}$ is not an edge of ${{\mathcal {Q}}}$ and there exists a quadrangle of ${{\mathcal {Q}}}$ containing v and $v^\prime$. Thus the first assertion follows. We make the complete list of elements of ${\text {Aut}}({{\mathcal {Q}}})$ by computer and verify the assertion on ${\text {Aut}}({{\mathcal {Q}}})\rightarrow {\text {Aut}}({{\mathcal {P}}})$. $\square$

Corollary 2.5

A $\mathrm{QP}$-covering map $\gamma :{{\mathcal {Q}}}\rightarrow {{\mathcal {P}}}$ from the graph ${{\mathcal {Q}}}$ is unique up to the action of ${\text {Aut}}({{\mathcal {P}}})$. $\square$

2.3 The configurations ${{\mathcal {L}}}_{40}$ and ${{\mathcal {L}}}_{112}$

In this section, following the argument of Shioda [6], we describe the Néron–Severi lattices $S_{0}$ of $X_0$ and $S_{3}$ of $X_3$ and investigate the embedding $\rho :S_{0}\hookrightarrow S_{3}$ induced by the specialization of $X_0$ to $X_3$.

By Theorem 1.1 (1), we have a distinguished set of

$$\begin{aligned} 6\times 4+4^2=40 \end{aligned}$$

smooth rational curves on $X_p$, where the $6\times 4$ curves are the irreducible components of the six singular fibers of $\sigma :X_p\rightarrow {{\mathbb {P}}}^1$ and the $4^2$ curves are the torsion sections of the Mordell–Weil group. We denote the configuration of these smooth rational curves by ${{\mathcal {L}}}_{40, p}$, or simply by ${{\mathcal {L}}}_{40}$. The specialization of $X_0$ to $X_p$ gives a bijection from ${{\mathcal {L}}}_{40, 0}$ to ${{\mathcal {L}}}_{40, p}$, because the specialization preserves the elliptic fibration $\sigma :X_p\rightarrow {{\mathbb {P}}}^1$ and its zero section. This bijection is obviously compatible with the specialization homomorphism $S_0\rightarrow S_p$.

The set of lines on the Fermat quartic surface $F_3$ in characteristic 3 has been studied classically by Segre [20]. The surface $F_3\subset {{\mathbb {P}}}^3$ contains exactly 112 lines, and every line on $F_3$ is defined over the finite field ${{\mathbb {F}}}_9$. We denote by ${{\mathcal {L}}}_{112}$ the set of these lines. We can easily make the list of defining equations of all lines on $F_3$ and calculate the dual graph of ${{\mathcal {L}}}_{112}$. It is also known ([2]) that the classes of 22 lines appropriately chosen from ${{\mathcal {L}}}_{112}$ form a basis of $S_{F_3}\cong S_{3}$. Fixing a basis of $S_{3}$, we can express all classes of lines as integer vectors of length 22 (see [18]).

We show that the specialization of $X_0$ to $X_3\cong F_3$ induces an embedding

$$\begin{aligned} \rho _{{{\mathcal {L}}}}:{{\mathcal {L}}}_{40}\hookrightarrow {{\mathcal {L}}}_{112} \end{aligned}$$

of configurations. We recall the construction of the isomorphism $X_3\cong F_3$ by Shioda [6]. Let $\sigma _F:F_3 \rightarrow {{\mathbb {P}}}^1$ be the morphism defined by

$$\begin{aligned} \sigma _F\;:\; [x_1: x_2: x_3: x_4]\;\mapsto \; [x_3^2- i\,x_4^2: x_1^2+i \,x_2^2]=[-x_1^2+i\,x_2^2: x_3^2+i\, x_4^2], \end{aligned}$$

(2.1)

where $i=\sqrt{-1}\in {{\mathbb {F}}}_9$. The generic fiber of $\sigma _F$ is a curve of genus 1, and $\sigma _F$ has a section (see the next paragraph). Hence the generic fiber of $\sigma _F$ is isomorphic to its Jacobian, which is defined by Eq. (1.1) by the result of Bašmakov and Faddeev [21]. Therefore $\sigma _F:F_3\rightarrow {{\mathbb {P}}}^1$ is isomorphic to $\sigma :X_3\rightarrow {{\mathbb {P}}}^1$ over ${{\mathbb {P}}}^1$.

Remark 2.6

In characteristic 0, morphism (2.1) with $i\in {{\mathbb {C}}}$ from the Fermat quartic surface to ${{\mathbb {P}}}^1$ has no sections.

Using the defining equations of lines and the vector representations of their classes, we confirm the following facts. These facts make the isomorphism between $\sigma _F:F_3\rightarrow {{\mathbb {P}}}^1$ and $\sigma :X_3\rightarrow {{\mathbb {P}}}^1$ over ${{\mathbb {P}}}^1$ more explicit. There exist exactly $6\times 4$ lines on $F_3$ that are contracted to points by $\sigma _F$. These 24 lines form, of course, a configuration of six disjoint quadrangles. Moreover, there exist exactly 64 lines on $F_3$ that are mapped to ${{\mathbb {P}}}^1$ isomorphically by $\sigma _F$. Let $z_F\in {{\mathcal {L}}}_{112}$ be one of these 64 sections of $\sigma _F$. To be explicit, we choose the following line as $z_F$. (See Remark in Section 4 of [6]):

$$\begin{aligned} x_1+i\, x_3- x_4=x_2+x_3 -i \,x_4=0. \end{aligned}$$

(2.2)

Let $\mathrm{MW}(\sigma _F, z_F)$ denote the Mordell–Weil group of $\sigma _F:F_3\rightarrow {{\mathbb {P}}}^1$ with the zero section $z_F$, and let $\mathrm{Triv}(\sigma _F, z_F)$ be the sublattice of $S_{3}$ generated by the classes of the zero section $z_F$ and the 24 lines in the singular fibers of $\sigma _F$. (This lattice is called the trivial sublattice of the Jacobian fibration $(\sigma _F, z_F)$ in the theory of Mordell–Weil lattices [22].) Let $\mathrm{Triv}^{-} (\sigma _F, z_F)$ denote the primitive closure of $\mathrm{Triv}(\sigma _F, z_F)$ in $S_{3}$. By [22], we have a canonical isomorphism

$$\begin{aligned} \mathrm{Triv}^{-} (\sigma _F, z_F)/\mathrm{Triv}(\sigma _F, z_F)\;\cong \; \text {the torsion part of }\mathrm{MW}(\sigma _F, z_F). \end{aligned}$$

(2.3)

Therefore a section $s:{{\mathbb {P}}}^1\rightarrow F_3$ of $\sigma _F$ is a torsion element of $\mathrm{MW}(\sigma _F, z_F)$ if the class of s belongs to $\mathrm{Triv}^{-} (\sigma _F, z_F)$. By this criterion, we find 16 lines among the 64 sections of $\sigma _F$ that form the torsion part of $\mathrm{MW}(\sigma _F, z_F)$. Thus we obtain the configuration ${{\mathcal {L}}}_{40, 3}$ on $X_3$ as a sub-configuration of ${{\mathcal {L}}}_{112}$. Combining this embedding ${{\mathcal {L}}}_{40, 3}\hookrightarrow {{\mathcal {L}}}_{112}$ with the bijection ${{\mathcal {L}}}_{40}={{\mathcal {L}}}_{40, 0}\cong {{\mathcal {L}}}_{40, 3}$ induced by specialization of $X_0$ to $X_3$, we obtain the embedding $\rho _{{{\mathcal {L}}}}:{{\mathcal {L}}}_{40}\hookrightarrow {{\mathcal {L}}}_{112}$ induced by the specialization of $X_0$ to $X_3$.

The dual graph of ${{\mathcal {L}}}_{40}$ is now calculated explicitly. Hence we can prove the following by a direct computation.

Proposition 2.7

The dual graph of ${{\mathcal {L}}}_{40}$ is isomorphic to the $\mathrm{QP}$-graph ${{\mathcal {Q}}}_1$. $\square$

Comparing the ranks and the discriminants of $\langle {{{\mathcal {L}}}_{40}} \rangle \cong \langle {{{\mathcal {Q}}}_1} \rangle$ and $S_{0}$, we obtain the following:

Corollary 2.8

The lattice $S_{0}$ is generated by the classes of curves in ${{\mathcal {L}}}_{40}$. $\square$

Corollary 2.9

The embedding $\rho _{{{\mathcal {L}}}}:{{\mathcal {L}}}_{40}\hookrightarrow {{\mathcal {L}}}_{112}$ induces the embedding $\rho :S_{0}\hookrightarrow S_{3}$ induced by the specialization of $X_0$ to $X_3$. This embedding $\rho$ is primitive. $\square$

The last assertion follows from the explicit matrix form of the embedding $\rho$ with respect to some bases of $S_0$ and $S_3$ (see [18]).

Remark 2.10

The existence of an isomorphism $X_3\cong F_3$ can be easily seen by the following argument. By [23], we know that $X_3$ is a supersingular K3 surface with Artin invariant 1, and hence is isomorphic to $F_3$ by the uniqueness of a supersingular K3 surface with Artin invariant 1.

2.4 All embeddings of ${{\mathcal {L}}}_{40}$ into ${{\mathcal {L}}}_{112}$

The embedding $\rho _{{{\mathcal {L}}}}:{{\mathcal {L}}}_{40}\hookrightarrow {{\mathcal {L}}}_{112}$ constructed in the preceding section depends on the choice of $\sigma _F$ and $z_F$. In this section, we make the complete list of all embeddings ${{\mathcal {L}}}_{40}\hookrightarrow {{\mathcal {L}}}_{112}$.

Let $a\mapsto {\bar{a}}:=a^3$ denote the Frobenius automorphism of the base field $k_3$. Then the projective automorphism group of $F_3\subset {{\mathbb {P}}}^3$ is equal to

$$\begin{aligned} {\mathrm {PGU}}_4({{\mathbb {F}}}_9):=\{\, {g\in {\mathrm {GL}}_4(k_3)} \mid {{}^\mathrm{T} g \cdot {\bar{g}}\text { is a scalar matrix} } \, \}/ k_3^{\times }, \end{aligned}$$

which is of order 13063680. We can calculate the action of ${\mathrm {PGU}}_4({{\mathbb {F}}}_9)$ on ${{\mathcal {L}}}_{112}$ and on $S_{3}=\langle {{{\mathcal {L}}}_{112}} \rangle$. Let ${{\mathcal {A}}}$ denote the set of all ordered five tuples $[z, \ell _0, \dots , \ell _3]$ of lines on $F_3$ that form the configuration whose dual graph is as follows:

(2.4)

Note that ${\mathrm {PGU}}_4({{\mathbb {F}}}_9)$ acts on ${{\mathcal {A}}}$ naturally. We have the following:

Proposition 2.11

The action of ${\mathrm {PGU}}_4({{\mathbb {F}}}_9)$ on ${{\mathcal {A}}}$ is simply transitive.

Proof

By [24], we have the following facts.

• (1) Since every line on $F_3$ is defined over ${{\mathbb {F}}}_9$, the intersection points of $\ell \in {{\mathcal {L}}}_{112}$ with other lines in ${{\mathcal {L}}}_{112}$ are ${{\mathbb {F}}}_9$-rational. For each ${{\mathbb {F}}}_9$-rational point P of $\ell$, there exist exactly three lines in ${{\mathcal {L}}}_{112} {\setminus }\{\ell \}$ that intersect $\ell$ at P. Hence there exist exactly $112-3\times 10-1=81$ lines in ${{\mathcal {L}}}_{112}$ that are disjoint from $\ell$. The group ${\mathrm {PGU}}_4({{\mathbb {F}}}_9)$ acts on the set of ordered pairs of disjoint lines in ${{\mathcal {L}}}_{112}$.

• (2) If $\ell _1, \ell _2, \ell _3\in {{\mathcal {L}}}_{112}$ satisfy $\langle \ell _1, \ell _2\rangle =\langle \ell _2, \ell _3\rangle =\langle \ell _3, \ell _1\rangle =1$, then there exist a plane $\Pi \subset {{\mathbb {P}}}^3$ containing $\ell _1, \ell _2, \ell _3$ and a point $P\in \Pi$ contained in $\ell _1, \ell _2, \ell _3$. The residual line $\ell _4=(F_3\cap \Pi )-(\ell _1+ \ell _2+ \ell _3)$ also passes through P.

• (3) Let $[\ell _1, \ell _2]$ be an ordered pair of disjoint lines in ${{\mathcal {L}}}_{112}$. Then there exist exactly ten lines that intersect both $\ell _1$ and $\ell _2$. Let $\mathrm{Stab}([\ell _1, \ell _2])$ denote the stabilizer subgroup of $[\ell _1, \ell _2]$ in ${\mathrm {PGU}}_4({{\mathbb {F}}}_9)$. Then the restriction homomorphism

  $$\begin{aligned} \mathrm{res}_{\ell }:\mathrm{Stab}([\ell _1, \ell _2])\rightarrow {\mathrm {PGL}}(\ell _1, {{\mathbb {F}}}_9) \end{aligned}$$

  to the group of linear automorphisms of $\ell _1\cong {{\mathbb {P}}}^1$ over ${{\mathbb {F}}}_9$ is surjective, and its kernel is of order 2. Let P be an ${{\mathbb {F}}}_9$-rational point of $\ell _1$, and let $m_P, m^\prime _P\in {{\mathcal {L}}}_{112}$ be the lines that intersect $\ell _1$ at P but are disjoint from $\ell _2$. Then the non-trivial element of ${\text {Ker}}(\mathrm{res}_{\ell })$ exchanges $m_P$ and $m^\prime _P$.

The transitivity of the action of ${\mathrm {PGU}}_4({{\mathbb {F}}}_9)$ on ${{\mathcal {A}}}$ follows from these facts. Moreover, we have

$$\begin{aligned} |{{\mathcal {A}}}|=112\cdot 81\cdot 10\cdot 9\cdot 16=13063680=|{\mathrm {PGU}}_4({{\mathbb {F}}}_9)|, \end{aligned}$$

where the factor 112 is the number of choices of $\ell _0$ in $[z, \ell _0, \dots , \ell _3]\in {{\mathcal {A}}}$, the factor 81 is the number of choices of $\ell _2$ when $\ell _0$ is given, the factor $10\cdot 9$ is the number of choices of $\ell _1$ and $\ell _3$ when $\ell _0$ and $\ell _2$ are given, and the factor 16 is the number of choices of z for a given quadrangle $[\ell _0, \dots , \ell _3]$. Therefore the action of ${\mathrm {PGU}}_4({{\mathbb {F}}}_9)$ on ${{\mathcal {A}}}$ is simply transitive. $\square$

Let ${{\mathcal {F}}}$ denote the set of sub-configurations of ${{\mathcal {L}}}_{112}$ isomorphic to ${{\mathcal {L}}}_{40}$. Let $\alpha =[z_{\alpha }, \ell _0, \dots , \ell _3]$ be an element of ${{\mathcal {A}}}$. Then there exists a unique Jacobian fibration

$$\begin{aligned} \sigma _\alpha :F_3\rightarrow {{\mathbb {P}}}^1 \end{aligned}$$

with the zero section $z_{\alpha }$ such that $\ell _0+\ell _1+\ell _2+\ell _3$ is a singular fiber of $\sigma _\alpha$. The Jacobian fibration $(\sigma _F, z_F)$ that was used in the construction of $\rho _{{{\mathcal {L}}}}$ is obtained as one of the $(\sigma _{\alpha }, z_{\alpha })$. By Proposition 2.11, all Jacobian fibrations $(\sigma _{\alpha }, z_{\alpha })$ are conjugate under the action of ${\mathrm {PGU}}_4({{\mathbb {F}}}_9)$. Therefore $(\sigma _{\alpha }, z_{\alpha })$ yields a sub-configuration ${{\mathcal {L}}}_{\alpha }$ of ${{\mathcal {L}}}_{112}$ isomorphic to ${{\mathcal {L}}}_{40}$, and the map $\alpha \mapsto {{\mathcal {L}}}_{\alpha }$ gives a surjection $\lambda :{{\mathcal {A}}}\rightarrow {{\mathcal {F}}}$ compatible with the action of ${\mathrm {PGU}}_4({{\mathbb {F}}}_9)$. The size of a fiber of $\lambda$ over ${{\mathcal {L}}}^\prime \in {{\mathcal {F}}}$ is

$$\begin{aligned} 30\times 2\times 16=960, \end{aligned}$$

where the factor 30 is the number of quadrangles in ${{\mathcal {L}}}^\prime \cong {{\mathcal {L}}}_{40}$, the factor 2 counts the flipping $\ell _1\leftrightarrow \ell _3$, and the factor 16 is the number of choices of the zero section $z_{\alpha }$. Thus we obtain the following:

Corollary 2.12

The number of sub-configurations of ${{\mathcal {L}}}_{112}$ isomorphic to ${{\mathcal {L}}}_{40}$ is $|{\mathrm {PGU}}_4({{\mathbb {F}}}_9)|/960=13608$, and ${\mathrm {PGU}}_4({{\mathbb {F}}}_9)$ acts on the set of these sub-configurations transitively. $\square$

2.5 An elliptic modular surface of level 4 over a discrete valuation ring

Let R be a discrete valuation ring such that $2\in R^{\times }$ and $i=\sqrt{-1}\in R$. We construct a model of the elliptic modular surface of level 4 over R, that is, we perform over R the resolution of the completion of the affine surface defined by (1.1). This construction explains the isomorphism ${{\mathcal {L}}}_{40}\cong {{\mathcal {Q}}}_1$ of graphs geometrically.

Fig. 3

Complete quadrangle

In this paragraph, all schemes and morphisms are defined over R. We consider the complete quadrangle on ${{\mathbb {P}}}^2$ (Fig. 3) such that each of the triple points $t_1, \dots , t_4$ is an R-valued point. Let $M\rightarrow {{\mathbb {P}}}^2$ be the blowup of ${{\mathbb {P}}}^2$ at $t_1, \dots , t_4$. Let ${\bar{l}}_1, \dots , {\bar{l}}_6$ be the strict transforms of the lines $l_1, \dots , l_6$, and let ${\bar{t}}_1, \dots , {\bar{t}}_4$ be the exceptional divisors over $t_1, \dots , t_4$. It is well known that these $6+4=10$ smooth rational curves on M form a configuration whose dual graph is the Petersen graph ${{\mathcal {P}}}$. Let

$$\begin{aligned} \varphi _M:M\rightarrow {{\mathbb {P}}}^1 \end{aligned}$$

(2.5)

be the fibration induced by the pencil of lines on ${{\mathbb {P}}}^2$ passing through $t_1$. (The dependence of the construction on the choice of this ${{\mathbb {P}}}^1$-fibration $\varphi _M$ will be discussed in Sect. 4.3. See Remark 4.5.) Then $\varphi _M$ has exactly three singular fibers ${\bar{l}}_1+{\bar{t}}_4$, ${\bar{l}}_2+{\bar{t}}_3$, ${\bar{l}}_3+{\bar{t}}_2$, and four sections ${\bar{t}}_1,{\bar{l}}_4, {\bar{l}}_5, {\bar{l}}_6$. Let $M^\prime \rightarrow M$ be the blowup at the nodes on ${\bar{l}}_1+{\bar{t}}_4$, ${\bar{l}}_2+{\bar{t}}_3$, ${\bar{l}}_3+{\bar{t}}_2$, and let $\varphi ^\prime _M:M^\prime \rightarrow {{\mathbb {P}}}^1$ be the composite of $\varphi _M$ and $M^\prime \rightarrow M$. We choose an affine parameter $\lambda$ on the base curve ${{\mathbb {P}}}^1$ of $\varphi ^\prime _M$ such that the singular fibers are located over $\lambda =0, 1, \infty$. Let ${\tilde{M}}^\prime \rightarrow {{\mathbb {P}}}^1$ be the pullback of $\varphi _M^\prime :M^\prime \rightarrow {{\mathbb {P}}}^1$ by the covering ${{\mathbb {P}}}^1\rightarrow {{\mathbb {P}}}^1$ given by

$$\begin{aligned} \sigma \mapsto \lambda =((\sigma +\sigma ^{-1})/2)^2, \end{aligned}$$

(2.6)

and let ${\tilde{M}}\rightarrow {\tilde{M}}^\prime$ be the normalization of ${\tilde{M}}^\prime$. Then ${\tilde{M}}$ is smooth over R, and the natural morphism ${{\tilde{\varphi }}}_M:{\tilde{M}}\rightarrow {{\mathbb {P}}}^1$ to the $\sigma$-line has exactly 6 singular fibers over $\sigma =0, \pm 1, \pm i, \infty$. Each singular fiber is a union of three smooth rational curves forming the configuration the middle of which is with multiplicity 2. Let ${\tilde{t}}_1,{\tilde{l}}_4, {\tilde{l}}_5, {\tilde{l}}_6$ be the pullbacks of the sections ${\bar{t}}_1,{\bar{l}}_4, {\bar{l}}_5, {\bar{l}}_6$ of $\varphi _M$ by ${\tilde{M}}\rightarrow M$. For a divisor D on ${\tilde{M}}$, let [D] denote the class of D in the Picard group ${\mathrm {Pic}}\, {\tilde{M}}$. Note that, via ${\tilde{M}}\rightarrow M$, a fiber F of $\varphi _M:M\rightarrow {{\mathbb {P}}}^1$ is pulled back to a sum of two fibers of ${{\tilde{\varphi }}}_M:{\tilde{M}}\rightarrow {{\mathbb {P}}}^1$, and hence the class $[{\tilde{F}}]$ of the pullback ${\tilde{F}}$ of F is divisible by 2 in ${\mathrm {Pic}}\, {\tilde{M}}$. Let $[H]\in {\mathrm {Pic}}\, {\tilde{M}}$ denote the class of the pullback of a general line of ${{\mathbb {P}}}^2$. We put $B:={\tilde{t}}_1+{\tilde{l}}_4+{\tilde{l}}_5+{\tilde{l}}_6$. Since $[{\tilde{F}}]=[H]-[{\tilde{t}}_1]$ and $[{\tilde{l}}_i]=[H]-[{\tilde{t}}_j]-[{\tilde{t}}_{k}]$ for $(i, j, k)=(4,3,4), (5,2,3), (6, 2, 4)$, we have

$$\begin{aligned}{}[B]=3[{\tilde{F}}]+2[2 {\tilde{t}}_1-{\tilde{t}}_2-{\tilde{t}}_3-{\tilde{t}}_4]. \end{aligned}$$

Therefore [B] is divisible by 2 in ${\mathrm {Pic}}\, {\tilde{M}}$, and we can construct a double covering ${{\mathcal {X}}}\rightarrow {\tilde{M}}$ branched along B. Then ${{\mathcal {X}}}$ is a model of the elliptic modular surface of level 4 over R, and the Jacobian fibration $\sigma :{{\mathcal {X}}}\rightarrow {{\mathbb {P}}}^1$ is obtained as the composite of the double covering ${{\mathcal {X}}}\rightarrow {\tilde{M}}$ and ${{\tilde{\varphi }}}_M:{\tilde{M}}\rightarrow {{\mathbb {P}}}^1$.

The $\mathrm{QP}$-covering map ${{\mathcal {L}}}_{40}\rightarrow {{\mathcal {P}}}$ (see Corollary 2.5) is constructed as follows. We consider an F-valued point of ${\text {Spec}}R$, where F is a field. We put $X_F:={{\mathcal {X}}}\otimes _R F$, and ${\tilde{M}}_F:={\tilde{M}}\otimes _R F$, $M_F:=M\otimes _R F$. Let ${{\mathcal {E}}}_F$ be the generic fiber of $\sigma \otimes F:X_F\rightarrow {{\mathbb {P}}}^1_F$, which is an elliptic curve over the function field $F(\sigma )$ defined by (1.1). Let $m_2:X_F\rightarrow X_F$ be the rational map induced by multiplication by 2 on ${{\mathcal {E}}}_F$. Then the rational map

$$\begin{aligned} \mu _F\;\;:\;\; X_F \; \smash {\mathop {\; \longrightarrow \; }\limits ^{m_2}}\; X_F\; \; \smash {\mathop {\; \longrightarrow \; }\limits ^{}}\; {\tilde{M}}_F \; \smash {\mathop {\; \longrightarrow \; }\limits ^{}}\; M_F \end{aligned}$$

(2.7)

gives a map from ${{\mathcal {L}}}_{40}$ to the Petersen graph ${{\mathcal {P}}}$ formed by $\{{\bar{t}}_1, \dots , {\bar{t}}_4, {\bar{\ell }}_1, \dots , {\bar{\ell }}_6\}$.

Proposition 2.13

The rational map $\mu _F$ induces a Galois extension of the function fields. Its Galois group ${\text {Gal}}(\mu )$ is isomorphic to $({{\mathbb {Z}}}/2{{\mathbb {Z}}})^5$ and is generated by the inversion $\iota :(X, Y, \sigma )\mapsto (X, -Y, \sigma )$ of the elliptic curve ${{\mathcal {E}}}_F$, two involutions

$$\begin{aligned} (X, Y, \sigma )\mapsto (X, Y, -\sigma ), \;\; (X, Y, \sigma )\mapsto (X, Y, 1/\sigma ), \end{aligned}$$

(2.8)

and the translations by the 2-torsion points of ${{\mathcal {E}}}_F$.

Proof

The inversion $\iota$ and the involutions in (2.8) fix each 2-torsion point of ${{\mathcal {E}}}_F$. Hence the involutions in the statement of Proposition 2.13 generate a group isomorphic to $({{\mathbb {Z}}}/2{{\mathbb {Z}}})^5$. By (2.6), the function field $F(\sigma )$ is a Galois extension of $F(\lambda )$ with Galois group generated by $\sigma \mapsto -\sigma$ and $\sigma \mapsto 1/\sigma$. Hence the covering ${\tilde{M}}_F \rightarrow M_F$ in (2.7) is the quotient by the involutions in (2.8). The covering $X_F\rightarrow {\tilde{M}}_F$ in (2.7) is the quotient by $\iota$, and the map $m_2$ is the quotient by the group of translations by the 2-torsion points of ${{\mathcal {E}}}_F$. Thus the proof is completed. $\square$

2.6 Another model of the elliptic modular surface of level 4

We give a much simpler construction of a $({{\mathbb {Z}}}/2{{\mathbb {Z}}})^5$-covering $X_{0}\rightarrow M_{{{\mathbb {C}}}}$ over the complex numbers by means of a Hirzebruch covering (see Hironaka [25]). This section is due to a suggestion by one of the referees of the first version of the paper. Let $M_{{{\mathbb {C}}}}$ be the complex surface obtained by blowing up ${{\mathbb {P}}}^2_{{{\mathbb {C}}}}$ at the triple points of the complete quadrangle on ${{\mathbb {P}}}^2_{{{\mathbb {C}}}}$, and let $M^{\circ }_{{{\mathbb {C}}}}$ be the complement of the ten $(-1)$-curves on $M_{{{\mathbb {C}}}}$. We have a canonical surjective homomorphism $\pi _1 (M^{\circ }_{{{\mathbb {C}}}}) \mathbin {\rightarrow \rightarrow }H_1(M^{\circ }_{{{\mathbb {C}}}}, {{\mathbb {Z}}}/2{{\mathbb {Z}}})\cong ({{\mathbb {Z}}}/2{{\mathbb {Z}}})^5$. It is known (see [25]) that the corresponding étale covering $W^{\circ }\rightarrow M^{\circ }_{{{\mathbb {C}}}}$ extends to a finite morphism $W\rightarrow M_{{{\mathbb {C}}}}$ from a smooth surface W and that W is a K3 surface.

Proposition 2.14

The surface W has a Jacobian fibration $\sigma _W:W\rightarrow {{\mathbb {P}}}^1$ that is isomorphic to $\sigma :X_0\rightarrow {{\mathbb {P}}}^1$.

Proof

Consider the $({{\mathbb {Z}}}/2{{\mathbb {Z}}})^5$-covering $\gamma :{{\mathbb {P}}}^5\rightarrow {\mathbf {P}}^5$ defined by

$$\begin{aligned}{}[x_0: x_1: \dots : x_6]\mapsto [X_0: X_1:\dots : X_6]=[x_0^2: x_1^2:\dots : x_6^2]. \end{aligned}$$

Let $P\subset {\mathbf {P}}^5$ be the linear plane defined by

$$\begin{aligned} X_1-X_2+X_3=-X_3+X_5+X_6=X_2+X_4-X_5=0, \end{aligned}$$

and, for $i=1, \dots , 6$, let $l_i\subset P$ denote the intersection of P and the coordinate hyperplane $X_i=0$. Then the six lines $l_1, \dots , l_6$ form the complete quadrangle in Fig. 3. The surface ${\overline{W}}:=\gamma ^{-1}(P)\subset {{\mathbb {P}}}^5$ is the complete intersection of three quadratic hypersurfaces

$$\begin{aligned} x_1^2-x_2^2+x_3^2=-x_3^2+x_5^2+x_6^2=x_2^2+x_4^2-x_5^2=0. \end{aligned}$$

(2.9)

The finite covering $\gamma |{\overline{W}}:{\overline{W}}\rightarrow P$ extends to the covering $\gamma _W:W\rightarrow M_{{{\mathbb {C}}}}$ by the blowing up of $M_{{{\mathbb {C}}}}\rightarrow P$ at the triple points $t_1, \dots , t_4$ of the complete quadrangle on P. The pullback of each line $l_i$ by $\gamma |{\overline{W}}$ is a union of four conics, and ${\overline{W}}$ has $4\times 4$ nodes over $t_1, \dots , t_4$. Thus we obtain a configuration ${{\mathcal {L}}}_{W}$ of 40 smooth rational curves on W consisting of $4\times 6$ pullbacks of conics on ${\overline{W}}$ and $4\times 4$ exceptional curves over the nodes of ${\overline{W}}$. By computing the intersection numbers of the 24 conics and the incidence relation between the conics and the 16 nodes, we can write the intersection matrix of the configuration ${{\mathcal {L}}}_{W}$ explicitly. Then we confirm that this configuration ${{\mathcal {L}}}_{W}$ is isomorphic to ${{\mathcal {L}}}_{40}$. In fact, by Proposition 2.4, there exist 7680 isomorphisms between ${{\mathcal {L}}}_{W}$ and ${{\mathcal {L}}}_{40}$. Among these isomorphisms, we have 1536 isomorphisms such that the 16 smooth rational curves corresponding to the nodes of ${\overline{W}}$ are mapped to the sections of $\sigma :X_0\rightarrow {{\mathbb {P}}}^1$ and the 24 smooth rational curves over the lines $l_i$ are mapped to the irreducible components of singular fibers of $\sigma$. Hence W has an elliptic fibration $\sigma _W:W\rightarrow {{\mathbb {P}}}^1$ with a section and 6 singular fibers of type $I_4$. By [26], such an elliptic K3 surface is unique up to isomorphism. Hence $\sigma _W:W\rightarrow {{\mathbb {P}}}^1$ is isomorphic to $\sigma :X_0\rightarrow {{\mathbb {P}}}^1$. $\square$

Remark 2.15

The Jacobian fibration $\sigma _W:W\rightarrow {{\mathbb {P}}}^1$ is obtained from the elliptic fibration $M_{{{\mathbb {C}}}}\rightarrow {{\mathbb {P}}}^1$ induced by the pencil of conics passing through all the triple points $t_1, \dots , t_4$. See Remark 4.5, which also explains the number $1536=7680/5$ of the special isomorphisms ${{\mathcal {L}}}_{W}\cong {{\mathcal {L}}}_{40}$ in the proof.

For $J\subset \{1, \dots , 6\}$, let ${\tilde{\tau }}_J$ denote the involution of ${{\mathbb {P}}}^5$ given by

$$\begin{aligned} x_m\mapsto -x_m \;\; \text {if}\;\; m \in J, \quad x_n\mapsto x_n \;\; \text {if}\;\; n \notin J. \end{aligned}$$

Note that ${\tilde{\tau }}_{J}={\tilde{\tau }}_{J^\prime }$ if $J\cap J^\prime =\emptyset$ and $J\cup J^\prime =\{1, \dots , 6\}$. The Galois group ${\text {Gal}}(\gamma _W)$ of the covering $\gamma _W:W\rightarrow M_{{{\mathbb {C}}}}$ consists of the restrictions $\tau _J:={\tilde{\tau }}_J|{\overline{W}}$ of these involutions ${\tilde{\tau }}_J$ to ${\overline{W}}$. Let $S_W$ denote the Néron–Severi lattice of W, which is equal to $\langle {{{\mathcal {L}}}_W} \rangle$. We can calculate the action of ${\text {Gal}}(\gamma _W)$ on $S_W$ explicitly.

For an isomorphism $\varphi :{{\mathcal {L}}}_W\cong {{\mathcal {L}}}_{40}$ of graphs, let $\langle {\varphi } \rangle :S_W\cong S_0$ denote the induced isometry of lattices, and let ${\mathrm {O}}(\langle {\varphi } \rangle ):{\mathrm {O}}(S_W)\cong {\mathrm {O}}(S_0)$ denote the induced isomorphism of the automorphism groups of lattices. By checking all the 7680 isomorphisms $\varphi :{{\mathcal {L}}}_W\cong {{\mathcal {L}}}_{40}$, we confirmed the following fact. See Remark 4.5 for a geometric reason of this result.

Proposition 2.16

For each isomorphism $\varphi :{{\mathcal {L}}}_W\cong {{\mathcal {L}}}_{40}$ of graphs, the isomorphism ${\mathrm {O}}(\langle {\varphi } \rangle )$ maps ${\text {Gal}}(\gamma _W)\subset {\mathrm {O}}^+(S_W)$ to ${\text {Gal}}(\mu )\subset {\mathrm {O}}^+(S_0)$ isomorphically. $\square$

By Barth–Hulek [8], we know that the sum I of the classes of sections of $\sigma :X_0\rightarrow {{\mathbb {P}}}^1$ is divisible by 2 in ${\mathrm {Pic}}\, X_0$. We put $h_8:=(1/2)I+F$, where $F\in {\mathrm {Pic}}\, X_0$ is a fiber of $\sigma$. Then $h_8$ is primitive in ${\mathrm {Pic}}\, X_0$ and nef of degree 8. The complete linear system $|h_8|$ is base-point-free, because there exist no vectors $f\in S_0$ such that $\langle f, f\rangle =0$ and $\langle f, h_8\rangle =1$ (see Nikulin [27] and Proposition 12 of [8]). Let $\varPhi _{8}:X_0\rightarrow {{\mathbb {P}}}^5$ be the morphism induced by $|h_8|$. The curves contracted by $\varPhi _8$ are exactly the sections of $\sigma :X_0\rightarrow {{\mathbb {P}}}^1$, and $\varPhi _8$ maps each irreducible component of singular fibers of $\sigma$ to a conic. Hence the image of $\varPhi _8$ is equal to ${\overline{W}}$. We consider the involutions $\tau _J$ of ${\overline{W}}$ as elements of ${\text {Aut}}(X_0)$ via the birational morphism $\varPhi _8$. By Proposition 2.16, we have the following description of ${\text {Gal}}(\mu )$ simpler than the one given in Proposition 2.13.

Proposition 2.17

The Galois group ${\text {Gal}}(\mu )$ consists of 32 involutions $\tau _J$. $\square$

Remark 2.18

In [28], Abo–Sasakura–Terasoma studied $X_p$, where $p\equiv 1 \bmod 4$, and obtained an isomorphism from $X_p$ to the reduction of the complete intersection (2.9) modulo p.

3 Borcherds’ method

3.1 Chambers

We fix notions about tessellation of a positive cone of an even hyperbolic lattice by chambers.

Let L be an even lattice. A vector $r\in L$ is called a root if $\langle r,r\rangle =-2$. The set of roots of L is denoted by ${{\mathcal {R}}}(L)$.

Let L be an even hyperbolic lattice. Let ${{\mathcal {P}}}(L)$ be one of the two connected components of $\{ {x\in L\otimes {{\mathbb {R}}}} \mid {\langle x, x\rangle >0} \}$. Then ${\mathrm {O}}^+(L)$ acts on ${{\mathcal {P}}}(L)$. For $v\in L\otimes {{\mathbb {Q}}}$ with $\langle v,v\rangle <0$, let $(v)^{\perp }$ denote the hyperplane of ${{\mathcal {P}}}(L)$ defined by $\langle x, v\rangle =0$. Let ${{\mathcal {V}}}$ be a set of vectors of $L\otimes {{\mathbb {Q}}}$ such that $\langle v, v\rangle <0$ for all $v\in {{\mathcal {V}}}$. We assume that the family$\{ {(v)^{\perp }} \mid {v\in {{\mathcal {V}}}} \}$of hyperplanes is locally finite in${{\mathcal {P}}}(L)$. A ${{\mathcal {V}}}$-chamber is the closure in ${{\mathcal {P}}}(L)$ of a connected component of

$$\begin{aligned} {{\mathcal {P}}}(L)\;\; {\setminus } \;\; \bigcup _{v\in {{\mathcal {V}}}} (v)^{\perp }. \end{aligned}$$

Typical examples are ${{\mathcal {R}}}(L)$-chambers defined by the set ${{\mathcal {R}}}(L)$ of roots of L.

Definition 3.1

Let N be a closed subset of ${{\mathcal {P}}}(L)$. We say that Nis tessellated by${{\mathcal {V}}}$-chambers if N is a union of ${{\mathcal {V}}}$-chambers. Suppose that N is tessellated by ${{\mathcal {V}}}$-chambers, and let H be a subgroup of ${\mathrm {O}}^+(L)$ that preserves N. We say that Hpreserves the tessellation ofNby${{\mathcal {V}}}$-chambers if any $g\in H$ maps each ${{\mathcal {V}}}$-chamber in N to a ${{\mathcal {V}}}$-chamber. Suppose that this is the case. We say that the tessellation of N is H-transitive if H acts transitively on the set of ${{\mathcal {V}}}$-chambers in N.

Remark 3.2

Let U be a subset of ${{\mathcal {V}}}$ such that the closed subset

$$\begin{aligned} N_U:=\{\, {x\in {{\mathcal {P}}}(L)} \mid {\langle x, v\rangle \ge 0\;\;\text {for all }v\in U} \, \} \end{aligned}$$

of ${{\mathcal {P}}}(L)$ contains an interior point. Then $N_U$ is tessellated by ${{\mathcal {V}}}$-chambers. In particular, if ${{\mathcal {V}}}^\prime$ is a subset of ${{\mathcal {V}}}$, then each ${{\mathcal {V}}}^\prime$-chamber is tessellated by ${{\mathcal {V}}}$-chambers.

Let D be a ${{\mathcal {V}}}$-chamber. We put

$$\begin{aligned} {\text {Aut}}(D):=\{\, {g\in {\mathrm {O}}^+(L)} \mid {D^g=D} \, \}. \end{aligned}$$

A wall ofD is a closed subset of D of the form $(v)^{\perp }\cap D$ such that the hyperplane $(v)^{\perp }$ of ${{\mathcal {P}}}(L)$ is disjoint from the interior of D and $(v)^{\perp }\cap D$ contains a non-empty open subset of $(v)^{\perp }$. We say that a hyperplane $(v)^{\perp }$ of ${{\mathcal {P}}}(L)$defines a wall ofD if $(v)^{\perp }\cap D$ is a wall of D. We say that a vector $v\in L\otimes {{\mathbb {Q}}}$ with $\langle v,v\rangle <0$defines a wall ofD if $(v)^{\perp }$ defines a wall of D and $\langle v, x\rangle \ge 0$ for all $x\in D$. Note that, for each wall of D, there exists a unique primitive vector in $L^{\vee }$ defining the wall. Let $(v)^{\perp }\cap D$ be a wall of D. Then there exists a unique ${{\mathcal {V}}}$-chamber $D^\prime$ such that the interiors of D and $D^\prime$ are disjoint and that $(v)^{\perp }\cap D$ is equal to $(v)^{\perp }\cap D^\prime$. (Hence $(v)^{\perp }\cap D^\prime$ is a wall of $D^\prime$.) We say that $D^\prime$ is a ${{\mathcal {V}}}$-chamber adjacent toDacross the wall$(v)^{\perp }\cap D$. A face of D is a closed subset of D of the form $F\cap D$ such that

$$\begin{aligned} F=(v_1)^{\perp }\cap \dots \cap (v_m)^{\perp }, \quad \text {where }(v_1)^{\perp }, \dots , (v_m)^{\perp }\text { define walls of }D, \end{aligned}$$

and that $F\cap D$ contains a non-empty open subset of F.

Example 3.3

We consider the tessellation of ${{\mathcal {P}}}(L)$ by ${{\mathcal {R}}}(L)$-chambers. Each root r of L defines a reflection$s_r\in {\mathrm {O}}^+(L)$ via $x\mapsto x+\langle x, r\rangle r$. Let W(L) denote the subgroup of ${\mathrm {O}}^+(L)$ generated by all the reflections with respect to the roots. Then the tessellation of ${{\mathcal {P}}}(L)$ by ${{\mathcal {R}}}(L)$-chambers is W(L)-transitive. An ${{\mathcal {R}}}(L)$-chamber N is a fundamental domain of the action of W(L) on ${{\mathcal {P}}}(L)$, and ${\mathrm {O}}^+(L)$ is equal to $W(L)\rtimes {\text {Aut}}(N)$. Moreover, W(L) is generated by the reflections $s_r$ associated with the roots r of L defining the walls of N, and the faces of codimension 2 of N give the defining relations of W(L) with respect to this set of generators.

Let $L_{26}$ be an even unimodular hyperbolic lattice of rank 26, which is unique up to isomorphism. The shape of an ${{\mathcal {R}}}(L_{26})$-chamber was determined by Conway [29], and hence we call an ${{\mathcal {R}}}(L_{26})$-chamber a Conway chamber. Let w be a nonzero primitive vector of $L_{26}$ with $\langle w, w\rangle =0$ such that w is contained in the closure of ${{\mathcal {P}}}(L_{26})$ in $L_{26}\otimes {{\mathbb {R}}}$. We say that w is a Weyl vector if the lattice $\langle {w} \rangle ^{\perp }/\langle {w} \rangle$ is isomorphic to the negative-definite Leech lattice, where $\langle {w} \rangle ^{\perp }$ is the orthogonal complement in $L_{26}$ of $\langle {w} \rangle :={{\mathbb {Z}}}w\subset L_{26}$. Let $w\in L_{26}$ be a Weyl vector. Then a root r of $L_{26}$ is called a Leech root with respect tow if $\langle w, r\rangle =1$. We put

$$\begin{aligned} {{\mathcal {C}}}(w):=\{\, {x\in {{\mathcal {P}}}(L_{26})} \mid {\langle x, r\rangle \ge 0\;\;\text {for all Leech roots }r\text { with respect to }w} \, \}. \end{aligned}$$

Theorem 3.4

(Conway [29]) The mapping $w\mapsto {{\mathcal {C}}}(w)$ gives a bijection from the set of Weyl vectors to the set of Conway chambers. $\square$

3.2 Borcherds’ method

Borcherds [3, 4] developed a method to analyze ${{\mathcal {R}}}(S)$-chambers of an even hyperbolic lattice S by means of Conway chambers. We briefly review this method, and fix some terminologies. See [30] for details of the algorithms.

Let S be an even hyperbolic lattice. Suppose that we have a primitive embedding $i:S\hookrightarrow L_{26}$ such that the orthogonal complement R of S in $L_{26}$ satisfies the following condition:

$$\begin{aligned} R\text { cannot be embedded into the negative-definite Leech lattice.} \end{aligned}$$

(3.1)

(This condition is fulfilled, for example, if R contains a root.) We choose ${{\mathcal {P}}}(S)$ so that the embedding $i:S\hookrightarrow L_{26}$ induces an embedding $i_{{{\mathcal {P}}}}:{{\mathcal {P}}}(S)\hookrightarrow {{\mathcal {P}}}(L_{26})$. Let

$$\begin{aligned} {\mathrm {pr}}_S:L_{26}\otimes {{\mathbb {Q}}}\rightarrow S\otimes {{\mathbb {Q}}}\end{aligned}$$

denote the orthogonal projection. A hyperplane $(v)^{\perp }$ of ${{\mathcal {P}}}(L_{26})$ intersects ${{\mathcal {P}}}(S)$ in a hyperplane if and only if $\langle {\mathrm {pr}}_S(v), {\mathrm {pr}}_S(v)\rangle <0$, and, if this is the case, we have ${{\mathcal {P}}}(S)\cap (v)^{\perp }=({\mathrm {pr}}_S(v))^{\perp }$. We put

$$\begin{aligned} {{\mathcal {V}}}(i):=\{\, {{\mathrm {pr}}_S(r)} \mid {r\in {{\mathcal {R}}}(L_{26}), \;\; \langle {\mathrm {pr}}_S(r), {\mathrm {pr}}_S(r)\rangle <0} \, \}. \end{aligned}$$

(3.2)

The tessellation of ${{\mathcal {P}}}(L_{26})$ by Conway chambers induces a tessellation of ${{\mathcal {P}}}(S)$ by ${{\mathcal {V}}}(i)$-chambers. Each ${{\mathcal {V}}}(i)$-chamber is of the form $i_{{{\mathcal {P}}}}^{-1}({{\mathcal {C}}}(w))$. It is easily seen (see [30]) that assumption (3.1) implies that each ${{\mathcal {V}}}(i)$-chamber has only a finite number of walls. The defining vectors of walls of a ${{\mathcal {V}}}(i)$-chamber $i_{{{\mathcal {P}}}}^{-1}({{\mathcal {C}}}(w))$ can be calculated from the Weyl vector $w\in L_{26}$ of the Conway chamber ${{\mathcal {C}}}(w)$. From this set of walls of $i_{{{\mathcal {P}}}}^{-1}({{\mathcal {C}}}(w))$, we can calculate the finite group ${\text {Aut}}(i_{{{\mathcal {P}}}}^{-1}({{\mathcal {C}}}(w)))\subset {\mathrm {O}}^+(S)$. Moreover, for each wall $(v)^{\perp }\cap i_{{{\mathcal {P}}}}^{-1}({{\mathcal {C}}}(w))$ of a ${{\mathcal {V}}}(i)$-chamber $i_{{{\mathcal {P}}}}^{-1}({{\mathcal {C}}}(w))$, we can calculate a Weyl vector $w^\prime$ such that $i_{{{\mathcal {P}}}}^{-1}({{\mathcal {C}}}(w^\prime ))$ is the ${{\mathcal {V}}}(i)$-chamber adjacent to $i_{{{\mathcal {P}}}}^{-1}({{\mathcal {C}}}(w))$ across the wall $(v)^{\perp }\cap i_{{{\mathcal {P}}}}^{-1}({{\mathcal {C}}}(w))$.

Since ${{\mathcal {R}}}(S)\subset {{\mathcal {V}}}(i)$, Remark 3.2 implies the following:

Proposition 3.5

An ${{\mathcal {R}}}(S)$-chamber is tessellated by ${{\mathcal {V}}}(i)$-chambers. $\square$

3.3 Discriminant forms

For the application of Borcherds’ method to K3 surfaces, we need the notion of discriminant forms due to Nikulin [31].

Let $q:A\rightarrow {{\mathbb {Q}}}/2{{\mathbb {Z}}}$ be a non-degenerate quadratic form with values in ${{\mathbb {Q}}}/2{{\mathbb {Z}}}$ on a finite abelian group A. We denote by ${\mathrm {O}}(q)$ the automorphism group of (A, q). For a prime p, we denote by $A_p$ the p-part of A and by $q_p:A_p\rightarrow {{\mathbb {Q}}}/2{{\mathbb {Z}}}$ the restriction of q to $A_p$. Then we have a canonical orthogonal direct-sum decomposition

$$\begin{aligned} (A, q)=\bigoplus (A_p, q_p). \end{aligned}$$

Hence ${\mathrm {O}}(q)$ is canonically isomorphic to the direct product of ${\mathrm {O}}(q_p)$.

Let L be an even lattice, and let $A(L)=L^{\vee }/L$ denote the discriminant group of L. We define the discriminant form ofL

$$\begin{aligned} q(L):A(L)\rightarrow {{\mathbb {Q}}}/2{{\mathbb {Z}}}\end{aligned}$$

by $q(L)({{\bar{x}}}):=\langle x, x\rangle \bmod 2{{\mathbb {Z}}}$, where $x\mapsto {\bar{x}}$ is the natural projection $L^{\vee }\rightarrow A(L)$. Then we have a natural homomorphism

$$\begin{aligned} \eta _L:{\mathrm {O}}(L)\rightarrow {\mathrm {O}}(q(L)). \end{aligned}$$

Let M be a primitive sublattice of an even lattice L, and N the orthogonal complement of M in L. Let ${\mathrm {O}}(L, M)$ denote the subgroup $\{ {g\in {\mathrm {O}}(L)} \mid {M^g=M} \}$ of ${\mathrm {O}}(L)$. Then we have a canonical embedding ${\mathrm {O}}(L, M)\hookrightarrow {\mathrm {O}}(M)\times {\mathrm {O}}(N)$. The submodule $L\subset M^{\vee }\oplus N^{\vee }$ defines a subgroup $\varGamma _L:=L/(M\oplus N)\subset A(M) \times A(N)$. By Nikulin [31], we have the following:

Proposition 3.6

Let p be a prime that does not divide $|A(M)|$. Then $N\hookrightarrow L$ induces an isomorphism $q(L)_p\cong q(N)_p$, which is compatible with the actions of ${\mathrm {O}}(L, M)$ on L and on N. $\square$

Proposition 3.7

Let p be a prime that does not divide $|A(L)|$. Then the p-part of $\varGamma _L$ is the graph of an isomorphism $q(M)_p\cong -q(N)_p$, which is compatible with the actions of ${\mathrm {O}}(L, M)$ on M and on N. $\square$

Proposition 3.8

Suppose that L is unimodular, and let $\gamma _L:q(M)\cong -q(N)$ be the isomorphism with the graph $\varGamma _L$. Let H be a subgroup of ${\mathrm {O}}(N)$. Then $g\in {\mathrm {O}}(M)$ extends to ${\tilde{g}}\in {\mathrm {O}}(L, M)$ with ${\tilde{g}}|_N\in H$ if and only if the isomorphism ${\mathrm {O}}( q(M))\cong {\mathrm {O}}(q(N))$ induced by $\gamma _L$ maps $\eta _M(g)\in {\mathrm {O}}(q(M))$ into $\eta _N(H)\subset {\mathrm {O}}(q(N))$. $\square$

3.4 Geometric application of Borcherds’ method

Let Z be a K3 surface defined over an algebraically closed field. We use the notation $S_{Z}$, ${{\mathcal {P}}}_{Z}$ and $N_{Z}$ defined in Sect. 1.1. The following is well known.

Proposition 3.9

The closed subset $N_{Z}$ of ${{\mathcal {P}}}_{Z}$ is an ${{\mathcal {R}}}(S_{Z})$-chamber. The mapping $C\mapsto ([C])^{\perp }\cap N_{Z}$ gives a one-to-one correspondence between the set of smooth rational curves on Z and the set of walls of $N_{Z}$. $\square$

Since the action of ${\mathrm {O}}^+(S_{Z})$ on ${{\mathcal {P}}}_{Z}$ preserves the tessellation by ${{\mathcal {R}}}(S_{Z})$-chambers and an ample class is an interior point of $N_{Z}\subset {{\mathcal {P}}}_{Z}$, we obtain the following.

Corollary 3.10

Let $a\in S_{Z}$ be an ample class. Then the following three conditions on $g\in {\mathrm {O}}^+(S_{Z})$ are equivalent: (i) $N_{Z}=N_{Z}^g$. (ii) $N_{Z}\cap N_{Z}^g$ contains an interior point of $N_{Z}$. (iii) There exist no roots r of $S_{Z}$ such that $\langle r, a\rangle$ and $\langle r, a^g\rangle$ have different signs. $\square$

Let Z be a complex K3 surface. Let $T_{Z}$ denote the orthogonal complement of $S_{Z}=H^2(Z, {{\mathbb {Z}}})\cap H^{1,1}(Z)$ in the even unimodular lattice $H^2(Z, {{\mathbb {Z}}})$ with the cup-product. Then $T_{Z}\otimes {{\mathbb {C}}}$ contains a one-dimensional subspace $H^{2, 0}(Z)={{\mathbb {C}}}\, \omega$, where $\omega$ is a nonzero holomorphic 2-form on Z. We put

$$\begin{aligned} {\mathrm {O}}(T_{Z}, \omega ):=\{\, {g\in {\mathrm {O}}(T_{Z})} \mid {{{\mathbb {C}}}\, \omega ^g={{\mathbb {C}}}\, \omega } \, \}. \end{aligned}$$

Recall that we have a natural homomorphism $\eta _{T_{Z}}:{\mathrm {O}}(T_{Z})\rightarrow {\mathrm {O}}(q(T_{Z}))$. We put

$$\begin{aligned} {\mathrm {O}}(q(T_{Z}), \omega ):=\text {the image of }{\mathrm {O}}(T_{Z}, \omega )\text { under }\eta _{T_{Z}}. \end{aligned}$$

The even unimodular overlattice $H^2(Z, {{\mathbb {Z}}})$ of $S_{Z}\oplus T_{Z}$ induces an isomorphism $\gamma _H$ between $q(S_{Z})$ and $-q(T_{Z})$. Let ${\mathrm {O}}(q(S_{Z}), \omega )$ denote the subgroup of ${\mathrm {O}}(q(S_{Z}))$ corresponding to ${\mathrm {O}}(q(T_{Z}), \omega )$ via the isomorphism ${\mathrm {O}}(q(T_{Z}))\cong {\mathrm {O}}(q(S_{Z}))$ induced by $\gamma _H$. By Proposition 3.8, an isometry $g\in {\mathrm {O}}(S_{Z})$ extends to an isometry ${\tilde{g}}$ of $H^2(Z, {{\mathbb {Z}}})$ that preserves $H^{2, 0} (Z)$ if and only if $\eta _{S_{Z}}(g)\in {\mathrm {O}}(q(S_{Z}), \omega )$.

Let Z be a supersingular K3 surface defined over an algebraically closed field $k_p$ of odd characteristic p. Then $A(S_{Z})$ is an ${{\mathbb {F}}}_p$-vector space, and we have the period of Z, which is a subspace of $A(S_{Z})\otimes k_p$. (See Ogus [32, 33].) Let ${\mathrm {O}}(q(S_{Z}), \omega )$ denote the subgroup of ${\mathrm {O}}(q(S_{Z}))$ consisting of automorphisms that preserve the period.

In the two cases where Z is defined over ${{\mathbb {C}}}$ or supersingular in odd characteristic, we call the condition

$$\begin{aligned} \eta _{S_{Z}}(g)\in {\mathrm {O}}(q(S_{Z}), \omega ) \end{aligned}$$

(3.3)

on $g\in {\mathrm {O}}^+(S_{Z})$ the period condition. In these two cases, we have the Torelli theorem. (See Piatetski-Shapiro and Shafarevich [34], Ogus [32, 33] for $p>3$ and Bragg and Lieblich [35] for $p\ge 3$.) By virtue of this theorem, we have the following:

Theorem 3.11

Let Z be a complex K3 surface or a supersingular K3 surface in odd characteristic, and let $\psi _Z:{\text {Aut}}(Z)\rightarrow {\mathrm {O}}^+(S_{Z})$ be the natural representation of ${\text {Aut}}(Z)$ on $S_{Z}$. Then an isometry $g\in {\mathrm {O}}^+(S_{Z})$ belongs to the image of $\psi _Z$ if and only if g preserves $N_{Z}$ and satisfies the period condition (3.3). $\square$

We explain the procedure of Borcherds’ method in the simplest case. See [30] for more general cases. In the following, we assume that Z is a complex K3 surface or a supersingular K3 surface in odd characteristic. We also assume that $\psi _Z$is injective, and regard${\text {Aut}}(Z)$as a subgroup of${\mathrm {O}}^+(S_{Z})$. We search for a primitive embedding $i:S_{Z}\hookrightarrow L_{26}$ inducing $i_{{{\mathcal {P}}}}:{{\mathcal {P}}}_{Z}\hookrightarrow {{\mathcal {P}}}(L_{26})$ and a Weyl vector $w_0\in L_{26}$ with the following properties, and look at the tessellation of the ${{\mathcal {R}}}(S_{Z})$-chamber $N_{Z}$ by ${{\mathcal {V}}}(i)$-chambers, where ${{\mathcal {V}}}(i)$ is defined by (3.2).

(I) Let R denote the orthogonal complement of $S_{Z}$ in $L_{26}$. We require that R satisfies (3.1), so that each ${{\mathcal {V}}}(i)$-chamber has only a finite number of walls. We also require that $\eta _R:{\mathrm {O}}(R)\rightarrow {\mathrm {O}}(q(R))$ is surjective. By Proposition 3.8, every isometry $g\in {\mathrm {O}}^+(S_{Z})$ extends to an isometry of $L_{26}$. Hence the action of ${\mathrm {O}}^+(S_{Z})$ preserves the tessellation of ${{\mathcal {P}}}_{Z}$ by ${{\mathcal {V}}}(i)$-chambers. In particular, the action of ${\text {Aut}}(Z)$ on $N_{Z}$ preserves the tessellation of $N_{Z}$ by ${{\mathcal {V}}}(i)$-chambers.

(II) Let D be the closed subset $i_{{{\mathcal {P}}}} ^{-1}({{\mathcal {C}}}(w_0))$ of ${{\mathcal {P}}}_{Z}$. We require that D contains an ample class in its interior. Then D is a ${{\mathcal {V}}}(i)$-chamber contained in $N_{Z}$.

Definition 3.12

The ${{\mathcal {V}}}(i)$-chamber D is called the initial chamber of this procedure. A wall $(v)^{\perp }\cap D$ of D is called an outer wall if $(v)^{\perp }$ defines a wall of the ${{\mathcal {R}}}(S_{Z})$-chamber $N_{Z}$, that is, if there exists a root r of $S_{Z}$ such that $(v)^{\perp }=(r)^{\perp }$. We call the wall $(v)^{\perp }\cap D$ an inner wall otherwise. Let ${{\mathcal {W}}}_{\mathrm{out}}(D)$ and ${{\mathcal {W}}}_{\mathrm{inn}}(D)$ denote the set of outer walls and inner walls, respectively.

We calculate the set of walls of the initial chamber D. Since each outer wall corresponds to a smooth rational curve on Z by Proposition 3.9, we obtain a configuration of smooth rational curves on Z from ${{\mathcal {W}}}_{\mathrm{out}}(D)$.

(III) We calculate ${\text {Aut}}( D):=\{ {g\in {\mathrm {O}}^+(S_{Z})} \mid { D^g= D} \}$. By Corollary 3.10, any element of ${\text {Aut}}( D)$ preserves $N_{Z}$. Therefore the group

$$\begin{aligned} {\text {Aut}}(Z, D):=\{\, {g\in {\text {Aut}}( D)} \mid {g\text { satisfies the period condition }(3.3)} \, \} \end{aligned}$$

(3.4)

is contained in ${\text {Aut}}(Z)$. We find an ample class h in the interior of D such that $h^g=h$ for all $g\in {\text {Aut}}(Z, D)$. Then ${\text {Aut}}(Z, D)$ is equal to the projective automorphism group ${\text {Aut}}(Z, h)$.

(IV) Note that ${\text {Aut}}(Z, D)={\text {Aut}}(Z, h)$ acts on ${{\mathcal {W}}}_{\mathrm{out}}(D)$ and ${{\mathcal {W}}}_{\mathrm{inn}}(D)$. We decompose ${{\mathcal {W}}}_{\mathrm{inn}}(D)$ into the orbits under the action of ${\text {Aut}}(Z, h)$:

$$\begin{aligned} {{\mathcal {W}}}_{\mathrm{inn}}(D)=O_1\cup \dots \cup O_J. \end{aligned}$$

From each orbit $O_j$, we choose a wall $(v_j)^{\perp }\cap D$ and calculate a Weyl vector $w_j\in L_{26}$ such that $D_j:=i_{{{\mathcal {P}}}}^{-1}({{\mathcal {C}}}(w_j))$ is the ${{\mathcal {V}}}(i)$-chamber adjacent to D across $(v_j)^{\perp }\cap D$. Since $(v_j)^{\perp }\cap N_{Z}$ is not a wall of $N_{Z}$, the ${{\mathcal {V}}}(i)$-chamber $D_j$ is contained in $N_{Z}$. For each $j=1, \dots , J$, we find an isometry $g_j$ of ${\mathrm {O}}^+(S_{Z})$ that satisfies the period condition (3.3) and $D^{g_j}= D_j$. Note that each $g_j$ preserves $N_{Z}$ by Corollary 3.10, and hence $g_j\in {\text {Aut}}(Z)$. Note also that, for each inner wall $(v^\prime )^{\perp }\cap D\in O_j$, there exists a conjugate $g^\prime \in {\text {Aut}}(Z)$ of $g_j$ by ${\text {Aut}}(Z, h)$ that maps D to the ${{\mathcal {V}}}(i)$-chamber adjacent to D across the wall $(v^\prime )^{\perp }\cap D$.

(V) Under the assumptions given in (I)–(IV), the group ${\text {Aut}}(Z)$ is generated by ${\text {Aut}}(Z, h)$ and the automorphisms $g_1, \dots , g_J$. Moreover, the tessellation of $N_{Z}$ by ${{\mathcal {V}}}(i)$-chambers is ${\text {Aut}}(Z)$-transitive, and the mappings $g\mapsto h^{g}$ and $g\mapsto D^{g}$ give one-to-one correspondences between the following sets:

• The set of cosets ${\text {Aut}}(Z, h)\backslash {\text {Aut}}(Z)$.

• The set of ${{\mathcal {V}}}(i)$-chambers contained in $N_{Z}$.

• The subset $\{ {h^{g}} \mid {g\in {\text {Aut}}(Z)} \}$ of $S_{Z}$.

Moreover, considering the reflections with respect to the roots r defining the outer walls $(r)^{\perp }\cap D$ of D, we see that, under the assumptions given in (I)–(IV), the tessellation of ${{\mathcal {P}}}_{Z}$ by ${{\mathcal {V}}}(i)$-chambers is ${\mathrm {O}}^+(S_{Z})$-transitive.

The method described in this section was applied by Kondo [36] to the calculation of the automorphism group of a generic Jacobian Kummer surface, and since then, many studies have been done on the automorphism groups of various K3 surfaces (see the references of [30]). This method was also applied to the study of automorphism group of an Enriques surface in [37, 38].

4 Borcherds’ method for $X_0$ and $X_3$

Recall from Sect. 1.1 that we use the following notation:

$$\begin{aligned} S_{3}:=S_{X_3}, \; {{\mathcal {P}}}_{3}:= {{\mathcal {P}}}_{X_3}, \; N_{3}:=N_{X_3}, \; \quad S_{0}:=S_{X_0}, \; {{\mathcal {P}}}_{0}:= {{\mathcal {P}}}_{X_0}, \; N_{0}:=N_{X_0}. \end{aligned}$$

4.1 Borcherds’ method for $X_3$

We identify $X_3$ and $F_3$ via Shioda’s isomorphism explained in Sect. 2.3. Hence $S_{3}$ is the Néron–Severi lattice of $F_3$. In [2], we have obtained a generating set of ${\text {Aut}}(X_3)$ by finding a primitive embedding $i_{3}:S_{3}\hookrightarrow L_{26}$ inducing $i_{3, {{\mathcal {P}}}}:{{\mathcal {P}}}_{3}\hookrightarrow {{\mathcal {P}}}(L_{26})$ and a Weyl vector $w_0\in L_{26}$ that satisfy the requirements in Sect. 3.4. The result is as follows. See [18] or [2] for the explicit descriptions of $i_{3}$, $w_0$, and other computational data.

Table 2 Inner walls of $D_3$

We have $A(S_{3})\cong ({{\mathbb {Z}}}/3{{\mathbb {Z}}})^2$. The group ${\mathrm {O}}(q(S_{3}))$ is a dihedral group of order 8, and ${\mathrm {O}}(q(S_{3}), \omega )$ is a cyclic subgroup of order 4. The orthogonal complement $R_3$ of $S_{3}$ in $L_{26}$ is a negative-definite root lattice of type $2A_2$. The order of ${\mathrm {O}}(R_3)$ is 288, the order of ${\mathrm {O}}(q(R_3))$ is 8, and the natural homomorphism ${\mathrm {O}}(R_3)\rightarrow {\mathrm {O}}(q(R_3))$ is surjective. We put

$$\begin{aligned} D_3:= i_{3, {{\mathcal {P}}}}^{-1}({{\mathcal {C}}}(w_0)). \end{aligned}$$

Then $D_3$ contains the class $h_3\in S_{3}$ of a hyperplane section of $X_3=F_3\subset {{\mathbb {P}}}^3$ in its interior. Hence $D_3$ is a ${{\mathcal {V}}}( i_{3})$-chamber. The set ${{\mathcal {W}}}_{\mathrm{out}} ( D_3)$ of outer walls of the initial chamber $D_3$ is equal to $\{ {(\ell )^{\perp }\cap D_3} \mid {\ell \in {{\mathcal {L}}}_{112}} \}$. Because

$$\begin{aligned} h_3=\frac{1}{28}\sum _{\ell \in {{\mathcal {L}}}_{112}} [\ell ], \end{aligned}$$

the group ${\text {Aut}}(X_3, D_3)$ defined by (3.4) is equal to ${\text {Aut}}(X_3, h_3)$, which is the projective automorphism group $\{ {g\in {\mathrm {PGL}}_4(k_3)} \mid {g(F_3)=F_3} \}={\mathrm {PGU}}_4({{\mathbb {F}}}_9)$ of $F_3\subset {{\mathbb {P}}}^3$. Hence ${\text {Aut}}(X_3, D_3)$ is of order 13063680. The class $h_3$ is in fact the image of $w_0$ under the orthogonal projection $L_{26}\otimes {{\mathbb {Q}}}\rightarrow S_{3}\otimes {{\mathbb {Q}}}$. Under the action of ${\text {Aut}}(X_3, h_3)={\mathrm {PGU}}_4({{\mathbb {F}}}_9)$, the set ${{\mathcal {W}}}_{\mathrm{inn}}( D_3)$ of inner walls of $D_3$ is decomposed into two orbits $O^\prime _{648}$ and $O^\prime _{5184}$ of size 648 and 5184, respectively. Each inner wall $(v)^{\perp }\cap D_3$ in the orbit $O^\prime _s$ is defined by a primitive vector v of $S_{3}^{\vee }$ with the properties given in Table 2, and there exists a double-plane polarization $b^\prime _d \in S_{3}$ such that the corresponding double-plane involution $g(b^\prime _d)\in {\text {Aut}}(X_3)$ maps $D_3$ to the ${{\mathcal {V}}}(i_3)$-chamber adjacent to $D_3$ across the wall $(v)^{\perp }\cap D_3$. These results prove the following:

Theorem 4.1

(Kondo–Shimada [2]) The automorphism group ${\text {Aut}}(X_3)$ is generated by the projective automorphism group ${\text {Aut}}(X_3, h_3)= {\mathrm {PGU}}_4({{\mathbb {F}}}_9)$ and two double-plane involutions $g(b^\prime _{10}), g(b^\prime _{31})$ corresponding the orbits $O^\prime _{648}, O^\prime _{5184}$ of the action of ${\mathrm {PGU}}_4({{\mathbb {F}}}_9)$ on the set ${{\mathcal {W}}}_{\mathrm{inn}} (D_3)$ of inner walls of the initial chamber $D_3$. $\square$

4.2 Borcherds’ method for $X_0$

Table 3 Inner walls of $D_0$

We define an embedding $i_0:S_{0}\hookrightarrow L_{26}$ by

$$\begin{aligned} i_{0}:= i_{3}\circ \rho , \end{aligned}$$

(4.1)

where $i_{3}:S_{3}\hookrightarrow L_{26}$ is the embedding used in Sect. 4.1, and $\rho :S_{0}\hookrightarrow S_{3}$ is the embedding given by the specialization of $X_0$ to $X_3$. The key observation of this article is that $i_{0}$ is equal to the embedding used by Keum–Kondo [1] for the calculation of ${\text {Aut}}(X_0)$.

We have $A(S_{0})\cong ({{\mathbb {Z}}}/4{{\mathbb {Z}}})^2$. The group ${\mathrm {O}}(q(S_{0}))$ is isomorphic to the dihedral group of order 8, and the subgroup ${\mathrm {O}}(q(S_{0}), \omega )$ is cyclic of order 4. The embedding $i_{0}$ is primitive and induces $i_{0, {{\mathcal {P}}}}:{{\mathcal {P}}}_{0}\hookrightarrow {{\mathcal {P}}}(L_{26})$. The orthogonal complement $R_0$ of $S_{0}$ in $L_{26}$ is a negative-definite root lattice of type $2A_3$. The order of ${\mathrm {O}}(R_0)$ is 4608, the order of ${\mathrm {O}}(q(R_0))$ is 8, and the natural homomorphism ${\mathrm {O}}(R_0)\rightarrow {\mathrm {O}}(q(R_0))$ is surjective. The vector

$$\begin{aligned} h_0:=\frac{1}{2}\sum _{\ell \in {{\mathcal {L}}}_{40}} [\ell ]\;\; \in \;\; S_{0}\otimes {{\mathbb {Q}}}\end{aligned}$$

(4.2)

is in fact in $S_{0}$, and we have $\langle h_0, h_0\rangle =40$. Since $\langle h_0, \ell \rangle =2$ for all $\ell \in {{\mathcal {L}}}_{40}$, the class $h_0$ is nef. Since there exist no roots r of $S_{0}$ such that $h_0\in (r)^{\perp }$, the class $h_0$ is ample. Let$w_0\in L_{26}$be the same Weyl vector that was used in Sect. 4.1. The orthogonal projection of $w_0$ to $S_{0}\otimes {{\mathbb {Q}}}$ is equal to $h_0/2$. (In [1], the vector $h_0/2$ is used instead of $h_0$.) We put

$$\begin{aligned} D_0:= i_{0, {{\mathcal {P}}}}^{-1}({{\mathcal {C}}}(w_0)). \end{aligned}$$

Then $D_0$ contains $h_0$ in its interior, and hence $D_0$ is a ${{\mathcal {V}}}( i_{0})$-chamber. The set ${{\mathcal {W}}}_{\mathrm{out}}( D_0)$ of outer walls of the initial chamber $D_0$ is equal to $\{ {(\ell )^{\perp }\cap D_0} \mid {\ell \in {{\mathcal {L}}}_{40}} \}$. We have

$$\begin{aligned} {\text {Aut}}(X_0, D_0)={\text {Aut}}(X_0, h_0), \end{aligned}$$

(4.3)

which is of order 3840 and acts on ${{\mathcal {W}}}_{\mathrm{out}}( D_0)$ transitively. Using the algorithms in Remark 1.3, we search for double-plane polarizations in $S_{0}$ and obtain the following proposition, which proves Theorem 1.4.

Proposition 4.2

The action of ${\text {Aut}}(X_0, h_0)$ decomposes the set ${{\mathcal {W}}}_{\mathrm{inn}}(D_0)$ of inner walls of the initial chamber $D_0$ into four orbits $O_{64}$, $O_{40}$, $O_{160}$, $O_{320}$, where $|O_s|=s$. For each inner wall $(v)^{\perp }\cap D_0\in O_s$, there exists a double-plane polarization $b_d\in S_{0}$ such that the corresponding double-plane involution $g(b_d)\in {\text {Aut}}(X_0)$ maps $D_0$ to the ${{\mathcal {V}}}(i_0)$-chamber adjacent to $D_0$ across the wall $(v)^{\perp }\cap D_0$. $\square$

Each inner wall $(v)^{\perp }\cap D_0\in O_s$ is defined by a primitive vector $v\in S_{0}^{\vee }$ with the properties given in Table 3. See [18] for the matrix representations of double-plane involutions $g(b_d)$.

4.3 The group ${\text {Aut}}(X_0, h_0)$

We investigate the finite group ${\text {Aut}}(X_0, h_0)$ more closely. Note that the order 3840 of this group is the maximum among all finite subgroups of automorphisms of complex K3 surfaces (see Kondo [39]). There exists a natural identification between ${{\mathcal {W}}}_{\mathrm{out}}(D_0)$ and ${{\mathcal {L}}}_{40}$. Therefore by (4.3), the group ${\text {Aut}}(X_0, h_0)$ acts on ${{\mathcal {L}}}_{40}$ faithfully, and hence ${\text {Aut}}(X_0, h_0)$ is embedded into the automorphism group ${\text {Aut}}({{\mathcal {L}}}_{40})$ of the dual graph of ${{\mathcal {L}}}_{40}$. On the other hand, since $\langle {{{\mathcal {L}}}_{40}} \rangle =S_{0}$ (Corollary 2.8), we have an embedding ${\text {Aut}}({{\mathcal {L}}}_{40}) \hookrightarrow {\mathrm {O}}^+(S_{0})$. In fact, we confirm by direct calculation the following:

and ${\text {Aut}}(X_0, h_0)$ is of index 2 in ${\text {Aut}}({{\mathcal {L}}}_{40})$. By Propositions 2.4 and 2.7, we have a natural homomorphism ${\text {Aut}}({{\mathcal {L}}}_{40})\rightarrow {\text {Aut}}({{\mathcal {P}}})$ to the automorphism group of the Petersen graph ${{\mathcal {P}}}$. Recall that, in Sects. 2.5 and 2.6, we have constructed a morphism $\mu _{{{\mathbb {C}}}} :X_0\rightarrow M_{{{\mathbb {C}}}}$ that induces the $\mathrm{QP}$-covering map ${{\mathcal {L}}}_{40}\rightarrow {{\mathcal {P}}}$, and calculated the Galois group ${\text {Gal}}(\mu )$ in Propositions 2.13 and 2.17.

Proposition 4.3

The homomorphism

$$\begin{aligned} {\text {Aut}}(X_0, h_0)\hookrightarrow {\text {Aut}}({{\mathcal {L}}}_{40})\rightarrow {\text {Aut}}({{\mathcal {P}}}) \end{aligned}$$

(4.4)

is surjective, and its kernel is equal to the Galois group ${\text {Gal}}(\mu )\cong ({{\mathbb {Z}}}/2{{\mathbb {Z}}})^5$.

Proof

By the list of elements of ${\text {Aut}}(X_0, h_0)$ (see [18]), we see that the homomorphism (4.4) is surjective, and its kernel is of order 32. Each generator of ${\text {Gal}}(\mu )$ given in Propositions 2.13 or 2.17 preserves ${{\mathcal {L}}}_{40}$, and hence ${\text {Gal}}(\mu )$ is contained in ${\text {Aut}}(X_0, h_0)$. Since $\mu$ induces the $\mathrm{QP}$-covering map ${{\mathcal {L}}}_{40}\rightarrow {{\mathcal {P}}}$, it follows that ${\text {Gal}}(\mu )$ is contained in the kernel of (4.4). Comparing the order, we complete the proof. $\square$

For $v\in S_{0}$, we put

$$\begin{aligned} {\text {Aut}}(X_0, v):=\{\, {g\in {\text {Aut}}(X_0)} \mid {v^g=v} \, \}. \end{aligned}$$

Let $f\in S_{0}$ be the class of a fiber of the Jacobian fibration $\sigma :X_0\rightarrow {{\mathbb {P}}}^1$ defined by (1.1). For each element g of ${\text {Aut}}(X_0, f)$, there exists an automorphism ${\bar{g}}\in {\text {Aut}}({{\mathbb {P}}}^1)$ such that the diagram

(4.5)

commutes and hence g preserves ${{\mathcal {L}}}_{40}$. Therefore ${\text {Aut}}(X_0, f)$ is contained in ${\text {Aut}}(X_0, h_0)$, and we have a homomorphism

$$\begin{aligned} \beta :{\text {Aut}}(X_0, f)\rightarrow \mathrm{Stab}(\mathrm{Cr}(\sigma )), \end{aligned}$$

where $\mathrm{Cr}(\sigma ):=\{0,\infty , \pm 1, \pm i\}$ is the set of critical values of $\sigma$ and $\mathrm{Stab}(\mathrm{Cr}(\sigma ))$ is the stabilizer subgroup of $\mathrm{Cr}(\sigma )$ in ${\text {Aut}}({{\mathbb {P}}}^1)$.

We have the inversion $\iota _{\sigma }:X_0\rightarrow X_0$ of the Jacobian fibration $\sigma$. We also have a subgroup $T_{\sigma }$ of ${\text {Aut}}(X_0, f)$ consisting of translations by the 16 sections of $\sigma$.

Proposition 4.4

The order of ${\text {Aut}}(X_0, f)$ is 768. The image of $\beta$ is isomorphic to ${{\mathfrak {S}}}_4$, and the kernel of $\beta$ is equal to the subgroup $T_{\sigma }\rtimes \langle {\iota _{\sigma }} \rangle$ of ${\text {Aut}}(X_0, f)$.

Proof

By means of $\rho _{{{\mathcal {L}}}}:{{\mathcal {L}}}_{40}\hookrightarrow {{\mathcal {L}}}_{112}$ and (2.1), we can calculate the quadrangle $F_c$ in ${{\mathcal {L}}}_{40}$ consisting of the classes of irreducible components of the singular fiber $\sigma ^{-1}(c)$ for each $c\in \mathrm{Cr}(\sigma )$. Then f is the sum of vectors in one of these $F_c$, and hence we can calculate ${\text {Aut}}(X_0, f)$ from the list of elements of ${\text {Aut}}(X_0, h_0)$. Looking at the action of ${\text {Aut}}(X_0, f)$ on the set of the quadrangles $F_c$, we see that the image of $\beta$ is isomorphic to ${{\mathfrak {S}}}_4$ generated by permutations $(0,-1,-i)(\infty ,1,i)$ and $(0,-i)(\infty , i)(1, -1)$ of $\mathrm{Cr}(\sigma )$. Therefore the kernel is of order 32. Since $T_{\sigma }\rtimes \langle {\iota _{\sigma , z}} \rangle$ is of order 32 and contained in the kernel, we complete the proof. $\square$

Remark 4.5

Since $|{\text {Aut}}(X_0, h_0)|/|{\text {Aut}}(X_0, f)|=5$, the orbit of f under the action of ${\text {Aut}}(X_0, h_0)$ consists of five elements $f=f^{(1)}, f^{(2)}, \dots , f^{(5)}$. We can easily confirm that

$$\begin{aligned} {\text {Gal}}(\mu )=\bigcap _{\nu =1}^{5} {\text {Aut}}(X_0, f^{(\nu )}). \end{aligned}$$

The five classes $f^{(\nu )}$ give rise to five elliptic fibrations $\sigma ^{(\nu )}:X_0\rightarrow {{\mathbb {P}}}^1$. These elliptic fibrations correspond to the choices of the ${{\mathbb {P}}}^1$-fibration $\varphi _M:M\rightarrow {{\mathbb {P}}}^1$ in (2.5): for $\nu =1, \dots , 4$, the class $f^{(\nu )}$ is induced by the pencil of lines passing through the triple point $t_\nu$, and $f^{(5)}$ is induced by the pencil of conics passing through all the triple points (see Remark 2.15). Let $h_8^{(\nu )}\in S_0$ be the polarization of degree 8 constructed from $\sigma ^{(\nu )}:X_0\rightarrow {{\mathbb {P}}}^1$ via the recipe of Barth–Hulek explained in Sect. 2.6. Then we have ${\text {Aut}}(X_0, f^{(\nu )})={\text {Aut}}(X_0, h_8^{(\nu )})$.

5 Proof of Theorems 1.7 and 1.8

We use the same notation as in Sect. 4. The following fact has been established.

Proposition 5.1

• (1) The tessellation of $N_{3}$ by ${{\mathcal {V}}}( i_{3})$-chambers is ${\text {Aut}}(X_3)$-transitive, and the tessellation of ${{\mathcal {P}}}_{3}$ by ${{\mathcal {V}}}( i_{3})$-chambers is ${\mathrm {O}}^+(S_{3})$-transitive.

• (2) The tessellation of $N_{0}$ by ${{\mathcal {V}}}( i_{0})$-chambers is ${\text {Aut}}(X_0)$-transitive, and the tessellation of ${{\mathcal {P}}}_{0}$ by ${{\mathcal {V}}}( i_{0})$-chambers is ${\mathrm {O}}^+(S_{0})$-transitive. $\square$

From now on, we consider $S_{0}$ as a sublattice of $S_{3}$ via $\rho :S_{0}\hookrightarrow S_{3}$ and ${{\mathcal {P}}}_{0}$ as a subspace of ${{\mathcal {P}}}_{3}$. For example, we use notation such as $h_0\in S_{3}$, $D_0\subset {{\mathcal {P}}}_{3}$, ${{\mathcal {P}}}_{0}\subset {{\mathcal {P}}}_{3}$, .... By definition (4.1) of $i_0$, we have the following:

Proposition 5.2

The tessellation of ${{\mathcal {P}}}_{0}$ by ${{\mathcal {V}}}( i_{0})$-chambers is obtained as the restriction to ${{\mathcal {P}}}_{0}$ of the tessellation of ${{\mathcal {P}}}_{3}$ by ${{\mathcal {V}}}( i_{3})$-chambers. $\square$

5.1 Proof of Theorem 1.7

First, we show that the restriction homomorphism ${\tilde{\rho }}$ from ${\mathrm {O}}^+(S_{3}, S_{0})$ to ${\mathrm {O}}^+(S_{0})$ maps ${\mathrm {O}}^+(S_{3}, S_{0})\cap {\text {Aut}}(X_3)$ to ${\text {Aut}}(X_0)$. By Theorem 3.11, it suffices to show that, for each $g\in {\mathrm {O}}^+(S_{3}, S_{0})\cap {\text {Aut}}(X_3)$, the restriction $g|_{S_{0}}\in {\mathrm {O}}^+(S_{0})$ satisfies the period condition (3.3) and preserves $N_{0}$.

Lemma 5.3

If $g\in {\mathrm {O}}^+(S_{3}, S_{0})$ satisfies the period condition $\eta _{S_{3}}(g)\in {\mathrm {O}}(q(S_{3}), \omega )$ for $X_3$, then $g|_{S_{0}}\in {\mathrm {O}}^+(S_{0})$ satisfies the period condition $\eta _{S_{0}}(g|_{S_{0}})\in {\mathrm {O}}(q(S_{0}), \omega )$ for $X_0$.

Proof

Let Q denote the orthogonal complement of $S_{0}$ in $S_{3}$. Then Q is an even negative-definite lattice of rank 2 with discriminant group isomorphic to $({{\mathbb {Z}}}/4{{\mathbb {Z}}})^2\times ({{\mathbb {Z}}}/3{{\mathbb {Z}}})^2$. By the classical theory of Gauss, such a lattice is unique up to isomorphism, and the lattice Q is given by a Gram matrix

$$\begin{aligned} \left( \begin{array}{cc} -\,12 &{}\quad 0 \\ 0 &{}\quad -\,12 \end{array} \right) . \end{aligned}$$

We consider the commutative diagram in Fig. 4. The two isomorphisms in the bottom line of this diagram are derived from the isomorphism $q(S_{3})\cong q(Q)_3$ given in Proposition 3.6 and the isomorphism $q(Q)_2\cong -q(S_{0})$ given in Proposition 3.7. It is easy to verify that ${\mathrm {O}}(Q)$ is a dihedral group of order 8, and the composites $p_3\circ \eta _Q:{\mathrm {O}}(Q)\rightarrow {\mathrm {O}}(q(Q)_3)$ and $p_2\circ \eta _Q:{\mathrm {O}}(Q)\rightarrow {\mathrm {O}}(q(Q)_2)$ are isomorphisms, where $p_2$ and $p_3$ are projections to the 2-part and the 3-part, respectively. Using the image of $\eta _Q:{\mathrm {O}}(Q)\rightarrow {\mathrm {O}}(q(Q))$ as the graph of an isomorphism between ${\mathrm {O}}(q(Q)_3)$ and ${\mathrm {O}}(q(Q)_2)$, we obtain an isomorphism ${\mathrm {O}}(q(S_{3}))\cong {\mathrm {O}}(q(S_{0}))$ that is compatible with the homomorphisms from ${\mathrm {O}}^+(S_{3}, S_{0})$. Recall that ${\mathrm {O}}(q(S_{3}), \omega )$ and ${\mathrm {O}}(q(S_{0}), \omega )$ are cyclic of order 4. Since the cyclic subgroup of order 4 is a characteristic subgroup of the dihedral group of order 8, the isomorphism ${\mathrm {O}}(q(S_{3}))\cong {\mathrm {O}}(q(S_{0}))$ maps ${\mathrm {O}}(q(S_{3}), \omega )$ to ${\mathrm {O}}(q(S_{0}), \omega )$. $\square$

Fig. 4

Commutative diagram for the period condition

Since we have calculated the embedding $\rho :S_{0}\hookrightarrow S_{3}$ in the form of a matrix and the set ${{\mathcal {W}}}_{\mathrm{out}}(D_3)\cup {{\mathcal {W}}}_{\mathrm{inn}}(D_3)$ of walls of the initial chamber $D_3$ for $X_3$ in the form of a list of vectors (see [18]), we can easily prove the following:

Lemma 5.4

• (1) The ample class $h_0$ of $X_0$ is contained in $D_3$, and no outer walls of $D_3$ pass through $h_0$. In particular, $h_0$ belongs to the interior of $N_{3}$ and hence is ample for $X_3$.

• (2) Among the walls $(v)^{\perp }\cap D_3$ of $D_3$, there exist exactly two walls such that the hyperplane $(v)^{\perp }$ of ${{\mathcal {P}}}_{3}$ contains ${{\mathcal {P}}}_{0}$. These two walls $(v_1)^{\perp }\cap D_3$ and $(v_2)^{\perp }\cap D_3$ belong to the orbit $O^\prime _{648}\subset {{\mathcal {W}}}_{\mathrm{inn}}(D_3)$. Moreover, we have $\langle v_1, v_2\rangle =0$. $\square$

Combining Lemma 5.4 with Propositions  5.1 and 5.2, we obtain the following:

Corollary 5.5

• (1) We have ${{\mathcal {P}}}_{0}=(v_1)^{\perp }\cap (v_2)^{\perp }$, where $(v_1)^{\perp }$ and $(v_2)^{\perp }$ are the hyperplanes of ${{\mathcal {P}}}_{3}$ given in Lemma 5.4.

• (2) For each ${{\mathcal {V}}}( i_{0})$-chamber $D_0^\prime \subset {{\mathcal {P}}}_{0}$, there exist exactly four ${{\mathcal {V}}}( i_{3})$-chambers that contain $D_0^\prime$.

• (3) The initial chamber $D_0$ for $X_0$ is a face $(v_1)^{\perp }\cap (v_2)^{\perp }\cap D_3$ of the initial chamber $D_3$ for $X_3$, and the interior of $D_0\subset {{\mathcal {P}}}_{0}$ is contained in the interior of $N_{3}\subset {{\mathcal {P}}}_{3}$.

• (4) The four ${{\mathcal {V}}}( i_{3})$-chambers containing $D_0$ are contained in $N_{3}$. In particular, we have $\gamma _1, \gamma _2, \varepsilon \in {\text {Aut}}(X_3)$ such that the four ${{\mathcal {V}}}( i_{3})$-chambers containing $D_0$ are $D_3$ and $D_3^{\gamma _1}$, $D_3^{\gamma _2}$, $D_3^{\varepsilon }$. See Fig. 5. $\square$

Fig. 5

${{\mathcal {V}}}( i_{3})$-chambers containing $D_0$

Remark 5.6

The automorphisms $\gamma _1$ and $\gamma _2$ of $X_3$ in Corollary 5.5 (4) can be obtained as conjugates of the double-plane involution $g(b^\prime _{10})$ by ${\mathrm {PGU}}_4({{\mathbb {F}}}_9)$. Let $(v^{\prime \prime })^{\perp }\cap D_3$ be the wall of $D_3$ that is mapped to the wall $(v_2)^{\perp }\cap D_3^{\gamma _1}$ of $D_3^{\gamma _1}$ by $\gamma _1$. Then $(v^{\prime \prime })^{\perp }\cap D_3$ is an inner wall belonging to $O^\prime _{648}$, and hence we have a conjugate $\gamma ^{\prime \prime }$ of $g(b^\prime _{10})$ by ${\mathrm {PGU}}_4({{\mathbb {F}}}_9)$ that maps $D_3$ to the ${{\mathcal {V}}}(i_3)$-chamber adjacent to $D_3$ across $(v^{\prime \prime })^{\perp }\cap D_3$. Then, as the automorphism $\varepsilon$, we can take $\gamma ^{\prime \prime }\gamma _1$. See Sect. 6.2 for another construction of $\varepsilon$.

Let ${\mathrm {pr}}_3:L_{26}\otimes {{\mathbb {Q}}}\rightarrow S_{3}\otimes {{\mathbb {Q}}}$, ${\mathrm {pr}}_0:L_{26}\otimes {{\mathbb {Q}}}\rightarrow S_{0}\otimes {{\mathbb {Q}}}$ and ${\mathrm {pr}}_{30}:S_{3}\otimes {{\mathbb {Q}}}\rightarrow S_{0}\otimes {{\mathbb {Q}}}$ be the orthogonal projections. Then we have ${\mathrm {pr}}_{30}\circ {\mathrm {pr}}_3={\mathrm {pr}}_0$. We put

$$\begin{aligned} {{\mathcal {V}}}(\rho ):=\{\, {{\mathrm {pr}}_{30}(r)} \mid {r\in {{\mathcal {R}}}(S_{3}), \;\;\; \langle {\mathrm {pr}}_{30}(r), {\mathrm {pr}}_{30}(r)\rangle <0} \, \}. \end{aligned}$$

The restriction to ${{\mathcal {P}}}_{0}$ of the tessellation of ${{\mathcal {P}}}_{3}$ by ${{\mathcal {R}}}(S_{3})$-chambers is the tessellation of ${{\mathcal {P}}}_{0}$ by ${{\mathcal {V}}}(\rho )$-chambers. The closed subset

$$\begin{aligned} N_{30}:=N_{3}\cap {{\mathcal {P}}}_{0} \end{aligned}$$

of ${{\mathcal {P}}}_{0}$ contains $D_0$ by Corollary 5.5 (3), and hence its interior is non-empty. Therefore $N_{30}$ is a ${{\mathcal {V}}}(\rho )$-chamber. We have

$$\begin{aligned} {{\mathcal {R}}}(S_{0})\subset {{\mathcal {V}}}(\rho )\subset {{\mathcal {V}}}( i_{0}), \end{aligned}$$

where the second inclusion follows from ${{\mathcal {R}}}(S_{3})\subset {{\mathcal {R}}}(L_{26})$ and ${\mathrm {pr}}_{30}\circ {\mathrm {pr}}_3={\mathrm {pr}}_0$. It follows from Remark 3.2 that

$$\begin{aligned} D_0\subset N_{30}\subset N_{0}, \end{aligned}$$

(5.1)

and that the ${{\mathcal {V}}}(\rho )$-chamber $N_{30}$ is tessellated by ${{\mathcal {V}}}( i_{0})$-chambers. If $g\in {\mathrm {O}}^+(S_{3}, S_{0})$ preserves $N_{3}$, then $g|_{S_{0}}\in {\mathrm {O}}^+(S_{0})$ preserves $N_{30}$ and hence preserves $N_{0}$ by Corollary 3.10. Combining this fact with Lemma 5.3, we conclude that every element of the image of ${\tilde{\rho }}|_{{\text {Aut}}}$ belongs to ${\text {Aut}}(X_0)$.

Next we calculate a generating set of the image of ${\tilde{\rho }}|_{{\text {Aut}}}$.

Lemma 5.7

The group ${\mathrm {PGU}}_4({{\mathbb {F}}}_9)={\text {Aut}}(X_3, h_3)$ acts transitively on the set of non-ordered pairs $\{(v)^{\perp }, (v^\prime )^{\perp }\}$ of hyperplanes of ${{\mathcal {P}}}_{3}$ such that $(v)^{\perp }\cap D_3$ and $(v^\prime )^{\perp }\cap D_3$ are inner walls of $D_3$ belonging to $O^\prime _{648}$, and such that $\langle v, v^\prime \rangle =0$.

Proof

As can be seen from the list [18] of walls of $D_3$, for each inner wall $(v)^{\perp }\cap D_3$ in $O^\prime _{648}$, the number of inner walls $(v^\prime )^{\perp }\cap D_3$ in $O^\prime _{648}$ satisfying $\langle v, v^\prime \rangle =0$ is 42. Comparing $42\times 648 /2=13608$ with Corollary 2.12, we obtain the proof. $\square$

Corollary 5.8

Let g be an element of ${\text {Aut}}(X_3)$ such that $D_0^\prime :={{\mathcal {P}}}_{0}\cap D_3^{g}$ is a ${{\mathcal {V}}}( i_{0})$-chamber, that is, $D_0^\prime$ has an interior point as a subset of ${{\mathcal {P}}}_{0}$. Then there exists an element $\gamma \in {\mathrm {PGU}}_4({{\mathbb {F}}}_9)$ such that $\gamma g\in {\text {Aut}}(X_3)$ maps the face $D_0$ of $D_3$ to the face $D_0^\prime$ of $D_3^{g}=D_3^{\gamma g}$.

Proof

We put $v_1^\prime :=v_1^{g^{-1}}$ and $v_2^\prime :=v_2^{g^{-1}}$, where $v_1$ and $v_2$ are given in Lemma 5.4. Then $D_0^{\prime g^{-1}}={{\mathcal {P}}}_{0}^{g^{-1}}\cap D_3=(v_1^\prime )^{\perp }\cap (v_2^\prime )^{\perp }\cap D_3$ is a face of $D_3$, which is the intersection of two perpendicular inner walls $(v_1^\prime )^{\perp }\cap D_3$ and $(v_2^\prime )^{\perp }\cap D_3$ in $O^\prime _{648}$. Hence the existence of $\gamma \in {\mathrm {PGU}}_4({{\mathbb {F}}}_9)$ follows from Lemma 5.7. $\square$

We put

$$\begin{aligned} {\text {Aut}}(X_3, D_0):=\{\, {g\in {\text {Aut}}(X_3)} \mid { D_0^g= D_0} \, \}, \end{aligned}$$

(5.2)

and compare it with ${\text {Aut}}(X_0, D_0)={\text {Aut}}(X_0, h_0)$. Note that ${\text {Aut}}(X_3, D_0)$ is a subgroup of ${\mathrm {O}}^+(S_{3}, S_{0})\cap {\text {Aut}}(X_3)$ containing the kernel of ${\tilde{\rho }}|_{{\text {Aut}}}$.

Lemma 5.9

The homomorphism ${\tilde{\rho }}|_{{\text {Aut}}}$ maps ${\text {Aut}}(X_3, D_0)$ to ${\text {Aut}}(X_0, h_0)$ isomorphically. In particular, the homomorphism ${\tilde{\rho }}|_{{\text {Aut}}}$ is injective, and the image of ${\tilde{\rho }}|_{{\text {Aut}}}$ contains ${\text {Aut}}(X_0, h_0)$.

Proof

By Corollary 5.5 (4), the subgroup ${\text {Aut}}(X_3, D_0)$ of ${\text {Aut}}(X_3)$ is contained in the finite subset

$$\begin{aligned} {\mathrm {PGU}}_4({{\mathbb {F}}}_9)\;\;\sqcup \;\; {\mathrm {PGU}}_4({{\mathbb {F}}}_9)\cdot {\gamma _1}\;\;\sqcup \;\; {\mathrm {PGU}}_4({{\mathbb {F}}}_9)\cdot {\gamma _2}\;\;\sqcup \;\; {\mathrm {PGU}}_4({{\mathbb {F}}}_9)\cdot {\varepsilon } \end{aligned}$$

(5.3)

of ${\text {Aut}}(X_3)$. For each element g of this subset, we determine whether g preserves ${{\mathcal {P}}}_{0}$ or not. We see that, in each coset ${\mathrm {PGU}}_4({{\mathbb {F}}}_9)\cdot \gamma$ in (5.3), exactly 960 elements g satisfy ${{\mathcal {P}}}_{0}^{g}= {{\mathcal {P}}}_{0}$, and that the set of restrictions $g|_{S_{0}}$ of these $960\times 4=3840$ elements g is equal to ${\text {Aut}}(X_0, h_0)$. $\square$

We discuss the following problem: Let $(v)^{\perp }$ be a hyperplane of ${{\mathcal {P}}}_{0}$ that defines a wall of $D_0$. Determine whether $(v)^{\perp }$ defines a wall of $N_{30}$ or not.

Since ${{\mathcal {L}}}_{40}\subset {{\mathcal {L}}}_{112}$, it immediately follows that, if $(v)^{\perp }\cap D_0$ is an outer wall of $D_0$, then $(v)^{\perp }\cap N_{30}$ is a wall of $N_{30}$.

Lemma 5.10

Let $(v)^{\perp }\cap D_0$ be an inner wall of $D_0$. Then $(v)^{\perp }\cap N_{30}$ is a wall of $N_{30}$ if and only if $(v)^{\perp }\cap D_0\in O_{64}$ or $(v)^{\perp }\cap D_0 \in O_{160}$.

Proof

Let $g\in {\text {Aut}}(X_0)$ be an automorphism that maps $D_0$ to the ${{\mathcal {V}}}(i_0)$-chamber adjacent to $D_0$ across the inner wall $(v)^{\perp }\cap D_0$ (for example, we can take as g a conjugate by ${\text {Aut}}(X_0, h_0)$ of the double-plane involution $g(b_d)$ corresponding to the orbit $O_s$ containing $(v)^{\perp }\cap D_0$). Then $(v)^{\perp }\cap N_{30}$ is a wall of $N_{30}$ if and only if $h_0$ and $h_0^{g}$ , regarded as vectors of $S_{3}$ via $\rho :S_{0}\hookrightarrow S_{3}$, are separated by a root in$S_{3}$, that is, the set

$$\begin{aligned} \{\, {r\in {{\mathcal {R}}}(S_{3})} \mid {\langle h_0, r\rangle \text { and }\langle h_0^g, r\rangle \text { have different sign}} \, \} \end{aligned}$$

is non-empty (see Corollary 3.10). We can calculate this set using the algorithm described in Section 3.3 of [9]. $\square$

Remark 5.11

The ‘if ’-part of Lemma 5.10 is refined as follows. For each positive integer d, we put

$$\begin{aligned} {{\mathcal {C}}}_d:=\{\, {[C]\in S_{3}} \mid {C\text { is a smooth rational curve on }X_3\text { such that }\langle h_3, [C]\rangle =d} \, \}. \end{aligned}$$

The walls of $N_{3}$ are in one-to-one correspondence with the union of these sets ${{\mathcal {C}}}_d$. We have ${{\mathcal {C}}}_1={{\mathcal {L}}}_{112}$. The set ${{\mathcal {C}}}_d$ can be calculated by induction on d. Indeed, a root r of $S_{3}$ satisfying $\langle h_3, r\rangle =d$ belongs to ${{\mathcal {C}}}_d$ if and only if there exists no class $r^\prime \in {{\mathcal {C}}}_{d^\prime }$ with $d^\prime <d$ such that $\langle r, r^\prime \rangle <0$. By this method, we obtain the following:

Proposition 5.12

For $d=2,3,5,6$, the set ${{\mathcal {C}}}_d$ is empty. We have

$$\begin{aligned} |{{\mathcal {C}}}_1|=112, \quad |{{\mathcal {C}}}_4|=18144, \quad |{{\mathcal {C}}}_7|=2177280=1632960+544320. \end{aligned}$$

The actions of ${\mathrm {PGU}}_4({{\mathbb {F}}}_9)$ on ${{\mathcal {C}}}_1$ and on ${{\mathcal {C}}}_4$ are transitive. The action of ${\mathrm {PGU}}_4({{\mathbb {F}}}_9)$ on ${{\mathcal {C}}}_7$ has two orbits of size 1632960 and 544320. $\square$

Then we have the following:

• Among the 64 walls in $O_{64}$, 32 walls are defined by $({\mathrm {pr}}_{30}(r))^{\perp }$ with $r\in {{\mathcal {C}}}_1$, and the other 32 walls are defined by $({\mathrm {pr}}_{30}(r))^{\perp }$ with $r\in {{\mathcal {C}}}_4$.

• Among the 160 walls in $O_{160}$, 40 walls are defined by $({\mathrm {pr}}_{30}(r))^{\perp }$ with $r\in {{\mathcal {C}}}_1$, 80 walls are defined by $({\mathrm {pr}}_{30}(r))^{\perp }$ with $r\in {{\mathcal {C}}}_4$, and 40 walls are defined by $({\mathrm {pr}}_{30}(r))^{\perp }$ with $r\in {{\mathcal {C}}}_7$.

Note that, if $g\in {\text {Aut}}(X_0)$ belongs to the image of ${\tilde{\rho }}|_{{\text {Aut}}}$, then g preserves $N_{30}\subset N_{0}$. Hence the double-plane involutions $g(b_{80})$ and $g(b_{296})$ corresponding to the orbits $O_{64}$ and $O_{160}$ are not in the image of ${\tilde{\rho }}|_{{\text {Aut}}}$.

Lemma 5.13

Let O be either $O_{40}$ or $O_{320}$, and let $(v)^{\perp }\cap D_0$ be an element of O. Let $D_0^\prime$ be the ${{\mathcal {V}}}( i_{0})$-chamber adjacent to $D_0$ across $(v)^{\perp }\cap D_0$. Then there exists an element $g^\prime$ of ${\mathrm {O}}^+(S_{3}, S_{0})\cap {\text {Aut}}(X_3)$ such that $g^\prime |_{S_{0}}$ maps $D_0$ to $D_0^\prime$.

Proof

Let F denote the hyperplane $(v)^{\perp }$ of ${{\mathcal {P}}}_{0}$ considered as a linear subspace of ${{\mathcal {P}}}_{3}$ of codimension 3. Let $D_3^\prime$ be one of the four ${{\mathcal {V}}}( i_{3})$-chambers such that $D_0^\prime ={{\mathcal {P}}}_{0}\cap D^\prime _3$. (See Corollary 5.5 (2).) We have $F\cap D_0=F\cap D_0^\prime =F\cap D_3=F\cap D_3^\prime$, and this set contains a non-empty open subset of F. Lemma 5.10 implies that there exists no root r of $S_{3}$ such that the hyperplane $(r)^{\perp }$ of ${{\mathcal {P}}}_{3}$ contains F. Since $F\cap D_3=F\cap D_3^\prime$, we see that $D_3$ and $D_3^\prime$ are on the same side of $(r)^{\perp }$ for any root r of $S_{3}$, and hence $D_3^\prime$ is contained in $N_{3}$. Therefore we have an element $g^\prime$ of ${\text {Aut}}(X_3)$ such that $D_3^{g^\prime }= D_3^\prime$. By Lemma 5.8, there exists an element $\gamma$ of ${\mathrm {PGU}}_4({{\mathbb {F}}}_9)$ such that $\gamma g^\prime$ maps the face $D_0$ of $D_3$ to the face $D_0^\prime$ of $D_3^\prime =D_3^{g^\prime }=D_3^{\gamma g^\prime }$. Since each of $D_0$ and $D_0^\prime$ contains a non-empty open subset of ${{\mathcal {P}}}_{0}$, we see that $\gamma g^\prime \in {\text {Aut}}(X_3)$ belongs to ${\mathrm {O}}^+(S_{3}, S_{0})$. Then $\gamma g^\prime |_{S_{0}}$ maps $D_0$ to $D_0^\prime$. $\square$

Lemmas 5.9 and 5.13 imply that $g(b_{112})$ and $g(b_{688})$ are in the image of ${\tilde{\rho }}|_{{\text {Aut}}}$. Let G be the subgroup of ${\text {Aut}}(X_0)$ generated by ${\text {Aut}}(X_0, h_0)$ and $g(b_{112})$ and $g(b_{688})$. Since G is contained in the image of ${\tilde{\rho }}|_{{\text {Aut}}}$, each $g\in G$ preserves $N_{30}$.

Lemma 5.14

If a ${{\mathcal {V}}}( i_{0})$-chamber $D^\prime$ is contained in $N_{30}$, then there exists an element $g\in G$ such that $D^\prime =D_0^g$.

Proof

Since $N_{30}$ is tessellated by ${{\mathcal {V}}}( i_{0})$-chambers, there exists a sequence

$$\begin{aligned} D^{(0)}= D_0, \; D^{(1)}, \; \dots \; , \; D^{(N)}= D^\prime \end{aligned}$$

of ${{\mathcal {V}}}( i_{0})$-chambers such that each $D^{(\nu )}$ is contained in $N_{30}$ and that $D^{(\nu )}$ is adjacent to $D^{(\nu -1)}$ for $\nu =1, \dots , N$. We prove the existence of $g\in G$ by induction on N. The case $N=0$ is trivial. Suppose that $N>0$, and let $g^\prime \in G$ be an element such that $D_0^{g^\prime }=D^{(N-1)}$. Note that $g^\prime$ preserves $N_{30}$. The ${{\mathcal {V}}}( i_{0})$-chambers $D_0$ and $D^{^\prime g^{\prime -1}}$ are adjacent, and both are contained in $N_{30}$. Hence, by Lemma 5.10, the wall of $D_0$ across which $D^{^\prime g^{\prime -1}}$ is adjacent to $D_0$ is either in $O_{40}$ or in $O_{320}$. Therefore we have an element $g^{\prime \prime }\in G$ (a conjugate of $g(b_{112})$ or $g(b_{688})$ by ${\text {Aut}}(X_0, h_0)$) such that $D^{^\prime g^{\prime -1}}= D_0^{g^{\prime \prime }}$. Then $g^{\prime \prime }g^\prime \in G$ maps $D_0$ to $D^\prime$. $\square$

Let g be an arbitrary element of the image of ${\tilde{\rho }}|_{{\text {Aut}}}$. Since g preserves $N_{30}$, there exists an element $g^\prime \in G$ such that $D_0^g=D_0^{g^\prime }$. Then $g^\prime g^{-1}\in {\text {Aut}}(X_0, h_0)$, and hence $g\in G$. Thus the proof of Theorem 1.7 is completed. $\square$

5.2 Proof of Theorem 1.8

By the commutativity of diagram (1.2) and Theorem 1.7, it suffices to prove that the image of $\mathrm{res}_0:{\text {Aut}}(\overline{{{\mathcal {X}}}/R})\rightarrow {\text {Aut}}(X_0)$ contains ${\text {Aut}}(X_0, h_0)$ and the double-plane involutions $g(b_{112})$ and $g(b_{688})$. Let $\pi :{{\mathcal {X}}}\rightarrow {\text {Spec}}R$ be the elliptic modular surface of level 4 over a discrete valuation ring R of mixed characteristic with residue field k of characteristic 3. Let K be the fraction field of R. We put $X_K:={{\mathcal {X}}}\otimes _R K$ and $X_{k}:={{\mathcal {X}}}\otimes _R k$ and identify $X_0$ with $X_K\otimes _K{\bar{K}}$ and $X_3$ with $X\otimes _k{{\bar{k}}}$, where ${\bar{K}}$ and ${\bar{k}}$ are algebraic closures of K and k, respectively.

Replacing R by a finite extension of R, we can assume that $h_0$ is the class of a line bundle $L_K$ on $X_K$ and that every element of ${\text {Aut}}(X_0, h_0)$ is defined over K. We can extend $L_K$ to a line bundle ${{\mathcal {L}}}$ on ${{\mathcal {X}}}$ by (21.6.11) of EGA, IV [40]. Then the class of the line bundle $L_{k}:={{\mathcal {L}}}|X_{k}$ on $X_{k}$ is $\rho (h_0)\in S_{3}$. Hence $L_{k}$ is ample by Lemma 5.4. Therefore ${{\mathcal {L}}}$ is ample relative to ${\text {Spec}}R$ by (4.7.1) of EGA, III [41]. We choose $n>0$ such that ${{\mathcal {L}}}^{\otimes n}$ is very ample relative to ${\text {Spec}}R$, embed ${{\mathcal {X}}}$ into a projective space ${{\mathbb {P}}}^N_R$ over ${\text {Spec}}R$ by ${{\mathcal {L}}}^{\otimes n}$, and regard ${\text {Aut}}(X_0, h_0)$ as the group of projective automorphisms of $X_K\subset {{\mathbb {P}}}^{N}_K$. Since $X_3$ is not birationally ruled, we can apply the theorem of Matsusaka–Mumford [42] and conclude that every element of ${\text {Aut}}(X_0, h_0)$ has a lift in ${\text {Aut}}({{\mathcal {X}}}/R)$.

Remark 5.15

The argument in the preceding paragraph is a special case of Theorem 2.1 of Lieblich and Maulik [43].

Let $b$ be either $b_{112}$ or $b_{688}$. Replacing R by a finite extension of R, we can assume that $b$ is the class of a line bundle $M_K$ on $X_K$, and that each smooth rational curve contracted by $\varPhi _{b}:X_K\rightarrow {{\mathbb {P}}}^2_K$ is defined over K. Let $\Sigma (b)\subset S_{0}$ be the set of classes of smooth rational curves contracted by $\varPhi _{b}$. We extend $M_K$ to a line bundle ${{\mathcal {M}}}$ on ${{\mathcal {X}}}$. Then the class of the line bundle $M_{k}:={{\mathcal {M}}}|X_{k}$ on $X_{k}$ is $\rho (b)\in S_{3}$. Using the algorithms in Remark 1.3, we can verify that $\rho (b)$ is a double-plane polarization of $X_3$ and calculate the set $\Sigma (\rho (b))\subset S_{3}$ of classes of smooth rational curves contracted by $\varPhi _{\rho (b)}:X_k\rightarrow {{\mathbb {P}}}^2_k$. Then we have the following equality:

$$\begin{aligned} \Sigma (\rho (b))=\rho (\Sigma (b)). \end{aligned}$$

(5.4)

Since the complete linear systems $|M_K|$ and $|M_k|$ are of dimension 2 and fixed-point-free, we see that $\pi _* {{\mathcal {M}}}$ is free of rank 3 over R and defines a morphism

$$\begin{aligned} \widetilde{\varPhi }:{{\mathcal {X}}}\rightarrow {{\mathbb {P}}}^2_R \end{aligned}$$

over R. We execute, over R, Horikawa’s canonical resolution for double coverings branched along a curve with only ADE-singularities (see Section 2 of [44]). Let $C_{1, K}, \dots , C_{\mu , K}$ be the smooth rational curves on $X_K$ contracted by $\varPhi _{b}$, where $\mu$ is the total Milnor number of the singularities of the branch curve of $\varPhi _{b}$ (and hence of $\varPhi _{\rho (b)}$). It follows from (5.4) that the closure ${{\mathcal {C}}}_j$ of each $C_{j, K}$ in ${{\mathcal {X}}}$ is a smooth family of rational curves over ${\text {Spec}}R$, that $\widetilde{\varPhi }$ contracts ${{\mathcal {C}}}_j$ to an R-valued point $q_{0j}$ of ${{\mathbb {P}}}^2_R$ (that is, a section of the structure morphism ${{\mathbb {P}}}^2_R\rightarrow {\text {Spec}}R$), and that $\widetilde{\varPhi }$ is finite of degree 2 over the complement of $\{q_{01}, \dots , q_{0\mu }\}$ in ${{\mathbb {P}}}^2_R$. We put $J_0:=\{1, \dots , \mu \}$, $P_0:= {{\mathbb {P}}}^2_R$, and let $\beta _0:P_0\rightarrow {{\mathbb {P}}}^2_R$ be the identity. Suppose that we have a morphism $\beta _i:P_i\rightarrow {{\mathbb {P}}}^2_R$ over R from a smooth R-scheme $P_i$ and a subset $J_i\subset J_0$ such that

• (i) $\widetilde{\varPhi }$ factors as

  $$\begin{aligned} {{\mathcal {X}}}\; \smash {\mathop {\; \longrightarrow \; }\limits ^{\alpha _i}}\; P_i \; \smash {\mathop {\; \longrightarrow \; }\limits ^{\beta _i}}\; {{\mathbb {P}}}^2_R, \end{aligned}$$

• (ii) $\alpha _i$ contracts ${{\mathcal {C}}}_j$ to an R-valued point $q_{ij}$ of $P_i$ for each $j\in J_i$, and

• (iii) $\alpha _i$ is finite of degree 2 over the complement of $\{ {q_{ij}} \mid {j\in J_i} \}$ in $P_i$.

Suppose that $J_i$ is non-empty. We choose an index $j_0\in J_i$, and let $\beta ^\prime :P_{i+1}\rightarrow P_{i}$ be the blowup at the R-valued point $q_{ij_0}$. Let $\beta _{i+1}:P_{i+1}\rightarrow {{\mathbb {P}}}^2_R$ be the composite of $\beta ^\prime$ and $\beta _i$. Then properties (i)–(iii) are satisfied with i replaced by $i+1$ for some $J_{i+1}\subset J_{i}$ with $J_{i+1}\ne J_{i}$. Indeed, $\alpha _{i+1}$ induces a finite morphism from at least one of the ${{\mathcal {C}}}_{j}$ with $j\in J_{i}$ to the exceptional divisor of $\beta ^\prime$. Therefore after finitely many steps, we obtain a finite double covering ${{\mathcal {X}}}\rightarrow P$ that factors $\widetilde{\varPhi }$, where P is obtained from ${{\mathbb {P}}}^2_R$ by a finite number of blowups at R-valued points. Then the deck-transformation of ${{\mathcal {X}}}\rightarrow P$ gives a lift of the double-plane involution $g(b)\in {\text {Aut}}(X_0)$ to ${\text {Aut}}({{\mathcal {X}}}/R)$. $\square$

Remark 5.16

The double-plane polarizations $\rho (b_{112}), \rho (b_{688})\in S_{3}$ have the following properties with respect to $h_3$:

$$\begin{aligned}&\langle h_3, \rho (b_{112})\rangle =9, \;\; \langle h_3, h_3^{g(b_{\rho (b_{112})})}\rangle =34, \\&\langle h_3, \rho (b_{688})\rangle =19, \;\; \langle h_3, h_3^{g(b_{\rho (b_{688})})}\rangle =178. \end{aligned}$$

6 Enriques surface of type $\mathrm{IV}$

Let Z be a K3 surface defined over an algebraically closed field of characteristic $\ne 2$. For an element $g\in {\mathrm {O}}^+(S_{Z})$ of order 2, we put

$$\begin{aligned} S_{Z}^{+g}:=\{\, {v\in S_{Z}} \mid {v^{g}=v} \, \}, \quad S_{Z}^{-g}:=\{\, {v\in S_{Z}} \mid {v^{g}=-v} \, \}. \end{aligned}$$

Suppose that $\varepsilon :Z\rightarrow Z$ is an Enriques involution, and let $\pi :Z\rightarrow Y:=Z/\langle {\varepsilon } \rangle$ be the quotient morphism. Note that the lattice $S_{Y}$ of numerical equivalence classes of divisors on the Enriques surface Y is an even unimodular hyperbolic lattice of rank 10, which is unique up to isomorphism. Then the pullback homomorphism $\pi ^*:S_{Y}\hookrightarrow S_{Z}$ induces an isometry of lattices from $S_{Y}(2)$ to $S_{Z}^{+\varepsilon }$, where $S_{Y}(2)$ is the lattice obtained from $S_{Y}$ by multiplying the intersection form by 2. Hence the following are satisfied: (i) $S_{Z}^{+\varepsilon }$ is a hyperbolic lattice of rank 10 and (ii) if M is a Gram matrix of $S_{Z}^{+\varepsilon }$, then (1 / 2)M is an integer matrix that defines an even unimodular lattice. Moreover, since $\pi$ is étale, we have that (iii) the orthogonal complement $S_{Z}^{-\varepsilon }$ of $S_{Z}^{+\varepsilon }$ in $S_{Z}$ contains no roots.

6.1 Proof of Proposition 1.11

We check conditions (i), (ii), (iii) for all involutions in the finite group ${\text {Aut}}(X_0, h_0)$. It turns out that there exist exactly six involutions $\varepsilon ^{(1)}, \dots , \varepsilon ^{(6)}$ satisfying these conditions. They are conjugate to each other, and they belong to the subgroup ${\text {Gal}}(\mu )$ of ${\text {Aut}}(X_0, h_0)$ (see Proposition 4.3). We show that these involutions are Enriques involutions of type $\mathrm{IV}$.

Let $\varepsilon _0$ be one of $\varepsilon ^{(1)}, \dots , \varepsilon ^{(6)}$. Recall that $\sigma :X_0\rightarrow {{\mathbb {P}}}^1$ is the Jacobian fibration defined by (1.1), and let $f\in S_{0}$ be the class of a fiber of $\sigma$. Since $\varepsilon _0\in {\text {Gal}}(\mu )$, we have $\varepsilon _0\in {\text {Aut}}(X_0, f)$ by Remark 4.5. Let $F_c\subset {{\mathcal {L}}}_{40}$ be the set of classes of irreducible components of the singular fiber $\sigma ^{-1}(c)$ over $c\in \mathrm{Cr}(\sigma )$. Looking at the action of $\varepsilon _0$ on these 6 quadrangles $F_{c}$, we see that the element ${\bar{\varepsilon }}_0\in \mathrm{Stab}(\mathrm{Cr}(\sigma ))$ defined by diagram (4.5) is of order 2 and fixes exactly 2 points of $\mathrm{Cr}(\sigma )$. Suppose that $F_{c}$ is fixed by $\varepsilon _0$. Then $\varepsilon _0$ acts on $F_{c}$ as $\ell _0\leftrightarrow \ell _2$ and $\ell _1\leftrightarrow \ell _3$, where $\ell _0, \dots , \ell _3$ are labeled as in (2.4). Therefore $\varepsilon _0$ is fixed-point-free, and $Y_0:=X_0/\langle {\varepsilon _0} \rangle$ is an Enriques surface.

The Enriques involution $\varepsilon _0$ acts on ${{\mathcal {L}}}_{40}$ in such a way that, for any curve $C\in {{\mathcal {L}}}_{40}$, we have $C\cap C^{\varepsilon _0}=\emptyset$. Hence we obtain a configuration of 20 smooth rational curves on $Y_0$. It is easy to check that this configuration is isomorphic to the configuration of type $\mathrm{IV}$. By Theorem 6.1 of [14], we see that $Y_0$ is an Enriques surface of type $\mathrm{IV}$. $\square$

Using Proposition 2.17, we can describe the six Enriques involutions $\varepsilon ^{(\nu )}$ in ${\text {Gal}}(\mu )$ as follows.

Proposition 6.1

The involution $\tau _J \in {\text {Gal}}(\mu )$ is an Enriques involution if and only if $|J|=3$ and J contains $\{1, 5\}$ or $\{2,6\}$ or $\{3, 4\}$. $\square$

6.2 Proof of Theorem 1.12

Let $\varepsilon _0\in {\text {Aut}}(X_0, h_0)$ be the image of $\varepsilon _3$ under ${\tilde{\rho }}|_{{\text {Aut}}}$, which is one of $\varepsilon ^{(1)}, \dots , \varepsilon ^{(6)}$. Since $\varepsilon _0\in {\text {Aut}}(X_0, h_0)$, the involution $\varepsilon _3$ preserves the face $D_0={{\mathcal {P}}}_{0}\cap D_3$ of $D_3$. Therefore $\varepsilon _3$ belongs to the finite group ${\text {Aut}}(X_3, D_0)$ defined by (5.2). We check all involutions in ${\text {Aut}}(X_3, D_0)$ and find $\varepsilon _3$ in the form of a matrix acting on $S_{3}$. We have $\langle h_3, h_3^{\varepsilon _3}\rangle =16$. Indeed, the ${{\mathcal {V}}}( i_{3})$-chamber $D_3^{\varepsilon _3}$ is the chamber $D_3^{\varepsilon }$ in Fig. 5. The action of $\varepsilon _3$ on the fibers of the Jacobian fibration $\sigma :X_3\rightarrow {{\mathbb {P}}}^1$ defined by (1.1) is exactly the same as the action of $\varepsilon _0$ on the fibers of the corresponding fibration of $X_0$. Hence $\varepsilon _3$ is fixed-point-free. Moreover, the configuration on $Y_3:=X_3/\langle {\varepsilon _3} \rangle$ of 20 smooth rational curves obtained from ${{\mathcal {L}}}_{40}\subset {{\mathcal {L}}}_{112}$ is isomorphic to the configuration of type $\mathrm{IV}$, and hence $Y_3$ is of type $\mathrm{IV}$ by Theorem 6.1 of [14]. The set of pullbacks of the smooth rational curves on $Y_3$ by $\pi _3$ is ${{\mathcal {L}}}_{40}\subset {{\mathcal {L}}}_{112}$. Hence they are lines on $F_3$. $\square$

Remark 6.2

Recently, we have shown in [38] that $X_0$ has exactly nine Enriques involutions modulo conjugation in ${\text {Aut}}(X_0)$ and that four of the quotient Enriques surfaces have finite automorphism groups (of types I, II, III, IV), whereas the other five have infinite automorphism groups.