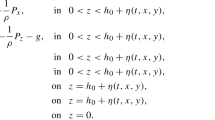Wave-breaking phenomena and persistence properties for the nonlocal rotation-Camassa–Holm equation

Abstract

Consideration in the present paper is a mathematical model proposed as an equation of long-crested shallow water waves propagating in one direction with the effect of Earth’s rotation. This model equation is analogous to the Camassa–Holm approximation of the two-dimensional incompressible and irrotational Euler equations, and its solution corresponding to physically relevant initial perturbations is more accurate on a much longer timescale. The effects of the Coriolis force caused by the Earth rotation and nonlocal higher nonlinearities on the blow-up criteria and wave-breaking phenomena in the periodic setting are investigated. Moreover, working with moderate weight functions that are commonly used in time–frequency analysis, some persistence results to the equation are illustrated.

1 Introduction

It is known that near the Equator the ocean waves propagate mainly along the Equator as two-dimensional waves, due to the joint action of the wind and the Coriolis force [11, 12]. We study here a model equation with the Coriolis effect derived from the incompressible and irrotational two-dimensional shallow water in the equatorial region [22]. This model equation called the rotation-Camassa–Holm(R-CH) equation has a cubic and even quartic nonlinearities and a formal Hamiltonian structure. More precisely, the motion of the fluid is described by the scalar equation in the following form:

$$\begin{aligned}&u_t-\beta \mu u_{xxt}+cu_x\ +3\alpha \varepsilon uu_x-\beta _0 \mu u_{xxx}+\omega _1\varepsilon ^2 u^2u_x+\omega _2 \varepsilon ^3u^3u_x\nonumber \\&\quad =\alpha \beta \varepsilon \mu (2u_xu_{xx}+uu_{xxx}), \end{aligned}$$

(1.1)

where u represents the horizontal velocity field at height $z_0$, the constants appearing in the equation are defined by $c=\sqrt{1+\Omega ^2}-\Omega$ with the parameter $\Omega$ which is the constant rotational frequency due to the Coriolis effect, $\alpha =\frac{c^2}{1+c^2}$, $\beta _0=\frac{c(c^4+6c^2-1)}{6(c^2+1)^2}$, $\beta =\frac{3c^4+8c^2-1}{6(c^2+1)^2}$ and $\omega _1=\frac{-3c(c^2-1)(c^2-2)}{2(1+c^2)^3}$ and $\omega _2=\frac{(c^2-2)(c^2-1)^2(8c^2-1)}{2(1+c^2)^5}$ satisfying $c\rightarrow 1$, $\beta \rightarrow \frac{5}{12}$, $\beta _0\rightarrow \frac{1}{4}$, $\omega _1,\omega _2\rightarrow 0$ and $\alpha \rightarrow \frac{1}{2}$ when $\Omega \rightarrow 0$. Using the rescaling, it is required that $0\le z_0\le 1$, where

$$\begin{aligned} z^2_0=\frac{1}{2}-\frac{2}{3}\frac{1}{(c^2+1)}+\frac{4}{3}\frac{1}{(c^2+1)^2}. \end{aligned}$$

Since it is also natural to require that the constant $\beta >0$, it must be the case

$$\begin{aligned} 0\le \Omega \le \sqrt{\frac{1}{6}(1+2\sqrt{19})}\approx 1.273, \end{aligned}$$

and

$$\begin{aligned} \frac{1}{\sqrt{2}}\le z_0< \sqrt{\frac{61-2\sqrt{19}}{54}}\approx 0.984. \end{aligned}$$

Equation (1.1) is derived in [22] by showing that after a double asymptotic expansion with respect to $\varepsilon$ and $\mu$, the free surface $\eta =\eta (\tau ,\xi )$ under the field variable $(\eta ,\xi )$ defined in 2D Euler’s dynamics is governed by the following equation:

$$\begin{aligned}&2(\Omega +c)\eta _\tau +3c^2\eta \eta _\xi +\ \frac{c^2}{3}\mu \eta _{\xi \xi \xi }+A_1\varepsilon \eta ^2\eta _\xi +A_2\varepsilon ^2\eta ^3\eta _\xi +A_0\varepsilon ^3\eta ^4\eta _\xi \\&\quad =\varepsilon \mu (A_3\eta _\xi \eta _{\xi \xi }+A_4\eta \eta _{\xi \xi \xi })+o(\varepsilon ^4,\mu ^2), \end{aligned}$$

where the constants $A_0, A_1, A_2, A_3$ and $A_4$ satisfy that

$$\begin{aligned} \displaystyle A_0= & {} \frac{c^2(c^2-2)(3c^{10}+228c^8-540c^6-180c^4-13c^2+42)}{12(c^2+1)^6}, \ A_1=\frac{3c^2(c^2-2)}{(c^2+1)^2}, \\ A_2= & {} -\frac{c^2(2-c^2)(c^6-7c^4+5c^2-5)}{(c^2+1)^4}, \ A_3=\frac{-c^2(9c^4+16c^2-2)}{3(c^2+1)^2}, \hbox { and } \\&\displaystyle A_4=\frac{-c^2(3c^4+8c^2-1)}{3(c^2+1)^2}. \end{aligned}$$

The free surface $\eta$ with respect to the horizontal component of the velocity u at $z=z_0$ under the CH regime $\varepsilon =O(\sqrt{\mu })$ is also given by

$$\begin{aligned} \eta =\frac{1}{c}u+\gamma _1\varepsilon u^2+\gamma _2\varepsilon ^2 u^3+\gamma _3\varepsilon ^3u^4+\gamma _4\varepsilon \mu u_{\xi \xi }+o(\varepsilon ^4,\mu ^2), \end{aligned}$$

where the constants in the expression are given by

$$\begin{aligned} \gamma _1&=\frac{2-c^2}{2c^2(c^2+1)}, \quad \gamma _2=\frac{(c^2-1)(c^2-2)(2c^2+1)}{2c^3(c^2+1)^3},\\ \gamma _3&=-\frac{(c^2-1)^2(c^2-2)(21c^4+16c^2+4)}{8c^4(c^2+1)^5}, \quad \mathrm{and} \; \, \gamma _4=\frac{-(3c^4+6c^2-5)}{12c(c^2+1)^2}. \end{aligned}$$

Denote $m=(1-\beta \mu \partial ^2_x)u$. One can rewrite the above equation in terms of the evolution of the momentum density m, namely

$$\begin{aligned} \partial _t m+\alpha \varepsilon (um_x+2mu_x)+cu_x-\beta _0\mu u_{xxx}+\omega _1\varepsilon ^2u^2u_x+\omega _2\varepsilon ^3u^3u_x=0. \end{aligned}$$

(1.2)

In the case that the Coriolis effect vanishes $(\Omega =0)$, the coefficients in the higher-power nonlinearities correspond to $\omega _1=0$ and $\omega _2=0$. In this case, using the scaling transformation $u(t,x)\rightarrow \alpha \varepsilon u(\sqrt{\beta \mu }t,\sqrt{\beta \mu }x)$ and then the Galilean transformation $u(t,x)\rightarrow u(t,x-\frac{3}{4}t)+\frac{1}{4}$, the R-CH equation (1.2) is then reduced to the classical CH equation:

$$\begin{aligned} u_t-u_{xxt}+3uu_x=2u_xu_{xx}+uu_{xxx}, \end{aligned}$$

which was derived [5, 18] (see also the rigorous derivation in [13]) as a model describing the unidirectional propagation of shallow water waves. It was later shown to model the propagation of axially symmetric waves in hyperelastic rods [15] and also derived by applying tri-Hamiltonian duality to the bi-Hamiltonian structure of the Korteweg–de Vries (KdV) equation [27]. In contrast to the KdV equation, the CH equation has many remarkable distinctive properties: The CH equation is completely integrable for a large class of initial data, for which it can be solved by the inverse scattering method [5, 8, 14, 17], it can describe wave-breaking phenomenon, the solution remains bounded while its slope becomes infinite in finite time [5, 9], it has peaked solutions, which are nonanalytic solitary waves that are global weak solutions, and interact cleanly like solitons [1, 5], and it has a variety of interesting geometric formulations [10, 26]. On the other hand, if we take formally $\beta =0$ and $\omega _2=0$ in (1.2), then we get the following integrable Gardner equation [20]:

$$\begin{aligned} u_t+cu_x+3\alpha \varepsilon uu_x-\beta _0\mu u_{xxx}+\omega _1 \varepsilon ^2u^2u_x=0. \end{aligned}$$

Note that the R-CH equation (1.2) has the following three conserved quantities:

$$\begin{aligned} I(u)=\int u \hbox {d}x, \quad E(u)=\frac{1}{2}\int u^2+\beta \mu u^2_x\hbox {d}x \end{aligned}$$

and

$$\begin{aligned} F(u)=\frac{1}{2}\int \left( cu^2+\alpha \varepsilon u^3+\beta _0 \mu u^2_x+\frac{\omega _1\varepsilon ^2}{6}u^4+\frac{\omega _2\varepsilon ^3}{10}u^5+\alpha \beta \varepsilon \mu uu^2_x \right) \hbox {d}x. \end{aligned}$$

Define that

$$\begin{aligned} B_1=\partial _x (1-\beta \mu \partial ^2_x), \end{aligned}$$

and

$$\begin{aligned} B_2&=\partial _x \left( \alpha \varepsilon m+\frac{c}{2}\right) +\left( \alpha \varepsilon m+\frac{c}{2}\right) \partial _x-\beta _0 \mu \partial ^3_x+\frac{2}{3}\omega _1\varepsilon ^2\partial _x(u\partial ^{-1}_x(u\partial _x)) \\&\quad +\frac{5}{8}\omega _2\varepsilon ^3\partial _x\left( u^{\frac{3}{2}}\partial ^{-1}_x\left( u^{\frac{3}{2}}\partial _x\right) \right) . \end{aligned}$$

A simple calculation then reveals that the R-CH equation (1.2) can be written as

$$\begin{aligned} m_t=-B_1\frac{\delta F}{\delta m}=-B_2\frac{\delta E}{\delta m}, \end{aligned}$$

where $B_1$ and $B_2$ are two skew-symmetric differential operators.

It is observed that the consideration of the Coriolis effect gives rise to a higher-power nonlinear term into the R-CH model, which has interesting implications for the fluid motion, particularly in the relation to the wave-breaking phenomena and the permanent waves. It is noted that in the process of the derivation of the asymptotic model equation, the rotation parameter $\Omega$ is treated as a fixed O(1) constant relevant to the nonlinearity parameter $\varepsilon$ and the shallowness parameter $\mu$. As is pointed out in [6, 22], the motivation for such a fixed $\Omega$ in the asymptotic expansion is to retain higher-degree nonlinearities in the asymptotic equation so that in the analytical aspect is studied with an emphasis of investigating whether rotation effects can defer or enhance the formation of singularity. For the other small parameter $\Omega$ due to the Coriolis force in the shallow water wave propagation regime, it is referred to recent works in [21, 24] for the geophysical applications.

One of our goals in the present paper is to investigate from this model in the periodic setting how the higher-power nonlinearities affect the wave-breaking phenomena and what conditions can ensure the occurrence of the wave-breaking phenomena or permanent waves. The dynamics of the blow-up quantity along the characteristics in the R-CH equation actually involves the interaction among three parts: a local nonlinearity, a nonlocal term and a term stemming from the weak Coriolis forcing. It is known that the nonlocal (smoothing) effect can help maintain the regularity while waves propagate and hence prevent them from blowing up, even when dispersion is weak or absent. See, for example, the Benjamin–Bona–Mahoney (BBM) equation [2]. As the local nonlinearity becomes stronger and dominates over the dispersion and nonlocal effects, singularities may occur in the sense of wave breaking. Examples can be found in the Whitham equation [9] and the Camassa–Holm (CH) equation [5, 13]. It is also found that the Coriolis effect will spread out waves and make them decay in time, delaying the onset of wave breaking. Understanding the wave-breaking mechanism such as when a singularity can form and what the nature of it is not only presents fundamental importance from mathematical point of view but also is of great physical interest, since it would help provide a key mechanism for localizing energy in conservative systems by forming one or several small-scale spots. For instance, in fluid dynamics, the possible phenomenon of finite-time breakdown for the incompressible Euler equations signifies the onset of turbulence in high Reynolds number flows.

The R-CH equation with a nonlocal structure can be reformulated in a weak form of nonlinear nonlocal transport type. From the transport theory, the blow-up criteria assert that singularities are caused by the focusing of characteristics, which involve the information on the gradient $u_x$. The dynamics of the wave-breaking quantity along the characteristics is established by the Riccati-type differential inequality. Inspired by the idea in study of the classical CH equation to show how local structure of the solution affects the blow-ups [4], the argument in our case is then approached by a refined analysis on evolution of the solution u and its gradient $u_x$. It is noted that the method in [4] relies heavily on the fact that the convolution terms are quadratic and positively definite. As for the R-CH equation, the convolution contains cubic even quartic nonlinearities which do not have a lower bound in terms of the local terms. Hence, the higher-power nonlinearities in the equation make it difficult to obtain a purely local condition on the initial data that can generate finite-time wave breaking. In our case, the blow-up can be deduced by the interplay between u and $u_x$. More precisely, this motivates us to carry out a refined analysis of the characteristic dynamics of $M=\gamma u-u_x$ and $N=\gamma u+u_x$. The estimates of M and N can be closed in the form of

$$\begin{aligned} M'(t)\ge -CMN+K_1,\quad N'(t)\le CMN+K_2, \end{aligned}$$

where the nonlocal terms $K_1,K_2$ can be bounded in terms of certain order conservation laws. From these Riccati-type differential inequalities, the monotonicity of M and N can be established, and hence the finite-time wave-breaking follows.

Another purpose of the present paper is to find a large class of weight functions $\varphi$ such that

$$\begin{aligned} \sup _{t\in [0,T)}(\Vert \varphi u(t)\Vert _p+\Vert \varphi u_x(t)\Vert _p)<\infty \end{aligned}$$

where $\Vert \cdot \Vert _{p}$ denotes the usual $L_p$ norm. We obtain a persistence result on solutions u in the weighted $L^p$ spaces $L_{p,\varphi }:L_p(\mathbb {R},\varphi ^p \hbox {d}x)$. As a consequence and an application, we determine the spatial asymptotic behavior of certain solutions to the R-CH equation. We will work with moderate weight functions which appear with regularity in the theory of time–frequency analysis [19].

The remainder of the paper is organized as follows. In Sect. 2, some preliminary estimates and results for the periodic R-CH equation are recalled and presented. Section 3 is devoted to proof the breakdown mechanisms to the R-CH equation. In Sect. 4, some fundamentals concerning moderate weight functions and the functional analytic setting for the R-CH equation are presented and persistence results for the R-CH equation to its supersymmetric extension are given.

2 Preliminaries and dynamics along the characteristics

In this section, we will recall some useful properties of solutions to (1.2) in the periodic setting. Using the scaling transformation $u(t,x)\rightarrow \alpha \varepsilon u(\sqrt{\beta \mu }t,\sqrt{\beta \mu }x)$, equation (1.2) can be written as the following R-CH equation:

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle u_t-u_{xxt}+cu_x+3uu_x-\frac{\beta _0}{\beta }u_{xxx}+\frac{\omega _1}{\alpha ^2}u^2u_x+\frac{\omega _2}{\alpha ^3}u^3u_x=2u_xu_{xx}+uu_{xxx},\\ u(t,x)=u(t, x + 1), \qquad \forall \ t > 0, \, x \in \mathbb {R}. \end{array}\right. } \end{aligned}$$

(2.1)

Then, we convert the above equation into the following weak form:

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle u_t+uu_x+\frac{\beta _0}{\beta }u_x+G*\partial _x{ \left( \left( c-\frac{\beta _0}{\beta } \right) u+u^2+\frac{1}{2}u^2_x+\frac{\omega _1}{3\alpha ^2}u^3+\frac{\omega _2}{4\alpha ^3}u^4 \right) }=0,\\ u(t, x)=u(t, x + 1), \qquad \forall \ t > 0, \, x \in \mathbb {R}, \end{array}\right. } \end{aligned}$$

(2.2)

where $\displaystyle G(x)=\frac{\cosh (x-[x]-\frac{1}{2})}{2\sinh (\frac{1}{2})}$ (here [x] represents the largest integer part of x), which is the fundamental solution of $(1-\partial ^2_x)^{-1}$ on the unit circle $\mathbb {S} = \mathbb {R}/\mathbb {Z}$, that is for any $x \in \mathbb {S},$

$$\begin{aligned} (1-\partial _x^2)^{-1}f(x)&= (G*f)(x) =\int ^1_0 \frac{\cosh \big ((x-y)-[x-y]-{\frac{1}{2}}\big )}{2\sinh \big (\frac{1}{2}\big )}f(y)\hbox {d}y\nonumber \\&=\int ^x_0\frac{\cosh \big (x-y-{\frac{1}{2}}\big )}{2\sinh \left( \frac{1}{2}\right) }f(y)\hbox {d}y+ \int ^1_x\frac{\cosh \big (x-y+{\frac{1}{2}}\big )}{2\sinh \left( \frac{1}{2}\right) }f(y)\hbox {d}y. \end{aligned}$$

(2.3)

The following conservation law is useful to establish the result of wave breaking.

Lemma 2.1

Let $u_0\in H^s(\mathbb {S}), s>\frac{3}{2},$ and T be the maximal existence time of the solution u in the R-CH equation (2.2) with initial value $u(0) = u_0.$ Then, for all $t\in [0,T)$, we have

$$\begin{aligned} E(u)=\frac{1}{2}\int _{\mathbb {S}} \left( u^2+u_x^2\right) {\mathrm{d}}x = \frac{1}{2} \int _{\mathbb {S}}(u_0^2+u^2_{0,x}){\mathrm{d}}x \equiv E_0. \end{aligned}$$

Proof

To see this, it is observed that

$$\begin{aligned} \int _{\mathbb {S}}u^2u_{xxx}{\mathrm{d}}x= - \int _{\mathbb {S}}2uu_xu_{xx}{\mathrm{d}}x \end{aligned}$$

and

$$\begin{aligned} \frac{\beta _0}{\beta }\int _{\mathbb {S}}uu_{xxx}\hbox {d}x=\frac{\beta _0}{\beta }\int _{\mathbb {S}}u{\mathrm{d}}u_{xx}=-\frac{\beta _0}{2\beta }\int _{\mathbb {S}}(u^2_x)_x {\mathrm{d}}x=0. \end{aligned}$$

Multiplying the first equation of (2.1) by u and integrating by parts then yields the required conservation law, which implies that for any $t\in (0,T)$, $\displaystyle \Vert u(t)\Vert _{H^1}=\Vert u_0\Vert _{H^1}.$$\square$

One of important ingredients in our development is a local existence theory for the initial-value problem for the periodic R-CH equation (2.2), which may be similarly obtained as in [13, 16] (up to a slight modification) and the proof is omitted.

Lemma 2.2

Let $u_0\in H^s(\mathbb {S})$ with $s>\frac{3}{2}$. Then, there exist a positive time $T^*_{u_0}>0$ and a unique solution $u\in C([0,T^*_{u_0});H^s(\mathbb {S}))\bigcap C^1([0,T^*_{u_0});H^{s-1}(\mathbb {S}))$ to the periodic R-CH equation (2.2) with $u(0)=u_0$. Moreover, the life span $T^*_{u_0}$ does not depend on the regularity index s of the initial data $u_0$ and the solution u depends continuously on the initial value $u_0$.

Now, we return to the original R-CH equation (1.1), and let

$$\begin{aligned} \Vert u\Vert ^2_{X^{s+1}_\mu }=\Vert u\Vert ^2_{H^s}+\mu \beta \Vert \partial _x u\Vert ^2_{H^s}. \end{aligned}$$

For some $\mu _0>0$ and $M>0$, we define the Camassa–Holm regime

$$\begin{aligned} P_{\mu _0,M}:={(\varepsilon ,\mu ):0<\mu \le \mu _0,0<\varepsilon \le M\sqrt{\mu }}. \end{aligned}$$

By following exact approach in [13], we have the local well-posedness result without proof.

Corollary 2.3

Let $u_0\in H^{s}(\mathbb {S}),s>\frac{3}{2}$ and $\mu _0>0$. Then, there exist $T>0$ and a unique family of solutions $(u_{\varepsilon ,\mu }|_{(\varepsilon ,\mu )\in P_{\mu _0,M}})$ in $C([0,\frac{T}{\varepsilon }]$;$X^{s+1}(\mathbb {S}))$$\bigcap C^1([0,\frac{T}{\varepsilon }];X^{s}(\mathbb {S}))$ to the following periodic initial-value problem:

$$\begin{aligned} {\left\{ \begin{array}{ll} \partial _t u-\beta \mu \partial _tu_{xx}+cu_x+3\alpha \varepsilon uu_x-\beta _0\mu u_{xxx}+\omega _1\varepsilon ^2u^2u_x+\omega _2\varepsilon ^3u^3u_x\\ \qquad =\alpha \beta \varepsilon \mu (2u_xu_{xx}+uu_{xxx}), \qquad t > 0, \, x \in \mathbb {S}, \\ u(0, x)=u_0(x), \qquad x \in \mathbb {S}.\\ \end{array}\right. } \end{aligned}$$

(2.4)

In order to study the dynamics along the characteristics of the R-CH equation (1.1), we introduce the associated Lagrangian scales as

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle \frac{\hbox {d}q(t,x)}{\hbox {d}t}= u(t,q(t,x)),\\ q(0,x)=x, \end{array}\right. } \qquad x \in \mathbb {S},\quad t\in [0,T), \end{aligned}$$

(2.5)

where $u\in C^1([0,T),H^{s-1}(\mathbb {S}))$ is the solution to Eq. (2.2).

Lemma 2.4

[22] Suppose $u_0 \in H^s(\mathbb {S})$ with $s>\frac{3}{2}$, and let $T>0$ be the maximal existence time of the strong solution u to the corresponding the periodic R-CH equation (2.2). Then, equation (2.5) has a unique solution $q \in C^1([0,T);\mathbb {S})$ such that $q(t,\cdot )$ is an increasing diffeomorphism of $\mathbb {S}$ for all $(t,x)\in [0,T)\times \mathbb {S}$ with

$$\begin{aligned} q_x(t,x)=\exp \left( 2\int _0^t u_x(s,q(s,x))\,{\mathrm{d}}s\right) > 0. \end{aligned}$$

The following Sobolev estimate is crucial to obtain the optimal blow-up result.

Lemma 2.5

[28] For every $f\in H^1(\mathbb {S}),$ we have

$$\begin{aligned} \underset{x\in [0,1]}{\max }f^2(x)\le \kappa _1\int _{\mathbb {S}}(f^2+\epsilon ^2f_x^2){\mathrm{d}}x, \end{aligned}$$

where

$$\begin{aligned} \kappa _1=\frac{\cosh \left( \frac{1}{2\epsilon }\right) }{2\epsilon \sinh \left( \frac{1}{2\epsilon }\right) }, \end{aligned}$$

and $\kappa _1$ is the optimal constant which is obtained by the associated Green function defined by

$$\begin{aligned} G_1=\frac{\cosh \left( \frac{x}{\epsilon }-\frac{[x]}{\epsilon }-\frac{1}{2\epsilon }\right) }{2\epsilon \sinh \left( \frac{1}{2\epsilon }\right) }. \end{aligned}$$

In particular, when the parameter $\epsilon =1$, the constant $\kappa _1=\displaystyle \frac{e+1}{2(e-1)}$ is sharp.

3 Wave-breaking criterion and wave-breaking data

Using the energy estimates, it enables us to obtain the following wave-breaking criterion to the R-CH equation. The wave-breaking phenomena could be illustrated by choosing certain initial data.

Theorem 3.1

Let $u_0\in H^s(\mathbb {S})$ with $s>\frac{3}{2}$, and $T^*_{u_0}>0$ be the maximal existence time of the solution u to (2.2) with initial data $u_0$. Then, the corresponding solution u blows up in finite time if and only if

$$\begin{aligned} \lim _{t\rightarrow T^*_{u_0}}\;\inf _{x\in \mathbb {S}}{u_x(t,x)}=-\infty , \end{aligned}$$

(3.1)

that is, the solution breaks down in finite time $T^*_{u_0}.$

Proof

Applying Lemma 2.2 and a simple density argument, we only need to show that the theorem holds for some $s\ge 3$. Here, we assume $s=3$ to prove the above theorem. Multiplying the equation in (2.1) by $- u_{xx}$ and integrating by parts again, we obtain

$$\begin{aligned} \frac{1}{2}\frac{\hbox {d}}{\hbox {d}t}\Vert u_x\Vert ^2_{H^1}&=-\frac{3}{2}\int _{\mathbb {S}}u_x(u^2_x+u^2_{xx})\hbox {d}x + \int _{\mathbb {S}}\left( \frac{\omega _1}{\alpha ^2}u^2u_x+ \frac{\omega _2}{\alpha ^3}u^3u_x\right) u_{xx}\hbox {d}x\nonumber \\&\le -\frac{3}{2}\int _{\mathbb {S}}u_x(u^2_x+u^2_{xx})\hbox {d}x+\int _{\mathbb {S}}\left| \frac{\omega _1}{2\alpha ^2}u^2+ \frac{\omega _2}{2\alpha ^3}u^3\right| (u^2_x+u^2_{xx})\hbox {d}x. \end{aligned}$$

(3.2)

Assume that $T^*_{u_0}<+\infty$ and there exists $m_0 >0$ such that

$$\begin{aligned} u_x(t,x)\ge - m_0,\quad \forall (t,x)\in [0,T^*_{u_0})\times \mathbb {S}. \end{aligned}$$

(3.3)

It then follows from Lemmas 2.1 and 2.5 that

$$\begin{aligned}&\frac{\hbox {d}}{\hbox {d}t} \int _{\mathbb {S}}(u^2+2u^2_x+u^2_{xx})\hbox {d}x\nonumber \\&\quad \le \, \left( \frac{3}{2}M+\frac{|\omega _1|}{2\alpha ^2}\Vert u\Vert ^2_{L^\infty }+\frac{|\omega _2|}{2|\alpha |^3}\Vert u\Vert ^3_{L^\infty }\right) \int _{\mathbb {S}}(u^2_x+u^2_{xx})\hbox {d}x\nonumber \\&\quad \le \,C(1+ m_0 +\Vert u_0\Vert ^3_{H^1})\int _{\mathbb {S}}(u^2_x+u^2_{xx})\hbox {d}x, \end{aligned}$$

(3.4)

where we used the Sobolev embedding theorem $H^s(\mathbb {S})\hookrightarrow L^\infty (\mathbb {S})$(with $s>\frac{1}{2}$) in the last inequality. Applying Gronwall’s inequality to (3.4) yields for every $t\in [0,T^*_{u_0})$

$$\begin{aligned} \Vert u(t)\Vert ^2_{H^2}&\le 2\Vert u_0\Vert ^2_{H^2({\mathbb {S}})}e^{Ct(1+ m_0 +\Vert u_0\Vert ^3_{H^1})}\nonumber \\&\le 2\Vert u_0\Vert ^2_{H^2({\mathbb {S}})}e^{CT^{*}_{u_0}(1+ m_0 +\Vert u_0\Vert ^3_{H^1})}. \end{aligned}$$

(3.5)

Differentiating the first equation in (2.1) with respect to x, and multiplying the result equation by $- u_{xxx}$, then integrating by parts, we get

$$\begin{aligned} \frac{1}{2}&\frac{\hbox {d}}{\hbox {d}t}\int _{\mathbb {S}}(u^2_{xx}+u^2_{xxx})\hbox {d}x\\&\quad =-\frac{15}{2}\int _{\mathbb {S}}u_xu^2_{xx}\hbox {d}x-\frac{5}{2}\int _{\mathbb {S}} (u_xu^2_{xxx}) \hbox {d}x + \int _{\mathbb {S}}\left( \frac{\omega _1}{\alpha ^2}u^2u_x+\frac{\omega _2}{\alpha ^3}u^3u_x\right) _xu_{xxx} \hbox {d}x\\&\quad \le \,C(1+ m_0 +\Vert u\Vert ^3_{L^\infty })\int _{\mathbb {S}}(u^2_{xx}+u^2_{xxx})\hbox {d}x+C(\Vert u\Vert ^2_{L^\infty }+\Vert u\Vert ^4_{L^\infty })\Vert u_x\Vert ^4_{L^4}, \end{aligned}$$

where use has been made of the assumption in (3.3). It now follows from the Sobolev embedding theorem and the interpolation inequality $\Vert f\Vert _{L^4({\mathbb {S}})}\le C\Vert f\Vert ^{\frac{3}{4}}_{L^2({\mathbb {S}})}\Vert f_x\Vert ^{\frac{1}{4}}_{L^4({\mathbb {S}})}$ that

$$\begin{aligned}&\frac{\hbox {d}}{\hbox {d}t} \int _{\mathbb {S}}(u^2_{xx}+u^2_{xxx})\hbox {d}x\le C(1+ m_0 +\Vert u_0\Vert ^3_{H^1})\int _{\mathbb {S}}(u^2_{xx}+u^2_{xxx})\hbox {d}x\nonumber \\&\qquad +\,C\Vert u_0 \Vert ^5_{H^1}(1+\Vert u_0\Vert ^2_{H^1})\Vert u_{xx}\Vert _{L^2}\nonumber \\&\quad \le \,C(1+ m_0 +\Vert u_0\Vert ^{14}_{H^1})\int _{\mathbb {S}}(u^2_{xx}+u^2_{xxx})\hbox {d}x. \end{aligned}$$

(3.6)

Hence, applying Gronwall’s inequality to (3.6) implies that for every $t\in [0,T^*_{u_0})$

$$\begin{aligned} \int _{\mathbb {S}}(u^2_{xx}+u^2_{xxx})\hbox {d}x\le e^{C(1+ m_0 +\Vert u_0\Vert ^{14}_{H^1})T^*_{u_0}}\int _{\mathbb {S}}(u^2_{0xx}+u^2_{0xxx})\hbox {d}x. \end{aligned}$$

Combining the above estimate together with (3.5) then yields

$$\begin{aligned} \Vert u(t)\Vert ^2_{H^3(\mathbb {S})}\le 3\Vert u_0\Vert ^2_{H^3(\mathbb {S})}e^{C(1+ m_0 +\Vert u_0\Vert ^{14}_{H^1})T^*_{u_0}}. \end{aligned}$$

This contradicts the assumption on the maximal existence time $T^*_{u_0}<+\infty .$ Conversely, the Sobolev embedding theorem $H^s\hookrightarrow L^\infty ,(s>\frac{1}{2})$ implies that if (3.1) holds, the corresponding solution u blows up in finite time. This completes the proof of Theorem 3.1. $\square$

It is also found that the solution of (2.2) cannot break up in any time because of the conserved energy.

Theorem 3.2

Suppose $u_0\in H^s$ with $s>\frac{3}{2}$. Let $T>0$ be the maximal time of existence of the corresponding solution u(t, x) of (2.2) with the initial data $u_0$. Then, for any $t \in [0, T)$

$$\begin{aligned} \sup _{x\in \mathbb {S}}u_x(t,x)\le \Vert \partial _x u_{0}\Vert _{L^\infty }+(2K)^{\frac{1}{2}}, \end{aligned}$$

where the constant K is given by $\displaystyle K=K_0+\frac{e^{\frac{1}{2}}}{2}K_1+\frac{3e^{\frac{3}{2}}}{2}K_1$ with

$$\begin{aligned} E_0&=\frac{1}{2}\int _{\mathbb {S}}(u^2_0+u^2_{0, x}) {\mathrm{d}}x,\\ K_0&= \left( \frac{e+1}{2(e-1)} \right) E_0+ \left| c-\frac{\beta _0}{\beta } \right| \left( \frac{e+1}{2(e-1)} \right) ^{\frac{1}{2}}E^{\frac{1}{2}}_0\\&\quad +\frac{|\omega _1|}{3\alpha ^2}\left( \frac{e+1}{2(e-1)} \right) ^{\frac{3}{2}}E^{\frac{3}{2}}_0+\frac{|\omega _2|}{4\alpha ^3}\left( \frac{e+1}{2(e-1)} \right) ^2 E^2_0, \quad \mathrm{and} \\ K_1&= \left| c-\frac{\beta _0}{\beta } \right| \left( \frac{e+1}{2(e-1)}\right) ^{\frac{1}{2}}E^{\frac{1}{2}}_0+ E_0 \\&\quad +\,\frac{|\omega _1|}{3\alpha ^2} \left( \frac{e+1}{2(e-1)} \right) ^{\frac{1}{2}}E^{\frac{3}{2}}_0+\frac{\omega _2}{4\alpha ^3}\left( \frac{e+1}{2(e-1)}\right) E^2_0. \end{aligned}$$

Proof

Applying the translation $u(t,x)\rightarrow u(t,x-\frac{\beta _0}{\beta }t)$ to Eq. (2.2) yields the equation in the form

$$\begin{aligned} u_t+uu_x+G_{x}*\left( \left( c-\frac{\beta _0}{\beta }\right) u+u^2+\frac{1}{2}u^2_x+\frac{\omega _1}{3\alpha ^2}u^3+\frac{\omega _2}{4\alpha ^3}u^4\right) =0. \end{aligned}$$

Taking the derivative $\partial _x$ to the above equation, we have

$$\begin{aligned} u_{xt}+uu_{xx}&=-\frac{1}{2}u^2_x+u^2+\left( c-\frac{\beta _0}{\beta }\right) u+\frac{\omega _1}{3\alpha ^2}u^3+\frac{\omega _2}{4\alpha ^3}u^4\nonumber \\&\quad -\,G*\left( \left( c-\frac{\beta _0}{\beta }\right) u+u^2+\frac{1}{2}u^2_x+\frac{\omega _1}{3\alpha ^2}u^3+\frac{\omega _2}{4\alpha ^3}u^4 \right) . \end{aligned}$$

(3.7)

Let $M_0 (t, x) =u_x(t,q(t, x))$ with the characteristic curve q(t, x) defined in (2.5). Then, we obtain the following equation:

$$\begin{aligned} \frac{\partial M_0(t,q)}{\partial t}&=-\frac{1}{2}M_0^2(t, q(t,x)) +u^2+\left( c-\frac{\beta _0}{\beta }\right) u+\frac{\omega _1}{3\alpha ^2}u^3+\frac{\omega _2}{4\alpha ^3}u^4(q)\nonumber \\&\quad -\,G*\left( \left( c-\frac{\beta _0}{\beta }\right) u+u^2+\frac{1}{2}u^2_x+\frac{\omega _1}{3\alpha ^2}u^3+\frac{\omega _2}{4\alpha ^3}u^4\right) (q), \end{aligned}$$

(3.8)

where

$$\begin{aligned} (G*f)(x)&={\frac{e^{x-\frac{1}{2}}}{2}}{\int _0^x e^{-y}f(y)\hbox {d}y}+{\frac{e^{{\frac{1}{2}}-x}}{2}}\int ^x_0 e^y f(y)\hbox {d}y\nonumber \\&\quad +\,{\frac{e^{x+\frac{1}{2}}}{2}}{\int _x^1 e^{-y}f(y)\hbox {d}y}+{\frac{e^{{-\frac{1}{2}}-x}}{2}}\int ^1_x e^y f(y)\hbox {d}y. \end{aligned}$$

(3.9)

Let

$$\begin{aligned} H(u(t, q(t,x))= & {} u^2+\left( c-\frac{\beta _0}{\beta }\right) u+\frac{\omega _1}{3\alpha ^2}u^3+\frac{\omega _2}{4\alpha ^3}u^4(q) -G*\left( \left( c-\frac{\beta _0}{\beta }\right) u+u^2\right. \\&\left. +\frac{1}{2}u^2_x+\frac{\omega _1}{3\alpha ^2}u^3+\frac{\omega _2}{4\alpha ^3}u^4\right) (q). \end{aligned}$$

Then, we have

$$\begin{aligned} \frac{\partial M_0(t,q)}{\partial t} = -\frac{1}{2}M_0^2(t, q(t,x)) +H(u (t, q(t,x))). \end{aligned}$$

On the other hand, a direct computation reveals that

$$\begin{aligned}&\left| u^2+\left( c-\frac{\beta _0}{\beta }\right) u+\frac{\omega _1}{3\alpha ^2}u^3+\frac{\omega _2}{4\alpha ^3}u^4 \right| \nonumber \\&\quad \le \, \Vert u\Vert ^2_{L^\infty }+\left| c-\frac{\beta _0}{\beta }\right| \Vert u\Vert _{L^\infty }+\frac{|\omega _1|}{3\alpha ^2}\Vert u\Vert ^3_{L^\infty } +\frac{|\omega _2|}{4\alpha ^3}\Vert u\Vert ^4_{L^\infty }\nonumber \\&\quad \le \,\left( \frac{e+1}{2(e-1)} \right) (2E_0)+ \left| c-\frac{\beta _0}{\beta }\right| \left( \frac{e+1}{2(e-1)} \right) ^{\frac{1}{2}}{(2E_0)}^{\frac{1}{2}} +\frac{|\omega _1|}{3\alpha ^2}\left( \frac{e+1}{2(e-1)} \right) ^{\frac{3}{2}}{(2E_0)}^{\frac{3}{2}}\nonumber \\&\qquad +\frac{|\omega _2|}{4\alpha ^3}\left( \frac{e+1}{2(e-1)} \right) ^2 {(2E_0)}^2\nonumber \\&\quad =\frac{(e+1)E_0}{e-1}+ \left| c-\frac{\beta _0}{\beta } \right| \left( \frac{(e+1)E_0}{e-1}\right) ^{\frac{1}{2}} +\frac{|\omega _1|}{3\alpha ^2}\left( \frac{(e+1)E_0}{e-1}\right) ^{\frac{3}{2}} +\frac{|\omega _2|}{4\alpha ^3}\left( \frac{(e+1)E_0}{e-1} \right) ^2 \nonumber \\&\quad =K_0 \end{aligned}$$

(3.10)

and

$$\begin{aligned}&\left| \frac{e^{x-\frac{1}{2}}}{2} {\int ^x_0} e^{-y}\left( \left( c-\frac{\beta _0}{\beta }\right) u+u^2+\frac{1}{2}u^2_x+\frac{\omega _1}{3\alpha ^2}u^3+\frac{\omega _2}{4\alpha ^3}u^4\right) \hbox {d}y \right| \nonumber \\&\quad \le \,\frac{e^{\frac{1}{2}}}{2}\left( \left| c-\frac{\beta _0}{\beta } \right| \left( \frac{(e+1)E_0}{e-1} \right) ^{\frac{1}{2}}+2E_0 +\frac{|\omega _1|}{3\alpha ^2}\left( \frac{(e+1)E_0}{e-1}\right) ^{\frac{3}{2}} \right. \nonumber \\&\qquad \left. +\frac{|\omega _2|}{4|\alpha |^3} \left( \frac{(e+1)E_0}{e-1}\right) ^2 \right) \nonumber \\&\quad =\frac{e^{\frac{1}{2}}}{2}K_1. \end{aligned}$$

(3.11)

Similarly,

$$\begin{aligned} \left| \frac{e^{\frac{1}{2}-x}}{2} {\int ^x_0} e^{y}\left( \left( c-\frac{\beta _0}{\beta }\right) u+u^2+\frac{1}{2}u^2_x+\frac{\omega _1}{3\alpha ^2}u^3+\frac{\omega _2}{4\alpha ^3}u^4\right) \hbox {d}y \right|&\le \frac{e^{\frac{3}{2}}}{2}K_1,\nonumber \\ \left| \frac{e^{x+\frac{1}{2}}}{2} {\int ^1_x} e^{-y}\left( \left( c-\frac{\beta _0}{\beta }\right) u+u^2+\frac{1}{2}u^2_x+\frac{\omega _1}{3\alpha ^2}u^3+\frac{\omega _2}{4\alpha ^3}u^4\right) \hbox {d}y \right|&\le \frac{e^{\frac{3}{2}}}{2}K_1, \quad \mathrm{and} \nonumber \\ \left| \frac{e^{-x-\frac{1}{2}}}{2} {\int ^1_x} e^{y}\left( \left( c-\frac{\beta _0}{\beta }\right) u+u^2+\frac{1}{2}u^2_x+\frac{\omega _1}{3\alpha ^2}u^3+\frac{\omega _2}{4\alpha ^3}u^4\right) \hbox {d}y \right|&\le \frac{e^{\frac{3}{2}}}{2}K_1. \end{aligned}$$

(3.12)

Putting Eqs. (3.10), (3.11) and (3.12) into (3.8), it follows that

$$\begin{aligned} H(u(t, q(t,x))\le K, \end{aligned}$$

where the constant K is defined by

$$\begin{aligned} K =K_0+\frac{e^{\frac{1}{2}}}{2}K_1+\frac{3e^{\frac{3}{2}}}{2}K_1. \end{aligned}$$

Hence, there appears the relation

$$\begin{aligned} -\frac{1}{2}M_0^2(t, q(t, x)) - K \le \frac{\partial M_0(t,q)}{\partial t} \le -\frac{1}{2}M_0^2(t, q(t, x)) +K. \end{aligned}$$

(3.13)

For any given $x \in \mathbb {S}$, we now consider a function P(t) defined by

$$\begin{aligned} P(t)=M_0(t)-\Vert u_{0,x}\Vert _{L^\infty }-(2K)^{\frac{1}{2}}. \end{aligned}$$

Note that P(t) is a $C^1$-differential function in [0, T) and satisfies

$$\begin{aligned} P(0)=M_0(0)-\Vert u_{0,x}\Vert _{L^\infty }-(2K)^{\frac{1}{2}}\le 0. \end{aligned}$$

We now claim that $\displaystyle P(t)\le 0,$ for any $t\in [0,T),$ by using the argument of continuous deduction. Indeed, since $M_0(t)$ is continuous on [0, T), if the above inequality does not hold, we can find a $t_0\in (0,T)$ such that $P(t_0)>0.$

Denote now that

$$\begin{aligned} t_1=\max \{t<t_0:P(t) = 0\}. \end{aligned}$$

Then, $P(t_1)=0$ and $P'(t_1)\ge 0.$ Consequently, $M_0'(t_1)\ge 0.$ On the other hand, in view of (3.13), we have

$$\begin{aligned} M_0'(t_1)&\le -\frac{1}{2}M_0^2(t_1)+K\\&\le -\frac{1}{2} \left( \Vert u_{0,x}\Vert _{L^\infty }+(2K)^{\frac{1}{2}} \right) ^2+K<0, \end{aligned}$$

which yields a contradiction. Consequently, it is concluded that for any $t \in [0, T)$

$$\begin{aligned} \sup _{x\in \mathbb {S}}u_x(t,x) = \sup _{x\in \mathbb {S}}M_0(t, q(t, x)) \le \Vert \partial _x u_{0}\Vert _{L^\infty }+(2K)^{\frac{1}{2}}. \end{aligned}$$

The proof of Theorem 3.2 is thus complete. $\square$

Attention is now given to searching initial data to illustrate the wave-breaking phenomena. It is known that a local-in-space type of blow-up mechanism in [4] (see also [7]) considerably simplifies the classical results and characterizes how the local structure of the solution both in periodic and in non-periodic cases can affect the formation of singularities. It is our purpose to study the issue that under what kind of condition the particular periodic initial data could generate the wave-breaking solution. We first present some notations and useful results obtained in [4] before stating our wave-breaking result.

For any real constant $\gamma$, define $I(\gamma )\ge -\infty$ by

$$\begin{aligned} I(\gamma )=\inf \left\{ \, \int ^1_0 (G+\gamma G_x)* (2u^2+u^2_x)\hbox {d}x \; \Big | \, u\in H^1(\mathbb {S}),u(0)=u(1)=1 \, \right\} , \end{aligned}$$

and the quantity $\gamma ^*\in [0,+\infty )$ by

$$\begin{aligned} \gamma ^*=\inf \{\gamma \in (0,+\infty ) \, | \, \gamma ^2+I(\gamma )-2\ge 0 \} \end{aligned}$$

which the usual convention that $\gamma ^*=+\infty$ if the infimum is taken on the empty set.

It is known in [4] that $I(\gamma )$ is even with respect to the variable $\gamma \in \mathbb {R}$ and $I(\gamma )>-\infty$ if and only if

$$\begin{aligned} -\frac{e+1}{e-1}\le \gamma \le \frac{e+1}{e-1}. \end{aligned}$$

Particularly, if $|\gamma |<\frac{e+1}{e-1}$, then $I(\gamma )$ is in fact a minimum with only one minimizer $u\in H^1(\mathbb {S})$ with $u(0)=u(1) = 1$. In addition, $\gamma ^*$ was computed numerically as the zero point of the function $\gamma \rightarrow \gamma ^2+I(\gamma )-2$ by

$$\begin{aligned} \gamma ^*=0.513\ldots . \end{aligned}$$

(3.14)

The following convolution estimate is crucial for the blow-up analysis.

Lemma 3.3

[4] For any $\gamma \in \mathbb {R}$ and all $u\in H^1(\mathbb {S})$, the following convolution estimate holds

$$\begin{aligned} (G\pm \gamma G_x)*(2u^2+u^2_x)(x)\ge I(\gamma )u^2(x),\quad \quad \forall x\in \mathbb {S}, \end{aligned}$$

and $I(\gamma )$ is the best possible constant.

We are now in a position to state the wave-breaking result to the R-CH equation (2.2).

Theorem 3.4

Suppose that $u_0\in H^s(\mathbb {S})$ with $s>\frac{3}{2}$. Let $T_0>0$ be the maximal time of existence of the corresponding solution u to (2.2) with the initial data $u_0$. Assume there is a point $x_0\in \mathbb {S}$ such that

$$\begin{aligned} u_{0, x}(x_0)<- \left| \gamma ^* \left( u_0(x_0) - \frac{k}{2} \right) \right| -\sqrt{2}C_0, \end{aligned}$$

where the constant $k = \frac{\beta _0}{\beta } - c,$$\gamma ^*$ is defined in (3.14) and $C_0>0$ is defined by

$$\begin{aligned} C^2_0 = \left( \frac{1}{2}+(|\gamma ^*|+1)(e^{\frac{1}{2}}+e^{\frac{3}{2}})\right) \left( \frac{|\omega _1|}{3\alpha ^2}\left( \frac{(e+1)E_0}{e-1} \right) ^{\frac{3}{2}} +\frac{|\omega _2|}{2|\alpha |^3} \left( \frac{(e+1)E_0}{e-1} \right) ^{2}\right) \end{aligned}$$

with

$$\begin{aligned} E_0=\frac{1}{2}\int _{\mathbb {S}}(u^2_0+u^2_x)\hbox {d}x. \end{aligned}$$

Then, the solution u(t, x) of the R-CH equation (2.2) breaks down such that

$$\begin{aligned} \lim _{t\rightarrow T_0^{-}}\;\inf _{x\in \mathbb {S}} \{ u_x(t,x) \}=-\infty \end{aligned}$$

at the time

$$\begin{aligned} T_0\le \frac{2}{\sqrt{u^2_{0,x}(x_0) -\left( \gamma ^* \left( u_{0}(x_0)- \frac{k}{2}\right) \right) ^2}-\sqrt{2}C_0}< \infty . \end{aligned}$$

Remark 3.5

In the case of the rotation frequency $\Omega = 0$, or the wave speed $c=1$, the corresponding constant $C_0$ in the theorem must be zero, because the parameters $\omega _1$ and $\omega _2$ vanish. The assumption on the wave breaking is then back to the case of the classical CH equation.

Proof

In view of (3.7), we have

$$\begin{aligned} u_{xt}+uu_{xx}&=-\frac{1}{2}u^2_x+u^2+\left( c-\frac{\beta _0}{\beta }\right) u+\frac{\omega _1}{3\alpha ^2}u^3+\frac{\omega _2}{4\alpha ^3}u^4\\&\quad -\,G*\big (\big (c-\frac{\beta _0}{\beta }\big )u+u^2+\frac{1}{2}u^2_x+\frac{\omega _1}{3\alpha ^2}u^3+\frac{\omega _2}{4\alpha ^3}u^4\big )\\&=-\frac{1}{2}u^2_x+ \left( u - \frac{k}{2} \right) ^2 +\frac{\omega _1}{3\alpha ^2}u^3+\frac{\omega _2}{4\alpha ^3}u^4\\&\quad -\,G*\left( \left( u - \frac{k}{2} \right) ^2 +\frac{1}{2}u^2_x+\frac{\omega _1}{3\alpha ^2}u^3+\frac{\omega _2}{4\alpha ^3}u^4\right) . \end{aligned}$$

Along with the trajectory of q(t, x), then using (3.7) and the above equation gives

$$\begin{aligned} \frac{\partial u(t,q)}{\hbox {d}t}&=-G_{x}*\left( \left( u - \frac{k}{2} \right) ^2 +\frac{1}{2}u^2_x+ \frac{\omega _1}{3\alpha ^2}u^3+\frac{\omega _2}{4\alpha ^3}u^4\right) ,\\ \frac{\partial u_x(t,q)}{\hbox {d}t}&=-\frac{1}{2}u^2_x+\left( u - \frac{k}{2} \right) ^2 + \frac{\omega _1}{3\alpha ^2}u^3+\frac{\omega _2}{4\alpha ^3}u^4\\&\quad -\,G*\left( \left( u - \frac{k}{2} \right) ^2 +\frac{1}{2}u^2_x+ \frac{\omega _1}{3\alpha ^2}u^3+\frac{\omega _2}{4\alpha ^3}u^4\right) . \end{aligned}$$

Denote now two functions M(t) and N(t) at $(t,q(t,x_0))$ by

$$\begin{aligned} M(t)= & {} \gamma ^* \left( u(t,q(t, x_0)) - \frac{k}{2} \right) - u_x(t,q(t, x_0)) \quad \mathrm{and}\\ N(t)= & {} \gamma ^* \left( u(t,q(t, x_0)) - \frac{k}{2} \right) +u_x(t,q(t, x_0)). \end{aligned}$$

It then follows from expressions $M(t,q(t,x_0))$ and $N(t,q(t,x_0))$ that

$$\begin{aligned} \frac{\hbox {d}M}{\hbox {d}t}&=\frac{1}{2}u^2_x- \left( u - \frac{k}{2} \right) ^2 -\frac{\omega _1}{3\alpha ^2}u^3-\frac{\omega _2}{4\alpha ^3}u^4\nonumber \\&\quad -\,\gamma ^* G_{x}*\left( \left( u - \frac{k}{2} \right) ^2 +\frac{1}{2}u^2_x+ \frac{\omega _1}{3\alpha ^2}u^3+\frac{\omega _2}{4\alpha ^3}u^4 \right) \nonumber \\&\quad +\,G*\left( \left( u - \frac{k}{2} \right) ^2 +\frac{1}{2}u^2_x+ \frac{\omega _1}{3\alpha ^2}u^3+\frac{\omega _2}{4\alpha ^3}u^4\right) , \end{aligned}$$

(3.15)

and

$$\begin{aligned} \frac{\hbox {d}N}{\hbox {d}t}&=-\frac{1}{2}u^2_x+ \left( u - \frac{k}{2} \right) ^2 +\frac{\omega _1}{3\alpha ^2}u^3+\frac{\omega _2}{4\alpha ^3}u^4\\&\quad -\,\gamma ^* G_{x}*\left( \left( u - \frac{k}{2} \right) ^2 +\frac{1}{2}u^2_x+ \frac{\omega _1}{3\alpha ^2}u^3+\frac{\omega _2}{4\alpha ^3}u^4\right) \\&\quad -\,G*\left( \left( u - \frac{k}{2} \right) ^2 +\frac{1}{2}u^2_x+ \frac{\omega _1}{3\alpha ^2}u^3+\frac{\omega _2}{4\alpha ^3}u^4\right) . \end{aligned}$$

Then, using Lemma 3.3, we have

$$\begin{aligned} \frac{\hbox {d}M}{\hbox {d}t}&=\frac{1}{2}\left( u^2_x-2 \left( u - \frac{k}{2} \right) ^2-\frac{2\omega _1}{3\alpha ^2}u^3-\frac{\omega _2}{2\alpha ^3}u^4\right) \nonumber \\&\quad -\,\frac{1}{2} \gamma ^* G_{x}*\left( 2 \left( u - \frac{k}{2} \right) ^2 +u^2_x+ \frac{2\omega _1}{3\alpha ^2}u^3+\frac{\omega _2}{2\alpha ^3}u^4\right) \nonumber \\&\quad +\,\frac{1}{2} G*\left( 2 \left( u - \frac{k}{2} \right) ^2+u^2_x+ \frac{2\omega _1}{3\alpha ^2}u^3+\frac{\omega _2}{2\alpha ^3}u^4\right) \nonumber \\&\ge \frac{1}{2}\left( u^2_x-2\left( u - \frac{k}{2} \right) ^2 +I(\gamma ^*)\left( u - \frac{k}{2} \right) ^2 -\frac{2\omega _1}{3\alpha ^2}u^3-\frac{\omega _2}{2\alpha ^3}u^4\right) \nonumber \\&\quad +\,\frac{1}{2} (G - \gamma ^* G_{x})*\left( \frac{2\omega _1}{3\alpha ^2}u^3+\frac{\omega _2}{2\alpha ^3}u^4\right) . \end{aligned}$$

(3.16)

Because $I(\gamma ^*) = 2-(\gamma ^*)^2$, it must be the case

$$\begin{aligned} \frac{\hbox {d}M}{\hbox {d}t}&\ge \frac{1}{2}\left( u^2_x-(\gamma ^*)^2 \left( u - \frac{k}{2} \right) ^2 -\frac{2\omega _1}{3\alpha ^2}u^3-\frac{\omega _2}{2\alpha ^3}u^4\right) \nonumber \\&\quad +\,\frac{1}{2} (G - \gamma ^* G_{x})*\left( \frac{2\omega _1}{3\alpha ^2}u^3+\frac{\omega _2}{2\alpha ^3}u^4\right) \nonumber \\&=-\frac{1}{2} \left( \gamma ^* \left( u - \frac{k}{2} \right) -u_x \right) \left( \gamma ^* \left( u - \frac{k}{2} \right) + u_x \right) +\frac{1}{2}\left( -\frac{2\omega _1}{3\alpha ^2}u^3-\frac{\omega _2}{2\alpha ^3}u^4\right) \nonumber \\&\quad +\,\frac{1}{2} (G -\gamma ^* G_{x})*\left( \frac{2\omega _1}{3\alpha ^2}u^3+\frac{\omega _2}{2\alpha ^3}u^4\right) . \end{aligned}$$

(3.17)

In view of (3.9) and applying Lemma 2.5, there appears the relation

$$\begin{aligned}&\left| \frac{1}{2}\left( -\frac{2\omega _1}{3\alpha ^2}u^3-\frac{\omega _2}{2\alpha ^3}u^4\right) + \frac{1}{2} (G - \gamma ^* G_{x})*\left( \frac{2\omega _1}{3\alpha ^2}u^3+\frac{\omega _2}{2\alpha ^3}u^4\right) \right| \nonumber \\&\quad \le \,\left( \frac{1}{2}+(|\gamma ^*|+1)\left( e^{\frac{1}{2}}+e^{\frac{3}{2}} \right) \right) \left( \frac{|\omega _1|}{3\alpha ^2}\Vert u\Vert ^3_{L^\infty }+\frac{|\omega _2|}{2|\alpha |^3}\Vert u\Vert ^4_{L^\infty }\right) \nonumber \\&\quad = \left( \frac{1}{2}+(|\gamma ^*|+1)\left( e^{\frac{1}{2}}+e^{\frac{3}{2}}\right) \right) \left( \frac{|\omega _1|}{3\alpha ^2}\left( \frac{(e+1)E_0}{e-1} \right) ^{\frac{3}{2}} +\frac{|\omega _2|}{2|\alpha |^3} \left( \frac{(e+1)E_0}{e-1} \right) ^{2}\right) \nonumber \\&\quad =C^2_0. \end{aligned}$$

(3.18)

It is then inferred from (3.17) that

$$\begin{aligned} \frac{\hbox {d}M}{\hbox {d}t}\ge -\frac{1}{2}MN-C^2_0. \end{aligned}$$

(3.19)

With the same approach, we have

$$\begin{aligned} \frac{\hbox {d}N}{\hbox {d}t}\le \frac{1}{2}MN+C^2_0. \end{aligned}$$

(3.20)

By the assumptions on $u_0(x_0)$, it is easy to see that

$$\begin{aligned} M(0)=\gamma ^* \left( u_0(x_0) - \frac{k}{2} \right) -u_{0,x}(x_0)>0,\quad N(0)=\gamma ^* \left( u_0(x_0) - \frac{k}{2} \right) + u_{0,x}(x_0)<0, \end{aligned}$$

and

$$\begin{aligned} \frac{1}{2}M(0)N(0)+C^2_0<0. \end{aligned}$$

By the continuity of M(t) and N(t), it then ensures that

$$\begin{aligned} \frac{\hbox {d}M}{\hbox {d}t}>0,\quad \frac{\hbox {d}N}{\hbox {d}t}<0,\quad \forall t\in [0,T). \end{aligned}$$

This in turn implies that

$$\begin{aligned} M(t)>M(0)>0,\quad N(t)<N(0)<0,\quad \forall t\in [0,T). \end{aligned}$$

Let $h(t)=\sqrt{-M(t)N(t)}$. It then follows that

$$\begin{aligned} \frac{\hbox {d}h}{\hbox {d}t}&= \frac{-M'(t)N(t)-M(t)N'(t)}{2h}\ge \frac{\left( -\frac{1}{2}MN-C^2_0\right) (-N)-M\left( \frac{1}{2}MN+C^2_0\right) }{2h}\\&=\frac{M-N}{2h}\left( -\frac{1}{2}MN-C^2_0\right) . \end{aligned}$$

Using the estimate $\displaystyle \frac{M-N}{2h}\ge 1$ and the fact that $h+\sqrt{2}C_0>h-\sqrt{2}C_0>0$, we obtain the following differential inequalities:

$$\begin{aligned} \frac{\hbox {d}h}{\hbox {d}t}\ge -\frac{1}{2}MN-C^2_0=\frac{1}{2}(h-\sqrt{2}C_0)(h+\sqrt{2}C_0)\ge \frac{1}{2}(h-\sqrt{2}C_0)^2. \end{aligned}$$

Hence, solving this inequality implies the wave breaks

$$\begin{aligned} \lim _{t\rightarrow T_0^{-}}\;h(t, q(t, x_0)) = \infty \end{aligned}$$

at the wave-breaking time

$$\begin{aligned} T_0\le \frac{2}{\sqrt{u^2_{0,x}(x_0) -\left( \gamma ^*\left( u_{0}(x_0)- \frac{k}{2}\right) \right) ^2}-\sqrt{2}C_0}< \infty . \end{aligned}$$

Using the fact that $\displaystyle - u_x(t, q(t, x_0)) = \frac{1}{2}(M-N) \ge h(t, q(t, x_0)),$ this in turn implies there exists $T_0<\infty$, such that

$$\begin{aligned} \lim _{t\rightarrow T_0^{-}}\;\inf _{x\in \mathbb {S}} \{ u_x(t,x) \}=-\infty . \end{aligned}$$

The proof of Theorem 3.4 is thus complete. $\square$

Remark 3.6

Returning to the original scale, our assumption for the wave breaking becomes

$$\begin{aligned} \sqrt{\beta \mu }u_{0,x}(\sqrt{\beta \mu }x_0)+ \left| \gamma ^* \left( u_0(\sqrt{\beta \mu }x_0) - \frac{k}{2} \right) \right| <-\frac{\sqrt{2}}{\alpha \varepsilon }C_1. \end{aligned}$$

Note that when $\Omega$ increases, $\alpha$ and $\beta$ decrease. It is then observed that with effect of the Earth rotation, a worse initial data $u_0(x_0)$ are required to make the breaking wave happen. On the other hand, in the original scale, we have the blow-up time $T_1$ bounded by

$$\begin{aligned} T_1\le \frac{2}{\alpha \varepsilon \left( \sqrt{\beta \mu u^2_{0,x}(\sqrt{\beta \mu }x_0)-\left( \gamma ^* \left( u_0(\sqrt{\beta \mu }x_0)- \frac{k}{2}\right) \right) ^2}-\frac{\sqrt{2}}{\alpha \varepsilon }C_1\right) }, \end{aligned}$$

where

$$\begin{aligned} C^2_1 = \left( \frac{1}{2}+(|\gamma ^*|+1)\left( e^{\frac{1}{2}}+e^{\frac{3}{2}}\right) \right) \left( \frac{|\omega _1|}{3\alpha ^2}\left( \frac{(e+1){\alpha ^2\varepsilon ^2}E_0}{e-1}\right) ^{\frac{3}{2}} +\frac{|\omega _2|}{2|\alpha |^3}\left( \frac{(e+1){\alpha ^2\varepsilon ^2}E_0}{e-1}\right) ^{2}\right) \end{aligned}$$

with

$$\begin{aligned} E(u_0)=\frac{1}{\alpha ^2\varepsilon ^2}E_0(\alpha \varepsilon u_0(\sqrt{\beta \mu }x_0)), \end{aligned}$$

which thus implies that a longer time is required for wave to break down when effect of the Earth rotation is considered.

The blow-up rate of the solution of (2.2) can be determined in the following result.

Corollary 3.7

Let u be the solution of the periodic R-CH equation (2.2) with initial data $u_0\in H^s({\mathbb {S}})$ with $s>\frac{3}{2}$. Assume there is a point $x_0\in \mathbb {S}$ such that

$$\begin{aligned} u_{0, x}(x_0)<- \left| \gamma ^* \left( u_0(x_0) - \frac{k}{2} \right) \right| -\sqrt{2}C_0. \end{aligned}$$

Let $T_0>0$ be the blow-up time of existence of the corresponding solution u(t, x) with the initial data $u_0$. Then, the blow-up rate to the corresponding solution at $T_0$ is determined by

$$\begin{aligned} \lim _{t\rightarrow T_0^-} \left( \inf _{x\in \mathbb {S}} \{ u_x(t,x) \}(T_0-t)\right) =-2. \end{aligned}$$

with the constant K defined in Theorem 3.2.

To prove Corollary 3.7, we need the following lemma due to Constantin and Escher [9]

Lemma 3.8

[9] Let $T > 0$ and $v \in C^1([0, T ); H^2(\mathbb {S})).$ Then, for every $t \in [0, T ),$ there exists at least one point $\xi (t) \in \mathbb {S}$ with

$$\begin{aligned} I (t) := \inf _{x \in \mathbb {S}} \{ v_x (t, x) \} = v_x (t, \xi (t)). \end{aligned}$$

The function I(t) is absolutely continuous on (0, T) with

$$\begin{aligned} \frac{\hbox {d}I(t)}{{\text {d}}t} = v_{t x} (t, \xi (t)), \quad a. \ e. \; \mathrm{on} \; (0, T ). \end{aligned}$$

Proof of Corollary 3.7

By Lemma 3.8, given $t \in [0, T_0),$ let $x_0(t) \in \mathbb {S}$ be such that

$$\begin{aligned} u_x(t, x_0(t)) = \inf _{x \in \mathbb {S}} \{u_x (t, x) \} \end{aligned}$$

which implies $u_{x x} (t, x_0(t)) = 0, \,$ a.e. on $(0, T_0).$ Let $M_1 (t) = u_x(t, x_0(t))$. In view of (3.13), there appears the relation

$$\begin{aligned} -\frac{1}{2}M_1^2(t) -K\le \frac{\hbox {d}M_1(t)}{\hbox {d}t} \le -\frac{1}{2}M_1^2(t) + K, \quad a. \ e. \; t \in (0, T_0). \end{aligned}$$

Choose $0<\varepsilon <\frac{1}{2}$. Since $M_1(t) \rightarrow -\infty$ as $t\rightarrow T_0^{-}$, we can find $t_0\in (0, T_0)$ such that

$$\begin{aligned} M_1(t_0)<-\sqrt{2K+\frac{K}{\varepsilon }}<-\sqrt{\frac{K}{\varepsilon }},\quad \quad t\in [t_0,T_0). \end{aligned}$$

This in turn implies that

$$\begin{aligned} \frac{1}{2}-\varepsilon<\frac{\hbox {d}}{\hbox {d}t}\left( \frac{1}{M_1(t)} \right) <\frac{1}{2}+\varepsilon ,\quad \quad a. \ e. \; t\in [t_0, T_0). \end{aligned}$$

Integrating the above relation on $(t, T_0)$ with $t\in [t_0,T_0)$ and noticing that $M_1(t)\rightarrow -\infty$ as $t\rightarrow T_0^-$, we obtain

$$\begin{aligned} \left( \frac{1}{2}-\varepsilon \right) (T_0-t)<-\frac{1}{M_1(t)}< \left( \frac{1}{2}+\varepsilon \right) (T_0-t). \end{aligned}$$

Since $\varepsilon \in (0,\frac{1}{2})$ is arbitrary, the above inequality implies the following equation:

$$\begin{aligned} \lim _{t\rightarrow T_0^-}(\inf _{x\in \mathbb {S}}\{u_x(t,x)\} (T_0-t))=-2. \end{aligned}$$

This completes the proof of Corollary 3.7. $\square$

4 Persistence properties for the R-CH equation

Attention in this section is now turned to asymptotic persistence for (2.1). The Sobolev space $H^s=H^s(\mathbb {R}), s \ge 0$ on the line is the Hilbert space

$$\begin{aligned} H^s=\{u\in L_2(\mathbb {R});\int _\mathbb {R}|\widehat{u}(\xi )|^2(1+\xi ^2)^sd \xi <\infty \} \end{aligned}$$

equipped with the norm

$$\begin{aligned} \Vert u\Vert ^2_{H^s}=\int _\mathbb {R}|\widehat{u}(\xi )|^2(1+\xi ^2)^s d \xi . \end{aligned}$$

The pseudodifferential operator $(1-\partial _x^2)^{-1}$ has the symbol $\frac{1}{1+ \xi ^2}$ and hence defines an isomorphism $H^s\rightarrow H^{s+2}$ for any $s\ge 0$. Moreover, $(1-\partial ^2_x)^{-1}f(x)=(p*f)(x)$ with the kernel $p(x)=\frac{1}{2}e^{-|x|}.$ One can rewrite Eq. (2.1) into the following weak form:

$$\begin{aligned} u_t+uu_x+\frac{\beta _0}{\beta }u_x+p*\partial _x \left( \left( c-\frac{\beta _0}{\beta }\right) u+u^2+\frac{1}{2}u^2_x+\frac{\omega _1}{3\alpha ^2}u^3+\frac{\omega _2}{4\alpha ^3}u^4 \right) =0. \end{aligned}$$

(4.1)

Some standard computations show that

$$\begin{aligned} (\partial _x p)(x)=-\frac{1}{2}e^{-x}1_{x\ge 0}+\frac{1}{2}e^{x}1_{x< 0}=-\frac{1}{2}sign(x)e^{-|x|} \end{aligned}$$

in the weak sense and that

$$\begin{aligned} \partial ^2_x p=p-\delta \end{aligned}$$

with the Dirac distribution $\delta$.

Now let us first recall some standard definitions. In general, a function $v:{\mathbb {R}}^n\rightarrow {\mathbb {R}}$ is called sub-multiplicative if

$$\begin{aligned} v(x+y)\le v(x)v(y), \quad \forall x,y\in {\mathbb {R}}^n. \end{aligned}$$

Let v be a sub-multiplicative function. A positive function $\varphi$ on ${\mathbb {R}}^n$ is called v-moderate if there exists a constant $c>0$ such that

$$\begin{aligned} \varphi (x+y)\le c v(x)\varphi (y),\quad \forall x,y\in {\mathbb {R}}^n. \end{aligned}$$

We say that $\varphi$ is moderate if it is v-moderate for some sub-multiplicative function v. Let us recall the most standard examples of such weights. Let

$$\begin{aligned} \varphi (x)=\varphi _{a,b,c,d}(x)=e^{|x|^b}(1+|x|)^c\log (e+|x|)^d. \end{aligned}$$

We have:

• (1) for $a,c,d>0$ and $0\le b\le 1$ such weight is sub-multiplicative.

• (2) If $a,c,d\in \mathbb {R}$ and $0\le b\le 1$, then $\varphi$ is moderate. More precisely, $\varphi _{a,b,c,d}$ is $\varphi _{\alpha ,\beta ,\gamma ,\delta -}$ moderate for $|a|\le \alpha ,b\le \beta ,|c|\le \gamma$ and $|d|\le \delta$.

The interest of imposing the sub-multiplicativity condition on a weight function is also made clearly by the following proposition.

Proposition 4.1

Let $v:{\mathbb {R}}^n\rightarrow {\mathbb {R}}^+$ and $C_0>0$. Then, the following conditions are equivalent: (1) $\forall x,y:v(x+y)\le C_0 v(x)v(y).$ (2) For all $1\le p,q,r\le \infty$ and for any measurable functions $f_1,f_2:\mathbb {R}\rightarrow \mathbb {C}$ the weighted Young inequalities hold:

$$\begin{aligned} \Vert (f_1*f_2)v\Vert _r\le C_0\Vert f_1 v\Vert _p\Vert f_2 v\Vert _q,\quad \quad 1+\frac{1}{r}=\frac{1}{p}+\frac{1}{q}. \end{aligned}$$

Definition 4.2

We say that $\varphi :\mathbb {R}\rightarrow (0,\infty )$ is an admissible weight function for the R-CH equation if it is locally absolutely continuous function $\phi :\mathbb {R}\rightarrow \mathbb {R}$ such that for some $A>0$ we have $|\varphi '(x)|\le A|\varphi (x)|$ and $\varphi$ is v-moderate with a sub-multiplicative function v satisfying $\inf v>0$ and

$$\begin{aligned} \int _\mathbb {R} v(x)e^{-|x|}\hbox {d}x<\infty . \end{aligned}$$

We recall that a locally absolutely continuous function is a.e. differentiable in $\mathbb {R}$. Moreover, its a.e. derivative belongs to $L^1_{loc}$ and agrees with its distributional derivative.

Theorem 4.3

Let $s>\frac{3}{2}$ and $2\le p\le \infty$. Let $u\in C([0,T),H^s)$ be the strong solution to (4.1) starting from $u_0$ so that $\varphi u_0,\varphi u_{0, x}\in L^p(\mathbb {R})$ for an admissible weight function $\varphi$ of the R-CH equation (4.1). Let

$$\begin{aligned} M^*=\sup _{t\in [0,T)}(\Vert u(t)\Vert _\infty +\Vert u_x(t)\Vert _\infty )<\infty . \end{aligned}$$

Then, there is a constant $C>0$ depending only on the weight $\varphi$ such that

$$\begin{aligned} \Vert \varphi u(t)\Vert _p+\Vert \varphi u_x(t)\Vert _p\le e^{CM^*t}(\Vert \varphi u_0\Vert _p+\Vert \varphi u_{0,x}\Vert _p) \end{aligned}$$

for all $t\in [0, T)$.

Remark 4.4

The basic example of application of Theorem 4.2 is obtained by choosing the standard weights $\varphi =\varphi _{a,b,c,d}$ as in with the following conditions

$$\begin{aligned} a\ge 0,\quad c,d\in \mathbb {R},\quad 0\le b\le 1,\quad ab<1. \end{aligned}$$

(For $a<0$, one has $\varphi (x)\rightarrow 0$ as $|x|\rightarrow \infty$: the conclusion of the theorem remains true but it is not interesting in the case.) The restriction $ab<1$ guarantees the validity of condition for a multiplicative function $v(x)\ge 1$. The limit case $a=b=1$ is not covered by Theorem 4.2. The result holds true, however, for the weight $\varphi =\varphi _{1,1,c,d}$ with $c<0,d\in \mathbb {R}$ and $\frac{1}{|c|}<p\le \infty$, or more generally when $(1+|\cdot |)^c\log (e+|\cdot |)^d\in \mathbb {R}$.

Remark 4.5

Let us consider a few particular cases:

• (1) Let $\varphi =\varphi _{0,0,c,0}, \, c>0$ and $p=\infty$ in Theorem 4.2. For this choice, Theorem 4.2 says that the algebraic decay of the initial datum $u_0$,

  $$\begin{aligned} |u_0(x)|+|u_{0,x}(x)|\le C(1+|x|)^{-c}, \end{aligned}$$

  for all $x\in \mathbb {R}$, is preserved by the solution u with $u_0$ on [0, T),  i.e.,

  $$\begin{aligned} |u(x,t)|+|u_x(x,t)|\le C'(1+|x|)^{-c}, \end{aligned}$$

  for all $(x,t)\in \mathbb {R}\times [0,T)$, where $C,C'>0$ are constant.

• (2) Let $\varphi =\varphi _{a,1,0,0}1_{x\ge 0}+1_{x<0},0\le a<1$. By our definitions, $\varphi$ is an admissible weight function for the R-CH. Let furthermore $p=\infty$ in Theorem 4.2. Then, one deduces that the R-CH preserves the point-wise decay $O(e^{-ax})$ of its solutions as $x\rightarrow \infty$, for any $t>0$. Analogously, one concludes that, for $x\rightarrow -\infty$, the decay $O(e^{ax})$ is preserved during the evolution. Hence, our Theorem 4.2 encompasses also Theorem 1.2 of [23].

Now, let us prove Theorem 4.2 using the ideas of [25].

Proof

Applying the translation $u(t,x)\rightarrow u(t,x-\frac{\beta _0}{\beta }t)$ to Eq. (4.1) yields the equation in the form

$$\begin{aligned} u_t+uu_x+p_x*\big (\big (c-\frac{\beta _0}{\beta }\big )u+u^2+\frac{1}{2}u^2_x+\frac{\omega _1}{3\alpha ^2}u^3+\frac{\omega _2}{4\alpha ^3}u^4\big )=0. \end{aligned}$$

(4.2)

Let $F(u)=\displaystyle (c-\frac{\beta _0}{\beta })u+u^2+\frac{1}{2}u^2_x+\frac{\omega _1}{3\alpha ^2}u^3+\frac{\omega _2}{4\alpha ^3}u^4$ and assume that $\varphi$ is v-moderate satisfying the conditions specified. For any $n\in \mathbb {N}$, let $\varphi _n(x)=\min \{\varphi (x),n\}$. Then, $\varphi _n:\mathbb {R}\rightarrow \mathbb {R}$ is locally absolutely continuous, $\Vert \varphi _n\Vert _{\infty }\le n$ and $\Vert \varphi '_n(x)\Vert \le A|\varphi _n(x)|$a.e.on $\mathbb {R}$. Moreover, as shown in [3], the n-truncations $\varphi _n$ are again v-moderate. Let $p\in [2,\infty ).$ We multiply the equation by $\varphi _n|\varphi _n u|^{p-2}\varphi _n u$ and integrate to obtain

$$\begin{aligned} \int _{\mathbb {R}}(\varphi _nu)_t\varphi _nu|\varphi _nu|^{p-2}\hbox {d}x+\int _{\mathbb {R}}|\varphi _nu|^{p}u_x\hbox {d}x+\int _{\mathbb {R}}\varphi _n(\partial _xp*F(u))|\varphi _n u|^{p-2}\varphi _nu\hbox {d}x=0. \end{aligned}$$

(4.3)

We then denote the three terms on the left-hand side as $I_1,I_2$ and $I_3$ and observe that

$$\begin{aligned} I_1=\frac{1}{p}\int _{\mathbb {R}}\frac{\hbox {d}}{\hbox {d}t}\left[ \sqrt{(\varphi _n u)^2}\right] ^p\hbox {d}x=\frac{1}{p}\frac{\hbox {d}}{\hbox {d}t}\Vert \varphi _n u\Vert ^p_p=\Vert \varphi _n u\Vert ^{p-1}_p\frac{\hbox {d}}{\hbox {d}t}\Vert \varphi _n u\Vert _p. \end{aligned}$$

Moreover, we have $|I_2|\le M^*\Vert \varphi _n u\Vert ^p_p$, where the $M^*$ is related to $E_0$. Applying Holder’s inequality then gives

$$\begin{aligned} |I_3|\le \Vert \varphi _n(\partial _x p*F(u))\Vert _p\Vert (\varphi _n u)^{p-1}\Vert _{\frac{1}{1-1/p}}=\Vert \varphi _n(\partial _x p*F(u))\Vert _p\Vert \varphi _n u\Vert ^{p-1}_p. \end{aligned}$$

Hence, (4.3) yields

$$\begin{aligned} \frac{\hbox {d}}{\hbox {d}t}\Vert \varphi _n u\Vert _p\le M^*\Vert \varphi _n u\Vert _p+\Vert \varphi _n (\partial _x p*F(u))\Vert _p \end{aligned}$$

(4.4)

and using the weighted Young inequality we have

$$\begin{aligned} \Vert \varphi _n(\partial _x p*F(u))\Vert _p\le C_1\Vert (\partial _x p)v \Vert _1\Vert \varphi _n F(u)\Vert _p\le C_2\Vert \varphi _n F(u)\Vert _p, \end{aligned}$$

(4.5)

and

$$\begin{aligned} \Vert \varphi _n F(u)\Vert _p&\le \left| c-\frac{\beta _0}{\beta }\right| \Vert \varphi _n u\Vert _p+\Vert \varphi _n u^2\Vert _p+\frac{1}{2}\Vert \varphi _n u_x^2\Vert _p+\left| \frac{\omega _1}{3\alpha ^2}\right| \Vert \varphi _n u^3\Vert _p\nonumber \\&\quad +\,|\frac{\omega _2}{4\alpha ^3}|\Vert \varphi _n u^4\Vert _p\nonumber \\&\le C_3M^*(\Vert \varphi _n u\Vert _p+\Vert \varphi _n u_x\Vert _p), \end{aligned}$$

(4.6)

where $C_1$,$C_2$ and $C_3$ are independent of n. From equation (4.2), we conclude

$$\begin{aligned} \frac{\hbox {d}}{\hbox {d}t}\Vert \varphi _n u\Vert _p\le (C_4+1)M^*(\Vert \varphi _n u\Vert _p+\Vert \varphi _n u_x\Vert _p), \end{aligned}$$

(4.7)

where the constant $C_4=C_2C_3$ is independent of n. Multiplying the identity $u_{tx}+u^2_x+uu_{xx}+\partial ^2_x p*F(u)=0$ with $\varphi _n |\varphi _n u_x|^{p-2}\varphi _n u_x$, we can obtain that

$$\begin{aligned}&\varphi _n u_{tx}|\varphi _n u_{x}|^{p-2}\varphi _n u_x +\varphi _n u^2_{x}|\varphi _n u_{x}|^{p-2}\varphi _n u_x+\varphi _n u u_{xx}|\varphi _n u_{x}|^{p-2}\varphi _n u_x\nonumber \\&\quad +\,\varphi _n |\varphi _n u_{x}|^{p-2}\varphi _n u_x\partial ^2_x p*F(u)=0. \end{aligned}$$

(4.8)

As before, we will have

$$\begin{aligned} I_4&=\int _{\mathbb {R}}\varphi _n u^2_{x}|\varphi _n u_{x}|^{p-2}\varphi _n u_x \hbox {d}x\le M^*\int |\varphi _n u_{x}|^{p}\hbox {d}x=M^* |\varphi _n u_{x}|_p^{p},\nonumber \\ I_5&=\int _{\mathbb {R}}\varphi _n u u_{xx}|\varphi _n u_{x}|^{p-2}\varphi _n u_x \hbox {d}x\le M^*\Vert \varphi _n u\Vert _p\Vert \varphi _n u_x\Vert ^{p-1}_p,\nonumber \\ I_6&=\int _{\mathbb {R}}\varphi _n |\varphi _n u_{x}|^{p-2}\varphi _n u_x\partial ^2_x p*F(u)\hbox {d}x\le \Vert \varphi _n (\partial ^2_xp*F(u)\Vert _p\Vert \varphi _n u_x\Vert ^{p-1}_p. \end{aligned}$$

(4.9)

Then,

$$\begin{aligned} \frac{\hbox {d}}{\hbox {d}t}\Vert \varphi _n u_x\Vert _p\le M^*(\Vert \varphi _n u\Vert _p+\Vert \varphi _n u_x\Vert _p)+\Vert \varphi _n(\partial ^2_x p*F(u))\Vert _p. \end{aligned}$$

(4.10)

Using that $\Vert vp\Vert _1< \infty$, we have

$$\begin{aligned} \Vert \varphi _n(\partial ^2_x p*F(u))\Vert _p&\le C_5\Vert \varphi _n F(u)\Vert _p\le C_5C_3M^*(\Vert \varphi _n u\Vert _p+\Vert \varphi _n u_x\Vert _p)\nonumber \\&=C_6M^*(\Vert \varphi _n u\Vert _p+\Vert \varphi _n u_x\Vert _p). \end{aligned}$$

(4.11)

Moreover, the above inequalities, we can obtain that

$$\begin{aligned} \frac{\hbox {d}}{\hbox {d}t}\Vert \varphi _n u_x\Vert _p\le (C_6+1)M^*(\Vert \varphi _n u\Vert _p+\Vert \varphi _n u_x\Vert _p). \end{aligned}$$

(4.12)

Combining (4.7) and (4.12), there exists a constant C, only depending on $\alpha ,\beta ,\beta _0,\omega _1,\omega _2$ and u , such that

$$\begin{aligned} \frac{\hbox {d}}{\hbox {d}t}(\Vert \varphi _n u\Vert _p+\Vert \varphi _n u_x\Vert _p)\le CM^*(\Vert \varphi _n u\Vert _p+\Vert \varphi _n u_x\Vert _p). \end{aligned}$$

(4.13)

So that, by Gronwall’s lemma, we obtain that

$$\begin{aligned} \Vert \varphi _n u\Vert _p+\Vert \varphi _n u_x\Vert _p \le (\Vert \varphi _n u\Vert _p+\Vert \varphi _n u_x\Vert _p)e^{CM^*t}, \quad \forall t\in [0,T). \end{aligned}$$

Since $\varphi _n(x),a.e.$ as $n\rightarrow \infty$ and $\varphi u_0,\varphi u_{0x}\in L_p(\mathbb {R})$ the assertion of the theorem follows for the case $p\in [2,\infty ).$ Since $\Vert \cdot \Vert _\infty =\lim _{p\rightarrow \infty }\Vert \cdot \Vert _p$, it is clear that the theorem also applies for $p=\infty .$$\square$

In the following corollary, however, we may choose $\varphi =\varphi _{1, 1, c, d}$, if $c<0,d\in \mathbb {R}$ and $\frac{1}{|c|}< p\le \infty .$

Corollary 4.6

Let $2 \le p \le \infty$ and let $\varphi :\mathbb {R}\rightarrow (0,\infty )$ be a locally absolutely continuous and v-moderate weight function satisfying $|\varphi '(x)|\le A|\varphi (x)|$ a.e., for some $A>0, \inf v>0$ and $ve^{-|\cdot |}\in L_p(\mathbb {R})$. For $s>3$, let $u\in C([0,T),H^s)\bigcap C^1([0,T),H^{s-1})$ be the strong solution to (4.1) starting from $u_0$. Then,

$$\begin{aligned} \sup _{t\in [0,T)}(\Vert \varphi u(t)\Vert _p+\Vert \varphi u_x(t)\Vert _p) \end{aligned}$$

and

$$\begin{aligned} \sup _{t\in [0,T)}(\Vert \varphi ^{\frac{1}{2}} u(t)\Vert _p+\Vert \varphi ^{\frac{1}{2}} u_x(t)\Vert _p) \end{aligned}$$

are finite. For the particular choice $c=d=0$ and $p=\infty$, we conclude from

$$\begin{aligned} |u_0(x)|+|u_{0,x}(x)|\le Ce^{-|x|} \end{aligned}$$

for any $x\in \mathbb {R}$ that the unique solution u with u(0) satisfies

$$\begin{aligned} |u(x)|+|u_{x}(x)|\le C'e^{-|x|} \end{aligned}$$

on $\mathbb {R}\times [0,T)$.

Proof

As explained in [3], the function $\varphi ^{\frac{1}{2}}$ is a $v^{\frac{1}{2}}$ moderate weight satisfying $|(\varphi ^{\frac{1}{2}})(x)|\le \frac{A}{2}\varphi ^{\frac{1}{2}}(x)$, $\inf v^{\frac{1}{2}}>0$ and $v^{\frac{1}{2}}e^{-|\cdot |}\in L_1(\mathbb {R})$. We apply Theorem 4.2 with $p=2$ to the weight $\varphi ^{\frac{1}{2}}$ and obtain

$$\begin{aligned} \Vert \varphi ^{\frac{1}{2}} u(t)\Vert _2+\Vert \varphi ^{\frac{1}{2}} u_x(t)\Vert _2\le (\Vert \varphi ^{\frac{1}{2}} u_0\Vert _2+\Vert \varphi ^{\frac{1}{2}} u_{0x}\Vert _2)e^{CM^*t}. \end{aligned}$$

(4.14)

Let $\varphi _n$ be as in the proof of Theorem 4.2. Then, (4.14) holds equally with $\varphi$ replaces by $\varphi _n$. By the definition of F(u) and Eq. (4.14), there is a constant $\widetilde{C_1}$ depended only on $\varphi$ and $z_0$ such that $\Vert \varphi _n F(u)\Vert _2\le \widetilde{C_1} e^{2CM^*t}$. Using this estimate, we conclude that $\Vert \varphi _n(\partial _x p*F(u))\Vert _p\le \widetilde{C_2}e^{2CM^*t}$ and, that

$$\begin{aligned} \Vert \varphi _n(\partial ^2_x p*F(u))\Vert _p&\le \Vert \varphi _n(p*F(u))\Vert _p+\Vert \varphi _nF(u)\Vert _p\\&\le \widetilde{C_3} e^{2CM^*t}+\widetilde{C_4}M^*(\Vert \varphi _n u\Vert _p+\Vert \varphi _n u_x\Vert _p). \end{aligned}$$

Using the same method in Theorem 4.2, this yields that

$$\begin{aligned} \frac{\hbox {d}}{\hbox {d}t} (\Vert \varphi _n u\Vert _p+\Vert \varphi _n u_x\Vert _p)\le \widetilde{C_5}M^*(\Vert \varphi _n u\Vert _p+\Vert \varphi _n u_x\Vert _p)+\widetilde{C_6}e^{2CM^*t}, \end{aligned}$$

(4.15)

and the constants $\widetilde{C_j}>0,j=1,...,6$, depend only on $\varphi$ and $u_0$. Integrating this equation and letting $n\rightarrow \infty$, we obtain the result of the corollary for $p\in [2,\infty )$. The case $p=\infty$ is again obtained from a standard limit argument. This achieves the proof. $\square$

Remark 4.7

We can also apply this theorem choosing $\varphi (x)=\varphi _{1,1,0,0}(x)=e^{|x|}$ and $p=\infty$. It follows that if $|u_0(x)|$ and $|\partial _x u_0(x)|$ are both bounded by $Ce^{-|x|}$, then the strong solution satisfies, uniformly in [0, T]

$$\begin{aligned} |u(x,t)|+|\partial _x u(x,t)|\le Ce^{-|x|}. \end{aligned}$$

(4.16)

The peakon-like decay is the fastest possible decay that is possible to propagate for a nontrivial solution u. Indeed, arguing as in the proof of Theorem 1.1 in [23], it is not difficult to see that, for fast enough decaying data, the following asymptotic profiles hold:

$$\begin{aligned} u(x,t)&\sim u_0(x)+e^{-x}t\Phi (x),\quad x\rightarrow +\infty ,\nonumber \\ u(x,t)&\sim u_0(x)-e^{x}t\Psi (x),\quad x\rightarrow -\infty , \end{aligned}$$

(4.17)

where $\Phi (t)\ne 0$ and $\Psi (t)\ne 0$ for all $t\in [0,T]$ (unless $u\equiv 0$). Thus, if $u_0(x)=o(e^{-|x|})$, only the zero solution can decay faster than $e^{-|x|}$ at a later time $0<t_1\le T$.