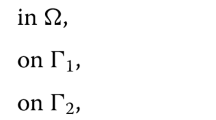Critical quasilinear elliptic problems using concave–convex nonlinearities

Abstract

It is established existence, multiplicity, and asymptotic behavior of nonnegative solutions for a quasilinear elliptic problem driven by the $\Phi$-Laplacian operator. One of these solutions is obtained as ground-state solution by applying the well-known Nehari method. The nonlinear term is a concave–convex function which presents a critical behavior at infinity. The concentration-compactness principle is used in order to recover the compactness required in variational methods.

1 Introduction

In this work, we deal with existence, multiplicity, and asymptotic behavior of nonnegative solutions of the problem

$$\begin{aligned} -\Delta _{\Phi } u = \lambda a(x)|u|^{q-2}u + b(x)|u|^{\ell ^*-2}u~ \quad \text{ in } \ \Omega ,~~u = 0 \, \quad \text{ on } \, \partial \Omega , \end{aligned}$$

(1.1)

where $\Omega \subset {\mathbb {R}}^{N}$ is a bounded smooth domain, $\lambda >0$ is a parameter, $\ell ^* := N \ell /(N - \ell )$ with $1< \ell < N$ and $a, b: \Omega \rightarrow {\mathbb {R}}$ are two indefinite functions in sign. The operator $\Delta _{\Phi }$ is named $\Phi$-Laplacian which is given by

$$\begin{aligned} \Delta _{\Phi } u = \text{ div } ( \phi (|\nabla u|) \nabla u) \end{aligned}$$

where $\phi : (0,\infty )\rightarrow (0,\infty )$ is a $C^{2}$-function satisfying

• $(\phi _1)$$\displaystyle \lim _{s \rightarrow 0} s \phi (s)= 0, \displaystyle \lim _{s \rightarrow \infty } s \phi (s)= \infty$;

• $(\phi _2)$$s\mapsto s\phi (s)$ is strictly increasing.

We extend $s \mapsto s \phi (s)$ to ${\mathbb {R}}$ as an odd function. The function $\Phi$ is given by

$$\begin{aligned} \Phi (t) = \int _{0}^{t} s \phi (s) ds,\quad ~ t \ge 0. \end{aligned}$$

As a consequence the function $\Phi$ satisfies $\Phi (t) = \Phi (-t)$ for each $t \in {\mathbb {R}}$. Without any loss of generality we assume $\Phi (1) = 1$. For further results on Orlicz and Orlicz–Sobolev framework, we refer the reader to [1, 36,37,38,39, 50]. At the same time, the Orlicz–Sobolev space $W^{1,\Phi }(\Omega )$ is a generalization of the classical Sobolev space $W^{1,p}(\Omega )$. Hence, several properties of the Sobolev spaces have been extended to Orlicz–Sobolev spaces. The interest regarding Orlicz–Sobolev spaces is motivated by their applicability in many fields of mathematics, such as partial differential equations, calculus of variations, nonlinear potential theory, differential geometry, geometric function theory, the theory of quasiconformal mappings, probability theory, non-Newtonian fluids, image processing. The class of problems introduced in (1.1) is related with several fields of physics based on the nature of the nonhomogeneous nonlinearity $\Phi$. For instance, we cite the following examples:

• (i) Nonlinear elasticity: $\Phi (t)=(1+t^{2})^{\gamma }-1$,   $1<\gamma <N/(N-2)$;

• (ii) Plasticity: $\Phi (t)=t^{\alpha }(\log (1+t))^{\beta }$,   $\alpha \ge 1$, $\beta >0$;

• (iii) Non-Newtonian fluid: $\Phi (t)=\frac{1}{p}|t|^{p}$,   for $p>1$;

• (iv) Plasma physics: $\Phi (t)=\frac{1}{p}|t|^{p}+\frac{1}{q}|t|^{q}$,   where $1<p<q<N$ with $q\in (p,p^{*})$;

• (v) Generalized Newtonian fluids: $\Phi (t)=\int _{0}^{t}s^{1-\alpha }[\sinh ^{-1}(s)]^{\beta }\;{\mathrm {d}}s$,   $0\le \alpha \le 1$, $\beta >0$.

For more details about nonhomogeneous differential operators with different types of nonlinearity $\Phi$, we refer the readers to [30, 33, 36, 37, 54] and references therein. Recall that when $\phi := 2$, $a = b := 1$ we obtain $\ell = 2$. Then problem (1.1) reads as

$$\begin{aligned} -\Delta u = \lambda |u|^{q-2}u + |u|^{2^{*}-2}u \quad in \;\; \Omega ,~ u = 0 \quad on \;\; \partial \Omega . \end{aligned}$$

(1.2)

In the pioneering paper [13], the authors proved results on existence of positive solutions of (1.2). A new variational technique was developed to overcome difficulties due to the presence of the critical Sobolev exponent $2^{*} = \frac{2N}{N - 2}$.

Problem (1.2) was later considered in [7] where among other results it was shown that there is some $\Lambda > 0$ such that (1.2) has

• (i)      a positive minimal solution $\;\; u_{\lambda } \in H_{0}^{1}~ \text{ for } \text{ each }~ \lambda \in (0, \Lambda ), \;\; \text{ with }$

  $$\begin{aligned}&\frac{1}{2} \int _{\Omega } \vert \nabla u_{\lambda } \vert ^{2}\mathrm{d}x - \frac{\lambda }{q + 1} \int _{\Omega } u_{\lambda }^{q + 1}\mathrm{d}x - \frac{1}{2^{*}} \int _{\Omega } u_{\lambda }^{2^{*}}\mathrm{d}x \;< \; 0\\&\quad \text{ when } \;\; 1< q < 2, ~N \ge 1, \end{aligned}$$

• (ii)      a positive weak solution $\;\; u_{\lambda } \in H_{0}^{1} \quad \text{ for } \;\; \lambda = \Lambda$

  $$\begin{aligned} \text{ when } \;\; 2< q < 3,\quad ~ N \ge 3, \end{aligned}$$

• (iii)      no positive solution    when $\;\; \lambda > \Lambda$.

Moreover, in the first case above, $\Vert u_{\lambda } \Vert _{\infty } \rightarrow 0$ as $\lambda \rightarrow 0$. We also refer the reader [2, 3] and references therein.

It is important to mention that when $\phi (t) = r t^{r-2}$, $1< r < \infty$ and $a = b := 1$ problem (1.1) becomes

$$\begin{aligned} \displaystyle - \Delta _r u = \lambda |u|^{q-2}u + |u|^{p-2}u ~ \text{ in }~ \Omega ,~~ u = 0\quad \text{ on }~ \partial \Omega . \end{aligned}$$

(1.3)

This problem was also studied in [8] and subsequently by many other researchers.

It is worthwhile to mention that conditions $(\phi _{1})- (\phi _{2})$ implies that the function $\Phi$ is an N-function. In addition due to the expression of $\Delta _{\Phi }$, it is natural to work in the framework of Orlicz–Sobolev spaces, and for basic results on Orlicz and Orlicz–Sobolev spaces, we infer the reader to [1, 38, 39, 50]. It is well known that $W^{1,\Phi }_{0}(\Omega )$ is not equal in general to $W^{1,q}_{0}(\Omega )$ for any $q \in [1, + \infty )$. As example we cite $\Phi (t) = |t|^{p} ln (1 + |t|), p > 1,$ which satisfies $W^{1,\Phi }_{0}(\Omega ) \ne W^{1,q}_{0}(\Omega )$ for any $q \in [1, + \infty )$. Hence it is not possible to consider the usual Sobolev spaces $W^{1,q}_{0}(\Omega )$ in order to ensure existence and multiplicity of solutions for the problem (1.1). In [21, 45, 46] the authors have been considered the following hypothesis

$$\begin{aligned} t \rightarrow \Phi (\sqrt{t}) \, \, \text{ is } \text{ a } \text{ strictly } \text{ convex } \text{ function }. \end{aligned}$$

(1.4)

Under this condition, the Orlicz–Sobolev spaces is uniformly convex. However, for the p-Laplacian operators, we observe that $\Phi (t) = t^{p}/ p$ and (1.4) says that $p \ge 2$. This is a serious restriction on Orlicz–Sobolev framework. In order to preserve the property, $W^{1,\Phi }_{0}(\Omega )$ is uniform convex, and we shall consider another hypothesis on the function $\Phi$ taking into account the p-Laplacian operator for any $p > 1$. Furthermore, using the Orlicz–Sobolev setting, we shall consider an additional hypothesis on the function $\phi$ which allow us to consider a huge class of quasilinear operators where the assumption (1.4) does not work anymore. Under this additional condition, we consider a minimization problem using the Nehari method. More precisely, the following additional condition on $\phi$ will be assumed:

• ($\phi _3$) $-1<\ell -2:=\displaystyle \inf _{t>0}\displaystyle \frac{(t\phi (t))''t}{(t\phi (t))'}\le \displaystyle \sup _{t>0}\displaystyle \frac{(t\phi (t))''t}{(t\phi (t))'}=:m-2<N-2.$

The usual norm on $L_{\Phi }(\Omega )$ is ( Luxemburg norm),

$$\begin{aligned} \Vert u\Vert _\Phi =\inf \left\{ \lambda >0~|~\int _\Omega \Phi \left( \frac{u(x)}{\lambda }\right) \mathrm{d}x \le 1\right\} \end{aligned}$$

and the Orlicz–Sobolev norm of $W^{1, \Phi }(\Omega )$ is

$$\begin{aligned} \displaystyle \Vert u\Vert = \Vert u\Vert _\Phi +\sum _{i=1}^N\left\| \frac{\partial u}{\partial x_i}\right\| _\Phi . \end{aligned}$$

We say that a N-function $\Psi$ grows essentially more slowly than $\Phi _*$, and we write $\Psi<<\Phi _*$ whenever

$$\begin{aligned} \lim _{t\rightarrow \infty }\frac{\Psi (\lambda t)}{\Phi _*(t)}=0,\quad \text{ for } \text{ all }~~\lambda >0. \end{aligned}$$

Recall that $\Phi _*$ is the N-function defined by

$$\begin{aligned} \Phi _{*}^{-1}(t) = \int _{0}^{t} \dfrac{\Phi ^{-1}(s)}{s^{1 + 1/N}} \mathrm{d}s,\quad t \ge 0 \end{aligned}$$

where we mention that

$$\begin{aligned} \int _{1}^{\infty } \dfrac{\Phi ^{-1}(s)}{s^{1 + 1/N}} \mathrm{d}s = + \infty \quad \text{ and } \,\, \int _{0}^{1} \dfrac{\Phi ^{-1}(s)}{s^{1 + 1/N}} \mathrm{d}s < \infty . \end{aligned}$$

Recall also that

$$\begin{aligned} \widetilde{\Phi }(t) = \displaystyle \max _{s \ge 0} \{ts - \Phi (s) \},\quad ~ t \ge 0. \end{aligned}$$

The imbedding below (cf. [1, 31]) will be used in this paper:

$$\begin{aligned} \displaystyle W_{0}^{1,\Phi }(\Omega ) {\mathop {\hookrightarrow }\limits ^{\tiny cpt}}L_\Psi (\Omega ),\quad \text{ if }~~\Psi<<\Phi _*, \end{aligned}$$

in particular, as $\Phi<<\Phi _*$ (cf. [39, Lemma 4.14]),

$$\begin{aligned} W_{0}^{1,\Phi }(\Omega ) {\mathop {\hookrightarrow }\limits ^{\tiny {cpt}}}L_\Phi (\Omega ). \end{aligned}$$

Furthermore, we have the following embeddings

$$\begin{aligned} W_0^{1,\Phi }(\Omega ) {\mathop {\hookrightarrow }\limits ^{{\tiny {\mathrm{cont}}}}} L_{\Phi _*}(\Omega ) \end{aligned}$$

and

$$\begin{aligned} L_{\Phi }(\Omega ) {\mathop {\hookrightarrow }\limits ^{{\tiny {\mathrm{cont}}}}} L^{\ell }(\Omega ), L_{\Phi _{*}}(\Omega ) {\mathop {\hookrightarrow }\limits ^{{\tiny {\mathrm{cont}}}}} L^{\ell ^{*}}(\Omega ). \end{aligned}$$

Under assumptions $(\phi _{1}) - (\phi _{3})$, it turns out that $\Phi$ and $\widetilde{\Phi }$ are N-functions satisfying the $\Delta _2$-condition; see [50].

Remark 1.1

Under assumption $(\phi _{3})$, we observe that

$$\begin{aligned} \ell -2\le \displaystyle \frac{\phi '(t)t}{\phi (t)}\le m-2,\ \ \ell \le \displaystyle \frac{\phi (t)t^2}{\Phi (t)}\le m,\quad t > 0. \end{aligned}$$

(1.5)

Moreover, we have that

$$\begin{aligned}\left\{ \begin{array}{rcl} t^2\phi ''(t)&{}\le &{} (m-4)t\phi '(t)+(m-2)\phi (t)\\ t^2\phi ''(t)&{}\ge &{} (\ell -4)t\phi '(t)+(\ell -2)\phi (t),\quad t \ge 0. \end{array}\right. \end{aligned}$$

Under conditions $(\phi _{1}),(\phi _{2}),(\phi _{3})$ the Orlicz–Sobolev space $W^{1,\Phi }_{0}(\Omega )$ is Banach and reflexive with respect to the standard norm denoted $\Vert . \Vert$. Notice also that $(\phi _{1}),(\phi _{2}),(\phi _{3})$ imply that $W_0^{1,\Phi }(\Omega )$ is uniformly convex. Here we mention that $\phi (t) = 2$ and $\phi (t) = rt^{r -2}$ satisfy $(\phi _{1})- (\phi _{2})$ and $(\phi _{3})$. Furthermore, when $\phi (t) = 2$ then $m = \ell = 2$, $\Delta _{\Phi } = \Delta$ and $W^{1,\Phi }_{0}(\Omega ) = H_0^1(\Omega )$. When $\phi (t) = rt^{r -2}$ then $m = \ell = r$, $\Delta _{\Phi } = \Delta _r$ and $W^{1,\Phi }_{0}(\Omega ) = W_0^{1,r}(\Omega )$.

Many other well-known operators are examples of $\Delta _{\Phi }$. For instance, if $\phi (t) = p_{1}t^{p_{1} -2} + p_{2}t^{p_{2} -2}$ with $1< p_{1}< p_{2} < \infty$, then $\phi$ satisfies hypotheses $(\phi _{1})-(\phi _{3})$ and the operator in problem (1.1) reads as $-\Delta _{p_{1}} u - \Delta _{p_{2}} u$ which is known as the $(p_{1},p_{2})$-Laplacian and was extensively studied in the last years; see [47, 55]. We mention that in this case $\ell = p_{1}$ and $m = p_{2}$.

Another class of operators is the so-called anisotropic elliptic problem included here as example for $\Delta _{\Phi }$ is obtained by setting

$$\begin{aligned} \phi (t) = \displaystyle \sum _{j=1}^{N} t^{p_{j}-2}, \Phi (t) = \displaystyle \sum _{j=1}^{N} \dfrac{t^{p_{j}}}{p_{j}} \end{aligned}$$

where $1< p_{1}< p_{2}< \cdots< p_{N} < \infty$ and

$$\begin{aligned} p^{\star } = \displaystyle \dfrac{N}{\left( \sum _{j =1}^{N}\frac{1}{p_{j}}\right) - 1}, \displaystyle \sum _{j=1}^{N} \dfrac{1}{p_{j}} > 1. \end{aligned}$$

(1.6)

Here we consider the case $p_{N} < p^{\star }$ and $\overline{p} = \dfrac{N}{\sum _{j =1}^{N}\frac{1}{p_{j}}}$ is the mean harmonic for the numbers $p_{j}$ with $j = 1, 2, \ldots , N$. This number satisfies $p^{\star } = \frac{N \overline{p}}{N - \overline{p}}$. It is no hard to verify that hypotheses $(\phi _{1})- (\phi _{3})$ are satisfied for the anisotropic elliptic problem. This operator have been considered during the lasts years which has a rich physical motivation; see [11, 12]. For further references, we refer the reader to [34, 35, 45, 46, 57] and references therein.

It is important to emphasize that a great interest on problem (1.1) for the Laplacian operator have been made since the seminal paper [6]. Our main purpose in this work is to guarantee existence and multiplicity of solutions for quasilinear elliptic equations driven by $\Phi$-Laplacian using indefinite concave–convex nonlinearities. More specifically, we shall consider problem (1.1) where the functions a and b are sign changing functions.

The main aim in this work is to consider the critical growth in problem (1.1). Elliptic problems with critical nonlinearities have been widely considered since the celebrated works [40,41,42,43]. For quasilinear elliptic problems, we infer the reader to [4, 9, 10, 36, 44, 49, 51, 58] and references therein. The main difficulty here is the loss of compactness for the embedding $W_0^{1,\Phi }(\Omega )$ into $L^{\ell ^{\star }}(\Omega )$. It is usual to consider some kind of compactness proving that the energy functional satisfies the Palais–Smale condition for any energy level below to a positive constant, see [58]. For the Laplace operator, the energy functional verifies the Palais–Smale condition for any energy level $c \in \left( 0, S^{N/2}/N \right)$. Here S denotes the best constant for the embedding $H^{1}_{0}(\Omega )\subset L^{2^{*}}(\Omega )$. In order to ensure that the energy level belongs to $\left( 0, S^{N/2}/N \right)$, many researchers considered some especial functions named as Talenti functions. The same situation occurs for the p-Laplace operator and (p, q)-Laplace operator. For the $\Phi$-Laplacian operator, this strategy is not applicable anymore. The main problem is due the fact that Talenti functions are not suitable for nonhomogeneous operators such as $\Phi$-Laplacian operator. In order to overcome these difficulties, we shall prove some kind of compactness taking into account the Nehari method. More specifically, we shall prove that any minimizer sequence on the Nehari manifold admits a convergent subsequence. This is crucial in our arguments showing that quasilinear elliptic problems involving nonhomogeneous operators and critical nonlinearities can be treated using a minimization procedure. The main idea here is to find a minimizer for the energy functional over the Nehari manifold. At the same time, recalling that there is no compact embedding $W_0^{1,\Phi }(\Omega )\subset L^{\ell ^{*}}(\Omega )$, problem (1.1) presents a critical behavior and the energy functional does not verify the Palais–Smale condition. In order to overcome this difficulty, we also apply the concentration-compactness principle together with variational methods ensuring our main results. In conclusion, the main objective in this work is to find existence and multiplicity of solutions for the problem (1.1) extending and complementing the early results above-mentioned.

In this paper, we shall assume the following set of technical conditions:

(H)         $1<q<\displaystyle \frac{\ell (\ell ^*-m)}{\ell ^*-\ell }\le \ell \le m<\ell ^*,\quad a,b \in L^\infty (\Omega ),~~~ a^+,b^+\not \equiv 0$.

The main feature in this work is to use the Nehari method in order to achieve our main results. The hypothesis (H) is essential for the minimization procedure which shows that the critical value on the Nehari manifold is negative; see Sect. 3 ahead. Moreover, hypothesis (H) is trivially satisfied for Laplacian operator, p-Laplacian operator for each $p > 1$ and many others quasilinear operators in divergent form.

Recall that under $(\phi _{1})-(\phi _{3})$ the functional $J_{\lambda } : W^{1, \Phi }_{0}(\Omega ) \rightarrow {\mathbb {R}}$ given by

$$\begin{aligned} J_{\lambda }(u)=\displaystyle \int _{\Omega }\Phi (|\nabla u|)\mathrm{d}x-\displaystyle \frac{\lambda }{q} \displaystyle \int _{\Omega }a(x)|u|^{q}\mathrm{d}x-\displaystyle \frac{1}{\ell ^*} \displaystyle \int _{\Omega }b(x)|u|^{\ell ^*}\mathrm{d}x,\ \ u\in W_0^{1,\Phi }(\Omega ), \end{aligned}$$

is well defined. Furthermore, the functional $J_{\lambda }$ is in $C^{1}$ class. The derivative of $J_{\lambda }$ is given by

$$\begin{aligned} \left<J'_{\lambda }(u),v\right> = \displaystyle \int _{\Omega }\phi (|\nabla u|)\nabla u\nabla v\mathrm{d}x-\lambda \displaystyle \int _{\Omega }a(x)|u|^{q-2}uv\mathrm{d}x- \displaystyle \int _{\Omega }b(x)|u|^{\ell ^*-2}uv\mathrm{d}x \end{aligned}$$

for any $u,v\in W_0^{1,\Phi }(\Omega )$. Hence finding weak solutions for the problem (1.1) is equivalent to find critical points for the functional $J_{\lambda }$. In general, under hypotheses $(\phi _{1})-(\phi _{3})$, the functional $J_{\lambda }$ is not of class $C^{2}$, i.e., the second derivative $J_{\lambda }''(u)(h_{1}, h_{2})$ does not exist for some directions $(h_{1}, h_{2}) \in W_0^{1,\Phi }(\Omega )^{2}$ where $u \in W_0^{1,\Phi }(\Omega )$ is some fixed function. For example, using the p-Laplacian operator where $\Phi (t) = t^{p}/p$ we know that $J_{\lambda }$ has the second derivative if and only if $p \ge 2$. This is another difficulty in order to apply the Nehari method. The fibering maps is linked to the Nehari method in order to find weak solutions for elliptic equations; see [14, 15]. These maps are defined by $\gamma _{u}(t) = J_{\lambda }(t u), t > 0$ for each $u \in W_0^{1,\Phi }(\Omega )$. Thanks to hypothesis $(\phi _{3})$, we stress that the fibering map is in $C^{2}$ class which is sufficient in order to consider the Nehari method given by

$$\begin{aligned} {\mathcal {N}}_{\lambda } = \left\{ u \in W_0^{1,\Phi }(\Omega )\setminus \{0\} : \langle J'_{\lambda }(u), u \rangle = 0 \right\} . \end{aligned}$$

More specifically, we have that $J_{\lambda }''(u)(u,u)$ is well defined for any $u \in W_0^{1,\Phi }(\Omega )$. Moreover, we mention that

$$\begin{aligned} \gamma _{u} ''(1) = J_{\lambda }''(u)(u,u) \quad \text{ for } \text{ any } \,\, u \in {\mathcal {N}}_{\lambda }. \end{aligned}$$

(1.7)

This is the key in order to apply the Nehari method for quasilinear elliptic problems which does not present any kind of homogeneity.

A weak solution $u \in W^{1,\Phi }_{0}(\Omega )$ for Eq.  (1.1) is said to be a ground-state solution when u is a minimal energy solution in the set of all nontrivial solutions. In this work, we shall prove existence nonnegative ground state solution using the Nehari method. Besides that, we find another nonnegative solution for the problem (1.1) using a minimization procedure. An overview on this subject can be found in [52, 53].

Quasilinear elliptic problems driven by $\Phi$-Laplacian operator have been extensively discussed during the last years. We refer the reader to the important works [5, 16, 18, 19, 21,22,23,24, 47, 54].

In [16] the authors considered existence of positive solutions for quasilinear elliptic problems where the nonlinear term is superlinear at infinity. In [21, 54] the authors studied existence and multiplicity of solutions where the nonlinear term is also superlinear. In [5] was studied the critical case using the well-known concentration-compactness argument. Regarding concave–convex nonlinearities, we further refer the reader to [20, 27,28,29, 59, 60].

It is worthwhile mentioning that in our main theorems the functions a, b may change sign and no homogeneity conditions either on the operator or on the nonlinear term is required. More specifically, we emphasize that our nonlinear operator $\Delta _{\Phi }$ is not homogeneous which is a serious difficulty in elliptic problems. To the best of our knowledge, there is no result on elliptic problems with concave–convex functions for the $\Phi$-Laplacian operator in the critical case.

Our main results are stated below.

Theorem 1.1

Suppose $(\phi _{1}) - (\phi _{3})$ and (H). Then there exists $\Lambda _1> 0$ such that for each $\lambda \in (0, \Lambda _{1})$, problem (1.1) admits at least one nonnegative ground-state solution $u = u_{\lambda }$ satisfying $J_{\lambda }(u) < 0$ and $\displaystyle \lim _{\lambda \rightarrow 0^{+}} \Vert u_{\lambda }\Vert = 0$.

Now we shall state our second result.

Theorem 1.2

Suppose $(\phi _{1}) - (\phi _{3})$ and (H). Then there exists $\Lambda _2 > 0$ in such way that for each $\lambda \in (0, \Lambda _{2})$, problem (1.1) admits at least one nonnegative weak solution $v = v_{\lambda }$ satisfying $J_{\lambda }(v) > 0$.

As a consequence of the results just above, we have the following multiplicity result.

Theorem 1.3

Suppose $(\phi _{1}) - (\phi _{3})$ and (H). Set $\Lambda = \min \{\Lambda _1, \Lambda _2 \}$. Then for each $\lambda \in (0, \Lambda )$, problem (1.1) admits at least two nonnegative weak solutions $u = u_{\lambda }, v = v_{\lambda } \in W_0^{1,\Phi }(\Omega )$ satisfying $J_{\lambda }(u)< 0 < J_{\lambda }(v)$. Furthermore, the function u is a ground-state solution for each $\lambda \in (0,\Lambda )$.

Remark 1.2

Our main results remain true for more general nonlinearities. For example, we can consider the following quasilinear elliptic problem

$$\begin{aligned} -\Delta _{\Phi } u = \lambda a(x)|u|^{q-2}u + b(x) \phi _{*}(|u|) u~ \quad \text{ in } \ \Omega ,~~u = 0\quad \text{ in } \partial \Omega , \end{aligned}$$

(1.8)

where $\Phi _{*}^{\prime }(t) = \phi _{*}(t)t$ for any $t \ge 0$ and $\phi _{*}$ is a suitable function. Here we put $\lambda > 0$ small enough and a, b can be two sign changing functions. The function $\Phi _{*}$ behaves like the critical Sobolev function where the continuous Orlicz–Sobolev embedding remains true; see [1, 31].

In order to achieve our results, we shall consider the Nehari manifold ${\mathcal {N}}_{\lambda }$ introduced in [48]. Here we also refer to [14, 15, 32, 52, 53] where the authors establish a precise description on the fibering maps.

A main point during this work is that due to the concave–convex nonlinearities present in (1.1), the Ambrosetti–Rabinowitz condition is not satisfied in general. Furthermore, when a, b are functions that change sign, the well-known nonquadraticity condition introduced by Costa–Magalhães [25] does not work anymore. Those conditions are used to prove that certain Palais–Smale sequences are bounded. In order to overcome this difficulty, we shall employ the Nehari manifold method.

In this work, we employ that the fibering maps $\gamma _{u}(t) = J_{\lambda }(t u), t > 0$ belongs to $C^{2}$ class for each $u \in W_0^{1,\Phi }(\Omega )$. This can be done thanks to hypothesis $(\phi _{3})$. This is the main reason in order consider the assumption $(\phi _{3})$ which permit us to consider the Nehari method for quasilinear elliptic problems. In particular, we also split the Nehari manifold into two parts. More specifically, in order to achieve our results we shall consider the Nehari manifold ${\mathcal {N}}_{\lambda }$ introduced in [48]. Here we also refer [14, 15, 32, 52, 53] where the authors establish a precisely description on the fibering maps. In the present work, the main difficulty is that a and b are not defined in sign, i.e., the functions a, b can be two sign changing functions. Furthermore, the nonlinear operator $\Delta _{\Phi }$ is not homogeneous. In order to overcome these difficulties, we split the Nehari manifold into two parts ${\mathcal {N}}_{\lambda }= {\mathcal {N}}_{\lambda }^{+} \cup {\mathcal {N}}_{\lambda }^{-}$. Moreover, taking into account hypothesis $(\phi _{3})$, is possible to ensure that there exists an unique projection in each part ${\mathcal {N}}_{\lambda }^{-}, {\mathcal {N}}_{\lambda }^{+}$, see Sect. 2 ahead. In this way, we obtain that problem (1.1) admits at least two nonnegative solutions. These solutions are finding by standard minimization procedure in each part $\mathcal {N_{\lambda }}^{\pm }$.

It is important to mention that we deal with to the lack of compactness in $W_0^{1,\Phi }(\Omega )\hookrightarrow L^{\ell ^{*}}(\Omega )$. In order to overcome the difficulty with compactness we apply the concentration-compactness principle, see [40,41,42,43], together with variational methods as in [13]. Furthermore, the Brezis–Lieb Lemma for convex functions plays a crucial role.

It is worthwhile to mention that problem (1.1) admits at least two nonnegative solutions thanks to the fact that the fibering maps give us an unique projection in each of $\mathcal {N_{\lambda }}^{\pm }$, see Sect. 2 in the sequel. Those solutions are found by standard minimization procedure in each of $\mathcal {N_{\lambda }}^{\pm }$. The main tool here is to use hypothesis $(\phi _{3})$ showing that the fibering maps admits an unique critical point. The reader is also referred to [4, 6, 9, 10, 36, 44, 51, 58] and references therein.

The paper is organized as follows: Section 2 is devoted to the main proprieties for Nehari manifold. In Sect. 3 we give a complete description for the fibering maps. Section 4 is devoted to find Palais–Smale sequences taking minimizers sequences on the Nehari manifold. Section 5 we consider the concentration-compactness principle for Orlicz–Sobolev setting. In Sect. 6 we consider the proof of our main results. In the present work, we use $C, C_{1}, \ldots$ to denote positive constants. The usual norm in $L^{p}(\Omega )$ is denoted by $\Vert .\Vert _{p}$ for any $p \in [1, \infty ]$. Throughout this work, the integral for a function $f: \Omega \rightarrow {\mathbb {R}}$ over $\Omega$ is denoted by $\int _{\Omega } f\mathrm{d}x$ for each $f \in L^{1}(\Omega )$. Furthermore, we shall use the following notation $f^+:=\max \{f,0\}$ for the positive part and $f^-:=\min \{f,0\}$ for the negative part of the function f.

2 The Nehari manifold

The main goal in this section is to gather information on the critical points for the fibering maps associated to the energy functional $J_{\lambda }$. For an overview on the Nehari method, we refer the reader to [14, 15, 58].

The Nehari manifold associated with the functional $J_\lambda$ is given by

$$\begin{aligned} \begin{array}{rcl} {\mathcal {N}}_\lambda &{}=&{}\{u\in W_0^{1,\Phi }(\Omega )\setminus \{0\}: \left<J'_{\lambda }(u),u\right>=0\}\\ &{}=&{}\left\{ u\in W_0^{1,\Phi }(\Omega )\setminus \{0\}:\displaystyle \int _{\Omega }\phi (|\nabla u|)|\nabla u|^2\mathrm{d}x=\displaystyle \int _{\Omega }\left[ \lambda a(x)|u|^{q}+b(x)|u|^{\ell ^*}\right] \mathrm{d}x\right\} . \end{array} \end{aligned}$$

(2.9)

Later on, we shall prove that $u \mapsto \langle J'_\lambda (u), u\rangle$ is in $C^{1}$ class. So that ${\mathcal {N}}_\lambda$ is a $C^1$-submanifold of $W^{1,\Phi }_{0}(\Omega )$. Let $u\in \mathcal {N_\lambda }$ be a fixed function. Using (2.9) we infer that

$$\begin{aligned} J_{\lambda }(u)=\displaystyle \int _{\Omega }\left[ \Phi (|\nabla u|) - \displaystyle \frac{1}{q} \phi (|\nabla u|)|\nabla u|^2+\left( \displaystyle \frac{1}{q}-\displaystyle \frac{1}{\ell ^*}\right) b(x)|u|^{\ell ^*}\right] \mathrm{d}x, \end{aligned}$$

(2.10)

or equivalently

$$\begin{aligned} J_{\lambda }(u)=\displaystyle \int _{\Omega }\left[ \Phi (|\nabla u|) - \displaystyle \frac{1}{\ell ^*} \phi (|\nabla u|)|\nabla u|^2-\lambda \left( \displaystyle \frac{1}{q}-\displaystyle \frac{1}{\ell ^*}\right) a(x)|u|^{q}\right] \mathrm{d}x. \end{aligned}$$

(2.11)

As a first step, we shall prove that $J_{\lambda }$ is coercive and bounded from below on ${\mathcal {N}}_\lambda$ which allows us to find a ground state solution for the problem (1.1). Initially, we have the following result

Proposition 2.1

Suppose $(\phi _{1}) - (\phi _{3})$ and (H). Then the functional $J_\lambda$ is coercive and bounded from below on ${\mathcal {N}}_\lambda$.

Proof

In view of (2.11), we get

$$\begin{aligned} J_{\lambda }(u)\ge \left( \displaystyle \frac{1}{m}-\displaystyle \frac{1}{\ell ^*} \right) \displaystyle \int _{\Omega }\phi (|\nabla u|)|\nabla u|^2\mathrm{d}x+\lambda \left( \displaystyle \frac{1}{\ell ^*}-\displaystyle \frac{1}{q}\right) \displaystyle \int _{\Omega }a(x)|u|^{q}\mathrm{d}x. \end{aligned}$$

Now due the fact that

$$\begin{aligned} \min \{||u||^\ell ,||u||^m\}\le \displaystyle \int _{\Omega }\Phi (|\nabla u|)\mathrm{d}x\le \displaystyle \frac{1}{\ell }\displaystyle \int _{\Omega }\phi (|\nabla u|)|\nabla u|^2\mathrm{d}x, \end{aligned}$$

we obtain

$$\begin{aligned} \begin{array}{rcl} J_{\lambda }(u)\ge & {} \ell \left( \displaystyle \frac{1}{m}-\displaystyle \frac{1}{\ell ^*} \right) \min \{||u||^\ell ,||u||^m\}+\lambda \left( \displaystyle \frac{1}{\ell ^*}-\displaystyle \frac{1}{q}\right) ||a^+||_{\infty }\displaystyle \int _{\Omega }|u|^{q}\mathrm{d}x. \end{array} \end{aligned}$$

(2.12)

Thus the functional $J_\lambda$ is coercive and bounded from below on ${\mathcal {N}}_\lambda$. Here was used hypothesis (H) and the fact that $|t|^{q}< < \Phi _{*}$ proving that $W_0^{1,\Phi }(\Omega )$ is embedding into $L^{q}(\Omega )$. This ends the proof. $\square$

At this moment, we shall define the fibering map $\gamma _u: [0,+\infty )\rightarrow {\mathbb {R}}$ by

$$\begin{aligned}\gamma _u(t):=J_{\lambda }(tu)=\displaystyle \int _{\Omega }\left[ \Phi (t|\nabla u|)-\displaystyle \frac{\lambda t^{q}}{q}a(x)|u|^{q}-\displaystyle \frac{t^{\ell ^*}}{\ell ^*}b(x)|u|^{\ell ^*}\right] \mathrm{d}x. \end{aligned}$$

Fibering maps have been considered together the Nehari manifold in order to ensure the existence of critical points for $J_{\lambda }$. In particular, for concave–convex nonlinearities is quite important to establish the geometry for the fibering map $\gamma _{u}$. Here we refer the reader to [14, 15, 59, 60].

Now we point out that $\gamma _{u}$ is in $C^{1}$ class thanks to hypotheses $(\phi _{1}) - (\phi _{2})$. More specifically, we obtain

$$\begin{aligned} \gamma '_u(t)= \displaystyle \int _{\Omega }\left[ t\phi (t|\nabla u|)|\nabla u|^2-\lambda t^{q-1}a(x)|u|^{q}-t^{\ell ^*-1} b(x)|u|^{\ell ^*}\right] \mathrm{d}x. \end{aligned}$$

It is easy to see that $tu\in {\mathcal {N}}_\lambda$ if and only if $\gamma '_u(t)=0.$ Therefore, $u\in {\mathcal {N}}_\lambda$ if and only if $\gamma '_u(1)=0.$ In other words, it is sufficient to find stationary points of fibering maps in order to get critical points for $J_{\lambda }$ on ${\mathcal {N}}_\lambda$. Notice also that, using $(\phi _{3})$, we deduce that $\gamma _{u}$ is of class $C^{2}$ with second derivative given by

$$\begin{aligned} \gamma ''_u(t)= & {} \displaystyle \int _{\Omega }\Big [t\phi '(t|\nabla u|)|\nabla u|^3+\phi (t|\nabla u|)|\nabla u|^2\\&\quad -\,\lambda (q-1)t^{q-2}a(x)|u|^{q} - (\ell ^*-1)t^{\ell ^*-2} b(x)|u|^{\ell ^*}\Big ]\mathrm{d}x, \,\, \forall ~ t > 0. \end{aligned}$$

As was pointed in [14, 15], it is natural to divide ${\mathcal {N}}_\lambda$ into three sets

$$\begin{aligned}&{\mathcal {N}}_\lambda ^+:=\{u\in {\mathcal {N}}_\lambda :\gamma ''_u(1)>0\};\\&{\mathcal {N}}_\lambda ^-:=\{u\in {\mathcal {N}}_\lambda :\gamma ''_u(1)<0\};\\&{\mathcal {N}}_\lambda ^0:=\{u\in {\mathcal {N}}_\lambda :\gamma ''_u(1)=0\}. \end{aligned}$$

Here we mention that ${\mathcal {N}}_\lambda ^+,~{\mathcal {N}}_\lambda ^-,~{\mathcal {N}}_\lambda ^0$ corresponds to critical points for the fibering map $\gamma _{u}(t)$ of minimum, maximum, and inflection points, respectively. Here we refer the reader also to [56].

Remark 2.1

It is not hard to verify that

$$\begin{aligned} \gamma ''_u(1)= & {} \displaystyle \int _{\Omega }\left[ \phi '(|\nabla u|)|\nabla u|^3+(2-q)\phi (|\nabla u|)|\nabla u|^2-(\ell ^*-q)b(x)|u|^{\ell ^*} \right] \mathrm{d}x\nonumber \\= & {} \displaystyle \int _{\Omega }\left[ \phi '(|\nabla u|)|\nabla u|^3+(2-\ell ^*)\phi (|\nabla u|)|\nabla u|^2-\lambda (q-\ell ^*)a(x)|u|^{q}\right] \mathrm{d}x\nonumber \\= & {} \displaystyle \int _{\Omega }\left[ \phi '(|\nabla u|)|\nabla u|^3+ 2 \phi (|\nabla u|)|\nabla u|^2 - \lambda q a(x)|u|^{q} - \ell ^{*} b(x)|u|^{\ell ^{*}}\right] \mathrm{d}x\nonumber \\ \end{aligned}$$

(2.13)

holds true for any $u\in {\mathcal {N}}_\lambda$. Here was used the fact that u belongs to the Nehari manifold.

Remark 2.2

Here we mention that $J_{\lambda }$ is not in $C^{2}$ class. However, there exist some directions $h \in W_0^{1,\Phi }(\Omega )$ such that $J_\lambda ^{''}(u)(h, h)$ is well defined. For example, we observe that $J_\lambda ^{''}(u)( u, u)$ is well defined and

$$\begin{aligned} J''_\lambda (u)\cdot (u,u)+\left<J'_\lambda (u),u\right>=\gamma ''_u(1), \quad \text{ for } \text{ any } \,\, u \in W_0^{1,\Phi }(\Omega ), u \ne 0. \end{aligned}$$

Now we shall prove that ${\mathcal {N}}_\lambda$ is a $C^1$-manifold. This step is crucial in our argument in order to get the main result in this work.

Lemma 2.1

Suppose $(\phi _{1}) - (\phi _{3})$. Then there exists $\lambda _{1} > 0$ such that

• (1) ${\mathcal {N}}_\lambda ^0=\emptyset$.

• (2) ${\mathcal {N}}_\lambda ={\mathcal {N}}_\lambda ^+\dot{\cup }{\mathcal {N}}_\lambda ^-$ is a $C^1$-manifold.

for each $\lambda \in (0, \lambda _{1})$.

Proof

First of all, we shall consider the proof for item (1). Arguing by contradiction we assume that ${\mathcal {N}}_\lambda ^0\ne \emptyset .$ Let $u\in {\mathcal {N}}_\lambda ^0$ be a fixed function. Clearly, we have $\gamma '_u(1)=\gamma ''_u(1)=0.$ Using (2.13) we obtain

$$\begin{aligned} \displaystyle \int _{\Omega }\left[ (2-q)\phi (|\nabla u| )|\nabla u|^2+\phi '(|\nabla u|)||\nabla u|^3+(q-\ell ^*)b|u|^{\ell ^*}\right] \mathrm{d}x = 0. \end{aligned}$$

Now taking into account hypothesis $(\phi _{3})$, we have that

$$\begin{aligned} (\ell -q)\displaystyle \int _{\Omega }\phi (|\nabla u| )|\nabla u|^2\mathrm{d}x\le (\ell ^*-q)||b^+||_{\infty }\Vert u\Vert _{\ell ^*}^{\ell ^*}\le (\ell ^*-q)S_{\ell ^*}||b^+||_{\infty }||u||^{\ell ^*}, \end{aligned}$$

where $S_{\ell ^*}$ is the best constant in the embedding $W_0^{1,\Phi }(\Omega )\hookrightarrow L^{\ell ^*}(\Omega ).$ On the other hand,

$$\begin{aligned} (\ell -q)\displaystyle \int _{\Omega }\phi (|\nabla u| )|\nabla u|^2\mathrm{d}x \ge \ell (\ell -q)\displaystyle \int _{\Omega }\Phi (|\nabla u|)\mathrm{d}x \ge \ell (\ell -q)\min \{||u||^\ell ,||u||^m\}. \end{aligned}$$

Taking into account the estimates just above, we observe that

$$\begin{aligned} \ell (\ell -q)\min \{||u||^\ell ,||u||^m\}\le (\ell ^*-q)S_{\ell ^*}||b^+||_{\infty }||u||^{\ell ^*}. \end{aligned}$$

Therefore, we obtain

$$\begin{aligned} ||u||^{\ell ^*}\ge \displaystyle \frac{\ell (\ell -q)}{(\ell ^*-q)S_{\ell ^*}||b^+||_{\infty }}\min \{||u||^\ell ,||u||^m\}=\left[ \displaystyle \frac{\ell (\ell -q)}{(\ell ^*-q)S_{\ell ^*}||b^+||_{\infty }}\right] ||u||^{\alpha }, \end{aligned}$$

where we put $\alpha =\ell$ for any $\Vert u\Vert \ge 1$ and $\alpha =m$ for any $\Vert u\Vert \le 1$. These facts imply that

$$\begin{aligned} ||u||\ge \left[ \displaystyle \frac{\ell (\ell -q)}{(\ell ^*-q)S_{\ell ^*}||b^+||_{\infty }}\right] ^{\frac{1}{\ell ^*-\alpha }}. \end{aligned}$$

(2.14)

Notice that, using $(\phi _3)$ and H$\ddot{o}$lder’s inequality for Sobolev spaces, we have

$$\begin{aligned} (\ell ^*-m)\displaystyle \int _{\Omega }\phi (|\nabla u| )|\nabla u|^2\mathrm{d}x\le \lambda (\ell ^*-q)||a^+||_{(\frac{\ell }{q})'}\Vert u\Vert _{\ell }^{q}\le \lambda (\ell ^*-q)S_{\ell }||a^+||_{(\frac{\ell }{q})'}||u||^{q}, \end{aligned}$$

where $S_{\ell }$ is a best constant in the embedding $W_0^{1,\Phi }(\Omega )\hookrightarrow L^{\ell }(\Omega )$. Here was used also the fact that $a \in L^{\infty }(\Omega )$ which is continuous embedding in $L^{(\frac{\ell }{q})'}(\Omega )$. Using the same ideas discussed in the previous case, we infer that

$$\begin{aligned} \ell (\ell ^*-m)\min \{||u||^\ell ,||u||^m\}\le \lambda (\ell ^*-q)S_{\ell }||a^+||_{(\frac{\ell }{q})'}||u||^{q}. \end{aligned}$$

Hence, the last assertion says that

$$\begin{aligned} \displaystyle \frac{\ell (\ell ^*-m)}{(\ell ^*-q)S_{\ell }||a^+||_{(\frac{\ell }{q})'}}||u||^\alpha =\displaystyle \frac{\ell (\ell ^*-m)}{(\ell ^*-q)S_{\ell }||a^+||_{(\frac{\ell }{q})'}}\min \{||u||^\ell ,||u||^m\}\le \lambda ||u||^{q}. \end{aligned}$$

In this way, we mention that

$$\begin{aligned} \left[ \displaystyle \frac{\ell (\ell ^*-m)}{(\ell ^*-q)S_{\ell }||a^+||_{(\frac{\ell }{q})'}}\right] ||u||^{\alpha -q}\le \lambda . \end{aligned}$$

(2.15)

Under these conditions, using (2.14) and (2.15), we get a contradiction for any

$$\begin{aligned} \lambda > \min _{\alpha \in \{ \ell , m \}} \left( \left[ \displaystyle \frac{\ell (\ell -q)}{(\ell ^*-q)S_{\ell ^*}||b^+||_{\infty }}\right] ^{\frac{\alpha -q}{\ell ^*-\alpha }}\left[ \displaystyle \frac{\ell (\ell ^*-m)}{(\ell ^*-q)S_{\ell }||a^+||_{(\frac{\ell }{q})'}}\right] \right) =:\lambda _1. \end{aligned}$$

(2.16)

This finishes the proof of item (1).

Now we shall prove the item (2). Without any loss of generality, we take $u\in {\mathcal {N}}_\lambda ^+$. Define $\psi (u):=\left<J'_\lambda (u),u\right>.$ It is no hard to see that

$$\begin{aligned} \psi '(u)=J''_\lambda (u)\cdot (u,u)+\left<J'_\lambda (u),u\right>=\gamma ''_u(1)>0,\,\,\ \forall \, u\in {\mathcal {N}}_\lambda ^+. \end{aligned}$$

Hence, 0 is a regular value for the functional $\psi$. Consequently, we see that ${\mathcal {N}}_\lambda ^+$ is a $C^1$-manifold. Similarly, we should be show that ${\mathcal {N}}_\lambda ^-$ is a $C^1$-manifold. As a consequence the proof of item (2) follows due the fact that ${\mathcal {N}}_\lambda ^{0}=\emptyset$ for any $\lambda > 0$ small enough. This completes the proof. $\square$

Now we are in a position to prove that any critical point for $J_{\lambda }$ on ${\mathcal {N}}_\lambda$ is a free critical point, i.e., any minimizer for $J_{\lambda }$ in the Nehari manifold ${\mathcal {N}}_{\lambda }$ is a critical point for $J_{\lambda }$ in the whole space $W^{1,\Phi }_{0}(\Omega )$. More precisely, we shall consider the following result

Lemma 2.2

Suppose $(\phi _{1}) - (\phi _{3})$. Let $u_0$ be a local minimum (or local maximum) for $J_\lambda$ on ${\mathcal {N}}_{\lambda }$. Then $u_0$ is a critical point of $J_\lambda$ on $W_0^{1,\Phi }(\Omega )$ for each $\lambda <\lambda _1$.

Proof

Let $u_{0} \in {\mathcal {N}}_\lambda$ be a local maximum or minimum for the functional $J_{\lambda }$ on ${\mathcal {N}}_\lambda$. Without any loss of generality, we assume that $u_0$ is a local minimum. Define the function

$$\begin{aligned} \theta (u)=\left<J_\lambda '(u),u\right>=\displaystyle \int _{\Omega }\left[ \phi (|\nabla u|)|\nabla u|^2-\lambda a(x) |u|^{q}-b(x)|u|^{\ell ^*}\right] \mathrm{d}x. \end{aligned}$$

It is easy to see that $u_0$ is a solution for the minimization problem

$$\begin{aligned} \left\{ \begin{array}{l} \min J_\lambda (u),\\ \theta (u)=0 \end{array}\right. \end{aligned}$$

(2.17)

From now on the proof for this lemma is standard, and we omit the details. $\square$

3 Analysis of the fibering maps

In this section, we give a complete description on the geometry for the fibering maps associated to the problem (1.1). Let $u \in W_0^{1,\Phi }(\Omega )\backslash \{0\}$ be a fixed function. To the best our knowledge, the essential nature of fibering maps is determined by the signs of $\displaystyle \int _{\Omega }a(x)|u|^q\mathrm{d}x$ and $\displaystyle \int _{\Omega }b(x)|u|^{\ell ^*}\mathrm{d}x$. Throughout this section is useful to consider the auxiliary function of $C^{1}$ class given by

$$\begin{aligned}m_u(t)=t^{2-q}\displaystyle \int _{\Omega }\phi (t|\nabla u|)|\nabla u|^2\mathrm{d}x-t^{\ell ^*-q}\displaystyle \int _{\Omega }b(x)|u|^{\ell ^*}\mathrm{d}x, t \ge 0, u \in W_0^{1,\Phi }(\Omega )\backslash \{0\}.\end{aligned}$$

Now we shall consider a result comparing points $t u \in {\mathcal {N}}_\lambda$ with the function $m_{u}$. More precisely, we have

Lemma 3.1

Suppose that $(\phi _{1}) - (\phi _{3})$ holds. Let $t>0$ be fixed. Then $tu\in {\mathcal {N}}_\lambda$ if and only if t is a solution of

$$\begin{aligned} m_u(t)=\lambda \displaystyle \int _{\Omega }a(x) |u|^{q}\mathrm{d}x, u \in W_0^{1,\Phi }(\Omega )\backslash \{0\}. \end{aligned}$$

Proof

The proof is quite standard and we omit the details. $\square$

The next lemma is a powerful tool in order to get a precise information around the function $m_{u}$ and the fibering maps. More precisely, we shall consider the following result

Lemma 3.2

Suppose that $(\phi _{1}) - (\phi _{3})$ hold.

• (1) Suppose that $\displaystyle \int _{\Omega }b(x)|u|^{\ell ^*}\mathrm{d}x\le 0$ holds. Then we obtain $\displaystyle m_{u}(0) := \lim _{t \rightarrow 0} m_{u}(t)=0 , m_{u}(\infty ) := \lim _{t \rightarrow \infty } m_{u}(t) = \infty$ and $m'_u(t)>0$ for any $t>0$.

• (2) Suppose $\displaystyle \int _{\Omega }b(x)|u|^{\ell ^*}\mathrm{d}x>0$. Then there exists an only critical point for $m_{u}$, i.e., there is an only point $\tilde{t}>0$ in such way that $m'_u(\tilde{t})=0$. Furthermore, we know that $\tilde{t} > 0$ is a global maximum point for $m_{u}$ and $m_{u}(\infty ) = - \infty$.

Proof

First of all, we observe that

$$\begin{aligned} m'_u(t)= & {} (2-q)t^{1-q}\displaystyle \int _{\Omega }\phi (t|\nabla u|)|\nabla u|^2\mathrm{d}x+t^{2-q}\displaystyle \int _{\Omega }\phi '(|\nabla (tu)|)|\nabla u|^3\mathrm{d}x\\&-\, (\ell ^*-q)t^{\ell ^*-q-1}\displaystyle \int _{\Omega }b(x)|u|^{\ell ^*}\mathrm{d}x. \end{aligned}$$

In this way the proof follows using the same ideas discussed in Lemma 4.2 and Lemma 4.3 given in [17]. The details are omit here. $\square$

Now we shall prove that $m_{u}$ has a behavior at infinity and at the origin given by the sings of $\int _{\Omega } a(x)|u|^{q}\mathrm{d}x$ and $\int _{\Omega } b(x)|u|^{\ell ^*}\mathrm{d}x$. This is crucial in to prove a complete description on the geometry for the fibering maps. The hypothesis (H) is the main tool in order to prove the uniqueness of projection in each part for ${\mathcal {N}}_{\lambda }^{\pm }$.

Lemma 3.3

Suppose that $(\phi _{1}) - (\phi _{3})$ and (H) hold. Let $u\in W^{1,\Phi }_0(\Omega )/\{0\}$ be a fixed function. Then we shall consider the following assertions:

• (1) Assume that $\displaystyle \int _{\Omega }b(x)|u|^{\ell ^*} \mathrm{d}x\le 0$. Then $\gamma '_u(t)\ne 0$ for any $t>0$ and $\lambda > 0$ whenever $\displaystyle \int _{\Omega }a(x)|u|^{q}\mathrm{d}x \le 0$. Furthermore, there exist an unique $t_1= t_1(u,\lambda )$ in such way that $\gamma '_u(t_1)=0$ and $t_1 u\in {\mathcal {N}}_\lambda ^+$ whenever $\displaystyle \int _{\Omega }a(x)|u|^{q} \mathrm{d}x> 0.$

• (2) Assume that $\displaystyle \int _{\Omega }b(x)|u|^{\ell ^*}\mathrm{d}x > 0$ holds. Then there exists an unique $t_1=t_1(u,\lambda )> {\tilde{t}}$ such that $\gamma '_u(t_1)= 0$ and $t_1 u\in {\mathcal {N}}_\lambda ^-$ whenever $\displaystyle \int _{\Omega }a(x)|u|^{q} \mathrm{d}x\le 0$.

• (3) For each $\lambda >0$ small enough, there exists unique $0<t_1=t_1(u,\lambda )<{\tilde{t}}<t_2=t_2(u,\lambda )$ such that $\gamma '_u(t_1)=\gamma '_u(t_2)=0$, $t_1 u\in {\mathcal {N}}_\lambda ^+$ and $t_2 u\in {\mathcal {N}}_\lambda ^-$ whenever $\displaystyle \int _{\Omega }a(x)|u|^{q}\mathrm{d}x> 0$, $\displaystyle \int _{\Omega }b(x)|u|^{\ell ^*}\mathrm{d}x> 0$ holds.

Proof

First of all, we shall consider the proof for the case $\displaystyle \int _{\Omega }b(x)|u|^{\ell ^*}\mathrm{d}x\le 0$ and $\displaystyle \int _{\Omega }a(x)|u|^{q}\mathrm{d}x\le 0$. Using Lemma 3.2 (1) it is easy to verify that

$$\begin{aligned} m_u(0)=0, m_u(\infty ) = \infty \,\,\text{ and } \,\, m'_u(t)>0, t \ge 0. \end{aligned}$$

Under these conditions we deduce that

$$\begin{aligned} m_u(t)\ne \lambda \displaystyle \int _{\Omega }a(x)|u|^{q} \mathrm{d}x\quad \text{ for } \text{ any } \,\,t>0, \lambda >0. \end{aligned}$$

According to Lemma 3.1 we obtain that $tu\not \in {\mathcal {N}}_\lambda$ for any $t>0$. In particular, we see also that $\gamma '(t)\ne 0$ for each $t>0$.

Now we shall consider the proof for the case $\displaystyle \int _{\Omega }a(x)|u|^{q}\mathrm{d}x > 0$ and $\displaystyle \int _{\Omega }b(x)|u|^{\ell ^*}\mathrm{d}x \le 0$. Using one more time Lemma 3.2 (1) we observe that $m_{u}(0)= 0 , m_{u}(\infty ) = \infty$ and $m_{u}$ is a strictly increasing function. In particular, the equation

$$\begin{aligned} m_u(t)= \lambda \displaystyle \int _{\Omega }a(x)|u|^{q}\mathrm{d}x \end{aligned}$$

admits exactly one solution $t_1= t_1(u,\lambda )>0$. Hence, using Lemma 3.1, we know that $t_1 u\in {\mathcal {N}}_\lambda$ proving that $\gamma '_u( t_1) =0$. Additionally, using the identity

$$\begin{aligned} m_u(t)=t^{1-q}\gamma _u'(t)+\lambda \displaystyle \int _{\Omega }a(x)|u|^{q}\mathrm{d}x, \end{aligned}$$

we easily see that

$$\begin{aligned} 0<m'_u(t_1) = t_1^{1-q}\gamma ''_u(t_1). \end{aligned}$$

In particular, we have been proven that $t_1u\in {\mathcal {N}}_\lambda ^+$.

Now we shall consider the proof for the case $\displaystyle \int _{\Omega }a(x) |u|^{q } \mathrm{d}x\le 0$ and $\displaystyle \int _{\Omega }b(x) |u|^{\ell ^*} \mathrm{d}x > 0$. Here the function $m_{u}$ admits an unique turning point $\tilde{t} > 0$, i.e., we have that $m^{\prime }_{u}(t) = 0, t > 0$ if only if $t = \tilde{t}$; see Lemma 3.2 (2). Moreover, $\tilde{t}$ is a global maximum point for $m_{u}$ in such way that $m_{u}(\tilde{t}) > 0, m_{u}(\infty ) = - \infty$. As a product, there exits an unique $t_1>{\tilde{t}}$ such that

$$\begin{aligned} m_u(t_1)= \lambda \displaystyle \int _{\Omega }a(x)|u|^{q}\mathrm{d}x. \end{aligned}$$

Here we emphasize that $m_u'(t_1)<0$ where we have used the fact that $m_{u}$ is a strictly decreasing function in $(\tilde{t}, \infty )$. As a consequence we obtain $0>m'_u(t_1)=t_1^{1-q}\gamma _u''(t_1)$ proving that $t_1u\in {\mathcal {N}}_\lambda ^-$.

At this moment, we shall consider the proof for the case $\displaystyle \int _{\Omega }a(x)|u|^{q}\mathrm{d}x > 0$ and $\displaystyle \int _{\Omega }b(x)|u|^{\ell ^*} \mathrm{d}x> 0$. Due the fact that $\displaystyle \int _{\Omega }a(x)|u|^{q}>0$ we obtain $\bar{\lambda }_1>0$ such that

$$\begin{aligned} m_u({\tilde{t}}) > \lambda \displaystyle \int _{\Omega }a(x)|u|^{q}\mathrm{d}x,\quad \text{ for } \text{ any } \,\, \lambda \in (0,\bar{\lambda }_1). \end{aligned}$$

(3.18)

It is worthwhile to mention that $m_{u}$ is increasing in $(0, \tilde{t})$ and decreasing in $(\tilde{t}, \infty )$. It is not hard to verify that there exist exactly two points $0<t_1=t_1(u,\lambda )<{\tilde{t}} < t_2=t_2(u,\lambda )$ such that

$$\begin{aligned} m_u(t_i)=\lambda \displaystyle \int _{\Omega }a(x)|u|^{q}\mathrm{d}x,\quad i=1,2. \end{aligned}$$

Additionally, we have that $m_u'(t_1)>0$ and $m_u'(t_2)<0$. Arguing as in the previous step we ensure that $t_1u\in {\mathcal {N}}_\lambda ^+$ and $t_2u\in {\mathcal {N}}_\lambda ^-$. This completes the proof. $\square$

The next lemma shows that for any $\lambda >0$ small enough the function $J_{\lambda }(u)$ assumes positive values. More specifically, we shall show also that $J_\lambda$ is away from zero on the Nehari manifold ${\mathcal {N}}_\lambda ^{-}$. In particular, any critical point for $J_{\lambda }$ on ${\mathcal {N}}_\lambda ^{-}$ provide us a nontrivial critical point. This is crucial for the proof of our main theorems proving that $\gamma _u$ admits one or two critical points.

Lemma 3.4

Suppose that $(\phi _{1}) - (\phi _{3})$ hold. There exist $\delta _1, \tilde{\lambda }_1>0$ in such way that $J_\lambda (u)\ge \delta _1$ for any $u\in {\mathcal {N}}_\lambda ^{-}$ where $0<\lambda < \tilde{\lambda }_1$.

Proof

Since $u\in {\mathcal {N}}_\lambda ^-,$ we have that $\gamma ''_{u}(1)<0$. Arguing as in the proof of Lemma 2.1, we obtain

$$\begin{aligned} ||u||>\left[ \displaystyle \frac{\ell (\ell -q)}{(\ell ^*-q)S_{\ell ^*}\Vert b^+\Vert _{\infty }}\right] ^{\frac{1}{\ell ^*-\alpha }}. \end{aligned}$$

Moreover, in view of (2.12) and the Sobolev imbedding, we have that

$$\begin{aligned}\begin{array}{rcl} J_{\lambda }(u)&{}\ge &{}\ell \left( \displaystyle \frac{1}{m}-\displaystyle \frac{1}{\ell ^*} \right) \min \{||u||^\ell ,||u||^m\}+\lambda \left( \displaystyle \frac{1}{\ell ^*}-\displaystyle \frac{1}{q}\right) \displaystyle \int _{\Omega }a(x)|u|^{q}\mathrm{d}x\\ &{}=&{}\ell \left( \displaystyle \frac{1}{m}-\displaystyle \frac{1}{\ell ^*} \right) ||u||^\alpha +\lambda \left( \displaystyle \frac{1}{\ell ^*}-\displaystyle \frac{1}{q}\right) \displaystyle \int _{\Omega }a(x)|u|^{q}\mathrm{d}x\\ &{}\ge &{}||u||^q\left[ \ell \left( \displaystyle \frac{1}{m}-\displaystyle \frac{1}{\ell ^*} \right) ||u||^{\alpha -q}+\lambda \left( \displaystyle \frac{1}{\ell ^*}-\displaystyle \frac{1}{q}\right) \Vert a^+\Vert _{\left( \frac{\ell }{q}\right) '}S_{\ell }\right] . \end{array}\end{aligned}$$

Using the inequalities just above we get

$$\begin{aligned}J_{\lambda }(u)>\left[ \displaystyle \frac{\ell (\ell -q)}{(\ell ^*-q)S_{\ell ^*}\Vert b^+\Vert _{\infty }}\right] ^{\frac{q}{\ell ^*-\alpha }}\left[ A +\lambda B \right] \end{aligned}$$

where

$$\begin{aligned}A = \ell \left( \displaystyle \frac{1}{m}-\displaystyle \frac{1}{\ell ^*} \right) \left( \displaystyle \frac{\ell (\ell -q)}{(\ell ^*-q)S_{\ell ^*}\Vert b^+\Vert _{\infty }}\right) ^{\frac{\alpha -q}{\ell ^*-\alpha }}\end{aligned}$$

and

$$\begin{aligned} B = \left( \displaystyle \frac{1}{\ell ^*} -\displaystyle \frac{1}{q}\right) \Vert a^+\Vert _{\left( \frac{\ell }{q}\right) '}S_{\ell }.\end{aligned}$$

Therefore, for each $0<\lambda <\tilde{\lambda }_1:=\displaystyle \frac{q}{m}\lambda _1$ where we take $\lambda _{1}>0$ given by (2.16). Here we put $\tilde{\lambda }_1:=\displaystyle \frac{q}{m}\lambda _1$ obtaining the desired result. This finishes the proof. $\square$

Now we shall prove that any minimizer on ${\mathcal {N}}_\lambda ^{+}$ has negative energy. More specifically, defining $\alpha _\lambda :=\displaystyle \inf _{u\in {\mathcal {N}}_\lambda }J_\lambda (u) , \alpha _\lambda ^+=\displaystyle \inf _{u\in {\mathcal {N}}_\lambda ^+} J_\lambda (u)$ we can be shown the following result

Lemma 3.5

Suppose that $(\phi _{1}) - (\phi _{3})$ and (H) hold. Then there exist $u \in {\mathcal {N}}_\lambda ^{+}$ and $\lambda _{1} > 0$ in such way that $\alpha _{\lambda }^{+} \le J_\lambda (u) < 0$ for each $0<\lambda < \lambda _1$. In particular, we obtain $\alpha _{\lambda } = \alpha _{\lambda }^{+}$ for each $0<\lambda < \lambda _1$.

Proof

Fix $u\in {\mathcal {N}}_\lambda ^+$. Here we observe that $\gamma _u''(1)>0$. Using hypothesis $(\phi _{3})$ we infer that

$$\begin{aligned} \begin{array}{rcl} \displaystyle (\ell ^*-q)\int _\Omega b(x)|u|^{\ell ^*}\mathrm{d}x&{}<&{}\displaystyle \int _{\Omega }\left[ \phi '(|\nabla u|)|\nabla u|^3+(2-q)\phi (|\nabla u|)|\nabla u|^2\right] \mathrm{d}x \\ &{}\le &{}\displaystyle \int _{\Omega }\left[ (m-2)\phi (|\nabla u|)|\nabla u|^2+(2-q)\phi (|\nabla u|)|\nabla u|^2\right] \mathrm{d}x\\ &{}=&{}(m-q)\displaystyle \int _{\Omega }\phi (|\nabla u|)|\nabla u|^2\mathrm{d}x. \end{array}\end{aligned}$$

The last inequalities imply that

$$\begin{aligned} \int _\Omega b(x)|u|^{\ell ^*}\mathrm{d}x<\displaystyle \frac{m-q}{\ell ^*-q}\displaystyle \int _{\Omega }\phi (|\nabla u|)|\nabla u|^2\mathrm{d}x. \end{aligned}$$

On the other hand, using the inequality just above and the fact that $u \in {\mathcal {N}}_{\lambda }$ we get

$$\begin{aligned}\begin{array}{rcl} J_\lambda (u)&{}\le &{} \left( \displaystyle \frac{1}{\ell }-\displaystyle \frac{1}{q}\right) \displaystyle \int _{\Omega }\left[ \phi (|\nabla u|)|\nabla u|^2\mathrm{d}x+\left( \displaystyle \frac{1}{q}-\displaystyle \frac{1}{\ell ^*}\right) b(x)|u|^{\ell ^*}\right] \mathrm{d}x\\ &{}<&{} \displaystyle \frac{1}{q}\left[ \displaystyle \frac{q-\ell }{\ell }\mathrm{d}x+\displaystyle \frac{m-q}{\ell ^*}\right] \displaystyle \int _{\Omega }\phi (|\nabla u|)|\nabla u|^2\mathrm{d}x. \end{array}\end{aligned}$$

In view of hypothesis (H) it follows that $\alpha ^+_\lambda \le J_{\lambda }(u) <0$. Additionally, we stress that ${\mathcal {N}}_\lambda ={\mathcal {N}}_\lambda ^-\cup {\mathcal {N}}_\lambda ^+$ and $\alpha _\lambda ^->0$ see Lemma 3.4. Hence we deduce that $\alpha _\lambda ^+=\alpha _\lambda$. This finishes the proof. $\square$

4 The Palais–Smale condition

In this section we shall prove some auxiliary results in order to get the Palais–Smale condition for the functional $J_{\lambda }$ on the Nehari manifold. In general, given any Banach space X endowed with the norm $\Vert .\Vert$ and taking $I : X \rightarrow {\mathbb {R}}$ a functional of $C^{1}$ class we recall that a sequence $(u_{n}) \in X$ is said to be a Palais–Smale sequence at level $c \in {\mathbb {R}}$, in short $(PS)_{c}$, when $I(u_{n}) \rightarrow c$ and $I^{\prime }(u_{n}) \rightarrow 0$ as $n \rightarrow \infty$. Recall that I satisfies the Palais–Smale condition at the level c, in short $(PS)_{c}$ condition, when any $(PS)_{c}$ sequence admits a convergent subsequence. We say simply that I verifies the Palais–Smale condition when $(PS)_{c}$ condition holds true for any $c \in {\mathbb {R}}$.

Now we follow same ideas discussed in [56]. The main feature here is to find a suitable sequence $(u_{n}) \in {\mathcal {N}}_{\lambda }$. Initially, we consider the following result

Lemma 4.1

Suppose $(\phi _{1})- (\phi _{3})$ and (H). Let $u \in {\mathcal {N}}_\lambda ^{+}$ be fixed. Then there exist $\epsilon >0$ and a differentiable function

$$\begin{aligned} \xi :B(0,\epsilon )\subset W_{0}^{1,\Phi }(\Omega )\rightarrow (0, \infty ),\ \ \ \xi (0)=1,\,\ \xi (v)(u-v)\in {\mathcal {N}}_\lambda ^{+}, v \in B(0,\epsilon ). \end{aligned}$$

Furthermore, for any $\lambda > 0$ small enough we get

$$\begin{aligned} \left<\xi '(0),v\right>= & {} \dfrac{1}{\gamma ''_u(1)} \displaystyle \int _{\Omega }\Big [(\phi '(|\nabla u|)|\nabla u|+2\phi (|\nabla u|))\nabla u\nabla v\nonumber \\&\quad -\,\ell ^*b(x)|u|^{\ell ^*-2}uv - q\lambda a(x)|u|^{q-2}uv \Big ]\mathrm{d}x. \end{aligned}$$

(4.19)

Proof

Initially, we define $\psi : W_0^{1,\Phi }(\Omega )\backslash \{ 0\} \rightarrow {\mathbb {R}}$ given by $\psi (u)=\left<J'_\lambda (u),u\right>$ for $u \in W_0^{1,\Phi }(\Omega )\backslash \{ 0\}$. It is easy to verify that

$$\begin{aligned} \left<\psi '(u),u\right>=\displaystyle \int _{\Omega }\left[ \phi '(|\nabla u|)|\nabla u|^3+2\phi (|\nabla u|)|\nabla u|^2-\ell ^*b(x)|u|^{\ell ^*}-q\lambda a(x)|u|^{q}\right] \mathrm{d}x. \end{aligned}$$

Recall that $\left<\psi '(u),u\right>=\gamma ''_u(1)$ holds for any $u\in {\mathcal {N}}_\lambda$ where $\gamma ''_u(1)$ is given by Remark 2.1.

Now we define $F_u : {\mathbb {R}} \times W_0^{1,\Phi }(\Omega )\backslash \{0\} \rightarrow {\mathbb {R}}$ given by

$$\begin{aligned} F_{u}(\xi ,w)= \left<J'_\lambda (\xi (u-w)),\xi (u-w)\right>. \end{aligned}$$

Here we observe that $F_u(1,0)=\psi (u)$. As a consequence

$$\begin{aligned} \partial _{1} F_u(\xi ,w)= & {} \displaystyle \int _{\Omega }\left[ 2\xi \phi (\xi |\nabla (u-w)|)|\nabla (u-w)|^2+\xi ^2\phi '(\xi |\nabla (u-w)|)|\nabla (u-w)|^3\right] \mathrm{d}x \\&- \displaystyle \int _{\Omega }\left[ \ell ^*\xi ^{\ell ^*-1} b(x)|u-w|^{\ell ^*} + q\xi ^{q-1}\lambda a(x)|u-w|^q\right] \mathrm{d}x. \end{aligned}$$

In particular, for each $u\in {\mathcal {N}}_\lambda ^{+}$, we mention that

$$\begin{aligned} \partial _{1} F_u(1,0)= & {} \displaystyle \int _{\Omega }\Big [2\phi (|\nabla u|)|\nabla u|^2+\phi '(|\nabla u|)|\nabla u|^3\mathrm{d}x - \ell ^*b(x)|u|^{\ell ^*}\\&+\, q\lambda a(x)|u|^q\Big ]\mathrm{d}x=\gamma _u''(1) > 0. \end{aligned}$$

As a product, using the inverse function theorem, there exist $\epsilon >0$ and a differentiable function $\xi :B(0,\epsilon )\subset W^{1,\Phi }(\Omega )\rightarrow (0, \infty )$ satisfying $\xi (0)=1$ and $F_u(\xi (w),w)= \left<J'_\lambda (\xi (u- w),\xi (u-w))\right> = 0,$ i.e. $\xi (w)(u-w)\in {\mathcal {N}}_\lambda ^{+},\ \ \forall w\in B(0,\epsilon )$. The main idea here is to apply the inverse function theorem for the function $F_{u}$ for some $u \in {\mathcal {N}}_\lambda ^{+}$. Furthermore, we also obtain

$$\begin{aligned} \left<\xi '(w),v\right>=-\,\displaystyle \frac{\left<\partial _2F_u(\xi (w),w),v\right>}{\partial _1F_u(\xi (w),w)}, \left<\xi '(0),v\right>=-\,\displaystyle \frac{\left<\partial _2F_u(\xi (0),0),v)\right>}{\partial _1F_u(\xi (0),0)}. \end{aligned}$$

Here $\partial _1F_u$ and $\partial _2F_u$ denote the partial derivatives on the first and second variable, respectively.

On the other hand, after some manipulations, we see that

$$\begin{aligned}\begin{array}{rcl} \left<\partial _2F_u(\xi (w),w),v\right>&{}=&{} -\, \xi ^2\displaystyle \int _{\Omega }\phi '(\xi |\nabla (u-w)|) |\nabla (u-w)| \nabla (u-w) \nabla v \mathrm{d}x\\ &{}&{}-\, 2\xi ^2\displaystyle \int _{\Omega }\phi (\xi |\nabla (u-w)) \nabla (u-w) \nabla v \mathrm{d}x\\ &{}&{}+\,\ell ^*\xi ^{\ell ^*}\displaystyle \int _{\Omega }b(x)|u-w|^{\ell ^*-2}(u-w) v\mathrm{d}x\\ &{}&{}+\,\lambda q \xi ^{q}\displaystyle \int _{\Omega }a(x)|u-w|^{q-2}(u-w)v\mathrm{d}x. \end{array} \end{aligned}$$

Hence, putting $w=0$ and $\xi =\xi (0)=1$, the last identity just above shows that

$$\begin{aligned} \left<\partial _2F_u(1,0),v\right>= & {} -\displaystyle \int _{\Omega }\Big [\phi '(|\nabla u|) |\nabla u| \nabla u \nabla v\\&\quad +\, 2 \phi (|\nabla u|) \nabla u \nabla v - \ell ^*b(x)|u|^{\ell ^*-2} uv -\lambda q a(x)|u|^{q-2}uv\Big ]\mathrm{d}x \end{aligned}$$

Here was used the fact that $\partial _1 F_u(1,0)=\gamma _{u}''(1)$ holds for any $u\in {\mathcal {N}}_\lambda ^{+}$. The proof is now finished. $\square$

Analogously, using the same ideas discussed in the previous result, we get the following result

Lemma 4.2

Suppose $(\phi _{1})- (\phi _{3})$ and (H). Let $u \in {\mathcal {N}}_\lambda ^{-}$ be fixed. Then there are $\epsilon >0$ and a differentiable function

$$\begin{aligned} \xi :B(0,\epsilon )\subset W^{1,\Phi }(\Omega )\rightarrow (0, \infty ),\ \ \ \xi (0)=1,\,\ \xi (v)(u-v)\in {\mathcal {N}}_\lambda ^{-}, \, v \in B(0,\epsilon ). \end{aligned}$$

Furthermore, for any $\lambda > 0$ small enough we obtain

$$\begin{aligned} \langle \xi ^{\prime }(0),v \rangle= & {} \dfrac{1}{\gamma ''_u(1)} \displaystyle \int _{\Omega }\Big [(\phi '(|\nabla u|)|\nabla u|+2\phi (|\nabla u|))\nabla u\nabla v\nonumber \\&-\,\ell ^*b(x)|u|^{\ell ^*-2}uv - q \lambda a(x)|u|^{q-2}uv\Big ]\mathrm{d}x. \end{aligned}$$

(4.20)

In the next result, we shall prove that any minimizer sequence for the functional $J_{\lambda }$ in ${\mathcal {N}}_{\lambda }^{-}$ or ${\mathcal {N}}_{\lambda }^{+}$ is bounded from below and above for some positive constants. This is crucial in order to get a minimizer on the Nehari manifold.

Proposition 4.1

Suppose $(\phi _{1})- (\phi _{3})$ and (H). Let $(u_n)$ be a minimizer sequence for the functional $J_{\lambda }$ on the Nehari manifold ${\mathcal {N}}_{\lambda }^{+}$. Then

$$\begin{aligned} \liminf _{n \rightarrow \infty } ||u_n|| \ge - \alpha _\lambda ^{\frac{1}{q}} \left[ \displaystyle \frac{\ell ^*q}{(\ell ^*-q)\lambda \Vert a\Vert _\infty S^{q}_{q}}\right] ^{\frac{1}{q}} > 0 \end{aligned}$$

(4.21)

and

$$\begin{aligned} ||u_n||< \left[ \displaystyle \frac{\lambda }{q}\left( \displaystyle \frac{\ell ^*-q}{\ell ^*-m}\right) \Vert a\Vert _\infty S^{q}_{q}\right] ^{\frac{1}{\alpha -q}}, \end{aligned}$$

(4.22)

where $\alpha \in \{\ell ,m\}$. The same property can be ensured for the Nehari manifold ${\mathcal {N}}_{\lambda }^{-}$, i.e., we have that $(u_n) \in {\mathcal {N}}_{\lambda }^{-}$ is bounded form above and below by positive constants.

Proof

Let $(u_n)\subset {\mathcal {N}}_\lambda$ be a fixed sequence. Recall that $m\Phi (t)\le \phi (t)t^2$ holds for any $t \in {\mathbb {R}}$. Using the inequalities just above, we obtain that

$$\begin{aligned} \begin{array}{rcl} 0> \alpha _\lambda ^{+} + o_{n}(1) &{}=&{}J_\lambda (u_n)=\displaystyle \int _{\Omega }\left[ \Phi (|\nabla u_n|) - \displaystyle \frac{1}{\ell ^*}\phi (|\nabla u_n|) |\nabla u_n|^{2}-\lambda \left( \frac{1}{q}-\frac{1}{\ell ^*}\right) a(x)|u_n|^q \right] \mathrm{d}x\\ &{}\ge &{} \displaystyle \int _{\Omega }\left[ \left( 1-\displaystyle \frac{m}{\ell ^*}\right) \Phi (|\nabla u_n|)-\lambda \left( \frac{1}{q}-\frac{1}{\ell ^*}\right) a(x)|u_n|^q\right] \mathrm{d}x \end{array} \end{aligned}$$

(4.23)

holds for any $n\in \mathbb {N}$ large enough. Under these conditions, using the above inequality and the continuous embedding $W_0^{1,\Phi }(\Omega )\hookrightarrow L^q(\Omega )$, we easily see that

$$\begin{aligned}0<-\left( \alpha _\lambda ^++\displaystyle \frac{1}{n}\right) \left[ \displaystyle \frac{\ell ^*q}{(\ell ^*-q)\lambda }\right] <\displaystyle \int _{\Omega }a(x)|u|^q\mathrm{d}x\le ||a||_\infty S^{q}_{q}||u_n||^q.\end{aligned}$$

Here $S_{q}$ is the best constant for the embedding $W_0^{1,\Phi }(\Omega )\hookrightarrow L^q(\Omega )$. As a product the last estimate says that

$$\begin{aligned} ||u_n||> \left[ -\left( \alpha _\lambda ^++\displaystyle \frac{1}{n}\right) \displaystyle \frac{\ell ^*q}{(\ell ^*-q)\lambda \Vert a\Vert _\infty S^{q}_{q}}\right] ^{\frac{1}{q}}. \end{aligned}$$

As a consequence using the last estimate and Lemma 3.5, we see also that (4.21) holds.

Furthermore, using (4.23) and arguing as in the previous inequalities, we can also shown that

$$\begin{aligned} \displaystyle \min \{||u_n||^\ell ,||u_n||^m\}\le \displaystyle \int _{\Omega }\Phi (|\nabla u_n|)\mathrm{d}x< & {} \lambda \left( \displaystyle \frac{\ell ^*}{\ell ^*-m}\right) \left( \displaystyle \frac{\ell ^*-q}{\ell ^*q}\right) \Vert a\Vert _\infty S^{q}_{q} ||u_n||^q\nonumber \\= & {} \displaystyle \frac{\lambda }{q}\left( \displaystyle \frac{\ell ^*-q}{\ell ^*-m}\right) \Vert a\Vert _\infty S^{q}_{q}||u_n||^q. \end{aligned}$$

(4.24)

Hence the last assertions give us

$$\begin{aligned}\min \{||u_n||^{\ell -q},||u_n||^{m-q}\}<\lambda \left( \displaystyle \frac{\ell ^*}{\ell ^*-m}\right) \left( \displaystyle \frac{\ell ^*-q}{\ell ^*q}\right) \Vert a\Vert _\infty S^{q}_{q}= \displaystyle \frac{\lambda }{q}\left( \displaystyle \frac{\ell ^*-q}{\ell ^*-m}\right) \Vert a\Vert _\infty S^{q}_{q}.\end{aligned}$$

As a consequence we obtain (4.22). $\square$

Now we consider two technical results in order to prove that any minimizer sequence for $J_{\lambda }$ on the Nehari manifold is a Palais–Smale sequence.

Proposition 4.2

Suppose $(\phi _{1})- (\phi _{3})$ and (H). Then any minimizer sequence $(u_n)$ on the Nehari manifold ${\mathcal {N}}_{\lambda }^{-}$ or ${\mathcal {N}}_{\lambda }^{+}$ satisfies

$$\begin{aligned} \left<J'_\lambda (u_n), \displaystyle \frac{u}{||u||}\right>\le \displaystyle \frac{C}{n}[||\xi '_n(0)||+1],~u\in W^{1,\Phi }(\Omega )/\{0\}, \end{aligned}$$

(4.25)

where $\xi _n:=\xi :B_{\frac{1}{n}}(0)\rightarrow (0,\infty )$ was obtained from Lemma 4.1 and Lemma 4.2.

Proof

Let $(u_n)$ be a minimizer sequence on the Nehari manifold ${\mathcal {N}}_{\lambda }^{-}$ or ${\mathcal {N}}_{\lambda }^{+}$. Here we shall consider the proof for the Nehari manifold ${\mathcal {N}}_{\lambda }^{+}$. The proof for the Nehari manifold ${\mathcal {N}}_{\lambda }^{-}$ follows arguing in the same way. According to Lemma 4.1, we obtain

$$\begin{aligned}\xi _n:B(0,\epsilon _n) \rightarrow {\mathbb {R}}^+,\ \ \ \xi (0)=1,\,\ \xi (w)(u_n-w)\in {\mathcal {N}}_\lambda ^+.\end{aligned}$$

Now, we put $\rho \in (0, \epsilon _n)$ and $u\in W^{1,\Phi }(\Omega )\backslash \{0\}$. Define the auxiliary function

$$\begin{aligned}w_\rho =\displaystyle \frac{\rho u}{||u||}\in B(0,\epsilon _n).\end{aligned}$$

Using one more time Lemma 4.1 and Ekeland’s variational principle, we mention that

$$\begin{aligned} \mu _\rho =\xi (w_\rho )(u_n-w_\rho )\in {\mathcal {N}}_\lambda ^+ \,\, \text{ and } \,\, J_\lambda (\mu _\rho )-J_\lambda (u_n)\ge - \frac{1}{n}||\mu _\rho -u_n||. \end{aligned}$$

(4.26)

Notice also that

$$\begin{aligned} w_\rho \rightarrow 0,\ \xi _n(w_\rho )\rightarrow 1, \ \mu _\rho \rightarrow u_n \text{ and } J'_\lambda (\mu _\rho )\rightarrow J'_\lambda (u_n) \end{aligned}$$

(4.27)

as $\rho \rightarrow 0$ holds true for any $n \in \mathbb {N}$.

At this moment, applying mean value theorem, there exists $t\in (0,1)$ in such way that

$$\begin{aligned} \begin{array}{rcl}J_\lambda (\mu _\rho )-J_\lambda (u_n)&{}=&{}\left<J'_\lambda ((1-t)\mu _\rho +tu_n),\mu _\rho -u_n\right>\\ &{}=&{}\left<J'_\lambda (\mu _\rho +t(u_n-\mu _\rho )) -J'_\lambda (u_n),\mu _\rho -u_n \right>\\ &{}&{}+\,\left<J'_\lambda (u_n),\mu _\rho -u_n\right>. \end{array}\end{aligned}$$

It is worthwhile to mention that $||u_n-\mu _\rho ||\rightarrow 0$ as $\rho \rightarrow 0$. Hence, using (4.26) and (4.27), we easily see that

$$\begin{aligned} -\frac{1}{n}||\mu _\rho -u_n||\le \left<J'_\lambda (u_n),\mu _\rho -u_n \right> + o_{\rho }(1)||\mu _\rho -u_n|| \end{aligned}$$

where $o_{\rho }(1)$ denotes a quantity that goes to zero as $\rho$ goes to zero. Taking into account that $\mu _\rho =\xi (w_\rho )(u_n-w_\rho )\in {\mathcal {N}}_\lambda ^+$ it follows that

$$\begin{aligned} -\frac{1}{n}||\mu _\rho -u_n|| +o_{\rho }(1)||\mu _\rho -u_n||\le \left<J'_\lambda (u_n),-w_\rho \right>+(\xi _n(w_\rho )-1)\left<J'_\lambda (u_n),u_n-w_\rho \right>. \end{aligned}$$

Furthermore, using the fact that $\left<J_\lambda ^{\prime }(\mu _\rho ),\mu _\rho \right>=0$, we mention that

$$\begin{aligned} -\frac{1}{n}||\mu _\rho -u_n||\le & {} o_{\rho }(1)||\mu _\rho -u_n|| - \rho \left<J'_\lambda (u_n),\frac{u}{||u||}\right>\\&+\,(\xi _n(w_\rho )-1)\left<J'_\lambda (u_n)-J'_\lambda (\mu _\rho ),u_n-w_\rho \right>. \end{aligned}$$

As a consequence, the last estimates and (4.27) say that

$$\begin{aligned} \left<J'_\lambda (u_n),\frac{u}{||u||}\right>\le & {} \displaystyle \frac{||\mu _\rho -u_n||}{n\rho }+o_{\rho }(1)\displaystyle \frac{||\mu _\rho -u_n||}{\rho } \\&+\, \displaystyle \frac{(\xi _n(w_\rho )-1)}{\rho }\left<J'_\lambda (u_n)-J'_\lambda (\mu _\rho ),u_n-w_\rho \right>. \end{aligned}$$

It is no hard to see that

$$\begin{aligned} ||\mu _\rho -u_n||\le \rho |\xi _n(w_\rho )|+|\xi _n(w_\rho )-1| \,||u_n|| \text{ and } \displaystyle \lim _{\rho \rightarrow 0}\displaystyle \frac{|\xi _n(w_\rho )-1|}{\rho }\le ||\xi '_n(0)||.\nonumber \\ \end{aligned}$$

(4.28)

The last inequality is justified due the fact that

$$\begin{aligned} \displaystyle \lim _{\rho \rightarrow 0}\displaystyle \frac{|\xi _n(w_\rho )-1|}{\rho }=\left<\xi '_n(0),\frac{u}{||u||}\right>\le ||\xi '_n(0)||. \end{aligned}$$

Therefore, using the fact that $(u_n)$ is bounded and (4.28), we infer that

$$\begin{aligned}\begin{array}{rcl} \displaystyle \lim _{\rho \rightarrow 0} \displaystyle \frac{||\mu _\rho -u_n||}{\rho }&{}\le &{}\displaystyle \lim _{\rho \rightarrow 0} \left[ ||\xi _n(w_\rho )||+\displaystyle \frac{|\xi _n(w_\rho )-1|}{\rho }||u_n||\right] \\ &{}\le &{} C \left[ 1+||\xi '_n(0)||\,\,||u_n||\right] \le C \left[ 1+||\xi '_n(0)||\right] . \end{array} \end{aligned}$$

Furthermore, using the fact that $\displaystyle \frac{\xi _n(w_\rho )-1}{\rho }$ and $\xi _n(w_\rho )$ are bounded for $\rho >0$ small enough, we easily see that

$$\begin{aligned}\begin{array}{rcl} \Vert \mu _\rho -u_n \Vert &{}=&{}|\rho |\left| \left| \displaystyle \frac{\xi _n(w_\rho )-1}{\rho }u_n-\xi _n(w_\rho )\displaystyle \frac{u}{||u||}\right| \right| \\ &{}\le &{} |\rho |\left[ \left| \displaystyle \frac{\xi _n(w_\rho )-1}{\rho }\right| ||u_n||+|\xi _n(w_\rho )|\right] . \end{array} \end{aligned}$$

Since $(u_n)$ is bounded, there exists a constant $C>0$ in such way that

$$\begin{aligned} \displaystyle \frac{||\mu _\rho -u_n||}{\rho }\le C[||\xi '_n(0)||+1]. \end{aligned}$$

Putting all these estimates together we employ that there exists a constant $C > 0$ which is independent in $\rho >0$. Thus, taking the limit as $\rho \rightarrow 0$ we obtain the inequality (4.25). This ends the proof. $\square$

Now we shall consider a technical result in order to get Palais–Smale sequences on the Nehari manifold ${\mathcal {N}}_{\lambda }^{+}$ or ${\mathcal {N}}_{\lambda }^{-}$.

Proposition 4.3

Suppose $(\phi _{1})- (\phi _{3})$ and (H). Then given any minimizer sequence $(u_n)$ on the Nehari manifold ${\mathcal {N}}_{\lambda }^{-}$ or ${\mathcal {N}}_{\lambda }^{+}$ we obtain

$$\begin{aligned} ||\xi '_n(0)|| \le C \, \, \text{ for } \text{ each } \,\, n \in \mathbb {N} \end{aligned}$$

(4.29)

where $C > 0$ is independent on n. Here we recall that $\xi _n:=\xi :B_{\frac{1}{n}}(0)\rightarrow (0,\infty )$ was obtained by Lemma 4.1.

Proof

In view of (4.19) we observe that

$$\begin{aligned} \left<\xi '_n(0),v\right>=\displaystyle \frac{\chi _n(v)}{\gamma ''_{u_n}(1)}, \end{aligned}$$

(4.30)

where we define the auxiliary function $\chi _n : W_0^{1,\Phi }(\Omega )\rightarrow {\mathbb {R}}$ by

$$\begin{aligned} \chi _n(v)= & {} \displaystyle \int _{\Omega }\Big [(\phi '(|\nabla u_n|)|\nabla u_n|+2\phi (|\nabla u_n|))\nabla u_n\nabla v\\&\quad -\, \ell ^*b(x)|u_n|^{\ell ^*-2}u_nv-q\lambda a(x)|u_n|^{q-2}u_nv \Big ]\mathrm{d}x. \end{aligned}$$

Now we claim that the numerator in (4.30) is bounded as follows: There exists a positive constant $c > 0$ in such way that $|\chi _n(v)| \le c \, ||v||$ holds true for any $v \in W_0^{1,\Phi }(\Omega )$. Furthermore, we claim also that there exists a positive constant d such that $\gamma ''_{u_n}(1)\ge d>0$ for any $n \in \mathbb {N}$.

In what follows we shall prove the claims given just above. It is easy to verity that

$$\begin{aligned} \begin{array}{rcl}|\chi _n(v)|&{}\le &{} \displaystyle \int _{\Omega }\left[ |\phi '(|\nabla u_n|)| |\nabla u_n|^2+2\phi (|\nabla u_n|)|\nabla u_n|\right] |\nabla v|\mathrm{d}x\\ &{}&{}+\,||b^+||_\infty \ell ^*\displaystyle \int _{\Omega }|u_n|^{\ell ^*-1}|v|\mathrm{d}x+\lambda q||a^+||_\infty \displaystyle \int _{\Omega }|u_n|^{q-1}|v|\mathrm{d}x. \end{array} \end{aligned}$$

Now using Remark 1.1, we see that $\displaystyle \frac{|\phi '(t)t|}{\phi (t)}\le \max \{|\ell -2|,|m-2|\}:=C_1$. Thus, using Hölder’s inequality, we also see that

$$\begin{aligned}\begin{array}{rcl}|\chi _n(v)|&{}\le &{} C_1\displaystyle \int _{\Omega }\phi (|\nabla u_n|)|\nabla u_n||\nabla v|\mathrm{d}x\\ &{}&{}+\,||b^+||_\infty \ell ^*\displaystyle \int _{\Omega }|u_n|^{\ell ^*-1}|v|\mathrm{d}x+\lambda q||a^+||_\infty \displaystyle \int _{\Omega }|u_n|^{q-1}|v|\mathrm{d}x\\ &{}\le &{} 2C_1||\phi (|\nabla u_n|)|\nabla u_n|||_{\tilde{\Phi }}||v||\\ &{}&{}+\,||b^+||_\infty \ell ^*\displaystyle \int _{\Omega }|u_n|^{\ell ^*-1}|v|\mathrm{d}x+\lambda q||a^+||_\infty \displaystyle \int _{\Omega }|u_n|^{q-1}|v|\mathrm{d}x\\ &{}\le &{} C_2 \max \left\{ \left( \displaystyle \int _{\Omega }\tilde{\Phi }(\phi (|\nabla u_n|)|\nabla u_n|)\mathrm{d}x\right) ^{\frac{\ell -1}{\ell }},\left( \displaystyle \int _{\Omega }\tilde{\Phi }(\phi (|\nabla u_n|)|\nabla u_n|)\mathrm{d}x\right) ^{\frac{m-1}{m}}\right\} ||v|| \\ &{}&{}+\,||b^+||_\infty \ell ^*\displaystyle \int _{\Omega }|u_n|^{\ell ^*-1}|v|\mathrm{d}x+\lambda q||a^+||_\infty \displaystyle \int _{\Omega }|u_n|^{q-1}|v|\mathrm{d}x. \end{array} \end{aligned}$$

In view of inequality $\widetilde{\Phi }(t\phi (t))\le \Phi (2t)\le 2^m\Phi (t), t \ge 0$ and (4.22), there exists a constant $C_3>0$ such that

$$\begin{aligned}\begin{array}{rcl}|\chi _n(v)| &{}\le &{} C_3\max \left\{ \left( \displaystyle \int _{\Omega }\Phi (|\nabla u_n|)\mathrm{d}x\right) ^{\frac{\ell -1}{\ell }},\left( \displaystyle \int _{\Omega }\Phi (|\nabla u_n|)\mathrm{d}x\right) ^{\frac{m-1}{m}}\right\} ||v||\\ &{}&{}+\,||b^+||_\infty \ell ^*\displaystyle \int _{\Omega }|u_n|^{\ell ^*-1}|v|\mathrm{d}x+\lambda q||a^+||_\infty \displaystyle \int _{\Omega }|u_n|^{q-1}|v|\mathrm{d}x\\ &{}\le &{} C_3 || u_n||^\beta ||v||+||b^+||_\infty \ell ^*\displaystyle \int _{\Omega }|u_n|^{\ell ^*-1}|v|\mathrm{d}x+\lambda q||a^+||_\infty \displaystyle \int _{\Omega }|u_n|^{q-1}|v|\mathrm{d}x\\ &{}\le &{} C_4||v||+||b^+||_\infty \ell ^*\displaystyle \int _{\Omega }|u_n|^{\ell ^*-1}|v|\mathrm{d}x+\lambda q||a^+||_\infty \displaystyle \int _{\Omega }|u_n|^{q-1}|v|\mathrm{d}x. \end{array} \end{aligned}$$

where $\beta \in \{\ell -1,\frac{\ell }{m}(\ell -1),m-1,\frac{m}{\ell }(m-1)\}$.

At this stage, we shall estimate the terms $\displaystyle \int _{\Omega }|u_n|^{\ell ^*-1}|v|\mathrm{d}x$ and $\displaystyle \int _{\Omega }|u_n|^{q-1}|v|\mathrm{d}x$. In order to do that we employ $\hbox {H}\ddot{o}\hbox {lder}$’s inequality and Sobolev imbedding proving that

$$\begin{aligned}\displaystyle \int _{\Omega }|u_n|^{\ell ^*-1}|v|\mathrm{d}x\le \left( \displaystyle \int _{\Omega }|u_n|^{\ell ^*}\mathrm{d}x\right) ^{\frac{\ell ^*-1}{\ell ^*}} \left( \displaystyle \int _{\Omega }|v|^{\ell ^*}\mathrm{d}x\right) ^{\frac{1}{\ell ^*}}\le C_5 \Vert u_n\Vert ^{\ell ^{*}-1} \Vert v\Vert \le C_6 \Vert v\Vert .\end{aligned}$$

In view of the estimates above, there exists a constant $c>0$ in such that $|\chi _n(v)|\le c||v||$. Here we emphasize that estimate (4.22) says that c is independent on $n \in \mathbb {N}$.

It remains to show that there exists a constant $d>0$, independent in n, in such way that $\gamma ''_{u_n}(1)\ge d$. The proof follows arguing by contradiction assuming that $\gamma ''_{u_n}(1) = o_n(1)$. It follows from (4.21) that there exists $a_\lambda >0$ satisfying

$$\begin{aligned} \displaystyle \liminf _{n \rightarrow \infty }||u_n||\ge a_\lambda >0 \end{aligned}$$

(4.31)

At this moment, we emphasize that $\gamma ''_{u_n}(1) = o_n(1)$. Using (2.13) we deduce that

$$\begin{aligned}o_n(1)=\gamma ''_{u_n}(1)=\displaystyle \int _{\Omega }\left[ (2-q)\phi (|\nabla u_n| )|\nabla u_n|^2+\phi '(|\nabla u_n|)||\nabla u|^3+(q-\ell ^*)b|u_n|^{\ell ^*}\right] \mathrm{d}x.\end{aligned}$$

Using (1.5) and Sobolev embeddings we also mention that

$$\begin{aligned} (\ell -q)\displaystyle \int _{\Omega }\phi (|\nabla u| )|\nabla u_n|^2\mathrm{d}x\le & {} (\ell ^*-q)||b^+||_{\infty }||u_n||_{\ell ^*}^{\ell ^*}+o_n(1)\\\le & {} (\ell ^*-q)S_{\ell ^*}||b^+||_{\infty }||u_n||^{\ell ^*}+o_n(1). \end{aligned}$$

On the other hand, we observe that

$$\begin{aligned} (\ell -q)\displaystyle \int _{\Omega }\phi (|\nabla u_n| )|\nabla u_n|^2\mathrm{d}x\ge \ell (\ell -q)\displaystyle \int _{\Omega }\Phi (|\nabla u_n|)\mathrm{d}x\ge \ell (\ell -q)\min \{||u_n||^\ell ,||u_n||^m\}. \end{aligned}$$

Using the estimates just above, we get

$$\begin{aligned} \ell (\ell -q)\min \{||u_n||^\ell ,||u_n||^m\}\le (\ell ^*-q)S_{\ell ^*}||b^+||_{\infty }||u_n||^{\ell ^*}+o_n(1). \end{aligned}$$

Hence, we have that

$$\begin{aligned} \ell (\ell -q)\le {(\ell ^*-q)S_{\ell ^*}||b^+||_{\infty }}||u_n||^{\ell ^*-\alpha }+\displaystyle \frac{o_n(1)}{||u_n||^\alpha } \end{aligned}$$

where $\alpha =\ell$ whenever $||u_n||\ge 1$ and $\alpha =m$ whenever $||u_n||\le 1$. Furthermore, using (4.31), we obtain

$$\begin{aligned} ||u_n||\ge \left[ \displaystyle \frac{\ell (\ell -q)}{(\ell ^*-q)S_{\ell ^*}||b^+||_{\infty }}\right] ^{\frac{1}{\ell ^*-\alpha }}+o_n(1). \end{aligned}$$

(4.32)

Using one more time (1.5), (2.13) and Hölder inequality, we deduce that

$$\begin{aligned} (\ell ^*-m)\displaystyle \int _{\Omega }\phi (|\nabla u_n| )|\nabla u_n|^2\mathrm{d}x\le & {} \lambda (\ell ^*-q)||a^+||_{(\frac{\ell }{q})'}||u_n||_{\ell }^{q}+o_n(1)\\\le & {} \lambda (\ell ^*-q)S_{q}||a^+||_{(\frac{\ell }{q})'}||u_n||^{q}+o_n(1). \end{aligned}$$

Here $S_{q}$ denotes the best Sobolev constant for the embedding $W_0^{1,\Phi }(\Omega )$ into $L^{q}(\Omega )$. Using the same ideas discussed here, we also mention that

$$\begin{aligned}\ell (\ell ^*-m)\min \{||u_n||^\ell ,||u_n||^m\}\le \lambda (\ell ^*-q)S_{\ell }||a^+||_{(\frac{\ell }{q})'}||u_n||^{q}+o_n(1).\end{aligned}$$

As a consequence we get

$$\begin{aligned}\displaystyle \frac{\ell (\ell ^*-m)}{(\ell ^*-q)S_{\ell }||a^+||_{(\frac{\ell }{q})'}}||u_n||^\alpha =\displaystyle \frac{\ell (\ell ^*-m)}{(\ell ^*-q)S_{\ell }||a^+||_{(\frac{\ell }{q})'}}\min \{||u_n||^\ell ,||u_n||^m\}\le \lambda ||u_n||^{q}+o_n(1).\end{aligned}$$

To sum up, using the estimate (4.31), we can be shown that

$$\begin{aligned} ||u_n||\le & {} \left[ \lambda \displaystyle \frac{(\ell ^*-q)S_{\ell }\Vert a^+\Vert _{\left( \frac{\ell }{q}\right) '}}{\ell (\ell ^*-m)}\right] ^{\frac{1}{\alpha -q}}+\displaystyle \frac{o_n(1)}{||u_n||^{\frac{q}{\alpha -q}}}\\= & {} \left[ \lambda \displaystyle \frac{(\ell ^*-q)S_{\ell }\Vert a^+\Vert _{\left( \frac{\ell }{q}\right) '}}{\ell (\ell ^*-m)}\right] ^{\frac{1}{\alpha -q}}+o_n(1). \end{aligned}$$

Arguing as in the proof of Lemma 2.1, using the above inequality and (4.32), we have a contradiction for each $\lambda < \lambda _1$ where $\lambda _1$ was given by (2.16). This finishes the proof. $\square$

At this stage we shall prove that any minimizer sequences on the Nehari manifold in ${\mathcal {N}}^{+}_{\lambda }$ or ${\mathcal {N}}^{-}_{\lambda }$ provides us a Palais–Smale sequences. More specifically, we can prove the following result

Proposition 4.4

Suppose $(\phi _{1})- (\phi _{3})$ and (H). Then we have the following assertions

• (1) there exists a sequence $(u_n)\subset {\mathcal {N}}_\lambda ^+$such that $J_\lambda (u_n)= \alpha ^+_\lambda +o_n(1) \ \text{ and } J'_\lambda (u_n)=o_n(1)\ \text{ in }~ W^{-1,\widetilde{\Phi }}(\Omega ).$

• (2) there exists a sequence $(u_n)\subset {\mathcal {N}}_\lambda ^-$ such that $J_\lambda (u_n)=\alpha ^-_\lambda +o_n(1) \ \text{ and } J'_\lambda (u_n)=o_n(1)\ \text{ in } W^{-1,\widetilde{\Phi }}(\Omega ).$

Proof

Here we shall prove the item (1). The proof of item (2) follows the same ideas discussed here using Lemma 4.2 instead of Lemma 4.1. Applying Ekeland’s variational principle, there exists a sequence $(u_n)\subset {\mathcal {N}}_\lambda ^+$ in such way that

• (i) $J_\lambda (u_n) \,= \,\alpha _\lambda ^+ + o_n(1)$,

• (ii) $J_\lambda (u_n)<J_\lambda (w)+\frac{1}{n}||w-u||, \,\,\forall \,\, w\,\in {\mathcal {N}}_\lambda ^+.$

According to Proposition 4.3, there exists $C>0$ independent on $n \in \mathbb {N}$ in such way that $\Vert \xi _n'(0)\Vert \le C$. This estimate together with Proposition 4.2 give us the following estimate

$$\begin{aligned}\left<J'_\lambda (u_n), \displaystyle \frac{u}{||u||}\right>\le \displaystyle \frac{C}{n},\quad ~u\in W^{1,\Phi }(\Omega )/\{0\}.\end{aligned}$$

As a consequence $\Vert J_\lambda '(u_n)\Vert \rightarrow 0$ as $n \rightarrow \infty$. This ends the proof. $\square$

5 The concentration-compactness method

In this section we shall discuss the concentration-compactness theorem for Orlicz–Sobolev framework. It is important to recover the compactness property in order to apply a minimization argument. This property allows us to prove our main results on existence and multiplicity of solutions to quasilinear elliptic problems.

In what follows we borrow the ideas discussed in [58]. Given any function $v\in {C}^\infty _0(\Omega )$ we extend the function v in the following form $v(x)=0$ for any $x\in \Omega ^c$. This function is also denoted by v which belongs to $v\in {C}_0^\infty ({\mathbb {R}}^N)$. Moreover, we observe that $\text{ supp }(v)\subset \Omega$. It is important to mention also that

$$\begin{aligned} \Vert v \Vert _{W^{1,\Phi }({\mathbb {R}}^N)}=\Vert v\Vert _{W^{1,\Phi }(\Omega )} \end{aligned}$$

and

$$\begin{aligned} \Vert v\Vert = \Vert v\Vert _{_{W^{1,\Phi }(\Omega )}} \,\, \text{ for } \text{ any } \,\, v \in W_0^{1,\Phi }(\Omega ). \end{aligned}$$

Furthermore, we observe that

$$\begin{aligned} W_0^{1,\Phi }(\Omega )=\overline{\{v\in {C}_0^\infty ({\mathbb {R}}^N)~|~\text{ supp }(v)\subset \Omega \}}^{W^{1,\Phi }({\mathbb {R}}^N)}. \end{aligned}$$

As a consequence, we know that $v \in {W^{1,\Phi }({\mathbb {R}}^N)}$ whenever $v\in W_0^{1,\Phi }(\Omega )$.

Now we shall consider the vectorial space

endowed with the norm $\displaystyle \Vert u\Vert _\infty =\sup _{x\in {\mathbb {R}}^N}|u(x)|$. Denote by ${\mathcal {M}}$ the space of finite measures on ${\mathbb {R}}^N$ using the norm

$$\begin{aligned} \Vert \mu \Vert _{{\mathcal {M}}}=\sup \left\{ \int _{{\mathbb {R}}^N} u d\mu ~|~u\in {C}_0,~ \Vert u\Vert _\infty =1\right\} . \end{aligned}$$

Here ${C}_0^*$ denotes the dual set for ${C}_0$. Recall that ${\mathcal {M}}$ satisfies the following properties

• (i) ${\mathcal {M}} = {C}_0^*$ and $\langle \mu ,u \rangle := \int u d\mu$,

• (ii) The convergence $\mu _n \rightharpoonup \mu$ in ${\mathcal {M}}$ occurs whenever $\displaystyle \lim _{n\rightarrow \infty }\int _{{\mathbb {R}}^N} u d\mu _n{\longrightarrow } \int _{{\mathbb {R}}^N} u d\mu ,~u\in {C}_0$,

• (iii) Let $(\mu _n)\subseteq {\mathcal {M}}$ be an bounded sequence. Then, up to a subsequence, we obtain $\mu _n \rightharpoonup \mu$ in ${\mathcal {M}}$.

At this moment we consider a minimizer sequence $(u_n) \subset {\mathcal {N}}_{\lambda }$ for the functional $J_{\lambda }$. Notice that $(u_{n})$ is bounded and there exists $u \in W_0^{1,\Phi }(\Omega )$ in such way that $u_{n} \rightharpoonup u$ in $W_0^{1,\Phi }(\Omega )$. Consider $\mu _n,\nu _n: {C}_0\rightarrow {\mathbb {R}}$ given by

$$\begin{aligned} \langle \mu _n, v\rangle =\int _{{\mathbb {R}}^N}\Phi (|\nabla u_n|)v\mathrm{d}x \qquad \text{ and }\qquad \langle \nu _n, v\rangle =\int _{{\mathbb {R}}^N}|u_n|^{\ell ^*}v\mathrm{d}x,~v\in {C}_0. \end{aligned}$$

Hence there exists a constant $C > 0$ in such way that

$$\begin{aligned} |\langle \mu _n,v\rangle | \le C \Vert v\Vert _\infty ~\text{ and }~ |\langle \nu _n,v\rangle |\le C\Vert v\Vert _\infty . \end{aligned}$$

In other words, we have been shown that $(\mu _n),(\nu _n)\subseteq {\mathcal {M}}$ are bounded measures. It follows from the last estimate that

$$\begin{aligned} \Phi (|\nabla u_n|)\rightharpoonup \mu ,~~|u_n|^{\ell ^*}\rightharpoonup \nu ~~\text{ in }~~{\mathcal {M}}. \end{aligned}$$

(5.33)

In what follows we shall consider the compactness-concentration theorem in the Orlicz–Sobolev framework, see for instance [40]. For a proof on compactness-concentration theorem in Orlicz–Sobolev spaces, we refer the reader to [36].

Lemma 5.1

There exist an enumerable set L, a family $\{x_j\}_{j\in L}\subseteq {\mathbb {R}}^N$ such that $x_i \ne x_j$ and nonnegative real numbers $\{\nu _j\}_{j\in L}$ and $\{\mu _j \}_{j\in L}$ satisfying

$$\begin{aligned} \nu =|u|^{\ell ^*}+\sum _{j\in L}\nu _j\delta _{x_j}~\qquad \text{ and }~\qquad \mu \ge \Phi (|\nabla u|)+\sum _{j\in L}\mu _j\delta _{x_j}, \end{aligned}$$

where $\delta _{x_j}$ is the Dirac measure with mass at $x_j$. Furthermore, we have

$$\begin{aligned} \nu _j\le \max \left\{ S_{\ell ^*}^{-\frac{\ell ^*}{\ell }}\mu _j^{\frac{\ell ^*}{\ell }}, S_{\ell ^*}^{-\frac{\ell ^*}{m}}\mu _j^{\frac{\ell ^*}{m}}\right\} ,~j\in L, \end{aligned}$$

where $S_{\ell ^*}$ is the best constant for the embedding $W^{1,\Phi }_{0}(\Omega ) \hookrightarrow L^{\ell ^{*}}(\Omega )$.

Lemma 5.2

The set $\widetilde{L} = \{j\in L~|~\nu _j>0\}$ is finite.

Proof

Initially we mention that $\{x_j\}_{j\in \widetilde{L}}\subseteq \overline{\Omega }$. Indeed, arguing by contradiction we suppose that $x_j\in \overline{\Omega }^c$ for some $j\in L$. Hence there exists $\epsilon > 0$ such that ${\overline{B}_\epsilon }(x_j)\subseteq \overline{\Omega }^c$. Consider $\varphi _\epsilon \in {C}_0^\infty ({\mathbb {R}}^N)$ satisfying the following conditions

$$\begin{aligned} supp(\varphi _\epsilon )\subset B_\epsilon (x_j),~~~ \varphi _\epsilon {\mathop {\longrightarrow }\limits ^{\epsilon \rightarrow 0}}\chi _{\{x_j\}}~ \text{ a.e. }~ \mathbf{R}^{N}. \end{aligned}$$

Now we extend the function $u_n$ in ${\mathbb {R}}^N$ putting $u_n(x)=0$ for any $x\in {\mathbb {R}}^N \backslash \Omega$. At this stage the proof follows the same lines discussed in [36]. Here we omit the details. $\square$

For the next result, we extend the function $u_n$ to ${{\mathbb {R}}}^{N}$ defining $u_n = 0~\text{ in }~ {{\mathbb {R}}}^{N} \backslash \Omega$. Moreover, we consider $L = \{x_1, \ldots , x_r \}$ for some $r \in \mathbb {N}$ which was obtained from the previous lemma. Under these conditions, we can consider the following result

Lemma 5.3

Let $u_{n} \subset {\mathcal {N}}_\lambda$ be a minimizer sequence for the functional $J_{\lambda }$. Then there exists $u \in W_0^{1,\Phi }(\Omega )$ in such way that $u_{n} \rightharpoonup u$ in $W_0^{1,\Phi }(\Omega )$. Furthermore, we have that

$$\begin{aligned} u_n \rightarrow u \, \, \text{ in } \,\, L^{\ell ^*}(K) \end{aligned}$$

(5.34)

for each compact set $K\subset {\mathbb {R}}^N \backslash \{x_1, \ldots , x_r \}$.

Proof

Initially, we observe that $\widetilde{L}$ is finite. Hence there exists $\delta >0$ such that $B_{\delta }(x_i)\cap B_{\delta }(x_j)=\emptyset$ for any $i\ne j$ with $i, j \in \widetilde{L}$. Now we consider the set $\displaystyle K_{\delta }\subset {\mathbb {R}}^N \backslash \cup _{j\in {L}} B_\delta (x_j)$ and $\chi \in {C}_0^\infty$ in such way that

$$\begin{aligned} 0\le \chi \le 1,~~\chi =1~\text{ in }~K_{\delta },~~\text{ supp }(\chi )\cap \left( \cup _{j\in \widetilde{L}} B_{\frac{\delta }{2}}(x_j)\right) =\emptyset . \end{aligned}$$

Notice also that

$$\begin{aligned} |u_n-u|^{\ell ^*}\rightharpoonup \nu ~~\text{ and }~~ \nu = \sum _{j\in \widetilde{L}}\nu _j\delta _{x_j}~\text{ in }~ {\mathcal {M}}. \end{aligned}$$

On the other hand, we observe that

$$\begin{aligned}&\displaystyle 0\le \int _{K_{\delta }} |u_n-u|^{\ell ^*}\mathrm{d}x \le \displaystyle \int _{{\mathbb {R}}^N}|u_n-u|^{\ell ^*}\chi \mathrm{d}x,\\&\quad \displaystyle \int _{{\mathbb {R}}^N}|u_n-u|^{\ell ^*}\chi \mathrm{d}x \rightarrow \int _{{\mathbb {R}}^N}\chi d\nu ,\\&\quad \int _{{\mathbb {R}}^N}\chi d\nu = \displaystyle \sum _{j\in \widetilde{J}} \chi (x_j) = 0. \end{aligned}$$

As a consequence we mention that

$$\begin{aligned} \int _{K_{\delta }}|u_n-u|^{\ell ^*}\mathrm{d}x \rightarrow 0. \end{aligned}$$

Putting the all estimates together and using the fact that $\delta > 0$ is arbitrary we conclude that (5.34) holds true for each compact set $K\subset {\mathbb {R}}^N \backslash \{x_j\}_{j\in \widetilde{L}}$. This ends the proof. $\square$

Lemma 5.4

Let $u_{n} \subset {\mathcal {N}}_\lambda$ be a minimizer sequence for the functional $J_{\lambda }$. Consider $u \in W_0^{1,\Phi }(\Omega )$ such that $u_{n} \rightharpoonup u$ in $W_0^{1,\Phi }(\Omega )$. Then we obtain the following properties:

(i) $\phi (|\nabla u_n|)\nabla u_n\rightharpoonup \phi (|\nabla u|)\nabla u$ in $\prod L_{\widetilde{\Phi }}(\Omega )$;

(ii) $|u_n|^{\ell ^*-2}u_n \rightharpoonup |u|^{\ell ^*-2}u$ in $L^{\frac{\ell ^*}{\ell ^*-1}}(\Omega )$.

Proof

Firstly, we shall prove the item (i). Consider $\{K_\nu \}_{\nu =1}^{\infty }$ a family of compact sets satisfying

$$\begin{aligned} \Omega \backslash \{x_j\}_{j \in \widetilde{L}}=\bigcup _{\nu =1}^\infty K_\nu . \end{aligned}$$

(5.35)

Choose any integer number $\nu \ge 1$. Let $\chi \in {C}_0^\infty ({\mathbb {R}}^N)$ be a function such that $0\le \chi \le 1$,  $\chi =1~\text{ in }~K_\nu$ and supp($\chi ) \cap \{x_j\}_{j\in \widetilde{L}} = \emptyset$. Using the fact that $\Phi$ is convex we obtain

$$\begin{aligned} A_n:=(\phi (|\nabla u_n|)\nabla u_n-\phi (|\nabla u|)\nabla u,\nabla u_n-\nabla u)\ge 0,~\text{ in }~{\mathbb {R}}^N.\end{aligned}$$

As a consequence we employ that

$$\begin{aligned} 0\le \int _{K_\nu }A_n(x)\mathrm{d}x\le & {} \int _{{\mathbb {R}}^n}(\phi (|\nabla u_n|)\nabla u_n,\nabla u_n-\nabla u)\chi \mathrm{d}x\\&-\int _{{\mathbb {R}}^n}(\phi (|\nabla u|)\nabla u,\nabla u_n-\nabla u)\chi \mathrm{d}x. \end{aligned}$$

Define $v_n =\chi (u_n-u)$. It follows easily that $v_n$ is bounded in $W^{1,\Phi }({\mathbb {R}}^N)$. Using $v_n$ as testing function, we deduce that

$$\begin{aligned} \int _{{\mathbb {R}}^N}\left[ \phi (|\nabla u_n|)\nabla u_n\nabla v_n \mathrm{d}x -\lambda a(x)|u_n|^{q-2}u_nv_n -b(x)|u_n|^{\ell ^*-2}u_nv_n\right] \mathrm{d}x =o_n(1). \end{aligned}$$

(5.36)

In other words, we know that

$$\begin{aligned} \int _{{\mathbb {R}}^N}\phi (|\nabla u_n|)\nabla u_n(\nabla u_n-\nabla u) \chi \mathrm{d}x + \int _{{\mathbb {R}}^N}(u_n-u)\phi (|\nabla u_n|)\nabla u_n\nabla \chi \mathrm{d}x\nonumber \\ = \displaystyle \int _{\Omega }\left[ \lambda a(x)|u_n|^{q-2}u_n+ b(x)|u_n|^{\ell ^*-2}u_n\right] v_n \mathrm{d}x+o_n(1). \end{aligned}$$

(5.37)

Note that

$$\begin{aligned} \displaystyle \int _{{\mathbb {R}}^N} \big |\phi (|\nabla u_n|)\nabla u_n\nabla \chi (u_n- u) \big | \mathrm{d}x\le \displaystyle \Vert \phi (|\nabla u_n|)|\nabla u_n|\Vert _{\widetilde{\Phi }} |\nabla \chi |_\infty \Vert (u_n-u)\Vert _\Phi = o_n(1). \end{aligned}$$

Moreover, we mention that $L_{\Phi }(\Omega )\hookrightarrow L^\ell (\Omega )\hookrightarrow L^q(\Omega )$ which shows that

$$\begin{aligned} \int _{{\mathbb {R}}^N}a(x)|u_n|^{q-1}|v_n| \mathrm{d}x\le & {} \Vert a\Vert _\infty \Vert u_n\Vert _q^{q-1}\Vert u_n-u\Vert _q\\\le & {} C \Vert a\Vert _\infty \Vert u_n\Vert _\Phi ^{q-1}\Vert u_n-u\Vert _\Phi =o_n(1). \end{aligned}$$

Additionally, using that $(|u_n|^{\ell ^*-1})$ is bounded in $L^{\frac{\ell ^*}{\ell ^*-1}}(\Omega )$ and Lemma 5.3, we conclude that

$$\begin{aligned} \displaystyle \int _{{\mathbb {R}}^N} |b(x)|| u_n|^{\ell ^*-1}|v_n | \mathrm{d}x \le \Vert b\Vert _\infty \Vert u_n\Vert _{\ell ^*}^{\ell ^*-1}\Vert u_n-u\Vert _{L^{\ell ^*}(S_{\chi })} = o_{n}(1) \end{aligned}$$

where $S_\chi :=\text{ supp }(\chi )$. In this way, using (5.37) we get

$$\begin{aligned} \int _{{\mathbb {R}}^N}\phi (|\nabla u_n|)\nabla u_n(\nabla u_n-\nabla u) \chi \mathrm{d}x=o_n(1). \end{aligned}$$

(5.38)

Furthermore, using that $u_n\rightharpoonup u$ in $W_0^{1,\Phi }(\Omega )$ and $\chi \phi (|\nabla u|)|\nabla u|\in L_{\widetilde{\Phi }}(\Omega )$, putting $u_n=u=0$ in ${\mathbb {R}}^n \backslash \overline{\Omega }$ we see that

$$\begin{aligned} \int _{{\mathbb {R}}^N}\phi (|\nabla u|)\nabla u(\nabla u_n-\nabla u)\chi \mathrm{d}x =o_n(1). \end{aligned}$$

(5.39)

At this stage using (5.38), (5.39) in (5.36), we ensure that $A_n$ is in $L^1(K_\nu )$. Now, up to a subsequence, we get

$$\begin{aligned} A_n(x)\rightarrow 0,\quad ~\text{ a.e. }~x\in K_\nu . \end{aligned}$$

Hence (5.35) implies that

$$\begin{aligned} A_n(x)\rightarrow 0,\quad ~\text{ a.e. }~x\in {\mathbb {R}}^N. \end{aligned}$$

It follows from [26, Lemma 6] that

$$\begin{aligned} \nabla u_n\rightarrow \nabla u,\quad ~\text{ a.e. } \text{ in }~{\mathbb {R}}^N. \end{aligned}$$

Moreover, using the fact that $u_n=0$ in ${\mathbb {R}}^N \backslash \overline{\Omega }$, we also see that

$$\begin{aligned} \nabla u_n\rightarrow \nabla u,\quad ~\text{ a.e. } \text{ in }~\Omega . \end{aligned}$$

Using the fact that $t\longmapsto \phi (t)t$ is a continuous function one has

$$\begin{aligned}\phi (|\nabla u_n|)\nabla u_n \rightarrow \phi (|\nabla u|)\nabla u,~\text{ a.e. } \text{ in }~\Omega .\end{aligned}$$

In this way, using that $\widetilde{\Phi }(\phi (t)t)\le \Phi (2t)$, we obtain $\phi (|\nabla u_n|)|\nabla u_n|$ is bounded in $L_{\widetilde{\Phi }}(\Omega )$. Therefore, using [38, Lemma 2], we have been shown that

$$\begin{aligned}\phi (|\nabla u_n|)\nabla u_n\rightharpoonup \phi (|\nabla u|)\nabla u,\quad ~\text{ in }~\prod L_{\widetilde{\Phi }}(\Omega ).\end{aligned}$$

This ends the proof of item (i).

Now we shall prove the item (ii). Note that $W_0^{1,\Phi }(\Omega ){\mathop {\hookrightarrow }\limits ^{cpt}}L_\Phi (\Omega )$ showing that $u_n\rightarrow u$ in $L_\Phi (\Omega )$. Up to a subsequence we have that $u_n\rightarrow u$ a. e. in $\Omega$. Hence we easily see that

$$\begin{aligned}|u_n|^{\ell ^*-2}u_n \rightarrow |u|^{\ell ^*-2}u,~\text{ a.e. } \text{ in } \Omega .\end{aligned}$$

Now using the fact that $(|u_n|^{\ell ^*-2}u_n)$ is bounded in $L^{\frac{\ell ^*}{\ell ^*-1}}(\Omega )$ and using one more time [38, Lemma 2] we conclude that

$$\begin{aligned}|u_n|^{\ell ^*-2}u_n \rightharpoonup |u|^{\ell ^*-2}u,\quad ~\text{ in } L^{\frac{\ell ^*}{\ell ^*-1}}(\Omega ).\end{aligned}$$

This completes the proof. $\square$

6 The Proof of our main theorems

6.1 The Proof of Theorem 1.1

Let $\lambda < \Lambda _1 = \displaystyle \min \{\lambda _1,\bar{\lambda }_1\}$ be fixed where $\lambda _1 > 0$ is given by (2.16) and $\bar{\lambda }_1>0$ is provided in (3.18). Taking into account Lemma 3.5, we infer that

$$\begin{aligned}\alpha _\lambda ^+:=\displaystyle \inf _{u\in {\mathcal {N}}_\lambda ^+}J_\lambda (u) < 0.\end{aligned}$$

The main feature here is to find a function $u=u_\lambda \in {\mathcal {N}}_\lambda ^+$ in such way that

$$\begin{aligned}J_\lambda (u)= \displaystyle \min _{w \in {\mathcal {N}}_\lambda ^+}J_\lambda (w)=:\alpha _\lambda ^+ \,\, \text{ and } \,\, J'_\lambda (u) \equiv 0.\end{aligned}$$

As a first step, using Proposition 4.1, there exists a minimizer sequence denoted by $(u_n)\subset W^{1,\Phi }(\Omega )$ such that

$$\begin{aligned} J_\lambda (u_n)=\alpha _\lambda +o_n(1) \text{ and } J'_\lambda (u_n)=o_n(1). \end{aligned}$$

(6.40)

Since the functional $J_\lambda$ is coercive in ${\mathcal {N}}_\lambda ^+$ we obtain that $(u_n)$ is now bounded in ${\mathcal {N}}_\lambda ^+$. Therefore, there exists a function $u = u_{\lambda } \in {W^{1,\Phi }_0(\Omega )}$ in such way that

$$\begin{aligned} u_n \rightharpoonup u \,\, \text{ in } \,\, W_0^{1,\Phi }(\Omega ),~~ u_n \rightarrow u \,\,\text{ a.e. }\,\, \text{ in } \Omega ,~~ u_n \rightarrow u \,\, \text{ in } \,\, L_{\Phi }(\Omega ). \end{aligned}$$

(6.41)

At this point we shall prove that u is a weak solution for the problem elliptic problem (1.1). First of all, using (6.40), we mention that

$$\begin{aligned}o_n(1)=\left<J'_\lambda (u_n),v\right>=\displaystyle \int _{\Omega }\left[ \phi (|\nabla u_n|)\nabla u_n\nabla v-\lambda a(x)|u_n|^{q-2}u_n v-b(x)|u_n|^{\ell ^*-2}u_nv\right] \mathrm{d}x\end{aligned}$$

holds for any $v \in W_0^{1,\Phi }(\Omega )$. In view of (6.41), Lemma 5.4 and Lebesgue convergence theorem we get

$$\begin{aligned}\displaystyle \int _{\Omega }\left[ \phi (|\nabla u|)\nabla u\nabla v-\lambda a(x)|u|^{q-2}u v-b(x)|u|^{\ell ^*-2}v\right] \mathrm{d}x = 0\end{aligned}$$

for any $v\in W^{1,\Phi }_{0}(\Omega )$ proving that u is a weak solution to the elliptic problem (1.1). Additionally, the weak solution u is not zero. In fact, using the fact that $u_n\in {\mathcal {N}}_\lambda ^{+},$ we obtain

$$\begin{aligned}\begin{array}{rcl} \lambda \displaystyle \int _{\Omega }a(x)|u_n|^q\mathrm{d}x&{}=&{} \displaystyle \frac{q\ell ^*}{\ell ^*-q}\displaystyle \int _{\Omega }\left[ \Phi (|\nabla u_n|)- \displaystyle \frac{1}{\ell ^*}\phi (|\nabla u_n|)|\nabla u_n|^2\right] \mathrm{d}x -J_\lambda (u_n) \displaystyle \frac{q\ell ^*}{\ell ^*-q}\\ &{}\ge &{} \displaystyle \frac{q\ell ^*}{\ell ^*-q} \left( 1 - \dfrac{m}{\ell ^*}\right) \displaystyle \int _{\Omega }\Phi (|\nabla u_n|) \mathrm{d}x -J_\lambda (u_n)\displaystyle \frac{q\ell ^*}{\ell ^*-q} \\ &{}\ge &{} -J_\lambda (u_n)\displaystyle \frac{q\ell ^*}{\ell ^*-q}. \end{array} \end{aligned}$$

Taking into account (6.40) and (6.41) we also obtain that

$$\begin{aligned} \lambda \displaystyle \int _{\Omega }a(x)|u|^q\mathrm{d}x\ge -\alpha ^{+}_\lambda \displaystyle \frac{q\ell ^*}{\ell ^*-q} > 0. \end{aligned}$$

(6.42)

As a consequence, we deduce that $u\not \equiv 0$.

At this stage, we shall prove that $J_\lambda (u)=\alpha _\lambda$ and $u_n\rightarrow u$ in $W_0^{1,\Phi }(\Omega )$. Since $u\in {\mathcal {N}}_\lambda$, we also see that

$$\begin{aligned}\alpha _\lambda \le J_\lambda (u)=\displaystyle \int _{\Omega }\left[ \Phi (|\nabla u|)-\displaystyle \frac{1}{\ell ^*}\phi (|\nabla u|)|\nabla u|^2-\lambda \left( \displaystyle \frac{1}{q}-\displaystyle \frac{1}{\ell ^*}\right) a(x)|u|^{q}\right] \mathrm{d}x. \end{aligned}$$

Now we define $\Psi : {\mathbb {R}} \rightarrow {\mathbb {R}}$ by $\Psi (t) =\Phi (t)-\displaystyle \frac{1}{\ell ^*}\phi (t)t^2$ which is a convex function. In fact, using hypothesis $(\phi _{3})$ and $m<\ell ^*$, we deduce that

$$\begin{aligned} (\Psi (t))''= & {} (t\phi (t))' \left[ \left( 1-\frac{2}{\ell ^*}\right) -\frac{1}{\ell ^*}\frac{t(t\phi (t))''}{(t\phi (t))'}\right] \\\ge & {} (t\phi (t))' \left[ \left( 1-\frac{2}{\ell ^*}\right) -\frac{m-2}{\ell ^*}\right] = (t\phi (t))'\left( 1-\frac{m}{\ell ^*}\right) > 0 \end{aligned}$$

for any $t > 0$. Hence the last assertion says that

$$\begin{aligned}u\longmapsto \displaystyle \int _{\Omega }\Psi (|\nabla u |)\mathrm{d}x\end{aligned}$$

is weakly lower semicontinuous. Therefore, we obtain

$$\begin{aligned} \alpha _\lambda \le J_\lambda (u)\le & {} \liminf _{n \rightarrow \infty } \displaystyle \int _{\Omega }\left[ \Psi (|\nabla u_n|) - \lambda \left( \displaystyle \frac{1}{q}-\displaystyle \frac{1}{\ell ^*}\right) a(x)|u_n|^{q}\right] \mathrm{d}x = \liminf _{n \rightarrow \infty } J_\lambda (u_n)= \alpha _\lambda . \end{aligned}$$

As a consequence, we have $J_\lambda (u)=\alpha _\lambda .$ Additionally, using (6.41), we also mention that

$$\begin{aligned}\begin{array}{rcl} J_\lambda (u)&{}=&{} \displaystyle \lim _{n \rightarrow \infty } \displaystyle \int _{\Omega }\left[ \Psi (|\nabla u_n|)-\lambda \left( \displaystyle \frac{1}{q}-\displaystyle \frac{1}{\ell ^*}\right) a(x)|u_n|^{q}\right] \mathrm{d}x\\ &{}=&{} \displaystyle \lim _{n \rightarrow \infty } \displaystyle \int _{\Omega }\Psi (|\nabla u_n|) \mathrm{d}x -\lambda \left( \displaystyle \frac{1}{q}-\displaystyle \frac{1}{\ell ^*}\right) \displaystyle \int _{\Omega }a(x)|u|^{q}\mathrm{d}x. \end{array} \end{aligned}$$

It follows from the last identity that

$$\begin{aligned}\lim _{n \rightarrow \infty } \displaystyle \int _{\Omega }\Psi (|\nabla u_n|) \mathrm{d}x =\displaystyle \int _{\Omega }\Psi (|\nabla u|)\mathrm{d}x.\end{aligned}$$

In view of Brezis–Lieb Lemma, choosing $v_n=u_n-u,$ we infer that

$$\begin{aligned} \lim _{n \rightarrow \infty } \displaystyle \int _{\Omega }\left[ \Psi (|\nabla u_n|) - \Psi (|\nabla v_n|)\right] \mathrm{d}x = \displaystyle \int _{\Omega }\Psi (|\nabla u|)\mathrm{d}x. \end{aligned}$$

In this way, the previous assertion implies that

$$\begin{aligned}0=\lim _{n \rightarrow \infty } \displaystyle \int _{\Omega }\Psi (|\nabla v_n|) \mathrm{d}x\ge \lim _{n \rightarrow \infty }\left( 1-\displaystyle \frac{m}{\ell ^*}\right) \displaystyle \int _{\Omega }\Phi (|\nabla v_n|)\mathrm{d}x\ge 0.\end{aligned}$$

Therefore, we obtain that $\displaystyle \lim _{n \rightarrow \infty } \int _{\Omega } \Phi (|\nabla v_n|)\mathrm{d}x=0$ and $u_n\rightarrow u \,\,\text{ in } \,\, W^{1,\Phi }(\Omega ).$ Hence we conclude that $u_{n} \rightarrow u$ in $W_0^{1,\Phi }(\Omega )$.

At this point, we claim that $u\in {\mathcal {N}}_\lambda ^+$ holds true. According to (6.42) we also obtain

$$\begin{aligned} \int _{\Omega } a(x)|u|^q \mathrm{d}x > 0. \end{aligned}$$

(6.43)

The proof for the claim just above follows arguing by contradiction. Here we suppose that $u\notin {\mathcal {N}}_\lambda ^+$ holds which implies that $u \in {\mathcal {N}}_\lambda ^-$. As a consequence

$$\begin{aligned} J_{\lambda }(u) \ge \inf _{w \in {\mathcal {N}}_\lambda ^-} J_{\lambda }(w) = \alpha _{\lambda }^{-} > 0. \end{aligned}$$

On the other hand, using the fact that $u_{n} \rightarrow u$, we mention also that

$$\begin{aligned} J_{\lambda }(u) = \lim _{n \rightarrow \infty } J_{\lambda }(u_{n}) = \alpha _{\lambda }^{+} < 0. \end{aligned}$$

This is a contradiction proving that u is in ${\mathcal {N}}_\lambda ^{+}$.

At this stage, due the fact that $J_\lambda (u)=J_\lambda (|u|)$ and $J'_\lambda (u) =J'_\lambda (|u|)$, we show that $|u|\in {\mathcal {N}}_\lambda ^+$ for each $u \in {\mathcal {N}}_\lambda ^{+}$. Taking into account Lemma 2.2 we conclude |u| is also a critical point of $J_\lambda$. Without any loss of generality, we can assume that our minimizer u for the functional $J_{\lambda }$ is nonnegative in $\Omega$.

Finally, we observe that $\displaystyle \lim _{\lambda \rightarrow 0}||u||=0$. Indeed, since $u\in {\mathcal {N}}_\lambda ^+$ and arguing as in Proof of Lemma 2.1, we get

$$\begin{aligned}||u||^{\alpha -q}\le \lambda \displaystyle \frac{\ell ^*-q}{\ell (\ell ^*-m)}S_{\ell }||a^+||_{(\frac{\ell }{q})'} \end{aligned}$$

where we put $\alpha \in \{\ell ,m\}$. This ends the Proof of Theorem 1.1.

6.2 The Proof of Theorem 1.2

Put $\Lambda _2 = \min \{\bar{\lambda }_1,\tilde{\lambda }_1\}$ where $\bar{\lambda }_1$ is provided in (3.18) and $\tilde{\lambda }_1$ is given by Lemma 3.4. Initially, due Lemma 3.4, there exists $\delta _1>0$ such that $J_\lambda (v)\ge \delta _1$ for any $v\in {\mathcal {N}}_\lambda ^{-}.$ As a consequence

$$\begin{aligned} \alpha ^{-}_{\lambda }:= \displaystyle \inf _{w \in {\mathcal {N}}_\lambda ^{-}}J_\lambda (w)\ge \delta _1>0. \end{aligned}$$

Now we shall consider a minimizer sequence $(v_n)\subset {\mathcal {N}}_\lambda ^{-}$ given in Proposition 4.1, i.e., $(v_n)\subset {\mathcal {N}}_\lambda ^{-}$ is a sequence satisfying

$$\begin{aligned} \displaystyle \lim _{n\rightarrow \infty }J_\lambda (v_n)=\alpha _{\lambda }^{-} \,\,\text{ and } \,\, \displaystyle \lim _{n\rightarrow \infty } J'_\lambda (v_{n}) = 0. \end{aligned}$$

(6.44)

Since $J_\lambda$ is coercive in ${\mathcal {N}}_\lambda$ and so on ${\mathcal {N}}_\lambda ^{-}$, using Lemma 2.1, we can show that $(v_n)$ is a bounded sequence in $W^{1,\Phi }_{0}(\Omega ).$ Up to a subsequence we assume that $v_n\rightharpoonup v$ in $W^{1,\Phi }_{0}(\Omega )$ holds for some $v = v_{\lambda } \in W_0^{1,\Phi }(\Omega )$. Additionally, using the fact that $q <\ell ^{*}$, we obtain $t^{q}<<\Phi _{*}(t)$ and $W_{0}^{1,\Phi }(\Omega )\hookrightarrow L^{q}(\Omega )$ is also a compact embedding. This fact ensures that $v_n\rightarrow v$ in $L^{q}(\Omega ).$ In this way, we easily seen that

$$\begin{aligned} \displaystyle \lim _{n\rightarrow \infty } \displaystyle \int _{\Omega }a(x) |v_n|^{q}\mathrm{d}x=\displaystyle \int _{\Omega }a(x) |v|^{q}\mathrm{d}x. \end{aligned}$$

(6.45)

Now we claim that $v \in W_0^{1,\Phi }(\Omega )$ given just above is a weak solution to the elliptic problem (1.1). In fact, using (6.44), we infer that

$$\begin{aligned}\left<J'_\lambda (v_n), w\right>=\displaystyle \int _{\Omega }\left[ \phi (|\nabla v_n|)\nabla v_n\nabla w-\lambda a(x)|v_n|^{q-2}v_n w-b(x)|v_n|^{\ell ^*-2}v_n w\right] \mathrm{d}x = o_{n}(1)\end{aligned}$$

holds for any $w \in W_0^{1,\Phi }(\Omega )$. Now using Lemma 5.4 we get

$$\begin{aligned}\displaystyle \int _{\Omega }\left[ \phi (|\nabla v|)\nabla v\nabla w-\lambda a(x)|v|^{q-2}v w-b(x)|v|^{\ell ^*-2}v w\right] \mathrm{d}x = 0, w \in W_0^{1,\Phi }(\Omega ).\end{aligned}$$

So that v is a critical point for the functional $J_{\lambda }$. Without any loss of generality, changing the sequence $(v_{n})$ by $(|v_{n}|)$, we can assume that $v \ge 0$ in $\Omega$.

Now we claim that $v \ne 0$. The proof for this claim follows arguing by contradiction assuming that $v \equiv 0$. Recall that $J_\lambda (t v_{n}) \le J_\lambda (v_{n})$ for any $t \ge 0$ and $n \in \mathbb {N}$. These facts imply that

$$\begin{aligned} \left( 1 - \dfrac{m}{\ell ^{*}}\right) \int _{\Omega } \Phi (|\nabla t v_{n}|)\mathrm{d}x\le & {} \lambda \left( t^{q} - 1\right) \left( \displaystyle \frac{1}{q}-\displaystyle \frac{1}{\ell ^*}\right) \int _{\Omega } a(x)|v_{n}|^{q}\mathrm{d}x\\&+ \left( 1 - \dfrac{\ell }{\ell ^{*}}\right) \int _{\Omega } \Phi (|\nabla v_{n}|)\mathrm{d}x. \end{aligned}$$

Using the last estimate together with the fact that $(v_{n})$ is bounded and [36, Lemma 2.1], we obtain

$$\begin{aligned} \min (t^{\ell }, t^{m}) \left( 1 - \dfrac{m}{\ell ^{*}}\right) \int _{\Omega } \Phi (|\nabla v_{n}|)\mathrm{d}x \le \lambda \left( t^{q} - 1\right) \left( \displaystyle \frac{1}{q}-\displaystyle \frac{1}{\ell ^*}\right) \int _{\Omega } a(x)|v_{n}|^{q}\mathrm{d}x + C \end{aligned}$$

holds for some $C > 0$. These inequalities give us

$$\begin{aligned} \min (t^{\ell }, t^{m}) \left( 1 - \dfrac{m}{\ell ^{*}}\right) \int _{\Omega } \Phi (|\nabla v_{n}|) \mathrm{d}x\le \lambda \left( t^{q} - 1\right) \left( \displaystyle \frac{1}{q}-\displaystyle \frac{1}{\ell ^*}\right) \Vert a\Vert _{\infty } \Vert v_{n}\Vert _{q}^{q} + C. \end{aligned}$$

It is no hard to verify that the fact $\Vert v_{n}\Vert \ge c > 0$ for any $n \in \mathbb {N}$. Using one more time [36, Lemma 2.1], we infer that

$$\begin{aligned} \min (t^{\ell }, t^{m}) \le o_{n}(1) t^{q} + C \end{aligned}$$

holds for any $t \ge 0$ where $C = C(\ell ,m,\ell ^{*}, \Omega , a,b) > 0$ where $o_{n}(1)$ denotes a quantity that goes to zero as $n \rightarrow \infty$. Here was used the fact $v_{n} \rightarrow 0$ in $L^{q}(\Omega )$. This estimate does not make sense for any $t > 0$ big enough using the fact that $q < \ell$. Hence $v \ne 0$ as claimed. As a consequence, v is in ${\mathcal {N}}_\lambda = {\mathcal {N}}_\lambda ^+ \cup {\mathcal {N}}_\lambda ^-$.

At this stage, we shall prove that $v_n\rightarrow v$ in $W_0^{1,\Phi }(\Omega )$. The proof follows arguing by contradiction. Assume that $\displaystyle \liminf _{n \rightarrow \infty } \int _{\Omega } \Phi (|\nabla v_{n} - \nabla v|) \mathrm{d}x\ge \delta$ holds for some $\delta > 0$. Recall that $\Psi : {\mathbb {R}} \rightarrow {\mathbb {R}}$ is defined by

$$\begin{aligned} \Psi (t) = \Phi (t)-\displaystyle \frac{1}{\ell ^*}\phi (t)t^2 \end{aligned}$$

(6.46)

is a convex function for each $t \ge 0$. The Brezis–Lieb Lemma for convex functions says that

$$\begin{aligned} \lim _{n \rightarrow \infty } \int _{\Omega }\left[ \Psi (|\nabla v_{n}|) - \Psi (|\nabla v_{n}- v|)\right] \mathrm{d}x= \int _{\Omega } \Psi (|\nabla v|)\mathrm{d}x \end{aligned}$$

In particular, the last estimate give us

$$\begin{aligned} \int _{\Omega } \Psi (|\nabla v|)\mathrm{d}x < \liminf _{n \rightarrow \infty } \int _{\Omega } \Psi (|\nabla v_{n}|)\mathrm{d}x. \end{aligned}$$

Now we claim that

$$\begin{aligned} \int _{\Omega } b(x) |v|^{\ell ^{*}} \mathrm{d}x > 0. \end{aligned}$$

(6.47)

The proof follows arguing by contradiction. Here we assume that

$$\begin{aligned} \int _{\Omega } b(x) |v|^{\ell ^{*}} \mathrm{d}x \le 0. \end{aligned}$$

(6.48)

Under these conditions, using Brezis–Lieb Lemma for convex functions, we have

$$\begin{aligned} \int _{\Omega } \Psi (|\nabla t v|) \mathrm{d}x < \liminf _{n \rightarrow \infty } \int _{\Omega } \Psi (|\nabla t v_{n}|)\mathrm{d}x \,\, \text{ for } \text{ any } \,\, t > 0 \end{aligned}$$

where $\Psi$ is given by (6.46). Recall also that

$$\begin{aligned} J_{\lambda }(t v_{n}) = \int _{\Omega } \Psi (|\nabla t v_{n}|) \mathrm{d}x + \lambda \int _{\Omega } \left( -\dfrac{1}{q} + \dfrac{1}{\ell ^{*}}\right) a(x)|t v_{n}|^{q} \mathrm{d}x. \end{aligned}$$

Using (6.45) the last identity implies that

$$\begin{aligned} J_{\lambda }(t v ) < \liminf _{n \rightarrow \infty } J_{\lambda }(t v_{n}) \le \liminf _{n \rightarrow \infty } J_{\lambda }(v_{n}) = \alpha _{\lambda }^{-} \,\, \text{ for } \text{ any } \,\, t > 0. \end{aligned}$$

(6.49)

On the other hand, using (6.48), we mention that

$$\begin{aligned} J_{\lambda }(t v )= & {} \int _{\Omega } \left[ \Phi (|\nabla t v|) \mathrm{d}x - \dfrac{\lambda }{q} \int _{\Omega } a(x)|t v|^{q} \mathrm{d}x - \dfrac{1}{\ell ^{*}}\int _{\Omega } b(x)|t v|^{\ell ^{*}} \right] \mathrm{d}x \nonumber \\\ge & {} \int _{\Omega }\left[ \Phi (|\nabla t v|) - \dfrac{\lambda }{q} a(x)|t v|^{\ell ^{*}}\right] \mathrm{d}x. \end{aligned}$$

(6.50)

As a consequence, using the last estimate together with Holder’s inequality, we obtain

$$\begin{aligned} J_{\lambda }(t v )\ge & {} \min \left( \Vert t v\Vert ^{\ell }, \Vert t v\Vert ^{m}\right) - \lambda \Vert a\Vert _{\infty } S_{q}\Vert t v\Vert ^{q}\nonumber \\= & {} t^{\ell } \Vert v\Vert ^{\ell } - \lambda t^{q} \Vert a\Vert _{\infty } S_{q}\Vert v\Vert ^{q} \end{aligned}$$

(6.51)

holds for any $t > 0$ big enough. Hence the last estimate implies that

$$\begin{aligned}\lim _{t \rightarrow \infty } J_{\lambda }(t v) = + \infty .\end{aligned}$$

This is a contradiction with (6.49). So that $\displaystyle \int _{\Omega } b(x)|v|^{\ell ^*} \mathrm{d}x \le 0$ is impossible proving that

$$\begin{aligned} \int _{\Omega } b(x) |v|^{\ell ^{*}} \mathrm{d}x > 0 \end{aligned}$$

(6.52)

holds true. Recalling that we argue by contradiction we assume that $(v_{n})$ does not converge strongly to v. According to Lemma 3.3, there exists an unique $t_{0}$ in $(0, \infty )$ such that $t_{0} v \in {\mathcal {N}}_\lambda ^{-}$. It is easy to verify that

$$\begin{aligned} \int _{\Omega } \Psi (|\nabla t_{0}v|) \mathrm{d}x< \liminf _{n \rightarrow \infty } \int _{\Omega } \Psi (|\nabla t_{0} v_{n}|)\mathrm{d}x. \end{aligned}$$

As a consequence we see that

$$\begin{aligned} \alpha ^{-}_\lambda\le & {} J_\lambda (t_{0}v ) = \displaystyle \int _{\Omega }\left[ \Psi (|\nabla t_{0} v|)-\lambda \left( \displaystyle \frac{1}{q}-\displaystyle \frac{1}{\ell ^*}\right) a(x)|t_{0} v|^{q}\right] \mathrm{d}x\\< & {} \liminf _{n \rightarrow \infty } \displaystyle \int _{\Omega }\left[ \Psi (|\nabla t_{0} v_{n}|)-\lambda \left( \displaystyle \frac{1}{q}-\displaystyle \frac{1}{\ell ^*}\right) a(x)|t_{0} v_{n}|^{q}\right] \mathrm{d}x\\= & {} \liminf _{n \rightarrow \infty } J_{\lambda }(t_{0}v_{n}) \le \liminf _{n \rightarrow \infty } J_{\lambda }(v_{n}) = \alpha _{\lambda }^{-}. \end{aligned}$$

This is a contradiction proving also that $v_{n} \rightarrow v$ in $W_0^{1,\Phi }(\Omega )$. As a consequence v is in ${\mathcal {N}}_\lambda ^-$. This follows from the strong convergence and the fact that $t_{0} = 1$ is the unique maximum point for the fibering map $\gamma _{v}$ for any $v \in {\mathcal {N}}_\lambda ^-$. Hence using the same ideas discussed in Proof of Theorem 1.1, we infer that

$$\begin{aligned} \alpha ^{-}_\lambda \le J_{\lambda }(v) \le \liminf _{n \rightarrow \infty } J_{\lambda }(v_{n}) = \alpha ^{-}_\lambda . \end{aligned}$$

In particular, we see that $\alpha ^{-}_\lambda = J_{\lambda }(v)$ and

$$\begin{aligned} \lim _{n \rightarrow \infty } \int _{\Omega }\left[ \Phi (|\nabla v_{n}|) - \dfrac{1}{\ell ^{*}} \phi (|\nabla v_{n}|)|\nabla v_{n}|^{2}\right] \mathrm{d}x= \int _{\Omega } \left[ \Phi (|\nabla v|) - \dfrac{1}{\ell ^{*}} \phi (|\nabla v|)|\nabla v|^{2}\right] \mathrm{d}x. \end{aligned}$$

In particular, we know that $J_{\lambda }(v)\ge \delta _{1} > 0$. So we finish the Proof of Theorem 1.2.

6.3 The Proof of Theorem 1.3

In view of Theorems 1.1 and 1.2, there are $u = u_{\lambda } \in {\mathcal {N}}_\lambda ^{+}$ and $v = v_{\lambda } \in {\mathcal {N}}_\lambda ^{-}$ in such way that

$$\begin{aligned}J_\lambda (u)=\displaystyle \inf _{w\in {\mathcal {N}}_\lambda ^{+}}J_\lambda (w)\ \ \ \text{ and }\ \ \ J_\lambda (v)=\displaystyle \inf _{ w\in {\mathcal {N}}_\lambda ^{-}}J_\lambda (w).\end{aligned}$$

Additionally, using the fact that $0< \lambda < \Lambda := \min \{\Lambda _1,\Lambda _2\}$ where $\Lambda _1, \Lambda _2>0$ are given by Theorem 1.1 and Theorem 1.2, we mention that ${\mathcal {N}}_\lambda ^{+}\cap {\mathcal {N}}_\lambda ^{-}= \emptyset$. Therefore, u, v are nonnegative weak solutions to the elliptic problem (1.1). As was mentioned before, using the fact that

$$\begin{aligned} J_\lambda (w)=J_\lambda (|w|)\,\, \text{ and }\,\, J^{\prime }_\lambda (w)=J^{\prime }_\lambda (|w|)\end{aligned}$$

holds true for any $w \in W_0^{1,\Phi }(\Omega )$ we can assume $u, v\ge 0$ in $\Omega$. Furthermore, u is a ground state solution for the problem (1.1). As a consequence problem (1.1) admits at least two nontrivial solutions whenever $0< \lambda < \Lambda$. This completes the proof.