Abstract
Using topological degree arguments, several existence theorems are proved for the following system of nonlocal resonant boundary value problem
where \(f : [0,1] \times \mathbb {R}^{k}\times \mathbb {R}^{k}\rightarrow \mathbb {R}^{k}\) is continuous and bounded, \(g = \text{ diag } (g_1,\ldots ,g_k) g_j : [0,1] \rightarrow \mathbb {R}\) has bounded variation \((j = 1,\ldots ,k)\).
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Let \(f : [0,1] \times \mathbb {R}^{k}\times \mathbb {R}^{k}\rightarrow \mathbb {R}^{k}\) be continuous and bounded, \(g = \text{ diag }(g_1,\ldots ,g_k)\) with \(g_j : [0,1] \rightarrow \mathbb {R}\) having bounded variation, and let us consider the boundary value problem on [0, 1]
Such a problem is called resonant because, when \(f \equiv 0\), the linear problem
has the family of nontrivial solutions \(x(t) = c\) with \(c \in \mathbb {R}^{k}\). It was recently considered by Szymańska-Dȩbowska [10] in the special case of
with \(f = f(t,x)\) such that the limit
exists uniformly in \(\xi \in S^{k-1}\), with \(S^{k-1}\) the unit sphere in \(\mathbb {R}^{k}\). The result of [10], presented here as Theorem 4.1, was proved there by considering an approximate sequence of perturbed problems with invertible linear part, solving each of those using Schauder fixed point theorem, getting a uniform bound for the corresponding solutions and going to the limit to deduce a solution of (1.3).
The class of functions f considered in [10] was introduced in 1971 by Nirenberg [7] for elliptic systems, generalizing the one introduced in 1970 by Landesman and Lazer [1] for semilinear elliptic equations with resonant linear part. More recently, Ortega and Sánchez [8] have used a similar class of functions in their study of periodic solutions of differential systems of the form
In this paper, we first show that the result of [10] for problem (1.3) follows in a straightforward way from the simplest form of Leray–Schauder continuation theorem [2] (sometimes referred as Schaefer’s fixed point theorem [9]), to some fixed point operator in \(C^1([0,1],\mathbb {R}^{k})\) constructed in Sect. 2 (Lemma 2.1). This approach provides a generalization of the existence theorem of [10] to some f which may depend upon \(x'\), need not to belong to the Landesman–Lazer–Nirenberg class, but satisfy a condition of the type introduced in 1966 by Villari [11] for periodic solutions of resonant third-order differential equations.
The use of more sophisticated techniques from coincidence degree theory [3, 5] provides other existence conditions for problem (1.1) in terms of the non-vanishing of the Brouwer degree of some mapping in \(\mathbb {R}^{k}\) depending upon f and g (Theorem 6.1). From this result follow also existence conditions for problem (1.3) with Landesman–Lazer–Nirenberg nonlinearities, in terms of the non-vanishing of the Brouwer degree of some mapping in \(\mathbb {R}^{k}\) depending upon h defined in (1.4) and g (Theorem 7.1).
When \(g \equiv 0\), problems (1.1) and (1.3) reduce to classical Neumann problems, for which existence results in the line of Theorem 6.1 can be traced to [4].
2 Equivalent fixed point problem
In order to study problem (1.1) using Leray–Schauder-type arguments, we embed problem (1.1) into the homotopy
Problem (2.1) reduces for \(\lambda = 1\) to (1.1), and for \(\lambda = 0\), to the linear problem
The first two equations imply that \(x(t) \equiv x(0)\), so that \(x'(t) \equiv 0\), and the third one implies \(x(0) = 0\) : For \(\lambda = 0\), problem (2.1) only has the trivial solution.
The following lemma shows that, for each \(\lambda \in [0,1]\), system (2.1) can be written as a fixed point problem in \(C^1([0,1],\mathbb {R}^{k})\), equipped with the norm
Lemma 2.1
For each \(\lambda \in [0,1]\), problem (2.1) is equivalent to the fixed point problem in \(C^1([0,1],\mathbb {R}^{k})\)
Proof
If \(x \in C^2([0,1],\mathbb {R}^{k})\) is a solution of (2.1) for some \(\lambda \in [0,1]\), then
so that
and hence x(t) verifies (2.2). Conversely, if \(x \in C^1([0,1],\mathbb {R}^{k})\) is a solution of (2.2) for some \(\lambda \in [0,1]\), then \(x \in C^2([0,1],\mathbb {R}^{k})\), and, from (2.2) we get, for all \(t \in [0,1]\),
Consequently, \(x'(0) = 0\) and, taking \(t = 0\) in (2.2), we get
which, combined with the first equation in (2.3) taken in \(t = 1\), gives the second boundary condition in (2.1). \(\square \)
Now it is standard, using Ascoli-Arzelá’s theorem, to show that the operator \({\mathcal {F}} : C^1([0,1],\mathbb {R}^{k}) \rightarrow C^1([0,1],\mathbb {R}^{k})\) defined by
is completely continuous, i.e., continuous and taking bounded subsets into relatively compact ones, and hence the same is true for the operator \((x,\lambda ) \mapsto \lambda {\mathcal {F}}x\) from \(C^1([0,1],\mathbb {R}^{k}) \times [0,1]\) to \(C^1([0,1],\mathbb {R}^{k})\).
3 Conditions of Villari type
In this section, we use the simplest version of Leray–Schauder’s continuation theorem for \({\mathcal {F}}\) [2, 9].
Lemma 3.1
If there exists \(R > 0\) such that, for any \(\lambda \in (0,1)\) and any possible fixed point x of \(\lambda {\mathcal {F}}\), one has \(\Vert x\Vert < R\), then \({\mathcal {F}}\) has a fixed point x such that \(\Vert x\Vert \le R\).
We first prove the following existence theorem, involving Villari-type conditions. \(\langle \cdot , \cdot \rangle \) denotes the usual inner product in \(\mathbb {R}^{k}\) and \(|\cdot |\) the corresponding Euclidean norm.
Theorem 3.1
Assume that the following conditions hold:
-
(h1)
There exists \(M > 0\) such that

-
(h2)
There exists \(r > 0\) such that
$$\begin{aligned} \left\langle x(0) , \int _0^1 f(s,x(s),x'(s))\,\mathrm{d}s - \int _0^1 \int _0^s f(\tau ,x(\tau ),x'(\tau ))\,\mathrm{d}\tau \, \mathrm{d}g(s) \right\rangle \le 0 \end{aligned}$$(3.1)for all \(x \in C^1([0,1],\mathbb {R}^{k})\) such that

Then, problem (1.1) has at least one solution.
Proof
Let \(\lambda \in (0,1)\) and let x be a possible fixed point of \(\lambda {\mathcal {F}}\). Then, x satisfies the first equation in (2.3), and hence, using Assumption (h1), we have, for all \(t \in [0,1]\)
Consequently, if \(\min _{t \in [0,1]}|x(t)| \ge r\), it follows from (2.4) and Assumption (h2) that,

a contradiction. Hence, there exists \(\tau \in [0,1]\) such that \(|x(\tau )| < r\), which, combined with (3.2), implies that, for all \(t \in [0,1]\),
and the result follows from Lemma 3.1. \(\square \)
Remark 3.1
When \(f(t,x,x') = f(t)\), it is easy to see that Assumption (h2) is equivalent to the necessary and sufficient condition
for the solvability of the non-homogeneous linear boundary value problem
Remark 3.2
The conclusion of Theorem 3.1 still holds if, in Assumption (h2), condition (3.1) is replaced by
It suffices to replace homotopy (2.1) by the homotopy
For \(\lambda = 1\), we still get problem (1.1), and for \(\lambda = 0\), we obtain the problem
which again has only the trivial solution. The corresponding fixed point operator is given by
and the proof of the variant of Theorem 3.1 proceeds like the one of this theorem, leading to the contradiction

4 Landesman–Lazer–Nirenberg nonlinearities
The following lemma will be useful for proving existence theorems when f(t, x) belongs to the Landesman–Lazer–Nirenberg class. Let \(f : [0,1] \times \mathbb {R}^{k}\rightarrow \mathbb {R}^{k}\) be continuous.
Lemma 4.1
Assume that, the following conditions hold.
-
(H1)
For each \(t \in [0,1]\), the limit (1.4) exists uniformly in \(\xi \in S^{k-1}\).
If there exists a sequence \((x_n)\) in \(C^1([0,1],\mathbb {R}^{k})\) such that \(\inf _{t \in [0,1]}|x_n(t)| \ge n\) and such that the sequence \((y_n) := \left( \frac{x_n}{|x_n|}\right) \) converges uniformly on [0, 1] to \(\eta \in S^{k-1}\), then, for each \(t \in [0,1]\),
Proof
Let \((x_n)\) be the sequence in \(C^1([0,1],\mathbb {R}^{k})\) given in the assertion. Given \(\varepsilon > 0\), for each \(t \in [0,1]\), one can find, by Assumptions (H1), a positive integer \(N_1\) such that, for all \(n \ge N_1\), and for all \(\xi \in S^{k-1}\), one has
By the continuity of h, one can find a positive integer \(N_2\) such that, for all \(n \ge N_2\)
Consequently, for \(n \ge N_0 = \max \{N_1,N_2\}\), one has
which shows that, for each \(t \in [0,1], (f(t,x_n(t)))\) converges to \(h(t,\eta )\). \(\square \)
The following result is the one proved in a different way in [10].
Theorem 4.1
Assume that condition (H1) holds and that
-
(H2)
For all \(\xi \in S^{k-1}\),
$$\begin{aligned} \left\langle \xi , \int _0^1 h(s,\xi )\,\mathrm{d}s - \int _0^1 \int _0^s h(\tau ,\xi )\,\mathrm{d}\tau \,\mathrm{d}g(s) \right\rangle < 0. \end{aligned}$$(4.2)
Then, problem (1.3) has at least one solution.
Proof
Assumption (H1) implies the existence of some \(M > 0\) such that
By Theorem 3.1, it suffices to prove that condition (h2) is satisfied for (1.3). If it is not the case, there exists a sequence \((x_n)\) in \(C^1([0,1],\mathbb {R}^{k})\) such that
and, for all \(n \in \mathbb {N}\),
Set \(y_n(t) = \frac{x_n(t)}{|x_n(t)|} \quad (n \in \mathbb {N})\), so that \(|y_n(t)| = 1 \quad (n \in \mathbb {N})\), and
By (4.4) and Ascoli-Arzelà’s theorem, going if necessary to a subsequence, there exists \(y \in C([0,1],\mathbb {R}^{k})\) such that \((y_n)\) converges uniformly on [0, 1] to y. Furthermore, \(|y(t)| = 1\) for all \(t \in [0,1]\), and, by (4.4) again, \((y'_n)\) converges to 0 uniformly on [0, 1]. Consequently, \(y \in C^1([0,1],\mathbb {R}^{k}), y' = 0\) on [0, 1] and y is constant, namely \(y(t) = \eta \in S^{k-1}\; (t \in [0,1])\). By Lemma 4.1, for each \(t \in [0,1], (f(t,x_n(t)))\) converges to \(h(t,\eta )\), and Lebesgue dominated convergence theorem implies that
which introduced in (4.3) gives the contradiction
\(\square \)
Remark 4.1
By using Remark 3.2, one can show that the conclusion is Theorem 4.1 remains valid if, in Assumption (H2), (4.2) is replaced by
5 Equivalent abstract semilinear equation
In order to obtain more general existence conditions, we apply a continuation theorem from coincidence degree theory [3, 4]. To this aim, we first write problem (1.1) in an equivalent form.
Lemma 5.1
x is a solution of (1.1) if and only if \(x \in C^1([0,1],\mathbb {R}^{k})\) is a solution of the integro-differential boundary value problem
Proof
If \(x \in C^2([0,1],\mathbb {R}^{k})\) is a solution of (1.1), then
and hence (5.1) follows from inserting the first equation in the second one. Conversely, if \(x \in C^1([0,1],\mathbb {R}^{k})\) is a solution of (5.1), then \(x \in C^2([0,1],\mathbb {R}^{k})\), and, by, respectively, differentiating the first equation, taking its value at 0, and inserting the first equation in the third one, we get
\(\square \)
Let us define the linear operator \(L : C^1([0,1],\mathbb {R}^{k}) \rightarrow C([0,1],\mathbb {R}^{k}) \times \mathbb {R}^{k}\) by
L is clearly continuous, and we denote its kernel by N(L) and its range by R(L). As

\(\text{ dim } N(L) = k\), and, for \((y,c) \in C([0,1],\mathbb {R}^{k}) \times \mathbb {R}^{k}\),

has a solution if and only if \(c = y(1)\), so that \(R(L) = N(Q)\) with Q the projector in \(C([0,1],\mathbb {R}^{k}) \times \mathbb {R}^{k}\) defined by
Thus, R(L) is closed and has codimension k, so that L is a continuous Fredholm operator of index 0. If we define \(N : C^1([0,1],\mathbb {R}^{k}) \rightarrow C([0,1],\mathbb {R}^{k}) \times \mathbb {R}^{k}\) by
it follows easily from standard arguments based upon Ascoli-Arzelá’s theorem that N is completely continuous. As L has a continuous right inverse, N is L-completely continuous in the sense of [5]. With those notations, problem (5.1), and hence problem (1.1), is equivalent to the abstract equation \(Lx = Nx\).
6 More general Villari-type conditions and Brouwer degree
We denote by B(r) the open ball of center 0 and radius r in \(\mathbb {R}^{k}\), define the continuous mapping \(\varphi : \mathbb {R}^{k}\rightarrow \mathbb {R}^{k}\) by
and denote by \(d_B[\varphi ,B(r),0]\), when it is defined, the Brouwer degree of \(\varphi \) with respect to B(r) and 0 [6]. We state the special case of Theorem IV.13 in [5] applied to \(L-N\) with L and N defined above.
Lemma 6.1
Assume there exists \(R > 0\) such that the following conditions hold:
-
(c1)
For each \(\lambda \in (0,1)\), any possible solution of \(Lx = \lambda Nx\) is such that \(\Vert x\Vert < R\).
-
(c2)
Any possible solution \(c \in \mathbb {R}^{k}\) of \(\varphi (c) = 0\) is such that \(|c| < R\).
-
(c3)
\(d_B[\varphi ,B(R),0] \ne 0\).
Then equation \(Lx = Nx\) has at least one solution x such that \(\Vert x\Vert \le R\).
We can now prove an existence theorem for (1.1) under a Villari-type condition.
Theorem 6.1
Assume that Assumption (h1) holds as well as the following conditions:
-
(a2)
There exists \(r > 0\) such that
$$\begin{aligned} \int _0^1 \int _0^s f(\tau ,x(\tau ),x'(\tau ))\,\mathrm{d}\tau \, \mathrm{d}g(s) - \int _0^1 f(s,x(s),x'(s))\,\mathrm{d}s \ne 0 \end{aligned}$$(6.1)for all \(x \in C^1([0,1],\mathbb {R}^{k})\) such that

-
(a3)
\(d_B[\varphi ,B(r),0] \ne 0\).
Then, problem (1.1) has at least one solution.
Proof
Let \(\lambda \in (0,1)\) and \(x \in C^1([0,1],\mathbb {R}^{k})\) be a possible solution of \(Lx = \lambda Nx\), i.e., of
Then, by Assumption (h1), we have
Now, it follows from (5.3) and (5.4) that
and as \(Lx = \lambda Nx \;(\lambda \in (0,1))\) implies \(QNx = 0\), we have
Assumption (a2) implies the existence of \(\tau \in [0,1]\) such that
Consequently, for all \(t \in [0,1]\), it follows from (6.2) and (6.3) that
and hence that
Thus, condition (c1) of Lemma 6.1 is satisfied, and the same is true, from Assumption (a2) restricted to constant functions, and from Assumption (a3), for conditions (c2) and (c3), because \(d_B[\varphi ,B(R),0] = d_B[\varphi ,B(r),0] \ne 0\) follows from \(\varphi (c) \ne 0\) for all \(|c| \ge r\) and the excision property of Brouwer degree. \(\square \)
Remark 6.1
Theorem 3.1 with the slightly stronger Assumption (h2) with a strict inequality in (3.1) (or in its variant (3.4)) is a special case of Theorem 6.1. Indeed, (3.1) (respectively, (3.4)) then implies that Assumption (a2) of Theorem 6.1 holds and, furthermore, by taking constant functions c, that

when \(|c| \ge r\). This immediately implies, using the homotopy \((1-\lambda )c + \lambda \varphi (c)\) (resp. \(-(1-\lambda )c + \lambda \varphi (c)\)) and homotopy invariance of Brouwer degree, that

so that Assumption (a3) of Theorem 6.1 is verified.
7 Landesman–Lazer–Nirenberg nonlinearities and Brouwer degree
When f belongs to the Landesman–Lazer–Nirenberg class, we can deduce from Theorem 6.1 new conditions of existence involving Brouwer degree. Let \(\psi : S^{k-1} \rightarrow \mathbb {R}^{k}\) be the continuous mapping defined by
where h is defined in (1.4), and recall that when \(0 \not \in \psi (S^{k-1})\), the Brouwer degree \(d_B[\psi ,S^{k-1}]\) is defined as the Brouwer degree \(d_B[\Psi ,B(1),0]\) of any continuous extension \(\Psi \) of \(\psi \) to the closed unit ball \(\overline{B}(1)\).
Theorem 7.1
Assume that Assumption (H1) holds as well as the following conditions:
-
(A2)
 .
. -
(A3)
\(d_B[\psi ,S^{k-1}] \ne 0\).
Then, problem (1.3) has at least one solution.
Proof
It follows from Assumption (H1) that Assumption (h1) of Theorem 3.1 applied to (1.3) holds for some \(M > 0\). If Assumption (a2) of Theorem 6.1 does not hold, there exists a sequence \((x_n)\) in \(C^1([0,1],\mathbb {R}^{k})\) such that
and, for all \(n \in \mathbb {N}\),
Set \(y_n(t) = \frac{x_n(t)}{|x_n(t)|} \quad (n \in \mathbb {N})\). Proceeding like in the proof of Theorem 4.1, we find that, going if necessary to a subsequence, \((y_n)\) converges uniformly on [0, 1] to some constant \(\eta \in S^{k-1}\), and
which introduced in (7.1) gives
a contradiction to Assumption (A2). Now, it follows from Assumption (a2) that

and hence, by the excision property of Brouwer degree, for all \(\rho \ge r\),
Consequently, as \(\varphi (\rho \, \cdot )\) on \(\overline{B}(1)\) is a continuous extension of \(\varphi (\rho \, \cdot )\) on \(S^{k-1}\), we have, for \(\rho \ge r\),
On the other hand, if follows from Assumption (H1) and Lebesgue dominated convergence theorem and Assumption (A2) that

which implies that, by the invariance of Brouwer degree under small perturbations, there exists \(R \ge r\) such that
It follows from (7.2), (7.3), (7.4), Assumption (A3) and the excision property of Brouwer degree, that
and Assumption (a3) of Theorem 6.1 is satisfied. \(\square \)
Remark 7.1
Theorem 4.1 follows from Theorem 7.1. Indeed, it follows from Assumption (H2) (respectively, from its alternative (4.5)), like in Remark 6.1, that \(\psi (\xi ) \ne 0\) for \(\xi \in S^{k-1}\) and that
The interest of the proof of Theorem 4.1 is that it depends only upon the simplest version of Leray–Schauder continuation theorem, which is equivalent to Schauder’s fixed point theorem.
Example 7.1
For \(n \ge 1\) an integer, \(\alpha \in (0,1), p \in C([0,1],\mathbb {R}^2), a \in \mathbb {R}\), and using in \(\mathbb {R}^2\) the complex notation, let us consider the boundary value problem
This is a special case of (1.3) with
For \(\xi \in S^1,\quad t \in [0,1]\),
Consequently, for \(\xi \in S^1\),
Hence, if

we have
and hence problem (7.5) has at least one solution.
In the special case of Neumann problem, problem (7.5) with \(a = 0\), has at least one solution for all \(p \in C([0,1],\mathbb {R}^2)\) such that
Notice that, in this case, if (7.5) has a solution z, then
which shows that condition (7.6) is necessary and sufficient for the existence of a solution to the Neumann problem (7.5) with \(a = 0\).
Remark 7.2
When \(n \ge 2\), the existence result for problem (7.5) cannot be deduced from Theorem 4.1 because, as shown in Remark 7.1, the assumptions of Theorem 4.1 correspond to problem with associated Brouwer degree 1 or \(-1.\)
References
Landesman, E.M., Lazer, A.C.: Nonlinear perturbations of linear elliptic boundary value at resonance. J. Math. Mech. 19, 609–623 (1970)
Leray, J., Schauder, J.: Topologie et équations fonctionnelles. Ann. Sci. École Norm. Supérieure (3) 51, 45–78 (1934)
Mawhin, J.: Equivalence theorems for nonlinear operator equations and coincidence degree theory for some mappings in locally convex topological vector spaces. J. Differ. Equ. 12, 610–636 (1972)
Mawhin, J.: Problèmes aux limites du type de Neumann pour certaines équations différentielles ou aux dérivées partielles non linéaires. In: Equations différentielles et fonctionnelles non linéaires, pp. 124–134. Hermann, Paris (1973)
Mawhin, J.: Topological Degree Methods in Nonlinear Boundary Value Problems, CBMS Regional Series in Mathematics No. 40. American Mathematical Society, Providence (1979)
Mawhin, J.: A simple approach to Brouwer degree based on differential forms. Adv. Nonlinear Stud. (4) 4, 535–548 (2004)
Nirenberg, L.: An application of generalized degree to a class of nonlinear problems. In: Troisième Colloque du C.B.R.M. d’analyse fonctionnelle, pp. 57–74. Vander, Louvain (1971)
Ortega, R., Sanchez, L.A.: Periodic solutions of forced oscillators with several degrees of freedom. Bull. Lond. Math. Soc. 34, 308–318 (2002)
Schaefer, H.H.: Ueber die Methode der a priori Schranken. Math. Ann. 129, 415–416 (1955)
Szymańska-Dȩbowska, K.: On a \(k\)-dimensional nonlocal boundary value problem at resonance. Electron. J. Differ. Equ. 2015, 1–8 (2015)
Villari, G.: Soluzioni periodiche di una classe di equazioni differenziali del terz’ordine quasi lineari. Ann. Mat. Pura Appl. (4) 73, 103–110 (1966)
Author information
Authors and Affiliations
Corresponding author
Additional information
Dedicated in the memory of Gaetano Villari.
Rights and permissions
About this article
Cite this article
Mawhin, J., Szymańska-Dȩbowska, K. Second-order ordinary differential systems with nonlocal Neumann conditions at resonance. Annali di Matematica 195, 1605–1617 (2016). https://doi.org/10.1007/s10231-015-0532-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10231-015-0532-9
Keywords
- Nonlocal boundary value problem
- Boundary value problem at resonance
- Leray–Schauder fixed point theorem
- Coincidence degree



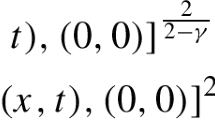



 .
.