On doubly periodic minimal surfaces in ${\mathbb {H}}^2 \times {\mathbb {R}}$ with finite total curvature in the quotient space

Abstract

In this paper, we develop the theory of properly immersed minimal surfaces in the quotient space $({{\mathrm{{\mathbb {H}}^2\times {\mathbb {R}}}}})/G,$ where G is a subgroup of isometries generated by a vertical translation and a horizontal isometry (without fixed points) in ${{\mathrm{{\mathbb {H}}^2}}}$. The horizontal isometry can be either a parabolic translation along horocycles in ${{\mathrm{{\mathbb {H}}^2}}}$ or a hyperbolic translation along a geodesic in ${{\mathrm{{\mathbb {H}}^2}}}.$ We prove that if a properly immersed minimal surface in $({{\mathrm{{\mathbb {H}}^2\times {\mathbb {R}}}}})/G$ has finite total curvature, then its total curvature is a multiple of $2\pi$ and, moreover, we understand the geometry of the ends. The results hold true more generally for properly immersed minimal surfaces in $M\times {\mathbb {S}}^1,$ where M is a hyperbolic surface with finite topology whose ends are isometric to one of the ends of the above spaces $({{\mathrm{{\mathbb {H}}^2\times {\mathbb {R}}}}})/G$.

1 Introduction

Among all the minimal surfaces in ${{\mathrm{{\mathbb {R}}}}}^3$, the ones of finite total curvature are the best known. In fact, if a minimal surface in ${{\mathrm{{\mathbb {R}}}}}^3$ has finite total curvature, then this minimal surface is either a plane or its total curvature is a nonzero multiple of $2\pi .$ Moreover, if the total curvature is $-4\pi ,$ then the minimal surface is either the Catenoid or the Enneper’s surface [21].

In the homogeneous space ${{\mathrm{{\mathbb {H}}^2\times {\mathbb {R}}}}},$ Nelli and Rosenberg [20] and Collin and Rosenberg [2] obtained the first examples of minimal surfaces with finite total curvature which are graphs over certain polygonal domains. Later, the first author jointly with H. Rosenberg [12] developed the theory of complete embedded minimal surfaces of finite total curvature in ${{\mathrm{{\mathbb {H}}^2\times {\mathbb {R}}}}}.$ In that work, they proved that the total curvature of such surfaces must be a multiple of $2\pi ,$ and they gave simply connected examples whose total curvature is $-2\pi m,$ for each nonnegative integer m.

In the last few years, many people have worked on this subject, constructed new examples and classified some minimal surfaces of finite total curvature in ${{\mathrm{{\mathbb {H}}^2\times {\mathbb {R}}}}}$ (see [10, 11, 14, 19, 22, 23, 26]).

In [19], Morabito and Rodríguez constructed for $k\ge 2$ a $(2k-2)$-parameter family of properly embedded minimal surfaces in ${{\mathrm{{\mathbb {H}}^2\times {\mathbb {R}}}}}$ invariant by a vertical translation which have total curvature $4\pi (1-k),$ genus zero and 2k vertical Scherk-type ends in the quotient by the vertical translation. Moreover, independently, Morabito and Rodríguez [19] and Pyo [22] constructed for $k\ge 2$ examples of properly embedded minimal surfaces with total curvature $4\pi (1-k),$ genus zero and k ends, each one asymptotic to a vertical plane. In particular, we have examples of minimal annuli with total curvature $-4\pi .$

It is natural to consider this kind of question for doubly periodic minimal surfaces (that is, surfaces invariant by a ${\mathbb {Z}}^2$ subgroup of isometries), and some similar results are obtained. For instance, we know that a doubly periodic minimal surface in ${{\mathrm{{\mathbb {R}}}}}^3,$ which is not a plane, is given by a properly embedded surface in ${{\mathrm{{\mathbb {T}}}}}\times {{\mathrm{{\mathbb {R}}}}},$ where ${{\mathrm{{\mathbb {T}}}}}$ is some flat torus, and Meeks and Rosenberg [17] proved that a finite topology complete embedded minimal surface in ${{\mathrm{{\mathbb {T}}}}}\times {{\mathrm{{\mathbb {R}}}}}$ has finite total curvature and they understood the geometry of the ends.

In the space ${{\mathrm{{\mathbb {H}}^2\times {\mathbb {R}}}}}$ quotiented by a subgroup of isometries generated by a parabolic translation along horocycles in ${{\mathrm{{\mathbb {H}}^2}}}$ and a vertical translation, the second author [16] constructed examples of minimal surfaces with total curvature $-4\pi$ and four ends. In one example, two ends are asymptotic to a horizontal slice and two ends are asymptotic to a vertical plane, while in the other example, two ends are asymptotic to a vertical plane and the other two are asymptotic to the quotient of a helicoidal plane. Here a helicoidal plane means a minimal surface in ${{\mathrm{{\mathbb {H}}^2\times {\mathbb {R}}}}}$ which is parameterized by $X(x,y)=(x,y,ax+b)$ when we consider the halfplane model for ${{\mathrm{{\mathbb {H}}^2}}}.$

In this paper, we consider the space ${{\mathrm{{\mathbb {H}}^2\times {\mathbb {R}}}}}$ quotiented by a subgroup of isometries $G\subset \hbox {Isom}\,({{\mathrm{{\mathbb {H}}^2\times {\mathbb {R}}}}})$ generated by a horizontal isometry $\phi$ in $H^2$ without fixed points and a vertical translation T(h),  for some $h>0.$ The isometry $\psi$ can be either a parabolic translation along horocycles in ${{\mathrm{{\mathbb {H}}^2}}}$ or a hyperbolic translation along a geodesic in ${{\mathrm{{\mathbb {H}}^2}}}.$ We prove that if a properly immersed minimal surface in ${{\mathrm{{\mathbb {H}}^2\times {\mathbb {R}}}}}/G$ has finite total curvature, then its total curvature is a multiple of $2\pi ,$ and moreover, we understand the geometry of the ends. More precisely, we prove the following result.

Main Theorem

Let $X: \Sigma \hookrightarrow {\mathcal {M}} = {{\mathrm{{\mathbb {H}}^2\times {\mathbb {R}}}}}/[\psi , T(h)]$ be a properly (oriented) immersed minimal surface with finite total curvature. Then

• 1. $\Sigma$ is conformally equivalent to a compact Riemann surface $\overline{M}$ with genus g minus a finite number of points, that is, $\Sigma =\overline{M}\setminus \{p_1,\ldots , p_k\}$.

• 2. The total curvature satisfies

  $$\begin{aligned} \int _{\Sigma }K\hbox {d}\sigma =2\pi (2-2g-k). \end{aligned}$$

• 3. Depending on the asymptotic geometry of the end of ${{\mathrm{{\mathbb {H}}^2\times {\mathbb {R}}}}}/G$ containing an end E of the surface $\Sigma ,$ we have only three possible asymptotic behaviors for the end E of $\Sigma$: E is either asymptotic to a vertical plane, or to a horizontal slice or to a quotient of a helicoidal plane.

• 4. If we parameterize each end of $\Sigma$ by a punctured disk, then either the holomorphic quadratic differential Q extends to a constant at the puncture (in the case where the end is asymptotic to a horizontal slice) or Q extends meromorphically to the puncture with a double pole and residue zero.

Let us mention that these results hold true for properly immersed minimal surfaces in $M\times {\mathbb {S}}^1,$ where M is a hyperbolic surface $(K_M=-1)$ with finite topology whose ends are either isometric to ${\mathcal {M}}_+$ (where the injectivity radius goes to zero) or ${\mathcal {M}}_-$ (where the injectivity radius goes to infinity) which we define in the next section.

2 Preliminaries

Unless otherwise stated, we use the Poincaré disk model for the hyperbolic plane, that is

$$\begin{aligned} {\mathbb {H}}^2=\left\{ (x,y)\in {{\mathrm{{\mathbb {R}}}}}^2|\ x^2+y^2<1\right\} \end{aligned}$$

with the hyperbolic metric $g_{{{\mathrm{{\mathbb {H}}^2}}}}=\sigma g_0=\frac{4}{(1-x^2-y^2)^2}g_0,$ where $g_0$ is the Euclidean metric in ${{\mathrm{{\mathbb {R}}}}}^2.$ In this model, the asymptotic boundary $\partial _{\infty }{\mathbb {H}}^2$ of ${\mathbb {H}}^2$ is identified with the unit circle.

We write $\overline{pq}$ to denote the geodesic arc between the two points p, q.

We consider the quotient spaces $({{\mathrm{{\mathbb {H}}^2\times {\mathbb {R}}}}})/G,$ where G is a subgroup of Isom (${{\mathrm{{\mathbb {H}}^2\times {\mathbb {R}}}}}$) generated by a horizontal isometry $\phi$ in $H^2$ without fixed points and a vertical translation T(h),  for some $h>0.$ The horizontal isometry $\psi$ can be either a horizontal translation along horocycles in ${{\mathrm{{\mathbb {H}}^2}}}$ or a horizontal translation along a geodesic in ${{\mathrm{{\mathbb {H}}^2}}}.$

Let us analyze each one of these cases for $\psi .$

For the first case, consider any geodesic $\gamma$ parameterized by arc length that limits to a point at infinity $p_0\in \partial _{\infty }{{\mathrm{{\mathbb {H}}^2}}}, \gamma (+\infty )=p_0.$ Let c(s) be the horocycles in ${{\mathrm{{\mathbb {H}}^2}}}$ tangent to $\partial _{\infty }{{\mathrm{{\mathbb {H}}^2}}}$ at $p_0$ that intersects $\gamma$ at $\gamma (s),$ and write d(s) to denote the horocylinder $c(s)\times {{\mathrm{{\mathbb {R}}}}}$ in ${{\mathrm{{\mathbb {H}}^2\times {\mathbb {R}}}}}.$ Taking two points $p,q \in c(s),$ let $\psi :{{\mathrm{{\mathbb {H}}^2\times {\mathbb {R}}}}}\rightarrow {{\mathrm{{\mathbb {H}}^2\times {\mathbb {R}}}}}$ be the parabolic translation along d(s) such that $\psi (p)=q.$ We have $\psi (d(s))=d(s)$ for all s. If the subgroup of isometries G is generated by $\psi$ and a vertical translation T(h),  that is, $G=[\psi , T(h)],$ then the manifold ${\mathcal {M}}$ which is the quotient of ${{\mathrm{{\mathbb {H}}^2\times {\mathbb {R}}}}}$ by G is diffeomorphic to ${{\mathrm{{\mathbb {T}}}}}^2\times {{\mathrm{{\mathbb {R}}}}},$ where ${{\mathrm{{\mathbb {T}}}}}^2$ is the 2-torus. Moreover, ${\mathcal {M}}$ is foliated by the family of tori ${{\mathrm{{\mathbb {T}}}}}(s)=d(s)/G,$ which are intrinsically flat and have constant mean curvature 1 / 2 (see Fig. 1). Observe that the end $\bigcup _{s\ge 0}d(s)/[\psi , T(h)]$ has injectivity radius zero since the length of $c(s)/[\psi ]$ goes to zero as $s\rightarrow +\infty ;$ the end $\bigcup _{s\le 0}d(s)/[\psi , T(h)]$ has injectivity radius strictly positive since it coincides with the injectivity radius of ${{\mathrm{{\mathbb {T}}}}}(0).$

Fig. 1

${\mathcal {M}}=({{\mathrm{{\mathbb {H}}^2\times {\mathbb {R}}}}})/[\psi , T(h)]$, where $\psi$ is a parabolic isometry

For the second case, take a geodesic $\gamma$ in ${{\mathrm{{\mathbb {H}}^2}}}$ and consider c(s) the family of equidistant curves to $\gamma ,$ with $c(0)=\gamma .$ Write d(s) to denote the plane $c(s)\times {{\mathrm{{\mathbb {R}}}}}$ in ${{\mathrm{{\mathbb {H}}^2\times {\mathbb {R}}}}}.$ Given two points $p,q\in c(s),$ let $\psi :{{\mathrm{{\mathbb {H}}^2\times {\mathbb {R}}}}}\rightarrow {{\mathrm{{\mathbb {H}}^2\times {\mathbb {R}}}}}$ be the hyperbolic translation along $\gamma$ such that $\psi (p)=q.$ We have $\psi (d(s))=d(s)$ for all s. If $G=[\psi , T(h)],$ then the manifold ${\mathcal {M}}$ which is the quotient of ${{\mathrm{{\mathbb {H}}^2\times {\mathbb {R}}}}}$ by G is also diffeomorphic to ${{\mathrm{{\mathbb {T}}}}}^2\times {{\mathrm{{\mathbb {R}}}}}$, and ${\mathcal {M}}$ is foliated by the family of tori ${{\mathrm{{\mathbb {T}}}}}(s)=d(s)/G,$ which are intrinsically flat and have constant mean cuvature $\frac{1}{2}$tanh(s) (see Fig. 2). Observe that both ends $\bigcup _{s\le 0}d(s)/[\psi , T(h)]$ and $\bigcup _{s\ge 0}d(s)/[\psi , T(h)]$ have injectivity radii strictly positive since it coincides with the injectivity radius of ${{\mathrm{{\mathbb {T}}}}}(0).$

Fig. 2

${\mathcal {M}}=({{\mathrm{{\mathbb {H}}^2\times {\mathbb {R}}}}})/[\psi , T(h)]$, where $\psi$ is a hyperbolic isometry

As remarked above, in these quotient spaces we have two different types of ends: one where the injectivity radius is zero, which we denote by ${\mathcal {M}}_+,$ and another one where the injectivity radius is strictly positive, which we denote by ${\mathcal {M}}_{-}$.

Hence ${\mathcal {M}}_+=\bigcup _{s\ge 0} d(s)/[\psi ,T(h)],$ where $\psi$ is a parabolic translation along horocycles, and ${\mathcal {M}}_-=\bigcup _{s\ge 0} d(s)/[\psi ,T(h)],$ for $\psi$ hyperbolic translation along a geodesic in ${{\mathrm{{\mathbb {H}}^2}}},$ or ${\mathcal {M}}_-=\bigcup _{s\le 0}d(s)/[\psi , T(h)],$ where $\psi$ can be either a parabolic translation along horocycles or a hyperbolic translation along a geodesic in ${{\mathrm{{\mathbb {H}}^2}}}$ (see Fig. 3).

Fig. 3

${\mathcal {M}}_+$ and ${\mathcal {M}}_-$

From now on, we will not distinguish between the two quotient spaces above, and we will denote both by ${\mathcal {M}}.$

Throughout this paper, we will only consider oriented surfaces.

Let $\Sigma$ be a Riemannian surface and $X:\Sigma \rightarrow {\mathcal {M}}$ be a minimal immersion. Since ${\mathcal {M}}=({{\mathrm{{\mathbb {H}}^2\times {\mathbb {R}}}}})/[\psi , T(h)]$ is diffeomorphic to the product manifold ${\mathbb {H}}^2/[\psi ]\times {\mathbb {S}}^1,$ we can write $X=(F, h): \Sigma \rightarrow {\mathbb {H}}^2/[\psi ]\times {\mathbb {S}}^1,$ where $F: \Sigma \rightarrow {\mathbb {H}}^2/[\psi ]$ and $h: \Sigma \rightarrow {\mathbb {S}}^1$ are harmonic maps. We consider local conformal parameters $z= x+iy$ on $\Sigma .$ Hence

$$\begin{aligned} \begin{array}{ccc} |F_x|^2_{{{\mathrm{{\mathbb {H}}^2}}}}+(h_x)^2= |F_y|^2_{{{\mathrm{{\mathbb {H}}^2}}}}+(h_y)^2&{}&{}\\ &{}&{}\\ \left\langle F_x,F_y\right\rangle _{{{\mathrm{{\mathbb {H}}^2}}}}+h_x \cdot h_y=0&{}&{}\\ \end{array} \end{aligned}$$

(2.1)

and the metric induced by the immersion is given by

$$\begin{aligned} \hbox {d}s^2=\lambda ^2(z)|\hbox {d}z|^2=(|F_z|_{{{\mathrm{{\mathbb {H}}^2}}}}+|F_{\bar{z}}|_{{{\mathrm{{\mathbb {H}}^2}}}})^2|\hbox {d}z|^2. \end{aligned}$$

(2.2)

Considering the universal covering $\pi :{{\mathrm{{\mathbb {H}}^2\times {\mathbb {R}}}}}\rightarrow {\mathbb {H}}^2/[\psi ]\times {\mathbb {S}}^1$, we can take $\widetilde{\Sigma },$ a connected component of the lift of $\Sigma$ to ${{\mathrm{{\mathbb {H}}^2\times {\mathbb {R}}}}},$ and we have $\widetilde{X}=(\widetilde{F}, \widetilde{h}): \widetilde{\Sigma }\rightarrow {{\mathrm{{\mathbb {H}}^2\times {\mathbb {R}}}}}$ such that $\pi (\widetilde{\Sigma })=\Sigma$ and $\widetilde{F}: \widetilde{\Sigma }\rightarrow {\mathbb {H}}^2, \widetilde{h}: \widetilde{\Sigma }\rightarrow {\mathbb {R}}$ are harmonic maps. We denote by $\widetilde{\partial _t}, \partial _t$ the vertical vector fields in ${{\mathrm{{\mathbb {H}}^2\times {\mathbb {R}}}}}$ and ${\mathbb {H}}^2/[\psi ]\times {\mathbb {S}}^1,$ respectively. Consider the function $n_3: \Sigma \rightarrow {{\mathrm{{\mathbb {R}}}}}$ given by $n_3=\left\langle \partial _t, N \right\rangle ,$ where N is the unit normal vector to $\Sigma ,$ and define the function $\tilde{n}_3: \widetilde{\Sigma }\rightarrow {{\mathrm{{\mathbb {R}}}}}$ by the relation $\tilde{n}_3=n_3\circ \pi .$ Now consider the function $\omega : \Sigma \rightarrow {{\mathrm{{\mathbb {R}}}}}$ so that $\hbox {tanh}(\omega )=n_3$ and define the function $\tilde{\omega }: \widetilde{\Sigma }\rightarrow {{\mathrm{{\mathbb {R}}}}}$ by the relation $\tilde{\omega }=\omega \circ \pi .$ Notice that the function $\tilde{\omega }$ has a pole at points where $\tilde{n}_3=\pm 1.$

Since we consider X a conformal minimal immersion, we have

$$\begin{aligned} n_3=\frac{|F_z|^2-|F_{\bar{z}}|^2}{|F_z|^2+|F_{\bar{z}}|^2} \end{aligned}$$

(2.3)

and

$$\begin{aligned} \omega =\frac{1}{2}\ln \frac{|F_z|}{|F_{\bar{z}}|}. \end{aligned}$$

(2.4)

Note that the same formulas are true for $\tilde{n}_3$ and $\tilde{\omega }.$

We know that for local conformal parameters $\tilde{z}$ on $\widetilde{\Sigma },$ the holomorphic quadratic Hopf differential associated with $\widetilde{F}$ is given by

$$\begin{aligned} \widetilde{Q}(\widetilde{F})=(\sigma \circ \widetilde{F})^2\widetilde{F}_{\tilde{z}}\bar{\widetilde{F}}_{\tilde{z}}(\hbox {d}\tilde{z})^2, \end{aligned}$$

where $\sigma$ is the conformal factor of the hyperbolic metric on ${{\mathrm{{\mathbb {H}}^2}}},$ can be written as $(\widetilde{h}_{\tilde{z}})^2(\hbox {d}\tilde{z})^2=-\widetilde{Q}$. Then, since $\widetilde{h}$ and h differ by a constant in a neighborhood, $(h_z)^2(\hbox {d}z)^2=-Q$ is also a holomorphic quadratic differential on $\Sigma$ for local conformal parameters z on $\Sigma .$ We note that Q has two square roots globally defined on $\Sigma .$ We will write $Q=\phi (z)(\hbox {d}z)^2.$ Writing $\widetilde{Q}=\widetilde{\phi }(z)(\hbox {d}z)^2,$ we denote by $\tilde{\eta }=\pm 2i\sqrt{\tilde{\phi }}\hbox {d}\tilde{z}$ a square root of $\widetilde{Q},$ where we choose the sign so that

$$\begin{aligned} \tilde{h}=\hbox {Re}\ \int \tilde{\eta }. \end{aligned}$$

(2.5)

Using (2.2), (2.4) and the definition of Q,  we have

$$\begin{aligned} \hbox {d}s^2=4(\hbox {cosh}^2\omega )|Q|. \end{aligned}$$

(2.6)

The sectional curvature of the tangent plane to $\Sigma$ at a point z is $-n_3^2$, and the second fundamental form is

$$\begin{aligned} II=\frac{\omega _x}{\hbox {cosh}\omega }\hbox {d}x\otimes \hbox {d}x-\frac{\omega _x}{\hbox {cosh}\omega }\hbox {d}y\otimes \hbox {d}y+2\frac{\omega _y}{\hbox {cosh}\omega }\hbox {d}x\otimes \hbox {d}y. \end{aligned}$$

Hence, using the Gauss equation, the Gauss curvature of $(\Sigma , \hbox {d}s^2)$ is given by

$$\begin{aligned} K_{\Sigma }=-\hbox {tanh}^2\omega -\frac{|\nabla \omega |^2}{4(\hbox {cosh}^4\omega )|\phi |}. \end{aligned}$$

(2.7)

The total curvature of $\Sigma$ is simply defined as the integral of the intrinsic curvature over the whole surface, that is,

$$\begin{aligned} C(\Sigma )=\int _{\Sigma }K_{\Sigma }\hbox {d}\sigma . \end{aligned}$$

Since the Jacobi operator of the minimal surface $\Sigma$ is given by

$$\begin{aligned} J=\frac{1}{4\cosh ^2\omega |\phi |}\left[ \Delta _0-4|\phi |+\frac{2|\nabla \omega |^2}{\cosh ^2\omega }\right] \end{aligned}$$

and $Jn_3=0,$ then

$$\begin{aligned} \Delta _0\omega =2\sinh (2\omega )|\phi |, \end{aligned}$$

(2.8)

where $\Delta _0$ denotes the Laplacian in the Euclidean metric $|\hbox {d}z|^2$, that is, $\Delta _0=4\partial ^2_{z\bar{z}}.$

3 Main results

In this section, besides proving the main theorem of this paper, we will demonstrate some properties of an end (which is, in our context, an immersion of ${\mathbb {S}}^1\times \left[ \left. 0,+\infty \right) \right.$) when it is properly immersed in ${\mathcal {M}}_+$ or in ${\mathcal {M}}_-,$ which are interesting by themselves.

We will write [d(0), d(s)] to denote the vertical slab $\cup _{0\le t \le s}d(t)$ in ${{\mathrm{{\mathbb {H}}^2\times {\mathbb {R}}}}}$ bounded by $d(0)\cup d(s).$

Lemma 1

There is no proper minimal end E in ${\mathcal {M}}_+$ with $\partial {\mathcal {M}}_+\cap E=\partial E$ whose lift is an annulus in ${{\mathrm{{\mathbb {H}}^2\times {\mathbb {R}}}}}.$

Proof

Let us prove it by contradiction. Suppose we have a proper minimal end E in ${\mathcal {M}}_+$ with $\partial {\mathcal {M}}_+\cap E=\partial E$ whose lift $\widetilde{E}$ is a proper minimal annulus in ${{\mathrm{{\mathbb {H}}^2\times {\mathbb {R}}}}}.$ Hence $\partial \widetilde{E}\subset d(0)$, $\widetilde{E}\subset \bigcup _{s\ge 0}d(s)$ and, since E is proper, $\widetilde{E}\cap d(s)\ne \emptyset$ for any $s\ge 0,$ where $d(s)=c(s)\times {{\mathrm{{\mathbb {R}}}}},$ c(s) a horocycle tangent to $\partial _\infty {{\mathrm{{\mathbb {H}}^2}}}$ at $p_0.$

Choose $p\ne p_0\in \partial _\infty {{\mathrm{{\mathbb {H}}^2}}}$ such that the vertical plane $\overline{pp_0}\times {{\mathrm{{\mathbb {R}}}}}$ does not intersect the (compact) boundary of the annulus $\partial \widetilde{E}.$

Now consider $q\in \partial _\infty {{\mathrm{{\mathbb {H}}^2}}}$ contained in the halfspace determined by $\overline{pp_0}\times {{\mathrm{{\mathbb {R}}}}}$ that does not contain $\partial \widetilde{E},$ such that $(\overline{pq}\times {{\mathrm{{\mathbb {R}}}}})\cap d(0)=\emptyset ,$ and let q go to $p_0.$ If there exists some point $q_1$ such that $(\overline{pq_1}\times {{\mathrm{{\mathbb {R}}}}})\cap \widetilde{E}\ne \emptyset ,$ then, since $p,q_1\notin d(s)$ for any s, and E is proper, the intersection $(\overline{pq_1}\times {{\mathrm{{\mathbb {R}}}}})\cap \widetilde{E}$ is a compact set in $\widetilde{E}.$ Thus, when we start with q close to p and let q go to $q_1,$ there will be a first contact point between $\overline{pq_0}\times {{\mathrm{{\mathbb {R}}}}}$ and $\widetilde{E},$ for some point $q_0.$ By the maximum principle, this yields a contradiction. Therefore, we conclude that $\overline{pp_0}\times {{\mathrm{{\mathbb {R}}}}}$ does not intersect $\widetilde{E}.$ Choosing another point $\bar{p}$ in the same halfspace determined by $\overline{pp_0}\times {{\mathrm{{\mathbb {R}}}}}$ as $\widetilde{E},$ such that $(\overline{\bar{p}p_0}\times {{\mathrm{{\mathbb {R}}}}})\cap \partial \widetilde{E}=\emptyset ,$ we can use the same argument above and conclude that $\widetilde{E}$ is contained in the region between $\overline{pp_0}\times {{\mathrm{{\mathbb {R}}}}}$ and $\overline{\bar{p}p_0}\times {{\mathrm{{\mathbb {R}}}}}.$ Call $\alpha =\overline{pp_0}$ and $\bar{\alpha }=\overline{\bar{p}p_0}.$

Fig. 4

Curve $\gamma$

Now consider a horizontal geodesic $\gamma$ with endpoints q and $\bar{q},$ such that q is contained in the halfspace determined by $\alpha \times {{\mathrm{{\mathbb {R}}}}}$ that does not contain $\widetilde{E},$ and $\bar{q}$ is contained in the halfspace determined by $\bar{\alpha }\times {{\mathrm{{\mathbb {R}}}}}$ that does not contain $\widetilde{E}$ (see Fig. 4). Up to a horizontal translation, we can suppose $\widetilde{E}\cap (\gamma \times {{\mathrm{{\mathbb {R}}}}})\ne \emptyset .$ Since E is proper, the part of $\widetilde{E}$ between $\partial \widetilde{E}$ and $\widetilde{E}\cap \left( \gamma \times {{\mathrm{{\mathbb {R}}}}}\right)$ is compact, then there exists $M\in {{\mathrm{{\mathbb {R}}}}}$ such that the function $\widetilde{h}$ restricting to this compact part satisfies $-M\le \widetilde{h}\le M.$

Let us consider a function v defined in the connected component of ${{\mathrm{{\mathbb {H}}^2}}}\setminus \gamma$ that does not contain $p_0,$ such that v satisfies the minimal surface graph equation with boundary values $+\infty$ on $\gamma$ and M on the asymptotic arc at infinity of ${{\mathrm{{\mathbb {H}}^2}}}.$ [For the existence and properties of such function v,  see for instance [25], section 4, equation (32)]. The graph of v is a minimal surface that does not intersect $\widetilde{E}.$ When we let $q,\bar{q}$ go to $p_0$ we get, using the maximum principle, that $\widetilde{E}$ is under the graph of v and then $\widetilde{h}|_{\widetilde{E}}$ is bounded above by M, since v converges to the constant function M uniformly on compact sets as $q,\bar{q}$ converge to $p_0.$ Using a similar argument, we can show that $\widetilde{h}|_{\widetilde{E}}$ is also bounded below by $-M$. Therefore $\widetilde{E}$ is an annulus contained in the region bounded by $\alpha \times {{\mathrm{{\mathbb {R}}}}}, \bar{\alpha }\times {{\mathrm{{\mathbb {R}}}}}, {{\mathrm{{\mathbb {H}}^2}}}\times \{-M\}$ and ${{\mathrm{{\mathbb {H}}^2}}}\times \{M\}.$

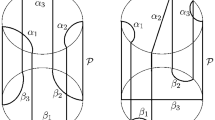
Take four points $p_1,p_2,p_3,p_4\in \partial _{\infty }{{\mathrm{{\mathbb {H}}^2}}}$ such that $p_1,p_2$ are contained in the halfspace determined by $\bar{\alpha }\times {{\mathrm{{\mathbb {R}}}}}$ that does not contain $\widetilde{E},$ and $p_3,p_4$ are contained in the halfspace determined by $\alpha \times {{\mathrm{{\mathbb {R}}}}}$ that does not contain $\widetilde{E}$. Moreover, choose these points so that there exists a complete minimal surface ${\mathcal {A}}$ taking value 0 on $\overline{p_1p_2}\cup \overline{p_3p_4}$ and $+\infty$ on $\overline{p_1p_4}\cup \overline{p_2p_3}$ (see Fig. 5). This minimal surface exists by [2].

Fig. 5

Minimal graph ${\mathcal {A}}$

Up to a vertical translation, ${\mathcal {A}}$ does not intersect $\widetilde{E}$ and ${\mathcal {A}}$ is above $\widetilde{E}.$ Pushing down ${\mathcal {A}}$ (under vertical translation) and using the maximum principle, we conclude that ${\mathcal {A}}=\widetilde{E},$ which is impossible. $\square$

Remark 1

We do not use any assumption on the total curvature of the end to prove the previous lemma.

Lemma 2

If a proper minimal end E with finite total curvature is contained in ${\mathcal {M}}_-$, then E has bounded curvature and infinite area.

Proof

To prove this lemma, we use a kind of blow-up argument. It is based on ideas presented in the paper by Rosenberg et al. [24].

Suppose E does not have bounded curvature. Then there exists a divergent sequence $\{p_n\}_{n\in {\mathbb {N}}}$ in E such that $|A(p_n)|\ge n,$ where A denotes the second fundamental form of E. Since the injectivity radius of ${\mathcal {M}}_-$ is strictly positive, there exists $\delta >0$ such that for all n,  the exponential map exp$_{{\mathcal {M}}}: D(0,\delta )\subset T_{p_n}{\mathcal {M}}\rightarrow B_{{\mathcal {M}}}(p_n,\delta )$ is a diffeomorphism, where $B_{{\mathcal {M}}}(p_n,\delta )$ is the extrinsic ball of radius $\delta$ centered at $p_n$ in ${\mathcal {M}}.$ Without loss of generality, we can suppose $B_{{\mathcal {M}}}(p_j,\delta )\cap B_{{\mathcal {M}}}(p_k,\delta )=\emptyset ,$ for $j\ne k$ (E is properly immersed).

The properness of the end implies the existence of a curve $c\subset E$ homotopic to $\partial E$ such that every point in the connected component of $E\setminus c$ that does not contain $\partial E$ is at an extrinsic distance greater than $\delta$ from $\partial E.$ Call $E_1$ this component. Hence each point of $E_1$ is the center of an extrinsic ball of radius $\delta$ disjoint from $\partial E.$

Denote by $C_n$ the connected component of $p_n$ in $B_{{\mathcal {M}}}(p_n,\delta )\cap E_1$ and consider the function $f_n:C_n\rightarrow {{\mathrm{{\mathbb {R}}}}}$ given by

$$\begin{aligned} f_n(q)=d(q,\partial C_n)|A(q)|, \end{aligned}$$

where d is the extrinsic distance.

The function $f_n$ restricted to the boundary $\partial C_n$ is identically zero and $f_n(p_n)=\delta |A(p_n)|>0.$ Then $f_n$ attains a maximum in the interior. Let $q_n$ be a point where such maximum is achieved. Hence $\delta |A(q_n)|\ge d(q_n,\partial C_n)|A(q_n)|=f_n(q_n)\ge f_n(p_n)=\delta |A(p_n)|\ge \delta n,$ which yields $|A(q_n)|\ge n.$

Now consider $r_n=\frac{d(q_n,\partial C_n)}{2}$ and denote by $B_n$ the connected component of $q_n$ in $B_{{\mathcal {M}}}(q_n,r_n)\cap E_1,$ in particular $B_n\subset C_n.$ If $q\in B_n,$ then $f_n(q)\le f_n(q_n)$ and

$$\begin{aligned} \begin{array}{rcl} d(q_n, \partial C_n)&{}\le &{} d(q_n,q) + d(q, \partial C_n)\\ &{}&{}\\ &{}\le &{} \frac{d(q_n,\partial C_n)}{2} +d(q, \partial C_n)\\ &{}&{}\\ \Rightarrow d(q_n, \partial C_n) &{}\le &{} 2d(q,\partial C_n), \end{array} \end{aligned}$$

hence we conclude that $|A(q)|\le 2|A(q_n)|.$

Call g the metric on E and take $\lambda _n=|A(q_n)|.$ Using the exponential map, consider the surface ${\Sigma }_n=\hbox {exp}_{q_n}^{-1}(B_n)\subset T_{q_n}{\mathcal {M}}$ endowed with the pullback metric $g_n=\hbox {exp}_{q_n}^{*}(\lambda _n g),$ and hence, $\Sigma _n$ is a minimal surface in ${{\mathrm{{\mathbb {R}}}}}^3$ with respect to the metric $g_n.$ Since $g_n=\lambda _n\hbox {exp}_{q_n}^{*}(g)$ and $\lambda _n\rightarrow \infty$ as $n\rightarrow \infty ,$ then $({{\mathrm{{\mathbb {R}}}}}^3,g_n)$ converges to $({{\mathrm{{\mathbb {R}}}}}^3, g_0),$ where $g_0$ is the canonical metric in the euclidean space (For more details about this convergence, see [24]).

We have $\Sigma _n \subset B_{{{\mathrm{{\mathbb {R}}}}}^3}(0,\lambda _nr_n),$ where $B_{{{\mathrm{{\mathbb {R}}}}}^3}(0,\lambda _nr_n)$ is the ball in ${{\mathrm{{\mathbb {R}}}}}^3$ centered at the origin with radius $\lambda _nr_n$ with respect to the canonical metric $g_0.$ Moreover, $|A_n(0)|=1$ and $|A_n(q)|\le 2$ for all $q\in \Sigma _n,$ where $A_n$ denotes the second fundamental form of $\Sigma _n.$ Since $(\Sigma _n,g_n)$ is a minimal surface in $({{\mathrm{{\mathbb {R}}}}}^3,g_n)$ of bounded curvature, then there is $\delta >0$ (only depending on the curvature bound) such that for each $p\in \Sigma _n$ far from the boundary (at a distance that depends only on $\delta$), a neighborhood of p is a graph over the disk $D(p,\delta )$ in the tangent plane to $\Sigma _n$ at p,  centered at p and of radius $\delta .$ Moreover each such local graph has bounded geometry.

Note that $2\lambda _nr_n=f_n(q_n)\ge f_n(p_n)\ge \delta n,$ hence $\lambda _nr_n\rightarrow +\infty$ as $n\rightarrow \infty ;$ and $\partial \Sigma _k\cap B_{{{\mathrm{{\mathbb {R}}}}}^3}(0,\lambda _nr_n)=\emptyset$ for k large enough.

Fix n. The sequence $\left\{ \widetilde{\Sigma }_k=\Sigma _k\cap B_{{{\mathrm{{\mathbb {R}}}}}^3}(0,\lambda _nr_n)\right\} _{k>> n}$ is a sequence of minimal surfaces in $({{\mathrm{{\mathbb {R}}}}}^3,g_n)$ contained in $B_{{{\mathrm{{\mathbb {R}}}}}^3}(0,\lambda _nr_n)$ of bounded curvature passing through the origin. Since $\partial \Sigma _k\cap B_{{{\mathrm{{\mathbb {R}}}}}^3}(0,\lambda _nr_n)=\emptyset ,$ we have uniform curvature estimates for every point $p\in \widetilde{\Sigma }_k.$ In particular, each surface in this sequence is a graph of bounded geometry over a $\delta$-disk in the tangent plane at the origin; in other words, we have a sequence of functions $u_k$ defined over a $\delta$-disk that satisfy the minimal surface equation in $({{\mathrm{{\mathbb {R}}}}}^3,g_n)$ and have bounded geometry (see for instance Proposition 2.3 in [24]). Therefore, we obtain a subsequence that converges to a minimal surface in $({{\mathrm{{\mathbb {R}}}}}^3, g_0)$ contained in $B_{{{\mathrm{{\mathbb {R}}}}}^3}(0,\lambda _nr_n)$ passing through the origin and with the norm of the second fundamental form at the origin equal to 1. We can apply this argument for each n, and using the diagonal sequence argument, we obtain a complete minimal surface $\widetilde{\Sigma }$ in ${{\mathrm{{\mathbb {R}}}}}^3,$ with $0\in \widetilde{\Sigma }$ and $|A(0)|=1.$ In particular, $\widetilde{\Sigma }$ is not the plane. Then by Osserman’s theorem [21], we have $\int _{\widetilde{\Sigma }}| A|^2\ge 4\pi .$

We know that the integral $\int _\Sigma |A|^2$ is a conformal invariant of $\Sigma$, and hence

$$\begin{aligned} \int _{B_n} |A|^2=\int _{\Sigma _n}|A|^2. \end{aligned}$$

Consider a compact $K\subset \widetilde{\Sigma }$ sufficiently large so that $\int _K|A|^2\ge 2\pi ,$ and fix n such that $K\subset B(0,\lambda _nr_n).$ Since a subsequence of $\{\Sigma _k\cap B_{{{\mathrm{{\mathbb {R}}}}}^3}(0,\lambda _nr_n)\}_{k\ge n}$ converges to $\widetilde{\Sigma }\cap B_{{{\mathrm{{\mathbb {R}}}}}^3}(0,\lambda _nr_n),$ then for k sufficiently large, we have that

$$\begin{aligned} \int _{\Sigma _k\cap B(0,\lambda _nr_n)}|A|^2\ge 2\pi -\epsilon , \end{aligned}$$

for some small $\epsilon >0.$ It implies $\int _{B_k}|A|^2\ge 2\pi -\epsilon ,$ for k sufficiently large. Since $B_i\cap B_j=\emptyset ,$ for $i\ne j,$ we conclude that $\int _{E}|A|^2=+\infty .$ But this is not possible, since

$$\begin{aligned} \int _{E}|A|^2=\int _{E}-2K_E+2K_{\mathrm{sec}_{{\mathcal {M}}}(E)}\le -2\int _E K_E<+\infty . \end{aligned}$$

Therefore, E has necessarily bounded curvature.

Now let us prove that the area of E is infinite. Since E is complete, there exist $\epsilon >0$ and a sequence of points $\{p_n\}_{n\in {\mathbb {N}}}$ in E such that $p_n$ diverges in ${\mathcal {M}}_-$ and $B_E(p_k,\epsilon )\cap B_E(p_j,\epsilon )=\emptyset ,$ for $k\ne j,$ where $B_E(p_k,\epsilon )\subset E$ is the intrinsic ball centered at $p_k$ with radius $\epsilon ,$ in particular $d(p_n,\partial E)>\epsilon .$ Since the injectivity radius is strictly positive, using Theorem 3 and Remark 4 in Appendix of [5], we conclude that area$\left( B_E(p_n,\epsilon )\right) \ge \pi \epsilon ^2$ for any n. Therefore,

$$\begin{aligned} \hbox {area}(E)\ge \sum _{n\ge 1}\hbox {area}\left( B_E(p_n,\epsilon )\right) =\infty . \end{aligned}$$

$\square$

Proposition 1

Let $E\subset {\mathcal {M}}$ be a properly immersed minimal end contained in ${\mathcal {M}}_+.$ If E is transversal to the torus ${{\mathrm{{\mathbb {T}}}}}(s)$ and the boundary $\partial E$ is contained in $\cup _{t<s}{{\mathrm{{\mathbb {T}}}}}(t),$ then $E\cap {{\mathrm{{\mathbb {T}}}}}(s)$ consists of $l_s+1$ curves $\alpha , d_1, d_2,\ldots , d_{l_s},$ where each $d_i$ is homotopically trivial in E and $\alpha$ generates $\pi _1(E),$ the fundamental group of E.

Proof

Suppose that $\partial E\subset \left( \cup _{t<s}{{\mathrm{{\mathbb {T}}}}}(t)\right)$ and E is transversal to ${{\mathrm{{\mathbb {T}}}}}(s).$ Then $E\cap {{\mathrm{{\mathbb {T}}}}}(s)$ is k jordan curves $d_1,\ldots ,d_{l_s},\alpha _1,\ldots ,\alpha _{j_s},l_s+j_s=k,$ where each $d_i$ is homotopically trivial in E and each $\alpha _i$ generates the fundamental group of $E,\pi _1(E).$

We will prove that $j_s=1$ necessarily and the subannulus bounded by $\alpha _1$ is contained in $\cup _{t\ge s}{{\mathrm{{\mathbb {T}}}}}(t)$.

Assume $j_s\ne 1.$ Then there exist $\alpha _1,\alpha _2\subset E\cap {{\mathrm{{\mathbb {T}}}}}(s)$ generators of $\pi _1(E).$ Since E is topologically an annulus, there exists a compact annulus $F\subset E$ such that $\partial F=\alpha _1\cup \alpha _2.$ So F is compact and its boundary is on ${{\mathrm{{\mathbb {T}}}}}(s).$

Using the maximum principle with the family of tori ${{\mathrm{{\mathbb {T}}}}}(t)$, we conclude $F\cap \left( \cup _{t<s}{{\mathrm{{\mathbb {T}}}}}(t)\right) =\emptyset .$ Hence $F\subset \left( \cup _{t\ge s}{{\mathrm{{\mathbb {T}}}}}(t)\right)$ and then, since $E\subset {\mathcal {M}}_+,$ there exists a third jordan curve $\alpha _3$ that generates $\pi _1(E)$ and another compact annulus G such that $G\cap \left( \cup _{t<s}{{\mathrm{{\mathbb {T}}}}}(t)\right) \ne \emptyset$ and $\partial G$ is either $\alpha _1\cup \alpha _3$ or $\alpha _2\cup \alpha _3,$ but we have just seen that such G cannot exist. Therefore $j_s=1,$ that is, $E\cap {{\mathrm{{\mathbb {T}}}}}(s)=\alpha \cup d_1\cup \cdots \cup d_{l_s},$ where $\alpha$ generates $\pi _1(E).$ Moreover, by the demonstration, we conclude that the subannulus bounded by $\alpha$ is contained in $\cup _{t\ge s}{{\mathrm{{\mathbb {T}}}}}(t),$ and each $d_i\subset E$ bounds a disk on E contained in $\cup _{t\ge s}{{\mathrm{{\mathbb {T}}}}}(t)$. $\square$

Remark 2

The same holds true for $E\subset {\mathcal {M}}_-,$ that is, if $E\subset {\mathcal {M}}_-$ is a properly immersed minimal end, and E is transversal to ${{\mathrm{{\mathbb {T}}}}}(s)$ with boundary $\partial E$ contained in the compact component of ${\mathcal {M}}_{-}\setminus {{\mathrm{{\mathbb {T}}}}}(s),$ then $E\cap {{\mathrm{{\mathbb {T}}}}}(s)$ is $l_s+1$ curves $\alpha ,d_1,\ldots ,d_{l_s},$ where $d_i$ is homotopically trivial in E and $\alpha$ generates $\pi _1(E).$

Lemma 3

Let $X=(F,h): U=\{|z|\ge R_0\}\rightarrow {\mathcal {M}}$ be a conformal minimal immersion of an end E that has finite total curvature in ${\mathcal {M}},$ and suppose that the function $\phi$ associated with the holomorphic quadratic differential $Q=\phi (z)(\hbox {d}z)^2$ can be written as

$$\begin{aligned} \phi (z)=\left( \sum _{j\ge 1}\frac{a_{-j}}{z^j}+P(z)\right) ^2, \end{aligned}$$

where P is a polynomial function and $\phi$ has no zeroes in U. Then the area of the end is infinite if, and only if, $P\not \equiv 0$ or $a_{-1}\ne 0.$ Moreover, if the area of the end is infinite, then the function $\omega$ converges to zero uniformly (exponentially fast) at infinity.

Proof

Since in a conformal parameter z,  we express the metric as $\hbox {d}s^2=\lambda ^2|\hbox {d}z|^2,$ where $\lambda ^2=4(\hbox {cosh}^2\omega )|\phi |,$ then by (2.7) we have

$$\begin{aligned} -K_{\Sigma }\lambda ^2=4(\sinh ^2\omega )|\phi |+\displaystyle \frac{|\nabla \omega |^2}{\cosh ^2\omega }\ge 0. \end{aligned}$$

(3.1)

Hence,

$$\begin{aligned} \begin{array}{rcl} -\displaystyle \int _UK\hbox {d}A&{}=&{}\displaystyle \int _U4(\sinh ^2\omega )|\phi ||\hbox {d}z|^2+\int _U\frac{|\nabla \omega |^2}{\hbox {cosh}^2\omega }|\hbox {d}z|^2\\ &{}&{}\\ &{}=&{} \displaystyle \int _U4(\hbox {cosh}^2\omega )|\phi ||\hbox {d}z|^2-\int _U4|\phi ||\hbox {d}z|^2+\int _U\frac{|\nabla \omega |^2}{4(\hbox {cosh}^4\omega )|\phi |}\hbox {d}A\\ &{}&{}\\ &{}=&{} \hbox {area}(E)-4\displaystyle \int _U|\phi ||\hbox {d}z|^2+\int _U\frac{|\nabla \omega |^2}{4(\hbox {cosh}^4\omega )|\phi |}\hbox {d}A, \end{array} \end{aligned}$$

where the last term in the right-hand side is finite by (2.7), because E has finite total curvature.

By the above equality, we conclude that area(E) is infinite if, and only if, $\phi =\left( \sum _{j\ge 1}\frac{a_{-j}}{z^j}+P(z)\right) ^2,$ with $P\not \equiv 0$ or $a_{-1}\ne 0.$

Now suppose that the area of the end is infinite. We will use estimates on positive solutions of $\sinh$-Gordon equations by Han [7], Minsky [18] and Wan [28] to our context in order to show that the function $\omega$ goes to zero uniformly at infinity.

Given V any simply connected domain of $U=\{|z|\ge R_0\},$ we have the conformal coordinate $w=\int \sqrt{{\phi }}\hbox {d}z=u+iv$ with the flat metric $|\hbox {d}w|^2=|{\phi }||\hbox {d}z|^2$ on V. Observe that w is a coordinate since $\phi$ does not vanish on U. In the case where $P\not \equiv 0,$ the disk D(w(z), |z| / 2) contains a ball of radius at least c|z| in the metric $|\hbox {d}w|^2$ where c does not depend on z. In the case where $P\equiv 0$ and $a_{-1}\ne 0$, we consider the conformal universal covering $\tilde{U}$ of the annulus U given by the conformal change of coordinate $w=\ln (z) + f(z),$ where f(z) extends holomorphically by zero at the puncture. Any point z in U lifts to the center w(z) of a ball $D(w(z), \ln ( |z|/2)) \subset \tilde{U}$ for $|z| >2R_0$ large enough.

The function $\omega$ lifts to the function $\tilde{\omega } \circ w (z):=\omega (z)$ on the w-plane which satisfies the equation

$$\begin{aligned} \Delta _{|\phi |} \tilde{\omega }= 2 \sinh 2 \tilde{\omega } \end{aligned}$$

(3.2)

where $\Delta _{|\phi |}$ is the Laplacian in the flat metric $|\hbox {d}w|^2$. On the disk $D_{|\phi |} (w(z), 1)$, we consider the hyperbolic metric given by

$$\begin{aligned} \hbox {d}\sigma ^2=\mu ^2|\hbox {d}w|^2=\frac{4}{(1-|w-w(z) |^2)^2}|\hbox {d}w|^2. \end{aligned}$$

Then $\mu$ takes infinite values on $\partial D(w(z),1)$, and since the curvature of the metric $\hbox {d}\sigma ^2$ is $K=-1,$ the function $\omega _2=\ln \mu$ satisfies the equation

$$\begin{aligned} \Delta _{|\phi |}\omega _2=e^{2\omega _2}\ge e^{2\omega _2}-e^{-2\omega _2}=2\sinh \omega _2. \end{aligned}$$

Since $\phi$ has no zeroes and $\hbox {d}s^2= 4(\cosh ^2 \omega )|\phi ||\hbox {d}z|^2,$ we know that $\tilde{\omega }=\omega \circ \pi$ has no poles. Hence, we can define the function $\eta (w) =\tilde{\omega } (w)-\omega _2 (w)$ and it satisfies

$$\begin{aligned} \Delta _{|\phi |}\eta =e^{2\tilde{\omega }}-e^{-2\tilde{\omega }}-e^{2\omega _2}=e^{2\omega _2}\left( e^{2\eta }-e^{-4\omega _2}e^{-2\eta }-1\right) , \end{aligned}$$

which can be written in the metric $\hbox {d}\tilde{\sigma }^2=e^{2\omega _2}|\hbox {d}w|^2$ as

$$\begin{aligned} \Delta _{\tilde{\sigma }}\eta =e^{2\eta }-e^{-4\omega _2}e^{-2\eta }-1. \end{aligned}$$

Since $\omega _2$ goes to $+\infty$ on the boundary of the disk $D_{|\phi |}(w(z),1),$ the function $\eta$ is bounded above and attains its maximum at an interior point $q_0.$ At this point $\eta _0=\eta (q_0)$ we have

$$\begin{aligned} e^{2\eta _0}-e^{-4\omega _2}e^{-2\eta _0}-1\le 0, \end{aligned}$$

which implies

$$\begin{aligned} e^{2\eta _0}\le \frac{1+\sqrt{1+4a^2}}{2}, \end{aligned}$$

where $a=e^{-2\omega _2(q_0)}\le \ \hbox {sup}\frac{1}{\mu ^2}\le \frac{1}{4}.$ Thus, at any point of the disk $D_{|\phi |}(w(z),1),$ $\tilde{\omega }$ satisfies

$$\begin{aligned} \tilde{\omega }\le \omega _2+\frac{1}{2}\ln \left( \frac{2+\sqrt{5}}{4}\right) . \end{aligned}$$

We observe that the same estimate above holds for $-\tilde{\omega }$. Then, at the point z,  we have

$$\begin{aligned} |{\omega }(z)|=|\tilde{\omega } (w(z))| \le \ln 2+\frac{1}{2}\ln \left( \frac{2+\sqrt{5}}{4}\right) :=K_0 \end{aligned}$$

uniformly on $R\ge R_0.$ Using this estimate, we can apply a maximum principle as considered by Minsky (see [18], Lemma 3.3). We know that for |z| large, we can find a disk $D_{|\phi |}(w(z),r)$ with r large too and the metric $|\hbox {d}w|^2=|\phi ||\hbox {d}z|^2$ is flat. If (u, v) are Euclidean coordinates based at w(z),  we define a comparison function G on the disk $D_{|\phi |}(w(z),r)$ by

$$\begin{aligned} G(u,v)=\frac{K_0}{\cosh r}\cosh \sqrt{2}u\cosh \sqrt{2}v. \end{aligned}$$

Then $G\ge K_0\ge \tilde{\omega }$ on $\partial D_{|\phi |}(w(z),r)$, $\Delta _{|\phi |}G=4G$ everywhere and $G(w(z))=\frac{K_0}{\cosh r}.$ Suppose the minimum of $G-\tilde{\omega }$ is a point $p_0$ where $\tilde{\omega }(p_0)> G(p_0).$ Then $0< \tilde{\omega }(p_0)\le 2\sinh 2\tilde{\omega }(p_0)$ and

$$\begin{aligned} \Delta _{|\phi |}(G-\tilde{\omega })(p_0)=4G(p_0)-2\sinh 2\tilde{\omega }(p_0)\le 4(G(p_0)-\tilde{\omega }(p_0))<0. \end{aligned}$$

Therefore we have necessarily $\tilde{\omega }\le G$ on the disk. Considering the same argument to $G+\tilde{\omega }$, we can conclude $|\tilde{\omega }|\le G.$ Hence

$$\begin{aligned} |\tilde{\omega }(w(z))|\le \frac{K_0}{\cosh r} \end{aligned}$$

(3.3)

and then $|\tilde{\omega }|\rightarrow 0$ uniformly at the puncture, consequently $|\omega |\rightarrow 0$ uniformly at infinity. $\square$

Lemma 4

Let $X=(F,h): U=\{|z|\ge R_0\}\rightarrow {\mathcal {M}}$ be a conformal minimal immersion of an end E that has finite total curvature in ${\mathcal {M}},$ and suppose that the function $\phi$ associated with the holomorphic quadratic differential $Q=\phi (z)(\hbox {d}z)^2$ can be written as

$$\begin{aligned} \phi (z)=\left( \sum _{j\ge 1}\frac{a_{-j}}{z^j}+P(z)\right) ^2, \end{aligned}$$

where P is a polynomial function and $\phi$ has no zeroes in U. If the end E is proper in ${\mathcal {M}},$ then $P\equiv 0.$

Proof

Suppose $P\not \equiv 0.$ Up to a change of variable, we can assume that the coefficient of the leading term of P is one. Then, for suitable complex number $a_0,\ldots , a_{k-1},$ we have

$$\begin{aligned} P(z) = z^k + a_{k-1}z^{k-1} +\cdots + a_0 \quad \hbox {and} \quad \sqrt{\phi }=z^{k}(1 + o(1)). \end{aligned}$$

Let us define the function

$$\begin{aligned} w(z)=\int \sqrt{\phi (z)}\hbox {d}z=\int \left( \sum _{j\ge 1}\frac{a_{-j}}{z^j}+a_0+\cdots +z^k\right) \hbox {d}z. \end{aligned}$$

If $a_{-1}=a+ib$ and we denote by $\theta \in {{\mathrm{{\mathbb {R}}}}}$ a determination of the argument of $z\in U,$ then locally

$$\begin{aligned} \hbox {Im}(w)(z)=b \, \hbox {ln}|z|+a\theta +\frac{|z|^{k+1}}{k+1}(\hbox {sin}(k+1)\theta +o(1)) \end{aligned}$$

(3.4)

and

$$\begin{aligned} \hbox {Re}(w)(z)=a \, \hbox {ln}|z|-b\theta +\frac{|z|^{k+1}}{k+1}(\hbox {cos}(k+1)\theta +o(1)). \end{aligned}$$

(3.5)

If $C_0 > \hbox {max}\{|\hbox {Im}(w)(z)|; |z|=R_0\},$ then the set $U\cap \{\hbox {Im}(w)(z) = C_0\}$ is composed of $k + 1$ proper and complete curves without boundary $L_0 ,\ldots , L_k$ (see Fig. 6).

Fig. 6

$L_j$ for $k=2$

Take ${\mathcal {R}}$ a simply connected component of $U\cap \{\hbox {Im}(w)(z) \ge C_0\}.$ The holomorphic map w(z) gives conformal parameters $w=u+iv, v\ge C_0,$ to $X({\mathcal {R}})\subset E.$

Then $\widetilde{X}(w)=(\widetilde{F}(w),v)$ is a conformal immersion of ${\mathcal {R}}$ in ${{\mathrm{{\mathbb {H}}^2\times {\mathbb {R}}}}}$ and we have

$$\begin{aligned} |\widetilde{F}_u|^2_{{{\mathrm{{\mathbb {H}}^2}}}}=|\widetilde{F}_v|^2_{{{\mathrm{{\mathbb {H}}^2}}}} +1 \quad \hbox {and} \quad \left\langle \widetilde{F}_u,\widetilde{F}_v\right\rangle _{{{\mathrm{{\mathbb {H}}^2}}}} =0. \end{aligned}$$

Hence the holomorphic quadratic Hopf differential is

$$\begin{aligned} Q_{\widetilde{F}}=\phi (w)(\hbox {d}w)^2=\frac{1}{4}\left( |\widetilde{F}_u|^2_{{{\mathrm{{\mathbb {H}}^2}}}}-|\widetilde{F}_v|^2_{{{\mathrm{{\mathbb {H}}^2}}}} -2i\left\langle \widetilde{F}_u,\widetilde{F}_v\right\rangle _{{{\mathrm{{\mathbb {H}}^2}}}}\right) (\hbox {d}w)^2=\frac{1}{4}(\hbox {d}w)^2 \end{aligned}$$

and the induced metric on these parameters is given by $\hbox {d}s^2=\hbox {cosh}^2\widetilde{\omega }|\hbox {d}w|^2.$

Since $\widetilde{X}_v=({\widetilde{F}}_v,1)$ and $|\widetilde{F}_u|^2_{{{\mathrm{{\mathbb {H}}^2}}}}=|\widetilde{F}_v|^2_{{{\mathrm{{\mathbb {H}}^2}}}} +1=\hbox {d}s^2(\widetilde{X}_v, \widetilde{X}_v )=\cosh ^2\omega ,$ we obtain

$$\begin{aligned} |\widetilde{F}_u|^2_{{{\mathrm{{\mathbb {H}}^2}}}}= \cosh ^2\omega \quad \hbox {and}\quad |\widetilde{F}_v|^2_{{{\mathrm{{\mathbb {H}}^2}}}}=\sinh ^2\omega . \end{aligned}$$

(3.6)

Consider the divergent curve $\gamma (v)=\widetilde{X}(u_0+iv)=(\widetilde{F}(u_0,v),v).$ We have

$$\begin{aligned} d_{{{\mathrm{{\mathbb {H}}^2}}}}(\widetilde{F}(u_0,C_0),\widetilde{F}(u_0,v))\le \int _{C_0}^v|\widetilde{F}_v|_{{{\mathrm{{\mathbb {H}}^2}}}}\hbox {d}v=\int _{C_0}^v|\sinh \tilde{\omega }|\hbox {d}v\le C<\infty , \end{aligned}$$

where C does not depend on v. We have this uniform estimate because by (3.3) in Lemma 3, we know that $|\tilde{\omega }|\rightarrow 0$ exponentially fast at infinity.

Thus, when we pass the curve $\gamma$ to the quotient by the third coordinate, we obtain a curve in E which is not properly immersed in the quotient space ${\mathcal {M}}.$ Therefore, if E is proper, we have $P\equiv 0$. $\square$

Definition 1

We write helicoidal plane to denote a minimal surface in ${{\mathrm{{\mathbb {H}}^2\times {\mathbb {R}}}}}$ which is parameterized by $X(x,y)=(x,y,ax+b)$ when we consider the halfplane model for ${{\mathrm{{\mathbb {H}}^2}}}.$

Observe that, considering the hyperbolic plane with the Poincaré model, a helicoidal plane in ${{\mathrm{{\mathbb {H}}^2\times {\mathbb {R}}}}}$ looks like a helicoid with vertical axis at infinity.

Now we can state the main result of this paper.

Theorem 1

Let $X: \Sigma \hookrightarrow {\mathcal {M}} = {{\mathrm{{\mathbb {H}}^2\times {\mathbb {R}}}}}/[\psi , T(h)]$ be a properly immersed (oriented) minimal surface with finite total curvature. Then

• 1. $\Sigma$ is conformally equivalent to a compact Riemann surface $\overline{M}$ with genus g minus a finite number of points, that is, $\Sigma =\overline{M}\setminus \{p_1,\ldots , p_k\}$.

• 2. The total curvature satisfies

  $$\begin{aligned} \int _{\Sigma }K\hbox {d}\sigma =2\pi (2-2g-k). \end{aligned}$$

• 3. The ends contained in ${\mathcal {M}}_-$ are necessarily asymptotic to a vertical plane $\gamma \times {\mathbb {S}}^1$, and the ends contained in ${\mathcal {M}}_+$ are asymptotic to either

  • a horizontal slice ${{\mathrm{{\mathbb {H}}^2}}}/[\psi ]\times \{c\},$ or

  • a vertical plane $\gamma \times {\mathbb {S}}^1$, or

  • the quotient of a helicoidal plane.

• 4. If we parameterize each end by a punctured disk, then either Q extends holomorphically to the puncture (in the case where the end is asymptotic to a horizontal slice) or Q extends meromorphically to the puncture with a double pole and residue zero.

Proof

The proof of this theorem uses arguments of harmonic diffeomorphisms theory as can be found in the work of Han, Tam, Treibergs and Wan [7, 8, 28] and Minsky [18].

From a well-known result by Huber [13], we deduce that $\Sigma$ is conformally a compact Riemann surface $\overline{M}$ minus a finite number of points $\{p_1,\ldots ,p_k\},$ and the ends are parabolic.

For each puncture $p_i$ take $B_i$ a small disk centered at $p_i$ and consider $\overline{M}^*=\overline{M}-\cup _{i=1}^{k}B_i,$ the surface minus a finite number of disks removed around the punctures $p_i.$ Since the ends are parabolic, each punctured disk $B^*_i=B_i\setminus \{p_i\}$ can be parameterized conformally by the exterior of a disk in ${\mathbb {C}},$ say $U=\{z\in {\mathbb {C}}; |z|\ge R_0\}.$

Using the Gauss–Bonnet theorem for $\overline{M}^*,$ we get

$$\begin{aligned} \int _{\overline{M}^*}K\hbox {d}\sigma +\sum _{i=1}^k\int _{\partial B_i}k_g\ \hbox {d}s=2\pi (2-2g-k). \end{aligned}$$

(3.7)

Therefore, in order to prove the second item of the theorem is enough to show that for each i,  we have

$$\begin{aligned} \int _{\partial B_i}k_g\ \hbox {d}s=\int _{B_i}K\hbox {d}\sigma . \end{aligned}$$

In other words, we have to understand the geometry of the ends. Let us analyze each end.

Fix i,  denote $E=B^*_i$ and let $X=(F,h):U=\{|z|\ge R_0\}\rightarrow {\mathbb {H}}^2/[\psi ]\times {\mathbb {S}}^1$ be a conformal parameterization of the end E. In this parameter, we express the metric as $\hbox {d}s^2=\lambda ^2|\hbox {d}z|^2$ with $\lambda ^2=4(\hbox {cosh}^2\omega )|\phi |,$ where $Q=\phi (z)(\hbox {d}z)^2$ is the holomorphic quadratic differential on the end.

If $Q\equiv 0$, then $\phi \equiv 0$ and h is constant, which yields that the end E of $\Sigma$ is contained in some horizontal slice ${{\mathrm{{\mathbb {H}}^2}}}/[\psi ]\times \{c_0\}.$ Then the minimal surface $\Sigma$ is necessarily the slice ${{\mathrm{{\mathbb {H}}^2}}}/[\psi ]\times \{c_0\}.$ Note that because $\Sigma$ has finite total curvature, this case is possible only when the horizontal slices of ${\mathcal {M}}$ have finite area. Therefore, we can assume $Q\not \equiv 0.$

Following the ideas of [8] and section 3 of [12], we can show that finite total curvature and nonzero Hopf differential Q imply that Q has a finite number of isolated zeroes on the surface $\Sigma .$ Moreover, for $R_0>0$ large enough, we can show that there is a constant $\alpha$ such that $(\cosh ^2\omega )|\phi |\le |z|^\alpha |\phi |$ and then, since the metric $\hbox {d}s^2$ is complete, we use a result by Osserman [21] to conclude that Q extends meromorphically to the puncture $z=\infty .$ Hence we can suppose that $\phi$ has the following form:

$$\begin{aligned} \phi (z)=\left( \sum _{j\ge 1}\frac{a_{-j}}{z^j}+P(z)\right) ^2, \end{aligned}$$

for $|z|>R_0$, where P is a polynomial function.

Since $\phi$ has a finite number of zeroes on U,  we can suppose without loss of generality that $\phi$ has no zeroes on U,  and then the minimal surface E is transverse to the horizontal sections ${{\mathrm{{\mathbb {H}}^2}}}/[\psi ]\times \{c\}.$

Suppose E is contained in ${\mathcal {M}}_+.$ Up to translation (along a geodesic not contained in ${{\mathrm{{\mathbb {T}}}}}(0)$), we can suppose that E is transverse to ${{\mathrm{{\mathbb {T}}}}}(0)$ and $\partial E\subset \cup _{s<0}{{\mathrm{{\mathbb {T}}}}}(s),$ and hence by Proposition 1, the intersection $E\cap {{\mathrm{{\mathbb {T}}}}}(0)$ is $l+1$ curves $\alpha , d_1, d_2,\ldots , d_l,$ where each $d_i$ is homotopically trivial in E and $\alpha$ generates the fundamental group $\pi _1(E).$

Take a point p in the horocycle $c(0)\subset {\mathbb {H}}^2$ and consider $e_1=c(0)/[\psi ],$ $e_2=p\times {{\mathrm{{\mathbb {R}}}}}/[T(h)].$ The curves $e_1,e_2$ are generators of $\pi _1({{\mathrm{{\mathbb {T}}}}}(0)).$

Since $E\subset {\mathcal {M}}_+$ and $\pi _1({\mathcal {M}}_+)=\pi _1({{\mathrm{{\mathbb {T}}}}}(0)),$ we can consider the inclusion map $i_*:\pi _1(E)\rightarrow \pi _1({{\mathrm{{\mathbb {T}}}}}(0))$ and we can write $i_*([\alpha ])=n[e_1]+m[e_2],$ where m, n are integers.

Observe that we cannot have $n=m=0,$ since this would imply that E lifts to an annulus in ${{\mathrm{{\mathbb {H}}^2\times {\mathbb {R}}}}}$ and we already know by Lemma 1 that this is not possible.

Remark 3

If $E\subset {\mathcal {M}}_+$ (resp. $E\subset {\mathcal {M}}_-$) is an end of $\Sigma ,$ we can assume without loss of generality that E is one of the noncompact connected components of $\Sigma \cap \bigcup _{s\ge 0} {{\mathrm{{\mathbb {T}}}}}(s)$ (resp. $\Sigma \cap \bigcup _{s\le 0} {{\mathrm{{\mathbb {T}}}}}(s)$), and then $\partial E\subset {{\mathrm{{\mathbb {T}}}}}(0).$

Claim 1

If $n \ne 0$ and $m=0,$ then the end $E\subset {\mathcal {M}}_+$ is asymptotic to a horizontal slice ${{\mathrm{{\mathbb {H}}^2}}}/[\psi ]\times \{c\}$, and the quadratic differential Q extends holomorphically to the puncture, and

$$\begin{aligned} \int _{E}K=\int _{\partial E} k_g. \end{aligned}$$

Proof

We can assume, without loss of generality, that $\partial E\subset {{\mathrm{{\mathbb {T}}}}}(0)$ and E is transverse to ${{\mathrm{{\mathbb {T}}}}}(1)$. Call $\widetilde{E}\subset {{\mathrm{{\mathbb {H}}^2\times {\mathbb {R}}}}}$ a connected component of $\pi ^{-1}(E\cap {\mathcal {M}}_+)$ such that $\pi (\widetilde{E})=E.$ We have that $\widetilde{E}$ is a proper minimal surface transverse to the horocylinder d(1) and its boundary $\partial \widetilde{E}=\pi ^{-1}(\partial E)$ is a curve in d(0) invariant by $\psi ^n.$

Since $\partial \widetilde{E}\subset d(0)$ is invariant by $\psi ^n, n\ne 0,$ and $\widetilde{E}$ is transversal to the horocylinder d(1),  then by the trapping theorem in [4], $\widetilde{E}$ is contained in a horizontal slab. Hence $\widetilde{h}|_{\widetilde{E}}$ is a bounded harmonic function, and then $h|_{E}$ is a bounded harmonic function defined on a punctured disk. Therefore h has a limit at infinity, and then Q extends to a constant at the puncture. In particular, $\widetilde{h}$ has a limit at infinity.

The end of $\widetilde{E}$ is contained in a slab of width $2\epsilon >0$, and by a result of Collin, Hauswirth and Rosenberg [3], $\widetilde{E}$ is a multigraph outside a compact domain of ${{\mathrm{{\mathbb {H}}^2\times {\mathbb {R}}}}}.$ This implies that $\widetilde{E}$ has bounded curvature. Then there exists $\delta >0$ such that for any $p\in E,$ a neighborhood $V_p$ of p is a minimal graph of bounded geometry over the $\delta$-geodesic disk (in exponential coordinates) $D(0,\delta )\subset T_pE$ centered at the origin of the tangent space at p.

Now fix s and consider a divergent sequence $\{p_n\}_{n\in {\mathbb {N}}}$ in E. Applying hyperbolic translations to each point $p_n$ (horizontal translations along a geodesic of ${{\mathrm{{\mathbb {H}}^2}}}$ that sends $p_n$ to a point in ${{\mathrm{{\mathbb {T}}}}}(s)$), we get a sequence of points in ${{\mathrm{{\mathbb {T}}}}}(s)$ which we still denote by $\{p_n\}_{n\in {\mathbb {N}}}.$ Since ${{\mathrm{{\mathbb {T}}}}}(s)$ is compact, up to extracting a subsequence, we can assume that the sequence $\{p_n\}_{n\in {\mathbb {N}}}$ converges to a point $p\in {{\mathrm{{\mathbb {T}}}}}(s)$ and the sequence of graphs $V_{p_n}$ converges to a minimal graph $V_p$ of bounded geometry over a small disk in $T_pE.$

Since h has a limit at infinity, this limit graph $V_p$ is contained in a horizontal slice. Then we conclude that $n_3\rightarrow 1$ and $|\nabla h|\rightarrow 0$ uniformly at infinity, which yields a $C^1$-convergence of E to a horizontal slice. Now using elliptic regularity, we get that E converges in the $C^2$-topology to a horizontal slice. In particular, the geodesic curvature of $\alpha _s$ goes to 1 and its length goes to zero, where $\alpha _s$ is the curve in $E\cap {{\mathrm{{\mathbb {T}}}}}(s)$ that generates $\pi _1(E).$

Denote by $E_s$ the part of the end E bounded by $\partial E$ and $\alpha _s.$ Applying the Gauss–Bonnet theorem for $E_s,$ we obtain

$$\begin{aligned} \int _{E_s}K + \int _{\alpha _s}k_g -\int _{\partial E}k_g=0. \end{aligned}$$

By our analysis in the previous paragraph, we have $\int _{\alpha _s}k_g\rightarrow 0,$ as $s\rightarrow \infty .$ Then when we let s go to infinity, we get

$$\begin{aligned} \int _E K=\int _{\partial E}k_g, \end{aligned}$$

as we wanted to prove. $\square$

Claim 2

If $m\ne 0$, then the area of the end is infinite.

Proof

In fact, consider $g:\Sigma \rightarrow {{\mathrm{{\mathbb {R}}}}}$ the extrinsic distance function to ${{\mathrm{{\mathbb {T}}}}}(0),$ that is, $g=d_{{\mathcal {M}}}(\ .\ , {{\mathrm{{\mathbb {T}}}}}(0)).$ Hence $|\nabla ^{{\mathcal {M}}} g|=1$ and $g^{-1}(s)=\Sigma \cap {{\mathrm{{\mathbb {T}}}}}(s).$ We know for almost every s,  $\Sigma \cap {{\mathrm{{\mathbb {T}}}}}(s)=\alpha _s\cup d_1\cup \cdots \cup d_l,$ where $\alpha _s$ generates $\pi _1(E)$ and $d_i$ is homotopic trivial in E. Then, by the coarea formula,

$$\begin{aligned} \begin{array}{rclrl} \displaystyle \int _{\{g\le s\}}1\hbox {d}A&{}=&{}\displaystyle \int _{-\infty }^s\left( \int _{\{g=\tau \}}\frac{\hbox {d}s_{\tau }}{|\nabla ^{\Sigma } g|}\right) \hbox {d}\tau &{}\ge &{}\displaystyle \int _{0}^s |\alpha _\tau |\hbox {d}\tau \\ &{}&{}\\ &{}\ge &{} \displaystyle \int _0^s |e_2|\hbox {d}\tau \ =\ s|e_2|, \end{array} \end{aligned}$$

where the last inequality follows from the fact we are supposing that $i_{*}[\alpha _s]$ has a component in $[e_2]$ and the curve $e_2$ has the least length in its class, and in the last equality, we use that the curve $e_2$ has constant length. Hence when we let s go to infinity, we conclude that the area of E is infinite. $\square$

So if $E\subset {\mathcal {M}}_+$ and $m\ne 0,$ the area of E is infinite. Moreover, we know by Lemma 2 that all the ends contained in ${\mathcal {M}}_-$ have infinite area. Thus we will analyze all the remaining cases together using the common fact of infinite area.

From now on, E will denote an end in ${\mathcal {M}}$ with infinite area. We can assume without loss of generality that $\partial E\subset {{\mathrm{{\mathbb {T}}}}}(0)$ (see Remark 3). Since E has infinite area, we have, by Lemma 3 and Lemma 4,

$$\begin{aligned} \phi =\left( \sum _{j\ge 1}\frac{a_{-j}}{z^j}\right) ^2, \end{aligned}$$

(3.8)

with $a_{-1}=a+ib\ne 0$ for $|z|\ge R_0$, and $|\omega |\rightarrow 0$ uniformly at infinity. In particular, the tangent planes to the end become vertical at infinity.

Let $X:U=\{|z|\ge 1\}\rightarrow {\mathcal {M}}$ be a conformal parameterization of the end E from the exterior of a disk (we suppose, without loss of generality, that the disk is the unit disk). Now consider the covering of U by the halfplane $HP:=\{z=x+iy, x\ge 0\}$ through the holomorphic exponential map $e^z:HP\rightarrow U.$ Hence, we can take $X\circ e^z:HP\rightarrow {\mathcal {M}}$ a conformal parameterization of the end from a halfplane. Since the halfplane is simply connected, consider $\widetilde{X}:HP\rightarrow {{\mathrm{{\mathbb {H}}^2\times {\mathbb {R}}}}}$ the lift of $X\circ e^z$ into ${{\mathrm{{\mathbb {H}}^2\times {\mathbb {R}}}}}.$

Using (2.5) and (3.8), we know that $\widetilde{X}=(\widetilde{F},\widetilde{h}),$ where for any $z\in HP$ we have $\widetilde{h}(z)=bx+ay+\widetilde{p}(z),$ with $|\widetilde{p}(z)|\rightarrow 0$ as $x\rightarrow \infty .$

Observe that $\partial \widetilde{E}=\widetilde{X}(\{x=0\})$ and the curve $\{\widetilde{h}=c\}$ is asymptotic to the straight line $\{bx+ay=c\}$ as $x\rightarrow \infty .$

Claim 3

Since the end E is proper, $b=0$ necessarily.

Proof

Suppose that $b\ne 0$ and consider the change of coordinates by the rotation $e^{i\theta }z: HP\rightarrow HP_{\theta },$ where $\tan \theta =\frac{b}{a}$ (notice that if $a=0,$ then $\theta =\pi /2$) and $HP_{\theta }=e^{i\theta }(HP)\subset \{\tilde{z}=\tilde{x}+i\tilde{y}\}.$ From now on, when we write one curve in the plane $\tilde{z}=\tilde{x}+i\tilde{y},$ we mean the part of this curve contained in $HP_\theta .$

In this new parameter $\tilde{z},$ we have $\partial \widetilde{E}=\widetilde{X}(\{a\tilde{x}+b\tilde{y}=0\})$ and the curve $\{\widetilde{h}=c\}$ is asymptotic to the straight line $\{\tilde{y}=\frac{c}{\sqrt{a^2+b^2}}\}.$

Now consider the conformal change of coordinates $\tilde{w}=\int \sqrt{\tilde{\phi }}\hbox {d}\tilde{z}=\tilde{u}+i\tilde{v},$ where $\tilde{v}=\widetilde{h}(\tilde{z})=\sqrt{a^2+b^2}\tilde{y}+\widetilde{p}(e^{-i\theta }\tilde{z}).$ Since $|\widetilde{p}(e^{-i\theta }\tilde{z})|\rightarrow 0$ as $\hbox {Re} (e^{-i\theta }\tilde{z})\rightarrow +\infty ,$ then the vertical curve $\beta (t)=(0,t)$ in the $\tilde{w}$-plane is the image of a curve $\alpha$ in the $\tilde{z}$-plane which is asymptotic at infinity to the curve $\{\tilde{x}=0\}.$ If we consider the asymptotic vector to a curve as the limit at infinity of the tangent vectors to that curve, we conclude that in the $\tilde{z}$-plane the angle between the asymptotic vector to $\alpha$ and the asymptotic vector to $\partial \widetilde{E}$ is $\theta \ne 0.$ (Here $\partial \widetilde{E}$ means the curve in the $\tilde{z}$-plane whose image by $\widetilde{X}$ is the boundary of $\widetilde{E}$). Since the parameterization is conformal, the angles are preserved. Hence, in the $\tilde{w}$-plane, the angle between the asymptotic vector to $\partial \widetilde{E}$ and the curve $\beta$ is $\theta \ne 0.$

In the $\tilde{w}$-coordinates, we have $\widetilde{X}(\tilde{w})=(\widetilde{F}(\tilde{w}),\tilde{v})$ a conformal immersion of $\widetilde{E},$ and

$$\begin{aligned} |{\widetilde{F}_{\tilde{u}}}|^2_{\sigma }=|{\widetilde{F}_{\tilde{v}}}|^2_{\sigma }+1=\cosh ^2\widetilde{\omega }. \end{aligned}$$

Now consider the curve $\beta (t)=(0,t), t\ge 0,$ in the $\tilde{w}$-plane. The angle between the asymptotic vector to $\partial \widetilde{E}$ and the curve $\beta$ is $\theta \ne 0,$ and then $\widetilde{X}(\beta )$ is a divergent curve in $\widetilde{E}$. However, the curve $\widetilde{F}(\beta )=\widetilde{F}(0,t)$ satisfies

$$\begin{aligned} l(\widetilde{F}(\beta ))=\int _0^t |\widetilde{F}_{\tilde{v}}|\hbox {d}\tilde{v}=\int _0^t|\sinh \widetilde{\omega }|\hbox {d}\tilde{v}\le C, \end{aligned}$$

for some constant C not depending on t,  since we know by (3.3) that $|\tilde{\omega }|\rightarrow 0$ at infinity (to see that $\tilde{\omega }$ goes to zero exponentially fast on $\beta$ as t goes to infinity, observe that the curve $\beta$ in the halfplane $HP_\theta$ is a curve asymptotic to the $\tilde{y}$-axis, and in the halfplane, HP it satisfies that the x-coordinate goes to infinity, and hence when we see $\beta$ as a curve in the exterior disk U, its norm $|\beta |$ goes to infinity, and therefore formula (3.3) can be applied). This implies that when we pass the curve $\widetilde{X}(\beta )$ to the quotient space ${\mathcal {M}},$ we obtain a curve in E that is not proper in ${\mathcal {M}},$ which is impossible, since the end E is proper. $\square$

Then, since $b=0,$ the third coordinate on the halfplane HP satisfies $\tilde{h}(z)=ay+\tilde{p}(z).$ Now let us go back to using the conformal parameterization of $\widetilde{E}$ given by $\widetilde{X}(u,v)=(\widetilde{F}(u,v), v),$ where $w=u+iv=\displaystyle \int \sqrt{\tilde{\phi }}\hbox {d}z.$

Claim 4

The asymptotic boundary of $\widetilde{E}$ at finite height (that is, $\partial _\infty \widetilde{E}\cap (\partial _{\infty }{{\mathrm{{\mathbb {H}}^2}}}\times {{\mathrm{{\mathbb {R}}}}})$) is contained in one unique vertical straight line $\bar{p}_0\times {{\mathrm{{\mathbb {R}}}}},$ for some point $\bar{p}_0\in \partial _\infty {{\mathrm{{\mathbb {H}}^2}}}$.

Proof

We have $\widetilde{X}(w)=(\widetilde{F}(w),v)$ a conformal immersion of $\widetilde{E}$, and

$$\begin{aligned} |\widetilde{F}_u|^2_{{{\mathrm{{\mathbb {H}}^2}}}}=|\widetilde{F}_v|^2_{{{\mathrm{{\mathbb {H}}^2}}}}+1 \quad \hbox {and} \quad \left\langle \widetilde{F}_u,\widetilde{F}_v\right\rangle _{{{\mathrm{{\mathbb {H}}^2}}}}=0. \end{aligned}$$

Hence the holomorphic quadratic Hopf differential is

$$\begin{aligned} \widetilde{Q}_{\widetilde{F}}=\tilde{\phi }(w)(\hbox {d}w)^2=\frac{1}{4}\left( |\widetilde{F}_u|^2_{{{\mathrm{{\mathbb {H}}^2}}}}-|\widetilde{F}_v|^2_{{{\mathrm{{\mathbb {H}}^2}}}}-2i\left\langle \widetilde{F}_u,\widetilde{F}_v\right\rangle _{{{\mathrm{{\mathbb {H}}^2}}}}\right) (\hbox {d}w)^2=\frac{1}{4}(\hbox {d}w)^2 \end{aligned}$$

and the induced metric on these parameters is given by $\hbox {d}s^2=\hbox {cosh}^2\widetilde{\omega }|\hbox {d}w|^2.$

Moreover, by (3.3), there exists a constant $K_0>0$ such that

$$\begin{aligned} |\widetilde{\omega }(w)|\le \frac{K_0}{\hbox {cosh}r}, \end{aligned}$$

(3.9)

for u sufficiently large, where $r=\sqrt{u^2+v^2}.$

Notice that for u sufficiently large, the point $w=u+iv$ is contained in a ball of radius r large such that any point in this ball is the center of a ball of radius r / 2 where the inequality (3.9) is satisfied for all points inside that smaller ball. Since the metric $|\hbox {d}w|^2=|\tilde{\phi }||\hbox {d}\tilde{z}|^2$ is flat, we are working in ${{\mathrm{{\mathbb {R}}}}}^2$. Consider the function $\widetilde{\omega }$ defined on D(w, r) and define $\hat{\omega }:D(w,1)\rightarrow {{\mathrm{{\mathbb {R}}}}}$ by $\hat{\omega }(z)=\widetilde{\omega }(rz),$ so by (3.2),

$$\begin{aligned} \Delta _{|\phi |}\hat{\omega }=2r^2\sinh 2\hat{\omega }. \end{aligned}$$

Hence by $L^p$ elliptic estimates (see [6], Theorem 9.11), we get

$$\begin{aligned} |\hat{\omega }|_{W^{2,p}(D(w,2/3))}\le C\left( |2r^2\sinh 2\hat{\omega }|_{L^{p}(D(w,1))}+|\hat{\omega }|_{L^{p}(D(w,1))}\right) \le C' r^2e^{-r}, \end{aligned}$$

where in the last inequality we use (3.9). Now applying the Sobolev embedding theorem for $p>2,$ we obtain

$$\begin{aligned} |\hat{\omega }|_{C^{1,\alpha }(D(w,1/2))}\le C''r^2e^{-r}, \end{aligned}$$

and that implies

$$\begin{aligned} r|\nabla \widetilde{\omega }|_{C^0(D(w,r/2))}\le C''r^2e^{-r}. \end{aligned}$$

Then

$$\begin{aligned} |\nabla \widetilde{\omega }|_{C^{0}(D(w,r/2))}\le C''re^{-r}. \end{aligned}$$

(3.10)

Now consider the curve $\gamma _c=\widetilde{E}\cap ({{\mathrm{{\mathbb {H}}^2}}}\times \{v=c\}),$ that is, $\gamma _c(u)=(\widetilde{F}(u,c),c).$ Let $(V,\sigma (\eta )|\hbox {d}\eta |^2)$ be a local parameterization of ${{\mathrm{{\mathbb {H}}^2}}}$ and define the local function $\varphi$ as the argument of $\widetilde{F}_u,$ hence

$$\begin{aligned} \widetilde{F}_u=\frac{1}{\sqrt{\sigma }}\cosh \widetilde{\omega } e^{i\varphi } \quad \hbox {and} \quad \widetilde{F}_v=\frac{i}{\sqrt{\sigma }}\sinh \widetilde{\omega } e^{i\varphi }. \end{aligned}$$

If we denote by $k_g$ the geodesic curvature of $\gamma _c$ in $(V,\sigma (\eta )|\hbox {d}\eta |^2)$ and by $k_e$ the Euclidean geodesic curvature of $\gamma _c$ in $(V,|\hbox {d}\eta |^2),$ we have

$$\begin{aligned} k_g=\frac{k_e}{\sqrt{\sigma }}-\frac{\left\langle \nabla \sqrt{\sigma }, n\right\rangle }{\sigma }, \end{aligned}$$

where $n=(-\sin \varphi ,\cos \varphi )$ is the Euclidean normal vector to $\gamma _c$. If t denotes the arc length of $\gamma _c,$ we have

$$\begin{aligned} k_e=\varphi _t=\frac{\varphi _u\sqrt{\sigma }}{\cosh \widetilde{\omega }} \end{aligned}$$

and

$$\begin{aligned} \frac{\left\langle \nabla \sqrt{\sigma }, n\right\rangle }{\sigma }= \frac{\left\langle \nabla \hbox {ln} \sqrt{\sigma }, n\right\rangle }{\sqrt{\sigma }}=\frac{1}{2\sqrt{\sigma }}\left( \cos \varphi (\ln \sigma )_{\eta _2}-\sin \varphi (\ln \sigma )_{\eta _1} \right) . \end{aligned}$$

Then,

$$\begin{aligned} k_g=\frac{\varphi _u}{\cosh \widetilde{\omega }}-\frac{1}{2\sqrt{\sigma }}\left( \cos \varphi (\ln \sigma )_{\eta _2}-\sin \varphi (\ln \sigma )_{\eta _1} \right) . \end{aligned}$$

(3.11)

In the complex coordinate w,  we have

$$\begin{aligned} \widetilde{F}_w=\frac{e^{\widetilde{\omega }+i\varphi }}{2\sqrt{\sigma }} \quad \hbox {and} \quad \widetilde{F}_{\bar{w}}=\frac{e^{-\widetilde{\omega }+i\varphi }}{2\sqrt{\sigma }}. \end{aligned}$$

(3.12)

Moreover, the harmonic map equation in the complex coordinate $\eta =\eta _1+i\eta _2$ of ${{\mathrm{{\mathbb {H}}^2}}}$ (see [27], p. 8) is

$$\begin{aligned} \widetilde{F}_{w\bar{w}}+(\ln \sigma )_{\eta }\widetilde{F}_w\widetilde{F}_{\bar{w}}=0. \end{aligned}$$

(3.13)

Then using (3.12) and (3.13), we obtain

$$\begin{aligned} (-\widetilde{\omega }+i\varphi )_w= & {} -\sqrt{\sigma }\left( \frac{1}{\sqrt{\sigma }}\right) _w-(\ln \sigma )_{\eta }\widetilde{F}_w\nonumber \\= & {} \frac{1}{2}(\ln \sigma )_w-(\ln \sigma )_{\eta }\widetilde{F}_w\nonumber \\= & {} \frac{1}{2}\left( (\ln \sigma )_{\eta }\widetilde{F}_w+(\ln \sigma )_{\bar{\eta }}\bar{\widetilde{F}}_w\right) -(\ln \sigma )_{\eta }\widetilde{F}_w\nonumber \\= & {} \frac{1}{2}(\ln \sigma )_{\bar{\eta }}\bar{\widetilde{F}}_w-\frac{1}{2}(\ln \sigma )_{\eta }\widetilde{F}_w, \end{aligned}$$

(3.14)

where $2(\ln \sigma )_{\eta }=(\ln \sigma )_{\eta _1}-i(\ln \sigma )_{\eta _2}$ and $\bar{\widetilde{F}_w}=\frac{1}{2\sqrt{\sigma }}e^{-\widetilde{\omega }-i\varphi }$.

Taking the imaginary part of (3.14), we get

$$\begin{aligned} \varphi _u+\widetilde{\omega }_v=\frac{\cosh \widetilde{\omega }}{2\sqrt{\sigma }}\left( \cos \varphi (\ln \sigma )_{\eta _2}-\sin \varphi (\ln \sigma )_{\eta _1}\right) . \end{aligned}$$

(3.15)

By (3.11) and (3.15), we deduce

$$\begin{aligned} k_g=-\frac{\widetilde{\omega }_v}{\cosh \widetilde{\omega }}. \end{aligned}$$

(3.16)

Therefore for each c, by (3.9) and (3.10), the geodesic curvature of the curve $\gamma _c$ goes to zero as u go to infinity. In particular, the asymptotic boundary of $\gamma _c$ consists of only one point (see [10], Proposition 4.1).

We will prove that the family of curves $\gamma _c$ has the same boundary point at infinity independently on the value c. In order to do that, fix $u_0$ and consider $\alpha _{u_0}$ the projection onto ${{\mathrm{{\mathbb {H}}^2}}}$ of the curve $\widetilde{X}(u_0,v)=(\widetilde{F}(u_0,v),v),$ that is, $\alpha _{u_0}(v)=\widetilde{F}(u_0,v)\in {{\mathrm{{\mathbb {H}}^2}}}.$ We have $\alpha _{u_0}'(v)=\widetilde{F}_v$ and $|\alpha _{u_0}'(v)|_{\sigma }=|\sinh \widetilde{\omega }|$. Then

$$\begin{aligned} \hbox {d}(\alpha _{u_0}(v_1),\alpha _{u_0}(v_2))\le l(\alpha _{u_0}{|_{[v_1,v_2]}})=\int _{v_1}^{v_2}|\sinh \widetilde{\omega }|\hbox {d}v\le \int _{v_1}^{v_2} \sinh K_1\mathrm{e}^{-r} \hbox {d}v, \end{aligned}$$

for some constant $K_1,$ where $r=\sqrt{u_0^2+v^2},$ and the last inequality follows from (3.9). Thus, for any $v_1,v_2,$ we have $d(\alpha _{u_0}(v_1),\alpha _{u_0}(v_2))\rightarrow 0$ as $u_0\rightarrow +\infty .$

Therefore, the asymptotic boundary of all horizontal curves $\gamma _c$ in $\widetilde{E}$ coincides, and therefore, $\partial _{\infty }\widetilde{E}\cap \partial _{\infty }{{\mathrm{{\mathbb {H}}^2}}}\times {{\mathrm{{\mathbb {R}}}}}\subset \bar{p}_0\times {{\mathrm{{\mathbb {R}}}}}$, for some point $\bar{p}_0\in \partial _\infty {{\mathrm{{\mathbb {H}}^2}}}$. $\square$

Observe that since $\widetilde{h}|_{\partial \widetilde{E}}$ is unbounded and $\partial E$ is a closed curve of ${\mathcal {M}}$, then we have two possibilities for $\partial \widetilde{E}:$ either $\partial \widetilde{E}$ is invariant by a vertical translation or is invariant by a screw motion $\psi ^n\circ T(h)^m, n,m\ne 0.$ Let us analyze each one of these possible cases.

Claim 5

If $\partial \widetilde{E}$ is invariant by vertical translation and $E\subset {\mathcal {M}}_+,$ then E is asymptotic to some vertical plane $\gamma \times {\mathbb {S}}^1$ and

$$\begin{aligned} \int _{E} K=\int _{\partial E} k_g. \end{aligned}$$

Proof

In this case, by the trapping theorem in [4], $\widetilde{E}$ is contained in a slab between two vertical planes that limit to the same vertical line at infinity. Moreover, since $|\widetilde{\omega }|\rightarrow 0$, we get bounded curvature by (2.7). In particular, E has bounded curvature too.

Then there exists $\delta >0$ such that for any $p\in E,$ a neighborhood $V_p$ of p is a minimal graph of bounded geometry over the $\delta$-geodesic disk (in exponential coordinates) $D(0,\delta )\subset T_pE$ centered at the origin of the tangent space at p.

Now fix s and consider a divergent sequence $\{p_n\}_{n\in {\mathbb {N}}}$ in E. Applying hyperbolic translations to each point $p_n$ (horizontal translations along a geodesic of ${{\mathrm{{\mathbb {H}}^2}}}$ that sends $p_n$ to a point in ${{\mathrm{{\mathbb {T}}}}}(s)$), we get a sequence of points in ${{\mathrm{{\mathbb {T}}}}}(s)$ which we still denote by $\{p_n\}_{n\in {\mathbb {N}}}.$ Since ${{\mathrm{{\mathbb {T}}}}}(s)$ is compact, the sequence $\{p_n\}_{n\in {\mathbb {N}}}$ converges to a point $p\in {{\mathrm{{\mathbb {T}}}}}(s)$ and the sequence of graphs $V_{p_n}$ converges to a minimal graph $V_p$ of bounded geometry over a small disk in $T_pE.$ Since the sequence of minimal graphs $V_{p_n}$ is contained between two vertical planes whose distance goes to zero at infinity, we conclude that the limit graph $V_p$ is vertical (otherwise we would get points of $V_{p_n}$ outside the region bounded by the two planes).

In particular, $n_3\rightarrow 0$ and the tangent planes $T_{p_n}E$ converge to a vertical plane contained between the two vertical planes given by the trapping theorem. Then, it yields a $C^1$-convergence of E to a vertical plane. Now using elliptic regularity, we get that E converges in the $C^2$-topology to a vertical plane. Therefore, the geodesic curvature of $\alpha _s$ goes to zero and its length stays bounded, where $\alpha _s$ is the curve in $E\cap {{\mathrm{{\mathbb {T}}}}}(s)$ that generates $\pi _1(E).$

Applying the Gauss–Bonnet theorem for $E_s,$ the part of the end E bounded by $\partial E$ and $\alpha _s,$ we obtain

$$\begin{aligned} \int _{E_s}K + \int _{\alpha _s}k_g -\int _{\partial E}k_g=0. \end{aligned}$$

By our analysis in the previous paragraph, we have $\int _{\alpha _s}k_g\rightarrow 0,$ as $s\rightarrow \infty .$ Then, when we let s go to infinity, we get

$$\begin{aligned} \int _E K=\int _{\partial E}k_g, \end{aligned}$$

as we wanted to prove. $\square$

Claim 6

If $\partial \widetilde{E}$ is invariant by vertical translation and $E\subset {\mathcal {M}}_-,$ then E is asymptotic to some vertical plane $\gamma \times {\mathbb {S}}^1$ and

$$\begin{aligned} \int _{E} K=\int _{\partial E} k_g. \end{aligned}$$

Proof

By Claim 4, we already know that the asymptotic boundary of $\widetilde{E}$ is contained in $\bar{p}_0\times {{\mathrm{{\mathbb {R}}}}},$ for some $\bar{p}_0\in \partial _{\infty }{{\mathrm{{\mathbb {H}}^2}}}.$ Since $\partial \widetilde{E}$ is invariant by vertical translation, then we can find a horizontal geodesic $\gamma$ in ${{\mathrm{{\mathbb {H}}^2}}}$ such that $\gamma$ limits to $\bar{p}_0$ at infinity and $\gamma \times {{\mathrm{{\mathbb {R}}}}}$ does not intersect $\partial \widetilde{E}$. Call $q_0$ the other endpoint of $\gamma .$ Take $q\in \partial _{\infty }{{\mathrm{{\mathbb {H}}^2}}}$ contained in the halfspace determined by $\gamma \times {{\mathrm{{\mathbb {R}}}}}$ that does not contain $\partial \widetilde{E}$. Since the asymptotic boundary of $\widetilde{E}$ is contained in $\bar{p}_0\times {{\mathrm{{\mathbb {R}}}}},$ then $\overline{qq_0}\times {{\mathrm{{\mathbb {R}}}}}$ does not intersect $\widetilde{E}$ for q sufficiently close to $q_0.$ Also note that for any q,  $\overline{qq_0}\times {{\mathrm{{\mathbb {R}}}}}$ cannot be tangent at infinity to $\widetilde{E}$, because E is proper in ${\mathcal {M}}.$ Thus, if we start with q close to $q_0$ and let q go to $\bar{p}_0,$ we conclude that in fact $\gamma \times {{\mathrm{{\mathbb {R}}}}}$ does not intersect $\widetilde{E}$, by the maximum principle. Now if we consider another point $\bar{q_0}\in \partial _{\infty }{{\mathrm{{\mathbb {H}}^2}}}$ contained in the same halfspace determined by $\gamma \times {{\mathrm{{\mathbb {R}}}}}$ as $\partial \widetilde{E}$ and such that $\bar{\gamma }\times {{\mathrm{{\mathbb {R}}}}}=\overline{\bar{q_0}\bar{p}_0}\times {{\mathrm{{\mathbb {R}}}}}$ does not intersect $\partial \widetilde{E},$ we can prove using the same argument above that $\bar{\gamma }\times {{\mathrm{{\mathbb {R}}}}}$ does not intersect $\widetilde{E}$. Thus we conclude that $\widetilde{E}$ is contained in the region between two vertical planes that limit to $\bar{p}_0\times {{\mathrm{{\mathbb {R}}}}}$.

Since $|\widetilde{\omega }|\rightarrow 0$, we have bounded curvature by (2.7). So $E\subset {\mathcal {M}}_-$ is a minimal surface with bounded curvature contained in a slab bounded by two vertical planes that limit to the same point at infinity. Hence, using the same argument as in Claim 5, we can show that E converges in the $C^2$-topology to a vertical plane and, moreover, we get

$$\begin{aligned} \int _E K=\int _{\partial E}k_g. \end{aligned}$$

$\square$

Claim 7

If $\partial \widetilde{E}$ is invariant by screw motion and $E\subset {\mathcal {M}}_+,$ then E converges to the quotient of a helicoidal plane and

$$\begin{aligned} \int _{E} K=\int _{\partial E}k_g. \end{aligned}$$

Proof

In this case, by the trapping theorem in [4], $\widetilde{E}$ is contained in a slab between two parallel helicoidal planes and, since $|\widetilde{\omega }|\rightarrow 0$, we have bounded curvature by (2.7). Then E is a minimal surface in ${\mathcal {M}}_+$ with bounded curvature contained in a slab between the quotient of two parallel helicoidal planes whose distance in ${\mathcal {M}}_+$ goes to zero at infinity.

Thus, using the same argument as in Claim 5, we can show that in fact E converges in the $C^2$-topology to the quotient of a helicoidal plane contained between the quotient of the two helicoidal planes given by the trapping theorem. In particular, the geodesic curvature of $\alpha _s$ goes to zero and its length stays bounded, where $\alpha _s$ is the curve in $E\cap {{\mathrm{{\mathbb {T}}}}}(s)$ that generates $\pi _1(E).$

Applying the Gauss–Bonnet theorem for $E_s,$ the part of the end E bounded by $\partial E$ and $\alpha _s,$ we obtain

$$\begin{aligned} \int _{E_{s}}K + \int _{\alpha _{s}}k_g -\int _{\partial E}k_g=0. \end{aligned}$$

By our previous analysis, we have $\int _{\alpha _{s}}k_g\rightarrow 0$, when $s\rightarrow \infty .$ Then, when we let s go to infinity, we get

$$\begin{aligned} \int _E K=\int _{\partial E}k_g, \end{aligned}$$

as we wanted to prove. $\square$

Claim 8

The case $\partial \widetilde{E}$ invariant by screw motion and $E\subset {\mathcal {M}}_{-}$ is not possible.

Proof

By Remark 2, we know that for almost every $s\le 0,$ $\widetilde{E}\cap d(s)$ contains a curve invariant by screw motion. Consider $\gamma$ a unit speed geodesic such that $\gamma (+\infty )=\bar{p}_0$, and for each n take $\alpha _n$, the geodesic orthogonal to $\gamma$ passing trough $\gamma (n).$ For n sufficiently large, one of the half spaces $P_n^+$ determined by $\alpha _n\times {{\mathrm{{\mathbb {R}}}}}$ contains $\bar{p}_0\times {{\mathrm{{\mathbb {R}}}}}$ and the other one $P_n^-$ contains $\partial \widetilde{E}.$ Observe that for each n,  we have, for s sufficiently large, that a curve invariant by screw motion in the plane d(s) contains points in both half spaces $P_n^+$ and $P_n^-.$ Hence we conclude that for every n,  $\widetilde{E}$ has points outside the half space $P_n^+$ which contains $\bar{p}_0\times {{\mathrm{{\mathbb {R}}}}}$. Then, the asymptotic boundary of $\widetilde{E}$ cannot be contained in $\bar{p}_0\times {{\mathrm{{\mathbb {R}}}}},$ a contradiction with Claim 4. Thus this case is not possible. $\square$

Therefore, analyzing the geometry of all possible cases for the ends of a properly immersed minimal surface with finite total curvature $\Sigma$ in ${\mathcal {M}}$, we have proved the theorem. $\square$