Abstract
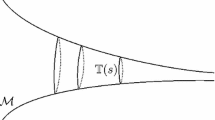
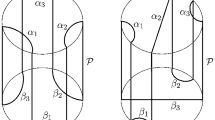
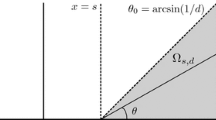
We prove that the ends of a properly immersed simply or one connected minimal surface in \({{\mathbb{H}} \times {\mathbb{R}}}\) contained in a slab of height less than \({\pi}\) of \({{\mathbb{H}} \times {\mathbb{R}}}\) are multi-graphs. When such a minimal surface is properly embedded, then the ends are graphs. When such a minimal surface is properly embedded and simply connected, it is an entire graph.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Bernstein J., Brenner C.: Conformal Structure of Minimal Surfaces with Finite Topology. Comment. Math. Helv. 86, 353–381 (2011)
T.H. Colding and W.P. Minicozzi, II The space of embedded minimal surfaces of fixed genus in a 3-manifold. I. Estimates off the axis for disks, Annals of Mathematics (2) 160 (2004), 27–68.
P. Collin, Topologie et courbure des surfaces minimales proprement plongées de \({\mathbb{R}^3}\), Annals of Mathematics 145 (1997), 1–31.
P. Collin, L. Hauswirth, and H. Rosenberg, The geometry of finite topology surfaces properly embedded in hyperbolic space with constant mean curvature one, Annals of Mathematics 153 (2001), 623–659.
Collin P., Rosenberg H.: Construction of harmonic diffeomorphisms and minimal graphs. Annals of Mathematics 172, 1879–1906 (2010)
B. Daniel, Isometric immersions into \({\mathbb{S}^n \times \mathbb{R}}\) and \({\mathbb{H}^n \times \mathbb{R}}\) and applications to minimal surfaces. Trans. Amer. Math. Soc. 361 (2009), 6255–6282.
Daniel B.: Isometric Immersion into three-dimensional homogeneous manifolds. Comment. Math. Helv. 82, 87–131 (2007)
Gulliver R.: Removability of singular points on surfaces of bounded mean curvature. J. Differential Geometry 11, 345–350 (1976)
Hauswirth L.: Minimal surfaces of Riemann type in three-dimensional product manifolds. Pacific J. Math. 224, 91–117 (2006)
D. Hoffman and W.H. Meeks, III ,The strong halfspace theorem for minimal surfaces, Invent. Math. 101 (1990), 373–377.
W.H. Meeks, III and H. Rosenberg, The uniqueness of the helicoid, Annals of Mathematics 161 (2005), 727–758.
B. Nelli and H. Rosenberg, Minimal surfaces in \({\mathbb{H}^2 \times \mathbb{R}}\). Bull. Braz. Math. Soc. (N.S.) 33 (2002), 263–292.
B. Nelli and H. Rosenberg, Errata: “Minimal surfaces in \({\mathbb{H}^2\times \mathbb{R}}\), [Bull. Braz. Math. Soc. (N.S.) 33 (2002), 263–292; MR1940353]. Bull. Braz. Math. Soc. (N.S.) 38 (2007), 661–664. 53A10.
R. Sa Earp and E. Toubiana, Screw motion surfaces in \({\mathbb{S}^2 \times \mathbb{R}}\) and \({\mathbb{H}^2 \times \mathbb{R}}\). Illinois J. Math. 49 (2005), 1323–1362.
L. Mazet, M. Rodriguez, and H. Rosenberg, Periodic constant mean curvature surfaces in \({\mathbb{H} \times \mathbb{R}}\)., Asian Journal of Mathematics 18 (2014), 829–858.
Author information
Authors and Affiliations
Corresponding author
Additional information
P. Collin, L. Hauswirth, and H. Rosenberg was partially supported by the ANR-11-IS01-0002 Grant.
Rights and permissions
About this article
Cite this article
Collin, P., Hauswirth, L. & Rosenberg, H. Properly immersed minimal surfaces in a slab of \({\mathbb {H} \times {\mathbb {R}}}\), \({\mathbb {H}}\) the hyperbolic plane. Arch. Math. 104, 471–484 (2015). https://doi.org/10.1007/s00013-015-0744-7
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00013-015-0744-7