Global dynamics of the Benoît system

Abstract

In this paper, we work with a two-degree polynomial differential system in $\mathbb R ^3$ related with the canard phenomena. We show that this system is completely integrable, and we provide its global phase portrait in the Poincaré ball using the Poincaré–Lyapunov compactification.

1 Introduction

We recall that the relevant canard phenomena were discovered by the French mathematicians Benoît et al. [4] in 1981 when they studied the two-dimensional van der Pol oscillator. These canard phenomena are generically persistent under small parameter changes in singular perturbed differential systems with two or more slow variables and one fast variable, see [2] and also [3, 8, 9] and [10].

In the paper of Benoît [2] of the year 1983, a slow–fast system in $\mathbb{R }^3$ was studied with two slow and one fast variable. This paper becomes seminal because it leads to the well-known mixed-mode oscillations investigated up to now. Choosing appropriate weights, the main part of the vector field is the quasi-homogeneous part of degree 2 that exhibits the more interesting dynamics. It is precisely this quasi-homogeneous part that we choose as the differential system to study in this paper. A reason for looking at this quasi-homogeneous part comes from the geometric approach of singular perturbations, due to Wechselberger and Szmolyan (see [10] and [9]), where a blowup (rescaling) is used and all terms of the vector field that do not belong to this quasi-homogeneous part become of higher order after the rescaling. Another reason is that up to now, nobody described the global dynamics of this interesting system.

In short, we consider the three-dimensional polynomial differential system in $\mathbb R ^3$ given by

$$\begin{aligned} \begin{array}{l} X^{\prime }=-2Y, \\ Y^{\prime }=1, \\ Z^{\prime }=-\frac{X+Z^2}{\varepsilon }. \\ \end{array} \end{aligned}$$

(1)

Here, $\varepsilon$ is a nonzero real parameter and the prime denotes the derivative with respect to the independent variable $T$ that we call the time. This system in this paper will be called the Benoît system.

The objective of this paper is to describe the global dynamics of the Benoît system (1). For doing this, first we rescale all the variables and we eliminate the redundant parameter $\varepsilon$. After, we will use the Poincaré–Lyapunov compactification of $\mathbb R ^3$. This compactification identifies $\mathbb R ^3$ with the interior of the unit ball in $\mathbb R ^3$ and the infinity of $\mathbb R ^3$ with the boundary $\mathbb S ^2$ of that ball, and the Benoît system is analytically extended to the closed ball which is called the Poincaré ball. This extended flow has the sphere $\mathbb S ^2$ invariant. We shall describe the phase portrait of the Benoît system in the Poincaré sphere using the Poincaré–Lyapunov compactification, see for more details Sect. 2.

All the results that we shall present and prove will be for $\varepsilon >0$. In fact, it is not difficult to see that the dynamics for the case $\varepsilon <0$ can be studied in a similar way to the case $\varepsilon >0$. In fact, it is easy to check that the phase portrait of the Benoît system in the Poincaré ball for $\varepsilon =\varepsilon ^*<0$ is the same that for $\varepsilon =-\varepsilon ^*>0$ but changing the sign of the $z$ coordinate.

Doing the rescaling $(X,Y,Z,T)\rightarrow (x,y,z,t)$ defined by $X= \varepsilon x, Y= \varepsilon ^{1/2} y, Z= \varepsilon ^{1/2} z$, and $T= \varepsilon ^{1/2} t$, the differential system (1) becomes

$$\begin{aligned} \begin{array}{ll} \dot{x}=-2y&=P_1(x,y,z), \\ \dot{y}=1&=P_2(x,y,z), \\ \dot{z}=-x-z^2&=P_3(x,y,z). \end{array} \end{aligned}$$

(2)

The strategy for providing the phase portrait in the Poincaré ball of the Benoît system is the following. First, we study the Benoît system (2) at infinity that corresponds to analyze the extended Benoît system restricted to the boundary $\mathbb S ^2$. Second, we state two independent first integrals for the Benoît system and we also provide the explicit solutions of the Benoît system in function of the new time $t$. Third, we describe its global dynamics in the Poincaré ball. We shall see that all the orbits of the Benoît system will have their $\alpha -$ and $\omega -$limit at infinity.

The main results of this paper are the following.

Proposition 1

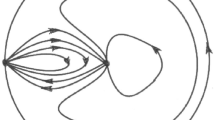
The extended Benoît system at infinity has as equilibrium points, at the Poincaré–Lyapunov sphere, the end of the $x$-axis (which are saddle-nodes) and $z$-axis (which are hyperbolic nodes). Moreover, the phase portrait of the extended Benoît system on the Poincaré–Lyapunov sphere is represented, in Fig. 1.

Fig. 1

Phase portrait of the Benoît system at the Poincaré–Lyapunov sphere at infinity

Proposition 1 is proved in Sect. 3.

Proposition 2

The Benoît system is completely integrable having the following two independent first integrals

$$\begin{aligned} H_1=x+y^2 \end{aligned}$$

and $H_2$ is equal to

$$\begin{aligned} \begin{array}{l} \left[8W_1\left(\frac{y^2}{4}\!+\!\frac{x}{4}, \frac{1}{4}, y^2\right)W_1\left(\frac{y^2}{4}\!+\!\frac{x}{4}\!+\!1, \frac{1}{4}, y^2\right) \!-\!2W_1\left(\frac{y^2}{4}\!+\!\frac{x}{4}, \frac{1}{4}, y^2\right)^2y^2\!+\!W_1\left(\frac{y^2}{4}\!+\!\frac{x}{4}, \frac{1}{4}, y^2\right)^2y^4\right.\\ +2 W_1\left(\frac{y^2}{4}+\frac{x}{4},\frac{1}{4},y^2\right)^2 x+W_1\left(\frac{y^2}{4}+\frac{x}{4},\frac{1}{4},y^2\right)^2 x^2 -2W_1\left(\frac{y^2}{4}+\frac{x}{4}, \frac{1}{4}, y^2\right)^2y^2x\\ -8W_1\left(\frac{y^2}{4}+\frac{x}{4}, \frac{1}{4}, y^2\right)y^2W_1(\frac{y^2}{4}\!+\!\frac{x}{4}\!+\!1, \frac{1}{4}, y^2) \! +\!8 W_1\left(\frac{y^2}{4}+\frac{x}{4},\frac{1}{4},y^2\right) W_1\left(\frac{y^2}{4}+\frac{x}{4}+1,\frac{1}{4},y^2\right) x \\ \left.+16 W_1\left(\frac{y^2}{4}+\frac{x}{4}+1,\frac{1}{4},y^2\right)^2+W_1 \left(\frac{y^2}{4}+\frac{x}{4},\frac{1}{4},y^2\right)^2\right]^{\frac{1}{2}}z^2\\ +\left[ 2 W_2\left(\frac{y^2}{4}\!+\!\frac{x}{4},\frac{1}{4},y^2\right) W_1\left(\frac{y^2}{4}\!+\!\frac{x}{4},\frac{1}{4},y^2\right) \!-\!8W_2\left(\frac{y^2}{4}\!+\!\frac{x}{4}\!+\!1, \frac{1}{4}, y^2\right)W_1\left(\frac{y^2}{4}+\frac{x}{4}+1, \frac{1}{4}, y^2\right)y^2 \right.\\ +2 z y W_1\left(\frac{y^2}{4}\!+\!\frac{x}{4},\frac{1}{4},y^2\right) +2 W_2\left(\frac{y^2}{4}\!+\!\frac{x}{4},\frac{1}{4},y^2\right) y^4 W_1\left(\frac{y^2}{4}\!+\!\frac{x}{4},\frac{1}{4},y^2\right)\\ 8W_2\left(\frac{y^2}{4}\!+\!\frac{x}{4}, \frac{1}{4}, y^2\right)y^2W_1\left(\frac{y^2}{4}\!+\!\frac{x}{4}\!+\!1, \frac{1}{4}, y^2\right) +8 W_2\left(\frac{y^2}{4}\!+\!\frac{x}{4},\frac{1}{4},y^2\right) W_1\left(\frac{y^2}{4}\!+\!\frac{x}{4}\!+\!1,\frac{1}{4},y^2\right)\\ -6W_2\left(\frac{y^2}{4}\!+\!\frac{x}{4}\!+\!1, \frac{1}{4}, y^2\right)W_1\left(\frac{y^2}{4}\!+\!\frac{x}{4}, \frac{1}{4}, y^2\right) -4W_2\left(\frac{y^2}{4}\!+\!\frac{x}{4}, \frac{1}{4}, y^2\right)W_1\left(\frac{y^2}{4}\!+\!\frac{x}{4}, \frac{1}{4}, y^2\right)y^2x\\ -8xW_1\left(\frac{y^2}{4}\!+\!\frac{x}{4}\!+\!1, \frac{1}{4}, y^2\right)W_2\left(\frac{y^2}{4}\!+\!\frac{x}{4}\!+\!1, \frac{1}{4}, y^2\right) \! +\!2 W_2\left(\frac{y^2}{4}\!+\!\frac{x}{4},\frac{1}{4},y^2\right) W_1\left(\frac{y^2}{4}\!+\!\frac{x}{4},\frac{1}{4},y^2\right) x^2\\ +8 W_2\left(\frac{y^2}{4}\!+\!\frac{x}{4},\frac{1}{4},y^2\right) W_1\left(\frac{y^2}{4}\!+\!\frac{x}{4}\!+\!1,\frac{1}{4},y^2\right) x -4W_2\left(\frac{y^2}{4}\!+\!\frac{x}{4}, \frac{1}{4}, y^2\right)W_1\left(\frac{y^2}{4}\!+\!\frac{x}{4}, \frac{1}{4}, y^2\right)y^2\\ -8W_2\left(\frac{y^2}{4}\!+\!\frac{x}{4}\!+\!1, \frac{1}{4}, y^2\right)W_1\left(\frac{y^2}{4}\!+\!\frac{x}{4}, \frac{1}{4}, y^2\right)x \! +\!4 W_2\left(\frac{y^2}{4}\!+\!\frac{x}{4}\!+\!1,\frac{1}{4},y^2\right) W_1\left(\frac{y^2}{4}\!+\!\frac{x}{4},\frac{1}{4},y^2\right) y^2\\ -24W_1\left(\frac{y^2}{4}\!+\!\frac{x}{4}\!+\!1, \frac{1}{4}, y^2\right)W_2\left(\frac{y^2}{4}\!+\!\frac{x}{4}\!+\!1, \frac{1}{4}, y^2\right)\\ +2 W_2\left(\frac{y^2}{4}+\frac{x}{4}+1,\frac{1}{4},y^2\right) W_1\left(\frac{y^2}{4}+\frac{x}{4},\frac{1}{4},y^2\right) y^4+4 W_2\left(\frac{y^2}{4}+ \frac{x}{4},\frac{1}{4},y^2\right) W_1\left(\frac{y^2}{4}+\frac{x}{4},\frac{1}{4},y^2\right) x\\ \left.-2W_2\left(\frac{y^2}{4}+\frac{x}{4}+1, \frac{1}{4}, y^2\right)W_1\left(\frac{y^2}{4}\!+\!\frac{x}{4}, \frac{1}{4}, y^2\right)x^2\right]z\\ +9 W_2\left(\frac{y^2}{4}+\frac{x}{4}+1,\frac{1}{4},y^2\right)^2+6 W_2\left(\frac{y^2}{4}+\frac{x}{4}+1,\frac{1}{4},y^2\right)^2 y^2 +6 W_2\left(\frac{y^2}{4}+\frac{x}{4}+1,\frac{1}{4},y^2\right)^2 x\\ +W_2\left(\frac{y^2}{4}+\frac{x}{4}+1,\frac{1}{4},y^2\right)^2 y^4 +W_2\left(\frac{y^2}{4}+\frac{x}{4}+1,\frac{1}{4},y^2\right)^2 x^2+2 W_2\left(\frac{y^2}{4}+\frac{x}{4}+1,\frac{1}{4},y^2\right)^2 y^2 x\\ +4 W_2\left(\frac{y^2}{4}+\frac{x}{4},\frac{1}{4},y^2\right) y^2 W_2\left(\frac{y^2}{4}\!+\!\frac{x}{4}\!+\!1,\frac{1}{4},y^2\right) \!+\!2 W_2\left(\frac{y^2}{4}\!+\!\frac{x}{4},\frac{1}{4},y^2\right) y^4 W_2\left(\frac{y^2}{4}+\frac{x}{4}\!+\!1,\frac{1}{4},y^2\right)\\ -8W_2\left(\frac{y^2}{4}+\frac{x}{4}, \frac{1}{4}, y^2\right)W_2\left(\frac{y^2}{4}+\frac{x}{4}+1, \frac{1}{4}, y^2\right)x\\ -2W_2\left(\frac{y^2}{4}+\frac{x}{4}, \frac{1}{4}, y^2\right)W_2\left(\frac{y^2}{4}+\frac{x}{4}+1, \frac{1}{4}, y^2\right)x^2 +2 z y W_2\left(\frac{y^2}{4}+\frac{x}{4},\frac{1}{4},y^2\right)\\ -2 W_2\left(\frac{y^2}{4}+\frac{x}{4},\frac{1}{4},y^2\right)^2 y^2 x +W_2\left(\frac{y^2}{4}+\frac{x}{4},\frac{1}{4},y^2\right)^2 y^4+2 W_2\left(\frac{y^2}{4}+\frac{x}{4},\frac{1}{4},y^2\right)^2 x\\ W_2\left(\frac{y^2}{4}+\frac{x}{4}, \frac{1}{4}, y^2\right)^2x^2-2W_2\left(\frac{y^2}{4}+\frac{x}{4}, \frac{1}{4}, y^2\right)^2y^2 +W_2\left(\frac{y^2}{4}+\frac{x}{4},\frac{1}{4},y^2\right)^2\\ -6W_2\left(\frac{y^2}{4}+\frac{x}{4}, \frac{1}{4}, y^2\right)W_2\left(\frac{y^2}{4}+\frac{x}{4}+1, \frac{1}{4},y^2\right). \end{array} \end{aligned}$$

The first integral $H_1$ is well known (see [2]), but as far as we know, the second integral $H_2$ is new.

Here, $W_1(\mu ,\nu ,z)$ and $W_2(\mu ,\nu ,z)$ represent the Whittaker functions that are two independent solutions of the differential equation

$$\begin{aligned} \ddot{y}+\left(-\frac{1}{4}+\frac{\mu }{\nu }+\frac{\frac{1}{4}-\nu ^2}{z^2}\right)y=0. \end{aligned}$$

They can be defined in terms of the Hypergeometric and Kummer functions in the following way:

$$\begin{aligned} W_2(\mu ,\nu ,z)=e^{-z/2}e^{1/2+\nu }H\left(\left[\frac{1}{2}+\nu -\mu \right], \left[1+2\nu \right],z\right) \end{aligned}$$

and

$$\begin{aligned} W_1(\mu ,\nu ,z)=e^{-z/2}e^{1/2+\nu }K\left(\frac{1}{2} +\nu -\mu ,1+2\nu ,z\right). \end{aligned}$$

For more details in these functions, see for instance [1].

Proposition 3

The solution $(x(t),y(t),z(t))$ of the Benoît system satisfying $(x(0),y(0), z(0))=(x_0,y_0,z_0)\in \mathbb R ^3$ is given by $x(t)=-t^2-y_0t+x_0, y(t)=t+y_0$, and $z(t)$ is equal to

$$\begin{aligned} \begin{array}{l} -\frac{1}{3d}\left\{ -3H\left(\left[\frac{5}{4}-\frac{x_0}{4}-\frac{y_0^2}{4}\right], \left[\frac{3}{2}\right], (t+y_0)^2\right)t\right.\\ -3H\left(\left[\frac{5}{4}-\frac{x_0}{4}-\frac{y_0^2}{4}\right], \left[\frac{3}{2}\right], (t+y_0)^2\right)y_0+3 H\left(\left[\frac{5}{4}-\frac{x_0}{4}-\frac{y_0^2}{4}\right], \left[\frac{3}{2}\right],(t+y_0)^2\right) x_0 t\\ +3 H\left(\left[\frac{5}{4}-\frac{x_0}{4}-\frac{y_0^2}{4}\right], \left[\frac{3}{2}\right],(t+y_0)^2\right) x_0 y_0+3 H\left(\left[\frac{5}{4}-\frac{x_0}{4}-\frac{y_0^2}{4}\right],\left[\frac{3}{2}\right], (t+y_0)^2\right) y_0^2 t\\ +3H\left(\left[\frac{5}{4}-\frac{x_0}{4}-\frac{y_0^2}{4}\right], \left[\frac{3}{2}\right],(t+y_0)^2\right) y_0^3+3 H\left(\left[\frac{1}{4}-\frac{x_0}{4}-\frac{y_0^2}{4}\right], \left[\frac{1}{2}\right], (t+y_0)^2\right) t\\ +3H\left(\left[\frac{1}{4}-\frac{x_0}{4}-\frac{y_0^2}{4}\right],\left[\frac{1}{2}\right],(t+y_0)^2\right) y_0-3z_0H\left(\left[\frac{7}{4}-\frac{x_0}{4}-\frac{y_0^2}{4}\right], \left[\frac{5}{2}\right], (t+y_0)^2\right)t^2\\ -6z_0H\left(\left[\frac{7}{4}-\frac{x_0}{4}-\frac{y_0^2}{4}\right], \left[\frac{5}{2}\right], (t+y_0)^2\right)y_0t-3z_0H\left(\left[\frac{7}{4}-\frac{x_0}{4}-\frac{y_0^2}{4}\right], \left[\frac{5}{2}\right], (t+y_0)^2\right)y_0^2\\ +z_0H\left(\left[\frac{7}{4}-\frac{x_0}{4}-\frac{y_0^2}{4}\right], \left[\frac{5}{2}\right], (t+y_0)^2\right)t^2x_0+2 z_0 H\left(\left[\frac{7}{4}-\frac{x_0}{4}-\frac{y_0^2}{4}\right], \left[\frac{5}{2}\right],(t+y_0)^2\right) y_0 t x_0\\ +z_0 H\left(\left[\frac{7}{4}-\frac{x_0}{4}-\frac{y_0^2}{4}\right], \left[\frac{5}{2}\right], (t+y_0)^2\right) y_0^2 x_0+z_0 H\left(\left[\frac{7}{4}-\frac{x_0}{4}-\frac{y_0^2}{4}\right], \left[\frac{5}{2}\right],(t+y_0)^2\right) y_0^2 t^2\\ +2 z_0 H\left(\left[\frac{7}{4}-\frac{x_0}{4}-\frac{y_0^2}{4}\right], \left[\frac{5}{2}\right], (t+y_0)^2\right) y_0^3 t+z_0 H\left(\left[\frac{7}{4}-\frac{x_0}{4}-\frac{y_0^2}{4}\right], \left[\frac{5}{2}\right],(t+y_0)^2\right) y_0^4\\ -3 z_0 H\left(\left[\frac{3}{4}-\frac{x_0}{4}-\frac{y_0^2}{4}\right], \left[\frac{3}{2}\right], (t+y_0)^2\right)+3 z_0 H\left(\left[\frac{3}{4}-\frac{x_0}{4}-\frac{y_0^2}{4}\right], \left[\frac{3}{2}\right],(t+y_0)^2\right) t^2\\ +6 z_0 H\left(\left[\frac{3}{4}-\frac{1}{4} -\frac{y_0^2}{4}\right], \left[\frac{3}{2}\right],(t+y_0)^2\right) y_0 t\left.+3z_0H\left(\left[\frac{3}{4}-\frac{x_0}{4}-\frac{y_0^2}{4}\right], \left[\frac{3}{2}\right], (t+y_0)^2\right)y_0^2\right\} , \end{array} \end{aligned}$$

where

$$\begin{aligned} \begin{array}{ll} d=&z_0H\left(\left[\frac{3}{4}-\frac{x_0}{4}-\frac{y_0^2}{4}\right], \left[\frac{3}{2}\right], (t+y_0)^2\right)t+z_0H\left(\left[\frac{3}{4}-\frac{x_0}{4}-\frac{y_0^2}{4}\right], \left[\frac{3}{2}\right], (t+y_0)^2\right)y_0\\&+H\left(\left[\frac{1}{4}-\frac{x_0}{4}-\frac{y_0^2}{4}\right], \left[\frac{1}{2}\right], (t+y_0)^2\right).\\ \end{array} \end{aligned}$$

Corollary 4

All the orbits of the Benoît system are unbounded in forward and backward time.

Theorem 5

The possible orbits of the Benoît system restricted to the level $H_1=h_1$ are of three types:

• (i) Disconnecting orbits: homoclinic orbits to the equilibrium point at infinity $(-1,0,0)\in \mathbb S ^2$.

• (ii) Intermediate orbits: heteroclinic orbits going from the equilibrium $(0,0,1)\in \mathbb S ^2$ to the equilibrium $(-1,0,0)\in \mathbb S ^2$, or going from the equilibrium $(-1,0,0)\in \mathbb S ^2$ to the equilibrium $(0,0,-1)\in \mathbb S ^2$.

• (iii) Passage orbits: heteroclinic orbits going from the equilibrium $(0,0,1)\in \mathbb S ^2$ to the equilibrium $(0,0,-1)\in \mathbb S ^2$.

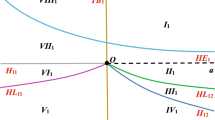
The three possible configurations of the orbits are drawn in Fig. 2.

Fig. 2

Possible phase portrait of the Benoît system restricted to the compactified level $H_1=h_1$. Picture (a) has a continuum of orbits of disconnecting type. Picture (b) has a unique orbit of disconnecting type. Picture (c) has no orbits of disconnecting type

Moreover, all these three possible types appear in the Benoît system but in different levels of $H_1$.

Propositions 2 and 3 and Corollary 4 are proved in Sect. 4, and Theorem 5 is proved in Sect. 5.

In the next section, we present the Poincaré–Lyapunov compactification in $\mathbb R ^3$.

2 Poincaré and Poincaré–Lyapunov compactification in $\mathbb R ^3$

A polynomial vector field $X$ in $\mathbb R ^3$ can be extended to a unique analytic vector field on the sphere $\mathbb S ^2$. The technique for doing such an extension is called the Poincaré compactification and allows to study a polynomial vector field in a neighborhood of infinity, which corresponds to the equator $\mathbb S ^2$ of the sphere $\mathbb S ^3$. Poincaré introduced this compactification for polynomial vector fields in $\mathbb R ^2$. Its extension to $\mathbb R ^3$ can be found in [5]. For completeness, we will give here a small introduction on this technic as it appears in [5].

In $\mathbb R ^3$, we consider the polynomial differential system

$$\begin{aligned} \dot{x}=P_1(x,y,z),\quad \dot{y}=P_2(x,y,z), \quad \dot{z}=P_3(x,y,z), \end{aligned}$$

or equivalently its associated polynomial vector field $X=(P_1,P_2,P_3)$. The degree $m$ of $X$ is defined as $m=max\,\left(deg(P_i);\,i=1,2,3\right)$.

Let $\mathbb S ^3=\{y=(y_1,y_2,y_3,y_4)\in \mathbb R ^4;\;\Vert y\Vert =1\}$ be the unit sphere in $\mathbb R ^4, \mathbb S _+=\{y\in \mathbb S ^3;\;y_4>0\}$ and $\mathbb S _-=\{y\in \mathbb S ^3;\;y_4<0\}$ be the northern and southern hemispheres of $\mathbb S ^3$, respectively. The tangent space to $\mathbb S ^3$ at the point $y$ is denoted by $T_y\mathbb S ^3$. Then, the tangent plane

$$\begin{aligned} T_{(0,0,0,1)}\mathbb S ^3=\{(x_1,x_2,x_3,1)\in \mathbb R ^4;\;(x_1,x_2,x_3)\in \mathbb R ^3\} \end{aligned}$$

is identified with $\mathbb R ^3$.

We consider the central projections $f_+:\,T_{(0,0,0,1)}\mathbb S ^3\rightarrow \mathbb S _+$ and $f_-:\,T_{(0,0,0,1)}\mathbb S ^3\rightarrow \mathbb S _-$ defined by $f_{\pm }(x)=\pm (x_1,x_2,x_3,1)/\Delta x$, where $\Delta (x)=\left(1+\displaystyle \sum \nolimits _{i=1}^3x_i^2\right)^{1/2}$. Through these central projection, $\mathbb R ^3$ is identified with the northern and southern hemispheres. The equator of $\mathbb S ^3$ is $\mathbb S ^2=\{y\in \mathbb S ^3;\;y_4=0\}$. Clearly, $\mathbb S ^2$ can be identified with the infinity of $\mathbb R ^3$.

The maps $f_+$ and $f_-$ define two copies of $X$ on $\mathbb S ^3$, one $Df_+\circ X$ in the northern hemisphere and the other $Df_-\circ X$ in the southern one. Denoted by $\bar{X}$, the vector field on $\mathbb S ^3\setminus \mathbb S ^2$ which, restricted to $\mathbb S _+$, coincides with $Df_+\circ X$ and restricted to $\mathbb S _-$ coincides with $Df_-\circ X$.

The expression for $\bar{X}(y)$ on $\mathbb S _+\cup \mathbb S _-$ is

$$\begin{aligned} \bar{X}(y)=y_4\left(\begin{array}{c@{\quad }c@{\quad }c} 1-y_1^2&-y_2y_1&-y_3y_1 \\ -y_1y_2&1-y_2^2&-y_3y_2 \\ -y_1y_3&-y_2y_3&1-y_3^2 \\ -y_1y_4&-y_2y_4&-y_3y_4 \\ \end{array}\right)\left(\begin{array}{c} P_1 \\ P_2 \\ P_3 \\ \end{array}\right), \end{aligned}$$

where $P_i=P_i(y_1/|y_4|,y_2/|y_4|,y_3/|y_4|)$. Written in this way, $\bar{X}(y)$ is a vector field in $\mathbb R ^4$ tangent to the sphere $\mathbb S ^3$.

Now, we can analytically extend the vector field $\bar{X}(y)$ to the whole sphere $\mathbb S ^3$ by considering $p(X)=y_4^{m-1}\bar{X}(y)$, where $m$ is the degree of $X$. This extended vector field $p(X)$ is called the Poincaré compactification of $X$ on $\mathbb S ^3$.

As $\mathbb S ^3$ is a differentiable manifold, in order to compute the expression for $p(X)$, we can consider the eight local charts $(\mathcal U _i,F_i),(\mathcal V _i,G_i)$, where $\mathcal U _i=\{y\in \mathbb S ^3;\;y_i>0\}$ and $\mathcal V _i=\{y\in \mathbb S ^3;\;y_i<0\}$ for $i=1,2,3,4;$ the diffeomorphisms $F_i:\,\mathcal U _i\rightarrow \mathbb R ^3$ and $G_i:\,\mathcal V _i\rightarrow \mathbb R ^3$ for $i=1,2,3,4$ are the inverses of the central projections from the origin to the tangent planes at the points $(\pm 1,0,0,0), (0,\pm 1,0,0), (0,0,\pm 1,0)$, and $(0,0,0,\pm 1)$, respectively. Therefore, $F_i(y)=-G_i(y)$. Now, we do the computations on $\mathcal U _1$. Suppose that the origin $(0,0,0,0)$, the point $(y_1,y_2,y_3,y_4)\in \mathbb S ^3$ and the point $(1,z_1,z_2,z_3)$ in the tangent plane to $\mathbb S ^3$ at $(1,0,0,0)$ are collinear. Then, we have $1/y_1=z_1/y_2=z_2/y_3=z_3/y_4$, and consequently, $F_1(y)=(y_2/y_1,y_3/y_1,y_4/y_1)=(z_1,z_2,z_3)$ defines the coordinates on $\mathcal U _1$. As

$$\begin{aligned} DF_1(y)=\left(\begin{array}{c@{\quad }c@{\quad }c@{\quad }c} -y_2/y_1^2&1/y_1&0&0 \\ -y_3/y_1^2&0&1/y_1&0 \\ -y_4/y_1^2&0&0&1/y_1 \\ \end{array}\right) \end{aligned}$$

and $y_4^{m-1}=\left(z_3/\Delta z\right)^{m-1}$, the analytical vector field $p(X)$ becomes

$$\begin{aligned} \frac{z_3^m}{(\Delta z)^{m-1}}\left(-z_1P_1+P_2,-z_2P_1+P_3,-z_3P_1\right), \end{aligned}$$

where $P_i=P_i\left(1/z_3,z_1/z_3,z_2/z_3\right)$.

In a similar way, we can deduce the expression of $p\left(X\right)$ in $\mathcal U _2$ and $\mathcal U _3$. These are

$$\begin{aligned} \frac{z_3^m}{(\Delta z)^{m-1}}\left(-z_1P_2+P_1,-z_2P_2+P_3,-z_3P_2\right), \end{aligned}$$

where $P_i=P_i(z_1/z_3,1/z_3,z_2/z_3)$ in $\mathcal U _2$, and

$$\begin{aligned} \frac{z_3^m}{(\Delta z)^{m-1}}\left(-z_1P_3+P_1,-z_2P_3+P_2,-z_3P_3\right), \end{aligned}$$

where $P_i=P_i(z_1/z_3,z_2/z_3,1/z_3)$ in $\mathcal U _3$.

The expression for $p(X)$ in $\mathcal U _4$ is $z_3^{m+1}(P_1,P_2,P_3)$ where $P_i=P_i(z_1,z_2,z_3)$. The expression for $p(X)$ in the local chart $\mathcal V _i$ is the same as in $\mathcal U _i$ multiplied by $(-1)^{m-1}$.

When we work with the expression of the compactified vector field $p(X)$ in the local charts, we shall omit the factor $1/\left(\Delta z\right)^{m-1}$. We can do that through a rescaling of the time variable.

We remark that all the points on the sphere at infinity $\mathbb S ^2$ in the coordinates of any local chart have $z_3=0$.

In what follows, we shall work with the orthogonal projection of $p(X)$ from the closed northern hemisphere to $y_4=0$ and we continue denoting this projected vector field by $p(X)$. Note that the projection of the closed northern hemisphere is a closed ball $B$ of radius one, whose interior is diffeomorphic to $\mathbb R ^3$ and whose boundary $\mathbb S ^2$ corresponds to the infinity of $\mathbb R ^3$. Of course, $p(X)$ is defined in the whole closed ball $B$ in such a way that the flow on the boundary is invariant. The new vector field on $B$ is called the Poincaré compactification of $X$, and $B$ is called the Poincaré ball, and $\partial B$ is called the Poincaré sphere at infinity.

The singularities at infinity in a Poincaré compactification can be quite degenerate, and sometimes there is the possibility of eliminating this degeneracy doing the so-called Poincaré–Lyapunov compactification. This compactification results to be an extension of the Poincaré compactification presented before, in the sense that we no longer keep the construction homogeneous, but make it quasi-homogeneous. In this context, the construction is very similar to the one done in the Poincaré compactification case and the representation of the vector field in the local charts $\mathcal U _i$ and $\mathcal V _i$ are obtained in the following way: in the local chart $\mathcal U _1$, we consider the coordinates $z_1,\;z_2,\,z_3$ where $x=1/z_3^\alpha ,\;y=z_1/z_3^\beta ,\,z=z_2/z_3^\gamma$. For the local charts $\mathcal U _2$ and $\mathcal U _3$, we take, respectively, $x=z_1/z_3^\alpha ,\;y=1/z_3^\beta ,\,z=z_2/z_3^\gamma$ and $x=z_1/z_3^\alpha ,\;y=z_2/z_3^\beta ,\,z=1/z_3^\gamma$. Observe that the difference between this new compactification and the Poincaré compactification is the presence of the constants $(\alpha ,\beta ,\gamma )$ for some well-choosing positive integer numbers. The correspondent ball $B$ obtained in this extended version is called Poincaré–Lyapunov ball, and its frontier $\partial B$ (that corresponds to the infinity of $\mathbb R ^3$) is called the Poincaré–Lyapunov sphere at infinity.

It is possible that for a system for which the usual Poincaré compactification has a non-elementary singular point at infinity, for well-chosen $\alpha , \beta$, and $\gamma$, the Poincaré–Lyapunov compactification has only elementary singular points at infinity or even no singular points at infinity at all. For more details in this construction, see for instance chapters 5 and 9 of [6].

3 Dynamical behavior of Benoît system at infinity

In this section, we will provide the dynamics of the Benoît system at infinity. For doing this, we will use the Poincaré–Lyapunov compactification with weights $(\alpha ,\beta ,\gamma )=(1,2,1)$.

In order to understand the behavior of the flow at the Poincaré–Lyapunov sphere, we have to describe the flow in each one of the six local charts $\mathcal U _i$ and $\mathcal V _i$ for $i=1,2,3$.

3.1 Local chart $\mathcal U _1$

We call the coordinates in this chart by $(z_1,z_2,z_3)$. In order to obtain the expression of the vector field in this chart, we must take $x=1/z_3, y=z_1/z_3^2$ and $z=z_2/z_3$ and, after this change, multiply the resultant vector field by $z_3$. After doing this, the Poincaré–Lyapunov compactification of the Benoît system in the local chart $\mathcal U _1$ is given by

$$\begin{aligned} \dot{z}_1=4z_1^2+z_3^2,\quad \dot{z}_2=-z_3-z_2^2+2z_1z_2, \quad \dot{z}_3=2z_1z_3. \end{aligned}$$

(3)

Restricting to the points of the Poincaré–Lyapunov sphere that corresponds to the points at infinity ($z_3=0$), the previous system becomes

$$\begin{aligned} \dot{z}_1= 4z_1^2,\quad \dot{z}_2= -z_2(z_2-2z_1),\quad \dot{z}_3= 0. \end{aligned}$$

The last equation reflects the fact that the infinity is invariant under the flow. From this system, we see that the Benoît system has a unique equilibrium point at the origin of the chart $\mathcal U _1$. Moreover, this equilibrium point is degenerate, and after performing a blowing-up, we have the phase portrait given in Fig. 3.

Fig. 3

The phase portrait in the local chart $\mathcal U _1$ at infinity

Observe that the equilibrium point $(0,0,0)$ is located at the end of the positive part of the $x$-axis.

3.2 Local chart $\mathcal U _2$

In a similar way, the Poincaré–Lyapunov compactification of the Benoît system in the local chart $\mathcal U _2$ is

$$\begin{aligned} \dot{z}_1=-4-z_1z_3^2,\quad \dot{z}_2=-2z_1z_3-z_2(2z_2+z_3^2),\quad \dot{z}_3= -z_3^4. \end{aligned}$$

At infinity ($z_3=0$), we have

$$\begin{aligned} \dot{z}_1=-4, \quad \dot{z}_2= -2z_2^2,\quad \dot{z}_3=0. \end{aligned}$$

This system has no equilibrium point and its dynamics is given in Fig. 4.

Fig. 4

The phase portrait in the local chart $\mathcal U _2$ at infinity

Note that in this figure, the invariant line $z_2=0$ is associated with half of the equator of the Poincaré–Lyapunov sphere that is located at the end of the half-plane $\pi _+=\{(x,y,0),$ $y\ge 0\}$.

3.3 Local chart $\mathcal U _3$

In the local chart $\mathcal U _3$, the Poincaré–Lyapunov compactification of the Benoît system is given by

$$\begin{aligned} \dot{z}_1= z_1-2z_2+z_1^2z_3,\quad \dot{z}_2= 2z_2(1+z_1z_3)+z_3^3,\quad \dot{z}_3= z_3(1+z_1z_3). \end{aligned}$$

Restricted to $z_3=0$, we obtain

$$\begin{aligned} \dot{z}_1= z_1-2z_2,\quad \dot{z}_2= 2z_2,\quad \dot{z}_3= 0.\end{aligned}$$

So, this system has a unique equilibrium point in $z_3=0$ at the origin of the local chart $\mathcal U _3$. Moreover, restricted to the invariant set $z_3=0$, we have a hyperbolic node that is unstable. Its phase portrait restrict to $z_3=0$ is given in Fig. 5.

Fig. 5

The local phase portrait at the origin of the local chart $\mathcal U _3$ restricted to $\mathbb S ^2$

Remark 6

We observe that the flows in the $\mathcal V _i$ charts for $i=1,2,3$ are the same than the ones in the respective $\mathcal U _i$ charts for $i=1,2,3$ but reversing the time because the compactified vector field in $\mathcal V _i$ coincides with the vector field in $\mathcal U _i$ multiplied by $-1$ for each $i=1,2,3$.

From the Subsects. 3.1–3.3, it follows the proof of Proposition 1.

4 First integrals of Benoît system, general solution, and local dynamics inside the levels of $H_1$

In this section, we will prove Proposition 2 that shows that the Benoît system admits two independent first integrals. Moreover, we prove Proposition 3 and Corollary 4 where we give an explicit form of the general solution of the Benoît system. We also study the local phase portrait at the equilibrium point on the compactified levels of the first integral $H_1$.

Proof of Proposition 2

First, by dividing the first and third equation of the Benoît system by the second one, we obtain the equivalent system

$$\begin{aligned} \frac{dx}{dy} =-2y,\quad \frac{dz}{dy} =-x-z^2. \end{aligned}$$

Solving this new system, we obtain

$$\begin{aligned}&\begin{array}{c} x(y)=-y^2+H_1, \\ \end{array}\\&\begin{array}{ll} z(y)=&-\frac{2H_2W_1\left(\frac{H_1}{4}+1, \frac{1}{4}, y^2\right)}{y\left(H_2W_1\left(\frac{H_1}{4}, \frac{1}{4}, y^2\right)+W_2\left(\frac{H_1}{4}, \frac{1}{4}, y^2\right)\right)}-\frac{(H_2-2H_2y^2+H_1H_2)W_1\left(\frac{H_1}{4}, \frac{1}{4}, y^2\right)}{2y\left(H_2W_1\left(\frac{H_1}{4}, \frac{1}{4}, y^2\right)+W_2\left(\frac{H_1}{4}, \frac{1}{4}, y^2\right)\right)}\\&+ \frac{(3+H1)W_2\left(\frac{H_1}{4}+1, \frac{1}{4}, y^2\right)}{2y\left(H_2W_1\left(\frac{H_1}{4}, \frac{1}{4}, y^2\right)+W_2\left(\frac{H_1}{4}, \frac{1}{4}, y^2\right)\right)} -\frac{(1-2y^2+H1)W_2\left(\frac{H_1}{4}, \frac{1}{4}, y^2\right)}{2y\left(H_2W_1\left(\frac{H_1}{4}, \frac{1}{4}, y^2\right)+W_2\left(\frac{H_1}{4},\frac{1}{4}, y^2\right)\right)}. \\ \end{array} \end{aligned}$$

Solving the above system with respect to $H_1$ and $H_2$, we obtain the two first integrals given in the statement of Proposition 2. Since their gradients are linearly independent except in a Lebesgue measure set of points of $\mathbb R ^3$, these two first integrals are independent. $\square$

Proof of Proposition 3

Solving the first and second equation of the Benoît system with initial conditions $x(0)=x_0$ and $y(0)=y_0$, we get $x(t)=-t^2-y_0t+x_0$ and $y(t)=t+y_0$.

Substituting these expressions into the third equation of the Benoît system, we obtain $\dot{z}=t^2+y_0t-x_0-z^2$. Now, by solving this Riccati differential equation with initial condition $z(0)=z_0$, we obtain the expression given in the statement of Proposition 3. $\square$

Before proving Corollary 4, we give a general definition of the $\alpha -$ and $\omega -$limit set. It is well known that any solution $\varphi (t)=(x(t),y(t),z(t))$ given in Proposition 3 has a maximal interval of definition $(\alpha ,\omega )$ with $-\infty \le \alpha <0$ and $0<\omega \le +\infty$. We say that a point $y$ is in the $\alpha -$limit set of the orbit $\varphi (t)$ if there exists a strictly decreasing sequence of times $\left(t_n\right)_{n\in \mathbb N }\subset (\alpha ,\omega )$ such that $t_n\rightarrow \alpha$ when $n\rightarrow \infty$ and $\varphi (t_n)\rightarrow y$. In this case, we denote $y\in \mathcal L _\alpha (\varphi )$ and call $\mathcal L _\alpha (\varphi )$ the $\alpha -$ limit set of the orbit $\varphi (t)$. In the same way, we say that a point $y$ is in the $\omega -$limit set of the orbit $\varphi (t)$ if there exists a strictly increasing sequence of times $\left(t_n\right)_{n\in \mathbb N }\subset (\alpha ,\omega )$ such that $t_n\rightarrow \omega$ when $n\rightarrow \infty$ and $\varphi (t_n)\rightarrow y$. In this case, we denote $y\in \mathcal L _\omega (\varphi )$ and call $\mathcal L _\omega (\varphi )$ the $\omega -$ limit set of the orbit $\varphi (t)$.

Remark 7

It is known (see Theorem 2.1 of [7]) that when in the maximal interval of definition $\alpha >-\infty$ (resp. $\omega <+\infty$), then the solution $\varphi (t)$ goes to the boundary of the phase space when $t\rightarrow \alpha$ (when $t\rightarrow \omega$, respectively). In this case, all the points in $\mathcal L _\alpha (\varphi )$ ($\mathcal L _\omega (\varphi )$, respectively) are in the boundary of the phase space.

Proof of Corollary 4

Note that if the solution $\varphi (t)=(x(t),y(t),z(t))$ given in Proposition 3 is such that its maximal interval of definition $(\alpha ,\omega )$ has $\omega =+\infty$, it follows from the first and second coordinates of the solution $\varphi (t)$ that $\varphi (t)$ is unbounded in forward time. On the other hand, if $\omega <+\infty$, it implies from Remark 7 that the solution goes to the boundary of the phase space when $t\rightarrow \omega$. But as the phase portrait of the Benoît system is the whole $\mathbb R ^3$, it follows that also in this case, the solution is unbounded in forward time. Of course, the same argument can be applied in backward time and we can conclude that all the solutions of the Benoît system are unbounded in forward and backward times. $\square$

The next result describes the geometry of the level sets of the first integral $H_1$ in $\mathbb R ^3$ and at infinity.

Proposition 8

For each $h_1\in \mathbb R$, the level surface $H_1=h_1$ is a parabolic cylinder in $\mathbb R ^3$. Moreover, these parabolic cylinders reach the infinity in the half great circle of the Poincaré sphere that is located at the infinity of the half-plane $\hat{\pi }_-=\{(x,0,z);\;x\le 0\}$.

Proof

It is easy to see that for each $h_1\in \mathbb R$, the surface $H_1=h_1$ is a parabolic cylinder in $\mathbb R ^3$. To see how these cylinders arrive at infinity, we have to see the form of these cylinders in the local charts $\mathcal V _1, \mathcal U _3$, and $\mathcal V _3$.

In the local chart $\mathcal V _1$, the level surface $H_1=h_1$ is given by $z_3^2+z_1^2-h_1z_3^4=0$. So, at infinity ($z_3=0$), we have $z_1^2=0$. So, we obtain points of the form $(0,z_2,0)$ that at infinity in this local chart correspond to the end of the half-plane $\hat{\pi }_-=\{(x,0,z),\;x\le 0\}$.

Now, in the local chart $\mathcal U _3$, we have $z_1z_3^3+z_2^2-h_1z_3^4=0$ that at infinity becomes $z_2=0$. So, the parabolic cylinder $x+y^2=h_1$ at infinity in $\mathcal U _3$ is contained in the straight line $(z_1,0,0)$. In this way, the parallel lines contained in the parabolic cylinders reach the infinity in the same point, the origin of the local chart $\mathcal U _3$.

The analysis in the local chart $\mathcal V _3$ follows in a similar way. $\square$

The dynamics of the Benoît system restricted to the levels of the $H_1$ first integral will be provided studying the local behavior around the equilibria that are in each level. For this purpose, we will use the next theorem that describes the topological type of degenerated singularities that have a single nonzero eigenvalue in the plane. This kind of singularities will be called semi-hyperbolic singularities. A proof of this result can be found in Theorem 2.19 of [6].

Theorem 9

Let $(0,0)$ be an isolated singularity of the system

$$\begin{aligned} \begin{array}{ll} \dot{x}&=X_1(x,y), \\ \dot{y}&=y+X_2(x,y), \\ \end{array} \end{aligned}$$

where $X_1$ and $X_2$ are analytic in a neighborhood of the origin and have expansions that begin with two-degree terms in $x$ and $y$. Let $y=f(x)$ be the solution of the equation $y+X_2(x,y)=0$ in the neighborhood of $(0,0)$ and assume that the series expansion of the function $g(x)=X_1(x,f(x))$ has the form $g(x)=a_mx^m+\ldots$, where $m\ge 2,a_m\ne 0$. Then,

• (i) If $m$ is odd and $a_m>0$, then $(0,0)$ is a topological node.

• (ii) If $m$ is odd and $a_m<0$, then $(0,0)$ is a topological saddle, two of whose separatrices tend to $(0,0)$ in the directions $0$ and $\pi$, the other two in the directions $\pi /2$ and $3\pi /2$.

• (iii) If $m$ is even, then $(0,0)$ is a saddle-node, that is, a singularity whose neighborhood is the union of one parabolic and two hyperbolic sectors, two of whose separatrices tend to $(0,0)$ in the directions $\pi /2$ and $3\pi /2$ and the other in the direction $0$ and $\pi$ according to $a_m<0$ or $a_m>0$.

The corresponding indices are $+1, -1,0$ so they may serve to distinguish the three types.

Going back to the Benoît system observe that for each $h_1$, the surface $H_1=h_1$ has in the Poincaré sphere three singular points where two of them are hyperbolic nodes (the equilibria $(0,0,1)\in \mathbb S ^2$ and $(0,0,-1)\in \mathbb S ^2$) and one is semi-hyperbolic (the equilibrium $(-1,0,0)\in \mathbb S ^2$).

Now, we have to study the local dynamics of the semi-hyperbolic singularity at the equator. This dynamics will be provided by the next result.

Proposition 10

For each fixed $h_1$, the semi-hyperbolic singularity $(-1,0,0)\in \mathbb S ^2$ in the level $H_1=h_1$ has two nodal sectors and two hyperbolic sectors. More precisely, the local phase portrait at $(-1,0,0)\in \mathbb S ^2$ and restricted to $H_1=h_1$ is described in Fig. 6.

Fig. 6

Local phase portrait at the equilibrium point $(-1,0,0)\in \mathbb S ^2$ on the level $H_1=h_1$. In the picture, we have indicated with the symbol $\infty$ the local invariant straight line of the parabolic cylinder at infinity. Picture (b) is the origin in coordinates $z_1,z_2$ and picture (a) (resp. (c)) is the origin in coordinates $z_2,\theta$ see (14) (resp. (10))

Proof

In order to study the local dynamics in a neighborhood of $(-1,0,0)\in \mathbb S ^2$ on the level $H_1=h_1$, we consider the local chart $\mathcal V _1$. In this chart, we take the coordinates given by the Poincaré compactification

$$\begin{aligned} x=\frac{1}{z_3},\quad y=\frac{z_1}{z_3},\quad z=\frac{z_2}{z_3}. \end{aligned}$$

Observe that the dynamics at the end of the half-plane $\hat{\pi }_-=\{(x,0,z);\;x\le 0\}$ in these coordinates is the same one obtained using the Poincaré–Lyapunov compactification. So $H_1$ takes the form

$$\begin{aligned} z_3+z_1^2-h_1z_3^2=0. \end{aligned}$$

(4)

Moreover, the dynamics in the local chart $\mathcal V _1$ is given by

$$\begin{aligned} \begin{array}{lll} \dot{z}_1&=-z_3(2z_1^2+z_3)&=f_1(z_1,z_2,z_3), \\ \dot{z}_2&=z_2^2+z_3-2 z_1z_2z_3&=f_2(z_1,z_2,z_3), \\ \dot{z}_3&=-2z_1z_3^2&=f_3(z_1,z_2,z_3). \\ \end{array} \end{aligned}$$

(5)

Note that the equilibrium at the infinity $(-1,0,0)\in \mathbb S ^2$ is represented in this local chart by $(0,0,0)$.

Now, we will divide the study in three cases depending on $h_1$.

• Case 1: $h_1=0$ (parabolic cylinder). In this case, (4) takes the form $z_3+z_1^2=0$. Substituting $z_3=-z_1^2$ in (5), we obtain that the dynamics in the level $H_1=0$ is given by

  $$\begin{aligned} \begin{array}{ll} \dot{z}_1&=f_1(z_1,z_2,-z_1^2)=z_1^4, \\ \dot{z}_2&=f_2(z_1,z_2,-z_1^2)=z_2^2-z_1^2+2z_1^3z_2. \\ \end{array} \end{aligned}$$

  (6)

In this differential system, the origin $(0,0)$ has the eigenvalue $0$ with multiplicity 2. In order to understand the behavior of the flow of (6) in a neighborhood of $(0,0)$, we will use a polar blowup. So, doing the change of variables $z_1=r_1\cos \theta _1, z_2=r_1\sin \theta _1$ and the rescaling of the time $s=r_1t$, system (6) becomes

$$\begin{aligned} \begin{array}{ll} r_1^{\prime }&=r_1\left(r_1^2 \cos ^5\theta _1+2 r_1^2 \sin ^2\theta _1 \cos ^3\theta _1-\sin \theta _1 \cos ^2\theta _1+\sin ^3\theta _1\right),\\ \theta _1^{\prime }&=\cos \theta _1 \left(r_1^2 \sin \theta _1 \cos ^3\theta _1-\cos ^2\theta _1+\sin ^2\theta _1\right), \\ \end{array} \end{aligned}$$

(7)

where the prime denotes the derivative with respect to the new time $s$.

Now, we study the zeroes of (7) restricted to $r_1=0$. For this, we solve $\theta _1^{\prime }=0, r_1=0$ that implies that

$$\begin{aligned} \theta _1=\pm \frac{\pi }{4},\pm \frac{\pi }{2},\pm \frac{3\pi }{4}. \end{aligned}$$

We must analyze the topological type of each one of these singularities.

Calling $X$ the vector field (7), we have for $\theta _1^*=\frac{\pi }{4}$

$$\begin{aligned} DX\left(0,\frac{\pi }{4}\right)= \left(\begin{array}{l@{\quad }l} 0&0 \\ 0&\sqrt{2} \\ \end{array}\right). \end{aligned}$$

So, $\left(0,\frac{\pi }{4}\right)$ is a semi-hyperbolic singularity of (7) and to decide about its topological type we use Theorem 9.

By a translation of the form $R_1=r_1$ and $\phi _1=\theta _1-\frac{\pi }{4}$ and a time reparametrization $\tau =\sqrt{2}\,s$, we obtain

$$\begin{aligned} \begin{array}{ll} \dot{R}_1=&\frac{1}{4}\left(\cos \phi _1-\cos (3 \phi _1)+ \sin \phi _1+\sin (3 \phi _1)\right)R_1+\\&\frac{\sqrt{2}}{2}\left(\cos ^5\left(\phi _1+\frac{\pi }{4}\right)\!+\!2 \sin ^2\left(\phi _1+\frac{\pi }{4}\right) \cos ^3\left(\phi _1+\frac{\pi }{4}\right)\right)R_1^3\!+\!O\left(R_1^4\right)\!= \!X_1(R_1,\phi _1),\\ \dot{\phi }_1=&\frac{1}{4} \left(-\cos \phi _1+\cos (3 \phi _1)+\sin \phi _1+\sin (3 \phi _1)\right)\\&+\frac{1}{\sqrt{2}} \cos ^4\left(\phi _1+\frac{\pi }{4}\right) \sin \left(\phi _1+\frac{\pi }{4}\right) R_1^2+O\left(R_1^4\right)=\tilde{X}_2(R_1,\phi _1),\\ \end{array} \end{aligned}$$

and the dots denotes derivative with respect to $\tau$.

Expanding $\tilde{X}_2(R_1,\phi _1)$ in Taylor series of $\phi _1$around $0$, we obtain $\tilde{X}_2(R_1,\phi _1)=\phi _1+X_2(R_1,\phi _1)$, where $X_2$ has terms of second order in $R_1$ and $\phi _1$. Solving $\phi _1+X_2(R_1,\phi _1)=0$ for $\phi _1$ as a function of $R_1$ in a neighborhood of $0$, we obtain

$$\begin{aligned} \phi _1=-\frac{1}{8}R_1^2+O\left(R_1^4\right)=f(R_1). \end{aligned}$$

Substituting in $X_1(R_1,\phi _1)$, we have

$$\begin{aligned} g(R_1)=X_1(R_1,f(R_1))=\frac{1}{4}R_1^3+O\left(R_1^4\right). \end{aligned}$$

Using the notation of Theorem 9, we have that $m=3$ and $a_3=\frac{1}{4}>0$. It follows from Theorem 9(i) that $(0,0)$ is a topological node.

Repeating this procedure for the equilibrium $\left(0,-\frac{\pi }{4}\right)$, also semi-hyperbolic, we get

$$\begin{aligned} g(R_1)=-\frac{1}{4}R_1^3+O\left(R_1^4\right). \end{aligned}$$

Then, Theorem 9 implies that the equilibrium is a topological saddle.

Consider now the equilibria $\left(0,\pm \frac{\pi }{2}\right)$. For these equilibria, the Jacobian matrix satisfies

$$\begin{aligned} DX\left(0,\pm \frac{\pi }{2}\right)=\left(\begin{array}{cc} \pm 1&0 \\ 0&\mp 1 \\ \end{array}\right). \end{aligned}$$

So, these two equilibria are hyperbolic saddles with expanding (resp. contracting) radial direction for $\left(0,\frac{\pi }{2}\right) \left(\text{ resp.} \left(0,-\frac{\pi }{2}\right)\right)$.

Taking into account the equilibria $\left(0,\pm \frac{3\pi }{4}\right)$, we have

$$\begin{aligned} DX\left(0,\pm \frac{3\pi }{4}\right)=\left(\begin{array}{l@{\quad }l} 0&0 \\ 0&\pm \sqrt{2}\\ \end{array}\right), \end{aligned}$$

and so both equilibria are semi-hyperbolic. Therefore, we can use again Theorem 9 for deciding about their topological type.

Similar calculations to the ones done for the equilibrium $\left(0,\frac{\pi }{4}\right)$ show that for $\left(0,\frac{3\pi }{4}\right)$, the function $g$ is given by $g(R_1)=-\frac{R_1^2}{8}+O\left(R_1^4\right)$, and $f(R_1)=-\frac{R_1^3}{4}+O\left(R_1^4\right)$ that implies from Theorem 9 that $\left(0,\frac{3\pi }{4}\right)$ is a topological saddle. Also, $\left(0,-\frac{3\pi }{4}\right)$ is such that $g(R_1)=-\frac{1}{8}R_1^2+O\left(R_1^4\right)$, and $f(R_1)=\frac{R_1^3}{4}+O\left(R_1^4\right)$, and from Theorem 9, it follows that $\left(0,-\frac{3\pi }{4}\right)$ is a topological node.

Finally, for the case $h_1=0$, the local phase portrait after a polar blowup is given in Fig. 7.

Fig. 7

The radial blowup at the equilibrium $(-1,0,0)\in \mathbb S ^2$ restricted to the level $H_1=0$

This implies that the local phase portrait of system (6) in a neighborhood of $(0,0)$ is given by Fig. 6b.

For the next steps consider $h_1\ne 0$. Here, we can write (4) as

$$\begin{aligned} \frac{z_1^2}{-\frac{1}{4h_1}}+\frac{\left(z_3- \frac{1}{2h_1}\right)^2}{\frac{1}{4h_1^2}}=1. \end{aligned}$$

(8)

Equation (8) implies that the invariant surfaces $H_1=h_1$ are represented in the local chart $\mathcal V _1$ by a hyperbolic cylinder if $h_1>0$ or by an elliptic cylinder if $h_1<0$.

• Case 2: $h_1>0$ (hyperbolic cylinder). In this case, Eq. (8) becomes

  $$\begin{aligned} -\frac{z_1^2}{a^2}+\frac{\left(z_3-b\right)^2}{b^2}=1 \end{aligned}$$

  (9)

  where $a=\sqrt{\frac{1}{4h_1}}$ and $b=\frac{1}{2h_1}$.

Performing the change of coordinates

$$\begin{aligned} z_1=ar\sinh \theta ,\quad z_2=z_2\quad \text{ and}\quad z_3=b-br\cosh \theta \end{aligned}$$

(10)

system (5) becomes

$$\begin{aligned} \begin{array}{ll} \dot{r}&=\frac{b}{a}(r \cosh \theta -1) \left(2 a^2 r^2+\left(b-2 a^2\right)r \cosh \theta -b\right) \sinh \theta ,\\ \dot{z}_2&=z_2^2+2 a b rz_2 (r \cosh \theta -1) \sinh \theta +b-b r \cosh \theta , \\ \dot{\theta }&=-\frac{b}{2ar} (r \cosh \theta -1) \left(r \left(2 a^2+b+\left(b-2 a^2\right) \cosh (2 \theta )\right)-2 b \cosh \theta \right) \\ \end{array} \end{aligned}$$

(11)

and (9) is given by $r^2=1$.

Observe that the equilibrium $(z_1,z_2,z_3)=(0,0,0)$ in the local chart $\mathcal V _1$ now is given, in the new coordinates by $(r,z_2,\theta )=(1,0,0)$. As we want to study the dynamics in a neighborhood of $(1,0,0)$ restricted to the level surface $r=1$, we can restrict to the reduced system

$$\begin{aligned} \begin{array}{ll} \dot{z}_2&=z_2^2+2 a b z_2(\cosh \theta -1) \sinh \theta +b-b \cosh \theta , \\ \dot{\theta }&=\frac{4b}{a} \left(2 a^2+\left(2 a^2-b\right) \cosh \theta \right) \sinh ^4\left(\theta /2\right). \\ \end{array} \end{aligned}$$

Now, we have to investigate the topological type of the equilibrium $(0,0)$ of this system. This equilibrium has all the eigenvalues zero and so we must use the blow-up technic again. Taking $z_2=r_1\cos \theta _1$ and $\theta =r_1\sin \theta _1$, the previous system becomes

$$\begin{aligned} \begin{array}{ll} \dot{r}_1=&8 a b \sin \theta _1 \sinh ^4\left(\frac{r_1}{2}\sin \theta _1\right)\\&+\cos \theta _1 \left(r_1^2 \cos ^2\theta _1+a b r_1 (\sinh (2 r_1 \sin \theta _1)-2 \sinh (r_1 \sin \theta _1)) \cos \theta _1+b\right)\\&-\frac{b}{a }\cosh (r_1 \sin \theta _1) \left(4 \left(b-2 a^2\right) \sin \theta _1 \sinh ^4\left(\frac{1}{2} r_1 \sin \theta _1\right)+a \cos \theta _1\right),\\ \dot{\theta }_1=&\frac{4 b}{ar_1} \cos \theta _1 \left(2 a^2+\left(2 a^2-b\right) \cosh (r_1 \sin \theta _1)\right) \sinh ^4\left(\frac{1}{2} r_1 \sin \theta _1\right)\!-\!r_1\sin \theta _1\cos ^2(\theta _1)\\&-\frac{\sin \theta _1}{r_1} \left(2 a b r_1 (\cosh (r_1 \sin \theta _1)-1) \sinh (r_1 \sin \theta _1) \cos \theta _1+b\!-\!b \cosh (r_1 \sin \theta _1)\right). \\ \end{array} \end{aligned}$$

(12)

Expanding both equations of system (12) in Taylor series of $r_1$ and rescaling $s=r_1t$, system 12 writes

$$\begin{aligned} \begin{array}{ll} r_1^{\prime }&=\left(\cos ^3\theta _1-\frac{b \cos \theta _1 \sin ^2\theta _1}{2 }\right) r_1+O\left(r_1^3\right), \\ \theta _1^{\prime }&= \frac{b \sin ^3\theta _1-2 \cos ^2\theta _1 \sin \theta _1}{2 }+\left(\frac{b \sin ^5\theta _1}{24}-\frac{b^2 \cos \theta _1 \sin ^4\theta _1}{4 a}\right) r_1^2+O\left(r_1^3\right),\\ \end{array} \end{aligned}$$

where the prime denotes derivative with respect to the new time $s$.

Now, as in the case $h_1=0$, we have to study the zeroes of this system restricted to $r_1=0$. By solving $\theta _1^{\prime }=0$ and $r_1=0$, we get

$$\begin{aligned} \theta _1=0,\;\;\arctan \sqrt{\frac{2}{b}},\;\;\pi - \arctan \sqrt{\frac{2}{b}},\;\;\pi ,\;\;\pi +\arctan \sqrt{\frac{2}{b}},\;\; -\arctan \sqrt{\frac{2}{b}}. \end{aligned}$$

Again, we have to study each one of these equilibria separately in order to obtain the dynamics in a neighborhood of $(0,0)$.

We begin with the equilibrium $(r_1^*,\theta _1^*)=(0,0)$ of the previous system. For this equilibrium, we have $DX(0,0)=\left(\begin{array}{cc} 1&0 \\ 0&-1 \\ \end{array}\right)$. So $(0,0)$ is a hyperbolic saddle with expanding radial direction. For $(r_1^*,\theta _1^*)=(0,\pi )$, we obtain $DX(0,\pi )=\left(\begin{array}{cc} - 1&0 \\ 0&1 \\ \end{array}\right)$ and this equilibrium is also a hyperbolic saddle but with contracting radial direction.

Now, $(r_1^*,\theta _1^*)=\left(0,\arctan \sqrt{\frac{2}{b}}\right)$. Here, $DX\left(0,\arctan \sqrt{\frac{2}{b}}\right)=\left(\begin{array}{cc} 0&0 \\ 0&\frac{2}{\sqrt{\frac{2+b}{b}}} \\ \end{array}\right)$. And as in case 1, we have a semi-hyperbolic equilibrium point. So we use one more time Theorem 9 for deciding about the topological type of this singularity.

By a translation of the form $r_1=R_1, \theta _1=\phi _1+\arctan \sqrt{\frac{2}{b}}$ and the time reparametrization $\tau =\sqrt{\frac{2+b}{b}} t$, we find

$$\begin{aligned} \begin{array}{ll} R_1^{\prime }&=X_1(R_1,\phi _1), \\ \phi _1^{\prime }&=\phi _1+X_2(R_1,\phi _2), \\ \end{array} \end{aligned}$$

where

$$\begin{aligned} \begin{array}{ll} X_1(R_1,\phi _1)=&-\frac{b}{4} \sqrt{\frac{b+2}{b}} \cos \left(\phi _1+\arctan \sqrt{\frac{2}{b}}\right) \sin ^2\left(\phi _1+\arctan \sqrt{\frac{2}{b}}\right)R_1 \\&+\frac{1}{2}\sqrt{\frac{b+2}{b}}\cos ^3 \left(\phi _1+\arctan \sqrt{\frac{2}{b}}\right) R_1+O\left(R_1^3\right),\\ \end{array} \end{aligned}$$

and $\phi _1+X_2(R_1,\phi _2)$ is

$$\begin{aligned} \begin{array}{l} \frac{1}{4} \sqrt{\frac{b+2}{b}} \left(b \sin ^3\left(\phi _1+\arctan \sqrt{\frac{2}{b}}\right)-2 \cos ^2\left(\phi _1+\arctan \sqrt{\frac{2}{b}}\right) \sin \left(\phi _1+ \arctan \sqrt{\frac{2}{b}}\right)\right) \\ \!-\!\frac{b}{48a} \sqrt{\frac{b+2}{b}} \sin ^4\!\left(\phi _1+\arctan \sqrt{\frac{2}{b}}\right) \!\left(6 b \cos \left(\phi _1\!+\!\arctan \sqrt{\frac{2}{b}}\right)\!-\!a \sin \left(\phi _1\!+\!\arctan \sqrt{\frac{2}{b}}\right)\right)\!R_1^2\\ \!+\,O\left(R_1^4\right). \\ \end{array} \end{aligned}$$

Solving $\phi _1+X_2(R_1,\phi _2)=0$ for $\phi _1$ as a function of $R_1$ in a neighborhood of $0$, we have

$$\begin{aligned} \begin{array}{ll} \phi _1=&f(R_1)=-\frac{b\left(a\sqrt{2}{b}-6b\right)}{12a(2+b)^2} R_1^2+ \\&\frac{b\left(-320 (b+2) a^3\!+\!\sqrt{\frac{2}{b}} (9 b-2) a^2\!+\!40 b (5 b+16) a+30 \sqrt{2} (5 b-2) b^{5/2}\right)}{480 a^2 (b+2)^4}R_1^4\\&+O\left(R_1^5\right) \\ \end{array} \end{aligned}$$

and so

$$\begin{aligned} g(R_1)=X_1(R_1,f(R_1))=-\frac{b-4 a^2}{2a(b+2)\sqrt{\frac{2}{b}}}R_1^3+O\left(R_1^4\right). \end{aligned}$$

Now observe that $a_3=-\frac{\left(b-4 a^2\right)}{2a(b+2)\sqrt{\frac{2}{b}}}>0$ because $h_1>0$. So, from Theorem 9, $\left(0,\arctan \sqrt{\frac{2}{b}}\right)$ is a topological node.

It is not difficult to see that for the equilibrium $\left(0,-\arctan \sqrt{\frac{2}{b}}\right)$, we have $DX\left(0,-\arctan \sqrt{\frac{2}{b}}\right)=\left(\begin{array}{cc} 0&0 \\ 0&\frac{2}{\sqrt{\frac{2+b}{b}}} \\ \end{array}\right)$, and in a similar way, we obtain for this equilibrium $g(R_1)=X_1(R_1,f(R_1))= \frac{b-4 a^2}{2a(b+2)\sqrt{\frac{2}{b}}}R_1^3+O\left(R_1^4\right)$. From Theorem 9, we get that $\left(0,-\arctan \sqrt{\frac{2}{b}}\right)$ is a topological saddle.

Consider now the equilibrium $\left(0,\pi +\arctan \sqrt{\frac{2}{b}}\right)$. Here, we have

$DX\left(0,\pi +\arctan \sqrt{\frac{2}{b}}\right)=\left(\begin{array}{cc} 0&0 \\ 0&-\frac{2}{\sqrt{\frac{2+b}{b}}} \\ \end{array}\right)$. Similar calculations show that for this case, we obtain

$$\begin{aligned} \begin{array}{ll} \phi _1=&f(R_1)=-\frac{b\left(a\sqrt{2}{b}-6b\right)}{12a(2+b)^2} R_1^2 \\&+\frac{b \left(-320 (b+2) a^3+ \sqrt{\frac{2}{b}} (9 b-2) a^2+40 b (5 b+16) a+30 \sqrt{2} (5 b-2) b^{5/2}\right) }{480 a^2 (b+2)^4}R_1^4\\&+O\left(R_1^5\right), \\ \end{array} \end{aligned}$$

and

$$\begin{aligned} g(R_1)=X_1(R_1,f(R_1))=-\frac{b-4 a^2}{2a(b+2)\sqrt{\frac{2}{b}}}R_1^3+O\left(R_1^5\right). \end{aligned}$$

As $a_3=-\frac{b-4 a^2}{2a(b+2)\sqrt{\frac{2}{b}}}>0$ for $h_1>0$, it follows from Theorem 9 that the equilibrium $\left(0,\pi +\arctan \sqrt{\frac{2}{b}}\right)$ is a topological node. In the same way, we can show that the equilibrium $\left(0,\pi -\arctan \sqrt{\frac{2}{b}}\right)$ is a topological saddle.

Altogether, for the case $h_1>0$, the local phase portrait after a polar blowup is given in Fig. 8.

Fig. 8

The radial blowup at the equilibrium $(-1,0,0)\in \mathbb S ^2$ restricted to the level $H_1=h_1>0$

So the dynamics restricted to the level $H_1=h_1$ in a neighborhood of the equilibrium at infinity $(-1,0,0)\in \mathbb S ^2$ is given by Fig. 6c.

• Case 3: $h_1<0$ (elliptic cylinder). In this case, Eq. (8) becomes

  $$\begin{aligned} \frac{z_1^2}{a^2}+\frac{\left(z_3-b\right)^2}{b^2}=1. \end{aligned}$$

  (13)

  Here, performing a change of coordinates of the form

  $$\begin{aligned} z_1=ar\cos \theta ,\quad z_2=z_2\quad \text{ and}\quad z_3=b+br\sin \theta \end{aligned}$$

  (14)

  we obtain a system very near to the system studied in case 2. The proof for this case is very close to the proof of case 2 and will be omitted.

$\square$

From the above proposition, we are in condition to prove Theorem 5. This will be done in the next section.

5 Proof of Theorem 5

The proof of Theorem 5 will be divided into two parts. First, we prove that all the possible configurations of the phase portrait restricted to the levels of the first integral $H_1$ are the ones given in Fig. 2. In the second step, we provide solutions of the Benoît system that shows that the three possible cases in fact occur at different levels of $H_1$.

Proof of the first part of Theorem 5

By the Poincaré-Bendixon theorem (see for instance [6]) at the compactified level $H_1=h_1$ inside the Poincaré ball, the only possible $\alpha -$ and $\omega -$limit sets of any orbit of the level set $H_1=h_1$ is an equilibrium point. Note that at $H_1=h_1$, there are exactly three equilibrium points which are the northern and southern poles that are hyperbolic nodes and the semi-hyperbolic equilibrium at $(-1,0,0)\in \mathbb S ^2$ which local dynamics is given by Proposition 10.

From the local dynamics of $(-1,0,0)\in \mathbb S ^2$ (see Proposition 6) in the level $H_1=h_1$, we note that there are two nodal zones with one attracting and other repeller. So if an orbit visits both nodal zones, this orbit is homoclinic for the equilibrium $(-1,0,0)\in \mathbb S ^2$, being an orbit of disconnecting type. Moreover, in this case, we can have a unique homoclinic orbit to $(-1,0,0)\in \mathbb S ^2$ (Fig. 2b) or a continuous of homoclinic orbits to $(-1,0,0)\in \mathbb S ^2$ (Fig. 2a). Note that the existence of two homoclinic orbits to $(-1,0,0)\in \mathbb S ^2$ in a same level $H_1=h_1$ implies the existence of a continuum of such orbits. Note that if such an orbit exists, it disconnects the cylinder $H_1=h_1$ into two connected components being one containing the northern pole and the other containing the southern pole. In this case, all the orbits in the connected component that contains the northern pole are such that their $\omega -$limit set is the equilibrium $(-1,0,0)\in \mathbb S ^2$, and their $\alpha -$limit set is either the northern pole and we have an heteroclinic orbits connecting the norther pole and the equilibrium $(0,0,1)$ (orbit of intermediate type), or the $\alpha -$limit set is the equilibrium $(-1,0,0)$ and we have a homoclinic orbit to $(-1,0,0)\in \mathbb S ^2$ (orbit of disconnecting type).

Similar analysis can be done for the orbits in the region that contain the southern pole and again we obtain orbits of intermediate type or disconnecting type.

Now, if the Benoît system does not admit homoclinic orbits for the equilibrium $(-1,0,0)$ at the level $H_1=h_1$, then all the orbits that have the northern pole as $\alpha -$limit set can have either $(-1,0,0)$ as $\omega -$limit and we obtain an orbit of intermediate type, or the southern pole as $\omega -$limit, and in this case, we obtain an orbit of passage type. $\square$

The next proposition provides an example where all the three different phase portraits for the levels $H_1=h_1$ are present in a Benoît system. So, we obtain the second part of Theorem 5.

Proposition 11

The Benoît system realizes the three different phase portraits for the levels $H_1=h_1$ described in Fig. 2.

Proof

By solving the Benoît system with initial condition $(0,0,z_0)$, we obtain

$$\begin{aligned} \varphi (t,z_0)=(x(t),y(t),z(t))=(-t^2,t,z(t,z_0)), \end{aligned}$$

(15)

with

$$\begin{aligned} z(t,z_0)=\left\{ \begin{array}{ll} \frac{\frac{\left(-\sqrt{2}\pi t\Gamma \left(\frac{3}{4}\right)^2+\pi ^2 z_0t\right)J_1\left(-\frac{3}{4}, \frac{t^2}{2}\right)}{\Gamma \left(\frac{3}{4}\right)^2}+2tJ_2\left(\frac{3}{4}, \frac{t^2}{2}\right)}{\frac{\left(-\sqrt{2}\pi \Gamma (\frac{3}{4})^2+\pi ^2z_0\right)J_1\left(\frac{1}{4}, \frac{t^2}{2}\right)}{\Gamma \left(\frac{3}{4}\right)^2}-2J_2\left(\frac{1}{4}, \frac{t^2}{2}\right)}&\mathrm{{if}}\;t<0,\\ z_0&\mathrm{{if}}\; t=0,\\ \frac{\frac{\left(\sqrt{2}\pi t\Gamma (\frac{3}{4})^2+\pi ^2 z_0t\right)J_1\left(-\frac{3}{4}, \frac{t^2}{2}\right)}{\Gamma \left(-\frac{3}{4}\right)^2}-2tJ_2\left(\frac{3}{4}, \frac{t^2}{2}\right)}{\frac{\left(\sqrt{2}\pi \Gamma (\frac{3}{4})^2+\pi ^2z_0\right)J_1\left(\frac{1}{4}, \frac{t^2}{2}\right)}{\Gamma \left(\frac{3}{4}\right)^2}-2J+2\left(\frac{1}{4}, \frac{t^2}{2}\right)}&\mathrm{{if}}\;t>0, \\ \end{array} \right. \end{aligned}$$

where the function $\Gamma (\nu )$ is the Gamma and the functions $J_1(\nu ,s)$ and $J_2(\nu ,s)$ are the modified Bessel functions of the first end second kinds, respectively. They satisfy the Bessel equation $s^2\ddot{y}+s\dot{y}+(s^2+\nu ^2)y=0$ (see for more detail [1]). Moreover, for this solution, we get $\lim _{t\rightarrow \pm \infty }z(t,z_0)/x(t)= \lim _{t\rightarrow \pm \infty }-z(t,z_0)/t^2=0$. This implies that in the local chart $\mathcal V _1$, this solution satisfies $z_1(t)=y(t)/x(t)\rightarrow 0$ when $t\rightarrow \pm \infty$ and $z_2(t)=z(t,z_0)/x(t)\rightarrow 0$ when $t\rightarrow \pm \infty$. Observing that the singularity at infinity $(-1,0,0)\in \mathbb S ^2$ is represented in the local chart $\mathcal V _1$ by the origin $(0,0,0)$, it follows that this solution is homoclinic to $(-1,0,0)\in \mathbb S ^2$ for each $z_0\in \mathbb R$. In this way, we have proved that the Benoît system has a phase portrait like Fig. 2a at the level $H_1=0$ (note that the solutions (15) are inside the level $H_1=0$).

On the other hand, by solving the Benoît system with initial condition $(x_0,y_0,z_0)=(2,0,0)$, we obtain

$$\begin{aligned} \varphi (t,x_0)=(x(t,x_0),y(t),z(t,x_0))=(-t^2+2,t,z(t)) \end{aligned}$$

(16)

where $z(t)$ is

$$\begin{aligned} \frac{\left(1\!-\!t^2\right)\pi J_1\left(\!-\!\frac{1}{4}, \!-\!\frac{t^2}{2}\right)\!+\!\left(-1\!+\!t^2\right)\sqrt{2}J_2\left(\frac{1}{4}, \!-\!\frac{t^2}{2}\right)\!-\!t^2\left(\sqrt{2}J_2\left(\frac{3}{4}, \!-\!\frac{t^2}{2}\right)\!+\!\pi J_1\left(\frac{3}{4}, -\frac{t^2}{2}\right)\right)}{t\left(-\sqrt{2}J_2\left(\frac{1}{4}, -\frac{t^2}{2}\right)+\sqrt{2}J_2\left(\frac{3}{4}, -\frac{t^2}{2}\right)+\pi J_1\left(-\frac{1}{4}, -\frac{t^2}{2}\right)+\pi J_1\left(\frac{3}{4}, -\frac{t^2}{2}\right)\right)} \end{aligned}$$

The denominator of this function has zeroes in $t_-\approx -1.162342261$ and $t_+\approx 1.16234226158$ moreover $\lim _{t\searrow t_-}z(t,2)=\infty$ and $\lim _{t\nearrow t_+}z(t,2)=-\infty$. This implies that this solution is a heteroclinic solution connecting the point $(0,0,1)\in \mathbb S ^2$ and $(0,0,-1)\in \mathbb S ^2$. So, the Benoît system has a phase portrait like Fig. 2c at the level $H_1=2$ (solution (16) is inside the level $H_1=2$).

These two particular solutions show that the Benoît system admits the three possible phase portraits given in Fig. 2. $\square$

Remark 12

It is not difficult to see that for the system in Proposition 11, a bifurcation in the phase portrait occurs for the value of the parameter $h_1=1$. In fact, for $h_1=1$, we have a unique homoclinic solution for the equilibrium point $(-1,0,0)\in \mathbb S ^2$ given by $\varphi (t)=(-t^2+1,t,-t)$ and for $h_1=1+\delta$ for $\delta >0$ sufficiently small; there is no homoclinic orbit at this level.

Remark 13

The computations of this paper has been checked with the help of the algebraic manipulator mathematica.