Dynamics of the Painlevé-Ince Equation

Abstract

The Painlevé-Ince differential equation $y'' + 3 y y' + y^3=0$ has been studied from many points of view. Here we complete its study providing its phase portrait in the Poincaré disc.

1 Introduction and Statement of the Main Results

The Painlevé-Ince differential equation

$$\begin{aligned} \frac{d^2y}{dt^2} + 3y\frac{dy}{dt} + y^3 = 0, \end{aligned}$$

(1)

has been studied for several authors due to its interesting properties:

• (i) It has eight Lie point symmetries with the Lie Algebra sl(2, R) consequently through a point transformation it is linearisable, see [12].

• (ii) It has a Riccati hierarchy based on the Riccati differential equation with the operator $\frac{d}{dy} +y$, see [5].

• (iii) It satisfies the Painlevé property, see [11].

• (iv) Its left Painlevé series together with its well known right Painlevé series have been studied in [6, 7, 9].

• (v) Its mixed Painlevé series together with their geometric interpretations were studied in [2, 8].

Extensions of the Painlevé-Ince differential Eq. (1) can be found in [10].

It is easy to check that the general solution of the Painlevé-Ince differential Eq. (1) is

$$\begin{aligned} y(t)=\frac{2 a (b+t)}{3+a b^2+2 a b t+a t^2}, \end{aligned}$$

where a and b are arbitrary constants. From this general solution we can determine the constants a and b for each particular solution y(t) such that $y(t_0)=y_0$ and $y'(t_0)=y'_0$. But to know these explicit solutions, it is not easy to determine the qualitative properties of these solutions, i.e. where they are born, where they die tells, if they define homoclinic orbits, or heteroclinic orbits, ...

In order to describe the dynamics of the Painlevé-Ince differential Eq. (1) we write this second order differential equation as the system of first order

$$\begin{aligned} \begin{array}{l} \dfrac{dx}{dt}= x'= -3 y x - y^3, \\ \dfrac{dy}{dt}= y'= x. \end{array} \end{aligned}$$

(2)

This differential system has the first integral

$$\begin{aligned} H(x,y)= \frac{\left( x+y^2\right) ^2}{2 x+y^2}, \end{aligned}$$

(3)

as it is easy to verify. But again it is not trivial to describe the dynamics of the orbits of the Painlevé-Ince differential Eq. (1) using this first integral.

Here we one to complete the studies on the Painlevé-Ince differential equation describing the dynamics of its differential system (2) in the Poincaré disc. The Poincaré disc is the closed unit disc centered at the origin of coordinates of $\mathbb {R}^2$, where its interior is identified with the whole plane $\mathbb {R}^2$ and its boundary (the circle $\mathbb {S}^1$) is identified with the infinity of $\mathbb {R}^2$. Note that in the plane $\mathbb {R}^2$ we can go to infinity in as many as directions as points has the circle $\mathbb {S}^1$. For a detailed introduction of the Poincaré disc see subsect. 2.2.

Fig. 1

The phase portrait of the differential system (2) in the Poincaré disc

Our main result is the follwing one.

Theorem 1

The phase portrait of the Painlevé-Ince differential system (2) in the Poincaré disc is shown in Fig. 1.

Theorem 1 is proved in the next section. From Fig. 1 we can see that the Painlevé-Ince differential system (2) has exactly five different kind of orbits:

• (i) A unique equilibrium point (0, 0).

• (ii) A continuum of homoclinic orbits starting and ending at the equilibrium point (0, 0).

• (iii) A continuum of heteroclinic orbits starting at the equilibrium point (0, 0) and ending at infinity at the equilibrium point localized at the origin of the local chart $V_1$ (see the proof of Theorem 1 for more details).

• (iv) A continuum of heteroclinic orbits starting at infinity at the equilibrium point localized at the origin of the local chart $V_1$ and ending at the equilibrium point (0, 0).

• (v) A continuum of homoclinic orbits starting and ending at the equilibrium point localized at the origin of the local chart $V_1$.

2 Proof of Theorem 1

2.1 Finite Equilibrium Points

Clearly that the differential system (2) has a unique finite equilibrium, the origin of coordinates. Since the linear part of this differential system at the origin has the matrix

$$\begin{aligned} \left( \begin{array}{cc} 0 &{} 0 \\ 1 &{} 0 \end{array} \right) , \end{aligned}$$

the origin is a nilpotent equilibrium point. By applying Theorem 3.5 of [4] its local phase portrait is formed by an elliptic and a hyperbolic sector, separated by two parabolic sectors. Using the first integral (3) it follows easily that the boundary of the elliptic sector is the parabola $x+y^2=0$, and that the boundary of the hyperbolic sector is the parabola $2x+y^2=0$. Between these two parabolas there are the two parabolic sectors. For a picture of the local phase portrait at this finite equilibrium point see the neighorbood of the origin in the Poincaré disc of Fig. 1.

2.2 Infinite Equilibrium Points

In this subsection we shall use the Poincaré compactification, done by Poincaré in [13, 14]. This compactification allows to study the dynamics near the infinity of a polynomial differential system in the plane $\mathbb {R}^2$. See Chapter 5 of [4] or the added Data File for additional information on this compactification and for the expressions in the local charts that we shall use in what follows for studying the phase portrait of system (2) the Poincaré disc.

We remark that for studying the infinite equilibrium points we only need to study the infinite equilibrium points of the local chart $U_1$, and to verify if the origin of $U_2$ is an infinite equilibrium point.

Now we shall use the local charts $U_1$ and $U_2$ for studying the infinite singular points of the polynomial differential system (2) extended to the Poincaré disc. Thus the polynomial differential system (2) in the local chart $U_1$ is

$$\begin{aligned} \begin{array}{l} u' = v^2 + 3 u^2 v+u^4, \\ v' = u v (3v+ u^2). \end{array} \end{aligned}$$

(4)

The unique infinite equilibrium of system (4), i.e. the unique equilibrium point (u, v) with $v=0$, is the origin (0, 0). Since the linear part of system (4) at the origin is the matrix identically zero, in order to study its local phase portrait we need to do changes of variables called blow ups, see [1] for more details on these changes of variables.

We do the blow up $(u,v)=(u_1,u_1 v_1)$. Then in the new variables $(u_1,v_1)$ the differential system (4) becomes

$$\begin{aligned} \begin{array}{l} u_1' = u_1^2 (u_1^2 + 3 u_1 v_1 + v_1^2), \\ v_1' = -u_1 v_1^3. \end{array} \end{aligned}$$

(5)

Doing the rescaling of the independent variable $t\rightarrow \tau$ through the change $d\tau =u_1 dt$ system (5) writes

$$\begin{aligned} \begin{array}{l} \dfrac{du_1}{d\tau } = u_1 (u_1^2 + 3 u_1 v_1 + v_1^2), \\ \dfrac{dv_1}{d\tau } = -v_1^3. \end{array} \end{aligned}$$

(6)

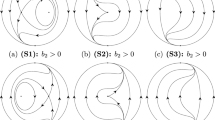
The differential system (6) is a polynomial homogeneous differential system of degree 3, the phase portraits of such systems have been studied in [3]. Thus system (6) has the following four invariant straight lines through the origin of coordinates $u_1 v_1 (u_1 + v_1) (u_1 + 2 v_1)=0$, studying the motion on these straight lines we obtain that the local phase portrait at the origin of the differential system (6) is given in Fig. 2a.

Going back to the differential system (5) we get that the local phase portrait at the origin of the differential system (5) is given in Fig. 2b. Finally going back to the differential system (4) we get that the local phase portrait at the origin of the differential system (4) is given in Fig. 2c.

Fig. 2

The local phase portraits of the blow up of the origin of the local chart $U_1$

Now we study if the origin of the local chart $U_2$ is an equilibrium point. Then the differential system (2) in the local chart $U_2$ writes

$$\begin{aligned} \begin{array}{l} u' = -1 - 3 u v - u^2 v^2, \\ v' = -u v^3. \end{array} \end{aligned}$$

(7)

Hence the origin of the local chart $U_2$ is not an infinite equilibrium points.

In summary the unique infinite equilibrium points are the origins of the local charts $U_1$ and $U_2$. In the Poincaré disc at the origin of $U_1$ we see the half phase portrait in $v\ge 0$ of Fig. 2c, and at the origin of $V_1$ the half phase portrait in $v\le 0$ of Fig. 2c. See Fig. 1. This completes the phase portrait in the Poincaré disc of the differential system (2). Therefore Theorem 1 is proved.