Introduction

In Denmark, the context of this study, school mathematics is structured by a government-specified curriculum that outlines in broad and largely non-prescriptive ways what children are expected to know by the end of each of three 3-year phases of compulsory education. With respect to the development of children’s arithmetic competence, the curriculum document asserts that teachers should (our translation) “challenge and support individual students to develop their arithmetic strategies based on their number understanding rather than learning procedures for setting-up and calculating standard algorithms. The aim is not to practice standardised algorithms” (Ministry of Children and Education, 2019a). Such ambitions, which accord with international expectations that students should develop strategy flexibility and adaptivity (Baroody, 2003; Hickendorff, 2018; Xu et al., 2017), have not been systematically evaluated, not least because Danish national assessments typically privilege answers and not strategies. Moreover, the loose specification of the Danish curriculum means that teachers have great didactical autonomy (Skott, 2004), with the consequence that little is known about what strategies children learn. This paper, drawing on a definition of strategy “as a procedure or set of procedures for achieving a higher level goal or task” (Lemaire & Reder, 1999, p.365), is a first attempt to conduct such an evaluation by focusing explicitly on grades three, six and eight (age 9, 12 and 14), as placeholders for each of the three phases of the Danish curriculum (grades 1–3, 4–6 and 7–9).

While research on multidigit arithmetic strategy adaptivity and strategy flexibility is extensive, the distinction between the two constructs is not always transparent (del Olmo-Muñoz et al., 2022; Heinze et al., 2009). Some scholars appear to construe flexibility and adaptivity as synonyms (see, for example, Baroody, 2003; Hickendorff, 2018), while others construe adaptivity as subsuming flexibility (see, for example, McMullen et al., 2016, 2020). A more widely accepted view construes adaptivity as subsumed by flexibility (Blöte et al., 2000; Hästö et al., 2019; Star & Rittle-Johnson, 2008), whereby strategy flexibility involves learners knowing multiple procedures and then applying them adaptively to different situations (Rathgeb-Schnierer & Green, 2017; Schneider et al., 2011). In other words, by way of working definitions for this paper, it seems reasonable to assume that for any given task, task-specific flexible students have access to a repertoire of strategies, while task-specific adaptive students are able to select an optimal strategy from those available (Heinze et al., 2009; Hickendorff, 2022; Verschaffel et al., 2009).

In the following, an examination of the literature on the development and significance of strategy flexibility and strategy adaptivity is structured according to these working definitions. In addition, particular attention has been paid to the role of shortcut strategies, which Torbeyns et al., (2009a, p.3) define as the “flexible adaptation of the numbers and operations in the sum or difference on the basis of one’s understanding of number relations and/or the properties of the arithmetic operations”. This definition has been repeatedly used in studies of Dutch-speaking students, albeit in different contexts, by the same small group of researchers (see, for example, De Smedt et al., 2010; Hickendorff, 2018; Peters et al., 2013; Torbeyns et al., 2017). However, as is discussed later with respect to the methods of this study, the ways in which this definition has been operationalised may limit a study’s outcomes.

The development and significance of strategy flexibility

In general, research has found students of all ages able to employ a range of multidigit arithmetic strategies. Much of this research, structured by goals relating to the efficacy of specific strategies, has been based on a choice/no choice methodology, whereby, in the choice condition, students are invited to choose a strategy from a set of researcher-determined strategies, while, in the no choice condition, a researcher-specified strategy is applied to all problems (Luwel et al., 2009). Many of these studies, which have been conducted in Flanders, the Dutch-speaking region of Belgium, have included investigations of third graders’ approaches to multidigit addition and subtraction tasks designed to elicit either a compensation or a jump strategy (Torbeyns et al., 2009b); fourth graders’ solutions to multidigit addition and subtraction tasks designed to stimulate either mental computation or standard written algorithms (Torbeyns & Verschaffel, 2013); fourth, fifth and sixth graders’ solutions to single digit addition problems (Imbo & Vandierendonck, 2007), and sixth graders’ solutions to multidigit subtraction tasks designed to elicit either direct subtraction or indirect addition (Torbeyns et al., 2018). Elsewhere, researchers have investigated Italian third and fifth graders’ solutions to multidigit subtractions (Caviola et al., 2018), Dutch fourth graders’ solutions to multidigit subtraction tasks designed to elicit either direct subtraction or indirect addition (Hickendorff, 2020) and French third, fifth and seventh graders’ approaches to multidigit addition and subtraction (Lemaire & Callies, 2009). Overall, these studies confirm that few students, when prompted, are unable to execute successfully a range of researcher-determined strategies, including shortcut.

The relatively few studies offering students an unrestricted free choice have yielded not dissimilar outcomes, typically finding that students, when prompted, can provide a range of strategies for a given operation, whether French third and fifth graders’ approaches to multidigit addition (Lemaire & Brun, 2017), Flemish second, third and fourth graders’ approaches to multidigit addition and subtraction (Torbeyns et al., 2009a), German third graders’ approaches to multidigit addition and subtraction (Heinze et al., 2009) or Dutch sixth graders’ approaches to all four operations (Hickendorff, 2018). Furthermore, in a hybrid study comprising both authentic choice and no choice components, Hickendorff (2022) investigated the multidigit subtraction strategies of Dutch third graders by means of an instrument designed to measure, first, the strategies students know and use and, second, the extent to which they know which strategy is optimal. She found that most students consistently used the same strategy across problems, but when prompted, knew more strategies than those used spontaneously. However, of relevance to this study, students have been rarely found to identify optimal solution strategies for a given task. Overall, such studies, whether free choice or choice/no choice, confirm that most students, irrespective of age, have access to and are able to execute successfully a range of multidigit arithmetic-related strategies.

The development and significance of strategy adaptivity

As with strategy flexibility, studies based on a choice/no choice methodology are first examined. While many of these studies have already been discussed from the perspective of strategy flexibility, here, they are analysed from the perspective of task-specific adaptivity. In order for students to identify a particular strategy as optimal, it would not be unreasonable to expect them to acknowledge and take account of various task characteristics (Verschaffel et al., 2009). However, as Flemish studies have shown, this tends not to be the case. For example, while third graders are able to execute a range of imposed addition and subtraction strategies, when given a free choice they rarely take account of either task or strategy efficiency characteristics (Torbeyns et al., 2009b). Similarly, fourth graders tend to resort to standard additive algorithms even on tasks designed to elicit number-based strategies (Torbeyns & Verschaffel, 2013), typically basing strategy choices on personal competence rather than task characteristics (Torbeyns & Verschaffel, 2016). However, as they progress from grade four to six, they become aware of a task’s characteristics and, from the perspective of subtraction, adopt indirect addition successfully (Torbeyns et al., 2018; Van Der Auwera et al., 2022). Elsewhere, with respect to tasks designed to elicit indirect addition, Dutch fourth grade children are able to adapt strategy choices on the basis of task characteristics, although this tendency diminishes when written computation is involved (Hickendorff, 2020). In a similar vein, a French study found third and fifth graders’ mental approaches to two-digit addition were influenced by whether tasks involved a carrying of a ten (Lemaire & Callies, 2009). The same study also found that fifth and seventh graders’ approaches to two-digit subtractions were influenced by the need to borrow. In sum, there is evidence that students’ awareness of task characteristics, and the impact of that acknowledgement on strategy choice, develops with age.

From the free-choice perspective, Flemish studies continue to dominate. For example, an intervention designed to encourage third graders’ use of indirect addition found few students adopting the strategy, although when it was used it was used efficiently (De Smedt et al., 2010). A study of traditionally taught students in grades two through four found, in relation to their chosen strategies on addition and subtraction, little evidence of shortcut strategies like compensation or indirect addition, although older students, when asked to identify additional strategies, were typically able to do so (Torbeyns et al., 2009a). This age-related shift towards an apparent awareness of task characteristics was confirmed by a later study of grade four and grade six children, which found, with respect to subtraction, students of all ages switching between indirect addition and direct subtraction according to whether the subtrahend was smaller or larger than the difference; in the former case, students tended to use direct subtraction, while in the latter, they tended to use indirect addition (Peters et al., 2013). Elsewhere, with respect to tasks designed to elicit shortcut strategies, a Dutch study found fewer than one in five sixth graders choosing shortcut strategies, which were used no more successfully than standard algorithms (Hickendorff, 2018). That being said, in relation to multidigit subtraction, by the end of grade six, Dutch special needs students not only frequently and spontaneously turn to indirect addition but do so on the basis of their interpretation of the different task characteristics (Peltenburg et al., 2012). Finally, with respect to Dutch speakers, a comparative study involving tasks designed to elicit number-based compensation strategies, evaluated, across grades three, four and five, Dutch and Flemish students’ approaches to subtraction. They found most children consistently rely on one strategy, with only a minority of the high-achieving or older students showing strategy variability (Torbeyns et al., 2017).

Moving beyond studies of Dutch speakers, a study of German third graders, undertaken before the introduction of standard algorithms, found not only considerable strategy variation but also that half the students who offered appropriate solution strategies did so adaptively (Heinze et al., 2009). That said, an earlier German study also found that third graders’ use of number-based strategies fell considerably after the introduction of the standard algorithm Selter (2001). Elsewhere, French third and fifth graders’ use of columnar retrieval, a mental application of a column-based algorithm, decreased with age, while their rounding down of both operands and use of direct retrieval increased (Lemaire & Brun, 2017). With respect to multiplication, a study of Swedish fifth graders found, due to students’ persistent use of either repeated addition or equal groups, almost no adaptive strategy choice (Larsson, 2016; Larsson et al., 2017). Finally, Hickendorff’s (2022) hybrid study found, with respect to subtraction tasks designed to elicit either indirect addition or compensation, few third graders using either strategy when given a free choice.

Overall, research has shown that while children of all ages typically have access to a range of multidigit arithmetic-related strategies, they rarely use them adaptively (Lemaire & Brun, 2017; Lemaire & Callies, 2009), even when tasks are designed to elicit shortcut strategies (Hickendorff, 2018; Torbeyns et al., 2009a). That said, adaptive strategy choices become more likely with age (Lemaire & Callies, 2009; Torbeyns et al., 2018; Van Der Auwera et al., 2022), although instruction and textbooks, particularly the timing of the introduction of standard algorithms, influence not only students’ strategy repertoires but their preferred strategies (Blöte et al., 2001; Csíkos, 2016; Heinze et al., 2009; Hickendorff et al., 2019; Karantzis, 2010; Selter, 2001; Sievert et al., 2019; Torbeyns et al., 2017).

The current study

Drawing on the above, the current study is motivated by a number of factors. First, much of the research undertaken over the last 25 years has focused on multidigit addition and subtraction, with few studies examining strategy choice in relation to multiplication (Hickendorff et al., 2019). Second, few free-choice studies have examined students’ strategy choices at different ages, leaving a substantial research gap in respect of strategy development. Indeed, as highlighted above, much influential research has employed a choice/no choice methodology, an approach still regarded as the default for eliciting students’ strategy use (Torbeyns et al., 2017). Third, few studies have examined the relationship between students’ strategy repertoires and computational accuracy. Fourth, despite curricular expectations, no systematic evaluation has been undertaken of Danish students’ strategy flexibility and strategy adaptivity. Such a study will contribute to the literature on the impact of culture on the development of students’ adaptivity (Hatano & Inagaki, 1984).

In light of the above, the research presented in this paper, focused on students in grades three, six and eight, is framed by the questions:

  • How is task-specific strategy flexibility manifested in students’ approaches to multidigit arithmetic?

  • How is task-specific strategy adaptivity manifested in students’ approaches to multidigit arithmetic?

  • In what ways are task-specific strategy flexibility and strategy adaptivity associated with accuracy?

Each grade-related component, representing a cross-sectional analysis, collectively contributes to a snapshot of how Danish students’ multidigit-related strategies may play out over time. In this sense, the study is not to be construed as a conventional longitudinal study in which the same students are scrutinised over time, but as a developmental perspective on the issue under scrutiny (Selter et al., 2001; van den Heuvel-Panhuizen & Treffers, 2009).

Methods

Participants

Schools in five demographically different municipalities in Jutland, the central region of Denmark, were contacted to elicit participation. This yielded 20 schools, large and small, urban and rural, whose classes and pupils are shown in Table 1. Prior to their child’s participation, parents received two letters. The first, delivered through their child’s school’s communication platform, outlined the project and clarified their right to withdraw the child’s participation. The second, by means of an email, included information about, for example, how personal data would be managed within the framework of the European Union’s general data protection regulation (GDPR). Over a period of 4 weeks, members of the project team undertook the TriFA with each participating class.

Table 1 Participant totals
Full size table

Assessment of strategy use

Acknowledging the above, this study draws on a procedural adaptation of a tri-phase assessment (TriFA) tool, previously exploited in a free-choice study of Chinese students’ linear equations-related strategy use (Xu et al., 2017). According to Xu et al. (p.3), during phase one students “solve each problem as quickly and accurately as possible”, during phase two, in addition to the strategy yielded during phase one, they “generate multiple strategies for each problem”. Finally, in phase three they “evaluate their own strategies generated in the former two phases for each problem”. In their analyses attention was paid to students’ use of “innovative” strategies, which were operationalised as those “that had the fewest steps and with the most simplified computation”. In this study, due to its focus on multidigit arithmetic, an adaptation of Torbeyns et al. and’s (2009a, 2009b) shortcut strategy has been used as an alternative to “innovative”, not least because the latter implies an invented solution different from any procedural norm and that expectations of the fewest steps would be too restrictive. However, from the perspective of additive operations, both Torbeyns et al., (2009a, 2009b) and Hickendorff (2018) distinguish shortcut strategies from both decomposition and sequential strategies, a distinction that may be unnecessarily restrictive. For example, a student who employs a sequential solution to 502 − 18 by writing 502 − 10 = 492; 492 − 8 = 484 has completed the task in only two steps and may well have demonstrated a “flexible adaptation of the numbers and operations” (Torbeyns et al., 2009a, p.3) beyond any expectations of a standard algorithm. In other words, implying that no strategy is of itself shortcut or non-shortcut, such a student may have applied a number-dependent approach to a strategy that both Torbeyns et al., (2009a, 2009b and Hickendorff, 2018) construe as number-independent. Consequently, drawing on modifications of Hickendorff (2018), Torbeyns et al., (2009a, 2009b) and Xu et al. (2017), shortcut strategies exploit the modification of a task’s numbers and/or operations in ways that both simplify the arithmetic and reduce the number of steps from those of standard algorithms.

Several pertinent factors informed the number and range of included tasks. First, to facilitate comparison some common tasks were included across all three grades, although it was necessary to strike a balance between the number of common tasks and the posing of appropriate challenges for each grade. Table 2 shows the task distribution for each grade level. Second, initial piloting indicated that intended common subtraction tasks were too complex for most third graders, who subsequently received simpler subtractions than the older students. Third, as it is not part of the intended experience for third graders, multidigit multiplication was included only for grades six and eight. Fourth, the 2019 national test’s finding that almost a third of all ninth graders were unable to divide 7021 by 7 (Ministry of Children and Education, 2019b) indicated that including division would result not in an evaluation of how students solve multidigit division tasks but whether they could solve them. Consequently, division was excluded from the instrument. Fifth, to ensure the assessment could take place within the familiarity of the students’ own classrooms, two equivalent tests were developed for each grade so that students sitting in adjacent seats would be unable to copy. Sixth, acknowledging the need to minimise disruption, the assessment was designed to be completed within 1 h.

Table 2 Number of tasks by grade and operation
Full size table

During phase one, students solved a range of multidigit arithmetic tasks by whatever strategy they preferred and wrote their solutions on the appropriate pages of a provided booklet. In addition, and on a separate sheet that was collected at the end of the phase, students also wrote down their answers for each task. During phase two, students returned to their booklet and, on the same pages as earlier, solved the same problems by whatever alternative strategies they could generate. During phase three, students were invited to identify which of the strategies generated during the first two phases they believed was optimal. Students who solved a task by means of a shortcut strategy during phase one were evaluated as adaptive with respect to that task, while those who offered multiple strategies across the phases were evaluated as flexible with respect to that task. Also, accuracy was determined solely from the answers provided during phase one in ways that ensured its measure was independent of any strategy used.

Multidigit addition tasks

Table 3 shows the tasks used to elicit students’ strategies for multidigit addition, each of which was designed to elicit shortcut strategies (Sievert et al., 2019; Torbeyns et al., 2009b). Importantly, while three tasks in each set are common across grades, a two-digit task was included for students in grade three, while a fourth 3-digit task was introduced for grade eight.

Table 3 Addition tasks used across the different tests
Full size table

Multidigit subtraction

Table 4 shows the different multidigit subtraction tasks. Typically, tasks were adapted from Hickendorff (2020) and included subtractions with both large (for example, 502 − 18) and small differences (for example, 703 − 686) intended to elicit strategies like compensation and indirect addition. Also, despite the original intention of including common tasks across the three grade levels, piloting indicated that many third graders had struggled to complete some of the intended three-digit subtractions. Consequently, two-digit tasks, which were incorporated uniquely for third graders, were supplemented by simpler three-digit tasks than those offered to sixth and eighth graders.

Table 4 Subtraction tasks used across the different tests
Full size table

Multidigit multiplication

Table 5 shows the various multidigit multiplication tasks, which were designed to elicit various shortcut strategies like compensation or decomposition.

Table 5 Multiplication tasks used across the different tests
Full size table

Coding

Two experts independently undertook the development of a coding schedule for the various strategies used with the different tasks. The outcomes were then compared and contrasted to produce an agreed set of shortcut strategies for each task based on the number of steps and simple calculations. Thus, as seen in Table 6, indirect addition could be coded as either shortcut or non-shortcut according to the student’s interpretation of the different task characteristics. That is, the indirect addition solution to 514 − 486 would have been coded as shortcut, while the same approach to 502 − 18 would not. In the case of uncertainty or disagreement, the opinion of a third expert was sought and a resolution was achieved.

Table 6 Examples of strategies coded as shortcut and non-shortcut strategies. In this context, non-shortcut strategies include both standard algorithms and other strategies not classified as shortcut
Full size table

Each student’s solutions, from the perspectives of both strategy use and accuracy, were coded by the first author and at least one of several research assistants trained to code the TriFA. With respect to phase one, each task was first coded for accuracy (correct, incorrect or no solution) and second for strategy (shortcut, non-shortcut, misconception or none). Finally, in phase one, non-shortcut strategies were further categorised as either standard algorithm or “other”, while the “none” category included both unsolved tasks and tasks solved with no written strategy. With respect to those tasks solved with no written strategy—tasks to which students submitted only an answer—and acknowledging our interest in observable strategies, no strategy was inferred. Importantly, coding for accuracy was undertaken independently of coding for strategy, being determined from students’ answer sheets and not the booklets in which they recorded their solution strategies. With respect to phase two, any solution involving a shortcut strategy was recorded as such. Also, solutions based on the same underlying principles but executed differently were evaluated as different. For each student, the total recorded for each task included all acceptable solution strategies, shortcut or not. With respect to phase three, each student’s optimal strategy was coded as either shortcut or not. All disagreements were checked, and in the event of any uncertainties, the opinion of a third expert was sought and the uncertainty was resolved. To facilitate analysis, students were grouped according to the levels of flexibility and adaptivity shown in Table 7. The group characteristics were in part determined by the very high numbers of students exhibiting neither flexibility nor adaptivity and the relatively low numbers exhibiting high levels of adaptivity and flexibility. Finally, Mann–Whitney U tests, conducted to determine the comparability of the two sets of tasks, confirmed no significant differences, thus warranting combining all data into a single set.

Table 7 Students’ adaptivity and flexibility levels
Full size table

Statistical procedures

In order to address the three research questions posed above, various descriptive statistics were calculated with respect to students’ grade levels, accuracy and strategy choices in the different phases of the investigation and in relation to the three examined arithmetical operations. In addition, one-way ANOVAs, with standard error nested at the classroom level, were undertaken to test for differences within the various configurations of student, strategy and accuracy data. In cases where ANOVAs indicated significant differences, Tukey post hoc tests were used to test for between-group differences. Finally, to investigate the association between flexibility and adaptivity as independent variables and accuracy as a dependent variable, a simple linear regression was undertaken, with standard error clustered at the classroom level.

Results

The results are presented in five parts. First, examining the extent to which participating students’ exhibit flexibility as assessed by their use of multiple strategies. Second, examining the extent to which participating students’ exhibit adaptivity measured by their use of shortcut strategies during phase one. Third, examining differences in students’ use of shortcut strategies as a preferred choice (phase one) or available strategy (phase two), across addition, subtraction and multiplication and grade levels. Fourth, examining students’ evaluation of their strategy choices from phase one to phase two. Finally, examining the relationship between students’ flexibility and adaptivity and accuracy.

Student flexibility

Figure 1 shows that the proportion of students exhibiting no flexibility falls from a high of 49% in grade three, through 24% in grade six to 21% in grade eight. Figure 1 also shows a remarkably similar flexibility distribution profile for grades six and eight. A one-way ANOVA, with students nested in classes, yielded significant differences in the proportions of flexibility across the three grade levels (\(F\left(\mathrm{2,119}\right)=6.7\), p < 0.0001), with Tukey post hoc tests revealing significant differences between grade three (\(M=0.21, SD=0.29)\) and grade six (\(M=0.35, SD=0.31\)) and between grade three and grade eight (\(M=0.36, SD=0.31)\), but not between grade six and grade eight.

Fig. 1
figure 1

Percentage of students in each level of flexibility by grade

Full size image

With respect to addition, a one-way ANOVA, with students nested in classes, identified significant differences between grade levels \((F\left(\mathrm{2,119}\right)=6.59, p<0.0001)\). Tukey post hoc tests found third graders’ flexibility (\(M=0.31, SD=0.38\)) to be significantly lower than both sixth (\(M=0.56, SD=0.45)\) and eight graders (\(M=0.55, SD=0.44\)). However, there were no significant differences the flexibility of sixth and eighth graders. In respect of subtraction, the ANOVA revealed significant flexibility-related differences between grades (\(F\left(\mathrm{2,119}\right)=3.76,p<0.0001\)), with Tukey post hoc tests revealing significantly higher levels of flexibility in grade six (\(M=0.24, SD=0.38)\) than grade three (\(M=0.11. SD=0.28\)), and grade eight (\(M=0.23, SD=0.36\)) than grade three, but not between grade six and grade eight. Finally, with respect to multiplication, the ANOVA revealed statistically significant differences between grade six and grade eight, \(F\left(\mathrm{1,81}\right)=3.85,p<0.0001,\) with eighth graders (\(M=0.31, SD=0.38\)) exhibiting significantly more flexibility than sixth (\(M=0.26, SD=0.38\)).

Student adaptivity

Figure 2 shows, irrespective of grade, very low proportions of students exhibiting high levels of adaptivity (3%). Also, the proportions of students with no adaptivity are high in grade three (70%), fall in grade six (46%) and then rise in grade eight (59%). A one-way ANOVA, with students nested in classes, identified significant differences between the grade levels \((F\left(\mathrm{2,119}\right)=4.59, p<0.0001)\), with Tukey post hoc tests showing that adaptivity was statistically significantly higher in grade six \((M=0.15, SD=0.22)\) than in either grade three \((M=0.10, SD=0.21)\) or grade eight \((M=0.11, SD=0.20)\). However, there were no statistically significant differences between grades three and eight.

Fig. 2
figure 2

Percentage (frequency) of students in each level of adaptivity by grade level

Full size image

The figures of Table 8 show students’ phase one strategy use as a percentage of all tasks, irrespective of accuracy, for each operation and grade level. They indicate, irrespective of operation, that the proportions of task solved by means of shortcut strategies, while never high, typically tends to diminish with age, although there is a slight exception with respect to grade six subtraction. They also show a marked increase in the use of standard algorithms alongside a commensurate decline in the use of other—neither shortcut nor standard algorithms—strategies. In addition, addition prompted few misconceptions, while both subtraction- and multiplication-related misconceptions become fewer with maturity. Finally, the proportions of unattempted tasks show addition to be a challenge to many grade 3 students, subtraction a challenge across the grades, particularly grade 3, and multiplication problematic for many students in both grades 6 and 8.

Table 8 Percentage of phase one tasks by strategy type and grade
Full size table

Student use of shortcut strategies by operation

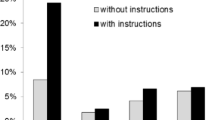
Figure 3 shows, for each operation and grade, the percentage of phase one tasks solved by a shortcut strategy (dark grey), the percentage of phase two tasks solved by at least one shortcut strategy (mid-grey) and the percentage of tasks solved with a shortcut strategy in phase one and at least one new shortcut strategy in phase two (light grey). With respect to addition, students’ use of shortcut strategies during phase one is more common in grade three than in the higher grades. Also, the use of shortcut strategies during phase two seems more commonplace in the higher grades. However, the situation with respect to subtraction seems different, with students’ use of shortcut strategies during phase one follows no clear pattern. The pattern for multiplication is similar to that of subtraction, with higher proportions of tasks being solved by shortcut strategies during phase one than phase two, though small difference in grade 8. Finally, across all three operations and grades, the use of shortcut strategies in both phase one and two is, in relative terms, rare.

Fig. 3
figure 3

Percentage of tasks solved uniquely by shortcut strategies at each phase of the study

Full size image

Student selection of an optimal strategy

The figures of Table 9 show when shortcut strategies were identified as optimal. By way of example, and reflecting a trend across all three grades, third graders solved 608 phase one tasks by means of shortcut strategies and that 80% of these were identified during phase three as optimal. By way of contrast, third graders first used shortcut strategies on 229 phase two occasions and that 21% of these were later identified as optimal. In short, students who first use shortcut strategies during phase one are considerably more likely than students who first used shortcut strategies in phase two to recognise those strategies as optimal.

Table 9 Percentage of shortcut solutions identified as optimal in relation to when they were introduced
Full size table

Adaptivity, flexibility and accuracy

Multiple linear regressions, with standard error clustered at the classroom level, were calculated for each grade level to examine the predictive strength on accuracy, as a percentage of correct solutions, of adaptivity and flexibility. With respect to grade three, a significant regression equation (\(F\left(\mathrm{2,38}\right)=52.65,p<0.001,{R}^{2}=0.24\)) identified both flexibility (\(\beta =0.44,p<0.001\)) and adaptivity (\(\beta =0.30,p<0.001\)) as significant predictors of accuracy. In similar vein, a significant regression equation for grade six (\(F\left(\mathrm{2,9}\right)=35.59,p<0.0001,{R}^{2}=0.15\)) identified both flexibility (\(\beta =0.23,p<0.0001\)) and adaptivity (\(\beta =0.19,p<0.0001\)) as significant predictors of accuracy. Finally, a significant regression equation for grade eight \(\left(F\left(\mathrm{2,42}\right)=44.66,p<0.001\right),{R}^{2}=0.14\)) also identified flexibility (\(\beta =0.25,p<0.0001\)) and adaptivity (\(\beta =0.09,p<0.0001\)) as significant predictors of accuracy.

Table 10 shows the results of the full linear regression model \(\left(F\left(\mathrm{8,120}\right)=58.48,p<0.0001\right),{R}^{2}=0.34)\), including all participants, clustered by classroom, grade as a dummy variable and testing for interactions between flexibility and grade and adaptivity and grade. The first five rows confirm that flexibility, adaptivity and, relative to earlier grades, grade level are significant predictors of accuracy, with flexibility appearing as a stronger predictor than adaptivity. When examining the influence of flexibility by grade and adaptivity by grade, flexibility has the greatest impact in grade three compared to grade six and grade eight. By way of contrast, adaptivity is not significantly different predictor for accuracy in grade six compared to grade three but is less predictive for grade eight compared to grade three.

Table 10 Regression analysis examining flexibility, adaptivity and grade level as predictors for accuracy. All students are clustered in classes
Full size table

Further, one-way ANOVA identified significant differences between different levels of flexibility and accuracy (full results in the Appendix), and different levels of adaptivity and accuracy (full results in the Appendix).

Discussion

In this paper, drawing on an adaptation of a tri-phase flexibility assessment tool (Xu et al., 2017), various aspects of Danish third, sixth and eighth graders’ multidigit arithmetic-related strategy flexibility and adaptivity have been examined in relation to accuracy. In so doing, students’ task-specific adaptivity was evaluated against their initial use of shortcut strategies and their task-specific flexibility against the number of solutions they supplied. This approach has exposed both expected and unexpected outcomes worthy of further investigation, both nationally and internationally. However, before discussing the findings in relation to the research questions posed above, four potential limitations are considered.

First, because the principal goal was to investigate students’ use of shortcut strategies at different ages, it seemed appropriate to use the same tasks whenever possible. However, for the reasons explained above, the instrument for third graders incorporated simplified subtraction and no multiplication. Consequently, differences in either flexibility or adaptivity between, say, third and sixth graders, are likely to be smaller than if the former had received the same tasks as their peers. By way of contrast, had the instruments used by sixth and eighth graders not been essentially identical, the unexpected difference between sixth and eighth graders’ adaptivity may have gone unnoticed. Second, irrespective of age and operation, the proportions of misconceptions and incomplete solutions highlighted in Table 8 indicate that many tasks posed challenges for substantial numbers of students and may have contributed to lower shortcut usage than might otherwise have been the case. Third, conscious of the criticisms of free-choice methods (Luwel et al., 2009; Siegler & Lemaire, 1997), the decision to ignore strategy efficiency, particularly speed, enabled the involvement of representative samples in time-efficient ways and a meaningful analysis of the impact of students’ strategy choices on accuracy. Moreover, at least as far as sixth graders are concerned, the limited use of shortcut strategies identified by this study accords with the outcomes of a similar free-choice study involving Dutch students (Hickendorff, 2018). Fourth, one consequence of the decision to analyse only written solutions, a problem frequently associated with large-scale assessments, was that no strategy-related insights could be inferred from solutions presented solely as answers. That said, the manner of the test’s implementation and lack of emphasis on speed gave students every chance to communicate their solution processes.

How is strategy flexibility manifested in students’ approaches to multidigit arithmetic?

The results indicated a higher level of flexibility in the older age groups, with the low flexibility of third graders resonating with that of their Flemish peers, who, even after instruction privileging informal strategies, rarely demonstrate subtraction-related strategy flexibility (De Smedt et al., 2010). More generally, students’ flexibility with respect to both subtraction and multiplication is, typically, around half that of addition. Indeed, in comparison with their grade four Dutch peers, who are typically able to solve subtractions by means of both direct subtraction and indirect addition, few Danish students, irrespective of age, were able to do the same. That being said, as implied by the data of Table 7, the generally low levels of strategy flexibility, as found elsewhere (Csíkos, 2016; Hickendorff, 2020; Lemaire & Brun, 2017; Lucangeli et al., 2003; Selter, 2001; Torbeyns & Verschaffel, 2013, 2016), may be due to students, having been taught standard algorithms, rejecting alternatives.

How is strategy adaptivity manifested in students’ approaches to multidigit arithmetic?

The results of this study, which seem to contradict international studies showing strategy adaptivity becoming more likely with age (Lemaire & Callies, 2009; Torbeyns et al., 2018; Van Der Auwera et al., 2022), indicate that levels of strategy adaptivity peaked in grade six rather than, as might reasonably be expected, grade eight. One explanation may lie in instructional practices that privilege standard algorithms, as found in studies undertaken in Belgium (Torbeyns & Verschaffel, 2013, 2016), France (Lemaire & Brun, 2017), Germany (Selter, 2001), Hungary (Csíkos, 2016), Italy (Lucangeli et al., 2003) and the Netherlands (Hickendorff, 2020). Indeed, assuming that standard algorithms for addition, subtraction and multiplication are introduced in that order, the figures of Table 7 indicate that students’ use of shortcut strategies seems to diminish as they become familiar with standard algorithms. What is clear, and in need of further investigation, is that students who first used a shortcut strategy during phase one were more than three times as likely as students who first used a shortcut strategy in phase two to identify that strategy as optimal (Table 9).

In what ways are task-specific strategy flexibility and strategy adaptivity associated with accuracy?

The various analyses have shown not only higher levels of accuracy with higher grade level, confirming an expected role of maturation, but, within each grade level, accuracy increasing with increases in both flexibility (Hästö et al., 2019) and adaptivity (McMullen et al., 2016). Indeed, with the linear regression confirming, at all grade levels, both strategy flexibility and strategy adaptivity as significant predictors of computational accuracy, the results may have implications for instructional practice, not least of which may be the need for teachers to facilitate students’ informed use of shortcut strategies as complements to standard algorithms. This is particularly the case for Demark, where the evidence of this study suggests that while flexibility is promoted in curriculum guidelines (Ministry of Education, 2019a), teachers, who have considerable autonomy in respect of what they teach and how they teach it (Skott, 2004), rarely seem to encourage it.

Conclusions and implications

In conclusion, this study’s novel use of the TriFA facilitated a nuanced understanding of not only the interrelationship of flexibility and adaptivity but also their differential relationship with accuracy. However, the various components of this study, not least its inclusion of older students, raise at least six issues worthy of further research. First, is the need to disentangle the impact of maturation and strategy choice on accuracy. Second, acknowledging students’ apparent age-related enthusiasm for standard algorithms, is the need to uncover why students abandon effective, insight-based strategies in favour of less efficient algorithms. Third, is the need to address how cultural expectations, both implicit and explicit, influence students’ strategy choices, particularly in contexts like Denmark, where children are expected to “develop their arithmetic strategies based on their number understanding rather than learning procedures for setting-up and calculating standard algorithms” (Ministry of Children and Education, 2019a). Fourth, and not unrelated to the third, is the need to investigate older students’ arithmetical strategy choices in contexts other than Denmark, not least because it is unclear if the decline in adaptivity of Danish students is unique. Fifth, as a way of complementing quantitative studies of the form presented here, is the need to elicit the strategy choices of those students who elect to write only an answer. Finally, is the need at the item level to uncover how different task types influence students’ strategy choice.