Introduction

The efficient and adaptive use of a variety of arithmetic strategies has become a major goal of primary mathematics education worldwide (Verschaffel et al. 2007). Instead of focusing on enhancing students’ mastery and efficient application of a limited range of standard strategies (routine expertise), mathematics education reform emphasizes the importance of students’ adaptive expertise (Hatano 2003): the ability to apply meaningfully learned procedures flexibly and creatively. In reform-oriented mathematics curricula, this striving for adaptive expertise is reflected in the instructional content and approaches, focusing on diversity of solution strategies. Reform movements throughout the world have identified adaptivity and flexibility of strategy use as an important competence (e.g., Star et al. 2015) although the implementation of this goal differs between countries. One relevant aspect of adaptive expertise is the use of so-called shortcut strategies, in which the solution process is made easier by adapting the numbers and/or the operation of the problem. For instance, the subtraction problem 843 – 299 = ? may be solved by changing the operation to addition by adding 1 and 543 to the minuend of 299. Or, one could change the numbers by subtracting 300 instead of 299, and compensating back the 1 subtracted too much.

In contrast to the importance attached to flexibility, adaptivity, and clever strategies, empirical results have shown that primary school students do not use shortcut strategies very frequently in Flanders (e.g., De Smedt et al. 2010; Torbeyns et al. 2009a, b), Germany (e.g., Heinze et al. 2009; Selter 2001), or The Netherlands (e.g., Blöte et al. 2001; Hickendorff et al. 2010). The current study aims to extend these results by investigating the use of shortcut strategies in very favorable conditions, that is, by studying older students (with higher levels of conceptual and procedural knowledge) who have received years of reform-based mathematics instruction focusing on fostering adaptivity and clever strategies. Furthermore, the problems were designed to maximally elicit shortcut strategies. Finally, the use of shortcut strategies was stimulated by an explicit instruction to look for a clever strategy. The current study’s results will shed light on the extent to which students use shortcut strategies in these very favorable conditions, making it possible to place previous studies’ findings of limited use of shortcut strategies in a broader perspective. Moreover, the results may have practical implications for (reform-based) mathematics education striving for adaptive expertise.

Adaptivity, flexibility, and shortcut strategies

Strategic flexibility and adaptivity are considered important components of mathematical proficiency (e.g., Baroody 2003; Xu et al. 2017). Although many different definitions and operationalizations exist in the literature, they converge on two central themes: the knowledge of different solution strategies and the ability to adapt them appropriately when solving a problem (Rathgeb-Schnierer and Green 2017). Furthermore, it also clear that conceptual knowledge of numbers, number relations, and operations is closely related to adaptivity and flexibility (McMullen et al. 2016). In the current paper, flexibility and adaptivity are used interchangeably as selecting the optimal strategy for a given problem in a given setting for a given person. Although many researchers stress the importance of metacognitive processes in regulated strategy selection, there is also ample evidence that strategies can be selected without involving consciousness (see for instance Verschaffel et al. 2009). Furthermore, it may be that one should speak of arriving at a strategy rather than selecting it, since it may rather be that students notice an (adaptive) approach based on aspects of the numbers and their relations in the problems instead of selecting it from a number of possible strategies before starting the solution (Threlfall 2009). Irrespective of these issues though, adaptivity and flexibility would show in the way students answer specific mathematical problems. In this framework of strategy flexibility and adaptivity, an important class of strategies are so-called shortcut strategies which involve the flexible adaptation of the numbers and/or operations in the problem to make the problem easier to solve (Torbeyns et al. 2009). Importantly, shortcut strategies are valued not so much because of the (alleged) benefits to the students, but rather because they signify something more “mathematical” than the acquisition of factual and procedural knowledge (Threlfall 2009).

Solution strategies for solving multidigit arithmetic problems in the additive domain have received ample research attention. There is a general consensus that there are three types of mental,Footnote 1 number-based solution strategies to solve multidigit addition and subtraction problems: (a) sequential strategies in which the subtrahend is decomposed: e.g., solving 45 − 29 via 45 − 20 = 25; 25 − 9 = 16, (b) decomposition strategies in which both operands are decomposed: e.g., solving 45 − 29 via 40 − 20 = 20; 5 − 9 = − 4; 20 − 4 = 16, and (c) varying (or shortcut) strategies: e.g., the compensation strategy 45 − 29 = 45 − 30 + 1 = 15 + 1 = 16 or the indirect addition strategy (also called subtraction by addition) in which one adds on from the subtrahend: e.g., 29 + 1 = 30; 30 + 15 = 45; so the answer is 1 + 15 = 16 (for overviews, see for instance Beishuizen et al. 1997; Heinze et al. 2009; Peltenburg et al. 2012; Peters et al. 2013).

By contrast, the multiplicative domain has received much less research attention. The major strategy categories to solve multidigit multiplication and division problems involve (a) repeated addition or subtraction: e.g., solving the multiplication problem 12 × 29 by repeatedly adding (multiples of) 29s or solving the division problem 736 : 23 by repeatedly subtracting (multiples of) 23s, (b) partitioning strategies in which one or both of the operands are decomposed: e.g., solving 12 × 29 via 10 × 29 = 290; 2 × 29 = 58; 290 + 58 = 348, and (c) simplifying (or shortcut) strategies, most notably compensation: e.g., solving 12 × 29 via 12 × 30 − 12 × 1 = 360 − 12 = 348 (Ambrose et al. 2003; Buijs 2008; Van Putten et al. 2005; Zhang et al. 2014).

Previous studies on shortcut strategy use

In the domain of multidigit addition and subtraction, studies with German third graders (Heinze et al. 2009; Selter 2001), Dutch second graders (Blöte et al. 2001), Flemish second to fourth graders (De Smedt et al. 2010; Peters et al. 2013; Torbeyns et al. b; c), and recently, a cross-national study of Dutch and Flemish third to sixth graders showed that students used the shortcut strategies indirect addition, compensation, and other simplifying strategies rather infrequently, usually below 20% (Torbeyns et al. 2017). In subtraction problems, compensation strategies seem to be used somewhat more often than indirect addition. The following general patterns of factors impacting shortcut strategy use emerge. The first factor is the instructional setting: generally speaking, students following a more reform-based investigative or problem-solving program focusing on a diversity of strategies were more likely to use shortcut strategies than children in a more traditional skills-oriented program focusing on the acquisition and mastery of standard strategies (Blöte et al. 2001; De Smedt et al. 2010; Heinze et al. 2009). The second factor is problem characteristics: besides the impact of number characteristics, the presentation format has also been found to have an effect, with word problems eliciting more shortcut strategies than symbolically presented problems (De Smedt et al. 2010). Third, the student factors gender, mathematics achievement level, and grade were related to shortcut strategy use: boys more often used shortcut strategies than girls (Blöte et al. 2001) and higher achievers and older students were also more likely to use shortcut strategies than lower achievers and younger students (Blöte et al. 2001; Heinze et al. 2009; Torbeyns et al. 2009; Torbeyns et al. 2017). Fourth and finally, characteristics of the task or task instructions were important. Stimulating shortcut strategies by asking students to solve a problem in different ways, or asking them to evaluate different strategies, showed that students know more about these strategies than their spontaneous use showed (Blöte et al. 2001; Torbeyns et al. 2009).

Very few studies have investigated the use of shortcut strategies in multiplication and division problems. The studies of Hickendorff et al. (2010) and Fagginger Auer et al. (2016a) with Dutch sixth graders showed that in multidigit division, shortcut strategies were used rather frequently but still in a minority of solutions, and more often when students calculated mentally (in the head) than when they wrote their solution steps down. However, since the factors that were identified to affect shortcut strategy use in addition and subtraction were not studied systematically in the studies addressing multiplication and division, it is yet unknown whether these factors’ effects generalize beyond the additive domain.

Current study

Researchers and practitioners in contemporary mathematics education agree on the importance of adaptive expertise, including the flexible, adaptive, and creative use of solution strategies to solve arithmetic problems. Empirical results, however, have shown that the extent to which students use clever, adaptive shortcut strategies spontaneously is rather limited. The current study aims to extend these results by investigating the use of shortcut strategies in very favorable conditions: (a) by studying older students who have, compared to younger children, higher conceptual and procedural knowledge which is a prerequisite for using these strategies, (b) by studying students who have received years of reform-based mathematics instruction in which fostering adaptivity and clever strategies are part of their daily educational practices, (c) by using arithmetic problems that all have number characteristics that maximally elicits these shortcut strategies and that were presented as word problems, and (d) by providing an explicit instruction to stimulate the use of these strategies. Furthermore, to give a more comprehensive account of the adaptive use of shortcut strategies in arithmetic, problems from both the additive and the multiplicative domains were included in the current study, allowing investigation of the extent to which student and task factors identified to affect shortcut strategy use in addition and subtraction problems generalize to multiplication and division problems.

To achieve these goals, a large sample of Dutch sixth graders was studied. In The Netherlands, mathematics education can be characterized as rather heavily reform-based, largely influenced by the principles of Realistic Mathematics Education (RME; Freudenthal 1973, 1991; Treffers 1993). In RME, the meaningful acquisition of a diversity of strategies is central to instruction, exemplified by the early and prolonged focus on (self-invented) computation strategies (e.g., van den Heuvel-Panhuizen 2008). RME became the dominant instructional approach in mathematics curricula for Dutch primary education at the end of the twentieth century (Royal Dutch Society of Arts and Sciences 2009) and almost all elementary schools use a mathematics textbook based on RME principles (Hop and Kraemer 2012; Scheltens et al. 2013; see also Van Zanten and van den Heuvel-Panhuizen 2014). Since teachers rely heavily on the textbook they use, it is very likely that all Dutch schools and classes follow these principles to some extent.

All participating students completed a task of 12 multidigit arithmetic problems (addition, subtraction, multiplication, and division) that had number characteristics expected to elicit specific shortcut strategies. For instance, the multiplication problem 6 × 34.95 was designed to elicit the compensation strategy 6 × 35 − 6 × 0.05. The students were required to show their working in a calculation box, which was used to infer whether a shortcut strategy was used or not. The effects of several factors that previous studies identified as impacting the use of shortcut strategies were investigated: the student factors gender and mathematics achievement level and the task instructions with or without explicit instructions to look for a shortcut strategy. Finally, the performance with the different strategies was analyzed, since the assumed efficiency of shortcut strategies has yet to be supported by empirical results.

This study was guided by four research questions. First, what is the overall extent to which the Dutch sixth graders use shortcut strategies? We hypothesized the frequency of shortcut strategies to be higher than that in previous studies, because the participating students were older and therefore most likely had higher conceptual knowledge facilitating the adaptation of numbers and/or operations that is required for using shortcut strategies (McMullen et al. 2016; Robinson et al. 2016; Torbeyns et al. 2009), as well as more years of schooling in a diversity of (shortcut) strategies. Since previous studies usually resulted in no more than 20% shortcut strategy use, we expected the use of shortcut strategies in the current study would be higher than 20%. Second, to which extents do the student factors gender and general mathematics achievement level affect the likelihood to use shortcut strategies? We hypothesized that boys are more inclined to use shortcut strategies than girls (e.g., Blöte et al. 2001; Hickendorff et al. 2010), and that students with higher mathematics achievement level are more likely to use shortcut strategies than students with lower level achievement (Heinze et al. 2009; Torbeyns et al. 2009; Torbeyns et al. 2006). Third, to what extent does stimulating the use of shortcut strategies by providing an explicit instruction to “have a close look at the numbers and use a clever strategy” increase shortcut strategy use? We hypothesized that students solving the problems with this explicit instruction would use a shortcut strategy more often than students who did not receive this instruction, given previous findings of the effect of task instructions (Blöte et al. 2001; Torbeyns et al. 2009). Fourth and finally, how well do the students perform with the different strategies? According to a rational task analysis, these shortcut strategies are more efficient than standard strategies because they require fewer computational steps (see also Torbeyns et al. 2009). However, the invention and execution of these strategies requires high levels of procedural and conceptual knowledge of numbers, number relations, and operations and the ample practice with the standard strategies most likely leads to a rather fluent efficiency in standard strategies (Lemaire and Siegler 1995; Torbeyns et al. 2009). An unresolved question is how these opposing mechanisms affect students’ performance with shortcut strategies. We hypothesized, however, that students who choose to use a shortcut strategy do this for its efficiency benefits, and that this would be reflected in their superior performance with shortcut strategies compared to standard strategies.

Method

Participants

Participants were 648 students from grade 6 with mean age 12 years 0 months (SD = 5 months) originating from 23 different primary schools, with 9 to 79 students participating per school (average 28 students per school). These schools were spread over the entire country of The Netherlands. The sample consisted of 288 boys, 323 girls, and 37 students with gender information missing.

The majority of the current study’s participants (N = 618) also completed CITO’s End of Primary School Test (CITO 2009), a widely used test in The Netherlands that aims to give an objective advice on the most suitable track of secondary education. This covers the domains of mathematics, language, and study skills with over 150,000 sixth graders participating each year. On the 60-item subtest on mathematics (KR20 = .91), the current sample scored on average 41.8 items correct (SD = 10.5), which was slightly lower than the national average of 42.8 correct (SD = 10.5). For each student, a percentile rank score based on this national sample could be computed. The median national percentile rank in the current sample was 50.0, with first and third quartiles 23.0 and 71.0, respectively. These figures indicate that the mathematics achievement distribution was slightly lower in the current sample than that of the national sample. Ethnic status information was available for 553 students, and the percentage of ethnic minority students in the current sample (21.7%) was markedly higher than that in the national sample (12.0%).

Material

The task consisted of 12 multidigit arithmetic problems. There were three problems per operation: addition, subtraction, multiplication, and division. Each problem was presented as a word problem (i.e., in a realistic context) as is common in current Dutch educational and testing setting (Hickendorff 2013). There were two problems printed per page (A4-sized). Each problem was presented with an empty “calculation box’ next to it, in which students had to write down their working. There was a written instruction at the start of the task stating (translated from Dutch) “It is important to show your working in the calculation box. Thereafter, note down your answer on the line. If you do not write anything in the calculation box, your answer will be scored as incorrect.’

Table 1 shows the number characteristics of the problems, which were chosen to make a shortcut strategy possible. In the addition problems, three numbers had to be added, and the first and third number made a round hundred (problems a and b) or a round thousand (problem c). Combining the first and third addend was the possible shortcut strategy for addition (e.g., 316 + 178 + 284 = 600 + 178 = 778). In the subtraction problems, the subtrahend was close to a round hundred (problems a and b) or a round thousand (problem c). This made two shortcut strategies possible: compensation of the subtrahend (e.g., 827 − 388 = 827 − 400 + 12 = 427 + 12 = 439) or indirect addition: adding-on from the dividend (388 + 12 = 400; 400 + 427 = 827, so the answer is 12 + 427 = 439). In the multiplication problems, one of the multiplicands was close to a round number, making compensation possible (e.g., 7 × 54.95 = 7 × 55 − 7 × 0.05 = 385 − 0.35 = 384.65). Finally, in the division problems, the dividend was close to one hundred times the divisor, also making compensation possible (e.g., 784 : 8 = 800 : 8 − 16 : 8 = 100 − 2 = 98).

Table 1 Number characteristics of the 12 problems
Full size table

There were two versions of the task: version A without an explicit instruction for the students to look for a clever shortcut strategy and version B with this explicit instruction for problems 5 through 12. The order of the problems was the same in both task versions and is shown in Table 2. The first four problems—one of each operation—were the baseline problems, presented without an instruction to look for a shortcut strategy. In task version B, these four baseline problems were followed by a written instruction (translated from Dutch) “Compute the answer to the following problems as cleverly as possible. Have a close look at the numbers in the problem. Show your working in the calculation box”. Furthermore, above each calculation box of problems 5 through 12, the reminder “Compute in a clever way!” Footnote 2 was printed.

Table 2 Design of the two task versions
Full size table

Procedure

The current task was administered as part of a pretest study for the CITO End of Primary School Test. A complete test booklet consisted of six subtests from the domains mathematics, language, and study skills. Students completed each subtest on a different day. One of the subtests on mathematics included the current task of 12 problems, and an additional 16 mathematics problems that were administered for other research purposes. Classroom assignment was used to assign students one of the two task versions A (320 students) or version B (328 students).

The task was administered in the classroom, and each student worked individually without time limit. At the start, teachers read the written instruction regarding the calculation box together with the students. The teachers in the classrooms where task version B was administered were instructed not to mention the upcoming instruction for shortcut strategy use, in order not to affect the spontaneous use of such strategies on the baseline problems.

The students completed the End of Primary School Test (CITO 2009) as part of their final year’s standardized assessment at most one month after the students participated in the current study.

Solution strategies

Students’ solution strategies were coded based on what they wrote in the calculation box. Of all 7776 trials (648 student × 12 problems), in 556 instances (7.2%), this was not possible because (a) the student did not write his/her working in the calculation box (3.8%), (b) the written work was unclear (0.5%), (c) a wrong operation was used; e.g., adding instead of subtracting the numbers (1.1%), or (d) the problem was skipped entirely (1.7%).

In the remaining trials, the solution strategies were categorized into whether a shortcut strategy was used or not. The solution strategy was coded as a shortcut strategy (a) in the addition problems if the first and third terms were combined, (b) in the subtraction problems if either adding-on from the subtrahend using round numbers or compensation of the subtrahend was used, (c) in the multiplication problems if compensation of the second term (i.e., rounding up) was used, and (d) in the division problems if compensation of the dividend (i.e., rounding up) was used.

Six independent raters (undergraduate research assistants) each coded one-sixth of the material. To assess the agreement in categorization, the solution strategies of 63 students (756 trials; 10–11 students per coder) were double-coded by another of the six raters using a rotational design (rater B coded 11 students originally coded by rater A; rater C coded 11 students originally coded by rater B; etc). The percentage agreement was 92.5% and Cohen’s kappa (Cohen 1960) was .75, indicating substantial and satisfactory agreement between raters.

Statistical analyses

The data had a hierarchical structure with problems nested in students and students nested in schools, which necessitated a multilevel modeling approach. Because the dependent variables were dichotomous (shortcut strategy used yes or no in research questions 1 to 3, and answer correct or incorrect in research question 4), we used binary logistic random effect models, or equivalently multilevel logistic regression models, (Jaeger 2008; see also applications by Fagginger Auer et al. 2016a, 2016b). We specified these models with random intercepts for students, schools, and items (De Boeck 2008). Likelihood ratio (LR) tests were used to statistically test whether certain main effects or interaction effects were significant. In LR-tests, the improvement in model fit (log-likelihood) of the more complex model containing a specific effect, compared with the simpler model without that effect, yields a χ2 statistics that is tested for statistical significance (Jaeger 2008). The logistic regression parameter estimates b are scaled on a logit scale. They are tested for statistical significance with the Wald statistics \( z=\frac{b}{SE_b} \). They can be converted to the effect sizes by computing the odds ratio: OR = e b. The analyses were carried out in the general computing platform R (R Core team 2015) using the glmer-function in the lme4-package (Bates et al. 2015).

Results

The results are presented along the four research questions, regarding (1) the overall extent of shortcut strategy use, (2) the influence of students’ gender and mathematics achievement level, (3) the effect of stimulating shortcut strategy use with the explicit instructions to “look for a clever strategy,” and (4) the performance with the different strategies.

Overall extent of shortcut strategy use

The overall frequency distribution of the number of problems solved with a shortcut strategy was very skewed: nearly half of the students (45%) solved none of the problems with a shortcut strategy, and a small percentage of students (3%) solved more than half of the problems with a shortcut strategy. On average, students solved 1.5 problems (SD = 2.1) out of the 12 problems with a shortcut strategy. Thus, shortcut strategies were not very common.

Influence of student factors: gender and mathematics achievement level

Table 3 shows the percentage of shortcut strategy use by problem type, gender, and general mathematics level. Twelve students who skipped half or more of the baseline problems and/or the remaining problems and 35 students without gender information and/or mathematics achievement level score were excluded from the multilevel logistic regression analyses, yielding an effective sample size of 600. The empty model showed that the between-schools variance accounted for 7.6% of all variance in shortcut strategy use (intra-class correlation of .076).

Table 3 Frequency of shortcut strategy use by problem type, gender, and general mathematics level (ML)
Full size table

Next, the effects of gender and mathematics achievement level were added to the model. Both variables significantly affected shortcut strategy use. Girls were less inclined to use a shortcut strategy than boys (b = − 0.51, z = − 3.08, p = 0.002, OR = 0.60), and the higher students’ mathematics level, the larger the probability to use a shortcut strategy (b = 0.52, z = 5.82, p < .001, OR = 1.68). The interaction between gender and mathematics achievement level was not significant (LR χ 2 (1) = 0.29, p > .05).

Spontaneous versus stimulated shortcut strategy use

To investigate whether including an explicit instruction to “have a close look at the numbers and use a clever strategy” affected students’ use of shortcut strategies, the difference between students completing task versions A (without this instruction) and B (with this instruction on problems 5–12) was analyzed in the multilevel logistic regression models. These two groups did not differ in their shortcut strategy use on the four baseline problems, which were presented without this instruction in both task versions (b = − 0.19, z = − 0.65, p > .05, OR = 0.83). Students who received the instructions to look for a clever strategy on problems 5–12 (task version B) were significantly more likely to use a shortcut strategy on those problems than students who did not receive these instructions (task version A), b = 0.71, z = 3.81, p < .001, OR = 2.03. Thus, the task instructions designed to stimulate the use of shortcut strategies did increase students’ shortcut strategy use.

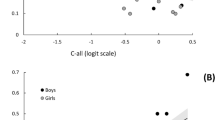
To investigate the influence of these task instructions further, interaction effects of task instruction with problem type, gender, and general mathematics level were tested. The interaction effect of task instruction with problem type was significant (LR χ 2 (3) = 17.07, p < .001), as was the interaction effect of task instruction with mathematics achievement level (LR χ 2 (1) = 16.66, p < .001). The interaction effect of task instruction with gender was not significant (LR χ 2 (1) = 0.37, p > .05). Furthermore, the three-way interaction between task instruction, problem type, and mathematics achievement level was significant (LR χ 2 (3) = 25.74, p < .001). Further inspection of this effect showed that the task instructions only affected the shortcut strategy use in the addition and multiplication problems, see Fig. 1. The effect of the instruction was significant on the addition and the multiplication problems (b = 1.24, z = 5.01, p < .001, OR = 3.54 and b = 0.65, z = 2.53, p = .011, OR = 1.91, respectively). The instruction did not have a significant effect on shortcut strategy use on the subtraction and the division problems (b = 0.52, z = 1.71, p > .05, OR = 1.68 and b = 0.28, z = 1.12, p > .05, OR = 1.32, respectively). Furthermore, the effect of the instruction was larger for students with a higher mathematics achievement level than for students with a lower level in the addition problems only (b = 1.06, z = 6.28, p < .001, OR = 2.89), see Fig. 2. For the other problem types, the effect of the instruction was not affected by students’ mathematics achievement level.

Fig. 1
figure 1

Estimated percentage of shortcut strategy use with and without the instructions to look for a clever strategy, by problem type (averaged across mathematics achievement level)

Full size image
Fig. 2
figure 2

Estimated percentage of shortcut strategy use with and without the instructions to look for a clever strategy on the addition problems, by mathematics achievement level

Full size image

Performance with the different strategies

Table 4 presents the average percentage of correct answers for trials solved with a shortcut strategy and with a standard strategy, by problem type and by gender. Mathematics achievement level was left out of these analyses because of its large overlap with task performance, and including it could obscure relevant effects of other variables. To statistically test the performance difference between shortcut and standard strategies, again, a multilevel logistic regression analysis with random intercepts for students, schools, and items was performed but now with accuracy (0 = incorrect; 1 = correct) as a dependent variable. The empty binary logistic random effect models showed that the between-schools variance accounted for 15.6% of all variance in performance (intra-class correlation of .156). Next, the variable strategy use (shortcut vs. standard) was added as a trial-specific predictor (see for more details Fagginger Auer et al. 2016a; Hickendorff et al. 2009). Overall, the effect of shortcut strategy use on accuracy was not significant (b = − 0.05, z = − 0.42, p > .05, OR = 0.95). However, the interaction effects of strategy use with problem type and with gender were both significant (LR χ 2 (3) = 15.34, p < .001 and LR χ 2 (1) = 7.17, p < .01, respectively).

Table 4 Percentage correct within shortcut and standard strategies, by problem type and by gender
Full size table

Figure 3 graphically illustrates these interaction effects. For addition problems, performance with shortcut strategies was significantly lower than that with standard strategies (b = − 0.55, z = 2.81, p < .01, OR = 0.58). For division problems, the opposite pattern emerged: performance with shortcut strategies was significantly higher than that with standard strategies (b = 0.52, z = 2.41, p = .02, OR = 1.68). On the subtraction and multiplication problems, the difference between shortcut and standard strategies was not significant (b = − 0.45, z = − 1.53, p > .05, OR = 0.64 and b = 0.11, z = 2.41, p > .05, OR = 1.12). Regarding gender, the performance difference between shortcut and standard strategies was not significant for boys (b = 0.24, z = 1.58, p < .001, OR = 1.27). By contrast, for girls, the performance with the shortcut strategies was significantly lower than that with the standard strategies (b = − 0.37, z = − 2.27, p = .024, OR = 0.69).

Fig. 3
figure 3

Estimated percentage of correct solution with shortcut and non-shortcut strategies, by problem type (averaged across gender; left plot) and gender (averaged across problem type; right plot)

Full size image

Discussion

One of the mathematics education reform aims is that children use efficient, clever strategies depending on the number characteristics of the problem (Verschaffel et al. 2007). The present study’s findings, however, show that Dutch children at the end of primary school are not very much inclined to use such shortcut strategies, although the characteristics of the problems administered were very favorable for shortcut strategies. The use of shortcut strategies—spontaneous as well as stimulated by explicit instruction—ranged between 6% (subtraction problems) and 21% (addition problems). In line with previous studies’ results on flexible and various strategy use, boys were more inclined to use shortcut strategies than girls and students with higher mathematics achievement used shortcut strategy more often than their lower achieving peers. Although an explicit instruction in the task to look for a clever strategy increased shortcut strategy use significantly, the effect was small and turned out to be significant for the addition and multiplication problems only. Moreover, in the addition problems, the effect of the instruction was stronger for higher achievers than for lower achievers, similar to the findings of Torbeyns, De Smedt, and colleagues (2009). Finally, overall, shortcut strategies were not more accurate than standard strategies. Thus, the assumed efficiency benefits of shortcut strategies are not reflected in the empirical performance.

One explanation for the overall rather low frequency of shortcut strategy use may be that since children this age have been instructed standard procedures for multidigit arithmetic, they prefer these standardized procedures (cf Selter 2001; Torbeyns and Verschaffel 2013, 2016) and are therefore less inclined to look for specific efficient strategies than before these procedures were instructed. Once students are explicitly taught the digit-based algorithms, they tend to prefer these algorithms over the previously learnt number-based strategies, also on tasks for which the use of shortcut strategies would be equally or even more efficient (Verschaffel et al. 2007). The current study’s findings may well be another example of such “procedural habituation,” even in a mathematics education setting that puts less emphasis on standard procedures, illustrating the pervasiveness of this phenomenon. A related issue is that the current study’s classroom administration procedure with the requirement to write down the solution steps in a calculation box may have implicitly (and unintendedly) conveyed the socio-mathematical norm that the use of a standardized procedure is preferred (see for instance Verschaffel et al. 2009), leading to an underestimation of spontaneous shortcut strategy use.

Similarly, previous studies have shown that what students do on a standard task (their strategic behavior) does not fully reflect what they know (their strategic knowledge) (e.g., Blöte et al. 2001). Xu et al. (2017) recently found this so-called potential flexibility (what students know) and practical flexibility (what students do) in the domain of equation solving to be distinct but related. The current study only measured practical flexibility, ignoring potential flexibility. That implies that some students may have known the shortcut strategies but did not use them (for instance because of procedural habituation, or because of the task administration procedure). Other administration procedures, such as individual interviews where students solve this kind of problems and verbally report their solution steps, may yield higher frequencies of shortcut strategies. Furthermore, other task instructions, for instance the request to generate multiple strategies, may yield a more complete account of whether students know shortcut strategies but do not use them in a setting like the current one. However, even if these results would show more knowledge and/or use of shortcut strategies, the finding, that in a standard school, mathematics task students hardly show this knowledge in their strategic behavior remains. An educational implication may be that the socio-mathematical norms should support the adaptive, flexible, and creative use of (shortcut) strategies also in mathematics tests, and should discourage the routine use of standard procedures without having had a close look at the numbers of the specific problem at hand.

Another interesting finding is the difference between problem types. Compared to the other three arithmetic operations, the addition problems were solved more frequently with a shortcut strategy and the effect of the explicit instruction to look for a clever strategy was larger. A possible explanation may be the specific shortcut strategy aimed for. In the subtraction, multiplication, and division problems, the compensation strategy was the intended shortcut strategy, because one of the operands was slightly below a round number. The addition problems targeted a different shortcut strategy, efficiently regrouping the three addends, which could require other processes, such as inhibiting the left-to-right procedure (Robinson et al. 2016). Future studies may overcome this in two different ways. The first possibility is to replace the current addition problems by ones facilitating the use of the compensation strategy (i.e., where one of the addends is slightly below a round number, such as 54.95 + 132 = ?). This would allow a more consistent comparison of the use of shortcut strategies between problem types/operations. The other possibility is to include a wider range of shortcut strategies, and consequently problems, for all four arithmetic operations, which would allow for a more complete picture of students’ (shortcut) strategy repertoire. Such a varied set of problems could form the basis of developing a measurement instrument of individual differences in shortcut strategy use, which might be used in research evaluating the impact of instruction on students’ adaptivity.

Another remarkable finding is that shortcut strategies generally did not yield more correct answers than the standard strategies, although this differed by problem type (shortcut strategies were more efficient than standard strategies in division problems, but less efficient than standard strategies in addition problems, whereas there was no efficiency difference in the subtraction and multiplication problems) and by gender (shortcut strategies were less efficient than standard strategies in girls, whereas there was no efficiency difference in boys). That means that the assumed efficiency benefits of shortcut strategies are not supported by the empirical efficiency data. This probably related to the normative definition of “efficient shortcut strategy” that was used, which ignores individual differences between students. A shortcut strategy is likely not an efficient strategy for all individual students, since it is not necessarily an easy strategy: it requires conceptual understanding and perhaps increased cognitive load (Robinson et al. 2016; Torbeyns et al. 2009). The finding that children with higher mathematical achievement levels used shortcut strategies more often than their lower achieving peers supports this idea. Moreover, they add to the body of literature questioning the desirability and feasibility of striving for adaptivity and flexibility for low mathematics achievers (e.g., Fagginger Auer et al. 2016a; Hickendorff et al. 2010; Torbeyns et al. 2006), although there are studies showing promising results (e.g., Peltenburg et al. 2012). Several scholars argue that low mathematics achievers might benefit from instruction in a single strategy instead of multiple strategies (Kroesbergen & Van Luit 2003; National Mathematics Advisory Panel 2008; Royal Dutch Society of Arts and Sciences 2009; Timmermans & van Lieshout 2003). Further research into the levels of flexibility and adaptivity low mathematical achievers can obtain in different domains and under different (instructional) conditions are necessary, to provide insights into the feasibility of fostering flexibility and adaptivity for students of all levels of mathematical competence. However, this cannot go without a discussion about the desirability of this aim. Since instructional time and efforts can only be spent once, it is important to prioritize the goals of mathematics education, in particular for low mathematics achievers.

Regarding the efficiency of shortcut strategies, it is important to note that the current study’s strategy performance data are possibly biased by selection effects (Siegler and Lemaire 1997). For instance, characteristics of the students that selected specific strategies may have biased the accuracy data. Such a selection effect may explain the opposite results for division and addition problems: in division, shortcut strategies were used rather infrequently and therefore possibly predominantly by high achieving students, explaining that shortcut strategies were more accurate than standard strategies. By contrast, shortcut strategies were used rather frequently in addition problems, and therefore by higher as well as lower achieving students, which may explain why shortcut strategies were less accurate than standard strategies.

Furthermore, the current study’s choice-only design does not allow for assessment of how students would have performed with the strategy they did not select. It might be that students did not choose a shortcut strategy since it was not the most efficient strategy for them, and consequently they made an adaptive strategy choice by not using the shortcut strategy. The gender differences in use and efficiency of shortcut strategies corroborate with this pattern: it may be that girls were less inclined to use shortcut strategies than boys because for girls, there were efficiency costs of using shortcut strategies, whereas for boys, there were no costs (nor benefits). To investigate such adaptivity with respect to individual strategy efficiency characteristics, a choice/no-choice design is necessary (Siegler and Lemaire 1997; see also Luwel et al. 2009). In such a study, students would solve problems in two different types of conditions: one in which they are free to choose between a shortcut or a non-shortcut strategy (the choice condition) and the other in which they are required to use one particular strategy (the no-choice conditions: one for shortcut strategies and another for non-shortcut strategies). However, such a procedure may negatively affect the ecological validity of the findings: the possible strategies are constrained to only two types or approaches and the artificiality of the situation may well affect students’ behavior (see for a more elaborate argumentation Threlfall 2009).

A final issue is that the characterization of mathematics instruction was based solely on the written materials (educational goals, curricular guidelines, and mathematics textbooks), and we did not collect data on how this “written curriculum” was implemented in the classroom (the “enacted curriculum”; Stein et al. 2009). Future research could attempt to measure how the use of shortcut strategies is implemented in the enacted curriculum, for instance by teacher interviews or classroom observations, to evaluate the effect of instruction on students’ adaptive use of shortcut strategies in a more direct way.

In conclusion, the present study is the first to investigate students’ use of shortcut strategies across the four arithmetic operations simultaneously, using a large and representative sample of sixth graders who followed an instructional trajectory based on mathematics education reform principles. By incorporating the current study’s problems in a regular mathematics test, the spontaneous use of shortcut strategies was assessed in an ecologically valid setting. Overall, this spontaneous use of shortcut strategies was low, in particular for students with below-average mathematics achievement level. Furthermore, an explicit written instruction to look for a clever strategy had minor effects at most. These outcomes have relevant implications for the instructional trajectories that emphasize the importance of these strategies, such as realistic mathematics education. In particular, the feasibility of striving for adaptive expertise in children of low mathematics level can be called into question.