Irr and equivalence of cash-flow streams, loans, and portfolios of bonds

Abstract

We show, through a Linear Algebra approach, that a general deterministic cash-flow stream admits a given Internal Rate of Return (irr, either constant or time-varying) if, and only if, it can be replicated by a suitable portfolio of bonds, each with yield to maturity equal to that same irr. Five particular replicating portfolios are examined, including and generalizing other representations known from the the literature, which allow for a unified, irr-based, interpretation of apparently diverse objects. Considering the amortization of a loan as a particular case, further equivalences are found and lead to some original consideration.

1 Introduction

The internal rate of return (irr) of any sequence of deterministic cash-flows—which we call, in full generality, a project—is usually defined as any interest rate which makes the project “fair”, meaning that, if the cash flows of the project are discounted according to such a rate, a null overall sum obtains. Its definition is often traced back to Keynes (1936), who called it marginal efficiency of capital, although (Dorfman 1981) reports that it appeared in the economic debate back since (Fisher 1907) and even (von Böhm-Bawerk 1889), thus making it one of the most famous and long established concepts in Financial mathematics.

Since irrs are root of polynomials, every project usually has several irrs in the complex field, and it may have more than one real irr, or no real irr at all. It is nevertheless a long-known result that, when the project under consideration is either a pure investment or a pure loan (that is, when the cash-flows change sign one single time, respectively, either from negative to positive or from positive to negative), a unique real irr exists, which traditionally is given a natural interpretation as either the yield on the invested capital (for pure investments) or the interest rate due on the borrowed amount (for pure loans). This allows for associating an easily interpretable irr to a wide class of projects. Furthermore, the irr comes in the form of a yearly percentage, which makes it very easy to understand and compare between projects or with other indices, such as roi/roe, or as the (opportunity) cost of capital. It is not surprising, thus, that the irr has enjoyed a great and time-standing popularity in several fields: for instance, Graham and Harvey (2001) find that irr is used by many firms for valuating investment decision-making, and Gredil et al. (2023) show how it is used (with other return rates) in private equity.

On the other hand, through the years, a lot of puzzles and flaws of the irr have been exposed and studied in the literature: see, for instance, Lorie and Savage (1955), Levi (1957), Hirshleifer (1958), Levi (1964), and Teichroew et al. (1965), or more recently Jensen and Smith (1984), Castagnoli (1986), and Brealey et al. (2009). A full analysis of such studies would go far beyond the scope of this paper, but the interested reader may find quite a thorough review in Magni (2013), who exhibits no less than eighteen flaws of the irr, in the introduction to Magni (2014), where several debates about the irr are put into an historical perspective, and in Magni (2016) (and references therein), which provide an extensive survey of the literature on irr and, in particular, of the solutions to its flaws. Remarkably, some of the results (most notably (Hazen 2003) and Magni (2010)) allow for classifying every project either as a “net investment” or a “net borrowing”, therefore allowing for an unambiguous interpretation of the irr.

What is relevant for the purpose of this paper is that several of the works addressing the limitations of the irr (see, e.g., Hazen (2003), Hartman and Schafrick (2004), Magni (2010), Cuthbert (2018), and again Magni (2013), and Magni (2016)) directly or indirectly employ a “decomposition” technique, consisting of building a suitable set of bonds or other projects, such that the overall cash-flow stream of the resulting portfolio coincides with the stream of the original operation: such an object, in Mathematical Finance, is called a “hedging portfolio”. Such decompositions are often linked to the irr of the original project, which also in most of the cases coincides with the yield (either constant or variable) of the bonds or projects that build the hedging portfolio. The same technique appeared in some works with national relevance in Italy (in particular, see Cacciafesta (2015), Fersini and Olivieri (2015), and Piacitelli et al. (2021)), where it was surprisingly used to try both proving and disproving the presence of “anatocism” (which, according to the Italian law, has a more strict and proper meaning than simply “compound interest”) in the usual amortization plan of a loan with constant rate and payments. In every cited paper, the used decompositions were introduced each as a “stand-alone” result, possibly just citing previous papers which used the exact same particular decomposition.

The main, and starting, result of the present paper is that all the above decompositions, and several other ones, are just particular cases of a unique result. Through standard Linear Algebra methods, we shall indeed prove that a given interest rate is an irr for a project if, and only if, the project can be hedged by a portfolio of bonds whose yields to maturity all equal the given rate itself. This does not depend at all on the nature of the original project, and therefore is completely independent on the given irr being a yield or a cost, which can still be investigated with the known methods from the cited literature: as such, our result can provide a visual interpretation of the irr to be put alongside the existing ones. Furthermore, we shall investigate the financial meaning of five particular, and quite natural, decompositions, both in the general case and in the special case of loans amortization, which will lead to some non trivial considerations and possibly to adding some new insights. In particular, one of these decompositions patently emphasizes the known fact that some concepts defined in independent frameworks, such as the outstanding capital of Peccati (1987), the outstanding balance of loans amortization, or the investment balance of Hartman and Schafrick (2004) are actually particular instances of the same concept, i.e., roughly speaking, the remaining value that the project is worth at a given date, also called in full generality an investment stream in, e.g., Hazen (2003) and Magni (2010) (see also Magni (2020), Chapter 1, for a more detailed and comprehensive discussion). Although our work may not directly affect the way irr can be used as a measure of profitability or as a choice criterion (which are investigated in the papers cited above), it will draw several connections who will allow, e.g., to apply to a wider set of objects some known results (as in some examples we provide).

For the sake of readability, most of the paper will deal with the particular case where the projects under consideration have equidistant cash flows and the irrs are supposed to be constant in time. We shall nevertheless explain how these results can be adapted to hold, unchanged, even in the case of nonconstant time periods and time-varying yield rates: notably, in such a case, our description will adapt to the model of Magni (2010) and to the internal financial laws of Peccati (1989), besides of course to loans with variable rates. Finally, we shall deal with real rates only: although our results work unchanged with complex irrs, we have found no deeper financial insight coming to taking them into consideration. Readers interested in complex rates of return may refer to Pierru (2010), Osborne (2010), and Osborne (2014) .

The paper is organized as follows.

In Sect. 2, the notations are set and the main definitions are given. Standard interpretations and considerations about the irr are recalled.

Section 3 contains the main result of the paper. After introducing some additional notation, which will make easier to handle the concepts under consideration, two technical lemmas will be stated and proved, namely, that the set of all projects with a given irr make a linear (sub)space, that the set of all bonds (either traditional or zero-coupon) with yield to maturity equal to such an irr make a spanning system of that space and, finally, that some particular choices of bonds form a basis for it. The main theorem will then follow as an immediate consequence, and some examples will be given. Some particular portfolios will be examined in detail, namely, portfolios of “single period bonds” (i.e., bonds with maturity immediately after the issue date), portfolios of bonds with common issue date at the earliest possible date and variable maturity, and portfolios of bonds with variable issue date and common maturity at the last possible date, where each of the last two may be composed by either zero-coupon or traditional bonds. Such portfolios make very natural and somewhat significant choices, but the reader will undoubtedly realize (and it will be recalled) that they are not the only possible ones, as lots of other combinations (even with general projects instead of bonds) may be taken under consideration.

The results of Sect. 3 are applied in Sect. 4 to the particular case of a loan amortization. First of all, the general rules of an elementary amortization are introduced, which build the simplest (and possibly the most used) framework for the amortization of a loan, here called a meal (Method for Elementary Amortization of Loans). Then, the five particular decompositions seen in Sect. 3 are applied, and examined to find some interesting (and sometimes not trivial) economic interpretations. In particular, it is argued that all loan amortization techniques, even the most exotic ones, can always be reduced to a meal with a suitable interest rate (which, not surprisingly, is of course equal to the irr of the original amortization plan, that is to say, with its so-called Annual Percentage Rate, or apr).

Finally, Sect. 5 is dedicated to pointing out how the results of the paper apply, without significant changes, to variable interest rates and to more general sets of maturities. Moreover, it is shown how our method has interesting links with the decomposition of the Net Present Value of an operation into yearly contributions as proposed by Peccati (1987).

2 Notation and classical interpretation

Let $n\in \mathbb {N}$. In this paper, any situation when an agent goes through the exchange of the monetary amounts $a_0, a_1, \ldots , a_n\in \mathbb {R}$ (with the usual convention that positive values represent inflows and negative values represent outflows) at the maturities $t_0< t_1< \ldots < t_n$ is called a project and denoted by

$$\begin{aligned} \begin{array}{c|c|c|c|c|c} t_0 &{} t_1 &{} t_2 &{} \cdots &{} t_{n-1} &{} t_n \\ \hline a_0 &{} a_1 &{} a_2 &{} \cdots &{} a_{n-1} &{} a_n \\ \end{array}. \end{aligned}$$

(1)

If a project is given, its discounted cash flow dcf function is defined by the position

$$\begin{aligned} \textsc {dcf}\ :(-1,+\infty )\rightarrow \mathbb {R}\,\quad \textsc {dcf} (r):= \sum _{k=0}^n a_k (1+r)^{t_0-t_k}: \end{aligned}$$

from the financial point of view, the dcf is the function that associates to every $r\in (-1,+\infty )$ the sum of the discounted values at time $t_0$, according to the interest rate r, of all the amounts involved in the project. The evaluation $\textsc {dcf} ({\overline{r}})$ of the dcf at a given interest rate ${\overline{r}}$ is called the net present value (npv) of the operation at that rate.

An evocative interpretation of the npv is given as follows. Suppose that all of the money movements of the project are deposited into, or withdrawn from, a bank account which produces and asks interests at rate ${\overline{r}}$ (the same for deposits and for loans). The final balance of the account will be the same that would obtain if an amount equal to the npv be invested from time $t_0$ until time $t_n$ at compound interest ${\overline{r}}$ (i.e., so to say, in that same account).

Every interest rate $r^*\in (-1,+\infty )$ such that $\textsc {dcf} (r^*)=0$ is called an internal rate of return irr of the project: note that irrs are roots of a polynomial equation, so that they need not be unique, nor even exist.

The irr can be immediately read as the yield of the project, in the case of an investment, or as its overall cost, in the case of a loan: significantly, the Annual Percentage Rate (apr) of a financing project can be calculated as its irr, properly taking into account all of the fees and charges. As such, an agent can evaluate the profitability of a project by comparing its irr with the typical yield of her/his usual investments: an investment is profitable if the irr is greater than her/his usual yield, and a loan is profitable in the opposite case.

The “bank account” interpretation seen for the npv is even crispier in the case of the irr: if the cash flows of the project are borrowed from, or invested into, a bank account with working interest rate $r^*$, such a rate $r^*$ is an irr for the project if, and only if, the final balance of the account is null.¹

All in all, the irr enjoys a good popularity among financial operators for at least two reasons. First of all, the irr can be easily expressed as a yearly “percentage” of profitability or cost, which makes it quite easy (at least apparently) to communicate and to understand. Furthermore, unlike other criteria (such as the npv itself), the irr of a project comes from an “objective” calculation, without the need to take into account any “subjective” conditions of the agent undertaking the project itself.

We already mentioned in the introduction that a long discussion can be found in the literature about irr ’s oddities and “flaws”. Since we shall use it as a working example for our decomposition theorem (Example 1 below), we just mention that Lorie and Savage (1955) started from a very sensible problem of firm management to end up with a project (the algebraic difference of the cash flows generated by two possible alternatives) which could not be easily to classify neither as an investment nor as a loan, and which admitted two different irrs without a clear financial meaning.

3 Decomposition into elementary projects

It is immediate to identify the project (1) with the vector $[a_0\ \,a_1\ \,a_2\ \,\cdots \ \,a_n]\in \mathbb {R}^{n+1}$, by orderly associating the amounts $a_0, a_1, \dots , a_n$ to the maturities $t_0, t_1, \dots , t_n$. Throughout this and the following section, the set of maturities is supposed (without loss of generality, as it will be argued in Sect. 5) to be $\{0, 1, 2, \dots , n\}$ ($n\in \mathbb {N}$).

The following two classes of simple projects, collectively called elementary projects, are introduced. They will be central in the interpretation proposed in this note.

Definition

Let $t, s\in \mathbb {N}$, $0\leqslant t<s\leqslant n$ and $r\in (-1,+\infty )$.

• (i) $\mathbb {I}_{t,s}(r)$ denotes the project with a single unit outflow at time t and a single inflow $(1+r)^{s-t}$ at time s:

  

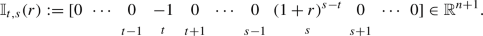
• (ii) $\mathbb {Y}_{t,s}(r)$ denotes the project with a single unit outflow at time t, inflows equal to r from time $t+1$ to time $s-1$ and a final inflow of $1+r$ at time s:

  

Remark 1

Classically, $\mathbb {I}_{t,s}(r)$ is called a zero-coupon bond issued at time t and with maturity s; its yield to maturity (i.e., its unique irr) is of course r. Analogously, $\mathbb {Y}_{t,s}(r)$ is called a traditional bond, or bullet bond issued at time t with maturity s and coupon rate r; again, its yield to maturity (and unique irr) is plainly r. Note that $\mathbb {I}_{t-1,t}(r) = \mathbb {Y}_{t-1,t}(r)$ for every $t=1,2, \dots , n$ and every $r\in (-1,+\infty )$: as such, bonds of this kind will be called single period bonds without the need to specify whether they are traditional or zero-coupon (such bonds coincide with the “very simple transactions” of Cuthbert (2018)).

In the case of bonds, the irr is unique and it has a crisp and immediate meaning: it is a cost for the issuer and a yield for the purchaser.

The main result of this paper will be proved through two preliminary lemmas.

Lemma 1

Let $n\in \mathbb {N}$, $r\in (1,+\infty )$, and denote by ${\mathcal {S}}_n(r)$ the set of all projects on the set $\{0, 1, 2, \dots , n\}$ of maturities with irr r. Then:

• (i) ${\mathcal {S}}_n(r)$ is a linear n-dimensional subspace of $\mathbb {R}^{n+1}$, containing all the elementary projects $\mathbb {I}_{t,s}(r)$ and $\mathbb {Y}_{t,s}(r)$ ($0\leqslant t<s \leqslant n$);

• (ii) the set $\{\mathbb {I}_{t-1,t}(r): t=1,2,\ldots ,n\}$ is a basis of ${\mathcal {S}}_n(r)$;

• (iii) the sets $\{\mathbb {I}_{t,s}(r): 0\leqslant t<s \leqslant n\}$ and $\{\mathbb {Y}_{t,s}(r): 0\leqslant t<s \leqslant n\}$ are both spanning systems for ${\mathcal {S}}_n(r)$.

Proof

(i) It is enough to note that

$$\begin{aligned} {\mathcal {S}}_n(r) = \left\{ [a_0\ \,a_1\ \,a_2\ \,\cdots \ \,a_n]\in \mathbb {R}^{n+1}: \sum _{t=0}^n a_t (1+r)^{-t} = 0 \right\} \end{aligned}$$

is the set of the solutions of a linear equation, i.e., a hyperplane in $\mathbb {R}^{n+1}$. Of course, all the elementary projects $\{\mathbb {I}_{t,s}(r): 0\leqslant t<s \leqslant n\}$ and $\{\mathbb {Y}_{t,s}(r): 0\leqslant t<s \leqslant n\}$ belong to ${\mathcal {S}}_n(r)$, because, as already pointed out, they have r as (the unique) irr.

(ii) It is a standard Linear Algebra result that a set of n vectors in an n-dimensional linear space is a spanning system if and only if it is linearly independent², so it is enough to check linear independence of $\{\mathbb {I}_{t-1,t}(r)\}_t$. Suppose that $\sum _{t=1}^n \beta _t \mathbb {I}_{t-1,t}(r)=[0\ \,0\ \,\cdots \ \,0]$: since it is also

$$\begin{aligned} \sum _{t=1}^n \beta _t \mathbb {I}_{t-1,t}(r) = [-\beta _1\quad (1+r)\beta _1 - \beta _2 \quad \cdots \quad (1+r)\beta _{n-1} - \beta _n \quad (1+r)\beta _n]\, \end{aligned}$$

it is straightforward to see that it has to be $\beta _1=0$, which makes the second component equal to $-\beta _2$, thus allowing to conclude that $\beta _2=0$ as well, and so on, thus proving linear independence of $\{\mathbb {I}_{t-1,t}(r)\}_t$.

(iii) It is enough to note that $\{\mathbb {I}_{t-1,t}(r)\}_t$ is contained both in $\{\mathbb {I}_{t,s}(r)\}_{t<s}$ and in $\{\mathbb {Y}_{t,s}(r)\}_{t<s}$, because, as already pointed out, $\mathbb {I}_{t-1,t}(r) = \mathbb {Y}_{t-1,t}(r)$ for every $t=1,2, \dots , n$. $\square$

Remark 2

In proving part (iii) of Lemma 1, it has been pointed out that $\{\mathbb {I}_{t-1,t}(r)\}_t \subseteq \{\mathbb {I}_{t,s}(r)\}_{t<s} \cap \{\mathbb {Y}_{t,s}(r)\}_{t<s}$. The opposite inclusion holds as well, because the only way for a bond to simultaneously have and not have intermediate payments is not having intermediate dates at all, which amounts to saying, reaching maturity in the date immediately following issue. Therefore, we can conclude that $\{\mathbb {I}_{t-1,t}(r)\}_t = \{\mathbb {I}_{t,s}(r)\}_{t<s} \cap \{\mathbb {Y}_{t,s}(r)\}_{t<s}$.

It is possible to explicitly show that $\{\mathbb {I}_{t-1,t}(r)\}_t$ is a spanning system for ${\mathcal {S}}_n(r)$. Given indeed any $[a_0\ \,a_1\ \,\cdots \ \,a_n]\in {\mathcal {S}}_n(r)$, set $\beta _1 = -a_0$, $\beta _2 = -a_1 - a_0(1+r)$, and, in general,

$$\begin{aligned} \beta _t = -\sum _{k=0}^{t-1} a_k (1+r)^{t-k-1} \qquad (t = 3, \dots , n); \end{aligned}$$

take into consideration the portfolio $\sum _{t=1}^n \beta _t \mathbb {I}_{t-1,t}(r)$. Recalling that each $\mathbb {I}_{t-1,t}(r)$ yields non null amounts at times $t-1$ and t only:

• at time 0, the portfolio yields the overall amount $\beta _1\cdot (-1) = a_0$;

• at the generic time $t=1,2,\ldots n-1$, the portfolio yields the amount $\beta _t(1+r)-\beta _{t+1} = - \sum _{k=0}^{t-1} a_k (1+r)^{t-k} + \sum _{k=0}^{t} a_k (1+r)^{t-k} = a_t$;

• at time n, the portfolio yields $\beta _n\cdot (1+r) = -\sum _{t=0}^{n-1} a_t (1+r)^{n-t} = -(1+r)^n\cdot \sum _{t=0}^{n-1}a_t (1+r)^{-t}$. Since $\sum _{t=0}^{n}a_t (1+r)^{-t}=0$, because r is an irr for the project, it follows that $-(1+r)^n\cdot \sum _{j=0}^{n-1}a_t (1+r)^{-t} = (1+r)^n\cdot a_n (1+r)^{-n} = a_n$.

As a particular case, it is immediate to see how $\{\mathbb {I}_{t-1,t}(r)\}_t$ spans both $\{\mathbb {I}_{t,s}(r)\}_{t<s}$ and $\{\mathbb {Y}_{t,s}(r)\}_{t<s}$: for every $0\leqslant t<s \leqslant n$,

$$\begin{aligned} \mathbb {I}_{t,s}(r) = \sum _{k=t+1}^{s} (1+r)^{k-t-1}\mathbb {I}_{k-1,k}(r) \quad \text {and}\quad \mathbb {Y}_{t,s}(r) = \sum _{k=t+1}^{s} \mathbb {I}_{k-1,k}(r). \end{aligned}$$

A final, but remarkable, consideration is in order. Given the expressions for the coefficients $\beta _t$, $t=1,2, \dots , n$, it is straightforward to check that

$$\begin{aligned} \beta _{t+1} = (1+r)\beta _t - a_t\, \end{aligned}$$

(2)

which describes the dynamic evolution of the capital ($\beta _t$) invested in the project, as dictated by the irr. Such a value is referred to as the “outstanding capital” in Peccati (1987) and as the “internal”, or “Hotelling”, value in Magni (2010, 2013). This recursive relation also serves as the foundational block in Hazen (2003). Magni (2010, 2013) extends this concept in a broader framework, referred to as the “fundamental economic relation” (eq. (1) in Magni (2013)) or the “law of motion” (eq. (1.1) in Magni (2020)), demonstrating its applicability to any economic (real or financial) asset and its role as a unifying principle in finance and accounting.

Example 1

(Lorie and Savage 1955) showed that, on the set $\{0, 1, 2\}$ of maturities, the project $[{-{1\,600}}\ \,{10\,000}\ \,{{-10\,000}}]$ has two irrs: $i^*_1 = 25\%$ and $i^*_2 = 400\%$. By Lemma 1(ii), the project can be decomposed as follows: according to $i^*_1 = 25\%$ (note that $-{8\,000} = -{10\,000} - ({-1\,600})\cdot {1.25} = -a_0 - a_1(1+r)$, as in Remark 2 above),

$$\begin{aligned} \begin{array}{c|c|c|c} \text {elementary project} &{} t=0 &{} t=1 &{} t=2 \\ \hline {1\,600}\cdot \mathbb {I}_{0,1}({0.25}) &{} {-1\,600} &{} {2\,000} &{} 0 \\ \hline {-8\,000}\cdot \mathbb {I}_{1,2}({0.25}) &{} 0 &{} {8\,000} &{} {-10\,000} \\ \hline \text {overall} &{} {-1\,600} &{} {10\,000} &{} {-10\,000} \end{array} \end{aligned}$$

and, according to $i^*_2 = 400\%$ (and with $-{2\,000} = -{10\,000} - ({-1\,600})\cdot {5}$),

$$\begin{aligned} \begin{array}{c|c|c|c} \text {elementary project} &{} t=0 &{} t=1 &{} t=2 \\ \hline {1\,600}\cdot \mathbb {I}_{0,1}(4) &{} {-1\,600} &{} {8\,000} &{} 0 \\ \hline {-2\,000}\cdot \mathbb {I}_{1,2}(4) &{} 0 &{} {2\,000} &{} {-10\,000} \\ \hline \text {overall} &{} {-1\,600} &{} {10\,000} &{} {-10\,000} \end{array}\quad . \end{aligned}$$

Example 2

The project $[{-302.4}\ \ {1\,650}\ \ {-3\,350}\ \ {3\,000}\ \ {-1\,000}]$, on the set $\{0,1,2,3,4\}$ of maturities, has four irrs: ${11.1111}\%$, ${25}\%$, ${42.8571}\%$, and ${66.6667}\%$.

• (a) With $r = {0.1111}$, the project can be decomposed as

  $$\begin{aligned} \begin{array}{c|c|c|c|c|c} \text {elementary project} &{} t=0 &{} t=1 &{} t=2 &{} t=3 &{} t=4 \\ \hline {302.4}\cdot \mathbb {I}_{0,1}({0.1111}) &{} {-302.4} &{} {336} &{} {0} &{} {0} &{} {0} \\ \hline {-1\,314}\cdot \mathbb {I}_{1,2}({0.1111}) &{} {0} &{} {1\,314} &{} {-1\,460} &{} {0} &{} {0} \\ \hline {1\,890}\cdot \mathbb {I}_{2,3}({0.1111}) &{} {0} &{} {0} &{} {-1\,890} &{} {2\,100} &{} {0} \\ \hline {-900}\cdot \mathbb {I}_{3,4}({0.1111}) &{} {0} &{} {0} &{} {0} &{} {900} &{} {-1\,000} \\ \hline \text {overall} &{} {-302.4} &{} {1\,650} &{} {-3\,350} &{} {3\,000} &{} {-1\,000} \\ \end{array}. \end{aligned}$$

• (b) With $r = {0.25}$, the project can be decomposed as

  $$\begin{aligned} \begin{array}{c|c|c|c|c|c} \text {elementary project} &{} t=0 &{} t=1 &{} t=2 &{} t=3 &{} t=4 \\ \hline {302.4}\cdot \mathbb {I}_{0,1}({0.25}) &{} {-302.4} &{} {378} &{} {0} &{} {0} &{} {0} \\ \hline {-1\,272}\cdot \mathbb {I}_{1,2}({0.25}) &{} {0} &{} {1\,272} &{} {-1\,590} &{} {0} &{} {0} \\ \hline {1\,760}\cdot \mathbb {I}_{2,3}({0.25}) &{} {0} &{} {0} &{} {-1\,760} &{} {2\,200} &{} {0} \\ \hline {-800}\cdot \mathbb {I}_{3,4}({0.25}) &{} {0} &{} {0} &{} {0} &{} {800} &{} {-1\,000} \\ \hline \text {overall} &{} {-302.4} &{} {1\,650} &{} {-3\,350} &{} {3\,000} &{} {-1\,000} \\ \end{array}. \end{aligned}$$

• (c) With $r = {0.4286}$, the project can be decomposed as

  $$\begin{aligned} \begin{array}{c|c|c|c|c|c} \text {elementary project} &{} t=0 &{} t=1 &{} t=2 &{} t=3 &{} t=4 \\ \hline {302.4}\cdot \mathbb {I}_{0,1}({0.4286}) &{} {-302.4} &{} {432} &{} {0} &{} {0} &{} {0} \\ \hline {-1\,218}\cdot \mathbb {I}_{1,2}({0.4286}) &{} {0} &{} {1\,218} &{} {-1\,740} &{} {0} &{} {0} \\ \hline {1\,610}\cdot \mathbb {I}_{2,3}({0.4286}) &{} {0} &{} {0} &{} {-1\,610} &{} {2\,300} &{} {0} \\ \hline {-700}\cdot \mathbb {I}_{3,4}({0.4286}) &{} {0} &{} {0} &{} {0} &{} {700} &{} {-1\,000} \\ \hline \text {overall} &{} {-302.4} &{} {1\,650} &{} {-3\,350} &{} {3\,000} &{} {-1\,000} \\ \end{array}. \end{aligned}$$

• (d) With $r = {0.6667}$, the project can be decomposed as

  $$\begin{aligned} \begin{array}{c|c|c|c|c|c} \text {elementary project} &{} t=0 &{} t=1 &{} t=2 &{} t=3 &{} t=4 \\ \hline {302.4}\cdot \mathbb {I}_{0,1}({0.6667}) &{} {-302.4} &{} {504} &{} {0} &{} {0} &{} {0} \\ \hline {-1\,146}\cdot \mathbb {I}_{1,2}({0.6667}) &{} {0} &{} {1\,146} &{} {-1\,910} &{} {0} &{} {0} \\ \hline {1\,440}\cdot \mathbb {I}_{2,3}({0.6667}) &{} {0} &{} {0} &{} {-1\,440} &{} {2\,400} &{} {0} \\ \hline {-600}\cdot \mathbb {I}_{3,4}({0.6667}) &{} {0} &{} {0} &{} {0} &{} {600} &{} {-1\,000} \\ \hline \text {overall} &{} {-302.4} &{} {1\,650} &{} {-3\,350} &{} {3\,000} &{} {-1\,000} \\ \end{array}. \end{aligned}$$

Lemma 2

Let $n\in \mathbb {N}$, $r\in (1,+\infty )$, and denote by ${\mathcal {S}}_n(r)$ the linear (sub)space of all projects on the set $\{0, 1, 2, \dots , n\}$ of maturities with irr r. The following sets:

• (i) $\{\mathbb {I}_{t-1,t}(r): t=1, 2,\ldots , n\}$,

• (ii) $\{\mathbb {I}_{t-1,n}(r): t=1, 2,\ldots , n\}$,

• (iii) $\{\mathbb {I}_{0,t}(r): t=1, 2,\ldots , n\}$,

• (iv) $\{\mathbb {Y}_{t-1,n}(r): t=1, 2,\ldots , n\}$, and

• (v) $\{\mathbb {Y}_{0,t}(r): t=1, 2,\ldots , n\}$

are bases of ${\mathcal {S}}_n(r)$.

Proof

Note that part (i) is simply a rewording of Lemma 1(ii), included here to gather all the bases in a single statement. Parts (ii-v) are proved just like (i) (see Lemma 1 again): all the involved sets have exactly n elements and therefore it is enough to see that each of them is a linearly independent set, which quickly follows from their definition. $\square$

Remark 3

It is straightforward (although a little toilsome here and there) to calculate the coefficients that yield the generic project $[a_0\ \,a_1\ \,\cdots \ \,a_n]$ as a linear combination of the bases shown in Lemma 2:

• (i) with the basis $\{\mathbb {I}_{t-1,t}(r)\}_t$, as seen in Remark 2, the coefficients $\beta _t = -\sum _{j=0}^{t-1} a_j (1+r)^{t-j-1}$ ($t = 1, 2, \dots , n$) are used;

• (ii) with $\{\mathbb {I}_{t-1,n}(r)\}_t$, the coefficients are $\beta _t = -a_{t-1}$ ($t = 1, 2, \dots , n$);

• (iii) with $\{\mathbb {I}_{0,t}(r)\}_t$, the coefficients are $\beta _t = a_t(1+r)^{-t}$ ($t = 1, 2, \dots , n$);

• (iv) with $\{\mathbb {Y}_{t-1,n}(r)\}_t$, the coefficients are $\beta _1 = -a_0$, $\beta _2 = -a_1 - ra_0$, $\beta _t = -a_{t-1} - r\cdot \sum _{j=0}^{t-2} a_j(1+r)^{t-j-2}$ ($t = 2, \dots , n$);

• (v) finally, with $\{\mathbb {Y}_{0,t}(r)\}_t$, the coefficients are $\beta _t = a_t(1+r)^{-1} - r\cdot \sum _{j=t+1}^n a_j(1+r)^{t-j-1}$ ($t = 1, 2, \dots , n-1$), $\beta _n = a_n(1+r)^{-1}$.

Note that the term $\sum _{j=0}^{t-2} a_j(1+r)^{t-j-2}$, which appears in (iv), equals the investment balance at time $t-2$ of the project (see, e.g., Hartman and Schafrick (2004)). Furthermore, the term $\sum _{j=t+1}^n a_j(1+r)^{t-j-1}$, which appears in (v), is the present value, at rate r and at time t, of the last $n-t$ cash-flows of the project (which, if r coincided with the market rate, would amount to its market price at time t after cashing $a_t$).

It is now possible to give the main result of the paper.

Theorem 1

If the interest rate r is the irr of a project on the set $\{0,1,2,\ldots ,n\}$ of maturities, then there exists suitable portfolios:

• (i) of single period bonds,

• (ii) of zero-coupon bonds with maturity n,

• (iii) of zero-coupon bonds with issue date 0,

• (iv) of traditional bonds with maturity n, and

• (v) of traditional bonds with issue date 0

(with all the involved bonds having yield r to maturity), which have the same payments as the project.

Proof

It is an immediate consequence of Lemmas 1 and 2, with the terminology seen in Remark 1. $\square$

Remark 4

Theorem 1 could actually be stated as a characterization: r is the irr of a project if and only if there exist porfolios of bonds with yield r to maturity which hedge the project. The opposite implication, though, is actually too straightforward to mention (for instance, it is a direct consequence of Lemma 1(i)). Furthermore, Theorem 1 points out just five of the infinitely many decompositions that may be conceived: it is clear that a decomposition of a financial project with irr r can be found with respect to any spanning system of ${\mathcal {S}}_n(r)$, and in particular with respect to every n linearly independent projects (not necessarily bonds!) with irr r.

In the five highlighted decompositions, the meaning of the irr is crisp for each of the bonds composing the portfolio: it is a yield for the buyer and a cost for the issuer. Remarkably, though, such a clarity of interpretation need not propagate to the entire portfolio: for instance, although the irr is unique for all of the elementary bonds, yet the project can show multiple ones. Indeed, generally speaking, some of the bonds in the portfolio are bought and some other are (short-)sold, and therefore the resulting cash-flow stream may not be immediate to tell as an investment or a borrowing. We refer the reader to, e.g., Magni (2010) again to understand how it is possible to classify every project as a net investment or a net borrowing with respect to each of its significant rates of return.

Note that, as seen in Examples 1 and 2, if a project has multiple irrs, each of them can be used to decompose it as in Theorem 1. Roughly speaking, it can be said that a project has (at least) five significant representations as a portfolio of bonds for each irr it admits.

Example 3

(follows from 2) It is immediate to check that the project of Example 2 is equivalent to the portfolio ${302.4}\cdot \mathbb {I}_{0,4}(r) - {1\,650}\cdot \mathbb {I}_{1,4}(r) + {3\,350}\cdot \mathbb {I}_{2,4}(r) - {3\,000}\cdot \mathbb {I}_{3,4}(r)$ (basis (ii)) for every $r\in \{{11.1111}\%, {25}\%, {42.8571}\%, {66.6667}\%\}$.

It is straightforward that, if $m>n$, then ${\mathcal {S}}_n(r) \subseteq {\mathcal {S}}_m(r)$. Such a trivial remark has the non-trivial consequence that a project with irr r and final maturity n can be “decomposed” in a portfolio of (elementary) projects with final maturity even greater than n.

Example 4

(follows from 2) The project of Example 2 is equivalent to the following portfolio, with $r = 11.1111\%$.

	$t=0$	$t=1$	$t=2$	$t=3$	$t=4$	$t=5$
302.4$\cdot \mathbb {Y}_{0,5}(r)$	$-$302.4	33.60	33.60	33.60	33.60	336
$-$1 616.4$\cdot \mathbb {I}_{1,4}(r)$	0	1 616.4	0	0	$-$2 217.28	0
3 383.6$\cdot \mathbb {Y}_{2,4}(r)$	0	0	$-$3 383.6	375.96	3 759.56	0
$-$2 590.44$\cdot \mathbb {I}_{3,5}(r)$	0	0	0	2 590.44	0	$-$3 198.08
2 575.87$\cdot \mathbb {Y}_{4,5}(r)$	0	0	0	0	$-$2 575.87	2 862.08
overall	$-$302.4	1 650	$-$3 350	3 000	$-$1 000	0

We point out that the decompositions seen in this section might just be theoretical, because no real market could be found where the needed bonds are actually traded. In such a case, the given representation maintains its value only from an interpretative, and no longer from an operational, point of view.

4 An application to loans’ amortization

A simple and yet fairly general definition of the amortization of a loan (based on Broverman (2017)) is given below, both to set the notations used in this section and for the convenience of the reader.

Suppose that the amount L is borrowed by a debtor from a bank (or a financial institution) and repaid by n payments of amounts $K_1$, $K_2$, ..., $K_n$ at times $1, 2, \dots , n$ which have to include interests according to a certain rate r, agreed upon by the two parties. For every time $t=0,1,\ldots , n$ the outstanding balance (or principal, or debt) $O\!B_t$ is defined, according to the following rules: at the time $t=0$ when the loan is started, $O\!B_0:=L$ (which simply amounts to say that the whole borrowed amount has to be entirely repaid) and, for every time $t=1,2,\ldots ,n$ of payment,

• (i) the interest due for the period from $t-1$ to t, denoted by $I_t$, is calculated as the rate r times the outstanding balance $O\!B_{t-1}$ at the beginning of the period;

• (ii) the difference $P\!R_t:=K_t-I_t$ between the agreed payment $K_t$ and the interest $I_t$ due is called the principal repaid at time t;

• (iii) the oustanding balance at time t is $O\!B_t:= O\!B_{t-1} - P\!R_t$.

Since these rules lead to split every payment in two elements (a principal and an interest), the method of amortization following such rules may be called a meal (a Method for Elementary Amortization of Loans).³

It is worth pointing out that a meal can also be defined starting from a given sequence $P\!R_1, P\!R_2, \dots , P\!R_n$ of principals repaid: it simply suffices to replace Rule (ii) with the equivalent rule

(ii$'$):

the payment $K_t$ due at time t is the sum $P\!R_t + I_t$ of the agreed principal $P\!R_t$ repaid and the interest $I_t$ due.

Finally, a meal can also be defined by a sequence $O\!B_1, O\!B_2, \dots , O\!B_{n}$ of outstanding balances (with $O\!B_0=L$), because of course they immediately allow to deduce the principals repaid as $P\!R_t = O\!B_{t-1}-O\!B_t$, $t = 1, \dots , n$.

Remark 5

The outstanding balances could be defined without explicitly splitting the payment in two components. Indeed, since for the period from $t-1$ to t the interest $I_t = r\cdot O\!B_{t-1}$ is due, the total debt due before the payment at time t amounts to $O\!B_{t-1}\cdot (1+r)$, and the outstanding balance at time t can therefore be calculated as $O\!B_t:= O\!B_{t-1}\cdot (1+r)-K_t$. Note that, taking Rule (ii) into consideration, the above formula can be written $O\!B_t:= (O\!B_{t-1} + I_t) - (P\!R_t + I_t)$, which shows its full equivalence with Rule (iii).

It is noteworthy that such a recursive formula for calculating $O\!B_t$ is again perfectly analogous to (2), thus emphasizing that the outstanding balances in meal play the same role as the outstanding capitals in npv decomposition and as the investment balance in general projects, that is, roughly speaking, the value that, at a given date, remains committed to the project. Given the obvious analogy between payments in loans and cash-flows in projects, this also highlights an analogous link between period operating profits and interests due (which is quite reasonable indeed, because such interests are the profit required by the institution which grants the loan).

The loan is said to be amortized by the payments $K_1$, $K_2$, ..., $K_n$ if the final outstanding balance is null, i.e., if $O\!B_n=0$. It is straightforward to check that this amounts to saying that the sum of the principals repaid equals the whole borrowed amount, i.e., that $P\!R_1 + P\!R_2 + \dots + P\!R_n=L$: such a condition is called the elementary balance condition for the amortization of the loan. Although less immediate, it is also possible to check that such condition holds if and only if the sum of the discounted values at time $t=0$ of the payments equals the borrowed amount, i.e., if $K_1(1+r)^{-1}+ K_2(1+r)^{-2}+\dots +K_n(1+r)^{-n}=L$: such a condition is called the initial balance condition for the amortization of the loan. A more general condition can also be proved in the same way, showing that, for every $t=1, 2, \dots , n-1$, the outstanding balance $O\!B_t$ is the sum of the discounted values of future payments, i.e., that $O\!B_t = K_{t+1}(1+r)^{-1}+ K_{t+2}(1+r)^{-2}+\dots +K_n(1+r)^{t-n}$, or, in a more compact form, $O\!B_t = \sum _{j=t+1}^{n} K_j (1+r)^{t-j}$.

From the point of view of the lending institution, the set of cash flows generated by a meal can be denoted as the project $[-L\ \,K_1\ \,K_2\ \,\cdots \ \,K_n]$ on the set $\{0,1,2,\ldots ,n\}$ of maturities. In such a setting, the initial balance condition amounts to saying that r is the unique irr of such a project (uniqueness follows from Descartes’s rule, because the cash flows have only one change of sign). This way, Theorem 1 (and Remark 3) can be applied, to show that, for the lender, granting a loan is financially equivalent to setting up one of the following portfolios of bond, whose calculations are explicitly carried out because they will suggest some non trivial economic considerations:

• (i) buying $\beta _1 = L$ units of $\mathbb {I}_{0,1}(r)$ at time 0 and, for every $t=1, \dots , n-1$,

  $$\begin{aligned} \begin{aligned} \beta _{t+1}&= \textstyle L(1+r)^{t} - \sum _{j=1}^{t} K_j (1+r)^{t-j} \\&= \textstyle \sum _{j=1}^n K_j(1+r)^{t-j} - \sum _{j=1}^{t-1} K_j (1+r)^{t-j} \\&= \textstyle \sum _{j=t}^n K_j(1+r)^{t-j} = O\!B_{t} \end{aligned} \end{aligned}$$

  units of $\mathbb {I}_{t,t+1}(r)$ at time t;

• (ii) buying $\beta _1 = L$ units of $\mathbb {I}_{0,n}(r)$ at time $t=0$ and issuing $-\beta _{t+1} = K_t$ units of $\mathbb {I}_{t,n}(r)$ at times $t=1, 2, \dots , n-1$;

• (iii) buying, at time 0, $\beta _t = K_t(1+r)^{-t}$ unit of $\mathbb {I}_{0,t}(r)$ for every maturity $t = 1, 2, \dots , n$;

• (iv) buying $\beta _1 = L$ units of $\mathbb {I}_{0,n}(r)$ at time $t=0$, issuing $-\beta _2 = K_1 - rL = P\!R_1$ units of $\mathbb {I}_{1,n}(r)$ at time $t=1$ and, in general, issuing

  $$\begin{aligned} \begin{aligned} -\beta _{t+1}&= \textstyle K_{t}-rL(1+r)^{t-1} + r\cdot \sum _{j=1}^{t-1} K_t(1+r)^{t-j-1} \\&= \textstyle K_{t-1}-r\cdot \Big [\sum _{j=1}^n K_t(1+r)^{(t-1)-j} - \sum _{j=1}^{t-1} K_t(1+r)^{t-j-1}\Big ] \\&= \textstyle K_{t-1}-r\cdot \sum _{j=t}^n K_t(1+r)^{t-j-1} \\&= K_{t} - rO\!B_{t-1} = K_{t} - I_{t} = P\!R_{t} \end{aligned} \end{aligned}$$

  units of $\mathbb {Y}_{t,n}(r)$ at times $t=2, \dots , n-1$;

• (v) buying, for every maturity $t = 1, 2, \dots , n-1$,

  $$\begin{aligned} \begin{aligned} \beta _t&= K_t(1+r)^{-1} - r\cdot \textstyle \sum _{j=t+1}^n K_j (1+r)^{t-j-1} \\&= \big (P\!R_t + rO\!B_{t-1})(1+r)^{-1} - r\cdot (1+r)^{-1} O\!B_t \\&= \big (P\!R_t + r(O\!B_{t-1}-O\!B_{t})\big )(1+r)^{-1} \\&= \big (P\!R_t + rP\!R_t\big )(1+r)^{-1} = P\!R_t \end{aligned} \end{aligned}$$

  units of $\mathbb {Y}_{0,t}(r)$ and, at time n,

  $$\begin{aligned} \begin{aligned} \beta _n&= K_n(1+r)^{-1} = (P\!R_{n} + I_{n})(1+r)^{-1} \\&= \big (P\!R_{n} + rP\!R_{n}\big )(1+r)^{-1} = P\!R_n \end{aligned} \end{aligned}$$

  units of $\mathbb {Y}_{0,n}(r)$.

Example 5

A bank loan of ${100\,000}$ €is paid back at $r = 6\%$ rate in five constant instalments, each of  €.⁴ The classical amortization table according to the meal is

t	K$_{t}$	I$_{t}$	PR$_{t}$	OB$_{t}$
0	–	–	–	100 000
1	23 740	6 000	17 740	82 260
2	23 740	4 936	18 804	63 456
3	23 740	3 807	19 932	43 524
4	23 740	2 611	21 128	22 396
5	23 740	1 344	22 396	0

The cash flows sequence generated from such a loan, from the bank’s point of view, amounts to the project $[{-100\,000}\ \,{23\,740}\ \,{23\,740}\ \,{23\,740}\ \,{23\,740}\ \,{23\,740}]$, whose unique irr is of course $6\%$. The project can be decomposed with respect to the five bases seen above as follows:

(i) with respect to $\{\mathbb {I}_{t-1,t}({0.06}): t=1,2,\ldots 5\}$,

elementary project	$t=0$	$t=1$	$t=2$	$t=3$	$t=4$	$t=5$
${100\,000}\cdot \mathbb {I}_{0,1}({0.06})$	${-100\,000}$	${106\,000}$	0	0	0	0
${82\,260}\cdot \mathbb {I}_{1,2}({0.06})$	0	${-82\,260}$	${87\,196}$	0	0	0
${63\,456}\cdot \mathbb {I}_{2,3}({0.06})$	0	0	${-63\,456}$	${67\,264}$	0	0
${43\,524}\cdot \mathbb {I}_{3,4}({0.06})$	0	0	0	${-43\,524}$	${46\,136}$	0
${22\,396}\cdot \mathbb {I}_{4,5}({0.06})$	0	0	0	0	${-22\,396}$	${23\,740}$
overall	${-100\,000}$	${23\,740}$	${23\,740}$	${23\,740}$	${23\,740}$	${23\,740}$

(ii) with respect to $\{\mathbb {I}_{t-1,5}({0.06}): t = 1, 2, \dots , 5\}$,

elementary project	$t=0$	$t=1$	$t=2$	$t=3$	$t=4$	$t=5$
${100\,000}\cdot \mathbb {I}_{0,5}({0.06})$	${-100\,000}$	0	0	0	0	${133\,823}$
${-23\,740}\cdot \mathbb {I}_{1,5}({0.06})$	0	${23\,740}$	0	0	0	${-29\,971}$
${-23\,740}\cdot \mathbb {I}_{2,5}({0.06})$	0	0	${23\,740}$	0	0	${-28\,274}$
${-23\,740}\cdot \mathbb {I}_{3,5}({0.06})$	0	0	0	${23\,740}$	0	${-26\,674}$
${-23\,740}\cdot \mathbb {I}_{4,5}({0.06})$	0	0	0	0	${23\,740}$	${-25\,164}$
overall	${-100\,000}$	${23\,740}$	${23\,740}$	${23\,740}$	${23\,740}$	${23\,740}$

(iii) with respect to $\{\mathbb {I}_{0,t}({0.06}): t = 1, 2, \dots , 5\}$,

elementary project	$t=0$	$t=1$	$t=2$	$t=3$	$t=4$	$t=5$
${22\,396}\cdot \mathbb {I}_{0,1}({0.06})$	${-22\,396}$	${23\,740}$	0	0	0	0
${21\,128}\cdot \mathbb {I}_{0,2}({0.06})$	${-21\,128}$	0	${23\,740}$	0	0	0
${19\,932}\cdot \mathbb {I}_{0,3}({0.06})$	${-19\,932}$	0	0	${23\,740}$	0	0
${18\,804}\cdot \mathbb {I}_{0,4}({0.06})$	${-18\,804}$	0	0	0	${23\,740}$	0
${17\,740}\cdot \mathbb {I}_{0,5}({0.06})$	${-17\,740}$	0	0	0	0	${23\,740}$
overall	${-100\,000}$	${23\,740}$	${23\,740}$	${23\,740}$	${23\,740}$	${23\,740}$

(iv) with respect to $\{\mathbb {Y}_{t-1,5}({0.06}): t = 1, 2, \dots , 5\}$,

elementary project	$t=0$	$t=1$	$t=2$	$t=3$	$t=4$	$t=5$
${100\,000}\cdot \mathbb {Y}_{0,5}({0.06})$	${-100\,000}$	${6\,000}$	${6\,000}$	${6\,000}$	${6\,000}$	${106\,000}$
${-17\,740}\cdot \mathbb {Y}_{1,5}({0.06})$	0	${17\,740}$	${-1\,064}$	${-1\,064}$	${-1\,064}$	${-18\,804}$
${-18\,804}\cdot \mathbb {Y}_{2,5}({0.06})$	0	0	${18\,804}$	${-1\,128}$	${-1\,128}$	${-19\,932}$
${-19\,932}\cdot \mathbb {Y}_{3,5}({0.06})$	0	0	0	${19\,932}$	${-1\,196}$	${-21\,128}$
${-21\,128}\cdot \mathbb {Y}_{4,5}({0.06})$	0	0	0	0	${21\,128}$	${-22\,396}$
overall	${-100\,000}$	${23\,740}$	${23\,740}$	${23\,740}$	${23\,740}$	${23\,740}$

(v) with respect to $\{\mathbb {Y}_{0,t}({0.06}): t = 1, 2, \dots , 5\}$,

elementary project	$t=0$	$t=1$	$t=2$	$t=3$	$t=4$	$t=5$
${17\,740}\cdot \mathbb {Y}_{0,1}({0.06})$	${-17\,740}$	${18\,804}$	0	0	0	0
${18\,804}\cdot \mathbb {Y}_{0,2}({0.06})$	${-18\,804}$	${1\,128}$	${19\,932}$	0	0	0
${19\,932}\cdot \mathbb {Y}_{0,3}({0.06})$	${-19\,932}$	${1\,196}$	${1\,196}$	${21\,128}$	0	0
${21\,128}\cdot \mathbb {Y}_{0,4}({0.06})$	${-21\,128}$	${1\,268}$	${1\,268}$	${1\,268}$	${22\,396}$	0
${22\,396}\cdot \mathbb {Y}_{0,5}({0.06})$	${-22\,396}$	${1\,344}$	${1\,344}$	${1\,344}$	${1\,344}$	${23\,740}$
overall	${-100\,000}$	${23\,740}$	${23\,740}$	${23\,740}$	${23\,740}$	${23\,740}$

Therefore, for the bank, the loan is equivalent to several possible portfolios of bonds, either traditional or zero-coupon, each bond yielding a $6\%$ rate to maturity.

Remark 6

It may be useful to point out that (almost) each one of the five “remarkable” decompositions proposed in this paper has a significant economic interpretation when applied to loans.

• (i) As already said, the bonds of the type $\mathbb {I}_{t-1,t}(r)$ feature full return at the date immediately after issue of the principal and the interests due. From the point of view of the debtor, then, issuing L units of $\mathbb {I}_{0,1}(r)$ at time $t=0$ means to assume the full obligation to repay $L (1+r)$ at time $t=1$; to meet such an obligation, she/he allocates a certain sum $K_1$ and contracts a new (and lower) debt, to repay at time $t=2$, for the reamining part. Note that, of course, the amount of such a debt is bound to be $L (1+r)-K_1 = L + I_1 - K_1 = L - P\!R_1 = O\!B_1$. This first decomposition, then, shows that every amortization of a loan is financially equivalent to a sequence of “chained debts” of amounts equal to the outstanding balance for every date of payment.

• (ii) This decomposition has an interpretation similar to the classical “bank account” characterization of irr. It indeed shows that, from the point of view of the debtor, the loan works as an obligation and an entitlement: the debtor assumes the obligation to repaying the principal L at time $t=n$ with compound interest (i.e., to repaying the sum $L(1+r)^n$), and she/he is entitled to put into place n “deposits”, at the payment dates, which will generate compound interests at the same rate r, thus concurring to the payment due at time $t=n$.

• (iii) The debt is here no longer seen as a single loan, but rather as a set of loans, each to be repaid with compound interest. Since the values at time 0 of such loans are of course the discounted values of the future payments, this decomposition immediately translates into the general initial balance condition. Notably enough, this interpretation has been misused, in legal contexts, to suggest that the meal inherently implies the payment of compound interest, which is forbidden by law in some states (see Pressacco et al. (2022), for an examination of the Italian case).

  It may be useful to point out that, even if in Example 5 the sequence of the discounted amounts of the loans is the reversed sequence of the principals repaid, this is not a general feature, but is due to a particular property of the constant rate amortization (namely, the well known fact that its principals repaid form a geometric progression).

• (v) This situation is examined before (iv), because it allows for better understanding a point that will come into play in that case as well. Note that the recursive relation $O\!B_t = O\!B_{t-1}-P\!R_t$, together with the initial budget condition, translates into the closed form expressions $O\!B_{t-1} = L-\sum _{j=1}^{t-1}P\!R_j = \sum _{j=t}^nP\!R_j$. In turn, this implies that $K_t = P\!R_t + r\cdot \sum _{j=t}^nP\!R_j$: the payment at time t includes its own principal repaid and the interests due on all principals repaid from t on. The cash flows that the loan generates for the issuer can therefore be written as in the following table (which unsurprisingly but notably resembles the method for deriving Makeham’s Formula, see, e.g., Broverman (2017), Figure 3.5), where the first row comes from the elementary balance condition itself.

  $$\begin{aligned} \begin{array}{ccccccccccc} -L &{}{}={}&{} -P\!R_1 &{}{}+{}&{} -P\!R_2 &{}{}+{}&{} -P\!R_3 &{}{}+{}&{} \cdots &{}{}+{}&{} -P\!R_n \\ K_1 &{}{}={}&{} (1+r)P\!R_1 &{}{}+{}&{} rP\!R_2 &{}{}+{}&{} rP\!R_3 &{}{}+{}&{} \cdots &{}{}+{}&{} rP\!R_n \\ K_2 &{}{}={}&{} &{}&{} (1+r)P\!R_2 &{}{}+{}&{} rP\!R_3 &{}{}+{}&{} \cdots &{}{}+{}&{} rP\!R_n \\ K_3 &{}{}={}&{} &{}&{} &{}&{} (1+r)P\!R_3 &{}{}+{}&{} \cdots &{}{}+{}&{} rP\!R_n \\ &{}\vdots &{} &{}&{} &{}&{} &{}&{} \ddots &{}&{} \vdots \\ K_n &{}{}={}&{} &{}&{} &{}&{} &{}&{} &{}&{} (1+r)P\!R_n \\ \end{array} \end{aligned}$$

  It is evident that the n columns after the “$=$” equal the sequences of payments of n bonds, issued at time $t=0$ at coupon rate r, with nominal value $P\!R_t$ and maturity date t for each $t=1,2,\ldots , n$.

• (iv) In the spirit of case (v) above, this decomposition becomes easier to understand. Buying the first bond for the full amount $L = \sum _{j=1}^nP\!R_n$ entitles to receive the coupon $r\big (\sum _{j=1}^nP\!R_n\big )$ at each time $t=1,2,\ldots ,n-1$ and the payment $(1+r)\big (\sum _{j=1}^nP\!R_n\big )$ at time n. Issuing the second bond adds $P\!R_1$ to the first intake, which thus becomes $P\!R_1 + rL = K_1$, and subtracts $rP\!R_1$ at each time $t=2,3,\ldots ,n-1$, for a temporary total of $r\big (\sum _{j=2}^nP\!R_n\big ) = rO\!B_1$, and $(1+r)P\!R_1$ at time t, for a temporary total of $(1+r)\big (\sum _{j=1}^nP\!R_n\big ) = (1+r)O\!B_1$. Issuing the third bond adds $P\!R_2$ to the second intake, which becomes $P\!R_2 + rO\!B_1 = K_2$, and further subtracts $rP\!R_2$ at times $t = 3, 4, \dots , n-1$, for a temporary total of $rO\!B_2$, and $(1+r)P\!R_2$ at time t, for a temporary total of $(1+r)O\!B_2$. Applying the same argument over and over shows that payments at each time $t=3, 4, \dots , n-1$ become equal to $P\!R_t +r\cdot \sum _{j=t}^nP\!R_n = P\!R_t + rO\!B_{t-1} = K_t$, and that the final payment becomes equal to $(1+r)O\!B_{n-1} = P\!R_n + rO\!B_{n-1} = K_n$.

Remark 7

The results of this section, as well as those of the previous one, admit a converse formulation: every portfolio of bonds with common yield r to maturity is naturally equivalent to a loan amortization scheme, built according to the meal rules. Such a result is obtained, for instance, by applying Lemma 2(iv) to decompose the resulting cash flows into a portfolio of traditional bonds with maturity n and, then, recalling that the number of bonds $\mathbb {Y}_{t,n}(r)$ in such a portfolio is numerically equivalent to the principal $P\!R_t$ repaid at time t. Analogously, a decomposition according to Lemma 2(ii) could be used, to directly deduce the payments. Of course, some principals repaid may turn out to be null, or negative (leading, in the second case, to an increase in the outstanding balance), or greater than the current outstanding balance (which will lead to a negative outstanding balance at the next maturity): although this may generate legal issues in practice, there are no mathematical obstacles to the interpretation.

It is well know that not every loan amortization is built according to the meal rules: in the market, several other types of loan amortization are sold (e.g., sinking fund, merchant’s rule, actuarial method, “german” amortization with anticipated interests, and so on). It is nevertheless generally true that every amortization scheme consists, for the debtor, in a single intake at time $t=0$ and a sequence of outflows at times $t=1,2, \dots , n$. This ensures existence and uniqueness of the irr of the overall cash flows (which is of course the apr, if all fees and charges are included into the cash flows) and, therefore, through the results of this paper, that the scheme is equivalent to a meal amortization with a suitable interest rate.

Example 6

(follows from 2) The decomposition seen in Example 2 for $r = 11.1111\%$ shows that the project $[{-302.4}\ \ {1\,650}\ \ {-3\,350}\ \ {3\,000}\ \ {-1\,000}]$ can be seen as a loan, amortized according to the meal rules, with outstanding balances (orderly equal to the number of bonds issued or bought, i.e.) $O\!B_0 = {302.4}$, $O\!B_1 = {-1\,314}$, $O\!B_2 = {1\,890}$, and $O\!B_3 = {-900}$, that is to say, with principals $P\!R_1 = {1\,616.4}$, $P\!R_2 = {-3\,204}$, $P\!R_3 = {2\,790}$, and $P\!R_4 = {-900}$ “repaid” (or “reborrowed”). It is indeed immediate to see that the table (built according to the meal rules)

t	K$_{t}$	I$_{t}$	PR$_{t}$	OB$_{t}$
0	–	–	–	302.4
1	1 650	33.6	1 616.4	$-$1 314
2	$-$3 350	$-$146	$-$3 204	1 890
3	3 000	210	2 790	$-$900
4	$-$1 000	$-$100	$-$900	0

induces “payments” that exactly match the cash flows of the original project.

5 Generalizations, further developments, and conclusions

Given an interest rate $r\in (-1,+\infty )$, this paper explicitly showed a fully general financial equivalence among:

• projects with irr r,

• portfolios of bonds with yield r to maturity, and

• loans, amortized according to the meal rules, with interest r due,

Saying that two such objects are financially equivalent means that they feature (or induce) the same cash flows in the various maturities under consideration, and that it is possible to find suitable (and essentially one-to-one, under technical conditions) correspondences that allow to transform either one into the other. As well as it happens in other fields of Mathematics (the simplest example that comes to mind is, e.g., the possibility to approach the solution of a geometrical problem either with Euclidean deductive arguments or with Descartes’s analytical description), it is then possible to examine a project in any of the three equivalent forms, possibly deducing from one of them some properties that may not be evident elsewhere.

In the paper, five possible cases of portfolios of bonds have been taken into particular consideration: the case of one period bonds, the two cases of traditional and zero-coupon bonds with common initial issue date and varying maturity, and the two cases of traditional and zero-coupon bonds with varying issue date and common maturity at the last date of the set into consideration. These are not, of course, the only possible portfolio types that can be taken into consideration: for instance, it has been said that the set of all “elementary projects” (i.e., classical bonds) $\{\mathbb {I}_{t,s}(r)\}_{t<s} \cup \{\mathbb {Y}_{t,s}(r)\}_{t<s}$ is a spanning system for the linear (sub)space ${\mathcal {S}}_n(r)$ of all projects with final maturity n and irr r and, therefore, any linear independent subset of such a set is a legitimate basis for the same space. For instance, it is possible to decompose any project in ${\mathcal {S}}_4(r)$ with respect to the basis $\{\mathbb {Y}_{0,4}(r), \mathbb {I}_{1,2}(r), \mathbb {I}_{2,4}(r), \mathbb {Y}_{2,4}(r)\}$, although the resulting decomposition may not lead to particularly interesting financial insights.

The discussion has been confined to the case of $n+1$ equidistant maturities, in order to keep the notation as simple as possible. In the general case of any set $\{t_0, t_1, \dots , t_n\}$ of increasing maturities, it is enough to define the elementary bonds by choosing two indices $i<j$ and setting

with coupon rates $r_k = (1+r)^{t_k - t_{k-1}}-1$ ($k = i+1, i+2, \dots , j$) calculated at compound interest (because other definitions may not guarantee r to be an irr for $\mathbb {I}_{i,j}(r)$). Nothing would then change in the main results of the paper, except of course a significant increase in complexity of the notation.

Note that, instead of a single irr r, a whole term structure of rates ${\textbf{r}} = \{r_k: k = 1, 2, \dots ,n\}$ could be considered over the generic set $\{t_0, t_1, \dots , t_n\}$ of maturities, with $r_1$ the spot rate from $t_0$ to $t_1$ and $r_k$ the forward rate from $t_{k-1}$ to $t_k$ for $k=2, 3, \dots , n$ (note that these will not be yearly rates, unless some $t_{k}$ is exactly one year away from $t_{k-1}$). This way, the present value at time $t_0$ of a cash flow $a_j$ at time $t_j$ ($j=1, 2, \dots , n$) would be $a_j\cdot \prod _{k=1}^{j}(1+r_k)^{-1}$. In such a setting, the elementary traditional bond would be defined with payments $[0\ \,\dots \ \,0\ \,{-1}\ \,r_{i+1}\ \,\dots \ \,r_{j-1}\ \,1+r_j\ \,0\ \,\dots \ \,0]$ as above, whereas in the zero-coupon bonds the payment at time $t_j$ would be replaced by $\prod _{k=i+1}^j(1+r_j)$. Of course, a new definition of generalized dcf would be needed, by discounting the cash flows accordingly to a whole n-dimensional vector of forward rates, and a vector ${\textbf{r}}^*$ would be defined a generalized irr , or a variable irr (or, as in Peccati (1989), an internal financial law) of a project whenever the generalized dcf of such a project with respect to ${\textbf{r}}^*$ were null. Such a setting is now fully compatible with the most general decomposition of a project with variable period yields such as introduced by Magni (2010), and therefore with the airr defined thereby. Analogously, a generalized meal would be defined, supposing that the interest $I_k$ due at time $t_k$ would be $r_k\cdot O\!B_{k-1}$ ($k=1, 2, \dots , n$). With such adjustments, the results of the present paper still hold true (although once again some major complication in the notation would appear), thus allowing for further analogies and possible practical consequences. Note, for instance, that the generalized meal allows to write an amortization which replicates not only the payments, but also the outstanding balances of the original plan (possibly considering as such the amounts due for early extinction of the debt): the period irrs deduced in such a way from the original plan would visibly show the actual costs sustained by the debtor and this, for instance, may help choosing suitable collateral projects to reduce the risk of her/his position.

A final consideration is in order. In the case of a constant irr r, it is possible to read the amortization of a loan according to the meal as a decomposition of the cash flows of the corresponding project in the spirit of Peccati (1987), where the outstanding balances play the role of the outstanding capitals: from each inlay (i.e., from every payment $K_t$, $t=1,2,\ldots ,n$) a part of profit is deduced, measured as a percentage r of the outstanding capital (which numerically equals the interest due according to the meal), while the remaining part (i.e., the principal repaid) is destined to reducing the outstanding capital invested in the project. Notably enough, the principals repaid are the coefficients used with respect to basis (v), reinforcing the interpretation that they are the various yearly contributions to the global npv of the project; in order to fully get the whole Peccati’s setup, it is then enough to introduce a subjective interest rate and to calculate the Economic Values Added year by year. Of course, such a reading of the meal could be carried out unchanged in the case of a variable irr, recovering the spirit of Peccati (1989) and, once again, of Magni (2010).