The impact of pharmaceutical innovation on premature cancer mortality in Switzerland, 1995–2012

Abstract

The premature cancer mortality rate has been declining in Switzerland, but there has been considerable variation in the rate of decline across cancer sites (e.g., breast or digestive organs). I analyze the effect that pharmaceutical innovation had on premature cancer mortality in Switzerland during the period 1995–2012 by investigating whether the cancer sites that experienced more pharmaceutical innovation had larger declines in premature mortality, controlling for the number of people diagnosed and mean age at diagnosis. Premature cancer mortality before ages 75 and 65 is significantly inversely related to the cumulative number of drugs registered 5, 10, and 15 years earlier. The number of drugs registered during 1980–1997 explains 63 % of the variation across cancer sites in the 1995–2012 log change in the premature (before age 75) mortality rate. Controlling for the cumulative number of drugs, the cumulative number of chemical subgroups does not have a statistically significant effect on premature mortality. This suggests that drugs (chemical substances) within the same class (chemical subgroup) are not “therapeutically equivalent”. Over 17,000 life-years before age 75 were gained in 2012 due to drugs registered during 1990–2007. The number of life-years before age 75 gained in 2012 from drugs registered during two earlier periods (1985–2002 and 1980–1997) were more than twice as great. Since mean utilization of new drugs is much lower than mean utilization of older drugs, more recent drug registrations may have a smaller effect on premature mortality than earlier drug registrations even if the average quality of newer drugs is higher. Estimates of the cost per life-year gained before ages 75 and 65 in 2012 from drugs registered during 1990–2007 are $21,228 and $28,673, respectively. These figures are below even the lowest estimates from the value-of-life literature of the value of a quality-adjusted life-year. The estimates indicate that the cost per life-year before age 75 gained from drugs registered during earlier periods (1985–2002 and 1980–1997) were considerably lower: $5299 and $3218, respectively. The largest reductions in premature mortality occur at least a decade after drugs are registered, when their utilization increases significantly. This suggests that if Switzerland is to obtain substantial additional reductions in premature cancer mortality in the future (a decade or more from now) at a modest cost, pharmaceutical innovation (registration of new drugs) is needed today.

Introduction

Previous authors have argued that “reducing premature mortality is a crucial public health objective” [16]. A widely used measure of premature mortality is years of potential life lost (YPLL) before a given age (e.g., age 70), i.e., the number of years not lived by an individual who died before that age [1]. Statistics of YPLL are published by the World Health Organization, the OECD, and government agencies of the U.S., Switzerland, and other countries. Burnet et al. [2] argue that YPLL “should be considered when allocating research funds”.

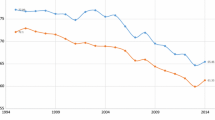
As shown in Fig. 1, in Switzerland in 2010, cancer (malignant neoplasms) was the largest cause of premature mortality: the number of years of potential life lost before age 70 (YPLL70) due to cancer was 44 % larger than YPLL70 due to external causes and 138 % larger than YPLL70 due to diseases of the circulatory system. However, as shown in Fig. 2, the premature cancer mortality rate has been declining; it declined about 27 % between 1995 and 2010. The cancer incidence rate remained approximately constant during that period.

Fig. 1

Premature (before age 70) mortality rates from three largest causes, Switzerland 2010

Fig. 2

Cancer incidence rate and premature (before age 70) cancer mortality rate, Switzerland 1995–2010

While the premature mortality rate from all cancers combined has been declining in Switzerland, Fig. 3 indicates that there has been considerable variation in the rate of decline across cancer sites. During the period 1995–2012, premature (before age 75) mortality from cancer of lymphoid, hematopoietic, and related tissue declined 31 %, and from breast cancer declined 38 %, but premature mortality from lip, oral cavity, and pharynx cancer increased 14 %, and from cancer of endocrine glands and related structures increased 19 %. This variation in the rate of decline of premature mortality cannot be explained by variation in the rate of decline of incidence.

Fig. 3

Log change in years of potential life lost before age 75, by type of cancer, Switzerland, 1995–2012

In this paper, I will analyze the effect that pharmaceutical innovation has had on premature cancer mortality in Switzerland during the period 1995–2012.¹ As shown in Fig. 4, the number of drugs used to treat cancer that had ever been launched in Switzerland increased almost fivefold between 1980 and 2010; the number of “cancer drugs” (antineoplastic and immunomodulating agents) used to treat cancer increased almost sixfold.

Fig. 4

Number of drugs used to treat cancer ever launched in Switzerland, 1980–2010

The analysis will be performed using fixed-effects and long-differences research designs (see McKinnish [12]) based on longitudinal disease-level data. In essence, I will investigate whether the cancer sites that experienced more pharmaceutical innovation had larger declines in the premature mortality rate, controlling for changes in the incidence rate. Figure 5 illustrates that the rate of pharmaceutical innovation, as measured by the number of drugs launched during the period 1986–2011, varied considerably across cancer sites. Twenty-nine drugs were launched for breast cancer, while only 15 or 16 drugs were launched for each of three other types of cancer: connective and soft tissue, male genital organs, and female genital organs.

Fig. 5

Number of drugs that had been launched in Switzerland for treating five types of cancer, 5-year intervals, 1986–2011

The analysis will be based on aggregate data—longitudinal data on 13 cancer sites²—rather than patient-level data. Stukel et al. [20] argue that comparisons of outcomes between patients treated and untreated in observational studies may be biased due to differences in patient prognosis between groups, often because of unobserved treatment selection biases. I believe that difference-in-differences estimates based on aggregate panel data are much less likely to be subject to unobserved treatment selection biases than estimates based on cross-sectional patient-level data.³ Moreover, the outcome measures that I analyze (premature mortality rates) are not subject to lead-time bias.⁴

In “Premature cancer mortality model “, I describe an econometric model of premature cancer mortality. The data sources used to construct the data to estimate this model are described in “Data”. Empirical results are presented in “Empirical results”. Key implications of the estimates are discussed in “Discussion”. “Summary and conclusions” provides a summary and conclusions.

Premature cancer mortality model

In his model of endogenous technological change, Romer [17] hypothesized an aggregate production function such that an economy’s output depends on the “stock of ideas” that have previously been developed, as well as on the economy’s endowments of labor and capital. The premature mortality model that I will estimate may be considered a health production function, in which premature mortality is an inverse indicator of health output or outcomes, and the cumulative number of drugs approved is analogous to the stock of ideas. The first model will be of the following form:

$${ \ln }({\text{YPLL75}} _{{{\text{s}},t}} ) = \beta_{k} {\text{CUM}}\_{\text{NCE}}_{{{\text{s}},t - k}} + \gamma { \ln }({\text{CASES}}\_{\text{LT75}} _{{{\text{s}},t - 1}} ) + \pi {\text{AGE}}\_{\text{DIAG}}_{{{\text{s}},t - 1}} + \alpha_{\text{s}} + \delta_{t} + \varepsilon_{{{\text{s}},t}}$$

(1)

where

YPLL75s,t	= years of potential life lost before age 75 from cancer at site s per 100,000 people below age 75 in year t (t = 1995, … , 2012)
CUM_NCEs,t–k	= ∑d INDds REGISTEREDd,t−k  = the number of new chemical entities (drugs) to treat cancer at site s that had been registered in Switzerland by the end of year t − k
INDds	= 1 if drug d is used to treat (indicated for) cancer at site s = 0 if drug d is not used to treat (indicated for) cancer at site s
REGISTEREDd,t–k	= 1 if drug d was registered in Switzerland by the end of year t − k = 0 if drug d was not registered in Switzerland by the end of year t – k
CASES_LT75s,t−1	= the number of new cases of cancer at site s diagnosed in people below age 75 per 100,000 people below age 75 in year t − 1
AGE_DIAGs,t−1	= the mean age at which people who were diagnosed with cancer at site s in year t − 1 were diagnosed
α s	= a fixed effect for cancer at site s
δ t	= a fixed effect for year t

1. The most recent available incidence data are for the year 2011

Inclusion of year and cancer-site fixed-effects controls for the overall decline in premature cancer mortality and for stable between-disease differences in premature mortality.⁵ A negative and significant estimate of β _k in Eq. (1) would signify that diseases for which there was more pharmaceutical innovation had larger declines in premature mortality. $\beta_{k} \times \, \left( {{\text{CUM}}\_{\text{NCE}}.,_{2012 - k} - {\text{CUM}}\_{\text{NCE}}.,_{1995 - k}}\right)$, where CUM_NCE., _t−k is the mean of CUM_NCE_s,t−k , is an estimate of the decline in Swiss premature cancer mortality during the sample period (1995–2012) that can be attributed to the introduction of new drugs. The functional form of Eq. (1) has the property of diminishing marginal productivity: the absolute reduction in premature mortality declines with each successive increase in the number of drugs.

As illustrated by Fig. 6, the data exhibit heteroskedasticity: cancer sites with larger total premature mortality during 1995–2012 had smaller (positive and negative) annual percentage fluctuations in YPLL75. Equation (1) will therefore be estimated by weighted least-squares, weighting by the mean premature mortality rate during 1995–2012 ((Σ_t YPLL75_s,t)/18). The standard errors of Eq. (1) will be clustered within cancer sites.

Fig. 6

Plot of the residuals from the (unweighted) regression ln(YPLL75st) = αs + δt + εst against total premature (before age 75) mortality during 1995–2012 (Σt YPLL75st)

Although one would expect an increase in true cancer incidence to increase premature cancer mortality, cancer incidence rates are subject to measurement error, so one should not necessarily expect the coefficient on measured cancer incidence (γ) to be positive. Let I and I* represent measured and true cancer incidence, respectively. Then I = (I/I*) × I*, and log(I) = log(I/I*) + log(I*). Measured cancer incidence can increase for two reasons: an increase in true cancer incidence, or an increase in the ratio of measured incidence to true incidence. The latter could occur as a result of increasing quantity or quality of cancer screening. More and better cancer screening could lead to earlier diagnosis, which might reduce premature mortality. Therefore the effect on premature mortality of increases in I* and increases in (I/I*) may offset one another: the former is likely to increase premature mortality, but the latter may reduce it. For this reason, although controlling (in an unrestrictive manner) for measured incidence in the premature mortality model seems appropriate, we should not be surprised if we don’t find a significant effect of measured incidence on premature mortality.

Equation (1) also includes mean age at time of diagnosis (AGE_DIAG) as an explanatory variable. Like the number of cases diagnosed, mean age at time of diagnosis could change for two reasons. First, the true mean age of onset of the disease could change; a reduction in the true mean age of onset would be likely to increase premature mortality. Second, the lag from time of onset to time of diagnosis could change; a reduction in this lag, which would reduce mean age at time of diagnosis, would be likely to reduce premature mortality. Hence, the sign of the coefficient (π) on AGE_DIAG_s,t−1 in Eq. (1) is ambiguous, a priori. Nevertheless, it seems desirable to control for mean age at time of diagnosis in the premature mortality equation.⁶

The measure of pharmaceutical innovation in Eq. (1)—the number of chemical substances previously commercialized to treat a disease—is not the theoretically ideal measure. Premature mortality is presumably more strongly related to the drugs actually used to treat a disease than it is to the drugs that could be used to treat the disease. A preferable measure is the mean vintage of drugs used to treat cancer at site s in year t, defined as ${\text{VINTAGE}}_{\text{st}} = \sum_{\text{d}} Q_{\text{dst}} {\text{LAUNCH}}\_{\text{YEAR}}_{\text{d}}/{\sum_{\text{d}}} Q_{\text{dst}}$, where Q _dst = the quantity of drug d used to treat cancer at site s in year t, and LAUNCH_YEAR_d = the world launch year of drug d.⁷ Unfortunately, measurement of VINTAGE_st is infeasible: even though data on the total quantity of each drug in each year (Q _d.t  = Σ_s Q_dst) are available, many drugs are used to treat multiple diseases,⁸ and there is no way to determine the quantity of drug d used to treat cancer at site s in year t.⁹ However, Lichtenberg [9] showed that in France, there is a highly significant positive correlation across drug classes between changes in the (quantity-weighted) vintage of drugs and changes in the number of chemical substances previously commercialized within the drug class.

Pharmaceutical innovation is not the only type of medical innovation that is likely to reduce premature mortality. Other medical innovation, such as innovation in diagnostic imaging, surgical procedures, and medical devices, is also likely to affect premature mortality. Therefore, measures of these other types of medical innovation should be included in the Eq. (1). Unfortunately, longitudinal disease-level measures of non-pharmaceutical medical innovation are not available for Switzerland. However, failure to control for non-pharmaceutical medical innovation is unlikely to bias estimates of the effect of pharmaceutical innovation on premature mortality, for two reasons. First, more than half of US funding for biomedical research came from pharmaceutical and biotechnology firms [4]. Much of the rest came from the federal government (i.e., the NIH), and new drugs often build on upstream government research [18]. The National Cancer Institute [14] says that it “has played an active role in the development of drugs for cancer treatment for 50 years… [and] that approximately one half of the chemotherapeutic drugs currently used by oncologists for cancer treatment were discovered and/or developed” at the National Cancer Institute.

Second, previous research based on US data indicates that non-pharmaceutical medical innovation is not positively correlated across diseases with pharmaceutical innovation. Lichtenberg [9] showed that, in the US during the period 1997–2007, the rate of pharmaceutical innovation was not positively correlated across diseases with the rate of medical procedure innovation and may have been negatively correlated with the rate of diagnostic imaging innovation. Also, Lichtenberg [10] found that estimates of the effect of pharmaceutical innovation on US cancer mortality rates were insensitive to the inclusion or exclusion of measures of non-pharmaceutical medical innovation. This suggests that failure to control for other medical innovation is unlikely to result in overestimation of the effect of pharmaceutical innovation on longevity growth.

In Eq. (1), premature mortality from cancer at site s in year t depends on the number of new chemical entities (drugs) to treat cancer at site s launched in Switzerland by the end of year t − k, i.e., there is a lag of k years. Eq. (1) will be estimated for different values of k: k = 0, 5, 10, 15, 20, 25, 30.¹⁰ One would expect there to be a substantial lag because new drugs diffuse gradually—they won’t be used widely until years after commercialization. Figure 7 shows data on the mean number of standard units¹¹ of cancer drugs sold (in thousands) in Switzerland in 2012, by period of launch in Switzerland. Mean utilization in 2012 of drugs launched after 2000 is only 19 % as high as mean utilization of drugs launched during 1951–1990, and 11 % as high as mean utilization of drugs launched during 1991–2000.

Fig. 7

Mean quantity (000s of standard units) of cancer molecules sold in Switzerland in 2012, by year of launch of molecule in Switzerland

The effect of a drug’s launch on premature mortality is likely to depend on both the quality and the quantity of the drug. Indeed, it is likely to depend on the interaction between quality and quantity: a quality improvement will have a greater impact on mortality if drug utilization (quantity) is high. Although newer drugs tend to be of higher quality than older drugs (see [11]), the relative quantity of very new drugs is quite low, so the impact on mortality of very new drugs is lower than the impact of older drugs.

Premature mortality in year t presumably depends more on the number of drugs actually used to treat patients in year t (N_NCE_TREAT_s,t ) than it does on the number of drugs registered by year t (or t − k). (Some drugs are not used until several years after registration.) CUM_NCE _s,t−k might be considered a “noisy indicator” of N_NCE_TREAT _s,t . In other words, CUM_NCE _s,t−k is subject to measurement error. Measurement error often biases coefficients towards zero. McKinnish [12] argued that when explanatory variables in panel data models are subject to measurement error, long-difference estimates may be less downward biased than fixed-effects estimates,¹² and that “it seems prudent for researchers to estimate both fixed-effects and long-differences models whenever feasible”. Therefore, in addition to estimating the fixed-effects model of the level of premature mortality (Eq. 1) using annual data, I will estimate a long-difference model that can be derived from Eq. (1). A special case of Eq. (1), when t = 2012 (the final year of the sample period) and incidence and mean age at diagnosis are excluded (for simplicity) is:

$${ \ln }\left( {{\text{YPLL75}} _{{{\text{s}}, 20 1 2}} } \right) = \beta_{k} {\text{CUM}}\_{\text{NCE}}_{{{\text{s}}, 20 1 2- k}} + \alpha_{\text{s}} + \delta_{ 20 1 2} + \varepsilon_{{{\text{s}}, 20 1 2}}$$

(2)

When t = 1995 (the initial year of the sample period) and incidence and mean age at diagnosis are excluded:

$${ \ln }\left( {{\text{YPLL75}} _{{{\text{s}}, 1 9 9 5}} } \right) = \beta_{k} {\text{CUM}}\_{\text{NCE}}_{{{\text{s}}, 1 9 9 5- k}} + \alpha_{\text{s}} + \delta_{ 1 9 9 5} + \varepsilon_{{{\text{s}}, 1 9 9 5}}$$

(3)

Subtracting (3) from (2) yields a simple linear regression:

$${ \ln }\left( {{\text{YPLL75}} _{{{\text{s}}, 20 1 2}} } \right) - { \ln }\left( {{\text{YPLL75}} _{{{\text{s}}, 1 9 9 5}} } \right) = \beta_{k} \left( {{\text{CUM}}\_{\text{NCE}}_{{{\text{s}}, 20 1 2- k}} - {\text{CUM}}\_{\text{NCE}}_{{{\text{s}}, 1 9 9 5- k}} } \right) + \, \left( {\delta_{ 20 1 2} - \delta_{ 1 9 9 5} } \right) + \left( {\varepsilon_{{{\text{s}}, 20 1 2}} - \varepsilon_{{{\text{s}}, 1 9 9 5}} } \right)$$

(4)

It is quite plausible that (CUM_NCE _s,2012−k − CUM_NCE _s,1995−k) is subject to less measurement error than CUM_NCE _s,t−k : the long-run (12-years) change in the number of drugs used to treat a condition can be measured more reliably than the number of drugs used to treat a condition in a particular year.

The measure of pharmaceutical innovation, CUM_NCE _s,t−k  = ∑_d IND_ds LAUNCH_d,t−k , is based on whether drug d had an indication for cancer at site s at the end of 2011. One would prefer to base the measure on whether drug d had an indication for cancer at site s at the end of year t − k. FDA data indicate that about one in four new molecular entities has supplemental indications, i.e., indications approved after the drug was initially launched.¹³

In Eq. (1), the measure of premature mortality is the number of years of potential life lost before age 75. To assess the robustness of my results, I will estimate models similar to Eq. (1), using the age threshold 65 as well as 75.

Chemical substances are divided into different groups according to the organ or system on which they act and their therapeutic, pharmacological, and chemical properties. In the anatomical therapeutic chemical (ATC) classification system developed by the World Health Organization Collaborating Centre for Drug Statistics Methodology, drugs are classified in groups at five different levels. The highest (1st) level is the “anatomical main group” level; there are 14 anatomical main groups. The 2nd, 3rd, 4th, and 5th levels are “therapeutic subgroup”, “pharmacological subgroup”, “chemical subgroup”, and “chemical substance”, respectively.¹⁴ Premature mortality from a disease may depend on the number of chemical (or pharmacological) subgroups that have previously been developed to treat the disease rather than, or in addition to, the number of chemical substances (drugs) that have previously been developed to treat the disease. This will be investigated by estimating versions of Eq. (4) in which (CUM_SUBGROUP_{s,2012 − k} − CUM_SUBGROUP_{s,1995 − k} ) is included in addition to or instead of (CUM_NCE_{s,2012 − k} − CUM_NCE_{s,1995 − k} ), where

CUM_SUBGROUPs,t−k	= ∑g IND_SUBGROUPgs REGISTERED_SUBGROUPg,t−k
IND_SUBGROUPgs	= 1 if any drugs in chemical subgroup g are used to treat (indicated for) cancer at site s = 0 if no drugs in chemical subgroup g are used to treat (indicated for) cancer at site s
REGISTERED_SUBGROUPg,t−k	= 1 if any drugs in chemical subgroup g had been registered in Switzerland by the end of year t − k = 0 if no drugs in chemical subgroup g had been registered in Switzerland by the end of year t − k

Data

NCE registrations in Switzerland (registered)

Data on new chemical entities registered in Switzerland were constructed from the expanded list of preparations of human and veterinary medicines published by the Swiss Agency for Therapeutic Products. This list includes WHO ATC codes and Swiss registration dates of pharmaceutical preparations.

Drug indications (IND)

Data on drug indications were obtained from Thériaque, a database of official, regulatory, and bibliographic information on all drugs available in France,¹⁵ intended for health professionals. This database is produced by the Centre National Hospitalier d’Information sur le Médicament. In this database, drugs are coded according to WHO ATC codes, and diseases are coded according to WHO ICD-10 codes.¹⁶

Appendix Table 3 shows drugs (sorted by Swiss launch year) used to treat various types of cancer in Switzerland.

Premature mortality data (YPLL75, YPLL65)

Data on years of potential life lost before ages 75 and 65, by cancer site and year (1995–2012), were constructed from data provided by the Federal Statistics Office.¹⁷

Cancer incidence data

Data on the number of new cancer cases, by cancer site, age, and year, were obtained from the National Institute for Cancer Epidemiology and Registration.¹⁸ This source also enabled calculation of the mean age of people diagnosed with cancer, by cancer site and year.

Appendix Table 4 shows data on the number of years of potential life lost and the number of new cases diagnosed (in the previous year) before ages 75 and 65, by cancer site, in 1995 and 2012.

Empirical results

Estimates of CUM_NCE coefficients from fixed-effects (FE) and long-difference (LD) models of premature cancer mortality are presented in Table 1. All models controlled for cancer incidence and mean age at diagnosis in the previous year. Controlling for these variables had little effect on estimates of the CUM_NCE coefficients; to conserve space, coefficients on cancer incidence and mean age at diagnosis are not shown in Table 1.

Table 1 Estimates of CUM_NCE coefficients from fixed-effects and long-difference models of premature cancer mortality

The estimates in the top part of the table (lines 1–3) are of models in which the age threshold for measuring premature mortality is age 75. The estimates in the bottom part of the table (lines 4–6) are of models in which the age threshold for measuring premature mortality is age 65. For each age threshold, estimates based on three alternative assumed lags (5, 10, and 15 years) between drug registration and premature mortality are presented.¹⁹

The left side of line 1 of Table 1 shows the FE model estimate of the effect of cumulative NCEs registered on the log of the premature (before age 75) cancer mortality rate 5 years later. The estimate is negative and significant (p value = 0.05). It indicates that premature cancer mortality was reduced by 1.2 % by an additional drug registered at least 5 years earlier. The right side of line 1 shows that the magnitude of the corresponding LD model estimate is 48 % larger; this is consistent with the hypothesis that the long-run (12-years) change in the number of drugs used to treat a condition can be measured more reliably than the number of drugs used to treat a condition in a particular year. This estimate is just slightly less significant (p value = 0.06).

In line 2, the assumed lag between cumulative NCE launches and premature mortality is 10 years. The FE estimate of β ₁₀ is 36 % larger than the FE estimate of β ₅, and the LD estimate of β ₁₀ is 73 % larger than the LD estimate of β ₅. As discussed above, since mean utilization of new drugs is much lower than mean utilization of older drugs, a more recent drug registration may have a smaller marginal effect on premature mortality than an earlier drug registration even if the average quality of newer drugs is higher. The LD estimate of β ₁₀ indicates that premature cancer mortality was reduced by 3.1 % by an additional drug registered at least 10 years earlier.

In line 3, the assumed lag between cumulative NCE launches and premature mortality is 15 years. The FE estimate of β ₁₅ is 33 % larger than the FE estimate of β ₁₀: the LD estimate of β ₁₅ is approximately equal to the LD estimate of β ₁₀. Both estimates are highly significant (p value <0.01). Figure 8 depicts the correlation across 13 cancer sites between the 1995–2012 log change in the premature (before age 75) mortality rate and the number of NCEs registered during 1980–1997 (i.e., the increase in cumulative NCEs registered until 15 years before).²⁰ The number of NCEs registered during 1980–1997 explains 63 % of the variation across cancer sites in the 1995–2012 log change in the premature (before age 75) mortality rate.

Fig. 8

Relationship across cancer sites between number of drugs launched, 1980–1997, and log change in premature mortality, 1995–2012

As shown in lines 4–6 of Table 1, the estimates of models in which the age threshold for measuring premature mortality is age 65 are qualitatively similar to the estimates of models in which the age threshold for measuring premature mortality is age 75.

Overall, the estimates in Table 1 indicate that premature cancer mortality before ages 75 and 65 is significantly inversely related to the cumulative number of NCEs registered 5, 10, and 15 years earlier (controlling for the number of people diagnosed and mean age at diagnosis); that LD estimates of the effect of NCE registrations are considerably larger than FE estimates (consistent with the presence of measurement error in the regressor); and that the marginal effect of more recently registered (and less frequently used) NCEs is smaller than the marginal effect of older NCEs.

As discussed earlier, premature mortality from a disease may depend on the number of chemical (or pharmacological) subgroups that have previously been developed to treat the disease rather than, or in addition to, the number of chemical substances (drugs) that have previously been developed to treat the disease. I investigated this possibility by estimating LD models with a 15-years lag in which (CUM_SUBGROUP_s,1997 − CUM_SUBGROUP_s,1980) was included in addition to (CUM_NCE_s,1997 − CUM_NCE_s,1980). In models of both premature mortality before age 75 and premature mortality before age 65, only the coefficients on (CUM_NCE_s,1997 − CUM_NCE_s,1980) were significant. That finding suggests that drugs (chemical substances) within the same class (chemical subgroup) are not “therapeutically equivalent”,²¹ i.e., they do not have essentially the same effect in the treatment of a disease or condition.

Discussion

Now I will use the estimates presented in Table 1 to calculate the number of life-years gained in 2012 from pharmaceutical innovation and drug expenditure per life-year gained. These calculations are shown in Table 2. Line 1 shows the premature (before ages 75 and 65) mortality rates of all cancers combined in 2012. The estimates imply that, in the absence of previous pharmaceutical innovation, these premature mortality rates would have been higher than they actually were. On the other hand, 2012 pharmaceutical expenditure would have been lower in the absence of previous pharmaceutical innovation. I will calculate 12 (=2 × 3 × 2) different estimates of life-years gained and their average cost, based on 2 estimation methods (FE and LD), 3 lags (5, 10, and 15 years), and 2 age thresholds (75 and 65).

Table 2 Calculation of number of life-years gained in 2012 from pharmaceutical innovation and of drug expenditure per life-year gained

As shown in line 4, the mean 1997–2012 increase in the cumulative number of drugs registered 5, 10, and 15 years earlier was 9.2, 11.8, and 11.3, respectively. As shown in line 6, the log change in premature mortality due to the increase in the cumulative number of drugs registered is β _k × ΔCUM_NCE _k . For example, the LD estimate of β ₅ × ΔCUM_NCE₅ (=−0.164) implies that the 2012 mortality rate before age 75 would have been 18 % (=exp(0.164) − 1) higher if ΔCUM_NCE₅ had been equal to zero: the mortality rate would have been 1513 rather than its actual value of 1284. As shown in line 7, that implies that 17,092 [=(1513 − 1284) × 7.5] life-years before age 75 were gained in 2012 due to pharmaceutical innovation during 1990–2007. The LD estimates of the number of life-years before age 75 gained from pharmaceutical innovation during 1985–2002 and 1980–1997 are more than twice as great.²²

Line 8 of Table 2 shows estimates of expenditure in 2012 on drugs used to treat cancer that were registered during the period 1995 − k to 2012 − k (k = 5, 10, 15). Data from IMS Health were used to estimate 2012 expenditure on each of the molecules listed in Appendix Table 3.²³ Our figures are likely to overstate expenditure on drugs used to treat cancer, for two reasons. First, some of these molecules [especially those not in anatomical main group L (antineoplastic and immunomodulating agents)] are used to treat diseases other than cancer. Second, the IMS data do not account for any rebates paid by drug manufacturers to payers, although according to pharmaceutical industry executives rebates play a much smaller role in Switzerland than they do in some other countries (e.g., the USA).

Table 3 Drugs (sorted by Swiss launch year) used to treat various types of cancer in Switzerland

The IMS Health data indicate expenditure by or on behalf of patients of all ages. Data from the National Institute for Cancer Epidemiology and Registration indicate that 70 % of patients diagnosed with cancer are diagnosed before the age of 75, and 41 % are diagnosed before the age of 65. I assumed that 70 % of 2012 expenditure on drugs used to treat cancer was for patients below age 75 and that 41 % of 2012 expenditure on drugs used to treat cancer was for patients below age 65. Since patients diagnosed before age 75 (for example) may continue to incur drug expenditure after age 75, these assumptions are also likely to be conservative, i.e., to overstate expenditure on drugs used to treat cancer on patients below age 75.

Line 9 of Table 2 shows estimates of the cost per life-year gained from previous pharmaceutical innovation. The FE estimates of the cost per life-year gained before ages 75 and 65 in 2012 from drugs launched during 1990–2007 are $32,287 and $40,010, respectively. However, as McKinnish [12] observed, “if the independent variable is an imprecise measure of the relevant factor, coefficient estimates from [FE] models can be severely attenuated towards zero”. Hence, the FE estimates may well understate the number of life-years gained, and we may also be overestimating the cost. The LD estimates of the cost per life-year gained before ages 75 and 65 in 2012 from drugs launched during 1990–2007, which are likely to be less attenuated towards zero, are at least 28 % lower: $21,228 and $28,673, respectively. Moreover, the LD estimates indicate that the cost per life-year before age 75 gained from drugs launched during 1985–2002 and 1980–1997 were considerably lower: $5299 and $3218, respectively.²⁴

Hirth et al. [6] performed a search of the value-of-life literature and identified 41 estimates of the value of life from 37 articles.²⁵ From estimates of the value of life, they calculated estimates of the value (in 1997 dollars) of a quality-adjusted life-year (QALY).²⁶ Four types of methods were used to produce those estimates: revealed preference/job risk, contingent valuation, revealed preference/non-occupational safety, and human capital. Median implied values (in 1997 and 2012 dollars²⁷) of a QALY estimated in those studies are shown in the following table.

Study method	Number of studies	Median value of a QALY
		1997 dollars	2012 dollars
Revealed preference/job risk	19	$428,286	$612,449
Contingent valuation	8	$161,305	$230,666
Revealed preference/non-occupational safety	8	$93,402	$133,565
Human capital	6	$24,777	$35,431

The LD estimates in line 9 of Table 2 of the cost per life-year gained before ages 75 and 65 in 2012 from drugs launched during 1990–2007 ($21,228 and $28,673, respectively) are lower than the median value in 2012 dollars of a QALY obtained from human capital studies ($35,431). Moreover, the median value of a QALY implied by other study methods was 3.8–17.3 times as high as the median value implied by human capital studies.

Summary and conclusions

The premature cancer mortality rate has been declining in Switzerland, but there has been considerable variation in the rate of decline across cancer sites. I analyzed the effect that pharmaceutical innovation has had on premature cancer mortality in Switzerland during the period 1995–2012, by investigating whether the cancer sites that experienced more pharmaceutical innovation had larger declines in premature mortality, controlling for the number of people diagnosed and mean age at diagnosis.

Premature cancer mortality before ages 75 and 65 is significantly inversely related to the cumulative number of NCEs registered 5, 10, and 15 years earlier. The number of NCEs registered during 1980–1997 explains 63 % of the variation across cancer sites in the 1995–2012 log change in the premature (before age 75) mortality rate.

Controlling for the cumulative number of drugs, the cumulative number of chemical subgroups does not have a statistically significant effect on premature mortality. This suggests that drugs (chemical substances) within the same class (chemical subgroup) are not “therapeutically equivalent”.

Over 17,000 life-years before age 75 were gained in 2012 due to drugs registered during 1990–2007. The number of life-years before age 75 gained from drugs registered during two earlier periods (1985–2002 and 1980–1997) were more than twice as great. Since mean utilization of new drugs is much lower than mean utilization of older drugs, more recent drug registrations may have a smaller effect on premature mortality than earlier drug registrations even if the average quality of newer drugs is higher.

Estimates of the cost per life-year gained before ages 75 and 65 in 2012 from drugs launched during 1990–2007 are $21,228 and $28,673, respectively. These figures are below even the lowest estimates from the value-of-life literature of the value of a QALY. The estimates indicate that the cost per life-year before age 75 gained from drugs launched during earlier periods (1985–2002 and 1980–1997) were considerably lower: $5299 and $3218, respectively.

The largest reductions in premature mortality occur at least a decade after drugs are registered, when their utilization increases significantly. This suggests that if Switzerland is to obtain substantial additional reductions in premature cancer mortality in the future (a decade or more from now) at a modest cost, pharmaceutical innovation (registration of new drugs) is needed today.

Appendix

See Tables 3 and 4.

Table 4 Premature cancer mortality and cancer incidence, by cancer site, Switzerland, 1995 and 2012