Robust estimation of fixed effect parameters and variances of linear mixed models: the minimum density power divergence approach

Abstract

Many real-life data sets can be analyzed using linear mixed models (LMMs). Since these are ordinarily based on normality assumptions, under small deviations from the model the inference can be highly unstable when the associated parameters are estimated by classical methods. On the other hand, the density power divergence (DPD) family, which measures the discrepancy between two probability density functions, has been successfully used to build robust estimators with high stability associated with minimal loss in efficiency. Here, we develop the minimum DPD estimator (MDPDE) for independent but non-identically distributed observations for LMMs according to the variance components model. We prove that the theoretical properties hold, including consistency and asymptotic normality of the estimators. The influence function and sensitivity measures are computed to explore the robustness properties. As a data-based choice of the MDPDE tuning parameter $\alpha$ is very important, we propose two candidates as “optimal” choices, where optimality is in the sense of choosing the strongest downweighting that is necessary for the particular data set. We conduct a simulation study comparing the proposed MDPDE, for different values of $\alpha$, with S-estimators, M-estimators and the classical maximum likelihood estimator, considering different levels of contamination. Finally, we illustrate the performance of our proposal on a real-data example.

1 Introduction

A major interest in statistics concerns the estimation of averages and their variation. The most commonly used method for this purpose is, probably, the Linear Model (LM). In this model, to give an example from a two-way layout, the expected value (mean) $\mu _{ij}$ of an observation $y_{ij}$ may be expressed as a linear combination of unknown parameters such as $\mu _{ij} = \mu + \alpha _i + \beta _j$, where $\mu$, $\alpha _i$ and $\beta _j$ are the constants which we are interested in estimating. The linearity in the parameters means that we can write a linear model in the form $\varvec{y}_i = \varvec{X}_i\varvec{\beta } + \varvec{\epsilon _i}$, where $\varvec{\beta }$ is the vector of unknown parameters, and the $\varvec{X}_i$s are known matrices. This formulation is the same as that used in case of linear regression model. In the present work, we consider the linear mixed models (LMMs), in which some (unknown) parameters are not treated as constants but as random variables. Random terms come into play when some items cannot be considered as fixed quantities, although their distributions are of interest. Hence, they are the tools to generalize the results to the entire population under study. The types of data that may be appropriately analyzed by LMMs include (i) Clustered data, where the dependent variable is measured once for each subject (the unit of analysis) and the units of analysis are grouped into, or nested within, clusters; (ii) Repeated-measures data, where the dependent variable is measured more than once on the same unit of analysis across levels of a factor, which may be time or other experimental conditions; (iii) Longitudinal data, where the dependent variable is measured at several points in time for each unit of analysis. For a general review of LMs and LMMs, see McCulloch and Searle (2001).

The standard methods used to estimate the parameters in LMMs are methods of maximum likelihood and restricted maximum likelihood. Generally, LMMs are based on normality assumptions, and it is well-known that these classical methods are not robust and can be greatly affected by the presence of small deviations from the assumptions. Furthermore, outlier detection for modern large data sets can be very challenging and, in any case, robust techniques cannot be replaced by the application of classical methods on outlier deleted data.

To answer the need for robust estimation in linear mixed models, a few methods have been proposed. The initial attempts were based on weighted versions of the log-likelihood function (see Huggins 1993a, b; Huggins and Staudte 1994; Stahel and Welsh 1994; Richardson and Welsh 1995; Richardson 1997; Welsh and Richardson 1997). Another attempt, discussed in Welsh and Richardson (1997), of robustifying linear mixed models consists of replacing the Gaussian distribution by the Student’s t distribution (see also Lange et al. 1989; Pinheiro et al. 2001). However, this modification of the error distribution is intractable and complicated to implement. In Copt and Victoria-Feser (2006), a multivariate high breakdown point S-estimator, namely the CVFS-estimator, has been adapted to the linear mixed models setup, while the estimator given by Koller (2013), namely the SMDM-estimator, attempts to achieve robustness by a robustification of the score equations. Robust estimators have been proposed, more generally, for generalized linear mixed models by Yau and Kuk (2002) and Sinha (2004).

The density power divergence (DPD) (Basu et al. (1998)), which measures the discrepancy between two probability density functions, has been successfully used to build robust estimators for independent and identically distributed observations. In Ghosh and Basu (2013), the construction of the DPD and the corresponding minimum DPD estimator (MDPDE) has been extended to the case of independent but non-identically distributed data. This approach and theory covers the linear regression model and has later been extended to more general parametric regression models (Ghosh and Basu 2016, 2019; Castilla et al. 2018, 2021; Ghosh 2019, etc.). This MDPDE has become widely popular in recent times due to its good (asymptotic) efficiency along with high robustness, easy computability and direct interpretation as an intuitive generalization of the maximum likelihood estimator (MLE).

In the present work, our aim is to propose a robust estimator of the fixed effect parameters and variances of random effects under the linear mixed model set up. In particular, we are going to consider independent random effects according to the standard variance components models. This is done by an application of the definition and properties of the MDPDE, as formulated by Ghosh and Basu (2013), to the linear mixed models scenario. However, in this case, the observations have a complicated, non-identically distributed structure, which makes this adaptation non-trivial, in the computation of the estimator as well as in the theoretical derivations. We show that under appropriate conditions on the model matrices, the asymptotic and robustness properties hold, and the resulting estimator outperforms the competing robust estimators both in the presence and in the absence of contamination in sample data. Furthermore, the calculation of the sensitivity measures allows us to find “optimal” values for the tuning parameter $\alpha$, where optimality is in terms of the right amount of data-specific downweighting needed to achieve robustness with minimal loss of efficiency. This is a valuable new contribution to the literature of DPD-based inference since, in contrast with the previous knowledge of $\alpha$ as trade-off between robustness and efficiency, our results lead to a small positive value of $\alpha$ as an optimum choice in practical applications. Furthermore, the estimation of random effects has been also considered, which is an important aspect in the study of LMMs. In particular, we provide a closed form to compute the random effects estimates based on the minimum DPD estimation. Large-scale numerical explorations, including an extensive simulation study, are provided to substantiate the theory developed and justify our claims of the superiority of the MDPDE in the proposed application domain of LMMs. Finally, our proposal is applied successfully (and robustly) to analyze two real-life data, one on orthodontic measures and another on foveal and extrafoveal vision acuity.

The rest of the paper is organized as follows. The MDPDE for non-homogeneous observations described in Ghosh and Basu (2013) is briefly presented in Sect. 2. In Sect. 3, we define the proposed estimator in case of linear mixed models, considering the estimation of fixed effect parameters and variances of random effects, and the prediction of random terms. The asymptotic and robustness properties of our procedures are considered in Sect. 4 together with the computational aspects and the case of balanced data. Section 5 reports the organization and results of the simulation study we conducted, comparing the performance of the MDPDE to the most recent methods, exploring also the case of contaminated data. Section 6 provides the application of the proposed estimator to the real-data example on orthodontic measures. Concluding remarks are presented in Sect. 7. The proof of the main theorem is reported in Appendix A, while the Supplementary Material contains the derivation of equivariance properties, some additional theoretical and Monte Carlo results, an example which shows the robustness of predicted random terms, and the application to the real-data example on foveal and extrafoveal vision acuity.

2 The MDPDE for independent non-homogeneous observations

The density power divergence family was first introduced by Basu et al. (1998) as a measure of discrepancy between two probability density functions. The authors used this measure to robustly estimate the model parameters under the usual setup of independent and identically distributed data. The density power divergence measure $d_\alpha (g,f)$ between two probability densities g and f is defined, in terms of a single tuning parameter $\alpha \ge 0$, as

$$\begin{aligned}&d_\alpha (g,f) = \int \left\{ f^{1+\alpha } - \left( 1 + \frac{1}{\alpha }\right) f^\alpha g + \frac{1}{\alpha }g^{1+\alpha }\right\}&\quad \text{ if } \alpha > 0, \end{aligned}$$

(1)

$$\begin{aligned}&\quad d_0 (g,f) = \int g \ln \left( \frac{g}{f}\right)&\text{ if } \alpha = 0, \end{aligned}$$

(2)

where $\ln$ denotes the natural logarithm. Basu et al. (1998) demonstrated that the tuning parameter $\alpha$ controls the trade-off between efficiency and robustness of the resulting estimator. With increasing $\alpha$, the estimator acquires greater stability with a slight loss in efficiency. Since the divergence is not defined for $\alpha = 0$, $d_0(g,f)$ in Equation (2) represents the divergence obtained in the limit of (1) as $\alpha \rightarrow 0$, which corresponds to a version of the Kullback–Leibler divergence. On the other hand, $\alpha = 1$ generates the squared $L_2$ distance.

Let G be the true data generating distribution and g the corresponding density function. To model g, consider the parametric family of densities $\mathcal {F}_{\varvec{\theta }} = \{f_{\varvec{\theta }}: \varvec{\theta } \in \Theta \subseteq \mathbb {R}^p \}$. The minimizer of $d_\alpha (g,f_{\varvec{\theta }})$ over $\varvec{\theta } \in \Theta$, whenever it exists, is the minimum DPD functional at the distribution point G. Note that the third term of the divergence $d_\alpha (g,f_{\varvec{\theta }})$ is independent of $\varvec{\theta }$; hence, it can be discarded from the objective function as it has no role in the minimization process. Consider a sequence of independent and identically distributed (i.i.d) observations $\varvec{Y}_1, \ldots , \varvec{Y}_n$ from the true distribution G. Using the empirical distribution function $G_n$ in place of G, the MDPDE of $\varvec{\theta }$ can be obtained by minimizing

$$\begin{aligned} \int f_{\varvec{\theta }}^{1+\alpha } - \left( 1+\frac{1}{\alpha }\right) \frac{1}{n}\sum _{i=1}^n f_{\varvec{\theta }}^\alpha (\varvec{Y}_i) \end{aligned}$$

over $\varvec{\theta } \in \Theta$. In the above equation, the empirical distribution function is used to approximate its theoretical version (or, alternatively, the sample mean is used to approximate the population mean). Note that, it is valid in case of continuous densities also. See Basu et al. (2011) for more details and examples.

Ghosh and Basu (2013) generalized the above concept of robust minimum DPD estimation to the more general case of independent non-homogeneous observations, i.e., they considered the case where the observed data $\varvec{Y}_1, \ldots , \varvec{Y}_n$ are independent but for each i, $\varvec{Y}_i \sim g_i$ where $g_1, \ldots , g_n$ are possibly different densities with respect to some common dominating measure. We model $g_i$ by the family $\mathcal {F}_{i,\varvec{\theta }} = \{f_i(\cdot ,\varvec{\theta }): \varvec{\theta } \in \Theta \}$ for $i \in \{1, \ldots , n\}$. While the distributions $f_i(\cdot ,\varvec{\theta })$ can be distinct, they share the same parameter vector $\varvec{\theta }$. Ghosh and Basu (2013) proposed to minimize the average divergence between the data points and the model densities which leads to the minimization of the objective function

$$\begin{aligned} H_n(\varvec{\theta })=\frac{1}{n} \sum _{i=1}^n \left[ \int f_i(\varvec{y},\varvec{\theta })^{1+\alpha }dy - \left( 1+\frac{1}{\alpha }\right) f_i(\varvec{Y}_i,\varvec{\theta })^\alpha \right] = \frac{1}{n}\sum _{i=1}^n H_i(\varvec{Y}_i,\varvec{\theta }), \end{aligned}$$

(3)

where $H_i(\varvec{Y}_i,\varvec{\theta })$ is the indicated term within the square brackets in the above equation. Differentiating the above expression with respect to $\varvec{\theta }$ , we get the estimating equations of the MDPDE for non-homogeneous observations. Note that the estimating equation is unbiased when each $g_i$ belongs to the model family $\mathcal {F}_{i,\varvec{\theta }}$, respectively. When $\alpha \rightarrow 0$, the corresponding objective function reduces to $- \sum _{i=1}^n \ln (f_i(\varvec{Y}_i,\varvec{\theta })) /n$, which is the negative of the log-likelihood function. In Section SM–1 of the Supplementary Material, we report Assumptions (A1)–(A7) which are used to prove the asymptotic normality of the MDPDE (Ghosh and Basu 2013).

3 The MDPDE for linear mixed models

The general formulation of a LMM may be expressed as

$$\begin{aligned} \varvec{Y} = \varvec{X}\varvec{\beta } + \varvec{Z} \varvec{\mathcal {U}} + \varvec{\epsilon }, \end{aligned}$$

(4)

where $\varvec{Y} \in \mathbb {R}^d$ is the response vector, $\varvec{X}$ and $\varvec{Z}$ are known design matrices, $\varvec{\beta }$ is the parameter vector for fixed effects, $\varvec{\mathcal {U}}$ is the vector of random effects, and $\varvec{\epsilon }$ is the random error vector. The vector $\varvec{\mathcal {U}}$ is assumed to be a random variable, in particular $\varvec{\mathcal {U}} \sim N_q (\varvec{0},\varvec{D})$, then $\mathbb {E}(\varvec{Y} \vert \varvec{\mathcal {U}} =\varvec{u}) = \varvec{X}\varvec{\beta } + \varvec{Z}\varvec{u}$. Notice that we will use $\varvec{\mathcal {U}}$ to indicate the random variable and $\varvec{u}$ for its realization. Finally, assume that $\varvec{\epsilon } \sim N_d(\varvec{0},\varvec{R})$ and $\varvec{\epsilon }$ and $\varvec{\mathcal {U}}$ are independent of each other, then

$$\begin{aligned} \varvec{Y} \sim N_d\left( \varvec{X}\varvec{\beta }, \varvec{Z}\varvec{D}\varvec{Z}^\top + \varvec{R} \right) . \end{aligned}$$

(5)

The estimation of the matrices $\varvec{D}$ and $\varvec{R}$ involves a large amount of parameters; indeed, we need to assume some additional structure to the mixed model. According to the variance components model, the levels of any random effect are assumed to be independent with the same variance. Different effects are assumed independent with possibly different variances. Let the model have r random factors $\varvec{\mathcal {U}}_j$ with $q_j$ levels, $j \in \{1,\ldots ,r\}$, with $q = \sum _{j=1}^r q_j$. As stated in Christensen (2011), a “natural generalization" of model 5 is to partition the vector $\varvec{\mathcal {U}} = [\varvec{\mathcal {U}}_1,\ldots ,\varvec{\mathcal {U}}_r]$ and matrix $\varvec{Z} = [\varvec{Z}_1 \ldots \varvec{Z}_r]$, such that $\varvec{\mathcal {U}}_j$ are independent between each other, i.e., $\mathbb {C} ov (\varvec{\mathcal {U}}_i,\varvec{\mathcal {U}}_j) = 0$ for $i \not = j$, and $\mathbb {C}ov(\varvec{\mathcal {U}}_j) = \varvec{D}_j= \sigma ^2_j\varvec{I}_{q_j}$, $j=1,\ldots ,r$. Finally, assume $\varvec{\epsilon }$ and $\varvec{\mathcal {U}_j}$ independent for all j and $\varvec{R} = \sigma _0^2 \varvec{I}_d$, where $\varvec{I}_n$ is the $n \times n$ identity matrix.

Then, $\varvec{Y} \sim N_d\left( \varvec{X}\varvec{\beta },\varvec{V} \right)$ where

$$\begin{aligned} \varvec{V} = \sigma _0^2\varvec{I}_{d} + \sum _{j=1}^r\varvec{Z}_{j}\varvec{Z}_{j}^\top \sigma ^2_j = \sigma _0^2\left( \varvec{I}_{d} + \sum _{j=1}^r \varvec{Z}_{j}\varvec{Z}_{j}^\top \gamma _j \right) , ~~~~ \text{ with } ~\gamma _j = \frac{\sigma ^2_j}{\sigma _0^2}. \end{aligned}$$

In case of multiple measurements on each of a collection of observational units $\varvec{Y}_1, \ldots , \varvec{Y}_n$, where $n_i$ denotes the size of each group and $\sum _{i=1}^nn_i = N$, the LMM in equation (4) can be written for each observation as

$$\begin{aligned} \varvec{Y}_i = \varvec{X}_i\varvec{\beta } + \sum _{j=1}^r\varvec{Z}_{ij}\varvec{\mathcal {U}}_{j} + \varvec{\epsilon }_i, ~~~~~~~i \in \{1, \ldots , n\}, \end{aligned}$$

(6)

where $\varvec{Y}_i$ $(n_i \times 1)$ is the response vector for group i, $\varvec{X}_i$ $(n_i \times k)$ and $\varvec{Z}_{ij}$ $(n_i \times q_j)$ are the model matrices, $\varvec{\beta }$ $(k \times 1)$ is the vector of unknown parameters for fixed effects, and $\varvec{\epsilon }_i$ $(n_i \times 1)$ is the error term. Then, assuming $\varvec{\epsilon }_i \sim \sigma _0^2 \varvec{I}_{n_i}$ and independent with respect to $\varvec{\mathcal {U}}_j$ for all i, j,

$$\begin{aligned} \varvec{Y}_i \sim N_{n_i}\left( \varvec{X}_i\varvec{\beta }, \varvec{V}_{i}\right) , ~~~~~~ i\in \{1, \ldots , n\}. \end{aligned}$$

where $\varvec{V}_i = \sigma ^2_0(\varvec{I}_{n_i} + \sum _{j=1}^r\varvec{Z}_{ij}\varvec{Z}_{ij}^\top \gamma _j)$.

Remark

Note that the covariance structure of the linear mixed models considered here also includes the case of standard random intercept and random slope models. The real-data application presented in Sect. 6 provides an example. Indeed, Christensen (Christensen 2011) also considered this model for the discussion of all the variance components estimation methods. Also note that all the methods and results described in this paper can be routinely derived for any other (low-dimensional) parametric structure specified for the variance components in the LMM as per the need, but such situations (beyond the structure considered here) would rarely occur in practice.

3.1 Robust parameter estimation

In this setting, we can obtain the MDPDE for the p-dimensional parameter vector $\varvec{\theta } = (\varvec{\beta }^\top ; \sigma _j^2,j \in \{0, \ldots ,r\})^\top$, with $p=k+r+1$, by minimizing the objective function given in Equation (3) with $f_i \equiv N_{n_i}(\varvec{X}_i\varvec{\beta }, \varvec{V}_i)$. Upon simplification, the objective function is given by

$$\begin{aligned} H_n(\varvec{\theta }) = \frac{1}{n}\sum _{i=1}^n \bigg [ \eta _{i\alpha } (\alpha +1)^{-\frac{n_i}{2}} -\bigg (1+\frac{1}{\alpha }\bigg ) w_i(\varvec{\theta }) \bigg ] \end{aligned}$$

(7)

where

$$\begin{aligned} \eta _{i\alpha } = {(2\pi )^{-\frac{n_i\alpha }{2}}\vert \varvec{V}_i\vert ^{-\frac{\alpha }{2}}} \end{aligned}$$

and

$$\begin{aligned} w_i(\varvec{\theta }) = \eta _{i\alpha }\exp \left\{ -\frac{\alpha }{2} (\varvec{Y}_i - \varvec{X}_i\varvec{\beta })^\top \varvec{V}_i^{-1}(\varvec{Y}_i - \varvec{X}_i\varvec{\beta })\right\} . \end{aligned}$$

(8)

Differentiating the above equation with respect to $\varvec{\beta }$, we get the corresponding estimating equation for the MDPDE of $\varvec{\beta }$ as

$$\begin{aligned} \frac{\partial H_n}{\partial \varvec{\beta }} = \frac{1}{n} \sum _{i=1}^n\bigg [-\left( 1+\alpha \right) w_i(\varvec{\theta }) \varvec{X}_i^\top \varvec{V}_i^{-1}(\varvec{Y}_i - \varvec{X}_i\varvec{\beta })\bigg ] = 0. \end{aligned}$$

(9)

Let $\varvec{U}_{ij}$ denote the partial derivative of the matrix $\varvec{V}_i$ with respect to $\sigma ^2_j$. We have that $\varvec{U}_{i0} = \varvec{I}_{n_i}$, and $\varvec{U}_{ij} = \varvec{Z}_{ij}\varvec{Z}_{ij}^\top$, $j \in \{1,\ldots ,r\}$. Then, the partial derivative of the objective function with respect to $\sigma ^2_j$, $j \in \{0, \ldots ,r\}$, leads to their MDPDE estimating equations as given by

$$\begin{aligned} \frac{\partial H_n}{\partial \sigma ^2_j} =&\frac{1}{n} \sum _{i=1}^n \bigg \{- \frac{\alpha \eta _{i\alpha } \textrm{Tr}(\varvec{V}_i^{-1}\varvec{U}_{ij})}{2(\alpha +1)^{\frac{n_i}{2}}} + \frac{\alpha }{2} \left( 1+\frac{1}{\alpha }\right) w_i(\varvec{\theta }) \nonumber \\&\times \Big [ \textrm{Tr}(\varvec{V}_i^{-1}\varvec{U}_{ij}) - (\varvec{Y}_i - \varvec{X}_i\varvec{\beta })^\top \varvec{V}_i^{-1}\varvec{U}_{ij}\varvec{V}_i^{-1}(\varvec{Y}_i - \varvec{X}_i\varvec{\beta }) \Big ]\bigg \} = 0, \end{aligned}$$

(10)

where $\textrm{Tr}(\cdot )$ denotes the trace of the argument matrix. Note that for the case $\alpha =0$ , the estimating equations (9)–(10) correspond to the MLE score equations. Thus, the MDPDE at $\alpha =0$ is nothing but the usual MLE under LMMs.

3.2 Robust estimation of the random effects

Finally, the estimates obtained by minimizing the objective function in (7) are used to predict the random realizations $\varvec{u}_{i}\vert \varvec{Y}_i$, $i=1,\ldots ,n$. Consider the joint distribution of $(\varvec{Y}_i,\varvec{\mathcal {U}}) \sim g_i(\varvec{y},\varvec{u})$ , and we have that $g_i(\varvec{y},\varvec{u}) = g_i(\varvec{y} \vert \varvec{u}) g(\varvec{u})$, where $g(\varvec{u})$ is the true density of $\varvec{\mathcal {U}}$. Let $f_i(\varvec{y},\varvec{u})$ be the parametric density to model $g_i(\varvec{y},\varvec{u})$, then it can be expressed as $f_i(\varvec{y},\varvec{u}) = f_i(\varvec{y} \vert \varvec{u})f(\varvec{u})$, which, by the plug-in principle, can be estimated using

$$\begin{aligned} f_i(\varvec{y}\vert \varvec{u}) = N_{n_i} (\varvec{X}_i \hat{\varvec{\beta }} + \varvec{Z}_i\varvec{u}_i, \hat{\sigma }_0^2 \varvec{I}_{n_i}) \text{ and } f(\varvec{u}) = N_q(\varvec{0}, \hat{\varvec{D}}). \end{aligned}$$

Hence, we can estimate the random coefficients by minimizing the density power divergence measure between the densities $g_i(\varvec{y},\varvec{u})$ and $f_i(\varvec{y},\varvec{u})$ given by

$$\begin{aligned} H_n(\varvec{u}_1,\ldots ,\varvec{u}_n) = \frac{1}{n}\sum _{i=1}^n \kappa _\alpha \bigg [ (\alpha +1)^{-\frac{n_i+q}{2}} +\bigg (1+\frac{1}{\alpha }\bigg ) c_i(\varvec{u}_i) \bigg ], \end{aligned}$$

where

$$\begin{aligned} c_i(\varvec{u}_i) = \exp \left\{ -\frac{\alpha }{2\hat{\sigma }_0^2}(\varvec{Y}_i - \varvec{X}_i\hat{\varvec{\beta }} - \varvec{Z}_i \varvec{u}_i)^\top (\varvec{Y}_i - \varvec{X}_i\hat{\varvec{\beta }} - \varvec{Z}_i \varvec{u}_i) - \frac{\alpha }{2} \varvec{u}_i^\top \hat{\varvec{D}}^{-1}\varvec{u}_i\right\} \end{aligned}$$

and

$$\begin{aligned} \kappa _\alpha = \frac{1}{(2\pi )^{\frac{(n_i+q)\alpha }{2}} (\hat{\sigma }_0^2)^{\frac{n_i\alpha }{2}} \vert \hat{\varvec{D}}\vert ^{\frac{\alpha }{2}}}. \end{aligned}$$

Differentiating the above equation with respect to $\varvec{u}_i$, $i=1,\ldots ,n$, we obtain the estimating equations for the MDPDE of $\varvec{u}_i$ as

$$\begin{aligned} \frac{\partial H_n}{\partial \varvec{u}_i} = \frac{(1+\alpha )\kappa _\alpha c_i(\varvec{u}_i)}{n} \bigg [ (\hat{\sigma }_0^2)^{-1} \varvec{Z}_i^\top (\varvec{Y}_i - \varvec{X}_i \hat{\varvec{\beta }} - \varvec{Z}_i \varvec{u}_i) - \hat{\varvec{D}}^{-1}\varvec{u}_i \bigg ] = 0. \end{aligned}$$

(11)

The computational aspects about how equations (9), (10) and (11) are solved numerically are treated in subsection 4.3.

Remark

The proposed estimating equations given in equation (11) for the random effects $\varvec{u}_i$ can be simplified to

$$\begin{aligned} \bigg [ (\hat{\sigma }_0^2)^{-1} \varvec{Z}_i^\top (\varvec{Y}_i - \varvec{X}_i \hat{\varvec{\beta }} - \varvec{Z}_i \varvec{u}_i) - \hat{\varvec{D}}^{-1}\varvec{u}_i \bigg ] = 0 \end{aligned}$$

since $\kappa _\alpha$ does not depend on $\varvec{u}_i$ and $c_i(\varvec{u}_i)>0$ $\forall i$. Then, the estimating equation depends on $\alpha$ only through the estimates of the unknown parameters $\hat{\varvec{\beta }}, \hat{\sigma }_0$ and $\hat{\varvec{D}}$. For $\alpha \rightarrow 0$ , the estimates of the unknown parameters correspond to the MLE, then the random effects predictions $\hat{{u}}_i$ correspond to the standard predictions of random effects. Hence, they are the Best Linear Unbiased Predictors (BLUPs). Our formula differs from the standard formula since we provide estimates of the random effects for each i-th observation, while they are usually reported for each random effect.

4 Theoretical properties of the MDPDE under the Linear mixed models

4.1 Asymptotic efficiency

In this subsection, we prove that the theorem stated in Ghosh and Basu (2013), about the asymptotic behavior of the MDPDE for non-homogeneous observations, holds for the LMM setup. In particular, we present some conditions on the independent variables and the variance–covariance matrices that are used to derive the asymptotic distribution of the estimator in the LMM application.

We assume that the true densities $g_i$, $i = 1,\ldots ,n$, belong to the model family, i.e., $g_i=f_i(\cdot ,\varvec{\theta })$ for some value of $\varvec{\theta } \in \Theta$. Consider the following assumptions.

• (MM1) Define $\varvec{X}_i^\prime = \left( \frac{\eta _{i\alpha }\varvec{V}_i^{-1}}{(1+\alpha )^{\frac{n_i}{2}+1}} \right) ^{\frac{1}{2}}\varvec{X}_i$, for each i, and $\varvec{X}^\prime =\text{ Block-Diag }(\varvec{X}_i^\prime : i \in \{1,\ldots , n\} )$. Then, the $\varvec{X}^\prime$ matrix satisfies

  $$\begin{aligned} \inf _n \left[ \text{ min } \text{ eigenvalue } \text{ of } \frac{{\varvec{X}^\prime }^\top \varvec{X}^\prime }{n}\right] > 0, \end{aligned}$$

  (12)

  and $\varvec{X}_i$ and $\varvec{Z}_i$ are full rank matrices for all i.

• (MM2) The values of $\varvec{X}_i$’s are such that, for all j, k, l

  $$\begin{aligned}{} & {} \sup _{n>1} \max _{1 \le i\le n} \vert \varvec{X}_{ij}^\top \varvec{V}_i^{-\frac{1}{2}}\vert = O(1), \qquad \sup _{n>1} \max _{1 \le i\le n} \vert \varvec{X}_{ij}^\top \varvec{V}_i^{-1}\varvec{X}_{ik}\vert = O(1), \end{aligned}$$

  (13)
  $$\begin{aligned}{} & {} \quad \frac{1}{n}\sum _{i=1}^{n} \vert \varvec{X}_{ij}^\top \varvec{V}_i^{-1} \varvec{X}_{ik}\varvec{X}_{il}^\top \varvec{V}_i^{-\frac{1}{2}}\textbf{1}\vert = O(1),\nonumber \\{} & {} \quad \frac{1}{n} \sum _{i=1}^n \vert \varvec{X}_{ij}^\top \varvec{V}_i^{-\frac{1}{2}}\vert diag(\varvec{V}_i^{-\frac{1}{2}}\varvec{X}_{ik}\varvec{X}_{il}^\top \varvec{V}_i^{-\frac{1}{2}})\textbf{1} = O(1), \end{aligned}$$

  (14)

  where $\varvec{1}(n_i \times 1)$ is a vector of 1’s.

• (MM3) The matrices $\varvec{V}_i$ and $\varvec{U}_{ij}$ are such that, for all $j,k,l \in \{0, \ldots , r\}$,

  $$\begin{aligned} \frac{1}{n}\sum _{i=1}^n \textrm{Tr}(\varvec{V}_i^{-1}\varvec{U}_{ij})&= O(1), \qquad \frac{1}{n}\sum _{i=1}^n \textrm{Tr}(\varvec{V}_i^{-1}\varvec{U}_{ij})\textrm{Tr}(\varvec{V}_i^{-1}\varvec{U}_{ik}) = O(1), \nonumber \\&\frac{1}{n}\sum _{i=1}^n \textrm{Tr}(\varvec{V}_i^{-1}\varvec{U}_{ik}\varvec{V}_i^{-1}\varvec{U}_{ij}) = O(1), \end{aligned}$$

  (15)
  $$\begin{aligned} \frac{1}{n}&\sum _{i=1}^n \textrm{Tr}(\varvec{V}_i^{-1}\varvec{U}_{ij}\varvec{V}_i^{-1} \varvec{U}_{ik}\varvec{V}_i^{-1}\varvec{U}_{il}) = O(1),\nonumber \\ \frac{1}{n}&\sum _{i=1}^n \textrm{Tr}(\varvec{V}_i^{-1}\varvec{U}_{ij}\varvec{V}_i^{-1}\varvec{U}_{ik})\textrm{Tr}(\varvec{V}_i^{-1}\varvec{U}_{il}) = O(1),\nonumber \\ \frac{1}{n}&\sum _{i=1}^n \textrm{Tr}(\varvec{V}_i^{-1}\varvec{U}_{ij})\textrm{Tr}(\varvec{V}_i^{-1}\varvec{U}_{ik})\textrm{Tr}(\varvec{V}_i^{-1}\varvec{U}_{il}) = O(1), \end{aligned}$$

  (16)

  where the determinant $\vert \varvec{V}_i\vert$ is bounded away from both zero and infinity $\forall i$.

• (MM4) Define $\varvec{X}_i^*= \left( \frac{\eta ^2_{i\alpha }\varvec{V}_i^{-1}}{(1+2\alpha )^{\frac{n_i}{2}+1}} \right) ^{\frac{1}{2}}\varvec{X}_i$, for each i, and ${\varvec{X}^*}=\text{ Block-Diag }(\varvec{X}_i^*: i \in \{1,\ldots , n \})$. Then, the $\varvec{X}^*$ matrix satisfies

  $$\begin{aligned} \max _{1 \le i \le n} \left[ \frac{({\varvec{X}^*}^\top \varvec{X}^*)^{-1}\varvec{X}_i^\top \varvec{V}_i^{-1}\varvec{X}_i}{n} \right] = O(1). \end{aligned}$$

  (17)

Theorem 1

Consider the setup of the linear mixed model presented in Sect. 3. Assume that the true data generating density belongs to the model family and that the independent variables satisfy Assumptions (MM1)–(MM4) for a given (fixed) $\alpha \ge 0$. Then, we have the following results as $n\rightarrow \infty$ keeping $n_i$ fixed for each i.

• (i) There exists a consistent sequence of roots $\hat{\varvec{\theta }}_n = (\hat{\varvec{\beta }}_n^\top , \hat{\sigma _n}^2_j, j \in \{ 0, \ldots , r\})^\top$ to the minimum DPD estimating equations given in (9)–(10).

• (ii) The asymptotic distributions of $\hat{\varvec{\beta }}$ and $\hat{\sigma }^2_j$ are independent for all $j \in \{0, \ldots , r\}$.

• (iii) The asymptotic distribution of $\varvec{\Omega }_n^{-\frac{1}{2}}\varvec{\Psi }_n \sqrt{n} (\hat{\varvec{\theta }}_n - \varvec{\theta })$ is p-dimensional normal with mean zero and covariance matrix $\varvec{I}_{p}$. In particular, the asymptotic distribution of $({\varvec{X}^*}^\top \varvec{X}^*)^{-\frac{1}{2}}({\varvec{X}^\prime }^\top \varvec{X}^\prime ) (\hat{\varvec{\beta }} - \varvec{\beta })$ is a k-dimensional normal with mean zero and covariance matrix $\varvec{I}_k$, where $\varvec{X}^\prime$ and $\varvec{X}^*$ are as defined in Assumptions (MM1) and (MM4), respectively.

The derivation of matrices $\varvec{\Omega }_n$ and $\varvec{\Psi }_n$ and the proof of Theorem 1 are presented in Section A.1 of Appendix.

4.2 Influence function

To explore the robustness properties of the coefficient estimates in our treatment of linear mixed models, we derive the influence function of the MDPDEs. Denote the density power divergence functional $T_\alpha = (T^{\varvec{\beta }}_\alpha , T^{\varvec{\Sigma }}_\alpha )$ for the parameter vector $\varvec{\theta }^\top = (\varvec{\beta }^\top , \varvec{\Sigma } =(\sigma ^2_0,\ldots ,\sigma ^2_r))$. We continue with the notation of the previous subsections.

The influence function of the estimator $T^{\varvec{\beta }}_\alpha$ with contamination at the direction $i_0$ at the point $\varvec{t}_{i_0}$ is computed to have the form

$$\begin{aligned} IF_{i_0}(\varvec{t}_{i_0},T_\alpha ^{\varvec{\beta }},G_1,\ldots ,G_n) = ({\varvec{X}^\prime }^\top \varvec{X}^\prime )^{-1} \varvec{X}_{i_0}^\top \varvec{V}_{i_0}^{-1}(\varvec{t}_{i_0} - \varvec{X}_{i_0}\varvec{\beta })f_{i_0}(\varvec{t}_{i_0};\varvec{\theta })^\alpha , \end{aligned}$$

(18)

and the corresponding influence function for the estimator $T_\alpha ^{\varvec{\Sigma }}$ has the form

$$\begin{aligned} IF_{i_0}(\varvec{t}_{i_0},T_\alpha ^{\varvec{\Sigma }},G_1,\ldots ,G_n) = \left[ \sum _{i=1}^n \frac{\eta _{i\alpha }}{4(1+\alpha )^{\frac{n_i}{2}+2}} T(\varvec{V}_i^{-1}\varvec{U}_{ij},\varvec{V}_i^{-1}\varvec{U}_{ik}) \right] ^{-1} \tau _{i_0}, \end{aligned}$$

(19)

where

$$\begin{aligned} \tau _i = \bigg ( \frac{1}{2} f_i(\varvec{t}_i;\varvec{\theta })^\alpha [\textrm{Tr}(\varvec{V}_i^{-1}\varvec{U}_{ij}) -&(\varvec{t}_i-\varvec{X}_i\varvec{\beta })^\top \varvec{V}_i^{-1}\varvec{U}_{ij}\varvec{V}_i^{-1}(\varvec{t}_i-\varvec{X}_i\varvec{\beta })] \\&-\frac{\eta _{i\alpha }\alpha \textrm{Tr}(\varvec{V}_i^{-1}\varvec{U}_{ij})}{2(1+\alpha )^{\frac{n_i}{2}+1}} \bigg ). \end{aligned}$$

Note that the influence functions in equations (18) and (19), seen as functions of the point $\varvec{t}$, are bounded for any $\alpha > 0$ since they are proportional to the functions $\varvec{z} e^{-\varvec{z}^\top \varvec{z}}$ and $\varvec{z}^\top \varvec{z} e^{-\varvec{z}^\top \varvec{z}}$, respectively, which are bounded for $\varvec{z} \in \mathbb {R}^{n_i}$. For $\alpha = 0$, the influence functions for $T_\alpha ^{\varvec{\beta }}$ and $T_\alpha ^{\varvec{\Sigma }}$ are seen to be unbounded; indeed, this case corresponds to the non-robust maximum likelihood estimator. Hence, unlike the MLE, the minimum DPD estimators are B-robust, i.e., their associated influence functions are bounded, for $\alpha >0$.

The influence function of the estimators $T_\alpha ^{\varvec{\beta }}$ and $T_\alpha ^{\varvec{\Sigma }}$ with contamination in all the n cases at the contamination points $\varvec{t}_1, \ldots , \varvec{t}_n$, can be derived with similar computations and correspond to the sum of equations (18) and (19), respectively, for $i_0 = 1,\ldots ,n$. In this case also the influence functions are bounded for $\alpha > 0$ and unbounded for $\alpha = 0$.

Several summary measures of robustness based on the influence function for i.i.d. observations have been introduced in Hampel (1968, 1974). Following the same approaches, some influence function-based gross summary measures can be defined for the non-homogeneous case. For $\alpha > 0$, the gross-error sensitivity and the self-standardized sensitivity of the estimator $T_\alpha ^{\varvec{\beta }}$ in the case of contamination only in the $i_0$-th direction are given by

$$\begin{aligned} \gamma _{i_0}^u(T_\alpha ^{\varvec{\beta }},G_1,\ldots ,G_n)&= \sup _{\varvec{t}} \{||IF_{i_0}(\varvec{t},T_\alpha ^{\varvec{\beta }},G_1,\ldots ,G_n)||\}\nonumber \\&= \frac{ \left[ \lambda _{max}\left( ({\varvec{X}^\prime }^\top \varvec{X}^\prime )^{-2}\varvec{X}_{i_0}^\top \varvec{V}_{i_0}^{-1}\varvec{X}_{i_0} \right) \right] ^{1/2}}{\sqrt{\alpha }(2\pi )^{\frac{n_i\alpha }{2}}\vert \varvec{V}_i\vert ^{\frac{\alpha }{2}} e^{1/2}} \end{aligned}$$

(20)

and

$$\begin{aligned} \gamma _{i_0}^s(&T_\alpha ^{\varvec{\beta }},G_1,\ldots ,G_n) \\&= \sup _{\varvec{t}} \{IF_{i_0}(\varvec{t},T_\alpha ^{\varvec{\beta }},G_1,\ldots ,G_n)^\top (\varvec{\Psi }_n^{-1} \varvec{\Omega }_{n} \varvec{\Psi }_n^{-1})^{-1} IF_{i_0}(\varvec{t},T_\alpha ^{\varvec{\beta }},G_1,\ldots ,G_n)\}^{\frac{1}{2}} \nonumber \\&= \frac{\left[ \lambda _{max}\left( ({\varvec{X}^*}^\top \varvec{X}^*)^{-1}\varvec{X}_{i_0}^\top \varvec{V}_{i_0}^{-1}\varvec{X}_{i_0} \right) \right] ^{1/2} }{n \sqrt{\alpha } (2\pi )^{\frac{n_i\alpha }{2}}\vert \varvec{V}_i\vert ^{\frac{\alpha }{2}} e^{1/2}} , \end{aligned}$$

(21)

where $\lambda _{max}(\varvec{A})$ indicates the largest eigenvalue of the matrix $\varvec{A}$, while they are equal to $\infty$ if $\alpha = 0$. Details of the computations are provided in Section SM–2 of the Supplementary Materials. The sensitivity measures for $T_\alpha ^{\varvec{\Sigma }}$ have no compact form and they are not reported.

4.3 Computational aspects

The estimating equations (9)–(10) previously introduced can be solved numerically in order to obtain the estimates of $\varvec{\theta } = (\varvec{\beta }^\top ; \sigma _j^2,j \in \{0, \ldots ,r\})^\top$.

Note that denoting $w_i = w_i(\varvec{\beta },\sigma ^2_j)$, $j = 0, \ldots ,r$, as defined in equation (8), the estimating equation for $\varvec{\beta }$ given in equation (9) corresponds to

$$\begin{aligned} -\sum _{i=1}^n w_i\varvec{X}_i^\top \varvec{V}_i^{-1}\varvec{Y}_i + \sum _{i=1}^n w_i\varvec{X}_i^\top \varvec{V}_i^{-1}\varvec{X}_i\varvec{\beta } =0. \end{aligned}$$

Solving for $\varvec{\beta }$, we get

$$\begin{aligned} \varvec{\beta } = \bigg (\sum _{i=1}^n w_i\varvec{X}_i^\top \varvec{V}_i^{-1}\varvec{X}_i\bigg )^{-1}\bigg (\sum _{i=1}^n w_i\varvec{X}_i^\top \varvec{V}_i^{-1}\varvec{Y}_i\bigg ), \end{aligned}$$

so that, in an iterative fixed point algorithm, the successive iterates have the relation

$$\begin{aligned} \varvec{\beta }^{(k+1)} = \bigg (\sum _{i=1}^n w_i(\varvec{\beta }^{(k)},\sigma _j^{(k)})\varvec{X}_i^\top \varvec{V}_i(\sigma _j^{(k)})^{-1}X_i\bigg )^{-1}\bigg (\sum _{i=1}^n w_i(\varvec{\beta }^{(k)},\sigma _j^{(k)})\varvec{X}_i^\top \varvec{V}_i(\sigma _j^{(k)})^{-1}\varvec{Y}_i\bigg ). \end{aligned}$$

The estimating equation (10) for the variance components cannot be written in a similar closed form, then it is solved numerically by a quasi-Newton method which allows box constraints, that is, each variable can be given a lower and/or upper bound.

Finally, the random coefficients can be predicted through the obtained estimates. Notice that the quantity $\kappa _\alpha$ can be removed to solve equation (11) since it does not depend on $\varvec{u}_i$, as well as $c_i(\varvec{u}_i)$ since $c_i(\varvec{u}_i) > 0$ for all i. Hence, equation (11) is simplified to

$$\begin{aligned} (\hat{\sigma }_0^2)^{-1} \varvec{Z}_i^\top (\varvec{Y}_i - \varvec{X}_i \hat{\varvec{\beta }}) - \left( (\hat{\sigma }_0^2)^{-1}\varvec{Z}_i^\top \varvec{Z}_i + \hat{\varvec{D}}^{-1}\right) \varvec{u}_i = 0. \end{aligned}$$

Then,

$$\begin{aligned} \hat{{u}}_i = \left( (\hat{\sigma }_0^2)^{-1}\varvec{Z}_i^\top \varvec{Z}_i + \hat{\varvec{D}}^{-1}\right) ^{-1} (\hat{\sigma }_0^2)^{-1} \varvec{Z}_i^\top (\varvec{Y}_i - \varvec{X}_i \hat{\varvec{\beta }}). \end{aligned}$$

(22)

This formulation provides a closed form to predict the realizations $\varvec{u}_i$, $i = 1,\ldots ,n$. It is worth noting that even if these estimates may appear not robust, in the sense that an outliers $(\varvec{Y}_i,\varvec{X}_i)$ can affect the predicted $\varvec{u}_i$, they are based on the robust estimates $\hat{\varvec{\beta }}$, $\hat{\sigma }_0^2$ and $\hat{\varvec{D}}$.

4.4 An example: the balanced data case

Consider the model defined by Equation (6). Here, we study the simplest case in which $n_i = p$, for all $i \in \{1, \ldots ,n\}$, and the associated random effects covariates ($\varvec{Z}_{ij}$) are also the same for all i. In this case, the covariance matrix of $\varvec{Y}_i$ is the same for all i and is denoted by $\varvec{V}$ having the form

$$\begin{aligned} \varvec{V}=\varvec{V}_i = \sigma _0^2 \left( \varvec{I}_p + \sum _{j=1}^r \varvec{U}_j \gamma _j\right) , \end{aligned}$$

where $\gamma _j = \sigma _j^2/\sigma _0^2$ and $\varvec{U}_j = \varvec{U}_{ij}$ as it is independent of i.

The influence function of the functional $T_\alpha ^{\varvec{\beta }}$ with contamination in the direction $i_0$, given in Equation (18), can be written as

$$\begin{aligned} IF_{i_0}(\varvec{t}_{i_0},T^{\varvec{\beta }}_\alpha ,G_1,\ldots ,G_n) = (1+\alpha )^{\frac{p}{2}+1}\left( \sum _{i=1}^n\varvec{X}_i^\top \varvec{V}^{-1}\varvec{X}_i\right) ^{-1} \varvec{X}_{i_0}^\top \varvec{V}^{-1}(\varvec{t}_{i_0}-\varvec{X}_{i_0}\varvec{\beta })w_{i_0}. \end{aligned}$$

Using this expression, the gross-error sensitivity for the functional $T_\alpha ^{\varvec{\beta }}$ is given by

$$\begin{aligned} \gamma _{i_0}^u(T_\alpha ^{\varvec{\beta }})= \frac{(1+\alpha )^{\frac{p}{2}+1}}{\sqrt{\alpha }} \left[ \lambda _{max}\left( \left[ \sum _{i=1}^n \varvec{X}_i^\top \varvec{V}^{-1} \varvec{X}_i\right] ^{-2}\varvec{X}_{i_0}^\top \varvec{V}^{-1}\varvec{X}_{i_0} \right) \right] ^{1/2} e^{-1/2}. \end{aligned}$$

(23)

Similarly, the self-standardized sensitivity of the functional $T_\alpha ^{\varvec{\beta }}$ can be written as

$$\begin{aligned} \gamma _{i_0}^s (T_\alpha ^{\varvec{\beta }}) = \frac{(1+\alpha )^{\frac{p+2}{4}}}{n\sqrt{\alpha }} {\left[ \lambda _{max}\left( \left[ \sum _{i=1}^n \varvec{X}_i^\top \varvec{V}^{-1} \varvec{X}_i\right] ^{-1}\varvec{X}_{i_0}^\top \varvec{V}_{i_0}^{-1}\varvec{X}_{i_0} \right) \right] ^{1/2}}(2e)^{-1/2}. \end{aligned}$$

(24)

The simpler form of the sensitivity measures allows us to assess their performance with respect to the tuning parameter $\alpha$. Indeed, the function $\frac{(1+\alpha )^{\frac{p}{2}+1}}{\sqrt{\alpha }}$ in the gross-error sensitivity (23) has a minimum for the value $\alpha ^*= \frac{1}{p+1}$, suggesting that this value of the parameter $\alpha$ gives the most robust estimator. Similarly, the function $\frac{(1+\alpha )^{\frac{p+2}{4}}}{\sqrt{\alpha }}$ in the self-standardized sensitivity (24) has a minimum for the value $\bar{\alpha } = \frac{2}{p}$. The existence of such minimum values for $\alpha$ is in contrast with the previously held knowledge about this parameter. It was introduced as a trade-off between efficiency and robustness, instead here we show that, passing some threshold, with increasing $\alpha$ , we lose both efficiency and robustness. Finally, the proposed optimal values $\alpha ^*$ and $\bar{\alpha }$ depend only on the dimension of observations and constitute valuable choices in practical situations.

In the following, we present a simple example for which we will compute the theoretical quantities introduced above. This example in linear mixed models has been chosen for its similarity to the case of longitudinal data; it is often also named as LMM with random intercept and random slope.

Notice that the MDPDE satisfies the equivariance properties. In particular, the regression equivariance allows us to assume, without loss of generality, any suitable value for the parameter $\varvec{\beta }$ while proving the asymptotic properties with the following example or for the Monte Carlo studies. Since the MDPDE is also scale and affine equivariant, such estimators do not depends on the choice of the coordinate system for the variables $\varvec{x}$ and on the measurement unit of $\varvec{y}$. The derivation of these properties is reported in Section SM–3 of the Supplementary Material. Furthermore, Section SM–4 reports an illustrative example which shows the robustness achieved by the random effects predictions computed according to equation (22).

We consider $n=50$ different subjects (groups), and for each of them, we have $p=10$ measurements taken with respect to the factor $u_{i2}$, $i=1,\ldots ,n$, with two levels, modeled here as a random effect. The $\varvec{X}$’s model matrices are simulated from a standard normal. In particular, the model is described by

$$\begin{aligned} \varvec{Y}_i = \beta _0 + \beta _1 \varvec{X}_i + \varvec{\mathcal {U}}_{1} + \varvec{\mathcal {U}}_{2}\varvec{Z}_{i2} + \varvec{\epsilon }_i, \end{aligned}$$

where $\varvec{\mathcal {U}}_{1} \sim N_p(0,\sigma ^2_1\varvec{I}_p)$, $\varvec{\mathcal {U}}_{2} \sim N_2(0,\sigma ^2_2\varvec{I}_2)$ and $\epsilon _i \sim N_p(0,\sigma _0^2\varvec{I}_p)$ , and they are independent. Hence, for this model, $\varvec{\theta } = (\beta _0,\beta _1,\sigma ^2_1,\sigma ^2_2,\sigma _0^2)$ , and we take $\varvec{\theta } = (1,2,0.25,0.5,0.25)$ as the true values of the parameters.

Fig. 1

Asymptotic relative efficiency with respect to $\alpha$ for $\beta _1$ and $\sigma ^2_2$, respectively

Using the given values, we compute the variance–covariance matrices $\varvec{V}_i$ and the matrices $\varvec{\Psi }_n$ and $\varvec{\Omega }_n$. First, we will look at the Asymptotic Relative Efficiency (ARE) of the minimum density power divergence estimators with respect to the fully efficient maximum likelihood estimator. Figure 1 shows the asymptotic relative efficiencies of the estimators of $\beta _1$ and $\sigma ^2_2$ for $\alpha \in [0,0.6]$. It is easy to see that there is a loss of efficiency which increases with $\alpha$. However, for small positive values of $\alpha$, the estimator retains reasonable efficiency. The ARE of the estimators of the other parameters are similar to those displayed here, and are given in Section SM–5 of the Supplementary Materials.

Fig. 2

Influence function for the functionals $T_\alpha ^{\beta _0}$(left panel) and $T_\alpha ^{\sigma _1^2}$ (right panel), for different values of the tuning parameter $\alpha$

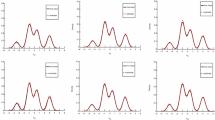
On the other hand, to study the robustness properties, Fig. 2 shows the influence functions of $T_\alpha ^{\beta _0}$ and $T_\alpha ^{\sigma _1^2}$, with respect to $\alpha = 0, 0.05, \alpha ^*, \bar{\alpha }$ where $\alpha ^*= 1/(p+1) = 1/11$ and $\bar{\alpha } = 2/p = 0.2$. Here, we have plotted $IF(\varvec{t}_1,\ldots ,\varvec{t}_n,T_\alpha ,G_1,\ldots ,G_n)$, the influence function of the estimator $T_\alpha$, computed with respect to constant vectors $\underline{\varvec{t}} = t (1,\ldots ,1)^\top$ for varying $t \in \mathbb {R}$. Note that except for the case $\alpha =0$, we can easily see that the influence function is bounded as may also be noted from equations (18) and (19); thus, the estimator will be robust with respect to outliers. The influence function for the estimators of other parameters behaves similarly; these plots are available in Section SM–5 of the Supplementary Materials.

Finally, Fig. 3 shows the gross-error sensitivity and the self-standardized sensitivity of the functional $T_\alpha ^{\varvec{\beta }}$. Here, we have considered a particular direction $i_0 \in \{1,\ldots ,n\}$. Note that in the present case of balanced data, the choice of $i_0$ does not change the behavior of the sensitivity measures with respect to $\alpha$.

Fig. 3

Gross-error sensitivity (left panel) and self-standardized sensitivity (right panel) of the functional $T_\alpha ^{\varvec{\beta }}$ with respect to $i_0 = 10$

5 Monte Carlo simulations

5.1 Model setting

We consider a simulation setting as introduced in Agostinelli and Yohai (2016) and reported here in order to facilitate the comparison of the considered estimators.

Consider an LMM for a two-way cross classification with interaction, where the model is given by

$$\begin{aligned} y_{fgh} = \varvec{x}^\top _{fgh}\varvec{\beta }_0 + a_f + b_g + c_{fg} + e_{fgh}, \end{aligned}$$

where $f=1,\ldots ,F, g= 1, \ldots ,G$, and $h=1,\ldots ,H$. Here, we set $F=2, G=2$ and $H=3$ getting $p=F\times G \times H= 12$. Also $\varvec{x}_{fgh}$ is a $k \times 1$ vector where the last $k - 1$ components are from a standard multivariate normal and the first component is identically equal to 1, and $\varvec{\beta }_{0}=(0,2,2,2,2,2)^{\top }$ is a $k \times 1$ vector of the fixed parameters with $k=6$. The random variables $a_{f}$, $b_{g}$ and $c_{fg}$ are the random effects which are normally distributed with variances $\sigma _{a}^{2}$, $\sigma _{b}^{2}$, and $\sigma _{c}^{2}$. Arranging the $y_{fgh}$ in lexicon order (ordered by h within g within f), we obtain the vector $\varvec{y}$ of dimension p, and in the similar way, the $p\times k$ matrix $\varvec{x}$ obtained arranging $\varvec{x}_{fgh}$. Similarly, we set $\varvec{a}=(a_{1},\ldots ,a_{F})^{\top }$, $\varvec{b}=(b_{1},\ldots ,b_{G})^{\top }$ and $\varvec{c}=(c_{11},\ldots ,c_{FG})^{\top }$, that is, $\varvec{a}\sim N_{F}(\varvec{0},\sigma _{a}^{2}\varvec{I}_{F})$ and similarly for $\varvec{b}$ and $\varvec{c}$, while $\varvec{e}=(e_{111},\ldots ,e_{FGH})^{\top }\sim N_{p}(\varvec{0},\sigma _{e}^{2}\varvec{I}_{p})$. Hence, $\varvec{y}$ is a p multivariate normal with mean $\varvec{\mu }=\varvec{x}\varvec{\beta }$ and variance matrix $\varvec{\Sigma }_{0}=\varvec{\Sigma }(\eta _{0},\varvec{\gamma }_{0}) =\eta _{0}(\varvec{V}_{0}+\sum _{j=0}^{J}\gamma _{j}\varvec{V}_{j})$, where $\varvec{V}_{0}=\varvec{I}_{p}$, $\varvec{V}_{1}=\varvec{I}_{F}\otimes \varvec{J}_{G}\otimes \varvec{J}_{H}$, $\varvec{V}_{2}=\varvec{J}_{F}\otimes \varvec{I}_{G}\otimes \varvec{J}_{H}$, and $\varvec{V}_{3}=\varvec{I}_{F}\otimes \varvec{I}_{G}\otimes \varvec{J}_{H}$; $\otimes$ is the Kronecker product and $\varvec{J}_k$ is a $k \times k$ matrix of ones. We took $\sigma _{a}^{2}=\sigma _{b}^{2}=1/16$ and $\sigma _{c}^{2}=1/8$. Then, $\varvec{\gamma _0}=(\gamma _{01},\gamma _{02},\gamma _{03})^{\top }=(\sigma _{a}^{2}/\sigma _{e}^{2},\sigma _{b}^{2}/\sigma _{e}^{2}, \sigma _{c}^{2}/\sigma _{e}^{2})^{\top }=(1/4,1/4,1/2)^{\top }$ and $\eta _{0}=\sigma _{e}^{2}=1/4$.

We consider a sample of size $n=100$ and four levels of contamination $\varepsilon =0,5,10$ and $15\%$. Hence, $n\times \varepsilon$ observations are contaminated according the following contamination scenarios. Let $\varvec{y}_0$ and $\varvec{x}_0$ indicate the response vector and the fixed effect model matrix for the contaminated observations.

• Complete contamination: $n\times \varepsilon$ elements of the vector $\varvec{y}$ are replaced by observations from $\varvec{y}_{0}\sim N_{p}(\varvec{x}_{0}\varvec{\beta }_{0}+\varvec{\omega }_{0},\varvec{\Sigma })$. The matrix $\varvec{x}_{0}$ is such that the first column is identically equal to 1, while the last $k - 1$ columns are from $N_{p\times (k-1)}(\varvec{\phi }_{0},0.005^{2}\varvec{I}_{p\times (k-1)})$ where $\varvec{\phi }_0$ indicates a p-vector of constants all equal to $\phi _0$ with $\phi _{0} = 1, 20$ in the case of low leverage outliers (lev1) or for large leverage outliers (lev20), respectively. $\varvec{\omega }_{0}$ is a p-vector of constants all equal to $\omega _{0}$ with $\omega _0 = 0, 1, \ldots , 30$.

• Contamination only on the response $\varvec{y}$: $\varvec{y}_{0}\sim N_{p}(\varvec{x}\varvec{\beta }_{0}+\varvec{\omega }_{0},\varvec{\Sigma })$ with $\omega _0$ as above.

• Contamination only on the $\varvec{x}$: $n\times \varepsilon$ rows of $\varvec{x}$ are replaced by $\varvec{x}_0$, as defined in the first scenario, with $\phi _0 = 0,1,3,5,10,15,20,25,30$. The corresponding elements of $\varvec{y}$ are replaced by observations sampled from $\varvec{y}_{0}\sim N_{p}(\varvec{x}_{0}\varvec{\beta }_{0},\varvec{\Sigma })$.

For each contamination scenario, we compute the CVFS-estimator described in Copt and Victoria-Feser (2006) with Rocke $\rho$ function and with asymptotic rejection probability set to 0.01 as implemented in the R R Core Team (2019) package robustvarComp (Agostinelli and Yohai (2019)), the SMDM estimator introduced by Koller (2013) as implemented in the R package robustlmm (Koller (2016)), the composite $\tau$-estimator proposed by Agostinelli and Yohai (2016) and available in the R package robustvarComp, and our proposed MDPDE with different choices of $\alpha$. In particular, $\alpha \in \{0, 0.01, 0.1, 0.2, \ldots ,1\}$; note that $\alpha ^*= 1/(p+1) = 1/13$ and $\bar{\alpha } = 2/p = 1/6$. For each case, we run 500 Monte Carlo replications.

5.2 Performance Measures

Let $(\varvec{y},\varvec{x})$ be an observation independent of the sample $(\varvec{y}_{1}, \varvec{x}_{1}), \ldots ,(\varvec{y}_{n}, \varvec{x}_{n})$ used to compute $\widehat{\varvec{\beta }}$ and let $\widehat{\varvec{y}}=\varvec{x} \widehat{\varvec{\beta }}$ be the predicted value of $\varvec{y}$ using $\varvec{x}$. Then, the squared Mahalanobis distance between $\widehat{\varvec{y}}$ and $\varvec{y}$ using the matrix $\varvec{\Sigma }_{0}$ is

$$\begin{aligned} m(\widehat{\varvec{y}}, \varvec{y}, \varvec{\Sigma }_{0})&= (\widehat{\varvec{y}}-\varvec{y})^{\top } \varvec{\Sigma }_{0}^{-1}(\widehat{\varvec{y}}-\varvec{y}) \\&= (\widehat{\varvec{\beta }}-\varvec{\beta }_{0})^{\top } \varvec{x}^{\top } \varvec{\Sigma }_{0}^{-1} \varvec{x} (\widehat{\varvec{\beta }}-\varvec{\beta }_{0}) + (\varvec{y}-\varvec{x} \varvec{\beta }_{0})^{\top } \varvec{\Sigma }_{0}^{-1} (\varvec{y}-\varvec{x} \varvec{\beta }_{0}). \end{aligned}$$

Since $\varvec{y}-\varvec{x}\varvec{\beta }_{0}$ is independent of $\varvec{x}$ and has covariance matrix $\varvec{\Sigma }_{0}$, putting $\varvec{A} = \mathbb {E}(\varvec{x}^{\top } \varvec{\Sigma }_{0}^{-1} \varvec{x})$ , we have

$$\begin{aligned} \mathbb {E} \left[ m(\widehat{\varvec{y}}, \varvec{y}, \varvec{\Sigma }_{0})\right]&= \mathbb {E}\left[ (\widehat{\varvec{\beta }} - \varvec{\beta }_{0})^{\top } \varvec{A} (\widehat{\varvec{\beta }} - \varvec{\beta }_{0}) \right] + {\text {trace}} \left[ \varvec{\Sigma }_{0}^{-1} (\varvec{y}-\varvec{x} \varvec{\beta }_{0}) (\varvec{y}- \varvec{x} \varvec{\beta }_{0})^{\top }\right] \\&= \mathbb {E}\left[ (\widehat{\varvec{\beta }}-\varvec{\beta }_{0})^{\top } \varvec{A}(\widehat{\varvec{\beta }}-\varvec{\beta }_{0})\right] + p. \end{aligned}$$

Then, to evaluate an estimator $\widehat{\varvec{\beta }}$ of $\varvec{\beta }$ by its prediction performance, we can use

$$\begin{aligned} \mathbb {E}\left[ m(\widehat{\varvec{\beta }},\varvec{\beta }_{0},\varvec{A}) \right] = \mathbb {E} \left[ (\widehat{\varvec{\beta }} - \varvec{\beta }_{0})^{\top } \varvec{A}(\widehat{\varvec{\beta }}-\varvec{\beta }_{0})\right] . \end{aligned}$$

Let N be the number of replications in the simulation study, and let $\widehat{\varvec{\beta }}_{j}$, $1\le j\le N$ be the value of $\widehat{\varvec{\beta }}$ at the j-th replication, then we can estimate $\mathbb {E}\left[ m(\widehat{\varvec{\beta }},\varvec{\beta }_{0},\varvec{A}) \right]$ by the mean square Mahalanobis distance as

$$\begin{aligned} \text {MSMD} = \frac{1}{N} \sum _{j=1}^{N} m(\widehat{\varvec{\beta }}_{j}, \varvec{\beta }_{0},\varvec{A}). \end{aligned}$$

It is easy to prove that as in this case, $\varvec{x}$ is a $p\times k$ matrix where the cells are independent N(0, 1) random variables, then $\varvec{A} = {\text {trace}}(\varvec{\Sigma }_{0}^{-1}) \varvec{I}_{k}$.

Given two p-dimensional covariance matrices $\varvec{\Sigma }_{1}$ and $\varvec{\Sigma }_{0}$, one way to measure how close $\varvec{\Sigma }_{1}$ and $\varvec{\Sigma }_{0}$ are is through the use of the Kullback–Leibler divergence between two multivariate normal distributions with the same mean and covariance matrices equal to $\varvec{\Sigma }_{1}$ and $\varvec{\Sigma }_{0}$, given by

$$\begin{aligned} \text {KLD}(\varvec{\Sigma }_{1},\varvec{\Sigma }_{0})=\text {trace} \left( \varvec{\Sigma }_{1}\varvec{\Sigma } _{0}^{-1}\right) -\log \left( \det (\varvec{\Sigma }_{1}\varvec{\Sigma }_{0}^{-1})\right) - p. \end{aligned}$$

Since $(\eta _{0},\varvec{\gamma }_{0})$ determines $\varvec{\Sigma }_{0}=\varvec{\Sigma }(\eta _{0},\varvec{\gamma }_{0})$, the covariance matrix of $\varvec{y}$ given $\varvec{x}$ for the particular LMM considered in our simulation (as described in Sect. 5.1), one way to measure the performance of an estimator $(\widehat{\eta },\widehat{\varvec{\gamma }})$ of $(\eta _{0},\varvec{\gamma }_{0})$ is by $\mathbb {E}\left[ \text {KLD}(\varvec{\Sigma }(\widehat{\eta },\widehat{\varvec{\gamma }}),\varvec{\Sigma }_{0})\right]$. Let $(\widehat{\eta }_{j},\widehat{\varvec{\gamma }}_{j}),1\le j\le N$, be the value of $(\widehat{\eta },\widehat{\varvec{\gamma }})$ at the j-th replication, then we can estimate $\mathbb {E}\left[ \text {KLD}(\varvec{\Sigma }(\widehat{\eta },\widehat{\varvec{\gamma }}),\varvec{\Sigma }_{0})\right]$ by the mean Kullback–Leibler divergence

$$\begin{aligned} \text {MKLD}=\frac{1}{N}\sum _{j=1}^{N}\text {KLD}(\varvec{\Sigma }(\widehat{\eta }_{j},\widehat{\varvec{\gamma }}_{j}),\varvec{\Sigma }_{0}). \end{aligned}$$

5.3 Results

We begin with the performance of the estimators in the absence of contamination. Table 1 shows the relative efficiency of the CVFS-estimator, the SMDM-estimator, the Composite $\tau$-estimator and the MDPDE for different values of $\alpha$ with respect to maximum likelihood. The efficiency of the estimators of $\varvec{\beta }$ has been measured by the MSMD ratio, while the MKLD ratio was used for the efficiency of an estimator of $(\eta ,\varvec{\gamma })$.

Table 1 Relative efficiency for the SMDM-estimator, CVFS-estimator, Composite $\tau$-estimator and MDPDE for different values of $\alpha$ with respect to the maximum likelihood computed by the MSMD for the fixed terms $\varvec{\beta }$ and by the MKLD for the random terms

The MDPDEs exhibit a high relative efficiency, even greater than the competitor estimators, for small values of $\alpha$, while the efficiency decreases with increasing $\alpha$. Note that the MDPDEs are far more successful in retaining the efficiency of the estimators of the random components. For very small values of $\alpha$ , the MDPDEs dominate either competitor (at least up to $\alpha = \alpha ^*$ for SMDM, and at least up to $\alpha = 0.2$ for CVFS) in terms of both (MSMD and MKLD) efficiency measures. As the value of $\alpha$ increases, the MSMD efficiency of the MDPDE eventually lags behind its competitors, but in terms of MKLD efficiency, it beats the competitors at least up to $\alpha = 0.4$, except for the Composite $\tau$-estimator that has a higher efficiency than the MDPDE for $\alpha > \bar{\alpha }$. On the whole, it is clear that under pure data, a properly chosen member of the MDPDE class can perform competitively, if not better, compared to the SMDM, the CVFS and the Composite $\tau$ -estimators.

Now, we consider the contamination settings. At first, Tables 2 and 3 report the maximum values of MSMD and MKLD over the values of $\omega _0$ and leverage $\phi _0$ considered for the complete contamination and separated contamination, respectively, of the MDPDE for different values of $\alpha$ compared to the CVFS-, the SMDM- and Composite $\tau$-estimators.

Table 2 Complete contamination. Maximum values of MSMD and MKLD for the CVFS-, SMDM-, Composite $\tau$-estimators and for the MDPDE at different values of $\alpha$ under $10\%$ of outlier contamination

Table 3 Contamination on $\varvec{x}$ and $\varvec{y}$ separately. Maximum values of MSMD and MKLD for the CVFS-, SMDM-, Composite $\tau$-estimators and for MDPDE considering different values of $\alpha$ under $10\%$ of outlier contamination

Small values of $\alpha$, as expected, provide much higher maximum values with respect to the other estimators in Table 2. However, for slightly larger values of $\alpha$, the MDPDEs are extremely competitive with the existing estimators. It may be easily observed that in case of complete contamination, the MDPDE at $\bar{\alpha }$ clearly beats the competitors (CVFS, SMDM and Composite $\tau$) over both performance measures at both leverage values (except in case of complete contamination at MSMD, lev20, where its performance measure is equal to that of CVFS). In this example, the MDPDE at $\alpha = 0.2$ fares even better. In case of contamination on the $\varvec{y}$, the estimators show similar performance, while, when only the $\varvec{x}$ is contaminated, the MSMD values are almost equal for all the considered estimators suggesting that the estimation of the fixed effects parameter $\varvec{\beta }$ is not affected. However, as in the previous case, the MDPDE for values of $\alpha$ close to zero show larger MKLD values, but slightly increasing $\alpha$ the MDPDE outperforms the competitors.

Fig. 4

Complete contamination. Performance of the MDPD-estimators of $\varvec{\beta }$ and $(\eta ,\varvec{\gamma })$ for $\alpha = \frac{1}{13}, \frac{1}{6},0.3$, compared to the CVFS-, SMDM- and Composite $\tau$-estimators, under $10\%$ outlier contamination

Fig. 5

Contamination on $\varvec{x}$ and $\varvec{y}$. Performance of the MDPD-estimators of $\varvec{\beta }$ and $(\eta ,\varvec{\gamma })$ for $\alpha = \frac{1}{13}, \frac{1}{6},0.3$, compared to the CVFS-, SMDM- and Composite $\tau$-estimators, under $10\%$ outlier contamination

Figures 4a and 4b display the MSMD and MKLD as function of $\omega _0$, comparing the CVFS-, SMDM- and Composite $\tau$-estimators with the MDPDEs for three chosen values of $\alpha$, under 10% of outlier contamination. In particular, we choose $\alpha ^*$ and $\bar{\alpha }$ since they are the values suggested by theory, and $\alpha =0.3$ since it shows the lowest (or very close to the lowest) maximum values of MSMD and MKLD. We can see that most of the MDPDEs outperform the CVFS- and SMDM-estimators, especially in case of leverage 20 (lev20), where the SMDM-estimator shows an unbounded behavior. On the other hand, in the case of leverage 1 (lev1), even if the CVFS-estimator presents lower maximum value of MSMD and MKLD for very small values of $\omega _0$, the MDPDEs show a better performance when $\omega _0$ increases. In fact, the MDPDE at $\alpha = 0.3$ is competitive or better than CVFS at all values of $\omega _0$. Finally, Fig. 5a and 5b shows the MSMD and MKLD as function of $\omega _0$ if the response $\varvec{y}$ is contaminated and as function of $\phi _0$ in case of contamination on the $\varvec{x}$. The CVFS-, SMDM- and Composite $\tau$-estimators are compared with the MDPDEs for three chosen values of $\alpha$, under 10% of outlier contamination. These results confirm that the MDPDEs, at least for one value of $\alpha$, outperform the competitor estimators. Complete results of the simulation study, for all the considered estimators and levels of contamination, are reported in Section SM–6 of the Supplementary Materials.

6 Real-data example: Orthodontic Distance Growth

Let us now present an application of the proposed estimation method to a real-data example on orthodontic measures, while Section SM–8 of the Supplementary Materials reports the analysis of the real-life data on foveal and extrafoveal vision acuity (and crowding) studying their interrelationships with one’s reading performances. We compare the estimates obtained by the minimum DPD method with those obtained using the classical (non-robust) restricted MLE, computed using the lmer function in R, as well as the robust competitors, that is, the SMDM-estimator, the CVFS-estimator and the Composite $\tau$-estimator. A very important consideration in real situations is the selection of an “optimum” value of $\alpha$ that applies to the given data set. We will consider the values $\alpha ^*$ and $\bar{\alpha }$, derived from theoretical computations, since they are the suggested optimal values.

We consider an orthodontic study conducted by Potthoff and Roy (1964) where the distance (in millimeters) between the pituitary and the pterygomaxillary fissure has been measured on 16 boys and 11 girls at 8, 10, 12, and 14 years. The data set is available as part of the R package nlme (Pinheiro et al. 2022). Figure 6 displays the measurements for each individual in the study together with the least-squares fit of the simple linear regression model.

Fig. 6

Orthodontic growth patterns in 11 girls (F) and 16 boys (M) from 8 to 14 years of age. Blue lines correspond to the individual least-squares fit of the simple linear regression model

From Fig. 6, it is possible to see that the data set possibly contains some outliers. In particular, the measurements for subject M09 have more variability around the fitted line with two possible within-subject outliers and the slope for subject M13 is larger than the others indicating a possible outlier at the level of random effects. Finally, subject M10 could be also considered as outlying observation for the large distance values since the first measurement. Overall, the intercept and the slope seem to vary with the subject, and the responses for the girls show less variation around the fitted lines than for boys.

According to the mentioned features, the orthodontic distance growth with respect to age can be modeled using the linear mixed model of the form

$$\begin{aligned} y_{ij} =&\beta _0 + \beta _1 I_i(F) + (\beta _2 +\beta _3 I_i(F))t_j + u_{i1} + u_{i2} t_j + \epsilon _{ij} \end{aligned}$$

for $i=1,\ldots ,27$ and $j=1,\ldots ,4$, where $y_{ij}$ denotes the distance for subject i at age $t_j$; $\beta _0$ and $\beta _1$ represent the fixed effect intercept for boys and girls, respectively; $\beta _2$ and $\beta _3$ represent the fixed effect slope for boys and girls, respectively; $I_i(F)$ indicates an indicator function for the girls group; ($\varvec{\mathcal {U}}_{1},\varvec{\mathcal {U}}_{2}$) is the vector of random terms and ($\varvec{u}_{i1},\varvec{u}_{i2}$) is the vector of realizations for subject i; $\epsilon _{ij}$ is the error term. Notice that in this example, the random effect for the age is nested into the random effect for the subject level, so a possible correlation between them has to be considered. According to this, the variance components to be estimated are $\sigma _j^2$, $j=0,1,2$ as previously described and the covariance $\sigma _{12}$ between the random variables $\varvec{\mathcal {U}}_1$ and $\varvec{\mathcal {U}}_2$.

Table 4 Orthodont data set. Estimates of fixed effects parameters obtained by the MLE (with and without the outlying observations), the SMDM-estimator, the CVFS-estimator, the Composite $\tau$-estimator and MDPDE for $\alpha = \alpha ^*= 0.2$ and $\alpha = \bar{\alpha }= 0.5$

Table 5 Orthodont data set. Estimates of variance components parameters obtained by the MLE (with and without the outlying observations), the SMDM-estimator, the CVFS-estimator, the Composite $\tau$-estimator and MDPDE for $\alpha = \alpha ^*= 0.2$ and $\alpha = \bar{\alpha }= 0.5$

Table 4 and Table 5 report the estimates for the fixed terms and for the variance components, respectively, obtained by the MLE, the SMDM-estimator, the CVFS-estimator, the Composite $\tau$-estimator and MDPDE for $\alpha = \alpha ^*= 0.2$ and $\alpha = \bar{\alpha }= 0.5$. Furthermore, we computed the maximum likelihood estimates for the reduced data set obtained removing the observations M09, M10 and M13, indicated as outliers. The estimates of $\beta _2$ and $\beta _3$ parameters are quite similar among the considered estimators. The fixed effect parameters differ mainly for the intercept $\beta _0$ and $\beta _1$, which indicates the effect of gender on the response $\varvec{y}_i$. Robust estimators show values closer to zero than the standard MLE, indicating that the orthodontic distance is less affected by gender. This can be explained by the fact that MLE is sensitive to the presence of outlying observations obtaining a bigger value. Indeed, when such observations are removed, the maximum likelihood estimates are similar to MDPDE. The main differences on the estimation of the random effects terms are both in size (error variance component) and shape (correlation components). The MDPDEs assign less variance to the error term, and the other estimates are in general smaller. As before, the estimates given by the MLE and MDPDE are very close when the outliers are removed. Notice that the SMDM- and CVFS-estimates are quite different with respect to the others, especially for the variance components parameters.

Fig. 7

Orthodont data set. QQ-plots of the random effects estimated by the MLE, the SMDM-estimator, the CVFS-estimator, the Composite $\tau$-estimator and MDPDE for $\alpha = \alpha ^*= 0.2$ and $\alpha = \bar{\alpha }= 0.5$

Figure 7 shows the QQ-plots of the estimates of the random terms $u_{ij}$ for $i=1,\ldots ,27$ and $j=1,2$, obtained by the MLE, the SMDM-estimator, the CVFS-estimator, the Composite $\tau$-estimator and MDPDE for $\alpha = \alpha ^*= 0.2$ and $\alpha = \bar{\alpha }= 0.5$. The QQ-plots seem to show some structure and confirm the larger variances estimated by MLE then those given by MDPDE; however, notice that the sample size ($n=27$) is quite low. Figure 13a and 13b, in Section SM–7 of the Supplementary Materials, shows the QQ-plots of the random effects estimated by different methods separately.

Fig. 8

Orthodontic growth patterns in 11 girls (F) and 16 boys (M) from 8 to 14 years of age. The fitted lines given by the MLE and MDPDE for $\alpha =0.2$ are represented in blue and orange, respectively

Finally, Fig. 8 shows the fitted lines given by fixed effects estimates and random effects predictions for the MLE and MDPDE with $\alpha =0.2$, represented in blue and orange, respectively. It is easy to see that the MDPDE achieves a better fit. In particular, notice the case of Subject M10 previously indicated as possible outlier.

Notice that for the simulation study in Sect. 5.2, the predictions of the response variable have been computed as $\widehat{\varvec{y}}=\varvec{x} \widehat{\varvec{\beta }}$, without considering the random effect estimates, since we were interested in evaluating the performance with respect to fixed effects estimation. In practical situations, such as the one presented in this section, when a linear mixed model is considered, both fixed effects and random effects estimates must be considered, i.e., $\widehat{\varvec{y}}_i=\varvec{X}_i \widehat{\varvec{\beta }} +\varvec{Z}_i \widehat{\varvec{u}}_i$.

7 Conclusions

In this paper, we have developed an estimator based on the density power divergences to deal with the robustness issues in the linear mixed model setup. We demonstrated that the desirable asymptotic properties of the MDPDE, such as consistency and asymptotic normality, hold for the linear mixed model setup. In order to assess the robustness properties, the influence function and sensitivity measures of the estimator were computed. We found that the estimator is B-robust for $\alpha > 0$. From a practical point of view, the choice of the value of the tuning parameter $\alpha$ is fundamental in applications. The behavior of the sensitivity measures suggested two optimal values, denoted by $\alpha ^*$ and $\bar{\alpha }$, depending on the dimension p, where the term “optimal” is in the sense of providing minimum sensitivity, and thus producing maximum robustness. The existence of such values is in contrast to the previous knowledge about the parameter $\alpha$. Indeed, it was shown that when $\alpha$ continues to increase beyond a certain value, we lose both robustness and efficiency.

The simulation study confirmed how the performance of the minimum density power divergence estimator changes with respect to $\alpha$. Furthermore, the MDPDE outperforms the competitor estimators; indeed our approach leads to more resistant estimators in the presence of case-wise contamination. Finally, the application of our estimator to a real-life data set indicated that the MDPDE has similar results to the classical maximum likelihood estimator.

We feel that many important extensions of this work are necessary and can be potentially useful. So far, the MDPDE has been implemented only for balanced data (although the theory that we have developed is perfectly general). In future, we propose to extend the implementation to the more general case of groups with possibly different dimensions. The problem of testing of hypothesis also deserves a deeper look in the linear mixed models scenario.

Appendix A

1.1 A.1 Proof of Theorem 1

First let us note that under the setup of the linear mixed models introduced in Sect. 3, given a fixed $\alpha \ge 0$, for each i, the matrices $\varvec{\Omega }_i$ and $\varvec{J}_i$ defined in Section SM–1 of Supplementary Material simplify to the forms

$$\begin{aligned} \varvec{J}^{(i)}&= \mathbb {E}_{g_i}[\nabla H_i(\varvec{Y}_i,\varvec{\theta })] = \left( \begin{array}{cc} \varvec{J}^{(i)}_{11} &{} 0 \\ 0 &{} \varvec{J}^{(i)}_{22} \end{array} \right) ,\\ \varvec{\Omega }^{(i)}&= \mathbb {V}\textrm{ar}_{g_i}(\nabla H_i(\varvec{Y}_i,\varvec{\theta })) = \left( \begin{array}{ccc} \varvec{\Omega }^{(i)}_{11} &{} 0 \\ 0 &{} \varvec{\Omega }^{(i)}_{22} \end{array} \right) , \end{aligned}$$

where

$$\begin{aligned} \varvec{J}^{(i)}_{11}= & {} \frac{4\varvec{X}_i^\top \varvec{V}_i^{-1}\varvec{X}_i}{(1+\alpha )^{\frac{n_i}{2}+1}}, \\ (j,k)\text{-th } \text{ element } \text{ of } \varvec{J}^{(i)}_{22}= & {} \frac{T(\varvec{V}_i^{-1}\varvec{U}_{ij},\varvec{V}_i^{-1}\varvec{U}_{ik})}{(1+\alpha )^{\frac{n_i}{2}+2}}, \\ \varvec{\Omega }^{(i)}_{11}= & {} \frac{4\varvec{X}_i^\top \varvec{V}_i^{-1}\varvec{X}_i}{(1+2\alpha )^{\frac{n_i}{2}+1}}, \\ (j,k)\text{-th } \text{ element } \text{ of } \varvec{\Omega }^{(i)}_{22}= & {} \frac{T(4,\varvec{V}_i^{-1}\varvec{U}_{ij},\varvec{V}_i^{-1}\varvec{U}_{ik})}{(1+2\alpha )^{\frac{n_i}{2}+2}} -\frac{\alpha ^2\textrm{Tr}(\varvec{V}_i^{-1}\varvec{U}_{ik})\textrm{Tr}(\varvec{V}_i^{-1}\varvec{U}_{ij})}{(1+\alpha )^{n_i+2}}, \end{aligned}$$

for $j, k \in \{ 0, \ldots , r\}$, with $T(c,\varvec{A},\varvec{B}) = c\alpha ^2\textrm{Tr}(\varvec{A})\textrm{Tr}(\varvec{B}) +2\textrm{Tr}(\varvec{AB})$

for general matrices $\varvec{A},\varvec{B}$ and a constant c ($c=1$ if not specified). Finally, put

$$\begin{aligned} \varvec{\Psi }_n = \frac{1}{n} \sum _{i=1}^n \frac{\eta _{i\alpha }}{4} \varvec{J}^{(i)} ~~~~ \text{ and } ~~ \varvec{\Omega }_n = \frac{1}{n} \sum _{i=1}^n \frac{\eta _{i\alpha }^2}{4} \varvec{\Omega }^{(i)}. \end{aligned}$$

Also, we assumed that the true data generating density belongs to the model family. Then, the proof of our Theorem 1 is immediate from the results stated by Ghosh and Basu (2013), provided we can show that the general Assumptions (A1)–(A7) are satisfied under the our assumed Conditions (MM1)–(MM4) for the special case of LMMs.

Now, the assumption that the true data generating density belongs to the model family, together with that the model density is normal with mean $\varvec{X}_i\varvec{\beta }$ and variance matrix $\varvec{V_i}$, ensures that Assumptions (A1)–(A3) are directly satisfied. Also, Assumption (A4) follows from Condition (MM1).

Next, we prove Equation (1) of Assumption (A6). For any $j = 1,\ldots ,p$, the j-th partial derivative with respect to $\varvec{\beta }$ is given by

$$\begin{aligned} \nabla _jH_i(\varvec{Y}_i,\varvec{\theta }) = -\alpha \left( 1+\frac{1}{\alpha } \right) \eta _{i\alpha }e^{-\frac{\alpha }{2}(\varvec{Y}_i - \varvec{X}_i\varvec{\beta })^\top \varvec{V}_i^{-1}(\varvec{Y}_i - \varvec{X}_i\varvec{\beta })}\varvec{X}_{ij}^\top \varvec{V}_i^{-1}(\varvec{Y}_i - \varvec{X}_i\varvec{\beta }). \end{aligned}$$

Then, considering $\varvec{Z}_i = \varvec{V}_i^{-\frac{1}{2}}(\varvec{Y}_i - \varvec{X}_i\varvec{\beta })$,

$$\begin{aligned}&\frac{(1+\alpha )}{n} \sum _{i=1}^n \textrm{E}_{g_i} \Bigg [ \bigg \vert \eta _{i\alpha }e^{-\frac{\alpha }{2}(\varvec{Y}_i - \varvec{X}_i\varvec{\beta })^\top \varvec{V}_i^{-1}(\varvec{Y}_i - \varvec{X}_i\varvec{\beta })}\varvec{X}_{ij}^\top \varvec{V}_i^{-1}(\varvec{Y}_i - \varvec{X}_i\varvec{\beta })\bigg \vert\\& \qquad \times \ uad I\Bigg (\bigg \vert \eta _{i\alpha }e^{-\frac{\alpha }{2}(\varvec{Y}_i - \varvec{X}_i\varvec{\beta })^\top \varvec{V}_i^{-1}(\varvec{Y}_i - \varvec{X}_i\varvec{\beta })}\varvec{X}_{ij}^\top \varvec{V}_i^{-1}(\varvec{Y}_i - \varvec{X}_i\varvec{\beta })\bigg \vert> \frac{N}{1+\alpha } \Bigg ) \Bigg ] \\& \quad \le \frac{(1+\alpha )}{n} \sum _{i=1}^n \eta _{i\alpha }\big \vert \varvec{X}_{ij}^\top \varvec{V}_i^{-\frac{1}{2}}\big \vert \textrm{E}_{g_i} \Bigg [e^{-\frac{\alpha }{2} \varvec{Z}_i^\top \varvec{Z}_i} \vert \varvec{Z}_i\vert\\&\qquad \times I \Bigg (e^{-\frac{\alpha }{2}\varvec{Z}_i^\top \varvec{Z}_i} \vert \varvec{Z}_i\vert> \frac{N}{(1+\alpha ) (\sup \limits _{n> 1} \eta _{i\alpha }) (\sup \limits _{n> 1} \max \limits _{1 \le i \le n} \vert \varvec{X}_{ij}^\top \varvec{V}_i^{-\frac{1}{2}}\vert )}\Bigg ) \Bigg ] \\&\quad = E_1 \Bigg [e^{-\frac{\alpha }{2} \varvec{Z}_1^\top \varvec{Z}_1} \vert \varvec{Z}_1\vert I \Bigg (e^{-\frac{\alpha }{2}\varvec{Z}_1^\top \varvec{Z}_1} \vert \varvec{Z}_1\vert> \frac{N}{(1+\alpha ) (\sup \limits _{n> 1} \eta _{i\alpha }) (\sup \limits _{n > 1} \max \limits _{1 \le i \le n} \vert \varvec{X}_{ij}^\top \varvec{V}_i^{-\frac{1}{2}}\vert )}\Bigg ) \Bigg ] \\&\qquad \times \Bigg ( \frac{1+\alpha }{n} \sum _{i=1}^n \eta _{i\alpha }\vert \varvec{X}_{ij}^\top \varvec{V}_i^{-\frac{1}{2}}\vert \Bigg ) \end{aligned}$$

Since the $\sup _{n > 1} \max _{1 \le i \le n} \vert \varvec{X}_{ij}^\top \varvec{V}_i^{-\frac{1}{2}}\vert = \mathcal {O}(1)$ by Assumption (MM2) and $\sup _{n > 1} \eta _{i\alpha }$ is bounded thanks to the boundness of $\vert \varvec{V}_i\vert$ in (MM3), by the dominated convergence theorem (DCT), we have

$$\begin{aligned} \lim _{N \rightarrow \infty } E_1\left[ e^{-\frac{\alpha }{2} \varvec{Z}_1^\top \varvec{Z}_1} \vert \varvec{Z}_1\vert I \left( e^{-\frac{\alpha }{2}\varvec{Z}_1^\top \varvec{Z}_1} \vert \varvec{Z}_1\vert> \frac{N}{(1+\alpha ) (\sup \limits _{n> 1} \eta _{i\alpha }) (\sup \limits _{n > 1} \max \limits _{1 \le i \le n} \vert \varvec{X}_{ij}^\top \varvec{V}_i^{-\frac{1}{2}}\vert )}\right) \right] = 0. \end{aligned}$$

Also

$$\begin{aligned} \sup _{n> 1} \left( \frac{1}{n} \sum _{i=1}^n \eta _{i\alpha }\vert \varvec{X}_{ij}^\top \varvec{V}_i^{-\frac{1}{2}}\vert \right) \le (\sup _{n> 1} \eta _{i\alpha }) (\sup _{n > 1} \max _{1 \le i \le n} \vert \varvec{X}_{ij}^\top \varvec{V}_i^{-\frac{1}{2}}\vert ) = \mathcal {O}(1) \end{aligned}$$

and this follows for all $j = 1, \ldots , p$. On the other hand, consider the partial derivative with respect to $\sigma ^2_j$, $j=0,1,\ldots ,r$, given in Equation (10). Hence, denoting with $\varvec{Z}_i = \varvec{V}_i^{-\frac{1}{2}}(\varvec{Y}_i - \varvec{X}_i\varvec{\beta })$, we have

$$\begin{aligned}&\frac{1}{n} \sum _{i=1}^n \textrm{E}_{g_i} \left[ \vert \nabla _{\sigma ^2}H_i(\varvec{Y}_i,\varvec{\theta })\vert \times I(\vert \nabla _{\sigma ^2_j}H_i(\varvec{Y}_i,\varvec{\theta })\vert>N) \right] \\&\quad \le \frac{\alpha }{2n}\sum _{i=1}^n \frac{\eta _{i\alpha }\textrm{Tr}(\varvec{V}_i^{-1}\varvec{U}_{ij})}{(1+\alpha )^{\frac{n_i}{2}}}\textrm{E}_{g_i}[I(\vert \nabla _{\sigma ^2_j}H_i(\varvec{Y}_i,\varvec{\theta })\vert>N)] \\&\qquad + \frac{1+\alpha }{2n}\sum _{i=1}^n \eta _{i\alpha }\textrm{Tr}(\varvec{V}_i^{-1}\varvec{U}_{ij})\textrm{E}_{g_i}[e^{-\frac{\alpha }{2} \varvec{Z}_i^\top \varvec{Z}_i}I(\vert \nabla _{\sigma ^2_j}H_i(\varvec{Y}_i,\varvec{\theta })\vert>N)] \\& \qquad + \frac{1+\alpha }{2n}\sum _{i=1}^n \eta _{i\alpha }\textrm{E}_{g_i}[\vert \varvec{Z}_i^\top \varvec{V}_i^{-1}\varvec{U}_{ij}\varvec{V}_i^{-1} \varvec{Z}_i\vert e^{-\frac{\alpha }{2} \varvec{Z}_i^\top \varvec{V}_i^{-1} \varvec{Z}_i}I(\vert \nabla _{\sigma ^2_j}H_i(\varvec{Y}_i,\varvec{\theta })\vert>N)] \\& \quad = \left( \frac{\alpha }{2n}\sum _{i=1}^n \frac{\eta _{i\alpha }\textrm{Tr}(\varvec{V}_i^{-1}\varvec{U}_{ij})}{(1+\alpha )^{\frac{n_i}{2}}} \right) \textrm{E}_1[I(\vert \nabla _{\sigma ^2_j}H_i(\varvec{Y}_i,\varvec{\theta })\vert>N)] \\& \qquad + \left( \frac{1+\alpha }{2n}\sum _{i=1}^n \eta _{i\alpha }\textrm{Tr}(\varvec{V}_i^{-1}\varvec{U}_{ij}) \right) \textrm{E}_1[e^{-\frac{\alpha }{2} \varvec{Z}_1^\top \varvec{Z}_1}I(\vert \nabla _{\sigma ^2_j}H_i(\varvec{Y}_i,\varvec{\theta })\vert>N)] + \\&\qquad + \frac{1+\alpha }{2n}\sum _{i=1}^n \eta _{i\alpha }\textrm{E}_{g_i}[\vert \varvec{Z}_i^\top \varvec{V}_i^{-1}\varvec{U}_{ij}\varvec{V}_i^{-1} \varvec{Z}_i\vert e^{-\frac{\alpha }{2} \varvec{Z}_i^\top \varvec{V}_i^{-1}\varvec{Z}_i}I(\vert \nabla _{\sigma ^2_j}H_i(\varvec{Y}_i,\varvec{\theta })\vert >N)] \end{aligned}$$

where in the last term $\varvec{Z}_i = (\varvec{Y}_i - \varvec{X}_i\varvec{\beta })$. Note that

$$\begin{aligned} \textrm{E}_{g_i}[\varvec{Z}_i^\top \varvec{V}_i^{-1}\varvec{U}_{ij}\varvec{V}_i^{-1} \varvec{Z}_i e^{-\frac{\alpha }{2} \varvec{Z}_i^\top \varvec{V}_i^{-1} \varvec{Z}_i}] = \frac{\textrm{Tr}(\varvec{V}_i^{-1}\varvec{U}_{ij})}{(1+\alpha )^{1+\frac{n_i}{2}}} \end{aligned}$$

; hence, by Equation (15),

$$\begin{aligned} \textrm{E}_{g_i}\left[ \vert \varvec{Z}_i^\top \varvec{V}_i^{-1}\varvec{U}_{ij}\varvec{V}_i^{-1} \varvec{Z}_i\vert e^{-\frac{\alpha }{2} \varvec{Z}_i^\top \varvec{V}_i^{-1} \varvec{Z}_i}I(\vert \nabla _{\sigma ^2}H_i(\varvec{Y}_i,\varvec{\theta })\vert >N)\right] \rightarrow 0, ~~~ \text{ as } N \rightarrow \infty . \end{aligned}$$

The expectation in the first two terms goes to zero as $N \rightarrow \infty$ by the DCT, as before, and the sums are bounded by Equation (15) in condition (MM3). This holds for all $j = 0,\ldots ,r$.

Finally, Assumptions (A5), (A7) and Equation (2) similarly hold using Equations (14) and (16), (17), (13) and (15), respectively.