Left-truncated health insurance claims data: theoretical review and empirical application

Abstract

From the inventory of the health insurer AOK in 2004, we draw a sample of a quarter million people and follow each person’s health claims continuously until 2013. Our aim is to estimate the effect of a stroke on the dementia onset probability for Germans born in the first half of the 20th century. People deceased before 2004 are randomly left-truncated, and especially their number is unknown. Filtrations, modelling the missing data, enable circumventing the unknown number of truncated persons by using a conditional likelihood. Dementia onset after 2013 is a fixed right-censoring event. For each observed health history, Jacod’s formula yields its conditional likelihood contribution. Asymptotic normality of the estimated intensities is derived, related to a sample size definition including the number of truncated people. The standard error results from the asymptotic normality and is easily computable, despite the unknown sample size. The claims data reveal that after a stroke, with time measured in years, the intensity of dementia onset increases from 0.02 to 0.07. Using the independence of the two estimated intensities, a 95% confidence interval for their difference is [0.053, 0.057]. The effect halves when we extend the analysis to an age-inhomogeneous model, but does not change further when we additionally adjust for multi-morbidity.

1 Introduction

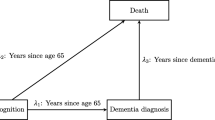
For Germany, Doblhammer et al. (2018) forecast an increase of up to 2.8 million people with dementia by 2050. One risk factor is a stroke, and we model life as a time-continuous, multi-state, Markovian history (see Fig. 1). The model is also called ‘disability model’ (see Hougaard 2001, Figure 1.6).

Fig. 1

Disease states and transitions

Note that ‘healthy’ exclusively stands for ‘neither having dementia nor having had a stroke’. Dementia onset of a person after a stroke (or precisely, after the first one) is, ceteris paribus, governed by the onset intensity, named $\lambda _{S^1D}$. We compare this intensity with the dementia onset intensity of a healthy person, $\lambda _{\text {HD}}$. By stroke effect on dementia onset, we refer to the difference (or the ratio) of these two intensities.

The population we will refer to are inhabitants of Germany born in the years 1900 to 1954, which we call ‘the first half of the 20th century’ (see Fig. 2, top box). Drawing a simple random sample (size n$_{\text {all}}$) from that population and then truncating, i.e. not observing, persons deceased before 2004, is similar to drawing a simple random sample (size n) of all Germans alive at the beginning of 2004. The latter is our situation. Note that in the first design, the number of observations is random, and in the second design, the number n$_{\text {all}}$ is unknown. That people are missing in the data due to an earlier death is called left-truncation (see Fig. 2, middle box and Fig. 8) and is a typical design defect in disease state models (see e.g. Putter et al. 2006). Ignoring truncation would lead to the ‘immortal time bias’ (see e.g. Hernán et al. 2016; Yadav and Lewis 2021).

Fig. 2

From population to the data of left-truncated persons subject to right-censoring (Population size: German Statistical Office (2004), without stillborn)

Efficient estimation in large samples is usually achieved by the maximum likelihood method. In order to render knowledge about truncated persons obsolete, marginalisation and conditioning are necessary here. We intend to do both a review of the methodological arguments and the application to a German data set. Right-censoring will always be accounted for (see Fig. 2, bottom box), and explanation will be sparse, because there is already an extensive literature. Explaining how the method reduces information is easier when the state ‘being alive’ is not subdivided into several disease states, and is presented in a lifetime state model (in the terminology of Hougaard, 2001) in Appendix A. Then, with all states of Fig. 1, Sect. 2 derives a confidence interval for the difference $\lambda _{S^1D}- \lambda _{\text {HD}}$ and a Wald-type test for the stroke effect. In the next Sect. 3, for two reasons, we allow intensities to depend on age. On the one hand, it enables a comparison of our case study with reputable international studies where age-inhomogeneous behaviour is routinely accounted for. On the other hand, we will see that accounting for age drastically changes the stroke effect, and is an insightful example of confounding. In Sect. 3 we additionally adjust for (vascular) multi-morbidity, in order to answer the question of whether the elevated dementia risk by stroke could be anticipated for multi-morbid persons. Sections 2 and 3.1 start with asymptotic theory, Section 2 continues with a Monte Carlo study to reveal that the asymptotic approximation with the normal distribution is adequate for our application. All sections end by fitting the model to the data of that section. Appendix A contains modelling, asymptotic theory as well as Monte Carlo simulations, and fits the data.

1.1 Data: AOK HCD

Although, for the purposes of our investigation, it would be ideal to have a sample from Germany in 2004, sampling is restricted to the 25 million members of Germany’s largest public health insurance company ‘Allgemeine Ortskrankenkasse’ (AOK), made available to us by its scientific research institute (WIdO). Compared with other statutory health insurance funds, or private health insurance, disease rates for the AOK are slightly elevated (see Schnee 2008). We refrain from studying selection bias in that respect, but as the AOK members represent one third of the population, results are expected to be representative. Also, a uniformly larger disease level, even when extending to incidences, will balance in the difference between the dementia incidences, with as compared to without a preceding stroke.

The AOK’s health claims data (HCD) include information on age, year of birth and date of exit (death or migration to another insurance company). From the insurance inventory on 01/01/2004, a simple random sample of 250,000 people is drawn. The health histories of those persons until the end of 2013 are retrieved. We exclude 4121 persons with implausible information on sex, birth year or region of living. In that form, the data are sufficient for the lifetime state model in Appendix A. The AOK HCD also contain information on outpatient and inpatient diagnoses for each insured person, with at least one day of insurance coverage, regardless of whether or not they sought medical treatment.

Recall our main focus. By sampling in 2004, we cannot strictly sample from the defined population because people who died earlier are not selectable, i.e. are left-truncated. We have argued why the second design effect resulting from the difference between the population in Germany and the insurants of the AOK is neglected by us. There is a third design effect which we now discuss briefly. In 2004 we draw only a sample of those persons aged 50 years or older. That age is typically the earliest at which a stroke or dementia occurs. Of course, 50 is not the earliest age at which a person may die and, thus a person who dies before age 50 is additionally left-truncated. We suppress this truncation reason, i.e. assume that death before 50 is impossible, for two reasons, in order to simplify the model. On the one hand, only $\approx$ 6.5% of the people die before age 50 in western civilisations.¹ Hence assuming that rate to be zero will not distort the results by much. On the other hand, our data donor WIdO allowed sampling 250,000 people, and without the restriction to those over 50 would have resulted in $\approx$ 50% younger,² and they would mostly remain healthy over the 10 years of observation. Half of the sample size means an increase in standard errors by a factor of $\sqrt{2}$, i.e. by 40%.

In the AOK HCD, all diagnoses are coded in the International Statistical Classification of Diseases and Related Health Problems (ICD), revision 10, issued by the WHO. Dementia was defined as having at least one of the following diagnoses coded by ICD-10: G30, G31.0, G31.82, G23.1, F00, F01, F02, F03, and F05.1. Note that by sampling at the beginning of 2004, a person with dementia diagnosis at that time (technically in that quarter or the next) may not indicate a dementia onset, but can be a pending case. We exclude those persons and n = 236,039 remain. For them, the mean follow-up time is 7.3 years, resulting in 1.7 million person-years at risk. Additional descriptive cross-sectional statistics as of 2004 are provided in Table 1.

Table 1 Descriptive statistics for AOK insurants 50+ sampled in 2004, cross-section mid of 2004, except (longitudinally): mean follow-up time and person-years at risk

Important longitudinal information for the models will entail 34 thousand persons who will experience dementia onset until 2013. Finally, in view of assessing the effect of a stroke (ICD-10: I63, I64) on dementia onset, 19,201 persons will have experienced a stroke by 2013. Additionally, due to the Markov property, the information about a stroke for 5864 persons in 2004 is likely to be an incidence, because a stroke is not a chronic disease and also likely to be the first stroke. We did not remove these individuals.

Six diseases (other than stroke) are considered in Mangialasche et al. (2012) as potential vascular risk factors for dementia. Along with age in Section 3.1, we adjust for vascular predisposition in Section 3.2. Hypertension (ICD-10: I10-I15) is the most frequent condition, with a prevalence of approximately 90% in the data. Hence, hypertension alone does not stratify sufficiently, so that we use the ‘two out of six’ rule for (vascular) multi-morbidity including the five other factors ‘type 2 diabetes’ (ICD-10: E11-E14), ‘ischemic heart diseases’ (ICD-10: I20-I25), ‘atrial fibrillation’ (ICD-10: I48), ‘hypercholesterolemia’ (ICD-10: E78.0) and ‘obesity’ (ICD-10: E66).

1.2 Literature review

Similar ideas of testing the effect of stroke on dementia are found in Desmond et al. (2002), Ivan et al. (2002), Reitz et al. (2008), Savva and Blossom (2010), Kuźma et al. (2018), Kim and Lee (2018) and Hbid et al. (2020). We now compare our contribution broadly to the adjacent literature, distinguishing between substantial and methodological similarities. Substantially, Vieira et al. (2013) report dementia incidences, as do Leys et al. (2005) after a stroke. Death incidences, after a stroke (van den Bussche et al. 2010) and with dementia (Garcia-Ptaceka et al. 2014), are of use to us, because they constitute elements of one of our models and will enter the calibration of simulations. Dementia prevalence is studied in Doblhammer et al. (2018), and risk factors are presented in Mangialasche et al. (2012). Community-based studies on the effect of a stroke on dementia include (Ivan et al. 2002) and (Reitz et al. 2008). Cerebrovascular processes are studied in more detail by Hu and Chen (2017). Statistical risk factors common to dementia and stroke are studied in Pendlebury and Rothwell (2009). With respect to the method, our work has considerable similarity to the study ‘Mortality of Diabetics in the County of Fyn’ in Andersen et al. (1993), and Andersen et al. (1988, Section 4) in particular. However, our truncation model is slightly easier, and our simple random sample of HCD is considerable larger than the data there. We reduce the arguments to those necessary for our model. We make considerable use of Fleming and Harrington (1991), even though the book does not cover left-truncation. Weißbach et al. (2009) and Weißbach and Walter (2010) apply a similar Markovian multi-state model, but to an economic question, and especially need to reduce their population in order to circumvent left-truncation. Note that right-truncation requires another method (see e.g. Dörre 2020; Weißbach and Dörre 2022; Weißbach and Wied 2022, and references therein). Finally, Weißbach et al. (2021) also analyse the same dataset and with dementia as the endpoint, but not using a multi-state model and with an emphasis on left-censoring.

2 Univariate analysis of health states

The set of assumptions in the present section is to some extent educational, because the assumptions will be too restrictive for realistic results on the development of dementia. The results cannot be compared to the epidemiological literature. Section 3.1 will present a first realistic model, requiring more notation. Here we only explain major modelling decisions. Following up on Sect. 1.1, let t count the years after a person’s 50th birthday, and we continue to call t ‘age’. The major methodological challenge is that people from our population of interest have died before 2004, the year when we started to observe. Their health histories have been deleted after their deaths, i.e. we cannot observe any of those histories, even if some of these people would belong to a simple sample from that population. Methodological arguments on how to proceed when drawing from the conditional population of alive people in 2004, are discussed in Appendix A in a lifetime state model with death being both the sole event of interest and the event of truncation. To augment the scope from mortality to morbidity, let here $X_t$ indicate a person’s disease state, H, $S^1$ or D, or d, at the age of t (see Figs. 1 and 3). A healthy individual’s status is set to $S^1$ at the time of the first stroke, and preserved (in the absence of further state transitions), also in cases of subsequent strokes. For a person with dementia we write $X_t=D$, irrespective of whether or not a stroke has preceded dementia onset at that age. A stroke after dementia onset is not recorded at all, as it is not relevant for the assessment of a stroke effect on dementia. Now, with the—in comparison with mortality analysis—two additional states, $S^1$ and D, no transition into any other state than d before 2004 prohibits observing the health history from 2004 onwards. Only death truncates a person. We will often refer the reader to Appendix A for detailed analytical arguments, and amend arguments in this section only when the disease state model differs methodologically from the lifetime state model.

2.1 Contribution of an observed person to inference

Roughly speaking, we aim at maximum likelihood inference. In the case of a simple sample, each randomly drawn person contributes with its density to the likelihood, and the estimation criterion is the maximisation of the joint density as a function of the parameter, i.e. the likelihood. We will see that people not observed do not contribute to our criterion function and we now derive the contribution for each observed history. We first collect all possible state transitions in the index set

$$\begin{aligned} {\mathcal {I}}:=\{H S^1, S^1 D, H D, H d, S^1 d, D d \} \quad \text {(see `arrows' in Figure 1)}. \end{aligned}$$

Furthermore, universally for all persons, we do not follow a health history any further than $\tau$ years. The continuous-time history $\textbf{X}=\{X_t, t\in [0,\tau ]\}$, observed in full, in parts or not at all, defined on the probability spaces $(\Omega , {\mathcal {F}}, P_{\varvec{\lambda }})$ represent either the population or one random draw from it. The Markov property is assumed for $\textbf{X}$, so that the history is determined by the transition intensities $\lambda _{hj}(t):= \lim _{s\searrow 0} P_{\varvec{\lambda }} (X_{t+s}=j \mid X_t=h)/s$. In this section, we model the population of Germany (at that time) as age-homogeneous, i.e. assume $\lambda _{hj}(t) \equiv \lambda _{hj}$. (The realistically age-inhomogeneous intensities follow in Sect. 3.1.) By parameter we mean the vector $\varvec{\lambda }:= (\lambda _{hj}, hj \in {\mathcal {I}})'$. We consider a simple random sample of size $n_{all}$ persons drawn from the population (see Fig. 2). The generalisation, compared to the lifetime state model in Appendix A, is less severe when we assume that all persons start in the same state, $X_0=H$, at the age origin, and all theoretical arguments assume alike. In practice, from those not truncated by death, with number denoted as n in Appendix A.2, $X_0 \in \{S^1,D\}$ is known to be very rare (see e.g. Doblhammer et al. 2018, Abb. 2.2). Moreover, excluding those exceptions from the data is impossible because, for example, for an observed person with $X_u=D$, $X_0$ is unknown. For the applications, we condition on the distribution of $X_0$, which leaves the criterion as a function of $\varvec{\lambda }$ unchanged, if the distribution of $X_0$ does not depend on $\varvec{\lambda }$. Essentially, with ${\mathcal {L}}$ denoting the distribution, this is because we can decompose

$$\begin{aligned} {\mathcal {L}}_{\varvec{\lambda }}(\textbf{X})={\mathcal {L}}_{\varvec{\lambda }}(\textbf{X}\mid X_0){\mathcal {L}}(X_0). \end{aligned}$$

(In the case of ${\mathcal {L}}_{\varvec{\lambda }}(X_0)$, efficiency gets lost.) Note that we again observe the same $n<n_{all}$ persons as in the lifetime state model of Appendix A, with histories that occur—completely or in part—during our observation period between 2003 and 2014 (see Fig. 2).

For each observed history, the ‘age-at-study-begin’, U, is the time between the calendar dates of the 50th birthday and the study begin on 01/01/2004. In Appendix A.2 we initially simplify to a non-random age-at-study-begin, u, and the age-at-death T is reformulated as (jump-diffusion) process $N_T$. Here we generalise and reformulate one history $\textbf{X}$ in several $N_{hj}(t) := \sum _{s \le t} \mathbbm {1}_{\{X_{s-} =h, X_s=j\}}$, the processes ‘counting’ the transition between states, up to age t, and $Y_h(t) := \mathbbm {1}_{\{X_{t-} =h\}}$, indicating residence in state h, at the age of t. The counting processes are collected in the vector $\textbf{N}_X(t):=(N_{hj}(t), hj \in {\mathcal {I}})'$. Now, as usual, statistical statements about parameters are inferred from statements about the location (the ‘signal’) of the random experiment. In order to define a location for a stochastic process, probabilities may be calculated on a filtration ${\mathcal {N}}_t:= \sigma \{\textbf{N}_X(s), 0 \le s \le t\}$. We can assume that $\textbf{N}_X(t)$ is adapted to it, because we theoretically assume $X_0=H$. We assume for the ‘true’, the population, parameter $\varvec{\lambda }_0$ (similar to Condition (A1) in Appendix A):

• (B1) It is $\lambda _{hj^0} \in \Lambda _{hj}:=[\varepsilon _{hj};1/\varepsilon _{hj}]$ for some small $\varepsilon _{hj} \in (0,1)$.

The compensator of $\textbf{N}_X$, the location concept here, has an intensity (the derivative of the compensator) with respect to ${\mathcal {N}}_t$ and $P_{\varvec{\lambda }}$ of $\varvec{\alpha }(t):=(Y_h(t) \lambda _{hj}, hj \in {\mathcal {I}})'$. (When only h appears, the first position of hj it meant. Especially $h \ne d$, because death is absorbing.) Starting with deterministic u, a person is not left-truncated in the case of $A:=\{X_u \ne d \}$. Different to the lifetime state model is that the history up to u is only known when $X_u=H$. If for instance $X_u=S^1$, the age-at-stroke is left-censored. This is an important incentive to start the observation only at u, i.e. ${}_u{\textbf{N}}(t):=\textbf{N}_X(t) - \textbf{N}_X(t \wedge u)$, where $t \wedge u := \min (t,u)$. Due to the Markovian property it is adapted to the filtration ${}_u{{\mathcal {G}}}_t := \sigma \{{}_u{\textbf{N}}(s), u \le s \le t\}$.

Lemma 1

With respect to the probability measure $P^{A}_{\varvec{\lambda }}(F):= P_{\varvec{\lambda }}(F \cap A)/P_{\varvec{\lambda }}(A)$ for $F \in {\mathcal {F}}$, the intensity of ${}_u{\textbf{N}}(t)$ is ${}_u{\varvec{\alpha }}(t):=\mathbbm {1}_{\{u < t\}} \varvec{\alpha }(t)$.

The proof is as in Section A.1.1. Note that $P^A_{\varvec{\lambda }}$ depends on the parameter $\varvec{\lambda }$ and on u. With ${}_u{Y}_h(t):= \mathbbm {1}_{\{u < t\}}Y_h(t)$, the coordinates of ${}_u{\varvec{\alpha }}$ are ${}_u{\alpha }_{hj}(t):= {}_u{Y}(t) \lambda _{hj}$. The observed left-truncated and right-censored counting process is ${}_u{\textbf{N}}^c(t) := \int _0^t C(s) d {}_u{\textbf{N}}(s)$, with $C(t):= \mathbbm {1}_{\{t \le u+10\}}$ and ${}_u{\textbf{Y}}^c(t):=C(t) {}_u{\textbf{Y}}(t)$ (compare Fleming and Harrington (1991), Example 1.4.2). It has intensity

$$\begin{aligned} {}_u{\varvec{\alpha }}^c(t) := \mathbbm {1}_{\{t \le u+10\}} {}_u{\varvec{\alpha }}(t)= \mathbbm {1}_{\{u < t \le u+10\}} \varvec{\alpha }(t) \end{aligned}$$

(1)

with respect to $P^A_{\varvec{\lambda }}$ and observed filtration ${}_u{{\mathcal {F}}}^c_t := \sigma \{{}_u{\textbf{N}}^c(s), u \le s \le t\}$. For the distinction between observable and unobservable filtrations, see Section A.1.2. As ${}_u{{\mathcal {F}}}^c_t$ is a required self-exciting filtration, by Jacod’s formula (see Andersen et al. 1988, Formula 4.3), the contribution of a person (truncated or not) to the marginal likelihood and its (natural) logarithm are:

(2)

Note ${}_u{\alpha }_{\cdot }^c(t) := \sum _{hj \in {\mathcal {I}}} {}_u{\alpha }_{hj}^c(t)$ together with ${}_u{N}_{\cdot }^c(t) := \sum _{hj \in {\mathcal {I}}} {}_u{N}_{hj}^c(t)$. The product integral is explained in Appendix A.1.1. Essentially, the discrete approximation of the history $\textbf{X}$ is a collection of random increments. The probability function (pf) of this collection can be a product of the increments’ pf’s. Decreasing the grid spacing defines an integral. The double-use of the integration symbol dt in the first line is still different to the line above Formula (A1) (in Appendix A.1.1), because Y(t) drops to zero after T, whereas $Y_h(t)$ is only one for a different state. The reason for the exponential function in the third line is explained shortly after Formula (A1). For the second equality, on the logarithmic scale, the logarithm of a product becomes a sum of logarithms, and no new integration for decreased grid spacing arises, the Stieltjes integration for discontinuous g ($\int fdg=\sum f \Delta g$) suffices. Note (generally $\Delta f(t):= f(t) - f( t-)$ (see Andersen et al. 1993, Sect. II.2) that $\Delta {}_u{N}^c_{hj}(t)$ is only not zero if ${}_u{N}^c_{hj}(t)$ jumps. These jumps are of height one. Further note that $\int _u^{u+10}$ can be replaced by $\int _0^{\tau }$, because ${}_u{Y}^c_h(t)$ already accounts for the limits, and similarly, in the product, $[u,u+10]$ is accounted for in ${}_u{\textbf{N}}^c(t)$. Note that, because almost surely ${}_u{N}^c_{hj} (u)=0$,

$$\begin{aligned} \frac{\partial }{\partial \lambda _{hj}} \ln dP = \frac{{}_u{N}^c_{hj} (\tau )}{\lambda _{hj}} - \int _0^{\tau } {}_u{Y}^c_h(t) dt. \end{aligned}$$

(3)

A truncated person does not contribute to the marginal likelihood, as argued in detail with Formula (A1) in Appendix A. As $\textbf{X}$ is random, so too must be the age-at-study-entry, U. Similar to Condition (A2) in Appendix A.1.2, together with independent truncation, we impose as additional assumption, that not everyone is dead, prior to 2004:

• (B2) U and $\textbf{X}$ are independent, it is $A:=\{ X_U \ne d\}$ and $\beta _{\varvec{\lambda }_0}:= \tilde{P}_{\varvec{\lambda }_0}(A) > 0$

The additional information by stopping time U, i.e. for $(\textbf{X},U)$, and at the same time the loss in information by truncation, is reflected by including ${}_U{\textbf{Y}}^c$ in the filtration ${}_u{{\mathcal {F}}}^c_t$, ${}_U{{\mathcal {F}}}^c_t := \sigma \{{}_U{\textbf{N}}^c(s), {}_U{\textbf{Y}}^c(s), u \le s \le t\}$. Consult Appendix A.1.2 to see that, similar to non-random truncation (2), conditional on the last two coordinates, by Jacod’s formula the logarithmic marginal density of $(\textbf{X},U, \mathbbm {1}_A)$ up to $\tau$ is

$$\begin{aligned} \ln {}_U{L}_{\tau }^c (\textbf{X},U \mid \varvec{\lambda }) = \int _0^{\tau } \sum _{hj \in {\mathcal {I}}} \ln ({}_U{Y}^c_h(t) \lambda _{hj}) d {}_U{N}^c_{hj} (t) - \sum _{hj \in {\mathcal {I}}} \int _0^{\tau } {}_U{Y}^c_h(t) \lambda _{hj} dt, \end{aligned}$$

(4)

where U replaces u in the definitions of ${}_u{N}^c_{hj} (t)$, ${}_u{Y}^c_h(t)$ and ${}_u{\varvec{\alpha }}^c(t)$ of (1). The expression uses the Doob–Meyer decomposition of $N_{hj}(t)$, stacked to $\textbf{N}_X$. Occasionally, we will denote the second term in (4), and in corresponding decompositions for more advanced models, the subtrahend, as ‘Y-term’. The first term, the minuend, will be denoted as the ‘N-term’, because Y will vanish after taking derivatives, essentially due to $\frac{d}{dx} \int =\int \frac{d}{dx}$ and $\ln (a x)=\ln (a)+ \ln (x)$. The observed left-truncated and right-censored versions thereof are

$$\begin{aligned} {}_U{\textbf{N}}^c(t) := \int _0^t C(s) d {}_U{\textbf{N}}(s) \quad \text {and} \quad {}_U{Y}^c_h(t):= C(t) \mathbbm {1}_{\{U < t\}}Y_h(t), \end{aligned}$$

with C(t) being one, as long as the person is not censored, i.e. for $t \le U+10$ and ${}_U{\textbf{N}}(t):=\textbf{N}_X(t) - \textbf{N}_X(t \wedge U)$. That the contribution of a truncated person is one, is argued in Appendix A.1.2, Formula (A2).

2.2 Point estimates and their standard errors

As in Appendix A.1.3, i denotes the person in $\textbf{X}^i$, $U_i$, ${}_{U}{N}^c_{hji}$ and ${}_U{Y}^c_{hi}$ and $n=\sum _{i=1}^{n_{all}} \mathbbm {1}_{A_i}$ with $A_i$ as in Condition (B2). The truncated persons without contribution to the conditional likelihood (marginalisation is not mentioned from now on) are sorted to the end of the unobserved sample, a convention already in Heckman (1976). All others contribute with (4) to

$$\begin{aligned} \ln {}_U{L}_{\tau }^c(data;\varvec{\lambda }) = \sum _{i=1}^n \ln {}_U{L}_{\tau }^c(\textbf{X}^i,U_i \mid \varvec{\lambda }). \end{aligned}$$

(5)

This requires $U_i$ to be random as explained in Appendix A.1.3. With ${}_U{N}^c_{hj\bullet }(t):= \sum _{i=1}^n {}_{U}{N}^c_{hji}(t)$ and ${}_U{Y}^c_{h\bullet }(t):=\sum _{i=1}^{n}{}_U{Y}^c_{hi}(t)$ (sketched in Fig. 3 for $n_{all}=4$)

Fig. 3

Four health histories (end of states is indicated by short vertical line, left-truncation events at $U_i$ are indicated by long vertical lines), unobservable $N_{S^1D\bullet }(t):=\sum _{i=1}^n N_{S^1D i}(t)$ and observed ${}_U{N}^c_{S^1D\bullet } (t)$ (offset between $N_{S^1D\bullet }$ and ${}_U{N}^c_{S^1D\bullet }$ for clarity)

the unique root of the derivatives of (5) - and hence the point estimates—are, by (3) simply

$$\begin{aligned} \hat{\lambda }_{hj} = \frac{{}_U{N}^c_{hj\bullet }(\tau )}{\int _0^{\tau } {}_U{Y}^c_{h\bullet }(t) dt}. \end{aligned}$$

(6)

One can avoid integration in the denominator in (6). Of the interesting states for h, H and $S^1$, rewrite e.g. for $h=H$:

$$\begin{aligned} \int _0^{\tau } {}_U{Y}^c_{H\bullet }(t) dt= & {} \sum _{i=1}^n \int _{U_i}^{U_i + 10} \mathbbm {1}_{\{X^i_{t-} =H\}} dt \\= & {} \sum _{i=1}^n \mathbbm {1}_{\{X^i_{U_i} = H\}} \left( 10 \, \mathbbm {1}_{\{X^i_{U_i+10} = H\}} + \mathbbm {1}_{\{X^i_{U_i+10} \in \{S^1,D\}\}} (\sup _t\{X^i_t=H\} - U_i) \right) \end{aligned}$$

Note that similar to (A5), by using the simple sample assumption, among those who survive $U_i$ (i.e. 2003), the portion in the study period at age t in state h is asymptotically the same in the observed sample and in the entire population. By the LLN, for fixed t,

$$\begin{aligned} \frac{{}_U{Y}^c_{h\bullet }(t)}{n}{\mathop {\longrightarrow }\limits ^{P}}m^A_h(t):=\tilde{P}_{\varvec{\lambda }_0}(X_t=h\mid A). \end{aligned}$$

(7)

The latter will typically be positive, but for our parametric model, we only need to assume (compare Condition (A3)):

• (B3) $\int _0^{\tau } \sum _{h \in \{H, S^1, D\}} m^A_h(t)dt > 0$

By verifying regularity conditions, we arrive at the (joint) asymptotic distribution of the estimators $\hat{\lambda }_{\text {HD}}$ and $\hat{\lambda }_{S^1D}$ by standard results on martingales. It depends on $m_h^A(t)$, the conditional prevalence of state h at age t in the population, and $\beta _{\varvec{\lambda }_0}$, the probability of a person from the sample to be observed, i.e. not to be truncated.

Theorem 1

Under Conditions (B1)–(B3) and $m^A_h(t)$ defined in (7) it is $\hat{\varvec{\lambda }}$, composed of (6), consistent and $\sqrt{n_{all}}(\hat{\varvec{\lambda }} - \varvec{\lambda }_0) {\mathop {\longrightarrow }\limits ^{{\mathcal {D}}}} {\mathcal {N}}(0,\varvec{\Sigma }^{-1}(\varvec{\lambda }_0))$ with diagonal matrix $\varvec{\Sigma }(\varvec{\lambda }_0)$ of diagonal elements

$$\begin{aligned} \sigma _{hj,hj}(\varvec{\lambda }_0):= \beta _{\varvec{\lambda }_0} \int _0^{\tau } \sum _{hj \in {\mathcal {I}}} \frac{ m^A_h(t) }{\lambda _{hj^0}}dt, \quad \text {for} \quad hj \in {\mathcal {I}}. \end{aligned}$$

Roughly speaking, the arguments of the proof, given in Appendix B, are similar to the case of the one-dimensional parameter space in Appendix A.1.3. Luckily, the multivariate parameter space here results in a diagonal matrix of asymptotic variance-covariance matrix, and positive definiteness follows from the positivity of the diagonal elements.

It remains to consistently estimate $\varvec{\Sigma }(\lambda _0)$, in order to construct a confidence interval for the difference $\hat{\lambda }_{S^1D^0}-\hat{\lambda }_{HD^0}$ with the standard error. This then allows a Wald-type test for the effect of a stroke $S^1$ on the intensity of dementia onset for the AOK HCD in Sect. 2.4. By Theorem 1, $Var(\hat{\varvec{\lambda }}) = Var (\sqrt{n_{all}}\hat{\varvec{\lambda }})/n_{all}{\mathop {=}\limits ^{\cdot }}\varvec{\Sigma }^{-1}(\varvec{\lambda }_0)/n_{all}$, so that, for estimating the asymptotic variance in Theorem 1, define $- {\mathcal {J}}_{\tau }(\varvec{\lambda }_0)$ as

$$\begin{aligned} diag \left( \frac{\partial ^2}{\partial \lambda _{hj}^2} \ln {}_U{L}_{\tau }^c(data \mid \varvec{\lambda })\mid _{\varvec{\lambda }=\varvec{\lambda }_0} ; hj \in {\mathcal {I}}\right) = - diag \left( \frac{{}_U{N}^c_{hj\bullet } (\tau )}{\lambda _{hj^0}^2}; hj \in {\mathcal {I}}\right) . \end{aligned}$$

Now, as ${\mathcal {J}}_{\tau }(\varvec{\lambda }_0)/n_{all} {\mathop {\longrightarrow }\limits ^{n_{all} \rightarrow \infty , P}} \varvec{\Sigma }(\lambda _0)$ (see Andersen et al. 1993, Formula 6.1.11), it is

$$\begin{aligned} \widehat{Var(\hat{\lambda }_{hj})} = {\mathcal {J}}_{\tau }^{-1}(\hat{\varvec{\lambda }})_{hj,hj} = \frac{{}_U{N}^c_{hj\bullet } (\tau )}{\left( \int _0^{\tau } {}_U{Y}^c_{h \bullet }(t) dt\right) ^2}, \end{aligned}$$

(8)

due to ${\mathcal {J}}_{\tau }^{-1}(\varvec{\lambda }_0)_{hj,hj} = \lambda _{hj^0}^2/{}_U{N}^c_{hj\bullet }(\tau )$, (6) and the CMT. The standard error of $\hat{\lambda }_{hj}$ is the square root thereof. Note that even though n$_{\text {all}}$, and with it the asymptotic variance - as component of $\varvec{\Sigma }(\lambda _0)$ -, is not observable, the standard errors are indeed observed.

2.3 Finite sample properties

We conduct a Monte Carlo simulation, primarily to visualize the asymptotic results on consistency, measured in (root) mean squared error, and on normality for small sample sizes, as indicated by Theorem 1. In particular, we find that the asymptotic approximation is rather precise for our statements on basis of the AOK HCD. Appendix A.1.4 does alike for the lifetime state model. We refrain from indicating the true parameter by the sub/superscript and drop 0 in this section. We arrange $\varvec{\lambda }$ as generator (left side):

$$\begin{aligned} Q:=\begin{pmatrix} -\lambda _{H \cdot } &{} \lambda _{H S^1} &{} \lambda _{H D} &{} \lambda _{H d} \\ 0 &{} -\lambda _{S^1 \cdot } &{} \lambda _{S^1 D} &{} \lambda _{S^1 d} \\ 0 &{} 0 &{} - \lambda _{D d} &{} \lambda _{D d}\\ 0 &{} 0 &{} 0 &{} 0 \end{pmatrix} = \begin{pmatrix} -0.08\bar{6} &{} 1/30 &{} 0.02 &{} 1/30 \\ 0 &{} -0.17 &{} 0.07 &{} 1/10 \\ 0 &{} 0 &{} - 0.1 &{} 1/10 \\ 0 &{} 0 &{} 0 &{} 0 \end{pmatrix} \end{aligned}$$

(9)

Here, the small dot signals summation over the respective index $\sum _{j}$.

2.3.1 Algorithm for simulating a history

We simulate a disease state history with the description in Albert (1962). As discussed in Sect. 2.1, we assume $X_0=H$, so that $X_t \equiv H$ on $[0,T_1)$ with $T_1$ having the cumulative hazard function $A_{H\cdot }(t)= \lambda _{H\cdot } t$ (i.e. $T_1 \sim Exp(\lambda _{H \cdot })$). Then, in $t=T_1$, $\textbf{X}$ migrates from H to $j \in \{S^1, D, d\}$ with $p_{Hj}=\tilde{P}_{\varvec{\lambda }}(X_{T_1}=j \mid X_{T_1-}=H)$, with $p_{Hj}= \lambda _{Hj} / \lambda _{H \cdot }$. Finally, (if $X_{T_1} \ne d$), $X_t \equiv j$ on $[T_1,T_2)$ with $T_2$ (and $j \in \{S^1,D\}$) having cumulative hazard function $A_{j\cdot }(t+T_1)- A_{j\cdot }(T_1)= \lambda _{j\cdot } t$ (i.e. $T_2 \sim Exp(\lambda _{j \cdot })$). In $t=T_2$, $\textbf{X}$ migrates from j to $k \in \{D, d\}$ with $p_{jk}$. Then (if $X_{T_2} \ne d$), $X_t \equiv D$ on $[T_2,T_3)$ with $T_3$ having cumulative hazard function $A_{Dd}(t+T_2)- A_{Dd}(T_2)= - \lambda _{Dd} t$ (i.e. $T_3 \sim Exp(\lambda _{Dd})$).

2.3.2 Selection of true parameter, sample size and birth distribution

For a true parameter $\varvec{\lambda }$ in a realistic region of the parameter space, intensities from the literature are reconciled with results the AOK HCD, anticipating Sect. 2.4. The theoretical relation between incidences and intensities is given by $P(t)=e^{tQ}$ (see e.g. Weißbach et al. 2009, Formula 2), where P(t) denotes the matrix of t-year probabilities $P(X_t=j \mid X_0=h)$. Similar to Section A.1.4, the approximation $e^Q \approx I + Q$ (for Q ‘small’) allows simply replacing the one-year incidences for the intensities. For dementia onset after a stroke (Leys et al. 2005) find a one-year incidence of 7%. The value $\lambda _{S^1 D}$ = 0.07 will be confirmed for the AOK HCD in Sect. 2.4 (Table 3). For dementia onset without a stroke, the AOK HCD result in $\lambda _{H D}$ = 0.02. Similarly, Vieira et al. (2013) collect, but independent of whether a stroke preceded, one-year incidences of 0.008, 0.001 and 0.002 (dependent on the country and age range) for individuals below age 65. The AOK HCD value of 0.02 is larger, but aims at high ages as well and we stick to 0.02.

There are other parameters which are necessary for the simulation, but not of primarily of interest for the main question and will thus not be reported in Sect. 2.4. However, we can still estimate them from the AOK HCD using (8) and compare with the literature. To start with, $\hat{\lambda }_{S^1 d}$ = 0.07; however, van den Bussche et al. (2010) find for Germany, also from some other HCD, that 17% of people die within one year after a stroke. We consider only the first stroke, which explains to some extent the smaller value. We use the value in between 0.1. From the AOK HCD, $\hat{\lambda }_{D d}$ of 9%, whereas Garcia-Ptaceka et al. (2014) find for Sweden from registry data that 11% die each year with dementia. Of course, conceptionally, those that had died from other causes would need to be excluded, but we use as value in between 0.1. From AOK HCD, $\hat{\lambda }_{H S^1}$ = 0.02, whereas Garcia-Ptaceka et al. (2012) find incidences above 0.01 only for French people above age 80 and for Italian and British above the age of 75. We even opt to increase $\lambda _{H S^1}$ slightly further to 1/30 $\approx$ 0.03. For the death intensity without stroke or dementia $\lambda _{H d}$, we did not find a relevant study. Our general death hazard from Appendix A.1.4 is $\lambda$ = 0.035 and we decrease slightly to 1/30. Our final choice is collected in (9) (right-hand side).

As sample sizes we let n$_{\text {all}}$ vary from one to five, ten, 20 (and later 100) thousand people. All are below the sample size latent to the AOK HCD. However, we will see convergence to kick in, so that more computational burden is unnecessary. For the distribution of the age-at-study-begin U, we follow (Weißbach and Wied 2022) and assume the distribution of U to be uniform.

The longer the birth period, the more people are left-truncated, our population is born within 54 years (see Fig. 2). However, to start with, we only use 30 years, i.e. $U \sim U[0,30]$. Combined with (9), on average, 48.7% in the simulated samples are unobserved due to left-truncation.

2.3.3 Interpretation

The number of simulation replications is 10,000. The simulation results in Table 2 (top) confirm consistency of $\hat{\varvec{\lambda }}$. Especially the root mean squared error drops, as a function of the sample size. The simulation averages of $\hat{\lambda }_{\text {HD}} - \lambda _{\text {HD}}$ (and similarly for transitions $S^1D$) reveal a generally small bias.

Table 2 Simulated bias (Bias) and root means squared error (rMSE) for (6) (top panel) and (8) (bottom panel) and actual level for confidence interval at the nominal level of 95% for $\lambda _{\text {HD}}$ and $\lambda _{S^1D}$ (top panel) (8) (n $\approx$ 0.513 $\times$ n$_{\text {all}}$, $\varvec{\lambda }$ of (9))

The standard error (8) can also be suspected to be consistent (see Table 2, bottom), without a formal proof in the above section. Simulations show similar behaviour for all other $\hat{\lambda }_{hj}$ (and their standard errors). The actual level of the confidence interval is close to the nominal.

To mimic our population of birth cohorts 1900 to 1953, we now use $U \sim U[0,54]$, and again (9). We chose n$_{\text {all}}$ = 100,000, being still below the sample size behind the AOK HCD, and run (only) 2000 simulation replications now. The left and middle panel of Fig. 4 confirm the asymptotic normality of $\hat{\lambda }_{\text {HD}}$ and $\hat{\lambda }_{S^1D}$ (of (6)) stated in Theorem 1. The theorem also states asymptotic independence of the two estimators, which will be important when subsequently deriving a confidence interval for the difference. The simulated correlation $corr(\hat{\lambda }_{\text {HD}}, \hat{\lambda }_{S^1D})$ = -0.02 confirms the independence.

Fig. 4

Distribution of estimators (6) of dementia intensities $\lambda _{\text {HD}}$ = 0.02 and $\lambda _{S^1D}$ = 0.07 (left/middle, $\approx$ 80% truncated units) and of estimator (A4) for death hazard $\lambda _0$ = 0.02 (right, 40,000 uncensored observations), kernel smoothed from 2000 simulated samples with each n = 250,000 observations (Explanation of panels and symbols is distributed over larger parts of text)

2.4 Result for AOK HCD

As the population, we consider the 76 million people born in Germany between 01/01/1900 and 31/12/1954 (see Fig. 2). The data, i.e. the truncated sample, was described in Sect. 1.1. We only remind readers here on the number of observations n = 236,039, and on the maximally observed timespan $\tau$ := 54+10 = 64 years (after a person’s 50th birthday). By doing so, n persons are at most followed until the age of 114 (see Fig. 8). The least possibly observed lifetime is just above 50 years, for a person turning 50 shortly before 01/01/2004 and dying shortly thereafter. Preliminary results for the lifetime state model are in Appendix A.2, where the hazard rate of the lifetime has been modelled, and we expand our perspective now to the history of vascular diseases. We start from the logarithmic conditional likelihood (5) for the model introduced during Sect. 2.1. In the disease history model pursued here, in contrast to ‘Mortality of Diabetics in the County of Fyn’ (see Andersen et al. 1993), the age-at-study-begin, U, is linked to the age-at-study-end by U + 10 (compare Andersen et al. 1993, Examples III.3.6, IV.1.7 and VI.1.4P). As in Hbid et al. (2020), we compare $\lambda _{\text {HD}}$ to $\lambda _{S^1D}$. The data cover the information relating 34,012 people with dementia onset in the monitoring period, split into 6275 after a stroke, and 27,737 not preceded by a stroke (see Table 3). Already with a stroke until 2004, 5864 persons (see Table 1) must be combined with 19,201 with newly diagnosed strokes between the third quarter 2004 and the end of 2013.

Table 3 Statistics, point estimates (6) and standard errors (SE, (8)) for age-homogeneous model

Point estimates (6) and standard errors (roots of (8)) are given in Table 3. Note that the 1,724,296 person-years at dementia risk of Table 1 are split into 85,645 after at stroke and 1,638,651 without a stroke. Even though 6275 dementia cases after a stroke does not appear to be very large, compared to the overall 25 thousand stroke cases, we find that a stroke increases the intensity of suffering from dementia from $\hat{\lambda }_{\text {HD}}$ $\approx$ 0.02 to $\hat{\lambda }_{S^1D}$ $\approx$ 0.07. Due to the asymptotic independence of both estimators, by Theorem 1, it is $Var(\hat{\lambda }_{S^1D}-\hat{\lambda }_{\text {HD}}) = Var(\hat{\lambda }_{S^1D}) + Var(\hat{\lambda }_{\text {HD}})$ and (see Table 3) estimated to be 0.00093$^2$ + 0.000102$^2$ = 8.6 $\times$ 10$^{-7}$. Hence, approximately $\hat{\lambda }_{S^1D}-\hat{\lambda }_{\text {HD}} \sim N(\lambda _{S^1D0}-\lambda _{HD0}, 0.000927^2)$, so that an approximate 95%-confidence interval of the intensity difference is [0.055 ± 0.00181] = [0.053,0.057]. As the aim of the study is to determine whether having had a stroke has an effect on dementia onset, the corresponding Wald-test rejects, at the 5% level, because the confidence interval does not overlap with zero. This is equivalent to the statement that the absolute of the standardised intensity difference, as test statistics, exceeds the 97.5% quantile of the normal distribution. The generalisation to the age-inhomogeneous model, in Sect. 3.1, will build on the equivalent formulation, that the squared test statistic exceeds the 95% quantile of the $\chi ^2_1$ distribution.

As a comparison, Desmond et al. (2002) reveal an increased relative risk (RR) for dementia of 3.8 after a stroke, adjusted for several demographic factors and cognitive status. Note that the similarity of incidences and intensities, argued in Sect. 2.3.2, enables comparing an RR, as the ratio of incidences, directly with a ratio of intensities. Our unadjusted intensity ratio is 0.072/0.017=4.2. Within the Framingham Study (Ivan et al. 2002), the adjusted RR of dementia with respect to stroke is estimated to be 2.0. The Rotterdam Study (Reitz et al. 2008) also indicates that a stroke doubles the risk of dementia (hazard ratio: HR=2.1). A systematic review and meta-analysis reveals a pooled HR of between 1.7 and 2.2 (Kuźma et al. 2018). Another result, but without multi-states, is that of Savva and Blossom (2010), who report a hazard ratio of 2. Based on South Korean HCD, and also using multi-state methods, Kim and Lee (2018) find a 2.4-fold risk of subsequent dementia after a stroke. Our intensity ratio of 4.2 exceeds the more recent studies, presumably because they adjust for covariates. We now, as the first covariate, adjust for age using age-inhomogeneous, namely piecewise-constant, intensities. We will see that the effect of a stroke on dementia onset becomes markedly smaller because of confounding and Simpson’s paradox: Simultaneously, intensities increase with age, and a stroke is more likely at higher ages.

3 Confounders

In Sect. 2, the probability of suffering either event, stroke or dementia onset, has been equal for all ages and independent of any other factor. Morbidity intensities vary with age, and in order to compare our results for Germany later in Sect. 3.1.2 internationally, we derive a model in Sect. 3.1 that adjusts for age inhomogeneity. Also, a risk-increasing effect of stroke on the dementia hazard might not be causal in the following sense. Assume that one group has a vascular predisposition and that a stroke (mainly) indicates the membership to that group. The information about the predisposition could have been achieved earlier and a stroke should not trigger additional medical effort with regard to dementia prevention. We aim in Sect. 3.2 at classification according to vascular predisposition.

3.1 Adjusting for age

We define (as in Weißbach et al. 2009; Weißbach and Walter 2010), for a partition $0=t_0, \ldots , t_b=\tau$, $\textbf{X}$ as a Markov process with piecewise constant intensities

$$\begin{aligned} \lambda _{hj}(t) := \sum _{l = 1}^b \mathbbm {1}_{[t_{l-1},t_l)}(t) \lambda _{hjl}. \end{aligned}$$

(10)

We do give neither the self-contained analysis of the lifetime state model of Appendix A, nor the still complete analysis of the age-homogeneous disease state model in Sect. 2. We restrict the display to the statement of the conditional likelihood and derive the estimator. The asymptotic arguments are developed to the extent that the standard errors can be derived.

3.1.1 Point estimate and standard error

The same two counting processes $N_{hj}(t)$ and $Y_h(t)$ of Sect. 2.1, reformulate a history. When stacking $\lambda _{hj}(t)$ to $\varvec{\lambda }(t)$ in the same way as $N_{hj}$ to $\textbf{N}_X$, $\textbf{N}_X$ has a compensator - with respect to ${\mathcal {N}}_t$ - with intensity $\varvec{\alpha }(t):=(Y_h(t) \lambda _{hj}(t), hj \in {\mathcal {I}})'$. The compensator is with respect to the probability measure $\tilde{P}_{\varvec{\lambda }}$, where $\varvec{\lambda }:= (\lambda _{HS^11}, \ldots , \lambda _{Ddb})'$ collects the 6b parameters.

Theorem 2

For model (10) and under regularity assumption similar to Theorem 1, the conditional maximum likelihood estimators, similar to (6), for the time interval $[t_l,t_{l-1}]$ are

$$\begin{aligned} \hat{\lambda }_{hjl} = A_{hj,l}/B_{h,l}, \end{aligned}$$

(11)

with transition counts $A_{hj,l}$ and time-at-risk $B_{h,l}$, per age-group:

$$\begin{aligned} A_{hj,l}:= & {} \sum _{{\mathop {[t_l,t_{l-1}) \cap [U_i,U_i+10) \ne \emptyset }\limits ^{i=1}}}^n\left[ {}_U{N}^c_{hji} (U_i+10 \wedge t_l) - {}_U{N}^c_{hji} (U_i \vee t_{l-1})\right] \\ B_{h,l}:= & {} \sum _{{\mathop {[t_l,t_{l-1})\cap [U_i,U_i+10) \ne \emptyset }\limits ^{i=1}}}^n \int _{U_i \vee t_{l-1}}^{U_i+10 \wedge t_l} {}_U{Y}_{hi}(t) dt \end{aligned}$$

Moreover, $\sqrt{n_{all}}(\hat{\varvec{\lambda }} - \varvec{\lambda }_0)$ converges in distribution to the central Gaussian distribution. The corresponding Hessian of the logarithmic conditional likelihood is a diagonal matrix with diagonal elements

$$\begin{aligned} - {\mathcal {J}}_{\tau }(\varvec{\lambda }_0)_{hjl,hjl} = \frac{\partial ^2}{\partial \lambda _{hjl}^2} \ln {}_U{L}^c(\text{data} \mid \varvec{\lambda })\mid _{\varvec{\lambda }=\varvec{\lambda }_0} = - A_{hj,l}/\lambda _{hjl^0}^2. \end{aligned}$$

Standard errors are hence similar to (8):

$$\begin{aligned} \widehat{Var(\hat{\lambda }_{hjl})} = A_{hj,l}/B_{h,l}^2 \end{aligned}$$

(12)

Proof

With little change, compared to (4), the conditional likelihood contribution is

$$\begin{aligned} \begin{aligned} \ln {}_U{L}^c(\textbf{X},U \mid \varvec{\lambda }) =&\int _U^{U+10} \sum _{hj \in {\mathcal {I}}} (\ln {}_U{Y}_h(t) + \ln \lambda _{hj}(t)) d {}_U{N}^c_{hj} (t) \\&- \sum _{hj \in {\mathcal {I}}} \int _U^{U+10} {}_U{Y}_h(t) \lambda _{hj}(t) dt. \end{aligned} \end{aligned}$$

(13)

Note that there are five possibilities for the intersection of $[t_l,t_{l-1})$ with $[U,U+10)$ (see Fig. 5), so that for the N-term (with $a \vee b := \max (a,b)$) for $[t_l,t_{l-1}) \cap [U,U+10) \ne \emptyset$ (0 else)

$$\begin{aligned}{} & {} \int _U^{U+10} \frac{\partial }{\partial \lambda _{hjl}} \ln \left( \sum _{\tilde{l}=1}^b \mathbbm {1}_{[t_{\tilde{l}-1},t_{\tilde{l}})} (t) \lambda _{hj\tilde{l}} \right) d {}_U{N}^c_{hj} (t) \\{} & {} \quad = \int _U^{U+10} \frac{\mathbbm {1}_{[t_{l-1},t_l)} (t)}{\sum _{\tilde{l}=1}^b \mathbbm {1}_{[t_{\tilde{l}-1},t_{\tilde{l}})} (t) \lambda _{hj\tilde{l}}} d {}_U{N}^c_{hj} (t) \\{} & {} \quad = \int _{U \vee t_{l-1}}^{U+10 \wedge t_l} \frac{1}{\lambda _{hjl}} d {}_U{N}^c_{hj} (t) = \frac{1}{\lambda _{hjl}} [{}_U{N}^c_{hj} (U+10 \wedge t_l) - {}_U{N}^c_{hj} (U \vee t_{l-1}) ] \end{aligned}$$

and for the Y-term

$$\begin{aligned}{} & {} - \frac{\partial }{\partial \lambda _{hjl}} \sum _{hj \in {\mathcal {I}}} \int _U^{U+10} {}_U{Y}_h(t) \left( \sum _{\tilde{l}=1}^b \mathbbm {1}_{[t_{\tilde{l}-1},t_{\tilde{l}})} (t) \lambda _{hj\tilde{l}} \right) dt \\{} & {} \quad = - \int _U^{U+10} {}_U{Y}_h(t) \mathbbm {1}_{[t_{l-1},t_l)} (t) dt = - \int _{U \vee t_{l-1}}^{U+10 \wedge t_l} {}_U{Y}_h(t) dt. \end{aligned}$$

Again by (4) with $\varvec{\lambda }$, and comparable to (5), it is $\ln {}_U{L}^c(data;\varvec{\lambda })$ the sum of the contributions (13), so that $(\partial /\partial \lambda _{hjl}) \ln {}_U{L}^c(data \mid \varvec{\lambda }) = A_{hj,l}/\lambda _{hjl} - B_{h,l}$, by interchanging differentiation and summation. For the multi-state Markov model with right-censoring (but without left-truncation), the proof of the asymptotic normality (assuming consistency) for the piecewise constant-intensity model (10) is found in Weißbach and Walter (2010). A simplified proof for consistency is found in Weißbach and Mollenhauer (2011). It is to be expected that the proofs easily generalise to the case of left-truncation, because, similarly, a Doob–Meyer decomposition of the counting process into compensator and martingale is applied and enables the martingale limit theorem. $\square$

Fig. 5

Possible intersections of $[t_l,t_{l-1})$ and $[U,U+10)$, possible situation for $\kappa$ in Sect. 3.2.1

3.1.2 Result for AOK HCD

The population and data, including the number of observation n, all remain the same as in the age-homogeneous model of Sect. 2. Section 2.4 revealed an effect of stroke on dementia onset that by far exceeds findings in contemporary epidemiology. An age-inhomogeneous dementia intensity has already been confirmed for the AOK HCD in Weißbach et al. (2021) and we now apply the piecewise constant intensities (10). Table 4 and Fig. 6 exhibit point estimates, standard errors and confidence intervals, due to (11), (12) and the generalisation of Theorem 1 with age intervals covering five years, i.e. with b = 12 pieces (see Table 4, column (1)).

Table 4 Statistics (columns (2),(3),(5),(6)), point estimates with standard errors (SE) (Formulae: (11) and root of (12)) (columns (4),(7)) and intensity ratio (column (8)) for 5-year age-classes (Oldest class [110-114) has no stroke or dementia events)

Fig. 6

Age-inhomogeneous intensity from stroke ($S^1$) to dementia onset (D) $\hat{\lambda }_{S^1D}(t)$ (top, grey) and healthy (H) to dementia onset (D) $\hat{\lambda }_{\text {HD}}(t)$ (bottom, black) on 5-year intervals: Point estimate ((11), solid line) and 95% confidence interval ((12), dashed line)

For instance, in the age-group with the most dementia events, namely from 80 to 85 years, the dementia intensity after a stroke of $\hat{\lambda }_{S^1D7}$ = 0.117 exceeds that without a stroke of $\hat{\lambda }_{HD7}$ = 0.047 (see framed numbers in Table 4). The ratio of 2.5 is now two thirds of the ratio 0.072/0.017 = 4.2 of Table 3, and more in line with the recent literature, e.g. of 2.4 for Korea, as reported by Kim and Lee (2018). The reason is Simpson’s paradox; the age-homogeneous $\hat{\lambda }_{S^1 D}$ $\approx$ 0.07 of Sect. 2.4 is implicitly an average over a later part of the time span $[0,\tau ]$ where dementia onset is generally more likely. That is, a stroke generally occurs at higher ages, so that the denominator in the stroke-specific point estimator (6), starts accumulating ‘time at risk’ at a high age. The higher dementia intensity at such ages then results in many events in the numerator of point estimator (6), not attributable to the stroke event. This defect is resolved by the age-specific ratios in (11). And the defect does not balance when calculating the relative risk, because the defect does not affect the healthy persons’ intensity $\hat{\lambda }_{\text {HD}}$.

The aim of the study is to determine whether a stroke has an effect on dementia. Following up on the arguments in Sect. 2.4, consider the squared test statistics for each of the b = 12 time intervals, and add those. Thus the sum for the 12 differences is distributed as $\chi ^2_{12}$, due to the independence between estimation differences, which must also hold in analogy to Theorem 1 for age-inhomogeneity, as the proof of Weißbach and Walter (2010, Theorem 1) suggests. The 95% quantile of the $\chi ^2_{12}$-distribution is 21.026 and the test statistic (using (12))

$$\begin{aligned} \sum _{l=1}^b \left( \frac{\hat{\lambda }_{S^1Dl}-\hat{\lambda }_{HDl}}{ \sqrt{\widehat{Var(\hat{\lambda }_{S^1Dl})} + \widehat{Var(\hat{\lambda }_{HDl})}}} \right) ^2=2413, \end{aligned}$$

so that the test is significant.

In order to explore the role of age further, we may notice a decreasing stroke-effect in age, measured in ratios. In the age group of the 55–60 year olds, the intensity ratio is 9.4 (see last column in Table 4). The higher the age, the smaller the intensity ratio. This coincides with the Framingham Study (Ivan et al. 2002) where the adjusted RR was higher for those younger than 80 (RR=2.6), compared to those aged 80 or older (RR=1.6). The b = 12 age-specific Wald-type tests for pairwise differences (suppressed here) show that there is no significant difference in the risk of dementia between persons with and without a stroke for the highest age groups (90 years and older). Similarly, the systematic review by Savva and Blossom (2010) also does not find an excess risk of dementia after a stroke in those aged 85 years or older.

3.2 Adjusting for multi-morbidity

Classification according to multi-morbidity at the time origin, i.e. at the age of 50, would impose a random dichotomous Z, but is not observed as some people are older in 2004. Moreover, multi-morbidity is age dependent, as acquisition of the first and second vascular disease could take place at any age after age 50. A time-dependent covariate $Z(t)=\mathbbm {1}_{\{[\text {age at the second disease onset},\tau )\}}(t)$ is necessary. For a dichotomous covariate, the additive model $\lambda ^{wo}_{hjl}+ \tilde{\beta }_{hjl}Z(t)$, as in Kremer et al. (2014, Formula 5), or the multiplicative $\lambda ^{wo}_{hjl}e^{\beta _{hjl}Z(t)}$ (Andersen et al. 1993, Formular 7.6.2) are equal and we may write the model as piecewise constant. Theory for an additive model and a fixed z is derived in Kremer et al. (2014), for a lifetime state model with left-censoring. For the multiplicative model and right-censoring, Borgan (1984, Theorem 2) derives the asymptotic distribution of the estimator. The full theory for left-truncation will not be reported here, only the point estimator and standard error shall be given. Observable data require a random Z, as usual, and we assume that the distribution of Z does not depend on $\varvec{\lambda }$ and condition again (after conditioning on U, $\mathbbm {1}_A$ and $X_0$) on Z. For the ease of notation, define the age of multi-morbidity onset as $\kappa :=\min \{t: Z(t)=1\}$. We refrain from developing an age-homogeneous model and directly follow up on Sect. 3.1 model age-inhomogeneously.

3.2.1 Point estimate and standard error

For each person only one additional split on one of the constant intensities pieces is necessary. For $\kappa$ before U or after U + 10, no further distinction is necessary (see Fig. 5). The idea is that a person now contributes to the estimation of a set of parameters without multi-morbidity, $\lambda ^{wo}_{hjl}$, , i.e. to the transition counts and the at-risk-times, until that $\kappa$. After the split, a set of parameters with multi-morbidity, $\lambda ^w_{hjl}$, is estimated. All parameters are collected in $\varvec{\lambda }$. In detail, conditional on $Z=z$ we define

$$\begin{aligned} \lambda _{hj}(t,z(t)) := \sum _{l = 1}^b \mathbbm {1}_{[t_{l-1},t_l)}(t) \left( \mathbbm {1}_{[0,\kappa )}(t) \lambda ^{wo}_{hjl}+ \mathbbm {1}_{[\kappa , \infty )}(t)) \lambda ^{w}_{hjl} \right) . \end{aligned}$$

(14)

Theorem 3

For model (14) and under regularity assumption similar to Theorem 2, the conditional maximum likelihood estimators are

$$\begin{aligned} \hat{\lambda }^{wo}_{hjl}= A^{wo}_{hj,l}/B^{wo}_{h,l} \quad \text {and} \quad \hat{\lambda }^w_{hjl}= A^w_{hj,l}/B^w_{h,l} \end{aligned}$$

(15)

with event counts $A^{wo}_{hj,l} := \sum _{i=1}^n ({}_U{N}^c_{hji} ((\kappa _i \wedge t_l) \vee t_{l-1}) - {}_U{N}^c_{hji} (t_{l-1}))$ and $A^w_{hj,l} := \sum _{i=1}^n ({}_U{N}^c_{hji} (t_l) - {}_U{N}^c_{hji} ((t_{l-1} \vee \kappa _i) \wedge t_l))$, as well as times at risk $B^{wo}_{h,l} := \sum _{i=1}^n \int _{t_{l-1}}^{(t_l \wedge \kappa _i)\vee t_{l-1}} {}_U{Y}_{hi}(t) dt$ and $B^w_{h,l} := \sum _{i=1}^n \int _{(t_{l-1} \vee \kappa _i) \wedge t_l}^{t_l} {}_U{Y}_{hi}(t) dt$.

The proof is in Appendix C. The squared standard errors are, similar to (12), $A^{wo}_{hj,l}/(B^{wo}_{h,l})^2$ and $A^w_{hj,l}/(B^w_{h,l})^2$.

3.2.2 Result for AOK HCD

Incorporating multi-morbidity by model (14), two tables that are similar to the unstratified Table 4, for the two groups with and without multi-morbidity are now given jointly in Table 5. Comparing the fourth and seventh columns, the dementia onset intensity is again larger when having had a stroke, as in the age-homogeneous model (of Sect. 2) and in the age-inhomogeneous model (of Sect. 3.1). Comparing the first and second rows, multi-morbidity does increase the dementia intensity, but by much less than a stroke does.

Table 5 Statistics as in Table 4 for point estimates (15) and standard errors (SE), 1st row without multi-morbidity $\hat{\lambda }^{wo}_{hjl}$, 2nd row with multi-morbidity $\hat{\lambda }^w_{hjl}$ (result above age 100 are too small to be reported)

The graphical analysis of the estimates (15) and confidence intervals (compare to Fig. 6 for age-inhomogeneous model) are displayed in Fig. 7. If multi-morbidity were a predominant predictive factor, a stroke would now not increase the dementia incidence. This is not the case, as the middle panel shows. The two panels (left and middle) reveal little differences between the stroke effect, comparing the strata (apart from larger confidence intervals, because group sizes are smaller than in Fig. 6). The differences $\lambda ^{wo}_{S^1Dl}-\lambda ^{wo}_{HDl}$ and $\lambda ^w_{S^1Dl}-\lambda ^w_{HDl}$ appear to be equal, and also equal to the unstratified difference $\lambda _{S^1Dl}-\lambda _{HDl}$ (right panel), hereby strongly suggesting that a stroke is a risk factor irrespective of multi-morbidity. It is tempting to construct a $\chi ^2$-test for the global hypothesis that a stroke is a significant risk factor, similar to that at the end of Sect. 3.1.2. However, it is not clear that the diagonal structure of the asymptotic variance-covariance matrix holds. Recall that in the linear regression, a regressor introduces dependence between the parameter estimators (see e.g. Bleymüller et al. 2020, Sect. 21.2 or 23.3).

Fig. 7

Estimates (15) for intensity model (14) as in Table 5 without multi-morbidity (left) from stroke ($S^1$) to dementia onset (D) $\lambda ^{wo}_{S^1Dl}$ (top, grey) and healthy (H) to dementia onset (D) $\hat{\lambda }^{wo}_{HDl}$ (bottom, black), intensity with multi-morbidity $\lambda ^w_{S^1Dl}$ and $\hat{\lambda }^w_{HDl}$ (middle) - (dashed: confidence intervals); and differences thereof $\lambda ^{wo}_{S^1Dl}-\lambda ^{wo}_{HDl}$ (right, dashed), $\lambda ^w_{S^1Dl}-\lambda ^w_{HDl}$ (right, dotted), combined with un-stratified from Table 4$\lambda _{S^1Dl}-\lambda _{HDl}$ (right, solid)

4 Discussion

In principle, left-truncation can be avoided by starting the observation period at the starting date of the population (as described in Weißbach et al. 2009). In the current context, this translates into defining the population as all people born after 01/01/1954. However, not only will the (many) events of stroke and dementia-onset for people born before 1954 be then un-analysed, the population will also not be of current interest, because dementia is a disease of old-age. More critical is that the similarity of the stroke effect from Sect. 3.1 to that of the related study in Kim and Lee (2018) for South Korea is authoritative, because the latter study takes more covariates into account. Multicollinearity can change the effect sizes. In addition, integrating exogenous continuous covariates in our left-truncated event history analysis other than the dichotomous covariate we considered, poses analytically and algorithmically new questions (see e.g. Kim et al. 2012). Also critical is that we assume three sorts of independence. First of all, we assume it within pairs $(T_i,U_i)$, even though this is likely to be untrue in our case study, because U is an affine transformation of the birthdate. Demographers typically assume younger cohorts to tend towards higher life expectancy. Theory about dependent truncation is currently developed in Emura and Pan (2020); Tanzer et al. (2021); de Uña-Álvarez and van Keilegom (2021); Rennert and Xie (2021). For dependent truncation, the truncation time distribution is essential, and different distributions are studied in Weißbach and Dörre (2022). Second, we can assume independence between pairs $(T_i,U_i)$, due to our data being a sample. However, for an observational study of event histories, stochastic independence must be concluded from irrelevance of the birthdate, as do Kaplan and Meier (1958). Third, close to longitudinal independence, probably the most critical assumption of our modelling strategy seems to be the Markovian. This is especially the case, as Pendlebury and Rothwell (2009) and Corraini et al. (2017) claim that the time elapsed since a stroke is a risk factor for the intensity of dementia onset. Such duration-dependence especially violates the assumption of multiplicative intensities (B8) and thus requires a different approach (see e.g. Weißbach and Schmal 2019). Another critical point is that, after the first age axis (time-since-birth) and the second axis (time-since-observation-start), a potential third time-dependent component is the cohort trend, found in Weißbach et al. (2021) for the same data, or in Kremer et al. (2014), for another dataset. Assuming steady health progress, here for Germany, the given intensity estimates must be interpreted as intensities averaged over cohorts, and are too high for today and are presumably lower for current/future cohorts. Differences, and hence the stroke effect, could still be valid.

Appendices

Appendix A: Lifetime state model

The population, the sample of size n$_{\text {all}}$, and among those, the n people not truncated, are as described in Sect. 2. Death before age 50 is considered impossible, i.e. has hazard zero. Let t, as in Sect. 2, count the years after a person’s 50$^{th}$ birthday. Of interest is the lifetime T after the 50$\text{th}$ birthday, called ‘age-at-death’ in the following (see Fig. 8). Assume hazard rate $\lambda _E(\cdot ) \equiv \lambda$ (i.e. T is Exponentially distributed) and CDF $F_E(\cdot )$.

Fig. 8

Three cases of the date of birth (white bullet), date of death (black circle), observed duration (solid line) and unobserved duration (dashed line). Top (observed person): Path for person born 1/1/1925 with death 01/01/2009, i.e. with T = 84–50, u (or U) $\le T \le u$ (or U) +10 Middle (un observed person): Path for person born 1/1/1915 with death 01/01/2000, i.e. with T = 85–50, $T < u$ (or U), u (or U) = 89–50 Bottom (partially observed person): Path for person born 1/1/1915 with death 1/1/2015, i.e. with T = 100–50, $T \ge u$ (or U) + 10, u (or U) + 10 = 99–50 (Explanation of graphs and symbols is distributed over larger parts of text)

For a person randomly drawn from the population, T is defined on the probability space $(\Omega , {\mathcal {F}}, P_{\lambda })$.

• (A1) It is for the true parameter $\lambda _0 \in \Lambda :=[\varepsilon ;1/\varepsilon ]$ for some small $\varepsilon \in (0;1)$.

The population is further described as second measurement, by the time elapsed for a person since the age of 50 at study begin, U, denoted ‘age at study begin’ (see Fig. 8). It is an affine transformation of the birthdate. The distribution of U will not be important. We observe over 10 years.

1.1 A.1 Filtration and conditional likelihood contribution

It is well-known for a simple random sample, that the maximum likelihood estimator for $\lambda$ is a ratio, where each person contributes a numerical one to the numerator and the observed time at risk, T, to the denominator. To be at risk or not, at a specific age, is formally $Y(t):= \mathbbm {1}_{\{T \ge t \}}$.

1.1.1 A.1.1 Non-random left-truncation and right-censoring

To start with, we assume u to be deterministic and known for any person in the sample. This is unrealistic for the AOK HCD and will be relaxed in Section A.1.2. Left-truncation means for an observable person (top path in Fig. 8) to be observably at risk of death only from 01/01/2004 on, i.e. $T-u$ = 34–29 = 5 years. The person should now contribute to the numerator of $\lambda$ estimator still with a numerical one, but to the denominator no longer with T, but only with $T-u$. Observing a person at all (whatever u), is indication of a small $\lambda$ and not observing a person is indication of a larger $\lambda$. Hence any left-truncated person (middle path in Fig. 8) must enter the likelihood, although we do not see its measurement T. Note that by assumption we still know how many, $n_{all} - n$, there are. The full maximum likelihood approach is worked out in Weißbach and Wied (2022).

Instead, we decide now to start observation at the age of u. When we express the lifetime T by the counting process $N_T(t):=\mathbbm {1}_{\{T \le t\}}$ (for $t \in {\mathbb {R}}^+$) (similar for $\textbf{X}$ in Sect. 2.1), this means we use the probability measure of $N_T$ after u, namely use a marginal likelihood (see Gouriéroux and Monfort 1995, Definition 7.2(i)).

In addition to ${\mathcal {F}}$, which describes the possible outcomes of T, potential outcomes of $N_T$ may use ‘being in t’, i.e. knowing the path until t, and require age-specific sigma-algebras, i.e. a filtration ${\mathcal {N}}_t:=\sigma \{\mathbbm {1}_{\{T \le s\}}, 0 \le s \le t\}$.

Reducing attention, in the stochastic process corresponds to a coarser filtration. (Increasing the filtration will be necessary when the random U introduces more information.) By starting attention at the age of u, earlier outcomes are deleted from the model, formally $\{ \emptyset , 0 \le s < u\}$. The remainder and observed filtration is now

$$\begin{aligned} {}_u{{\mathcal {G}}}_t := \sigma \{ \mathbbm {1}_{\{u \le T \le s\}}, u \le s \le t\}. \end{aligned}$$

For $T < u$ a person is truncated (middle path in Figure 8), i.e. $N_T(u)=1$, and no observable development will occur after u. Observable is, truncated or not, ${}_u{N}_T(t):=N_T(t) - N_T(\min (t,u))$, i.e. ${}_u{N}_T$ is $N_T$ if $u \le T$ and constantly zero otherwise. Note that ${}_u{{\mathcal {G}}}_t = \sigma \{{}_u{N}_T(s), u \le s \le t\}$.

A likelihood is a density, similarly, the marginal likelihood is the marginal density starting from u, with respect to some dominating measure. (The marginal density is then evaluated at the observed data.) The $N_T$, but also ${}_u{N}_T$, can be regarded as collection of Bernoulli increments (simplifying multinomial increments of $\textbf{X}$ in Sect. 2.1). The random measure of an experiment will usually contain the location, and for a Bernoulli-experiment, only the expectation. Over infinitely short intervals, expectations of the increments define the intensity process. After a deterministic u, intuitively, the expected increase of ${}_u{N}_T$ over an interval of length dt, at age t, is $\lambda dt$ if death is not reached, i.e. $t \le T$, and if the person is no left-truncated, i.e. in case of $A:=\{T > u\}$. Else it is zero. We assume $P_{\lambda }(A) > 0$. Formally, the intensity process of ${}_u{N}_T(t)$ after u is ${}_u{\alpha }(t):=\mathbbm {1}_{\{u < t \le T\}} \lambda$, with respect to the dominating probability measure

$$\begin{aligned} P^{A}_{\lambda }(F):= \frac{P_{\lambda }(F \cap A)}{P_{\lambda }(A)}, \quad \text {for} \quad F \in {\mathcal {F}}, \end{aligned}$$

that conditions on A. Due to the zero-intensity of a truncated person (Fig. 8, middle), the marginal likelihood contribution is one, i.e. ineffective. Hence even not observing the person, as will be the realistic case of the random U in Section A.1.2, still renders the marginal likelihood observable. That the dominating measure depends on $\lambda$ can be interpreted as information loss (for the untruncated person), ‘remaining’ in the dominating measure. For a proof that ${}_u{N}_T$, reduced by $\int _u^t{}_u{\alpha }(s) ds$, really is a $(P_{\lambda }(A),{}_u{{\mathcal {G}}}_t)$-martingale, with deterministic u, see Proposition 4.1 in Andersen et al. (1988).

Extending ${}_u{{\mathcal {G}}}_t$ to censoring will end this section, and is needed in our case study. Right-censored is the age-at-death if it occurs after 2013, or after having left the AOK (see Figs. 2 and 8, bottom). As in Andersen et al. (1993, Examples III.3.6, IV.1.7 and VI.1.4) we superimpose right-censoring on left-truncation. The observed left-truncated and right-censored counting process is the Stieltjes integral ${}_u{N}^c_T(t) := \int _0^t C(s) d {}_u{N}_T(s)= \mathbbm {1}_{\{u \le T \le \min (t, u+10)\}}$ with $C(t):= \mathbbm {1}_{\{t \le u+10\}}$ (compare Fleming and Harrington 1991, Example 1.4.2). It has intensity ${}_u{\alpha }_T^c(t) := \lambda \mathbbm {1}_{\{u \le t \le \min (T,u+10) \}}$ with respect to $P^A_{\lambda }$ and observed filtration

$$\begin{aligned} {}_u{{\mathcal {F}}}^c_t := \sigma \{{}_u{N}^c_T(s), u \le s \le t\}= \sigma \{\mathbbm {1}_{\{u \le T \le \min (s, u+10)\}}, u \le s \le t\}. \end{aligned}$$

The ${}_u{{\mathcal {F}}}^c_t$ is self-exciting (see Andersen et al. 1988, p4), as required (see Andersen et al. 1988, p23), so that the density is determined by Jacod’s formula (see Andersen et al. 1988, Formula 4.3), (see also Andersen et al. 1993, Formula 2.7.2” (and in extension 3.2.8)):

(A1)

For an explanation of the second and third line, see page 24 and, respectively, Example 2.2 in Andersen et al. (1988). For the first line note that whatever process Z, one defines $d Z(t):= Z(t)-Z(t - dt)$ for some ‘small’ dt (see Fleming and Harrington 1991, Section 1.4), here $d{}_u{N}_T^c(t) \equiv 0$. And also $\mathbbm {1}_{\{u \le T \le \min (t,u+10)\}} \equiv 0$. Note that the exponential function arises similar to $e^x=\lim _{dt \rightarrow 0} (1+ x dt)^{dt^{-1}}$.

Independent persons are, due to different $u_i$, not identically distributed. Each density is a Radon-Nikodym derivative with respect to a different measure, all of which are even dependent on the parameter, $P_{\lambda }^{A_i}$. Even worse, measures are conditional on observation. That the density for a collection of independent persons is the product of the persons’ densities (see e.g. Bleymüller et al. (2020, Sect. 8.2) or Feller (1971, Sect. III.1.Example(a))), relies on the equal (and parameter-independent) dominating measure (usually being Lebesgues). To achieve equal dominating measures for all persons, we will and can follow Examples IV.1.7 and VI.1.4 of Andersen et al. (1993) in using a random U. Also, if T is considered random, U should equally be, as already argued after (3).

1.1.2 A.1.2 Random left-truncation and conditional right-censoring

Let the probability space for (T, U) be denoted as $(\Omega , {\mathcal {F}}, \tilde{P}_{\lambda })$, where the distribution of U will not be important and we suppress its parameter (and indicate the difference to $P_{\lambda }$ with the tilde instead).

• (A2) U and T are independent and $\beta _{\lambda _0}:=\tilde{P}_{\lambda _0}(A) > 0$ with redefined $A:=\{T > U\}$.

Defer censoring as in Section A.1.1. As is the case for the AOK HCD, we observe durations U and T in the case of A, and neither measurement U nor T - nor the person at all - when $T< U$ (see again Fig. 8). The filtration ${\mathcal {G}}_t := \sigma \{ \mathbbm {1}_{\{T \le s\}}, \mathbbm {1}_{\{U \le s\}}, 0 \le s \le t\}$ is unobservable. We may still start from the ${\mathcal {G}}_t$-intensity, with respect to $\tilde{P}_{\lambda }$ of the bivariate $(N_T(t),\mathbbm {1}_{\{t > U\}})$ (see Andersen et al. 1993, Example III.3.2), being $\lambda \mathbbm {1}_{\{T \ge t\}}$ because U is independent of T. To be at risk after study begin is now formally ${}_U{Y}(t):=Y(t) \mathbbm {1}_{\{t> U\}}= \mathbbm {1}_{\{T \ge t > U\}}$. The intuition is for univariate ${}_U{N}_T(t):=N_T(t) - N_T(t \wedge U)$ is unchanged as compared to that for the fixed u. Due to U being a ${\mathcal {G}}_t$-stopping time, now ${}_U{{\mathcal {F}}}_t:= \{ {}_U{N}_T(s), {}_U{Y}(s), U \le s \le t\}$, is an observable filtration. Precisely, the intensity process of ${}_U{N}_T(t)$ is ${}_U{\alpha }_T(t)=\mathbbm {1}_{\{U < t \le T\}} \lambda$, with respect to ${}_U{{\mathcal {F}}}_t$ and the probability measure $\tilde{P}^{A}_{\lambda }(F):= \tilde{P}_{\lambda }(F \cap A )/\tilde{P}_{\lambda }(A)$, for $F \in {\mathcal {F}}$, by optional stopping. Left-truncation thus preserves the multiplicative intensity form (see Andersen et al. 1988, Proposition 4.1). Now, as ${}_U{{\mathcal {F}}}_t$ is self-exciting, we may again apply Jacod’s formula (see Andersen et al. 1988, Formula 2.1) in order to determine a conditional version of the marginal likelihood (see Andersen et al. (1988), Formula 4.3). It is for $T \le U$ one and else (see Andersen et al. (1988, Example 4.1) or Andersen et al. (1993, Formula 3.3.3 with $\Delta$ instead of d)) .

For acknowledging censoring, first note that now $T > U+10$ is known, conditionally on A, because U is observable. The deterministic censoring renders unnecessary a further increase in filtration. Hence, similar to Section A.1.1, we apply Definition III.2.1 in Andersen et al. (1993), with ${}_U{N}_T$ in the role of N, $({}_U{{\mathcal {F}}}_t)$ in the role of $({\mathcal {F}}_t)$, ${}_U{\alpha }_T$ in the role of $\lambda ^{\theta }$ and $\tilde{P}^{A}_{\lambda }$ in the role of $P_{\theta \psi }$. Being conditionally deterministic, $C(t):= \mathbbm {1}_{\{t \le U+ 10\}}$ is independent and predictable. We define ${}_U{Y}^c(t):=C(t) {}_U{Y}(t)= \mathbbm {1}_{\{U \le t < \min (T,U+10)\}}$, so that ${}_U{N}_T^c(t):= \int _U^t C(s) d {}_U{N}_T(s) = \mathbbm {1}_{\{U \le T \le \min (t,U+10)\}}$ has intensity ${}_U{\alpha }_T^c(t)=\mathbbm {1}_{\{U < t \le \min (T,U+10)\}} \lambda$, with respect to the observable filtration ${}_U{{\mathcal {F}}}^c_t:= \{ {}_U{N}^c_T(s), {}_U{Y}^c(s+), U \le s \le t\}$ and conditional distribution $\tilde{P}^A_{\lambda }$ (see Andersen et al. 1993, Section III.2.2). By Formula 3.2.8 in Andersen et al. (1993), the conditional (marginal) likelihood is for $T \le U$ again one and otherwise:

(A2)

For the second line, similar to $\Delta {}_U{N}^c_T(t)$ from Section 2.1, $d {}_U{N}^c_T(t)$ is only one if ${}_u{N}^c_T(t)$ jumps.

1.1.3 A.1.3 Large sample properties and standard error

We now combine the contribution (A2) for each person i (truncated or not) to the conditional likelihood (‘marginalisation’ will not be mentioned from now on) for the (latent) simple sample of size n$_{\text {all}}$. The number of observations is n := $\sum _{i=1}^{n_{all}} \mathbbm {1}_{A_i}$ (see Fig. 2 and Condition (A2)). Again, those truncated are sorted to the end of the sample. Due to the assumption of a simple sample, the logarithmic conditional likelihood for the data is the sum of logarithms for contributions (A2) (including zeros for the truncated). We denote by N$_{cens}$ := $\sum _{i=1}^n \mathbbm {1}_{\{T_i > U_i+10\}}$ the number of right-censored and by N$_{uncens}$ := n - N$_{cens}$ = $\sum _{i=1}^n \mathbbm {1}_{\{U_i < T_i \le U_i+10\}}$ the number of neither truncated nor censored people and can write $\ln {}_U{\textbf{L}}_{\tau }^c(\lambda )$ as

$$\begin{aligned} \sum _{i=1}^n \ln {}_U{L}_{\tau }^c(\lambda )_i = N_{uncens} \ln (\lambda ) - \lambda \sum _{i=1}^{n} \mathbbm {1}_{\{U_i \le T_i \le U_i +10 \}} (T_i- U_i) - 10 \lambda N_{cens}, \end{aligned}$$

(A3)

so that the unique estimator (if in $\Lambda$, see Condition (A1)) becomes

$$\begin{aligned} \hat{\lambda } =argmax_{\lambda \in \Lambda } \ln {}_U{\textbf{L}}_{\tau }^c(\lambda ) = \frac{N_{uncens}}{\sum _{i=1}^{n} \mathbbm {1}_{\{U_i \le T_i < U_i+10\}} (T_i- U_i) + 10 N_{cens}}. \end{aligned}$$

(A4)

For our parametric model, we assume

• (A3) $\int _0^{\tau } \tilde{P}_{\lambda }(U < t \le \min (T,U+10)\mid A)dt > 0$.

Theorem 4

Under Conditions (A1)-(A3) it is $\hat{\lambda }$ of (A4) consistent and $\sqrt{n_{all}}(\hat{\lambda } - \lambda _0) {\mathop {\longrightarrow }\limits ^{{\mathcal {D}}}} {\mathcal {N}}(0,\sigma ^{-1}(\lambda _0))$, for $n_{all} \rightarrow \infty$, with

$$\begin{aligned} \sigma (\lambda _0): = \frac{\beta _{\lambda _0}}{\lambda _0} \int _0^{\tau } \tilde{P}_{\lambda _0}(U < t \le \min (T,U+10)\mid T > U) dt. \end{aligned}$$

Proof

Due to the uniqueness of $\hat{\lambda }$, for both consistency and asymptotic normality, we need to verify Conditions (A)-(E) of Andersen et al. (1993, Theorems VI.1.1+2). In order to map the notations, note that n becomes n$_{\text {all}}$, $a_n:= \sqrt{n_{all}}$, $\varvec{\theta }$ becomes $\lambda$ and h is redundant. The $\lambda (t;\theta )$ becomes, by interchanging conditional expectations with summation, the multiplicative intensity process of ${}_U{N}^c_{T\bullet }(t):= \sum _{i=1}^n {}_U{N}^c_{Ti}(t)$, namely ${}_U{\alpha }^c_{\bullet }(t;\lambda )= \lambda \sum _{i=1}^n \mathbbm {1}_{\{U_i < t \le \min (T_i,U_i+10)\}}$. By Condition (A1), (A) is fulfilled for intensity ${}_U{\alpha }_T^c(t)$ and therefore for ${}_U{\alpha }_{T\bullet }^c(t;\lambda )$ and the logarithm of the likelihood (see Formula (A2)). For (B), because by the LLN, for fixed $t \in [0,\tau ]$, for the portion in the study period alive at the age t and observed it is

$$\begin{aligned} \frac{1}{n}\sum _{i=1}^n \mathbbm {1}_{\{U_i< t \le \min (T_i,U_i+10)\}} {\mathop {\longrightarrow }\limits ^{P}} \tilde{P}_{\lambda } (U < t \le \min (T,U+10)\mid A), \end{aligned}$$

(A5)

due to the simple sample assumption. Furthermore $n/n_{all} {\mathop {\longrightarrow }\limits ^{P}} \tilde{P}_{\lambda _0}(A)=\beta _{\lambda _0}$, so that Slutzky’s Lemma and the CMT yield $n_{all}^{-1} \int _0^{\tau } ((d/d \lambda ) \ln \lambda )^2\vert _{\lambda =\lambda _0} \lambda _0 \sum _{i=1}^n \mathbbm {1}_{\{U_i< t \le \min (T_i,U_i+10)\}} dt = (n/n_{all}) n^{-1} \sum _{i=1}^n \int _0^{\tau } (1/\lambda _0^2) \lambda _0 \mathbbm {1}_{\{U_i < t \le \min (T_i,U_i+10)\}} dt \rightarrow \sigma (\lambda _0)$. For (C), because (i) n $\le$ n$_{\text {all}}$, (ii) $1/(n \lambda _0) {\mathop {\rightarrow }\limits ^{P}} 0$ by Condition (A1) and $n {\mathop {\rightarrow }\limits ^{P}} \infty$ (due to n following a Binomial distribution with parameters $n_{all}$ and the selection probability $\beta _{\lambda _0}$) and (iii) Condition (A3), we have

$$\begin{aligned}{} & {} \frac{n}{n_{all}} \frac{1}{n} \int _0^{\tau } \left( \frac{d}{d \lambda } (\ln \lambda )\vert _{\lambda =\lambda _0}\right) ^2 \mathbbm {1}_{\{\vert \frac{1}{n} \frac{d}{d \lambda } (\ln \lambda )\vert _{\lambda =\lambda _0}\vert> \varepsilon \}} \lambda _0 \sum _{i=1}^n \mathbbm {1}_{\{U_i< t \le \min (T_i,U_i+10)\}} dt \nonumber \\{} & {} = \frac{n}{n_{all}} \frac{1}{\lambda _0^2 } \mathbbm {1}_{\{\vert 1/(n \lambda _0) \vert > \varepsilon \}} \lambda _0 \int _0^{\tau } \frac{1}{n} \mathbbm {1}_{\{U_i < t \le \min (T_i,U_i+10)\}} dt {\mathop {\rightarrow }\limits ^{P}} 0. \end{aligned}$$

(A6)

For (D), by Condition (A3), it is $\sigma (\lambda _0)$ positive. Condition (E) consists of six conditions: For the first four, note that $\sup _{\lambda } \vert (\partial ^3/d \lambda ^3)(\lambda \sum _{i=1}^n \mathbbm {1}_{\{U_i < t \le \min (T_i,U_i+10)\}})\vert =0$, $\sup _{\lambda } \vert (\partial ^3/d \lambda ^3) \ln (\lambda )\vert = sup_{\lambda } \mid \lambda ^{-3}/2\mid =: H < \infty$ and $(\int _0^{\tau } H dt)/n_{all} \rightarrow 0$. For the fifth, note (A6) (and also Condition (A1)). For the sixth, note (A6) and then $H/\sqrt{n_{all}} {\mathop {\rightarrow }\limits ^{P}} 0$. $\square$

It remains to consistently estimate $\sigma (\lambda _0)$, in order to construct a confidence interval. To start with, $- {\mathcal {J}}_{\tau }(\lambda _0) := (d^2/d \lambda ^2) \ln {}_U{\textbf{L}}_{\tau }^c(\lambda )\vert _{\lambda =\lambda _0} = - N_{uncens}/\lambda _0^2$ by Formula (A3). By Andersen et al. (1993, Formula 6.1.11) it is ${\mathcal {J}}_{\tau }(\lambda _0)/n_{all} {\mathop {\longrightarrow }\limits ^{P}} \sigma (\lambda _0)$, for $n_{all} \rightarrow \infty$. As a consequence, ${\mathcal {J}}_{\tau }^{-1}(\lambda _0) = N_{uncens}/\lambda _0^2$ and $n_{all} {\mathcal {J}}_{\tau }^{-1}(\lambda _0) {\mathop {=}\limits ^{\cdot }} \sigma ^{-1}(\lambda _0)$. Hence by (A4) and the CMT, as $\hat{\lambda }$ is consistent:

$$\begin{aligned} Var(\hat{\lambda }) {\mathop {=}\limits ^{\cdot }} {\mathcal {J}}_{\tau }^{-1}(\hat{\lambda }) = N_{uncens}^{-1} \left( \sum _{i=1}^{n} \mathbbm {1}_{\{U_i \le T_i < U_i+10\}} (T_i- U_i) + 10 N_{cens}\right) ^2 \end{aligned}$$

(A7)

Note that even though $Var(\hat{\lambda }) = Var (\sqrt{n_{all}}\hat{\lambda })/n_{all}{\mathop {=}\limits ^{\cdot }}\sigma ^{-1}(\lambda _0)/n_{all}$, by Theorem 4, $Var(\hat{\lambda })$ formally depends on the unobservable n$_{\text {all}}$, the standard error of $\hat{\lambda }$ (SE), as the square root of (A7), is still observable.

1.1.4 A.1.4 Finite sample properties

We visualise now consistency and asymptotic normality stated in Theorem 4, as does Section 2.3 for Theorem 1. We again find the approximations suitable for the AOK HCD data of n $\approx$ 250,000 observations in the next Section A.2.

We select the parameter for the Exponential distribution of T empirically, similar to Sect. 2.3.2. To this end, note first that $P(T \le 1)$ = 1 - $e^{-\lambda _0}$ $\approx$ $\lambda _0$ for small $\lambda _0$ (by the well-known $e^x$ $\approx$ 1 + x, for small x). For a contemporaneous one-year death incidence (and hence intensity) in Germany, approximately 0.96 mio. dead in 2020, restricted to the over 50 year-old’s (DeStatis 2021b), are to be set in relation to 35.5 mio. alive over 50 year old’s in 2019 (DeStatis 2021a), i.e. $F_E(1) \approx \lambda _0$ $\approx$ 0.035. The point estimate in the case study (applying estimator (A4)) will be $\hat{\lambda }$ = 0.0353. Because smaller parameters are more difficult to estimate we use $\lambda _0$ = 0.02.

In order to mimic the portion of uncensored lifetimes in our case study, we simulate, independent of T, $U \sim Exp(0.004)$, so that (on average) from n = 250,000 observations n$_{uncens}$ = 40,000. For different sample sizes and 2,000 simulation replication each, Table 6 shows that the mean squared error. As to be expected, it decreases with increasing sample size, and reaches an irrelevant magnitude far below the size of the AOK HCD.

Table 6 Mean squared error (MSE, $\times$ 10$^2$) for estimator (A4) of death hazard $\lambda _0=0.02$

For the assessment of normality, n = 250,000 observations correspond in this simulation model to a sample size of n$_{\text {all}}$ = 1.5 million. Figure 4 (right panel) plots the empirical distribution of (A4) and supports the normal shape.

1.2 A.2 Result for AOK HCD

As the population, we aim at Germans born in the first half of the $20^{th}$ century, as in the univariate model of Section 2.4, see first line in Fig. 2. For ease of argumentation, we retain the assumption of Sect. 2.4, that a person cannot die before age 50. Again the same n = 236,039 people from AOK HCD 2004 are not truncated. We monitor histories for transitions up to 31/12/2013, so that the maximally observed timespan is $\tau$ := 54 + 10 = 64 years (after a person’s 50$^{th}$ birthday). The conditional likelihood contributions are given in Formula (A3). Within the observation period 2004 until 2013, n$_{uncens}$ = 64,442 persons, out of the n, die (see Table 7).

Table 7 Statistics (as counts $\#$, or in years) for point estimate (A4) and standard error (SE) by (A7) for death hazard, $\sum _{i=1}^{n_{uncens}}$ requires corresponding ordering

For the Exponentially distributed age-at-death, T, according to (A4), point estimation of $\lambda _0$ divides n$_{uncens}$ by the observed time at the risk of dying. Each person surviving 2013 has been 10 years at risk in the observation period. For an observed death, the person contributes with the residual lifetime to the time at risk. The two contributions are listed in Table 7 and add up to 1.8 million years, i.e. $\hat{\lambda }$ = 0.035. Note that the person-years at dementia risk in Table 1 are by definition smaller. Recall that neither for the point estimate (A4) nor for its standard error (A7) is the knowledge of n$_{\text {all}}$ necessary. Theorem 4 yields the confidence interval $\hat{\lambda } \pm z_{1 - 0.025} \sqrt{\sigma ^{-1}(\lambda _0)}/\sqrt{n_{all}}$, with 97.5% quantile of the standard Gaussian distribution z$_{1 - 0.025}$, being very narrow due to a small standard error ${\mathcal {J}}_{\tau }^{-1/2}(\hat{\lambda })= [n_{all} \sigma (\hat{\lambda })]^{-1/2}$ by (A7) (see again Table 7). The expected lifetime is 1/0.035 $\approx$ 28 (plus 50) years, which may not be appropriate, due to the assumption of a constant hazard and by the impossibility of death before age 50 in this model. An age-inhomogeneous increase in the hazard is well-documented, and in basic demography, usually modelled as a Gompertz distribution. Piecewise constant hazards would be as in Sect. 3.1.

Appendix B: Proof of Theorem 1

Due to the uniqueness of $\hat{\varvec{\lambda }}$, for consistency (see Andersen et al. 1993, Theorem VI.1.1) and asymptotic normality (see Andersen et al. 1993, Theorem VI.1.2), we need to verify their Condition VI.1.1. Specifically, to map the notations, n becomes n$_{\text {all}}$, $a_n:= \sqrt{n_{all}}$, $\varvec{\theta }$ becomes $\varvec{\lambda }$, h becomes hj and $\lambda _h(t;\varvec{\theta })$ becomes

$$\begin{aligned} {}_U{\alpha }^c_{hj\bullet }(t;\varvec{\lambda })=\lambda _{hj} {}_U{Y}^c_{h\bullet }(t),\ hj \in {\mathcal {I}}, \end{aligned}$$

(B8)

because by interchanging conditional expectations, the multiplicative intensity process of ${}_U{N}^c_{hj\bullet }(t)$ is the sum of the compensators for each person’s counting process.

The fulfilment of Condition VI.1.1.’s (A) is now as in Theorem 4 of Appendix A.1.3. For (B), note first that for mixed derivatives, terms are only non-zero when $h_1j_1=h_2j_2=h_3j_3$ due to (B8). In that case $n_{all}^{-1} \int _0^{\tau } \sum _{hj \in {\mathcal {I}}} [(\partial /\partial \lambda _{hj}) \ln {}_U{\alpha }_{hj\bullet }^c(t;\varvec{\lambda }_0)]^2 {}_U{\alpha }_{hj\bullet }^c(t;\varvec{\lambda }_0) dt = (n/n_{all}) n^{-1} \int _0^{\tau } \sum _{hj} (1/\lambda _{hj^0}^2) \lambda _{hj^0} {}_U{Y}^c_{h\bullet }(t) dt \rightarrow \sigma _{hj,hj}(\varvec{\lambda }_0)$, because, by the LLN, for fixed $t \in [0,\tau ]$, (including Slutzky’s Lemma, the CMT, and (7) (as in Theorem 4)) it is $n/n_{all} {\mathop {\longrightarrow }\limits ^{P}} \beta _{\varvec{\lambda }_0} >0$ by Condition (B2). For (C),

$$\begin{aligned}{} & {} \frac{1}{n_{all}} \int _0^{\tau } \sum _{hj \in {\mathcal {I}}} \left( \frac{\partial }{\partial \lambda _{hj}} \ln {}_U{\alpha }_{hj\bullet }^c(t;\varvec{\lambda }_0) \right) ^2 \\{} & {} \quad \mathbbm {1}_{\left\{ \left| \frac{1}{\sqrt{n_{all}}} \frac{\partial }{\partial \lambda _{hj}} \ln {}_U{\alpha }_{hj\bullet }^c(t;\varvec{\lambda }_0)\right|> \varepsilon \right\} } {}_U{\alpha }_{hj\bullet }^c(t;\varvec{\lambda }_0) dt \\{} & {} \quad = \frac{1}{n_{all}} \int _0^{\tau } \sum _{hj \in {\mathcal {I}}} \frac{1}{\lambda _{hj^0}^2} \mathbbm {1}_{\left\{ \left| \frac{1}{\sqrt{n_{all}}} \frac{1}{\lambda _{hj^0}}\right| > \varepsilon \right\} }\lambda _{hj^0} {}_U{Y}^c_{h\bullet }(t) dt \rightarrow 0, \end{aligned}$$

because $1/\sqrt{n_{all}} \rightarrow 0$ and $\lambda _{hj^0}>0$ due to Condition (B1). For (D), $\varvec{\Sigma }(\varvec{\lambda }_0)$ is diagonal with $\sigma _{hj,hj}(\varvec{\lambda }_0)>0$ due to Conditions (B2) and (B3). Now in (E), generally (first line) and if $h_1j_1=h_2j_2=h_3j_3$ (second line), it is $\sup _{\varvec{\lambda } \in \varvec{\Lambda }} \vert (\partial ^3/\partial \lambda _{h_1j_1} \partial \lambda _{h_2j_2} \partial \lambda _{h_3j_3}) \lambda _{hj} {}_U{Y}^c_{h\bullet }(t) \vert = 0$ and $\sup _{\varvec{\lambda } \in \varvec{\Lambda }} \vert (\partial ^3/(\partial \lambda _{h_1j_1} \partial \lambda _{h_2j_2} \partial \lambda _{h_3j_3}) \ln ({}_U{\alpha }_{hj\bullet }^c(t;\varvec{\lambda }))\vert = \sup _{\lambda _{hj} \in \Lambda _{hj}} 2 \lambda _{hj}^{-3}$. Now $1/(2 \lambda _{hj}^3) \le 1/(2\varepsilon _{hj^0}^3)< \infty$ by Condition (B1). (This explains the third and fourth requirement.) For the fifth, $n_{all}^{-1} \int _0^{\tau } \sum _{hj \in {\mathcal {I}}} [(\partial ^2/\partial \lambda _{hj}^2) \ln {}_U{\alpha }_{hj\bullet }^c(t;\varvec{\lambda }_0)]^2 {}_U{\alpha }_{hj\bullet }^c(t;\varvec{\lambda }_0) dt = (n/n_{all}) n^{-1} \int _0^{\tau } \sum _{(h,j)}\lambda _{hj^0}^{-4} \lambda _{hj^0} {}_U{Y}^c_{h\bullet }(t) dt \rightarrow \sigma _{hj,hj}(\varvec{\lambda }_0)/\lambda _{hj^0}^2$. The latter are finite due to Conditions (B1) and (B3). The sixth is fulfilled with the same argument as in (C). $\square$

Appendix C: Proof of Theorem 3

Obviously, generalising (4), as in (13), the logarithmic conditional likelihood contribution is

$$\begin{aligned} \begin{aligned} \ln {}_U{L}^c(\textbf{X},U,\textbf{Z} \mid \varvec{\lambda }) =&\int _U^{U+10} \sum _{hj \in {\mathcal {I}}} (\ln {}_U{Y}_h(t) + \ln \lambda _{hj}(t,z(t))) d {}_U{N}^c_{hj} (t) \\&- \sum _{hj \in {\mathcal {I}}} \int _U^{U+10} {}_U{Y}^c_h(t) \lambda _{hj}(t,z(t)) dt. \end{aligned} \end{aligned}$$

(C9)

Now, in extension to Sect. 3.1.1, for $\kappa \in [U,U+10)$, the derivative with respect to $\lambda ^{wo}_{hjl}$ of the N-term of $\ln {}_U{L}^c(\textbf{X},U,\textbf{Z} \mid \varvec{\lambda })$ is

$$\begin{aligned}{} & {} \int _U^{U+10} \frac{\partial }{\partial \lambda ^{wo}_{hjl}} \ln \left( \sum _{\tilde{l} = 1}^b \mathbbm {1}_{[t_{\tilde{l}-1},t_{\tilde{l}})}(t) \left( \mathbbm {1}_{[0,\kappa )}(t) \lambda ^{wo}_{hj\tilde{l}} + \mathbbm {1}_{[\kappa , \infty )}(t) \lambda ^{w}_{hj\tilde{l}} \right) \right) d {}_U{N}^c_{hj} (t) \\{} & {} \quad = \int _U^{U+10} \frac{\mathbbm {1}_{[t_{l-1},t_l) \cap [0,\kappa )} (t) }{ \sum _{\tilde{l} = 1}^b \mathbbm {1}_{[t_{\tilde{l}-1},t_{\tilde{l}})}(t) \left( \mathbbm {1}_{[0,\kappa )}(t) \lambda ^{wo}_{hj\tilde{l}}+ \mathbbm {1}_{[\kappa , \infty )}(t) \lambda ^{w}_{hj\tilde{l}} \right) } d {}_U{N}^c_{hj} (t) \\{} & {} \quad = \left\{ {\begin{array}{ll} 0 &{} \text {if} \; \kappa \le t_{l-1} \\ \frac{1}{\lambda ^{wo}_{hjl}} \int _U^{U+10} \mathbbm {1}_{[t_{l-1},t_l)} (t) d {}_U{N}^c_{hj} (t)= \frac{1}{\lambda ^{wo}_{hjl}}({}_U{N}^c_{hj} (t_l) - {}_U{N}^c_{hj} (t_{l-1})) &{} \text {if} \; \kappa \ge t_l \\ \frac{1}{\lambda ^{wo}_{hjl}} \int _U^{U+10} \mathbbm {1}_{[t_{l-1},\kappa )} (t) d {}_U{N}^c_{hj} (t)=\frac{1}{\lambda ^{wo}_{hjl}}({}_U{N}^c_{hj} (\kappa ) - {}_U{N}^c_{hj} (t_{l-1})) &{} \quad \text {if} \; \kappa \in [t_{l-1}, t_l] \end{array}} \right. \end{aligned}$$

and with respect to $\lambda ^w_{hjl}$ it is:

$$\begin{aligned}{} & {} \int _U^{U+10} \frac{\partial }{\partial \lambda ^w_{hjl}} \ln \left( \sum _{\tilde{l} = 1}^b \mathbbm {1}_{[t_{\tilde{l}-1},t_{\tilde{l}})}(t) \left( \mathbbm {1}_{[0,\kappa )}(t) \lambda ^{wo}_{hj\tilde{l}} + \mathbbm {1}_{[\kappa , \infty )}(t) \lambda ^{w}_{hj\tilde{l}} \right) \right) d {}_U{N}^c_{hj} (t) \\{} & {} \quad = \int _U^{U+10} \frac{\mathbbm {1}_{[t_{l-1},t_l) \cap [\kappa ,\infty )} (t) }{ \sum _{\tilde{l} = 1}^b \mathbbm {1}_{[t_{\tilde{l}-1},t_{\tilde{l}})}(t) \left( \mathbbm {1}_{[0,\kappa )}(t) \lambda ^{wo}_{hj\tilde{l}}+ \mathbbm {1}_{[\kappa , \infty )}(t) \lambda ^{w}_{hj\tilde{l}} \right) } d {}_U{N}^c_{hj} (t) \\{} & {} \quad = \left\{ {\begin{array}{ll} \frac{1}{\lambda ^w_{hjl}}\int _U^{U+10} \mathbbm {1}_{[t_{l-1},t_l)} (t) d {}_U{N}^c_{hj} (t)=\frac{1}{\lambda ^w_{hjl}}({}_U{N}^c_{hj} (t_l) - {}_U{N}^c_{hj} (t_{l-1})) &{} \text {if} \; \kappa \le t_{l-1} \\ 0 &{} \text {if} \; \kappa \ge t_l \\ \frac{1}{\lambda ^w_{hjl}} \int _U^{U+10} \mathbbm {1}_{[\kappa ,t_l)} (t) d {}_U{N}^c_{hj} (t)=\frac{1}{\lambda ^w_{hjl}}({}_U{N}^c_{hj} (t_l) - {}_U{N}^c_{hj} (\kappa )) &{} \text {if} \; \kappa \in [t_{l-1}, t_l] \end{array}} \right. \end{aligned}$$

For $\kappa \ge U+10$, the N-term in $\frac{\partial }{\partial \lambda ^{wo}_{hjl}} \ln {}_U{L}^c(\textbf{X},U,\textbf{Z} \mid \varvec{\lambda })$ is $(\lambda ^{wo}_{hjl})^{-1}({}_U{N}^c_{hj} (t_l) - {}_U{N}^c_{hj} (t_{l-1}))$ and taking derivative with respect to $\lambda ^w_{hjl}$ becomes zero. For $\kappa < U$, the N-term after taking the derivative with respect to $\lambda ^{wo}_{hjl}$ is zero and with respect to $\lambda ^w_{hjl}$ it is $(\lambda ^w_{hjl})^{-1}({}_U{N}^c_{hj} (t_l) - {}_U{N}^c_{hj} (t_{l-1}))$.

Now, the derivative with respect to $\lambda ^{wo}_{hjl}$ of the Y-term in $\ln {}_U{L}^c(\textbf{X},U,\textbf{Z} \mid \varvec{\lambda })$ is, in extension to Sect. 3.1.1:

$$\begin{aligned}{} & {} \frac{\partial }{\partial \lambda ^{wo}_{hjl}} \sum _{hj \in {\mathcal {I}}} \int _U^{U+10} {}_U{Y}_h(t) \left( \sum _{\tilde{l} = 1}^b \mathbbm {1}_{[t_{\tilde{l}-1},t_{\tilde{l}})}(t) \left( \mathbbm {1}_{[0,\kappa )}(t) \lambda ^{wo}_{hj\tilde{l}}+ \mathbbm {1}_{[\kappa , \infty )}(t) \lambda ^{w}_{hj\tilde{l}} \right) \right) dt \\{} & {} \quad = \int _U^{U+10} {}_U{Y}_h(t) \mathbbm {1}_{[t_{l-1},t_l) \cap [0,\kappa )} (t) dt \\{} & {} \quad = \left\{ {\begin{array}{ll} 0 &{} \kappa \in [U,U+10)\; \text {and} \; \kappa \le t_{l-1} \\ \int _{t_{l-1}}^{\kappa } {}_U{Y}_h(t) dt &{} \text {if} \; \kappa \in [U,U+10)\; \text {and} \; \kappa \in [t_{l-1}, t_l] \\ \int _{t_{l-1}}^{t_l} {}_U{Y}_h(t) dt &{} \text {if} \; \kappa \in [U,U+10)\; \text {and} \; \kappa \ge t_l \\ 0 &{} \text {if} \; \kappa < U \\ \int _{t_{l-1}}^{t_l} {}_U{Y}_h(t) dt &{} \text {if} \; \kappa \ge U+10 \\ \end{array}} \right. \\ \end{aligned}$$

With respect to $\lambda ^w_{hjl}$ it is:

$$\begin{aligned}{} & {} \frac{\partial }{\partial \lambda ^w_{hjl}} \sum _{hj \in {\mathcal {I}}} \int _U^{U+10} {}_U{Y}_h(t) \left( \sum _{\tilde{l} = 1}^b \mathbbm {1}_{[t_{\tilde{l}-1},t_{\tilde{l}})}(t) \left( \mathbbm {1}_{[0,\kappa )}(t) \lambda ^{wo}_{hj\tilde{l}}+ \mathbbm {1}_{[\kappa , \infty )}(t) \lambda ^{w}_{hj\tilde{l}} \right) \right) dt \\{} & {} \quad = \int _U^{U+10} {}_U{Y}_h(t) \mathbbm {1}_{[t_{l-1},t_l) \cap [\kappa , \infty )} (t) dt \\{} & {} \quad = \left\{ {\begin{array}{ll} \int _{t_{l-1}}^{t_l} {}_U{Y}_h(t) dt &{} \kappa \in [U,U+10)\; \text {and} \; \kappa \le t_{l-1} \\ \int _{\kappa }^{t_l} {}_U{Y}_h(t) dt &{} \text {if} \; \kappa \in [U,U+10)\; \text {and} \; \kappa \in [t_{l-1}, t_l] \\ 0 &{} \text {if} \; \kappa \in [U,U+10)\; \text {and} \; \kappa \ge t_l \\ \int _{t_{l-1}}^{t_l} {}_U{Y}_h(t) dt &{} \text {if} \; \kappa < U \\ 0 &{} \text {if} \; \kappa \ge U+10 \\ \end{array}} \right. \\ \end{aligned}$$

These summarized, as in (5), to $\ln {}_U{L}_{\tau }^c(data;\varvec{\lambda }) = \sum _{i=1}^n \ln {}_U{L}_{\tau }^c(\textbf{X}^i,U_i,\textbf{Z}_i \mid \varvec{\lambda })$ must be set to zero. $\square$