Small area estimation of socioeconomic indicators for sampled and unsampled domains

Abstract

Socioeconomic indicators play a crucial role in monitoring political actions over time and across regions. Income-based indicators such as the median income of sub-populations can provide information on the impact of measures, e.g., on poverty reduction. Regional information is usually published on an aggregated level. Due to small sample sizes, these regional aggregates are often associated with large standard errors or are missing if the region is unsampled or the estimate is simply not published. For example, if the median income of Hispanic or Latino Americans from the American Community Survey is of interest, some county-year combinations are not available. Therefore, a comparison of different counties or time-points is partly not possible. We propose a new predictor based on small area estimation techniques for aggregated data and bivariate modeling. This predictor provides empirical best predictions for the partially unavailable county-year combinations. We provide an analytical approximation to the mean squared error. The theoretical findings are backed up by a large-scale simulation study. Finally, we return to the problem of estimating the county-year estimates for the median income of Hispanic or Latino Americans and externally validate the estimates.

1 Introduction

Socioeconomic indicators, such as the median income of sub-populations, are key both for policy recommendations and policy evaluation. Regional indicators of income, poverty, employment, or well-being are omnipresent in current projects and research. To better reflect regional heterogeneity, their focus has shifted to deeper regional levels.

Regional information is normally published on an aggregated level. The estimation of these aggregates is usually based on survey data. Although the demand for more detailed regional social indicators has increased, the underlying surveys tend to focus on higher regional or national level so that the survey costs do not become too high. Even though survey data provide reliable direct estimates at these levels, for more detailed regional levels they usually do not. At a regionally lower level, direct estimates are usually associated with high standard errors or unavailable. Estimates can be unavailable if the region is unsampled and thus no direct estimate could be given. In addition, the publication of regional estimates can be suppressed when the associated standard errors are high. For the investigation of regional indicators a researcher is therefore usually confronted with regional aggregates which are associated with high standard errors and contain a non-negligible proportion of unpublished data.

Small area estimation (SAE) methods are increasingly used to deal with highly volatile direct estimates on regional level. For a comprehensive overview, see Rao and Molina (2015). The key idea behind SAE techniques is to borrow strength by combining regional indicators in a common model framework. Within this model, additional related information, such as registration data, can be exploited.

The model-based approach allows the introduction of best predictors (BP) that minimize the mean square errors (MSE) in the class of unbiased predictors. Since the BPs depend on the model parameters, substituting them for appropriate estimators gives the empirical BPs (EBP) that stabilize the estimates in small domains.

For aggregated univariate target data, the most prominent model is the Fay–Herriot (FH) model by Fay and Herriot (1979). Many extensions were made to the FH predictor to meet different practical problems. Inter alia, Prasad and Rao (1990) and Datta and Lahiri (2000) propose MSE estimators for the FH predictor, Li and Lahiri (2010) and Yoshimori and Lahiri (2014) introduce new adjusted maximum likelihood fitting methods, Jiang and Tang (2011) study the influence of the fitting algorithm in the empirical best prediction, Molina et al. (2015) derive preliminary testing predictors, Moura et al. (2017) modified the basic model to analyze skewed business survey data, Ybarra and Lohr (2008), Bell et al. (2019), Burgard et al. (2019) and Burgard et al. (2019) study the effect of measurement errors in the covariates, Pratesi and Salvati (2008), Gonzáalez-Manteiga et al. (2010), Articus and Burgard (2014), and Morales et al. (2015) allow for a heterogeneous dependency structure in the FH model, Esteban et al. (2012) and Marhuenda et al. (2013) estimate small area poverty proportions under temporal and spatiotemporal Fay–Herriot models, respectively.

For aggregated multivariate target data, a widely employed model is the multivariate FH model. Fay (1987) and Datta et al. (1991) investigated the gain of precision achieved by the multivariate modeling. Datta et al. (1996) employed a multivariate FH model for obtaining hierarchical Bayes predictors. González-Manteiga et al. (2008) considered a multivariate FH model with a common domain random effect for the target vector, Arima et al. (2017) and Burgard et al. (2020) study multivariate measurement errors FH models, Porter et al. (2015), Benavent and Morales (2016), Ubaidillah et al. (2019), Esteban et al. (2019) and Benavent and Morales (2021) investigate and give further applications of multivariate FH models. Many other authors have studied further variants of the FH model and the multivariate FH model adapted to different setups.

In the context of survey sampling, there are two main types of missing data. First, missingness due to non-response refers to situations where data were planned to be collected by the nature of the sampling design, but failed to be collected due to some kind of response mechanism. This may occur because individuals in the sample refuse or fail to respond, or because of processing issues. The response mechanisms are of special concern in voluntary surveys where ignoring the response mechanism could lead to biased direct estimates. The treatment of this kind of missing data is therefore of great interest for applied statisticians as shown by Matei and Ranalli (2015) and Nguyen and Zhang (2020) in their recent studies on latent modeling approaches and reweighting methods for non-response. More generally, the book of Longford (2005) gives an introduction to missing data modeling and imputation methods. In the present study, we do not consider any kind of non-response, but deal solely with aggregate information such as domain-specific direct estimates which might have been adjusted to non-response by the statistical agencies.

Second, missing data can occur from the sampling design, if the design does not allocate samples to domains of interest. These domains could, for example, be a cross-combination of small geographic units and demographic characteristics such as age classes. In this case, the domain-specific sample sizes are random and can be zero or so small that corresponding direct estimates are not published due to the estimated variances being too high. This is the kind of missing information we are considering in this paper. The problem of estimating small area indicators with missing data, i.e., with unsampled domains or simply with unavailable data, has been scarcely treated in the literature. For unit-level data, Longford (2004) did some contributions related to multivariate shrinkage estimators, where the estimation is integrated with a multiple imputation procedure. For area-level small area models, to our knowledge, the existing SAE approaches using the FH model give empirical best predictors (EBP) only for domains with observed direct estimates. For unavailable direct estimates, the existing variants of the FH model only provide synthetic estimates with vague mean squared error approximations.

As an example, we can take a look at Articus et al. (2020) where the FH model is applied to local-level rental markets based on direct estimates from the German Microcensus. We can see that in the application of FH models missing direct estimates either appear as blank spots on a map (Articus et al. 2020, Figure 6) or are filled by synthetic predictions (Articus et al. 2020, Figure 7).

We attempt to fill this research gap with the introduction of a new model based on the FH model and bivariate modeling, called MBFH. It is an extension of the bivariate FH model, see, e.g., Rao and Molina (2015), Section 4.4.1, that allows for partially missing direct estimates. On the basis of this model, we derive the corresponding empirical best predictor under missing values (MBFH-EBP). In contrast to the FH or bivariate FH model, the MBFH model provides best predictors for both missing and observed values. We furthermore provide analytical mean squared error approximations of the MBFH-EBPs.

This best predictor is applicable to any indicator that is predictable by the Fay–Herriot model. For example, the dependent variables may consist of direct estimators labor market indicators (total of employed and unemployed people and unemployment rates), living conditions indicators (head count ratio, poverty gap, poverty housing, average per capita income), family budget indicators (per capita expenditure in food or housing), and others. In addition, the new predictor is applicable to setting where the target variable has missings, but a second correlated variable is observed in all domains.

The choice of auxiliary data can be made for each variable separately. We illustrate the use of the proposed method with an application to US ACS data at the county level, where direct estimates of median income for Hispanics or Latin Americans are partially missing.

The manuscript is structured as follows: Sect. 2 describes the problem of interest and the data which we use for an illustration. Section 3 provides the methodological foundation. Section 3.1 introduces the bivariate Fay–Herriot model, which is the basis for the development of the EBP theory under partially missing target estimates, the proposed MBFH predictor. Section 3.2 divides the set of domains in three groups depending on the missing structure of the direct estimates and gives the corresponding MBFH-EBPs. Section 3.3 gives an approximation to the MSE of the MBFH-EBP and proposes an explicit-formula estimator. With a model-based simulation, Sect. 4 validates the theoretical results and empirically investigates the introduced MBFH-EBPs and MSE estimators in different settings. Section 5 applies the new MBFH predictor to the publicly available US county-level ACS data on median income of Hispanic or Latino Americans. Section 6 presents a short summary and outlook. This contribution is the extension of a related working paper Burgard et al. (2019). Finally, the manuscript has four appendixes in the supplementary material. Section 1 gives algorithms for calculating the maximum likelihood and residual maximum likelihood estimators of the model parameters. Section 2 contains proofs of the derivation of best predictions under the new model. Section 3 contains the mathematical derivations for approximating the MSE of the MBFH-EBP. Section 4 presents a parametric bootstrap procedure for estimating the mean squared error of the MBFH-EBPs. Section 5 shows the MSE of the synthetic Fay–Herriot predictor for missing direct estimates.

Section 6 contains additional results from the model-based simulation study with 5% and 10% missing direct estimates.

2 The problem of interest

2.1 Aim

To illustrate the new MBFH predictor, we take a look at the publicly available county-level US ACS estimates of the median income of Hispanic or Latino Americans. Income is strongly related to the concepts of poverty and well-being and thereby has an essential impact on the regional distribution of resources. The US Office of Management and Budget (OMB) requires federal agencies to use at least two ethnicities in data collection and reporting: ’Hispanic or Latino’ and ’not Hispanic or Latino’. Most official US survey publications, including those on income and poverty, pay extra attention to people who consider themselves as Hispanic or Latino Americans, see, e.g., Guzman (2019) and Semega et al. (2019). Therefore, we consider regional estimates of the median income of Hispanic or Latino Americans.

The ACS estimates on county-level for the years 2010 and 2011 are partly estimated with high standard errors or are not published for certain counties and years. We can use additional publicly available data from the US Census Bureau to construct bivariate FH models based on these estimates. The statistical issue is that we cannot apply the statistical methodology based on the multivariate FH model to the domains with missing direct estimates. This paper introduces a new model-based approach to address this problem. The approach makes use of the fact that some regional estimates missing in 2010 are available in 2011 and the other way around. Intuitively, the random effect correlation of the median income between two years is expected to be highly positive. As the simulation study in Sect. 4 shows, in such a situation an application of the introduced MBFH predictor is profitable for stabilizing volatile estimates and predicting missing estimates. In the following, we describe the county-level US ACS data and the collection and choice of publicly available auxiliary data.

2.2 Data description

We use the freely available US American Community Survey (ACS) data. Detailed information about the ACS is given in US Census Bureau (2014). The US Census Bureau provides aggregated county-level data of ACS 1-year estimates with associated margins of error. We take the median annual income (dollars) Hispanic or Latino origin (of any race) (HC02_EST_VC12) in 2010 and 2011 as variables of interest.¹ This is the target vector of the statistical study.

We partition our finite population, the USA, into $D=3141$ ($d=1,\ldots ,D$) US counties, our domains of interest. There are publicly available county-level data from the US Census Bureau which can be used as auxiliary data.²

As 2010 and 2011 are temporary close, we choose the same auxiliary data for both variables, HC02_EST_VC12 in 2010 and 2011. Among the available auxiliary data, we chose the final model considering correlation patterns to the variables of interest, resulting coefficients, and model diagnostics. The chosen auxiliary variables are: Intercept, death rate in period 7/1/2010 to 6/30/2011 (RDEATH2011), and civilian labor force unemployment rate 2010 RTE (CLF040210D).

The ACS 1-year estimates are published only for certain counties in certain years to ensure disclosure control (U.S. Census Bureau 2016). For the variable of interest, there are direct estimates available for 704 counties in 2010 and 684 counties in 2011, after excluding counties where auxiliary data were missing. Of these, there are 626 counties with both variables observed, 58 counties with missing estimates in 2010 which are available in 2011 and 78 counties with missing estimates in 2011 which are available in 2010. Thereby, for the application $D=762$ counties remain as domains of interest, where $D_{1}=78$, $D_{2}=58$, and $D_{3}=626$. Due to this missing pattern, the use of the new MBFH-EBP is recommended.

To validate the results of the MBFH-EBP, especially the prediction of missing direct domain estimates, we need comparable county-level data. From the ACS also 5-year direct estimates are available for the variable of interest (HC02_EST_VC12).³ ACS 5-year estimates pool data from the last 5 years, such that direct estimates in 2012 refer to ACS data from 2008-2012 and are available for more counties than the 1-year estimates. It is not recommended to directly compare overlapping ACS datasets such as ACS 1- and 5-year data. As we, however, want to evaluate whether the MBFH-EBPs of missing ACS 1-year estimates are realistic, the ACS 5-year direct estimates are chosen as benchmarks. They are available for many counties where ACS 1-year direct estimates are missing, but MBFH-EBPs can be computed.

Although ACS 5-year estimates of HC02_EST_VC12 are available for some counties where 1-year estimates are missing, they do not cover all areas either. We therefore use an additional dataset for validation, the Census-ACS 2010 estimates. Census estimates for variable HC02_EST_VC12 are not available. We therefore choose Census estimates of variable median household income in the past 12 month (in 2009 inflation-adjusted dollars) in 2005–2009 (INC110209D) for validation. INC110209D is close to the variable of interest HC02_EST_VC12, and its estimates in 2005–2009 are available for all counties.⁴ For this comparison, one should keep in mind that these variables can only be used as proxies, as their definitions differ.

3 Best prediction under the missing data bivariate Fay–Herriot model

3.1 The bivariate Fay–Herriot model

Let U be a finite population partitioned into D domains $U_1,\ldots ,U_D$. Let $\mu _{d}=\left( \mu _{d1},\mu _{d2}\right) ^{\prime }$ be a vector of characteristics of interest in domain d and let ${y}_{d}=\left( {y}_{d1},{y}_{d2}\right) ^{\prime }$ be a vector of direct estimates of $\mu _d$ calculated by using the data of the target survey sample.

The bivariate Fay–Herriot model is defined in two stages. The first stage indicates that direct estimators $y_d,\,\forall d\in \{1,\ldots D\}$, are unbiased and follow the sampling model

$$\begin{aligned} {y}_{d}=\mu _{d}+{e}_{d},\quad \forall d\in \{1,\ldots ,D\}, \end{aligned}$$

(3.1)

where the vectors ${e}_{d}=(e_{d1},e_{d2})^\prime \sim N_{2}\left( 0,{V}_{ed}\right)$ are independent and the $2\times 2$ covariance matrices ${V}_{ed}$ are known. In most cases, ${V}_{ed}$ is taken to be the design-based covariance matrix of direct estimators $y_d$, $\forall d\in \{1,\ldots ,D\}$. The covariance matrices ${V}_{ed}$ are

$$\begin{aligned} {V}_{ed}= \left( \begin{array}{cc} \sigma _{ed1}^2 &{} \sigma _{ed12}\\ \sigma _{ed12}&{}\sigma _{ed2}^2 \end{array}\right) ,\quad \sigma _{ed12}=\rho _{ed12}\sigma _{ed1}\sigma _{ed2},\quad \forall d\in \{1,\ldots ,D\}. \end{aligned}$$

In the second stage, the true domain characteristic $\mu _{dk}$ is assumed to be linearly related to $p_k$ explanatory variables, $k=1,2$, $d\in \{1,\ldots ,D\}$. Let $x_{dk}^\prime =(x_{dk1},\ldots ,x_{dkp_k})$ be a row vector containing the true aggregated (population) values of $p_k$ explanatory variables for $\mu _{dk}$ and let ${X}_{d}=\text{ diag }({x}_{d1}^\prime ,{x}_{d2}^\prime )$ be a ${2\times p}$ block-diagonal matrix with $p=p_1+p_2$. Let $\beta _{k}=(\beta _{k1},\ldots ,\beta _{kp_k})^\prime$ be a column vector of size $p_k$ containing the regression parameters $\beta _{kj}$ for $\mu _{dk}$ and let $\beta =\left( \beta _{1}^{\prime },\beta _{2}^{\prime }\right) ^{\prime }_{p\times 1}$. The linking model is

$$\begin{aligned} \mu _{d}={X}_{d}\beta +{u}_{d},\quad {u}_{d}=(u_{d1},u_{d2})^\prime \sim N_2(0,{V}_{ud}),\quad \forall d\in \{1,\ldots ,D\}, \end{aligned}$$

(3.2)

where the vectors ${u}_{d}$’s are independent of the vectors ${e}_{d}$’s. The $2\times 2$ covariance matrix ${V}_{ud}$ depends on three unknown parameters, $\theta _{1}=\sigma _{u1}^2$, $\theta _{2}=\sigma _{u2}^2$ and $\theta _{3}=\rho$, i.e.,

$$\begin{aligned} {V}_{ud}= \left( \begin{array}{cc} \sigma _{u1}^2 &{} \rho \sigma _{u1}\sigma _{u2}\\ \rho \sigma _{u1}\sigma _{u2}&{}\sigma _{u2}^2 \end{array}\right) ,\quad \forall d\in \{1,\ldots ,D\}. \end{aligned}$$

The bivariate Fay–Herriot (BFH) model can be expressed as a single model in the form

$$\begin{aligned} y_d=X_d\beta +u_d+e_d, \quad \forall d\in \{1,\ldots ,D\}, \end{aligned}$$

(3.3)

or in the matrix form

$$\begin{aligned} y=X\beta +u+e, \end{aligned}$$

with

$$\begin{aligned} {y}=\underset{1\le d \le D}{\hbox {col}}({y}_{d}),\,\, {u}=\underset{1\le d \le D}{\hbox {col}}({u}_{d}),\,\, {e}=\underset{1\le d \le D}{\hbox {col}}({e}_{d}),\,\, X=\underset{1\le d \le D}{\hbox {col}}({X}_{d}),\,\, \end{aligned}$$

where “col” is the matrix operator stacking by columns. We finally assume that $u_d$, $e_d$, $d\in \{1,\ldots ,D\}$, are independent. The BFH model (3.3) is a reparametrization of Model 3 introduced by Benavent and Morales (2016).

Let us define ${V}_{d}={V}_{ud}+{V}_{ed}$, $\forall d\in \{1,\ldots ,D\}$. Under model (3.3), it holds that

$$\begin{aligned} E\left( {y}\right) ={X}\beta \quad \text{ and }\quad {V}=\text{ var }({y})={V}_u+{V}_e={V}_u+{V}_e =\underset{1\le d \le D}{\hbox {diag}}({V}_d). \end{aligned}$$

3.2 Prediction with missing target values

Let us assume that some of the $y_{dk}$ are missing and partition the domains into three groups:

• ${\mathbb {D}}_1 = \{d\in {\mathbb {N}} : 1\le d\le D_1\}$ contains the $D_1$ domains where only $y_{d1}$ is observed.

• ${\mathbb {D}}_2 = \{d\in {\mathbb {N}} : D_1+1\le d\le D_1+D_2\}$ contains the $D_2$ domains where only $y_{d2}$ is observed.

• ${\mathbb {D}}_3 = \{d\in {\mathbb {N}} : D_1+D_2+1\le d\le D\}$ contains the remaining domains where $y_d=(y_{d1},y_{d2})^\prime$ is fully observed.

If the BFH model (3.3) holds for $d\in \{1,\ldots ,D\}$ and the missing data obey scheme $\{1,\ldots ,D\}={\mathbb {D}}_1\cup {\mathbb {D}}_2\cup {\mathbb {D}}_3$, we say that target vectors $y_d$ obey a missing data BFH (MBFH) model. If the MBFH model holds, then

• 1. $y_{d1}\sim N_1 \left( x_{d1}^\prime \beta _1,\sigma _{u1}^2+\sigma _{ed1}^{2} \right)$ and $y_{d1}|_{u_d}\sim N_1 \left( x_{d1}^\prime \beta _1+u_{d1},\sigma _{ed1}^{2} \right)$ if $d\in {\mathbb {D}}_1$,

• 2. $y_{d2}\sim N_1 \left( x_{d2}^\prime \beta _2,\sigma _{u2}^2+\sigma _{ed2}^{2} \right)$ and $y_{d2}|_{u_d}\sim N_1 \left( x_{d2}^\prime \beta _2+u_{d2},\sigma _{ed2}^{2} \right)$ if $d\in {\mathbb {D}}_2$, and

• 3. $y_{d}\sim N_2 \left( X_{d}\beta ,V_{ud}+V_{ed} \right)$ and $y_{d}|_{u_d}\sim N_2 \left( X_{d}\beta +u_{d},V_{ed} \right)$ if $d\in {\mathbb {D}}_3$.

The supplementary material gives fitting algorithms to calculate the maximum likelihood (ML) and residual maximum likelihood (REML) estimators of the MBFH model parameters.

In a real situation where the target data follow a MBFH model, the BFH model is strictly applicable to ${\mathbb {D}}_3$, but not to ${\mathbb {D}}_1$ or ${\mathbb {D}}_2$. For example, under the BFH model we can only calculate EBLUPs of $\mu _d$ or $u_d$ for $d\in {\mathbb {D}}_3$. However, in what follows we show that it is possible to calculate EBPs for $d\in {\mathbb {D}}_1\cup {\mathbb {D}}_2$ under the MBFH model. We have the following three results. For the corresponding proofs, see the supplementary material.

R1. If $d\in {\mathbb {D}}_1$, then the BP of $u_d$ under the MBFH model is

$$\begin{aligned} {\hat{u}}_d^{bp}=E[u_d|y_{d1}]= \Phi _{d1}\left( \begin{array}{cc}\sigma _{ed1}^{-2}&{}0 \\ 0&{} 0 \end{array}\right) (y_{{\bar{d}}1}-X_d\beta ),\quad \Phi _{d1}=\left[ \left( \begin{array}{cc}\sigma _{ed1}^{-2}&{}0 \\ 0&{} 0 \end{array}\right) +V_{ud}^{-1}\right] ^{-1}, \end{aligned}$$

where $y_{{\bar{d}}1}=(y_{d1},0)^\prime$.

R2. If $d\in {\mathbb {D}}_2$, then the BP of $u_d$ under the MBFH model is

$$\begin{aligned} {\hat{u}}_d^{bp}=E[u_d|y_{d2}]= \Phi _{d2}\left( \begin{array}{cc}0&{}0 \\ 0&{} \sigma _{ed2}^{-2} \end{array}\right) (y_{{\bar{d}}2}-X_d\beta ),\quad \Phi _{d2}=\left( \left( \begin{array}{cc}0&{}0 \\ 0&{} \sigma _{ed2}^{-2} \end{array}\right) +V_{ud}^{-1}\right) ^{-1}, \end{aligned}$$

where $y_{{\bar{d}}2}=(0,y_{d2})^\prime$.

R3. If $d\in {\mathbb {D}}_3$, then BP of $u_d$ under the MBFH model is

$$\begin{aligned} {\hat{u}}_d^{bp}=E[u_d|y_d]= \Phi _dV_{ed}^{-1}(y_d-X_d\beta ),\quad \Phi _d=\left( V_{ed}^{-1}+V_{ud}^{-1}\right) ^{-1}. \end{aligned}$$

As a consequence of R1-R3, the BP of $\mu _d$, $d=1,\ldots ,D$, under the MBFH model is

$$\begin{aligned} {\hat{\mu }}_d^{bp}=X_d\beta +{\hat{u}}_d^{bp}. \end{aligned}$$

(3.4)

The EBP of $\mu _d$, $d=1,\ldots ,D$, under the MBFH model (MBFH-EBP) is obtained from formula (3.4) by plugging estimators ${\hat{\beta }}$, ${\hat{\sigma }}_{u1}^2$, ${\hat{\sigma }}_{u2}^2$ and ${{\hat{\rho }}}$ in the places of $\beta$, $\sigma _{u1}^2$, $\sigma _{u2}^2$ and $\rho$, respectively, i.e.,

$$\begin{aligned} {\hat{\mu }}_d^{ebp}=X_d{{\hat{\beta }}}+{\hat{u}}_d^{ebp}. \end{aligned}$$

(3.5)

3.3 Analytic approximation of the mean squared error of the MBFH predictor

This section gives an analytical approximation of the MSE of the MBFH-EBP for each of the three considered groups of domains. The corresponding mathematical derivations are presented in the supplementary material. Alternatively, the supplementary material also introduces a parametric bootstrap procedure for estimating the MSE of the MBFH-EBPs.

3.3.1 Empirical best predictors in domains of groups ${\mathbb {D}}_1$ and ${\mathbb {D}}_2$

As the estimators for groups ${\mathbb {D}}_1$ and ${\mathbb {D}}_2$ are somehow symmetric, we only present those corresponding to group ${\mathbb {D}}_1$:

$$\begin{aligned} h_d({{\hat{\beta }}},{{\hat{\theta }}})\triangleq {\hat{\mu }}_d^{ebp}=X_d{{\hat{\beta }}}+{{\hat{\Phi }}}_{d1}A_{d1}(y_{{\bar{d}}1}-X_d{{\hat{\beta }}}) =\left( \begin{array}{c}x_{d1}^\prime {{\hat{\beta }}}_1\\ x_{d2}{{\hat{\beta }}}_2 \end{array}\right) +\frac{y_{d1}-x_{d1}^\prime {{\hat{\beta }}}_1}{\sigma _{ed1}^{2}}\left( \begin{array}{c}{{\hat{\phi }}}_{d1,11} \\ {{\hat{\phi }}}_{d1,12} \end{array}\right) , \end{aligned}$$

where

$$\begin{aligned} {{\hat{\Phi }}}_{d1}=\Phi _{d1}({{\hat{\theta }}})=\left( A_{d1}+{\hat{V}}_{ud}^{-1}\right) ^{-1},\, {\hat{V}}_{ud}=V_{ud}({{\hat{\theta }}})= \left( \begin{array}{cc} {{\hat{\sigma }}}_{u1}^2 &{} {{\hat{\rho }}}{{\hat{\sigma }}}_{u1}{{\hat{\sigma }}}_{u2}\\ {{\hat{\rho }}}{{\hat{\sigma }}}_{u1}{{\hat{\sigma }}}_{u2}&{}{{\hat{\sigma }}}_{u2}^2 \end{array}\right) ,\, A_{d1}=\left( \begin{array}{cc}\sigma _{ed1}^{-2}&{}0 \\ 0&{} 0 \end{array}\right) . \end{aligned}$$

The derivatives of matrix $\Phi _{d1}(\theta )$ with respect to $\theta _\ell$, $\ell =1,2,3$, are

$$\begin{aligned} \frac{\partial \Phi _{d1}}{\partial \theta _\ell }=\big (A_{d1}+V_{ud}^{-1}\big )^{-1}V_{ud}^{-1}V_{ud\ell }V_{ud}^{-1}\big (A_{d1}+V_{ud}^{-1}\big )^{-1}= \left( \begin{array}{cc}\phi _{d1\ell ,11}&{}\phi _{d1\ell ,12} \\ \phi _{d1\ell ,12}&{} \phi _{d1\ell ,22} \end{array}\right) . \end{aligned}$$

The derivatives of $h_d(\beta ,\theta )$ with respect to $\beta _{kj}$ and $\theta _\ell$, $k=1,2$, $j=1,\ldots ,p_k$, $\ell =1,2,3$, are

$$\begin{aligned} \frac{\partial h_d}{\partial \beta _{1j}}= & {} \left( \begin{array}{c}x_{d1j}\\ 0 \end{array}\right) -\frac{x_{d1j}}{\sigma _{ed1}^{2}}\left( \begin{array}{c}\phi _{d1,11} \\ \phi _{d1,12} \end{array}\right) \triangleq \left( \begin{array}{c}h_{d\beta _{1j},1} \\ h_{d\beta _{1j},2} \end{array}\right) ,\quad \frac{\partial h_d}{\partial \beta _{2j}}= \left( \begin{array}{c}0\\ x_{d2j} \end{array}\right) \triangleq \left( \begin{array}{c}h_{d\beta _{2j},1} \\ h_{d\beta _{2j},2} \end{array}\right) \\ \frac{\partial h_d}{\partial \theta _{\ell }}= & {} \frac{\partial \Phi _{d1}}{\partial \theta _\ell }A_{d1}(y_{{\bar{d}}1}-X_d\beta ) = \frac{y_{d1}-x_{d1}^\prime \beta _1}{\sigma _{ed1}^{2}}\left( \begin{array}{c}\phi _{d1\ell ,11} \\ \phi _{d1\ell ,12} \end{array}\right) \triangleq \frac{y_{d1}-x_{d1}^\prime \beta _1}{\sigma _{ed1}^{2}}\left( \begin{array}{c}g_{d\theta _\ell ,1} \\ g_{d\theta _\ell ,2} \end{array}\right) . \end{aligned}$$

The $p_k\times 1$ vectors containing the derivatives with respect to $\beta _{k}$, $k=1,2$, are

$$\begin{aligned} h_{d\beta _k,1}=\underset{1\le j \le p_k}{\hbox {col}}\big (h_{d\beta _{kj},1}\big ),\quad h_{d\beta _k,2}=\underset{1\le j \le p_k}{\hbox {col}}\big (h_{d\beta _{kj},2}\big ). \end{aligned}$$

and the corresponding $p_{k_1}\times p_{k_2}$ matrices are $H_{d\beta _{k_1}\beta _{k_2},ab}=h_{d\beta _{k_1},a}h_{d\beta _{k_2},b}^\prime$, $k_1,k_2,a,b=1,2$.

The $3\times 1$ vectors containing the derivatives with respect to $\theta$ are

$$\begin{aligned} g_{d\theta ,1}=\underset{1\le \ell \le 3}{\hbox {col}}\big (g_{d\theta _{\ell },1}\big ),\quad g_{d\theta ,2}=\underset{1\le \ell \le 3}{\hbox {col}}\big (g_{d\theta _{\ell },2}\big ) \end{aligned}$$

and the corresponding $3\times 3$ matrices are $G_{d\theta \theta ,ab}=g_{d\theta ,a}g_{d\theta ,b}^\prime$, $a,b=1,2$.

For $d\in {\mathbb {D}}_1$, we have the following approximation to $MSE({\hat{\mu }}^{ebp}_d)$.

$$\begin{aligned} MSE({\hat{\mu }}^{ebp}_d)=G_{d1}(\theta )+G_{d2}(\theta )+G_{d3}(\theta )+O_{2\times 2}(D^{-1}), \end{aligned}$$

where $G_{d2}(\theta )=G_{d2,11}(\theta )+G_{d2,22}(\theta )+G_{d2,12}(\theta )+G_{d2,12}^\prime (\theta )$ and

$$\begin{aligned} G_{d1}(\theta )&= \Phi _{d1}(\theta )A_{d1}(\theta )(V_{ud}(\theta )+V_{ed}(\theta ))A_{d1}(\theta )\Phi _{d1}(\theta ) +V_{ud}(\theta )-2\Phi _{d1}(\theta )A_{d1}(\theta )V_{ud}(\theta ), \\ G_{d2,ab}(\theta )&= \left( \begin{array}{cc} \text{ tr }\{H_{d\beta _b\beta _a,11}(\theta )\, \text{ cov }({{\hat{\beta }}}_a,{{\hat{\beta }}}_b)\}&{} \text{ tr }\{H_{d\beta _b\beta _a,21}(\theta )\, \text{ cov }({{\hat{\beta }}}_a,{{\hat{\beta }}}_b)\}\\ \text{ tr }\{H_{d\beta _b\beta _a,12}(\theta )\, \text{ cov }({{\hat{\beta }}}_a,{{\hat{\beta }}}_b)\}&{} \text{ tr }\{H_{d\beta _b\beta _a,22}(\theta )\, \text{ cov }({{\hat{\beta }}}_a,{{\hat{\beta }}}_b)\} \end{array}\right) ,\,\, a,b=1,2, \\ G_{d3}(\theta )&= \frac{\sigma _{ud1}^2+\sigma _{ed1}^2}{\sigma _{ed1}^4}\,\left( \begin{array}{cc} \text{ tr }\{G_{d\theta \theta ,11}(\theta )\, \text{ var }({{\hat{\theta }}})\}&{} \text{ tr }\{G_{d\theta \theta ,21}(\theta )\, \text{ var }({{\hat{\theta }}})\}\\ \text{ tr }\{G_{d\theta \theta ,12}(\theta )\, \text{ var }({{\hat{\theta }}})\}&{} \text{ tr }\{G_{d\theta \theta ,22}(\theta )\, \text{ var }({{\hat{\theta }}})\} \end{array}\right) . \end{aligned}$$

Similarly as Prasad and Rao (1990), Datta and Lahiri (2000), and Das et al. (2004), we estimate $MSE({\hat{\mu }}^{ebp}_d)$ with

$$\begin{aligned} mse({\hat{\mu }}^{ebp}_d)=G_{d1}({{\hat{\theta }}})+G_{d2}({{\hat{\theta }}})+2G_{d3}({{\hat{\theta }}}). \end{aligned}$$

Note that when using ML instead of REML estimation an additional bias correction term has to be considered, see Datta and Lahiri (2000) for further details.

3.3.2 Empirical best predictors in domains of group ${\mathbb {D}}_3$

Let us consider the group ${\mathbb {D}}_3$. We write

$$\begin{aligned} h_d({{\hat{\beta }}},{{\hat{\theta }}})\triangleq {\hat{\mu }}_d^{ebp}=X_d{{\hat{\beta }}}+{{\hat{\Phi }}}_{d}V_{ed}^{-1}(y_{d}-X_d{{\hat{\beta }}}), \end{aligned}$$

where

$$\begin{aligned} {{\hat{\Phi }}}_{d}=\Phi _{d}({{\hat{\theta }}})=\left( V_{ed}^{-1}+{\hat{V}}_{ud}^{-1}\right) ^{-1},\quad {\hat{V}}_{ud}=V_{ud}({{\hat{\theta }}})= \left( \begin{array}{cc} {{\hat{\sigma }}}_{u1}^2 &{} {{\hat{\rho }}}{{\hat{\sigma }}}_{u1}{{\hat{\sigma }}}_{u2}\\ {{\hat{\rho }}}{{\hat{\sigma }}}_{u1}{{\hat{\sigma }}}_{u2}&{}{{\hat{\sigma }}}_{u2}^2 \end{array}\right) . \end{aligned}$$

The derivatives of matrix $\Phi _{d}(\theta )$ with respect to $\theta _\ell$, $\ell =1,2,3$, are

$$\begin{aligned} \frac{\partial \Phi _{d}}{\partial \theta _\ell }=\big (V_{ed}^{-1}+V_{ud}^{-1}\big )^{-1} V_{ud}^{-1}V_{ud\ell }V_{ud}^{-1}\big (V_{ed}^{-1}+V_{ud}^{-1}\big )^{-1}= \left( \begin{array}{cc}\phi _{d\ell ,11}&{}\phi _{d\ell ,12} \\ \phi _{d\ell ,12}&{} \phi _{d\ell ,22} \end{array}\right) . \end{aligned}$$

The derivatives of $h_d(\beta ,\theta )$ with respect to $\beta _{kj}$ and $\theta _\ell$, $k=1,2$, $j=1,\ldots ,p_k$, $\ell =1,2,3$, are

$$\begin{aligned} \frac{\partial h_d}{\partial \beta _{1j}}= & {} \left( \begin{array}{c}x_{d1j}\\ 0 \end{array}\right) -\Phi _{d}V_{ed}^{-1}\left( \begin{array}{c}x_{d1j}\\ 0 \end{array}\right) =\big (I-\Phi _{d}V_{ed}^{-1}\big )\left( \begin{array}{c}x_{d1j}\\ 0 \end{array}\right) \triangleq \left( \begin{array}{c}h_{d\beta _{1j},1} \\ h_{d\beta _{1j},2} \end{array}\right) , \\ \frac{\partial h_d}{\partial \beta _{2j}}= & {} \left( \begin{array}{c}0\\ x_{d2j} \end{array}\right) -\Phi _{d}V_{ed}^{-1}\left( \begin{array}{c}0\\ x_{d2j} \end{array}\right) =\big (I-\Phi _{d}V_{ed}^{-1}\big )\left( \begin{array}{c}0\\ x_{d2j} \end{array}\right) \triangleq \left( \begin{array}{c}h_{d\beta _{2j},1} \\ h_{d\beta _{2j},2} \end{array}\right) , \\ \frac{\partial h_d}{\partial \theta _{\ell }}= & {} \frac{\partial \Phi _{d}}{\partial \theta _\ell }V_{ed}^{-1}(y_{d}-X_d\beta ) \triangleq \left( \begin{array}{c}h_{d\theta _\ell ,1} \\ h_{d\theta _\ell ,2} \end{array}\right) . \end{aligned}$$

For $k,k_1,k_2=1,2$, the $p_k\times 1$ vectors containing the derivatives with respect to $\beta _{k}$ and the corresponding $p_{k_1}\times p_{k_2}$ matrices are

$$\begin{aligned} h_{d\beta _k,1}=\underset{1\le j \le p_k}{\hbox {col}}\big (h_{d\beta _{kj},1}\big ),\,\,\, h_{d\beta _k,2}=\underset{1\le j \le p_k}{\hbox {col}}\big (h_{d\beta _{kj},2}\big ),\,\,\, H_{d\beta _{k_1}\beta _{k_2},ab}=h_{d\beta _{k_1},a}h_{d\beta _{k_2},b}^\prime ,\,\,\, a,b=1,2. \end{aligned}$$

The $3\times 1$ vectors containing the derivatives with respect to $\theta$ are

$$\begin{aligned} h_{d\theta ,1}= & {} \underset{1\le \ell \le 3}{\hbox {col}}\big (h_{d\theta _{\ell },1}\big )= \frac{y_{d1}-x_{d1}^\prime \beta _1}{\sigma _{ed1}^2}g_{d\theta ,11} +\frac{y_{d2}-x_{d2}^\prime \beta _2}{\sigma _{ed2}^2}g_{d\theta ,12}, \\ h_{d\theta ,2}= & {} \underset{1\le \ell \le 3}{\hbox {col}}\big (h_{d\theta _{\ell },2}\big )= \frac{y_{d1}-x_{d1}^\prime \beta _1}{\sigma _{ed1}^2}g_{d\theta ,12} +\frac{y_{d2}-x_{d2}^\prime \beta _2}{\sigma _{ed2}^2}g_{d\theta ,22}, \\ g_{d\theta ,11}= & {} \underset{1\le \ell \le 3}{\hbox {col}}\big (\phi _{d\ell ,11}\big ),\,\,\, g_{d\theta ,12}=\underset{1\le \ell \le 3}{\hbox {col}}\big (\phi _{d\ell ,12}\big ),\,\,\, g_{d\theta ,22}=\underset{1\le \ell \le 3}{\hbox {col}}\big (\phi _{d\ell ,22}\big ) \end{aligned}$$

and the corresponding $3\times 3$ matrices are

$$\begin{aligned} H_{d\theta \theta ,11}&= h_{d\theta ,1}h_{d\theta ,1}^\prime = \frac{(y_{d1}-x_{d1}^\prime \beta _1)^2}{\sigma _{ed1}^4}\,g_{d\theta ,11}g_{d\theta ,11}^\prime +\frac{(y_{d2}-x_{d2}^\prime \beta _2)^2}{\sigma _{ed2}^4}\,g_{d\theta ,12}g_{d\theta ,12}^\prime \\&\quad +\,\frac{(y_{d1}-x_{d1}^\prime \beta _1)(y_{d2}-x_{d2}^\prime \beta _2)}{\sigma _{ed1}^2\sigma _{ed2}^2} \,\big (g_{d\theta ,11}g_{d\theta ,12}^\prime +g_{d\theta ,12}g_{d\theta ,11}^\prime \big ), \end{aligned}$$

$$\begin{aligned} H_{d\theta \theta ,12}&= H_{d\theta \theta ,21}^\prime =h_{d\theta ,1}h_{d\theta ,2}^\prime = \frac{(y_{d1}-x_{d1}^\prime \beta _1)^2}{\sigma _{ed1}^4}g_{d\theta ,11}g_{d\theta ,12}^\prime +\frac{(y_{d2}-x_{d2}^\prime \beta _2)^2}{\sigma _{ed2}^4}g_{d\theta ,12}g_{d\theta ,22}^\prime \\&\quad +\,\frac{(y_{d1}-x_{d1}^\prime \beta _1)(y_{d2}-x_{d2}^\prime \beta _2)}{\sigma _{ed1}^2\sigma _{ed2}^2} \big (g_{d\theta ,11}g_{d\theta ,22}^\prime +g_{d\theta ,12}g_{d\theta ,12}^\prime \big ), \\ H_{d\theta \theta ,22}&= & h_{d\theta ,2}h_{d\theta ,2}^\prime = \frac{(y_{d1}-x_{d1}^\prime \beta _1)^2}{\sigma _{ed1}^4}\,g_{d\theta ,12}g_{d\theta ,12}^\prime +\frac{(y_{d2}-x_{d2}^\prime \beta _2)^2}{\sigma _{ed2}^4}\,g_{d\theta ,22}g_{d\theta ,22}^\prime \\&\quad+\,\frac{(y_{d1}-x_{d1}^\prime \beta _1)(y_{d2}-x_{d2}^\prime \beta _2)}{\sigma _{ed1}^2\sigma _{ed2}^2} \,\big (g_{d\theta ,12}g_{d\theta ,22}^\prime +g_{d\theta ,22}g_{d\theta ,12}^\prime \big ). \end{aligned}$$

For $D_1+D_2+1\le d\le D$, we have the following approximation to $MSE({\hat{\mu }}^{ebp}_d)$.

$$\begin{aligned} MSE({\hat{\mu }}^{ebp}_d)=G_{d1}(\theta )+G_{d2}(\theta )+G_{d3}(\theta )+O_{2\times 2}(D^{-1}), \end{aligned}$$

where $G_{d2}(\theta )=G_{d2,11}(\theta )+G_{d2,22}(\theta )+G_{d2,12}(\theta )+G_{d2,12}^\prime (\theta )$ and

$$\begin{aligned} G_{d1}(\theta )&= \Phi _{d}(\theta )V_{ed}^{-1}(\theta )(V_{ud}(\theta )+V_{ed}(\theta ))V_{ed}^{-1}(\theta )\Phi _{d}(\theta ) +V_{ud}(\theta )-2\Phi _{d}(\theta )V_{ed}^{-1}(\theta )V_{ud}(\theta ),\\ G_{d2,ab}(\theta )&= \left( \begin{array}{cc} \text{ tr }\{H_{d\beta _b\beta _a,11}(\theta )\, \text{ cov }({{\hat{\beta }}}_a,{{\hat{\beta }}}_b)\}&{} \text{ tr }\{H_{d\beta _b\beta _a,21}(\theta )\, \text{ cov }({{\hat{\beta }}}_a,{{\hat{\beta }}}_b)\}\\ \text{ tr }\{H_{d\beta _b\beta _a,12}(\theta )\, \text{ cov }({{\hat{\beta }}}_a,{{\hat{\beta }}}_b)\}&{} \text{ tr }\{H_{d\beta _b\beta _a,22}(\theta )\, \text{ cov }({{\hat{\beta }}}_a,{{\hat{\beta }}}_b)\} \end{array}\right) ,\,\, a,b=1,2,\\ G_{d3}(\theta )&= \left( \begin{array}{cc} \text{ tr }\{H_{d\theta \theta ,11}(\theta )\, \text{ var }({{\hat{\theta }}})\}&{} \text{ tr }\{H_{d\theta \theta ,21}(\theta )\, \text{ var }({{\hat{\theta }}})\}\\ \text{ tr }\{H_{d\theta \theta ,12}(\theta )\, \text{ var }({{\hat{\theta }}})\}&{} \text{ tr }\{H_{d\theta \theta ,22}(\theta )\, \text{ var }({{\hat{\theta }}})\} \end{array}\right) . \end{aligned}$$

Similarly as Prasad and Rao (1990), Datta and Lahiri (2000), and Das et al. (2004), we estimate $MSE({\hat{\mu }}^{ebp}_d)$ with

$$\begin{aligned} mse({\hat{\mu }}^{ebp}_d)=G_{d1}({{\hat{\theta }}})+G_{d2}({{\hat{\theta }}})+2G_{d3}({{\hat{\theta }}}). \end{aligned}$$

Note that when using ML instead of REML estimation an additional bias correction term has to be considered, see Datta and Lahiri (2000) for further details.

4 Simulation

A model-based Monte Carlo simulation study is conducted to validate the theoretical derivations and reveal the performance of the MBFH predictor under various correlation settings. The simulation aims to empirically investigate the effect that the correlation parameters and the percentage of unobserved data have on the behavior of the predictors and estimators of MSEs. The values of the variance parameters are chosen all equal in order to have a neutral setting. The results can help researchers in the selection of dependent variables for the proposed MBFH predictor. Per variable 5%, 10%, and 20% of direct estimates are considered missing to reveal how well the MBFH-EBP can predict the missing values and how accurate the corresponding MSE estimates are. Often, the univariate FH estimator is used to stabilize volatile regional estimates. Therefore, we compare the MBFH EBP and MSE estimates to the EBLUP and MSE estimates of the corresponding univariate FH estimator. The FH estimator leads to an empirical best linear unbiased predictors (FH-EBLUP) only for observed direct estimates. For missing direct estimates, the FH provides synthetic predictors (FH-SYN) only. Let us write the model (3.3) in the form

$$\begin{aligned} {y}_d={X}_d\beta +{u}_d+{e}_d,\quad \forall d\in \{1,\ldots ,D\} \end{aligned}$$

(4.1)

with $D=600$ domains. Take $p_1=p_2=3$, $p=6$, $\beta =(\beta _1^\prime ,\beta _2^\prime )^\prime$ and $\beta _1=(\beta _{11},\beta _{12},\beta _{13})^\prime = \beta _2=(\beta _{21},\beta _{22},\beta _{23})^\prime = (2,3,4)^\prime$. For $k=1,2$, $d\in \ {1,\ldots ,D}$, generate $X_{d} = \text{ diag }(x_{d1}, x_{d2})_{2\times 6}$, with components $x_{d1}=(x_{d11}, x_{d12}, x_{d13}) = x_{d2}=(x_{d21}, x_{d22}, x_{d23})$, $x_{d11}=x_{d21}=1$, $x_{d12}=x_{d22}=U_{d2}$, $x_{d13}=x_{d23}=U_{d3}$, where $U_{d2}\sim Uniform (10,20)$ and $U_{d3}\sim Uniform (20,40)$, $d=1,\ldots ,D$ are all independent. The matrix of auxiliary variables is fixed for all simulation runs. Take $\sigma _{u1}^2=\sigma _{u2}^2=\sigma _{ed1}^2=\sigma _{ed2}^2=2$ and simulate ${u}_{d}\sim N_{2}(0,{V}_{ud})$, ${e}_d\sim N_{2}(0,{V}_{ed})$ $\forall d\in \{1,\ldots ,D\}$, where

$$\begin{aligned} V_{ud} = \left( \begin{array}{cc} 2 &{} \rho \sqrt{2}\sqrt{2}\\ \rho \sqrt{2}\sqrt{2}&{} 2\\ \end{array}\right) ,\quad V_{ed}= \left( \begin{array}{cc} 2&{} \rho _{ed12} \sqrt{2}\sqrt{2}\\ \rho _{ed12} \sqrt{2}\sqrt{2}&{}2\\ \end{array}\right) . \end{aligned}$$

We consider different combinations of random effect correlation $\rho \in \{-0.9,-0.6, -0.3, 0, 0.3, 0.6 ,0.9\}$ and sampling error correlation $\rho _{ed12} \in \{-0.3, 0, 0.6\}$. From experience, the chosen sampling correlations reflect common sampling scenarios. In the simulation, we estimate the model parameters via REML.

The steps of the simulation are

• 1. For all scenarios repeat $I=2000$ times ($i=1,\ldots ,2000$)

  • (a) Generate $u_d^{(i)}\sim N_2(0,V_{ud})$, $e_d^{(i)}\sim N_2(0,V_{ed})$ $\forall d\in \{1,\ldots ,D\}$, $y_{d1}^{(i)}=x_{d1}^\prime \beta _1+u_{d1}^{(i)}+e_{d1}^{(i)}$ $\forall d\in {\mathbb {D}}_1$, $y_{d2}^{(i)}=x_{d2}^\prime \beta _2+u_{d2}^{(i)}+e_{d2}^{(i)}$ $\forall d\in {\mathbb {D}}_2$ and $y_d^{(i)}={X}_d\beta +{u}_d^{(i)}+{e}_d^{(i)}$ $\forall d\in {\mathbb {D}}_3$, where $D_1=100$ and $D_2=100$.

  • (b) Calculate the true means $\mu _{d}^{(i)}={X}_d\beta +{u}_d^{(i)}$ $\forall d\in \{1,\ldots ,D\}$.

  • (c) Calculation of the MBFH-EBP of $\mu _d$.

    • i. Fit model (4.1) to the simulated data: $(y_{d1}^{(i)},X_d)$ $\forall d\in {\mathbb {D}}_1$, $(y_{d2}^{(i)},X_d)$ $\forall d\in {\mathbb {D}}_2$, $(y_{d}^{(i)},X_d)$ $\forall d\in {\mathbb {D}}_3$.

    • ii. Calculate the MBFH-EBPs ${\hat{\mu }}^{mbfh.ebp(i)}_{d}$ under the fitted model (4.1).

    • iii. Calculate the MSE predictor

      $$\begin{aligned} mse_{d}^{(i)}=G_{d1,d}({\hat{\theta }}^{(i)})+G_{d2,d}({\hat{\theta }}^{(i)})+2G_{d3,d}({\hat{\theta }}^{(i)}),\quad \end{aligned}$$

      with the formulas of $G_{d1,d}, G_{d2,d}$ and $G_{d3,d}$ depending on the group affiliation of the respective domain.

  • (d) Calculation of the FH-EBLUPs and FH-SYNs of $\mu _{d1}$ and $\mu _{d2}$.

    • i. Fit the corresponding univariate FH models of model (4.1) to the simulated data: $(y_{d1}^{(i)},X_d)$ $\forall d \in {{\mathbb {D}}_1 \cup {\mathbb {D}}_3 }$, $(y_{d2}^{(i)},X_d)$ $\forall d \in {{\mathbb {D}}_2 \cup {\mathbb {D}}_3 }$.

    • ii. Calculate the FH-EBLUPs ${\hat{\mu }}^{fh.eblup(i)}_{d}$ for variable 1 $\forall d \in {{\mathbb {D}}_1 \cup {\mathbb {D}}_3 }$ and variable 2 $\forall d \in {{\mathbb {D}}_2 \cup {\mathbb {D}}_3 }$.

    • iii. Calculate the univariate synthetic estimates FH-SYN ${\hat{\mu }}^{fh.syn(i)}_{d1}=x_{d1}^\prime {\hat{\beta }}_1^{fh(i)}$ for variable 1 $\forall d \in {{\mathbb {D}}_2 }$ and ${\hat{\mu }}^{fh.syn(i)}_{d2}=x_{d2}^\prime {\hat{\beta }}_2^{fh(i)}$ for variable 2 $\forall d \in {{\mathbb {D}}_1 }$.

    • iv. Calculate the MSE predictor for FH-EBLUP (cf. Prasad and Rao 1990; Datta and Lahiri 2000).

    • v. Calculate the MSE predictor for FH-SYN using the derivations in Appendix C. For variable 1 ${{\mathcal {D}}}_0 = {\mathbb {D}}_1 \cup {\mathbb {D}}_3$, ${{\mathcal {D}}}_1 = {\mathbb {D}}_2$. For variable 2 ${{\mathcal {D}}}_0 = {\mathbb {D}}_2 \cup {\mathbb {D}}_3$, ${{\mathcal {D}}}_1 = {\mathbb {D}}_1$.

• 2. For ${\hat{\mu }}^{*} \in \{{\hat{\mu }}^{mbfh.ebp}, {\hat{\mu }}^{fh.eblup}, {\hat{\mu }}^{fh.syn}\}$ and $mse^{*} \in \{mse^{mbfh.ebp}, mse^{fh.eblup}, mse^{fh.syn}\}$, calculate

  $$\begin{aligned} \begin{aligned} RBIAS( {\hat{\mu }}^{*}_{d} )&=\frac{1}{I}\sum _{i=1}^{I} \frac{{\hat{\mu }}^{*(i)}_{d} - \mu _{d}^{(i)}}{ \mu _{d}^{(i)} }\,, \quad RRMSE( {\hat{\mu }}^{*}_{d} ) = \left( \frac{1}{I}\sum _{i=1}^{I}\frac{( {\hat{\mu }}^{*(i)}_{d} - \mu _{d}^{(i)} )^2}{ (\mu _{d}^{(i)})^{2} } \right) ^{1/2}, \\ MSE( {\hat{\mu }}^{*}_{d} )&= \frac{1}{I}\sum _{i=1}^{I}({\hat{\mu }}^{*(i)}_{d} - \mu _{d}^{(i)})^2 \quad \text {and} \quad RBIAS( mse^{*}_{d} )= \frac{ \frac{1}{I}\sum _{i=1}^{I} mse_{d}^{*(i)} - MSE( {\hat{\mu }}^{*}_{d} ) }{ MSE( {\hat{\mu }}^{*}_{d} ) }. \end{aligned} \end{aligned}$$

The simulation population can be split in three domain groups, ${\mathbb {D}}_1$, ${\mathbb {D}}_2$, and ${\mathbb {D}}_3$. For ${\mathbb {D}}_3$ direct estimates are observed for both variables of interest. For ${\mathbb {D}}_1$ direct estimates are observed for variable one, but missing for variable two. For ${\mathbb {D}}_2$ direct estimates are observed for variable two, but missing for variable one. The MBFH-EBP can be calculated for all domain-variable combinations. The FH-EBLUP, on the other hand, can be calculated only for domain-variable combinations with available direct estimates. When there are no direct estimates of a variable available, the FH model only provides the synthetic predictors FH-SYN.

The simulation results are presented in Figs. 1, 2, 3, and 4. We show the results for 20% missing values in both variables of interest. The same plots with 5% and 10% missings look very similar and are displayed in Sect. 6 of the supplementary material. The figures differ with respect to the performance measure shown and their underlying sampling error correlation. They show the performance of the predictors MBFH-EBP, FH-EBLUP, and FH-SYN and their corresponding MSE estimates. The ML and REML methods are standard estimation methods in linear mixed models. However, REML estimators of the variance component parameters tend to have a lower bias and have a lower computational cost. This is why we obtain model parameters using the REML Fisher-scoring algorithm. The results under ML are similar and therefore not shown.

The performance measures are depicted separately for the three domain groups, ${\mathbb {D}}_1$, ${\mathbb {D}}_2$, and ${\mathbb {D}}_3$, and the two variables of interest, resulting in six panels. The gray-shaded panels indicate domain-variable combinations where direct estimates are missing. Each panel presents the results for different underlying correlations of random effects $\rho$. This way the interplay of the estimators efficiency with the correlation of sampling errors and random effects can be retrieved. In each panel, a boxplot of the RRMSE or RBias over the corresponding domains is drawn for the different random effect correlations. In panels with observed direct estimates, the boxplots are shown for FH-EBLUP and MBFH-EBP, whereas in panels with missing direct estimates, i.e., in gray-shaded panels, the boxplots are shown for FH-SYN and MBFH-EBP. For facilitating the comparison, in our application in Sect. 5 we have $D=762$, $D_1=78$, $D_2=58$, $D_3=626$ such that about 10% of the first and 7.6% of the second variable of interest are missing. Furthermore, in the application the sampling error correlation is $\rho _{ed12}=0$, and the correlation of random effects $\rho$ is estimated at 0.97.

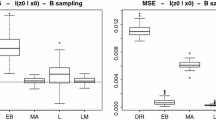
We first evaluate the performance of the predictors MBFH-EBP, FH-EBP, and FH-SYN via their RRMSE. Figures 1, 2, and 3 show the corresponding RRMSE for different underlying sampling error correlation $\rho _{ed12} \in \{0.6, -0.3, 0\}$. The nonzero sampling error correlations in Figs. 1 and 2 correspond to situations where both variables stem from the same survey. A zero sampling error correlation as in Fig. 3 applies if both variables stem from independent surveys. It is visible for all three Figs. 1, 2, and 3 that in terms of RRMSE the introduced MBFH-EBP is at least as efficient as the respective FH-EBLUP or FH-SYN. This observation holds for positively, negatively, and uncorrelated sampling errors. Thus, the application of the MBFH instead of the FH estimator is profitable for various combinations of sampling error and random effect correlations.

The prediction of missing values is visible in the gray-shaded panels. There, the efficiency gain of the MBFH-EBP over the FH-SYN in terms of RRMSE is especially high for high random effect correlation, positive or negative. This finding applies to all sampling error correlations, i.e., Figs. 1, 2, and 3 with $\rho _{ed12} \in \{0.6, -0.3, 0\}$. Thus, for the prediction of missing values the application of MBFH instead of FH is profitable as long as the absolute value of the underlying random effect correlation gets away from zero.

The performance of the MBFH-EBP for domains with no missing values is visible in the panels of group ${\mathbb {D}}_3$. For these, in Figs. 1, 2, and 3, the efficiency gain of MBFH-EBP over FH-EBLUP is especially high when the correlation of random effects and sampling errors is of opposite sign and high magnitude. This coincides with the findings in Datta et al. (1999) for unit-level multivariate small area models without missing values.

Fig. 1

RRMSE of point estimates, 20% missing domains, $\rho _{ed12}=0.6$

Fig. 2

RRMSE of point estimates, 20% missing domains, $\rho _{ed12}=-0.3$

Fig. 3

RRMSE of point estimates, 20% missing domains, $\rho _{ed12}=0$

Next, we take a look at the corresponding MSE estimates. Figure 4 presents the simulation results of the relative Bias (RBias) of the different MSE estimators under REML and sampling correlation $\rho _{ed12}=-0.3$ for varying random effect correlations $\rho$. The MSE estimates of MBFH-EBP lead good results for both missing and observed domains. The MSE estimates of FH-SYN, which derivation is shown in Appendix C, also lead good results. The relative bias of the MBFH-EBP MSE is around zero in most panels and for all random effect correlations. We can see that in group ${\mathbb {D}}_3$ there is a slight positive bias in the mse estimate for $\rho =0.9$ with $\rho _{ed12}=-0.3$. This bias is not visible when $\rho _{ed12}=0$ as in the application.

Fig. 4

RBias of MSE estimates, 20% missing domains, $\rho _{ed12}=-0.3$

The MBFH-EBP is best for both observed and missing estimates when (1) there are many domains with both variables observed while in case a variable is missing the other variable is observed and (2) the correlation of random effects and sampling errors is of opposite sign and high magnitude. One would, for example, expect the random effects of a variable in two consecutive years to be highly positively correlated, e.g., in the application in Sect. 5, we focus on the median income of Hispanic or Latino Americans in two consecutive years). On the other hand, random effects of variables like employment and unemployment would be expected to be highly negatively correlated. The correlation of sampling errors is determined by the sampling design. As we see from the MSE estimation in Fig. 4 in case a researcher is unsure whether applying the MBFH instead of the FH estimator is improving the predictions, a comparison of the MBFH and FH MSE estimates is recommended. For the selection of variables of interest, we would therefore advise researchers to pay special attention to the missing patterns of the two variables before considering the correlation patterns.

5 Estimating county-level median income of Hispanic or Latino Americans

5.1 Model results

Let ${y}_{d}=\left( {y}_{d1},{y}_{d2}\right) ^{\prime }$ be the vector of direct estimates of the US county-level median annual incomes of Hispanic or Latino origin people in 2010 and 2011. We assume that ${y}_{d}$ follows model (3.3)

$$\begin{aligned} {y}_d={X}_d\beta +{u}_d+{e}_d,\quad \forall d\in \{1,\ldots ,D\}, \end{aligned}$$

(5.1)

where ${u}_{d}=(u_{d1},u_{d2})^\prime \sim N_2(0,{V}_{ud})$, ${e}_{d}=(e_{d1},e_{d2})^\prime \sim N_{2}\left( 0,{V}_{ed}\right)$ are independent of each other. The number of considered US counties (domains of interest) is $D=3,141$. Let $\mu =(\mu _{1}^\prime ,\mu _{2}^\prime )^\prime$ be the vector of characteristics of interest HC02_EST_VC12 in 2010 and 2011 for the D domains. The vector of direct estimates y of $\mu$ is given by the ACS 1-year direct estimates. We take the estimated variances of the ACS 1-year direct estimates as input for the covariance matrices $V_{ed}$. The ACS 1-year direct estimates are provided with $\text {margin of error} = 1.645 * \sqrt{variance}$ (U.S. Census Bureau 2014, Chapter 12.3). Assuming the sampling errors between two years to be independent the covariance matrices $V_{ed}$ are defined by

$$\begin{aligned} V_{ed}&= \left( \begin{array}{cc} \sigma ^{2}_{ed1} &{} 0\\ 0 &{} \sigma ^{2}_{ed2}\\ \end{array}\right) , \ \forall d \in {1,\ldots ,D}, \end{aligned}$$

where $\sigma ^{2}_{ed1}$ and $\sigma ^{2}_{ed2}$ are given by the respective $(\text {margin of error} / 1.645)^2$. The off-diagonal elements of $V_{ed}$ are zero as the covariances of the sampling errors of the direct estimates between 2010 and 2011 are expected to be zero.

We fit the MBFH model to the data of

$D=762$ counties ($D_{1}=78$, $D_{2}=58$, $D_{3}=626$), the description of the data and auxiliary information is given in Sect. 2.2. The dependent variables y are ACS 1-year direct estimates of the median income (dollars) Hispanic or Latino origin (of any race) (HC02_EST_VC12) in 2010 and 2011. Tables 1 and 2 present the REML estimates of the regression parameters of the selected MBFH model. Columns with labels beta, std.error, t-value, and p-value, respectively, contain the values of the regression parameter estimator, the standard error, the t-statistic and the p-value, respectively. The estimated coefficients are very similar for HC02_EST_VC12 in 2010 and 2011 and highly significant. They furthermore seem plausible considering that counties with higher death rate and higher civilian labor force unemployment rate tend to have lower values of HC02_EST_VC12. Any thematic conclusions from the few freely available auxiliary data are, however, limited, e.g., due to high correlations among variables.

Table 1 Regression parameters for variable HC02_EST_VC12 in 2010

Table 2 Regression parameters for variable HC02_EST_VC12 in 2011

The $2\times 2$ covariance matrix ${V}_{ud}$ depends on three unknown parameters, $\theta _{1}=\sigma _{u1}^2$, $\theta _{2}=\sigma _{u2}^2$, and $\theta _{3}=\rho$, i.e.,

$$\begin{aligned} {V}_{ud}= \left( \begin{array}{cc} \sigma _{u1}^2 &{} \rho \sigma _{u1}\sigma _{u2}\\ \rho \sigma _{u1}\sigma _{u2}&{}\sigma _{u2}^2 \end{array}\right) ,\,\,\, \forall d\in \{1,\ldots ,D\}. \end{aligned}$$

As we consider the same variable in two consecutive years, we expect the correlation of random effects to be highly positive. Table 3 contains the estimates of the variance component parameters and the corresponding asymptotic 95% confidence intervals. The estimated random error correlation is highly positive.

Table 3 Variance component parameters and corresponding asymptotic 95% confidence intervals

Figure 5 plots the MBFH-EBPs versus the corresponding standardized model residuals in 2010 and 2011. The raw residuals are $r_{dk}^{ebp}=y_{dk}-{\hat{\mu }}_{dk}^{ebp}$, $d=1,\ldots ,D$. The standardized residuals of component k, $k=1,2$, are calculated from the raw residuals after subtracting the mean and dividing by the standard deviation of $\{r_{dk}^{ebp}:\, d=1,\ldots ,D\}$. Figure 6 plots the histograms of the standardized residuals. From the model, the residuals are expected to be normally distributed with mean zero and both figures show that the mass of the residuals is distributed near and around zero. At the same time, we detect some major outliers. In 2010 and 2011, about 2% of the standardized residuals have an absolute value greater 3. A further treatment of these outliers is necessary, but beyond the scope of this paper where we use the data for an illustration of the presented MBFH model. Unfortunately, we do not have access to new auxiliary variables that could explain the behavior of the target variables in the few domains where the model performs poorly. For further studies, an investigation of the outliers and of a robust version of the proposed model would be interesting. We refer to Sinha and Rao (2009) for general information on robust SAE, Schmid and Münnich (2014) for robust SAE including spatial effects, and Baldermann et al. (2018) for the additional consideration of spatial non-stationarity. For an implementation of robust FH models in R, see package rsae (Schoch 2014).

Fig. 5

MBFH-EBPs versus corresponding standardized model residuals of HC02_EST_VC12 in 2010 and 2011

Fig. 6

Histograms of standardized residuals of MBFH-EBPs in 2010 and 2011

5.2 Validating predictions of observed direct estimates

We compare the resulting MBFH-EBPs to the ACS 1-year direct estimates of the variable of interest, the median income (dollars) Hispanic or Latino origin (of any race) (HC02_EST_VC12) in 2010 and 2011. For the comparison we only include counties in which ACS 1-year direct estimates are available. Figure 7 plots the standard error of ACS 1-year direct estimates versus the difference between the direct estimates and MBFH-EBPs of HC02_EST_VC12 in 2010 and 2011. As the FH estimator is a shrinkage estimator, it is expected that the more reliable the direct estimates, and thereby the lower the ACS 1-year standard error, the closer are MBFH-EBPs and direct estimates. This shrinkage property is visible in Fig. 7 for the MBFH.

Fig. 7

Difference between ACS 1-year direct estimates and MBFH-EBPs versus standard error of ACS 1-year direct estimates of HC02_EST_VC12 in 2010 and 2011

Due to the shrinkage property of the MBFH, the root MSE of the MBFH-EBPs is expected to be close to the ACS standard errors for reliable direct estimates. For highly volatile direct estimates, on the other hand, it is expected to be much lower. The total number of persons HIS010210D⁵ in a county is expected to be an indicator of the reliability of the direct estimates, the more persons in a county, the more reliable the resulting estimate. Figure 8 plots log HIS010210D versus the ratio of the ACS 1-year direct estimate standard errors to estimated MBFH root MSE in 2010 and 2011. For counties with high total number of persons MBFH root MSE and ACS standard errors are close as the corresponding point estimates are close. For counties with lower total number of persons MBFH root MSE estimates are substantially lower than ACS 1-year standard errors as the estimator is more shrunk to the model-part than to the volatile direct estimate.

Fig. 8

Ratio of root MSEs of ACS 1-year direct estimates to root MSEs of MBFH-EBPs of HC02_EST_VC12 in 2010 and 2011 versus log of total persons in 2010 (HIS010210D)

5.3 Validating predictions of missing direct estimates

To validate the MBFH-EBPs also for missing direct estimates, ACS 5-year estimates of the variable of interest and Census 2010 estimates of a similar variable are used. Table 4 shows the quantiles of the relative difference (in %) of the ACS 1-year direct estimates and the MBFH-EBPs to the ACS 5-year direct estimates of HC02_EST_VC12. We compare 1-year direct estimates and EBPs in 2010 and 2011 to ACS 5-year direct estimates in 2008-2012 and 2009-2013, respectively. The results for the MBFH-EBPs are shown both for domains with available direct estimates and those without direct estimates, but were MBFH-EBPs could be computed. Due to their larger sample sizes the ACS 5-year estimates are less volatile than the ACS 1-year estimates and available for more counties (Table 4). Even though differently aggregated ACS estimates are not directly comparable, a comparison between ACS 1-year direct estimates and MBFH-EBPs to the ACS 5-year estimates should give a suitable image of the reliability of the MBFH-EBPs. As can be seen in Table 4, for domains with given direct estimate the quantiles of the relative differences of the MBFH-EBPs are smaller than those of the ACS 1-year direct estimates. Furthermore, the quantiles of the relative difference of the MBFH-EBPs of domains with no available direct estimate are close to those of the ACS 1-year direct estimates. The proximity of quantiles is more visible in 2011 than in 2010. This indicates that for both domains with available and missing ACS 1-year direct estimate, the MBFH predictor accomplishes more realistic predictions in 2011 than in 2010.

Table 4 Quantiles of the relative difference of estimates in 2010 and 2011 to ACS 5-year estimates in 2008–2012 and 2009–2013 of variable HC02_EST_VC12 (in %)

Figure 9 shows the different estimates exemplary for the states Indiana and Ohio in 2010 (left plots) and 2011 (right plots). In rows one, two and three are the ACS 1-year direct estimates, the ACS 5-year direct estimates, and the MBFH-EBPs, respectively. In both years, many ACS 1-year and some ACS 5-year direct estimates are missing, indicated by the white-shaded domains. Framed counties indicate those with ACS 1-year direct estimates missing in one year, but available in the other. For these counties the MBFH model provides EBPs in contrast to the commonly used univariate FH model. Therefore, in row three the framed counties are filled by MBFH-EBPs. The plot confirms the results from Table 4 that MBFH-EBPs are relatively close to the ACS 5-year, especially when considering counties, where the direct estimate is missing in one year, but available in the other. This indicates that the predictions of the missing values by the MBFH model are realistic.

Fig. 9

ACS 1-year direct estimates and MBFH-EBPs of 2010 and 2011 and ACS 5-year direct estimates of 2008–2012 and 2009–2013 of HC02_EST_VC12 shown for the counties in Indiana and Ohio

For further validation of the MBFH-EBPs, similar to Table 4, we display the quantiles of the relative difference (in %) to the Census-ACS 2005–2009 estimates of the median household income in the past 12 month (in 2009 inflation-adjusted dollars) in 2005–2009 (INC110209D) in Table 5. The Census-ACS estimates of INC110209D are available for all counties, and variables HC02_EST_VC12 and INC110209D are expected to be close. Similar to Table 4, we see that especially for 2011 the MBFH-EBPs are close to the Census estimates. This finding further supports the validity of the predicted missing values by the MBFH model.

Table 5 Quantiles of the relative difference of estimates in 2010 and 2011 to Census-ACS 2005–2009 estimates of variable INC110209D (in %)

For the analysis of the county-level median income of Hispanic or Latino Americans, the MBFH estimator shows promising results. The validation indicates that the MBFH-EBPs are realistic for both observed and missing direct estimates. It should be noted that this result is already achieved under the rather small number of freely available auxiliary data. Even better results are to be expected when more detailed auxiliary data are considered. With the use of the MBFH estimator, researchers are able to improve inter-regional and temporal comparisons of subgroup-specific indicators.

6 Summary and outlook

Socioeconomic indicators, such as the median income of sub-populations, are key to both policy recommendations and evaluation. Taking the freely available US ACS data on county-level median income of Hispanic or Latino Americans as an example, many county-specific direct estimates for 2010 and 2011 are associated with high standard errors or unpublished. Thereby, a comparison of different counties or time-points is partly not possible.

We present a new estimator based on small area estimation techniques and bivariate modeling, the MBFH predictor. It provides best predictors for many missing direct estimates, is easily applicable, allows for variable-specific choices of auxiliary data, and is flexible with respect to the correlation patterns and choice of the variables of interest. The MBFH predictor is a generalization of the bivariate FH model. That means in all situations where a bivariate FH model can be applied, the MBFH predictor can be applied as well, with the difference that the MBFH predictor also includes information of domains for which only one direct estimate is available. We furthermore derive an MSE estimator for the MBFH predictor and the synthetic FH predictor for observed and missing domains. Both are comparable in their relative bias. They therefore allow for a comparison of the MBFH and FH predictor for observed and missing values. The MSE estimator is convenient from a computational point of view because no resampling methods are needed to specify the uncertainty of the MBFH predictor.

A large-scale model-based Monte Carlo simulation study reveals the advantages of the MBFH predictor over the corresponding univariate FH models. For that, we consider the effects separately for the groups of domains with complete information and those where one direct estimate is missing. First, for domains with complete information the predictor can be advantageous over the FH-EBP when the variable random effects are highly correlated, positively or negatively. Thereby, it preserves the good qualities of the bivariate FH model but includes also information of domains with partially missing information in the parameter estimation. Second, for domains with one missing direct estimate we have to distinguish between the performance of the EBP for the variable with an observed and that with a missing direct estimate. For the variable with an observed direct estimate, the MBFH predictor does not give any performance gains over the corresponding FH model. On the other hand, there is also no performance loss visible in the simulation studies. For the variable with a missing direct estimate, the MBFH predictor gives significant performance gains over the corresponding FH synthetic predictor when the variable random effects are highly correlated. These are precisely the cases for which the MBFH predictor is designed and where we see the main contribution of the proposed approach.

We emphasize that we do not use imputation methods in the common way, as our goal is not to do analysis on the imputed data set. Our goal is to get best predictions of socioeconomic indicators for the domains. Hence, our method does not stand in concurrence against imputation, as these two methods have different goals. We do not have any information on the units in the domains with missing direct estimates. Hence, the only possibility is to assume that this area follows the selected model. We do not work with missing data in the sense of non-response. We deal with unpublished direct estimates in some domains, where the sample size is typically null or too small. A basic imputation method under a selected model would be using a synthetic estimator. Instead, we propose an EBP based on the MBFH model.

For an illustration, we applied the MBFH predictor to the median income of Hispanic or Latino Americans in 2010 and 2011 where publicly available direct estimates are volatile and partially missing. The validation with external data shows that the MBFH-EBP provides realistic results in practice. We therefore recommend the use of the MBFH-EBP for the estimation of regional indicators, especially in the context of unavailable direct domain estimates and unsampled domains. In the application, we detected some heavy outliers, and an investigation of a robust version of the proposed MBFH model therefore represents an interesting further area of study. In the future, we plan to publish the presented algorithm in an R package. In any case, the current R codes are available on request.